Graphical abstract
Keywords: Ribavirin, Solubility, Jouyban-Acree, Inverse Kirkwood–Buff integrals, Preferential solvation
Highlights
-
•
Solubility of ribavirin (II) in co-solvent + water were determined and correlated.
-
•
Apparent dissolution enthalpy was computed.
-
•
Preferential solvation parameters were obtained by Inverse Kirkwood–Buff integrals.
-
•
Ribavirin (II) was preferentially solvated by water in intermediate composition and co-solvent-rich mixtures.
Abstract
The equilibrium solubility of ribavirin in solvent mixtures of {methanol (1) + water (2)}, {n-propanol (1) + water (2)}, {acetonitrile (1) + water (2)} and {1,4-dioxane (1) + water (2)} was determined experimentally by using isothermal dissolution equilibrium method within the temperature range from (278.15 to 318.15) K under atmospheric pressure (101.1 kPa). At the same temperature and mass fraction of methanol (n-propanol, acetonitrile or 1,4-dioxane), the mole fraction solubility of ribavirin is greater in (methanol + water) than in the other three solvent mixtures. The preferential solvation parameters were derived from their thermodynamic solution properties by means of the inverse Kirkwood–Buff integrals. The preferential solvation parameters for methanol, n-propanol, acetonitrile or 1,4-dioxane (δx1,3) were negative in the four solvent mixtures with a very wide compositions, which indicated that ribavirin was preferentially solvated by water. Temperature had little effect on the preferential solvation magnitudes. The higher solvation by water could be explained in terms of the higher acidic behaviour of water interacting with the Lewis basic groups of the ribavirin. Besides, the solubility of the drugs was mathematically represented by using the Jouyban-Acree model, van’t Hoff-Jouyban-Acree model and Apelblat-Jouyban-Acree model obtaining average relative deviations lower than 1.57% for correlative studies. It is noteworthy that the solubility data presented in this work contribute to expansion of the physicochemical information about the solubility of drugs in binary solvent mixtures and also allows the thermodynamic analysis of the respective dissolution and specific solvation process.
1. Introduction
The drugs solubility in solvent mixtures as a function of temperature and composition is evaluated essentially for the aims of raw material purification, design of liquid dosage forms, and understanding of the mechanisms regarding to the physical and chemical stability of pharmaceutical dissolutions [1], [2]. Therefore, the solubility of active ingredients is a significant physicochemical property to be considered in pharmaceutical design because it affects the drug efficacy, influencing several biopharmaceutical and pharmacokinetic properties [3], [4]. Moreover, temperature-dependence of the solubility allows evaluating the preferential solvation of the solute by the solvent components in mixtures, which gives a powerful tool in the understanding of molecular interactions in relation to the dissolution processes of drug [5], [6], [7].
Ribavirin (II) (CAS Registry No. 36791-04-5, chemical structure shown in Fig. S1 of Supporting material) is a well-known antiviral drug with a broad spectrum of action. Because of its activity against both RNA and DNA viruses [8], it is recommended for the treatment of some infectious disorders including herpes [9], respiratory syncytial viral disease, and acute respiratory infections caused by adenovirus [10]. At present, ribavirin is also part of a combination therapy for the treatment of hepatitis C [11], [12], [13], [14], [15], [16] and Lassa fever [14], [15]. Furthermore, it has been evaluated for severe acute respiratory syndrome (SARS) and as an anti-cancer drug with successful results for the treatment of leukemia and breast cancer [16], [17], [18]. Due to its good properties, ribavirin has been received great attention. Nevertheless, in spite of the usefulness of this drug, the physicochemical properties of ribavirin in aqueous and organic solutions have not been studied systematically in the previous works [19], [20], [21], [22], [23], [24].
Although several theoretical and semi-empirical models have employed to predict drug solubility in solvent mixtures, the availability of experimental data is still fundamental for the pharmaceutical scientists [1], [25]. It is well-known that solvent mixtures has been widely used in pharmacies long ago [1], [2], [3], [4], only recently the mechanisms involving in the increase or decrease in drugs’ solubility start to be approached from a deep thermodynamic point of view, including the analysis of the preferential solvation of solute by the components of mixtures [5], [6], [7], [26], [27], [28], [29], [30]. In terms of the considerations mentioned above, the main goal of this work is to report the equilibrium solubility of ribavirin in {methanol (1) + water (2)}, {n-propanol (1) + water (2)}, {acetonitrile (1) + water (2)}+ and {1,4-dioxane (1) + water (2)} mixtures at different temperatures in order to evaluate the respective thermodynamic quantities of the solution, as well as the preferential solvation of the drug by these organic solvents. This research expands the available solubility data about drug in neat organic solvents and solvent mixtures [1] and also allows the thermodynamic analysis of the respective dissolution and specific solvation process. It is noteworthy that methanol and 1,4-dioxane is not used to develop liquid medicines due to its high toxicity. But in some instances methanol is used in drug purification procedures [31], as well as solvent in some drug microencapsulation techniques [32]. Moreover, methanol is widely used as mobile phase in high performance liquid chromatography [33]. In addition, 1,4-dioxane is widely used as a model co-solvent because it is miscible with water in all the range of compositions although it exhibits a low polarity as described by its dielectric constant [34]. Even more, the Jouyban–Acree model has been used to correlate the solubility of a lot of drugs in {methanol/1,4-dioxane (1) + water (2)} mixtures [35]. n-Propanol and acetonitrile are green solvents [36] and miscible with water in all compositions. In addition, although n-propanol is not widely used as co-solvent for design of liquid medicines, it has been used as solvent in the pharmaceutical industry for resins and cellulose esters [37], [38]. Acetonitrile is most widely utilized because of the high resolution attainable probably due to the low viscosity of water-acetonitrile mixtures [39]. Moreover, the water-acetonitrile mixtures may have a partially hydrophobic character similar to the methanol system since only the OH group in methanol is replaced by the CN group in acetonitrile.
2. Experimental
2.1. Materials and apparatus
Ribavirin (II) was provided by Shanghai Sharing Technologies Co., Ltd., China with a mass fraction of 0.983. It was purified three times in methanol. The final composition of ribavirin (II) used for solubility measurement was 0.996 in mass fraction, which was analysed by using a high-performance liquid chromatography (HPLC, Agilent 1260). The four neat solvents (methanol, n-propanol, acetonitrile and 1,4-dioxane) were provided by Sinopharm Chemical Reagent Co., Ltd., China, the mass fraction purities of which were all no less than 0.994 determined by gas chromatography {Smart (GC-2018)}. The water was twice distilled water prepared in our lab, which conductivity was less than 2 μS·cm−1. The detailed information of these chemicals was presented in Table S1 of Supporting material.
The diagram of solubility determination apparatus was given in Fig. S2 of Supporting material. The experimental apparatus consisted of a 100 ml jacketed glass vessel with a circulating (water + isopropanol) system and a magnetic stirrer. The temperature of circulating (water + isopropanol) mixture was kept by a thermostatic bath (Model: QYHX-1030), which was provided by Shanghai Joyn Electronic CO., Ltd., China and had a standard uncertainty of 0.05 K. The actual temperature of solution was displayed by a mercury glass micro thermometer (standard uncertainty: 0.02 K) inserted in the inner chamber of the jacket glass vessel. A condenser was employed to avoid escaping of the solvent. An analytical balance (model: BSA224S) having a standard uncertainty of 0.0001 g and provided by Satorius Scientific Instrument (Beijing) was used to determine the mass of the solute, solvent, and saturated solution. The reliability of apparatus was verified in advance by determining the benzoic acid solubility in toluene [40], [41].
2.2. Preparation of solvent mixtures
During the experiment, we use the analytical balance (model: BSA224S) to prepare the solvent mixtures. Each mixed solvent in the glass vessel was about 60 mL, and the relative standard uncertainty of which was estimated to be 0.0002. The mass fractions of organic solvent in the binary mixtures varied from 0 to 1. The glass vessel was covered with a stopper to prevent the solvent from escaping during the preparation procedure of solvent mixtures. During the experiment, the atmospheric pressure was about 101.1 kPa.
2.3. Solubility measurement
In this work the solid-liquid equilibrium for ribavirin in binary solvent mixtures of (methanol + water), (n-propanol + water), (acetonitrile + water) and (1,4-dioxane + water) was determined by an isothermal dissolution equilibrium method [40], [41], [42], [43], [44], [45], and the high-performance liquid phase chromatograph was employed to determine the solubility of ribavirin in equilibrium liquid phase.
For each experiment, saturated solutions of ribavirin (II) were prepared in the jacketed glass vessel. An excessive amount of ribavirin (II) was introduced into the jacketed glass vessel filled with about 60 ml solvent mixtures. Continuous stirring was achieved by using a magnetic stirrer at a given temperature to mix the solution intensively. The temperature of the solutions was kept at a desired value by circulating (water + isopropanol) mixture from the thermostatic bath through the outer jacket. So as to obtain the equilibration time of the studied systems, about 0.5 ml liquid phase was withdrawn every one hour by using a 2 mL of preheated syringe equipped with a pore syringe filter (PTFE 0.2 μm), and then analysed by the high-performance liquid phase chromatograph (Agilent-1260). Once the composition of liquid phase didn’t vary, the system was believed to reach equilibrium. In order to make sure that sampling was performed at equilibrium conditions, two types of experiments were carried out, one starting from a supersaturated solution, in which the solid phase precipitated to reach equilibrium and the other starting from a non-saturated solution, in which solid dissolved to reach equilibrium. The results revealed that it took about 13 h to reach equilibrium for all the studied systems. Once the mixture arrived at equilibrium, stirring was turned off to allow any undissolved solute to be precipitated. One hour later, the upper liquid phase was withdrawn using the 2 ml of preheated or precooled syringe, and transferred rapidly to a pre-weighed volumetric flask equipped with a rubber stopper. The volumetric flask filled with sample was weighed again with the analytical balance. Subsequently, the sample was diluted with methanol, and 1 μl of the solution was withdrawn for analysis by using the high-performance liquid chromatography.The equilibrium mole fraction solubility of ribavirin (II) in the four binary solvent mixtures are obtained with Eq. (1), and the initial composition of binary solvent mixtures (w) is calculated with Eqs. (2), (3).
| (1) |
| (2) |
| (3) |
where m 1 is the mass of ribavirin; m 2 is the mass of methanol, n-propanol, acetonitrile and 1,4-dioxane, and m 3 is the mass of water. M 1, M 2 and M 3 are the corresponding molar mass.
2.4. Analysis method
The concentration of ribavirin was analysed by the Agilent-1260 high-performance liquid chromatography (HPLC). The chromatographic column was a reverse phase column with a type of LP-C18 (250 mm × 4.6 mm), which temperature was kept at 303 K. The wavelength of the UV detector was set to 210 nm, which was determined by continuous UV-Scanning. The mobile phase comprised two component, which were methanol and water with a flow rate of 0.8 ml·min−1. The volume ratio of methanol to water was 25:75. Each analysis was carried out three times, and the average value of three measurements was regarded as the final value of the analysis. The relative standard uncertainty is estimated to be 4.5% in mole fraction solubility.
2.5. X-ray powder diffraction
The crystal of ribavirin was identified by X-ray powder diffraction (XPRD) carried out on a HaoYuan DX-2700B (HaoYuan, China) instrument. The samples were determined by Cu Ka radiation (λ = 1.54184 nm), and the tube voltage and current were set at 40 kV and 30 mA, respectively. The data were collected at room temperature from 5° to 80° (2-Theta) at a scan speed of 6 deg·min−1 under atmospheric pressure.
3. Results and discussion
3.1. X-ray powder diffraction analysis
Ribavirin has long been known to exist in two enantiotropically related polymorphic forms (I and II) [46], [47], [48]. Form II is the stable form at ambient temperature and melts at 439–441 K; while form I, the metastable polymorph, melts at (447–449) K [47], [48]. In order to demonstrate the existence of polymorph transformation or solvate formation of ribavirin during the solubility determination, the equilibrium solid phase is collected and analysed by XRD. The patterns of the raw material and the solids crystallized in neat solvents and solvent mixtures are plotted in Fig. S3 of Supporting material. It is confirmed by XRD pattern that all the XRD patterns of solid phase of ribavirin in equilibrium with its solution have the same characteristic peaks with the raw material, which corresponds to form II reported in literatures [46], [47], [48]. Therefore, it can be concluded that there was no polymorph transformation or solvate formation during the entire experiment.
3.2. Solubility results
The determined mole fraction solubility of ribavirin in binary solvent mixtures of (methanol + water), (n-propanol + water), (acetonitrile + water) and (1,4-dioxane + water) are presented in Table 1, Table 2, Table 3, Table 4 , respectively. In addition, the relationship between the mole fraction solubility and temperature and solvent composition are shown graphically in Fig. 1, Fig. 2, Fig. 3, Fig. 4 . It can be seen that, for the studied solvent mixtures, the ribavirin solubility is a function of temperature and solvent composition. The solubility of ribavirin increase with increasing temperature and mass fraction of water for the binary systems studied. The maximum solubility of ribavirin is observed in water. It can also be seen from Table 1, Table 2, Table 3, Table 4 that, at the same temperature and solvent composition, the solubility of ribavirin in (methanol + water) is greater than those in (n-propanol + water), (acetonitrile + water) and (1,4-dioxane + water). This behaviour may be due to the relative strong polarity of ribavirin molecule. At the same composition, the polarities of the four mixed solvents rank as (methanol + water) > (n-propanol + water) > (acetonitrile + water) > (1,4-dioxane + water) [49]. Therefore, the solubilities of ribavirin in (methanol + water) are larger than those in the other solvent mixtures.
Table 1.
Experimental mole fraction solubility of ribavirin in mixed solvent of methanol (w) + water (1 − w) with various mass fractions within the temperature range from T/K = (278.15 to 318.15) under p = 101.1 kPa.a
| T/K |
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
w | |||||||||||
| 1 | 0.8994 | 0.7988 | 0.7005 | 0.5992 | 0.4998 | 0.3999 | 0.3001 | 0.2013 | 0.0991 | 0 | |
| 278.15 | 0.03788 | 0.08134 | 0.1308 | 0.1892 | 0.2436 | 0.2783 | 0.3223 | 0.3731 | 0.4335 | 0.5198 | 0.5803 |
| 283.15 | 0.05168 | 0.1124 | 0.1847 | 0.2601 | 0.3143 | 0.3734 | 0.4277 | 0.4967 | 0.5831 | 0.6939 | 0.7755 |
| 288.15 | 0.07109 | 0.1513 | 0.2424 | 0.3362 | 0.4317 | 0.5013 | 0.5778 | 0.6679 | 0.7811 | 0.9040 | 1.039 |
| 293.15 | 0.09523 | 0.1998 | 0.3232 | 0.4470 | 0.5496 | 0.6577 | 0.7549 | 0.8748 | 1.023 | 1.197 | 1.354 |
| 298.15 | 0.1278 | 0.2652 | 0.4275 | 0.5893 | 0.7267 | 0.8507 | 0.9801 | 1.127 | 1.319 | 1.528 | 1.741 |
| 303.15 | 0.1710 | 0.3457 | 0.5433 | 0.7411 | 0.9312 | 1.076 | 1.254 | 1.432 | 1.665 | 1.939 | 2.190 |
| 308.15 | 0.2231 | 0.4424 | 0.7165 | 0.9509 | 1.152 | 1.346 | 1.553 | 1.819 | 2.085 | 2.422 | 2.732 |
| 313.15 | 0.2929 | 0.5844 | 0.9178 | 1.204 | 1.463 | 1.698 | 1.988 | 2.242 | 2.584 | 2.981 | 3.347 |
| 318.15 | 0.3791 | 0.7427 | 1.179 | 1.547 | 1.891 | 2.113 | 2.424 | 2.756 | 3.158 | 3.630 | 4.053 |
Standard uncertainties u are u(T) = 0.02 K, u(p) = 0.45 kPa; Relative standard uncertainty ur is ur (x) = 0.045. Solvent mixtures were prepared by mixing different masses of the solvents with relative standard uncertainty ur(w) = 0.0002. w represents the mass fraction of methanol in mixed solvents of methanol (w) + water (1 − w).
Table 2.
Experimental mole fraction solubility of ribavirin in mixed solvent of n-propanol (w) + water (1 − w) with various mass fractions within the temperature range from T/K = (278.15 to 318.15) under p = 101.1 kPa.a
|
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T/K |
w |
||||||||||
| 1 | 0.8998 | 0.7991 | 0.7009 | 0.5999 | 0.5002 | 0.3989 | 0.2991 | 0.2003 | 0.0999 | 0 | |
| 278.15 | 0.005986 | 0.03793 | 0.1153 | 0.1750 | 0.2235 | 0.2459 | 0.2773 | 0.3418 | 0.4509 | 0.5644 | 0.5803 |
| 283.15 | 0.008689 | 0.05375 | 0.1436 | 0.2415 | 0.3014 | 0.3329 | 0.3743 | 0.4625 | 0.6113 | 0.7555 | 0.7755 |
| 288.15 | 0.01219 | 0.07412 | 0.1934 | 0.3214 | 0.4028 | 0.4415 | 0.5048 | 0.6187 | 0.8041 | 1.024 | 1.039 |
| 293.15 | 0.01715 | 0.1013 | 0.2618 | 0.4269 | 0.5343 | 0.5866 | 0.6658 | 0.8146 | 1.042 | 1.339 | 1.354 |
| 298.15 | 0.02417 | 0.1347 | 0.3486 | 0.5669 | 0.7155 | 0.7718 | 0.8736 | 1.057 | 1.375 | 1.677 | 1.741 |
| 303.15 | 0.03320 | 0.1838 | 0.4716 | 0.7366 | 0.9113 | 0.9928 | 1.120 | 1.364 | 1.723 | 2.119 | 2.190 |
| 308.15 | 0.04547 | 0.2438 | 0.6207 | 0.9532 | 1.153 | 1.286 | 1.429 | 1.727 | 2.190 | 2.654 | 2.732 |
| 313.15 | 0.06169 | 0.3214 | 0.7960 | 1.218 | 1.489 | 1.619 | 1.796 | 2.155 | 2.683 | 3.242 | 3.347 |
| 318.15 | 0.08289 | 0.4186 | 1.014 | 1.538 | 1.836 | 2.012 | 2.258 | 2.664 | 3.311 | 3.955 | 4.053 |
Standard uncertainties u are u(T) = 0.02 K, u(p) = 0.45 kPa; Relative standard uncertainty ur is ur (x) = 0.045. Solvent mixtures were prepared by mixing different masses of the solvents with relative standard uncertainty ur(w) = 0.0002. w represents the mass fraction of n-propanol in mixed solvents of n-propanol (w) + water (1 − w).
Table 3.
Experimental mole fraction solubility of ribavirin in mixed solvents of acetonitrile (w) + water (1-w) with various mass fractions within the temperature range from T/K = (278.15 to 318.15) under p = 101.1 kPa.a
| T/K |
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
w | |||||||||||
| 1 | 0.8993 | 0.7998 | 0.7006 | 0.5997 | 0.5008 | 0.3995 | 0.3007 | 0.2008 | 0.0999 | 0 | |
| 278.15 | 0.0008602 | 0.01479 | 0.07012 | 0.1471 | 0.1991 | 0.2249 | 0.2573 | 0.3174 | 0.4258 | 0.5564 | 0.5803 |
| 283.15 | 0.001331 | 0.02185 | 0.09971 | 0.2062 | 0.2788 | 0.3119 | 0.3543 | 0.4339 | 0.5759 | 0.7429 | 0.7755 |
| 288.15 | 0.001941 | 0.03044 | 0.1349 | 0.2767 | 0.3715 | 0.4180 | 0.4746 | 0.5827 | 0.7726 | 0.9993 | 1.039 |
| 293.15 | 0.002769 | 0.04141 | 0.1817 | 0.3643 | 0.4875 | 0.5486 | 0.6225 | 0.7628 | 1.010 | 1.301 | 1.354 |
| 298.15 | 0.003961 | 0.05662 | 0.2414 | 0.4814 | 0.6410 | 0.7174 | 0.8120 | 0.9910 | 1.312 | 1.664 | 1.741 |
| 303.15 | 0.005644 | 0.07711 | 0.3187 | 0.6285 | 0.8302 | 0.9241 | 1.041 | 1.263 | 1.654 | 2.107 | 2.190 |
| 308.15 | 0.007877 | 0.1037 | 0.4151 | 0.8106 | 1.072 | 1.182 | 1.325 | 1.613 | 2.068 | 2.638 | 2.732 |
| 313.15 | 0.01097 | 0.1377 | 0.5382 | 1.037 | 1.337 | 1.483 | 1.654 | 2.009 | 2.574 | 3.238 | 3.347 |
| 318.15 | 0.01501 | 0.1791 | 0.6911 | 1.311 | 1.673 | 1.868 | 2.087 | 2.459 | 3.153 | 3.937 | 4.053 |
Standard uncertainties u are u(T) = 0.02 K, u(p) = 0.45 kPa; Relative standard uncertainty ur is ur (x) = 0.045. Solvent mixtures were prepared by mixing different masses of the solvents with relative standard uncertainty ur(w) = 0.0002. w represents the mass fraction of acetonitrile in mixed solvents of acetonitrile (w) + water (1-w).
Table 4.
Experimental mole fraction solubility of ribavirin in mixed solvents of 1,4-dioxane (w) + water (1 − w) with various mass fractions within the temperature range from T/K = (283.15 to 318.15) under p = 101.1 kPa.a
| T/K |
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
w | |||||||||||
| 1 | 0.8992 | 0.7998 | 0.7003 | 0.5988 | 0.4999 | 0.4007 | 0.3011 | 0.2009 | 0.0994 | 0 | |
| 283.15 | 0.007057 | 0.04835 | 0.1382 | 0.2338 | 0.2965 | 0.3376 | 0.3847 | 0.4661 | 0.5939 | 0.7362 | 0.7755 |
| 288.15 | 0.01009 | 0.06709 | 0.1892 | 0.3181 | 0.4015 | 0.4550 | 0.5161 | 0.6271 | 0.7976 | 0.9885 | 1.039 |
| 293.15 | 0.01453 | 0.09314 | 0.2586 | 0.4279 | 0.5376 | 0.6069 | 0.6894 | 0.8294 | 1.036 | 1.288 | 1.354 |
| 298.15 | 0.02028 | 0.1267 | 0.3438 | 0.5632 | 0.7064 | 0.7925 | 0.8975 | 1.073 | 1.342 | 1.651 | 1.741 |
| 303.15 | 0.02823 | 0.1682 | 0.4534 | 0.7368 | 0.9179 | 1.026 | 1.168 | 1.364 | 1.725 | 2.111 | 2.190 |
| 308.15 | 0.03869 | 0.2244 | 0.5920 | 0.9516 | 1.180 | 1.287 | 1.468 | 1.759 | 2.164 | 2.644 | 2.732 |
| 313.15 | 0.05272 | 0.2956 | 0.7644 | 1.219 | 1.487 | 1.656 | 1.857 | 2.165 | 2.682 | 3.235 | 3.347 |
| 318.15 | 0.07122 | 0.3894 | 0.9817 | 1.543 | 1.883 | 2.092 | 2.288 | 2.693 | 3.271 | 3.930 | 4.053 |
Standard uncertainties u are u(T) = 0.02 K, u(p) = 0.45 kPa; Relative standard uncertainty ur is ur (x) = 0.045. Solvent mixtures were prepared by mixing different masses of the solvents with relative standard uncertainty ur(w) = 0.0002. w represents the mass fraction of 1,4-dioxane in mixed solvents of 1,4-dioxane (w) + water (1 − w).
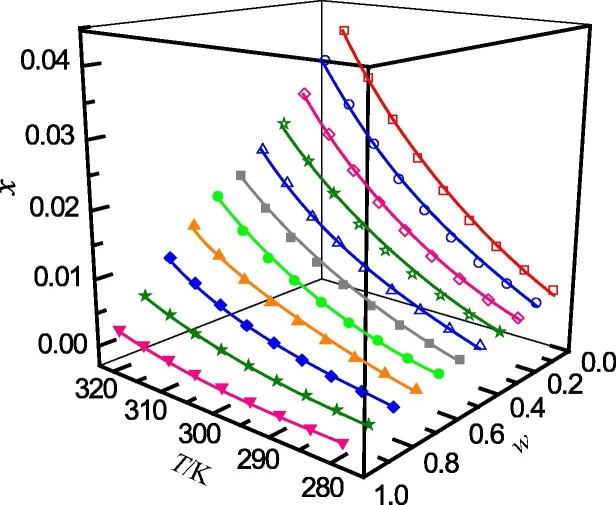
Fig. 1.
Mole fraction solubility (x) of ribavirin in methanol (w) + water (1 − w) mixed solutions with various mass fractions at different temperatures: w, mass fraction of methanol; □, w = 0; ○, w = 0.0991; ♢, w = 0.2013; ☆, w = 0.3001; △, w = 0.3999; ■, w = 0.4998; ●, w = 0.5992; ▲, w = 0.7005; ◆, w = 0.7988; ★, w = 0.8994; ▾; w = 1. —, calculated curves by the Jouyban − Acree model.
Fig. 2.
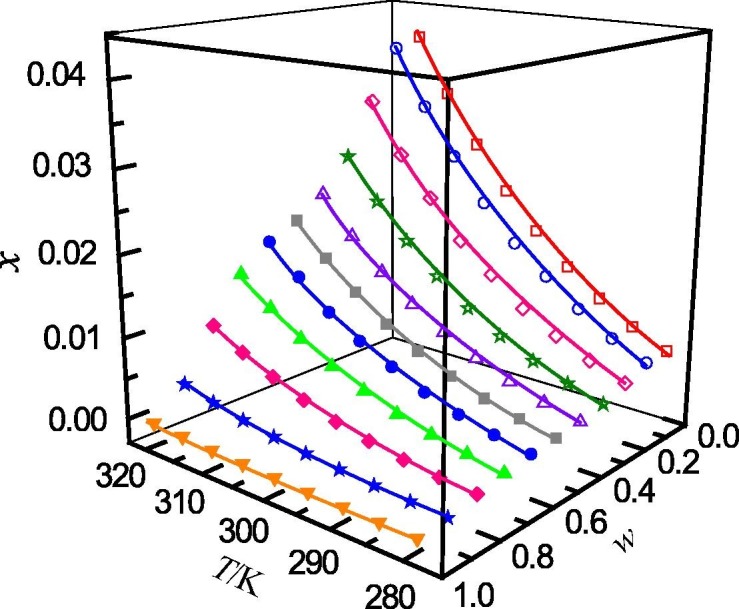
Mole fraction solubility (x) of ribavirin in n-propanol (w) + water (1 − w) mixed solutions with various mass fractions at different temperatures: w, mass fraction of n-propanol; □, w = 0; ○, w = 0.0999; ♢, w = 0.2003; ☆, w = 0.2991; △, w = 0.3989; ■, w = 0.5002; ●, w = 0.5999; ▲, w = 0.7009; ◆, w = 0.7991; ★, w = 0.8998; ▾; w = 1. —, calculated curves by the Jouyban − Acree model.
Fig. 3.
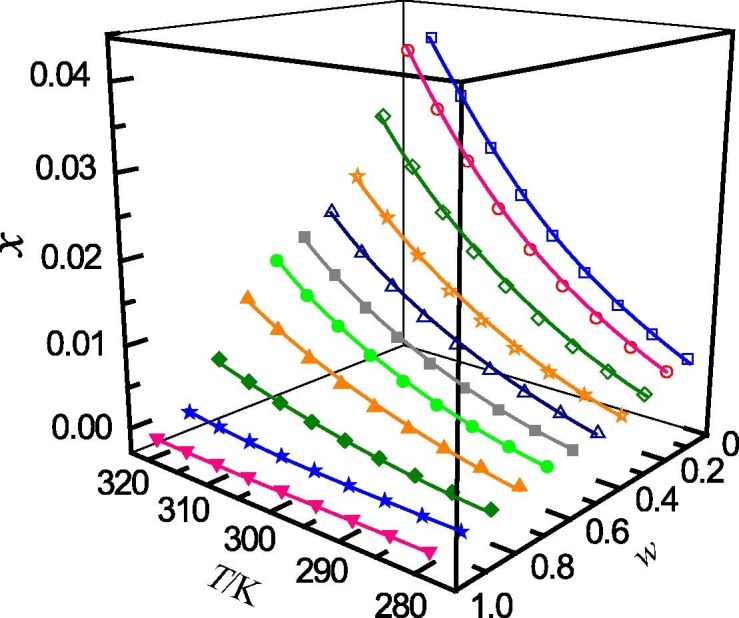
Mole fraction solubility (x) of ribavirin in acetonitrile (w) + water (1 − w) mixed solutions with various mass fractions at different temperatures: w, mass fraction of acetonitrile; □, w = 0; ○, w = 0.0999; ♢, w = 0.2008; ☆, w = 0.3007; △, w = 0.3995; ■, w = 0.5008; ●, w = 0.5997; ▲, w = 0.7006; ◆, w = 0.7998; ★, w = 0.8993; ▾; w = 1. —, calculated curves by the Jouyban − Acree model.
Fig. 4.
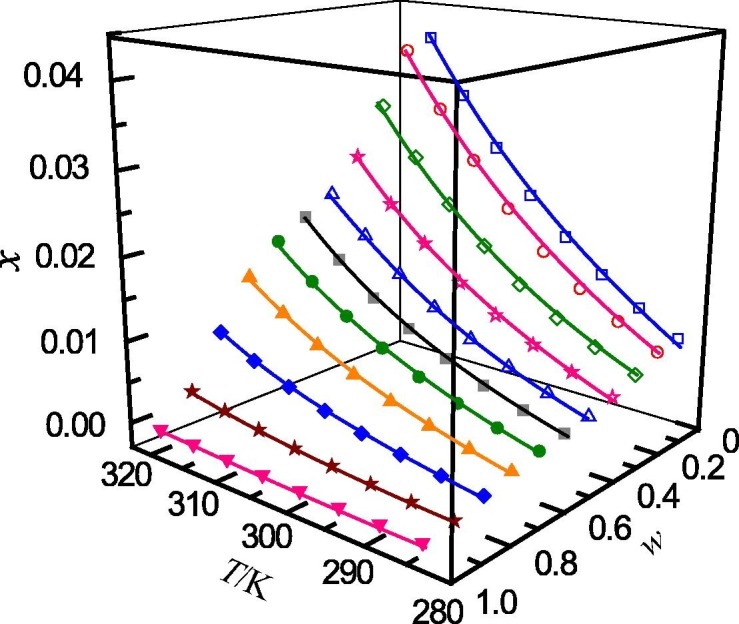
Mole fraction solubility (x) of ribavirin in 1,4-dioxane (w) + water (1 − w) mixed solutions with various mass fractions at different temperatures: w, mass fraction of 1,4-dioxane; □, w = 0; ○, w = 0.0994; ♢, w = 0.2009; ☆, w = 0.3011; △, w = 0.4007; ■, w = 0.4999; ●, w = 0.5988; ▲, w = 0.7003; ◆, w = 0.7998; ★, w = 0.8992; ▾; w = 1. —, calculated curves by the Jouyban − Acree model.
It is noteworthy that the mole-fraction solubility of ribavirin (II) in water at 298.15 K determined in this work is 0.01741, which is a little larger than 0.0103 (142 mg·mLl−1) reported by Benet [19], Goodarzi [20], Dave [21] and Chen [22], 0.0109 (149 mg·mL−1) reported by Vasa [23], and 0.0124 (169.99 mg·mL−1) reported by Prasanthi [24]. The difference may be due to many factors, such as determination method, equilibration time, purity, sampling, analysis method and so on. Based on study made by Vasa and Wildfong [23], ribavirin (II) reached a maximum solubility within 30 min. On the other hand, it can also be seen from the plots of the ribavirin (II) concentrations in distilled water as a function of time that, when the dissolution time is 180 min, the concentration of ribavirin (II) in water remains increased obviously. Therefore, it can be speculated that if the time is prolonged, the ribavirin (II) concentration will also increase. In other words, the concentration (149 mg·ml−1) at 30 min is not the equilibrium solubility of ribavirin (II) in water at studied temperature.
3.3. Solubility modelling
The models presented from 1960 to 2007 for correlating the solubility of a solid in solvent mixtures have been reviewed in Ref. [25]. In the present work, three models are used to correlate the solubility of ribavirin in binary solvent mixtures of (methanol + water), (n-propanol + water), (acetonitrile + water) and (1,4-dioxane + water) at different temperatures, which correspond to Jouyban−Acree model [25], [41], [50], a combination of the Jouyban−Acree model with van’t Hoff equation [41], [50], and a combination of the Jouyban−Acree model with modified Apelblat equation [41], [50].
3.3.1. Jouyban-Acree model
The Jouyban-Acree model is expressed as Eq. (4). This model can provide accurate mathematical description for the dependence of solute solubility on both temperature and solvent composition for binary and ternary mixed solvents [25], [41], [50].
| (4) |
where x w,T denotes the mole fraction solubility of solute in solvent mixtures at temperature T/K; w 1 and w 2 are the mass fraction of solvents 1 (methanol, n-propanol, acetonitrile or 1,4-dioxane) and 2 (water) in the absence of the solute (ribavirin), respectively; x 1,T and x 2,T are the solute solubility in mole fraction in neat solvent; and J i are the Jouyban-Acree model parameters.
3.3.2. Van’t Hoff-Jouyban-Acree model
The van’t Hoff equation is an ideal model, which is described as
| (5) |
Combining Eq. (4) and Eq. (5), the van’t Hoff-Jouyban-Acree model can be obtained [41], [50] and expressed as Eq. (6).
| (6) |
A 1, B 1 and A 2, B 2 are equation parameters.
3.3.3. Modified Apelblat-Jouyban-Acree model
The modified Apelblat equation is a semi-empirical model having three parameters. It may be employed to describe a nonlinear relationship between solubility in neat solvent and reciprocal of absolute temperature (1/T) and is described as
| (7) |
where A, B, and C are equation parameters; and also x T is the mole fraction solubility of ribavirin in studied mixed solvents at absolute temperature T in Kelvin.
By substituting Eq. (7) into Eq. (4), the modified Apelblat-Jouyban-Acree model can be obtained as Eq. (8) [41], [50].
| (8) |
The experimental solubility values of ribavirin in (methanol + water), (n-propanol + water), (acetonitrile + water) and (1,4-dioxane + water) mixtures are correlated and calculated with Eqs. (4), (6), (8). The objective function is described as
| (9) |
In order to show the error and evaluate the different models, the relative average deviation (RAD) and root-mean-square deviation (RMSD) are employed, which are described as Eqs. (10), (11).
| (10) |
| (11) |
where N is the number of experimental data points. denotes the mole fraction solubility determined in this work; and , the mole fraction solubility calculated with the corresponding solubility model.
The parameters in Eqs. (4), (5), (6), (7), (8) were acquired by using Mathcad software based on the experimental solubility values. The obtained values of model parameters together with the RAD and the RMSD values are presented in Table S2 of the Supporting material. The solubility of ribavirin in the four binary mixtures of (methanol + water), (n-propanol + water), (acetonitrile + water) and (1,4-dioxane + water) are evaluated on the basis of the regressed parameters’ values. The calculated solubilities using the Jouyban−Acree model are plotted in Fig. 1, Fig. 2, Fig. 3, Fig. 4. It can be seen from Table S2 that for the studied binary solvent mixtures, the maximum value of relative average deviations (RAD) is 1.57%, which is obtained with the van’t Hoff-Jouyban-Acree model for the system of (n-propanol + water). Besides, the root-mean-square deviations (RMSD) are no greater than 2.14 × 10−4. Comparison with the other models, the values of RAD and RMSD obtained with the Jouyban-Acree model is relatively small. On the whole, the three models can all be employed to correlate the solubility of ribavirin in the binary mixtures of (methanol + water), (n-propanol + water), (acetonitrile + water) and (1,4-dioxane + water) at all initial composition ranges, and the Jouyban-Acree model provides better correlation results than the other two models.
3.4. Dissolution property
Thermodynamic property of a solute dissolved in mixed solvent can provide significant information for the dissolution process. The standard dissolution enthalpy for dissolution process of ribavirin in the studied solvent mixtures may be attained from the famous van’t Hoff analysis [38], [41].
| (12) |
here R is the universal gas constant (8.314 J·K−1·mol−1). T hm stands for the mean harmonic temperature which is calculated via Eq. (13).
| (13) |
The values of can be obtained from the slope of the curves of lnx w,T vs (1/T − 1/T hm), which are shown graphically in Figs. S4–S7 of Supporting material. The standard dissolution enthalpy of ribavirin in the solvent mixtures of (methanol + water), (n-propanol + water), (acetonitrile + water) and (1,4-dioxane + water) are computed from Eq. (12) and tabulated in Table S3 of Supporting material. It can be found that the values of standard molar enthalpy of dissolution are all positive, which demonstrates that the dissolution process of ribavirin in the four binary mixed solvents is endothermic, and the entropy is driving force for the dissolution process.
3.5. Preferential solvation of ribavirin
Inverse Kirkwood–Buff integrals (IKBI) are widely used for evaluating the preferential solvation of non-electrolyte or non-dissociated weak electrolyte compounds in solvent mixtures, describing the local solvent proportions around the solute with respect to the composition of the solvent mixtures [6], [7]. This treatment depends on the standard molar Gibbs energies of transfer of ribavirin (3) from neat water (2) to the solvent mixtures and also on the excess molar Gibbs energy of mixing for the solvent binary mixtures free of drug. Thus, the results are expressed in terms of the variation of preferential solvation parameter (δx 1,3) of the solute ribavirin (3) by the solvent molecules with the mixtures composition. The inverse Kirkwood-Buff integral equation is given by the following general expression:
| (14) |
where, g i,3 is the pair correlation function for molecules of solvent i in the solvent mixtures around the solute ribavirin (3); r is the distance between the centers of molecules of ribavirin (3) and those of solvent (1) or water (2); and r cor is a correlation distance for which g i,3 (r > r cor) ≈ 1. Accordingly, for all distances r > r cor up to infinite, the value of the integral is essentially zero.
The preferential solvation parameter of ribavirin (compound 3) by the solvent (compound 1) in solvent (1) + water (2) mixtures is defined as [5], [6], [7], [26], [27], [28], [29], [30]:
| (15) |
where is the local mole fraction of solvent (1) in the environment near to ribavirin (3) and x 1 is the bulk mole fraction composition of solvent (1) in the initial binary solvent. If δx1,3 > 0 then the solute is preferentially solvated by solvent (1); on the contrary, if δx1,3 is <0 the solute is preferentially solvated by water (2). Values of δx 1,3 may be obtained from the inverse Kirkwood-Buff integrals for the individual solvent components analysed according to some thermodynamic quantities as shown in the following equations [5], [6], [7], [26], [27], [28], [29], [30]:
| (16) |
with,
| (17) |
| (18) |
| (19) |
In Eqs. (16), (17), (18), (19), κ T is the isothermal compressibility of the solvent (1) + water (2) mixtures (expressed in GPa−1); V 1 and V 2 are the partial molar volumes of the solvents in the mixtures (expressed in cm3·mol−1); similarly, V 3 is the partial molar volume of ribavirin in these mixtures (expressed in cm3·mol−1). The function D express by Eq. (20) is the derivative of the standard molar Gibbs energies of transfer of ribavirin from neat water (2) to solvent (1) + water (2) mixtures with respect to the solvent composition (expressed in kJ·mol−1, as is RT). The function Q defined by Eq. (21) involves the second derivative of the excess molar Gibbs energy of mixing of the two solvents with respect to the water proportion in the mixtures (also expressed in kJ·mol−1). V cor is the correlation volume and r 3 is the molecular radius of ribavirin calculated by using Eq. (22) with N Av as the Avogadro’s number.
| (20) |
| (21) |
| (22) |
Because of the dependence of κ T on composition, this term is not known for all the systems investigated. In addition, due to the minor contribution of RTκ T to the inverse Kirkwood-Buff integral, the dependence of κ T upon composition can be calculated approximated as an additive property by using the mixture compositions and the reported values for neat solvents by [5], [6], [26], [27], [28], [29], [30]:
| (23) |
where xi is the mole fraction of component i in solution and is the isothermal compressibility of the neat component i. The RTκT values can be calculated with the reported values for methanol (1.248 GPa–1), n-propanol (1.025 GPa–1), acetonitrile (1.070 GPa−1), 1,4-dioxane (0.738 GPa–1) and water (0.457 GPa–1) at 298.15 K, taken as independent of the temperature [51].
Standard molar Gibbs energy of transfer of ribavirin from neat water (2) to {methanol (1) + water (2)}, {n-propanol (1) + water (2)}, {acetonitrile (1) + water (2)} and {1,4-dioxane (1) + water (2)} mixtures is computed by using Eq. (24) from the solubility values.
| (24) |
The calculated values of are tabulated in Tables S4 and S5 of Supplementary material and correlated with polynomial presented as Eq. (25). Fig. S8 of Supporting material shows the values of Gibbs energy of transfer at five temperatures. The obtained coefficients in Eq. (25) are shown in Table S6 of Supplementary material.
| (25) |
Thus, D values are calculated from the first derivative of Eq. (25) solved according to the solvent mixture composition varying by 0.05 in mole fraction of methanol (1), n-propanol (1), acetonitrile (1) or 1,4-dioxane (1). The D values obtained are reported in Table S7 of Supplementary material.
The excess molar Gibbs energies of mixing at all the temperatures considered are needed in order to calculate the Q values. However, these values are reported only at one temperature, i.e. normally at 298.15 K. For this reason, it is necessary to calculate these values at the other temperatures required. For {methanol (1) + water (2)}, {acetonitrile (1) + water (2)} and {1,4-dioxane (1) + water (2)} solvent mixtures, values are calculated at 298.15 K using Eqs. (26), (27), (28), respectively, as reported by Marcus [6]; while for {n-propanol (1) + water (2)} mixtures, using Eq. (29) taken from Ref. [52]. On the other hand, the values at the other temperatures are calculated using Eq. (30). Here is the excess molar enthalpy of the solvent mixtures, T 1 is 298.15 K and T 2 is one of the other temperatures under consideration [6]. In turn, values are calculated by using Eqs. (31), (32), (33), (34) at 298.15 K for {methanol (1) + water (2)} [6], {n-propanol (1) + water (2)} [52], {acetonitrile (1) + water (2)} [6] and {1,4-dioxane (1) + water (2)} [6] solvent mixtures, respectively.
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
| (33) |
| (34) |
In similar manner, the partial molar volumes of both solvents in the mixtures are calculated from the reported density values of the solvent mixtures at the studied temperatures under study by Mikhail and Aliaj for methanol + water mixtures [53], [54], by Pang for (n-propanol + water) mixtures [55], by Saleh and Handa for {acetonitrile (1) + water (2)} mixtures [56], [57], and by Ruidiaz for (1,4-dioxane + water) mixtures [58] using Eqs. (35), (36). In these equations V is the molar volume of the mixtures calculated as V =(x 1·M 1+x 2·M 2)/ρ. Here, M 1 is 32.04 g·mol–1 for methanol, 60.06 g·mol–1 for n-propanol, 41.05 g·mol–1 for acetonitrile, 88.11 g·mol–1 for 1,4-dioxane and M 2 is 18.02 g·mol–1 for water.
| (35) |
| (36) |
Because no partial molar volumes of ribavirin (3) in these mixtures are acquired in the literature, in this work this property is considered as similar to that for the pure compound as a good approximation [26], [27], [28], [29], [30]. In this way, the molar volume of ribavirin (3) is calculated by using Advanced Chemistry Development (ACD/Labs) Software V 11.02 (○c1994-2016 ACD/Labs) as 117.0 cm3·mol–1. From this volume value, solute radius value (r 3) is calculated using Eq. (22) as 0.359 nm. The values of G 1,3 and G 2,3 can be obtained and shown in Tables S8–S11 of Supplementary material.
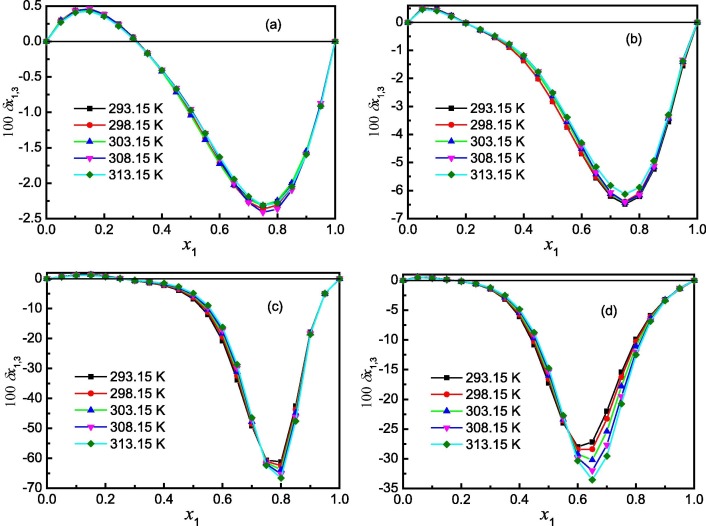
Definitive correlation volume requires iteration because it depends on the local mole fractions around the solute. This iteration is done by replacing δx 1,3 and V cor in the Eqs. (15), (16), (19) to recalculate until a non-variant value of V cor is acquired. The obtained values of correlation volume V cor and δx 1,3 are listed in Tables S12–S15 of Supplementary material for {methanol (1) + water (2)}, {n-propanol (1) + water (2)}, {acetonitrile (1) + water (2)} and {1,4-dioxane (1) + water (2)} solvent mixtures, respectively. In addition, the dependence of δx 1,3 values on solvent composition in mole fraction is shown graphically in Fig. 5 . It shows that the values of δx 1,3 vary non-linearly with the solvent (1) proportion in all the aqueous mixtures. According to Fig. 5, addition of water (1) makes negative the δx 1,3 values of ribavirin (3) from neat methanol (n-propanol, acetonitrile or 1,4-dioxane) (1) up to x 1 = 0.31 mol fraction of methanol, x 1 = 0.20 mol fraction of n-propanol, x 1 = 0.26 mol fraction of acetonitrile, and x 1 = 0.20 mol fraction of 1,4-dioxane. Maximum negative values are obtained with the composition x 1 = 0.75 with δx 1,3 = −2.314 × 10−2 to −2.411 × 10−2 for the methanol (1) + water, x 1 = 0.75 with δx 1,3 = −6.129 × 10−2 to −6.488 × 10−2 for the n-propanol (1) + water (2), x 1 = 0.80 with δx 1,3 = −61.20 × 10−2 to −66.60 × 10−2 for the {acetonitrile (1) + water (2)}, and x 1 = 0.60 to 0.65 with δx 1,3 = −78.98 × 10−2 to −33.52 × 10−2 for {1,4-dioxane (1) + water (2)} mixtures. In the other regions for the {methanol (1) + water (2)}, {n-propanol (1) + water (2)} and {1,4-dioxane (1) + water (2)} mixtures, the δx 1,3 values of ribavirin (3) are positive. However they are all less than 1.0 × 10−2. For the acetonitrile (1) + water (2) mixtures in water-rich composition, the δx 1,3 values are positive and slightly greater than 1.0 × 10−2 (e.g. 1.47 × 10−2 at 293.15 K). Nevertheless these values are much smaller than that in intermediate and acetonitrile-rich composition (e.g. -61.20 × 10−2 at 293.15 K). Therefore they are just qualitative because of uncertainties propagation effects instead of preferential solvation [59], [60], [61]. So the conclusion can be made that ribavirin is preferentially solvated by water for the four solvent mixtures with a very wide compositions. Probably the structuring of water molecules around the ribavirin molecule contributes to lowering of the net δx 1,3 to negative values in the four solvent mixtures. It can also be seen from Fig. 5 that the temperature has little effect on the preferential solvation magnitudes of ribavirin in the four solvent mixtures.
Fig. 5.
δx1,3 values of ribavirin (3) from water (2) to methanol (1) + water (2), n-propanol (1) + water (2), acetonitrile (1) + water (2) and 1,4-dioxane (1) + water (2) mixtures at several temperatures. (a), methanol (1) + water (2); (b), n-propanol (1) + water (2); (c), acetonitrile (1) + water (2); (d), 1,4-dioxane (1) + water (2).
Ribavirin can act as a Lewis base because of the free electron pairs in nitrogen atoms of —N and —N and oxygen atoms of O and —O— (Fig. S1 of Supporting materials), which interact with acidic hydrogen atoms of water. So it is conjecturable that ribavirin could be acting mainly as a Lewis base in front to water because the Kamlet–Taft hydrogen bond donor parameters are, α = 0.990 for methanol, 0.84 for n-pronanol, 0.19 for acetonitrile, 0.00 for 1,4-dioxane and 1.17 for water, respectively [51], [62].
Fig. S9 of Supporting material compares the preferential solvation of ribavirin in {methanol (1) + water (2)}, {n-propanol (1) + water (2)}, {acetonitrile (1) + water (2)} and {1,4-dioxane (1) + water (2)} at 298.15 K. The preferential solvation magnitudes of ribavirin by water is highest in acetonitrile mixtures, followed by 1,4-dioxane and n-propanol mixtures, and finally, by methanol mixtures in different solvent proportions, i.e. x 1 = 0.75, δx 1,3 = −2.367 × 10−2 for {methanol (1) + water (2)}; x 1 = 0.75, δx 1,3 = −6.396 × 10−2 for {n−propanol (1) + water (2)}; x 1 = 0.80, δx 1,3 = −62.50 × 10−2 for {acetonitrile (1) + water (2)}; and x 1 = 0.60, δx 1,3 = −28.43 × 10−2 for {1,4-dioxane (1) + water (2)}, respectively.
Finally, it is noteworthy that in our previous studies [63], [64], [65], the solute is preferentially solvated by co-solvent in co-solvent-rich mixtures. However, ribavirin (II) is preferentially solvated by water in this region. The reason is not clear at present. This case may be due to the chemical structure of solute.
4. Conclusion
The equilibrium solubility of ribavirin in four binary mixed solvents of {methanol (1) + water (2)}, {n-propanol (1) + water (2)}, {acetonitrile (1) + water (2)} and {1,4-dioxane (1) + water (2)} at temperature range from (278.15 to 318.15) K were reported. At the same composition of methanol, n-propanol, acetonitrile or 1,4-dioxane and temperature, the mole fraction solubility of ribavirin was highest in {methanol (1) + water (2)} mixtures, and lowest in {1,4-dioxane (1) + water (2)} mixtures. By using the Jouyban-Acree model, van’t Hoff-Jouyban-Acree model and Apelblat-Jouyban-Acree model, ribavirin solubility were well correlated obtaining ARD lower than 1.57% and RMSD lower than 2.14 × 10−4. Quantitative values for the local mole fraction of methanol (n-propanol, acetonitrile or 1,4-dioxane) and water around the ribavirin were calculated based on the IKBI method applied to the solubility values determined. Ribavirin was preferentially solvated by water for the four solvent mixtures over a very wide range of compositions. The preferential solvation magnitude of ribavirin by water was highest in acetonitrile mixtures, followed by 1,4-dioxane and n-propanol mixtures, and finally, by methanol mixtures. It is conjecturable that ribavirin could be acting mainly as a Lewis base in front to water.
Acknowledgments
The authors would like to express their gratitude for the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Footnotes
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.jct.2017.07.027.
Appendix A. Supplementary data
References
- 1.Jouyban A. CRC Press; BocaRaton, FL: 2010. Handbook of Solubility Data for Pharmaceuticals. [Google Scholar]
- 2.Rubino J.T. In: Encyclopedia of Pharmaceutical Technology. Swarbrick J., Boylan J.C., editors. Marcel Dekker; New York, NY: 1988. Cosolvents and cosolvency. [Google Scholar]
- 3.Avdeef A. Permeability and Charge State. Wiley-Interscience; Hoboken, NJ: 2003. Absorption and drug development, solubility. [Google Scholar]
- 4.Aulton M.E. second ed. Churchill Livingstone; London: 2002. Pharmaceutics: The Science of Dosage Forms Design. [Google Scholar]
- 5.Jouyban A., Martinez F., Acree W.E., Jr. Further calculations on solubility of 3-amino-1-adamantanol in ethanol + water binary solvent mixtures at various temperatures. J. Mol. Liq. 2016;219:211–215. [Google Scholar]
- 6.Marcus Y. Marcel Dekker Inc; New York, NY: 2002. Solvent Mixtures: Properties and Selective Solvation. [Google Scholar]
- 7.Marcus Y. In: Fluctuation Theory of Solutions: Applications in Chemistry, Chemical Engineering, and Biophysics, CRC, Press. Smith P.E., Matteoli E., O’Connell J.P., editors. Taylor & Francis Group; BocaRaton, FL: 2013. Preferential solvation in mixed solvents. [Google Scholar]
- 8.Zhu T.M., Fawzi M.B., Flint M., Kong F.M., Szeliga J., Tsao R., Howe A.Y.M., Pan W.T. Design and synthesis of HCV agents with sequential triple inhibitory potentials. Bioorg. Med. Chem. Lett. 2010;20:5212–5216. doi: 10.1016/j.bmcl.2010.06.156. [DOI] [PubMed] [Google Scholar]
- 9.Gangemi J.D., Nachtigal M., Barnhart D., Krech L., Jani P. Therapeutic efficacy of liposome-encapsulated ribavirin and muramyl tripeptide in experimental infection with influenza or herpes simplex virus. J. Infect. Dis. 1987;155:510–517. doi: 10.1093/infdis/155.3.510. [DOI] [PubMed] [Google Scholar]
- 10.Hayden F.G. Combination antiviral therapy for respiratory virus infections. Antivir. Res. 1996;29:45–48. doi: 10.1016/0166-3542(95)00914-0. [DOI] [PubMed] [Google Scholar]
- 11.Bellobuono A., Mondazzi L., Tempini S., Chiodo F., Magliano E., Furione L., Ideo G. Early addition of ribavirin to interferon in chronic hepatitis C not responsive to interferon monotherapy. J. Hepatol. 2000;33:463–468. doi: 10.1016/s0168-8278(00)80283-4. [DOI] [PubMed] [Google Scholar]
- 12.Chudinov M.V., Konstantinova I.D., Ryzhova O.I., Esipov R.S., Yurkevich A.M., Shvets V.I., Miroshnikov A.I. A new effective method for the synthesis of 1,2,4-triazole-3-carboxamide and ribavirin derivatives. Pharm. Chem. J. 2005;39:212–215. [Google Scholar]
- 13.Li Y.S., Zhang J.J., Mei L.Q., Tan C.X. An improved procedure for the preparation of ribavirin. Org. Prep. Proced. Int. 2012;44:387–391. [Google Scholar]
- 14.Konstantinova I.D., Fateev I.V., Galegov G.A., Deryabin P.G., Botikov A.G., Muzyka I.S., L’vov D.K., Miroshnikov A.I. Vol. 39. 2013. The arsenolysis reaction in the biotechnological synthesis of ribavirin. The in vitro and in vivo inhibition of influenza A virus replication with a combination of ribavirin and ozeltamivir; pp. 530–538. (Russ. J. Bioorg. Chem.). [DOI] [PubMed] [Google Scholar]
- 15.Paeshuyse J., Dallmeier K., Neyts J. Ribavirin for the treatment of chronic hepatitis C virus infection: a review of the proposed mechanisms of action. Curr. Opin. Virol. 2011;1:590–598. doi: 10.1016/j.coviro.2011.10.030. [DOI] [PubMed] [Google Scholar]
- 16.Rivero C.W., De Benedetti E.C., Lozano M.E., Trelles J.A. Bioproduction of ribavirin by green microbial biotransformation. Process Biochem. 2015;50:935–940. doi: 10.1016/j.procbio.2015.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Borden K.L.B., Culjkovic-Kraljacic B. Ribavirin as an anti-cancer therapy: acute myeloid leukemia and beyond. Leukemia lymphoma. 2010;51:1805–1815. doi: 10.3109/10428194.2010.496506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pettersson F., Yau C., Dobocan M.C., Culjkovic-Kraljacic B., Retrouvay H., Puckett R., Flores L.M., Krop L.E., Rousseau C., Cocolakis E., Borden K.L.B., Benz C.C., Miller W.H. Ribavirin treatment effects on breast cancers overexpressing eIF4E, a biomarker with prognostic specificity for luminal B-type breast cancer. Clin. Cancer Res. 2011;17:2874–2884. doi: 10.1158/1078-0432.CCR-10-2334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Benet L.Z., Broccatelli F., Oprea T.I. BDDCS Applied to over 900 Drugs. AAPS J. 2011;13:519–547. doi: 10.1208/s12248-011-9290-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Goodarzi N., Morgani A.B., Abrahamsson B., Cristofoletti R., Groot D.W., Langguth P., Mehta M.U., Polli J.E., Shah V.P., Dressman J.B. Biowaiver monographs for immediate release solid oral dosage forms: Ribavirin. J. Pharm. Sci. 2016;105:1362–1369. doi: 10.1016/j.xphs.2016.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dave R.A., Morris M.E. Novel high/low solubility classification methods for new molecular entities. Int. J. Pharm. 2016;511:111–126. doi: 10.1016/j.ijpharm.2016.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen J.M., Li S., Lu T.B. Pharmaceutical cocrystals of ribavirin with reduced release rates. Cryst. Growth Des. 2014;14:6399–6408. [Google Scholar]
- 23.Vasa D.M., Wildfong P.L.D. Solid-state transformations of ribavirin as a result of high-shear mechanical processing. Int. J. Pharm. 2017;524:339–350. doi: 10.1016/j.ijpharm.2017.04.002. [DOI] [PubMed] [Google Scholar]
- 24.Prasanthi G.D., Kumar P.P., Manohar B.S. Formulation and evaluation of immediate release film coated ribavirin tablets. World J. Pharm. Pharm. Sci. 2016;5:2227–2236. [Google Scholar]
- 25.Jouyban A. Review of the cosolvency models for predicting solubility of drugs in water-cosolvent mixtures. J. Pharm. Pharmaceut. Sci. 2008;11:32–58. doi: 10.18433/j3pp4k. [DOI] [PubMed] [Google Scholar]
- 26.Tooski H.F., Jabbari1 M., Farajtabar A. Vol. 45. 2016. Solubility and preferential solvation of the flavonoid naringenin in some aqueous/organic solvent mixtures; pp. 1701–1714. (J. Solution Chem.). [Google Scholar]
- 27.Delgado D.R., Martínez F. Preferential solvation of sulfadiazine, sulfamerazine and sulfamethazine in ethanol + water solvent mixtures according to the IKBI method. J. Mol. Liq. 2014;193:152–159. [Google Scholar]
- 28.Cárdenas Z.J., Jiménez D.M., Delgado D.R., Almanza O.A., Jouyban A., Martínez F., Acree W.E., Jr Solubility and preferential solvation of some n-alkyl-parabens in methanol + water mixtures at 298.15 K. J. Chem. Thermodynamics. 2017;108:26–37. [Google Scholar]
- 29.Jabbari M., Khosravi N., Feizabadi M., Ajloo D. Solubility temperature and solvent dependence and preferential solvation of citrus flavonoid naringin in aqueous DMSO mixtures: an experimental and molecular dynamics simulation study. RSC Adv. 2017;7:14776–14789. [Google Scholar]
- 30.Jouyban A., Acree W.E., Jr, Martínez F. Modelling the solubility and preferential solvation of gallic acid in cosolvent + water mixtures. J. Mol. Liq. 2016;224:502–506. [Google Scholar]
- 31.Chen B., Du Y., Wang H. Study on enantiomeric separation of basic drugs by NACE in methanol-based medium using erythromycin lactobionate as a chiral selector. Electrophoresis. 2010;31:371–377. doi: 10.1002/elps.200900343. [DOI] [PubMed] [Google Scholar]
- 32.Thote A.J., Gupta R.B. Formation of nanoparticles of a hydrophilic drug using supercritical carbon dioxide and microencapsulation for sustained release. Nanomedicine. 2005;1:85–90. doi: 10.1016/j.nano.2004.12.001. [DOI] [PubMed] [Google Scholar]
- 33.Kazakevich Y., Lobrutto R. John Wiley & Sons Inc; Hoboken, NJ: 2007. HPLC for Pharmaceutical Scientists. [Google Scholar]
- 34.Martin A., Bustamante P., Chun A.H.C. 4th ed. Lea & Febiger; Philadelphia (PA): 1993. Physical Chemical Principles in the Pharmaceutical Sciences. [Google Scholar]
- 35.Jouyban A. In silico prediction of drug solubility in water-dioxane mixtures using the Jouyban-Acree model. Pharmazie. 2007;62:46–50. [PubMed] [Google Scholar]
- 36.Byrne F.P., Jin S., Paggiola G., Petchey T.H.M., Clark J.H., Farmer T.J., Hunt A.J., McElroy C.R., Sherwood J. Tools and techniques for solvent selection: green solvent selection guides. Sustain Chem. Process. 2016 doi: 10.1186/s40508-016-0051-z. [DOI] [Google Scholar]
- 37.Yalkowsky S.H., He Y. CRC Press; Boca Raton: 2003. Handbook of Aqueous Solubility Data. [Google Scholar]
- 38.Delgado D.R., Martínez F. Solubility and solution thermodynamics of some sulfonamides in 1-propanol + water mixtures. J. Solution Chem. 2014;43:836–852. [Google Scholar]
- 39.Gekko K., Ohmae E., Kameyama K., Takagi T. Acetonitrile-protein interactions: amino acid solubility and preferential solvation. BBA. 1998;1387:195–205. doi: 10.1016/s0167-4838(98)00121-6. [DOI] [PubMed] [Google Scholar]
- 40.Han S., Meng L., Du C.B., Xu J., Cheng C., Wang J., Zhao H.K. Solubility measurement and thermodynamic modeling of 4-nitrophthalimide in twelve pure solvents at elevated temperatures ranging from (273.15 to 323.15) K. J. Chem. Eng. Data. 2016;61:2525–2535. [Google Scholar]
- 41.Cheng C., Cong Y., Du C.B., Wang J., Yao G.B., Zhao H.K. Solubility determination and thermodynamic models for dehydroepiandrosterone acetate in mixed solvents of (ethyl acetate + methanol), (ethyl acetate + ethanol) and (ethyl acetate + isopropanol) J. Chem. Thermodynamics. 2016;101:372–379. [Google Scholar]
- 42.Yao G.B., Xia Z.X., Li Z.H., Shao C. Determination and modeling for solid–liquid phase equilibrium of ternary caprolactam + cyclohexanone oxime + methyl tert-butyl ether system. Fluid Phase Equilibr. 2016;417:242–247. [Google Scholar]
- 43.Xu A.L., Xu R.J., Wang J. Solubility determination and thermodynamic modeling of terephthaldialdehyde in ten organic solvents from T = (273.15 to 318.15) K and mixing properties of solutions. J. Chem. Thermodynamics. 2016;102:188–198. [Google Scholar]
- 44.Yao G.B., Li Z.H., Xia Z.X., Yao Q.C. Solubility of N-phenylanthranilic acid in nine organic solvents from T = (283.15 to 318.15) K: Determination and modeling. J. Chem. Thermodynamics. 2016;103:218–227. [Google Scholar]
- 45.Yao G.B., Xia Z.X., Li Z.H. Thermodynamic study of solubility for 2-amino-4-chloro-6-methoxypyrimidine in twelve organic solvents at temperatures from 273.15 K to 323.15 K. Thermodynamics. 2017;105:187–197. [Google Scholar]
- 46.Prusiner P., Sundaralingam M. A new class of synthetic nucleoside analogues with broad-spectrum antiviral properties. Nat. New Biol. 1973;244:116–117. doi: 10.1038/newbio244116a0. [DOI] [PubMed] [Google Scholar]
- 47.Witkowski J.T., Robins R.K., Sidwell R.W., Simon L.N. Design, synthesis, and broad spectrum antiviral activity of 1-betad-ribofuranosyl-1,2,4-triazole-3-carboxamide and related nucleosides. J. Med. Chem. 1972;15:1150–1154. doi: 10.1021/jm00281a014. [DOI] [PubMed] [Google Scholar]
- 48.Tong H.H.Y., Shekunov B.Y., Chan J.P., Mok C.K.F., Hung H.C.M., Chow A.H.L. An improved thermoanalytical approach to quantifying trace levels of polymorphic impurity in drug powders. Int. J. Pharmaceut. 2005;295:191–199. doi: 10.1016/j.ijpharm.2005.02.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Smallwood I.M. Amoled; London: 1996. Handbook of Organic Solvent Properties. [Google Scholar]
- 50.Jouyban A., Fakhree M.A.A., Acree W.E., Jr. Comment on “Measurement and correlation of solubilities of (z)-2-(2-aminothiazol-4-yl)-2-methoxyiminoacetic acid in different pure solvents and binary mixtures of water + (ethanol, methanol, or glycol) J. Chem. Eng. Data. 2012;57:1344–1346. [Google Scholar]
- 51.Marcus Y. John Wiley & Sons; Chichester: 1998. The Properties of Solvents. [Google Scholar]
- 52.Delgado D.R., Martínez F. Preferential solvation of some structurally related sulfonamides in 1-propanol + water co-solvent mixtures. Phys. Chem. Liq. 2015;55:293–306. [Google Scholar]
- 53.Milkhail S.Z., Kimel W.R. Densities and viscosities of methanol-water mixtures. J. Chem. Eng. Data. 1961;6:533–537. [Google Scholar]
- 54.Aliaj F., Syla N., Bytyqi-Damoni A. Refractive indices, densities and excess molar volumes of binary systems methanol + water and ethanol + water at T = 293.15 K. AKTET J. Inst. Alb-Shkenca. 2006;9:36–42. [Google Scholar]
- 55.Pang F.M., Seng C.E., Teng T.T., Ibrahim M.H. Densities and viscosities of aqueous solutions of 1-propanol and 2-propanol at temperatures from 293.15 K to 333.15 K. J. Mol. Liq. 2007;136:71–78. [Google Scholar]
- 56.Saleh M.A., Akhtar S., Ahmed M.S. Density, viscosity and thermodynamic activation of viscous flow of water1acetonitrile. J. Mol. Liq. 2006;44:551–562. [Google Scholar]
- 57.Handa Y.P., Benson G.C. Thermodynamics of aqueous mixtures of nonelectrolytes. IV. Excess volumes of water-acetonitrile mixtures from 15 to 35 °C. J. Solution Chem. 1981;10:291–300. [Google Scholar]
- 58.Ruidiaz M.A., Martínez F. Volumetric properties of the pharmaceutical model cosolvent system 1,4-dioxane + water at several temperatures. Vitae Rev. Fac. Quím. Farm. 2009;16:327–337. [Google Scholar]
- 59.Ben-Naim A. Theory of preferential solvation of nonelectrolytes. Cell Biophys. 1988;12:255–269. doi: 10.1007/BF02918361. [DOI] [PubMed] [Google Scholar]
- 60.Ben-Naim A. Preferential solvation in two- and in three-component systems. Pure Appl Chem. 1990;62:25–34. [Google Scholar]
- 61.Marcus Y. Solubility and solvation in mixed solvent systems. Pure Appl Chem. 1990;62:2069–2076. [Google Scholar]
- 62.Taft R.W., Kamlet M.J. The solvatochromic comparison method. II. The alpha-scale of solvent hydrogen-bond donor (HBD) acidities. J. Am. Chem. Soc. 1976;98:2886–2894. [Google Scholar]
- 63.Chen J., Chen G.Q., Cong Y., Du C.B., Zhao H.K. Solubility modelling and preferential solvation of paclobutrazol in cosolvent mixtures of (ethanol, n-propanol and 1,4-dioxane) + water. J. Chem. Thermodynamics. 2017;112:249–258. doi: 10.1016/j.jct.2017.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Chen G.Q., Chen J., Cheng C., Cong Y., Du C.B., Zhao H.K. Solubility and preferential solvation of econazole nitrate in binary solvent mixtures of methanol, ethanol and 1,4-dioxane in water. J. Chem. Thermodynamics. 2017;111:228–237. doi: 10.1016/j.jct.2017.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Wang S.L., Du C.B., Zhao H.K. Solubility, solution thermodynamics and preferential solvation for 4-bromopyrazole in mixed solvents of (methanol/ethanol + water) from T = (283.15 to 318.15) K. J. Chem. Thermodynamics. 2017;112:146–154. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.