Probabilistic risk assessment of the energy saving shortfall in energy performance contracting projects–A case study

Highlights

• •A method to evaluate the probability of saving shortfall for energy performance contracting projects is proposed.
• •Two calibrated building energy models are developed using EnergyPlus.
• •The influential parameters affecting the chiller plant energy use are identified.
• •The probability distributions functions are developed using empirical data.
• •A case study is analysed to illustrate the methodology.

Abstract

Lack of a proper assessment method on performance risks in Energy Performance Contracting (EPC) projects is one of the reasons hindering the further development of energy service companies (ESCOs) market. This paper proposes a simulation-based method to evaluate the probability of energy saving shortfall taking into account the variations in the influential parameters, including weather conditions, occupancy, operating hours, thermostat set-point, etc., during the contract period. The proposed method involves the use of a detailed building energy simulation programme, sensitivity analysis and Monte Carlo simulation techniques. Empirical data is also used to develop the probability distribution functions for the identified parameters to simulate the actual yearly variations in the post-retrofit conditions. A real case study of replacement of heat rejection system for a central chiller plant in Hong Kong is used to demonstrate the application of this probabilistic method. The result shows that the possible energy savings after a 1-year retrofit period ranges from 393,000 kW h (2.86%) to 1098,000 kW h (10.8%) with 90% statistical significance.

1. Introduction

Buildings account for 40% of the world's energy use, and most of the existing buildings are not so energy efficient as modern technology allows [1], [2]. As such, energy retrofitting of existing building services equipment can yield significant amount of energy savings. However, the lack of upfront capital and technological know-how are usually hurdles to undertaking energy improvement projects although the benefits of such works, for example, a substantial reduction in utility costs and improvement of the built environment, are obvious. Energy Performance Contracting (EPC) is recognised as a means to tackle this problem in many countries, including the United States, Australia, Germany, Japan, Singapore and China [3], [4]. The European Parliament defines EPC in the Directive 2006/32/EC as “a contractual arrangement between the beneficiary and the provider (normally an ESCO) of an energy efficiency improvement measure, where investments in that measure are paid for in relation to a contractually agreed level of energy efficiency improvement.” [5] . It means that, under an EPC arrangement, energy service companies (ESCOs) guarantee or share the energy savings with building owners. Building owners only make a series of payment to ESCOs when the actual energy savings are materialised. In the case of shortfall in savings, ESCOs will compensate the loss incurred by building owners. To ensure the guaranteed energy saving can be achieved, a proper assessment method on the probability of energy saving shortfall is needed to evaluate such project risks.

Mills et al. [6] identified the risks associated with energy-efficiency projects and classified them into five aspects, namely economic, contextual, technology, operation, and measurement and verification (M&V) risks. Several risk management approaches (e.g. financial hedging, careful design, proper metering, etc.) were also introduced to mitigate the associated risks in their study. However, even though ESCOs can better manage the performance risks by ensuring system efficiency, optimisation control and better maintenance, the actual energy saving is still uncertain. This is attributed to various extrinsic factors including weather conditions, economic circumstances, as well as occupants’ behaviour, which can significantly affect the actual energy savings. For example, the occupancy rate of hotel may decrease dramatically due to economic downturn, resulting in a significant reduction in the actual energy savings. Therefore, a dilemma is often observed from the ESCOs’ perspective in determining the amount of guaranteed energy savings. On one hand, ESCOs try to mitigate the performance risks by being conservative on the guaranteed savings, but on the other hand, to increase chances of winning bids by offering higher energy saving guarantee and shorter contract period.

Several attempts were made to develop such an assessment method. Rickard et al. [7] adopted the technique of coefficient of variation (CV) to compare saving uncertainties in different energy efficiency measures. However, some drawbacks were found in this technique, for example, several simplified assumptions had to be made for project comparison and a number of risk factors were excluded in the analysis. Mathew et al. [8] indicated the possible use of actuarial pricing approach to quantify the associated risks for project decision-making. However, this approach requires a large number of actual EPC project data, but the non-standardised project information and poor data quality often hinder the development of a reliable actuarial database [9]. Mills et al. [6] and Jackson [10] suggested using the Monte Carlo technique for quantifying the risks related to EPC projects, but their studies only focused on the illustration of a proposed methodology and no real project data is used to demonstrate the credibility of their findings.

This paper aims at developing a simulation-based method to evaluate the probability of energy saving shortfall taking into account the variations in the influential parameters. It is structured as follows. First, the probabilistic method is presented to quantify performance risks for energy saving shortfall under guaranteed EPC projects. The method involves the use of a detailed building energy simulation programme, sensitivity analysis and the Monte Carlo simulation techniques. Second, a case study of replacement of heat rejection system for a central chiller plant in Hong Kong is used for illustrating the application of this probabilistic method. Finally, the results of this case study are presented.

2. Probabilistic risk assessment of energy saving shortfall procedure and methods

Fig. 1 shows the procedure and methods used for quantifying the probability of energy saving shortfall in guaranteed EPC projects. The whole procedure consists of four main steps.

• I Development of pre- and post-retrofit models: The first step is to develop two energy models that can predict representative energy consumption of the building at the pre- and post-retrofit stages. With the two models, the actual energy savings can be predicted taking into account any deviation in the post-retrofit conditions from the baseline conditions. The models should be developed by using a detailed building energy simulation programme, which allows users to input all essential building information, system & equipment specifications, as well as operational characteristics for realistic energy use predictions. The two models should be basically identical except the retrofitted systems and the conditions with significant changes (e.g. change of occupancy). To ensure the representativeness of the models, the models should be calibrated with the measured energy use data. Details of the calibration procedures can be referred to other published literature and guidelines [11], [12], [13], [14].
• II Sensitivity analysis: The second step is to identify the importance of influential parameters affecting energy use. In general, the influential parameters can be summarised into three categories, namely “Building Load”, “System Control and Operation” and “Equipment, System and Plant”. For the selection of influential parameters, attention should be paid to those parameters that are likely to change during the EPC contract period, for example, weather conditions, occupancy rate, operating hours, etc. Some of the influential parameters may be excluded, for example, building height, materials used in building facade, orientation, etc., since these parameters are unlikely to change during the contract period. In some projects, an exclusion clause is incorporated to protest the interest of ESCOs and hosts in case of significant changes in the baseline conditions (e.g. large scale renovation works are conducted during the contract period). Those parameters can also be discarded in the sensitivity analysis.

  There are three common techniques to conduct sensitivity analysis, namely differential sensitivity analysis (DSA), random sensitivity analysis (RSA) and stochastic sensitivity analysis (SSA) in the field of building energy study [15], [16]. In comparison with these techniques, differential analysis by finite differences (FD) is most widely used because the calculations are easy and there are fewer problems to incorporate into the simulation programme. This technique has been widely used by researchers to determine the most sensitive parameters affecting building energy use [16], [17], [18], [19], [20]. The selection of a proper range and interval is essential to obtain accurate results in sensitivity analysis. Therefore, the range and intervals selected should cover the two extreme scenarios with a reasonably narrow interval. Nonlinearity issues should also be studied when the standard deviation of the influence coefficient (IC) is large. The procedure of performing differential sensitivity analysis is presented in the later part of this paper.

• III Development of probability distribution for selected parameters: The third step is to develop the probabilistic distribution function (PDF) for each of the selected parameters. The selection of the representative PDF is critical in this analysis as it is used to simulate the yearly variations in those selected parameters during the post-retrofit period. Empirical data from official database and previous research are used to determine the corresponding PDF for the selected parameters using curve-fitting techniques. Three goodness-of-fit tests, namely the Chi-square test, the Kolmogorov–Smirnov (K–S) test, and the Anderson–Darling (A–D) test, are performed to evaluate how well the assumed distributions fit a set of sample data [21]. The Chi-square test is used to determine the validity of two or more theoretical distribution models. The K–S test serves the same purpose, but with fewer limitations in application such as a large number of intervals. The A–D test is particularly useful when the tails of a distribution reflect an essential distribution characteristic. The lower the goodness-of-fit value of these tests is, the more representative the assumed PDF is selected. For those parameters without empirical data to determine, a triangular distribution is proposed to be the representative PDF, and the most likely value should be regarded as the baseline condition.
• IV Simulation of possible energy saving: The fourth step is to simulate energy saving taking into account all possible combinations of selected parameters during the post-retrofit period. Monte Carlo simulation is performed to generate a common set of post-retrofit condition data based on the PDF of the selected parameters. Monte Carlo simulation is a mathematical method where output values are randomly generated based on the assumed distributions of the independent parameters. A smooth approximation of the output distribution is obtained with large sample sizes (e.g. by iterating 10,000 simulation runs). This technique has been applied in a number of probabilistic analysis [22], [23], [24], [25], [26] .The Latin Hypercube Sampling method is proposed to generate those random numbers, because it more precisely reflects the shape of a defined distribution with relative small sample sizes [26].

Fig. 1.

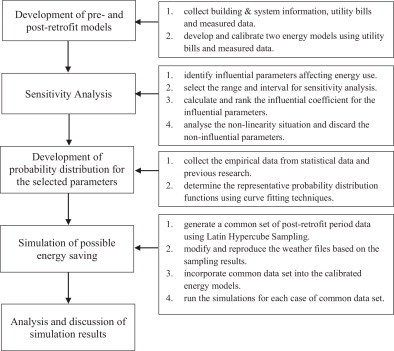
Probabilistic risk assessment of energy saving shortfall procedure and methods.

Detailed building energy simulation programmes usually require the weather and input data files to run the simulation. To simulate the energy saving uncertainty associated with yearly weather variations, it is necessary to modify and reproduce the typical weather file 10,000 times in accordance with the results of each Monte Carlo simulation. The algorithm of weather adjustment for the original weather file is based on a “morphing” method, developed by Belcher et al. [27] who constructed design weather data for future climates. Chan [28] also adopted this morphing method to modify the Hong Kong typical meteorological year (TMY) weather file taking into accounts the effect of urban heat islands. The procedure of this method will be illustrated in the later part of this paper. Similarly, 10,000 input files are required to generate based on the result of Monte Carlo simulation. Each weather and input file represents one of the possible yearly conditions during the post-retrofit period. These weather and input files are run on the detailed energy building simulation programme for the pre- and post-retrofit models to simulate possible range of energy savings.

3. Case study

3.1. Description of composite buildings

The above method for quantifying the probability of energy saving shortfall is illustrated through a real EPC project in the composite buildings. This development consists of three commercial towers with a total gross floor area (GFA)1 of around 240,000 m², which were built in the late 1990s. The first two towers, denoted as A and B, are symmetrical in building shape, and each comprises 14 serviced apartment (SA) storeys and 16 office storeys. The remaining tower, denoted as C, is solely for 30 storeys of office premises. Similar to other typical high-rise buildings below 30 storeys [29], a reinforced concrete structure was adopted and the building facades are made up of curtain walls while the window-to-wall ratio (WWR) is around 0.79 for four orientations. Reflective double glazing glasses are used for all towers. Table 1 shows the design parameters of these towers.

Table 1.

The design parameters of the building towers in the case study.

	Unit	Tower A	Tower B	Tower C
Location	–	City district in Hong Kong
Total gross floor area (GFA)a	m2	77,000	77,000	84,000
Total air-conditioned area	m2	50,000	50,000	54,500
Number of stories	–	30	30	30
		(SA:14; office:16)	(SA:14; office:16)	(All office premises)
Aspect ratio	Length/depth	1.91	1.91	1.91
Orientation	Degrees	335	335	335
Window U-value (N,S,E,W)	W/m2 K	2.67	2.67	2.67
Window SHGCb(N,S,E,W)	–	0.635	0.635	0.635
Wall U-value (N,S,E,W)	W/m2 K	3.3	3.3	3.3
Window-to-wall ratio (N,S,E,W)	–	0.79	0.79	0.79

^aGross floor area is a statutory building parameter measured to the external walls of building without deductions for lift, stair voids and other openings.

^bSHGC = Solar heat gain coefficient.

A central chiller plant system is used to provide cooling to these towers. This chiller plant system comprises 3 units of the day-mode 1800 ton chiller and 2 units of the night-mode 450 ton chiller. The primary–secondary pumping system is adopted and the seawater cooling system was used for heat rejection. The three day-mode chillers operating from 08:00 to 19:00 are capable of providing air conditioning for both the office and SA premises. For the remaining time, the AC operation is switched from the day-mode to the night mode, and only the SA premises are provided with air conditioning service.

3.1.1. Heat rejection system retrofit under guaranteed saving package

An energy audit was conducted by the ESCO after 5 years operation of the building. A design problem was found in the seawater cooling system in that the central chilled water plant was supplied with seawater, which was discharged from an adjacent central chiller plant for chiller condenser cooling, after the seawater had been used to cool the chillers in the adjacent plant. As the “indirect” seawater supply was at much higher temperatures than the original design level, the chiller plant had been running at rather low coefficient of performance (COP). The poor quality of the seawater also exacerbated corrosion of condenser tubes, causing further lowering of the COP. In order to address these problems, the ESCO and host agreed that the existing seawater cooling system should be replaced with a fresh-water evaporative cooling tower system, and the project was implemented under an EPC guaranteed saving package.

The actual energy saving was calculated based on the common set of post-retrofit period conditions per annum. The isolation approach [12] was adopted to measure the annual energy consumption of the whole chiller plant, including chillers, chilled water pumps and seawater pumps. Other energy and cost-avoided savings (e.g. reduction in maximum demand use and maintenance costs) were not considered in this study. Table 2 shows the component of chiller plant equipment for energy saving calculation in this retrofit project.

Table 2.

The component of chiller plant equipment for energy saving calculation in the case study.

	Pre-retrofit stage	Post-retrofit stage
Chiller plant	Annual chiller energy use	Annual chiller energy use
	Annual chilled water pump energy use	Annual chilled water pump energy use
Heat rejection	Annual sea water pump energy use	–
	–	Annual condensing water pump energy use
Annual energy use	A = sum of the above	B = sum of the above
Actual energy saving	Energy savings = A−B (calculated based on the post-retrofit conditions)

3.2. Development of building energy models

Two building energy models, representing the energy consumption at the pre- and post-retrofit stages, were developed using EnergyPlus [30]. EnergyPlus is a detailed building energy simulation program developed by the Department of Energy (DOE) in the United States. This program has been tested and validated according to ASHRAE standard 140 [31] and a number of researchers have utilised EnergyPlus to carry out sensitivity and parametric analysis for building energy use [19], [24].

3.2.1. Pre-retrofit model

The composite buildings consist of two types of premises: office and serviced apartment, on a total of 90 usable floors. For simplicity, a model for only three typical floors was developed to represent the whole composite buildings. As tower A and tower B are symmetrical to each other in shape, the first typical floor model, denoted as TY1, represents the SA premises of towers A and B. Similarly, the second typical floor model, denoted as TY2, represents the office premises of towers A and B. The third typical floor model, denoted as TY3, represents the office premises of the whole tower C. No roof and ground floors were modelled, because the top floors of all the three towers are used to house lift machine rooms, potable water, flush water and fire services water tank while the towers are atop a basement floor. Therefore, it would be reasonable to assume that heat transfers to the air-conditioned area caused by direct solar heat gain and ground temperature variations would be limited.

To ensure that the operating conditions of the chiller plant in the pre-retrofit period could be realistically modelled, a complete year of monthly energy use data of the chiller plant was collected and used as the basis for comparison while the operating conditions were tuned. A spot measurement was also conducted to evaluate the overall COP of the chiller plant. The other baseline conditions, including the occupancy rate of the office and SA premises, were obtained from relevant documentary records. Table 3 shows the EnergyPlus input details.

Table 3.

Description of EnergyPlus inputs.

		Unit	Office	Serviced apartment
Internal loads	Occupant	–	8 m2/person	42 person/floor
	Lighting	W/m2	15	15
	Electric equipment	W/m2	25	12
	Operating schedule	–	Based on the local BECa	Based on the local BECa
Shading		–	No shading device	No shading device
Thermostat set point	Cooling	°C	24.5	24.5
	Heating	°C	22	22
HVAC system	Air side	–	VAV	VAV
	Water side	–	Direct seawater cooled chiller; COP: 4.135; Partload performance: default curves from EnergyPlusb
Supply air temperature		°C	Summer: 14 Winter: 18	Summer: 14 Winter: 18
Infiltration		ACH	0.1	0.1
Ventilation		–	0.01 m3/s/person	0.63 m3/s/floor
Exterior wall		–	Concrete wall with gypsum	Concrete wall with gypsum
Interior Wall		–	Concrete wall with gypsum	Concrete wall with gypsum
Window construction		–	Curtain wall with double glazing	Curtain wall with double glazing
Thermal zoning		–	Core and perimeter zoning	Core and perimeter zoning

^aBEC = Building energy code (EMSD) [30].

^bSeawater-cooled chiller system is not directly supported in EnergyPlus. A “DistrictCooling” object with the specified leaving temperature on condenser loop is used to simulate the effect of using seawater as a heat rejection method in this study.

The pre-retrofit model was calibrated with reference to equipment nameplate data, operating schedules, occupancy patterns, etc. For those missing data which were required as inputs to EnergyPlus, estimates were made based on common practices and regulatory requirements, such as the building energy code [32]. The simulated results were compared to the monthly electricity bills data. The calibration procedures and requirements were in accordance with the ASHRAE Guideline 14 [12].

3.2.2. Post-retrofit model

The post-retrofit model was developed based on the pre-retrofit model except the retrofitted part. Similarly, one complete year of post-retrofit data was collected for calibration of the post-retrofit model. Other data and information, including new occupancy rate, operating schedules, as well as plant performance after retrofit, were also recorded.

Better chiller performance was observed after the retrofit. It was mainly attributed to the lower incoming condenser water temperature for chiller heat rejection (approximately 5 °C reduction). Apart from the chiller plant, there was no significant change from the baseline conditions, except the occupancy rate, which was 31% higher than the pre-retrofit conditions.

The predictions of the calibrated models and the actual consumption figures are shown for comparison in Table 4 as well as Fig. 2, Fig. 3 . It should be noted that the measured values of total chiller plant energy use on April and September in the post-retrofit case were discarded, as these data were found erroneous. Much effort had been made to account for the large deviation between the measured and predicted values of these two months, for example, checking on (1) maintenance records; (2) occupancy rate; (3) monthly outdoor temperature; (4) monthly relative humidity; (5) numbers of holiday happening on weekdays; (6) monthly billing period. The investigation concluded that the large deviation was most likely due to missing sub-meter readings but records of those readings could not be retrieved.

Table 4.

Calibration errors for the pre- and post-retrofit models and its requirement.

	ASHRAE guideline 14 requirement	Pre-retrofit energy model	Post-retrofit energy model
Minimum period spanned by baseline data	12 months	12 months	10 months
CV(RMSE)a	15%	7.98%	8.50%
NMBEb	5%	4.55%	1.23%

^aCV(RMSE) = the coefficient of variation of the root mean squared errors.

^bNMBE = normalised mean bias error.

Fig. 2.

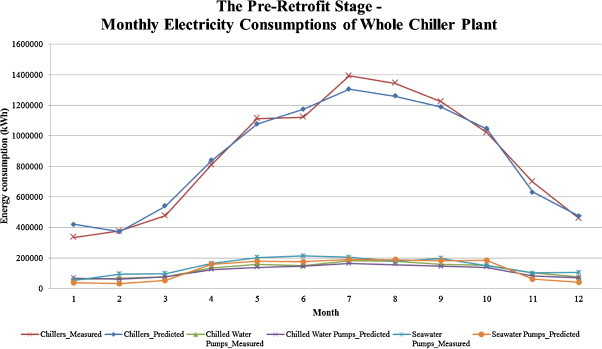
Comparison of the measured data with the predicted results on the chiller plant electricity consumption at the pre-retrofit stage.

Fig. 3.

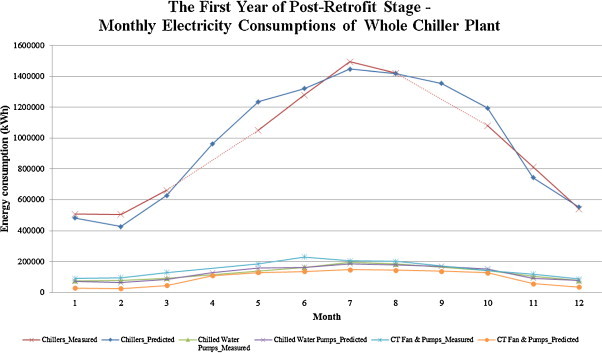
Comparison of the measured data with the predicted results on the chiller plant electricity consumption after the first year of post-retrofit stage.

According to the ASHRAE 14 guideline, the two statistical indices, namely coefficient of variation of the root mean squared errors (CVRMSE) and normalised mean bias error (NMBE), were used to assess how well the predicted values match with the measured values [12]. The models may be declared to be calibrated when CVRMSE and NMEB are less than 15% and 5% with monthly data respectively. Both models in this study complied with the calibration requirements.

3.3. Sensitivity analysis

Twenty-two parameters were finally identified for sensitivity analysis. These are summarised in Table 5 . The range and intervals selected are plausible values found from the previous studies on parametric and sensitivity analysis [16], [19], with attention being paid to the selection of range and intervals, they should cover the two extreme scenarios with a reasonably narrow interval. For example, the range of annual mean dry bulb temperature was selected based on the highest and lowest values throughout the 16 years of the Hong Kong Observatory weather data, and the interval was selected based on the measurement error ±0.1 °C for temperature sensor.

Table 5.

Results of sensitivity analysis.

Parameter(s)	Unit	Minimum	Base case	Maximum	Interval	Number	Influential coefficient	Ranking
Building Load
Annual mean dry bulb temperaturea	°C	22.066	23.066	24.066	0.1	21	1.080	1
Annual mean dew point temperaturea	°C	17.907	18.907	19.907	0.1	21	0.460	4
Annual mean global solar radiationa	W h/m2	192.907	292.907	392.907	10	21	0.124	11
Occupant density (office)	m2/person	5	8	20	1	15	−0.104	14
Occupant density (SA)	Person/floor	35	42	45	1	10	0.0428	17
Lighting load (office)	W/m2	10	20	30	1	20	0.113	13
Lighting load (SA)	W/m2	10	20	30	1	20	0.0646	15
Equipment load (office)	W/m2	10	25	40	1	30	0.148	9
Equipment load (SA)	W/m2	10	12	40	1	30	0.0310	18
AC operating hours (office)b	h	17:00	19:00	22:00	0.25	20	0.627	3
AC operating hours (SA) c	h	24	24	24	–	–	–	–
Annual mean occupancy rate (office)d	% (floor)	50% (31)	73.4% (47)	100% (62)	1	31	0.239	6
Annual mean occupancy rate (SA)d	% (floor)	50% (14)	73.4% (21)	100% (28)	1	14	0.215	7
Ventilation rate (office)	m3/s/person	0.005	0.01	0.015	0.002	6	0.0243	19
Ventilation rate (SA)	m3/s/person	0.005	0.01	0.015	0.002	6	0.0199	20
Infiltration rate (office)	ACH	0.05	0.1	0.25	0.02	11	−0.00113	22
Infiltration rate (SA)	ACH	0.05	0.1	0.25	0.02	11	0.00470	21
System control and operation
Supply air temperature (office)	°C	10	14	18	0.1	80	−0.116	12
Supply air temperature (SA)	°C	10	14	18	0.1	80	−0.151	8
Thermostat set point (office)	°C	20	24	28	0.1	80	−0.290	5
Thermostat set point (SA)	°C	20	24	28	0.1	80	−0.131	10
HVAC plant
Chilled water supply (CHWS) temperature	°C	4	6.7	9	0.1	50	−0.0614	16
Overall COP of chiller plant	–	3	4.1365	5	0.1	21	−0.864	2

^aThis SA study focused on the importance of parameters affecting the energy use of a chiller plant. The seasonal variation in these weather variables, therefore, was not included. The annual mean temperature was taken as the average value of the daily mean air temperature throughout a year.

^bAC operating hours (office) involves two parameters, the AC start-up time and operating duration, would be adjusted. In this study, the AC start-up time, which is 8:00 am, remained unchanged and only the operating duration was changed.

^cAC operating hours (SA) was assumed to be unchanged as it is very unlikely for SA operators to reduce the operating hours.

^dThe data on occupancy rate is in terms of the annual mean percentage. The occupancy rate was converted into the number of floors being fully occupied. Besides, it was assumed that a tenant rents the office floor in terms of a whole floor, instead of half-floor. Similarly, the SA operator will try to occupy the whole floor for minimising the operation costs.

The differential sensitivity analysis (DSA) was employed in this study, and the sensitivity influence coefficient (IC) was calculated as follows:

$$\text{IC}=\frac{\text{percentage}\text{change}\text{in}\text{energy}\text{use}\text{of}\text{chiller}\text{plant}}{\text{percentage}\text{change}\text{in}\text{input}\text{parameter}}=\frac{\text{OP}-{\text{OP}}_{\text{bc}}}{{\text{OP}}_{\text{bc}}}/\frac{\text{IP}-{\text{IP}}_{\text{bc}}}{{\text{IP}}_{\text{bc}}}$$ (1)

where OP is the new energy use in chiller plant; OP_bc is the base case energy use in chiller plant; IP is the new input parameter value; IP_bc is the base case input parameter value.

The base case value was same as the corresponding condition used to calibrate the pre-retrofit energy model. The advantage of using the above calculation approach is that IC is dimensionless, which can be used for comparison among different parameters.

Table 5 shows the results of sensitivity analysis for the case study buildings. These parameters are ranked according to their absolute value of IC. It can be seen that the four most sensitive parameters affecting energy use are the annual mean dry bulb temperature, chiller COP, AC operating hours and annual mean dew point temperature. Their IC values are at least 1.5 times larger than those of other parameters ranging from the fifth to the seventh, which include the thermostat set point for office premise, occupancy rate for office and SA premises, with the IC values ranging from 0.290 to 0.215.

Other parameters, such as occupant density, lighting load, equipment load, chilled water supply temperature, ventilation rate and infiltration have relatively small effects on the building energy use in comparison with the first seven parameters. This suggests that the ESCO can neglect their impacts on actual energy savings even when a large deviation is observed between the pre- and post-retrofit conditions. It is worth noting that the significance of the parameters may vary in different climatic conditions. For example, the ventilation rate is usually one of the most significant parameters contributing to the energy use of air-conditioning systems. However, for the Hong Kong weather conditions where four seasons are clearly distinct, the change of ventilation rate is insensitive to the total air-conditioning energy use on an annual basis because although the greater fresh air flow rate provides a larger rate of free cooling when the outdoor temperature is cool (thus reducing the energy use for air-conditioning during cool winter days), the saving would be compensated by the increase in air-conditioning energy use during hot summer days.

High nonlinearity was found in several parameters. This means that the value of IC varies significantly from point to point. For instance, the parameter of AC operating hours is more sensitive to energy use when the presumed hour for switching off AC system is toward day-time in comparison to night-time due to the impact of solar radiation. However, the purpose of sensitivity analysis is to eliminate some parameters which are relatively less sensitive to energy use. The exact average IC value and ranking are not important in this study. The issue of high nonlinearity can be neglected when the average value of the most sensitive interval is still much lower than that of other parameters.

3.4. Probability distribution of the selected parameters

Based on the results of the sensitivity analysis, the first seven parameters were considered as the influential parameters and, for them, representative PDF were developed to simulate their yearly variations during the post-retrofit period. The selection of the representative distribution followed the three established tests, namely the Chi-square test, the Kolmogorov–Smirnov (K–S) test, and the Anderson–Darling (A–D) test [21], [26]. The K–S test was used when the sample sizes were less than 30. The Chi-square test and A–D test were employed while the sample sizes equal to 30 or more. All the calculated values from these tests were tested by the corresponding criteria values at the 5% significance level. When the calculated value is less than the critical value at the specified significance level, the assumed distribution can be declared as an acceptable model to describe sample data. For example, the observed data of dry bulb mean temperature (sample sizes = 16) was assumed to be inferred by the normal distribution. In the K–S test, the calculated value of maximum discrepancy between the assumed and observed cumulative frequencies was 0.08, which was less than the critical value of $D_{n=16}^{\alpha =0.05}=0.33$ at 5% significance level. By the K–S test, the normal distribution was verified as an acceptable model at 5% significance level for the dry bulb mean temperature parameter. The test results for all the selected parameters are listed in Table 6 .

Table 6.

Results of Chi-square, K–S and A–D tests and the assumed distribution for the selected parameters.

Parameter(s)	Unit	Distribution	5% level	Mean	95% level	Standard deviation	Chi-square test	K–S test	A–D test	Sample sizes
Building load
Annual mean dry bulb maximum temperature	°C	Logistic continuous	25.24	25.79	26.35	0.34	0.13	0.16	0.37	16
Annual mean dry bulb mean temperature	°C	Normal continuous	22.95	23.45	23.95	0.3	0.13	0.08	0.12	16
Annual mean dry bulb minimum temperature	°C	Logistic continuous	21.02	21.58	22.15	0.35	0.13	0.11	0.3	16
Annual mean dew point temperature	°C	Logistic continuous	18.56	19.25	19.95	0.43	2.0	0.14	0.3	16
AC operating hours (office)a	H	Logistic continuous	17.30	18.75	20.19	0.89	2392.2	0.19	22.2	521
Occupancy rate (office) b	%(Floor)	Triangular continuous	81.1%(50)	90.2%(56)	97.3%(61)	4.9	0.15	0.17	0.34	13
Occupancy rate (SA) b	%(Floor)	Normal continuous	69.9% (20)	81.3%(23)	92.6% (26)	7.06	1.08	0.16	0.45	13
System control and operation
Thermostat set point (office)	°C	Triangular continuous	19.48	21.64	24.43	1.52	2.59	0.054	0.15	61
HVAC Plant
Overall COP of chiller plant after retrofit	–	Triangular continuous	4.031	4.137	4.45	0.089	–	–	–	–

^aThe unit of AC operating hours is in terms of hours, for example, 19:30 = 19.5.

^bAs there is no occupancy rate of individual tower for office and SA premises in the annual report, the mean value of the whole composite buildings was used.

All the parameters above are in term of annual mean.

3.4.1. Annual mean dry bulb temperature and dew point temperature

Weather condition is one of the most critical factors affecting building energy consumption [28]. Although it is well recognised that mean temperature is generally increasing due to global warming and urbanisation [33], considerable variations may still be observed from year to year. For example, the location of this case study, Hong Kong, has a humid sub-tropical climate with four distinct seasons. In summer, the mean outdoor temperature reaches up to 28.7 °C but it can drop significantly to 16.1 °C in winter [34]. The cooling degree-days (CDD) and heating degree-days (HDD) are 3556 and 426 with a base of 18.3 °C, respectively [35]. With such seasonal climate characteristics, the annual mean temperature varied from 22.91 °C to 23.53 °C within 4 years (from 2009 to 2012), and the differences between the numbers of very hot days (daily maximum temperatures ≥33 °C) and cold days (daily minimum temperatures ≤12 °C) for two consecutive years can be as large as 22 days (from 2006 to 2007) and 23 days (from 2007 to 2008) respectively in Hong Kong [36]. This uncertainty in year-round weather conditions can lead to volatility in energy savings for weather dependent retrofit measures.

Based on the latest 16 years’ daily measured data (1997–2012) obtained from the Hong Kong Observatory [36], the four climatic variables, including annual maximum, mean and minimum daily dry bulb temperature and dew point temperature, were assigned to the most representative PDF using a distribution curve fitting technique. It is noted that the variations in diurnal temperature range is also considered in this study. Diurnal temperature range is the temperature difference between the daily maximum and minimum temperature. The change in diurnal temperature range is an indication of the severity of global warming [37].

3.4.2. Occupancy rate for office and SA premises

Occupancy rates in office and SA buildings vary from time to time, especially during the periods of economic growth or downturn. In many EPC projects, the ESCO and host both bear the risk of variations in occupancy, leading to uncertainty in actual energy savings. In this study, a large variation in occupancy rate was observed. In 2003, the average occupancy rate dropped dramatically from 90.5% to 81.3% for the office premises and from 80.2% to 69.6% for the SA premises due to the economic impact of the Severe Acute Respiratory Syndrome (SARS) outbreak in that year, and these figures increased gradually to nearly the highest (office: 94% and SA: 88%) in recent years. In this study, the PDFs of occupancy rate for the office and SA premises were derived from the 11 years’ data (2001–2011) of the developer's annual reports.

3.4.3. Operating hours of AC system for office premise

To control the energy use within budget, the building owners provide tenants with air-conditioning service in fixed periods only. The operating hours of AC system for office premises in Hong Kong vary from buildings to buildings. In general, the AC operating hours is in line with the office working hours, which is typically from 8:30 am to 5:30 pm in Hong Kong. However, overtime working is very common in Hong Kong. There may be frequent requests for extension of AC operating hours, especially when there are changes of tenants. Since the contract period is relatively long in EPC projects (e.g. 4–5 years for chiller replacement), it is reasonable to expect that the operating hours in the first year of an EPC contract would be different from those in the past year. Therefore, the impact of possible extension or reduction of operating hours on the energy saving must be addressed.

However, there are hardly any reliable records or research studies that report the long term variations in the operating hours of AC systems in buildings. An alternative way to estimate this variation is based on the AC operating hour data given by real estate agents. This approach assumed that the operating hours would be dependent on tenants’ preference and relative negotiation power. As such, this study was based on the information from Primeoffice to determine the PDF of operating hours. Primeoffice is a property search website with the database of over 1800 Hong Kong office buildings. It provides the building information such as typical floor area, air-conditioning hours and system types (e.g. central AC, split type) [38]. Based on the Primeoffice database, the PDF of operating hours was determined. As real estate agents operate in a very competitive environment in Hong Kong and they pay particular attention to solicit patronage with good services, the data on this website is assumed to be adequate for the demonstration of methodology rather than reporting the actual results.

3.4.4. Thermostat set point for office premises

The choice of indoor air temperature set-point can substantially affect the energy consumption of chiller plant [39], [40]. The indoor air temperature setting can vary significantly as different occupants could have different thermal sensation to indoor environment. In the recent years, the government launched the “Energy Conservation Charter” programme to encourage occupants to raise the indoor temperature to 25.5 °C for energy savings [41], but the thermostat set-point is not often adjusted as recommended. Mui and Wong's field survey [42] on 61 offices found that the average air temperature in typical office buildings is 23 ± 1.5 °C.

The PDF of thermostat set point was determined based on the survey results of Mui and Wong [42]. Despite the fact that this study was not focused on the variation of indoor air temperature in a single development as this case study represents, the finding was applicable since in general the decision on thermostat set point would be in relation to occupants’ behaviours, instead of building characteristics and location.

3.4.5. Overall COP of chiller plant

Coefficient of performance (COP) is a primary indicator to reflect the actual energy efficiency of chillers; the higher the COP of chillers is, the less energy is consumed to provide the same amount of cooling. The performance of chiller plant will deteriorate with time of use due to two main factors: (1) normal wear and tear over a long operating period; and (2) contamination of chilled water tubes. Masaaki et al. [43] studied the degree of deterioration of chiller performance after 5 years of operation. It was found that no performance deterioration was observed for the first 21 months. After that, the COP deteriorated at an annual average of 2.53%. The study also suggested that 7.6% of chiller performance could be recovered when preventive maintenance, such as tube chemical cleaning, is regularly performed.

The PDF of COP is difficult to determine, because the variations in the operating COP due to equipment deterioration depend on a number of factors, including operating hours, operation conditions (whether it is close to the standard operating conditions), the frequency and quality of maintenance work. As the maintenance is part of the scope of the contract in most EPC projects, the ESCO has an incentive to ensure that the plant performance shall be maintained at the expected COP. When the plant performance is much lower than the expected COP, active maintenance, such as tube chemical cleaning, replacement of parts, would be carried out to avoid energy saving shortfall. In this case study, the existing chillers were still used after the retrofit. Based on the previous study of existing chiller performance [43], an annual average of 2.53% COP deterioration rate was assumed for the worst case while 7.6% improvement of chiller performance will be used for the best case (assuming with high quality of maintenance work during the contract period). A triangular distribution was assumed for the PDF of COP. The most likely value in this PDF will be set equal to the existing COP.

3.5. Simulation of energy saving

Fig. 4 illustrates the calculation procedures of 10,000 simulation runs. A risk analysis tool based on Monte Carlo simulation (@Risk) [44] was utilised to generate 10,000 common data sets of 7 input parameters for two calibrated building energy models. The purpose of generating this common data set is to simulate all the possible cases for the yearly post-retrofit period conditions taking into account the variations in these selected parameters.

Fig. 4.

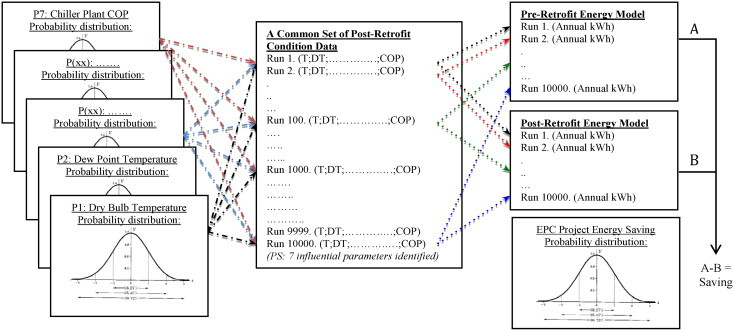
The procedures for calculation of energy saving shortfall (Guaranteed model) using Monte Carlo and EnergyPlus simulation.

In EnergyPlus, the Hong Kong typical meteorological year (TMY) weather data file is used to represent the long-term typical weather condition over a year. This weather file consists of 8760 hourly climatic variable data, including dry bulb temperature, wet bulb temperature, solar radiation, wind speed, etc. In order to simulate all the possible yearly weather conditions during the post-retrofit period, this Hong Kong TMY weather file was modified and reproduced 10,000 times in accordance with the results of each Monte Carlo simulation run. The algorithm of weather adjustment is based on a “morphing” method, developed by Belcher et al. [27] who constructed design weather data for future climates. The main advantage of this method is that it preserves the characteristics of standard weather pattern after modification. In the “morphing” method, three operations: (1) a shift; (2) a liner stretch; and (3) a shift and a stretch, as listed in Eqs. (2) to (4) are used to modify the weather file.

$$x=x_0+\Delta x_y$$ (2)

$$x={\alpha }_y{x}_0$$ (3)

$$x=x_0+\Delta x_y+{\alpha }_y\times \left(x_0-{〈x_0〉}_y\right)$$ (4)

where x ₀ is the existing hourly climatic variable; Δx _y is the absolute change in yearly mean climatic variable for the year y; α _y is the fractional change in yearly mean climatic variable for year y; 〈x ₀〉_y is the climatic variable x ₀ average over year y.

In this study, the hourly dry bulb temperature (DBT) of the existing Hong Kong TMY weather file was morphed by a combination of a shift and a stretch to generate another set of Hong Kong TMY weather file. The equation for morphing is shown as follows (Eq. (6)):

$$\alpha db{t}_y=\frac{\Delta TMA{X}_y-\Delta TMI{N}_y}{{〈db{t}_{0\text{max}}〉}_y-{〈db{t}_{0\min }〉}_y}$$

$$dbt=db{t}_0+\Delta TEM{P}_y+\alpha db{t}_y\times \left(db{t}_0-{〈db{t}_0〉}_y\right)$$

where 〈dbt _0max〉_y, 〈dbt ₀〉_y and 〈dbt _0min〉_y  = yearly mean daily maximum, average and minimum temperature of EnergyPlus weather file data respectively; ΔTMAX _y, ΔTEMP _y and ΔTMIN _y  = absolute change in yearly mean daily maximum, average and minimum temperature of Hong Kong weather data respectively; dbt ₀  = existing hourly temperature of EnergyPlus weather file.

A stretch method was adopted to adjust the current hourly dew point temperature (DPT). As required in EPW weather file, the other climatic variable—relative humidity (RH), was calculated from the hourly value of DBT and DPT using ASHRAE psychrometric formulae [35]. All the morphing processes involved above were automatically performed using Excel VBA. By using the morphing method, a set of 10,000 modified weather files was developed, taking into account the yearly weather variations.

After the generation of 10,000 TMY weather files, jEPlus, an open-source parametric analysis tool for managing the EnergyPlus simulations, was used to automatically substitute the base case value of two calibrated models with the results of Monte Carlo simulation. Based on the representative PDF of those seven influential parameters, a group of values representing one of the post-retrofit conditions is randomly generated using the Latin Hypercube Sampling method (please refer to Fig. 4). To instruct jEPlus running all the possible conditions of the post-retrofit period, a CSV-styled text file containing 10,000 different values of each influential parameter was created. By incorporating the calibrated energy model, TMY weather files and a CSV-styled text file, jEPlus can simultaneously perform the eight instructed simulations at maximum in each run, and the simulation results are automatically grouped together for a probabilistic analysis of actual energy savings [45]. The 20,000 EnergyPlus iterations (10,000 iterations for each model) were performed in 10 computers with two quad-core processors, taking 8 h to complete the calculation. In this demonstration, 4 timesteps per hour was used and the conduction transfer function was adopted as a heat balance algorithm in EnergyPlus. A point worth noting is that the common data set was applied to all selected parameters for both models, except the parameter “Overall COP of chiller plant” in the pre-retrofit model, which remains unchanged as the pre-retrofit condition.

4. Results and discussion

4.1. Probability of energy saving shortfall

Fig. 5, Fig. 6 show the actual energy saving for all possible combination of the selected parameters and the fitted distributions of energy savings in the case study buildings. The possible energy savings after 1 year retrofit period ranges from 393,000 kW h (2.86%) to 1098,000 kW h (10.8%) with 90% statistical significance, which is best fitted by a weibull distribution with a mean 711,054 kW h (5.18%) and a standard deviation 215,182 kW h (1.57%). This suggests that the variations in actual yearly energy savings can be significant. The maximum energy savings can be 3 times higher than the minimum one. The results also provide information on the probability of energy saving shortfall when a certain amount of energy savings is anticipated. For example, only by a 46.5% chance the ESCO will successfully achieve the mean value of energy saving per year 711,054 kWh (5.18%) for the replacement of heat rejection system in this study. Further studies are needed to benchmark this sort of probability values when data on more buildings are available, but since the objective of this paper is to demonstrate a plausible methodology, it still serves its purpose.

Fig. 5.

Probability density of energy savings in the case study.

Fig. 6.

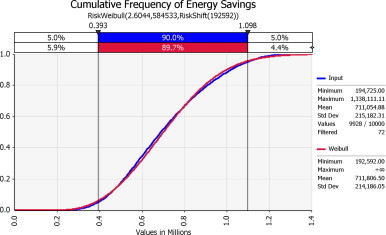
Cumulative frequency of energy savings in the case study.

5. Conclusions

This paper proposes a simulation-based method to evaluate the probability of energy saving shortfall taking into account the variations in the influential parameters. A real case study of replacement of heat rejection system for a central chiller plant in Hong Kong is used to demonstrate the application of this probabilistic method. The result shows that the possible energy savings after a 1-year retrofit period can range from 393,000 kW h (2.86%) to 1098,000 kW h (10.8%) with 90% statistical significance. This assessment method can be useful for evaluating the performance risks when certain amount of energy saving is guaranteed for retrofit measures.

It should be noted that the confidence of the result relies on the representativeness of two building energy models, the selection of proper ranges and intervals for sensitivity analysis, as well as the goodness-of-fits of probabilistic distribution functions for selected parameters. Besides, this study only focuses on the energy savings from the retrofit work. However, the financial benefits from EPC projects also include the avoided-cost savings, for instance, a reduction in operation and maintenance costs. The future works on the risk assessment in EPC projects should include the variations in such avoided-cost savings. With the use of this proposed methodology, the risks of EPC will be better understood and managed.