Can rewiring strategy control the epidemic spreading?

Abstract

Relation existed in the social contact network can affect individuals’ behaviors greatly. Considering the diversity of relation intimacy among network nodes, an epidemic propagation model is proposed by incorporating the link-breaking threshold, which is normally neglected in the rewiring strategy. The impact of rewiring strategy on the epidemic spreading in the weighted adaptive network is explored. The results show that the rewiring strategy cannot always control the epidemic prevalence, especially when the link-breaking threshold is low. Meanwhile, as well as strong links, weak links also play a significant role on epidemic spreading.

Highlights

• •A novel epidemic spreading model in weighted adaptive network is proposed.
• •The relation intimacy among individuals is considered in rewiring strategy.
• •The effect of the modified rewiring strategy is evaluated.
• •As well as strong links, weak links play an important role in the epidemic spreading.

1. Introduction

Recent global infectious diseases, including H1N1 (Swine Influenza), SARS (Severe Acute Respiratory Syndrome), H7N9 (Avian Influenza) and Ebola (Ebola virus disease), have caused major public health threats due to the potential high mortalities and substantial economic impacts. To analyze the spreading process of infectious diseases and make better decisions on the controlling strategy, epidemic spreading process is usually modeled based on complex networks, with nodes representing individuals and links denoting their interactions  [1], [2], [3].

Meanwhile, facing the epidemic threat, individuals may take some self-protective actions such as reducing outside activities, wearing face masks, washing hands frequently, taking the vaccination and so on  [4], [5], [6], [7]. Such self-protective actions will influence the network topology and may significantly change the predicted course of epidemic dynamic  [8], [9]. Based on the Susceptible–Infected–Susceptible (SIS) model, Gross et al. proposed the adaptive network to depict the impact of the dynamic change of network structure on epidemic spreading  [10]. In their model, the network structure changed all the time according to the states of neighboring nodes and this in turn affected epidemic dynamics. Specifically, the susceptible individuals might protect themselves by rewiring their links. The susceptible node would break the link (SI link) with the infected node based on a fixed probability and form a new link with another randomly selected susceptible node. Following this, there are many literatures studying the epidemic propagation on an adaptive network. Shaw et al. analyzed the epidemic spreading process in adaptive networks based on Susceptible–Infected–Recovered–Susceptible (SIRS) model  [11]. Lagorio et al. studied the critical effect of quarantine on the epidemic propagation on an adaptive social contact network  [12]. Guo et al. proposed a continuous-time Adaptive Susceptible–Infected–Susceptible (ASIS) model to study the interplay between epidemic dynamics and the dynamics of network structure  [13]. Song et al. introduced a new preferentially reconnecting edge strategy of adaptive networks depending on spatial distance. For this rewiring strategy, when an SI link was broken, the S node would reconnect to a random node with probability $p$ and a neighboring node with probability 1-$p$. They found that a smaller value of probability $p$ led to a slower epidemic spreading  [14].

However, prior works have several main limitations. First, rewiring strategy in adaptive network has been accepted as an effective strategy to suppress the epidemic spreading  [15], [16]. Many factors that influence the rewiring strategy were explored  [14], [17]. However, interpersonal relations, generally present in the social network, are seldom considered. Though relation has attracted more and more attention in the static network research  [18], [19], it is still unclear how the relation affects the epidemic propagation in adaptive networks. Second, the rewiring mechanism of adaptive network models  [20] includes two processes, that is, link-breaking and link-creating, which are explored by most studies. But these studies only considered the influencing factors of link-creating process (such as spatial space  [14], [17]), and the influencing factors related with link-breaking process were ignored. In this study, we incorporated interpersonal relation as the influencing factor of link-breaking process. Thus the link would not be broken randomly but according to the relation intimacy between two nodes that lie in two sides of a link. Third, vaccination is an important fundamental method to block transmission of diseases for the fixed network topology  [21], [22], [23], [24], [25]. Although some previous literatures studied the selection method of vaccinated nodes and explored the effect of vaccination strategy in adaptive networks  [26], the interplay between rewiring strategy and vaccination is less investigated.

Incorporating the interpersonal relations and vaccination strategy, this paper develops a novel epidemic spreading model in weighted adaptive network. We divide our model into three processes, including epidemic spreading process, network evolution process and learning process. Then we study the epidemic spreading in adaptive network based on relation intimacy. Our results demonstrate that the rewiring strategy has a close relationship with the epidemic spreading, and this strategy cannot always suppress the disease, which is different from some previous studies  [15], [27]. When breaking some weak links, the epidemic size is still very large. However, as strong links gradually being cut, the epidemic can be controlled effectively. Meanwhile, the results also show that weak links play an important role on the epidemic spreading as well as strong links.

This study contributes to the literature in three important aspects. First, this study proposes a new model to examine the influencing factors of epidemic spreading in adaptive networks. The new model consists of three main processes, which describe the epidemic spreading, network structure adjustment and individuals’ strategy learning respectively. Second, interpersonal relation has significant influence on individuals’ behavior. The proposed model takes the interpersonal relation into consideration and analyzes the impact of interpersonal relation on epidemic spreading. Third, this study also investigates the interplay between rewiring strategy and vaccination strategy. The result shows that, without vaccination, the disease cannot be suppressed very well only through rewiring strategy.

The rest of this paper is organized as follows. In Section  2, we describe the proposed model in detail, including epidemic spreading process, network evolution process and learning process. The relationship between rewiring strategy and epidemic spreading is investigated in Section  3. Finally, we conclude this study and discuss future work in Section  4.

2. Model

Many infectious diseases, such as influenza, are hard to be eradicated and may spread for many seasons. Inspired by prior studies  [28], [29], in this paper, each step is divided into three processes, namely, epidemic spreading process, network evolution process and learning process. Schematic of the proposed model is given in Fig. 1 .

Fig. 1.

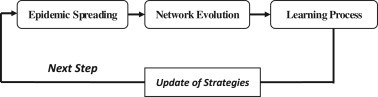
Schematic of the proposed model.

At the beginning of a season, each susceptible individual can choose vaccination or not. Normally only a small part of population ${\rho }_V^{\prime }$ takes vaccination. In this study, we assume that the vaccine is not fully effective and the successful rate of the vaccination is $e$.

A vaccinated individual ($V$) will pay a cost $v$ that accounts for not only the monetary cost of the vaccine, but also the side effect. If an individual gets infected during the epidemic season, he/she has to pay a cost $r$. Obviously, $r>v>0$. Without loss of generality, we take the cost of being infected as $r=1$. Because of the imperfect vaccine, the population will have the following four types of individuals:

• (1)Vaccinated individuals that remain healthy ($V_e$) during the epidemic season have payoff $\pi =-v$.
• (2)Vaccinated individuals that were infected ($V_i$) during the epidemic season have payoff $\pi =-v-r$.
• (3)Individuals that are not vaccinated and remain healthy during the epidemic season have payoff $\pi =0$.
• (4)Those individuals that are not vaccinated but, unfortunately, are infected are assigned a payoff $\pi =-r$.

2.1. Epidemic spreading

We employ a weighted Susceptible–Infected–Recovered (SIR) epidemic model to describe the epidemic spreading process. The nodes in the network can be divided into three states: susceptible state ($S$), infected state ($I$) and recovered state ($R$). Besides, contact weight is defined to measure the relation closeness level. The larger the weight is, the closer two individuals’ relation is. Initially, a small part of nodes ($I_0$) are randomly set to be infected and other nodes are susceptible. In each season, we assume that the probability of a susceptible individual getting infected through an SI link with unit weight (${\omega }_1$) is $\beta$. So for any SI link with weight $\omega$, the infection probability is $\beta \left(\omega \right)=1-{(1-\beta )}^{\omega /{\omega }_1}$. Without loss of generality, we set ${\omega }_1=1$ and have $\beta \left(\omega \right)=1-{(1-\beta )}^{\omega }$. If a susceptible node $i$ has $\left|B_i\right|$ infected neighbors, the infected probability is $\lambda =1-{\prod }_{j\in B_i}[1-\beta \left({\omega }_{ij}\right)]$, where ${\omega }_{ij}$ is the link weight between node $i$ and its infected neighbor $j$. In this paper, we investigate two types of weight distributions: uniform distribution (U(0, 2)) and normal distribution (N(1, 1/3))  [30]. At the same time, the probability that the infected individual becomes recovered is $\mu$. Once the infected node is recovered, it will not be infected again until next season.

2.2. Network evolution

The network evolution is caused by rewiring strategy. To mitigate the possible infection risk of epidemic diseases, individuals will adjust their behaviors and break the connection with the infected nodes, namely, link-breaking [Fig. 2 (a)]. Meanwhile, they will form a new link to another randomly selected susceptible or recovered node  [10], that is, link-creating [Fig. 2(b)].

Fig. 2.

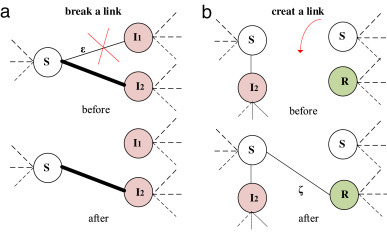
Link rewiring based on the node state. The thickness of link represents the size of weight. (a) Break the link between the susceptible node ($S$) and the infected nodes ($I_1,I_2$) based on the weight; (b) Create the link between susceptible node ($S$), recovered node ($R$) and susceptible node ($S$).

2.2.1. Link-breaking process

Previous adaptive network models normally take the direct breaking of SI links as an effective way to control the epidemic spreading. However, an individual usually has some inevitable contacts with those people of closer relationships, which implies a different link-breaking strategy. In this model, we propose a new link-breaking strategy which contains an important parameter, that is, link-breaking threshold (${\theta }_o$). ${\omega }_{\max }$ represents the maximum value of the weight. The links with the weights that are higher than the link-breaking threshold will be preserved. Otherwise, the SI links will be broken with a probability $\epsilon$. The new link-breaking probability $\tau$ is given as follows.

$$\tau =\{\begin{array}{cc}0\hfill & \text{when }\omega \in ({\theta }_o{\omega }_{\max },{\omega }_{\max })\text{,}\hfill \\ \epsilon \hfill & \text{when }\omega \in (0,{\theta }_o{\omega }_{\max })\text{.}\hfill \end{array}$$ (2.1)

2.2.2. Link-creating process

Because of the imperfect vaccine in the population, the network includes successful vaccinated individuals ($V_e$) and unsuccessful vaccinated individuals ($V_i$). Since the $V_e$ nodes cannot be infected again, they can be regarded as $R$ nodes. In the similar way, $V_i$ nodes can still be infected, so they are treated as $S$ nodes. Therefore, the susceptible node can connect $R$ nodes with probability $\zeta$ or S nodes with probability $1-\zeta$   [10].

2.3. Learning process

After the epidemic spreading process and network evolution, individuals will evaluate their neighbors’ payoffs and update their strategy by imitating their neighbors’ strategies (vaccination or not). The individual randomly chooses one neighbor and decides whether to adopt this neighbor’s strategy or not. Here, we employ one of the most used method, Fermi rule  [31], [32], to calculate the learning probability, which represents the probability that node $j$ adopt the strategy of the neighbor $i$:

$$P(s_j\to s_i)=\frac{1}{1+exp[-\kappa ({\pi }_j-{\pi }_i)]}\text{.}$$ (2.2)

Where $s_i$ and ${\pi }_i$ denote the strategy and payoff of individual $i$ respectively. $\kappa$ characterizes the strength of selection: small $\kappa$ ($\kappa \ll 1$) means random selection and large $\kappa$ ($\kappa \gg 1$) represents strong selection. Here we set $\kappa =1$   [28]. The update of strategies takes place simultaneously for all the individuals. Once their new strategies are taken, a new step begins.

3. Simulation results and discussion

In this section, we verify our model by simulation and present the results. Initially, we randomly choose 1% and 5% of all individuals to be infected and vaccinated. Without specific statement, we use the number of final recovered nodes, $R\infty$, to denote the epidemic size. The larger $R\infty$ is, the severer the disease is. Besides, ${\rho }_S$, ${\rho }_I$, ${\rho }_R$, ${\rho }_V$ are set to describe the fractions of susceptible, infected, recovered and vaccinated nodes, respectively. The simulation will be ended when no infected individuals exist in the network, and each data is obtained by averaging over 50 independent runs.

We first apply the model in square lattices network  [33] (nodes $N=40\times 40$) with uniform weight distribution. The impact of the link-breaking threshold on the epidemic size ($R\infty$) and the fractions of six links (SS, SI, SR, II, RI and RR) are shown in Fig. 3 . The term “Proportion of different links” in Fig. 3 denotes proportion of six links with each ${\theta }_o$. This term in other figures has the similar meaning. Clearly, the whole figure can be divided into three regions by two red dash lines based on the change of the epidemic size. In region I (${\theta }_o$ lies in the interval $\sim [0,0.65]$), the infection keeps in the high level as the increase of ${\theta }_o$, which points out that breaking small weight links does not influence the epidemic size. It is consistent with the real contact network. The susceptible individuals seldom contact with infected nodes on the end of small weight links, so breaking those links hardly helps to control the disease spreading. The epidemic size becomes smaller and smaller when ${\theta }_o$ lies in the middle range ($\sim [0.65,0.9]$). The disease can be controlled very well at ${\theta }_o=0.9$. That is because, when ${\theta }_o$ increases, some large weight SI links are cut and those infected individuals are the ones that the susceptible often or inevitably contact with. But when ${\theta }_o>0.9$ (region III), the epidemic size hardly changes. After breaking plenty of connections with the infected, SI links are sparse and infected individuals are relatively isolated, which cut off the disease spreading path. Thus the impact of the SI link removal process on lowering epidemic size gradually diminishes. Some previous literatures  [15], [27] mainly concluded that rewiring strategy can suppress the disease completely. However, different from these studies, our results exhibit that the rewiring strategy cannot always control the epidemic based on the above description. At the same time, there exist two critical points for ${\theta }_o$ (one is about ${\theta }_o^1=0.65$ and the other is about ${\theta }_o^2=0.9$), which can be treated as an important index for effective link removal. According to these critical points, Fig. 3 can be divided into two types of regions. In regions I and III, the epidemic size hardly changes as ${\theta }_o$ increases and these regions are defined as “ineffective region” for controlling epidemic spreading. The region II, which can effectively lower the epidemic size, is called “effective region”.

Fig. 3.

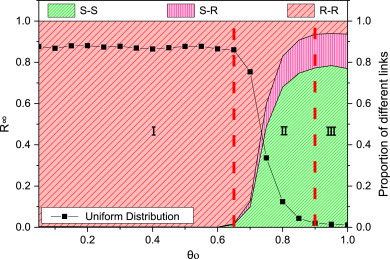
How do the epidemic size ($R\infty$) and the fractions of the six links (SS, SI, SR, II, IR and RR) change with the link-breaking threshold in square lattice network under uniform weight distribution. Parameters are set to be $N=40\times 40$, $\beta =0.03$, $\mu =0.02$, $\epsilon =0.8$, $\zeta =0.5$, ${\rho }_V^{\prime }=0.05$, $e=0.5$, $v=0.2$, $\kappa =1$.

Furthermore, to better understand the impact of rewiring strategy on the epidemic spreading, we consider node and link dynamics of four kinds of link-breaking thresholds in lattice network with uniform weight distribution. From ${\theta }_o=0.3$ (Fig. 4 (a)) to ${\theta }_o=0.8$ (Fig. 4(c)), the time that the density of recovered nodes (${\rho }_R$, green upper triangle symbols) tends to be stable gradually shifts (from A to C, where A corresponds to the time 350, C corresponds to the time 1200). That suggests that the disease spreads out more and more difficultly. Whereas when ${\theta }_o=0.95$, the epidemic cannot outbreak. Besides, the proportion of RR links (red slash area) goes up with time, which demonstrates that $R$ nodes are more inclined to be clustered. The cluster of $R$ nodes also helps to control the disease propagation to some extent. In Fig. 4(d), since plenty of large weight links are removed, the disease cannot spread out and the infection (${\rho }_R$) keeps in the low level.

Fig. 4.

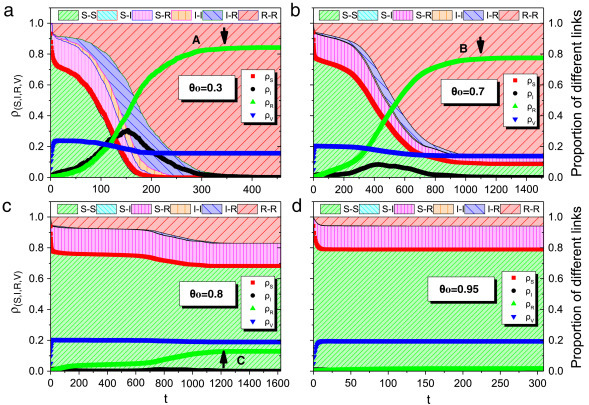
The final fraction of four kinds of nodes (susceptible, infected, recovered and vaccinated node) and six types of links (SS, SI, SR, II, IR and RR) with different link-breaking thresholds in square lattice network under uniform weight distribution. The parameters are set as $N=40\times 40$, $\beta =0.03$, $\mu =0.02$, $\epsilon =0.8$, $\zeta =0.5$, ${\rho }_V^{\prime }=0.05$, $e=0.5$, $v=0.2$, $\kappa =1$.

With respect to link strength, disparate types of links play disparate roles in epidemic spreading  [34]. To further explain the above results, it is imperative to investigate the epidemic spreading when breaking the same number of SI links with different weight. $E_{[{\omega }_1,{\omega }_2]}$ is defined as the set of SI links with weight in the interval $\sim \left[{\omega }_1{\omega }_2\right]$. Here we take lattice network with uniform distribution (U(0, 2)) as an example. In this type of weighted network, different weighted links are distributed uniformly in the network. The number of links in $E_{[{\omega }_1,{\omega }_2]}$ is approximately equal to that of $E_{[{\omega }_3,{\omega }_4]}$ (where ${{\omega }_2-{\omega }_1=\omega }_4-{\omega }_3$). Fig. 5 shows the change of the density of recovered nodes (${\rho }_R$) with time when SI links in $E_{[{\omega }_1,{\omega }_2]}$ are removed. In Fig. 5, A, B and C represent the time that ${\rho }_R$ reaches the stable state when the SI links in the corresponding set are removed. For example, in the subpanel (a), the point A represents that in the time 350 ${\rho }_R$ reaches the stable state when the links in $E_{[0.6,1]}$ are removed. It is found that the value of ${\rho }_R$ in the stable state hardly changes as the increase of weight of removed SI links, which indicates that only breaking large weight links cannot lower the epidemic size (For instance, the stable values of ${\rho }_R$ in Fig. 5(a) are almost the same for three different scenarios). Moreover, when some large weight SI links are broken, it is more effective to slower the epidemic spreading, which can be exhibited from the time that ${\rho }_R$ tends to be stable (such as A, B and C in Fig. 5(a) and (b)). But the gap of three time points in Fig. 5(a) and (b) is small. Therefore, we just show two cases ($E_{[0,1.2]}$ and $E_{[0.8,2.0]}$) in Fig. 5(c) and one side of weight intervals takes the extremum, which exhibit the different stable time of ${\rho }_R$ (A and C) more clearly. Comparing subpanels (a) and (b) in Fig. 5, we can find that breaking more SI links can slower the epidemic spreading more effective, because A corresponds to the time 350 and 400 in subpanels (a) and (b) respectively. We also find that when more weak links are broken, the stable time will be longer and the disease is suppressed more effectively. For instance, C in subpanel (a) is equivalent to the time 500, and C in subpanel (b) is equivalent to the time 600. Besides, when the set $E_{[0.2,1.0]}$ in subpanel (b) is expanded to $E_{[0,1.2]}$ in subpanel (c) from two sides or in other words more weak and strong links are removed, the effect of disease control is much better. Since the point A in subpanel (b) is approximately equal to the time 400, while A in subpanel (c) reaches to the time 500 and the difference can be exhibited more obviously from C in subpanels (b) and (c). The above results suggest that both small and large weight links (or we can treat them as weak and strong links) play important roles on epidemic spreading, which has been concluded by many previous literatures  [34], [35]. Based on previous studies, we try to show the disparity between strong links and weak links. The difference may be that strong links lead to high infection rate (infection rate $\beta \left(\omega \right)$ increases with weight $\omega$) and contribute to the epidemic spreading, while the weak links mainly stabilize the network structure  [34], [35]. Therefore, when ${\theta }_o$ lies in the interval $\sim [0,0.65]$, rewiring strategy just destroys the stability of the network. As ${\theta }_o$ increases, rewiring strategy rapidly lowers susceptible individuals’ infection rate by removing strong links, which results in disease control.

Fig. 5.

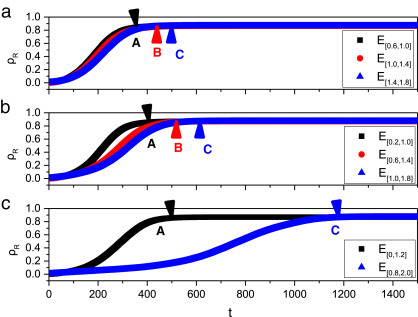
The impact of cutting SI links in the similar interval on epidemic spreading. The parameters are set as $N=40\times 40$, $\beta =0.03$, $\mu =0.02$, $\epsilon =0.8$, $\zeta =0.5$, ${\rho }_V^{\prime }=0.05$, $e=0.5$, $v=0.2$, $\kappa =1$.

Previous studies have shown that the contact patterns can dramatically influence the disease dynamics  [36], [37], so we also verify the proposed model on other types of networks. For this purpose, we apply our model with two kinds of weight distributions (uniform distribution and normal distribution) on different networks including the square lattice network, the Erdös–Rényi (ER) network  [38], the Barabási–Albert (BA) network  [39] and Watts–Strogatz (WS) network  [40]. Fig. 6 exhibits that, in despite of disparate degree and weight distribution, the dynamic relation between epidemic size and ${\theta }_o$ is similar to the result in Fig. 3.

Fig. 6.

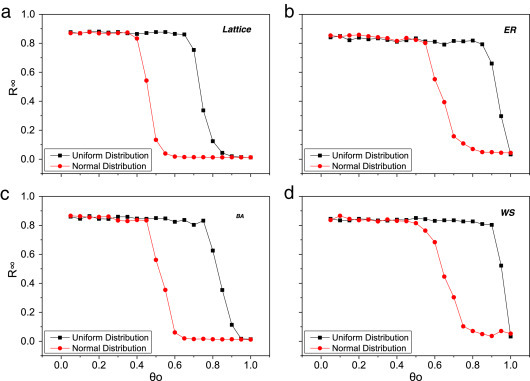
Insensitivity to the weight distribution and network structure. The parameters are set as $\beta =0.03$, $\mu =0.02$, $\epsilon =0.8$, $\zeta =0.5$, ${\rho }_V^{\prime }=0.05$, $e=0.5$, $v=0.2$, $\kappa =1$. The average degree of the lattices, ER network, BA network and WS network are all set to be 4. The sizes of the ER, BA and WS networks are set to be $N=1000$ and the square lattice is $N=40\times 40$.

Although the main results are qualitatively universal, there are still some quantitative differences for different types of networks with two weight distributions. (i) In ER, BA and WS networks, region II appears in a certain range of ${\theta }_o$. Taking the case of BA network with uniform weight distribution in Fig. 6(c) as an example, rewiring strategy could effectively block the disease when ${\theta }_o$ lies in a range between 0.75 and 0.95; (ii) the critical value of ${\theta }_o^1$ with normal weight distribution is smaller than that with uniform weight distribution. For instance, ${\theta }_o^1$ is about 0.45 in BA network with normal weight distribution, whereas ${\theta }_o^1$ ​approximate is equal to 0.75 with uniform weight distribution. (iii) In Fig. 6(b) and (d), there is no region III in the ER and WS networks with uniform weight distribution, which may be related to the coaction of special network structure and weight distribution.

The initial vaccination rate, vaccine effective rate and the cost of vaccine may have impact on the disease propagation   [41], [42], so we investigate the stability of the results under different kinds of vaccine in square lattice network with uniform weight distribution. Each subpanel in Fig. 7 is associated with a given ($v$, $e$). As a result, the similar results like Fig. 3 come out, but there are some quantitative differences between the results. First, the epidemic size becomes small with the increase of initial vaccination rate (${\rho }_V^{\prime }$) in each subpanel. For example, when $v=0.2$ and $e=0.2$  (Fig. 7(a)), the blue triangle symbols (${\rho }_V^{\prime }=0.08$) is lower than the black square symbols (${\rho }_V^{\prime }=0.02$) as ${\theta }_o$ is small. Second, when $v$ is fixed (such as $v=0.2$), the final recovered density ($R\infty$) gradually reduces as vaccine effective rate ($e$) increases. The main reason resulting in the decline of epidemic size is that more rational individuals prefer to take high effective vaccine. Third, when $v$ gets larger (from 0.2 to 0.8), less individuals incline to take vaccination and different initial vaccination rate (${\rho }_V^{\prime }=0.2$, 0.5, 0.8) leads to more similar epidemic size with small ${\theta }_o$. Especially, when $e=0.2$ and ${\rho }_V^{\prime }=0.02$ (the black square symbols in Fig. 7(a), (d), (g)), the disease can only be controlled to some extent even with high link-breaking threshold, especially when $v=0.8$. That is because, compared with expensive but low effective vaccine, most individuals prefer to low-cost strategy, namely, rewiring strategy. According to the above analysis, we can conclude that, without vaccination, the disease cannot be suppressed very well only through rewiring strategy, which implies that vaccination plays an important role on lowering the epidemic size.

Fig. 7.

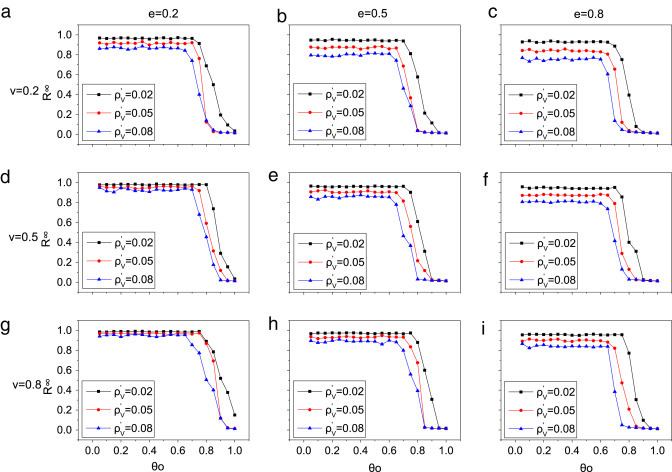
The effect of the vaccination in square lattice network with uniform weight distribution. For each of the 9 panels, the $x$-axis and $y$-axis are $\theta o$ and $R\infty$ respectively. In each subpanel, top-to-bottom in sequence is for the case of ${\rho }_V^{\prime }=0.02$ (black square symbols), ${\rho }_V^{\prime }=0.05$ (red circle symbols), ${\rho }_V^{\prime }=0.08$ (blue triangle symbols). The total population $N=40\times 40$, and other parameters were $\beta =0.03$, $\mu =0.02$, $\epsilon =0.8$, $\zeta =0.5$, $\kappa =1$.

The network evolution, caused by rewiring strategy (link-breaking and link-creating strategy), may affect the epidemic spreading  [43], [44]. Results presented in Fig. 8 clearly display that under different link-breaking probability $\epsilon$ and reconnecting probability $\zeta$, “ineffective region” and “effective region” still appear and our results are stable. Besides, we observe that larger link-breaking probability ($\epsilon$), inducing lower critical value (${\theta }_o^1$ and ${\theta }_o^2$), may speed up the extinction of disease.

Fig. 8.

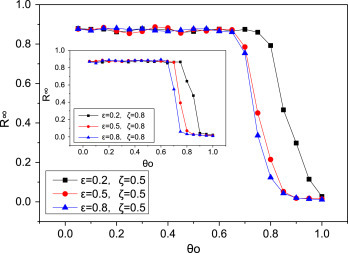
The effect of the link-breaking probability $\epsilon$ and reconnecting probability $\zeta$ in square lattice network with uniform weight distribution. Top-to-bottom in the panel is for the case of $\epsilon =0.2$, $\zeta =0.5$ (black square symbols), $\epsilon =0.5$, $\zeta =0.5$ (red circle symbols), $\epsilon =0.8$, $\zeta =0.5$ (blue triangle symbols). The inset shows the result with the same $\epsilon$ and different $\zeta (\zeta =0.8)$. The parameters are set as $N=40\times 40$, $\beta =0.03$, $\mu =0.02$, ${\rho }_V^{\prime }=0.05$, $e=0.5$, $v=0.2$, $\kappa =1$.

4. Conclusions and future work

Spontaneous behavioral responses to epidemic situation have significant impacts on disease spreading. Therefore, incorporating human behavior into epidemiological models could improve models’ utility in mimicking the reality and studying controlling measures  [45], [46], [47]. Meanwhile, such human behaviors influence the network topology and may significantly change the predicted course of epidemic dynamic. The adaptive network studied by many scholars depicts the impact of the dynamic change of network structure on epidemic spreading very well. However, most existing literatures of adaptive network ignore some important factors that generally exist in the social network, such as interpersonal relations. In this paper, considering individuals’ contact relations, we proposed a new epidemic propagation model to study how the rewiring strategy affects the epidemic spreading. We divided our model into three processes, that is, epidemic spreading process, network evolution process and learning process. In the first process, a weighted SIR model was given to describe the epidemic propagation. In network evolution process, we introduced a new rewiring strategy which took individuals’ relations into consideration. The link-breaking threshold parameter was given to describe the extent to which relation can be broken. Finally, susceptible individuals could evaluate their neighbors’ payoffs and update their strategies in the last process. Fermi rule was introduced to calculate their learning probability.

Our results show that rewiring strategy has an obvious impact on the epidemic spreading. Unexpectedly, regarding disease control, rewiring strategy does not always work. When ${\theta }_o$ is small, some weak links that susceptible individuals seldom connect with are removed, which does not influence the epidemic spreading. This is the reason why the infection remains at a high level. However, as the gradual increase of ${\theta }_o$, rewiring strategy rapidly lowers susceptible individuals’ infection rate by cutting strong links, which results in the decline of epidemic size. Besides, the importance of different types of links is also exhibited in our research. As well as strong links, weak links play an important role in the disease spreading. Moreover, our results are insensitive to network topology, weight distribution and vaccination strategy.

However, there are still some limitations for our research. First, we use the link weight to define the relation closeness level among individuals and study the model with two weight distributions. While there are some other ways to measure the relation intimacy  [48], [49] and how to measure the relation is also a research issue. Second, as a kind of self-protective actions, rewiring strategy is a complex pattern and affected by many factors. Our research just considers the relation intimacy, which may miss some meaningful details. Third, although the link-creating process is considered in this paper, much effort is put on the effect of link-breaking process. Future work can study the influence of link-creating mechanism on the epidemic spreading. Finally, real data will be helpful to evaluate the correctness and generality of the proposed model. Limited by the attainability of real data, we did not validate the proposed model with real data. Future work can find appropriate real data and evaluate the proposed model.