Characterization of expiration air jets and droplet size distributions immediately at the mouth opening

Abstract

Size distributions of expiratory droplets expelled during coughing and speaking and the velocities of the expiration air jets of healthy volunteers were measured. Droplet size was measured using the interferometric Mie imaging (IMI) technique while the particle image velocimetry (PIV) technique was used for measuring air velocity. These techniques allowed measurements in close proximity to the mouth and avoided air sampling losses. The average expiration air velocity was 11.7 m/s for coughing and 3.9 m/s for speaking. Under the experimental setting, evaporation and condensation effects had negligible impact on the measured droplet size. The geometric mean diameter of droplets from coughing was 13.5 μm and it was 16.0 μm for speaking (counting 1–100). The estimated total number of droplets expelled ranged from 947 to 2085 per cough and 112–6720 for speaking. The estimated droplet concentrations for coughing ranged from 2.4 to 5.2 cm⁻³ per cough and 0.004–0.223 cm⁻³ for speaking.

Nomenclature

C_p,d

heat capacity of water, J/g K

d_p

droplet diameter, m

D_v

binary diffusivity of water vapor in air, m²/s

f_n

droplet number fraction

I_d

evaporation/condensation rate of droplet, g/s

K_a

thermal conductivity of air, W/m K

L

latent heat of fusion/vaporization, J/g

L₀

length of core zone (zone 1) of air jet, m

m_s

number of mole of solute, M

M_v

molecular weight of water vapor, g/M

m_w

number of mole of water, M

n

refractive index

p

total pressure, Pa

p_v,a

vapor pressure at droplet surface, Pa

p_v,∞

saturation vapor pressure of air, Pa

r_p

droplet radius, m

R

universal gas constant

R₀

radius of jet opening, m

t

time, s

T_d

droplet temperature, K

T_∞

air temperature, K

V_x

horizontal air velocity, m/s

X_w

mole fraction of water

y

vertical distance, m

λ

wavelength of laser light, m

Δφ

fringe spacing, m

ϕ

observation angle, rad

1. Introduction

Expiratory droplets are potential carriers of pathogens that cause airborne diseases. Expiratory droplets are polydispersed and the size of the droplets has high impact on the disease transmission process. Smaller droplets evaporate quickly and become ‘droplet nuclei’. Droplet nuclei can remain airborne for long periods of time and can be dispersed widely by following the airflow pattern. Airborne mode transmission refers to infection via inhalation of these airborne pathogenic particles. Larger droplets settle out of the air more quickly but, due to the larger size, a vast majority of expelled pathogens are carried in the large droplets. Infection via direct spray of large pathogen-laden droplets onto mucous membranes or conjunctiva is known as droplet mode transmission. Droplet size also affects the infectivity of pathogen-laden droplets. Although larger droplets have higher pathogen-carrying capacities, their ability to penetrate deep into the respiratory tract is lower than that of smaller droplets. Smaller pathogen-laden droplets have higher infectivity (Nicas, Nazaroff, & Hubbard, 2005) compared to the larger ones for diseases that have the lower respiratory tract as the target infection site (e.g., tuberculosis). Droplet size is a key factor for the disease to be transmitted and for the size of the spreading zone. Tuberculosis, for example, can be transmitted via the airborne route and, thus, can have a wide spreading zone depending on the airflow conditions. Diseases such as influenza and severe acute respiratory syndrome (SARS) are primarily transmitted via the droplet mode. Persons in close contact with the source patient are considered at high risk (Hawkey, Bhagani, & Gillespie, 2003).

Given the importance of droplet size in disease transmission, size profile information of droplets expelled during expiratory actions is of primary interest. Over the past few decades, different methods were employed to measure the size profiles of expiratory droplets and different findings were reported. Most early studies (e.g., Duguid, 1946; Loudon & Roberts, 1967) used collection media (e.g., glass slides and filters) with subsequent microscopic analysis of the expiratory droplets collected on the media. Droplets measured by these methods were mainly in the supermicron size range. Sampling-based optical particle counters were employed in some more recent studies (e.g., Fairchild & Stamper, 1987; Papineni & Rosenthal, 1997). Most of the droplets measured were in the submicron size-range in their studies. Another recent study by Yang, Lee, Chen, Wu, and Yu (2007), which also employed sampling-based optical particle counters, reported droplet size spectra spanning from about 0.6–16 μm, with the average mode at 8.35 μm during coughing. Though different methods were employed, a common problem of these previous studies was that the expiratory droplets were not measured immediately at the mouth/nose exit. Instead, the expiratory droplets went through evaporation, dilution, sampling losses and other influences from the environment before being measured or collected, posing error and limitations in estimating the droplets size profile immediately at the mouth/nose exit (or the ‘original’ size distribution).

Remote sensing techniques may be possible solutions since they do not require air sampling and the sensing volume can be placed very close to the mouth/nose without disturbing the expiratory flow. Jennison (1942) conducted such measurements using high-speed photography. However, this technique requires high magnification to resolve small droplets, restricting the ability to detect small droplets and the size of the field of detection (only droplets of larger than 10 μm were detected in the study by Jennison, 1942). The more recently developed interferometric imaging technique overcomes these shortcomings to a great extent (Glover, Skippon, & Boyle, 1995). Interferometric imaging uses de-focused images of the droplets instead of focused images to lower down the magnification requirement. Scattering properties of droplets under the illumination of coherent optical radiation are analyzed using the Mie scattering theory to determine droplet size. This method is sometimes called the IMI (interferometric Mie imaging) method.

This study aimed at measuring the expiration air jet velocities and the size profiles of expiratory droplets during speaking and coughing in close proximity to the mouths with the help of the PIV (particle image velocimetry) and the IMI method. Total droplet counts and number concentrations of the droplets would also be estimated.

2. Experimental method

2.1. The expiratory droplet measurement setup

The experiments were conducted in an expiratory droplet measurement setup at the International Laboratory for Air Quality and Health (ILAQH), Queensland University of Technology (QUT). The setup was modified from the Expiratory Droplet Investigation System (EDIS) developed by QUT to fit the installation of the IMI and PIV instruments. Fig. 1 shows the schematic of the setup related to the IMI and PIV experiments. The setup consisted of a 500 mm diameter (490 mm internal diameter)×800 mm long acrylic glass tube supported on a rack mount and a chair for the volunteers. Both ends of the tube were open and there was no mechanically induced background airflow in the tube. A 70 mm wide laser safety shield with a 30 mm×30 mm opening was installed at one end of the tube. The center of the 30 mm² opening was 145 mm above the bottom interior of the tube. The safety shield also helped the volunteers to position their head correctly by leaning their head against the shield and placing their mouths on the opening. The safety shield was made from a 1-mm thick galvanized steel base plate covered with light-absorbing black-out material (Edmunds Optics, Flock Paper #40). The bottom of the tube was also covered with the black-out material to stop the laser sheet and to avoid laser light ray reflection. During the measurements, volunteers were asked to lean their heads on the safety shield and to place their mouths on the 30 mm² opening. The chair was mounted on a motorized seat lift to allow the volunteers to adjust the height to the correct position. All volunteers were asked to wear laser safety goggles (OD 10 at 532 nm, Yamamoto) throughout the measurements. The setup was placed inside an air-conditioned room so that the air temperature and relative humidity (RH) inside the tube remained fairly stable. The air temperature and RH inside the tube were monitored in real-time by a digital thermo-hygrometer. The air temperature and RH averaged from all experiments were 24.9 °C and 73.9%, respectively. All the side walls and windows of the room were covered with black cardboard paper with rough surface finishing to avoid refracted light rays. The door of the room was interlocked with the power supply of the laser source. The laser power supply could be switched on only if the door was fully closed.

Fig. 1.

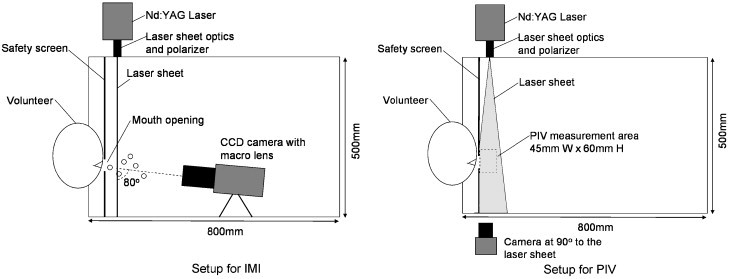
Schematic diagrams of the expiratory droplet investigation setup.

2.2. Optical settings for the IMI and PIV measurements

Detailed descriptions and derivations of the IMI technique and sizing calculation are provided by Glover et al. (1995) and Glantschnig and Chen (1981). Briefly, when there is a laser light ray illuminating a transparent droplet in a flow field, due to refraction and reflection, the incident laser light ray is split into several rays. The reflected and refracted light from the droplet is dominant in the wide-angle forward-scatter region, around 30–80°. At an observation angle in the off-axis alignment, the two components of the scattered light appear to emanate from small spots. The two spots are observed as glare points on the focal plane. On the non-focal plane, the two rays interfere with each other and the regular fringes are easily observed, and their origin can be understood in terms of a simplified geometric theory (Glantschnig & Chen, 1981). The fringe spacing can be related to the droplet diameter by the following equation:

$$d_p=\frac{2\lambda }{\mathrm{\Delta }\phi }{\left[\cos \left(\frac{\varphi }{2}\right)+\frac{n\sin \left({\displaystyle \frac{\varphi }{2}}\right)}{\sqrt{1+n^2-2n\cos \left({\displaystyle \frac{\varphi }{2}}\right)}}\right]}^{-1}$$ (1)

When a set of fringes can be observed for individual droplets, they provide a potentially accurate measurement of the droplet diameter.

For the IMI measurement, the laser light source and the sheet optics with a polarizer were mounted above the tube that produced a laser light sheet to cut downward through the tube diameter, perpendicular to the direction of the expiration jets (cut through the cross section of the expiration jet). The laser light source was a double-pulsed Nd:YAG laser at 532 nm wavelength (New Wave Research, Solo II), operated at 30 mJ with a pulse width of 3–5 ns. The sheet optics produced a laser sheet with an aperture angle of 7.1°. The thickness of the laser sheet was about 1 mm. A CCD camera (LaVision, ImagerIntense) was placed inside the tube at the downstream of the laser sheet. The camera was aligned at an observation angle of 80° to the laser sheet. The observation angle of the camera was monitored by a direct reading dial inclinometer (Empire) attached on the camera. The progressive-scan, dual-frame CCD camera had a resolution of 1376×1040 pixels and a maximum frame rate of 10/s. The exposure time of each image was 100 μs. A macro lens (Zeiss Makro-Planar T∗2.8/100) was mounted on the CCD camera to provide a magnification ratio of 1:1. A circular aperture of 20 mm diameter was mounted in front of the lens to produce de-focused droplet images of about 80 pixels in diameter. The laser source and the camera were synchronized by a PC-based control system (LaVision, Davis 7). The lower size detection limit of the IMI system was about 2 μm. The front end of the lens was about 100 mm away from the laser sheet. The measurement plane was 8.9 mm×6.7 mm (W×H). The center of the measurement plane was aligned with the center of the mouth opening on the laser safety shield. IMI measurements were made at two distances, 10 and 60 mm, from the mouth. The IMI system could only measure transparent droplets. The disturbance by background aerosol to the measurement was essentially screened out. A measurement of background aerosol by aerodynamic particle sizer (APS) showed that the majority of them were smaller than 0.523 μm in size with an average concentration of 1.6/cm³. They were smaller than the lower size detection limit of the IMI system.

The same laser source and CCD camera were used for the measurements of the velocity of expiration air jet by PIV. For the PIV measurements, the laser sheet was twisted by 90° to align along the direction of the expiration air jet. The laser sheet aperture angle was adjusted to 14.2° to produce a wider laser sheet. The camera was placed at the side of the tube and aligned at a 90^o observation angle to the laser sheet. An objective lens (Nikkor 50 mm/f1.8 D) with a 532 nm optical filter was mounted on the camera. The measurement area was 45 mm×60 mm (W×H), located immediately in front of the mouth opening. The PIV images were taken in dual-frame pairs for cross-correlation post-processing. The images were taken at a frequency of 5 pairs/s. At the camera's viewing position, an opening was made on the tube wall and a 51 mm×70 mm planer acrylic glass window was fitted on the opening to avoid image distortion by the curved surface of the tube. Flow seeding was provided by an aerosol generator (LaVision, Aerosol Generator) using saline solution.

2.3. Experiment protocol

The experiments with volunteers and the use of the laser setup were approved by the Human Research Ethics Committee and the Safety Office of Queensland University of Technology. Eleven healthy volunteers (3 men and 8 women) were recruited via a broadcast email invitation with a small financial reward. The volunteers were university students and postgraduate research students (under 30 years old). Smokers, asthma sufferers, people who were experiencing illness, who had recently experienced expiratory problems or were likely to experience discomfort in confined spaces were excluded.

Every volunteer was asked to cough and to speak following a standard protocol. When the volunteer was seated comfortably in the correct position with his/her mouth placed at the opening of the safety shield, they were asked to speak by counting 1–100 10 times loudly and slowly with a pause after speaking each number. The volunteers produced expiration air jets in the horizontal forward direction with the help of the safety shield. The volunteers were allowed to take a brief rest after finishing every round of speaking 1–100. After 10 rounds of counting 1–100 were finished, the volunteers were given a 5-minute break and they were allowed to drink water. After the break, the volunteers were asked to cough 50 times during the cough test. They were instructed to close their lips before each cough. Therefore, the volunteers were well-prepared before each cough and started each cough with same mouth shape. The volunteers were allowed to take a brief rest and drink water whenever they needed to during the cough test. Every volunteer was asked to conduct two rounds of tests following this protocol. The first round was for measurement at 10 mm from the mouth opening and the second round was for measurement at 60 mm. A 20-min break was given to the volunteers after finishing the first round to allow time for the experimenters to move the IMI system from the 10 mm to the 60 mm distance and to realign the optical setup. PIV measurements were made on two volunteers (one man and one woman). The coughing and speaking protocol was the same as in the IMI measurements except that the volunteers were asked to do one round of coughing and one round of speaking only.

3. Results

3.1. Expiration air jet velocity

The maximum expiration air velocity during coughing by the male volunteer was 13.2 m/s and that by the female volunteer was 10.2 m/s. The average expiration air velocity during coughing was 11.7 m/s. During speaking, the maximum expiration air velocity was 4.6 m/s for the male and 3.6 m/s for the female volunteer, with an average velocity of 3.9 m/s. Fig. 2 shows an example of the measured air velocity field during coughing and speaking. During coughing, a high velocity core of about 15 mm in diameter was formed at the mouth exit. A significant gradient of air velocity can be seen from the center of the jet towards the outer of the jet envelope. Entrainment of the surrounding air by the cough jet could be found along the jet making the jet envelope expand. The high momentum of air expulsion during coughing produced an air jet having a throw even longer than the viewable area of the camera. Comparatively, the initial air jet velocity was much lower during speaking so that the throw of the air jet was about 40 mm in the example shown in Fig. 2. Air entrainment was also observed in the speaking case.

Fig. 2.

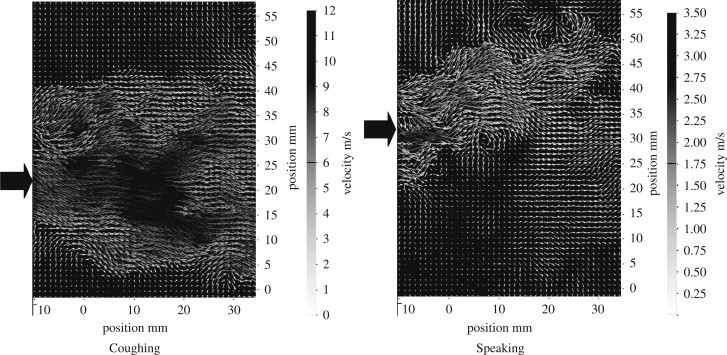
Measured air velocity fields for coughing and speaking from a male volunteer. The block arrows indicate mouth position.

3.2. Measured droplet size distributions

Table 1 shows the average count of droplets per person during coughing and speaking at the two distances from the mouth opening. The coughing droplet count was aggregated across 50 coughs while the speaking droplet count was aggregated across 10 times of counting 1–100. The standard deviation of the 11-volunteer data pool is also shown. The droplets were classified into 16 size classes as adopted from Duguid (1946). Narrower size classes were used for smaller sizes of droplets since most of the droplets measured were in the lower size end. During coughing, the size class that has the highest number count was 6 μm at the two measurement distances. At the 10 mm distance an average total of 110 droplets were counted in 50 coughs but this average reduced to 42 droplets at the 60 mm distance. The size class that had the highest droplet count for speaking was also 6 μm. However, the number of droplets was much smaller with speaking, compared to coughing. An average total of 61 droplets were counted at the 10 mm distance after counting 1–100 10 times. The average total number of droplets per person was reduced to 40 at the 60 mm distance. The observation of having the same size class that had the highest droplet count for coughing and speaking was similar to that reported in Duguid (1946). However, in Duguid (1946), this size was in the 8–16 μm size class. Another study (Papineni & Rosenthal, 1997) reported that highest counts were found in the size class of less than 0.6 μm for both talking and coughing.

Table 1.

Average droplet number count per person measured at the 10 and 60 mm distances

Size range (μm)	Size class (μm)	Speaking (averaged number per person, counting 1–100 for 10 times)				Coughing (average number per person, coughing 50 times)
		10 mm	S.D.	60 mm	S.D.	10 mm	S.D.	60 mm	S.D.
2–4	3	1.7	1.62	4.6	3.41	4.0	3.46	3.5	2.28
4–8	6	26.8	8.94	16.1	3.28	55.0	15.88	17.6	7.47
8–16	12	9.2	4.67	6.9	3.35	20.4	15.44	6.5	5.15
16–24	20	4.8	4.07	4.3	2.95	6.7	4.60	2.8	2.98
24–32	28	3.2	2.36	2.6	2.07	2.5	2.42	1.4	1.71
32–40	36	1.6	1.03	1.9	0.74	2.4	2.37	0.6	0.97
40–50	45	1.7	0.90	1.0	0.47	2.0	2.67	0.2	0.48
50–75	62.5	1.8	0.98	1.4	0.97	2.0	1.41	0.9	2.16
75–100	87.5	1.3	0.65	1.2	0.79	1.4	1.84	0.5	0.85
100–125	112.5	1.7	1.01	1.2	0.92	1.7	1.77	1.0	1.56
125–150	137.5	1.6	1.03	0.4	0.70	1.6	1.84	0.7	1.25
150–200	175	1.7	1.01	1.0	0.94	4.4	2.80	0.6	0.67
200–250	225	1.5	0.82	0.4	0.52	2.5	1.84	0.5	1.07
250–500	375	1.4	0.50	0.6	0.70	2.1	1.20	0.9	0.82
500–1000	750	0.5	0.82	0.1	0.32	1.4	0.97	0.4	0.71
1000–2000	1500	0.0	0.00	0.0	0.00	0.0	0.00	0.0	0.00

Key: S.D.—standard deviation.

The measured droplet size profiles are presented in terms of df_n/d ln  d_p and are fitted by the log-normal distribution as shown in Fig. 3 a and b. The geometric mean (GM) diameters are also shown for comparison. Although the droplet size peaked at 6 μm for both speaking and coughing, the GM diameter was larger for speaking compared to that of coughing (16.0 μm vs 13.5 μm at the 10 mm distance). This suggests that the expulsion of air at higher velocity during coughing might promote the production of smaller droplets compared to the lower expiration velocity experienced during speaking. The results reported by Duguid (1946) and Loudon and Roberts (1967) are also plotted on Fig. 3 for comparison. It shows that the GM diameters obtained in the current study were fairly close to that reported by Duguid (1946) but differed rather significantly from that reported by Loudon and Roberts (1967). Fig. 3a and b also show that the GM diameter reduced modestly at the 60 mm distance when compared to the 10 mm distance. The reduction in the GM diameter might be caused by the shrinkage of the droplets by evaporation but this hypothesis is questionable since the traveling time might be very short considering the high velocity of the expiration jets. The RH of the surrounding air might still be high under the influence of the expiration jet. Another reason could be that the droplets became more widely dispersed at the 60 mm distance. The chance for capturing the large droplets by the camera became even less compared to the 10 mm distance.

Fig. 3.

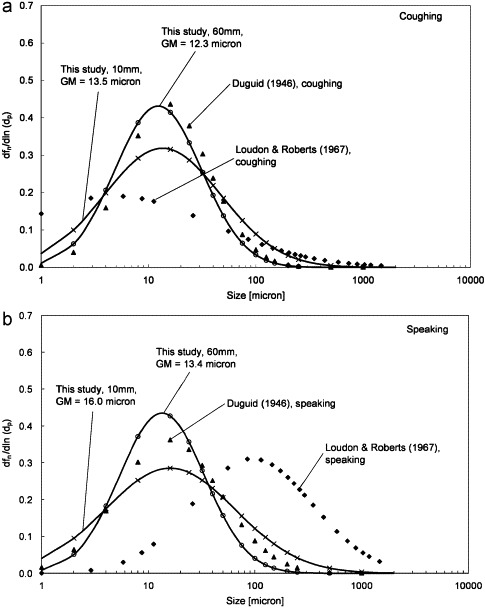
(a) Droplet size distribution for coughing and (b) droplet size distribution for speaking.

4. Discussion

4.1. Estimation of droplet evaporation/condensation

Expiratory droplets experience evaporation/condensation once they are produced and introduced into the air, leading to changes in droplet size. In the current study, droplet measurements were made at 10 and 60 mm from the mouth. The effects of evaporation/condensation on the droplet size at these two distances were estimated to access if the current results are representative of the ‘original’ size profile. For such estimation, information about the surrounding air temperature and RH along the trajectory of the droplets is essential. Numerical simulations were performed for the coughing and speaking cases. A two-dimensional numerical geometry with dimensions adopted from the expiratory droplet investigation setup (800 mm×490 mm) was used. An opening of 15 mm in diameter was created at the position corresponding to the mouth position in the experimental setup. One mm hexahedral meshing was generally used in the geometry with grid adaptations near the tube walls to keep the y ⁺ value of the first layer of mesh within 30–60. The standard log-law wall function was adopted for the turbulence near-wall treatment. The numerical geometry was constructed and meshed using the GAMBIT (version 2.2) pre-processor. Conservation equations of mass, momentum and energy plus the species transport equation for water vapor were solved using the SIMPLE algorithm and the second-order upwind solution scheme by FLUENT (version 6.2). The density of the air–water vapor mixture was set to follow a second-order polynomial function of temperature to capture the buoyancy effect. Inputs of the numerical simulations are summarized in Table 2 .

Table 2.

Input conditions for the numerical simulations

Ambient air conditions	24.9 °C, 73.5%RH
Expiration air conditions	37 °C, 100%RH McFadden et al. (1985)
Expiration air velocity	11.7 m/s (coughing); 3.9 m/s (speaking)
Mouth diameter	15 mm

The profiles for the predicted horizontal air velocity along the center-line of the mouth opening up to the 100 mm distance are shown in Fig. 4 a. The figure shows that the changes in horizontal air velocities at the two measurement distances were very modest compared to that at the mouth opening. This suggests that the two droplet measurement distances, 10 and 60 mm, were essentially within the core zone (or zone 1 in the classical jet theory, Rajaratnam, 1976) where the center-line velocity is the same as the jet's initial velocity. Fig. 4b shows the numerically predicted air temperature and RH at horizontal distances of up to 100 mm from the mouth opening. The figure shows that, at the 10 mm distance, the air temperature and RH were the same as at the mouth exit (37 °C and 100%, respectively) for both coughing and speaking. The RH was reduced by about 0.5% at the 60 mm distance for coughing but, for speaking, the air became slightly supersaturated (RH>100%) at this distance. This happened because the warm and saturated air front of the exhalation air jet met with the cooler surrounding air. In reality, this may trigger the nucleated condensation of water droplets and may lower the RH back to the saturation state but modeling this rather complex phenomenon was not the intention of the current simulations. Considering that the solutes might lower the vapor saturation pressure on the droplet surface, the droplets were more likely to grow by condensation rather than shrink by evaporation. The evaporation/condensation of droplets was estimated using the model proposed by Kukkonen, Vesala, and Kulmala (1989) with some simplifications. The models for diffusive mass flux of vapor from a droplet surface and droplet temperature were

$$\frac{\mathrm{d}{r}_p}{\mathrm{d}t}=-\frac{M_v{D}_{v}p}{\mathit{rR}{T}_{\infty }}\ln \left(\frac{p-p_{v,a}}{p-p_{v,\infty }}\right)$$ (2)

and

$$\frac{\mathrm{d}{T}_d}{\mathrm{d}t}=\frac{3K_a}{C_{p,d}{r}^2}(T_{\infty }-T_d)-\frac{3L{I}_d}{4\pi r^3}$$ (3)

The effect of forced convection due to the difference in velocity between the droplets and the surrounding air was neglected in this estimation since the initial air velocity was more or less maintained throughout the 60-mm distance, as shown in Fig. 4a. However, it is worth noting that significant velocity difference between the droplets and the air may develop at longer distances. The convective heat and mass transfers should be considered if a longer traveling distance is concerned. Dependence on temperature by the vapor diffusion coefficient was not considered since such a correction would be less than 3% under atmospheric conditions (Kukkonen et al., 1989). Radiation heat exchange between the droplets and the surroundings was also neglected. The effect of the solute on the saturation vapor pressure on the droplet surface was included using Raoult's law:

$$p_{v,a}=X_w{p}_{v,a}(T_d)\mathrm{where}{X}_w=\frac{m_w}{m_w+m_s}$$ (4)

The expiratory fluid was considered as a saline solution with NaCl content of 150 mM (Nicas et al., 2005). This solute content led to about 0.3% drop in the saturation vapor pressure on the surface of freshly produced expiratory droplets. The effect of other non-volatile components, e.g., glycoprotein, on the hygroscopic behavior is still uncertain and was ignored in this estimation. The temperature and vapor pressure of the surrounding air along the trajectory of the droplets were taken from the FLUENT simulation results. The system of equations was numerically solved by the fourth-order Runge–Kutta method.

Fig. 4.

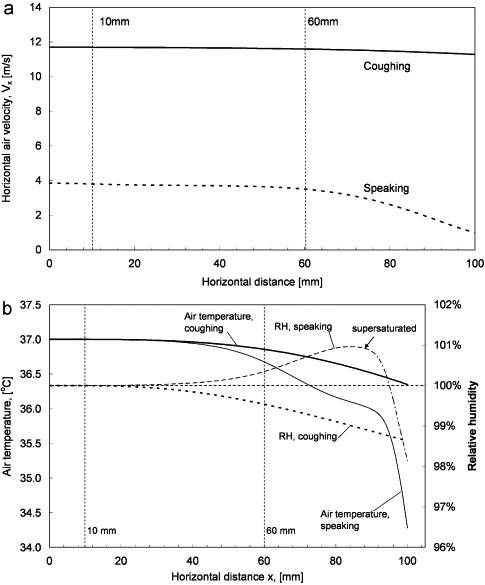
(a) Predicted horizontal air velocities at horizontal distances up to 100 mm and (b) predicted distribution of air temperature and RH at horizontal distances up to 100 mm.

Table 3 shows the average number count per person before and after the evaporation/condensation correction at the 60 mm distance. Changes in average number were found only for droplets smaller than 12 μm for speaking and 6 μm for coughing by the correction. This is because the rate of change in droplet size was inversely proportional to the droplet size as indicated in Eq. (2). The average number for the smallest size class increased while the average number decreased for larger size classes. This indicates that the droplets experienced growth by condensation during their travel. However, the change in size distribution was minor due to the short traveling time and the small difference in vapor pressure between the droplet surface and the surroundings. The traveling time for reaching 60 mm was 5.13 ms for coughing and 15.4 ms for speaking, as estimated from the expiratory air jet velocity. This estimation suggests that the hygroscopic property of the droplets was not the reason for the reduction in the GM diameter measured at 60 mm compared to 10 mm. Droplets falling out of the IMI measurement area by gravitation settling was also not likely to be the major reason. This can be seen by a simple estimation of a free falling object. The maximum droplet traveling time to the measurement positions was about 20 ms. The downward distance traveled by a free falling object without air resistance after 20 ms can be calculated by y=(1/2)at ². With a gravitational acceleration, a, of −9800 mm/s², at 20 ms, y=−1.96 mm, this is shorter than half of the vertical height of the IMI measurement area, 8.9 mm/2=4.45 mm. The falling distance should be even less in reality due to air resistance. From the above analysis, the change in GM diameter could be caused mainly by the wider dispersion of droplets at the 60 mm distance induced by the expansion of the air jet. The estimated evaporation/condensation did not affect the size distribution at the 10 mm distance since the traveling time was even shorter than that for the 60 mm distance. The traveling time for reaching 10 mm was 0.86 and 2.56 ms for coughing and speaking, respectively. These results suggest that the size distribution obtained at the 10 mm distance may essentially represent the ‘original’ size distribution at the mouth opening.

Table 3.

Average droplet number count per person at 60 mm before and after the condensation correction

Size range (μm)	Size class (μm)	Speaking (averaged number per person, counting 1–100 for 10 times)		Coughing (average number per person, coughing 50 times)
		Measured	Corrected	Measured	Corrected
2–4	3	4.6	5.0	3.5	3.8
4–8	6	16.1	16.4	17.6	17.3
8–16	12	6.9	6.2	6.5	6.5
16–24	20	4.3	4.3	2.8	2.8
24–32	28	2.6	2.6	1.4	1.4
32–40	36	1.9	1.9	0.6	0.6
40–50	45	1.0	1.0	0.2	0.2
50–75	62.5	1.4	1.4	0.9	0.9
75–100	87.5	1.2	1.2	0.5	0.5
100–125	112.5	1.2	1.2	1.0	1.0
125–150	137.5	0.4	0.4	0.7	0.7
150–200	175	1.0	1.0	0.6	0.6
200–250	225	0.4	0.4	0.5	0.5
250–500	375	0.6	0.6	0.9	0.9
500–1000	750	0.1	0.1	0.4	0.4
1000–2000	1500	0.0	0.0	0.0	0.0

4.2. Estimation of total droplet number and concentration

The measurement volume of the IMI system covered a 6.7 mm×8.9 mm plane that was 1 mm thick (about 60 mm³ in volume), which is much smaller than the expiration jet envelope. Therefore, the IMI measurement results can only give the statistical size distribution. To estimate the total number of droplets produced in each of the activities, two projection methods were used. One method was to divide the total volume of droplets produced by the statistical size profiles obtained by IMI. This method requires information about the total volume of droplets produced for the particular expiratory action tested but this information is rare. Zhu, Kato, and Yang (2006) reported that the total mass of expiratory droplets in a cough was 6.7 mg but no data for speaking was reported. Total expiratory droplet volumes estimated from the droplet size profile reported by Duguid (1946) and Loudon and Roberts (1967) may also be used for this purpose. This is because the methods employed by these two studies were intended to collect all the expiratory droplets using collection media instead of using sampling-based instruments (e.g., Papineni & Rosenthal, 1997; Yang et al., 2007). Employing the data from studies using collection media should give better estimations of the expelled fluid volume compared to those using sampling-based instruments. This is because the sampling-based instruments tend to miss the larger droplets but they are the major contributors to the total expelled fluid volume. The speaking activity in Duguid's (1946) and Loudon and Roberts's (1967) studies was also counting from 1 to 100, as in the current study. The droplet number concentrations in the expiration jets were roughly estimated by assuming that a tidal volume of air (≈0.4 L for adults) was exhaled in a cough. It was also assumed that the air volume exhaled per vocalization during speaking followed the ratio of expiration jet velocity obtained from PIV measurements. Therefore, for example, an air volume of (3.1/11.7)×0.4 L was exhaled by counting ‘one’. Three times of this volume was exhaled when counting ‘ninety-four’. Table 4 shows the estimated total droplet numbers using the measured size profile at 10 mm. For coughing, the estimated total number ranged from 1085 to 2085 per cough using different data from the literature. However, due to the large difference in the reported droplet size profiles for speaking between Duguid (1946) and Loudon and Roberts (1967), the estimated total number differed significantly for using the data from different studies. The estimated droplet number concentrations are shown in Table 5 .

Table 4.

Estimated total expiratory droplet numbers produced during coughing and speaking using the measured size profile at 10 mm

Size class (μm)	Speaking			Coughing
	D	L&R	Z	D	L&R	Z
3	3	191		76	39	67
6	50	2972		1041	542	924
12	17	1018		386	201	343
20	9	534		127	66	113
28	6	353		47	25	42
36	3	181		45	24	40
45	3	191		38	20	34
62.5	3	201		38	20	34
87.5	2	141	N.A.	27	14	24
112.5	3	191		32	17	29
137.5	3	181		30	16	27
175	3	191		83	43	74
225	3	161		47	25	42
375	3	151		40	21	35
750	1	60		27	14	24
1500	0	0		0	0	0
Total	112	6720		2085	1085	1850

Key: D—refers to Duguid (1946); L&R—refers to Loudon and Roberts (1967); and Z—refers to Zhu et al. (2006).

Table 5.

Estimated droplet number concentrations during coughing and speaking using the measured size profile at 10 mm

Size class (μm)	Speaking (L−1)				Coughing (L−1)
	D	L&R	Z	L.V.	D	L&R	Z	L.V.
3	0.11	6.36		4.59	168	189	99	86
6	1.65	98.74		66.21	2311	2604	1355	1187
12	0.56	33.81		22.23	857	966	501	444
20	0.30	17.74		11.33	281	317	165	144
28	0.20	11.71		7.87	105	118	62	54
36	0.10	6.02		4.32	101	114	59	50
45	0.11	6.36		4.47	84	95	49	41
62.5	0.11	6.69		4.57	84	95	49	43
87.5	0.08	4.69		3.44	59	66	35	30
112.5	0.11	6.36	N.A.	4.52	71	80	42	36
137.5	0.10	6.02		4.31	67	76	39	34
175	0.11	6.36		4.52	185	208	108	93
225	0.09	5.36		3.85	105	118	62	53
375	0.08	5.02		3.45	88	99	52	44
750	0.03	2.01		1.11	59	66	35	30
1500	0.00	0.00		0.00	0	0	0	0
Total (in cm−3)	3.72 (0.004)	223.25 (0.223)		150.80 (0.151)	5212 (5.212)	2713 (2.713)	4625 (4.625)	2368 (2.368)

Key: D—refers to Duguid (1946); L&R— refers to Loudon and Roberts (1967); Z—refers to Zhu et al. (2006); and L.V.—estimation using laser measurement volume.

Another estimation method was to divide the total number of droplets captured by the total laser measurement volume. For example, if a total of 50 droplets was captured in a measurement in which 1000 IMI images were taken, the droplet concentration would be 50/(1000×60 mm³)=8.3×10⁻⁴  mm⁻³. The estimated droplet number concentrations using this laser volume method are shown in Table 5, in the column marked ‘L.V.’. Using the exhalation air volumes defined above, the estimated total number of droplets expelled was 947 per cough and 4539 droplets were expelled when counting 1–100. This estimation method does not require information on the total expelled liquid volume (or mass), which is uncertain. However, in determining the total laser measurement volume, the images taken between coughs (or vocalizations) and during pauses were also counted. This could induce uncertainties into the estimation. Another possible source of error is that the droplet concentration in the measurement volume did not necessarily represent the droplet concentration in the entire exhalation jet envelope. The maximum droplet concentration found in the current study was 5.2/cm³. With a maximum traveling time of around 20 ms, the likelihood of droplet coalescence, that might subsequently affect the size distribution measurements, was estimated to be insignificant via a simple scale analysis.

Both of the estimation methods have limitations. The above estimations are by no means comments on the accuracy of droplet number and total expiration droplet volume measurements provided in previous studies. However, our results suggest that further studies are needed for better estimation of total expiratory droplet number during different expiratory activities. This information is important for estimating the amount of pathogens disseminated to the air by the source patient, which is crucial for exposure and infection risk analysis studies.

4.3. Uncertainties and limitations of the droplet size measurement

According to Eq. (1), the refractive index of the droplet material and the camera's observation angle are two parameters that can affect the calculation of the final droplet size. In the current study, the refractive index of water (n=1.33) was used in the calculation but the presence of solutes in the expiratory fluid may alter the refractive index. Using Eq. (1), the effect of shifting the refractive index on the calculated droplet size was estimated. The estimation is shown in Fig. 5 for n between 1.00 and 2.00. It shows that the difference in the calculated droplet sizes within this range of refractive index compared to the calculated droplet size using n=1.33 are within 4%. A major change in the solute content due to evaporation/condensation was not likely according to the estimations discussed in Section 4.1. Using the same method, the difference in the calculated droplet size due to errors in observation angle measurements is estimated and shown in Fig. 5 for a range of ±5° for the preset observation angle, 80°. The figure shows that the difference in calculated sizes is within ±1.5% for this error range of observation angle measurement.

Fig. 5.

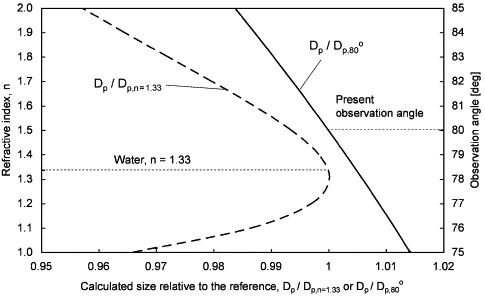
Effect of the shifting of the refractive index and the observation angle on the calculated droplet size.

It is also worth noting that the lower size detection limit of the IMI system was about 2 μm. Several other studies employing sampling-based instruments reported size peaks that are outside the IMI detection limit (e.g., <0.6 μm for both coughing and talking by Papineni & Rosenthal, 1997), which suggests that the IMI system might not cover the entire size range of expiratory droplets and other size modes exist outside the IMI detection limit. Another set of measurements using APS conduced in the EDIS showed that it was the case. The APS measurements found size modes at 0.8 μm for different expiratory activities. Details of the APS measurements are reported in another paper (Morawska et al., 2008). Discrepancies between results obtained by different instruments in the similar measurement setup indicate that instrumentation is still a major limitation in this kind of research. An instrument that is able to cover the entire size range of expiratory droplets with minimal sampling loss is still lacking.

The volunteers followed certain protocols when coughing and speaking. Although real human subjects were involved, the question of how representative the ‘artificially produced’ expiratory activities in the current study of the real expiratory activities is worth further considering. For example, the volunteers were asked to close their lips before each cough. They were also allowed to drink water any time as they need. From the experimenters’ observation, each volunteer drank around 1–2 cups (regular foam coffee cup size) of water in each set of experiments. These practices might have an impact on the expiration jet velocity and droplet size distribution, compared to coughs made in other mouth patterns, e.g., coughing several times in a row without closing the lips. This study involved healthy volunteers only. The speaking activity tested in the current study was counting 1–100. Different mouth movements can be involved if different speaking patterns are tested. Different speech patterns may affect the droplet size distribution and expiration jet velocity as well. On the other hand, a recent study by Hersen et al. (2008) indicated that the size distributions of exhaled respiratory aerosols from symptomatic individuals were different from that exhaled by healthy individuals. However, a specific size distribution for symptomatic individuals was not identified in their study and the reason for causing such a difference remains unclear. This also gives rise to the question that the exhalation jet velocity could be different according to health conditions.

5. Conclusion

The size distributions of the droplets expelled during coughing and speaking (counting 1–100) were measured by a series of experiments involving 11 human subjects. IMI method was used to obtain droplet sizing measurements at very close distances from the mouth, i.e., 10 and 60 mm in the current study. The optical remote sensing technique could eliminate the errors induced by air sampling techniques. The average expiration air jet velocity was 11.7 m/s for coughing and 3.1 m/s for speaking using the PIV technique. Impacts of the evaporation/condensation effects on the droplet size distributions were estimated by numerical method and the effect of the hygroscopic behavior was found to be negligible on the droplet size distributions at such close distances. Our numerical results indicate that the measured droplet size distributions can essentially represent the ‘original’ size distributions immediately in front of the mouth. The geometric mean diameter of the droplets expelled during coughing was 13.5 μm and it was 16.0 μm for speaking. It was estimated that 947–2085 droplets were expelled per cough and 112–6720 droplets were expelled during speaking. Using different estimation methods and literature reference data, the droplet concentrations were found to range from 2.4 to 5.2 cm⁻³ per cough and 0.004–0.223 cm⁻³ for speaking.

Comparison between the results obtained at the two measurement distances (10 and 60 mm) suggests that the measured size distributions might be distorted if the measurement was not made as close as possible to the mouth opening. In this particular setup, the distortion was mainly due to wider spread of the droplets following the expansion of the expiration jet, resulting in fewer droplets being detected at the 60 mm location Our analysis also suggests that other influential factors, including hygroscopic behavior and droplet falling, would become more significant if the droplet sensing element was placed at further distances.

This study is the first one employing the IMI technique to measure the original droplet size profiles from human expiratory activities. The droplet size distributions obtained in the current study are more in line with that reported by Duguid (1946), who employed collection media in his study. Estimating from Duguid's (1946) results, the geometric diameters for coughing and speaking were 14 and 16 μm, respectively. The geometric mean diameters reported by Loudon and Roberts (1967) differed from the current study more significantly compared to Duguid (1946) but their measured droplet size ranges (about 3–1500 μm) were also similar to the current study. Size peaks in the submicron range were reported by some previous studies using sampling-based instruments (e.g., 0.8 μm in Morawska et al., 2008, less than 0.6 μm in Papineni & Rosenthal, 1997 and less than 0.3 μm in Fairchild & Stamper, 1987), indicating that there are expiratory droplets smaller than the detection limit of the IMI system. Limitations and uncertainties of the IMI technique were also addressed in the paper. It seems that instrumentation is still a major limitation for this kind of research and the IMI technique can only capture the droplet profiles at the larger size range.