Epidemic dynamics on information-driven adaptive networks

Highlights

• •We propose an information-driven adaptive model in epidemic spreading.
• •Results show information and adaptive process can inhibit epidemic spreading.
• •We show a bifurcation diagram to describe the evolution of four dynamical behaviors.

Abstract

Research on the interplay between the dynamics on the network and the dynamics of the network has attracted much attention in recent years. In this work, we propose an information-driven adaptive model, where disease and disease information can evolve simultaneously. For the information-driven adaptive process, susceptible (infected) individuals who have abilities to recognize the disease would break the links of their infected (susceptible) neighbors to prevent the epidemic from further spreading. Simulation results and numerical analyses based on the pairwise approach indicate that the information-driven adaptive process can not only slow down the speed of epidemic spreading, but can also diminish the epidemic prevalence at the final state significantly. In addition, the disease spreading and information diffusion pattern on the lattice as well as on a real-world network give visual representations about how the disease is trapped into an isolated field with the information-driven adaptive process. Furthermore, we perform the local bifurcation analysis on four types of dynamical regions, including healthy, a continuous dynamic behavior, bistable and endemic, to understand the evolution of the observed dynamical behaviors. This work may shed some lights on understanding how information affects human activities on responding to epidemic spreading.

1. Introduction

The spreading dynamic is one of the core issues in network science [1], [2], [3], where most of the related researches focus on epidemic spreading and information diffusion in recent years. Much of the work to date focuses on the analysis of these two processes independently, such as the spread of single contagion [4], [5], [6] or concurrent diseases [7], [8], and the diffusion of various kinds of information (e.g., news [9], rumor [10], innovation [11].). However, the epidemic spreading process is closely coupled with the corresponding disease information diffusion (or saying individuals’ awareness of the disease) in the real world. For instance, during the severe acute respiratory syndrome (SARS) outbreak in China in 2003, overwhelming number of disease reports have been posted. These kind of information about SARS may affect the individuals’ behavior in keeping away from SARS and thus help to make the disease under control [12], [13]. Therefore, disease information diffusion may play an important role in the control of the epidemic outbreak, but it is not easy to quantitatively measure the strength of its impact [14].

Nowadays, some models have been proposed to model the interaction between epidemic spreading and information diffusion on complex networks [14], [15], [16], [17]. The fundamental assumption is that, when a disease starts to spread in the population, people may get the disease information from their friends or media before the advent of the epidemic and take some preventive measures to keep away from being infected [15], [18], [19]. By depicting preventive measures as the reduction of transmitting probability [20], [21] or particular states of individuals (immune or vaccination) [22], previous models showed that the disease information diffusion indeed inhibits the epidemic spreading significantly (reduce the epidemic prevalence as well as enhance the epidemic threshold) [15], [23]. Therefore, the emergence of mutual feedback between information diffusion and epidemic spreading [14] exhibits the intricate interplay between these two types of spreading dynamics. The interplay between these two types of spreading dynamics is similar to the competing epidemics [24], [25] to some extent, that is to say, there is a competitive mechanism between epidemic spreading and the information diffusion. Most of aforementioned studies of such complex interacted spreading dynamics are based on static network, i.e., the network structure stays fixed when the two processes are spreading on the network. However, individuals would sometimes cut off the connections with the infected ones when they become aware of the disease, leading to the change of network structure. Consequently, how to characterize the mutual spreading process on the adaptive networks is a crucial issue we want to address in this work.

Generally, the network dynamic researches could be classified into two lines: (i) one is the dynamics of the network, which focuses on the time evolution of network structure [26], [27], [28]; (ii) the other is considered as the dynamics on the network, which concerns the state change of the nodes (or interactions) on networks, such as the epidemic spreading and information diffusion process [29], [30], the evolutionary game [31] and so forth. Currently, researchers became to study how the epidemic would spread on adaptive networks, i.e., considering one epidemic spreading process on dynamical changing networks [32]. In [32], the author proposed a model by considering that the susceptible individuals are allowed to protect themselves by rewiring their links from the infected neighbors to some other susceptible ones [33], [34], [35]. Many researches indicate that segregating infected (or susceptible) individuals with the adaptive behavior is an efficient strategy to reduce the fraction of susceptible-infected (SI) interactions, as well as hinder the outbreak of the whole epidemic spreading [36], [37], [38]. In addition, abundant temporal behaviors are presented to illustrate the spreading dynamics on the adaptive network, such as the coexistence of multiple stable equilibrium and the appearance of an oscillatory region, which are absent in the spreading dynamics on static networks [32], [39]. Besides the edge rewiring strategy, the link cutting or temporarily deactivating is also a commonly used rule in the adaptive models [40], [41].

In this work, we consider a more complicated case that two dynamical processes (i.e., epidemic spreading and disease information diffusion) are spreading on adaptive networks. Therefore, three dynamical processes are coupled in this case, we aim to illustrate how the adaptive behavior can affect the interplay between epidemic spreading and information diffusion. The adaptive behavior is aroused by the individuals awareness of the disease. In this model, those who have been informed of the emergence of disease can break their neighbouring connections to prevent further infection. Additionally, epidemic spreading and disease information diffusion are described by the SI and SIS model, respectively. The disease information generation of the infected individuals is considered to form a mutual feedback loop between these two types of spreading dynamics [20]. Therefore, the effect of information diffusion on epidemic spreading could be interpreted by two aspects: (i) reduce the epidemic spreading probability with protective measures; and (ii) cut off SI links with the information-driven adaptive process. Both numerical analyses based on the pairwise approach and simulation results indicate that the information diffusion and the adaptive behavior of the nodes can inhibit the epidemic outbreak significantly. In addition, we present a full local bifurcation diagram to show the abundant dynamical behaviors in the proposed model.

The paper is organized as follows. In Section 2, we give a detailed description of the model as well as mathematical expressions based on the mean-field model and the pairwise model. In Section 3, we first analyze the case of epidemic and disease information spreading on static network, i.e., the case of no adaptive behavior is taken into account. We further give the results of how the epidemic and disease information spreading processes interact with each other on adaptive network. The sensitivity analysis of the parameters and dynamical characterization of the model is given in the end of Section 3. We conclude the paper with some future directions of the work in Section 4.

2. Model

2.1. Model description

We give a detailed illustration of our model in Fig. 1 . The vertical transformation describes the diffusion of disease information by an SIS model, where individuals can be at one of the two states: (i) + : indicates that the individuals have known the existence of the disease, denoted as the informed ones; (ii) −: indicates that the individuals have not known the existence of the disease. At each time step, the informed nodes will transmit the information to their unknown (−) neighbours with probability α, and each informed individual may forget the information of the disease with a probability λ. Besides, the one who has been infected by the disease will become to know the information of the disease with a corresponding rate ω [14], [16].

Fig. 1.

Transmission diagram of epidemic spreading (SI model in the horizontal direction) and disease information diffusion model (SIS model in the vertical direction).

In the horizontal transformation of Fig. 1, the epidemic spreading is described by an SI model. Each node is at one of two states, susceptible (S) or infected (I). The disease can be transmitted through the SI links, where the S-state individuals could be infected with the probabilities β, σ_Iβ, σ_Sβ and σ_SIβ respectively through $S_{-}{I}_{-},$ $S_{-}{I}_{+},$ $S_{+}{I}_{-}$ and $S_{+}{I}_{+}$ links, where σ_I, σ_S and σ_SI are the impact factors of the information on epidemic spreading. Generally, when people know the occurrence of the disease (informed individuals), they would like to take some measures to protect themselves, leading to the reduction in infectivity (0 < σ_S, σ_I < 1). In particular, the influence coefficient of the epidemic spreading probability through $S_{+}{I}_{+}$ links could be calculated as ${\sigma }_{SI}={\sigma }_S{\sigma }_I,$ with the assumption of the independent effect of the infection probability.

Additionally, we consider an information-driven adaptive process which the informed individuals would reduce physical contacts to protect themselves or their friends. That is to say, the informed susceptible individuals ($S_{+}$) will keep away from their infected neighbors to protect themselves from being infected, and informed infected individuals ($I_{+}$) will also avoid contacting their susceptible neighbors to prevent the epidemic from further spreading. Consequently, the edge-breaking rule of adaptive behavior is adopted [40]. Thus, at each time step, the $S_{+}$ ($I_{+}$) state individuals will break the links connected to their I (S)-state neighbors with rate r_S (r_I) respectively. Specially, the breaking rate of the $S_{+}{I}_{+}$ pairs could be interpreted as $1-(1-r_S)(1-r_I)$ with the independent assumption. It is worth noting that the deactivation of SI links only represents the avoidance of physical contacts between the S- and I-state individuals. That is to say, the edge-breaking process will not affect the diffusion of disease information for it can be transmitted through other types of connections such as phone, internet and so forth. The dynamic of the epidemic spreading degenerates to a classical SI model when we set $r_S=r_I=0,$ i.e., there is no edge-breaking in this case.

According to the model described above, the spreading process can be summarized as follows. At the beginning, an individual is randomly selected as the $I_{+}$ node, which is considered as the seed of both the epidemic spreading and information diffusion, and all other individuals are set as $S_{-}$ ones. At each time step, (i) the infected individuals would transmit the disease to their susceptible neighbors with the corresponding probabilities; (ii) the informed individuals would transmit the disease information to their un-informed neighbors; (iii) the informed individuals can forget the information; (iv) the informed individuals would also break the links with their relevant neighbors by considering the adaptive mechanism. Finally, the spreading process would be terminated when the size of the infected individuals becomes stable.

2.2. Numerical mathematical analysis

Firstly, we develop theoretical analysis to depict the dynamic processes of both information diffusion and epidemic spreading. In particular, mean-field analysis and the pairwise analysis are adopted. Let χ be the state variable, thus [χ] denotes the expected values of individuals of different types on the population (e.g. $\left[S_{+}\right]$ and $\left[S_{+}{I}_{+}\right]$ represent the expected number of informed susceptible nodes and expected number of links connecting an informed susceptible node to an informed infected node respectively).

Therefore, with the classical mean-field approach, we can obtain:

$$\begin{array}{ccc}\hfill \frac{d\left[I_{+}\right]}{dt}& =& 〈k〉\left[S_{+}\right]({\sigma }_S\beta \left[I_{-}\right]+{\sigma }_S{\sigma }_I\beta \left[I_{+}\right])\hfill \\ & & +\alpha \left[I_{-}\right](\left[S_{+}\right]+\left[I_{+}\right])+\omega \left[I_{-}\right]-\lambda \left[I_{+}\right]\hfill \end{array}$$ (1)

comparatively, with the pairwise approach, we can obtain:

$$\begin{array}{ccc}\hfill \frac{d\left[I_{+}\right]}{dt}& =& ({\sigma }_S\beta \left[S_{+}{I}_{-}\right]+{\sigma }_S{\sigma }_I\beta \left[S_{+}{I}_{+}\right])\hfill \\ & & +\alpha (\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])+\omega \left[I_{-}\right]-\lambda \left[I_{+}\right]\hfill \end{array}$$ (2)

where, the first terms of Eqs. (1) and (2) describe the infection of the $S_{+}$-state individuals, the second terms describe the information acceptance of the $I_{-}$-state individuals, the third terms describe the information generation of the $I_{-}$-state individuals and the last terms represent the information loss of the $I_{+}$-state individuals. Simultaneously, the full set of differential equations based on those two approaches can be illustrated in Appendix A. By the way, the adaptive process could be described by the last terms of ${\displaystyle \frac{d\left[S_{+}{I}_{-}\right]}{dt}},$ ${\displaystyle \frac{d\left[S_{-}{I}_{+}\right]}{dt}}$ and ${\displaystyle \frac{d\left[S_{+}{I}_{+}\right]}{dt}}$ in the pairwise approach of Eq. (4). It should be noted that the pairwise analysis is based on a well-known closure approximation given by $\left[ABC\right]={\displaystyle \frac{\left[AB\right]\left[BC\right]}{\left[B\right]}}$ with the assumption that the degree of each individual obeys Poisson distribution [42], [43]. In general, it might be very hard to get exact solutions of such complex differential equations, thus we give numerical solutions of the equations instead of the theoretical analysis in the following analysis.

3. Results

3.1. Simulation and numerical analysis without adaptive behaviour

In this work, we perform our model on the ER network with a total population of $N=10,000$ and average degree $〈k〉=6$ unless otherwise stated. Moreover, all the simulation results are given by 10,000 realizations. We first consider a simple case of no adaptive behavior when the epidemic and disease information are spreading in the network, i.e., the case of spreading on static network. Fig. 2 gives the simulation result of the fraction of infected nodes evolving with time for various information diffusion probabilities α, with the epidemic spreading probability $\beta =0.3$. For the SI process, the whole population would be infected when β > 0 for the connected social networks, resulting in that the final infected density equals to 1 for all the values of α in Fig. 2. That is to say, the disease information diffusion cannot avoid the epidemic spreading to the whole population when we perform our model on static network. However, we find that the disease information diffusion can slow down the epidemic spreading when we increase the value of α. Furthermore, the time cost for the whole population becomes infected when $\alpha =1$ is about three times longer than that of $\alpha =0$. In this sense, the diffusion of the disease information can slow down the epidemic spreading significantly. In addition, the inset of Fig. 2 indicates that the epidemic spreading can enhance the disease information diffusion. Actually, according to model illustrated in Fig. 1, on the one hand, we realize that the epidemic spreading could be influenced by information diffusion where the epidemic spreading probability of the informed individuals would change; and on the other hand, the information diffusion could be influenced by the epidemic spreading where the social disease information level (namely Info in the inset of Fig. 2) would be higher if more people are infected for the information generation, denoted by the parameter ω. In this way, a mutual feedback between disease spreading and information diffusion emerges: higher prevalence of the infected individuals makes more disease information generated in the population, which in turn gives rise to more informed individuals, thereby weakening the spread of epidemic.

Fig. 2.

The epidemic spreading dynamics of various information diffusion probabilities α without considering the effect of adaptive process. The horizontal axis (T) is the time step for the Monte Carlo simulation, the vertical axis (I) is the density of infected (the vertical axis of the inset figure is the density of informed population in the network). The parameters are set as $\beta =0.3,{\sigma }_S=0.5,{\sigma }_I=0.7,\lambda =0.2,\omega =0.75,r_S=r_I=0.$ The inset shows the information diffusion dynamics (Info) of various β for $\alpha =0.6$.

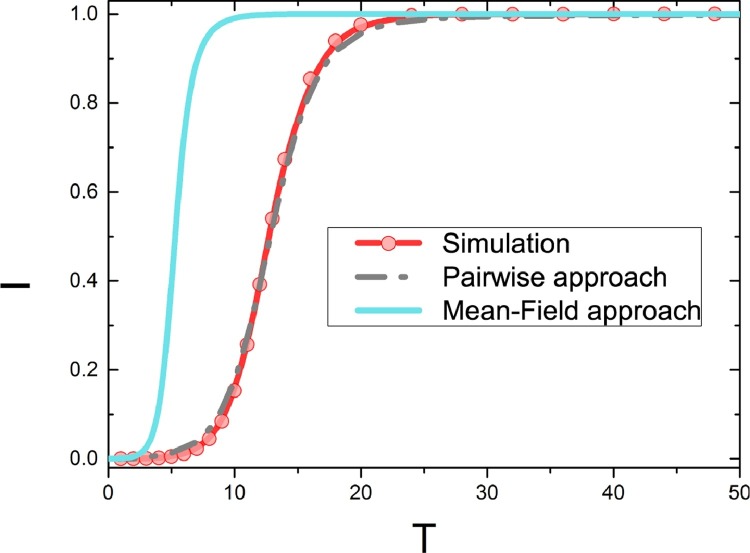
Fig. 3 shows a comparison of the evolution of infected density from the numerical analysis according to Eqs. (3) and (4) and the simulation results on ER network. Infected density curve based on the classical mean-field approach is much quicker than that of the simulation result, which would be caused by the mean-field assumption on the SI model. In the mean-field assumption, the I- and S-state individuals are well-distributed in the system. However, in the SI process, the I-state individuals are all well clustered, resulting in that many I-state individuals have no chance to contact the S-state individuals. In this way, the classical mean-field approach can not exactly describe the SI model. However, such problem is not so significant in the pairwise approach, which consider the time evolution of the links as well. Fig. 3 shows that the infected density curve of the pairwise approach finds good agreement with the simulation results.

Fig. 3.

Comparison of simulation results with the mean-field model and the pair approximation model without considering the effect of adaptive process. The horizontal axis (T) is the time step for the Monte Carlo simulation, the vertical axis (I) is the density of infected. The parameters are set as $\beta =0.3,{\sigma }_S=0.5,{\sigma }_I=0.7,\lambda =0.2,\omega =0.75,\alpha =0.6,r_S=r_I=0$.

3.2. Spreading dynamics with the adaptive process

In this part, we shall present the spreading dynamics with the information-driven adaptive process, the results are shown in Fig. 4 . Different from the results of Fig. 2, the saturation value of the infected density at the final state is much smaller than 1 in Fig. 4(a). That is to say, with the adaptive process based on the information diffusion, many individuals could avoid being infected via reducing some contacts. In addition, we also plot the numerical solution based on the pairwise approach in Fig. 4(a). It can be seen that the pairwise solution is not well consistent with simulation for the spreading dynamic on the adaptive network. The difference might be caused by the network structure variation in the adaptive process, where the assumption of the pairwise approach is the Poisson degree distribution. This conjecture is proved in Fig. 4(b), where the degree distribution of the original network is approximate to the Poisson-distribution with mean degree around 6 (pink circle markers), while the distribution of the network at the final state (gray diamond markers) deviates from the original distribution. In addition, Fig. 4(a) shows that the difference becomes larger with the increase of time, where the degree distribution deviates more away from the original distribution when the process goes on.

Fig. 4.

Dynamical analysis of the spreading model with adaptive process. (a) Comparison of the pairwise model with the simulation results, the horizontal axis (T) is the time step for the Monte Carlo simulation, the vertical axis (I) is the density of infected. (b) Degree distribution of the original network and that after the adaptive process, the horizontal axis (k) represents degree, the vertical axis (p(k)) is degree probability. The parameters are set as $\beta =0.2,{\sigma }_S=0.5,{\sigma }_I=0.7,\lambda =0.2,\omega =0.2,\alpha =0.5,r_S=0.15,r_I=0.1$.

The information-driven adaptive process can not only slow down the speed of epidemic spreading, but also can diminish the epidemic prevalence at the final state significantly according to Figs. 2 and 4. For simplicity, we assume $r_S=r_I=r$ in the following analysis. In order to exhibit the influence of information diffusion in detail, we show the full phase diagram $\alpha -\beta$ with $r=0.1$ in Fig. 5 , the color gives the infected density in the final state for each combination of α and β. The Fig. 5(a) and (b) are the numerical solution of the pairwise approach and the simulation result, respectively. As stated previously, the numerical solution is not very precise, but it can match the overall trend of simulation result well. For a fixed epidemic spreading probability β, epidemic outbreak size reduces with the increase of α. That is to say, the disease information diffusion can inhibit the epidemic spreading. Analogously, the quicker and broader of the information diffusion (larger α) is, the more efficient inhibition on the epidemic spreading will be. In addition, the curve of the color mutation (the dashed green curve) in Fig. 5 could be considered as the transition point, where the epidemic can’t spread out if α and β locate at the area on the left of this curve (the white range). The threshold value of the epidemic spread probability becomes larger with the increase of α.

Fig. 5.

The fraction of infected individuals in the stationary state (colors in the phase diagram represent the density of infected individuals at the final state, the dashed green curve shows that the prevalence value transmits from near 0 to significantly larger than 0) versus α and β for (a) pairwise analysis and (b) simulation result. The parameters are set as ${\sigma }_S=0.5,{\sigma }_I=0.7,\lambda =0.2,\omega =0.2,r_S=r_I=r=0.1$. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In order to intuitively demonstrate the epidemic spreading and the information diffusion process on adaptive network, we show the simulation results of those two types of spreading processes for various α on two different networks, i.e., a 100 × 100 lattice with degree $k=4$ as well as a real-world network, e.g., Haggle network [44]. The contacts in Haggle network represent connection between people measured by carrying wireless devices. The statistics of the network is given in Table 1 . The visualization of how epidemic and disease information interact with each other for these two networks are given in Fig. 6 and Fig. 7 , respectively. Taking Lattice as an example, we present four kinds of different levels of information spreading processes (corresponding to different α), and observe how the information diffusion affects the spreading of epidemic. In addition, as the adaptive edge-breaking process is merely executed on the epidemic spreading process, while these edges can still transmit information, thus the density of informed people can still maintain at a high level in the network. For each α in Fig. 6, firstly we give the fraction of the infected individuals at each time step (the red curve in each subfigure). For some particular time steps, we show the states of each individual with the gridding patterns, where the red dots and the gray dots represent the infected and informed individuals respectively (the contact networks and the un-informed susceptible individuals are not shown in the figures). We can intuitively see the distribution of the infected and informed individuals and conclude that when the diffusion of information is slower than the epidemic, we cannot stop the epidemic from spreading (Fig. 6(a) and (b)), however, when the information is diffusing faster, the epidemic will be trapped into an isolated area and cannot spread anymore (Fig. 6(c) and (d)). Furthermore, the visualization of these two processes on Haggle network displays similar results as the results on Lattice.

Table 1.

Statistics of haggle network, where N, E, C represent the number of nodes, the number of links, clustering coefficient of each system respectively.

Network	N	E	C
Haggle	274	2124	0.0337

Fig. 6.

Illustration to dynamic spreading process by considering the adaptive effect on the lattice. The square gridding patterns show the distribution of the infected and informed individuals in some particular time steps. The red area represents the nodes that are infected by the epidemic, while the gray area represents the informed individuals. The red curves (lower panels) describe the fraction of infected individuals over time with corresponding (the horizontal axis (T) is the time step for the Monte Carlo simulation, the vertical axis (I) is the density of infected). (a) $\alpha =0.1$; (b) $\alpha =0.3$; (c) $\alpha =0.5$; (d) $\alpha =0.7$. Other parameters are set as $\beta =0.4,{\sigma }_S=0.4,{\sigma }_I=0.8,\lambda =0.1,\omega =0.2,r_S=r_I=r=0.1.$ (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 7.

Illustration to dynamic spreading process by considering the adaptive effect on haggle network, while the purple, green and red circles represent individuals in S$-,$ S+ and I state respectively. The red curves (lower panels) describe the fraction of infected individuals over time with corresponding parameters. (a) $\alpha =0.02$; (b) $\alpha =0.3$; (c) $\alpha =0.5$; (d) $\alpha =1.0$. Other parameters are set as $\beta =0.1,{\sigma }_S=0.3,{\sigma }_I=0.5,\lambda =0.08,\omega =0.2,r_S=r_I=r=0.08.$ (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.3. Sensitivity analysis of the model

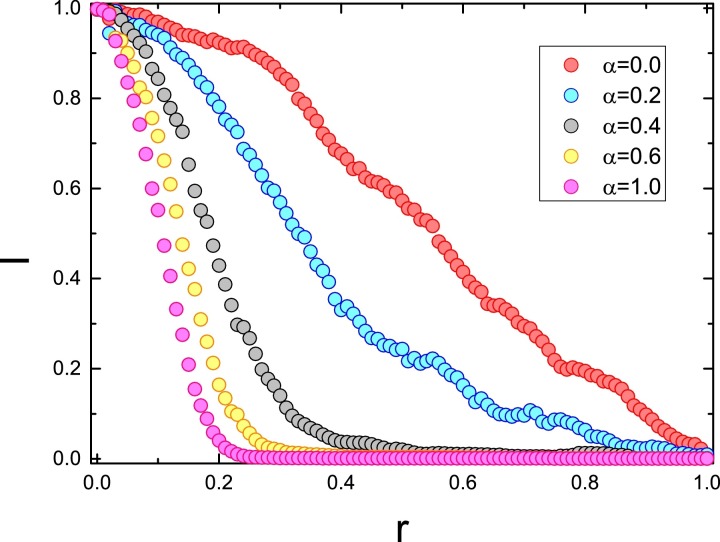
The sensitivity of the edge-breaking probability on epidemic spreading dynamics. The phase diagram in Fig. 5 shows the impact of information diffusion rate α on the epidemic spreading dynamics. In general, the adaptive edge-breaking probability r_S and r_I are also important parameters in affecting the epidemic spreading process. Fig. 8 illustrates the epidemic prevalence in the final state versus the adaptive edge-breaking rate (r) for various information diffusion rate α. It can be found that the epidemic prevalence diminishes with the increase of r, i.e., the epidemic could be controlled if people are very sensitive with the disease information and subsequently keep away from the infected. It should be noted that there is no disease information diffusion when $\alpha =0,$ but with considering the information generation, the infected individuals could stop contacting with the susceptible neighbors to impede the further spreading of epidemic. With the increase of α, the epidemic prevalence reduces sharply versus r and the continuous transition could be observed. By the way, it will change to a total isolation of infected individuals for $r=1,$ which seems to be the most effective way in controlling the contagion [45], [46].

Fig. 8.

Final fraction of infected individuals versus r. Different curves correspond to different α. Other parameters are set as $\beta =0.2,{\sigma }_S=0.5,{\sigma }_I=0.7,\lambda =0.2,\omega =0.2.$

Dynamical characterization of the information-driven rewiring. In order to deeply characterize the complex dynamical features of the proposed process, we concentrate on the distribution of the infected density in the final state (I*) rather than the simple average value [32], [39]. Fig. 9 shows four different types of dynamical behavior by calculating the distribution of the final fraction of infected for various β and r . For the distribution of Fig. 9(a), we have carried out 10,000 realizations of the infected density, and above 94% of the infected density is 0.0001, and the maximal is 0.0007, i.e., the infected density I* → 0, thus we consider this distribution indicates a healthy state (the disease can’t spread out) under the parameters setting here. Similarly, as to the distribution of Fig. 9(d), above 90% of the infected density is higher than 0.8, indicates a case of endemic state (epidemic outbreaks). Whereas the case illustrated in Fig. 9(c) is very different, where the infected density I* is around either zero or a nonzero value. This indicates that a bistable state [32] is located in this model, where healthy state and endemic state are both stable in this case. In addition, a continuous dynamic behavior can also be observed in particular parameter settings (Fig. 9(b)).

Fig. 9.

Distribution of the infected density in the final state versus different values of r and β. Each distribution is obtained by carrying out 10,000 independent realizations for the final fraction of infected. The parameters are set as $r_S=r_I=r=0.7,0.35,0.15,0;\beta =0.05,0.35,0.25,0.4$ for (a), (b), (c) and (d) respectively. Other parameters are ${\sigma }_S=0.5,{\sigma }_I=0.7,\lambda =0.2,\omega =0.2,\alpha =0.6$.

According to the dynamical behavior illustrated in Fig. 9 under different parameter sets, bifurcation diagram of the density of the infected as a function of infected probability β for different values of the edge-breaking rate r is given in Fig. 10 (a). Without the adaptive edge-breaking mechanism ($r=0$), the disease can spread out only if β > 0 for the SI process. When r > 0, the dynamical behaviors become more complicated, where the discontinuous phase transitions, bistable, oscillatory are observed. A fast edge-breaking (large r) leads to a broad healthy and bistable state range (shows by the range in the arrows) in Fig. 10(a). In Fig. 10(b), we give a full $r-\beta$ bifurcation diagram according to our simulation results, and we can clearly identify the areas of healthy, a continous dynamic behavior, bistability and endemic state in this model. At last, we present the dependence of the average value of infected density over 10,000 independent realizations on r and β in Fig. 10(c), where the changing of the density is consistent with the area classification in Fig. 10(b).

Fig. 10.

(a) Bifurcation diagram of the density of the infected I as a function of the infection probability β for different values of the edge-breaking rate r based on the results of simulation of the full network (diamonds). (b) Two parameter bifurcation diagram showing the dependence on the edge-breaking rate r and the infection probability β based on the results of simulation of the full network. (c) Full phase diagram $r-\beta$ for the simulation of the adaptive process. The parameters are the same as Fig. 8.

4. Conclusions

In order to understand the interplay between the dynamics on the network (the spread of epidemic spreading and disease information) and the dynamics of the network (the time varying of network links), we present two types of spreading dynamics with SI and SIS process respectively on an information-driven adaptive network, where the individuals who have known the disease information would probably cut off their links with others. Firstly, we illustrate the mutual feedback between epidemic spreading and information diffusion without considering the edge-breaking process ($r_S=r_I=0$), where the high epidemic prevalence preserves high disease information level, which in turn slows down the epidemic spreading. In this case, the numerical analysis based on the pairwise approach is consistent with the simulation result very well. Secondly, the results are very different when the information-driven edge-breaking process is considered (r_S, r_I > 0). The epidemic cannot spread out if the spreading probability is smaller than the threshold (shown in Fig. 5). In addition, the disease spreading and information diffusion pattern on the lattice as well as on a real-world network give visual representations that the disease might be trapped into an isolated field with information-driven adaptive process. Therefore, the information-driven adaptive process can inhibit the epidemic spreading significantly that it can not only slow down the epidemic spreading speed, but also reduce the epidemic prevalence. Finally, we give the local bifurcation analysis on four types of dynamical phenomena, including healthy, a continuous dynamic behavior, bistable and endemic, indicating that the state changes from healthy to a continuous dynamic behavior, bistable, endemic state as β increases.

In summary, we study the dependence of the epidemic spreading on the disease information diffusion and the information-driven adaptive process, with considering the simplest spreading model (SI) and adaptive process (edge-breaking). Recent researches show the different features between the epidemic and the information diffusion [47], [48], and this difference would also impact the interplay between epidemic spreading and disease information diffusion significantly. Another area for future extension is to adopt networks prediction [49] or other adaptation rules rather than the simple edge-breaking strategy, such as the temporarily deactivating, where the broken links would be active again after a fixed time [41] or, if the corresponding infected node becomes recovered [40].

Denote [χ] as the expected values of individuals of different types described in Section 2.2, the epidemic spreading is depicted by the parameters β, σ_Iβ, σ_Sβ and σ_SIβ, while the diffusion of disease information is controlled by the parameters: α, λ, ω. All these parameters have been explained in Section 2.1. According to the model described above, the differential equations of the mean-field approach (Eq. (3)) and pairwise approach (Eq. (4)) are given as follows.

$$\{\begin{array}{c}\frac{d\left[S_{-}\right]}{dt}=-〈k〉\beta \left[I_{-}\right]\left[S_{-}\right]-〈k〉{\sigma }_I\beta \left[I_{+}\right]\left[S_{-}\right]\hfill \\ -\alpha (\left[S_{+}\right]+\left[I_{+}\right])\left[S_{-}\right]+\lambda \left[S_{+}\right]\hfill \\ \frac{d\left[S_{+}\right]}{dt}=-〈k〉{\sigma }_S\beta \left[I_{-}\right]\left[S_{+}\right]-〈k〉{\sigma }_S{\sigma }_I\beta \left[I_{+}\right]\left[S_{+}\right]\hfill \\ +\alpha (\left[S_{+}\right]+\left[I_{+}\right])\left[S_{-}\right]-\lambda \left[S_{+}\right]\hfill \\ \frac{d\left[I_{-}\right]}{dt}=〈k〉\beta \left[I_{-}\right]\left[S_{-}\right]+〈k〉{\sigma }_I\beta \left[I_{+}\right]\left[S_{-}\right]\hfill \\ -\alpha (\left[S_{+}\right]+\left[I_{+}\right])\left[I_{-}\right]-\omega \left[I_{-}\right]+\lambda \left[I_{+}\right]\hfill \\ \frac{d\left[I_{+}\right]}{dt}=〈k〉{\sigma }_S\beta \left[I_{-}\right]\left[S_{+}\right]+〈k〉{\sigma }_S{\sigma }_I\beta \left[I_{+}\right]\left[S_{+}\right]\hfill \\ +\alpha (\left[S_{+}\right]+\left[I_{+}\right])\left[I_{-}\right]+\omega \left[I_{-}\right]-\lambda \left[I_{+}\right]\hfill \end{array}$$ (3)

$$\{\begin{array}{c}\frac{d\left[S_{-}\right]}{dt}=-\beta \left[S_{-}{I}_{-}\right]-{\sigma }_I\beta \left[S_{-}{I}_{+}\right]-\alpha (\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])+\lambda \left[S_{+}\right]\hfill \\ \frac{d\left[S_{+}\right]}{dt}=-{\sigma }_S\beta \left[S_{+}{I}_{-}\right]-{\sigma }_S{\sigma }_I\beta \left[S_{+}{I}_{+}\right]+\alpha (\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])-\lambda \left[S_{+}\right]\hfill \\ \frac{d\left[I_{-}\right]}{dt}=\beta \left[S_{-}{I}_{-}\right]+{\sigma }_I\beta \left[S_{-}{I}_{+}\right]-\alpha (\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])-\omega \left[I_{-}\right]+\lambda \left[I_{+}\right]\hfill \\ \frac{d\left[I_{+}\right]}{dt}={\sigma }_S\beta \left[S_{+}{I}_{-}\right]+{\sigma }_S{\sigma }_I\beta \left[S_{+}{I}_{+}\right]+\alpha (\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])+\omega \left[I_{-}\right]-\lambda \left[I_{+}\right]\hfill \\ \frac{d\left[S_{-}{I}_{-}\right]}{dt}=-\beta \left[S_{-}{I}_{-}\right]+\lambda (\left[S_{+}{I}_{-}\right]+\left[S_{-}{I}_{+}\right])-\omega \left[S_{-}{I}_{-}\right]+\beta \frac{\left[S_{-}{I}_{-}\right](\left[S_{-}{S}_{-}\right]-\left[S_{-}{I}_{-}\right])}{\left[S_{-}\right]}+{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right](\left[S_{-}{S}_{-}\right]-\left[S_{-}{I}_{-}\right])}{\left[S_{-}\right]}\hfill \\ -\alpha \frac{\left[S_{-}{I}_{-}\right](\left[S_{-}{I}_{+}\right]+\left[S_{-}{S}_{+}\right])}{\left[S_{-}\right]}-\alpha \frac{\left[S_{-}{I}_{-}\right](\left[I_{-}{I}_{+}\right]+\left[S_{+}{I}_{-}\right])}{\left[I_{-}\right]}\hfill \\ \frac{d\left[S_{-}{I}_{+}\right]}{dt}=-{\sigma }_I\beta \left[S_{-}{I}_{+}\right]+\omega \left[S_{-}{I}_{-}\right]+\lambda \left[S_{+}{I}_{+}\right]-\alpha \left[S_{-}{I}_{+}\right]-\lambda \left[S_{-}{I}_{+}\right]-\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{I}_{+}\right]}{\left[S_{-}\right]}-{\sigma }_I\beta \frac{{\left[S_{-}{I}_{+}\right]}^2}{\left[S_{-}\right]}+{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{+}\right]}\hfill \\ +{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{+}\right]}+\alpha \frac{\left[S_{-}{I}_{-}\right](\left[I_{-}{I}_{+}\right]+\left[S_{+}{I}_{-}\right])}{\left[I_{-}\right]}-\alpha \frac{\left[S_{-}{I}_{+}\right](\left[S_{-}{I}_{+}\right]+\left[S_{-}{S}_{+}\right])}{\left[S_{-}\right]}-r_I\left[S_{-}{I}_{+}\right]\hfill \\ \frac{d\left[S_{+}{I}_{-}\right]}{dt}=-{\sigma }_S\beta \left[S_{+}{I}_{-}\right]+\lambda \left[S_{+}{I}_{+}\right]-\lambda \left[S_{+}{I}_{-}\right]-\alpha \left[S_{+}{I}_{-}\right]-\omega \left[S_{+}{I}_{-}\right]-{\sigma }_S\beta \frac{{\left[S_{+}{I}_{-}\right]}^2}{\left[S_{+}\right]}-{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{+}{I}_{-}\right]}{\left[S_{+}\right]}+\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{-}\right]}\hfill \\ +{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{-}\right]}+\alpha \frac{\left[S_{-}{I}_{-}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}-\alpha \frac{\left[S_{+}{I}_{-}\right](\left[I_{-}{I}_{+}\right]+\left[S_{+}{I}_{-}\right])}{\left[I_{-}\right]}-r_S\left[S_{+}{I}_{-}\right]\hfill \\ \frac{d\left[S_{+}{I}_{+}\right]}{dt}=-{\sigma }_S{\sigma }_I\beta \left[S_{+}{I}_{+}\right]+\alpha \left[S_{-}{I}_{+}\right]+\alpha \left[S_{+}{I}_{-}\right]+\omega \left[S_{+}{I}_{-}\right]-2\lambda \left[S_{+}{I}_{+}\right]+{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right](\left[S_{+}{S}_{+}\right]-\left[S_{+}{I}_{+}\right])}{\left[S_{+}\right]}\hfill \\ +{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right](\left[S_{+}{S}_{+}\right]-\left[S_{+}{I}_{+}\right])}{\left[S_{+}\right]}+\alpha \frac{\left[S_{-}{I}_{+}\right](\left[S_{-}{I}_{+}\right]+\left[S_{-}{S}_{+}\right])}{\left[S_{-}\right]}+\alpha \frac{\left[S_{+}{I}_{-}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}-[1-(1-r_S)(1-r_I)]\left[S_{+}{I}_{+}\right]\hfill \\ \frac{d\left[I_{-}{I}_{-}\right]}{dt}=2\beta \left[S_{-}{I}_{-}\right]+2\lambda \left[I_{-}{I}_{+}\right]-2\omega \left[I_{-}{I}_{-}\right]+2\beta \frac{{\left[S_{-}{I}_{-}\right]}^2}{[S-]}+2{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right]\left[S_{-}{I}_{-}\right]}{\left[S_{-}\right]}-2\alpha \frac{\left[I_{-}{I}_{-}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}\hfill \\ \frac{d\left[I_{-}{I}_{+}\right]}{dt}={\sigma }_I\beta \left[S_{-}{I}_{+}\right]+{\sigma }_S\beta \left[S_{+}{I}_{-}\right]+\omega (\left[I_{-}{I}_{-}\right]-\left[I_{-}{I}_{+}\right])+\lambda (\left[I_{+}{I}_{+}\right]-\left[I_{-}{I}_{+}\right])-\alpha \left[I_{-}{I}_{+}\right]+\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{I}_{+}\right]}{\left[S_{-}\right]}+{\sigma }_I\beta \frac{{\left[S_{-}{I}_{+}\right]}^2}{\left[S_{-}\right]}\hfill \\ +{\sigma }_S\beta \frac{{\left[S_{+}{I}_{-}\right]}^2}{\left[S_{+}\right]}+{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{+}{I}_{-}\right]}{\left[S_{+}\right]}+\alpha \frac{\left[I_{-}{I}_{-}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}-\alpha \frac{\left[I_{-}{I}_{+}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}\hfill \\ \frac{d\left[I_{+}{I}_{+}\right]}{dt}=2{\sigma }_S{\sigma }_I\beta \left[S_{+}{I}_{+}\right]+2\alpha \left[I_{-}{I}_{+}\right]+2\omega \left[I_{-}{I}_{+}\right]-2\lambda \left[I_{+}{I}_{+}\right]+2{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right]\left[S_{+}{I}_{+}\right]}{\left[S_{+}\right]}+2{\sigma }_S{\sigma }_I\beta \frac{{\left[S_{+}{I}_{+}\right]}^2}{\left[S_{+}\right]}+2\alpha \frac{\left[I_{-}{I}_{+}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}\hfill \\ \frac{d\left[S_{-}{S}_{-}\right]}{dt}=2\lambda \left[S_{-}{S}_{+}\right]-2\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{S}_{-}\right]}{\left[S_{-}\right]}-2{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right]\left[S_{-}{S}_{-}\right]}{\left[S_{-}\right]}-2\alpha \frac{\left[S_{-}{S}_{-}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}\hfill \\ \frac{d\left[S_{-}{S}_{+}\right]}{dt}=\lambda \left[S_{+}{S}_{+}\right]-\lambda \left[S_{-}{S}_{+}\right]-\alpha \left[S_{-}{S}_{+}\right]-{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{+}\right]}-{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{+}\right]}-\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{-}\right]}-{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{-}\right]}\hfill \\ +\alpha \frac{\left[S_{-}{S}_{-}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}-\alpha \frac{\left[S_{-}{S}_{+}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}\hfill \\ \frac{d\left[S_{+}{S}_{+}\right]}{dt}=2\alpha \left[S_{-}{S}_{+}\right]-2\lambda \left[S_{+}{S}_{+}\right]-2{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right]\left[S_{+}{S}_{+}\right]}{\left[S_{+}\right]}-2{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{+}{S}_{+}\right]}{\left[S_{+}\right]}+2\alpha \frac{\left[S_{-}{S}_{+}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}\hfill \end{array}$$ (4)