Supply chain disruption management and evolutionarily stable strategies of retailers in the quantity-setting duopoly situation with homogeneous goods

Abstract

This paper develops an indirect evolutionary game model with two-vertically integrated channels to study evolutionarily stable strategies (ESS) of retailers in the quantity-setting duopoly situation with homogeneous goods and analyzes the effects of the demand and raw material supply disruptions on the retailers’ strategies. Every channel consists of one manufacturer and many (a sufficiently large number of) retailers that sell products in different markets by adopting two pure marketing strategies: profit maximization and revenue maximization. We find that revenue maximization strategy may prevail and profit maximization strategy may become extinct. Two strategies may coexist, i.e., all retailers in one channel will choose profit maximization strategy and all retailers in the other will choose revenue maximization strategy. The ESS of retailers depends on the relative size of the market scale and unit cost. The supply chain disruptions affect the ESS of retailers. We also introduce a recovery model of the supply chain under disruptions and illustrate the effect of disruptions on the ESS and on the average profits of channels in a market using a numerical simulation.

1. Introduction

Recently, there has been a widespread interest in using evolutionary game theory to study economic system, which remedies some drawbacks of orthodox game theory. In particular, orthodox game theory assumes that (a) players are fully rational and can take an optimal action (sophisticated); (b) they have the common knowledge of rationality; (c) they know the rules of the game. But, in reality players often have bounded rationality, can not take an optimal action (naïve), may not know the others’ rationality and the rules of the game, which are the assumptions made in evolutionary game theory. Even rational players often make mistakes that will affect the strategies of other players. Other fully rational players often make noise in the form of mutations or mistakes (see Young, 1993). There may be multiple solutions of general non-cooperative games. How do players choose among multiple solutions? It is very difficult for orthodox game theory to answer this question, but rather straightforward for evolutionary game theory. From a particular starting point, a unique steady state will be reached in a evolutionary game. The selected equilibrium is path-dependent, and the observed equilibrium depends on the initial condition.

Our study is closely related to the disruption management and evolutionary management of a supply chain, and duopoly competition. There are literatures studying oligopoly competition from evolutionary perspective. For the competition of the quantity-setting homogeneous oligopoly, see, for example, Tanaka (1999) studied the stochastically stable output of the asymmetric homogeneous oligopoly with low cost and high cost firms and showed that a stochastically stable output equals the competitive (Walrasian) output. Bischi and Kopel (2001) considered a simple Cournot-type duopoly market where competitors produce homogeneous goods and offer them at discrete time periods on a common market. They showed that for the nonlinear model multiple (locally) stable equilibriums may be observed. In this paper, we will study the quantity-setting homogeneous duopoly. Xiao and Yu (2005) studied the evolutionarily stable marketing strategies of retailers in two vertically integrated channels with differentiated goods. In the model, they analyzed the effects of the type of strategic interaction (strategic substitutes or complements). In this paper, we consider the two vertically integrated channels with homogeneous goods. There are literatures studying the differentiated goods competition (see, Tanaka, 2000, Xiao and Yu, 2005). Tanaka (2000) presented evolutionary game theoretic analyses of symmetric price-setting and quantity-setting oligopolies with differentiated goods. Jin (2001) showed that a simple and optimal price strategy could lead the market to a unique steady state. He found that the price convergence does not necessarily require almost perfect information and full rationality. In our model, we investigate the quantity-setting duopoly other than the price-setting duopoly. Xiao and Yu (2005) showed that profit maximization is a unique ESS in the price-setting duopoly situation with differentiated goods and linear inverse demand functions. Hence, we do not consider the price-setting duopoly situation.

Güth and Yaari (1992) brought forth an indirect evolutionary approach to study the effect of the preferences of individuals on their strategies. They assumed that players rationally take actions based on their preferences, but their preferences evolve over time. For the indirect evolutionary perspective, one can also refer to Bester and Güth (1998) and Huck and Oechssler (1999). In our model, we study the evolutionarily stable strategies (ESS) of preferences of retailers from an indirect evolutionary perspective. The retailers will maximize their utilities (revenues or profits) based on their preferences.

In general, economic literatures on evolutionary game theory assume the existence of many players and analyze what percentage of the population would choose a given strategy. Others analyze the change of the probability for choosing a specific strategy (Morrison, 1996). In our model, we focus on the distribution of strategies (the fraction of using a corresponding strategy) in the population rather than on the strategies of rational individuals.

On the evolutionary management of a supply chain, Kosfeld (2002) argued that the ‘solution’ to the coordination problem between stores and customers depends on the specific cost structure of stores and the preferences of customers. In his model, the demand is deterministic. However, a typical supply chain frequently faces disruptions caused by internal or external factors including demand fluctuations (new orders, order cancellations), raw material shortages, delivery delays due to transportation problems or inclement weather (such as storm, heavy fog), resource unavailability, natural disasters, etc. The supply chain disruption management is a new and interesting field. Qi et al. (2004) considered the coordination of a supply chain with one supplier and one retailer under demand disruptions. In their model, the demand disruptions incur a penalty to the supplier. Xia et al. (2004b) considered disruption management for a two-stage production and inventory system. Xia et al. (2004a) introduced a production and inventory management model with raw material supply disruptions. Xiao et al. (2005) considered the coordination of a supply chain with one manufacturer and two competing retailers when the demand is disrupted. Huntington (2003) studied the effect of energy disruptions on the decision-making of firms and aggregate economy. In addition to the disruption caused by accidental events, strategic disruption is often used by some firms. Strategic disruption refers to a firm’s intentional manipulation of its competitor’s transaction cost structure in an attempt to weaken the competitor’s alignment of its governance structure. Averyt and Ramagopal (1999) used the auto industry as a case to examine the policy of strategic disruption pursued by American producers against Japanese competitors since the 1980s. In their model, a firm destroys its competitor’s alignment of transactions and governance structures but leaves the firm’s own alignment relatively unchanged through altering governance rules. Thus, its competitor’s cost increases. In 1992, the United States and Japan signed the ‘Global Partnership Plan of Action’, which is a strategic disruption management policy of breaking the established ties between Japanese auto producers and Japanese parts suppliers (Lewis and Weiler, 1996). To our best knowledge, an evolutionary perspective on the effect of disruptions on a supply chain has not yet been studied in the literature. This paper will study the effect of the supply chain disruptions including the raw material supply and demand disruptions on the retailers’ strategies by employing an indirect evolutionary game model. We neglect the penalty cost incurred by the supply chain disruptions when we consider the long-term equilibrium because the manufacturers will adjust their production scales and plans rapidly. In Section 6, we will also consider the case with a penalty cost. We will illustrate our findings using a numerical simulation.

Economic literature often assumes that a firm is a profit-maximizer. But, is a profit maximization strategy evolutionary stable? Bester and Güth (1998) argued that altruism preferences may be evolutionarily stable. In other words, a profit maximization strategy may be evolutionarily unstable (see Bolle, 2000). Schaffer (1989) applied the finite population evolutionarily stable strategy to study whether profit-maximizers are the best survivors. He showed that the strategy that survives in an economic natural selection is the relative, not absolute, payoff maximization strategy. Güth and Peleg (2001) studied when a payoff maximization strategy will survive by employing an indirect evolutionary game. Xiao and Yu (2005) introduced an indirect evolutionary game approach to explain why there exists revenue maximization behavior and argued that a revenue maximization strategy may be a stable strategy and a profit maximization strategy may be unstable in the quantity-setting duopoly situation with differentiated goods. In this paper, we assume that a retailer has two strategies: profit maximization and revenue maximization. We will study the stability conditions of the profit maximization strategy. Our dynamic system is a special ordinary differential equation system that satisfies the admissible conditions given in Friedman (1991). We find that profit maximization strategy may become extinct and revenue maximization strategy prevails when the market scale is large enough. In this case, the retailers choosing revenue maximization strategy will gain more profit through selling more goods although the unit profit decreases. We also find that the relative unit cost affects the retailers’ strategies and the coexistence phenomenon often happens. Supply chain disruption is often recovered within a finite desired time, so we also introduce a disruption recovery model.

The rest of the paper is organized as follows. Section 2 gives some basic descriptions. Section 3 presents a main theorem and a corollary on the stability of equilibrium. Section 4 analyzes the effects of demand disruptions on the supply chain, in particular, on the retailers. Section 5 analyzes the effects of the raw material supply disruptions on the supply chain. In this section, we analyze the effects in two cases: the unit production cost change synchronously and asynchronously. We also analyze the effects when the demand and raw material supply are simultaneously disrupted using a numerical example. Section 6 introduces a recovery model of the supply chain under disruptions and analyzes the effect of the disruptions on the average profit of channels in a market. Section 7 gives a brief summary and conclusions.

2. The model

Assume that an economic system consists of two vertically integrated channels denoted by A and B. Every channel consists of one manufacturer and many (a sufficiently large number of) retailers. The manufacturer in channel i denoted by i, i  =  A,  B. The manufacturers need some raw materials to produce homogeneous products. The retailers respectively sell products in many (a sufficiently large number of) independent markets (Boyaci and Gallego, 2002). We call a retailer in channel i an individual in population i consisting of all retailers in channel i, i  =  A,  B. An individual in population A randomly competes with an individual in population B in a market (there are exactly two retailers in a given market, we will eliminate a market if neither a pair of retailers is matched in this market). For simplicity, we do not consider the intra-population’s competition that two individuals in the same population compete. Every individual has two (pure) strategies: profit maximization (for short P) and revenue maximization (for short R). In a one-shot game, two individuals simultaneously determine their marketing strategies, and determine optimal quantities according to their strategies. Hosomatsu (1969) showed how oligopoly firms reach a Cournot equilibrium without knowing the demand function and rivals’ costs. Hehenkamp et al. (1999) showed that the quantity distribution always converges under monotonic selection dynamic system to a distribution with probability one on a quantity equal or similar to a classical Cournot equilibrium. For simplicity, we assume that every retailer can take its optimal quantity reaction based on its preference (P or R). We focus on the ESS of the preferences. In other words, we study the ESS of the populations by employing an indirect evolutionary game. Friedman and Mezzetti (2002) set up a quantity choice model of dynamic oligopoly with bounded rationality. However, they retained an important feature of rational behavior strategy, profit maximization. We also assume that the individuals have bounded rationality. We focus on the distribution of the individual strategies in the population. In our model, the individuals repeatedly play an evolutionary game other than a one-shot game with each other. Let the unit production cost of manufacturer i be c _i and the quantity of goods of a retailer in channel i be q _i, i  =  A,  B. We normalize the unit cost of retailers to zero. 1 The unit price is p. We assume that every market faces the same inverse demand function and two channels monopolize markets. Without loss of generality, we assume that c _A  ⩾  c _B and the inverse demand function is p  =  a  −  q _A  −  q _B, or q _A  +  q _B  =  a  −  p. The parameter a represents the market scale and a  > max{c _A,  c _B} =  c _A. The analysis can be extended to the case with nonlinear inverse demand function.

We first consider the one-shot game. According to the above descriptions, in a market the profit function of channel i is π _i(q _A,  q _B) = (a  −  q _A  −  q _B  −  c _i)q _i, the revenue function of channel i is R _i(q _A,  q _B) = (a  −  q _A  −  q _B)q _i.

We have assumed that a retailer (individual A) in population A randomly competes with a retailer (individual B) in population B for a given market. If both individuals choose strategy P, the Cournot quantities of individuals A and B are

$$q_A^{\mathit{PP}}={\displaystyle \frac{1}{3}}(a+c_B-2c_A)\text{,}{q}_B^{\mathit{PP}}={\displaystyle \frac{1}{3}}(a+c_A-2c_B)\text{.}$$

Furthermore, the profits of the channels in the market are

$${\pi }_A^{\mathit{PP}}(q_A^{\mathit{PP}}\text{,}{q}_B^{\mathit{PP}})={\displaystyle \frac{1}{9}}(a+c_B-2c_A{)}^2\text{,}{\pi }_B^{\mathit{PP}}(q_A^{\mathit{PP}}\text{,}{q}_B^{\mathit{PP}})={\displaystyle \frac{1}{9}}(a+c_A-2c_B{)}^2\text{.}$$

If individual A chooses strategy P and individual B chooses strategy R, the Cournot quantities for individuals A and B are

$$q_A^{\mathit{PR}}={\displaystyle \frac{1}{3}}(a-2c_A)\text{,}{q}_B^{\mathit{PR}}={\displaystyle \frac{1}{3}}(a+c_A)\text{.}$$

The profits of the channels in the market are

$${\pi }_A^{\mathit{PR}}(q_A^{\mathit{PR}}\text{,}{q}_B^{\mathit{PR}})={\displaystyle \frac{1}{9}}(a-2c_A{)}^2\text{,}{\pi }_B^{\mathit{PR}}(q_A^{\mathit{PR}}\text{,}{q}_B^{\mathit{PR}})={\displaystyle \frac{1}{9}}(a+c_A)(a+c_A-3c_B)\text{.}$$

If individual A chooses strategy R and individual B chooses strategy P, the Cournot quantities for individuals A and B are

$$q_A^{\mathit{RP}}={\displaystyle \frac{1}{3}}(a+c_B)\text{,}{q}_B^{\mathit{RP}}={\displaystyle \frac{1}{3}}(a-2c_B)\text{.}$$

The profits of the channels in the market are

$${\pi }_A^{\mathit{RP}}(q_A^{\mathit{RP}}\text{,}{q}_B^{\mathit{RP}})={\displaystyle \frac{1}{9}}(a+c_B)(a+c_B-3c_A)\text{,}{\pi }_B^{\mathit{RP}}(q_A^{\mathit{RP}}\text{,}{q}_B^{\mathit{RP}})={\displaystyle \frac{1}{9}}(a-2c_B{)}^2\text{.}$$

If both individuals choose strategy R, the Cournot quantities of individuals A and B are

$$q_A^{\mathit{RR}}=q_B^{\mathit{RR}}={\displaystyle \frac{1}{3}}a\text{.}$$

The profits of the channels in the market are

$${\pi }_A^{\mathit{RR}}(q_A^{\mathit{RR}}\text{,}{q}_B^{\mathit{RR}})={\displaystyle \frac{1}{9}}a(a-3c_A)\text{,}{\pi }_B^{\mathit{RR}}(q_A^{\mathit{RR}}\text{,}{q}_B^{\mathit{RR}})={\displaystyle \frac{1}{9}}a(a-3c_B)\text{.}$$

Some economists suggested that a linear incentive mechanism is optimal (Groves and Loeb, 1979, Ugarte and Oren, 2000, Tirole, 1988). We assume that the manufacturers use a linear incentive mechanism to the individuals in their own populations, respectively, i.e., b _i  +  d _i π _i, i  =  A,  B, where 0 <  d _i  < 1 and π _i is the profit of channel i in a given market. Note that the magnitude of b _i does not affect the ESS and the magnitude of d _i only affects the speed of evolution. However, we focus on the ESS of populations other than their speeds. Thus, without loss of generality, we assume that the evolution of populations’ strategy is based on the profit bi-matrix given in Table 1 .

Table 1.

Profit bi-matrix

A	B
	P	R
P	${\pi }_A^{\mathit{PP}}$, ${\pi }_B^{\mathit{PP}}$	${\pi }_A^{\mathit{PR}}$, ${\pi }_B^{\mathit{PR}}$
R	${\pi }_A^{\mathit{RP}}$, ${\pi }_B^{\mathit{RP}}$	${\pi }_A^{\mathit{RR}}$, ${\pi }_B^{\mathit{RR}}$

Table 1 has the same form as that in Xiao and Yu (2005). But, Xiao and Yu (2005) focused on differentiated goods (substitutes or complements) and the ESS of the marketing objectives without considering the supply chain disruptions. However, in this paper, we focus more on the effect of the raw material supply and demand disruptions on the ESS of retailers with homogeneous products. The most fitting strategy becomes more prevalent and the other strategies may gradually become extinct.

Since individuals random compete, the matched individuals play a one-shot game other than a multi-stage game. Aggregate strategies of populations do not change too abruptly, and they continuously update their strategies over time. Let the fraction of individuals using strategy P in population i be s _i, so the fraction of individuals using strategy R in population i is 1 −  s _i, i  =  A,  B. The fraction differs from the probability in the mixed-strategy. The former emphasizes the relative size of subpopulation using a strategy in the population, and the latter emphasizes the stochasticity of using a strategy. The change of the fraction reflects the evolution of the population’s strategies, and the change of the probability reflects the change of the individuals’ subjective beliefs or strategy. In the former case, the evolution of the population’s strategies is based on the fitness of a strategy. The fitness depends only on the individual’s strategy set and the strategy fractions of two populations. In the latter case, the individual makes decisions based on the expected payoff.

We may see that there are simultaneously two Nash equilibriums (P,  R) and (R,  P) for the one-shot game. Individual A chooses strategy P when individual B chooses strategy R for equilibrium (P,  R). Individual A chooses strategy R when individual B chooses strategy P for equilibrium (R,  P). However, individual A does not know if individual B chooses P or R. But, which equilibrium will be selected? Moreover, which equilibrium will an initial state evolve to? Without loss of generality, we assume that the population’s strategy evolve in the form of a Malthusian dynamic system (or replicator dynamic system) which is a very general dynamic system in evolutionary game theory (for detailed, see Friedman, 1991, Cressman, 1992, Xiao, 2004). In a replicator dynamic system, the growth rate ${\dot{s}}_A/s_A$ equals the strategy P’s fitness e ₁ A(s _B, 1 −  s _B)^T less the average fitness (s _A, 1 −  s _A)A(s _B, 1 −  s _B)^T of population A, where ${\dot{s}}_A=\mathrm{d}{s}_A/\mathrm{d}t$, e ₁  = (1, 0), represents that all individuals in population A choose strategy P, and $A=\left[\begin{array}{cc}\hfill {\pi }_A^{\mathit{PP}}\hfill & \hfill {\pi }_A^{\mathit{PR}}\hfill \\ \hfill {\pi }_A^{\mathit{RP}}\hfill & \hfill {\pi }_A^{\mathit{RR}}\hfill \end{array}\right]$, represents the payoff matrix of individual A. Hence, the replicator dynamic system for population A is

$${\dot{s}}_A=s_A(e_1-(s_A\text{,}1-s_A))A(s_B\text{,}1-s_B{)}^{\mathrm{T}}\text{,}$$

Inserting the profits into ${\dot{s}}_A$ and rewrite the dynamic system, we have

$${\dot{s}}_A={\displaystyle \frac{1}{9}}{c}_A{s}_A(1-s_A)(4c_A-a-c_B{s}_B)\text{.}$$ (1)

Similarly, the replicator dynamic system for population B is

$${\dot{s}}_B={\displaystyle \frac{1}{9}}{c}_B{s}_B(1-s_B)(4c_B-a-c_A{s}_A)\text{.}$$ (2)

Eqs. (1), (2) are the continuous frequency dynamic systems for the two populations consisting of the retailers in channels A and B, respectively.

3. Evolutionarily stable strategies under normal operation

The populations are said to be at ESS, if they cannot be invaded by a small (relative to the number in the initial population) subpopulation of individuals using a different individual strategy. ESS is a static conception of evolutionary game theory. In order to study the dynamic characteristic of an evolutionary game, a dynamic system is often incorporated such as replicator dynamic system. An equilibrium of the replicator dynamic system (1), (2) is a point (s _A,  s _B) ∈ [0, 1] × [0, 1] such that ${\dot{s}}_A={\dot{s}}_B=0$. ESS of two populations differs from that of one population (Cressman, 1992). In the one population model, ESS and payoff matrix must be symmetrical for two individuals. But, in the two populations model, ESS and payoff matrix may be asymmetric for two individuals in different populations. For example, for hawk-dove game, two types of models have different ESS even when there are the same payoff bi-matrixes (Xiao, 2004).

From Eqs. (1), (2), we derive the following.

Theorem 1

For the replicator dynamic system given by Eqs. (1), (2) , we have the following:

• (i) (0,   0), (0,   1), (1,   0) and (1,   1) are its equilibriums (fixed points).
• (ii)
  If the unit costs satisfy $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$ , $(s_A^{\ast }\text{,}{s}_B^{\ast })$ is also an equilibrium of the replicator dynamic system (1), (2) on [0,   1]  ×  [0,   1] for 4c _A  −  c _B  ⩽  a  ⩽  4c _B , where

  $$s_A^{\ast }=(4c_B-a)c_A^{-1}\text{,}{s}_B^{\ast }=(4c_A-a)c_B^{-1}\text{.}$$

Proof

It is obvious that Part (i) holds. We now show Part (ii). A point (s _A,  s _B) is an equilibrium of the replicator dynamic system (1), (2) if and only if

$$4c_A-a-c_B{s}_B=0\text{and}4c_B-a-c_A{s}_A=0\text{,}$$

where (s _A,  s _B) ∈ [0, 1] × [0, 1], i.e.,

$$s_A^{\ast }=(4c_B-a)c_A^{-1}\text{,}{s}_B^{\ast }=(4c_A-a)c_B^{-1}\text{.}$$

From $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$, it follows that $(s_A^{\ast }\text{,}{s}_B^{\ast })$ is an equilibrium point if and only if

$$4c_A-c_B⩽a⩽4c_B\text{,}$$

i.e., Part (ii) holds. □

From Theorem 1, the point $(s_A^{\ast }\text{,}{s}_B^{\ast })$ becomes the point (0, 0) if a  = 4c _B  = 4c _A; the point $(s_A^{\ast }\text{,}{s}_B^{\ast })$ becomes the point (0, 1) if a  = 4c _B and $c_A={\displaystyle \frac{5}{4}}{c}_B$; the point $(s_A^{\ast }\text{,}{s}_B^{\ast })$ becomes the point (1, 1) if a  = 4c _A  −  c _B and c _A  =  c _B. From Theorem 1 and c _A  ⩾  c _B, we know that $s_A^{\ast }⩽s_B^{\ast }$. Hence, the point $(s_A^{\ast }\text{,}{s}_B^{\ast })$ does not become the point (1, 0).

Hofbauer and Sigmund (1998) gave the linearization method of using a Jacobian matrix. We linearize the system (1), (2) using the Jacobian method. The Jacobian matrix of the system is

$$J=\left[\begin{array}{cc}\hfill {\displaystyle \frac{1}{9}}{c}_A(1-2s_A)(4c_A-a-c_B{s}_B)\hfill & \hfill -{\displaystyle \frac{1}{9}}{c}_A{c}_B{s}_A(1-s_A)\hfill \\ \hfill -{\displaystyle \frac{1}{9}}{c}_A{c}_B{s}_B(1-s_B)\hfill & \hfill {\displaystyle \frac{1}{9}}{c}_B(1-2s_B)(4c_B-a-c_A{s}_A)\hfill \end{array}\right]\text{.}$$

The local stability of linear differential equations is determined by both determinant and trace. The determinant of the Jacobian matrix is

$$\det J={\displaystyle \frac{1}{81}}{c}_A{c}_B\left[(1-2s_A)(1-2s_B)(4c_A-a-c_B{s}_B)(4c_B-a-c_A{s}_A)-c_A{c}_B{s}_A{s}_B(1-s_A)(1-s_B)\right]\text{,}$$

the trace of the Jacobian matrix is

$$\mathrm{tr}J={\displaystyle \frac{1}{9}}{c}_A(1-2s_A)(4c_A-a-c_B{s}_B)+{\displaystyle \frac{1}{9}}{c}_B(1-2s_B)(4c_B-a-c_A{s}_A)\text{.}$$

Furthermore, we can derive the following.

Theorem 2

Assume that $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$ and 4c _A  −  c _B  ⩽  a  ⩽  4c _B , we have the following:

• (i) The equilibrium (0,   0) is unstable if a  <  4c _B or a   =   4c _B  <  4c _A but stable if a   =   4c _B   =   4c _A .
• (ii) The equilibrium (0,   1) is an ESS if 4c _A  −  c _B  <  a  <  4c _B , stable if a   =   4c _B  >  4c _A  −  c _B or a   =   4c _A  −  c _B  <  4c _B ; but unstable if a   =   4c _B   =   4c _A  −  c _B .
• (iii) The equilibrium (1,   0) is an ESS if c _B  <  c _A , or both c _A   =   c _B and 4c _A  −  c _B  <  a  <  4c _B , and it is stable if c _A   =   c _B and either a   =   4c _A  −  c _B or a   =   4c _B .
• (iv) The equilibrium (1,   1) is unstable if 4c _A  −  c _B  <  a  ⩽  4c _B or both a   =   4c _A  −  c _B and c _A  >  c _B , but stable if a   =   4c _A  −  c _B and c _A   =   c _B .
• (v) The equilibrium $(s_A^{\ast }\text{,}{s}_B^{\ast })$ is a saddle point if 4c _A  −  c _B  <  a  <  4c _B , unstable if a   =   4c _A  −  c _B and $c_B<c_A<{\displaystyle \frac{5}{4}}{c}_B$ , but stable if a   =   4c _B and $c_B<c_A<{\displaystyle \frac{5}{4}}{c}_B$ .

Proof of Theorem 2 is given in Appendix A. According to Cressman (1992), a locally and asymptotically stable equilibrium of a bi-matrix game with two players and two strategies is an ESS. Hence, in this paper, we can use ESS instead of the locally and asymptotically stable property. From Theorem 2, we derive the following.

Corollary 1

If 4c _A  −  c _B  <  a  <  4c _B and $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$ , the equilibriums (0,   1) and (1,   0) are ESS.

From Corollary 1. we know that all individuals in one population will choose profit maximization strategy and all individuals in the other will choose revenue maximization strategy when 4c _A  −  c _B  <  a  < 4c _B and $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$. It follows from Corollary 1 that s _A  =  s _B is a trajectory of the system (1), (2) if c _A  =  c _B and 4c _A  −  c _B  <  a  < 4c _B. The initial state (s _A0,  s _B0) evolves to the equilibrium (1, 0) if s _A0  >  s _B0, to the equilibrium $(s_A^{\ast }\text{,}{s}_B^{\ast })$ if s _A0  =  s _B0 and to the equilibrium (0, 1) if s _A0  <  s _B0. But, the equilibrium $(s_A^{\ast }\text{,}{s}_B^{\ast })$ is not an ESS and it is even unstable. In other words, when the fraction of individuals using profit maximization strategy in a population is larger than the fraction for the other population, its ESS is profit maximization and the other’s ESS is revenue maximization. We know roughly the equilibrium into which a point will evolve by using numerical simulation. For example, for the value of parameters:

$$a=3.9\text{,}{c}_A=1.2\mathrm{and}{c}_B=1\text{,}\mathrm{and}\mathrm{initial}\mathrm{state}(0.5\text{,}0.3)\text{,}$$

which are used throughout the paper (unless otherwise stated). We can depict Fig. 1 for the system (1), (2).

Fig. 1.

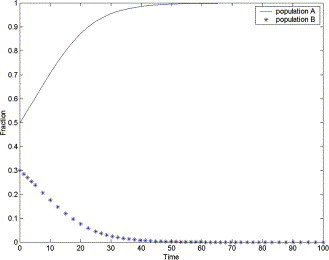
The fractions of individuals using strategy P as a function of time.

For different values of parameters, the evolutionary paths often are different. But, the basic characteristics of the effect of the disruptions on the evolutionary paths are similar. In the above, we have studied the evolution of the populations’ strategies, which will affect the average profits and production quantities of the channels in a market. The average profit of channel A is (s _A, 1 −  s _A)A(s _B, 1 −  s _B)^T and its average quantity is

$$(s_A\text{,}1-s_A)\left[\begin{array}{cc}\hfill q_A^{\mathit{PP}}\hfill & \hfill q_A^{\mathit{PR}}\hfill \\ \hfill q_A^{\mathit{RP}}\hfill & \hfill q_A^{\mathit{RR}}\hfill \end{array}\right](s_B\text{,}1-s_B{)}^{\mathrm{T}}\text{.}$$

Similarly, we can write the average profit and average quantity of channel B in a market. We assume that the production of a manufacturer allows a small flexibility such that a small production deviation does not incur a deviation cost, but a large production deviation will incur a deviation cost. Thus, a manufacturer will not be penalized with a deviation cost when the fractions s _A and s _B change continuously. We will consider two types of disruptions including the demand disruption and the raw material supply disruption, respectively.

4. Demand disruptions and evolutionary stable strategies of retailers

In practice, the demand is often disrupted by technological innovation, haphazard event, new policy, entrance of a new firm, promotional events of the firm and/or its competitors, etc. The factors will result in the increase or decrease of demand for the channels. For example, Severe Acute Respiratory Syndrome (SARS) has been reported in Asia, North America, and Europe in 2003. SARS affected to a large degree the demand for tourism, recreation, food, medicine and the related industries in the regions. Some rumors on the fact that vinegar can prevent SARS were released after SARS was discovered in Guangzhou, China, and then the demand for vinegar increased dramatically. People feared to catch SARS in the recreational place, which has resulted in the decrease of the demand for recreation. We assume that Δa is the changed amount of the market scale, i.e., the market scale after disruptions is a  + Δa. In this section, we will study how the demand disruptions affect a supply chain, and in particular, the retailers. We assume that there are only demand disruptions and other settings are unchanged. Note that the retailers do not concern the production deviation cost. The change of a retailer’s quantity may not incur a penalty cost for the manufacturer because the change may not result in the deviation of the total production quantity of the manufacturer. In this section, we can neglect the penalty cost incurred due to the supply chain disruptions because we consider long-term equilibrium without disruption recovery.

According to Corollary 1, we know that the equilibriums under disruptions have the same local stability as that without disruptions when 4c _A  −  c _B  −  a  < Δa  < 4c _B  −  a. But, the incremental demand Δa is sometimes either more than 4c _B  −  a or less than 4c _A  −  c _B  −  a. When Δa  = 4c _B  −  a, the equilibriums have the same stability as the case a  = 4c _B in Section 3. Similar argument applies to the case Δa  = 4c _A  −  c _B  −  a. Thus, we only consider the cases Δa  > 4c _B  −  a and Δa  < 4c _A  −  c _B  −  a. Similar to Theorem 2, we can derive the following.

Theorem 3

Assume that $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$ and Δa  >  4c _B  −  a. For the system (1), (2) , we have

• (i) If Δa  >  4c _A  −  a, the equilibrium (0,   0) is a unique ESS.
• (ii) If 4c _B  −  a  < Δa  <  4c _A  −  a, the equilibrium (1,   0) is a unique ESS.
• (iii) If Δa   =   4c _A  −  a, there is no ESS.

From Corollary 1 and Theorem 3, the disruptions will induce the population whose strategies originally evolved to profit maximization to choose revenue maximization strategy if Δa  > 4c _A  −  a. In other words, although profit maximization strategy for a population prevails currently, it may become extinct and revenue maximization strategy will prevail in the case that the incremental demand is sufficiently large. The disruptions will induce the retailers in the channel with lower cost to choose revenue maximization strategy and the retailers in the channel with higher cost to choose profit maximization strategy if 4c _B  −  a  < Δa  < 4c _A  −  a. In other words, the initial state originally evolved to the equilibrium (0, 1) will evolve to the equilibrium (1, 0) when the demand increases within the above range. Similar to Theorem 2, we can also derive the following from Theorem 1.

Theorem 4

Assume that $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$ and c _A  −  a  < Δa  <  4c _A  −  c _B  −  a. For the system (1), (2) , we have

• (i) If Δa  <  4c _B  −  c _A  −  a, the equilibrium (1,   1) is a unique ESS.
• (ii) If 4c _B  −  c _A  −  a  < Δa  <  4c _A  −  c _B  −  a, the equilibrium (1,   0) is a unique ESS.
• (iii) If Δa   =   4c _B  −  c _A  −  a, there is no ESS.

In Theorem 4, c _A  −  a  < Δa or a  + Δa  >  c _A, assures that the equilibrium price and quantity are positive. From Corollary 1 and Theorem 4, we know that the disruptions will induce the population whose strategies originally evolved to revenue maximization to choose profit maximization strategy if Δa  < 4c _B  −  c _A  −  a. In other words, although revenue maximization strategy for one population prevails currently, it may become extinct and profit maximization strategy will prevail when the decrement in demand is sufficiently large. The populations’ strategies evolve to profit maximization when the demand is sufficiently small. Similar to Theorem 3, the disruptions will induce the retailers in the channel with lower cost to choose revenue maximization strategy and that with higher cost to choose profit maximization strategy if the demand decreases within the above range.

In Theorem 3, Theorem 4, we have studied the effects of the demand disruptions on the ESS of the retailers from the theoretical point of view. Although some results are given, it is difficult for us to understand the results. For a given initial state, it is very difficult to understand the effects of the demand disruptions on its evolutionary path from a theoretical point of view. Now, we study the effect by using numerical simulation, which may also facilitate the readers. When the demand is disrupted, we can depict Fig. 2 . In Fig. 2, ‘delta a’ denotes Δa.

Fig. 2.

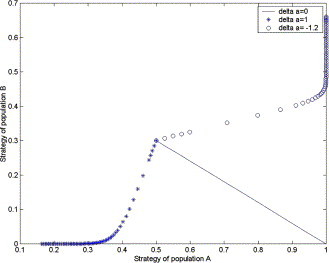
The ESS of retailers under demand disruptions with t ∈ [0, 100].

Theorem 3, Theorem 4 study the effects of demand disruptions on the ESS of retailers. In fact, the demand disruptions also indirectly affect the supplier due to the change of order quantity of manufacturers. For the demand disruptions, see Fig. 3 .

Fig. 3.

The effects of the demand disruptions on the supply chain.

In Fig. 3, the demand disruptions affect the retailer’s order quantity on which the manufacturer’s order quantity depends. In order to induce a right order quantity of the retailer, the manufacturer may change the incentive mechanism. Furthermore, the raw material supplier will be affected by the change of the manufacturer’s order quantity. At the ESS point, the quantities and the profits of the channels in a market are given in Table 2 .

Table 2.

The effects of the demand disruptions on the supply chains

Δa	qA	qB	πA	πB
−1.2	0.43	0.63	0.19	0.40
0	0.50	1.70	0.25	1.19
1	1.63	1.63	0.70	1.03

In Table 2, we only give the (ESS) equilibrium quantities and the equilibrium profits of the supply chains. We can also give the equilibrium profits of the raw material suppliers if we know the production functions of the manufacturers and the cost functions of the raw material suppliers. Furthermore, we know the effects of the demand disruptions on the raw material suppliers. In this paper, we do not consider the latter.

5. The raw material supply disruptions and evolutionary stable strategies of retailers

Besides demand disruptions, the raw material supply is often disrupted. In the real world, the disruptions of raw material supplies often result in the change of raw material price. If the raw material supplier launches a promotion, it will reduce price. The material supplier desires to earn more profit by increasing its unit price. Sometimes, the raw material price increases due to a shortage. When some crises are anticipated, the price will increase although there is ample supply currently. Examples on the raw material price increase could be seen from the crude oil price change in our daily life (the oil supply disruptions from the Middle East often result in the change of the crude oil price). We assume that Δc _i, is the changed amount of the unit production cost of manufacturer i, i  =  A,  B, i.e., the unit production cost after disruptions is c _i  + Δc _i. For example, the production cost of a manufacturer whose raw material supply depends on other countries increases (decreases) if the tariff increases (decreases). In general, we have sign (Δc _A) = sign(Δc _B), i.e., the unit production costs of the two manufacturers increase or decrease simultaneously because they produce homogeneous goods. But, the changed amounts can be different. In this section, we will study how the raw material supply disruptions affect the ESS of retailers without considering recovery. We assume that the demand is not disrupted. We can also regard the case in which the manufacturers do not know the recovery time as the case without considering recovery. In this case, the manufacturers do not expect recovery and thus adjust their production scale rapidly. Although they will suffer loss, the loss is transient and it does not affect the ESS of retailers. For example, according to the Canada–US Free Trade Agreement, the manufacturers will receive lower tariff even zero-tariff is applied in the free trade area, this results in a lower cost in the long run.

We first consider the case Δc _A  = Δc _B, i.e., the disruptions have the same effects on the unit production costs of the manufacturers. Similar to Theorem 2, we derive from Theorem 1 and Corollary 1 the following.

Theorem 5

When 4c _A  −  c _B  <  a  <  4c _B and $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$ , we have

• (i) If $0<\mathrm{\Delta }{c}_A=\mathrm{\Delta }{c}_B<{\displaystyle \frac{1}{3}}(a-4c_A+c_B)$ , the equilibriums (0,   1) and (1,   0) are ESS.
• (ii) If $\mathrm{\Delta }{c}_A=\mathrm{\Delta }{c}_B>{\displaystyle \frac{1}{3}}(a-4c_B+c_A)$ , the equilibrium (1,   1) is a unique ESS.
• (iii) If ${\displaystyle \frac{1}{3}}(a-4c_A+c_B)<\mathrm{\Delta }{c}_A=\mathrm{\Delta }{c}_B<{\displaystyle \frac{1}{3}}(a-4c_B+c_A)$ , the equilibrium (1,   0) is a unique ESS.
• (iv) If $\max \left\{4c_A-5c_B\text{,}{\displaystyle \frac{1}{4}}(a-4c_B)\right\}<\mathrm{\Delta }{c}_A=\mathrm{\Delta }{c}_B<0$ , the equilibriums (0,   1) and (1,   0) are ESS.
• (v) If $4c_A-5c_B<\mathrm{\Delta }{c}_A=\mathrm{\Delta }{c}_B<{\displaystyle \frac{1}{4}}(a-4c_A)$ , the equilibrium (0,   0) is a unique ESS.
• (vi) If $\max \left\{{\displaystyle \frac{1}{4}}(a-4c_A)\text{,}4c_A-5c_B\right\}<\mathrm{\Delta }{c}_A=\mathrm{\Delta }{c}_B<{\displaystyle \frac{1}{4}}(a-4c_B)$ , the equilibrium (1,   0) is a unique ESS.

For the decreased unit cost case, Theorem 5 implies that c _i  + Δc _i  > 0, i  =  A,  B, i.e., the raw material price is always positive. Moreover, Theorem 5 also assures that the assumption a  >  c _A  + Δc _A, holds. In Theorem 5, we do not consider some critical cases due to the fact that these cases are not ESS. From Corollary 1, Theorem 1, Theorem 5, we know that the system (1), (2) under disruptions has the same ESS as that without disruption if the changed amounts of the unit production costs ∣Δc _i∣ are equal and sufficiently small. The disruptions induce the individual originally inclining revenue maximization strategy to choose profit maximization if the increased amounts Δc _i are equal and sufficiently large. In other words, the synchronous and large increase of the unit production costs results in the profit maximization strategies of the two manufacturers.

We also find that the proper and synchronous increase or decrease of the unit production costs may induce the retailers in the channel with higher cost to choose profit maximization strategy and the retailers in the other to choose revenue maximization strategy. The sufficiently large and synchronous decrease of the unit production costs may induce the retailers to choose revenue maximization strategy. In other words, the profit maximization strategies will gradually become extinct if the unit costs decrease sufficiently and synchronously.

When the unit production costs synchronously increase or decrease, i.e., Δc _A  = Δc _B  = Δc, we depict the results in Fig. 4 .

Fig. 4.

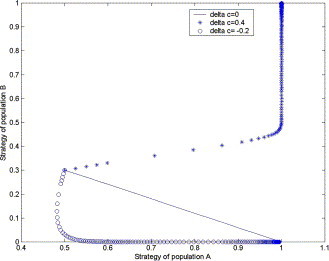
The ESS of retailers under raw material supply disruptions with t ∈ [0, 500].

In practice, we often see that the resulting effects of the disruptions on the two manufacturers are different, i.e., Δc _A  ≠ Δc _B. ∣Δc _i∣ > ∣Δc _j∣ means that the resulting effect of the disruptions on manufacturer i is larger than on manufacturer j, where i  ≠  j and i,  j  =  A,  B. With the increased unit cost, we derive the following.

Theorem 6

When 4c _A  −  c _B  <  a  <  4c _B , $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$ and 0  < Δc _A  < Δc _B  ⩽  2c _A , we have

• (i) If $c_A+\mathrm{\Delta }{c}_A-c_B⩽\mathrm{\Delta }{c}_B⩽{\displaystyle \frac{5}{4}}(c_A-c_B)+{\displaystyle \frac{1}{4}}\mathrm{\Delta }{c}_A$ , the equilibriums (0,   1) and (1,   0) are ESS.
• (ii) If $\max \left\{{\displaystyle \frac{5}{4}}(c_A-c_B)+{\displaystyle \frac{1}{4}}\mathrm{\Delta }{c}_A\text{,}{c}_A+\mathrm{\Delta }{c}_A-c_B\right\}<\mathrm{\Delta }{c}_B<{\displaystyle \frac{1}{4}}(c_A+\mathrm{\Delta }{c}_A)$ , the equilibriums (1,   0) and (0,   1) are ESS for a  ∈  (4(c _B   +  Δc _B )  −  (c _A   +  Δc _A ),   4c _B ); the equilibrium (0,   1) is a unique ESS for a  ∈  (max{4c _A  −  c _B ,   4(c _A   +  Δc _A )  −  (c _B   +  Δc _B )},   4(c _B   +  Δc _B )  −  (c _A   +  Δc _A )).

Proof

Part (i). From $\mathrm{\Delta }{c}_B⩽{\displaystyle \frac{5}{4}}(c_A-c_B)+{\displaystyle \frac{1}{4}}\mathrm{\Delta }{c}_A$ and 4c _A  −  c _B  <  a  < 4c _B, it follows that

$$4(c_B+\mathrm{\Delta }{c}_B)-(c_A+\mathrm{\Delta }{c}_A)<a<4(c_A+\mathrm{\Delta }{c}_A)\text{.}$$

Furthermore, it follows from c _A  + Δc _A  −  c _B  ⩽ Δc _B that

$$c_A+\mathrm{\Delta }{c}_A⩽c_B+\mathrm{\Delta }{c}_B<{\displaystyle \frac{5}{4}}(c_A+\mathrm{\Delta }{c}_A)\text{.}$$

Similar to Corollary 1, it follows that the equilibriums (0, 1) and (1, 0) are ESS. This case exists only when $\mathrm{\Delta }{c}_A⩽{\displaystyle \frac{1}{3}}(c_A-c_B)$. Note that ${\displaystyle \frac{1}{4}}(c_A+\mathrm{\Delta }{c}_A)<{\displaystyle \frac{5}{4}}(c_A+\mathrm{\Delta }{c}_A)-c_B$. Similarly, it follows Part (ii). □

Since in the real world it is almost impossible for $c_B+\mathrm{\Delta }{c}_B>{\displaystyle \frac{5}{4}}(c_A+\mathrm{\Delta }{c}_A)$, we do not consider the case in Theorem 6. In Theorem 6, the conditions 0 < Δc _A  < Δc _B  ⩽ 2c _A and a  > 4c _A  −  c _B assure that assumption a  >  c _B  + Δc _B  = max{c _A  + Δc _A,  c _B  + Δc _B} holds. From Corollary 1, Theorem 1, Theorem 6, with the increased unit cost, we know that the retailers have the same ESS as that without disruption when Δc _B  > Δc _A and the incremental unit cost Δc _B, is sufficiently small. If the incremental unit cost Δc _B is within a certain range, the equilibrium the initial state evolves to depends on the market scale a. In this case, one population’s ESS is the profit maximization strategy and the other’s ESS is the revenue maximization strategy. Similar to Theorem 6, we have the following.

Theorem 7

When 4c _A  −  c _B  <  a  <  4c _B , $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$ and 0  < Δc _B  < Δc _A  ⩽  2c _A , we have

• (i) When $\mathrm{\Delta }{c}_A⩾\max \left\{{\displaystyle \frac{1}{4}}\mathrm{\Delta }{c}_B+{\displaystyle \frac{5}{4}}{c}_B-c_A\text{,}4\mathrm{\Delta }{c}_B-c_A\right\}$ , the equilibrium (1,   0) is a unique ESS if 4c _A  −  c _B  ⩾  4(c _B   +  Δc _B )  −  (c _A   +  Δc _A ), or 4c _A  −  c _B  <  4(c _B   +  Δc _B )  −  (c _A   +  Δc _A ) and 4(c _B   +  Δc _B )  −  (c _A   +  Δc _A )  <  a  <  4(c _A   +  Δc _A )  −  (c _B   +  Δc _B ), the equilibrium (1,   1) is a unique ESS if 4c _A  −  c _B  <  a  <  4(c _B   +  Δc _B )  −  (c _A   +  Δc _A ).
• (ii) When $4\mathrm{\Delta }{c}_B-5(c_A-c_B)⩽\mathrm{\Delta }{c}_A<{\displaystyle \frac{1}{4}}\mathrm{\Delta }{c}_B+{\displaystyle \frac{5}{4}}{c}_B-c_A$ , the equilibriums (0,   1) and (1,   0) are ESS if 4(c _A   +  Δc _A )  −  (c _B   +  Δc _B )  <  a  <  4c _B , and the equilibrium (1,   0) is a unique ESS if 4c _A  −  c _B  <  a  <  4(c _A   +  Δc _A )  −  (c _B   +  Δc _B ).

Proof

Part (i). From $\mathrm{\Delta }{c}_A⩾\max \left\{{\displaystyle \frac{1}{4}}\mathrm{\Delta }{c}_B+\frac{5}{4}{c}_B-c_A\text{,}4\mathrm{\Delta }{c}_B-c_A\right\}$ and 4c _A  −  c _B  <  a  < 4c _B, it follows that a  < 4c _B  ⩽ 4(c _A  + Δc _A) − (c _B  + Δc _B) and 4(c _B  + Δc _B) − (c _A  + Δc _A) < 4c _B. If 4c _A  −  c _B  ⩾ 4(c _B  + Δc _B) − (c _A  + Δc _A), we have 4(c _B  + Δc _B) −(c _A  + Δc _A) <  a  < 4(c _A  + Δc _A) − (c _B  + Δc _B).

If 4c _A  −  c _B  < 4(c _B  + Δc _B) − (c _A  + Δc _A), we should consider two cases:

$$4(c_B+\mathrm{\Delta }{c}_B)-(c_A+\mathrm{\Delta }{c}_A)<a<4(c_A+\mathrm{\Delta }{c}_A)-(c_B+\mathrm{\Delta }{c}_B)$$

and

$$4c_A-c_B<a<4(c_B+\mathrm{\Delta }{c}_B)-(c_A+\mathrm{\Delta }{c}_A)\text{.}$$

Similar to Theorem 2, we can show that the equilibrium (1, 0) is a unique ESS if 4(c _B  + Δc _B) − (c _A  + Δc _A) <  a  < 4(c _A  + Δc _A) − (c _B  + Δc _B), the equilibrium (1, 1) is a unique ESS if 4c _A  −  c _B  <  a  < 4(c _B  + Δc _B) − (c _A  + Δc _A).

Part (ii). From $\mathrm{\Delta }{c}_A<{\displaystyle \frac{1}{4}}\mathrm{\Delta }{c}_B+{\displaystyle \frac{5}{4}}{c}_B-c_A$, it follows that 4(c _A  + Δc _A) − (c _B  + Δc _B) < 4c _B. From Δc _A  > Δc _B  > 0 and $\mathrm{\Delta }{c}_A<{\displaystyle \frac{1}{4}}\mathrm{\Delta }{c}_B+{\displaystyle \frac{5}{4}}{c}_B-c_A$, it follows that $c_B+\mathrm{\Delta }{c}_B<c_A+\mathrm{\Delta }{c}_A<{\displaystyle \frac{5}{4}}(c_B+\mathrm{\Delta }{c}_B)$. Similar to Part (i), it follows that the equilibrium (0, 1) and (1, 0) are ESS if 4(c _A  + Δc _A)− (c _B  + Δc _B) <  a  < 4c _B.

From Δc _A  ⩾ 4Δc _B−5(c _A  −  c _B), we know that 4(c _B  + Δc _B) − (c _A  + Δc _A)⩽4c _A  −  c _B. Furthermore, similar to Theorem 2, it follows that the equilibrium (1, 0) is a unique ESS if 4c _A− c _B  <  a  < 4(c _A  + Δc _A) − (c _B  + Δc _B). □

In Theorem 7, the conditions 0 < Δc _B  < Δc _A  ⩽ 2c _A and a  > 4c _A  −  c _B assure that the Assumption a  >  c _A  + Δc _A  = max{c _A  + Δc _A,  c _B  + Δc _B} holds. Similar to the explanations of Theorem 5, Theorem 6, we can also give an explanation of Theorem 7.

Theorem 6, Theorem 7 study the case with the increased unit production cost. In the real world, we often find the case with the decreased unit production cost. For the latter, we have the following.

Theorem 8

When 4c _A  −  c _B  <  a  <  4c _B , $c_B⩽c_A⩽{\displaystyle \frac{5}{4}}{c}_B$ , Δc _B  < Δc _A  <  0 and Δc _i   +   c _i  >  0, i   =   A,   B, we have

• (i) If $c_A+\mathrm{\Delta }{c}_A>{\displaystyle \frac{5}{4}}(c_B+\mathrm{\Delta }{c}_B)$ and Δc _B  ⩾  4Δc _A  ⩾  4(c _B  −  c _A ), the equilibrium (1,   0) is a unique ESS.
• (ii) If $\mathrm{\Delta }{c}_A>\max \left\{{\displaystyle \frac{5}{4}}(c_B+\mathrm{\Delta }{c}_B)-c_A\text{,}4\mathrm{\Delta }{c}_B-5(c_A-c_B)\right\}$ and $c_A-{\displaystyle \frac{5}{4}}{c}_B<\mathrm{\Delta }{c}_B<4\mathrm{\Delta }{c}_A$ , the equilibrium (1,   0) is a unique ESS for a  ∈  (4c _A  −  c _B ,4(c _B   +  Δc _B )) or a  ∈  (4(c _B   +  Δc _B ), min{4c _B ,   4(c _A   +  Δc _A )  −  (c _B   +  Δc _B )}).
• (iii) If $c_B+\mathrm{\Delta }{c}_B⩽c_A+\mathrm{\Delta }{c}_A⩽{\displaystyle \frac{5}{4}}(c_B+\mathrm{\Delta }{c}_B)$ and $\mathrm{\Delta }{c}_B⩾\max \left\{4\mathrm{\Delta }{c}_A\text{,}{c}_A-{\displaystyle \frac{5}{4}}{c}_B\right\}$ , the equilibriums (0,   1) and (1,   0) are ESS for a  ∈  (4c _A  −  c _B ,   4(c _B   +  Δc _B )), the equilibrium (1,   0) is a unique ESS for a  ∈  (4(c _B   +  Δc _B ), min{4c _B , 4(c _A   +  Δc _A )}).

Proof

Part (i). From $c_A+\mathrm{\Delta }{c}_A>{\displaystyle \frac{5}{4}}(c_B+\mathrm{\Delta }{c}_B)$ and Δc _B  ⩾ 4Δc _A, it follows that

$$4(c_B+\mathrm{\Delta }{c}_B)<4(c_A+\mathrm{\Delta }{c}_A)-(c_B+\mathrm{\Delta }{c}_B)⩽4c_A-c_B\text{.}$$

From Δc _A  ⩾  c _B  −  c _A, we know that 4c _B  ⩽ 4(c _A  + Δc _A). Similar to Theorem 2, it follows that the equilibrium (1, 0) is a unique ESS. Similarly, we can also follow Part (ii) and Part (iii). □

In Theorem 8, the condition Δc _i  +  c _i  > 0 means that the raw material price and the unit cost after disruptions are positive. From a  > 4c _A  −  c _B, c _A  ⩾  c _B and Δc _B  < Δc _A  < 0, we know that the Assumption a  > max{c _A  + Δc _A,  c _B  + Δc _B} holds.

Theorem 5, Theorem 6, Theorem 7, Theorem 8 study the effects of the raw material supply disruptions on the retailers. In practice, the raw material supply disruptions also affect the suppliers due to the change of the needed raw material quantities of manufacturers. For the raw material supply disruptions, see Fig. 5 .

Fig. 5.

The effects of the raw material supply disruptions on the supply chain.

In Fig. 5, the raw material supply disruptions will result in the change of the raw material price, which will affect the order quantity of the manufacturer and the incentive mechanism. The change of the incentive mechanism will affect the retailer’s order quantity. Furthermore, the raw material supplier will be affected.

In practice, we often find that the raw material supply disruptions and the demand disruptions coexist. According to the above ideas, we can study the case where both disruptions occur. We can also give a similar figure on the effects of disruptions on the supply chain. A formal analysis of the coexisting case is beyond the scope of this paper. Now, we illustrate the effects of the disruptions in this case on the ESS of retailers by using numerical simulation. We depict Fig. 6 with t  ∈ [0, 1000].

Fig. 6.

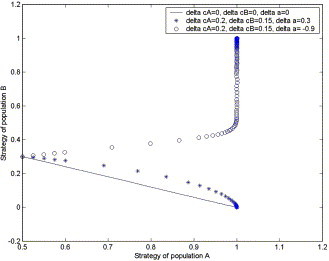
The ESS of retailers under demand and raw material supply disruptions.

At the ESS point, the quantities and the profits of channels are given in Table 3 .

Table 3.

The effects of the disruptions on channels

Δa	ΔcA	ΔcB	qA	qB	πA	πB
−0.9	0.2	0.15	0.45	0.70	0.20	0.49
0	0	0	0.50	1.70	0.25	1.19
0.3	0.2	0.15	0.47	1.87	0.22	1.34

In Fig. 6 and Table 3, we consider the case in which the effects of the raw material supply disruptions on manufacturer A is larger than that on manufacturer B. Similarly, we can also consider the contrary case.

6. A recovery model with supply chain disruptions

Sections 4, 5 studied the effects of the supply chain disruptions on the ESS of the populations without considering the recovery of disruptions. In fact, in the real world, the supply chain will gradually recover after the disruptions. In this section, we introduce a recovery model. Trimarchi (2003) suggested that, irrespective of any consideration of subjective utility, unexpected and substantial wealth transfers lead to a disruption cost. Disruptions often cause extra damage. The disruptions of a supply chain also incur extra cost for its members, and we call the extra cost a penalty cost. In this section, we assume that a unit penalty cost is c _u for the increased production and a unit penalty cost is c _s, for the decreased production quantity, c _u  > 0 and c _s  > 0.

We assume that the retailers do not bear any production deviation cost, i.e., the manufacturers bear fully the production deviation costs. We leave the case in which the retailers bear a part of deviation costs for future research.

6.1. A recovery model with demand disruptions

In this subsection, we introduce a recovery model of the supply chain with demand disruptions. Without loss of generality, we assume that the demand disruptions happen at time t  = 0 and are fully recovered at time T. Let a(t) denote the market scale at time t. Moreover, we assume that the demand recovers uniformly, i.e., we have a(t) =  a  + Δa(T  −  t)/T for t  ∈ [0,  T] and a(t) =  a for t  >  T. Thus, the evolutionary dynamic system of the populations’ strategies for t  ∈ [0,  T] is

$${\dot{s}}_A={\displaystyle \frac{1}{9}}{c}_A{s}_A(1-s_A)\{4c_A-c_B{s}_B-[a+\mathrm{\Delta }a(T-t)/T]\}\text{,}$$ (3)

$${\dot{s}}_B={\displaystyle \frac{1}{9}}{c}_B{s}_B(1-s_B)\{4c_B-c_A{s}_A-[a+\mathrm{\Delta }a(T-t)/T]\}\text{.}$$ (4)

The evolutionary dynamic system is the same as the system (1), (2) for t  >  T. Note that the stability of the four corner equilibriums of the system (3), (4) is the same as that of the system (1), (2) if T is finite, but the initial state of the system (1), (2) has become the state at time T. Hence, our task is to describe the evolutionary path of the initial state of the system (3), (4) and give the state at time T using numerical simulation. We assume that Δa  = −1, T  = 10 and t  ∈ [0, 500]. In order to well illustrate the effect of the demand disruptions on the evolutionary path, we assume that the initial state is (0.02, 0.75). The evolutionary paths of the retailers’ strategies are shown in Fig. 7 .

Fig. 7.

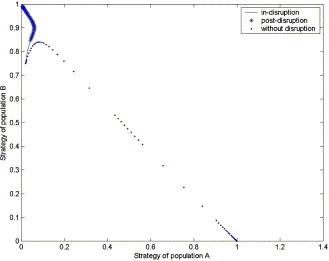
The ESS of retailers under demand disruptions with recovery consideration.

From Fig. 7, we know that the evolutionary path is distorted by the demand disruptions. Sometimes, the initial state even evolves to a different equilibrium due to the demand disruptions. For the manufacturer with higher (lower) cost, the retailers’ strategies should evolve to profit maximization (revenue maximization), but may evolve to revenue maximization (profit maximization) due to the demand disruptions.

Similar to Xiao et al. (2005), we know that the profit function of channel i in a market for t  ∈ [0,  T] is

$${\tilde{\pi }}_i^{\mathit{MN}}\left({\tilde{q}}_A^{\mathit{MN}}\text{,}{\tilde{q}}_B^{\mathit{MN}}\right)=\left[a+\mathrm{\Delta }a(T-t)/T-{\tilde{q}}_A^{\mathit{MN}}-{\tilde{q}}_B^{\mathit{MN}}-c_i\right]{\tilde{q}}_i^{\mathit{MN}}-c_u{\left({\overline{\tilde{q}}}_i(s_A\text{,}{s}_B)-{\overline{q}}_i(s_A\text{,}{s}_B)\right)}^{+}-c_s{\left({\overline{q}}_i(s_A\text{,}{s}_B)-{\overline{\tilde{q}}}_i(s_A\text{,}{s}_B)\right)}^{+}\text{,}i=A\text{,}B\text{,}M\text{,}N=P\text{,}R\text{,}$$ (5)

where

$$\begin{array}{cc}\hfill & {\overline{q}}_A(s_A\text{,}{s}_B)=s_A\left[s_B{q}_A^{\mathit{PP}}+(1-s_B)q_A^{\mathit{PR}}\right]+(1-s_A)\left[s_B{q}_A^{\mathit{RP}}+(1-s_B)q_A^{\mathit{RR}}\right]={\displaystyle \frac{1}{3}}a-{\displaystyle \frac{2}{3}}{c}_A{s}_A+{\displaystyle \frac{1}{3}}{c}_B{s}_B\text{,}\hfill \\ \hfill & {\overline{q}}_B(s_A\text{,}{s}_B)={\displaystyle \frac{1}{3}}a+{\displaystyle \frac{1}{3}}{c}_A{s}_A-{\displaystyle \frac{2}{3}}{c}_B{s}_B\hfill \end{array}$$

and (x)⁺  = max{x, 0}. ${\overline{q}}_i(s_A\text{,}{s}_B)$ represents the average production quantity of channel i in a market without disruption. We substitute a  + Δa(T  −  t)/T for a in the expression of $q_i^{\mathit{MN}}$, we can obtain the expression of ${\tilde{q}}_i^{\mathit{MN}}$ for t  ∈ [0,  T], and ${\tilde{q}}_i^{\mathit{MN}}=q_i^{\mathit{MN}}$ for t  ⩾  T, i  =  A,  B, M,  N  =  P,  R. Similar to the average production quantity ${\overline{q}}_A(s_A\text{,}{s}_B)$, we have for t  ∈ [0,  T]

$$\begin{array}{cc}\hfill & {\overline{\tilde{q}}}_A(s_A\text{,}{s}_B)={\displaystyle \frac{1}{3}}[a+\mathrm{\Delta }a(T-t)/T]-{\displaystyle \frac{2}{3}}{c}_A{s}_A+{\displaystyle \frac{1}{3}}{c}_B{s}_B\text{,}\hfill \\ \hfill & {\overline{\tilde{q}}}_B(s_A\text{,}{s}_B)={\displaystyle \frac{1}{3}}[a+\mathrm{\Delta }a(T-t)/T]+{\displaystyle \frac{1}{3}}{c}_A{s}_A-{\displaystyle \frac{2}{3}}{c}_B{s}_B\text{.}\hfill \end{array}$$

Furthermore, it follows from Eq. (5) that

$${\tilde{\pi }}_i^{\mathit{MN}}\left({\tilde{q}}_A^{\mathit{MN}}\text{,}{\tilde{q}}_B^{\mathit{MN}}\right)=[a+\mathrm{\Delta }a(T-t)/T-{\tilde{q}}_A^{\mathit{MN}}-{\tilde{q}}_B^{\mathit{MN}}-c_i]{\tilde{q}}_i^{\mathit{MN}}-{\displaystyle \frac{1}{3}}(T-t)T^{-1}[c_u(\mathrm{\Delta }a{)}^{+}+c_s(-\mathrm{\Delta }a{)}^{+}]\text{,}\text{for}t\in [0\text{,}T]\text{,}i=A\text{,}B\text{,}M\text{,}N=P\text{,}R\text{.}$$ (6)

Thus, the average profit of channel i in a market is for t  ∈ [0,  T]

$$\begin{array}{cc}\hfill & {\overline{\tilde{\pi }}}_A(s_A\text{,}{s}_B)=s_A[s_B{\tilde{\pi }}_A^{\mathit{PP}}+(1-s_B){\tilde{\pi }}_A^{\mathit{PR}}]+(1-s_A)[s_B{\tilde{\pi }}_A^{\mathit{RP}}+(1-s_B){\tilde{\pi }}_A^{\mathit{RR}}]\text{,}\hfill \\ \hfill & {\overline{\tilde{\pi }}}_B(s_A\text{,}{s}_B)=s_B[s_A{\tilde{\pi }}_B^{\mathit{PP}}+(1-s_A){\tilde{\pi }}_B^{\mathit{RP}}]+(1-s_B)[s_A{\tilde{\pi }}_B^{\mathit{PR}}+(1-s_A){\tilde{\pi }}_B^{\mathit{RR}}]\text{.}\hfill \end{array}$$

We assume that c _u  =  c _s  = 0.1 and T  = 10. We obtain Fig. 8, Fig. 9 for the average profits in a market.

Fig. 8.

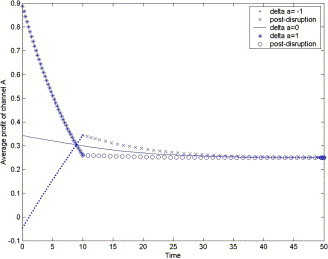
The average profit of channel A as a function of time under demand disruptions with recovery consideration.

Fig. 9.

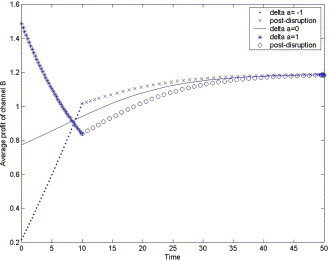
The average profit of channel B as a function of time under demand disruptions with recovery consideration.

From Fig. 8, Fig. 9, we find that the average profit of the channel with higher (lower) cost decreases (increases) as time increases if the demand is not disrupted, which means that the cost advantage of the channel with lower cost gradually materializes. For the increased demand, the average profit will decrease as time increases in the in-disruption period, even lower than the average profit without disruption. But, for the decreased demand, the average profit will increase as time increases in the in-disruption period, even higher than the average profit without disruption. For the demand disruption cases, we also see that the average profits of the channels will converge to the average profit without disruption, but the average profits at the end of the disruption period are not equal to the average profit without disruption.

6.2. A recovery model with the raw material supply disruptions

In Section 6.1, we set up a recovery model of supply chain with demand disruptions. In this subsection, we will study the effects of recovery of the raw material supply disruptions on the supply chains. For simplicity, we assume that Δc _A  = Δc _B  = Δc and the costs recover uniformly, i.e., we have c _i(t) =  c _i  + Δc(T  −  t)/T for t  ∈ [0,  T] and c _i(t) =  c _i, for t  >  T, i  =  A,  B. Similar to the dynamic system (3), (4), we have for t  ∈ [0,  T]

$${\dot{s}}_A={\displaystyle \frac{1}{9}}{s}_A(1-s_A)[c_A+\mathrm{\Delta }c(T-t)/T][4c_A-c_B{s}_B-a+(4-s_B)\mathrm{\Delta }c(T-t)/T]\text{,}$$ (7)

$${\dot{s}}_B={\displaystyle \frac{1}{9}}{s}_B(1-s_B)[c_B+\mathrm{\Delta }c(T-t)/T][4c_B-c_A{s}_A-a+(4-s_A)\mathrm{\Delta }c(T-t)/T]\text{.}$$ (8)

The evolutionary dynamic system is the same as the system (1), (2) for t  >  T.

We assume that Δc  = 1, T  = 10 and t  ∈ [0, 1000]. In order to well illustrate the effect of the raw material supply disruptions on the evolutionary path, we assume that the initial state is (0.03, 0.82). Fig. 10 describes the evolutionary path of the system with the raw material supply disruptions.

Fig. 10.

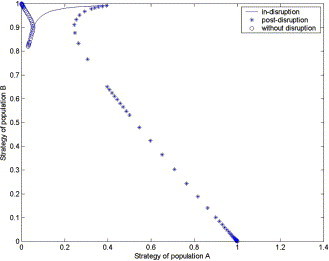
The ESS of retailers under raw material supply disruptions with recovery consideration.

From Corollary 1, we know that the equilibriums (0, 1) and (1, 0) are ESS for the system without disruption. From Fig. 10, we find that the initial state (0.03, 0.82) will evolve to ESS (0, 1) if the supply chain is not disrupted, but it may evolve to ESS (1, 0) if the supply chain is disrupted. Fig. 10 illustrates that the disruptions may affect the ESS of populations for a given initial state. The disruptions may result in a reverse ESS for a population.

Similar to Eq. (6), it follows that for t  ∈ [0,  T]

$${\tilde{\pi }}_i^{\mathit{MN}}({\tilde{q}}_A^{\mathit{MN}}\text{,}{\tilde{q}}_B^{\mathit{MN}})=\left\{a-{\tilde{q}}_A^{\mathit{MN}}-{\tilde{q}}_B^{\mathit{MN}}-[c_i+\mathrm{\Delta }c(T-t)/T]\right\}{\tilde{q}}_i^{\mathit{MN}}-{\displaystyle \frac{1}{3}}{c}_u(T-t)T^{-1}(\mathrm{\Delta }c(s_j-2s_i){)}^{+}-{\displaystyle \frac{1}{3}}{c}_s(T-t)T^{-1}(\mathrm{\Delta }c(2s_i-s_j){)}^{+}\text{,}i\text{,}j=A\text{,}B\text{,}j\ne i\text{,}M\text{,}N=P\text{,}R\text{.}$$ (9)

Given the same parameter values and the initial state as that in Fig. 8, we can depict similar Figures and give a similar explanation. In this paper, we only consider the case that disruptions occur at only one time. In practice, the disruptions may occur from lime to time. In the latter case, the populations continually adjust their Strategies.

7. Conclusions

The strategies of a firm affects to a large degree its success or survival. A good strategy is beneficial to its development. What is a good strategy? The answer depends on the market environment. The good strategy in one market may be unacceptable in another. Even the answer may be different for the same market at different times. For example, the demand disruptions often affect the retailer’s strategy. The raw material supply disruptions also affect the retailer’s strategy. The indirect evolutionary approach does not deny rational decision-making. This paper employs the usual rationality assumptions of game theory to endogenize preference strategies (revenue maximization and profit maximization), and analyzes the ESS of preference. In our model, the retailers can maximize their utilities, revenue or profit of the channel, based on their preferences. And then we focus on the preference strategies.

In a quantity-setting duopoly situation with homogeneous goods, the ESS of the populations consisting of retailers depends on the relative sizes of the market scale and unit costs. We find that there may be two evolutionarily stable strategies under some conditions. Revenue maximization strategy may coexist with profit maximization strategy. Revenue maximization strategy may prevail in the situation that the demand is large enough. We find that the disruptions affect not only the ESS of the retailers, but also the optimal strategies of manufacturers and suppliers.

There are several directions that this research could continue. First, an important extension of the paper will be the case with multiple manufacturers by employing a finite population evolutionary game. Second, one can also consider a model with a nonlinear demand function and the effects of the disruptions on the members of a decentralized supply chain. Finally, the effect of the disruptions on the ESS of populations in other economic systems is an interesting field for future research.

Appendix A.

Proof of Theorem 2

Part (i). At the equilibrium point (0, 0), it follows from c _B  ⩽  c _A that if a  < 4c _B, we have $\det J={\displaystyle \frac{1}{81}}{c}_A{c}_B(4c_A-a)(4c_B-a)>0$, and $\mathrm{tr}J={\displaystyle \frac{1}{9}}{c}_A(4c_A-a)+{\displaystyle \frac{1}{9}}{c}_B(4c_B-a)>0$. Hence, the equilibrium (0, 0) is unstable if a  < 4c _B.

If a  = 4c _B, we have det  J  = 0 and tr  J  ⩾ 0, and further analysis is required. The further analysis is divided into two cases:

When a  = 4c _B  < 4c _A. the system (1), (2) becomes

$${\dot{s}}_A={\displaystyle \frac{1}{9}}{c}_A{s}_A(1-s_A)(4c_A-4c_B-c_B{s}_B)\text{,}{\dot{s}}_B=-{\displaystyle \frac{1}{9}}{c}_A{c}_B{s}_A{s}_B(1-s_B)\text{.}$$

Given function V ₁(s _A,  s _B) =  s _A s _B, it follows from c _A  >  c _B that there exists a sufficiently small ε  > 0 such that

$$\frac{\mathrm{d}{V}_1(s_A\text{,}{s}_B)}{\mathrm{d}t}=\frac{1}{9}{c}_A{s}_A{s}_B(4c_A-4c_B-c_B{s}_B)-\frac{1}{9}{c}_A{s}_A^2{s}_B(4c_A-3c_B)+\frac{2}{9}{c}_A{c}_B{s}_A^2{s}_B^2>0$$

for all (s _A,  s _B) ∈ (0,  ε) × (0,  ε). s _A s _B equals zero on the boundary s _A  = 0 or s _B  = 0. According to Хetaeb Theorem, we know that the equilibrium (0, 0) is unstable if a  = 4c _B  < 4c _A.

When a  = 4c _B  = 4c _A, the system (1), (2) becomes

$${\dot{s}}_A=-{\displaystyle \frac{1}{9}}{c}_A{c}_B{s}_A{s}_B(1-s_A)\text{,}{\dot{s}}_B=-{\displaystyle \frac{1}{9}}{c}_A{c}_B{s}_A{s}_B(1-s_B)\text{.}$$

The function V ₂(s _A,  s _B) = −ln(1 −  s _A)(1 −  s _B) is a Lyapunov function since

$$\frac{\mathrm{d}{V}_2(s_A\text{,}{s}_B)}{\mathrm{d}t}=\frac{{\dot{s}}_A}{1-s_A}+\frac{{\dot{s}}_B}{1-s_B}=-\frac{2}{9}{c}_A{c}_B{s}_A{s}_B⩽0$$

for all (s _A,  s _B) ∈ [0, 1) × [0, 1). Note that all trajectories for the system (1), (2) lie in the square [0, 1] × [0, 1], which allows us to only consider the points in the square [0, 1] × [0, 1]. Hence, the equilibrium (0, 0) is stable but not asymptotically stable if a  = 4c _B  = 4c _A. Similarly, we can follow Parts (ii) through (V). □