Simulating and forecasting the cumulative confirmed cases of SARS-CoV-2 in China by Boltzmann function-based regression analyses

Highlights

• •Cumulative confirmed cases in China were well fitted with Boltzmann function.
• •Potential total numbers of confirmed cases in different regions were estimated.
• •Key dates indicating minimal daily number of new confirmed cases were estimated.
• •Cumulative confirmed cases of 2003 SARS-CoV were well fitted to Boltzmann function.
• •The Boltzmann function was, for the first time, applied to epidemic analysis.

Dear editor,

As reported in this Journal¹ and elsewhere,² an outbreak of atypical pneumonia caused by the zoonotic 2019 novel coronavirus (SARS-CoV-2) is on-going in China and has spread to the world. As of Feb 16, 2020 (24:00, GMT+8), there have been 70,548 confirmed patients and more than 1700 deaths from SARS-CoV-2 infection in China, and 58,182 confirmed patients and 1696 deaths in the most affected province, Hubei Province. Much research progress has been made in dissecting the evolution and origin of SARS-CoV-2 and characterizing its clinical features.3, 4, 5, 6, 7

While the outbreak is on-going, people raise grave concerns about the future trajectory of the outbreak, especially given that the working and schooling time has been already dramatically postponed after the Chinese Lunar New Year holiday was over (scheduled on Jan 31). In particular, a precise estimation of the potential total number of infected cases and/or confirmed cases is highly demanding. Earlier studies based on susceptible-exposed-infectious-recovered metapopulation and susceptible-infected-recovered-dead models revealed the number of potentially infected cases and the basic reproductive number of SARS-CoV-2.^{3 , 8 , 9} These traditional epidemiological models apparently require much detailed data for analysis.^{3 , 8}

Here we explored a simple data-driven, Boltzmann function-based approach for estimation only based on the daily cumulative number of confirmed cases of SARS-CoV-2 (Note: the rational for Boltzmann function-based regression analysis is presented in supporting information (SI) file). We decided to collect data (initially from Jan 21 to Feb 10, 2020) in several typical regions of China, including the center of the outbreak (i.e. Wuhan City and Hubei Province), other four most affected provinces (i.e., Guangdong, Zhejiang, Henan, Hunan) and top-4 major cities in China (i.e., Beijing, Shanghai, Guangzhou, Shenzhen). During data analysis on Feb 13, 2020, the number of new confirmed cases on Feb 12 in Hubei Province and Wuhan City suddenly increased by 14,840 and 13,436, respectively, of which 13,332 and 12,364 are those confirmed by clinical features (note: all the number of confirmed cases released by Feb 12 were counted according to the result of viral nucleic acid detection rather than by referring to clinical features). We thus arbitrarily distributed these suddenly added cases to the reported cumulative number of confirmed cases from Jan 21 to Feb 14 for Hubei Province by a fixed factor (refer to Table S1), assuming that they were linearly accumulative in those days. It is the same forth with the data for Wuhan City.

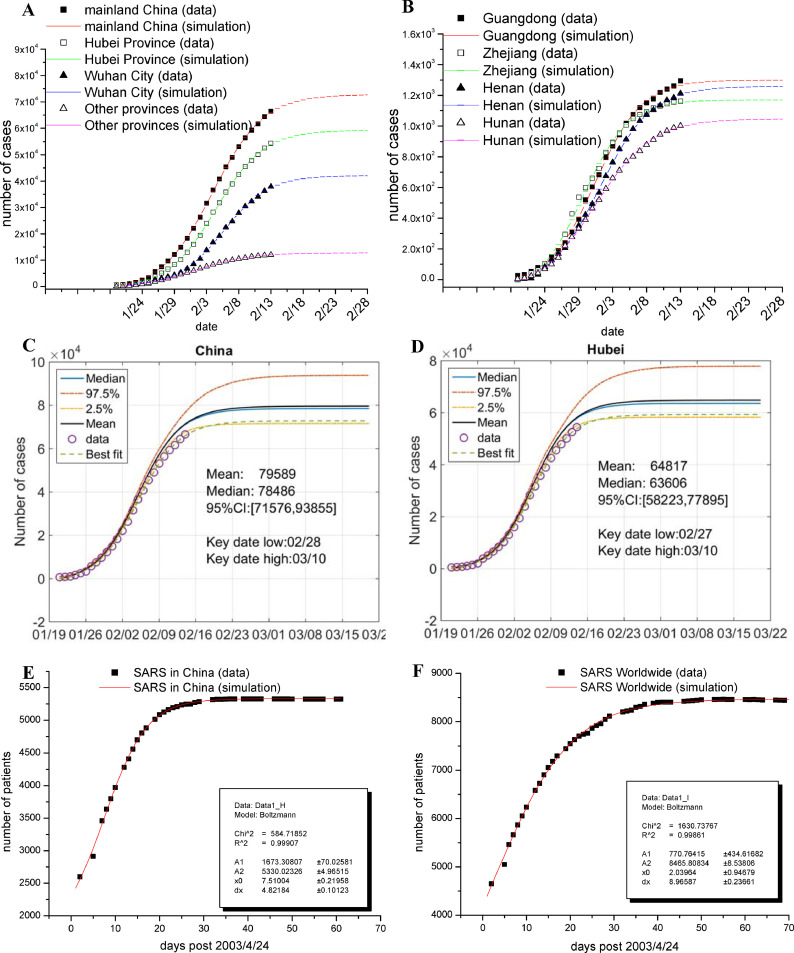
Regression analyses indicate that all sets of data were well fitted with the Boltzmann function (all R² values being close to 0.999; Figs. 1 A, B, S1, and Table 1 ). The potential total number of confirmed cases for mainland China, Hubei Province, Wuhan City, and other provinces were estimated as 72,800±600, 59,300±600, 42,100±700 and 12,800±100; respectively; those for provinces Guangdong, Zhejiang, Henan and Hunan were 1300±10, 1170±10, 1260±10, 1050±10, 1020±10 and 940±10, respectively (Table 1); those for Beijing, Shanghai, Guangzhou and Shenzhen were 394±4, 328±3, 337±3 and 397±4, respectively. In addition, we estimated the key date, on which the number of daily new confirmed cases is lower than 0.1% of the potential total number as defined by us subjectively (refer to Table 1).

Fig. 1.

Fitting the cumulative number of confirmed cases from different geographic regions of China to the Boltzmann function.

(A) Plots of the cumulative number of confirmed cases of SARS-CoV-2 as of Feb 14, 2020, in mainland China (■), in Hubei Province (□), in Wuhan City (▲) and in other provinces (△), with the simulation results being plotted as color lines. Note: the reported cumulative number of confirmed cases of Hubei Province and Wuhan City were re-adjusted for data fitting due to the suddenly added cases by clinical features (for detail, refer to Table S1). (B) Plots of the cumulative number of confirmed cases of SARS-CoV-2 as of Feb 14, 2020, in the most affected provinces (Guangdong, ■; Zhejiang, □; Henan, ▲; Hunan, △), with the simulation results being plotted as color lines. (C, D) Data of mainland China (panel C) and Hubei Province (panel D) were fitted to the Boltzmann function assuming that the relative uncertainty of the data follows a single-sided normal distribution with a mean of 1.0 and a standard deviation of 10%. Original data are shown as circles; simulated results are presented as colored lines as indicated. Inserts show key statistics. The key date is defined as the date when the number of daily new confirmed cases is less than 0.1% of the potential total number. The low and high key dates were determined by the simulated curve of confidence interval (CI) at 2.5% and 97.5%, respectively. (E, F) The cumulative number of confirmed cases of 2003 SARS in China (panel E) and worldwide (panel F) are shown as black squares, and the simulation results are plotted as red short lines and parameters of each established function are shown in inserts. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 1.

Regression analysis results of confirmed cases of SARS-CoV-2 in China.

Regions	without uncertainty			with uncertaintya
	potential total number	key dateb	R2	potential total number (mean, 95% CI)	key date (95% CI)b
China	72,800±600	2/28	0.999	79,589 (71,576, 93,855)	(2/28, 3/10)
Hubei Province	59,300±600	2/27	0.999	64,817 (58,223, 77,895)	(2/27, 3/10)
Wuhan City	42,100±700	2/27	0.999	46,562 (40,812, 57,678)	(2/28, 3/10)
Other provinces	12,800±100	2/27	0.999	13,956 (12,748, 16,092)	(2/27, 3/13)
Guangdong Province	1300±10	2/22	0.999	1415 (1324, 1550)	(2/22, 3/01)
Zhejiang Province	1170±10	2/20	0.997	1269 (1204, 1364)	(2/21, 2/27)
Henan Province	1260±10	2/24	0.999	1372 (1271, 1559)	(2/26, 3/09)
Hunan Province	1050±10	2/26	0.999	1140 (1050, 1279)	(2/28, 3/11)
Beijing City	394±4	2/25	0.999	429 (395, 486)	(2/25, 3/11)
Shanghai City	328±3	2/22	0.999	356 (334, 388)	(2/22, 3/01)
Guangzhou City	337±3	2/20	0.998	365 (346, 393)	(2/20, 2/28)
Shenzhen City	397±4	2/18	0.998	430 (407, 461)	(2/17, 2/25)

^aThe reported cumulative number of confirmed cases may have uncertainty. Assuming the relative uncertainty follows a single-sided normal distribution with a mean of 1.0 and a standard deviation of 10%, the potential total number and key dates were estimated at 95% CI. For detail, refer to the Methods section and Figs. 1C, D, S2 and S3.

^bKey date is determined when the number of daily new confirmed cases is less than 0.1% of the potential total number.

The above analyses were performed assuming that the released data on the confirmed cases are precise. However, there is a tendency to miss-report some positive cases such that the reported numbers represent a lower limit. One typical example indicating this uncertainty is the sudden increase of more than 14 000 new confirmed cases in Hubei Province on Feb 12 after clinical features were officially accepted as a standard for infection confirmation. Another uncertainty might result from insufficient kits for viral nucleic acid detection at the early stage of the outbreak. We thus examined the effects of such uncertainty using a Monte Carlo method (for detail, refer to the Methods section in SI file). For simplicity, we assumed that the relative uncertainty of the reported data follows a single-sided normal distribution with a mean of 1.0 and a standard deviation of 10%.

Under the above conditions, the potential total numbers of confirmed cases of SARS-CoV-2 for different regions were estimated (Figs. 1C, D, S2 and S3) and summarized in Table 1. The potential total numbers for China, Hubei Province, Wuhan City and other provinces were 79,589 (95% CI 71,576, 93,855), 64,817 (58,223, 77,895), 46,562 (40,812, 57,678) and 13,956 (12,748, 16,092), respectively, indicating that overall the outbreak may not be so bad as previously estimated.⁹ Such uncertainty analysis also allowed us to estimate the key dates at 95% CI. As summarized in Table 1, the key dates for mainland China, Hubei Province, Wuhan City, and other provinces would fall in (2/28, 3/10), (2/27, 3/10), (2/28, 3/10) and (2/27, 3/13), respectively.

Finally, the ongoing SARS-CoV-2 outbreak has undoubtedly caused us the memories of the SARS-CoV outbreak in 2003. We thus collected the data from the WHO officiate website for analysis, and found that the cumulative numbers of confirmed cases of 2003 SARS-CoV both in China and worldwide were fitted well with the Boltzmann function, with R² being 0.999 and 0.998, respectively (Figs. 1E and F).

In summary, we found that all data sets, including both the on-going outbreak of SARS-CoV-2 in China and the 2003 SARS-CoV epidemic in China and worldwide, were well fitted to the Boltzmann function (Fig. 1 and S1). These results strongly suggest that the Boltzmann function is suitable for analyzing the epidemics of coronaviruses like SARS-CoV and SARS-CoV-2. One advantage of this model is that it only needs the cumulative number of confirmed cases, somehow as simple as the recently proposed model.¹⁰ In addition, the estimated potential total numbers of confirmed cases and key dates may provide valuable guidance for Chinese central and local governments to deal with this emerging threat at current critical stage.

Declaration of Competing Interest

None.