Intervention time series analysis of crime rates: The case of sentence reform in Virginia

Abstract

We review the basic concepts of intervention analysis in the context of structural time series models and we apply this methodology to investigate the possible reduction in monthly crime rates reported from January 1984 up to and including December 2010 after Virginia abolished parole and reformed sentencing in January 1995. We find that the change in legislation has significantly reduced the burglary rates and to a lesser extent the murder rates in Virginia. The robustness of our results is investigated with an automatic detection of breaks procedure as well as with analyses of quarterly rather than monthly data.

• •We investigate the impact of sentence reform in Virginia on monthly crime rates.
• •Both univariate and multivariate structural time series models are used.
• •The effects of both step and of gradual level break interventions are examined.
• •The new legislation had an immediate negative effect on burglary and murder.
• •The new legislation had a gradual negative effect on larceny and murder.

1. Introduction

The contributions of Levitt, 2001, Cantor and Land, 2001 have prompted an active and interesting debate on effective intervention time series analysis. These discussions have become more prominent given the increasing interest in the effects of policy changes by governments promoting different crime-prevention programs. Different approaches to intervention time series analysis have been adopted in the evaluation of programs and policies in a number of criminal justice settings (McCleary and Hay, 1980, McDowall et al., 1980, Orwin, 1997). The standard approach to time series analysis in this framework aims at discriminating between the behaviour of the time series prior to the intervention and after the intervention. In other words, “given a known intervention, is there evidence that change in the series of the kind expected actually occurred, and, if so, what can be said of the nature and magnitude of the change,” (Box and Tiao, 1975). From the effective crime policy perspective it is important to assess whether a known intervention (policy change) has had the intended effect. For example, it is important to know whether an increased reliance on prisons, an increased number of police, tougher gun control laws, and innovative criminal justice programs and policies reduce crime rates and deter potential criminals from committing crimes.

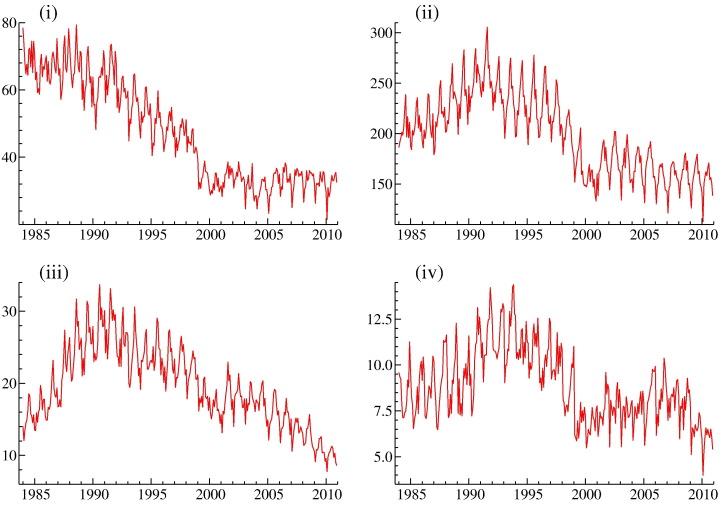
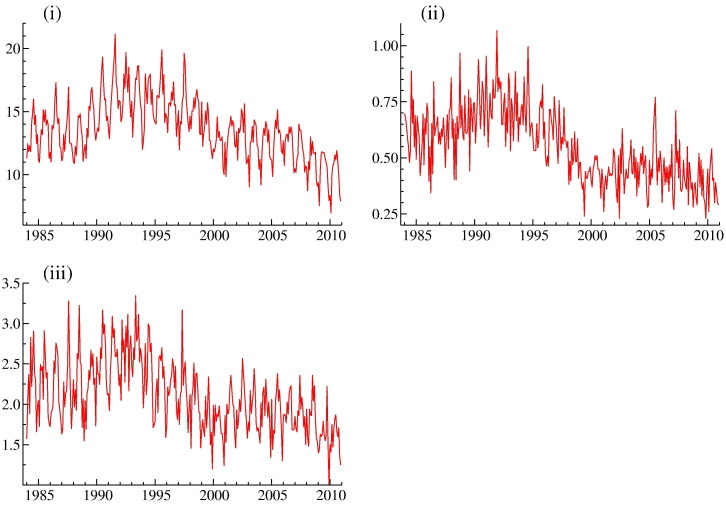
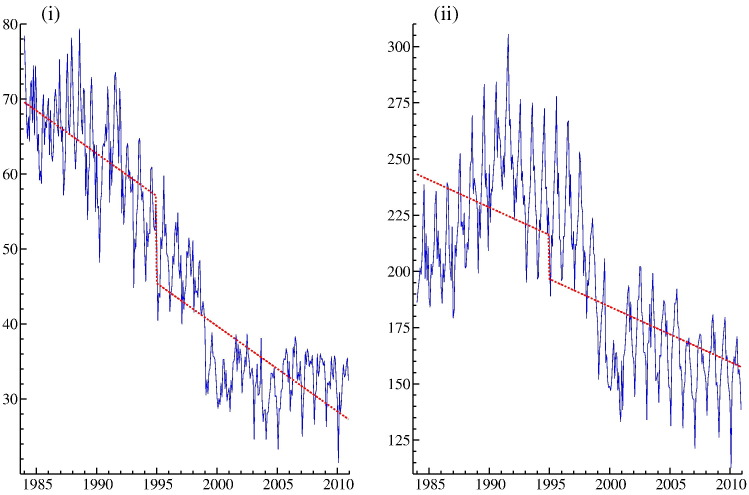
In this paper we investigate the impact of parole abolition and sentence reform in Virginia on crime rates reported from January 1984 up to and including December 2010. The crime rate series examined are monthly data on burglary, larceny, motor vehicle theft, robbery, aggravated assault, murder, and rape. The Commonwealth of Virginia abolished parole and reformed sentencing for all felony offences committed on or after January 1, 1995. This law was passed in a special legislative session in the autumn of 1994. Parole abolition was accompanied with substantially enhanced sentences for violent offenders.1 Visual inspection of the crime time series analysed in this paper (Fig. 1, Fig. 2 ) shows that most of them are declining from about the same time that Virginia enacted these major legislative initiatives to reduce violent crime. However, research to date is unable to determine if these reductions in crime rates are due to specific anti-crime initiatives.2 Reductions have occurred in the types of crimes that were targeted by these initiatives, indicating that they may have had their intended effect.

Fig. 1.

Monthly time series, from January 1984 to December 2010, of property crime rates: (i) burglary, (ii) larceny, (iii) motor vehicle theft, and (iv) robbery.

Fig. 2.

Monthly time series, from January 1984 to December 2010, of violent crimes rates: (i) aggravated assault, (ii) murder, and (iii) rape.

To examine the impact of Virginia's abolition of parole on crime rates, we consider different empirical approaches to the intervention analysis. First, we adopt a univariate structural time series approach to the intervention analysis of time series data, which are serially correlated, often non-stationary, and with strong seasonal and/or cyclical effects. Second, in order to address the problem of confounding variables, we apply the approach of Harvey (1996) and estimate multivariate structural time series models with control groups. Finally, the robustness of our results is investigated with an automatic detection of breaks procedure, as well as with analyses of quarterly rather than monthly data, thus showing that our results are independent of a particular time series method applied or the data frequency used.

The contribution of our paper to the existing literature is three-fold. Policy changes that increase the expected punishment per crime can lead to both greater deterrence and greater incapacitation. The empirical evidence which links increased punishment with lower crime rates is consistent.3 According to Levitt and Dubner (2005), increases in the prison population account for roughly one-third of the drop in crime in the US. However, most empirical tests on deterrence do not differentiate between the effect of deterrence and of incapacitation. Short-run declines in crime are likely to be attributable to deterrence, whereas the incapacitation effect of sentence enhancements will occur only in the long-run (Kessler and Levitt, 1999). In the case of Virginia, the 1994 legislation abolishing parole and establishing a truth-in-sentencing system was a single, most significant factor affecting the size of the prison population. Although it took time for the longer prison sentences imposed under the 1994 sentencing reform to have a significant growth effect on Virginia's prison population, decrease in the parole grant rate had an almost immediate effect on the size of the prison population.4 By looking at changes in crime immediately after the introduction of a sentence reform in Virginia, we hope to isolate a pure deterrent effect of the new legislation that is not contaminated by the effect of incapacitation. Hence, to the extent that severity of punishment serves as a deterrent to committing crimes in the short run, we would expect the reported crimes to drop especially for the violent offences. Disentangling deterrence and incapacitation effects of the introduced sentence reform in Virginia is the first contribution of our paper.

Our sample includes the 1990 to 1999 period when considerable social and economic changes occurred in the United States. There were declines in crime trends throughout the US during this decade. Furthermore, the second half of the 1990s was an economically prosperous period for the US. For example, unemployment rates declined sharply through most of this period. It was also a period in which a number of innovative criminal justice programs and policies were enacted both at the state level and at the local communities level. Favourable changes in patterns of drug use and access to guns were put in place. These factors could serve as alternative explanations for the decline in crime throughout the US in general, and Virginia in particular. Disentangling the impact of parole abolition on crime rates in Virginia from these other factors poses a considerable methodological challenge. We endeavour to tackle this problem of confounding variables by applying the approach of Harvey (1996) and estimating multivariate structural time series models with control groups. Understanding better the statistical relationship between Virginia anti-crime efforts and crime reductions over time in the presence of confounding variables is the second contribution of our paper.

Structural time series models may provide an effective approach to the modelling of interventions. The structural approach to time series analysis was popularized by Harvey, 1989, Commandeur and Koopman, 2007, and Durbin and Koopman (2012), and has been applied in various policy and intervention analysis applications. For example, Harvey and Durbin (1986) investigate the effects of the introduction of the seat belt law in 1983 in Great Britain on the number of car drivers killed and seriously injured. Harvey (1996) analyses the effects of the same British seat belt legislation using a multivariate structural time series framework with control groups. Balkin and Keith Ord (2001) investigate the relationship between speed limit increases and traffic-related fatalities in the US.

The structural time series approach has not been used extensively in crime data analysis.5 To our knowledge, the structural time series methodology applied to crime data is carried out by Harvey and Fernandes, 1989, Atkinson et al., 1997, who look at the number of outliers and breaks in the monthly number of purse (handbag) snatches in Hyde Park in Chicago. Koopman et al. (2008) model recidivism behaviour of juveniles from a Dutch judicial juvenile institution, using a non-Gaussian structural time series model. Nunley et al. (2011b) examine the impact of inflation, unemployment, and stock market growth on a battery of property crime rates in the U.S. over the period from 1948 to 2009. The authors use the structural time series approach in order to circumvent the problem associated with omitted variable bias. Finally, Vujić et al. (2012) model cyclical behaviour in property crime series (burglary and theft) in relation to the macroeconomic activity indicators in England and Wales in the period from 1955 to 2001. This paper extends further the structural intervention time series approach to the crime data analysis. We consider this to be the third contribution of our paper.

The paper is organised as follows. In Section 2 we describe the data used in the analysis. The structural time series models for intervention analysis used in this paper are discussed in Section 3. The empirical results of the investigation of the effects of parole abolition and sentence reform on the crime rates in Virginia are presented in Section 4. In Section 5 we provide a discussion of our methodological approach in the context of other intervention approaches and we provide some evidence of the robustness of our findings. Section 6 concludes the paper.

2. Data description

A major crime sentence reform in Virginia was proposed during the 1993 campaign of George Allen running for Governor. A key element of the campaign was to reduce the disparity between the sentence imposed in court and the actual time-served. This reform abolished parole, established a guidelines-based truth-in-sentencing system, and increased sentence length for violent offenders on or after January 1, 1995. The net result of the implementation of the legislation was a substantial increase in the sentences for the violent offences (especially rape and murder) and also for offenders with a violent past.6

We have obtained a data set of monthly time series on burglary, larceny, motor vehicle theft, robbery, aggravated assault, murder, and rape from the Uniform Crime Reports (UCR) collected by the Virginia State Police in the period from January 1984 up to, and including, December 2010. The UCR includes a data summary with counts of aggregated offences known to police and arrests. The pre-intervention period corresponds to the period from January 1984 to December 1994. The post-intervention period corresponds to the period from January 1995 to December 2010.7 Fig. 1, Fig. 2 present the reported crimes rates per 100,000 population, for property and violent crimes, respectively, from January 1984 to December 2010.8

It is clear from these graphs that the crime series are all trending and contain strong seasonal patterns. As explained in Section 3 we therefore explicitly incorporate trends and seasonal components in all our analyses.

3. Structural intervention time series analysis

An observed time series can be regarded as the realization of the cumulation of stochastic dynamic processes, exogenous effects and independent random shocks. In a structural time series analysis, these components can be treated and modelled separately. For a given time series, the extraction of the components and the estimation of parameters, including regression coefficients, are carried out by state space methods based on the Kalman filter; see Durbin and Koopman (2012).

The basic structural time series model (BSM) represents the time series by the additive model

$$y_t={\mu }_t+{\gamma }_t+{\epsilon }_t,{\epsilon }_t\sim \text{NID}\left(0,{\sigma }_{\epsilon }^2\right),t=1,\dots ,n,$$ (1)

where y _t is a scalar observation, μ _t is the slowly changing trend component, γ _t is the periodic or seasonal component, and ε _t is the irregular component. Each component is formulated as a dynamic stochastic process. The irregular ε _t is assumed to be normally and independently distributed (NID) with mean zero and unknown variance ${\sigma }_{\epsilon }^2$. The trend is assumed to evolve stochastically over time as a random walk process with a fixed drift, that is μ _t  =  μ _t −1  +  β  +  η _t, for t  = 1,…,n, with ${\eta }_t\sim \text{NID}\left(0,{\sigma }_{\eta }^2\right)$ where β and ${\sigma }_{\eta }^2$ are treated as unknown coefficients. The disturbance η _t and the irregular ε _s are independent of each other for all time periods t,s  = 1,…,n. The trend with β  = 0 is referred to as the local level component. A more general trend is obtained when β is replaced by an independent time-varying process. When it is replaced by another random walk process, we refer to μ _t as the local linear trend component. The seasonal component can be composed of seasonal dummy variables that may also evolve stochastically over time under appropriate restrictions, so that the component can treat the dynamic properties of the series y _t at the seasonal frequencies effectively and that it does not confound with the trend and irregular components. A more detailed discussion of structural time series models is given by Harvey (1989).

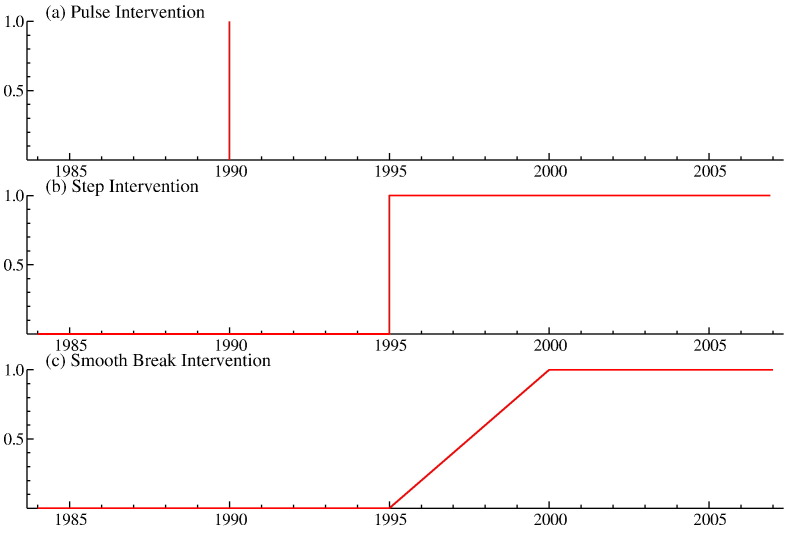
More components can be included when other features in the time series are present. For example, when variations in the time series coincide with other variables, contemporaneously or lagged, regression effects can be added to the model specification. We can collect such variables in the vector x _t, for t  = 1,…,n, and the regression effect x′ _t δ, where δ is the corresponding unknown vector of regression coefficients, can be added to the basic model specification (1). Also other effects can be added in this way. A single special event, a change in the mean or a change in the growth, at some time index τ, can be treated by means of an intervention variable. In our analysis below we consider three types of intervention effects which are presented graphically in Fig. 3 . The first graph illustrates a pulse intervention which is used to capture a single special event at some time period 1 < τ < n such as a special holiday or a strike. Such events may cause outlying observations within the time series; the pulse intervention variable, denoted by I _t(τ), can isolate such observations from the model. The second graph in Fig. 3 presents a step intervention that enables to break up the time series into two distinct segments with two different overall means, one for the pre-intervention period t  = 1,…,τ  − 1 and one for the post-intervention period t  =  τ,…,n for some 1 < τ < n. The step intervention, denoted by B _t(τ), is introduced in the model to capture events such as the introduction of new policy measures or changes in regulations. However, a policy change may not be felt instantaneously, but can also have a gradual effect; its full impact is only reached after some time. We do not want to rule out such interventions and therefore also consider the smooth break intervention as presented in the third graph of Fig. 3. The smooth break intervention, denoted by S _t (τ ₁, τ ₂), starts to take effect from time point τ ₁ onwards but it only reaches its full impact after a time period of length τ ₂  −  τ ₁, with 1 < τ ₁ < τ ₂ < n. In case we have τ ₂  =  n, the smooth break intervention reduces to a so-called growth or slope intervention.

Fig. 3.

Intervention effects: (a) pulse intervention, I_t(τ); (b) step intervention or a level break, B_t(τ); (c) smooth break intervention or a gradual level break, S_t (τ₁, τ₂).

We collect the various intervention variables for a pre-defined set of time events in the vector w _t(Π), where Π is given and represents all selected values for τ, τ ₁ and τ ₂. We notice that for each selected intervention type, a range of different values of τ can be selected. We typically only consider values of τ that represent potential events. Hence the vectors Π and w _t(Π) are treated as known and given. The selection of Π and the construction of w _t(Π) are part of the task of the econometrician. The time series model with intervention effects is then given by

$$y_t=x_t^{\prime }\delta +w_t{(\Pi )}^{\prime }\lambda +{\mu }_t+{\gamma }_t+{\epsilon }_t,{\epsilon }_t\sim \text{NID}\left(0,{\sigma }_{\epsilon }^2\right),t=1,\dots ,n,$$ (2)

where λ is a vector of regression coefficients and measures the actual intervention effects implied by w _t(Π).

More generally, when we carry out an intervention analysis to investigate a possible break at some point in time in the crime series, the estimated break may be confounded with other features in the series such as the general trend, the seasonal pattern, and/or the changes in other unobserved variables also affecting the crime rates. By adopting the basic structural time series model (1) with a local linear trend specification for μ _t and a step or smooth break intervention for January 1995, at least the possible confounding effects of a general trend and a seasonal pattern are adequately handled.

However, even when our models for the crime series allow for different factors, including the intervention for January 1995, omitted factors may still affect the crime series. In a bivariate analysis, the omitted factors may also affect a related time series that is not subject to the intervention of interest. We therefore also consider bivariate structural time series models with a treatment and a control time series as in Harvey (1996). In this multivariate approach the model is designed to simultaneously analyse a series representing an eligible crime, that is, a crime that is expected to be affected by the intervention, together with a series representing a non-eligible crime, that is, a crime which is not expected to be affected by the intervention. The former series is often referred to as the treatment series, while the latter series can be referred to as the control or reference series.

The two series are analysed simultaneously using the basic structural time series model (1). In particular, we denote the treatment series as $y_t^{(1)}$ and the reference series as $y_t^{(2)}$ with their model equations given by

$$\begin{array}{ll}\hfill & y_t^{(1)}={\mu }_t^{(1)}+{\gamma }_t^{(1)}+\lambda w_t+{\epsilon }_t^{(1)},\hfill \\ \hfill & y_t^{(2)}={\mu }_t^{(2)}+{\gamma }_t^{(2)}+{\epsilon }_t^{(2)},\hfill \end{array}$$ (3)

for $t=1,\dots ,n$, where the intervention variable w _t is only applied to the treatment series $y_t^{(1)}$. Apart from the intervention variable, the structure of the two model equations in Eq. (3) is the same. The stochastic components for trend ${\mu }_t^{(j)}$, seasonal ${\gamma }_t^{(j)}$ and irregular ${\epsilon }_t^{(j)}$ are mutually independent, for j  = 1,2. However, the trend components in both equations are correlated with each other. Also the two seasonal components and the two irregulars can be correlated with their counterparts in the two equations. When a correlation is equal to one, the stochastic evolution over time of the corresponding component is common to both equations. When a correlation is equal to zero, both components still evolve stochastically over time but independently of each other. The multivariate extension of structural time series models is discussed in more detail in Harvey, 1989, Commandeur and Koopman, 2007.

The empirical results presented in the next section are based on different specifications of the BSM models (univariate and bivariate, with and without intervention variables) and are computed by the time series package STAMP of Koopman et al. (2010). It is able to carry out all computations related to the estimation of parameters by the method of maximum likelihood, estimation of the trend, seasonal and irregular components using filtering and smoothing methods, residual statistics and graphics for diagnostic checking, and forecasting. The computations are based on the Kalman filter and related methods which are extensively discussed in Durbin and Koopman (2012).

4. The impact of sentence reform on crime rates

For all crime series displayed in Fig. 1, Fig. 2, the overall trends display downward patterns. The crime rates before 2000 are overall higher than those after 2000; in some cases even substantially higher. Although it has taken some time for the longer prison sentences imposed under the 1994 sentencing reform to have a significant effect on Virginia's prison population growth,9 decreases in the parole grant rate had an almost immediate effect on the size of the prison population.10 We next investigate the possible instantaneous or more gradual effects of parole abolition and sentence reform on crime rates in Virginia starting in January 1995.

4.1. Intervention without dynamic effects

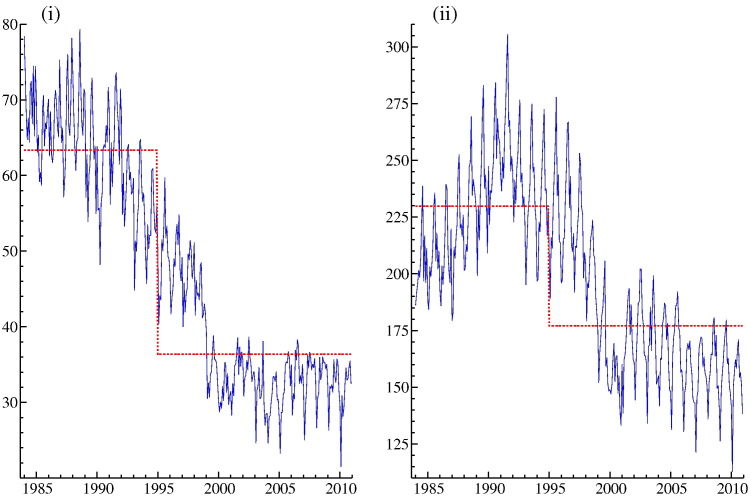
The main feature of our model (2) is the dynamic stochastic specifications of the unobserved components trend μ _t and seasonal γ _t. However, we first take μ _t  =  μ, a fixed constant, and γ _t as a fixed seasonal dummy effect. In this case model (2) reduces to a standard linear regression model and we can jointly estimate the regression coefficients, including those for the intervention effects. It is evident that even for this simplified regression model, the estimated intervention effect, and its possible statistical significance, depends on the specifications for μ _t and γ _t in the model. In graphs (i) and (ii) in Fig. 4 the sample means are presented for the burglary and the larceny crime series, before and after the intervention. The large decreases in the levels after January 1995 for these two crimes series are clearly visible. We confirm that both estimated level breaks are significant.

Fig. 4.

Level change in property crime rates: burglary (left) and larceny (right). The monthly time series are from January 1984 to December 2010.

However, these results may present a misleading picture of the magnitude of the intervention effects because the overall trend in the series is possibly not well represented by μ _t  =  μ in the model. Next we consider a model with a fixed trend as μ _t  =  μ  +  βt, where μ and β are regression coefficients. By adopting this specification for trend in our model with a step intervention in January 1995, we obtain the results presented in graphs (i) and (ii) in Fig. 5 for burglary and larceny. Although the estimated intervention effects are still visible after correcting for time trends in the series, they are clearly much less pronounced compared to the intervention effects presented in graphs (i) and (ii) in Fig. 4. We can conclude that model specification has an effect on the estimated intervention effects.

Fig. 5.

Trend change in property crime rates: burglary (left) and larceny (right). The monthly time series are from January 1984 to December 2010.

4.2. Intervention with dynamic effects

The results above do not account for the stochastic dynamic features in the time series. For all series, the Ljung-Box Q-statistic strongly indicates that the regression residuals are serially correlated. The dynamic stochastic properties of the trends and seasonal effects in the time series are not appropriately accounted for. The possible break in the time series can also be confounded with the dynamic properties of the trend and seasonal. To address these issues and challenges, we adopt the basic structural time series model (1) with stochastic trend and seasonal components, and with a step or smooth break intervention for January 1995.

4.2.1. Step intervention analysis results

For all seven crime rate series in Fig. 1, Fig. 2, we adopt the basic structural time series model as defined in Eq. (1) with the trend component as a random walk with fixed drift, together with a step intervention variable in January 1995. For the burglary and larceny series we also controlled for an outlier with a pulse intervention variable (see Fig. 3 (a)) in December 1989.

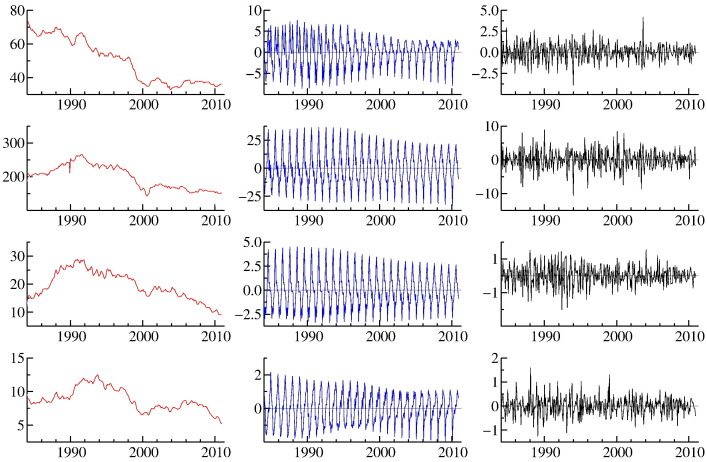
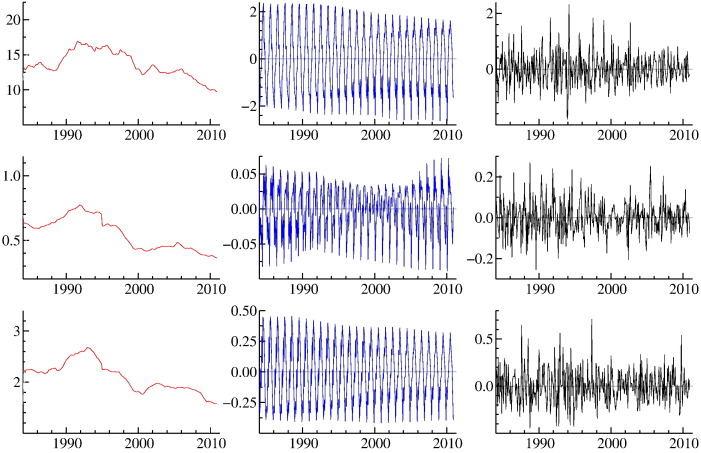
The estimation results are presented in Table 1 , while the smooth estimated trend and seasonal components are displayed in Fig. 6, Fig. 7 for the property and violent crimes, respectively. The estimated regression coefficients of the step intervention variable for January 1995 are negative for burglary, larceny, murder, and rape. However, a statistically significant effect of the new legislation is only found for burglary and murder. The values of the regression coefficients of the step intervention variable for January 1995 are positive for motor vehicle theft, robbery, and aggravated assault, but these are not significantly different from zero. From these analyses we conclude that the new legislation only resulted in a drop for the burglary and murder offences, but not for the other crime categories.

Table 1.

Estimated step interventions for univariate structural time series models.

		Burglary	Larceny	MVT	Robbery	AA	Murder	Rape
Interventions
Structural break		− 3.98	− 8.00	1.67	0.52	0.20	− 0.09	− 0.12
(95:01)		( − 1.95)	( − 1.24)	(1.39)	(0.85)	(0.32)	( − 1.83)	( − 0.96)
Outlier		− 12.57	− 36.88
(89:12)		( − 5.84)	( − 5.95)
Variances
	${\sigma }_{irr}^2$	2.34	18.49	0.73	0.28	0.48	0.01	0.04
		[1.00]	[1.00]	[1.00]	[1.00]	[1.00]	[1.00]	[1.00]
	${\sigma }_{lvl}^2$	1.17	15.07	0.50	0.09	0.06	0.0002	0.001
		[0.50]	[0.82]	[0.69]	[0.33]	[0.13]	[0.02]	[0.03]
	${\sigma }_{seas}^2$	0.01	0.04	0.001	0.001	0.00	0.00	0.00
		[0.00]	[0.00]	[0.00]	[0.00]	[0.00]	[0.00]	[0.00]
Diagnostics
Serial correlation	r(1)	0.10	0.04	0.09	0.10	0.06	0.02	− 0.01
Portmanteau test	Q(24)	33.13	41.27	40.51	27.52	26.60	32.70	10.41
Homoscedasticity	H(103)	0.49	0.59	0.39	0.52	0.55	0.62	0.57
Normality	N	2.97	11.63	5.08	4.96	7.81	5.67	3.49
Goodness-of-fit
	LogL	− 324.15	− 653.60	− 128.87	42.63	7.34	671.04	419.87
	p.e.v.	6.87	57.54	1.91	0.64	0.79	0.01	0.05
	$R_s^2$	0.31	0.34	0.11	0.23	0.33	0.40	0.42
	AIC	2.03	4.15	0.74	− 0.36	− 0.14	− 4.44	− 2.82

In our analysis we consider the BSM with a deterministic slope for the trend component and with intervention effects; the sample size is 324; for intervention effects, we report the t-statistic between round brackets; for the variances, we report the q-ratio in square brackets (it is the ratio of the component variance against the irregular variance); MVT = motor vehicle theft; AA = aggravated assault.

Fig. 6.

Trend (left), seasonal (middle), and irregular (right) components in property crime rates: burglary (first row); larceny (second row); motor vehicle theft (third row); robbery (fourth row). The monthly time series are from January 1984 to December 2010.

Fig. 7.

Trend (left), seasonal (middle), and irregular (right) components in violent crime rates: aggravated assault (first row); murder (second row); rape (third row). The monthly time series are from January 1984 to December 2010.

4.2.2. Gradual break intervention analysis results

The results of the univariate structural time series analysis with a step intervention variable (see Fig. 3 (b)) indicate a deterrent impact of the new legislation for burglary and murder. This evidence is based on the intervention variable B _t for which the impact starts in January 1995. In order to investigate the robustness of this result and whether the impact was instantaneous or more gradual, we repeat the empirical analyses of the previous section on the basis of a smooth break intervention S _t instead of a step intervention B _t. Our smooth break intervention S _t is shown in Fig. 3 (c); we let the break start in January 1995 and we let it end in different years. Table 2 contains the absolute values of the t-statistics of the estimated intervention effects based on B _t and S _t (for different lengths of the gradual break).

Table 2.

Estimated step (B_t) and smooth break (S_t) interventions from structural time series models for both property and violent crimes.

Offence	Break 1995	Gradual 1996	Gradual 1998	Gradual 2000	Gradual 2002	Gradual 2004	Gradual 2006
	Bt	St	St	St	St	St	St
Burglary	1.95	0.48	0.10	1.48	0.60	0.94	0.07
Larceny	1.24	0.35	0.38	2.37	1.39	1.44	1.26
Motor vehicle theft	1.39	0.02	0.06	0.91	0.65	0.62	0.75
Robbery	0.85	0.09	0.37	1.71	0.76	0.89	0.15
Aggravated assault	0.32	0.24	0.16	1.45	0.82	1.21	0.74
Murder (2nd degree)	1.83	0.55	1.34	2.68	1.78	1.09	0.69
Rape (forcible)	0.96	0.55	0.69	1.79	0.78	0.61	0.47

Note: We report t-tests (absolute values) for the step B_t and smooth break S_t interventions. The break for B_t takes place in January 1995. The start of the smooth break S_t is τ₁ and corresponds with January 1995 while τ₂ is the end of the gradual break and is January in the year indicated by the column headings.

The results provide some evidence that a gradual break (S _t) has been more likely than an abrupt break (B _t) in 1995. In particular, the gradual break that ends in 2000 shows a significant effect for larceny and murder. The estimated regression coefficients associated with this gradual break S _t are found to be negative for all crime series.

The more gradual breaks also lead to less precise interpretations of the break. A smooth break affects the overall trend in the period 1995–2000 and therefore cannot be exclusively associated with an event in, say, January 1995. However, in our empirical study the longer prison sentences imposed under the 1994 sentencing reform are likely to have had gradual effect on Virginia's prison population. For example, when we consider the inmates confined for offences committed in early 1996, about 25% of this new inmate population admitted to the prison came in under the old parole system, before 1995, while at the end of 2000 this number was about 1%. This provides some justification that the gradual intervention S _t should also be considered in our intervention analysis.

4.3. Bivariate intervention analysis results

In our bivariate analyses we consider burglary and murder as ‘eligible’ crimes. The new legislation also targeted robbery and rape offences, hence we consider these crimes to be ‘eligible’ as well. Larceny, motor vehicle theft, and aggravated assaults are considered as ‘non-eligible’ crimes. We analyse sets of two time series simultaneously using the bivariate structural time series model as discussed in Section 3 with one variable treated as a treatment group (burglary, robbery, murder, rape) and one variable treated as a control group (larceny, motor vehicle theft, aggravated assaults). We have twelve combinations of two variables and therefore present the estimation results for twelve bivariate models.

The bivariate structural time series model for crime series is also used to assess the effect of parole abolition and of reformed sentencing in Virginia. Since more data is used and since we explicitly model eligible (or treatment) and non-eligible (or control) crime series jointly, we expect an increase of the statistical significance of the intervention from a bivariate analysis in comparison to a univariate analysis. If the treatment variable is affected by the new legislation while the control variable is not, we expect to obtain a strong significant effect of the intervention from our estimation procedure.

The economic interpretation for having treatment and control crime groups can be given as follows. Observed changes in crime around the time of the introduction of the new legislation “may reflect a combination of the true deterrent impact of harsher repeat-offender enhancements and of other factors correlated with but not caused by the law change, such as changes in demographics, in other state policies, and in broad social norms against crime,” see Kessler and Levitt (1999).

The estimation results for burglary as a treatment series and three different control series are presented in Table 3 . The analogous specifications for robbery, murder, and rape as “treatment” series are presented in Table 4, Table 5 , and 6 , respectively. We find significant negative effects in two out of three of the bivariate structural time series specifications for burglary, with motor vehicle theft and aggravated assault as control groups. The estimated regression coefficient ranges from  −3.99 to  −5.19, which is in the neighbourhood of the univariate estimate of  −3.98. The estimated bivariate models for burglary satisfy all of the diagnostic requirements of residual independence, homoscedasticity, and normality. Inspection of the Akaike information criterion indicates that the fit of the bivariate models (all around 2.02) is about as good as the fit of the univariate model (2.03).

Table 3.

Estimated interventions for multivariate STS models — Burglary as a treatment series.

	Statistic	Burglary	Larceny	Burglary	MVT	Burglary	AA
Intervention		−2.75		−5.19		−3.99
(95:01)		( −1.55)		( −2.69)		( −2.00)
Outlier		−12.47	−38.36	−12.03		−11.92
(89:12)		( −5.79)	( −5.79)	( −5.73)		( −5.79)
Variances of disturbances
	${\sigma }_{irr}^2$	2.38	16.61	2.35	0.69	2.32	0.43
		[1.00]	[1.00]	[1.00]	[1.00]	[1.00]	[1.00]
	${\sigma }_{lvl}^2$	1.13	10.30	1.22	0.45	1.18	0.06
		[0.48]	[0.62]	[0.52]	[0.65]	[0.51]	[0.14]
	${\sigma }_{seas}^2$	0.01	0.01	0	0	0.01	0.00
		[0.00]	[0.00]	[0.00]	[0.00]	[0.00]	[0.00]
Diagnostics
Independence	Q(24)	32.65	37.03	33.09	38.00	35.22	24.90
First-order ACF	r(1)	0.10	0.03	0.09	0.04	0.10	0.06
Homoscedasticity	H(103)	0.48	0.58	0.48	0.38	0.51	0.54
Normality	N	2.93	18.14	3.28	5.06	3.04	7.58
Goodness-of-fit
	LogL	−935.38		−434.61		−303.26
	p.e.v.	6.84		6.76		6.87
		9.72	56.83	1.06	1.76	0.63	0.79
	$R_s^2$	0.32	0.35	0.33	0.18	0.32	0.33
	AIC	2.02	4.13	2.01	0.65	2.03	−0.16

Note: Sample size is 324; t-statistic in round brackets; q-ratio (ratio of the estimated standard deviations of the state disturbances and estimated standard deviation of the irregular) in square brackets; BSM model fitted to all specifications; MVT = motor vehicle theft; AA = aggravated assault.

Table 4.

Estimated interventions for multivariate STS models — Robbery as a treatment series.

	Statistic	Robbery	Larceny	Robbery	MVT	Robbery	AA
Intervention		0.73		−0.14		0.41
(95:01)		(1.33)		( −0.27)		(0.72)
Outlier			−33.57
(89:12)			( −5.61)
Variances of disturbances
	${\sigma }_{irr}^2$	0.28	18.35	0.27	0.68	0.28	0.45
		[1.00]	[1.00]	[1.00]	[1.00]	[1.00]	[1.00]
	${\sigma }_{lvl}^2$	0.09	10.34	0.10	0.27	0.09	0.05
		[0.32]	[0.56]	[0.39]	[0.40]	[0.32]	[0.11]
	${\sigma }_{seas}^2$	0.00	0.03	0.00	0.00	0.00	0.00
		[0.00]	[0.00]	[0.00]	[0.00]	[0.00]	[0.00]
Diagnostics
Independence	Q(24)	25.65	41.04	21.94	41.22	26.65	27.29
First-order ACF	r(1)	0.09	0.05	0.06	0.09	0.10	0.07
Homoscedasticity	H(103)	0.52	0.58	0.46	0.41	0.52	0.54
Normality	N	6.97	16.81	7.78	6.02	5.40	8.47
Goodness-of-fit
	LogL	−593.87		−65.95		63.57
	p.e.v.	0.63		0.63		0.64
		1.95	57.55	0.36	1.90	0.19	0.79
	$R_s^2$	0.24	0.34	0.24	0.12	0.23	0.33
	AIC	−0.37	4.15	−0.37	0.73	−0.35	−0.15

Note: Sample size is 324; t-statistic in round brackets; q-ratio (ratio of the estimated standard deviations of the state disturbances and estimated standard deviation of the irregular) in square brackets; BSM model fitted to all specifications; MVT = motor vehicle theft; AA = aggravated assault.

Table 5.

Estimated interventions for multivariate STS models — Murder as a treatment series.

	Statistic	Murder	Larceny	Murder	MVT	Murder	AA
Intervention		−0.08		−0.10		−0.10
(95:01)		( −2.52)		( −2.32)		( −2.55)
Outlier			−36.57
(89:12)			( −5.93)
Variances of disturbances
	${\sigma }_{irr}^2$	0.01	18.07	0.01	0.68	0.01	0.47
		[1.00]	[1.00]	[1.00]	[1.00]	[1.00]	[1.00]
	${\sigma }_{lvl}^2$	0.00	2.43	0.00	0.27	0.00	0.02
		[0.00]	[0.13]	[0.02]	[0.39]	[0.02]	[0.05]
	${\sigma }_{seas}^2$	0.00	0.00	0.00	0.00	0.00	0.00
		[0.00]	[0.00]	[0.00]	[0.00]	[0.00]	[0.00]
Diagnostics
Independence	Q(24)	31.13	44.16	29.16	44.84	29.45	25.45
First-order ACF	r(1)	0.01	0.06	0.01	0.09	0.04	0.06
Homoscedasticity	H(103)	0.61	0.60	0.59	0.39	0.62	0.54
Normality	N	7.30	13.94	7.45	6.53	4.30	8.75
Goodness-of-fit
	LogL	25.10		547.51		684.11
	p.e.v.	0.01		0.01		0.01
		0.04	57.22	0.01	1.90	0.01	0.79
	$R_s^2$	0.44	0.34	0.43	0.12	0.42	0.33
	AIC	−4.49	4.14	−4.47	0.73	−4.46	−0.15

Note: Sample size is 324; t-statistic in round brackets; q-ratio (ratio of the estimated standard deviations of the state disturbances and estimated standard deviation of the irregular) in square brackets; BSM model fitted to all specifications; MVT = motor vehicle theft; AA = aggravated assault.

Table 6.

Estimated interventions for multivariate STS models — Rape as a treatment series.

	Statistic	Rape	Larceny	Rape	MVT	Rape	AA
Intervention		−0.14		−0.19		−0.24
(95:01)		( −1.29)		( −1.67)		( −2.63)
Outlier			−35.37
(89:12)			( −5.79)
Variances of disturbances
	${\sigma }_{irr}^2$	0.04	18.20	0.04	0.69	0.04	0.48
		[1.00]	[1.00]	[1.00]	[1.00]	[1.00]	[1.00]
	${\sigma }_{lvl}^2$	0.00	9.20	0.00	0.33	0.00	0.02
		[0.02]	[0.51]	[0.03]	[0.48]	[0.02]	[0.04]
	${\sigma }_{seas}^2$	0.00	0.04	0.00	0.00	0.00	0.00
		[0.00]	[0.00]	[0.00]	[0.00]	[0.00]	[0.00]
Diagnostics
Independence	Q(24)	10.37	41.18	11.43	41.35	9.10	25.21
First-order ACF	r(1)	0.01	0.04	0.00	0.08	0.02	0.07
Homoscedasticity	H(103)	0.56	0.59	0.56	0.39	0.59	0.54
Normality	N	3.51	14.23	3.27	5.36	2.41	7.78
Goodness-of-fit
	LogL	−227.63		296.91		434.44
	p.e.v.	0.05		0.05		0.05
		0.33	57.84	0.05	1.92	0.03	0.78
	$R_s^2$	0.43	0.33	0.43	0.11	0.43	0.33
	AIC	−2.84	4.15	−2.84	0.74	−2.84	−0.16

Note: Sample size is 324; t-statistic in round brackets; q-ratio (ratio of the estimated standard deviations of the state disturbances and estimated standard deviation of the irregular) in square brackets; BSM model fitted to all specifications; MVT = motor vehicle theft; AA = aggravated assault.

A similar picture is obtained for the bivariate structural time series analyses of the murder series, see Table 5. Negative significant effects of the new legislation are found in all three bivariate structural time series models with control groups. When motor vehicle theft and aggravated assault are treated as non-eligible crimes, the estimated effect of the new legislation on murder is  −0.10, which is almost identical to the univariate result of  −0.09, see Table 1. The bivariate model residuals for murder also satisfy all of the model assumptions, while the fit of the bivariate models is similar to that of the univariate model (with AIC value  −4.45).

When we treat robbery as a treatment series, we do not find significant results in any of the three bivariate model specifications, see Table 4. This finding suggests that although the new legislation targeted robbery as a most violent property crime, we do not find any confirmation that the behaviour of this series has been significantly altered by the new legislation. When we consider the bivariate results in Table 6, where rape is handled as a treatment series, we find a significant negative effect for rape when it is modelled together with aggravated assault as a control group. The estimated effect is  −0.24, which is larger in absolute value than the univariate estimate of  −0.12. The AIC values of  −2.84 for rape in the bivariate model and of  −2.82 in the univariate model again indicate that these two models fit the rape crime series about equally well.

In summary, the multivariate estimation results confirm that new legislation significantly affected burglary ( −3.99 to  −5.19) and murder ( −0.10). As far as rape is concerned, we find a significant drop of  −0.24 in one of the three bivariate model specifications, which is a larger effect than the (insignificant) univariate estimation result of  −0.15. We have also considered the simultaneous treatment of all seven crime series in a unified model but this multivariate analysis has not led to an improvement of the univariate or bivariate specifications presented above. Also, we have not found a common trend in the seven crime variables.

5. Discussion

5.1. Alternative econometric methodologies for detecting breaks

Many forecasting and time series studies are based on the autoregressive moving average (ARMA) model and on the methodology of Box and Jenkins (1976). While the time series analysis based on the structural time series model of Harvey (1989) is somewhat less used in economics, sociology, crime, and other fields, we believe that the structural time series analyses carried out in Section 4 are especially appropriate when various non-stationary features need to be treated. We will not embark on a complete and detailed discussion of both approaches to time series modelling. For such an endeavour we refer to the discussions in Harvey, 1989, Commandeur and Koopman, 2007, Durbin and Koopman, 2012.

Among others, Harvey (1996) has argued strongly how a structural time series analysis can be adopted effectively in an intervention analysis. We have confirmed in our study that a structural time series analysis can indeed be effective in capturing non-stationary features such as trends and seasonal effects simultaneously in a unified manner. In addition, we have shown that an effective intervention analysis can also be accomplished in a multivariate structural time series analysis. The multivariate extension is straightforward in many ways although computationally somewhat more involved. In all cases, the analysis is based on state space methods such as the Kalman filter which can handle various messy features in a time series including missing values.

For the purpose of intervention analysis, many approaches have been developed on the basis of time series methodologies that are different from structural time series analysis. An early reference is Box and Tiao (1975) where a thorough approach is developed for intervention analysis in the context of stationary ARMA modelling. The more recent developments in detecting and testing for breaks in time series (in mean, regression coefficients, variance) have been initiated by Andrews, 1993, Zivot and Andrews, 1992. The key developments for identifying multiple structural breaks have been initiated by Bai and Perron (Bai and Perron, 2003, Bai and Perron, 1998) and Caporale and Grier (2005a) for non-trending data, and Lumsdaine and Papell, 1997, Lee and Strazicich, 2003, and Narayan and Popp (2013) for trending data.11

These different econometric approaches for the detection of structural breaks have been adopted and illustrated in various empirical studies. For example, Nelson (2000) adopts the Box–Tiao intervention analysis methodology to establish the impact of the Bankruptcy Reform Act of 1978. Miguel and Kremer (2008) assess whether two events, the 9-21 Earthquake in 1999 and the Severe Acute Respiratory Syndrome outbreak in 2003, had a temporary or long-term impact on the inbound tourism demand from Japan. Harvey and Fernandes, 1989, Atkinson et al., 1997 examine the number of outliers and breaks in a monthly time series of number of purse (handbag) snatches in Hyde Park in Chicago. The latter analyses are based on structural time series models. Caporale and Grier (2005a) verify the influence of political dummy variables while controlling for different inflation regimes, using the Bai–Perron methodology. Similarly interesting studies that assess the impact of breaks due to political and associated social and economic events are presented in Caporale and Grier (2005b), concerned with detecting breaks in real interest rates, Smyth and Narayan (2006), estimating both the number and location of structural breaks in concurring and dissenting opinions on the U.S. Supreme Court, and Chen and Wang (2014), investigating the impact of political events on monetary policy.

5.2. Robustness of results: automatic detection of breaks

Our study has aimed to capture the statistical effects of policy interventions with a known date. It is also possible within a structural time series analysis to develop a statistical procedure for determining the number of interventions and the locations of these. Hence we do not need to set a-priori the dates of the interventions but they can be treated as unknown. Such a procedure is implemented in the STAMP package of Koopman et al. (2010). It is based on a first analysis where a sequential inclusion of outlier and level break dummies in the model, over each time point t, is considered and the dummy parameters are estimated. All significant dummies (or those close to significance) are recorded. In a second analysis, all recorded dummies are included in the model and all parameters are estimated simultaneously. Then a general-to-specific estimation and testing methodology is adopted to determine the final model specification. In the structural time series analysis adopted in STAMP, each estimation round is based on a model where the trend and seasonal unobserved components are included such that it always accounts for the possible non-stationary dynamic features in the time series. The methodology is different from cointegration and Bai and Perron (Bai and Perron, 1998, Bai and Perron, 2003) analyses. In STAMP, the computations rely on the Kalman filter and the analytical methods developed by Harvey and Koopman (1992).

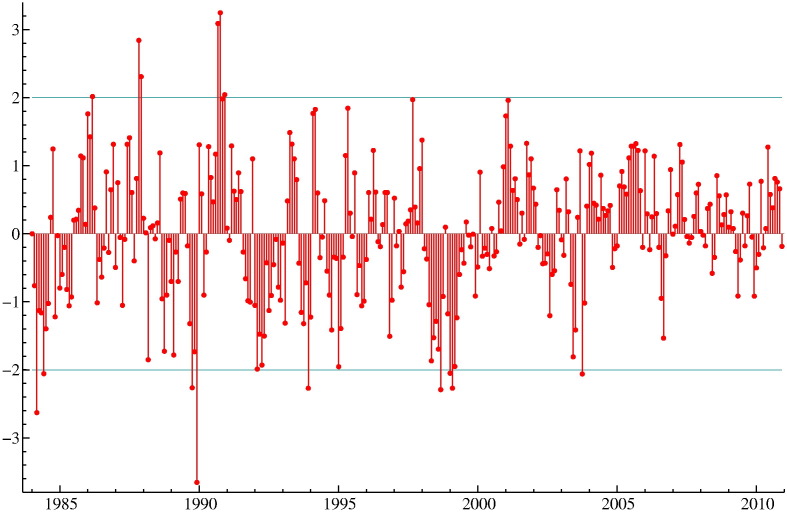
To assess the robustness of our empirical results presented in Section 4, we have carried out the outlier and level break detection procedures of STAMP. We present these additional results for the key time series of burglary12 and adopt the univariate structural time series model from Table 1. In the first step, we introduce outlier and level break interventions at each consecutive time point and record the resulting t-statistic for the related dummy variables. In Fig. 8 we present the t-statistics for the level break interventions in a time series index plot. We find that significant level breaks are detected in the series while the break for the reformed sentencing change from 1995 is not outstanding. In the next step we consider the univariate model that includes all significant outlier and level breaks from the first step (the level break intervention variables are for March 1984, November 1987, and October 1990) plus our parole policy intervention for January 1995. The resulting t-statistic for the policy change has now risen from  −1.95 in Table 1 to  −2.51 for this extended model. Hence the evidence of a significant change due to the parole abolition and reformed sentencing in Virginia has become stronger. However, this result is not found for all other six crime series, in most cases the additional analysis has not changed our conclusions as presented in this study.

Fig. 8.

The t-statistics for a level break at each time period for the univariate model of the burglary variable as considered in Table 1. The monthly time series is from January 1984 to December 2010.

5.3. Robustness of results: different time frequencies

To investigate whether our analysis is robust to analyses of different sample time frequencies, we have re-considered the monthly univariate structural time series analysis with the results reported in Table 1. Instead of analysing the monthly time series, we have aggregated all underlying time series of crime rates into quarterly time series and re-estimated the parameters of the same underlying model but now based on the quarterly time series. We expect the estimates, and in particular the estimated structural, or step, break for the first month/quarter of 1995, to have the same corresponding values and significance levels. The estimated step break coefficients for month and quarter sample frequencies are presented in Table 7 .

Table 7.

Estimated step break 1995 for monthly and quarterly sample frequencies.

	Burglary	Larceny	MVT	Robbery	AA	Murder	Rape
Step break 95:01
Monthly freq	−3.98*	−8.00	1.67	0.52	0.20	−0.09*	−0.12
Quarterly freq	−3.77*	−4.58	3.00*	0.65	0.16	−0.10*	−0.10
Abs.diff	0.21	3.42*	1.33	0.13	0.04	0.01	0.02

In our analysis we consider the BSM with a deterministic slope for the trend component and with intervention effects; the sample sizes are 324 (monthly) and 108 (quarterly); MVT = motor vehicle theft; AA = aggravated assault; abs.diff = absolute difference between monthly and quarterly estimates; the asterisk* indicates statistical significance.

The reported results indicate that the estimates of the step break dummy for the first month/quarter in 1995 are robust to the different monthly and quarterly sample frequencies. For all crime series, the differences between the two estimates (month/quarter) are statistically not different from zero, except for the larceny crime series. The monthly and quarterly analyses are based on the same models, but in case of the larceny series, the behaviour of the trend component is somewhat different (more variation in the quarterly case) and this affects the estimate of the step break dummy. Finally, apart from the burglary time series, the 1995 break estimates in the quarterly case are also significant for the motor vehicle theft and murder series.

6. Conclusions

We have adopted univariate and bivariate structural time series models to investigate the impact of parole abolition and sentence reform in Virginia on reported crime rates. The examined crime rate series are monthly data on burglary, larceny, motor vehicle theft, robbery, aggravated assault, murder, and rape in the years 1984–2010. We have verified our results with the same but quarterly data set. The empirical results have indicated that the legislation of January 1, 1995 has significantly affected only burglary (−3.99) and murder (−0.09). Significant gradual drops in crime rates based on a smooth break intervention variable for the 1995–2000 period have been found for larceny and murder. The bivariate analyses for burglary have yielded two significant drops of  −3.99 (with aggravated assault as reference) and  −5.19 (with motor vehicle theft as reference). In the case of rape, we found a significant drop of  −0.24 in one of the three bivariate model specifications. We have not found an effect of the new legislation for aggravated assault which is also a violent offence.

Virginia's abolition of parole and reform of the sentencing system provides a useful social experiment to study. First, the legislation had a big impact on society and it focussed on all felonies. Second, the legislation was enacted at a time in which there were various, favourable changes in a number of social and economic indicators. Third, the 1990s also witnessed the implementation of a number of initiatives focused on reducing crime at the Federal, State and Community levels. Disentangling the impact of parole abolition from the other factors poses multiple design and analytical challenges. According to the Virginia crime officials, research to date has been unable to determine if the observed reductions in crime rates were due to specific anti-crime initiatives. Hence, adopting a structural intervention time series analysis, we have aimed to contribute to a better understanding of the statistical relationship between anti-crime efforts and crime reductions over time.