Mechano-Electric and Mechano-Chemo-Transduction in Cardiomyocytes

Abstract

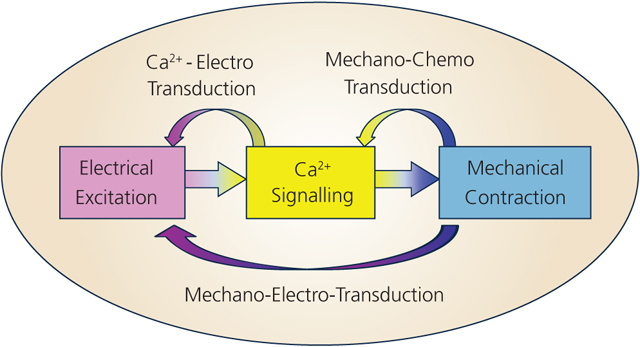
Cardiac excitation-contraction (E-C) coupling is influenced by (at least) three dynamic systems that couple and feedback to one another (Abstract Figure). Here we review the mechanical effects on cardiomyocytes that include mechano-electro-transduction (commonly referred to as mechano-electric coupling, MEC) and mechano-chemo-transduction (MCT) mechanisms at cell and molecular levels which couple to Ca²⁺-electro and E-C coupling reviewed elsewhere. These feedback loops from muscle contraction and mechano-transduction to the Ca²⁺ homeodynamics and to the electrical excitation are essential for understanding the E-C coupling dynamic system and arrhythmogenesis in mechanically loaded hearts. This white paper is comprised of two parts each reflects the key aspects from the 2018 UC Davis symposium: MEC (how mechanical load influences electrical dynamics) and MCT (how mechanical load alters cell signaling and Ca²⁺ dynamics). Of course, such separation is artificial since Ca²⁺ dynamics profoundly affects ion channels and electrogenic transporters and vice-versa. In time these dynamic systems and their interactions must become fully integrated, and that should be a goal for a comprehensive understanding of how mechanical load influences cell signaling, Ca²⁺ homeodynamics and electrical dynamics. In this white paper we will emphasize current understanding, consensus, controversies, and the pressing issues for future investigations. Space constraints make it impossible to cover all relevant articles in the field, so we will focus on the topics discussed in the symposium.

Graphical Abstract

Cardiac excitation-contraction coupling and feedback pathways by mechano-electro- and mechano-chemo-transduction.

§1. Preamble

Recognizing the critical need to combine experimental methods and mathematical models in studying complex heart disease mechanisms, the UC Davis Cardiovascular Symposia series provides an on-going forum for experimentalists, modelers, physicians and scientists to exchange ideas and build collaborations. The goal of this meeting series is to develop an in-depth quantitative understanding of the interplay of cardiac electrical, Ca²⁺ and mechanical signaling and how each of these systems feeds back on each other dynamically (Abstract Figure). Such feedback systems can both stabilize physiological function and cause pathological dysfunction. Such understanding is critically important for identification of causes of cardiac arrhythmias and contractile dysfunction (e.g. in heart failure) and the development of effective therapies.

The UC Davis Cardiovascular Symposium series has been organized to integrate such experimental and modeling studies in a series of meetings. The first symposium (2010) took an integrative view of the E-C coupling and arrhythmia mechanisms that set the stage for a series of more focused topics: on Ca⁺ channels and Ca²⁺ signaling system (2012), Na⁺ channels and Na⁺ regulation (2014), and K⁺ channels and K⁺ regulation (2016) and mechanics and energetics (2018). Each of these are essential to our integrated understanding and benefit greatly from combining experimental investigations with mathematical modeling studies and clinical perspectives. We shall come full circle from the first 2010 meeting in 2020 when we return to focus on integration among these areas. (See basicscience.ucdmc.ucdavis.edu)

§2. Mechano-Electric-Coupling

2.1: Mechano-electric coupling (MEC)

Clinical awareness of mechanical modulation of heart rate and rhythm can be traced back by at least a century in the Western medical literature, with examples both for mechanical induction (Meola, 1879) and mechanical termination (Schott, 1920) of heart rhythm disturbances. Following early experimental work that identified the intra-cardiac nature of mechanically-induced changes in cardiac electrophysiology (Schlomka & Hinrichs, 1932), mechano-electric coupling (MEC) was conceptualised as part of cardiac electro-mechanical auto-regulation by Ursula Ravens (née Thophile) in 1967 (Kaufmann & Theophile, 1967). Since then, pioneering work by Max Lab, Frederick Sachs, Michael Franz and others has moved MEC from a footnote in cardiac electrophysiology to appreciation as a fundamental part of cardiac functional integration (for a comprehensive collection of international research on the topic, see multi-author textbook (Kohl et al., 2011)).

MEC is based on at least two interacting molecular mechanisms: mechano-sensitive ion channels (see section 2.2) and mechanical modulation of intracellular calcium handling (section 2.3).

2.2: MEC effects via mechano-sensitive ion channels

General aspects

Mechano-sensitive ion channels can be split into channels that require a change in cell volume (cell volume-activated ion channels: VAC) and those that activate directly in response to membrane deformation (stretch-activated ion channels: SAC). Since acute effects of mechanical stimulation on cardiac electrophysiology, including beat-by-beat responses, are thought to not involve cell volume changes, SACs are usually considered a primary target for MEC research as it pertains to acute electrophysiological responses to mechanical stimulation.

It is important, however, to note that VAC contributes to cardiac MEC responses in cells subjected to swelling, for example during ischaemia or upon reperfusion. Interestingly, VAC are constitutively activated in the enlarged cells of failing hearts (Clemo et al., 1999), suggesting the presence of a ‘set point’ for cardiomyocyte cell volume by an as yet unidentified mechanism. Like many other changes in cardiac structure and function, causal chains of events occurring during chronic tissue remodelling are difficult to explore. This represents an important area for further study.

SAC can be sub-divided by their ion selectivity into cation non-selective (SAC_NS) and potassium-selective (SAC_K) channels. While somewhat arbitrary, this division is helpful when considering effects on cell electrophysiology, as SAC_NS will depolarise resting cardiomyocytes, while SAC_K will have a re- or hyperpolarizing effect. Given that resting cardiomyocytes respond to mechanical stimulation (if they show any response at all) by depolarization, it is thought that SAC_NS dominate MEC effect in healthy cells under normal conditions (Kohl et al., 2006).

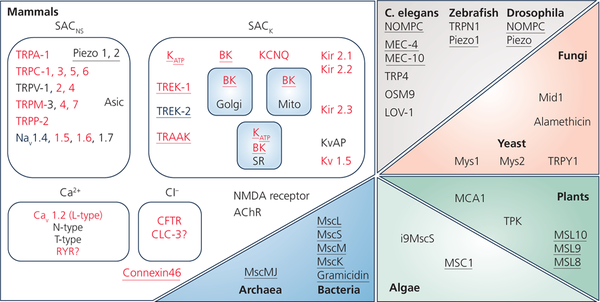
In addition to ion channels whose open probability is primarily graded by mechanical events, many ligand- and voltage-gated ion channels are mechanically modulated – both in terms of their open probability (Morris, 2011) and in terms of their functional integration into the surface sarcolemma (Boycott et al., 2013). Figure 1 provides a recent overview of mechano-sensitive ion channels that highlights both their ubiquitous presence across living kingdoms and the breadth of proteins identified (from (Peyronnet et al., 2016)). This listing is in constant flux, and the relatively recently identified Piezo channels (Coste et al., 2012) that appear to be gated by bilayer tension (Cox et al., 2016), have now been found in the heart as well (Liang et al., 2017). In addition, we now appreciate that there are individual mutations that may convey increased mechano-sensitivity to ion channels such as TREK-1, which may be associated with an increased risk for arrhythmogenesis in patients (Decher et al., 2017). These findings could open up pathways to ‘mechano-transduction targeting’ for personalised therapeutic strategies.

Figure 1:

Mechanically-gated and modulated ion channels across living organisms. Proteins highlighted in red have been identified in the mammalian heart, channels confirmed as stretch-activated are underlined. From (Peyronnet et al., 2016).

That said - in general, it has remained challenging to identify biologically relevant biophysical input signals for mechano-sensitive ion channel gating. Part of the challenge is that – while we are getting better at tracking cell strain in native tissue (Botcherby et al., 2013) – we are still far from true readouts of cell stress in the myocardium. While suitable fluorescent probes for measuring cytoskeletal stress have been developed (Rahimzadeh et al., 2011), challenges remain in terms of their calibration and use within native tissue, such as the heart.

Given our current inability to accurately identify biologically relevant input parameters – can we at least unequivocally identify the respondents to mechanical stimulation? Well – to some extent yes. As underlying molecular targets are increasingly being identified, both up- and down-regulation approaches have been used to substantiate the players involved in stretch-effects on cardiac electrophysiology. Of course, genetic modification is burdened by the possibility (probability) of compensatory changes in the presence and/or activity of other pathway elements.

This can, in part, be compensated using acute pharmacological interventions. A problem here is that we are lacking target-specific blockers and activators (as reviewed in detail elsewhere (Peyronnet et al., 2016)). To assess SAC_NS-contributions, GsMTx-4, a peptide from the venom of the Chilean tarantula Grammostola spatulata (Suchyna et al., 2000) is the intervention tool of choice. GsMTx-4 shows good selectivity for SAC_NS and utility for use not only in cardiac cells, but also in native tissue (Bode et al., 2001). This is not ‘a given’ and has led to false-negative observations with other, less suitable pharmacological agents such as Gadolinium and streptomycin (Cooper & Kohl, 2005; Zhang et al., 2018). A note of caution is warranted here for all cell culture studies: streptomycin, an obligatory component of most commercial culture media, is a formidable blocker of SAC_NS and stretch-induced changes in Ca²⁺ handling (Gannier et al., 1994; Belus & White, 2003).

The experimental difficulties in linking biophysical inputs to molecular players, and cellular responses to organ-level mechano-sensitivity, have contributed to the high relevance of computational models in the quantitative assessment of potential pathways of cardiac MEC (see section 2.4).

Healthy myocardium

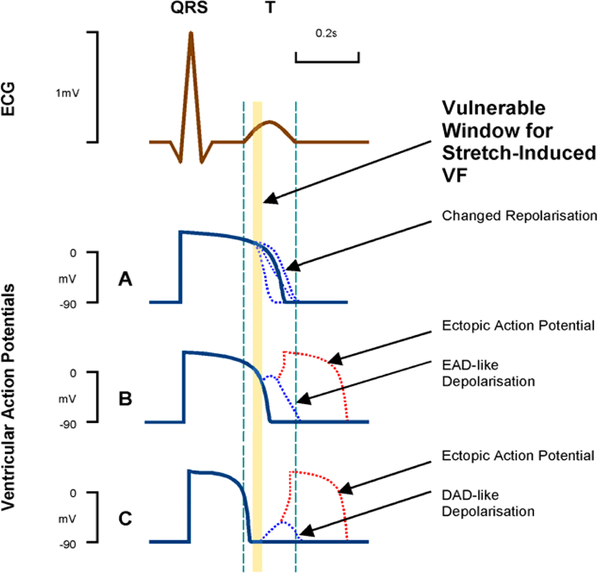
The physiological response of cardiac myocytes to acute mechanical stimulation is diastolic depolarization, which facilitates diastolic depolarisation in pacemaker (Cooper et al., 2000) and conduction cells (Kaufmann & Theophile, 1967). This can trigger excitation in resting atrial (Bode et al., 2001) and ventricular myocardium (Franz et al., 1992). This is in line with a major contribution by SAC_NS, whose pharmacological block can abolish ectopy. During the action potential (AP), acute stretch responses depend on the difference between current cellular membrane potential and reversal potential of stretch-activated channels (for SAC_NS between 0 and −15 mV), causing abbreviation of early and prolongation of late AP time courses, including early and delayed afterdepolarization-like potential changes (EAD, DAD; see Figure 2 (Kohl et al., 2001)).

Figure 2:

Schematic representation of cardiomyocyte action potential (AP) responses to stretch-activated ion channel (SAC) opening at different timings during the AP. Within a short critical time-window during early ventricular repolarization (just prior to the peak of the T wave; see schematic ECG trace), these can combine to render both trigger (red) and sustaining mechanisms (blue) for ventricular rhythm disturbances (Commotio cordis). Reproduced from (Kohl et al., 2001).

It has been difficult to identify an evolutionary advantage for cardiac MEC. One line of thought is that mechano-regulation of the ionic milieu would have been an early requirement during the emergence of multicellular life forms, whose presence/ preservation did not exert a negative evolutionary pressure – so mechano-modulation of ion channels is conserved in all cell types that have been assessed. Alternatively, the electrophysiological consequences of mechano-sensitive ion channel activation could be a side-effect of a different, more important role in the heart: the local matching of cellular Ca²⁺ load (and, hence, contractile performance) to global circulatory demand (Markhasin et al., 2003). This would be relevant for an organ that relies on synchronised and force-balanced contraction of millions of muscle cells that lack targeted external control mechanisms (such as individual neuro-muscular junctions), in particular as each of these cells experiences slightly different stress-strain dynamics during normal cardiac activity. Relevant mechanisms would include both (i) mechanical modulation of trans-sarcolemmal Ca²⁺ flux (whether directly by permeation Ca²⁺ through via SAC, or indirectly, e.g. by via SAC-medicated Na⁺ influx that alters NCX (Gannier et al., 1996; Jin et al., 2017; Zhao et al., 2017)) and (ii) mechanical modulation of Ca²⁺ flux between intracellular stores and cytosol (for example via a stretch-induced increase in ryanodine receptor (RyR) open probability (Iribe et al., 2009a) or mitochondrial Ca²⁺ release (Belmonte & Morad, 2008)). Whatever the explanation, the physiological benefit of cardiac mechano-electric cross-talk – beyond potential contributions to preload-adjusted sino-atrial node pacemaking (Quinn & Kohl, 2012) – remains a matter of debate.

What is well-established is that the arrhythmogenic potential of mechanical stimulation if ill-timed, may trigger sustained ventricular tachyarrhythmias (Schlomka & Hinrichs, 1932; Kohl et al., 2001; Link, 2012). Interestingly, this is an example of cardiac MEC research, where conceptual (Kohl et al., 2001) and computational prediction of quantitatively plausible mechanisms in 2-D (Garny & Kohl, 2004) and 3-D (Li et al., 2004) computational models of ventricular myocardium preceded experimental confirmation by many years (Quinn et al., 2017). We now know that focal electrical excitation, for example triggered by a precordial impact in myocardium just underneath the impact site (Link, 2012), may give rise to reentrant excitation if this ectopic focus occurs just on the trailing edge of the preceding repolarization wave, which acts as a functional block zone preventing uniform spread of the ectopic wave (Quinn et al., 2017). While this may give rise to sustained tachyarrhythmia, the vulnerable window for this is impact location-dependent and short (Figure2), so that most mechanically-induced ectopic beats are benign in healthy myocardium.

Diseased myocardium

Overall, mechanistic insight into MEC in diseased tissue is limited. Reasons include the aforementioned inability to determine local stress levels in native tissue and the often significant structural and functional remodelling in chronic disease settings.

Functional remodelling includes alterations in ion channel presence and activity, such as an upregulation of VAC in hypertrophied cells (Clemo et al., 1999), or metabolic and mechanical co-activation of ATP_K channels (Van Wagoner, 1993) in ischaemic tissue (Huang et al., 2013), with demonstrable knock-on effects on local intra- and extracellular ion concentrations and arrhythmogenesis (Bollensdorff & Lab, 2011). In addition, mutations that alter ion channel mechano-sensitivity are starting to emerge as clinically relevant contributors to arrhythmogenesis (Decher et al., 2017).

Structural remodelling gives rise to significant heterogeneity in active and passive mechanical properties, which will affect MEC responses. Examples include inhomogeneous stress-strain behaviour in and around ischaemic foci (where paradoxical segment lengthening can be observed), scar border zones (BZ; where stiff scar tissue gives rise to varying stress gradients as the surrounding tissue changes from resting to contracted and back), or asynchronous activation of different cardiac tissue regions (for example as a result of bundle branch block or during cardiac resynchronisation therapy). Some of the scenarios in which nonuniform contraction contributes to arrhythmogenesis are explained in sections 2.3 and 2.4.

2.3. MEC effects via changes in intracellular Ca²⁺ handling

General aspects

E-C coupling is traditionally seen as a sequence of events, where electrical activity (e.g. an AP) results in the rise and decay of an intracellular Ca²⁺ transient, with the consequential rise and fall of contraction. Yet there is feedback from mechanics to Ca²⁺ and electrophysiology, as well as from Ca²⁺ to electrophysiology. This could be called reverse mode E-C coupling. A key signaling molecule involved is intracellular Ca²⁺. A typical example of Ca²⁺–related arrhythmogenesis is when Ca²⁺ is released from the sarcoplasmic reticulum (SR) stores by ‘leaky’ Ryanodine receptors (RyR2) during diastole, or during AP repolarization. This Ca²⁺ can initiates a Ca²⁺ wave, followed by DAD or EAD (Bers, 2014). Below we will focus on an example that depends on Ca²⁺ release from myofilaments, rather than the SR.

Ectopy secondary to non-uniform EC coupling

In failing hearts, wall stress increases as a result of dilation of the left ventricle (LV). This increased wall stress aggravates regional differences in contractile strength around the impaired muscle. Regional differences in contractile strength may cause paradoxical stretching of impaired muscle by contractions of neighboring more viable muscle. This forms a BZ between regions of stretch and shortening.

In 2005, Wakayama et al. (Wakayama et al., 2005) described spatially non-uniform muscle contractions that lead to DAD induced arrhythmias. Quite different from Ca²⁺ leak induced Ca²⁺ waves (Ter Keurs & Boyden, 2007), the arrhythmogenic Ca²⁺ waves initiating these triggered propagated contractions in this multicellular cardiac preparation arise from acute reduction of myofilament Ca²⁺ binding in regions near damaged areas. In this latter case, Ca²⁺ waves are dependent on mechanical stretch and release at the border between the damaged and intact regions.

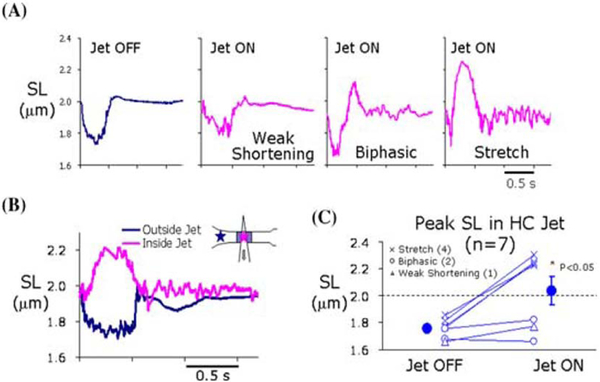
For these experiments, ter Keurs et al. created a controlled local reduction of myofilament force development in a length of normal multicellular rat trabecula. This was accomplished by exposing the preparation to a small jet of a solution that contained either 2,3-butanedione monoxime (BDM), or low external Ca²⁺ concentration ([Ca²⁺]_o; see Figure 3B inset). They measured sarcomere length (SL) and with this jet off there was SL shortening in this region. However, when the jet was on, the weakened region near the center of the jet experience stretch by the strong regions on either side of the jet (increased SL Figure 3A-right and 3B).

Figure 3:

Experimental model to mimic for nonuniform EC coupling in rat trabeculae. Sarcomere length (SL) changes measured from different regions during experiments in a single trabecula when jet of butane BDM was ON or OFF. Note: In some regions there was weak shortening while in others stretch was present. This set up conditions of nonuniform EC coupling. From (ter Keurs et al., 2006).

Here the initial Ca²⁺ rise during the wave initiation was shown to be caused by Ca²⁺ dissociation from myofilaments as a result of quick release and shortening of active sarcomeres (Wakayama et al., 2001). This is because the Ca²⁺ binding affinity is positively correlated with the number of Ca²⁺-activated force-bearing cross-bridges (Allen & Kentish, 1985). Rapid shortening of sarcomeres in the BZ during relaxation causes Ca²⁺ release from troponin C on the thin filaments. This release can initiate the Ca²⁺ waves. Elimination of SL shortening will inhibit the initiation of Ca²⁺ waves, while SR Ca²⁺ load and release will enhance such waves. Thus the initiation is not caused by Ca²⁺ leak from SR, but caused by an intracellular Ca²⁺ surge from myofilaments that are a major site of Ca²⁺ buffering in myocytes (Bers, 2001). Such a Ca²⁺ surge can then induce SR Ca²⁺ release waves which lead to DADs that under certain conditions, trigger electrical activity (Figure 4). Indeed, the amount of Ca²⁺ dissociated from the myofilaments affects the frequency of the arrhythmias. For example, the maximum rate of muscle relaxation was inversely correlated with the cycle length of the arrhythmia. An unresolved issue is that these waves propagate in multicellular preparations at 0.2–2.8 mm/sec which is too fast for SR-mediated Ca²⁺ waves travelling via Ca-induced Ca-release (~0.1 mm/sec; (Brette et al., 2005)) that normally do not cross gap junctions between myocytes, but is much slower than expected for full-blown AP propagation in tissue (>200 mm/sec; (Myles et al., 2012)). While the mechanism may be a hybrid, some mechanistic details about this potentially important MEC mechanism in arrhythmogenesis need further testing.

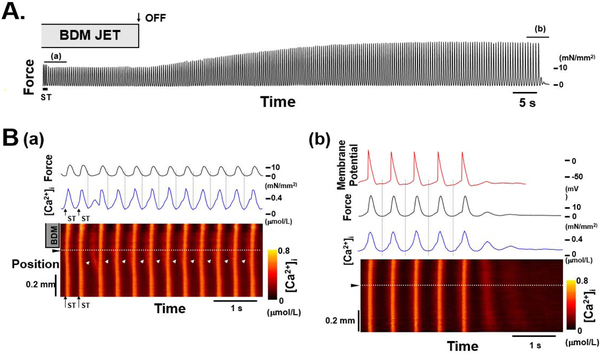
Figure 4:

Effect of regional application of BDM via a jet on a sustained arrhythmia. A, Continuous chart recording of force during a sustained arrhythmia induced by electric stimulation (ST). Arrow with OFF indicates when the BDM jet was turned off. After the jet was turned off, the contractions became larger and slower, B, Expanded recordings of force (black lines), membrane potential (red line), [Ca²⁺]i at the position indicated by the dotted white lines on the bottom (blue lines), and regional changes in [Ca2+]i (bottom) during the periods indicated by lines a and b in A. Note initiation of arrhythmia by Ca²⁺ wave seen in B(a). This Ca²⁺ wave is dependent on the amount of Ca²⁺ released from Troponin C upon quick release. From (Miura et al., 2010).

EAD generation secondary to myofilament protein dynamics: computational model

Recent computational modeling has concluded that myofilament protein dynamics in a hypertropic cardiomyopathy model could affect EAD-formation and possibly arrhythmias in this heritable substrate (Zile & Trayanova, 2017). The paper concluded that incorporation of Troponin C buffering of cytosolic Ca²⁺ alters AP repolarization reserve which leads to EAD emergence and triggers for arrhythmia. The utility of computational modelling at the organ level is discussed in more detail in section 2.4.

2.4. Modelling MEC at the Organ Level

We focus on organ-level electro-mechanical modeling studies, as these have advanced over recent years, progressing through different scopes of mechanistic research and corresponding model complexity. MEC effects at the level of individual cells, in contrast, have been modelled before the turn of the Millennium (Kohl et al., 1998; Rice JJ et al., 1999; Landesberg and Sideman, 1994; Noble et al., 1998), and they are thus not discussed in detail here. In short: experimentally observed responses of single cardiac cells to stretch have generally lent themselves to being reproduced using computational models (for reviews, see (Kohl et al., 1999; Trayanova and Rice, 2011)). Below we present the main areas of MEC exploration by computational modeling at the whole heart level.

Role of mechanical impact in arrhythmogenesis and arrhythmia termination in the heart.

In early whole-heart studies, mechanical stimulation was incorporated through its impact on the electrophysiology of the heart, namely through uniform regional SAC activation. In the modeling study by Li et al. (Li et al., 2004), both SAC_NS and SAC_K are recruited upon mechanical impact. The impact is administered at various coupling intervals following pacing at the apex. The results demonstrated that the impact induces sustained reentrant excitation only when (1) a new activation is elicited by mechanical stimulation (caused by activation of SAC_NS), and (2) upon return to the original region of impact, this activation does not encounter an extension of AP duration (prevented by activation of SAC_K, such as K_ATP). Furthermore, a subsequent study by Li et al. (Li et al., 2006) elucidated the mechanisms involved in termination of ventricular tachycardia by precordial thump and its decreased rate of success in ischemia. Results demonstrate that precordial thump-induced SAC_NS opening in normoxia reduces heterogeneity in transmembrane potential by partially repolarizing excited tissue and depolarizing resting myocardium, causing foci of excitation that eradicate the excitable gap, thus facilitating tachycardia-termination. Decreased precordial thump efficacy in ischemia was caused by recruitment of K_ATP, which diminishes the depolarizing effect of SAC_NS on resting tissue and caused pronounced AP shortening, thus facilitating establishment of reentry.

Electromechanical transduction and arrhythmogenesis in the diseased heart

In these studies, model complexity has increased, with representation of both electrical and mechanical function and their coupling. Past research explored the role of acute stretch as a trigger of arrhythmia under the conditions of acute ischemia, as well as the effect of acute stretch on the substrate for ventricular fibrillation (VF; Figure 5; (Jie et al., 2010)). In Jie et al., the ventricles had a central ischemic zone (CIZ) and an intermediate BZ, and this was used to represent the electrophysiological and mechanical milieu in the heart at several stages post-occlusion. The study found that large muscle strain developed in the ischemic region during contraction. In both BZ and CIZ, cell membranes underwent mechanically induced subthreshold depolarizations, or DAD–like events, whereas such depolarizations were absent in the normal zone. The DAD–like events resulted in mechanically induced ventricular premature beats (VPB), originating from the ischemic border (particularly in the LV endocardium where muscle strain and strain rate were largest), but not from CIZ, since in the latter ischemic injury suppressed excitability. VPB beats then traveled intramurally until emerging from the ischemic border on the epicardium, initiating reentry.

Figure 5:

Mechanically-induced arrhythmia in the regionally-ischemic rabbit heart. A. Distribution of muscle strain (E_ff) in the normal and ischemic heart during systole. B. Evolution of a mechanically-induced ventricular premature beats (VPB). C. Vm traces at sites 1 and 2 marked in the 191-ms inset in B. Black arrow and dashed circle denote mechanically-induced depolarization at these sites. Red arrow indicates activation at site 2 by propagation of the mechanically-induced VPB. D. Activation maps for the full model, model No_SAC, and model No_Ischemia during VPB. No_SAC incorporates all the electrophysiological changes in ischemia, but without involvement of SAC, and, thus, without mechanically-induced DADs; external stimuli were applied at the same time and locations where the mechanically-induced VPB originated in the full model (arrows in 191-ms inset in B). No_Ischemia included SAC and thus the spatial distribution of mechanically-induced DADs, but without ischemia-induced electrophysiological changes. Black lines denote conduction block. Asterisk: reentry exit site. Snapshots of transmembrane potentials are also presented for models No_SAC and No_Ischemia. Modified from (Jie et al., 2010).

A subsequent study by Hu et al. (Hu et al., 2013) examined the role of SAC recruitment on scroll wave stability in VF using an even more complex model, and image-based human ventricular electromechanics model. In VF, SAC recruitment is heterogeneous, and this affects electrophysiology and VF complexity. The study used a wide variety of SAC reversal potentials and channel conductances. Opening of SAC with a reversal potential of −60 mV diminished scroll wave breakup for all values of conductances by flattening heterogeneously the AP duration restitution curve. Opening of SAC with a reversal potential of −10 mV inhibited partially scroll wave breakup at low conductance values by flattening heterogeneously the conduction velocity restitution relation. For large conductance values recruitment of SAC with a reversal potential of −10 mV did not reduce the likelihood of scroll wave breakup, because Na⁺ channel inactivation in regions of large stretch led to conduction block, which counteracted the increased scroll wave stability due to an overall flatter conduction velocity restitution.

The role of mechano-electric coupling in defibrillation

Finally, mechano-electric transduction effects in defibrillation were explored through a bidomain electromechanics model suitable for the delivery of external electrical shocks (Li et al., 2008). This is a computationally complex model of the heart, particularly its electrophysiology component. The results of these whole heart studies demonstrated that volume overload in the ventricles could lead to up to 20% increase in the upper limit of vulnerability, a surrogate for a defibrillation threshold.

The theoretical studies discussed above demonstrate very nicely the quantitative feasibility that SACs and MEC effects can contribute significantly to cardiac arrhythmias (for rationally designed models and properties of myofilaments and SACs. What would be especially nice to see going forward is direct experimental validation that these mechanisms suffice to mediate arrhythmogenesis in the functioning mammalian heart, and for example can be prevented by the inhibition of these implicated MEC perpetrators.

§3. Mechano-Chemo-Transduction (MCT)

§3.1. Frank-Starling mechanism and Anrep effect

The heart has the remarkable ability to adapt its output to tremendous variations in the hemodynamic demand of the body, with the cardiac output ranging from 3 L/min at resting level to 21 L/min during vigorous exercise. The heart must not only be able to increase the output but also do so in the face of afterloads (arterial pressure) that range from <100 to >300 mmHg (MacDougall et al., 1985). As Ernest Starling writes in his Linacre Lecture these adaptations to changing demands “occurs equally well after total destruction of the nerves connecting the heart with the central nervous system” (p.5, (Starling, 1915)). In other words, the adaptive ability of the heart lies largely within the heart itself. Otto Frank (Frank, 1895) is equally credited for what is usually called the Frank-Starling effect. The quest for molecular understanding has occupied physiologists since that time.

In this section we will not recapitulate the excellent recent review on MCT (Schonleitner et al., 2017). Instead, we will recount some old and new research that bring into focus fundamental questions that remain unanswered and suggest modern experiments that may likely cast new light onto the intrinsic mechanisms that underlie the adaptation of the heart to changing mechanical loads.

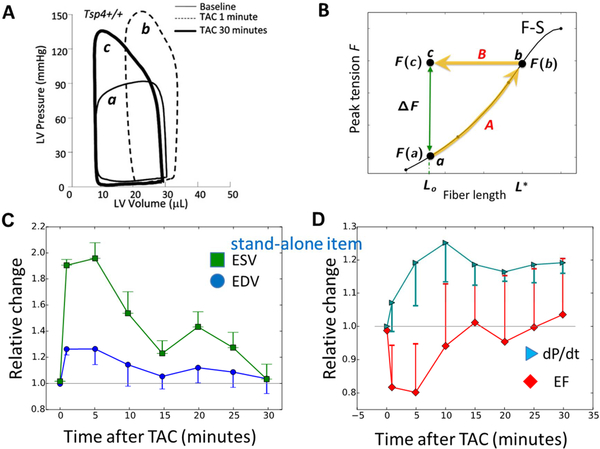
Starling’s promulgation of the “law of the heart” (Patterson et al., 1914) and Anrep’s work on the heart’s adaptation to afterload (von Anrep, 1912)) mark the modern period of investigating the heart’s adaptive response to mechanical load. Starling (Patterson et al., 1914) (Starling, 1915) described the law of the heart as “the energy of contraction … is a function of the length of the muscle fiber.” The Frank-Starling mechanism and Anrep effect are both illustrated by the pressure-volume (P-V) loops obtained from the LV in a mouse in Figure 6A. Curve A is the P-V loop before the outflow resistance was increased by transaortic constriction (TAC). Immediately after TAC, the LV end-diastolic volume (EDV) expands (note the rightward shift of P-V loop b). This expansion engages the Frank-Starling mechanism resulting in more forceful contraction that manifests itself in the higher developed pressure. The relationship between increasing contraction force and increasing muscle length stands as one of the great foundation stones of cardiac physiology. This fundamental relationship at the sarcomeric level is shown by the monotonically increasing Frank-Starling curve (F-S) in Figure 6B that is based on experiments using trabeculae (Allen & Kurihara, 1982) which shows developed force (F) as a function of sarcomere length (L).

Figure 6: Frank-Starling law and Anrep effect.

A. Pressure-volume (P-V) loops before TAC (light black), 1 min after TAC (dashed curve), and 30 min after TAC (heavy black). From Cingolani et al. (Cingolani et al., 2011). B. Black curve shows the relationship between fiber length and force generated by Frank-Starling (F-S) mechanism. L_ss is the steady state fiber length after the chamber volume has decreased due to stress-stimulated contractility (SSC) increase. ΔF (green arrow) is the force SSC needs to generate. F-S curve redrawn from Allen and Kurihara (Allen & Kurihara, 1982). C, D: Time evolution of left ventricular (LV) hemodynamic parameters following transaortic constriction (TAC). Values are normalized to initial values, when TAC imposed. EDV, end-diastolic volume; ESV, end-systolic volume; EF, ejection fraction; dP/dt, maximum rate of LV pressure change. Data redrawn from Cingolani et al. (2011).

The Frank-Starling law of the heart has stood the test of time, but even as it was being established, evidence emerged that muscle length was not the sole determinant of contractile force. Gleb von Anrep (von Anrep, 1912) found that increasing the outflow resistance caused an initial increase in LV EDV (the rightward shift from P-V loop a to b in Figure 6A) but after 10–30 min EDV recovered almost completely (P-V loop b to c), exhibiting the normal stroke volume at much higher pressure and stroke work (SW). Indeed, compared to P-V loop a the LV was producing much higher pressure at the same ESV (or SL). This is the eponymous Anrep effect.

Figure 6C–6D shows the time course of P-V loop changes (from 6A) in finer detail for EDV, ESV, ejection fraction (EF), and dP/dt_max upon TAC at time 0. These data show that immediately following TAC there is an expansion of the EDV and ESV (panel C), a decrease in ejection fraction, and an increase in contraction force as indexed by a greater dP/dt (panel D). The increase in contraction force is expected from Starling’s law as a consequence of the increased EDV. After 30 min, both the EDV and ESV have returned to their pre-TAC values. Despite the heart’s return to the initial LV chamber volume, the contractile force remains sufficiently large (measured by dP/dt) so that the ejection fraction—and therefore the stroke volume (indicated by the equal widths of the P-V loops before and 30 min after TAC in panel A) —recovers completely. At the 30 min time point the increased force cannot be due to the Frank-Starling mechanism because the EDV is at its initial value so the muscle lengths are the same.

§3.2. Load-tuning property of cardiac muscle: generation of different forces under different mechanical loads at the same muscle length

We can use Figure 6B to interpret these results shown in panels A and C. Let L_o be the muscle length at end-diastole (~EDV^1/3) before outflow resistance increase. At this time the muscle develops force F(a). Let F* be the force needed to eject the blood at the higher outflow resistance. The initial increase in EDV engages the Frank-Starling mechanism and after a few beats the LV expands to the point where the force of contraction is sufficient to eject the volume of blood equal to the venous return. This chamber volume corresponds to length L* and the muscle generates force F(b). During this phase, the muscle length travels along path A of the Allen-Kurihara F-S curve. As the EDV decreases (Figure 6A and 6C) the force of contraction must be maintained to eject blood against the higher output resistance, so the trajectory of the muscle length is horizontal along path B. After about 15 min the EDV stops decreasing to a value equal to its initial value L_o. At the steady state the muscle length equals L_o but must generate force F(c)=F(b). Therefore, the muscle of length L_o can generate different forces, as seen in F(a) and F(c). The difference between these two forces, ΔF=F(c)-F(a) reflects the increase in contractility. We call the property of the muscle to generate different forces under different loads at a given muscle length the load-tuning property.

In fact, such load tuning is an inherent property of the heart, whose contractions have to be ‘internally heterogeneous’ to achieve ‘externally homogeneous’ pump function (Katz & Katz, 1989). The auto-regulatory ability of the heart to adjust its regional contractility to spatio-temporally varying alterations that are driven by hemodynamic demand has been studied extensively, including ‘duplex models’ of isolated interacting muscle segments. These are kept in defined mechanical and biochemical conditions (interacting mechanically, while positioned in two separate baths), including more recent approaches where biological muscle segments ‘interacted’ mechanically and in real time with actuators that were controlled by computational models of cardiac electro-mechanical activity (Tyberg et al.; 1969; Wiegner et al., 1978; Markhasin et al., 2003). These studies highlight that MCT is the basis on which individual myocardial segments match their contractility to actual demand – in the absence of neuro-muscular junctions that grade skeletal muscle performance (for review, see Solovyova et al. 2014).

Given the muscle’s load-tuning force output, it is clear that muscle length cannot be the sole determinant of contractile force. Other than strain (fractional length change), what mechanical stimulus could also be involved? A logical candidate is the mechanical stress (force/area). Laplace’s law tells us that the wall stress is proportional to the product of the chamber pressure and chamber radius. Anrep’s observation was the first indication that the heart responded not only to mechanical strain as described by Starling’s law but also to mechanical stress. The response of the heart to an increase in the outflow resistance shown in Figure 6 actually has four names. The Anrep effect honors its discoverer; homeometric autoregulation (Sarnoff et al., 1960) emphasizes the increase of contractility at the same muscle length; slow force response (Allen & Kurihara, 1982; Kentish & Wrzosek, 1998; Donald et al.1976; Parmley & Chuck. 1973) emphasizes the slow time-dependent signaling (up to tens of minutes) to increase inotropy; and stress-stimulated contractility (Seo et al., 2014) that highlights the role of stress instead of strain in increasing contraction force. We think that the attachment of four different names to the same phenomenon attests to the long history of trying to understand this puzzling phenomenon. The Anrep effect presents two fundamental challenges that were addressed in this Symposium: (1) How does the cardiomyocyte distinguishes mechanical stress from strain? (2) What are the cellular and molecular mechanisms underlying the stress-stimulated contractility?

§3.3. Stress-stimulated contractility is caused by increased Ca²⁺ transient

The ability of cardiac muscle to generate two different forces at the same muscle length suggest that the cardiomyocyte could distinguish stress from strain. Around the 1980s, researchers used the multicellular preparations such as trabeculae and papillary muscle to measure strain and stress as well as cytosolic Ca²⁺ level. In a typical experiment, the muscle was stretched to a fixed length and isometric tension was measured. The consensus emerged from these studies is that stretch of the muscle caused an immediate increase in the contractile force (Frank-Starling), followed by a gradual further increase of force over minutes, called the slow force or Anrep response (Allen & Kurihara, 1982; Kentish & Wrzosek, 1998; Donald et al.1976; Parmley & Chuck. 1973) Importantly, the immediate force increase did not involve any change in the Ca²⁺ transient, which is caused by the strain-dependent myofilament-based Frank-Starling mechanism (Moss & Fitzsimons, 2002) (Solaro, 2007), whereas the slow force response involves increased cytosolic Ca²⁺ transients and in some cases enhanced myofilament Ca sensitivity to enhance contractility (Allen & Kurihara, 1982)(Kentish & Wrzosek, 1998).

Since the 1990s, researchers further developed techniques to study the strain and stress effects on single cardiomyocytes that allow in-depth exploration of the cellular and molecular mechanisms. a classical technique is to attach a pair of micro-cantilevers (i.e. carbon fibers, glass rods) to the surface of cardiomyocyte and then stretch the cell along the longitudinal direction. (Shaw, 2013)

This one-dimensional (1-D) stretch technique applies longitudinal strain and stress on the cell but not transverse compression, because the cell is free to expand transversely in bath solution. The Kass group (Seo et al., 2014) found that myocyte stretch during auxotonic contraction caused an immediate increase of the force, and then a gradual increase of contractility accompanied by increased Ca²⁺ transient; this single cell response recapitulates the Frank-Starling and Anrep effects. Kohl’s group (Iribe et al., 2009b) and Lederer’s group (Prosser et al., 2011) found that stretch of the resting cardiomyocyte caused a transient rise of Ca²⁺ sparks and waves, and repetitive stretches caused sustained rise of Ca²⁺ sparks. (Prosser et al., 2013).

The Chen-Izu group developed a Cell-in-Gel system to embed single cardiomyocytes in a 3-D hydrogel made of polymer matrix in solution (Jian et al., 2014). When the cell is paced to contract in the gel, the viscoelastic gel resists both the cell shortening and broadening to exert 3-D stress (i.e. longitudinal tension, transverse compression, and surface traction with normal and shear stresses). (Shaw, 2013) The stiffness of the gel reduces shortening, but increases Ca²⁺ transient amplitude and Ca²⁺ spark frequency (Figure 7). A distinct novelty of the Cell-in-Gel approach is to apply stress on the myocyte during auxotonic contraction against a 3-D viscoelastic matrix, without pre-stretching the cell, and thereby separating the stress from strain. How mechanical stresses affect the electrical dynamics in the Cell-in-Gel system are yet to be studied.

Figure 7: Stress-stimulated Ca²⁺ transient and Ca²⁺ sparks.

A: Schematic of a myocyte embedded in 3-D hydrogel matrix containing red fluorescence beads. B: Confocal imaging of the myocyte and beads demonstrating cell contraction and gel deformation as seen in the movement of the cell’s edge. (C) Cell contracting in normal Tyrode solution provides load-free control. (D) Cell contracting in-gel under load. (E) Fractional shortening of cell contraction in-gel (n=17 Cells) compared with load-free control (n=17). (F) Systolic Ca²⁺ transient (CaT) peak in cell-in-gel (n=17) compared with load-free control (n=17). (G) Diastolic Ca2+ spark frequency in the cells for load-free (n=18), in soft gel made of 5% crosslinker (Gel5%, n=9), in gel with 7.5% crosslinker (Gel7.5%, n=18), and after blebbistatin treatment (n=5). One-way ANOVA with Bonferroni post-test was used for pair-wise comparison: P< 0.001***. (Jian et al. 2014)

§3.4. Mechano-chemo-transduction pathways linking mechanical forces to Ca²⁺ dynamics

Research from the 1990s to present has focused on delineating the molecular pathways, or MCT that links cellular mechanics to changing Ca²⁺ dynamics. These pathways have been the subject of excellent reviews by Cingolani et al. (Cingolani et al., 2013) and Schönleitner et al. (Schonleitner et al., 2017). Here we briefly catalog the known pathways and highlight some differences that might reveal different mechanosensing modalities. We also consider that different experimental settings involve different strain and/or stress on the cell (Chen-Izu & Izu, 2017), which need to be taken into account in order to understand and compare the data obtained using different experimental settings.

Integrin-angiotensin-NHE pathway.

Mechanical stretch of β₁ integrin at the cardiomyocyte surface initiates a number of different signaling pathways by causing release of angiotensin II (Ang II) from myocytes (Browe & Baumgarten, 2004). The Ang II then activates angiotensin II type 1 receptor (AT₁ receptor) that begins a cascade that ultimately activates chloride-permeant stretch-activated channel (Browe & Baumgarten, 2004) or the Na⁺-H⁺ exchanger (NHE) and Na⁺-Ca²⁺ exchanger that leads to a secondary increase in the Ca²⁺ transient (Alvarez et al., 1999; Calaghan & White, 2004; Cingolani et al., 2013).

Thrombospondin pathway.

Thrombospondin-4 (TSP4) is an matricellular protein that increases in hypertension and heart failure. Cingolani et al. (2011) found that in mice lacking TSP4 the P-V loops did not have the evolutionary hallmark characteristics of the Anrep effect shown in Figure 6A following acute TAC. Instead, 30 min post-TAC the P-V loop remained right-shifted and the stroke volume was not restored. This paper shows the interaction of the extracellular matrix and the myocyte in mechano-sensing.

TRPC6/3-PKG pathway.

Using the 1-D stretch system with compliant carbon fibers attached on the cardiomyocyte, Seo et al. (2014) tested the hypothesis that the transient receptor potential canonical channel 6 (TRPC6) participates in stress-stimulated contractility. Inhibiting TRPC6 using cGMP to activate protein kinase G (PKG) or using a TRPC6 knockout eliminated the increase in Ca²⁺ transient amplitude and slow force response of papillary muscle to stretch. In whole animal studies where outflow resistance was increased by acute transaortic constriction (TAC), the pressure-volume loops in control animals exhibited the kind of response shown in Figure 6A. Immediately following TAC, the P-V loop shifted to the right and narrowed but after 15 min the end-diastolic volume of the P-V loop shifted back to the left (in fact below the control volume in their figure) and the stroke volume increased indicating an increase of stress-stimulated contractility. The TRPC6 knockout lacked the decrease in the end-diastolic volume after 15 minutes. These elegant studies reveal the importance of TRPC6 in stress-stimulated contractility increase but leaves open the identity of the mechanosensor, a possible G-coupled protein receptor.

NOX-ROS pathway.

Using the 1-D stretch system with glass rods attached on the cardiomyocyte, Iribe et al. (Iribe et al., 2009b) showed that stretch of resting cardiomyocytes elicited a transient increase in the Ca²⁺ spark rate. Subsequently, Prosser et al. (Prosser et al., 2011) showed that reactive oxygen species (ROS) production linked to isoform 2 of NADPH oxidase (NOX2), which they call X-ROS signaling, was responsible for the stretch-induced Ca²⁺ spark rate increase. The link between cellular mechanics and X-ROS signaling is compelling because an intact microtubular network is essential for the stretch-induced Ca²⁺ spark rate increase (Iribe et al., 2009b; Prosser et al. 2011; (Khairallah et al., 2012; Robison et al., 2016). In an editorial accompanying the Iribe paper, Mark Cannell (Cannell, 2009) suggested that the stretch-induced Ca²⁺ spark rate increase could underlie the slow force response. In support of this possibility, modeling studies by Limbu et al. (Limbu et al., 2015) show that X-ROS activation during the diastolic filling phase of the heart could increase the magnitude of the Ca²⁺ transient.

NOS-NO pathway.

Using a cell-in-agar technique, Vila Petroff et. al. (Petroff et al., 2001) found that stretching the tubing encasing cell-in-agar increased Ca²⁺ transient amplitude and the Ca²⁺ spark rate in cardiomyocytes. This MCT pathway involves nitric oxide (NO) signaling because the both the Ca²⁺ sparks and Ca²⁺ transient increase was abolished by inhibiting nitric oxide synthases (NOSs) using L-NAME (N^G-nitro-L-arginine methyl ester) or by genetic knockout of eNOS (eNOS^−/−). Using the 3-D Cell-in-Gel system, Jian et al. (Jian et al., 2014) found that stress stimulated Ca²⁺ sparks were abolished by pharmacological inhibition of nNOS or by genetic knockout of nNOS (nNOS^−/−). Furthermore, both constitutive nNOS and eNOS are involved in stress-stimulated increase of Ca²⁺ transient, and the stress effect on Ca²⁺ transient was abolished by inhibiting NOS. (Jian et al., 2014) These data strongly support that NOSs and NO signaling serve as a critically important chemo-transducer in the stress-stimulated MCT pathway.

The above studies show that mechanical strain and stress on cardiomyocytes activate various chemotransducers that lead to modulation of the intracellular Na⁺ and Ca²⁺ handling system. The effects of mechanical strain and stress on the Ca²⁺ homeodynamics manifest to several functional consequences. For example, stress induced increase of systolic Ca²⁺ transient through TRPC6/3 pathway and NOS-NO pathway is expected to enhance the cardiomyocyte contractility. Strain and stress induced spontaneous Ca²⁺ sparks and waves are expected to promote arrhythmogenic activities. However, the electrophysiological and Ca²⁺ handling systems in rodent myocytes differs significantly from that of larger mammalian (e.g. rabbit, dog, pig, human; Bers, 2001). Rodent (mouse and rat) ventricular myocytes exhibit very brief APD driven by robust transient outward current (I_to) and a late low plateau level that is dominated by inward NCX current. In contrast, larger mammals have long APDs with positive plateaus, little I_to and repolarization that is driven by delayed rectifier K⁺ currents (I_Kr and I_Ks) that are absent in rodents. Furthermore, in rodents Ca²⁺ handling is overwhelmingly dominated by SR Ca release and reuptake, with little Ca²⁺ influx via Ca²⁺ current, and SR Ca²⁺ stores are higher at baseline and maintained in resting cardiomyocytes. In larger mammals, a greater fraction of E-C coupling related Ca²⁺ enters each beat via Ca²⁺ current and leaves via NCX, and SR Ca²⁺ content increases with heart rate are critical to inotropic reserve. Another complicating factor is that experiments are often performed at room temperature, which can alter electrophysiological, Ca²⁺ handling and contractile properties. Hence, caution needs to be taken in translating the experimental findings in rodent models to human pathophysiology.

§3.5. Different mechano-sensing modalities

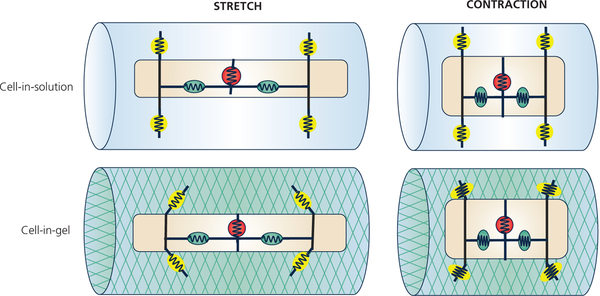
Interestingly, the involvement of NOS-NO signaling in the MCT pathway differs drastically in different experimental settings. As mentioned before, the NOS-NO signaling has been found critically involved in stress-stimulated MCT in the 3-D Cell-in-Gel system (Jian et al., 2014) and in the 3-D cell-in-agar experiment (Petroff et al., 2001). In contrast, inhibiting NOS with L-NAME did not affect strain-stimulated MCT in the 1-D stretch system, as found in the studies by Calaghan and White (Calaghan & White, 2004), Seo et al. (Seo et al., 2014), Iribe et al. (Iribe et al., 2009b), and Prosser et al. (Prosser et al., 2011) To resolve this apparent controversy, Chen-Izu and Izu (Chen-Izu & Izu, 2017) proposed an hypothesis on different mechano-sensing modalities based on “dimensionality” of the mechanosensors (i.e. 1-D longitudinal strain vs. 3-D stresses).

The apparent controversy on the NOS-NO involvement in MCT pathways opens a window into the different mechano-sensing modalities. One critical difference between the 1-D stretch experiments and the 3-D Cell-in-Gel experiments is the engagement of cell-surface mechanosensors (Chen-Izu & Izu, 2017). Figure 8 illustrates a conceptual model on how different mechanosensors may respond to different strain and stress. The surface mechanosensors are illustrated as the yellow circles (or ellipses if under strain/stress), and the internal mechanosensors seen as the red or green circles (or ellipses if under strain/stress). When the myocyte lengthens (or contracts) along the longitudinal axis, the cell also narrows (or widens) in the transverse direction because cell volume is conserved. The internal mechanosensors experience the same strain (relative length change) for a given cell strain during stretch or contraction, regardless of the external environment. By contrast, the surface mechanosensors are profoundly affected by the stiffness of the external environment. Specifically, in the 1-D stretch experiments, myocytes were immersed in bath solution and stretched along the long axis, so the myocyte is largely under longitudinal strain and stress. The bath solution imposes little transverse compression or shear stress on the cardiomyocyte; hence, the cell-surface mechanosensors are not under stress during stretch or contraction. However, in the Cell-in-Gel system, the myocyte embedded in a 3-D viscoelastic gel must pull the gel along the long axis as it contracts, push the gel along the transverse axis as it widens, and the cell surface pulls against shear force (Shaw et al., 2013); hence, the surface mechanosensors are subject to transverse and shear stresses during stretch or contraction (as in the myocardium, extracellular matrix, or hydrogel polymer matrix). Therefore, we propose a simple hypothesis, according to Occam’s Razor, that the cell-surface mechanosensors activate the NOS-NO signaling pathway.

Figure 8:

Conceptual model on how different mechanosensors may sense different strain and stress. Upper row: When the cell is in solution, the surface mechanosensors (yellow circle with spring) are not under transverse stress and surface traction.

Lower row: When the cell is contracting in 3-D viscoelastic environment, the surface mechanosensors are under transverse compression and shear stresses. The internal mechanosensors (green circle with spring) are under longitudinal tension during stretch or compression during contraction.

§4. Perspectives

§4.1. Linking modeling and experiments

The study of the heart has enjoyed a stronger interaction between mathematical modeling and experimental work than many other areas of physiology. Niederer et al. (Niederer et al., 2019) give an excellent history of the development of mathematical models of cardiac mechanics. A special issue in the JMCC (introduced by Smith and Niederer (Smith & Niederer, 2016)) focuses on cardiac modeling at both the cellular and tissue and whole-organ scales. An important theme from this special issue is the increased specificity of the models that enables a closer comparison between experimental data and simulation results.

Here we focus first on what we consider success stories and later on challenges that arise in studying mechano-electrical coupling and mechano-chemo-transduction. Our understanding of the mechanisms underlying the Anrep effect in the whole heart and its correlates slow force response and stress-stimulated contractility in cardiac muscle and single cardiomyocytes remains incomplete. Because experimental work in the 1980s showed that the SFR required Ca²⁺ entry, a stretch-sensitive L-type Ca²⁺ channel (LTCC) would seem to be important for the SFR. The importance of modeling is highlighted by Bluhm et al. (Bluhm et al., 1998) who showed that a stretch-sensitive Ca²⁺ channel would not account for the slow increase of force characteristic of the Anrep effect. Rather they were able to model both the magnitude and timing of the SFR by assuming that the Na⁺-K⁺ pump or the Na⁺ leak current were stretch-dependent. Later Niederer and Smith (Niederer & Smith, 2007) were able to model the SFR using a non-specific stretch-activated current (SAC) that allowed Na⁺ entry in conjunction with the Na⁺-H⁺ exchanger (NHE). A surprising and important finding was that the stretch-sensitive NHE could not, by itself, generate the SFR contrary to the view arising from extensive experimental studies. These studies illustrate some of the important contributions modeling can make to understanding cardiac physiology.

The Niederer and Smith (2007) study showed how the interaction of SACs and NHE generate the SFR. Importantly, they explained how the experimental protocol of preincubation with NHE blockers might have led to a misinterpretation of the primary role of the NHE in SFR. The explanation is subtle; SFR depends on the balance between Na⁺ influx and efflux that can shift with the resting Na⁺ level because of the cubic [Na⁺]_i-dependence of the NCX flux. Long incubation with NHE blocker reduced [Na⁺]_i to the point that that limits the ability of NCX to raise [Ca²⁺]_i to support the development of the SFR. It would probably be difficult to disentangle these interactions by experiments alone.

Iribe et al. (Iribe et al., 2009a) and Prosser et al. (Prosser et al., 2011, 2013) showed that stretch immediately increases Ca²⁺ spark rate, possibly through X-ROS signaling. In an editorial Mark Cannell (Cannell, 2009) suggested that the stretch-induced Ca²⁺ spark rate increase might contribute to Starling’s law of the heart and in particular the SFR. Limbu et al. (Limbu et al, 2015) modeled X-ROS signaling under cyclic stretching in a single myocyte and calculated spark rates and Ca²⁺ transients. The model faithfully reproduced the Ca²⁺ spark data from experiments but the Ca²⁺ transient results diverged from experimental data. In their simulations the initial stretch caused an immediate increase in the Ca²⁺ transient magnitude but its peak magnitude declined on subsequent stretches. These results are inconsistent with the body of experimental results showing no increase in the Ca²⁺ transient in the initial stretch and slowly increasing Ca²⁺ transient amplitude. Such trenchant differences between model results and experiments should be viewed positively because they open opportunities for modelers and experimentalists to focus on how the model got some things right and where the model needs modification.

We think the current computational models of cardiac excitation-contraction (E-C) coupling need to be further improved. Many parameters in the current models were derived from experimental data obtained in different species and under various artificial conditions. Hence the models need to be improved based on new data obtained under more physiological conditions, such as using mechanically loaded cardiomyocytes (instead of load-free cells). Furthermore, adding mechanical load and mechano-chemo-electro-transduction feedbacks into the E-C coupling model will be a necessary step towards developing more realistic models. Recognizing the importance of the back-and-forth dialog between modeling and bench experiments, it is critically important to bring together modelers and experimentalists to have this dialog, to learn from each other, and to develop interdisciplinary collaborations.

§4.2. Plurality of mechano-chemo-electro-transduction pathways

The plurality of mechano-chemo-electro-transduction pathways discovered so far suggest that mechanical strain and stress on the cardiomyocyte can be sensed and transduced by various mechano-sensors located in different sub-cellular structures. In this white paper we focus only on a few mechano-electro-transduction and mechano-chemo-transduction pathways discussed in the symposium and depicted in Figure 9. We recognize the existence of many other mechanosensors and their mechano-electro-transduction and mechano-chemo-transduction pathways and recommend excellent reviews on the Anrep effect (Cingolani et al., 2013), stretch-activated channel (Peyronnet et al., 2016) (Baumgarten, 2007), on mechano-sensitivity of Ca²⁺ signaling by (Schonleitner et al., 2017), etc. Here we wish to emphasize that different experimental settings involve different mechanical strain and stress, which would affect different mechanosensors depending on their sub-cellular localization and dimensionality. It is plausible that the internal mechanosensors are poised to sense longitudinal strain and tension, whereas cell-surface mechanosensors are poised to sense surface traction and transverse compression. Therefore, caution needs to be taken to clarify the precise mechanical stimuli in analyzing molecular mechanisms and comparing the data from different experimental settings. It is also important to use different mechanical stimuli to interrogate different mechanosensors in order to piece together a more precise and comprehensive map of the mechano-chemo-electro-transduction pathways.

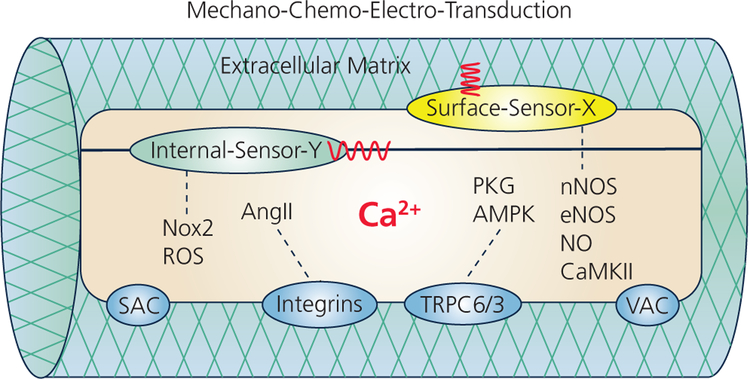
Figure 9:

Schematic of the mechano-chemo-electro-transduction (MCET) pathways in the cardiomyocyte embedded in extracellular matrix (ECM). Stretching the cell applies mechanical strain that can be sensed by Internal mechanosensors (green). Cell contraction against ECM applies mechanical stress that can be sensed by Surface-mechanosensors (yellow). The molecular identities of many mechanosensors are yet to be discovered (labeled X, Y). Depicted are known several MCET pathways: Nox2-ROS, integrin-AngII, TRPC6/3, and nNOS-eNOS-NO-CaMKII pathway; all these pathways lead to modulation of intracellular Ca2+ homeodynamics (see §3).; all these pathways lead to modulation of intracellular Ca2+ homeodynamics (see §3). Stretch-activated channels (SAC) and volume activated channels (VAC) have also been linked to Ca²⁺ permeability that may affect the Ca²⁺ entry and intracellular Ca²⁺ homeodynamics (see §2).

Why so many pathways? The heart has a plethora of ion channels, electrogenic exchangers, and pumps that are needed to adapt the action potential to the changing demands of the body. One wonders whether the plurality of mechanosensors and MCT pathways might be needed to adapt the force generation to different stressors and demands. Different mechanosensors and MCT pathways might stratify into different time and force hierarchies. Time hierarchy: The Frank-Starling mechanism and the Anrep effect have distinct time domains. The Frank-Starling mechanism is fully engaged within one or two heartbeats while the Anrep effect develops over many minutes. Teleologically such a separation into rapid and slow time domains make sense. Changes in venous return due to postural changes or left-right ventricular flow mismatch are transient disturbances that the Frank-Starling mechanism rapidly corrects without the expense of increased Ca²⁺ signaling. Adjusting to sustained increase in afterload caused by activities with large static component such as boxing (Mitchell et al., 2005) or shoveling snow (Franklin et al., 1995) on the other hand requires a different strategy. The heart might be trading off the cost of Ca²⁺ signaling to reduce the energetic cost of contracting against higher wall tension resulting from wall stretch. Research discussed here focused on acute changes of mechanical loading where the response time of the heart is on the order of a few seconds to a few tens of minutes. How chronic hypertension, operating on time scales of months to years, affects MEC and MEC remains largely unexplored.

Force hierarchy: Systolic blood pressure is around 120 mmHg but can reach 350 mmHg while doing double leg presses (MacDougall et al., 1985). Just as different scales are used for measuring milligrams and metric tons it seems reasonable that different mechanosensors and MCET pathways might respond to different levels of strain and stress.

To go beyond teleological speculation, future experiments must pay careful attention to the characteristics of mechanical loading (i.e. strain, stress, location, magnitude) imposed on the myocyte and determine which MCET pathway is operative by pharmacological or genetic dissection. Sequential application of specific channel blockers enabled electrophysiologists to “peel back” the layers of ionic currents that underlie the action potential (Hegyi et al., 2018; Banyasz et al., 2011). Perhaps a similar approach might be useful to determine how different MCET pathways stratify in time and force hierarchies.

§4.3. MCT and MEC feedbacks in cardiac excitation-contraction coupling

The heart pumps blood against an ever-changing mechanical load. The heart also has intrinsic mechanisms to sense the strain and stress and autoregulate contractile force to maintain a constant cardiac output. Although the heart’s response to mechanical loading was described by Frank-Starling and Anrep more than a century ago, the cellular and molecular mechanisms that transduce mechanical load to influence the Ca²⁺ handling and electrical activities in the cardiomyocyte are far from fully understood. The classic description of excitation-contraction coupling has information flowing from the electrical system to the Ca²⁺ control system and then to the contractile system. MCT and MEC reverse the flow of information enabling a continuously bidirectionally information feedforward and feedback between these three dynamic systems. According to control theory, such closed-loop feedback is necessary for autoregulation of the system. Continuing research on MCT and MEC is essential for understanding the heart as a smart pump that senses mechanical strain and stress and autoregulates contractile force to maintain cardiac output. But as with any control system operating out of its design space, Ca²⁺ dysregulation and arrhythmias can emerge.

MEC Consensus, Controversies and Open Issues.

There is consensus about the following:

• Many ion channels (incl. sarcolemmal and non-sarcolemmal) are mechanically modulated

  • Ion channels that change their open probability primarily in response to mechanical stimulation (mechano-sensitive channels) can be divided into cell-stretch and cell-volume activated ion channels (SAC, VAC, respectively).
  • VAC increase their open probability in response to cell swelling; they are constitutively active in hypertrophic myocardium – but they are not believed to be major determinant of beat-by-beat mechano-sensory behaviour or drivers of responses to acute mechanical stimulation.
  • SAC can be divided into cation-nonselective (SAC_NS) and potassium selective channels (SAC_K).
  • Non-myocytes (fibroblasts, macrophages) are mechano-sensitive; they express SAC and can contribute to cardiac electrophysiology.
• Mechano-sensitive channels affect cardiac electrophysiology

  • SAC_NS appear to contribute to acute electrical responses to stretch, so much so that electrophysiological responses to mechanical stimuli can generally be accounted for in quantitative models by simply invoking SAC_NS.
  • SAC_K cause re/hyperpolarization; they may contribute to action potential (AP) shortening, in particular in pathological settings such as ischaemia.
  • SAC_NS activation can increase intracellular Ca²⁺, either directly or indirectly (via Na⁺/Ca²⁺-exchange, NCX). The resulting intracellular Ca²⁺ signals can be highly compartmentalized
  • Drug actions, including drug effects on ion channels, can be mechano-modulated.

Controversies and Open Issues:

• Amplitudes and kinetics of SAC and VAC in physiological and pathological states and how they affect the delicate balance of currents during the cardiac AP are ill-explored.

  • We can track strain, but not stress, at the cell level in native cardiac tissue. As a result, for many mechano-electric coupling processes we do not know key biophysical input parameters.
  • The explicit in vivo molecular mechanisms of activation and how best to mimic them experimentally are unclear.
  • Our ability to interpret dynamic mechanical effects on electrophysiology is equally limited by difficulties in identifying ‘differential’ and ‘proportional’ signalling pathways.
  • The dynamics of 3-D deformation of subcellular nano-structures, and their relevance for micro-to-macro cardiac function are ill-explored and form a key frontier for further research.
  • Mechanistic links between acute (beat-by-beat time scale or faster), intermediate (second to minutes) and chronic effects (e.g. involving cell and tissue remodelling) of stretch-induced changes in cardiac electrophysiology are unclear.
  • In general, we know more about MEC effects in pathological settings (arrhythmo–genic effects) than about the role of VAC and SAC in normal homeostasis.

MCT Consensus, Controversies and Open Issues.

There is consensus on the following:

• Frank-Starling mechanism and Anrep effect

  • Heart has the intrinsic ability to adapt to changes in preload and afterload. Intrinsic adaptation has two components: Frank-Starling mechanism (heterometric) and Anrep Effect (homeometric or inotropic).
  • Frank-Starling (F-S) mechanism is activated by elevated End Diastolic Volume (and sarcomere length) and is thus heterometric regulation. The F-S mechanism is instantaneous (beat to beat) without requiring Ca²⁺ changes.
  • Anrep effect occurs gradually over many beats (minutes timescale) to enhance contractility by increasing the cytosolic Ca²⁺ transients and/or myofilament Ca sensitivity. Multiple biochemical signaling pathways have been implicated. Anrep can restore EDV and sarcomere length towards the initial state (and is thus homeometric).
• Mechano-chemo-transduction (MCT) pathways

  • MCT activate various chemo-transducers that lead to modulation of the Ca2+ handling system in the cardiomyocyte.
  • MCT pathways, involving cardiac mechanosensors, chemotransducers, and effectors.
  • The mechanical sensors may include myofilament proteins (e.g. titin and crossbridges) and cytoskeletal and transmembrane protein complexes that interact with extracellular matrix and neighbouring cells (e.g. at focal adhesions, dystrophin, integrins and desmosomes).

Controversies and Open Issues:

• Different labs found different role of nitric oxide (NO) signaling in mechano-chemo-transduction: some found that NO plays no role in stretch induced Ca²⁺ sparks, but the others found NO is critically important for MCT.

• The apparent controversy above might be explained by hypothesizing that different “dimensionality” of the mechanical strain or stress imposed on surface versus internal mechanosensors may activate different MCT pathways.

• How do cardiomyocytes distinguish mechanical strain (e.g. stretch) and mechanical stress (e.g. stiffness)?

• What are the mechanosensors activated by longitudinal strain and stress?

• What are the mechanosensors activated by transverse compression?

• What are the mechanosensors activated by surface traction and shear stress?

• What are the mechano-chemo-transduction pathways downstream from each mechanosensors to chemotransducers and to effectors: who, where, and how?

• How does mechano-chemo-transduction orchestrate concerted modulations of multiple Ca²⁺ handling molecules to autoregulate the Ca²⁺ transient and contractility?