Abstract
The National Strategy for Pandemic Influenza outlines a plan for community response to a potential pandemic. In this outline, state and local communities are charged with enhancing their preparedness. In order to help public health officials better understand these charges, we have developed a visual analytics toolkit (PanViz) for analyzing the effect of decision measures implemented during a simulated pandemic influenza scenario. Spread vectors based on the point of origin and distance traveled over time are calculated and the factors of age distribution and population density are taken into effect. Healthcare officials are able to explore the effects of the pandemic on the population through a geographical spatiotemporal view, moving forward and backward through time and inserting decision points at various days to determine the impact. Linked statistical displays are also shown, providing county level summaries of data in terms of the number of sick, hospitalized and dead as a result of the outbreak. Currently, this tool has been deployed in Indiana State Department of Health planning and preparedness exercises, and as an educational tool for demonstrating the impact of social distancing strategies during the recent H1N1 (swine flu) outbreak.
Keywords: Pandemic influenza, Visual analytics, Risk assessment, Geovisualization
Highlights
► We provide an interactive toolkit for pandemic modeling. ► Users can explore the spread of the pandemic through interactive visualizations. ► Users can interactively employ decisions measures and explore their impact.
1. Introduction
Federal, state, and local community public health officials must prepare and exercise complex plans to deal with a variety of potential mass casualty events [13], [16], [22]. In recent years, one of the most notable potential mass casualty events that require appropriate planning is pandemic influenza. However, officials responsible for developing such plans must often rely on information and trends provided via very complex modeling (requiring supercomputers so that only a few cases can be considered due to resource constraints) or, at the opposite extreme, modeling that has incorporated very drastic simplifying assumptions so as to be computationally practical. Moreover, such plans are developed with only a few specific scenarios or pre-event concepts in mind and often ignore the fact that the solutions dealing with a pandemic are very dependent on its underlying traits and actual characteristics, which cannot be known with any certainty a priori. Thus, there is a critical need to better equip public health officials responsible for pandemic influenza planning, or planning for other mass casualty events, with sophisticated yet easy to use tools that capture the complex elements, especially individual social behaviors, of traumatic events and that can also adjust as additional information is obtained and conditions evolve over time.
While desktop pandemic influenza modeling tools do exist (e.g., FluAid [1], FluSurge [12]), these tools are often restrictive in their scope and provide little to no spatiotemporal support to allow users to observe conditions evolving over time and space. To address this gap, visual analytics has emerged as a relatively new field formed at the intersection of analytical reasoning and interactive visual interfaces [38]. It is primarily concerned with presenting large amounts of information in a comprehensive and interactive manner. By doing so, the end user is able to quickly assess important data and, if required, investigate points of interest in detail. As such, we have developed a visual analytics toolkit (PanViz – Fig. 1 ) to aid in the modeling, analysis and exploration of pandemic influenza. Our interface utilizes linked views for displaying statistical information about populations under study, filtering controls for age and demographic data, and detailed bed capacity information at the county level. We provide end users with the means to interactively explore the model, make parameter changes, and engage in a variety of user created scenarios. As such, PanViz is able to provide healthcare officials with training and education scenarios for a variety of pandemic situations. Model parameters such as spread origin, mortality rate, etc. are all modifiable through a graphical user interface designed to support and enhance training exercises. Our toolkit was most recently deployed as a portion of the Indiana State Department of Health pandemic readiness training exercises, and was utilized as an educational tool for illustrating the potential impact of social distancing measures during the recent H1N1 outbreak [39].
Fig. 1.
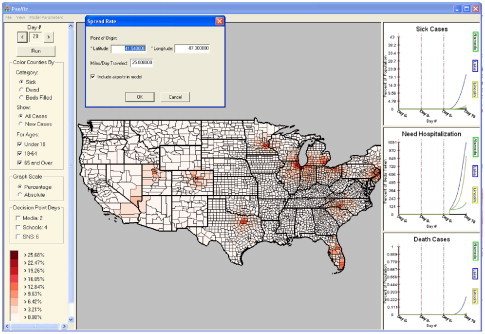
PanViz – a visual analytics environment for the modeling and exploration of pandemic influenza. In this image, an outbreak which began in Chicago, IL has quickly spread as a result of heavy air travel across major US airports.
Furthermore, the U.S. National Strategy for Pandemic Influenza [22] outlines three pillars of strategic intent: (1) preparedness and communication; (2) surveillance and detection; and (3) response and containment. PanViz is an effective method of communicating information between healthcare officials, first responders and the media, as well as providing insight into the impact of various responses and containment. The rationale for such a system is that mass casualty event response planning can be done with higher accuracy and more realism so that if an event happens, mitigation strategies can be invoked to minimize casualties as the event evolves. The potential impact of such a system is a reduction in the number of casualties associated with a mass casualty event and the overall health of U.S. citizens. This can be achieved via a mechanism to delineate decisions on mitigative measures, especially as additional information is gathered during the course of a pandemic or other mass casualty event. Thus, public health officials can use our tool as an operational research to both plan and rapidly assess health impacts, required community level resources, and the effect of potential decision strategies associated with a pandemic. The main thrust of our work is not creating an advanced model of influenza; instead, we provide a visual analytics environment in which users may effectively explore decision points and potential scenarios.
2. Related work
Previous work in pandemic influenza modeling has focused on understanding the spread of the disease at the micro-level (person-to-person contact) in order to help officials evaluate the effectiveness that their mitigation policies might have. This includes analyzing how viruses change and adapt [8], modeling the effects of immunization on influenza transmission [14], forecasting the economic impact of an influenza pandemic [31], and evaluating the general preparedness of the emergency response community [18], [19]. Other research focuses on containment and control of possible outbreaks [27], [28], [29]. Work by Guo focused down to the level of individual daily movements, studying pandemic spread as a spatial interaction problem [20]. Inglesby et al. [23] present an overview of a variety of mitigation measures and discuss their potential effectiveness. Nuno et al. [35] modeled the effects of antivirals and community transmission controls on the spread of influenza, and Simchi-Levi et al. [11] modeled the transportation of antivirals as a supply chain problem demonstrating how current production risks will lead to insufficient vaccine supplies. Larson et al. [25] studied how a population's heterogeneity affects the disease progression and analyzed how social distancing could effectively reduce disease spread. Nigmatulina et al. [34] utilized a series of spreadsheet models to analyze the effects of infection spread between several linked heterogeneous communities in order to evaluate the use of non-pharmaceutical intervention strategies. Atkinson and Wein modeled modes of influenza transmission routes [3] and studied the efficacy of other forms of control such as face masks and ventilators [4].
In all of the above modeling work, it is clear that there are a variety of strategies that can be implemented to reduce the impact of a pandemic, if the strategies are implemented early during the decision making process. However, these models are typically self-contained, unavailable to health care officials, or unlinked to any interactive visual interfaces. What is needed now are tools to help health officials prepare for an outbreak and disseminate information to the public in the event of a possible pandemic situation. Various modeling tools do exist which are meant to aid in pandemic preparation. FluAid is provided by the United States Department of Health and Human Services in order to assist state and local level planners in preparing for the next influenza pandemic [1]. This software provides a range of estimates of impact in terms of deaths, hospitalizations, and outpatients visits. FluSurge is a spreadsheet-based model which provides hospital administrators and public health officials estimates of the surge in demand for hospital-based services during the next influenza pandemic [12]. While these simulation tools provide excellent statistical support to planners, they are fairly restrictive in their scope, and do not provide any spatiotemporal support. Work done by Germann et al. [19] begins addressing this shortcoming. They developed a simulation which allows various intervention strategies to be set and simulations to be run. Results are displayed via a heat map displaying illness attack rates over the entire nation, and charts of incidence rates. However, this is a complex, large scale simulation which requires a supercomputing platform in order to run. User interaction is largely absent, and investigating the effect of decision changes requires a re-running of the entire simulation. In response, our application provides a desktop pandemic modeling tool with interactive, spatiotemporal support. This allows users to observe conditions evolving over time and space. Decision changes can be made interactively, and results modeled immediately as users simulate each time step.
In terms of creating complex mathematical models based on population distributions, highway travel, and spread vectors, much work is being done by the IBM Eclipse STEM project [17]. This work focuses on helping scientist and public health officials create and use models of emerging infectious diseases. It uses built-in Geographical Information System (GIS) data for almost every country in the world, including travel routes for modeling disease spread. The difficulty of this type of approach is that these detailed models often require a great deal of hand-crafting and fine tuning. This work currently provides an interface to Google Earth in which users can visualize their data. With respect to our current work, our tool provides a system in which a pandemic simulation has been developed and is directly linked to an interactive visualization tool, allowing for easier use by general public health officials at all level of government.
3. PanViz
Our pandemic influenza modeling and visualization system (PanViz) adopts the common method of displaying geo-referenced data on a map and allowing users to temporally scroll through their data. However, such exploration only provides slices of spatial data at a given time or an aggregate thereof. In order to understand these slices, users need to know the trends of previous data (and, if possible, model future data trends). Fig. 1 shows our visual analytics system. Population, demographic [40], and hospital bed [2] data are provided as input to the back-end modeling functions. The modeling functions output information on the number of sick, dead and hospitalized individuals by county and PanViz provides color coded geographical representations of the data. Users may interact with the system through a variety of viewing and modeling modalities. As shown in Fig. 1, the main viewing area is the spatiotemporal view, and the three windows on the right provide a time series view of the population statistics (number of people sick, hospitalized or dead due to the modeled pandemic) of any county selected (county selections are indicated by a darker border) in the main viewing area. These linked views allow for a quick comparison of trends across various spatial regions. Both the geospatial and time series viewing windows are linked to the time control at the upper left portion of the screen. This allows users to view the spatial changes in the data as they scroll across time.
3.1. Epidemic model
The PanViz visualization framework uses a mathematical epidemic model to calculate population dynamics and infection rate data. Specifically, disease dynamics are calculated per county (z=92 counties in Indiana) by a system of non-linear difference equations derived from traditional compartment epidemic models with homogeneous population mixing. Model parameters are defined and equations for disease dynamics are presented in Table 1, Table 2 . Individuals in the population are assigned to a compartment by disease state (susceptible (S), infectious/sick (I), recovered(R)). The population is demographically stratified by age into three groups: infant to 18, 18–64 and over 64 years old. Population numbers for each age group are taken from the 2000 U.S. census.
Table 1.
Pandemic influenza model.
| Model parameters | |
| Population of county y=1 to z counties. Indiana: z=92 | |
| t | time index from the first day of a disease outbreak (integer value) |
| mortality rate: percentage of those infected with pandemic influenza that will ultimately die | |
| recovery rate: percentage of those infected with pandemic influenza that will ultimately recover | |
| hospitalization rate: percentage of those infected with pandemic influenza that will ultimately require hospitalization | |
| time, in days, to recover once infectious, at rate (integer value) | |
| time, in days, until death once infectious, at rate (integer value) | |
| time, in days, of hospitalization duration due to disease, at rate (integer value) | |
| disease spread rate modifier in county y, by county density c of l | |
| c=1 | Rural: |
| c=2 | Small towns: |
| c=3 | Urban: |
| Proportion of county population in the age group, j, of m age groups (m=3 in initial model setup) | |
| disease prevalence modifier for age group j | |
| j=1 | |
| j=2 | |
| j=3 | |
| Preventative measure reduction (%) in baseline prevalence due to decision measure, k, of n measures | |
| kmod | Decision measure, k, prevalence modifier (in %) |
| Time between the beginning of the outbreak until decision measure, k, is initiated, measured in days | |
| Time until decision measure, k, reaches full efficacy, measured in days | |
| k=1 | Decision measure: school closures |
| k=2 | Decision measure: media alerts |
| k=3 | Decision measure: strategic national stockpile deployment |
| Baseline prevalence () derived from polynomial fitting of epidemic data reported in [7] | |
| Prevalence () after decision measures are implemented | |
| incidence of infectious in county y, age group j, at time t | |
| incidence of deceased in county y, age group j, at time t | |
| incidence of recovered in county y, age group j, at time t | |
| incidence of hospitalized y, age group j, at time t | |
| Number of individuals who were infectious or are currently infectious in county y, age group j, at time t | |
| Number of deceased individuals in county y, age group j, at time t | |
| Number of individuals who have been hospitalized or are currently hospitalized in county y, age group j, at time t | |
| Number of individuals who were infectious or are currently infectious in county y, at time t | |
| Number of deceased individuals in county y, at time t | |
| Number of individuals who have been hospitalized or are currently hospitalized in county y, at time t | |
| Influenza dynamics | |
| delay | |
| p | [7] |
| [7] | |
Table 2.
Population dynamics.
We also track infection severity by tabulating those hospitalized (H) and mortality as deceased (D) because of infection by pandemic influenza. The mortality rate () is the percentage infected that will ultimately die due to complications from pandemic influenza with average time to death of . Conversely, the recovery rate () is the percentage of those infected with pandemic influenza that will ultimately recover, with average time to recover of . Individuals are hospitalized at rate for an average of days. In the model, the user is asked to specify typical hospital capacity which is set to a default value of 70% (research indicates that typical hospital capacities may be as large as 80–90%). Hospital capacity is the percentage of total beds in use out of the total beds available.
We use the following terminology and definitions throughout our models. The functional form used to assign an individual's probability of being infected with pandemic influenza is listed in Table 1. This function is parameterized with user entered approximations for the center of the epidemic curve (default 70), the measure of the spread of the epidemic curve (default 11) and the peak amplitude of the epidemic curve (default 2.0%), see [30] for details. The form of this curve is based on epidemic curves experienced during the 1918 influenza pandemic and presented by (though not necessarily endorsed by) M. Cetron (DGMQ, CDC) which originated with S. Barrett and MIDAS.
The baseline prevalence () of an individual being infected with pandemic influenza, no decision measures yet implemented, can be approximated from the gross attack rate (GAR). The percent gross attack rate (GAR) is the percentage of the entire U.S. population that will have a clinical case of influenza. GAR is closely related to the mean number of secondary cases a typical single infected case will cause in a population with no immunity to the disease in the absence of interventions to control the infection [37], called the basic reproduction number (R 0). In the initial setup and default values for the model, we did assume a GAR of and as indicated. This leads us to an analytic expression for a prevalence curve (or the baseline probability mentioned above) that is used to drive the model and compute the daily number of new infected individuals as provided in Table 1. The specific parameter values for this expression are defined by Brigantic et al. [7]. A rough way to calculate R 0 for a simple single population is to take the product of the attack rate and the duration of infection (in this case the sum of the incubation and shedding periods). The incubation period is the time elapsed between exposure to a pathogenic organism and when symptoms and signs are first apparent [37] and the shedding period is the time that infected person can expel virus particles from the body, important routes include respiratory tract. These parameter values are based on a literature review that was further vetted by subject matter experts to arrive at appropriate values representative of pandemic influenza. These values are not necessarily specific to only air travel/airports, but are completely appropriate for cities or small towns. Moreover, these parameter values can be modified by the user of the PanViz tool, either to mimic alternate assumptions for pandemic influenza as desired and/or to model other potential infectious disease (e.g., smallpox) as well.
The user specifies coordinates and time of the first clinical pandemic influenza case in the state. These coordinates might correspond to a major city center or an airport, such as Indianapolis International Airport (IND). The time (day) at which pandemic influenza enters in a county (delay) is determined by the distance between the index case and target county centroid, and the approximate outbreak spread speed. Population density effects contact rates and thus disease spread rate. Counties are labeled as one of three categories: rural (less than 100 people per square mile), small (100–250 people per square mile), and urban (over 250 people per square mile). The disease spread rate modifier for population density (c of three categories in county y) is . Moreover, the model allows for variability in prevalence in the age groups, to account for population specific susceptibility or lack of immunity. The disease prevalence modifier due to age stratification (age group j) is given by the parameter . A future version of the tool will include additional options to establish associated impact parameters (e.g., hospitalization rates) by demographic group as found in the literature, such as provided by Meltzer et al. [31].
In the model, the user can evaluate diverse what-if scenarios for a 60-day period by varying decision measure k's efficacy (k mod), where the decision measures are school closures, media alerts, and strategic national stockpile deployment. Specifically, the modification to pandemic influenza prevalence due to a decision measure () is dependent on the baseline prevalence (), decision measure efficacy (k mod), time the measure is implemented () and the time at which the decision measure is fully effective (). The resulting pandemic influenza prevalence () is the baseline prevalence () minus the sum of all prevalence modifications due to decision measures ().
Disease dynamics are evaluated by combining the user supplied values for county demographics, population density, mortality and recovery rate, hospitalization rate, baseline and modified pandemic influenza prevalence. The number of infectious/sick in county y, age group j and at time t () is the product of the total county population (), county density modifier (), proportion of population in target age group (), age group disease modifier () and the decision measure modified pandemic influenza prevalence (). The number of deaths due to pandemic influenza in county y, age group j, at time t () is the product of the mortality rate () and the number of sick at time t −. The number of individuals recovered from pandemic influenza in county y, age group y, at time t () is the product of the recovery rate () and the number of sick at time . The number of hospitalizations due to pandemic influenza in county y, age group j, at time t () is the product of the hospitalization rate () and the number of sick at time t. The total number of individuals who have become sick due to pandemic influenza in county y, age group j, and at time t () is the sum of the sick minus the recovered and deceased each day, from the start of the pandemic to time t (). The total sick population in county y at time t () is the sum of the sick per age group in the county (). The total number of deceased, recovered, and hospitalized are calculated similarly, the exact equations are listed in Table 1.
Default parameters to our model are based on information from the U.S. National Strategic Plan [22]. In this plan, states are charged with the task of preparing for a pandemic influenza wave under the prediction that up to 35% of the population could be infected, 50% of the infected population will seek medical care, 20% of those seeking care will require hospitalization, and up to 2% of the infected population will die. These numbers are based on rates from the 1918 influenza pandemic [5], [14]. Unless otherwise specified, all images generated in this document use the default parameters found in Table 3 .
Table 3.
Default parameter settings.
| Outbreak speed=25.00 | ||||
3.2. Pandemic influenza visualization
The PanViz toolkit makes use of a person-to-person contact model spread with a constant rate of diffusion in order to simulate a spatiotemporal outbreak. The model employed by PanViz was designed to determine the number of influenza outbreak infections, hospitalizations, and deaths on a daily basis. As input, it requires the pandemic influenza characteristics, county data such as population, demographics [40], and hospital beds [2], and potential decision measures like closing schools. Spread vectors based on the point of origin and distance traveled per day are calculated, and effects on different age groups and population densities are taken into account.
Fig. 2 (Left) illustrates the infection probability model utilized by PanViz. In this case, users may vary the magnitude of the pandemic through a simple graphical user interface, Fig. 2 (Right). Users can directly control the mortality and infection rates, allowing for the creation of multiple scenarios and the ability to adapt this model to various ranges of pandemics. As the pandemic spreads over time, the peak wave hits various counties at different days as shown in Fig. 2 (Middle). In this case, the left curve is for a higher population density county that is also closer to the origin county than the right curve. Under the person-to-person contact model, the pandemic spreads diffusely from a single point source location at a constant rate. Fig. 3 shows the effects of modifying the spread origin. Previous work in disease modeling has looked at other means of spread vectors such as generation interval [24] in which a transmission delay is introduced between the host and those agents the host infects, and at the transmission of severe acute respiratory syndrome in household contacts [36]. In order to more realistically demonstrate the speed with which influenza can travel, we have also included travel between the 15 largest airports as part of the model. For a given location, the amount of time required for it to be affected is now determined by the minimum of the distance either from that point to the pandemic origin, or from that point to the nearest airport plus the distance from the pandemic origin to the airport closest to the pandemic origin. Once the disease reaches the nearest airport, it will begin spreading to all other cities with airport hubs on the subsequent day. Fig. 4 illustrates the difference between a single point source spread and the utilization of air travel routes for spread. Future work will focus on better parameterizing the airport spread models based on typical hub transportation.
Fig. 2.
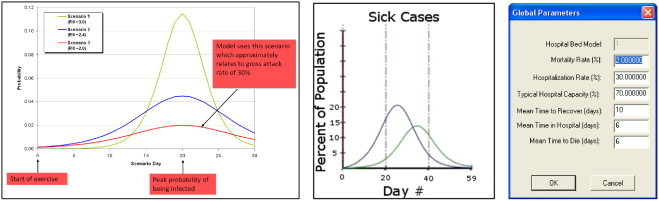
This figure (Left) illustrates the probability of infection for a variety of attack scenarios and (Middle) the impact that the spread factor and population density (which is controllable in the user interface) has on the time of the peak infection based on distance from the source. Note the lag between the two curves and the difference in magnitude. The smaller magnitude curve is due to a more rural population. (Right) shows the user interface for modifying the infection curve magnitude and duration parameters.
Fig. 3.
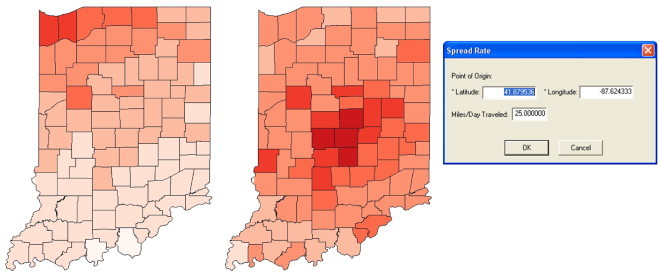
This figure (Left) showsDay 20 of a spread originating in Chicago, IL and (Middle) shows Day 20 of a spread originating in Indianapolis, IN. (Right) shows the user interface for modifying the spread center and rate.
Fig. 4.
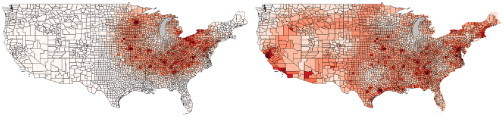
Modeling a pandemic spread originating in Chicago, IL. (Left) The effects of an outbreak after 40 days using a single source point spread model. (Right) The effects of an outbreak after 40 days including air travel between the 15 largest United States airports.
Along with modeling the spread from a given point of origin, our model also allows users to input an estimate of the number of days a person will remain sick, how many days a hospitalized person will remain in the hospital, and, if a person is going to die from the pandemic, how many days it will take the person to succumb. Fig. 5 provides a quick overview of the a simulated pandemic in a single county in Indiana. Here, we can observe the number of sick, hospitalized and dead individuals and note the lag between the sick and dead curves due to the user specified parameter. Again, many influenza models have been tested, from looking at the transmissibility of swine flu at Fort Dix in 1976 [26], to simulating pandemic influenza in San Antonio, Texas [32]. Our system enhances these modeling capabilities by allowing users to interactively adjust parameters and then visualize the result in an interactive environment.
Fig. 5.
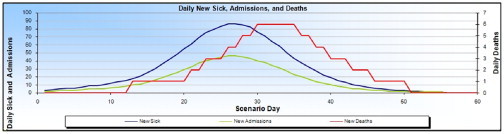
This figure shows our model of patients who have become ill, need hospitalization, or have died from the pandemic. Note the lag in deaths from time of infection as specified by the user.
Our system also allows for interactive filtering based on population demographics. Fig. 6 shows the number of people affected by the pandemic as a percentage of their given age range. Here we can observe which counties are hit the hardest for a given population. Furthermore, users may also modify the infection probability model of the pandemic based on the age ranges and population density of a county. In our system, we classify ages into three ranges (under 18, 18–65, and 65 plus) and counties into three ranges (rural, small town or major metropolitan).
Fig. 6.
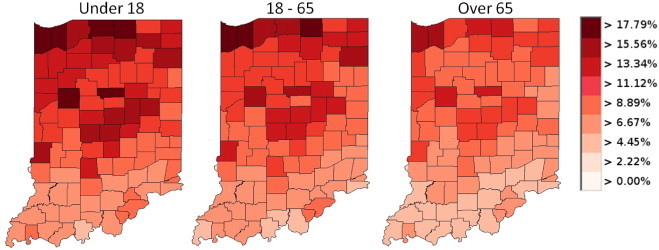
This figure shows the use of our filtering tools to analyze the population of ill patients for a given age range on Day 25 of a pandemic originating in Chicago, IL.
Users may interactively adjust the model parameters to define a magnification factor which will increase/decrease the probability of infection for a given age and/or county type. The impact of this can be seen in Fig. 2 (Middle). Note that each curve in that image represents a county; however, the magnitude of the pandemic is less in one county as compared to the other. This is due to the effects of modeling counties as different types. A similar result would be achieved by modifying the age parameters. Note that studies have been done on the distribution of influenza vaccine to high-risk groups (e.g., [28]), and future work will incorporate these factors into a more robust parameter set.
3.3. Decision measures
Within our modeling tool, we also account for various decision measures. These decision measures were decided on based on requirements from the Indiana State Department of Health in order to best accommodate their training exercises. In our system, we focus on three decision measures: (1) school closures; (2) media alerts; and (2) strategic national stockpile deployment.
The choice of these decision measures is also influenced by previous work. Historical records of past pandemics illustrate the efficacy of social distancing with regards to lessening the impact of a pandemic [6], [21]. Furthermore, other researchers have noted the expected reduction of influenza transmission based on school closures [9] or quarantines [15], and the effects of containing pandemic influenza through the use of antiviral agents and stockpiles have been well documented [27], [29]. However, other work suggests that for multiple outbreak sites, the idea of quarantines will prove ineffectual [33]. Detailed descriptions of the effects of various decision measure strategies can also be found in [19], [32], along with others.
Fig. 7 shows how an user can simply toggle on and off decision points within PanViz to see their effects on the pandemic impact. Fig. 7 (Left) shows the model on Day 40 with no decision measures employed. Using the controls on the lower left portion of the screen, the analyst chooses to deploy the strategic national stockpile (SNS) antivirals. The control widget shown in Fig. 9 allows the user to set the day of the simulation on which the decision measure was enacted, the number of days it will take the decision measure to reach full effect, and the impact the decision measure is expected to have in reducing the infection. In the graphs of Fig. 7 (Right), the user can immediately see how the use of the (SNS) has helped mitigate the magnitude of the pandemic. Through these controls, the user can interactively toggle decision points on and off and explore the effects that decisions taking place in the past would have on the current situation. Interactive toggling allows the user to understand the magnitude of the change by watching both the graphs and map display colors change for a given day as decision measures are implemented. Future work will include the use of more advanced decision measures and allow for both local and national measures. Note that this software is available online at http://pixel.ecn.purdue.edu:8080/rmacieje/PanViz/ and can be freely downloaded for experimentation.
Fig. 7.
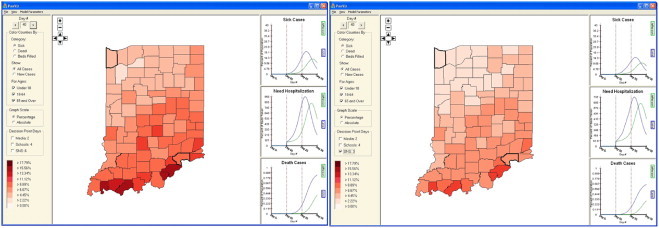
Here we illustrate the effects of utilizing decision measures within the confines of PanViz. In the left image, the analyst has used no decision measures. In the right image, the analyst has decided to see what effects deploying the strategic national stockpile on Day 3 would have had on the pandemic.
Fig. 9.
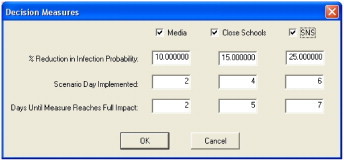
This figure shows the interactive widget for modifying the decision measure impacts on the probability of infection model.
4. Pandemic preparedness exercises
The main thrust of our work is to provide a means for enhancing pandemic preparedness exercises and providing tools for public education through easy to understand visuals. In 2008, the Indiana State Department of Health tasked its 10 districts to increase their level of preparedness and response through a series of functional exercises designed to test their readiness for a pandemic influenza. Here it was noted that we would not have a vaccine during the first wave of the pandemic [41] and that antivirals would be insufficient in supply and potential ineffective [22]. Hospitals would be overwhelmed and the public health community would be urging home care. In the absence of pharmaceutical measures, the general populace will need to rely on infection control measures (school closures and enhanced hygiene practices). As part of these functional exercises, four objectives were identified:
-
1.
Participants will determine the ability of their County Emergency Operations Center to establish and implement an order of command succession during an influenza pandemic.
-
2.
Participants will utilize their existing plans, policies and procedures to develop, coordinate, disseminate and manage public information during an influenza pandemic.
-
3.
Participants will utilize their existing plans, policies and procedures to manage Strategic National Stockpile (SNS) Pandemic Countermeasures including receipt, storage, security, distribution, dispensing and monitoring.
-
4.
Participants will determine existing medical surge capacity within their county and identify alternate care site needs during an influenza pandemic.
As a portion of these objectives, the PanViz tool kit was utilized as a means of providing situational awareness during the functional injects. The functional exercise assumed a 30% attack rate with a 2% mortality rate with the point of origin of the outbreak being Chicago, Illinois. Participants were able to input decision measures (such as when to deploy their SNS countermeasures) and observe the impact of their decisions. All scenarios utilized the default parameter settings documented in Table 3.
This tool was utilized as a demonstration of decisions taken during the tabletop exercise. Participants were able to provide input to the model as part of a web seminar. A single controller then modified the input parameters to the tool, and the resultant changes were visualized and shown within the webinar. PanViz was able to actively engage participants in discussions on issues with the medical surge capacity. Fig. 8 was used as an educational component of the functional exercises to illustrate the importance of advanced surge capacity plans. In Fig. 8 the number of available hospital beds (as noted in the Emergency Preparedness Atlas: U.S. Nursing Home and Hospital Facilities [2]) is displayed for each county. In our model, it is assumed that 70% of all beds are full due to general medical needs. As an example, on Day 1 of the pandemic, our model estimates that Hamilton County will need 32 of its 144 beds for patients as a direct result of the pandemic influenza. By Day 10, Hamilton County will need 762 of its 144 beds for patients as a direct result of the pandemic. One can quickly observe (by color) that all counties across the state have quickly reached their bed capacity. These striking visuals created wide spread discussion amongst participants and provided greater gravitas for the exercises.
Fig. 8.
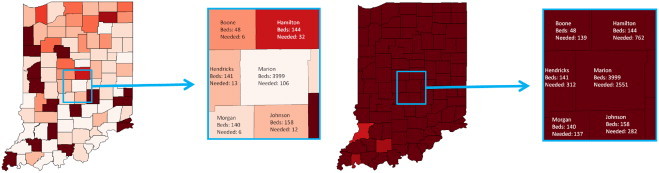
Here we illustrate the potential impact that a pandemic may have on the available health care facilities. In this case, each county is assumed to have 70% of all beds filled in a hospital on a given day. On Day 1 of the simulated pandemic, it is projected that Hamilton County will required 32 additional hospital beds over its baseline capacity usage to support the pandemic. By Day 10, Hamilton County has 762 patients needing hospitalization; however, the county resources are approximately 144 beds.
5. Public awareness and education
More recently, PanViz has been used as a means of providing educational information about the impact of implementing social distancing measures during the recent H1N1 outbreak. Utilizing attack and mortality rates similar to the 1918 pandemic, we created a series of graphics illustrating the impact that social distancing could have on reducing the pandemic's magnitude. Fig. 10 illustrates the spread of the pandemic when no decision measures are employed with that of the spread of the pandemic when social distancing and vaccinations have been employed early in the outbreak stages. Note the significant reduction of the magnitude of the outbreak. These educational materials were distributed through Purdue University's pandemic education website and details were also reported on by the United Press International [39].
Fig. 10.
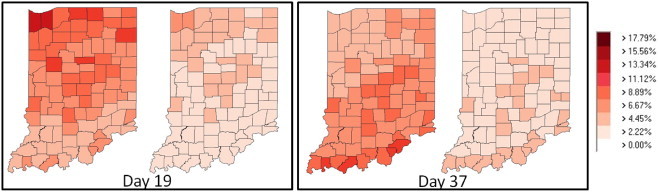
Here we illustrate the potential impact that social distancing and early vaccination could have on magnitude of a pandemic influenza. For Days 19 and 37 we present a comparison of the effects of a pandemic when no social distancing or vaccinations have been employed (the left map for each day) with the effect of an application of social distancing and vaccinations (the right map for each day). One can immediately see that the magnitude of the pandemic is substantially lessened.
In a situation similar to the recent H1N1 outbreak, PanViz could be deployed as an operational research tool in which officials could input the current known attack and mortality rates of the given pandemic. As data comes in, analysts can quickly adjust model parameters and settings within the PanViz framework in order to gain a rough prediction of the potential magnitude and spread. In this way, PanViz can provide officials with a means of communicating information amongst agencies, and providing public service announcements similar to our current press release.
6. Conclusions and future work
The interactive approach and ease of use of our visualization modeling methodology makes complex modeling and simulation tools available directly to public health officials and decision makers for their own use. Moreover, these tools and techniques have the potential to be updated in near real-time as actual data and observations are made during the course of a pandemic or epidemic such as the current Swine Flu outbreak that first appeared in April, 2009 [10]. In future work, we intend to refine the underlying modeling algorithms to be more sophisticated and accurate via detailed simulations and agent based modeling driven by basic input parameters from the user. These simulations can run underneath the top level model structure via a simple button click and can be transparent to the user, but returned results will have greater robustness increasing their power and overall effectiveness.
Furthermore, we plan to incorporate more advanced temporal and spatiotemporal analytics tools into future versions of the framework. Currently, the model does allow users to scroll through time as well as adjust the timing of different mitigation measures and the time it takes for these to reach full effect. Our plan is to include side-by-side temporal comparison and/or potentially include difference map views so that users can better ascertain temporal differences.
Our partners at the Indiana State Department of Health have shown immense interest in expanding their use of this tool, and current steps are underway to deploy this to all 92 county health officials in Indiana. While our tool's use cannot be directly quantified in terms of its impact in raising Indiana's preparedness rating, our contribution was a major component of the training and preparedness exercise program. Furthermore, the educational value of easy to understand visuals as a means for conveying information to the public cannot be overstated. As such, our PanViz tool provides an easy to use interface for both the modeling and exploration of pandemics for use in both training and operational research. We plan to further pursue our collaborations to port this into a fully functional emergency response tool where more detailed critical tasks can be solved.
Acknowledgments
This project was conducted by Purdue University under contract with the Indiana State Department of Health and was supported by Grant Award No. 5U90TP517024-08 from the Centers for Disease Control & Prevention (CDC) as well as the U.S. Department of Homeland Security's VACCINE Center under Award Number 2009-ST-061-CI0001. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the CDC.
Footnotes
This paper has been recommended for acceptance by Gennady Andrienko, Natalia Andrienko, Daniel Keim, Alan M. MacEachren and Stefan Wrobel.
References
- 1.Availability of influenza pandemic preparedness planning FluAid, 2.0, Journal of the American Medical Association 284 (14) (2000) 1782. [PubMed]
- 2.Agency for Healthcare Research and Quality, Emergency preparedness atlas: U.S. nursing home and hospital facilities, AHRQ Publication No. 07-0029-2, April 2007.
- 3.Atkinson M.P., Wein L.M. Quantifying the routes of transmission for pandemic influenza. Bulletin of Mathematical Biology. 2008;70:820–867. doi: 10.1007/s11538-007-9281-2. [DOI] [PubMed] [Google Scholar]
- 4.Atkinson M.P., Wein L.M. Assessing infection control measures for pandemic influenza. Risk Analysis. 2009;29:949–962. doi: 10.1111/j.1539-6924.2009.01232.x. [DOI] [PubMed] [Google Scholar]
- 5.M. Billings, The Influenza Pandemic of 1918, 1997.
- 6.Bootsma M.C., Ferguson N.M. The effect of public health measures on the 1918 influenza pandemic in US cities. Proceedings of the National Academy of Science. 2007;104(18):7588–7593. doi: 10.1073/pnas.0611071104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brigantic R., Malone J., Muller G., Lee R., Kulesz J., Delp W., McMahon B. Simulation to assess the efficacy of U.S. airport entry screening of passengers for pandemic influenza. International Journal of Risk Assessment & Management. 2009;12(2–4):290–310. [Google Scholar]
- 8.Bush R., Bender C., Subbarao K., Cox N., Fitch W. Predicting the evolution of human influenza A. Science. 1999;286(5446):1921–1925. doi: 10.1126/science.286.5446.1921. [DOI] [PubMed] [Google Scholar]
- 9.Cauchemez S., Valleron A.J., Boëlle P.Y., Flahault A., Ferguson N.M. Estimating the impact of school closure on influenza transmission from sentinel data. Nature. 2008;452(7188):750–754. doi: 10.1038/nature06732. [DOI] [PubMed] [Google Scholar]
- 10.Centers for Disease Control and Prevention, H1N1 Flu (Swine Flu), May 2009.
- 11.Chick S.E., Mamani H., Simchi-Levi D. Supply chain coordination and influenza vaccination. Operations Research. 2008;56(6):1493–1506. [Google Scholar]
- 12.Christian M.D., Kollek D., Schwartz B. Emergency preparedness: what every healthcare worker needs to know. Canadian Journal of Emergency Medicine. 2005;7(5):330–337. doi: 10.1017/s1481803500014548. [DOI] [PubMed] [Google Scholar]
- 13.D. Dausey, J. Aledort, N. Lurie, Tabletop exercises for pandemic influenza preparedness in local public health agencies, TR-319-DHHS, prepared for the U.S. Department of Health and Human Services Office of the Assistant Secretary for Public Health Emergency Preparedness, 2005.
- 14.Elveback L.R., Fox J.P., Ackerman E., Langworthy A., Boyd M., Gatewood L. An influenza simulation model for immunization studies. American Journal of Epidemiology. 1976;103(2):152–165. doi: 10.1093/oxfordjournals.aje.a112213. [DOI] [PubMed] [Google Scholar]
- 15.Ferguson N.M., Cummings D.A., Fraser C., Cajka J.C., Cooley P.C., Burke D.S. Strategies for mitigating an influenza pandemic. Nature. 2006;442(7101):448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.A.C. for Disease Control and Prevention, Community strategy for pandemic influenza mitigation in the United States—early, targeted, layered use of nonpharmaceutical interventions, Centers for Disease Control and Prevention, Atlanta, 2007.
- 17.Ford D.A., Kaufman J.H., Eiron I. An extensible spatial and temporal epidemiological modeling system. International Journal of Health Geographics. 2006;5(4) doi: 10.1186/1476-072X-5-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gensheimer K.F., Meltzer M.I., Postema A.S., Strikas R. Influenza pandemic preparedness. Emerging Infectious Diseases. 2003;9(12):1645–1648. doi: 10.3201/eid0912.030289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Germann T.C., Kadau K., Longini I.M., Macken C.A. Mitigation strategies for pandemic influenza in the United States. Proceedings of the National Academy of Sciences. 2006;103(15):5935–5940. doi: 10.1073/pnas.0601266103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Guo D. Visual analytics of spatial interaction patterns for pandemic decision support. International Journal of Geographical Information Science. 2007;21(8):859–878. [Google Scholar]
- 21.Hatchett R.J., Mecher C.E., Lipsitch M. Public health interventions and epidemic intensity during the 1918 influenza pandemic. Proceedings of the National Academy of Sciences. 2007;104(18):7582–7587. doi: 10.1073/pnas.0610941104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Homeland Security Council, National strategy for pandemic influenza, The White House website, November 2005.
- 23.Inglesby T.V., Nuzzo J.B., Henderson D.A. Disease mitigation measures in the control of pandemic influenza. Biosecurity and Bioterrorism. 2006;4(4):366–375. doi: 10.1089/bsp.2006.4.366. [DOI] [PubMed] [Google Scholar]
- 24.Kenah E., Lipsitch M., Robins J. Generation interval contraction and epidemic data analysis. Mathematical Biosciences. 2008;213(1):71–79. doi: 10.1016/j.mbs.2008.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Larson R.C. Simple models of influenza progression within a heterogeneous population. Operations Research. 2007;55(3):339–412. [Google Scholar]
- 26.Lessler J., Cummings D.A., Fishman S., Vora A., Burke D.S. Transmissibility of swine flu at Fort Dix, 1976. Journal of The Royal Society Interface. 2007;4(15):755. doi: 10.1098/rsif.2007.0228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lipsitch M., Cohen T., Murray M., Levin B.R. Antiviral resistance and the control of pandemic influenza. PLoS Medicine. 2007;4(1):111. doi: 10.1371/journal.pmed.0040015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Longini I.M., Halloran M.E. Strategy for distribution of influenza vaccine to high-risk groups and children. American Journal of Epidemiology. 2005;161(4):303–306. doi: 10.1093/aje/kwi053. [DOI] [PubMed] [Google Scholar]
- 29.Longini I.M., Halloran M.E., Nizam A., Yang Y. Containing pandemic influenza with antiviral agents. American Journal of Epidemiology. 2004;159(7):623–633. doi: 10.1093/aje/kwh092. [DOI] [PubMed] [Google Scholar]
- 30.Malone J., Brigantic R., Muller G., Gadgil A., Delp W., McMahon B., Lee R., Kulesz J., Mihelic F. U.S. airport entry screening in response to pandemic influenza: modeling and analysis. Travel Medicine and Infectious Disease. 2009;7(4):181–191. doi: 10.1016/j.tmaid.2009.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Meltzer M., Cox N., Fukuda K. The economic impact of pandemic influenza in the United States: priorities for intervention. Emerging Infectious Diseases. 1999;5(5):659–671. doi: 10.3201/eid0505.990507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Miller G., Randolph S., Patterson J. Responding to simulated pandemic influenza in San Antonio, Texas. Infection Control and Hospital Epidemiology. 2008;29(4):320–326. doi: 10.1086/529212. [DOI] [PubMed] [Google Scholar]
- 33.Mills C.E., Robins J.M., Bergstrom C.T., Lipsitch M. Pandemic influenza: risk of multiple introductions and the need to prepare for them. PLoS Medicine. 2006;3(6) doi: 10.1371/journal.pmed.0030135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nigmatulina K.R., Larson R.C. Living with influenza: impacts of government imposed and voluntarily selected interventions. European Journal of Operational Research. 2009;195(2):613–627. [Google Scholar]
- 35.Nuno M., Chowell G., Gumel A.B. Assessing the role of basic control measures, antivirals and vaccine in curtailing pandemic influenza: scenarios for the US, UK and the Netherlands. Journal of the Royal Society Interface. 2007;4(14):505–521. doi: 10.1098/rsif.2006.0186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.I.R. Douglas Scott, E. Gregg, M.I. Meltzer, Collecting data to assess SARS interventions, Emerging Infectious Diseases, May 2009. [DOI] [PMC free article] [PubMed]
- 37.Scott R., Gregg E., Meltzer M. Collecting data to assess SARS interventions. Emerging Infectious Diseases. 2004;10(7):1290–1292. doi: 10.3201/eid1007.030749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.J.J. Thomas, K.A. Cook (Eds.), Illuminating the Path: The R&D Agenda for Visual Analytics, IEEE Press, 2005.
- 39.United Press International, Program simulates spread of pandemic flu, UPI.com Science News, 2009.
- 40.United States Census Bureau, Population demographics, 2000.
- 41.US Department of Health and Human Services, HHS pandemic influenza plan, US Department of Health and Human Services, Washington, DC, November 2005.


