Effects of awareness diffusion and self-initiated awareness behavior on epidemic spreading - An approach based on multiplex networks

Highlights

• •The interplay between the epidemic spreading and the diffusion of awareness is studied in multiplex networks.
• •Unaware individuals can be informed by aware neighbors in information network and self-awareness induced by the infected neighbors in contact networks.
• •The effects of awareness diffusion and self-initiated awareness on the epidemic threshold and the density of infection are investigated.
• •Our findings show that the local or global information based self-awareness can reduce the density of infection but cannot alter the epidemic threshold.

Abstract

In this paper, we study the interplay between the epidemic spreading and the diffusion of awareness in multiplex networks. In the model, an infectious disease can spread in one network representing the paths of epidemic spreading (contact network), leading to the diffusion of awareness in the other network (information network), and then the diffusion of awareness will cause individuals to take social distances, which in turn affects the epidemic spreading. As for the diffusion of awareness, we assume that, on the one hand, individuals can be informed by other aware neighbors in information network, on the other hand, the susceptible individuals can be self-awareness induced by the infected neighbors in the contact networks (local information) or mass media (global information). Through Markov chain approach and numerical computations, we find that the density of infected individuals and the epidemic threshold can be affected by the structures of the two networks and the effective transmission rate of the awareness. However, we prove that though the introduction of the self-awareness can lower the density of infection, which cannot increase the epidemic threshold no matter of the local information or global information. Our finding is remarkably different to many previous results on single-layer network: local information based behavioral response can alter the epidemic threshold. Furthermore, our results indicate that the nodes with more neighbors (hub nodes) in information networks are easier to be informed, as a result, their risk of infection in contact networks can be effectively reduced.

1. Introduction

The outbreaks of diseases can involve the diffusion of information in regard to the diseases, including the risk of infection, rumors, fears and so on, which can stimulate individuals to take spontaneous behavioral responses to protect themselves, thereby bring profound impacts on the spreading of disease [1], [2], [3], [4], [5], [6]. For example, recent outbreaks of the H1N1 flu, the bird flu, and the severe acute respiratory syndrome (SARS) have brought the reduction of going out and the plenty of people wearing face masks. For this reason, there has been an increasing focus on the development of formal models aimed at investigating the interplay of epidemic spreading and information-based behavioral responses [7], [8], [9], [10]. Such as, based on the assumption that the probability of susceptible individual going to the alter state is proportional to the number of infected neighbors, Sahneh et al., extended the SIS (Susceptible-Infected-Susceptible) model to a Susceptible-Alter-Infected-Susceptible (SAIS) model [11], [12], and they found that the way of behavioral response can enhance the epidemic threshold; Meloni et al. studied a meta-population model that incorporates several scenarios of self-initiated behavioral changes into the mobility patterns of individuals, and they found that such behavioral changes do not alter the epidemic threshold, but may produce a negative impact on disease, i.e., the density of infection is increased [13]; In Refs. [14], [15], [16], authors investigated the effects of the information-based behavioral responses on the epidemic dynamics by designing the transmission rate as a function of the local infected density or the global infected density.

Though the effects of information-based behavioral responses on the epidemic dynamics have been studied by many authors, most of works assumed the spreadings of information and epidemic are in the same network. As we know, with the development of technology, information can fast diffuse through many different channels, such as, the word of mouth, news media, online social networks, and so on. In view of this, recent well-studied multiplex network theory has been used to mimic the interplay of information or related awareness and the epidemic dynamics [17], [18], [19], [20]. For instance, Sahneh et al., have shown that the information dissemination spread in another network can help boost the resilience of the agents’ population against the spreading and found optimal information dissemination for different topologies [21]; Wang et al., investigated the interplay of the epidemic dynamics and the information dynamics in multiplex network based on the SIR (R-recovery) model, and focused on the two fundamental quantities underlying any spreading process: epidemic threshold and the final epidemic prevalence [22]; Granell et al., established an SIS-UAU model to investigate the competing effects of the spreading of awareness and the epidemic dynamics in multiplex with the transmission rate of awareness as well as the structure of information network [23]. More recently, they further generalized their model by reducing the probability of infected individuals becoming awareness and including the effect of a mass broadcast of awareness (mass media) on the epidemic dynamics [24].

In Refs. [23], [24], authors assumed that susceptible individuals can only be informed by other aware neighbors. In reality, individuals may become aware (i.e., self-initiated awareness) when they find that their neighbors are infected. Inspired these factors, in the current work, we study the interplay between the diffusion of awareness by incorporating the self-awareness effects and the epidemic dynamics under the framework of multiplex network. In the model, an infectious disease first spreads among population represented by the contact network, and then the outbreak of the disease stimulates some people (infected or susceptible individuals) become aware of the risk of infection, and they take some protections to reduce the probability of infection. Meanwhile, unaware individuals can be informed by other aware individuals through the information network or become self-awareness induced by the infected neighbors in contact network or mass media. The finding indicates that the additional self-initiated awareness mechanism can reduce the density of infection, however, which can not alter the epidemic threshold. Moreover, we show that since the hub nodes in information networks are easier to be informed, which can much lower their infection probability in contact networks. The results are verified by the Monte-Carlo simulations and the microscopic Markov chain approach (MMCA).

The layout of the paper is as follows: we introduce the model in Section 2. The simulation results and theoretical analysis are presented in Section 3. Finally, Conclusions and discussions are presented in Section 4. The results for the global information-based self-initiated awareness are given in Appendix A.

2. Model

In this work, we generalize the model of Ref. [23], [24]. In that model, a multiplex network includes two layers, one is physical layer representing the spreading of epidemic (contact network), and the other is information layer on where the diffusion of the awareness evolves (information network). All nodes represent the same individuals in both layers, but the connectivity is different in each of them. In the contact layer, a Susceptible - Infected - Susceptible (SIS) model is used to mimic the epidemic dynamics. That is to say, a susceptible node can be infected by one infected neighbor with certain probability, and the infected node can return to susceptible state with probability μ. On the information layer, the dynamical process of awareness is assumed to be similar to the SIS model, that is, an unaware node (U) can be informed by an aware neighbor (A) with probability λ, and the aware node can loss awareness and back to unaware state with probability δ. The interplay of the two processes is modelled as follows: once an individual is infected, s/he will certainly become aware, that is, the probability is $\sigma =100\%$. In addition, to distinguish the protective behaviors between the aware individuals and unaware individuals, let β and ${\beta }^A=\gamma \beta$ (here 0 ≤ γ < 1. If $\gamma =0,$ the aware individuals are completely immune to the infection.) be the probabilities of unaware and aware susceptible nodes to get infected, respectively.

From the description of the model, one can find that, on the one hand, the authors assumed that the infected individuals will automatically become aware and are willing to inform the disease information. As we know, in many cases, infected individuals are unwilling to tell others since they can be discriminated or isolated by others once others know they are infected by one certain disease. For example, if one person is infected by AIDS or hepatitis B, who may be alienated by his friends. So we assume that infected individuals becoming aware with probability 0 ≤ σ ≤ 1. On the other hand, in the model, individuals can only be informed by their neighbors through the information network, that is to say, one individual has no chance to become aware once their neighbors are unaware. However, individuals can become self-awareness once their friends are infected or they are informed by the mass media, and the probability of becoming awareness increases with the number of infected people [12]. Thus, in our model, we assume that, for a susceptible individual, besides being informed by the aware neighbors in the information network, which can also self-awareness when contacting one infected neighbors in contact network, the probability is represented by parameter κ. Note that, for the original model in Ref. [23], awareness cannot break out if the probability $\sigma =0,$ so the roles of awareness cannot be played, however, in our model, the awareness can diffuse among population even though $\sigma =0$ since susceptible individuals can become aware by their self-initiated responses.

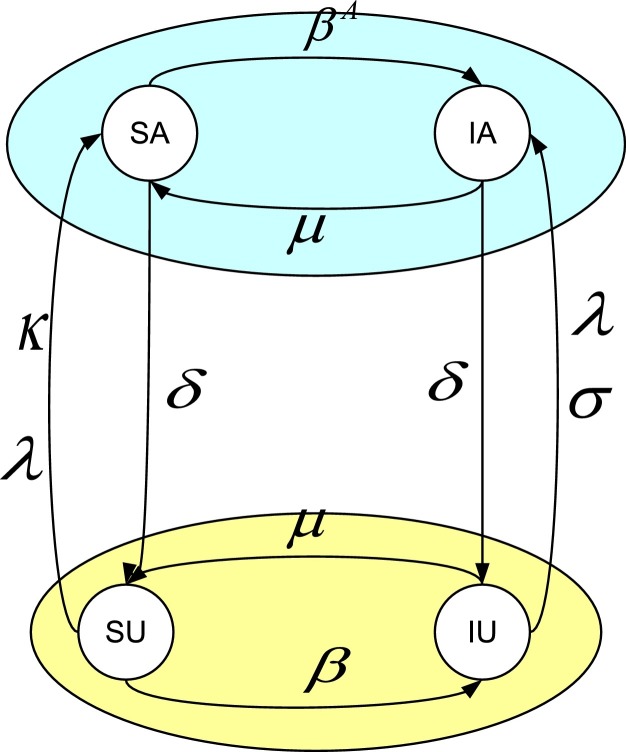
According to this scheme, an individual can be in four different states: susceptible and unaware(SU), susceptible and aware(SA), infected and unaware(IU), infected and aware(IA). The flow diagram of the model is given in Fig. 1 .

Fig. 1.

Model description for the UAU-SIS dynamic. An individual can be in four different states: SU, SA, IU, and IA. The top (bottom) layer is the epidemic process for the aware (unaware) individuals, respectively. SU (SA) can be infected by an infectious neighbor in contact layer with a probability β (${\beta }^A=\gamma \beta$). IU and IA recovers to SU and SA, respectively, with the same probability μ; The left (right) flow is the awareness process for the susceptible (infected) individuals, respectively. SU can go to SA with a probability λ of being informed by an aware neighbor through information network, or induced by the infected neighbors in contact network with a probability κ. SA recovers to SU with a probability δ. IU can go to IA by informed the aware neighbors in information layer with a probability λ, or self-awareness with a probability σ, which is not related to the neighbor’s states. SA and IA can become unaware and return to SU and IU with the same probability δ.

3. Main results

3.1. Theoretical analysis

Denoting a_ij and b_ij be the adjacency matrices that support the SIS and UAU processes, respectively. The probability of i in one of four states at time t is denoted by $p_i^{SU}\left(t\right),$ $p_i^{SA}\left(t\right),$ $p_i^{IU}\left(t\right)$ and $p_i^{IA}\left(t\right)$ respectively. Assuming the probability of susceptible (infect) node i not being informed by any neighbors is θ_i(t) (r_i(t)), and the probability of unaware (aware) susceptible node i not being infected is $q_i^U\left(t\right)$ ($q_i^A\left(t\right)$). They are described as [23]:

$$\begin{array}{ccc}\hfill {\theta }_i\left(t\right)& =& \prod _j(1-b_{ji}{p}_j^A\left(t\right)\lambda )(1-a_{ji}{p}_j^I\left(t\right)\kappa ),\hfill \end{array}$$ (1)

$$\begin{array}{ccc}\hfill r_i\left(t\right)& =& \prod _j(1-b_{ji}{p}_j^A\left(t\right)\lambda ),\hfill \end{array}$$ (2)

$$\begin{array}{ccc}\hfill q_i^U\left(t\right)& =& \prod _j(1-a_{ji}{p}_j^I\left(t\right)\beta ),\hfill \end{array}$$ (3)

$$\begin{array}{ccc}\hfill q_i^A\left(t\right)& =& \prod _j(1-a_{ji}{p}_j^I\left(t\right){\beta }^A),\hfill \end{array}$$ (4)

where $p_j^A\left(t\right)=p_j^{SA}\left(t\right)+p_j^{IA}\left(t\right)$ and $p_j^I\left(t\right)=p_j^{IU}\left(t\right)+p_j^{IA}\left(t\right)$ (Note: to simplify the model, we do not distinguish the infectivity of IA and IU, meanwhile, the diffusion capabilities of awareness for SA and IA are also the same).

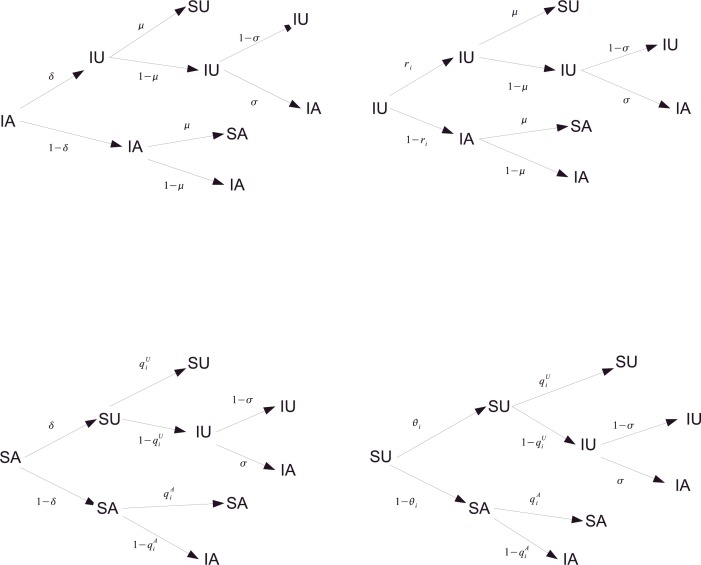
For each possible state at time t, which may give rise to four possible states at time $t+1$ with certain probability, the transition probability trees for node i are illustrated in Fig. 2 . According to the scheme in Fig. 2, one can easily write the Markov Chain Approach (MMCA) equations [25], [26] for each state, for example, along the top branch of the four trees, one can read the probability $p_i^{SU}(t+1)$ of SU at $t+1$ as:

$$\begin{array}{ccc}\hfill p_i^{SU}(t+1)& =& p_i^{IA}\left(t\right)\delta \mu +p_i^{IU}\left(t\right){\gamma }_i\left(t\right)\mu +p_i^{SA}\left(t\right)\delta q_i^U\left(t\right)+p_i^{SU}\left(t\right){\theta }_i\left(t\right)q_i^U\left(t\right).\hfill \end{array}$$ (5)

Similarly, the other three MMCA equations can be written as:

$$\begin{array}{ccc}\hfill p_i^{SA}(t+1)& =& p_i^{IA}\left(t\right)(1-\delta )\mu +p_i^{IU}\left(t\right)(1-r_i\left(t\right))\mu \hfill \\ & & +p_i^{SA}\left(t\right)(1-\delta )q_i^A\left(t\right)+p_i^{SU}\left(t\right)(1-{\theta }_i\left(t\right))q_i^A\left(t\right),\hfill \end{array}$$ (6)

$$\begin{array}{ccc}\hfill p_i^{IU}(t+1)& =& (1-\sigma )\{p_i^{IA}\left(t\right)\delta (1-\mu )+p_i^{IU}\left(t\right)r_i\left(t\right)(1-\mu )\hfill \\ & & +p_i^{SA}\left(t\right)\delta (1-q_i^U\left(t\right))+p_i^{SU}\left(t\right){\theta }_i\left(t\right)(1-q_i^U\left(t\right))\},\hfill \end{array}$$ (7)

$$\begin{array}{ccc}\hfill p_i^{IA}(t+1)& =& \sigma \{p_i^{IA}\left(t\right)\delta (1-\mu )+p_i^{IU}\left(t\right)r_i\left(t\right)(1-\mu )+p_i^{SA}\left(t\right)\delta (1-q_i^U\left(t\right))\hfill \\ & & +p_i^{SU}\left(t\right){\theta }_i\left(t\right)(1-q_i^U\left(t\right))\}+p_i^{IA}\left(t\right)(1-\delta )(1-\mu )\hfill \\ & & +p_i^{IU}\left(t\right)(1-r_i\left(t\right))(1-\mu )+p_i^{SA}\left(t\right)(1-\delta )(1-q_i^A\left(t\right))\hfill \\ & & +p_i^{SU}\left(t\right)(1-{\theta }_i\left(t\right))(1-q_i^A\left(t\right)),\hfill \end{array}$$ (8)

where $p_i^{SU}\left(t\right)+p_i^{SA}\left(t\right)+p_i^{IU}\left(t\right)+p_i^{IA}\left(t\right)\equiv 1$. When the system goes to the stationary state, we have $p_i^{SU}(t+1)=p_i^{SU}\left(t\right)=p_i^{SU}$ for SU state and equivalently for the SU, SA and IU states.

Fig. 2.

Transition probability trees for the states of UAU-SIS dynamics in the multiplex for per time step. The denotations of θ_i, r_i, $q_i^U$ and $q_i^A$ are given in Eqs. (1)–(4). Other parameters have the same denotations as in Fig. 1.

Since the epidemic threshold determines whether the epidemic can outbreak or die out, it is vital to analyze the effects of the different parameters on the epidemic threshold β_c. Near the threshold, the probability of nodes being infected is very low, i.e., $p_i^I={\varepsilon }_i\ll 1$. Consequently, $q_i^A\approx 1-{\beta }^A{\sum }_j\left(a_{ji}{\varepsilon }_j\right)$ and $q_i^U\approx 1-\beta {\sum }_j\left(a_{ji}{\varepsilon }_j\right)$. Further approximate $q_i^A\approx 1$ and $q_i^U\approx 1$ by assuming $p_i^I={\varepsilon }_i\to 0,$ and then substitute both of them into Eqs. (5) and (6), we obtain

$$p_i^{SU}=p_i^{SA}\delta +p_i^{SU}{\theta }_i$$ (9)

$$p_i^{SA}=p_i^{SA}(1-\delta )+p_i^{SU}(1-{\theta }_i)$$ (10)

Combing (8), (9), (10)), then a simple formula is obtained:

$$\mu {\varepsilon }_i=(p_i^{SU}\beta +p_i^{SA}{\beta }^A)\sum \left(a_{ji}{\varepsilon }_j\right),$$ (11)

with ${\beta }^A=\gamma \beta ,$ $p_i^U=p_i^{SU}+p_i^{IU}\approx p_i^{SU},$ $p_i^A=p_i^{SA}+p_i^{IA}\approx p_i^{SA}$ and ${\varepsilon }_i=p_j^{IU}\left(t\right)+p_j^{IA}\left(t\right)\ll 1,$ then Eq. (11) can be rewritten as:

$$\sum [(1-(1-\gamma )p_i^A)a_{ji}-\frac{\mu }{\beta }{\delta }_{ji}]{\varepsilon }_j=0,$$ (12)

here ${\delta }_{ji}=1$ if $i=j$; otherwise, ${\delta }_{ij}=0$.

Defining matrix H with elements:

$$h_{ji}=(1-(1-\gamma )p_i^A)a_{ji},$$ (13)

Eq. (12) can be read as

$$H\mathit{\varepsilon }=\frac{\mu }{\beta }\mathit{\varepsilon },$$ (14)

where $\mathit{\varepsilon }={({\varepsilon }_1,{\varepsilon }_2,\dots ,{\varepsilon }_N)}^T$ with T be the vector transportation.

The non-trivial solutions of Eq. (14) are eigenvectors of H, whose eigenvalues are equal to μ/β. Therefore, the onset of the epidemics is given by the largest eigenvalue of H, i.e., ${\bigwedge }_{max}\left(H\right),$

$${\beta }_c=\frac{\mu }{{\bigwedge }_{max}\left(H\right)}.$$ (15)

From Eqs. (13) and (15), one can see that the epidemic threshold depends on the structure of contact network (a_ij), the parameter γ and the density of awareness ρ^A. The value of ρ^A is further determined by the structure of information network, the transmission rate λ and the recovery rate δ.

3.2. Numerical simulations

To verify our theoretical results, as in Ref. [23], we first build a configuration network with degree distribution $P\left(k\right)\sim k^{-2.5}$ and network size $N=2000$ as the contact network, and for the information network, which is generated by adding 800 extra random links in the contact network. a_ij and b_ij represent the adjacency matrices of the contact network and the information network, respectively. All simulation results are obtained by averaging 20 realizations.

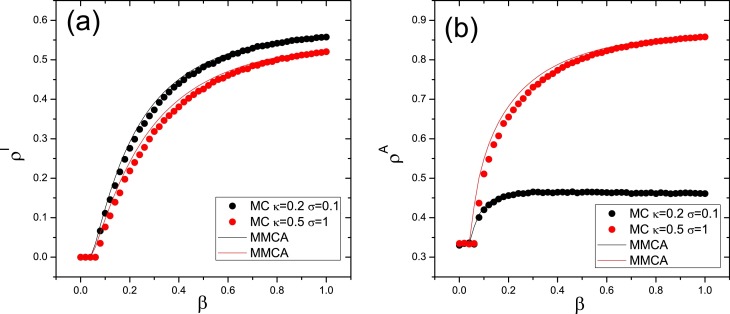
We first compare the results from MMCA with Monte–Carlo simulation in Fig. 3 to check the effectiveness of our analysis based on MMCA, from Fig. 3, one can observe that the results based on the two approaches are in good agreement. So in the next figures, our main results are obtained from MMCA.

Fig. 3.

Comparison of MMCA(solid line) with Monte–Carlo simulation(dotted line) for $\lambda =0.15,$$\gamma =0,$$\delta =0.6$ and $\mu =0.4$. The fraction of infected (a) and aware (b) nodes as a function of the infectivity parameter β for two different conditions of the parameters κ and σ.

Then we investigate the effects of the two main parameters of the model—κ and σ on the epidemic threshold and the density of infected individuals. Here, we will present the results for $\gamma =0,$ meaning that ${\beta }^A=0$ and $q^A=0$. Obviously, once the value of γ is increased, the epidemic threshold is decreased and the density of infected individuals in enhanced correspondingly.

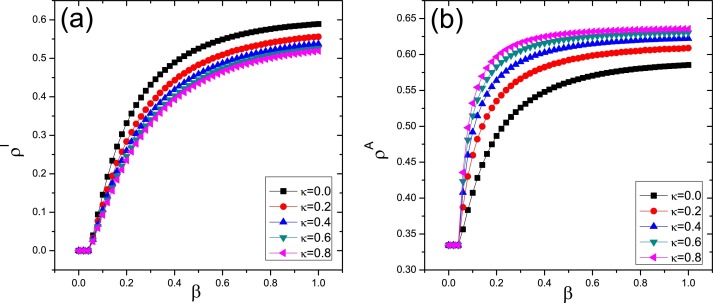
Fig. 4 plots the density of infection [ρ^I, see Fig. 4(a)] and aware individuals [ρ^A, see Fig. 4(b)] as a function of β for different values of κ, respectively. Observing the figure, one can see that though the larger value of κ can cause more individuals become aware and reduce the density of infection. However, one can find that the increasing of λ has no influence on the epidemic threshold. The result is remarkably different from many previous results which claim that the local information-based behavioral response in the single-layer network can alter the epidemic threshold. For instance, Wu et al., [14] compared the roles of the three forms of information-based awareness, i.e., local, global, and contact awareness, in the epidemic threshold, and concluded that global awareness cannot alter the epidemic threshold while both local awareness can enhance the epidemic threshold. Sahneh et al., [11], [12] and us also illustrated that the local information based behavioral responses can effectively increase the epidemic threshold, no matter of SIS model or SIR model [16].

Fig. 4.

Fraction of infected (a) and aware (b) nodes as a function of the infectivity parameter β for different values of the parameter κ. Here $\lambda =0.15,$$\gamma =0,$$\delta =0.6,$$\mu =0.4$ and $\sigma =0.4$.

How to understand this nontrivial result? Since the UAU awareness dynamic is the same to the SIS epidemic process. When the epidemic has not broken out, the density of awareness in information network (i.e., ρ^A) is only determined by the transmission rate of awareness, λ, recovery rate δ and the structure of information network, but is not related to the value of κ. Namely, near or below the epidemic threshold point, increasing the value of κ only means that the initial number of the aware individuals is increased, which cannot affect the density of aware individuals at stationary state. In this case, the value of $p_i^A$ is independent of the value of κ or σ, which gives rise to the same value of ρ^A [see Fig. 4(b)]. Thus, according to Eqs. (13) and (15), the epidemic threshold β_c is invariable owing to the same value of ρ^A. It is worth noting that, for the case of single-layer network, the local information-based behavioral response directly reduce the transmission rate of epidemic, leading to the change of the epidemic threshold. For our model, the self-awareness behavior first diffuses through the information network, and then play roles in the epidemic dynamics through the contact network. Thus, the effect of the awareness behavior on the transmission rate is indirect.

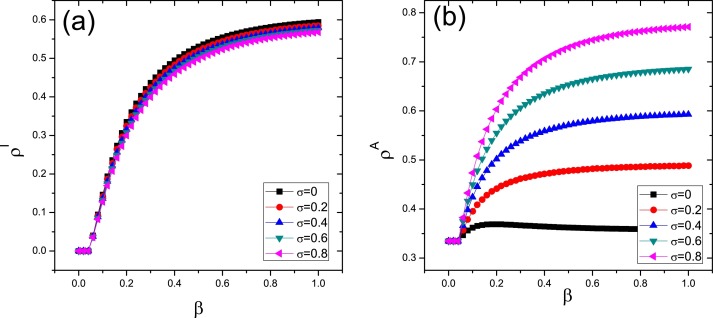
The density of infected individuals and aware nodes as functions of β for different values of parameter σ are also shown in Fig. 5 (a) and Fig. 5(b), respectively. One can see that, similar to Fig. 4, varying the value of σ has no effect on the epidemic threshold. However, differ to the above case, from Fig. 5(a) we find that the value of σ also has negligible effect on the density of infection, even in the extreme cases where infected unaware individuals remain unaware of its sickness ($\sigma =0$) or certainly become aware of it ($\sigma =1$). The result in Fig. 5 is in accord with the Fig. 3 in Ref. [24].

Fig. 5.

Fraction of infected (a) and aware (b) nodes as a function of the infectivity parameter β for different values of the parameter σ. Here $\lambda =0.15,$$\gamma =0,$$\delta =0.6,$$\mu =0.4$ and $\kappa =0.05$.

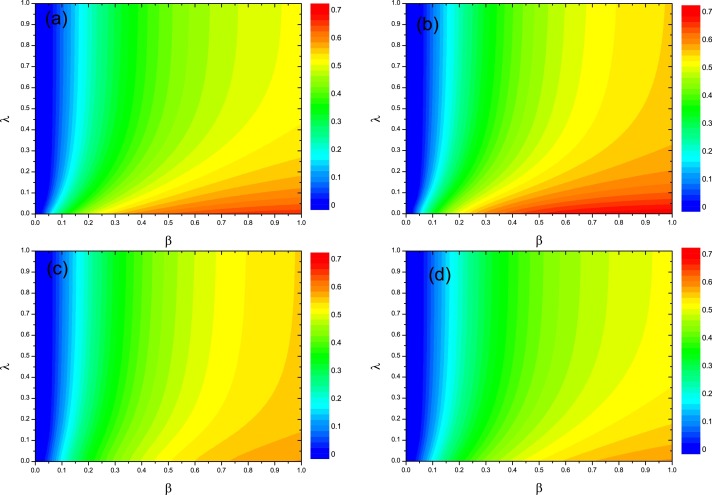
In order to systematically study the effects of κ and σ on the ρ^I, we further explore the full phase diagram ($\lambda -\beta$) in Fig. 6 . Overall, we can see that ρ^I is not influenced by λ when β is smaller than the epidemic threshold, since epidemic will die out by itself. Once β overpasses the epidemic threshold, ρ^I decreases with λ for different values of κ or σ. More specifically, by comparing Fig. 6(a) with Fig. 6(b) (or comparing Fig. 6(c) with Fig. 6(d)), we can see that ρ^I is not remarkably influenced by the value of σ. Likewise, by comparing the Fig. 6(a) with Fig. 6(d) (or comparing Fig. 6(b) with Fig. 6(c)), ρ^I decreases with κ, especially for the large value of β.

Fig. 6.

The fraction ρ^I of infected individuals in the stationary state. Full phase diagram $\lambda -\beta$ for the same multiplex described before. Where $\gamma =0,$$\lambda =0.15,$$\delta =0.6$ and $\mu =0.4$. (a): $\kappa =0,$$\sigma =1$; (b): $\kappa =0,$$\sigma =0.2$; (c): $\kappa =0.2,$$\sigma =0.2$; (d): $\kappa =0.2,$$\sigma =1$.

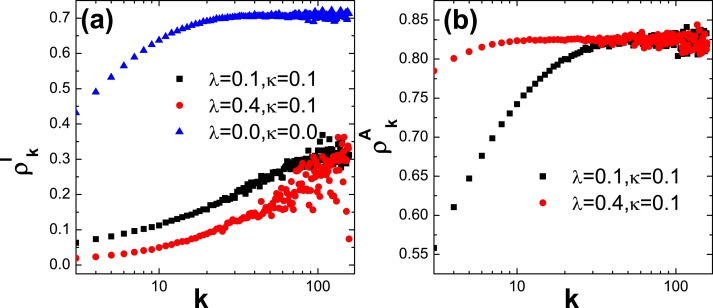
Finally, the density of infection for different degree k (labeled ${\rho }_k^I$) and the density of awareness for different degree k (labeled ${\rho }_k^A$) are plotted in Fig. 7 . From Fig. 7(a), one can observe that, when $\lambda =0.0$ and $\kappa =0.0$ (in this case, the awareness cannot diffuse in information network), the value of ${\rho }_k^I$ is very large and increases to a stable value finally. However, when λ is increased, the information can better diffuse in information network (see Fig. 7(b)), as a result, the value of ${\rho }_k^I$ is totally reduced. Moreover, Fig. 7(b) suggests that larger value of λ causes that the hub nodes in information networks have higher probability of being informed (i.e., larger value of ${\rho }_k^A$), which gives rise to the value of ${\rho }_k^I$ is not very large even for large degree k (see Fig. 7(a)).

Fig. 7.

For different values of λ and κ, (a) the density of infection ${\rho }_k^I,$ and (b) the density of awareness ${\rho }_k^A$ as the function of degree k. Here, $\beta =0.2,$$\gamma =0,$$\sigma =0.0,$$\delta =0.2$ and $\mu =0.4$.

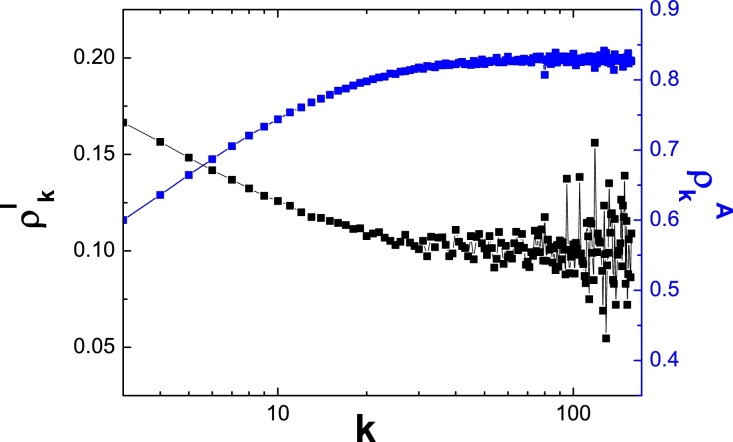
In Fig. 7, since the information network is constructed by adding 800 edges based on the contact network, thus, if a node is a hub node in one layer which means it is also a hub nodes in the other layer. In this situation, as shown in Fig. 8, even these hub nodes have more chances to be informed, they still have larger probability of being infected, thus, the effect of the information network cannot be well presented. In the next, we first construct a regular random network with degree $k=8$ for each node, which is constructed by random link rewiring from a regular network such that the degree of each node remains unchanged. In particular, a pair of edges, $A-B$ and $C-D,$ are randomly selected. They are then rewired to generate new link pairs $A-D$ and $B-C$. Multiple edges connecting the same pair of nodes are prohibited. The process continues for pE steps, where E is the number of edges in the network and p characterizes the randomness of the network. The information network is a configuration network with degree distribution $P\left(k\right)\sim k^{-2.5}$. Fig. 8 reports the values of ${\rho }_k^I$ and ${\rho }_k^A$ as a function of degree k (Note: here the node’s degree refers to the information network rather the contact network, since each node has the same degree in contact network). In this figure, we can clearly find that the nodes with larger degree in information network have larger value of ${\rho }_k^A,$ leading to smaller value of ${\rho }_k^I$. That is to say, if a node has more neighbors in information network, who can reduce the risk of infection in contact network.

Fig. 8.

The values of ${\rho }_k^I$ and ${\rho }_k^A$ as the function of degree k. Here the contact network is a regular random network with $k=8$ and switching probability $p=0.1,$ and the information network is the configuration network with $P\left(k\right)\sim k^{-2.5}$. The parameters: $\lambda =\kappa =\sigma =0.1,$$\delta =0.2,$$\gamma =0,$$\beta =0.3$ and $\mu =0.4$.

4. Conclusions and discussions

Recognizing that, on the one hand, outbreak of an epidemic through a physical-contact network can trigger the spreading of information awareness through other different channels, such as on-line social networks, mass media; on the other hand, an individual can not only be informed by other aware neighbors but also can become self-awareness once some friends in contact network are infected. By introducing the self-awareness mechanism for susceptible individuals, we have investigated interplay between the spreading of epidemic and the diffusion of awareness based on the framework of the multiplex networks. We mainly studied the two parameters κ and σ characterizing the self-awareness probability of susceptible individuals and infected individuals, respectively. Analysis based on the Markov chain approach as well as the extensive computations reveal that the density of infection can be reduced once the two parameters are increased, however, we found that the impact of self-awareness behavior for susceptible individuals on inhibiting the spreading of epidemic is significantly better than the self-awareness of the infected individuals, since self-awareness from susceptible individuals can directly reduce their probabilities of being infected. Meanwhile, we found that the self-awareness behavior cannot alter the epidemic threshold no matter of the local or global information, which are in stark contrast with the results obtained from the single-layer networks. In addition, our findings have shown that the introduction of information layer may cause some individuals has more chances to be informed, which can greatly reduce their risks of infection.

The challenges of studying the intricate interplay between social and biological contagions in human populations are generating interesting science. In this work, we consider the effects of the self-awareness behavior based on the multiplex networks on the density of infection and the epidemic threshold, our result implies that the conclusions obtained from single-layer networks may need to be re-examined and some new phenomena can emerge when the models are extended to multiplex networks.

Appendix A. Global information-based awareness

In recent work, Granell et al., considered the effect of the mass media on the epidemic process and awareness diffusion [24]. In the model, each individual becomes aware with probability m by assuming that they are informed by a broadcast or mass media. Thus, it can be regarded as a global information-based awareness. One questionable point is that the probability of being awareness m is irrelevant to the density of infection. As a result, even the epidemic is almost eliminated, individuals still have the fix probability of being aware. In reality, becoming awareness often means that individuals need to take some protective measures, such as, washing hands, wearing masks or reducing outgoings. These measures indicate certain inconveniences or some cost [27], [28]. Thus, a more realistic situation is that the probability of being awareness should be related to the density of infection. To mimic this case, here we assume the probability of awareness from global information is given as: mI(t) with I(t) is the density of infection at time t, which indicates that the probability of being awareness adaptively varies with the density of infection.

For this case, we only need to slightly change the local model described in Section 3.1. We only need to change γ_i(t) and θ_i(t) as follows:

$${\gamma }_i\left(t\right)=\prod _j(1-b_{ji}{p}_j^A\left(t\right)\lambda )(1-m{p}^I\left(t\right)),$$ (16)

$${\theta }_i\left(t\right)=\prod _j(1-b_{ji}{p}_j^A\left(t\right)\lambda )(1-a_{ji}{p}_j^I\left(t\right)\kappa )(1-m{p}^I\left(t\right))$$ (17)

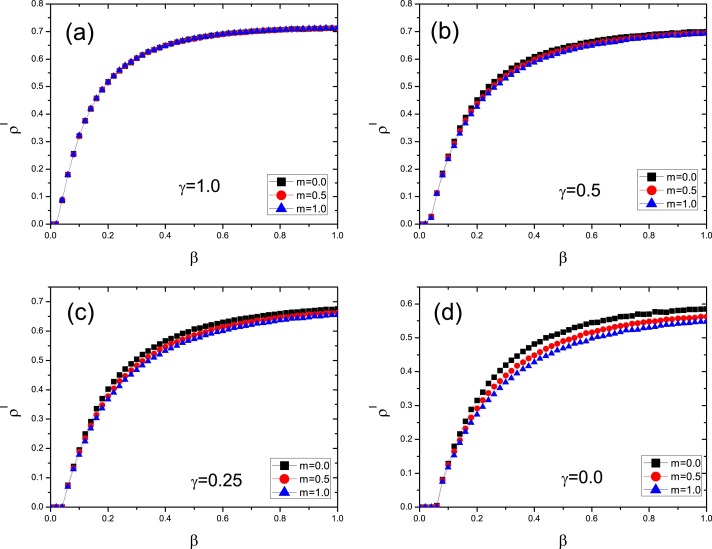
Similarly to the above analysis, we can get that the epidemic threshold is still determined by Eq. (15), i.e., the epidemic threshold is also independent of the value of m, which is different from the result in Ref. [24]. The result is verified by Fig. 9 for different values of γ.

Fig. 9.

The density of infected individuals as a function of β for different values of m. Here $\lambda =0.3,$$\sigma =0.5$$\delta =0.6,$$\mu =0.4$ and $\kappa =0.0$. (a): $\gamma =1$; (b): $\gamma =0.5$; (c): $\gamma =0.25$; (d): $\gamma =0$.