Skip to main content
PMC home page
Cerebral Cortex (New York, NY) logoLink to Cerebral Cortex (New York, NY)
. 2019 Sep 5;30(3):1357–1365. doi: 10.1093/cercor/bhz171

Topography Impacts Topology: Anatomically Central Areas Exhibit a “High-Level Connector” Profile in the Human Cortex

Jiahe Zhang 1, Lianne H Scholtens 2, Yongbin Wei 2, Martijn P van den Heuvel 2,3, Lorena Chanes 4,#,✉, Lisa Feldman Barrett 1,5,#,✉
PMCID: PMC7132940  PMID: 31504277

Abstract

Degree centrality is a widely used measure in complex networks. Within the brain, degree relates to other topological features, with high-degree nodes (i.e., hubs) exhibiting high betweenness centrality, participation coefficient, and within-module z-score. However, increasing evidence from neuroanatomical and predictive processing literature suggests that topological properties of a brain network may also be impacted by topography, that is, anatomical (spatial) distribution. More specifically, cortical limbic areas (agranular and dysgranular cortices), which occupy an anatomically central position, have been proposed to be topologically central and well suited to initiate predictions in the cerebral cortex. We estimated anatomical centrality and showed that it positively correlated with betweenness centrality, participation coefficient, and communicability, analogously to degree. In contrast to degree, however, anatomical centrality negatively correlated with within-module z-score. Our data suggest that degree centrality and anatomical centrality reflect distinct contributions to cortical organization. Whereas degree would be more related to the amount of information integration performed by an area, anatomical centrality would be more related to an area’s position in the predictive hierarchy. Highly anatomically central areas may function as “high-level connectors,” integrating already highly integrated information across modules. These results are consistent with a high-level, domain-general limbic workspace, integrated by highly anatomically central cortical areas.

Keywords: connectome, cortical type, degree centrality, limbic cortices, predictive processing

Introduction

Novel approaches to brain organization and function consider the brain as a complex network (Sporns 2011). Within these approaches, the topological properties of brain networks have been studied, highlighting the relevance of a set of densely connected areas, known as “rich club hubs” (van den Heuvel and Sporns 2011) or “core hubs” (Hagmann et al. 2008), which have been proposed to function as the backbone of neural integration (van den Heuvel et al. 2013). When these areas are damaged, modularity in the brain increases dramatically (Crossley et al. 2014), making the brain less able to integrate information across sensory modalities (de Reus and van den Heuvel 2014). These hubs have been defined based on their topological properties as those areas with the highest degree (number of connections) within the brain (e.g., Collin et al. 2017). Degree has been shown to relate to other topological centrality measures. More specifically, high-degree nodes exhibit high betweenness centrality (number of shortest paths) (van den Heuvel and Sporns 2011), high participation coefficient (distribution of connections across different modules), and high within-module z-score (number of connections within module) (van den Heuvel and Sporns 2013). Within the cerebral cortex, although rich club hubs have been extensively studied, the anatomical (spatial) distribution of cortical areas, that is, “topography,” has received less attention. However, classical (e.g., Sanides 1970) and more recent works (e.g., Barbas and Rempel-Clower 1997; Beul et al. 2015, 2017; Goulas et al. 2016, 2019; Huntenburg et al. 2017, 2018) highlight the relevance of topography and its relationship with cortical type (overall laminar structure) and cytoarchitecture for cortical organization.

The present study is motivated by an increasing body of literature (initially from the neuroanatomical domain and more recently from predictive processing perspectives) that has suggested a relationship between the anatomical (spatial) distribution of cortical areas and their organization as a network. This relationship is based on the systematic variation in the degree of laminar differentiation across cortical areas. Areas with a simple laminar elaboration (agranular and dysgranular tissue, known as cortical limbic areas) form a ring at the core of each hemisphere, defining its edge (edge = limbus). Gradients of laminar differentiation irradiate from this core of cortical limbic areas into isocortical areas (6 layers) with a progressively better developed layer IV, reaching the highest degree of laminar elaboration in primary exteroceptive sensory areas (reviewed in Sanides 1970; Mesulam 1985, 1998; Barbas 2015; Pandya et al. 2015; García-Cabezas et al. 2019). Thus, laminar elaboration gradients follow a specific spatial distribution across the cerebral cortex, with cortical limbic areas occupying an anatomically central position at the core of each hemisphere and laminar differentiation progressively increasing as one moves away from them into outer areas. As pointed out by Marshall and Magoun (1998), in mammalian brains, six-layered cortex mushroomed around limbic cortices as the phylogenetic scale moved forward. Some authors use the term “intermedius” or “mesopallium” to refer to agranular and dysgranular areas because they occupy an intermediate position between allocortical areas (hippocampal formation and olfactory areas) and six-layered cortex (see García-Cabezas et al. 2019 for a recent review).

In the present paper, we explore the relationship between topography (spatial distribution) and topology (network properties) in the human cerebral cortex, focusing on the relationship between a measure of anatomical centrality (based on the distance to the approximate center of the brain) and different topological measures (betweenness centrality, participation coefficient, within-module z-score, and communicability). We hypothesized that anatomical centrality is a contributor to topological centrality, distinct from degree. This hypothesis emerged from recent work within the predictive processing literature (Barrett and Simmons 2015; Chanes and Barrett 2016), based on a solid neuroanatomical model relating corticocortical connections to the laminar differentiation gradients mentioned above (Barbas and Rempel-Clower 1997; see also Barbas 2015). This work proposed that cortical limbic regions, which are anatomically central, are well suited to initiate predictive signals that are confirmed or corrected by incoming sensory information. Thus, cortical limbic areas occupy high levels in a cortical predictive hierarchy in which lower levels correspond to successively better-laminated areas (see also, “sensory-fugal” processing, Mesulam 1998, 2012). Moreover, fundamental work by Jones and Powell (1970) showed that the sequential connections from primary sensory to association to limbic areas reflect the flow of sensory representations that become progressively more integrated. Given their proposed high position in a predictive hierarchy and the highly integrated nature of the information they process, we expected topographically (anatomically, spatially) central areas to exhibit high topological centrality. A better understanding of topological properties across the entire cortex, taking into account anatomical features, may provide insights into the neural substrate of predictive processing and information integration (dimension reduction).

Materials and Methods

Connectome Reconstruction

Human connectome project (HCP) high-resolution diffusion-weighted data (Van Essen 2013; S500-release, n = 487, males and females mixed, age 22–35 years, imaging parameters: voxel size 1.25 mm isotropic, TR/TE 5520/89.5 ms, 270 diffusion directions with diffusion weighting 1000, 2000, or 3000 s/mm2) were used to reconstruct an average human connectome map. The diffusion-weighted images were eddy current and susceptibility distortion corrected, after which a voxel-wise diffusion profile was reconstructed using generalized q-sampling and whole-brain streamline tractography was performed (see de Reus and van den Heuvel 2014, for details on HCP connectome reconstruction).

Parcellation and Group Average Connectome Formation

For each subject, a high-resolution T1-weighted image (voxel size: 0.7 mm isotropic) was used for cortical segmentation and parcellation with FreeSurfer (Fischl et al. 2004; version 5.3.0). Each individual’s cortical surface (represented as vertex points) was parcellated into 219 nonoverlapping regions (111 left, 108 right hemisphere) using a subdivision of the Desikan-Killiany 68-region cortical FreeSurfer atlas (Cammoun et al. 2012), after which the parcellation was combined with the individual whole-brain streamline tractography to form a 219 × 219 connectivity matrix, representing each pair of cortical regions and their reconstructed white matter pathways. The strength of corticocortical connections was quantified as the reconstructed number of streamlines and computed as the number of streamlines touching both cortical regions. Finally, a weighted group-level averaged connectome was formed by including those connections consisting of at least 5 streamlines and observed in at least 60% of all individuals (van den Heuvel and Sporns 2011). We conducted all subsequent analyses with alternative thresholds (1 minimum streamline, 60% prevalence; 10 minimum streamlines, 60% prevalence; 5 minimum streamlines, 50% prevalence; 5 minimum streamlines, 70% prevalence; also consistency-thresholded connectome, same density as 5 minimum streamlines, 60% prevalence; Roberts et al. 2017) and found similar results (see Supplementary Texts S1−S5).

Graph Analysis

Analyzing the group average connectome map as a graph, describing cortical regions as nodes and their interconnections as edges, nodal degree was computed as the number of edges of a node (Fig. 1). We computed, for each node, the following measures related to network topology: 1) betweenness centrality, the number of all shortest paths in the cerebral cortex that go through a node (Freeman 1978); 2) participation coefficient, the distribution of a node’s edges among different modules (Guimerà and Amaral 2005); 3) within module z-score, a node’s connectedness to other nodes in its module (Guimerà and Amaral 2005); 4) communicability (de Reus and van den Heuvel 2014; Betzel et al. 2016), which takes into account all possible—not only the shortest—walks from a node to all other nodes in the cortex, reflecting the extent to which a region can compensate for the removal of another area (Betzel et al. 2016). Among these measures, participation coefficient and within module z-score were calculated based on 8 structural connectivity modules found by the Newman community detection algorithm (Newman 2006) (see Supplementary Fig. S1). All measures were computed using the Brain Connectivity Toolbox (Rubinov and Sporns 2010).

Figure 1.

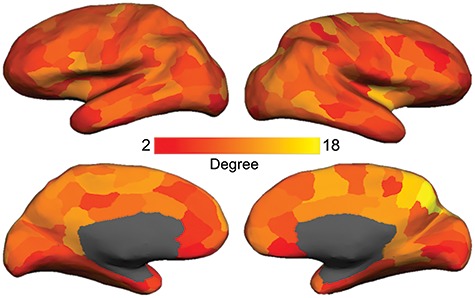
Figure 1

Open in a new tab

Degree map. Cortical parcellation scheme included 219 nodes and was based on a subdivision of the Desikan-Killiany 68 region cortical FreeSurfer atlas (Cammoun et al. 2012). Degree equals the number of connections of each node. We found high-degree nodes (e.g., the entire cingulate cortex, ventral prefrontal cortex, supplementary motor area, precuneus, anterior insula, and some lateral frontoparietal regions) to be consistent with previous literature (e.g., van den Heuvel and Sporns 2013).

Anatomical Centrality Estimation

To estimate anatomical centrality, we used the anterior commissure as a proxy for the center point of the brain, since it is approximately equidistant from the most distal points of the cerebrum on the x-, y-, and z-axes (Fig. 2A). First, we calculated the Euclidean distance between each vertex (MNI x, y, z) and the anterior commissure (MNI 0, 0, 0): 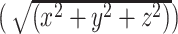Inline graphic. To facilitate regression analyses using 219-node-based graph theory measures, we averaged the distances for all vertices within a node to obtain a mean distance value for each of the 219 nodes. We then computed a normalized measure of anatomical centrality for each node defined as (maximal distance–node distance)/maximal distance, where maximal distance is the distance for the node with maximal distance from the anterior commissure, so that the anterior commissure would have an anatomical centrality of 1 and the most distant node would have an anatomical centrality of 0 (Fig. 2B). To verify that our anatomical centrality measure was related to cortical type, we compared anatomical centrality across nodes with a known distinct degree of laminar differentiation. Specifically, we compared three classes of nodes: 1) cortical limbic areas (cingulate cortex, posterior orbitofrontal cortex, ventral anterior insula, entorhinal cortex, parahippocampal gyrus, and temporal pole; defined following Mesulam 1985, noted as paralimbic areas), with a low degree of laminar elaboration; 2) primary exteroceptive sensory cortices (visual, auditory, and somatosensory; V1, A1, and S1), with a high degree of laminar elaboration; 3) association areas (rest of the areas), with an expected intermediate degree of laminar elaboration (Fig. 3A). We also correlated our measure of anatomical centrality with neuronal density and intracortical myelin, two measures also related to laminar elaboration (for a recent review, see García-Cabezas et al. 2019). For each node, we computed neuronal density as a weighted sum based on layer-specific neuron count and thickness data reported by von Economo and Koskinas (1925) (Scholtens et al. 2016):

graphic file with name M2.gif (1)

where l ranges from 1 to n, where n is the total number of identified cortical layers (see Supplementary Fig. S2A). Myelin content was assessed by T1w/T2w images (Glasser and Van Essen 2011; Glasser et al. 2016), and we computed one myelin estimate per node by averaging myelin estimates of all vertices within the node (see Supplementary Fig. S2B). As a related measure, we assessed whether mean BigBrain profile (or simply BigBrain profile, referring to the averaged profile within each node; Wei et al. 2018), reflecting a combination of cell size and neuronal density computed based on the high-resolution BigBrain histological volume (Amunts et al. 2013), is similarly related to anatomical centrality (see Supplementary Fig. S2C). Lastly, we correlated our anatomical centrality measure, as well as neuronal density, myelin and BigBrain profile, with the topological measures explored to assess whether they are related to topology.

Figure 2.

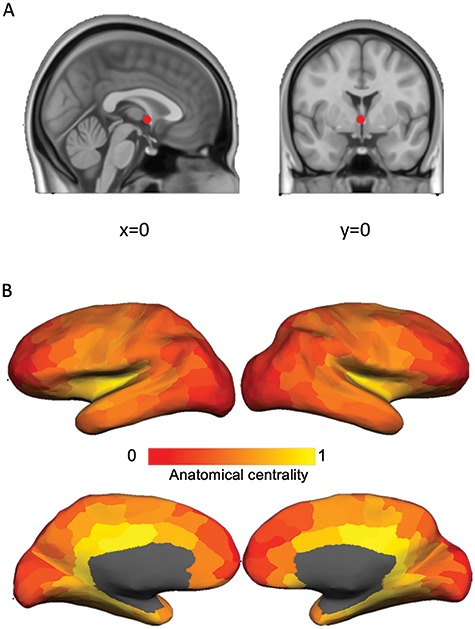
Figure 2

Open in a new tab

We created a measure of anatomical centrality to index the laminar differentiation gradient. (A) The anterior commissure (red dot), with MNI coordinates (0, 0, 0), was used as a proxy for the center point of the brain since it is approximately equidistant from the most distal points of the cerebrum. (B) Anatomical centrality map. Anatomical centrality for each node was computed as (maximal distance–node distance)/maximal distance, where maximal distance is the distance for the node with maximal distance from the anterior commissure. An anatomical centrality of 0 indicates minimal anatomical centrality (at maximal distance from the anterior commissure) and 1 indicates maximal centrality (at the anterior commissure).

Figure 3.

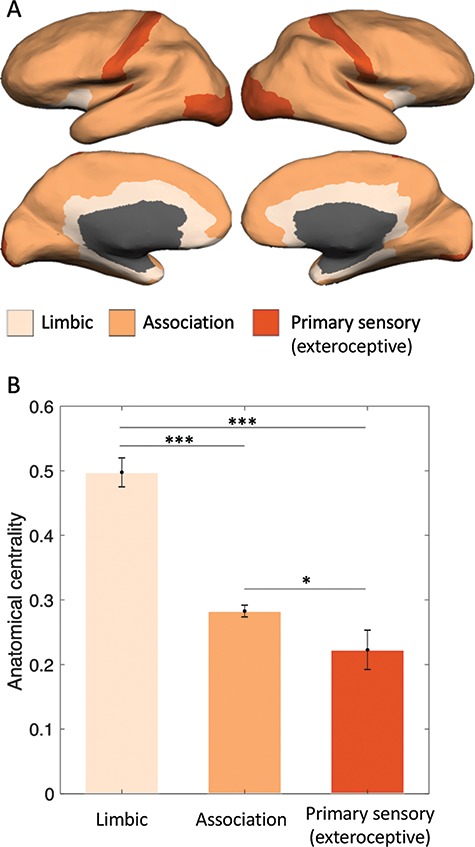
Figure 3

Open in a new tab

Anatomical centrality across groups of areas with different cortical types. (A) Limbic (agranular and dysgranular cortex), association, and primary exteroceptive sensory cortices (visual, auditory, and somatosensory; V1, A1, and S1). (B) Anatomical centrality of limbic, association, and primary exteroceptive sensory cortices followed the expected decreasing pattern, consistent with an increasing degree of laminar differentiation. *P < 0.05, ***P < 0.001, two-tailed t-test. Error bars indicate one standard error of the mean.

Statistical Analyses

A summary of the descriptive statistics can be found in Table 1. Residual plots indicated that the assumptions of normality, linearity, and homoscedasticity were all satisfied. We first ran a total of four hierarchical linear regression analyses, one for each network topology measure (betweenness centrality, participation coefficient, within-module z-score, and communicability). In each analysis, the measure was the dependent variable, while degree and anatomical centrality were introduced as independent variables. We computed the F statistic (F) and total variance (total R2) of the regression model, as well as the standardized regression coefficient (β) and t statistic (t) associated with each independent variable. We also computed additional variance explained by each independent variable when entered last in the model (∆R2). We obtained similar regression analysis results when removing outliers that were more than 1.5 interquartile ranges above or below the mean for all measures (Tukey 1977) (see Supplementary Text S6 for changes in descriptive statistics and regression tables). Lastly, we conducted a multivariate multiple regression analysis to assess the effects of degree and anatomical centrality on all four topology measures at the same time.

Table 1.

Summary of descriptive statistics for all variables involved in the study: degree, anatomical centrality, and four network topology measures (betweenness centrality, participation coefficient, within-module z-score, and communicability)

Measure Minimum Maximum Mean Std. dev.
Degree 2.00 18.00 7.74 2.44
Anatomical centrality 0.00 0.65 0.30 0.14
Betweenness centrality 0.00 3700.61 471.17 625.24
Participation coefficient 0.00 0.74 0.23 0.22
Within-module z-score −1.77 2.99 0.00 0.98
Communicability 0.00 0.01 0.01 0.00
Open in a new tab

Results

In agreement with previous reports (e.g., van den Heuvel and Sporns 2011, 2013), nodes with high degree were found in mid-to-posterior cingulate cortex, precuneus, retrosplenial cortex, insula, intraparietal sulcus, and lateral occipitotemporal cortex (Fig. 1). Anatomical centrality (Fig. 2) was related to the degree of laminar elaboration. Anatomical centrality of limbic, association, and primary sensory cortices (Fig. 3A) followed the expected decreasing pattern [limbic > association: t(193) = 7.92, P < 0.001; limbic > primary sensory: t(43) = 7.11, P < 0.001; association > primary sensory: t(196) = 2.24, P < 0.03; two-tailed t-test; Fig. 3B]. Anatomical centrality negatively correlated with neuronal density [r(217) = −0.33, P < 0.001], myelin [r(217) = −0.15, P < 0.030], and BigBrain profile [r(211) = −0.19, P < 0.004], showing that this measure is associated with other measures related to laminar elaboration. However, whereas degree and anatomical centrality significantly correlated with all topological measures, neuronal density, myelin, and BigBrain profile did not predict topology (see Supplementary Table S1).

Degree and anatomical centrality were not correlated [bivariate correlation; r(217) = −0.01, P < 0.91, two-tailed]. Both degree and anatomical centrality uniquely predicted network topological properties (Fig. 4). More specifically, as expected, higher degree was associated with higher centrality for all four measures [betweenness centrality: t(216) = 9.98, P < 0.001; participation coefficient: t(216) = 4.16, P < 0.001; within-module z-score: t(216) = 10.49, P < 0.001; communicability: t(216) = 15.77, P < 0.001; Table 2]. Higher anatomical centrality was also associated with higher betweenness centrality [t(216) = 3.60, P < 0.001], participation coefficient [t(216) = 2.52, P < 0.01], and communicability [t(216) = 8.34, P < 0.001] (Table 2). In contrast to degree, however, higher anatomical centrality was associated with lower within-module z-score [t(216) = −5.25, P < 0.001; Table 2].

Figure 4.

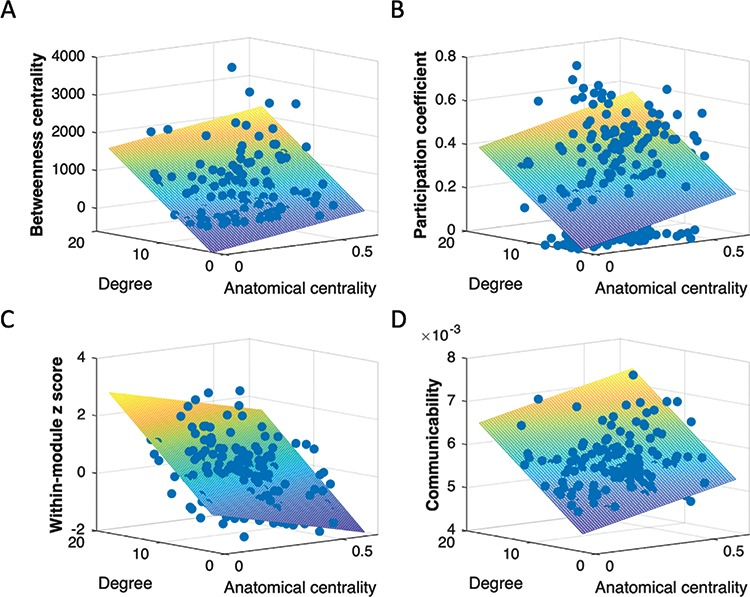
Figure 4

Open in a new tab

Degree and anatomical centrality separately contribute to network topological features: (A) betweenness centrality, (B) participation coefficient, (C) within-module z-score, and (D) communicability. Both degree and anatomical centrality were positively associated with betweenness centrality, participation coefficient, and communicability. Within-module z-score was positively associated with degree but negatively associated with anatomical centrality. Warmer color in mesh plot indicates higher value on topological measure and cooler color indicates lower value on topological measure.

Table 2.

Summary of hierarchical regression analyses. The table displays standardized regression coefficient (β), t statistic (t), and incremental variance (∆R2) associated with each independent variable, as well as the F statistic (F) and total variance (total R2) of the model. ∆R2 indicates additional variance explained by respective independent variables when entered last in the model

β t ∆R2 F Total R2
Betweenness centrality
Degree 0.55 9.98*** 0.30 56.03*** 0.34
Anatomical centrality 0.20 3.60*** 0.04
Participation coefficient
Degree 0.27 4.16*** 0.07 11.77*** 0.10
Anatomical centrality 0.16 2.52* 0.03
Within-module z-score
Degree 0.56 10.49*** 0.31 69.24*** 0.39
Anatomical centrality −0.28 −5.25*** 0.08
Communicability
Degree 0.68 15.77*** 0.47 158.12*** 0.59
Anatomical centrality 0.36 8.34*** 0.13
Open in a new tab

* P < 0.05.

** P < 0.01.

*** P < 0.001.

Together, participation coefficient (P) and within-module z-scores (z) may be used to classify nodes according to their patterns of connections within and across modules (Guimerà and Amaral 2005): low z/low P (peripheral nodes), low z/high P (nonhub connector nodes), high z/low P (provincial hubs), and high z/high P (connector hubs). Our results indicated dissociable impacts of degree and anatomical centrality on z/P ratio. Higher degree was associated with higher z/higher P and therefore resembled the connector hubs in their connectivity profile (van den Heuvel and Sporns 2013). In other words, a node with a higher degree tended to be more central within its own module and participate in more modules. In contrast, higher anatomical centrality was associated with lower z/higher P and therefore rather resembled the nonhub connector nodes in their connectivity profile. In other words, a node with higher anatomical centrality tended to be less central within its own module but participate in many modules. The differential contributions of degree and anatomical centrality would yield different connectivity profiles (illustrated in Fig. 5).

Figure 5.

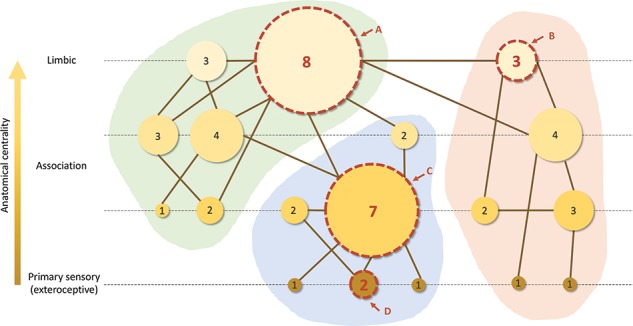
Figure 5

Open in a new tab

Schematic illustration of distinct contributions of degree (represented by node size; larger nodes have more connections; number inside the node indicates the exact number of connections) and anatomical centrality (represented by node color; lighter color indicates higher anatomical centrality) to topological centrality in a hypothetical graph. The graph is split into three modules (green, blue, and red background shading). Four specific nodes are highlighted with a dashed boundary to schematically reflect connectivity profiles resulting from the combination of both contributions (degree and anatomical centrality). Node A has high degree and high anatomical centrality, node B has low degree and high anatomical centrality, node C has high degree and low anatomical centrality, and node D has low degree and low anatomical centrality. In general, nodes with more anatomical centrality and degree are more topologically central in the network.

When both degree and anatomical centrality were entered into the model, they accounted for 34% of the variance in betweenness centrality, 10% of the variance in participation coefficient, 39% of the variance in within-module z-score, and 59% of the variance in communicability (Table 2). Lastly, a multivariate multiple regression analysis (two predictors: degree and anatomical centrality; four dependent variables: betweenness centrality, participation coefficient, within-module z-score, and communicability) showed that degree (F(4, 213) = 311.68, P < 0.001) and anatomical centrality (F(4, 213) = 21.20, P < 0.001) both significantly predicted all four topology measures, even when controlling for any potential correlation between those measures (size and significance of regression coefficients can be found in Supplementary Table S2).

Discussion

In the present paper, we explored the contributions of degree and anatomical centrality to topological properties of a human cortex network. Our initial interest on anatomical centrality emerged from classical observations that the structure of the cerebral cortex varies systematically along spatially successive areas (Sanides 1970; for reviews, see Barbas and Rempel-Clower 1997; Barbas 2015). We created a measure of anatomical centrality that may be considered a proxy for the laminar differentiation gradient, where cortical limbic areas (with a simple laminar structure) exhibit high anatomical centrality and association and primary sensory areas (with progressively better-laminated structure) exhibit progressively lower anatomical centrality. Our results reveal that anatomical centrality is a relevant feature for network topology, with topographically central (anatomically central) areas being also topologically central. These results stress the importance of taking into account anatomy as a relevant feature to understand the brain as a complex brain network (see also, e.g., Huntenburg et al. 2018). Our findings are also consistent with a variety of hypotheses about brain evolution. For example, evidence suggests that anatomically central cortical areas have expanded over primate evolution (e.g., Hill et al. 2010) in a way that has been linked to cognitive functioning (e.g., Finlay and Uchiyama 2015) and recent predictive processing perspectives highlight a key central role of highly anatomically central (limbic) areas in guiding cortical processing (Barrett and Simmons 2015; Chanes and Barrett 2016; Hutchinson and Barrett 2019). More anatomically central (limbic) cortical regions are responsible for maintaining allostasis and energy regulation in the core systems of the body (e.g., Kleckner et al. 2017), considered to be a main driver of brain evolution in general (e.g., Niven and Laughlin 2008) and primate brain evolution in particular (e.g., Pontzer 2015). And the link between anatomical centrality and cortical type is also consistent with the dual origin hypothesis of brain evolution, which proposes that each hemisphere of the cerebral cortex developed in concentric circles of progressively better-laminated tissue that folded in a mushroom-like shape, such that the degree of laminar differentiation is seen to increase radially (Sanides 1970; Pandya et al. 2015; García-Cabezas et al. 2019).

Our data suggest that degree and anatomical centrality reflect distinct contributions to cortical organization, as the two measures were not correlated among themselves and they explained unique variance in all the topological features explored. Degree and anatomical centrality both positively predicted betweenness centrality, participation coefficient, and communicability. However, while degree was positively correlated with within-module z-score, anatomical centrality was negatively correlated with this measure. In other words, as degree increased, areas increasingly showed a connectivity profile that resembled that of connector hubs (i.e., dense connections both intermodule and intramodule; high z/high P); on the other hand, as anatomical centrality increased, areas increasingly showed high intermodule but low intramodule connectivity (low z/high P). This suggests that areas with high anatomical centrality (limbic) may be particularly well suited to function as “high-level connectors,” integrating already highly integrated (low dimensional) information across domains (modules). This remarkable difference in connectivity profiles is consistent with tract-tracing studies in nonhuman primates, showing that limbic regions, in particular the cingulate cortex and anterior insula, have more distributed cortical connections (i.e., “participation” in different modules) compared with better-laminated areas such as the somatosensory, motor, and premotor cortices, which have more restricted connections with local and adjacent areas (Morecraft et al. 2004, 2012, 2015). This may help to explain why damage to limbic areas leads to more fundamental disturbances in motility and motivation than damage to more peripheral (less anatomically central) regions (Giaccio 2006; see also Mesulam 1998). While degree may be more closely related to the amount of information integrated (number of areas that a given node is integrating information from), anatomical centrality may be more closely related to the position that a node occupies in the cortical predictive hierarchy. Both the amount of information integration and the position in the hierarchy lead to different connectivity profiles (Fig. 5) and contribute to topological centrality, which suggests that a more nuanced characterization of rich club (high degree) hubs in terms of anatomical centrality may be relevant in order to further understand cortical organization and identify potential functional differences among them. For example, anatomically peripheral rich club hubs, associated with high z and medium-to-high P (e.g., Fig. 5, node C), would resemble connector hubs (van den Heuvel and Sporns 2013), integrating large amounts of low-level information both within and across modules, whereas more anatomically central rich club hubs (e.g., Fig. 5, node A), involving lower z and higher P, would exhibit a connectivity profile closer to nonhub connector nodes and integrate higher-level information across modules.

Our study presents some limitations, and our findings may be extended in several ways. Our analyses were anchored on a 219-node parcellation scheme. Some parcels within this scheme included regions with different degrees of laminar differentiation (e.g., orbitofrontal cortex). Future studies may examine more fine-grained parcels that are more homogeneous in cortical type (e.g., the orbitofrontal cortex could be further divided into its posterior and anterior portions, as the degree of laminar differentiation increases from posterior to anterior; Beck 1949). Moreover, as mentioned above, our measure of anatomical centrality, based on distance to the center of the brain, is one proxy for the spatial distribution of the laminar differentiation gradient, although it does not capture the full complexity of such distribution (e.g., we observed an intermediate anatomical centrality for primary somatosensory cortex, which is known to have a high degree of laminar elaboration). Other measures, such as neuronal density or intracortical myelin, have also been related to the degree of laminar differentiation, although they also present important limitations in capturing cortical type (for a detailed discussion, see García-Cabezas et al. 2019). The neuronal density map (see Supplementary Fig. S2A) displays extremely high values in the primary visual cortex and lacks differentiation between lateral frontal cortex and cortical limbic areas, for example. In the myelin map using T1w/T2w images (see Supplementary Fig. S2B), some of the exceptions reported by Glasser and van Essen (2011) can be observed, notably a relatively high myelin content in known agranular/dysgranular areas, such as the posterior cingulate/retrosplenial cortex or the posterior orbitofrontal cortex. Moreover, unlike anatomical centrality, these two measures were not predictive of topology (see Supplementary Table S1). Whether this was a result of the limited ability of the measures themselves (neuronal density and myelin) to capture cortical type or rather reflected additional relevant contributions to topology captured by our anatomical centrality measure, other than cortical type, remains to be explored in the future. Lastly, future studies may perform similar analyses using tract-tracing data from macaques, which may contribute to assess the impact of technical limitations of diffusion imaging such as ambiguous fiber crossing, lack of directionality, and lack of single tract precision (Shen et al. 2019).

The topological features exhibited by highly anatomically central areas are consistent with their role as a high-level, domain-general limbic workspace (Chanes and Barrett 2016), which would initiate predictions that cascade to progressively more specialized, better-laminated areas (Barrett and Simmons 2015; Chanes and Barrett 2016; Barrett 2017). Taken together, our findings enhance our understanding of the neural bases for how the brain can function predictively and implement information integration across the cortex, and they provide a relevant new feature to further characterize nodes, including extensively studied rich club hubs.

Funding

MPvdH was funded by a Vidi (NWO-VIDI 452-16-015) and ALWopen (ALWOP.179) grant from the Netherlands Organization for Scientific Research and a Fellowship by MQ. LC was funded by the Ministry of Science, Innovation and Universities of Spain (PSI2017-88416-R) and the Government of Catalonia (2017 SGR 1612). LFB was funded by the National Institute of Mental Health (R01 MH113234, R01 MH109464) and the National Cancer Institute (U01 CA193632).

Notes

Conflict of Interest: None declared.

Supplementary Material

Supplementary_Material_Final_bhz171
Click here for additional data file. (10.4MB, pdf)

References

  1. Amunts K, Lepage C, Borgeat L, Mohlberg H, Dickscheid T, Rousseau M É, Bludau S, Bazin P-L, Lewis L B, Oros-Peusquens A-M, et al. . 2013. BigBrain: an ultrahigh-resolution 3D human brain model. Science. 340(6139):1472–1475. doi: 10.1126/science.1235381. [DOI] [PubMed] [Google Scholar]
  2. Barbas H. 2015. General cortical and special prefrontal connections: principles from structure to function. Annu Rev Neurosci. doi: 10.1146/annurev-neuro-071714-033936. [DOI] [PubMed] [Google Scholar]
  3. Barbas H, Rempel-Clower N. 1997. Cortical structure predicts the pattern of corticocortical connections. Cereb Cortex. 7(7):635–646. [DOI] [PubMed] [Google Scholar]
  4. Barrett LF. 2017. How emotions are made. New York (NY): Houghton Mifflin Harcourt. [Google Scholar]
  5. Barrett LF, Simmons WK. 2015. Interoceptive predictions in the brain. Nat Rev Neurosci. 16(7):419–429. doi: 10.1038/nrn3950. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Beck E. 1949. A cytoarchitectural investigation into the boundaries of cortical areas 13 and 14 in the human brain. J Anat. 83(Pt 2):147–157. [PubMed] [Google Scholar]
  7. Betzel RF, Gu S, Medaglia JD, Pasqualetti F, Bassett DS. 2016. Optimally controlling the human connectome: the role of network topology. Sci Rep. 6(30770). doi: 10.1038/srep30770. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Beul SF, Barbas H, Hilgetag CC. 2017. A predictive structural model of the primate connectome. Sci Rep. 7(43176). doi: 10.1038/srep43176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Beul SF, Grant S, Hilgetag CC. 2015. A predictive model of the cat cortical connectome based on cytoarchitecture and distance. Brain Struct Funct. 220(6):3167–3184. doi: 10.1007/s00429-014-0849-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cammoun L, Gigandet X, Meskaldji D, Thiran JP, Sporns O, Do KQ, Maeder P, Meuli R, Hagmann P. 2012. Mapping the human connectome at multiple scales with diffusion spectrum MRI. J Neurosci Methods. 203(2): 386–397. doi: 10.1016/j.jneumeth.2011.09.031. [DOI] [PubMed] [Google Scholar]
  11. Chanes L and Barrett LF. 2016. Redefining the role of limbic areas in cortical processing. Trends Cogn Sci. 20(2):96–106. doi: 10.1016/j.tics.2015.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Collin G, Scholtens LH, Kahn RS, Hillegers MHJ, Heuvel MP.. 2017. Affected anatomical rich club and structural–functional coupling in young offspring of schizophrenia and bipolar disorder patients. Biol Psych. 82(10):746–755. doi: 10.1016/j.biopsych.2017.06.013. [DOI] [PubMed] [Google Scholar]
  13. Crossley NA, Mechelli A, Scott J, Carletti F, Fox PT, Mcguire P, Bullmore ET. 2014. The hubs of the human connectome are generally implicated in the anatomy of brain disorders. Brain. 137(8):2382–2395. doi: 10.1093/brain/awu132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Reus M, Heuvel M. 2014. Simulated rich club lesioning in brain networks: a scaffold for communication and integration? Front Hum Neurosci. 8:647. doi: 10.3389/fnhum.2014.00647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Finlay BL and Uchiyama R. 2015. Developmental mechanisms channeling cortical evolution. Trends Neurosci. 38(2):69–76. doi: 10.1016/j.tins.2014.11.004. [DOI] [PubMed] [Google Scholar]
  16. Fischl B, Van Der Kouwe A, Destrieux C, Halgren E, Ségonne F, Salat DH, Busa E, Seidman LJ, Goldstein J, Kennedy D, et al. . 2004. Automatically parcellating the human cerebral cortex. Cereb Cortex. 14(1):11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
  17. Freeman LC. 1978. Centrality in social networks conceptual clarification. Soc Networks. 1(3):215–239. doi: 10.1016/0378-8733(78)90021-7. [DOI] [Google Scholar]
  18. García-Cabezas MÁ, Zikopoulos B, Barbas H. 2019. The structural model: a theory linking connections, plasticity, pathology, development and evolution of the cerebral cortex. Brain Struct Funct. 224(3):985–1008. doi: 10.1007/s00429-019-01841-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Giaccio RG. 2006. The dual origin hypothesis: an evolutionary brain-behavior framework for analyzing psychiatric disorders. Neurosci Biobehav Rev. 30(4):526–550. doi: 10.1016/j.neubiorev.2005.04.021. [DOI] [PubMed] [Google Scholar]
  20. Glasser MF and Van Essen DC. 2011. Mapping human cortical areas in vivo based on myelin content as revealed by T1- and T2-weighted MRI. J Neurosci. 31(32):11597–11616. doi: 10.1523/JNEUROSCI.2180-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M, et al. . 2016. A multi-modal parcellation of human cerebral cortex. Nature. doi: 10.1038/nature18933. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Goulas A, Majka P, Rosa MGP, Hilgetag CC. 2019. A blueprint of mammalian cortical connectomes. 17(3):e2005346. PLoS Biol. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Goulas A, Werner RR, Beul SF, Saering D, Heuvel M, Triarhou LC, Hilgetag CC.. 2016. Cytoarchitectonic similarity is a wiring principle of the human connectome. BioRxiv. 068254. doi: 10.1101/068254. [DOI] [Google Scholar]
  24. Guimerà R and Amaral LAN.. 2005. Functional cartography of complex metabolic networks. Nature. 433(7028):895–900. doi: 10.1038/nature03288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Van Wedeen J, Sporns O.. 2008. Mapping the structural core of human cerebral cortex. PLoS Biol. 6(7):1479–1493. doi: 10.1371/journal.pbio.0060159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hill J, Inder T, Neil J, Dierker D, Harwell J, Van Essen D. 2010. Similar patterns of cortical expansion during human development and evolution. Proc Natl Acad Sci. 107(29):13135–13140. doi: 10.1073/pnas.1001229107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Huntenburg JM, Bazin PL, Goulas A, Tardif CL, Villringer A, Margulies DS. 2017. A systematic relationship between functional connectivity and intracortical myelin in the human cerebral cortex. Cereb Cortex. 27(2):981–997. doi: 10.1093/cercor/bhx030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Huntenburg JM, Bazin PL, Margulies DS.. 2018. Large-scale gradients in human cortical organization. Trends Cogn Sci. 22(1):21–31. doi: 10.1016/j.tics.2017.11.002. [DOI] [PubMed] [Google Scholar]
  29. Hutchinson JB and Barrett LF.. 2019. The power of predictions: an emerging paradigm for psychological research. Curr Dir Psychol Sci. 28(3):280–291. doi: 10.1177/0963721419831992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Jones EG, Powell TP. 1970. An anatomical study of converging sensory pathways within the cerebral cortex of the monkey. Brain. 93(4):793–820. [DOI] [PubMed] [Google Scholar]
  31. Kleckner IR, Zhang J, Touroutoglou A, Chanes L, Xia C, Simmons WK, Quigley KS, Dickerson BC, Barrett LF.. 2017. Evidence for a large-scale brain system supporting allostasis and interoception in humans. Nat Hum Behav. 1: 69. doi: 10.1038/s41562-017-0069. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Marshall LH, Magoun HW. 1998. Discoveries in the human brain: neuroscience prehistory, brain structure, and function. Totowa (NJ): Humana Press. [Google Scholar]
  33. Mesulam MM. 1985. Patterns in behavioral neuroanatomy. Association areas, the limbic system, and hemispheric specialization. In: Mesulam MM, editor. Principles of Behavioral Neurology. 1–70. New York (NY): Oxford University Press. [Google Scholar]
  34. Mesulam MM. 1998. From sensation to cognition. Brain. 121(Pt 6):1013–1052. http://www.ncbi.nlm.nih.gov/pubmed/9648540. [DOI] [PubMed] [Google Scholar]
  35. Mesulam MM. 2012. The evolving landscape of human cortical connectivity: facts and inferences. NeuroImage. 62(4):2182–2189. doi: 10.1016/j.neuroimage.2011.12.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Morecraft RJ, Cipolloni PB, Stilwell-Morecraft KS, Gedney MT, Pandya DN.. 2004. Cytoarchitecture and cortical connections of the posterior cingulate and adjacent somatosensory fields in the rhesus monkey. J Comp Neurol. 469(1):37–69. doi: 10.1002/cne.10980. [DOI] [PubMed] [Google Scholar]
  37. Morecraft RJ, Stilwell-Morecraft KS, Cipolloni PB, Ge J, McNeal DW, Pandya DN. 2012. Cytoarchitecture and cortical connections of the anterior cingulate and adjacent somatomotor fields in the rhesus monkey. Brain Res Bull. 87(4–5):457–497. doi: 10.1016/j.brainresbull.2011.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Morecraft RJ, Stilwell-Morecraft KS, Ge J, Cipolloni PB, Pandya DN.. 2015. Cytoarchitecture and cortical connections of the anterior insula and adjacent frontal motor fields in the rhesus monkey. Brain Res Bull. 119(Pt A):52–72. doi: 10.1016/j.brainresbull.2015.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Newman MEJ. 2006. Modularity and community structure in networks. Proc Natl Acad Sci. 103(23):8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Niven JE and Laughlin SB.. 2008. Energy limitation as a selective pressure on the evolution of sensory systems. J Exp Biol. 211(Pt 11):1792–1804. doi: 10.1242/jeb.017574. [DOI] [PubMed] [Google Scholar]
  41. Pandya DN, Petrides M, Seltzer B, Cipolloni PB. 2015. Cerebral cortex: architecture, connections, and the dual origin concept. New York (NY): Oxford University Press. [Google Scholar]
  42. Pontzer H. 2015. Energy expenditure in humans and other primates: a new synthesis. Annual Review of Anthropology. 44:169–187. doi: 10.1146/annurev-anthro-102214-013925. [DOI]
  43. Roberts JA, Perry A, Roberts G, Mitchell PB, Breakspear M.. 2017. Consistency-based thresholding of the human connectome. NeuroImage. 145(Pt A):118–129. doi: 10.1016/j.neuroimage.2016.09.053. [DOI] [PubMed] [Google Scholar]
  44. Rubinov M and Sporns O.. 2010. Complex network measures of brain connectivity: uses and interpretations. NeuroImage. 52(3):1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
  45. Sanides F. 1970. Functional architecture of motor and sensory cortices in primates in the light of a new concept of neocortex evolution In: Noback CR, Montagna W, editors. The primate brain: advances in primatology. , pp. 137–208. New York: Appleton-Century Crofts Education Division/Meredith Corporation. [Google Scholar]
  46. Scholtens LH, Reus MA, Lange SC, Schmidt R and Heuvel MP.. 2016. An MRI Von Economo – Koskinas atlas. NeuroImage. 170:249–256. doi: 10.1016/j.neuroimage.2016.12.069. [DOI] [PubMed] [Google Scholar]
  47. Shen K, Goulas A, Grayson DS, Eusebio J, Gati JS, Menon RS, AR McIntosh, Everling S.. 2019. Exploring the limits of network topology estimation using diffusion-based tractography and tracer studies in the macaque cortex. NeuroImage. doi: 10.1016/j.neuroimage.2019.02.018. [DOI] [PubMed] [Google Scholar]
  48. Sporns O. 2011. The human connectome: a complex network. Ann N Y Acad Sci. 1224:109–125. doi: 10.1111/j.1749-6632.2010.05888.x. [DOI] [PubMed] [Google Scholar]
  49. Tukey JW. 1977. Box-and-Whisker Plots. In Exploratory data analysis. pp. 39–43. Reading (MA): Addison_Wesley. [Google Scholar]
  50. Heuvel MP and Sporns O.. 2011. Rich-club organization of the human connectome. J Neurosci. 31(44):15775–15786. doi: 10.1523/JNEUROSCI.3539-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Heuvel MP, Kahn RS, Goni J, Sporns O.. 2013. High-cost, high-capacity backbone for global brain communication. Proc Natl Acad Sci. 109(28):11372–11377. doi: 10.1073/pnas.1203593109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Heuvel MP and Sporns O. 2013. An anatomical substrate for integration among functional networks in human cortex. J Neurosci Off J Soc Neurosci. 33(36):14489–14500. doi: 10.1523/JNEUROSCI.2128-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Van Essen DC. 2013. Cartography and connectomes. Neuron. doi: 10.1016/j.neuron.2013.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. von Economo C, Koskinas G. 1925. Die cytoarchitektonik der hirnrinde des erwachsenen menschen. Berlin: Springer. [Google Scholar]
  55. Wei Y, Scholtens LH, Turk E, van den Heuvel MP.. 2018. Multiscale examination of cytoarchitectonic similarity and human brain connectivity. Network Neurosci. 3(1):124–137. doi: 10.1162/netn_a_00057. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary_Material_Final_bhz171
Click here for additional data file. (10.4MB, pdf)

Articles from Cerebral Cortex (New York, NY) are provided here courtesy of Oxford University Press

RESOURCES