Short abstract
Machine learning has been used successfully to improve the accuracy of computer-aided diagnosis systems. This paper experimentally assesses the performance of models derived by machine learning techniques by using relevant features chosen by various feature-selection methods. Four commonly used heart disease datasets have been evaluated using principal component analysis, Chi squared testing, ReliefF and symmetrical uncertainty to create distinctive feature sets. Then, a variety of classification algorithms have been used to create models that are then compared to seek the optimal features combinations, to improve the correct prediction of heart conditions. We found the benefits of using feature selection vary depending on the machine learning technique used for the heart datasets we consider. However, the best model we created used a combination of Chi-squared feature selection with the BayesNet algorithm and achieved an accuracy of 85.00% on the considered datasets.
Keywords: Classification, data analysis, feature selection, heart disease, machine learning, prediction
Introduction
In the 21st century, data science has become an important part of the healthcare industry, appreciated by healthcare professionals for its ability to provide useable information and insights quickly. Typically, healthcare data come in the form of electronic medical records collected from patients. A common use of data in healthcare is for building decision support systems, which use patient data along with domain knowledge and artificial intelligence. These can provide information to aid healthcare professionals in their work as well as detect critical situations or errors and alert the healthcare professionals accordingly.1,2
Among the methods that are often built into clinical decision support systems are diagnostic models based on machine learning (ML) that can predict the presence of a disease in a patient based on a set of risk features.3 In this paper we will be building a predictive model for cardiovascular heart disease. According to the World Health Organization4 17.9 million people die each year from heart disease, which accounts for around 31% of deaths worldwide, making it the leading cause of death.
Although ML models have been widely studied5–8 and found to be greatly successful, heart-disease prediction is a complicated problem and there are still many improvements to be made and methods to explore. This kind of problem falls under the supervised learning task of classification within ML. We use classification algorithms to learn the relationship between a set of features and the target class.9 In our case we have heart-disease risk features such as age, cholesterol and the results of other medical tests and our class is the presence of heart disease for that patient.
This research focuses on the filter-based feature selection methods for data pre-processing before building the predictive models by classification algorithms. We use principal component analysis (PCA),10 Chi squared, ReliefF and symmetric uncertainty filters11–13 to find and use the most relevant risk features. These features are then passed into the classification algorithms to produce a range of models to predict heart conditions. These models are then compared for accuracy.
The aim of this research is to identify the combination of filter and classification methods that work well together for enhanced heart-disease prediction. To achieve this aim, we follow an experimental methodology in which extensive experimentations using filter and classification methods are conducted on real datasets related to heart disease published at the University of California Irvine data repository (UCI).14 The experiment aims to answer two research questions: will using a combination of filter and classification methods increase the performance of heart-disease prediction models using the heart-disease dataset considered, and what are the most influential features for the heart-disease dataset?
The experiment takes some inspiration from previous experimental literature as we have used some of the ML algorithms that have had the most success when building heart-disease prediction models. Our approach differs in the feature selection methods that are used, as well as in using a combined heart-disease dataset built from four commonly used datasets. We build several predictive models and compare them using specific performance metrics including accuracy, precision and recall, identifying the most effective ones that could be used for heart-disease prediction and could also be useful to the medical community. This research will be of interest to anyone working in medical diagnosis using ML technology.
This paper is organised as follows: we first survey common methods in ML related to heart-disease prediction, then discuss the research approach including the data and methods used. Next we analyse the results and finally present conclusions.
Literature review
Gokulnat and Shantharajah (2018) used a genetic algorithm to select features from the Cleveland dataset. This approach gave the authors a subset of seven features to which they applied four ML methods: SVM, multilayer perceptron, J48 and K Nearest Neighbours (KNN) to build models for heart-disease prediction.15 They evaluated their models using 10-fold cross-validation and compared the results to models built on the original feature set as well as feature sets selected using some commonly used feature selection techniques. The genetic algorithm when used with Support Vector Machine (SVM) achieved the highest accuracy of 88.34% compared to 83.70% accuracy with the original dataset.
Weng et al. (2017) proposed ML as an alternative to the established heart-disease risk assessment methods.16 The authors took a dataset derived from the UK’s Clinical Practice Research Datalink in RStudio and tested four simple classification algorithms: logistic regression, random forest, gradient boosting machines and neural networks as well as the American Heart Association/American College of Cardiology (ACC/AHA) baseline model. The data were split, 75% into a training set and 25% into a validation set. They found that all ML methods performed better than the ACC/AHA model, the neural network algorithm achieved the best result with an accuracy of 76.4% followed by gradient boosting and logistic regression with accuracies of 76.1% and 76.0% respectively. Random forest achieved an accuracy of 74.5%, whereas the ACC/AHA model achieved an accuracy of only 72.8%.
Khateeb and Usman (2017) tested four different classification techniques on the Cleveland heart-disease dataset: naive Bayes, KNN, decision tree and bagging.17 Rather than using a feature selection algorithm to pick the most statistically significant features they chose features based on domain knowledge. They found that this approach increased the accuracy of their models made with naive Bayes and KNN but decreased the accuracy of their decision tree and bagging models. Their most accurate model achieved an accuracy of 79.2% and was built by resampling the original dataset and the KNN ML algorithm.
Kavitha and Kannan (2016) created a framework for heart-disease classification that included feature extraction using PCA.18 The authors state the benefits of reducing the data dimensionality as increasing the prediction accuracy of the classifier and reducing the computational cost of the prediction. This can be achieved either by feature extraction methods, which create a new set of features that are somehow derived from the original features, or by feature selection, which takes a subset of the most relevant features from the dataset.
Badaruddoza et al. (2015) applied PCA to a dataset of commonly known heart-disease risk features on a minority population of Punjabi Indians across three generations.19 The dataset included features such as weight, waist circumference, body mass index, blood pressure and pulse rate. The authors noted that many of these features are inter-correlated and prescribed PCA to extract independent factors. Interestingly they found that across different generations and genders, PCA would produce a different number of component features and these component features would be loaded with different combinations of the original features. Generally, the first component that accounted for between 42–52% of the variation was the same across generations and genders and was mainly made up of obesity features such as body mass index and waist circumference. However, the second component that accounted for between 13–22% of the variation was different across genders and generations.
Jabbar et al. (2015) used feature selection with a Chi-squared feature evaluator in conjunction with the random forest ML algorithm to build a model for heart-disease prediction on the statlog heart-disease dataset.20 This dataset is made up of the same features as the Cleveland dataset and contains 270 instances. The authors used Chi squared with backwards elimination, whereby they rank the features by the Chi-squared test then one by one remove the lowest-ranked feature and build and test a model at each step until the accuracy of the model stops increasing. The best model they found achieved an accuracy of 83.7%.
Ziasabounchi and Askerzade (2014) employed PCA to extract features from the Cleveland Clinic Foundation heart-disease dataset before running two separate clustering methods: K-means and fuzzy C-means, for the purpose of diagnosing heart-disease patients.21 The authors compared the results of the clustering methods on the original dataset as well as a dataset of the PCA extracted features. They found that on the original dataset, K-means achieved an accuracy of 81.0% and fuzzy C-means achieved an accuracy of 80.0%; however, on the PCA-applied dataset accuracy improved to 87.0% with K-means and 82.0% with fuzzy C-means.
Santhanam and Ephzibah (2013) used PCA in conjunction with feature selection to extract PCA datasets from a variety of different feature sets, again based on the Cleveland heart-disease dataset.22 In total they obtained six different datasets including the original set with 14 features. The authors then applied regression and a feed-forward neural network algorithm to each dataset to create a prediction model. They found that one of the PCA datasets when used with the feed-forward neural network achieved an accuracy of 95.2%.
Rouhani and Abdoli (2011) compared different feature selection methods for diagnosing valvular heart disease based on phonocardiography, a diagnostic tool that the authors described as having a ‘high potential for detecting various heart diseases’ (p. 1).23 They used four different feature selection methods to reduce their set of 32 raw features: PCA, which extracted four significant features, gaussian discriminant analysis (GDA), a genetic algorithm and a genetic programming algorithm. After extracting a set of features for each method they tested the results using three different classification algorithms: a multilayer perceptron (MLP) and radial basis function (RBF) (which are types of neural networks) and support vector machine; however, they found that PCA performed very poorly achieving a maximum accuracy of only 65.54% compared to the other methods, which achieved high predictive accuracy. The authors concluded that the linear nature of PCA meant that it was a bad fit when using phonocardiography to diagnose heart disease.
Research approach
The research methodology followed in this research is experimental, as shown in Figure 1. The four heart-disease datasets discussed later are integrated into one training dataset. Then, different filter and feature extraction methods (Chi squared, ReliefF, symmetrical uncertainty (SU), PCA) discussed in detail in this section are applied to the training dataset. This results in four distinct feature sets that may overlap on the selected features. Each of these feature sets along with the original dataset are fed into eight different classification algorithms. The reason for using eight algorithms is to ensure that models are derived using different learning schemes. For example, JRip (RIPPER) produces a rule-based classifier and uses a global optimisation procedure to prune and evaluate the rules, and BayesNet is a probabilistic classifier that employs the Bayes theorem to predict the class labels. The classification algorithms used are discussed in detail later in this section.
Figure 1.
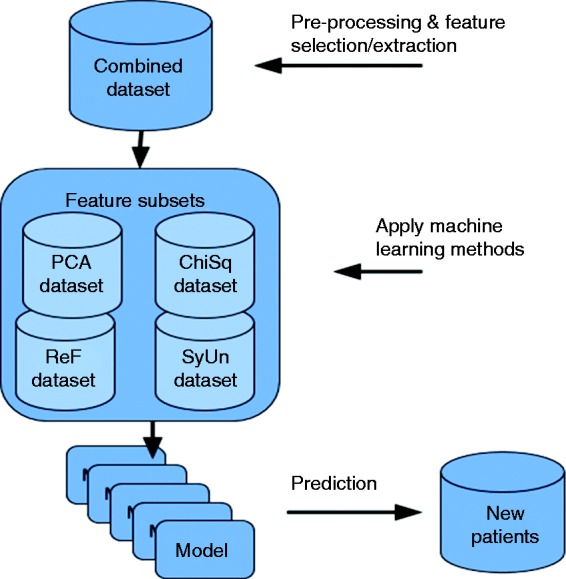
Experimental approach.
Once the models are derived by the classifiers, they are compared using different evaluation metrics to report their effectiveness in predicting heart disease. The end-user (clinicians) will be able to exploit the models derived and check their predictive power.
Dataset
The dataset we have used is a combination of four heart-disease datasets obtained from the UCI ML Repository.14 The datasets used and their authors are as follows: The Cleveland-Dataset (Cleveland Clinic Foundation: Robert Detrano), The Long-Beach-VA-Dataset (VA Medical Center, Long Beach: Robert Detrano), The Hungarian-Dataset (Hungarian Institute of Cardiology, Budapest: Andras Janosi), and The Switzerland-Dataset (University Hospital, Zurich, Switzerland: William Steinbrunn and University Hospital, Basel, Switzerland: Matthias Pfisterer). The reason for combining the four datasets is to obtain larger numbers of instances so more stable predictive models are derived by the ML techniques.
The new combined dataset contains 14 features and 720 instances. The features and their description are depicted in Table 1. There were a significant number of missing values particularly in the ca and thal features. We replaced these missing values using the ReplaceMissingValues filter within the Waikato Environment and Knowledge Analysis tool (WEKA),24 which replaces the missing values with the mean for numerical features and mode for nominal features. When we imported the data into WEKA some of the nominal features were interpreted as numerical, so we changed them back using the NumericToNominal filter.
Table 1.
Data features.
| Feature | Description | Type | Values |
|---|---|---|---|
| age | Age in years | Numerical | 28–77, mean: 51.9 |
| sex | Gender | Nominal | 0 = female (188)1 = male (532) |
| cp | Chest pain type | Nominal | 1 = typical angina (38)2 = atypical angina (160)3 = non-anginal pain (157)4 = asymptomatic (365) |
| trestbps | Resting blood pressure in mmHg | Numerical | 80–200, mean: 131.8missing values (2) |
| chol | Serum cholesterol in mg/dl | Numerical | 0–603, mean: 204missing values (23) |
| Fbs | Fasting blood sugar >120 mg/dl | Nominal | 0 = false (567)1 = true (70) |
| restecg | Resting electrocardiographic results | Nominal | 0 = normal (471)1 = having ST-T wave abnormality (86)2 = showing probable left ventricular hypertrophy (161)missing values (2) |
| thalach | Maximum heart rate achieved | Numerical | 60–202, mean: 140.6missing values (2) |
| exang | Exercise induced angina | Nominal | 0 = no (476)1 = yes (242)missing values (2) |
| oldpeak | ST depression induced by exercise relative to rest | Numerical | −2.6–6.2, mean: 0.8missing values (6) |
| slope | The slope of the peak exercise ST segment | Nominal | 1 = upsloping (187)2 = flat (292)3 = downsloping (34)missing values (207) |
| Ca | Number of major vessels colored by fluoroscopy | Nominal | 0 (179)1 (67)2 (41)3 (20)missing values (413) |
| Thal | Heart rate | Nominal | 3 = normal (192)6 = fixed defect (38)7 = reversible defect (170)missing values (320) |
| target | The predicted class: if the patient has heart disease | Nominal | 0 = heart disease not present (360)1 = heart disease present (360) |
Most existing ML experiments (discussed below) have been done with these 14 features. Many of the medical dataset features are irrelevant or intercorrelated. This can cause overfitting in the predictive models when it comes to classification. In a real-world context, many of these features require an in-depth testing of the patient, which may not be available at the time of needing a heart-disease prediction. Through feature selection, we want to find out the relevant features of heart conditions and see if by getting rid of or underrepresenting the less relevant features we can build a more accurate model. These assumptions are evaluated in below.
Filter and data extraction methods used
PC features
PCA works by extracting a new set of features (PCs) that are linear combinations of the original features.25 The PCs are generated in such a way that they are each orthogonal or uncorrelated and are created in order of how much variance they account for in the original dataset. For example, PC1 will be the linear combination of the original features that can explain the maximum variance, PC2 will be an orthogonal vector to PC1 that explains the next best amount of variance, and so on. The hope of PCA is that you can extract a feature set that is smaller than the original yet still accounts for most of the variance in the original feature set. The drawback of PCA is that it is hard to derive physical meaning from the PCs; however, in classification this is not a big concern as we are mainly interested in the model’s performance and not the inner workings.
To compute the PCs we first need to create a covariance matrix. For a dataset with N features this is an N by N matrix where each element is the covariance between two features, A and B, and is computed as follows:
| (1) |
After the covariance matrix has been created the next step is to find the Eigen vectors and Eigen values for this matrix. The Eigen vectors will be our PCs and are ranked by their corresponding Eigen values.
Chi squared
The Chi-squared feature evaluation simply tells the significance of each of the original features. Based on this the user can choose to keep the most and discard the least significant features. In Chi-squared feature selection, a feature’s significance is measured by the Chi-squared test statistic between the feature and the target class. Equation (2) is used to calculate the Chi-squared statistic where observed is the actual number of class observations and expected is the number of class observations that would be expected if there were no relationship between the feature and class. The sum is over each value of the feature, because of this chi squared requires that numeric features be discretised before calculating.26
| (2) |
A high Chi-squared test score indicates the feature and the target class are not likely to be independent and therefore we should keep the feature in our new dataset.
ReliefF
The ReliefF calculates the scores of features based on the differences in feature values and class values between neighbouring instances. If a set of neighbouring instances has different values for a feature but the same class value, then ReliefF decreases the score of that feature. Alternatively, if neighbouring instances have different values for a feature and different class values then ReliefF increases the feature’s score. This is repeated for a set of sampled instances and their nearest neighbours to calculate an overall score for each feature.27
The rank of each feature can be calculated using an equation such as the following:
| (3) |
Where X is the feature value for a random sample, Miss is the feature value of a nearest neighbour with the opposite class value of X and Hit is the feature value of a nearest neighbour with the same class value as X.
SU
The symmetrical uncertainty method evaluates features based on calculating the SU correlation metric between the feature and the class. To calculate SU, we first need the formula for mutual information (MI), which in our case is a measure of interdependence between a feature and the class:
| (4) |
where A is the feature, B is the class and P is the probability function. The sum is over the values of the feature. Now we can calculate the SU by normalising the MI with respect to the entropy of the feature and class:
| (5) |
where H is the Entropy function.28
Classification methods used
We used eight different supervised ML algorithms, which are all available and implementable within WEKA. They are: BayesNet, Logistic, Stochastic Gradient Descent (SGD), KNN (or in WEKA: IBK with K=21), Adaboost M1 with Decision Stump, Adaboost M1 with Logistic, repeated incremental pruning to produce error reduction (RIPPER or in WEKA: JRip) and random forest.29–36
The BayesNet or Bayesian Network algorithm creates a graphical model of the data where the features are represented by nodes and the causal relationships between features are represented by edges.37
Logistic fits a logistic regression model to the data with a ridge estimator.38 SGD seeks to find the function that best fits the training set by using Support Vector Machine as a loss function and estimating the gradient of the empirical risk or the difference between the model and the training set.39 IBK is also known as KNN and is a simple classification technique that selects the class value of a new instance by looking at a set of the K closest instances in the training set and picking the most frequent class value among them.
Adaboost M1 is not a classification method but instead hopes to increase the performance of another ML algorithm by repeatedly running that algorithm on samples of the training set and combining the results.33 In our experiment we used Adaboost M1 with two different ML algorithms, first with Decision Stump, which is a decision tree with a height of one and classifies instances based on one feature. Although this is a fairly weak classifier on its own, when used with Adaboost it can achieve good results. Secondly, we used Adaboost along with the logistic algorithm that has been described above.
The JRip algorithm is a rule-based learner, which first creates a set of rules that describes the training set, then iteratively prunes rules to minimise error and reduce over fitting.35 Finally, random forest grows a set of classification trees from samples of the training set. New instances are classified by taking a weighted vote from each tree.
Results analysis
Experimental setup and evaluation measures
All experiments were undertaken using the WEKA platform on a computer with a 2.4 GHz processor and 4 GB of RAM. We applied the eight ML algorithms to each of the datasets using 10-fold cross-validation to evaluate their performance. We used the default parameters in WEKA for all ML algorithms except for IBK and AdaboostM1. For IBK we set K to 21, and for AdaboostM1 we changed the ‘classifier’ parameter to work with the Logistic algorithm.
The measures we used to evaluate the performance of each model were predictive accuracy, precision and recall. These measures are based on the confusion matrix, which is a two by two matrix comparing the model’s predicted class values to the actual class values. In the first quadrant we have true positives (TP), which is the number of patients with heart disease who are correctly classified. Next we have false positives (FP), or the patients without heart disease who were incorrectly classified as having heart disease. Following this is false negatives (FN) or patients who have heart disease but are not classified correctly by the model. And finally, true negatives (TN), which are patients without heart disease that are correctly classified.
The evaluation metrics can then be defined as follows: predictive accuracy is the proportion of correctly classified outcomes either true positive or true negative.
| (6) |
Precision is the proportion of positively classified outcomes that are correctly classified. In our case, we want positive to mean target = 1, or the patient has heart disease.
| (7) |
Recall is the proportion of positive cases that are correctly classified. We again want positive to mean patients with heart disease. In medical diagnosis recall is very important since we do not want to miss diagnosing patients who really do have an illness or condition.
| (8) |
Feature selection results
To apply PCA to the heart-disease dataset we first needed to normalise the data because PCA looks for the maximum variation. If the data are not normalised the generated PCs will be skewed. After normalising the training dataset, we used the PCA evaluator with the Ranker search method. This attribute evaluator allows the user to specify the proportion of variance they want to be covered. The higher the variance required, the greater the number of PC; however, there is a diminishing return on the amount of variance covered by each principal component. We selected 73% variance coverage, which generated 11 PCs (features).
In the experiments, we used the Chi-Squared Attribute evaluator with the Ranker search method. The Chi-squared test only works with nominal and binary features so any numerical features must be discretised. However, this attribute evaluator automatically does this so we did not need to do any pre-processing. The Ranker search method orders the features and scores them based on their Chi-squared test statistic. The most significant features were found to be cp, exang and oldpeak, which had ranker scores of 214.6, 151.5 and 139.8 respectively. The least significant features were found to be restecg, fbs and trestbps, which had scores of 4.9, 1.6, <0.001 respectively. We removed these three features and selected the dataset of the remaining 10 features that we will refer to as the Heart-ChiSq dataset.
We used the ReliefF Attribute evaluator with the Ranker search method to order features. We left the methods parameters as the default, which compares every instance with its 10 nearest neighbours. The features that scored highest with ReliefF were cp, sex and thal with scores of 0.1661, 0.0793 and 0.0674. The features thalach, age, fbs and trestbps had scores that were significantly lower than other features: 0.0165, 0.0142, 0.0121 and 0.0108. We removed these four features and saved the remaining nine into a dataset that we will refer to as the Heart-ReF dataset.
We used the SU attribute evaluator with the Ranker search method. The most significant features according to SU were cp, exang and oldpeak with scores of 0.1956, 0.1678 and 0.1194. The lowest ranked features this time were slope, restecg, fbs and trestbps with scores of 0.0251, 0.0044, 0.0022 and <0.0001. We removed these four features and selected the remaining nine features to create a dataset that we will refer to as the HeartSyUn dataset.
Table 2 shows the features that were selected by the Chi-squared, ReliefF and SU methods. The order of the features in this table is based on their ranker scores. The Heart-PCA dataset has been excluded from this table because it is made up of PCs, which are combinations of all the original features.
Table 2.
Feature sets created by feature selection methods.
| Heart-ChiSq dataset | Heart-Refdataset | Heart-SyUndataset |
|---|---|---|
| cp | cp | cp |
| exang | sex | exang |
| oldpeak | thal | chol |
| chol | ca | oldpeak |
| thalach | chol | thal |
| thal | exang | thalach |
| sex | restecg | sex |
| age | slope | age |
| ca | oldpeak | ca |
| slope |
As we can see from Table 2, the three methods select many of the same features. In fact, the cp, exang, oldpeak, chol, thal, sex and ca features are included in all three feature sets. The Heart-ChiSq dataset only differs from the Heart-SyUn dataset in that the latter is missing the slope feature.
The cp feature is ranked the highest in all three feature sets and the exang, chol and thal features are also ranked high across all of our feature sets. This means these features, at least in a statistical sense, are the most influential for predicting heart disease. This information can be very useful to clinicians because when diagnosing a patient they can start by testing for the most influential features before the least influential ones.
Classification methods results
Figures 2, 3 and 4 show the accuracy, precision and recall of the eight classification models when applied to each dataset.
Figure 2.
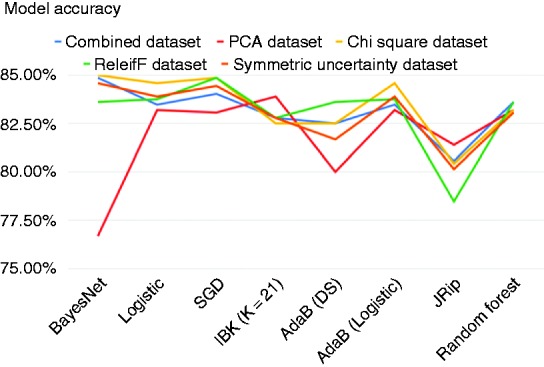
Accuracy across models.
Figure 3.
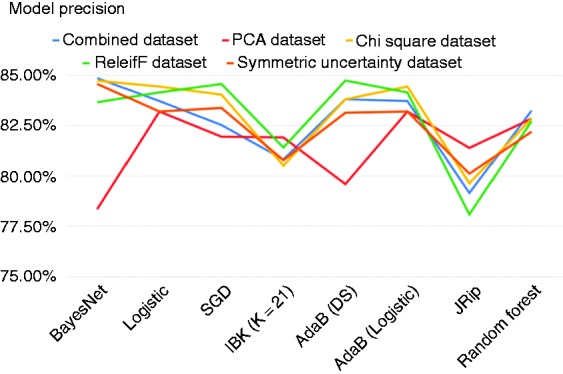
Precision across models.
Figure 4.
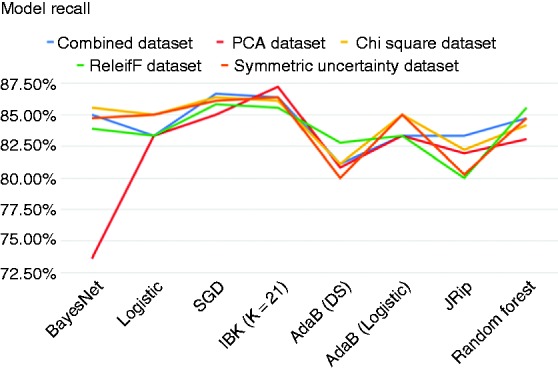
Recall across models.
As we can see from Figures 2, 3 and 4, applying feature selection and extraction to the combined heart-disease dataset had varying results depending heavily on what classification algorithm it was paired with to construct a model. Even some of the models built on the original dataset performed better than many of the models built on selected feature subsets. The model built using the original combined dataset by the BayesNet algorithm had the highest precision of any model that we created and this model achieved an accuracy of 84.86%, precision of 84.86% and a recall of 85.00%.
Moreover, many of the models that were built on the Heart-PCA dataset performed worse than the models built on the original dataset by the ML algorithms. However, the classification model that was built against this features set using IBK achieved the highest recall of any model and had the highest accuracy of any model applied on the PCA features set. To be exact, IBK was able to derive a classification model from the Heart-PCA features set with accuracy of 83.89%, precision of 81.91% and recall of 87.22%.
The classification models that were built on the Heart-ChiSq features set performed better than the models built on the original and Heart-PCA datasets for most of the ML algorithms considered, although in some cases the improvements were marginal. The best-performing model overall in terms of accuracy was built against the Heart-ChiSq dataset using BayesNet algorithm. It achieved an accuracy of 85.0%, precision of 84.73% and recall of 85.56%.
Models built using the ML algorithms on the Heart-ReF and SyUn features sets were mostly unremarkable, achieving accuracies generally higher than those derived from the combined dataset but lower than those derived from the Heart-ChiSq features set using the same ML algorithms. Notably some of the models generated from the Heart-ReF have higher precision and recall rates than those generated from the Heart-ChiSq features set while having comparable accuracy. The most accurate Heart-Ref model was built using SGD algorithm, and achieved an accuracy of 84.86%, precision of 84.57% and recall of 85.83%. The most accurate HeartSyUn model was built using BayesNet and achieved an accuracy of 84.58%, precision of 84.57% and recall of 84.72%.
The marginal differences of models across ML methods means that clinicians may choose to use a model that is easy to implement without a major loss in accuracy. Although the model with the highest accuracy, built using BayesNet and Chi-squared feature selection, would be an effective model, in a medical context such as this it is important that as few patients who really have heart disease are misclassified so the model with the highest recall built using IBK and PCA could also be useful.
A clinician may also want to use a rule-based model such as the those built using the JRip algorithm. These particular models are useful because they are easy to understand and can tell the clinician, in a step-by-step manner, what they need to test for up until the point of making a diagnosis. The Heart-PCA feature set when processed using JRip the most accurate model in terms of accuracy is derived, which is 81.39%. However, it would not be useful to use this model because the principal component features are made up of all the original features and all tests must be carried out before you can use them. The model created using JRip from the original combined dataset had the next highest accuracy with 80.56% and the highest recall with 83.33% so this method should be used if a rule-based model is needed.
Conclusions
Data analysis techniques, especially ML, are playing an ever-growing role in the worldwide medical battle against heart disease. This research investigated the performance of classification models produced by ML techniques and various feature selection methods against distinctive features set selected from four commonly used heart-disease datasets.
Our results show it is possible to create a more accurate model for heart-disease prediction by applying feature selection and extraction to the combined heart-disease dataset. The improvements over using the original dataset vary greatly depending on which ML algorithm is used; therefore to get the best possible model, it is necessary to review a wide range of combinations of feature selection techniques with ML algorithm. The most accurate model we found achieved an accuracy of 85.0%, precision of 84.73% and recall of 85.56%, using Chi-squared feature selection with BayesNet classifier. The model built using ReliefF feature selection alongside the SGD algorithm had a comparable accuracy and precision of 84.86% and 84.57% respectively, with an improved recall of 85.83%. Another model that could still prove useful is the pairing of PCA feature extraction with IBK, which had the highest recall of any model at 87.22% as well as an accuracy of 83.89% and precision of 81.91%. This model could be used as an initial screening for heart disease, followed by a more definitive test to get rid of the FPs.
The ranking of features by our feature selection methods shows us that cp is universally the most influential feature for predicting heart disease followed by exang, chol and thal features; however, these features are ranked differently across feature selection methods.
Our paper is limited in that we have only looked at a selection of ML and feature selection methods. It would be possible to build a better heart-disease prediction model by trying different methods; however, it is difficult to anticipate which are going to be effective without some extensive experimentations and analyses. In future research, it would be interesting to look at different combinations of feature selection methods with ML algorithms including wrapper feature selection, which tailors feature subsets specifically to a selected ML algorithm.
The models that were built in this study can be used by clinicians and healthcare professionals to detect heart disease in new patients, provided that patient data for the features used are available. Which specific features were selected in pre-processing is also useful because it shows which are the most statistically significant when predicting heart disease.
Conflict of Interest
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Contributorship
We declare that all authors have contributed to this research paper.
Ethical Approval
No primary data were collected. The data used in this study were retrieved from the UCI Machine Learning Repository (Dua and Graff, 2019) and are available publicly for research purposes.
Funding
The author received no financial support for the research, authorship, and/or publication of this article.
ORCID iDs
Fadi Thabtah https://orcid.org/0000-0002-2664-4694
Neda Abdelhamid https://orcid.org/0000-0003-3638-8919
Peer Review
This manuscript was reviewed by reviewers, the authors have elected for these individuals to remain anonymous.
References
- 1.Hersh WR. Medical informatics: Improving health care through information. Jama 2002; 288(16): 1955. [DOI] [PubMed] [Google Scholar]
- 2.Cresswell K, Majeed A, Bates DW, et al. Computerised decision support systems for healthcare professionals: An interpretative review. J Innov Health Inform 2013; 20(2): 115–128. [DOI] [PubMed] [Google Scholar]
- 3.Berner ES, Lande TJL. Overview of clinical decision support systems. Health Inform Clin Dec Supp Sys 2007; 3–22.
- 4.World Health Organization. Cardiovascular diseases. Available from https://www.who.int/cardiovascular_diseases/en/ (n.d., accessed 9 June 2019)
- 5.Wilson PWF, D’Agostino RB, Levy D, et al. Prediction of coronary heart disease using risk factor categories. Circ 1998; 97(18): 1837–1847. [DOI] [PubMed] [Google Scholar]
- 6.Palaniappan S, Awang R. Intelligent heart disease prediction system using data mining techniques. In: 2008 IEEE/ACS International Conference on Computer Systems and Applications, 31 March 2008, pp. 108--115.
- 7.Gonsalves AH, Thabtah F, Mohammad RMA, et al. Prediction of coronary heart disease using machine learning: an experimental analysis. In: Proc 2019 3rd International Conf Deep Learning Technologies 2019; 51–56.
- 8.Thabtah F. Machine learning in autistic spectrum disorder behavioral research: A review and ways forward. Informatics Health Social Care 2019; 44(3): 278–297. [DOI] [PubMed] [Google Scholar]
- 9.Loog M. Supervised classification: Quite a brief overview. Machine Learning Technique Space Weather 2018; 113–145.
- 10.Jolliffe I. Principal component analysis In: M Lovric. (ed) International Encyclopedia of Statistical Science. Berlin, Heidelberg: Springer, 2011. [Google Scholar]
- 11.Kira K, Rendell LA. A practical approach to feature selection. Machine Learning Proceedings 1992; 249–256.
- 12.Liu H, Setiono R. Chi2: feature selection and discretization of numeric attribute. In: Proc 7th IEEE International Conference Tools Artificial Intelligence 1995; 388–391.
- 13.Liu H, Yu L. Toward integrating feature selection algorithms for classification and clustering. IEEE Transactions Knowledge Data Engineering 2005; (4): 491–502. [Google Scholar]
- 14.Dua D, Graff C. UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science, 2009. [Google Scholar]
- 15.Gokulnath CB, Shantharajah SP. An optimized feature selection based on genetic approach and support vector machine for heart disease. Cluster Computing 2018.
- 16.Weng SF, Reps J, Kai J, et al. Can machine-learning improve cardiovascular risk prediction using routine clinical data? Plos One 2017; 12(4). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Khateeb N and, Usman M. Efficient Heart Disease Prediction System using K-Nearest Neighbor Classification Technique. In: Proc Int Conf Big Data Internet Things - BDIOT2017 2017.
- 18.Kavitha R and, Kannan E. An efficient framework for heart disease classification using feature extraction and feature selection technique in data mining. In: 2016 International Conference on Emerging Trends in Engineering, Technology and Science (ICETETS). 2016.
- 19.Badaruddoza, Kumar R, Kaur M. Principal component analysis of cardiovascular risk traits in three generations cohort among Indian Punjabi population. J Advanced Res 2015; 6(5): 739–746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jabbar MA, Deekshatulu BL, Chandra P. Prediction of heart disease using random forest and feature subset selection. Advances Intelligent Syst Comp Innovations Bio-Inspired Comp App 2015; 187–196. [Google Scholar]
- 21.Ziasabounchi N, Askerzade I. A comparative study of heart disease prediction based on principal component analysis and clustering methods. Turk J Mathematics Comp Sci 2014, 2: 39–50. [Google Scholar]
- 22.Santhanam T, Ephzibah EP. Heart Disease Classification Using PCA and Feed Forward Neural Networks. Mining Intell Knowledge Exploration Lecture Notes Comp Sci 2013; 90–99. [Google Scholar]
- 23.Rouhani M, Abdoli R. A comparison of different feature extraction methods for diagnosis of valvular heart diseases using PCG signals. J Medical Eng Tech 2011, 36(1): 42–49. [DOI] [PubMed] [Google Scholar]
- 24.Hall M, Frank E, Holmes G, et al. The WEKA data mining software: An update. SIGKDD Explor Newsl, 2009.
- 25.Ringnér M. What is principal component analysis? Nature Biotech 2008; 26(3): 303. [DOI] [PubMed] [Google Scholar]
- 26.Chugh A. ML: chi-square test for feature selection. Available from: https://www.geeksforgeeks.org/ml-chi-square-test-for-feature-selection/ (2018, accessed 25 September 2019)
- 27.Robnik-Šikonja M, Kononenko I. Theoretical and empirical analysis of ReliefF and rReliefF. Mach Learn 2003; 53(1–2): 23–69. [Google Scholar]
- 28.Sarhrouni E, Hammouch A and, Aboutajdine D. Application of symmetric uncertainty and mutual information to dimensionality reduction and classification of hyperspectral images. Int J Eng Technol 2012; 4, 268–276. [Google Scholar]
- 29.Pearl J. Bayesian networks: A model of self-activated memory for evidential reasoning. In: Proc 7th Conf Cognitive Science Society 1985; pp. 329–334.
- 30.Berkson J. Maximum likelihood and minimum X 2 estimates of the logistic function. J Am Stat Assoc 1955; 50(269), 130–162. [Google Scholar]
- 31.Kiefer J, Wolfowitz J. Stochastic estimation of the maximum of a regression function ann Math Statist 1952; 23(3), 462–466. [Google Scholar]
- 32.Fix E, Hodges Discriminatory analysis-nonparametric discrimination: Consistency properties. California: Berkeley University, 1951. [Google Scholar]
- 33.Freund Y and, Schapire RE. Experiments with a new boosting algorithm. In icml 1996; 96: 148–156. [Google Scholar]
- 34.Iba W, Langley P. Induction of one-level decision trees In: M Kaufmann. (ed) Mach Learn Proc 1992. Aberdeen, Scotland: Morgan Kaufmann, 1992, pp. 233–240. [Google Scholar]
- 35.Cohen WW. Fast effective rule induction In: M Kaufmann. (ed) Mach Learn Proc 1995. Tahoe City, California, USA: Morgan Kaufmann, 1995, pp. 115–123. [Google Scholar]
- 36.Ho TK. Random decision forests. In: Proceedings of 3rd international conference on document analysis and recognition 1995; 1: 278–282.
- 37.Kotsiantis SB, Zaharakis I, Pintelas P. Supervised machine learning: A review of classification techniques. Emerging Artificial Intelligence Applications Comp Eng 2007; 160, 3–24. [Google Scholar]
- 38.Le Cessie S, Van Houwelingen JC. Ridge estimators in logistic regression. J Royal Statistical Society: Series C (Applied Statistics ) 1992; 41(1): 191–201. [Google Scholar]
- 39.Bottou L. Stochastic gradient descent tricks. In: Neural networks: Tricks of the trade Berlin, Heidelberg: Springer, 2012, pp. 421–436.


