The Price equation and the causal analysis of evolutionary change

Abstract

Though the Price equation in itself is simply a statistical identity, biologists have often adopted a ‘causal interpretation’ of the equation, in the sense that its component terms have been supposed to correspond to distinct causal processes in evolution, such as natural selection and transmission bias. In this paper, we bring the issue of causal interpretation to the fore, by studying the conditions under which it is legitimate to read causal meaning into the Price equation. We argue that only if substantive assumptions about causal structure are made, which can be represented in the form of a causal model, can the component terms of the Price equation be interpreted as causally meaningful. We conclude with a reflection on the epistemic uses of the Price equation, emphasizing the difference between the description, explanation and prediction of evolutionary change.

This article is part of the theme issue ‘Fifty years of the Price equation’.

1. Introduction

The Price equation is a simple statistical identity that can be used to describe the change in gene (or mean phenotype) frequency in a population over a single generation. Evolutionary biologists have been interested in the Price equation for three main reasons. Firstly, the equation provides a quite general description of an evolving population, that rests on minimal assumptions. Secondly, the equation appears to isolate the effect of natural selection on the total evolutionary change, by partitioning the change into two components (‘Cov’ and ‘Exp’), which are often ascribed to ‘natural selection’ and ‘transmission bias’, respectively ([1–3]). Thirdly, the equation lends itself naturally to a description of multi-level selection, as Price [4] himself showed, for it admits of a simple hierarchical expansion. This point was elaborated by Hamilton [5], who wrote that the Price equation yields a ‘formal separation of levels of selection’; and the equation continues to be used in contemporary work on multi-level selection.

Considered simply as a piece of abstract mathematics, the Price equation is of course beyond reproach. However, the biological interest of the equation stems from interpreting it in a certain way. Typically, biologists adopt a causal interpretation of the Price equation, that is, they take its components to correspond to distinct causal processes in evolution. Both the idea that the ‘Cov’ and ‘Exp’ terms in the simple Price equation correspond to natural selection and transmission bias, and the idea that the terms in the hierarchically expanded Price equation correspond to distinct levels of selection, are examples of such causal interpretations. It is important to realize that any causal interpretation of the Price equation goes beyond the mathematics itself.

Our aim in this paper is to bring the issue of causal interpretation to the fore. While not disputing the usefulness of the Price equation for certain purposes, we argue that confusion has arisen from a failure to think carefully about how statistical formulae relate to causality. Sections 2 and 3 prepare the ground, by explaining how the commonly assumed causal interpretations of the simple and hierarchically expanded Price equations, respectively, are less straightforward than they appear. Section 4 discusses the general relation between causal assumptions and statistical descriptions, introduces the notion of a causal model, and examines conditions under which some forms of the Price equation can be interpreted causally. Section 5 argues that models and the Price equation have different theoretical natures and epistemic purposes, and suggests that a failure to recognize this distinction has led to confusion regarding causal interpretations of the Price equation. Section 6 draws conclusions.

2. Selection and transmission bias

(a). The simple Price equation

We adopt a standard formulation of the Price equation. A parent population contains n individuals, indexed by i, who vary from one another genetically. We are interested in the population-wide frequency of a particular allele at a given genetic locus. The ‘genetic value’ of the ith organism, z_i, is defined as the frequency of the allele within that individual (= 0, 1/2 or 1 for diploids). The average genetic value is $\overline{z}=(1/n)\sum _i{z}_i$, which equals the allele’s population-wide frequency. A second population, of size n′, contains offspring of the individuals in the parent population. The fitness of the ith individual, w_i, is defined as the number of successful gametes it produces. Average fitness is $\overline{w}=(1/n)\sum _i{w}_i$. The frequency of the allele among the successful gametes of the ith individual is $z_i^{\mathrm{\prime }}$. The transmission bias of the ith individual is defined as ${\delta }_i=z_i^{\mathrm{\prime }}-z_i$. Note that a non-zero value of δ_i may reflect mutation, gametic selection, or random genetic drift. Average transmission bias is $\overline{\delta }=(1/n)\sum _i{\delta }_i$.

The quantity of interest is $\mathrm{\Delta }\overline{z}$, the change in allele frequency between the parent and offspring populations. Following Price [1] (with a slight change of notation), this can be expressed as

$$\mathrm{\Delta }\overline{z}=\text{Cov}(\frac{w_i}{\overline{w}},z_i)+\frac{\text{Exp}(w_i{\delta }_i)}{\overline{w}},$$ 2.1

where ‘Cov’ and ‘Exp’ denote covariance and expectation respectively, taken over the whole population. Note that the ‘Cov’ term is the covariance of relative fitness $w_i/\overline{w}$ with genetic value z_i, while the ‘Exp’ term is the expectation of the product of relative fitness and transmission bias δ_i. (The term Exp(w_iδ_i) could equally be written $\overline{w_i{\delta }_i}$, but given its popularity in the literature we adopt the former notation.) We refer to equation (2.1) as the simple Price equation.

One under-appreciated issue in the derivation of (2.1) concerns the value of δ_i for an individual that leaves no successful gametes, i.e. with fitness w_i = 0. Price [1] stipulated that if w_i = 0 then δ_i = 0, but this is of course a convention. Other conventions are also possible. For example, we could stipulate that if w_i = 0 then ${\delta }_i=\overline{\delta }$, i.e. an individual with no offspring is assigned the average transmission bias in the population. A third possibility is to define δ_i as the transmission bias the individual would have had if it had left offspring—a quantity that is of course not directly observable (though $\overline{\delta }$ may be a good proxy for it). Let us call these conventions A, B and C, respectively. Note that the simple Price equation holds true whichever convention we adopt, since δ_i is multiplied by w_i in equation (2.1). This explains why the issue is rarely discussed; however, for certain purposes it is important.

(b). Causal interpretation: two issues

What then of the idea that the two r.h.s. terms of equation (2.1) correspond to natural selection and transmission bias, respectively? For all its popularity, this interpretation is questionable, for two distinct reasons. The first reason is the familiar point that statistical association between two variables does not imply that one causes the other. So a non-zero value of Cov(w_i, z_i), in a given population, does not mean that the differences in w are caused by differences in z; it is equally possible that w and z are joint effects of a common cause, for example. Now as some authors use the term, natural selection on a gene (or trait) means that genetic (or trait) differences must cause fitness differences (this is what Sober [6] calls ‘selection for’). Based on this usage, a non-zero value of Cov(w_i, z_i) does not imply that natural selection is occurring; therefore equation (2.1) itself, in the absence of further causal assumptions, does not isolate the portion of the total evolutionary change that is due to natural selection on z.

The second reason why the causal interpretation of equation (2.1) is questionable is much less familiar, and is independent of the first reason. The point is this. Suppose we define natural selection to mean that a gene (or trait) is systematically associated with fitness, irrespective of whether the former causes the latter—that is, we employ what Sober [6] calls ‘selection of’. It then follows by definition that whenever Cov(w_i, z_i) ≠ 0, there is selection on z. But even so, it does not immediately follow that equation (2.1) partitions the total change into components due to natural selection and transmission bias. For in general, when an effect is the result of multiple causal factors, there is no a priori reason why the factors’ respective contributions should be additively separable. So although natural selection in the sense of ‘selection of’ (i.e. differential reproduction), and biased transmission (i.e. mutation, gametic selection and random drift) are certainly distinct causal factors, both capable of affecting evolutionary change, it is not necessarily possible to express $\mathrm{\Delta }\overline{z}$ as the sum of components corresponding to each.

In this section, we focus on the second reason for questioning the causal interpretation of equation (2.1), setting aside the first reason (which we return to later). Therefore, in accordance with some though not all of the Price equation literature, we employ the ‘selection of’ concept throughout this section. That is, we take it as true by definition that if Cov(w_i, z_i) ≠ 0, then natural selection is occurring (though not vice versa, for z could be subject to stabilizing selection even if Cov(w_i, z_i) = 0.) And we assume that natural selection, in this sense, and biased transmission are the only factors that affect $\mathrm{\Delta }\overline{z}$. Our question is: can we legitimately regard (2.1) as partitioning the total change $\mathrm{\Delta }\overline{z}$ into components attributable to natural selection and biased transmission, respectively, as many authors believe?

(c). Isolating the difference made by natural selection

One reason for doubting that equation (2.1) achieves this is the fact that the variable w_i appears in both r.h.s. terms (as noted in [7–9]). That is, the fitness differences in the population affect the ‘Exp’ term as well as the ‘Cov’ term, so intuitively the latter term does not seem to isolate the effect of natural selection on $\mathrm{\Delta }\overline{z}$.

This worry can be fleshed out as follows. Intuitively, natural selection (i.e. differential reproduction) and biased transmission (i.e. mutation, gametic selection and random drift) represent distinct causal factors, both capable of affecting the total evolutionary change. If this is right, then presumably it should be possible, in principle, to alter the strength of natural selection in a population, or to eliminate it altogether, while leaving the transmission bias unchanged, and vice versa. But to eliminate selection, or to alter its strength, involves changing the fitness values of some individuals in the population, which will potentially affect both r.h.s. terms of equation (2.1). So how can it be correct to regard equation (2.1) as isolating the effects of natural selection and transmission bias on $\mathrm{\Delta }\overline{z}$?

Partly in response to this worry, an alternative form of the Price equation is sometimes used in the literature ([3,7–10]). To derive this alternative form, note that the ‘Exp’ term of equation (2.1) can be decomposed as follows:

$$\frac{\text{Exp}(w_i{\delta }_i)}{\overline{w}}=\text{Cov}(\frac{w_i}{\overline{w}},{\delta }_i)+\overline{\delta }.$$ 2.2

Substituting (2.2) into (2.1) and adding the covariance terms, using the definition $z_i^{\mathrm{\prime }}=z_i+{\delta }_i$, yields

$$\mathrm{\Delta }\overline{z}=\text{Cov}(\frac{w_i}{\overline{w}},z_i^{\mathrm{\prime }})+\overline{\delta }.$$ 2.3

Equation (2.3) expresses the total change as the sum of the covariance between an individual’s relative fitness and the frequency of the allele among its successful gametes, plus the average transmission bias in the population (unweighted by fitness). Importantly, the partition in equation (2.2), and therefore also (2.3), is sensitive to the convention adopted about the value of δ_i when w_i = 0. Depending on the convention adopted, equation (2.3) will divide up $\mathrm{\Delta }\overline{z}$ in different ways (except in the case where w_i > 0 for all i).

Some authors suggest that equation (2.3) better isolates the effect of natural selection on the total change, so admits of a more natural causal interpretation than the simple Price equation (2.1) (see [8,9]). For note that in equation (2.3), w_i does not appear in the second term $\overline{\delta }$, which suggests that term reflects transmission bias alone, while the ‘Cov’ term captures all the effects of differential fitness. However, against this argument, other authors have observed that since the ‘Cov’ term in (2.3) now contains $z_i^{\mathrm{\prime }}$, it is not independent of transmission bias, unlike the ‘Cov’ term in equation (2.1) (see [10–13]). So in one respect equation (2.1) yields a ‘cleaner’ partition of $\mathrm{\Delta }\overline{z}$ into two, while in another respect equation (2.3) does better.

This suggests that the method of inspecting terms in the Price equation then trying to deduce their causal meaning is fraught with difficulty. A more systematic approach is needed. One promising avenue is to use counterfactual reasoning, a widely-used technique for assessing causal relations (see [14,15]). Suppose that the evolutionary change in a given population is $\mathrm{\Delta }\overline{z}$, and that natural selection and biased transmission are the only causal factors at work. We then ask what the change would have been if there had been no transmission bias, but everything else had remained the same, from which we can deduce the difference made by transmission bias to $\mathrm{\Delta }\overline{z}$. Similarly, by hypothetically eliminating natural selection while keeping everything else fixed, we can deduce the difference made by selection to $\mathrm{\Delta }\overline{z}$.

To implement this for transmission bias, we simply set the value of δ_i to zero for each individual, while leaving unchanged the values of n, n′, z_i and w_i. This amounts to setting the ‘Exp’ term of equation (2.1) to zero while leaving the ‘Cov’ term unchanged. So the difference made by transmission bias to the actual change $\mathrm{\Delta }\overline{z}$ is equal to $\text{Exp}(w_i{\delta }_i)/\overline{w}$.

The corresponding argument for selection is trickier. For it is not entirely obvious what it means to hypothetically eliminate selection from the population. Clearly, it requires that Cov(w_i, z_i) should go to zero, but of course there are many ways to make this term zero. In accordance with the standard logic of counterfactuals (see [14]), to assess what would have happened in the absence of selection, we need to make the minimum modification to the actual state of the population that eliminates selection. Intuitively, this involves eliminating the fitness differences between individuals while leaving everything else unchanged. So we need to equalize the w_i for all i, while holding z_i, δ_i, n and n′ fixed at their actual values. Now fixity of n and n′ implies fixity of $\overline{w}$, so each w_i must be set equal to $\overline{w}$. These changes amount to setting the ‘Cov’ term of (2.3) to zero, while leaving the $\overline{\delta }$ term unchanged. So the difference made by natural selection to the actual change $\mathrm{\Delta }\overline{z}$ is equal to $\text{Cov}(w_i/\overline{w},z_i^{\mathrm{\prime }})$.

Note that, in principle, there are other hypothetical modifications that would also make Cov(w_i, z_i) go to zero. (For example, we could leave w_i unchanged for each i, but suitably alter the joint distribution of w and z.) However, all such modifications either are more complicated than the one described in the paragraph above, as they involve changing more than one variable, or else fail to eliminate the fitness differences in the population, so do not necessarily eliminate selection on z. (Recall that Cov(w_i, z_i) = 0 is compatible with there being stabilizing selection on z.) Therefore, the simplest modification that eliminates natural selection on z is to set w_i equal to $\overline{w}$ while leaving all other variables unchanged.

Three important points should be noted here. Firstly, our argument that this is the simplest way to eliminate natural selection implicitly rests on a causal assumption. It assumes that, in the actual population, an individual’s fitness w_i does not causally influence its genetic value z_i nor its transmission bias δ_i. For otherwise, equalizing the w_i while holding z_i and δ_i fixed would require us to modify the causal pathways leading from w_i to z_i, and from w_i to δ_i, so would not constitute the minimum modification that eliminates natural selection. Biologically, this assumption is perfectly realistic. But it is important to see that without this causal assumption, or some other one, there is no determinate way of saying how much difference natural selection makes to $\mathrm{\Delta }\overline{z}$, because there is no determinate way of saying what $\mathrm{\Delta }\overline{z}$ would have been in the absence of selection.

This is quite a striking result, which is not widely appreciated. One might easily think that if natural selection is understood as ‘selection of’, i.e. if Cov(w_i, z_i) ≠ 0 is taken to imply that selection is acting on z, then no causal assumptions are necessary in order to isolate the component of $\mathrm{\Delta }\overline{z}$ that is due to selection. However, this is not so. Isolating the difference made by selection requires comparing the actual change $\mathrm{\Delta }\overline{z}$ with the change that would have resulted had selection not acted; and computing this hypothetical change requires that we identify the minimum modification to the population that eliminates natural selection, which requires an assumption about causal structure. So even if natural selection is taken in the sense of ‘selection of’, causal assumptions are needed in order to justify interpreting the ‘Cov’ term of equation (2.3) as the change due to natural selection.

Secondly, computing the difference made by natural selection depends on the convention we adopt regarding the value of δ_i for an individual with w_i = 0. (The difference made by transmission bias, by contrast, is independent of this convention). For purposes of causal analysis, the ‘right’ convention is surely convention C—that is, assigning to a w_i = 0 individual the value of δ_i it would have had if it had left any offspring. Price’s own convention A (which assigns δ_i = 0 to such individuals), by contrast, may lead to an under- or over-estimation of the difference that natural selection makes; for in the context of our counterfactual reasoning, it amounts to assuming that if individuals that left no offspring had left offspring, they would have transmitted their genetic value with perfect fidelity, which is biologically implausible.

Thirdly, whichever convention we adopt, the difference made by transmission bias, and the difference made by natural selection, do not in general add up to the total change $\mathrm{\Delta }\overline{z}$. To see why, it helps to use yet another form of the Price equation (found in [11]). This form is derived by substituting (2.2) into (2.1) but without adding the covariance terms

$$\mathrm{\Delta }\overline{z}=\stackrel{\mathrm{difference}\hspace{0.17em}\mathrm{made}\hspace{0.17em}\mathrm{by}\hspace{0.17em}\mathrm{selection}}{\overbrace{\mathrm{Cov}(w_i/\overline{w},z_i)+\underset{\mathrm{difference}\hspace{0.17em}\mathrm{made}\hspace{0.17em}\mathrm{by}\hspace{0.17em}\mathrm{transmission}\hspace{0.17em}\mathrm{bias}}{\underbrace{\mathrm{Cov}(w_i/\overline{w},{\delta }_i)+\overline{\delta }}}}}$$ 2.4

Equation (2.4) partitions $\mathrm{\Delta }\overline{z}$ into three components. The first two r.h.s. terms sum to $\text{Cov}(w_i/\overline{w},z_i^{\mathrm{\prime }})$, which our counterfactual reasoning identifies as the difference made by selection. The second two r.h.s. terms sum to $\text{Exp}(w_i{\delta }_i)/\overline{w}$, which our counterfactual reasoning identifies as the difference made by transmission bias. These two differences add up to $\mathrm{\Delta }\overline{z}$ if and only if $\text{Cov}(w_i/\overline{w},{\delta }_i)=0$—which means that the two causes do not interact. A somewhat similar situation arises in a two-way ANOVA (analysis of variance): the main effects of the two independent variables only sum to the total effect if non-additive interaction is absent (as noted in [16]).

It might be thought that the condition $\text{Cov}(w_i/\overline{w},{\delta }_i)=0$ will often obtain empirically. This may be true—for mutation and sampling error, which are two sources of transmission bias, will typically be uncorrelated with individual fitness. However, another source of transmission bias is gametic selection (meiotic drive), which empirically is often associated with reduced viability. And moreover, the value of $\text{Cov}(w_i/\overline{w},{\delta }_i)$ is sensitive to the convention we adopt about the value of δ_i for the w_i = 0 individuals. If for example, we adopt Price’s convention A, then even if δ_i and w_i are entirely uncorrelated among individuals with w_i > 0, the value of $\text{Cov}(w_i/\overline{w},{\delta }_i)$ will generally be non-zero.

What is the upshot? The idea that the Price equation partitions the total change into components due to natural selection and transmission bias is murkier than it seems, even if we take a non-zero value of Cov(w_i, z_i) to imply, by definition, that selection is occurring. The ‘best-case scenario’ for this idea is when w_i > 0 for all i (which implies that any selection is by differential fecundity or fertility, rather than differential survival); and when mutation and sampling error are the only sources of transmission bias. For if w_i > 0 for all i, then no convention is needed about the value of δ_i when w_i = 0; while if transmission bias arises only from mutation and sampling error, then $\text{Cov}(w_i/\overline{w},{\delta }_i)$ should be close to zero in a large population. But in the general case, equation (2.4), taken in conjunction with our counterfactual reasoning, shows that selection and transmission bias do not make additively separable contributions to the total evolutionary change.

3. Levels of selection

In §2, we identified two reasons why causal interpretation of the Price equation is problematic. The first was that two variables, such as w and z, can be statistically associated for many reasons, even if one does not cause the other. The second was that even if natural selection is defined as statistical association between trait and fitness, it is still not obvious which form of the Price equation, if any, isolates the effect of natural selection on the total evolutionary change. Our focus in §2 was on the second problem. In this section, we return to the first problem, and focus on a special case of the problem that arises in the context of multi-level selection.

A version of the Price equation is often employed in discussions of multi-level selection, for example to analyse evolution in group-structured populations. Suppose that our population of n individuals is subdivided into N groups, assumed for convenience to be of equal size. We let z_jk and w_jk denote the genetic value and fitness, respectively, of the jth individual in the kth group. We let Z_k and W_k denote, respectively, the average genetic value and average fitness of the kth group. As before, we let i index the individuals in the global population, without regard to grouping. We can then partition the overall covariance between w_i and z_i into between-group and within-group components

$$\text{Cov}(w_i,z_i)=\stackrel{\mathrm{between}\text{-}\mathrm{group}}{\overbrace{\text{Cov}(W_k,Z_k)}}+\stackrel{\mathrm{within}\text{-}\mathrm{group}}{\overbrace{{\text{Exp}}_k(\text{Cov}(w_{\hspace{0.17em}jk},z_{\hspace{0.17em}jk}))}}.$$ 3.1

The first r.h.s. term of (3.1) is the covariance between the group means, while the second r.h.s. term is the average, across groups, of the within-group covariance between w and z. We can then substitute equation (3.1) into the simple Price equation (2.1). Ignoring individual-level transmission bias, this gives

$$\mathrm{\Delta }\overline{z}=\frac{\text{Cov}(W_k,Z_k)}{\overline{w}}+\frac{{\text{Exp}}_k(\text{Cov}(w_{\hspace{0.17em}jk},z_{\hspace{0.17em}jk}))}{\overline{w}},$$ 3.2

which is a multi-level version of the Price equation, which was first derived, in a slightly different form, by Price [4].

Equation (3.2) is a useful tool for modelling the evolution of altruism, as both Price [4] and Hamilton [5] saw. If the gene in question encodes an altruistic trait, then the between-group term will be positive, since groups with more altruists will have higher average fitness, while the within-group term will be negative, since within any group altruists suffer a fitness penalty relative to non-altruists. So the equation captures the idea, already known to Darwin [17], that altruism will be favoured by between-group selection, but disfavoured by within-group selection. The overall evolutionary outcome will depend on which selective force is stronger.

The example of altruism encourages the idea that equation (3.2) is a quite general formalization of the ‘levels of selection’ question in evolutionary biology. In particular, one might reasonably suppose that the debate over the importance of ‘group selection’ in nature can be interpreted as a debate about whether, in actual biological populations, the term Cov(W_k, Z_k) is substantial or not. This appears to be what Price [4] and Hamilton [5] thought, and it is still a widely held view today.

In fact, however, this interpretation of equation (3.2) is questionable. For it is quite possible that the term Cov(W_k, Z_k) be non-zero, even in the absence of what would ordinarily be regarded as group-level selection ([9,18]). To see this point, suppose that the gene whose evolution we are concerned with encodes a purely non-social trait, i.e. an individual’s fitness w_jk depends only on its own genetic value z_jk, but not on the genetic values of its group members, nor therefore on the group’s genetic value Z_k. In such a situation, it seems clear that $\overline{z}$ evolves by individual-level selection alone, i.e. because some individuals are fitter than others. But unless all groups happen to have exactly the same gene frequency, the term Cov(W_k, Z_k) will be non-zero. Simply put, group fitness W_k correlates with genetic value Z_k, but this is simply a side-effect of the fact that some groups contain a higher proportion of the fitter individuals than others.

Another way to see this point is in terms of G. C. Williams’s distinction between genuine group adaptation and ‘fortuitous group benefit’ [19]. The former refers to a trait that evolved because it is group-advantageous, the latter to a trait that, although group-advantageous, did not evolve for that reason but rather because it benefits individuals who happen to live in groups. Thus, for example, if faster deer have a selective advantage over slower deer, then a consequence of this is that a herd of fast deer will do better than a herd of slow deer, but this is a fortuitous group benefit, not a group adaptation. In effect, the problem with treating the term Cov(W_k, Z_k) as a measure of ‘group selection’ is that it ignores Williams’s distinction. A non-zero value of Cov(W_k, Z_k) may be indicative of a causal process of selection at the group level, but it may equally be a side-effect, or by-product, of individual-level selection.

The general moral here is that we must be wary of reading causal meaning into bare statistical formulae. This danger is particularly acute in a multi-level context, where it is easily missed. The partition of $\mathrm{\Delta }\overline{z}$ in equation (3.2) does not distinguish between two causal models: (i) individual fitness w_jk is caused by z_jk alone; and (ii) w_jk is caused by both z_jk and Z_k (figure 1). The value of Cov(W_k, Z_k) could be identical in both cases; but in case (i) it is both intuitively inappropriate, and untrue to the history of the concept, to talk about ‘group selection’. This is the fundamental reason why the multi-level Price equation (3.2), for all its usefulness as a conceptual tool for thinking about altruism, does not cleanly yield a ‘formal separation of levels of selection’, contrary to what Price and Hamilton thought.

Figure 1.

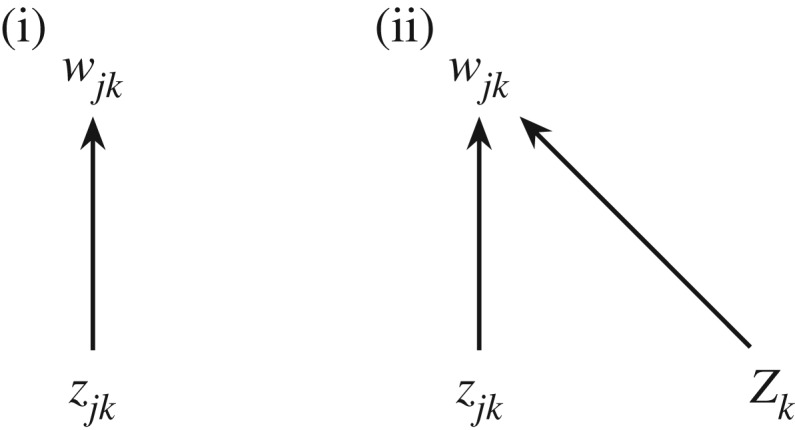
Causal dependence of individual fitness on individual genetic value alone (i); and on both individual and group genetic value (ii).

Of course, if we were to content to understand selection in the ‘selection of’ sense, this worry would not arise. That is, if we simply take it as true by definition that whenever Cov(W_k, Z_k) is non-zero, group selection is occurring, then our objection to the causal interpretation of the multi-level Price equation (3.2) could be side-stepped. However, in the context of multi-level selection, this is an inadvisable move, for it is tantamount to rejecting Williams’s distinction between group adaptation and fortuitous group benefit, and would lead to a conflation of evolutionary processes that are clearly distinct. If we accept (as most biologists appear to) that Williams’s distinction is an important one, and that it is intuitively wrong to speak of group selection in the absence of group effects on individual fitness, and thus that Cov(W_k, Z_k) ≠ 0 is not sufficient for group selection, then we must conclude that equation (3.2) does not, in fact, isolate the component of evolutionary change due to group selection.

4. Causal models

Our discussion thus far has revealed the difficulty of taking the components of the Price equation to correspond to distinct causal processes in evolution. The difficulty arises for both the single- and multi-level versions of the Price equation, and whether selection is understood as ‘selection for’ (where z causally influences w) or ‘selection of’ (where z and w are statistically associated, irrespective of whether z is a cause of w). In each case, we saw that the ‘Cov’ and ‘Exp’ terms of the Price equation admit of a causal interpretation only under specific conditions.

In this section, we change gear and explore the opposite approach. Instead of starting with the Price equation and trying to infer its causal meaning in particular circumstances, an alternative is to explicitly model causal assumptions up front and use this to decompose the evolutionary change (as done in [7,8,20]). This approach expresses causal relationships with a directed causal graph and draws on the general relationship between causality and probability [15,21]. In the present context, we are interested in the causal relationships among the three variables appearing in the Price equation (2.3), namely fitness w, genetic value z and the allelic frequency among the successful gametes z′. In the case of ‘selection for’, the parent’s genetic value z affects both w (through selection) and z′ (through transmission). Letting ε_w, ε_z and ε_z′ summarize all other causes of w, z and z′ respectively, we obtain figure 2 as the default causal model [7].

Figure 2.

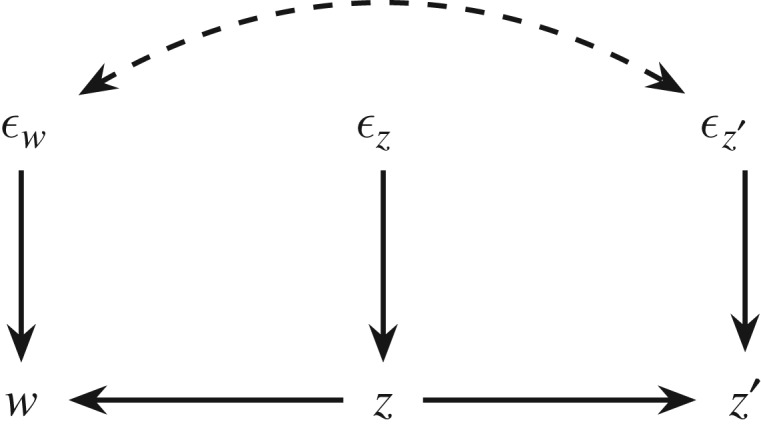
A simple causal graph over the three variables appearing in the Price equation, adopted with modification from Frank [7].

The causal model explicates the conditions for counterfactual reasoning. When we resorted to hypothetical interventions to separate out the differences made by selection and transmission bias in §2c, we noted that the reasoning depends on causal assumptions. For example, in eliminating transmission bias by setting δ_i = 0 for each individual, we stipulated that this leaves the other variables (apart from z′) unchanged. Given the causal model in figure 2, such an intervention amounts to setting ε_z′ = 0 for each individual, and at the same time assuming that there is no arrow from z′ to z or w. Likewise, that the elimination of selection by setting $w=\overline{w}$ does not change the other variables is warranted by the absence of an arrow from w to z or z′. Figure 2 satisfies all these requirements and thus provides an exemplar causal structure in which the difference made by selection and transmission bias are captured by $\text{Cov}(w_i/\overline{w},z_i^{\prime })$ and $\text{Exp}(w_i{\delta }_i)/\overline{w}$, respectively.

Another advantage of making explicit causal assumptions is that it allows a yet further decomposition of the Price equation, as shown by a number of authors [7,22]. Figure 2 contains two pathways that contribute to the ‘Cov’ term of equation (2.3): the top dashed arrows through the ε variables, and the bottom path through z. The contribution of the former is Cov(ε_w, ε_z′), while that of the latter is given by multiplying the regression coefficients β_wz, β_z′z, and the variance of z, according to Sewall Wright’s method of path coefficients [23]. Since a regression coefficient is nothing but covariance divided by variance, the whole equation becomes

$$\mathrm{\Delta }\overline{z}=\text{Cov}(\frac{w_i}{\overline{w}},z_i)\cdot \frac{\text{Cov}(z_i,z_i^{\prime })}{\text{Var}(z_i)}+\text{Cov}({ϵ}_w,{ϵ}_{z^{\prime }})+\overline{\delta }.$$ 4.1

The first term is a product of the selection differential $\text{Cov}(w_i/\overline{w},z_i)$ and the (narrow sense) heritability Cov(z_i, z′_i)/Var(z_i). When the average transmission bias and confounding are absent so that $\overline{\delta }=\text{Cov}({ϵ}_w,{ϵ}_{z^{\prime }})=0$, equation (4.1) reduces to the breeder’s equation, as discussed by ([3,7,22,24]). For the sake of simplicity, we henceforth assume Cov(ε_w, ε_z′) = 0.

With this assumption in place, equation (4.1) divides the ‘Cov’ term of equation (2.3) into two components. In §2, we saw that in order for the total change $\mathrm{\Delta }\overline{z}$ to be partitioned into the difference made by transmission bias and that by natural selection, the second term $\text{Cov}(w_i/\overline{w},{\delta }_i)$ of equation (2.4) must be zero. In equation (4.1), this condition translates to Cov(z_i, z′_i)/Var(z_i) = 1, that is, heritability must be perfect. If z represents a genetic value this condition is satisfied by the absence of mutation, random drift, or gametic selection, as we noted. But the Price equation is also used to describe a change in a phenotypic mean, in which case this condition of perfect heritability, and thus also the partition of the total change into the differences made by selection and transmission bias, is unlikely to obtain.

Do the r.h.s. terms of equation (4.1), in particular, the selection differential and heritability, correspond to distinct causal processes? The selection differential is often interpreted as capturing just the effects of selection and not those arising from reproduction because it does not contain z′, but as we have seen in §2, mere inspection of the terms in the equation is an unreliable guide here. Indeed, the heritability term shares z and z′ with the selection differential and the average transmission bias, respectively, so parity of argument would imply that none of the three r.h.s. terms in equation (4.1) represents distinct causal factors.

To address this issue, we again resort to counterfactual reasoning, but now in the context of a specific causal model. Let us ask whether there are hypothetical interventions that eliminate just one of the three r.h.s. components of equation (4.1) while leaving the others intact (note that we are assuming Cov(ε_w, ε_z′) = 0). The answer is yes. First, it is easily seen that setting $w=\overline{w}$ as before eliminates the selection differential but leaves the other two terms unchanged. Second, in order to eliminate the average transmission bias $\overline{\delta }$ alone, we manipulate ε_z′ in such a way that its mean becomes zero, i.e. Exp(ε_z′) = 0, but the other moments, including its variance, stay the same. This effectively makes $\overline{\delta }=0$, while leaving the other components intact. Finally, heribability can be manipulated by changing the variance of z′. Hence setting z′ to the mean Exp(ε_z′) eliminates the heritability without affecting the transmission bias or selection differential. So despite the apparent overlap of variables, the three components do seem to reflect distinct causal processes, in that they can be independently controlled by hypothetical interventions.

Note that, although the difference made by selection, $\text{Cov}(w_i/\overline{w},z_i^{\prime })$, decomposes into the selection differential and the heritability (given figure 2), the latter two components combine multiplicatively rather than additively. So the selection differential and the heritability do not constitute distinct shares of the total evolutionary change: it does not make sense to ask what portion of $\mathrm{\Delta }\overline{z}$ is due to each, nor which of them makes a greater contribution. This is also clear from figure 2, where the selection differential and heritability correspond to two consecutive links that constitute one causal path w ← z → z′. This means that they do not represent independent sources that affect the change due to selection (as measured by $\text{Cov}(w_i/\overline{w},z_i^{\prime })$), but rather two interactive components that together produce that change.

We saw in §2 that the interpretation of equation (2.3) depends on the convention we adopt regarding the value of δ_i for an individual with w_i = 0. The same issue arises with respect to equation (4.1), which includes z′_i and δ_i in its second and fourth components. Let us ask, then, which convention is needed in order to ensure that these two components correctly capture the corresponding causal factors. It is easy to see that Price’s convention A—assigning δ_i = 0 to offspringless individuals—does not work here, for it will underestimate both the heritability and transmission bias. By contrast, convention B (setting ${\delta }_i=\overline{\delta }$ if w_i = 0) gives a correct estimate of the transmission bias as long as the bias-generating mechanisms (ε_z, ε_z′) are independent from fitness w, which is satisfied if Cov(ε_w, ε_z′) = 0; but it overestimates the heritability because it amounts to assuming that such individuals would have perfect heritability. This leaves us with convention C, which counterfactually imputes the value of δ_i. Although this is conceptually plausible, such counterfactual values, being unobservable, cannot help us to estimate model parameters. A practical solution, in this case, is to ignore individuals with w_i = 0 and calculate the heritability and transmission bias based solely on those who beget offspring [10]. If we assume that all individuals are independent identically distributed samples from the model described in figure 2, discarding some of them (i.e. those with w_i = 0) will not introduce a bias in the estimation of the causal parameters.

That the Price equation can be used to partition the total change into the selection differential and the heritability has previously been shown by Queller ([22,24]) and Frank ([3,7]). What our analysis adds is the following key point: the components of equation (4.1) can only be interpreted causally if a certain causal structure, embodied in figure 2, is assumed. To see this point, consider the alternative causal structure in figure 3. This depicts a case of pleiotropy, in which the gene has two phenotypic effects. The first effect is to increase fertility via the arrow from z to w. The second effect is to encode a behaviour u which causes the individual to disperse towards a mutagenic region of the environment (e.g. with high radiation). This has a negative effect on viability (the arrow from u to w), and also has an effect on the mutation rate, thus affecting the transmission fidelity (the arrow from u to z′). In such a case u affects all the components of equation (4.1), including Cov(ε_w, ε_z′), so that the selection differential, heritability and transmission bias no longer represent distinct causal mechanisms.

Figure 3.

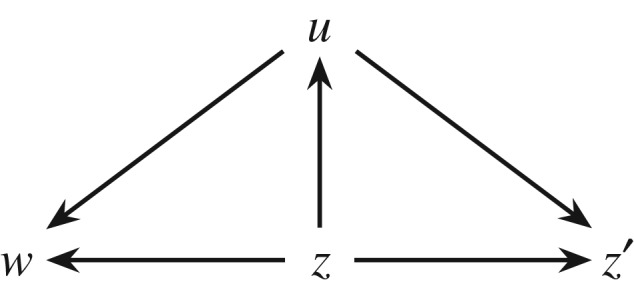
A case of pleiotropy, where gene z affects fitness w and successful gamete z′ through both direct and indirect pathways.

The moral of this example is that there is no unique or universally correct causal decomposition of the Price equation: all depend on an underlying causal structure, which must be specified separately from the equation. As a statistical relationship, the Price equation is causally neutral and by itself does not support any causal readings. It is only by making specific causal assumptions that we can interpret its components in causal terms.

5. Description versus explanation of evolutionary change

The moral drawn above invites a philosophical reflection. Why does the Price equation, taken alone, not admit of a causal interpretation, appearances to the contrary notwithstanding? The basic reason is that the Price equation is a descriptive principle, in contrast to the explanatory or predictive models used in population genetics [25,26]. The r.h.s. of the Price equation always correctly records an actual change in the gene frequency of a population, but one cannot calculate it before observing the l.h.s.. This reflects the fact that the Price equation is a mathematical identity, so that its r.h.s. is a redescription of the l.h.s.. Since algebraic transformations add no new information, the resulting identity contains nothing that one could not know from the original data. Reading out more, therefore, requires making an empirical assumption that is external to the equation itself.

At first sight, ascribing the total evolutionary change to selection and transmission bias does not seem to go beyond descriptive book-keeping, for it looks like sorting out the cash in your purse into coins and notes. In reality, however, it is more like asking how much of your money comes from where, because selection and transmission bias are understood as two different sources that contribute to evolutionary change. And to consider the relative contribution of each factor is to imagine a hypothetical situation in which the source in question is absent. It is for this reason that we needed to resort to counterfactual reasoning in order to determine the difference made by each factor.

To answer such counterfactual questions requires a certain structure that stays invariant across different possibilities [15]. Counterfactual reasoning evaluates the consequences that would obtain under different conditions, and this is possible only if we assume that the mechanism connecting conditions and outcomes is the same in both the actual and counterfactual scenarios. The causal graph we saw in §4 is one way to express this invariance assumption. The graphical structure is a representation of the causal mechanism that generates statistical data, and tells us what does and does not stay invariant under interventions to or modifications of the graph. The framework thus allows us to assess how the components of the Price equation are affected if we hypothetically eliminate selection or transmission bias, and to determine the possible interventions that keep a given statistical component fixed.

Adding causal assumptions makes the Price equation, which by itself is a mathematical identity, into a predictive model. The goal of a model is not to describe or record actual evolutionary changes, but rather to explain them or to predict unobserved changes. In this respect, equation (4.1) should be sharply distinguished from the preceding variants of the Price equation. For while the Price equation itself is always exact, the l.h.s. and r.h.s. of equation (4.1) rarely match if calculated from observed data, because the independence conditions implied by figure 2 only obtain asymptotically and will not hold exactly in any finite population, even if the figure correctly captures the causal structure of the population [10]. Hence if the breeder’s equation is taken as a description of an actual evolutionary change, it is almost always false. Nevertheless, it has long served for breeders to predict a change in the mean phenotype before performing artificial selection, or for ecologists to explain relatively slow responses to strong selective pressures in terms of the lack of heritability. This is because the equation gives evolutionary responses that would obtain under specific boundary conditions, given the model’s assumptions. Hence to the extent that those assumptions approximate reality, it allows us to make inferences about unobserved or unobservable evolutionary changes under future or hypothetical conditions.

The key to such inductive inferences is the assumption of invariance. As discussed above, explaining an evolutionary change in terms of a particular factor such as selection or transmission requires a stable structure to support counterfactual reasoning. Moreover, predicting the future based on past observations presupposes a certain kind of ‘uniformity of nature’ [27]. In the present context, this amounts to assuming that the causal structure that generates an evolutionary response does not itself change over time, despite the change in the frequency of genes and/or phenotypic variables. Clearly, such an assumption cannot be justified a priori or by past observations alone, but must be posited as an empirical hypothesis. This is the reason we needed to introduce a causal model in order to evaluate counterfactual claims, and to derive the equational form (4.1) which is capable of making predictions.

What the above discussion suggests is that it is impossible, in principle, to read off causal implications from the Price equation itself, unless causal assumptions are made (at least implicitly). As we noted, partitioning the total change into distinct components is already an explanatory task, for it amounts to attributing portions of evolutionary response to their corresponding causes. This cannot be achieved solely by inspecting data, but only by introducing an additional empirical hypothesis in the form of an invariant model. To think otherwise is to confuse description with explanation, and a priori identities with predictive models.

Might one argue that although the components of the Price equation do not by themselves make any causal claims, they may serve as evidence for the latter, just as an observed correlation between two variables is often taken as evidence of their causal connection? After all, such ‘inference to the best explanation’ is a common inferential pattern in science. The problem with this type of inference, however, is that the candidate explanations are rarely exhaustive. The presence or absence of a statistical association does not entail causal dependence nor independence, for two variables having no direct causal relationship may still show a spurious correlation owing to some confounding factor, while a genuine cause may be statistically independent from its effect if there are multiple causal pathways whose influences cancel each other (a situation called unfaithful [21]). We have already seen this when we noted that a non-zero between-group covariance Cov(W_k, Z_k) in the multi-level Price equation (3.2) may not reflect group selection, but rather a ‘fortuitous group benefit’ that arises as a side-effect of individual-level selection. Conversely, it is also possible that individual-level and group-level effects offset each other to yield zero between-group covariance [28]. The individual covariance term $\text{Cov}(w_i/\overline{w},z_i)$ in the single-level Price equation (2.1) fares no better, for on the one hand, it may be non-zero because of non-selective factors or selection on linked genes, and on the other, it may be zero despite genuine selection on z if this is counterbalanced by selection on another gene/trait.

Given these uncertainties, we believe that it is safer to treat these statistics as estimates of parameters of a pre-specified model. Calling them estimates makes it explicit that their interpretation is always relative to a model. For instance, the selection differential $\text{Cov}(w_i/\overline{w},z_i)$ can be taken as an estimate of the strength of linear selection only under a specific causal model such as figure 2. With a different model such as figure 3, the same statistic may correspond to a different parameter and no longer be properly called the selection differential. Of course, in most cases, we do not know which model is true. But at least the causal interpretation, along with the partitioning of the total change into distinct components, becomes a falsifiable hypothesis, which can be tested through an examination of the model’s assumptions.

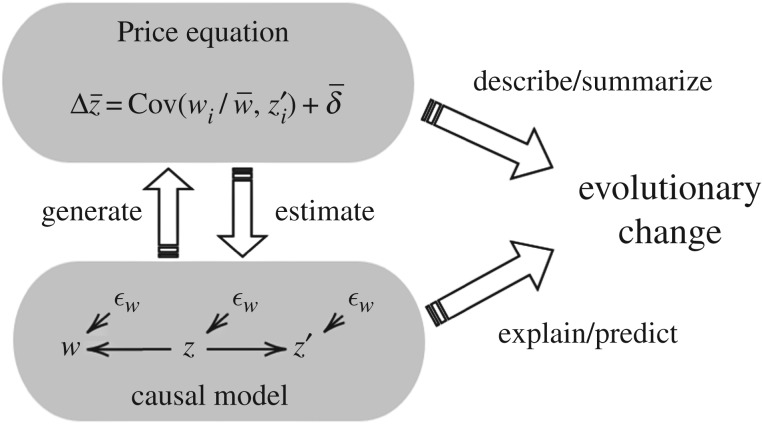
The resulting situation is summarized in figure 4, which illustrates the three-way relation between evolution, the Price equation and a causal model. Evolution is an empirical phenomenon, and the role of the Price equation is to describe and summarize it in concise statistical terms. The equation itself, however, is silent about the causal underpinnings that generate these statistics. The generating mechanism is represented by a causal model, which explains observed evolutionary changes and predicts future changes so long as the model’s assumptions stay valid. Since a causal model is an empirical hypothesis, its structure and parameters must be inferred and estimated from observed data. This is a fallible process, but necessary for making the a priori Price equation into a predictive model. This might not be news, but the neat form of the Price equation has sometimes given an impression that its terms by themselves admit of a causal interpretation. Attention to causal models dispels this illusion and reminds us that a causal reading of the statistical formulae is possible only with a predetermined causal hypothesis.

Figure 4.

The three-way relation between evolution, the Price equation, and a causal model.

6. Conclusion

In this paper, we have examined the oft-made claim that the r.h.s. components of the Price equation (the ‘Cov’ and ‘Exp’ terms) correspond to distinct evolutionary processes, such as natural selection and transmission bias. It turns out that this correspondence is neither straightforward nor universal. Our counterfactual argument showed that computing the difference made by natural selection depends on a convention about the value of δ_i for an individual who leaves no successful gametes, and on an assumption about the minimum modification needed to hypothetically eliminate selection from the population, which is tantamount to an assumption about causal structure. Furthermore, the differences made by selection and by transmission bias only add up to the total change under a specific condition, which in effect says that the two causal processes do not interact. Such a condition can be formally represented in terms of a causal graph, where each component of the Price equation finds a definite causal interpretation as its parameter. An explicit causal model also converts the Price equation, which by itself is an a priori descriptive principle, into an empirical model capable of explaining and predicting evolutionary changes. The Price equation thus has a distinct logical status, and plays a different role in the study of evolution, from other evolutionary models. A failure to recognize this can easily encourage the unwarranted view that the terms in the Price equation always admit of a univocal causal interpretation.

Data accessibility

This article has no additional data.

Authors' contributions

Both authors were equally involved in the research and writing of the paper.

Competing interests

We declare we have no competing interests.

Funding

No funding has been received for this article.