Universal rules for the interaction of selection and transmission in evolution

Abstract

The Price equation shows that evolutionary change can be written in terms of two fundamental variables: the fitness of parents (or ancestors) and the phenotypes of their offspring (descendants). Its power lies in the fact that it requires no simplifying assumptions other than a closed population, but realizing the full potential of Price’s result requires that we flesh out the mathematical representation of both fitness and offspring phenotype. Specifically, both need to be treated as stochastic variables that are themselves functions of parental phenotype. Here, I show how new mathematical tools allow us to do this without introducing any simplifying assumptions. Combining this representation of fitness and phenotype with the stochastic Price equation reveals fundamental rules underlying multivariate evolution and the evolution of inheritance. Finally, I show how the change in the entire phenotype distribution of a population, not simply the mean phenotype, can be written as a single compact equation from which the Price equation and related results can be derived as special cases.

This article is part of the theme issue ‘Fifty years of the Price equation’.

1. Introduction

Model building in biology, as in other fields, usually starts with identification of the process that one wishes to model, then simplifying assumptions are introduced that isolate the process of interest and facilitate mathematical analysis. Different simplifying assumptions are used for different problems. For example, models of selection often assume very large, or fixed, population size; models of drift often assume no selection is acting; models that combine selection and drift often assume that both processes are weak, in the sense that neither causes allele frequency to change by more than a small amount in a generation.

The Price equation [1] is notable because, though Price clearly had a process—selection—in mind, he introduced no simplifying assumptions. The only assumptions required are basically essential properties of the things—populations of organisms—under study. It is assumed that phenotypes can be represented with real numbers, that individuals reproduce, and that there is a population of said organisms that is closed, meaning that there is no immigration.

Aside from the no immigration condition, these assumptions seem so obvious that we usually do not bother to list them. I will refer to assumptions like these, which are widely held to be exactly true (i.e. not approximations) as scientific axioms [2]. A goal of the axiomatic method in mathematics is to start out with a minimal set of necessary axioms and then derive further results from these. The analogue in science would be to start out with a minimal set of scientific axioms and ask how far we can get deriving new results from these before we have to introduce simplifying assumptions. The Price equation (for closed populations) is one result arrived at in this way; I will argue that many others can be found, especially if we introduce a few new mathematical methods.

In the notation used in this paper (table 1), the deterministic Price equation can be written compactly as

$$\mathrm{\Delta }\overline{\varphi }=[[{\varphi }^o,\mathit{\Omega }]]+\overline{\delta },$$ 1.1

where ϕ represents (parental) phenotype; ϕ^o represents the mean phenotype of an individual’s descendants; Ω is relative fitness, defined as individual fitness divided by mean population fitness; and δ is the difference between an individual’s mean offspring phenotype and their own phenotype (i.e. δ = ϕ^o − ϕ). A bar over a term denotes the mean across the population, and double square brackets ([[, ]]) denotes the covariance across the entire population (table 1). The notion of ‘descendants’ used here is very broad; it includes not only offspring but the individual itself at a future time. (Note that if we are combining sexually produced offspring with asexual offspring or the individual itself, we weight each sexually produced offspring by 1/2 when calculating an individual’s fitness, so as not to count them twice when calculating $\overline{w}$. Note that this counting scheme is unnecessary if all reproduction is sexual, or if it is all asexual, since then all offspring are counted the same. Note also that the amount of genetic (or other) information passed to offspring is not relevant to the weighting of descendants in defining fitness; that information goes into the definition of transmission (i.e. defining ϕ^o).)

Table 1.

Symbols and notation.

$\overline{X}$	average value of X across its frequency distribution
$\hat{A}$ or E(A)	expected value of random variable A
$[[X,Y]]$	frequency covariance of X and Y
$⟨⟨A,B⟩⟩$	probability covariance of random variables A and B
$\left[\left[{\hspace{0.17em}}_b^a\right]\right]$	simple regression of a on b
w	absolute fitness (number of descendants after one generation)
Ω	relative fitness ($\mathit{\Omega }=w/\overline{w}$), conditional on $\overline{w}\ne 0$
ϕ	phenotype of an individual
ϕo	average phenotype of an individual’s offspring
δ	ϕo − ϕ
${\mathbb{P}}^j$	simple biorthogonal polynomial in trait ϕj
${\mathbb{P}}_{\bullet }^j$	conditional biorthogonal polynomial in trait ϕj

Equation (1.1) should hold for any closed population, but that is not the same as saying that it addresses all of our questions about evolution. Some of the major issues in evolution that are not obviously amenable to analysis using equation (1.1) are

• Stochasticity: As written, equation (1.1) is deterministic; treating offspring phenotype and relative fitness as determinate values. Strictly, this is valid only if we look at the system in hindsight, after reproduction has taken place. Looking forward in time, the exact values of both fitness and offspring phenotype cannot be predicted with certainty prior to reproduction. This means that we should treat them as random variables, having distributions of possible values.

• Multiple traits with complex transmission: The Price equation includes the effects of both selection and transmission (inheritance), but it is difficult to tease apart their contributions. This is a particular problem when we wish to study the joint evolution of several traits. Simply applying the Price equation separately to each trait does not allow us to see how correlations—as well as more complex relationships—between traits influences their joint evolution.

• Sequences: In principle, a DNA (or RNA, or protein) sequence is a phenotype, so the Price equation should apply. In practice, however, it is difficult to describe a nucleotide using a single numerical value. Nucleotides (or amino acids in a protein) are more appropriately described using vectors, so we will need to adapt our Price-based equations to apply to vector-valued phenotypes.

• The closure problem: The Price equation takes a mixed second moment of a population—the covariance between (offspring) phenotype and relative fitness—and gives us only the change in the mean of one of those variables. This means that some information is lost each generation, so we cannot iterate the equation across multiple future generations.

A common approach to dealing with issues like these is to introduce simplifying assumptions. Sometimes this eliminates the problem altogether. For example, the closure problem disappears if we assume that phenotypes are always normally distributed. This is because the normal distribution is characterized completely by the mean and variance, so we would need to only calculate those two values in the next generation. (Assuming a binomial distribution—requiring that the trait is controlled by one locus, and that individuals mate randomly and exhibit Mendelian transmission—makes things even simpler.)

Even when we do not completely evade the problem, we often introduce assumptions that make the math easier. For example, introducing stochasticity is made easier by holding population size fixed—meaning that mean population fitness is not a random variable—even as we allow some uncertainty in individual fitness.

These are simplifying assumptions because nobody thinks that they are always—or even often—true. Phenotypes are often not normally distributed (in a strict sense they never are, since the normal distribution is continuous and has non-zero values from −∞ to ∞), individuals often mate non-randomly, and all populations vary in size over time.

While all theories must start with some assumptions, they need not be simplifying assumptions. Rather, we can begin with only a set of premises that we believe to be true. The goal of this paper is to show how we can address each of the problems listed above while making only the following assumptions:

• —populations are finite;
• —we can define ancestor–descendant relationships;
• —phenotypes can be quantified with finite valued numbers or tensors;
• —for any individual, there is a probability distribution of possible numbers of descendants that they may leave; and
• —for each potential descendant, there is a probability distribution of possible phenotypic values.

In the following sections, I will discuss how some new mathematical approaches can allow us to address each of these issues.

2. Stochastic fitness and inheritance

The covariance in equation (1.1) is calculated over all individuals in a population. If we are treating the change in mean phenotype ($\mathrm{\Delta }\overline{\varphi }$) as a determinate value, then we are tacitly assuming that each individual has a single value of ϕ^o and of Ω. In this case, ϕ^o and Ω are not strictly random variables—since they are not the result of any random process. Of course, if we were calculating the covariance of values in a random sample from a larger population, which is what statisticians are most often concerned with, then these terms would be random variables, inheriting their randomness from the sampling process. The Price equation, however, is concerned with the entire population, not a sample from it. We are thus (in the case of equation (1.1)) dealing with a covariance between determinate values.

This distinction becomes important when we want to introduce true stochasticity into our analysis. Now, ϕ^o and Ω for a particular individual become true random variables—meaning that we can not assign determinate values to them, but rather must treat them as having probability distributions of possible values. As random variables, they can covary; but this covariance is different from the covariance in equation (1.1).

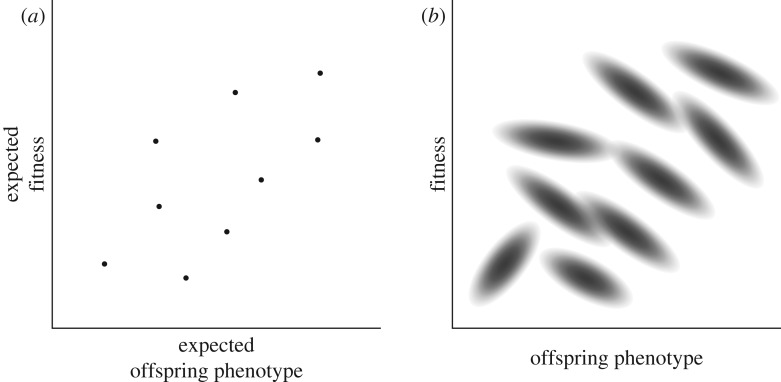
Figure 1 illustrates this distinction. Figure 1a plots expected fitness against expected offspring phenotype for a hypothetical population. Since these are expected values, they are not random variables—each individual has a single determinate value for each variable. The covariance between these values is calculated across the frequency distribution of the population, so we will call it a frequency covariance (denoted [[, ]]). The covariance term in the Price equation (equation (1.1)) is of this kind.

Figure 1.

Distinction between frequency and probability operations. (a) The joint distribution of expected fitness and expected offspring phenotype for a hypothetical population. Each individual corresponds to a distinct point. (b) The complete distributions of offspring phenotype and fitness for the population. Each individual now corresponds to a distinct joint distribution.

In figure 1b, we plot fitness and offspring phenotype directly (not their expected values). Since, in reality, these cannot be known with certainty prior to reproduction, each individual has a joint distribution of ϕ^o and Ω. For each individual organism, there is now a covariance between ϕ^o and Ω (represented by density in figure 1b). Since these covariances are each calculated over a probability distribution of possible future values, we refer to them as probability covariances (denoted 〈〈, 〉〉). There is no biological reason for these probability covariances to bear any resemblance to the frequency covariance between expected values in figure 1a.

Though frequency and probability operations are distinct, there are rules for combining them. Two such rules that are particularly useful are

$$\begin{array}{rl}& \hat{\overline{x}}=\overline{\hat{x}}\\ \text{and}& \widehat{[[x,y]]}-[[\hat{x},\hat{y}]]=\overline{⟨⟨x,y⟩⟩}-⟨⟨\overline{x},\overline{y}⟩⟩.\end{array}\}$$ 2.1

When ϕ^o and Ω become random variables, the change in mean phenotype ($\mathrm{\Delta }\overline{\varphi }$) also becomes a random variable, having a distribution of possible values. If we calculate the expected value of change in mean phenotype, using equation (2.1), we get the stochastic Price equation [3]

$$\widehat{\mathrm{\Delta }\overline{\varphi }}=[[\widehat{{\varphi }^o},\hat{\mathit{\Omega }}]]+\overline{⟨⟨{\varphi }^o,\mathit{\Omega }⟩⟩}+\hat{\overline{\delta }}.$$ 2.2

The first term on the right-hand side of equation (2.2), $[[\widehat{{\varphi }^o},\hat{\mathit{\Omega }}]]$, is the same as the covariance in equation (1.1), except that it involves the expected values of ϕ^o and Ω. This would capture the covariance between the points in figure 1a. The second term, $\overline{⟨⟨{\varphi }^o,\mathit{\Omega }⟩⟩}$, is the frequency average (i.e. the average across all individuals in the population) of the probability covariances between ϕ^o and Ω for each individual. This is like the average of the covariances for the different probability distributions in figure 1b.

Allowing fitness to be a random variable does more than simply introduce uncertainty into the equation, it leads to the appearance of new evolutionary processes that are invisible to the deterministic case. One of these new processes is captured by the mean probability covariance between offspring phenotype and relative fitness ($\overline{⟨⟨{\varphi }^o,\mathit{\Omega }⟩⟩}$), on which we will elaborate in the next section.

There is another, less obvious, way in which equation (2.2) is much more complex than equation (1.1). The term Ω in the frequency covariance in equation (1.1) is the relative fitness of an individual, which is just individual fitness divided by mean population fitness. In the deterministic case, this is just a number. The corresponding term in equation (2.2), $\hat{\mathit{\Omega }}$, looks similar but exhibits much more complex behaviour. This is because both individual fitness (w) and mean population fitness ($\overline{w}$) are now random variables, so $\hat{\mathit{\Omega }}$ is the expected value of a ratio of random variables that are correlated with one another. This value is a function of the entire distribution of possible fitness values, not just the mean.

Some of the consequences of $\hat{\mathit{\Omega }}$ being a function of the entire probability distribution of fitness values are discussed in Rice [3], and these results are extended to include migration in Rice & Papadopoulos [2]. Some of the main conclusions of those papers are:

• Populations are pulled towards phenotypes that minimize the set of even moments of w.

• Populations are pulled towards phenotypes that maximize the odd moments of w.

• The selection differential—the change due only to selection—increases when the variance in $\overline{w}$ increases, as it is expected to as population size declines.

• When migration is included, the impact of immigration on evolution of the population is greatest when the variance in immigration rate is zero (i.e. when the same number of immigrants arrives each generation). As immigration rates become less predictable, it has a smaller effect on evolution.

3. Selection and transmission with multiple traits

By highlighting the importance of the relationship between offspring phenotype and relative fitness, equations (1.1) and (2.2) remind us that transmission plays as important a role in evolution as does selection. Unfortunately, these equations, as written, make it difficult to tease apart the contributions of transmission and selection. In fact, both selection and transmission are wrapped up in both the first and second term on the right-hand side of equation (2.2).

We thus seek results that are as universal as equation (2.2) but more clearly illuminate different biological processes involving both transmission and selection. To achieve this goal, we need to be able to write both offspring phenotype (ϕ^o) and relative fitness (Ω) as functions of parental phenotype (ϕ). The problem here is not just to capture the distribution of variation in a population, which has been approached by using deviations from the normal distribution [4] or using cumulant methods [5], but to construct a space within which we can model selection and transmission.

One approach would be to simply fit a nonlinear function to ϕ^o and Ω. Unfortunately, this will not suffice if our goal is to write a universal equation composed of terms with meaningful biological interpretations. This is because all of the coefficients in a simple polynomial regression are functions of the degree of polynomial that we choose to fit.

To see this, consider the data for offspring and midparent phenotype shown in figure 2 (data from Ryan [6]). Fitting first- and second-order polynomials to this data yields the following functions:

$$\begin{array}{rl}& 1\text{st}\hspace{0.17em}\text{order}:\hspace{0.17em}{\varphi }^o=4.775+0.824\varphi \\ \text{and}& 2\text{nd}\hspace{0.17em}\text{order}:\hspace{0.17em}{\varphi }^o=-417.1+31.685\varphi -0.5636{\varphi }^2\end{array}\}$$ 3.1

Figure 2.

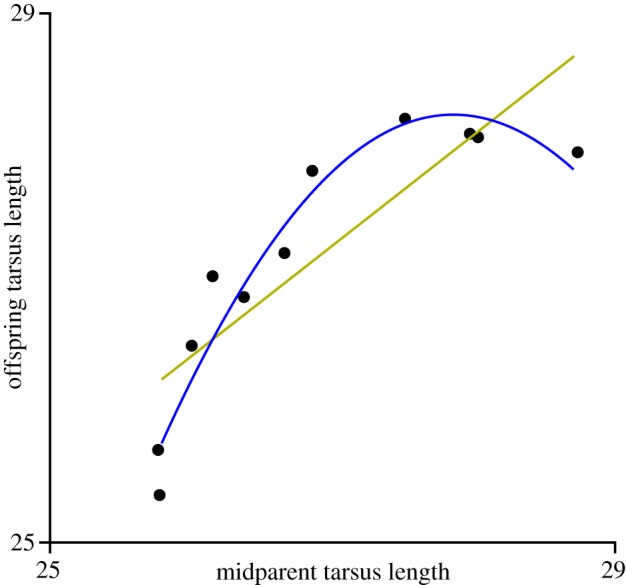
Data from Ryan [6] for offspring versus midparent tarsus length in hybrid buntings. The straight line is the best-fit linear function, the curve is the best-fit quadratic function. (Online version in colour.)

In the first-order function in equations (3.1), the coefficient of ϕ, 0.824, is the heritability of this trait among these individuals. In the second-order approximation, there is also a first-order term, but the coefficient corresponding to it is now 31.685—clearly different from the first-order case and no longer bearing any resemblance to heritability. If we find the best-fit third-order function, the coefficient of ϕ will change yet again, and the coefficient of ϕ² will be different as well. The reason for this is that, as we fit higher and higher order polynomials, effects are being partitioned according to different powers of ϕ, and these are not independent of one another (e.g. ϕ³ is correlated with ϕ).

Because the order of polynomial that we choose to fit to the population is arbitrary, the coefficients have no consistent biological meaning. The way around this problem is to construct a set of orthogonal polynomials in ϕ [7–9]. This is a set of polynomials of increasing order that are constructed so that the first-order polynomial has a mean of zero, and higher order polynomials are constructed to be orthogonal to all lower order polynomials, as well as having means of zero.

Orthogonal polynomials are defined with respect to a ‘weight function’ that determines the region over which the functions are required to be orthogonal. For instance, the Legandre polynomials sometimes used in evolutionary theory to study function valued traits [10–12] use as a weight function a uniform distribution between −1 and 1. The key to solving our problem is to use the population distribution itself as the weight function [8]. (A similar approach, going only to second order, was mentioned in the appendix to Lande & Arnold [13].)

For the data shown in figure 2, the first- and second-order orthogonal polynomials (constructed using only the midparent phenotype values) are

$$\begin{array}{rl}& {\mathbb{P}}^{[1]}=\varphi -27.1237\\ \text{and}& {\mathbb{P}}^{[2]}={\varphi }^2-54.754\varphi +\mathrm{748.509.}\end{array}\}$$ 3.2

Projecting offspring phenotype onto these functions yields a description of transmission in which the coefficients at a given order do not change as we add higher order terms to our analysis. Thus, the coefficient of ${\mathbb{P}}^{[1]}$ is the same, and the same as the heritability of this trait, in both first- and second-order projections in equation (3.3).

$$\begin{array}{rl}& 1\text{st}\hspace{0.17em}\text{order}:\hspace{0.17em}{\varphi }^o=27.133+0.824{\mathbb{P}}^{[1]}\\ \text{and}& 2\text{nd}\hspace{0.17em}\text{order}:\hspace{0.17em}{\varphi }^o=27.133+0.824{\mathbb{P}}^{[1]}-0.5636{\mathbb{P}}^{[2]}.\end{array}\}$$ 3.3

Note that the first-order polynomial differs from the (mid)parent phenotype only by the subtraction of a constant, which does not change covariances or variances. As a result, the regression of offspring on ${\mathbb{P}}^{[1]}$ is the same as the regression of offspring and ϕ—the heritability. The second-order coefficient is the regression of ϕ^o on the second-order orthogonal polynomial. This captures the quadratic relationship between offspring and parents, independent of the linear relationship (which regression on ϕ² would not, since ϕ² and ϕ are likely correlated in the population.

The example above is for a single trait. When we are considering multiple traits, there are multiple polynomials of each order. In this case, we construct a pair of biorthogonal bases [8,14]. This is a pair of bases with the property that each polynomial in one basis is orthogonal to all but one polynomial in the other basis (the definition of biorthogonality) and all polynomials of one order are orthogonal to all in other orders.

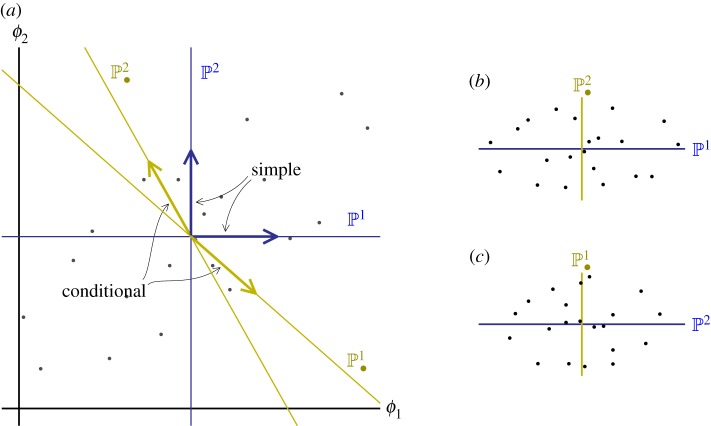
Figure 3 illustrates the first-order biorthogonal bases for two traits. For the first order, the ‘simple’ basis, $({\mathbb{P}}^1,{\mathbb{P}}^2)$, is just the trait values with their means subtracted out (so the population mean is zero). The ‘conditional’ basis, $({\mathbb{P}}_{\bullet }^1,{\mathbb{P}}_{\bullet }^2)$, designated by subscript dots, is biorthogonal to the simple basis. This means that ${\mathbb{P}}_{\bullet }^2$ is orthogonal to ${\mathbb{P}}^1$ and ${\mathbb{P}}_{\bullet }^1$ is orthogonal to ${\mathbb{P}}^2$. Projecting a variable onto the first-order simple polynomial ${\mathbb{P}}^j$ is the same as taking the simple regression on trait ϕ_j. Projecting onto the conditional polynomial, ${\mathbb{P}}_{\bullet }^j$, is the same as taking the partial regression on ϕ_j. Higher order polynomials are orthogonal to all those of lower order, so projections on them are independent of projections on lower order polynomials. The full method for constructing a biorthogonal basis for a population is given in Rice [8].

Figure 3.

(a) Simple and conditional bases for two traits in a population (grey dots denote individuals) in which the traits are positively correlated. The simple bases are just the trait values with the means subtracted out. The conditional bases are constructed so that ${\mathbb{P}}_{\bullet }^1$ is orthogonal to ${\mathbb{P}}^2$, and ${\mathbb{P}}_{\bullet }^2$ is orthogonal to ${\mathbb{P}}^1$. (Note that, because ϕ₁ and ϕ₂ are correlated, orthogonality does not correspond to right angles in this system.) (b,c) Projection of the points into the two pairs of orthogonal bases. (Online version in colour.)

The reason that we use biorthogonal bases is that we need to calculate covariances (such as between offspring phenotype and relative fitness) and this can be done by projecting one variable (e.g. ϕ^o) into the simple basis and the other (e.g. Ω) into the conditional basis [8]. Doing this, and then taking the inner product, yields our equation for multivariate evolution

$$\begin{array}{rl}\widehat{\mathrm{\Delta }{\overline{\varphi }}_i}& =\sum _j[[{\widehat{{\varphi }^o}}_i,{\mathbb{P}}^j]]\hspace{0.17em}\left[\left[{\hspace{0.17em}}_{{\mathbb{P}}_{\bullet }^j}^{\hat{\mathit{\Omega }}}\right]\right]+\sum _j\sum _{k\ge j}[[{\widehat{{\varphi }^o}}_i,{\mathbb{P}}^{\hspace{0.17em}jk}]]\hspace{0.17em}\left[\left[{\hspace{0.17em}}_{{\mathbb{P}}_{\bullet }^{\hspace{0.17em}jk}}^{\hat{\mathit{\Omega }}}\right]\right]\\ & +\sum _j\sum _{k\ge j}\sum _{l\ge k}[[{\widehat{{\varphi }^o}}_i,{\mathbb{P}}^{\hspace{0.17em}jkl}]]\hspace{0.17em}\left[\left[{\hspace{0.17em}}_{{\mathbb{P}}_{\bullet }^{\hspace{0.17em}jkl}}^{\hat{\mathit{\Omega }}}\right]\right]+\cdots \\ & +\sum _j⟨⟨[[{\varphi }_i^o,{\mathbb{P}}^j]],\left[\left[{\hspace{0.17em}}_{{\mathbb{P}}_{\bullet }^j}^{\mathit{\Omega }}\right]\right]⟩⟩+\sum _j\sum _{k\ge j}⟨⟨[[{\varphi }_i^o,{\mathbb{P}}^{\hspace{0.17em}jk}]],\left[\left[{\hspace{0.17em}}_{{\mathbb{P}}_{\bullet }^{\hspace{0.17em}jk}}^{\mathit{\Omega }}\right]\right]⟩⟩\\ & +\cdots +\hat{\overline{{[[{\varphi }^o,\mathit{\Omega }]]}_{\varphi .}}}\end{array}$$ 3.4

The last term in equation (3.4), $\hat{\overline{{[[{\varphi }^o,\mathit{\Omega }]]}_{\varphi }}}$, is the covariance within groups of individuals that have exactly the same phenotypic values for all traits (since, for these, the polynomials pass through the mean values of ϕ^o and Ω for those identical individuals). If any of the traits are continuous, then this term will generally be zero.

Equation (3.4) can be written more compactly, and its structure clarified, by introducing a summation convention. We can write ${\mathbb{P}}^{()}$ to indicate summation over all orders (1st, 2nd, etc. up to N − m, for m traits in a population of size N) and over all combinations (with repetition) of traits within an order. (For two traits, we are thus summing over ϕ₁, ϕ₂, ${\varphi }_1^2$, ${\varphi }_2^2$, ϕ₁ϕ₂, ….). Equation (3.4) now becomes

$$\widehat{\mathrm{\Delta }{\overline{\varphi }}_i}=[[{\widehat{{\varphi }^o}}_i,{\mathbb{P}}^{()}]]\hspace{0.17em}\left[\left[{\hspace{0.17em}}_{{\mathbb{P}}_{\bullet }^{()}}^{\hat{\mathit{\Omega }}}\right]\right]+⟨⟨[[{\varphi }_i^o,{\mathbb{P}}^{()}]],\left[\left[{\hspace{0.17em}}_{{\mathbb{P}}_{\bullet }^{()}}^{\mathit{\Omega }}\right]\right]⟩⟩+\widehat{\overline{[[{\varphi }^o,\mathit{\Omega }]{]}_{\varphi }}}+\hat{\overline{\delta }}.$$ 3.5

The above equation is equivalent to equation (2.2), but it disentangles transmission and selection. The $[[{\varphi }_i^o,{\mathbb{P}}^{()}]]$ terms capture transmission; the first-order ones—$[[{\varphi }_i^o,{\mathbb{P}}^j]]$—being additive genetic covariances between traits ϕ_i and ϕ_j ($[[{\varphi }_i^o,{\mathbb{P}}^i]]$ being the additive genetic variance in ϕ_i). The $[{[}_{{\mathbb{P}}_{\bullet }^{()}}^{\mathit{\Omega }}]]$ terms capture the partial regressions of relative fitness on different combinations of traits. These capture selection, as well as directional stochastic effects.

Because ϕ^o and Ω are random variables, so are $[[{\varphi }_i^o,{\mathbb{P}}^{()}]]$ and $[{[}_{{\mathbb{P}}_{\bullet }}^{\mathit{\Omega }}]]$—meaning that there can be a probability covariance between transmission and selection. These are captured by the $⟨⟨[[{\varphi }_i^o,{\mathbb{P}}^{()}]],[{[}_{{\mathbb{P}}_{\bullet }^{()}}^{\mathit{\Omega }}]]⟩⟩$ terms, which would be invisible to a deterministic model.

Equations (3.4) and (3.5) show that selection and transmission terms of the same order always go together. This is a result of doing our calculations in the space of orthogonal polynomials, and involves no simplifying assumptions about how fitness and transmission are related to one another. One interesting result of this fact is that a particular selection term is relevant to change in mean phenotype only if the corresponding transmission term (of the same order) is non-zero. Thus, for example, third-order selection does not influence $\widehat{\mathrm{\Delta }\overline{\varphi }}$ unless there is also third-order transmission. (Note, though, that the stochastic terms may still be non-zero even when the expected value of selection or transmission is zero.)

There is good reason to expect that transmission and selection will covary in some natural systems. Heritability, or additive genetic variance, are often different in different environments [15–20]. If the different environments impose different selection regimes, then a population that encounters both environments will experience a covariance between transmission and selection. In such a case, selection in the environment with higher heritability will lead to a larger magnitude of change than will selection in the low heritability environment.

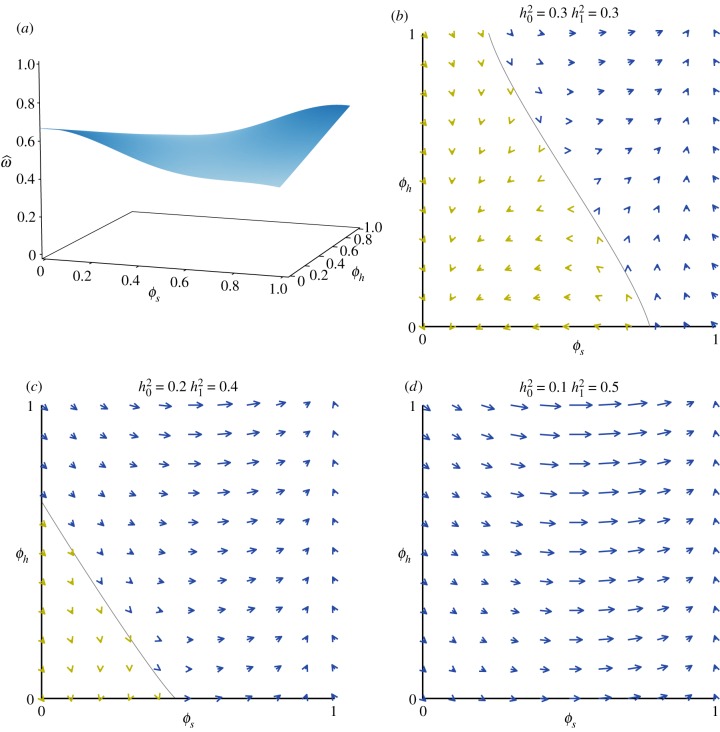
Figure 4 shows a case with two traits; one (ϕ_s) experiences different selection in the two different habitats. The other (ϕ_h) is a habitat preference trait that influences the probability that an individual experiences one or the other habitat. If ϕ_h = 0 the individual has a preference for habitat 0, and if ϕ_h = 1 they have a preference for habitat 1. ϕ_h = 1/2 corresponds to no preference (for details, see [8]).

Figure 4.

(a) A fitness landscape for two traits when individuals encounter one of two environments. ϕ_s has different optima in the two environments (ϕ_s = 0 optimum in environment 0, ϕ_s = 1 optimum in environment 1), and ϕ_h determines the probability that an individual encounters one or the other environment. (b–d) Vectors of evolutionary change at different starting points. The diagonal grey line in (b) and (c) indicates the boundary between points from which the population eventually evolves towards (0,0) and the points from which it eventually evolves towards (1,1). (Online version in colour.)

Figure 4a shows the expected fitness function for these two traits. There are peaks at [ϕ_s = 0, ϕ_h = 0] (being adapted to habitat 0 and preferring habitat 0), and at [ϕ_s = 1, ϕ_h = 1] (being adapted to habitat 1 and preferring habitat 1).

Using equation (3.5) for these two traits, we can calculate the expected change in each trait from any starting point. Doing this for a set of values yields a vector field that shows the direction and magnitude of evolution at each point. Figure 4b shows this vector field for the case in which heritability is the same (0.3) in both environments. In this case, the population evolves uphill on the landscape—following the fitness gradient—as would be predicted by quantitative genetics models. (I use heritability in the example, instead of additive genetic variance, because it is easier to intuitively evaluate. Because the phenotypic variance is held constant, there is a linear relationship between heritability and additive genetic variance in these examples.)

Things change when the heritabilities are different in the two environments. Figure 4c shows the case in which the heritability in environment 0 is 0.2, while that in environment 1 is 0.4 (the fitness function is still that shown in 4a). In this case, the population does not follow the fitness gradient, and in fact may be pulled across a fitness valley. In figure 4d, the difference in heritability is greater; 0.1 in environment 0 and 0.5 in environment 1. Here, the population evolves towards [ϕ_s = 1, ϕ_h = 1] from every starting point in this region, even though the fitness landscape is still the same. All of these heritability values, including the most extreme ones (0.1 and 0.5) are well within the range commonly seen in natural populations [19,21].

This example illustrates one way in which heritability can evolve—as individuals end up preferring environments in which heritability is relatively high. Note that there is no direct selection on heritability in this case. Rather, the trait ϕ_s tends to adapt to the environment with higher heritability. This, in turn, produces selection on the habitat preference trait (ϕ_h) to evolve towards preference for that environment because individuals have higher fitness there. Heritability evolves as a secondary consequence.

(Note that the orthogonal polynomial methods discussed here are different from statistical methods of hypothesis testing such as analysis of variance. Here, we are not trying to compare means or variances, nor are we trying to define test statistics for anything. Rather, our goal is to construct a space, with a corresponding coordinate system, within which we can do all of our calculations—plotting functions, integrating them, finding inner products, etc.—without making any simplifying assumptions about the distribution of variation in the population.)

4. Phenotypes that are sequences

Building meaningful theories requires that we represent biological entities in such a way that mathematical operations on our representations yield biologically meaningful results. We have, so far, been able to represent phenotypic values as real numbers, but this approach runs into problems when the traits of interest are sequences.

Consider the sequence of nucleotides in a DNA molecule (the same reasoning will apply to RNA as well as to the sequence of amino acids in a protein). Ideally, we would like to treat each site in the sequence as a distinct trait, then construct a basis using biorthogonal polynomials of these traits so that we can project some value of interest, such as offspring phenotype, into it; allowing us to represent that trait as a function of the sequence.

One approach to quantifying nucleotides, used sometimes in computational biology, is to represent each possible nucleotide as a number. Using binary numbers, we would have something like this

$$\begin{array}{cccc}\text{A}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& \text{C}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& \text{G}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& \text{T}\\ 00\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& 01\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& 10\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& 11\end{array}$$ 4.1

Here, we note an important difference between computational and mathematical biology. For purely computational problems, the numerical value assigned to a nucleotide is just a name, which could be interpreted in various different ways by an algorithm. By contrast, if we want to do analytical theory, then our representations of nucleotides must obey the rules of mathematics, and applying these rules must yield the correct biological result. Applying simple arithmetic to the numerical values given in (4.1) quickly shows that they do not pass this test.

For example: we often need to calculate the mean value of a phenotype, but under the scheme given in (4.1) the mean of an A and a G is a C (since the mean, in binary, of 00 and 10 is 01), and the sum of a C and a G is a T.

$$\begin{array}{cc}& \overline{(\mathrm{A},\hspace{0.17em}\mathrm{G})}=\text{C}\\ \text{and}& \text{C + G}=\text{T.}\end{array}\}$$ 4.2

These results are clearly biologically (and chemically) meaningless; the sum of two nucleotides is not a different nucleotide.

The way around this is to represent monomers as vectors that are orthogonal to one another. For simplicity, we will consider a DNA sequence; so the vectors are four dimensional. The approach can be modified for use with amino acid sequences by simply making the vectors bigger. We represent the DNA nucleotides as

$$\begin{array}{r}\begin{array}{cccc}\text{A}& \text{C}& \text{G}& \text{T}\\ \left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]& \left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]& \left[\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right]& \left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right].\end{array}\end{array}$$ 4.3

Using this representation, the mean of a set of nucleotides is not another nucleotide, but rather a different vector that represents the combination of nucleotides in the sample

$$\overline{(\mathrm{A},\hspace{0.17em}\mathrm{G})}=\left[\begin{array}{c}\frac{1}{2}\\ \\ 0\\ \frac{1}{2}\\ 0\end{array}\right].$$ 4.4

Beyond simply avoiding the nonsense results in (4.2), this representation yields more information than would a set of numbers. If we take the mean of a set of numerical (scalar) values, we lose information about the original distribution. For example, saying that the mean height of a group of people is 5′ 10″ is consistent both with everyone being 5′ 10″, and with nobody being that height. By contrast, the mean of a set of orthogonal vectors gives us the distribution of those vectors. So, for example, the vector in equation (4.4) tells us that, in this sample, $\frac{1}{2}$ of the nucleotides are ‘A’ and $\frac{1}{2}$ are ‘G’.

Unfortunately, standard theory of orthogonal polynomials considers only scalar-valued polynomials. We can extend it to apply to the case of nucleotides, however, with a slight modification. (Note that we are not talking about a vector of polynomials, which would simply be a variant of the multivariate case described above, but polynomials in which the variable is a vector, and higher powers of it are higher rank tensors. Such polynomials have non-commutative coefficients, and while some cases of non-commutative polynomials have been studied, I am not aware of any that include the cases that we encounter in representing sequences.)

(a). Vector-based orthogonal polynomials

I will illustrate the approach with an example of four individuals, each with a two base sequence (the two bases that we are considering need not be adjacent to one another)

$$\begin{array}{c}\text{individual}\\ \text{sequence}\end{array}\hspace{0.17em}|\hspace{0.17em}\begin{array}{cccc}1& 2& 3& 4\\ \mathrm{AC}& \mathrm{CG}& \mathrm{CC}& \mathrm{GA}\end{array}$$

We designate the ith monomer as μ_i. The first-order phenotype vectors for the four individual sequences above look like this

$$\begin{array}{rl}& \mathrm{individual}:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2\hspace{0.17em}3\hspace{0.17em}\\ & {\mu }_1{\mu }_2{\mu }_1{\mu }_2\hspace{0.17em}{\mu }_1{\mu }_2\hspace{0.17em}{\mu }_1{\mu }_2\\ & \left(\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]\right)\left(\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]\left[\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right]\right)\left(\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]\right)\left(\left[\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right]\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]\right).\end{array}$$ 4.5

As with the scaler case, we construct the first order simple basis by subtracting the mean from each value. We use ${\mathbb{M}}^1$ and ${\mathbb{M}}^2$ to denote the first-order simple basis for monomers in a sequence (these are the vector-based analogues of ${\mathbb{P}}^1$ and ${\mathbb{P}}^2$).

The second-order phenotypes are matrices, giving the combination of nucleotides at two different sites. For the example in (4.5), these are

$$\begin{array}{rl}& \mathrm{individual}:12\hspace{0.17em}\hspace{0.17em}3\hspace{0.17em}\hspace{0.17em}4\\ & {\mu }_{12}{\mu }_{12}{\mu }_{12}{\mu }_{12}\\ & \left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 1& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\end{array}$$ 4.6

Note that for the case of two sites, there is only one second-order phenotype that matters, μ₁₂, as opposed to three in the case of two scalar traits (${\varphi }_1^2$, ϕ₁ϕ₂, and ${\varphi }_2^2$). This is because all the terms in the μ vectors are 0 or 1, both of which remain unchanged when we square them. For the same reason, there are no third or higher order terms if we are considering only two sites (there will, of course, be third-order terms, and more than one second-order term, if we consider three sites).

The second-order orthogonal polynomials, ${\mathbb{M}}^{12}$ in this example, are constructed to be orthogonal to the first-order polynomials, and to have a mean of zero.

As with the scalar-based polynomials in the previous section, our goal is to represent other variables by projecting them into the set of $\mathbb{M}$ polynomials. Regression of a trait on a vector is done separately for each term in the vector; and this presents a problem because, though the vectors are orthogonal to one another, the terms within each vector are correlated with one another.

The solution to this problem is to pre-multiply each $\mathbb{M}$ term by a tensor defined as the outer product of the corresponding phenotype with itself. With this modification, we can write any variable of interest as a function of the set of monomers in the sequence. For the case of only two monomers (nucleotides, amino acids, etc.), the projection of ϕ^o looks like this.

$$\begin{array}{rl}{\varphi }^o& =\overline{{\varphi }^o}+[{[}_{{\mathbb{M}}^1}^{{\varphi }^o}]]\cdot ({\mu }_1\otimes {\mu }_1\cdot {\mathbb{M}}^1)+[{[}_{{\mathbb{M}}_{\bullet }^2}^{{\varphi }^o}]]\cdot ({\mu }_2\otimes {\mu }_2\cdot {\mathbb{M}}_{\bullet }^2)\\ & +[{[}_{{\mathbb{M}}^{12}}^{{\varphi }^o}]]\cdot ({\mu }_{12}\otimes {\mu }_{12}\cdot {\mathbb{M}}^{12}).\end{array}$$ 4.7

Though the individual terms in equation (4.7) are more complicated than those in the scalar polynomial case, the fact that any particular monomer is either present or absent, rather than a continuous variable, means that there are far fewer terms in the series than there would be for a continuous scalar phenotype. Using this approach, we can apply results like equation (3.5) to sequence-based traits.

5. Beyond the mean: following the entire population

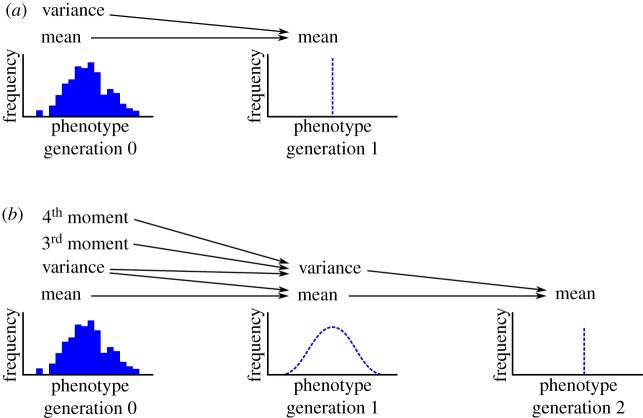
The Price equation requires information about the first and second moments of variation in one generation to calculate the mean in the next generation (figure 5a). This poses a problem if we want to extend our prediction to the generation after that, since we would need the variance in the next generation, which we did not calculate. We could, of course, calculate the variance in generation 1 using higher moments of the distribution in generation 0, but this would involve a separate calculation—and would only get us to the mean in generation 2 (figure 5b).

Figure 5.

Loss of information with each iteration of the Price equation. (Online version in colour.)

The loss of information each generation means that the Price equation approach does not give us a single equation—or even a closed set of equations—that can be iterated forward in time indefinitely. This is the closure problem in evolutionary theory.

Some authors, including me [3], have taken this to be an inescapable consequence of the complexity of phenotypes, which can be avoided only by introducing simplifying assumptions [3,22]. In fact, there is a way around it that will allow us to write a complete description of evolutionary change with no loss of information each generation.

(a). A solution: the population transform

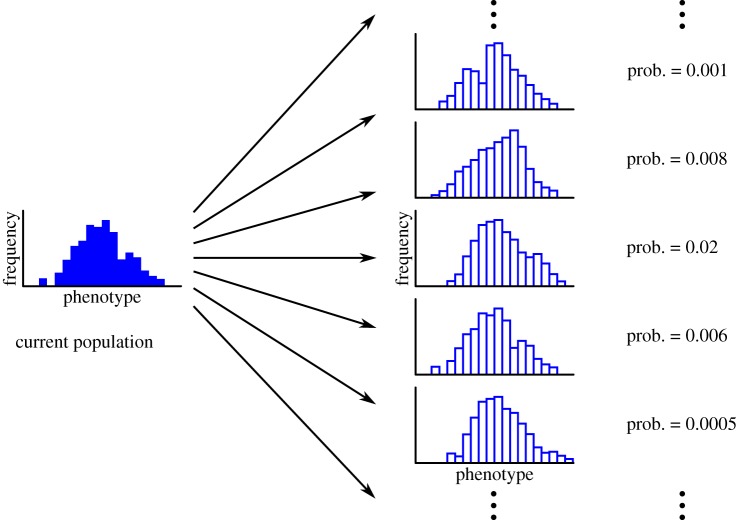
We need to capture the entire phenotype distribution of a population in a single mathematical unit, and then describe how the probability distribution of these frequency distributions changes over time. Figure 6 shows schematically what we want to achieve.

Figure 6.

The challenge: construct the probability distribution of future populations (represented by frequency distributions), given the current population distribution and patterns of fitness and transmission. (Online version in colour.)

The state of a population is captured by a frequency distribution. We can capture this distribution, for a particular group of individuals, using the number of individuals and the moment generating function

$$n\overline{{\text{e}}^{\hspace{0.17em}f\varphi }}.$$ 5.1

Here, n is the number of individuals and f is a transform variable. The bar indicates frequency mean. Thus, for a group of three individuals, one with phenotype ϕ = 1.5 and two with phenotype ϕ = 4, equation (5.1) would be: (3 · ((1/3)e^1.5f + (2/3)e^4f)).

The fact that all populations are finite, and the stipulation that the phenotype, ϕ, is finite, ensure that all moments exist; meaning that the moment generating function in equation (5.1) is a compact way to capture the population distribution.

The next step is to capture the probability distribution of possible populations. This is accomplished by defining a characteristic function of the moment generating function, which I will refer to as the population transform.

$$\text{The population transform}:\hspace{0.17em}{\mathcal{E}}_{\varphi ,n}=\hat{{\mathrm{e}}^{ipn\overline{{\mathrm{e}}^{\hspace{0.17em}f\varphi }}}}.$$ 5.2

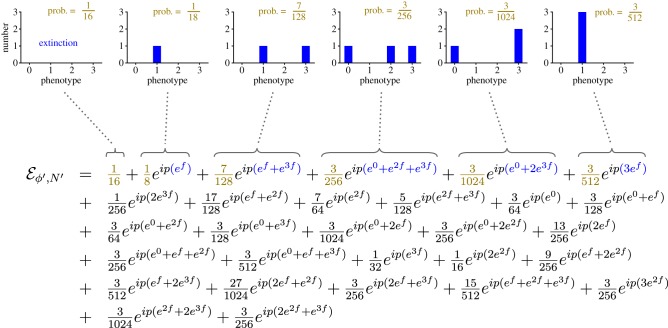
Here, p is the probability transform variable, and $i=\sqrt{-1}$. The hat denotes the expected value over all possible phenotype distributions, so equation (5.2) can be expanded to yield a set of terms, each of which corresponds to a different possible distribution of phenotypes, multiplied by the probability of that particular distribution arising (figure 8).

Figure 8.

Expansion of ${\mathcal{E}}_{{\varphi }^{\prime },N^{\prime }}$ illustrating how it contains all possible populations (after one generation) descended from the parents who's fitness and offspring distributions are given in figure 7. The phenotype distributions shown above the equation illustrate the population states corresponding to the first six terms in the expansion. (Online version in colour.)

The reason for adding all of these layers is that we now have a compact way to write the distribution of distributions that we can follow from one generation to the next. We will see below that this is easier than one might expect.

(Equation (5.2) is analogous to a Fourier transform of a Laplace transform. Note that the transform variables f and p do not correspond to any biological process. They serve to keep the different distributions and phenotypes distinct. We will see below that they also allow us to derive special cases, including the Price equation, from our main result.)

Equation (5.2) can uniquely describe any probability distribution of frequency distributions—whether for an entire population or for any subset of individuals. For example, the possible fitness values for an individual j (w_j) and the possible phenotypes of any descendants that it leaves (${\varphi }_j^o$) are jointly captured by:

$$\text{Individual}\hspace{0.17em}{j}^{\prime }s\hspace{0.17em}\text{descendants}:\hspace{0.17em}{\mathcal{E}}_{{\varphi }_j^o,w_j}=\hspace{0.17em}\hspace{0.17em}\hat{{\mathrm{e}}^{ip{w}_j\overline{{\mathrm{e}}^{\hspace{0.17em}f{\varphi }_j^o}}}}.$$ 5.3

The distribution of possible mated pairs is also a probability distribution of frequency distributions (each of size 2). To distinguish the sexes in each pair, we define two frequency transform variables, f_f and f_m for females and males, respectively. The transform of the distribution is then:

$$\begin{array}{rl}& \text{Distribution of possible mated pairs}:\\ & {\mathcal{E}}_{{\varphi }_m,{\varphi }_{\hspace{0.17em}f},2}=\hspace{0.17em}\hat{{\mathrm{e}}^{ip2{\mathrm{e}}^{\hspace{0.17em}{f}_f{\varphi }_f+f_m{\varphi }_m}}}.\end{array}$$ 5.4

Finally, the transform of the entire distribution of possible population states in the next generation is given by:

$$\text{Future populations}:\hspace{0.17em}{\mathcal{E}}_{{\varphi }^{\prime },N^{\prime }}=\hat{{\mathrm{e}}^{ipN\overline{{\mathrm{e}}^{\hspace{0.17em}f{\varphi }^o}}}}.$$ 5.5

Here, N is a random variable denoting population size. By including population size as well as the distribution of phenotypes, we are following both population dynamics and evolution.

The reason for writing everything in terms of the population transform is that it allows us to write a surprisingly simple equation for the transform of the entire population in the next generation as a function of the transforms of all individuals in the current generation

$${\mathcal{E}}_{{\varphi }^{\prime },N^{\prime }}=\prod _{\hspace{0.17em}j=1}^N{\mathcal{E}}_{{\varphi }_j^o,w_j}+\mathcal{A}.$$ 5.6

The product term on the right-hand side of equation (5.6) combines the independent contributions of each individual (or mated pair) to each phenotypic value in the next generation. The $\mathcal{A}$ term has the same general form as equation (5.2), but captures non-independence between the contributions of different individuals. (So, for instance, if the probability of individual j producing an offspring with phenotypic value ϕ* is influenced by whether or not individual k also does so, then this would enter into the terms in $\mathcal{A}$ that contain ϕ*.)

Equation (5.6) works because, in the absence of migration, the next generation is the convolution of the contributions of individuals in the current generation. This just means that we calculate the number of individuals with phenotypic value ϕ* in the next generation as the sum of contributions of each individual in the current population to ϕ*. Certain transforms, including the Laplace transform (used in equation (5.1)) and the Fourier transform (used in equation (5.2)), greatly facilitate calculation of convolutions. Specifically, the Convolution Theorem [23] states that, for these transforms, the transform of the convolution of two distributions is simply the product of the transforms of the distributions.

As to why we choose the particular transforms used here: we can always capture the frequency distribution in a population with equation (5.1) because the fact that populations and phenotypes are finite (axioms 1 and 3) insures that all moments exist, along with the moment generating function (mgf). When we are considering all possible future populations, however, it is not clear that the mgf will be defined (for example, it is not defined for the log-normal distribution). This is why we use the characteristic function in equation (5.2), since it is defined even when the mgf is not.

As an example: consider a population of two individuals, with phenotypic values 1 and 2, respectively, and the fitness and offspring phenotype distributions shown in figure 7. For simplicity, we will assume that the phenotypes of each individual’s offspring are independent, so $\mathcal{A}=0$.

Figure 7.

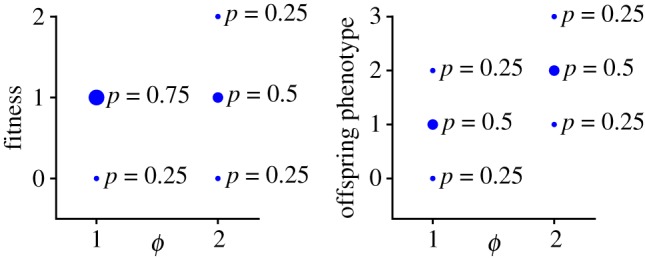
Example distributions of fitness and offspring phenotype for two different individuals, one with phenotype ϕ = 1 and the other with phenotype ϕ = 2. (Online version in colour.)

The individual fitness/offspring transforms (equation (5.3)) for these two individuals are

$$\begin{array}{rl}& {\mathcal{E}}_{{\varphi }_1^o,w_1}=\frac{1}{4}{\text{e}}^{ip\cdot 0}+\frac{3}{4}(\frac{1}{4}{\text{e}}^{ip\cdot {\mathrm{e}}^{0\cdot f}}+\frac{1}{2}{\text{e}}^{ip{\mathrm{e}}^{1\cdot f}}+\frac{1}{4}{\text{e}}^{ip{\mathrm{e}}^{2\cdot f}})\\ \text{and}& {\mathcal{E}}_{{\varphi }_2^o,w_2}=\frac{1}{4}{\text{e}}^{ip\cdot 0}+\frac{1}{2}(\frac{1}{4}{\text{e}}^{ip{\mathrm{e}}^{1\cdot f}}+\frac{1}{2}{\text{e}}^{ip{\mathrm{e}}^{2\cdot f}}+\frac{1}{4}{\text{e}}^{ip{\mathrm{e}}^{3\cdot f}})\\ & \hspace{0.17em}+\frac{1}{4}{(\frac{1}{4}{\text{e}}^{ip{\mathrm{e}}^{1\cdot f}}+\frac{1}{2}{\text{e}}^{ip{\mathrm{e}}^{2\cdot f}}+\frac{1}{4}{\text{e}}^{ip{\mathrm{e}}^{3\cdot f}})}^2.\end{array}\}$$ 5.7

(Note that e⁰ = 1, so the first term in both of equations (5.7) could be written simply as $\frac{1}{4}$.)

Using equation (5.6), we can find ${\mathcal{E}}_{{\varphi }^{\prime },N^{\prime }}$. Figure 8 shows how this gives the complete probability distribution of possible future populations. Each term in ${\mathcal{E}}_{{\varphi }^{\prime },N^{\prime }}$ corresponds to a different possible population in the next generation.

The distributions above the first six terms in figure 8 show how to interpret each term in the expansion. The coefficients of f in the secondary exponent (e.g. 3 in the term $\frac{1}{256}{\text{e}}^{ip(2{\mathrm{e}}^{3f})}$) give the phenotypic value of individual descendants. The coefficient of a secondary exponent itself (e.g. 2 in the term $\frac{1}{256}{\text{e}}^{ip(2{\mathrm{e}}^{3f})}$) gives the number of individuals with that phenotypic value (here, two individuals each with ϕ = 3). Finally, the coefficient of the entire term (e.g. $\frac{1}{256}$ in the term $\frac{1}{256}{\text{e}}^{ip(2{\mathrm{e}}^{3f})}$) gives the probability of that particular future population. Thus, the term $\frac{1}{256}{\text{e}}^{ip(2{\mathrm{e}}^{3f})}$ tells us that there is a probability of $\frac{1}{256}$ that there will be two descendants each with a phenotypic value of 3. Similarly, the term $\frac{1}{1024}{\text{e}}^{ip({\mathrm{e}}^0+2{\mathrm{e}}^{3f})}$ means that there is a probability of $\frac{1}{1024}$ that the population of descendants will contain one individual with phenotypic value 0 and two individuals with phenotypic value 3.

The first term in figure 8 corresponds to the case in which there are no descendants (it could be written $\frac{1}{16}{\text{e}}^{ip\cdot 0}$). It thus tells us that the probability of extinction in this case is $\frac{1}{16}$.

Equation (5.6) is in some ways analogous to the Schrödinger equation from physics, in that it describes how the distribution of possible states of a system changes over time. Here, however, the ‘state’ of a population is itself a frequency distribution. As with the Schrödinger equation, analytically solving equation (5.6) for anything larger than a tiny population will become prohibitively difficult. It is still of value, though, both as a conceptual foundation and as a tool for deriving other results.

From a conceptual standpoint, equation (5.6) shows that the closure problem in evolutionary theory is not an inevitable consequence of biological complexity. It is possible to follow all possible future states of a population with no loss of information each generation. (Of course, accurately iterating the equation forward would require either knowing what the fitness distributions will be, or including all phenotypes that influence fitness.) The solution is complicated—but it exists.

This formulation also brings extinction—an important evolutionary process that is often ignored except in models designed specifically to study it—into the same mathematical framework that describes change in allele frequency or mean phenotype.

From a practical standpoint, it may be possible to use equation (5.6) to solve for important special cases, such as when the phenotype is binary. Furthermore, as discussed below, a variant of equation (5.6) can be used to derive a variety of simpler results—including the Price equation.

(b). Deriving the Price equation and related results

If equation (5.6) really encompasses all possible evolutionary outcomes, then we should be able to derive the stochastic Price equation from it, as the expected change in the mean of the population. To do this, note that with a slight modification, the population transform, $\mathcal{E}$, becomes a moment generating function.

As figure 8 shows, equation (5.6) gives the numbers—as opposed to the frequencies—of individuals with each phenotypic value in each possible future population. In order to get a moment generating function for the future population, we need to divide each individual’s absolute fitness, w, by the total number of descendants, which is just $N\overline{w}$. We thus just need to substitute ΩN⁻¹ for w in equation (5.6)—turning the distributions in figure 8 into frequency distributions. The result is a moment generating function for the future population distribution

$${\mathcal{G}}_{{\varphi }^{\prime }}=\prod _{\hspace{0.17em}j=1}^N{\mathcal{E}}_{{\varphi }_j^o,{\mathit{\Omega }}_j{N}^{-1}}.$$ 5.8

We can find the nth probability moment of the mth frequency moment in the next generation by differentiating equation (5.8) n times with respect to ip and m times with respect to f, then setting both p and f equal to zero.

(i). Expected change in the mean (Price)

For example, if we want to know the expected mean phenotype in the next generation ($\widehat{{\overline{\varphi }}^{\prime }}$), we differentiate equation (5.8) once with respect to f (to get the frequency mean) and once with respect to ip (to get the expected value) and then set f and p equal to zero. Doing this yields

$$\widehat{{\overline{\varphi }}^{\prime }}={\frac{{\mathrm{\partial }}^2{\mathcal{G}}_{{\varphi }^{\prime }}}{\mathrm{\partial }p\mathrm{\partial }f}|}_{\hspace{0.17em}p=f=0}=\widehat{\overline{{\varphi }^o\mathit{\Omega }}}.$$ 5.9

The expected change in mean phenotype is then just

$$\widehat{\mathrm{\Delta }\overline{\varphi }}=\widehat{\overline{{\varphi }^o\mathit{\Omega }}}-\overline{\varphi }.$$ 5.10

Applying the rules for manipulating frequency and probability operations (equations (2.1)) to equation (5.10) quickly yields the stochastic Price equation (equation (2.2)), or the original Price equation if we just remove the hats.

(ii). Change in the covariance

The example above considers only one phenotypic trait, but a slight extension allows us to consider multiple traits. For two traits, the transform for an individual’s possible offspring distributions would be

$${\mathcal{E}}_{{\varphi }_1^o,{\varphi }_2^o,w_j}=\hspace{0.17em}\hat{{\mathrm{e}}^{ip{w}_j\overline{{\mathrm{e}}^{\hspace{0.17em}{f}_1{\varphi }_1^o+f_2{\varphi }_2^o}}}}.$$ 5.11

Each trait has a separate frequency transform variable, f, since we can consider the frequency of each trait separately from the others. There is still only one probability transform variable (p) though.

To find the expected covariance after selection, we use the bivariate transform in equation (5.11), substituting Ω_jN⁻¹ for w_j. Differentiating with respect to f₁, f₂ and ip, then setting each of these equal to zero

$${\frac{{\mathrm{\partial }}^3{\mathcal{G}}_{{\varphi }_1^{\prime },{\varphi }_2^{\prime }}}{\mathrm{\partial }p\mathrm{\partial }{f}_1\mathrm{\partial }{f}_2}|}_{\hspace{0.17em}p=f_1=f_2=0}=\widehat{\overline{{\varphi }_1^o{\varphi }_2^o\mathit{\Omega }}}.$$ 5.12

Equation (5.12) gives the expected value of $\overline{{\varphi }_1{\varphi }_2}$ after selection. Subtracting the product of the expected values of ${\overline{\varphi }}_1^{\prime }$ and ${\overline{\varphi }}_2^{\prime }$ (from equation (5.9)) we find the expected covariance in the next generation.

Both selection and transmission contribute to change in covariation between traits, and they interact in complex ways. Here, we will focus just on the effects of selection. Setting ${\varphi }_i^o={\varphi }_i$, we find the change in covariance between ϕ₁ and ϕ₂, due only to the action of selection, to be

$$\begin{array}{rl}\widehat{\mathrm{\Delta }[[{\varphi }_1,{\varphi }_2]]}& =[[{\varphi }_1{\varphi }_2,\hat{\mathit{\Omega }}]]-[[{\varphi }_1,\hat{\mathit{\Omega }}]][[{\varphi }_2,\hat{\mathit{\Omega }}]]\\ & -⟨⟨[[{\varphi }_1,\mathit{\Omega }]],[[{\varphi }_2,\mathit{\Omega }]]⟩⟩.\end{array}$$ 5.13

The first term on the right-hand side of equation (5.13) suggests that, as one would expect, selection on the product of two traits, all else held equal, will increase the covariance between them. The second term, however, shows that independent selection for two different traits to each increase (or to each decrease) contributes to a negative covariance between them. Conversely, if one trait is selected to increase while the other is selected to decrease, then this selection will tend to create a positive covariance between them. The third term shows that if the traits tend to be both positively or negatively selected at the same times, then this also contributes to a negative covariance.

This is a generalization of the fact, associated with the Hill-Robertson effect [24], that selection for alleles at two different loci leads to a negative gametic disequilibrium between them (gametic—or ‘linkage’—disequilibrium can be interpreted as a covariance between the presence of alleles at different loci [25]). It is also consistent with the observation from quantitative genetics that selection to increase two traits that are positively correlated tends to reduce the correlation between them [26].

6. Conclusion

The Price equation showed that it is possible to build axiomatic theories—useful mathematical theories based only on assumptions that we think are actually true—in evolutionary biology. We have seen that with some new mathematical tools, this generality can be extended, without introducing simplifying assumptions, to a range of evolutionary problems that are not, at first glance, amenable to the Price equation. We have also seen that the Price equation itself is not the only—or even the most general—axiomatic result possible.

Note that while I have emphasized the idea of axiomatic theories, simplifying assumptions have nonetheless played an important role in our discussion. For example, the results in figure 4 assumed that transmission is linear within each environment, to highlight the effects of there being different heritabilities in different environments. Similarly, equation (5.13) assumed that ϕ^o = ϕ, to highlight the effects of selection alone on changing covariation between traits.

The difference between this approach and conventional model building is that instead of starting out with simplifying assumptions, and letting these determine the mathematics that we will use and the results that we can see, we start with only assumptions that we think are exactly true (scientific axioms) and derive our main results from these. These general results, when expanded, are likely to be complicated (cf. equation (3.4)), but are made up of terms that have clear biological meaning. Introducing simplifying assumptions at this stage allows us to zoom in on particular terms of interest, such as $⟨⟨[[{\varphi }^o,{\mathbb{P}}^1]],[{[}_{{\mathbb{P}}_{\bullet }^1}^{\mathit{\Omega }}]]⟩⟩$. One advantage of this is that it makes it easy to relax or change our assumptions, and to see what we are excluding. If we wanted to see what the example in figure 4 would look like if transmission were nonlinear, we need only look at the second-order terms in equation (3.4). Axiomatic theories, inspired by Price [1], thus serve not only as unifying principles, but also as formulae for building new special case models.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interest.

Funding

This work was supported in part by NSF grant EF 0928772 to S.H.R.