Dormancy dampens the microbial distance–decay relationship

Abstract

Much of Earth's biodiversity has the capacity to engage in dormancy, a reversible state of reduced metabolic activity. By increasing resilience to unfavourable conditions, dormancy leads to the accumulation of ‘seed banks’. These reservoirs of genetic and phenotypic diversity should diminish the strength of environmental filtering and increase rates of dispersal. Although prevalent among single-celled organisms, evidence that dormancy influences patterns of microbial biogeography is lacking. We constructed geographical and environmental distance–decay relationships (DDRs) for the total (DNA) and active (RNA) portions of bacterial communities in a regional-scale 16S rRNA survey of forested ponds in Indiana, USA. As predicted, total communities harboured greater diversity and exhibited weaker DDRs than active communities. These observations were robust to random resampling and different community metrics. To evaluate the processes underlying the biogeographic patterns, we developed a platform of mechanistic models that used the geographical coordinates and environmental characteristics of our study system. Based on more than 10⁶ simulations, our models approximated the empirical DDRs when there was strong environmental filtering along with the presence of long-lived seed banks. By contrast, the inclusion of dispersal generally decreased model performance. Together, our findings support recent theoretical predictions that seed banks can influence the biogeographic patterns of microbial communities.

This article is part of the theme issue ‘Conceptual challenges in microbial community ecology’.

1. Introduction

Dormancy is a reversible state of reduced metabolic activity that has independently evolved numerous times across the tree of life [1,2]. Among plants, animals and the microbial life that dominates our planet, many organisms contribute to the collection of dormant individuals known as a seed bank [2–4]. Seed banks are often viewed as the outcome of a bet-hedging strategy that allows populations to distribute reproductive effort among long-lived individuals over time [1,5,6]. By increasing survival in fluctuating environments, dormancy reduces the probability of local extinctions, while maintaining genetic and phenotypic diversity via the storage effect [2,7–9]. Although crucial for understanding the local dynamics of populations and communities [10–12], dormancy is often neglected when attempting to predict and explain spatial patterns of biodiversity.

Dormancy may contribute to the biogeography of some species by allowing propagules to tolerate conditions that would otherwise prohibit dispersal and colonization [2,9,13,14]. This effect may be particularly strong among microorganisms, which are well known for forming cysts, spores and other morphological resting stages that are highly resilient to fluctuations in a wide range of environmental conditions. For example, there are more than 10²⁹ bacterial endospores in the marine subsurface alone [15]. However, microorganisms can also engage in less conspicuous forms of dormancy that involve the downregulation of metabolic activities, which allows individuals to extend their lifespan for prolonged periods of time [16]. As a result, microbial seed banks can account for the vast majority of individuals and biomass in some ecosystems [1,15,17,18]. Often, the biogeographic patterns of microbial communities are attributed to the unhindered capacity for dispersal among single-celled organisms. However, this perception may be influenced in part by dormancy, which should improve the odds of successful migration and colonization [9]. By influencing dispersal and environmental filtering, microbial dormancy is expected not only to increase the number of species in a given habitat (α-diversity), but also to decrease species turnover (β-diversity) reflecting the loss or replacement of species across space or time [9,19].

One classical biogeographic pattern that is likely to be influenced by seed banks is the distance–decay relationship (DDR). The DDR characterizes how community similarity changes across increasing geographical distance [20], often reflecting the influence of dispersal limitation and spatially autocorrelated environmental conditions [21–24]. The DDR has attracted attention among microbial ecologists for testing predictions of island biogeography [25], for elucidating scale-dependency of β-diversity [26] and for revealing the relative influence of geographical isolation versus environmental conditions [27–29]. Because it can decrease environmental filtering and dispersal limitation, and hence increase stochasticity in abundance and occurrence, dormancy should flatten the slope of the DDR [19,30]. For the same reasons, we expect dormancy to decrease the similarity between communities at the smallest scales of geographical and environmental distance, which would be reflected in a lower y-intercept of the DDR.

In the current study, we sampled and analysed bacterial communities from a regional distribution of freshwater ponds. Using 16S rRNA sequencing, we constructed geographical and environmental DDRs for both the total (DNA) and active (RNA) portions of the bacterial communities. We then developed simulation models with ecological mechanisms to evaluate our empirical DDRs and differences between DNA- and RNA-based assessments of bacterial composition. Specifically, we challenged our models to reproduce a large set of empirical results, and tested whether greater environmental filtering, decreased death in dormancy, and increased dormant dispersal led our models to more closely approximate our empirical results.

2. Material and methods

(a). Field study

(i). Study system and environmental data

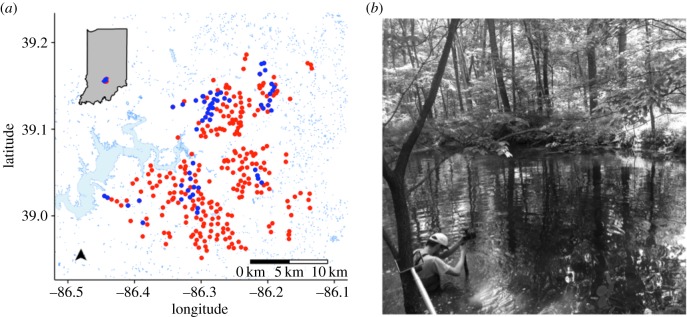
Between 1950 and 1960, approximately 300 ponds were constructed as wildlife habitat in Brown County State Park (BCSP), Yellowwood State Forest (YSF) and Hoosier National Forest (HNF) in south central Indiana, USA (figure 1). Built along topographical ridgelines, the ponds are hydrologically disconnected from one another within the forested landscape. We identified a subset (n = 49) of ponds to sample based on their representation across watersheds and their accessibility, which was influenced by proximity to recreational trails, fire trails or a logging road. Because surrounding vegetation can shade these small ponds and affect community structure [31], we quantified the percentage of visible sky above the centre of every pond by capturing hemispherical images of the forest canopy. In addition to measuring other spatial and physical properties (elevation, depth and diameter), we used a YSI 556 MPS multiprobe to quantify water temperature (°C), redox potential (ORP, mV), specific conductivity (SpC, µS cm⁻¹), dissolved oxygen (DO, mg l⁻¹), total dissolved solids (TDS, g l⁻¹) and salinity (PSU, ppm). We then collected surface water samples (0.1 m) from the centre of each pond using an extended pole to prevent sedimentary disturbance and transported them back to the laboratory for additional analyses. Specifically, we measured dissolved organic carbon (DOC) and dissolved organic nitrogen (DON) concentrations on 0.7 µm filtrates via high-temperature combustion and chemiluminescence with a Shimadzu TOC-V/TNM instrument. We measured water colour (a₄₄₀) as a surrogate for terrestrial-derived dissolved organic matter [32]. We quantified total phosphorus (TP) after persulfate digestion via spectrophotometric analysis using a molybdenum blue analysis [33]. Last, we estimated algal biomass by quantifying chlorophyll a with a Turner Designs fluorometer after cold-extracting biomass that was retained on 0.7 µm glass fibre filters in 95% ethanol [34].

Figure 1.

(a) A map of our study area depicting the locations of forested ponds constructed in south central Indiana, USA. For this study, we sampled 49 of the ponds (blue symbols); the remaining ponds were not sampled (red symbols). Surrounding surface water is depicted as light blue shapes. (b) A typical pond showing its relatively small size and surrounding vegetation.

(ii). Sampling and sequencing bacterial communities

We characterized bacterial communities by sequencing 16S rRNA genes and transcripts from pond water samples. This approach has been previously used to analyse the composition of the active (RNA) and total (DNA) taxa in complex bacterial communities [14,35,36] based on the following logic. Sequences recovered from the DNA pool can be derived from organisms that are dead, dormant or active [37]. By contrast, ribosomal RNA, which is required for protein synthesis, has a short half-life and is only produced by metabolically active individuals [38,39]. Thus, through the simultaneous analysis of 16S rRNA genes and transcripts, we can gain insight into how seed banks contribute to biogeographic patterns of microbial communities [1]. Importantly, we did not attempt to identify dormant bacteria cells or dormant bacterial taxa but instead operated under a simplifying assumption that dormant bacteria should contribute minimally to 16S rRNA transcripts and that bacterial taxa represented by 16S rRNA transcripts would be more likely to reflect active individuals.

For each pond sample, we harvested planktonic microbial biomass by filtering surface water onto a 47 mm 0.2 µm Supor Filter (Pall) using vacuum filtration. We then co-extracted nucleic acids from one half of the filter using the QIAGEN RNeasy PowerWater kit and a DNA elution accessory kit. We eliminated DNA from RNA samples using the RTS DNase kit (QIAGEN) and synthesized first-strand cDNA using the SuperScript III first-strand synthesis kit (Invitrogen) with random hexamer primers. Then, we amplified the V4 region of the 16S rRNA gene from the DNA and cDNA templates using barcoded 515F and 806R primers [40]. After purifying with the AmPure XP kit (Beckman), we quantified amplicons using the Quant-iT kit (Invitrogen) and then pooled libraries at approximately equal molar ratios (20 ng each). Following procedures outlined in greater detail elsewhere [37,41], we sequenced the pooled library on the Illumina MiSeq platform using 250 × 250 base pair (bp) paired-end reads (Illumina Reagent kit v2) at the Indiana University Center for Genomics and Bioinformatics Sequencing Facility. Raw sequence reads were assembled into contigs, quality-filtered to remove long sequences and sequences with ambiguous bases, and aligned to the Silva reference database (version 123). We used the UCHIME algorithm [42] to detect and remove chimeric sequences. Additionally, we removed mitochondrial, archaeal and eukaryotic sequences following detection with the Ribosomal Database Project's 16S rRNA reference sequences and taxonomy version 6 [43]. Finally, we split sequences based on taxonomic class using the Ribosomal Database Project (RDP) taxonomy and binned them into operational taxonomic units (OTUs) based on 97% sequence similarity. All initial sequence processing was completed using the software package ‘mothur’ (v. 1.32.1, [44]).

(iii). Quantifying distance–decay relationships

We constructed DDRs for both the active (RNA) and total (DNA) communities by calculating pairwise community similarity among sites (i.e. ponds). Because community similarity is not an absolute measure and depends on the aspects of the communities being compared (e.g. dominance, rarity, presence-only), we used three distance-based metrics that capture contrasting properties of similarity. First, we used Bray–Curtis similarity, a common metric that emphasizes the influence of abundant taxa:

$${\mathrm{BC}}_{ij}=1-\frac{\sum |n_{ik}-n_{\hspace{0.17em}jk}|}{\sum (n_{ik}+\hspace{0.17em}{n}_{\hspace{0.17em}jk})},$$

where n_ik is the abundance of taxon k at the ith and jth sites. Second, we calculated the Sørensen metric, which is a binary form of Bray–Curtis that accounts for the presence of taxa in a sample, and hence gives equal weight to rare and abundant taxa. Finally, we used the Canberra similarity metric, which places emphasis on the abundance of rare taxa:

$$C_{ij}=1-\left(\sum \frac{|n_{ik}-n_{\hspace{0.17em}jk}|}{|n_{ik}|+|n_{\hspace{0.17em}jk}|}\right)/l,$$

where l is the length of the community vector in the site-by-taxa matrix. For both the Bray–Curtis and Canberra measures, we used relative abundances to decrease the site-specific bias that occurs when total sample abundances of two sites greatly differ. We calculated each measure of community similarity using the vegdist() function in the ‘vegan’ R package [45].

We then calculated geographical and environmental distances among our sample ponds. For geographical distances, we used the ‘fossil’ R package [46]. For environmental distances, we used pairwise differences in scores from the first axis of the principle components analysis (PCA), which was conducted on centred and rescaled environmental data using the ‘vegan’ R package [45]. Given the disparate ranges in environmental and geographical distance, we relativized distances to values between 0 and 1 by dividing each pairwise distance by the maximum distance. This procedure also made environmental and geographical distance scale across the same range as community similarity, i.e. 0–1.

To test for the effect of dormancy on bacterial biogeography, we calculated the regression coefficient (hereafter ‘slope’) and intercepts of environmental and geographical DDRs for the active and total communities using ordinary least-squares regression [20,29,47]. We then tested whether differences in slopes and intercepts of DDRs were statistically significant using a permutation-based linear regression approach [20], which was implemented using the diffslope() function in the ‘simba’ R package. We also quantified DDRs using 5, 10, 15, 20, 25, 30, 35 and 45 ponds chosen at random to control for the influence of the sample size, and then repeated this procedure 1000 times to obtain mean values for each sample size. Additionally, we evaluated the effect of taxon richness on DDR parameters by randomly selecting different numbers of OTUs (1000, 4000, 8000, … 22 000) and rerunning our analyses. Because this process involved randomly selecting columns from the site-by-taxa matrices, we could not randomly select OTUs based on relative abundance or numbers of reads in individual samples (i.e. communities).

(b). Mechanistic modelling

(i). Rationale

Empirical relationships like the DDR are often used to test ecological hypotheses but cannot, by themselves, demonstrate whether hypothesized mechanisms can reproduce observed relationships. This is further complicated by assumptions and idiosyncrasies that are inherent to empirical data. For example, studies that characterize microbial communities using high-throughput DNA sequencing implicitly assume that primer coverage, extraction efficiency and amplification bias do not prevent molecular surveys from reflecting actual community structure [48]. There are also assumptions regarding the relationship between growth rate and rRNA content, when making inferences about the metabolic activity of bacterial and archaeal taxa using 16S ribosomal DNA and RNA sequencing [49,50]. However, these caveats and limitations can, in part, be addressed by coupling empirical efforts with models that explicitly encode hypothesized mechanisms and that are independent of methodological assumptions. Therefore, we developed a simulation platform to test whether the environmental and geographical DDRs observed among ponds could be reproduced by focusing on ecological mechanisms that influence community assembly: environmental filtering, dormancy and dispersal.

(ii). Overview

To evaluate the relative importance of dispersal and dormancy, we modelled population abundances within and among communities by simulating site-by-taxa matrices and using the same geographical coordinates, environmental PCA coordinates, the number of sites and maximum number of taxa across sites as in our field survey. In this way, we simulated the approximate dimensions of our empirical site-by-species matrices. By using the same magnitudes of richness and maximum abundance as in our field surveys, we avoided conflating the influence of environmental filtering, dormancy and dispersal with general numeric disparities between simulated and empirical data. As with species-abundance models of community ecology, our models did not simulate across time but instead provided a ‘snapshot in time’ [51]. Nevertheless, our approach yielded 10⁶ models, each simulating four matrices having more than 1.3 million elements each.

(iii). Simulating environmental filtering

To simulate environmental filtering, local abundances of dormant and active populations were determined by the match between site-specific scores of the first PCA axis (PCA₁) and species-specific environmental optima. For simplicity, a single optimum was chosen at random for each species by randomly selecting values within the range of scores from the first PCA axis (PCA₁). For example, if the PCA₁ scores ranged between −6 and 6, then a species was assigned a single optimum by drawing a uniform random number between −6 and 6. To simulate greater degrees of environmental filtering, we increased the range of randomly chosen environmental optima beyond the range of PCA₁ scores. For example, a species could have a randomly chosen environmental optimum ranging from −10 to 10. In this way, greater environmental filtering led to a greater number of species being poorly fitted to a greater number of locations. The match (m_ij) between the environmental optimum of the ith taxon (O_j) and the PCA₁ score at the jth site (E_i) was calculated as follows:

$$m_{ij}=\hspace{0.17em}\frac{1}{1+\hspace{0.17em}|E_i-O_j|}.$$

Values of m_ij ranged between 0.0 and 1.0, corresponding to a zero match and perfect match, respectively. For each species, a larger m_ij would result in greater active abundance while a smaller m_ij resulted in greater death within the active populations, greater transitions to dormancy, and hence larger dormant populations.

(iv). Simulating dormant and active abundances

Using a simple niche-based assumption, the active populations of each species occurred at each location with a probability equal to m_ij. To approximate the general magnitude of the greatest active OTU abundances in our field-based survey, active populations were initiated with 50 000 individuals. For dormant populations, we assumed they were primarily influenced by stochastic dynamics, were essentially invisible to environmental filtering and could occur at a location regardless of whether an active counterpart was present [9,52]. Thus, we initiated the occurrence of dormant populations with a binomial probability of 0.08, i.e. the average frequency of occurrence for taxa within our empirical data. We then assigned randomly chosen abundances ranging between 1 and 10 000 to each of these dormant populations. A fraction of each active population equal to 1 − m_ij was then assigned to its corresponding dormant subpopulation; hence dormant abundances were also made directly proportional to the species' environmental mismatch.

To simulate death, active populations were decreased in proportion to their environmental mismatch (1–m_ij). Hence, occurrence, abundance and death among active populations were determined by environmental filtering (via m_ij). By contrast, dormant populations were decreased by a randomly chosen percentage (0–100), the value of which varied across simulations. This parameter and its randomly chosen value allowed us to test for the influence of dormant death. Hence, death in dormancy was independent of environmental conditions, while overall, dormant abundances were partly influenced by deterministic environmental filtering, partly by random placement, and partly by the strength of dormancy in preventing death.

(v). Simulating dispersal

We simulated dispersal between dormant populations and between active populations by allowing the portions of dormant and active populations from randomly chosen donor sites to immigrate into recipient sites. For both active and dormant portions of simulated communities, the number of propagules (n_j) received by an OTU at site j from the same OTU at site i was equal to 1/(1 + d_ij) × n_i × p. Here, d_ij is the distance between site i and site j, n_i is the abundance of the dormant (or active) population of the OTU at site i, and p is a model-specific parameter that modifies the overall strength of dispersal limitation. The parameter p ranged between 0 and 1, where if p = 0 then n_j = 0 and if p = 1 then n_j = 1/(1 + d_ij) × n_i). Values for p were chosen independently and at random for active (i.e. p_active) and dormant (i.e. p_dormant) communities.

(vi). Model runs and analysis

We ran 10⁶ simulations, each with randomly drawn parameter values that influenced environmental filtering, dormant death rate, whether dispersal occurred at all, and if so, at what rates. This random sampling of parameters was designed to explore the complete space of model behaviour and to allow us to examine the relative importance of dormancy, dispersal and environmental filtering. When each model was completed, our platform combined the simulated active and dormant site-by-species matrices to form the site-by-species matrix for the total community. We then analysed our simulated communities in an identical manner to the data collected from our field survey. Specifically, for each model, our platform estimated the slopes and y-intercepts of geographical and environmental DDRs for the active and total communities for three similarity metrics (Bray–Curtis, Sørensen, Canberra). To draw inferences about the effects of environmental filtering, dormancy and dispersal on the biogeographic patterns of the active and dormant fractions, we calculated the per cent error (100 × |simulated − empirical|/empirical) between the slopes and y-intercepts of field-based and simulation-based DDRs. We also evaluated how many aspects of our empirical data, out of 50 (electronic supplementary material, table S1), each model was able to reproduce.

3. Results

(a). Field survey

(i). Environmental and geographic features

In the 500 km² study region, the sampled ponds were separated by an average distance of 9.7 km (± 6.15 s.d.), and had an average nearest neighbour distance of 2.18 km (± 3.70 s.d.) and an average furthest neighbour distance of 24.9 km (± 5.10 s.d.). Despite being constructed by the same team of people over a relatively short period of time, the morphological characteristics of the ponds were quite different. There was an approximately four-fold range in pond diameter (range = 7.0–32.5 m) and an approximately six-fold range in maximum depth (range = 0.3–2.0 m). In addition, environmental conditions substantially varied among the sampled ponds, often with greater than 100% difference between minimum and maximum values (table 1). The first two axes of the PCA explained 40.3 and 12.5% of the variation, respectively, in environmental conditions across sampled ponds. Along the first PCA axis, larger ponds with a more open canopy and elevated oxygen levels separated from smaller ponds with higher concentrations of nutrients and suspended solids (electronic supplementary material, figure S1). These multivariate observations are consistent with other strong relationships among environmental variables, including a positive correlation between specific conductivity and dissolved organic nitrogen (electronic supplementary material, figure S2).

Table 1.

Descriptive statistics for 16 environmental variables measured from 49 forested ponds in southern Indiana, USA.

variable	mean	s.d.	max.	min.
diameter (m)	17.9	6.2	32.5	7
depth (m)	1.3	0.4	2	0.3
elevation (m)	259.3	34.1	309	126
canopy cover (%)	0.28	0.15	0.76	0.1
temperature (°C)	22.0	1.7	25.8	18.6
pH	6.4	0.20	6.9	5.8
dissolved oxygen (mg l−1)	2.2	1.4	6	0.2
specific conductivity (µS cm−1)	44.3	17.0	98	12
total dissolved solids (g l−1)	0.028	0.011	0.064	0.008
colour (a440)	0.04	0.02	0.10	0.01
oxidative reduction potential (mV)	146.6	58.1	326	30
dissolved organic carbon (mg l−1)	9.5	2.5	18.4	5.0
dissolved organic nitrogen (mg l−1)	0.488	0.382	1.699	0.081
total phosphorus (μg l−1)	272	177	737	62
chlorophyll a (μg l−1)	1.8	0.5	3.4	0.7

Importantly, geographical and environmental distances between ponds were unrelated (p > 0.5), a result that was insensitive to sample size (electronic supplementary material, figure S3). This finding means that, unlike many other ecological studies, similarity in environmental conditions did not decay with increasing geographic distance. In fact, there was no relationship between environmental distance and geographical distance, whatsoever (electronic supplementary material, figure S3). Because of this natural decoupling, we were able to directly compare environmental DDRs and geographic DDRs for bacterial communities without additional statistical treatment.

(ii). Diversity of active and total communities

As expected, active communities (RNA) were less diverse than the total (DNA) community. Across all ponds, we observed 21 568 OTUs among our active communities and 27 446 OTUs among our total communities. Within a pond, we observed on average 1854 (± 586 s.d.) active OTUs and 2083 (± 733 s.d.) total OTUs, which corresponded to a site-specific difference of 229 (± 507 s.d.) taxa.

(iii). Distance decay of bacterial communities

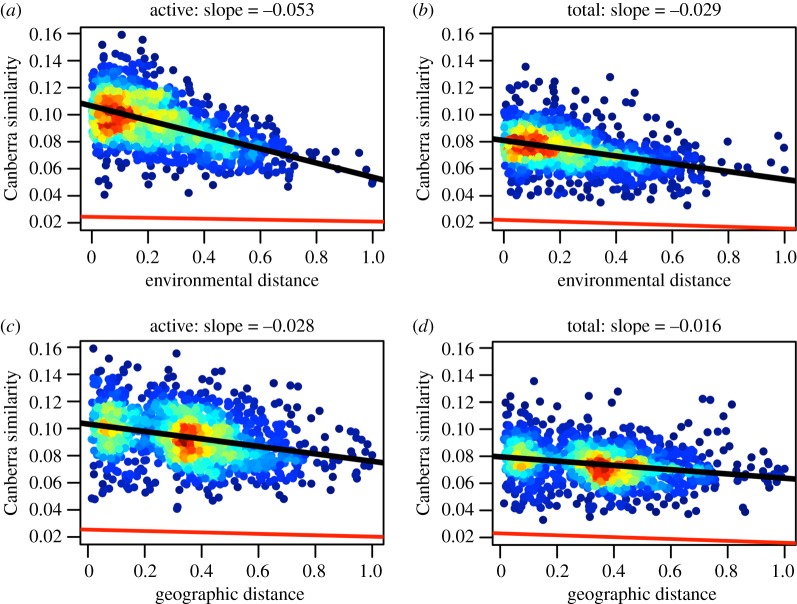
As predicted, DDRs for the active (RNA) community were characterized by steeper slopes and, in most cases, greater y-intercepts than those of the total (DNA) community (figure 2; electronic supplementary material, figures S4 and S5; tables 2 and 3). This was most evident when examining environmental DDRs. These findings are consistent with the view that environmental conditions have stronger filtering effects on active organisms than on taxa residing in seed banks. Through random resampling, we showed that differences in DDRs between RNA and DNA were independent of the number of sites (electronic supplementary material, figure S6) and the number of OTUs (electronic supplementary material, figure S7). While our findings were generally robust to community similarity metrics, the distinction between DDRs for the active and total communities was greatest when rare taxa were emphasized via the Canberra or Sørensen index (figure 2; electronic supplementary material, figures S4 and S5; tables 2 and 3). However, DDR slopes were steepest (and intercepts were greatest) when similarity was measured via the Bray–Curtis metric (electronic supplementary material, figure S4). Bringing these results together, community similarity was driven largely by dominant OTUs while differences between the active and total communities were driven by rare OTUs.

Figure 2.

Distance–decay relationships (DDRs) for active (RNA) and total (DNA) bacterial communities sampled from forested ponds. Using the Canberra metric of similarity, which emphasizes rare taxa, we found that environmental DDRs (a,b) were 58.5% steeper for the active community than for the total community (p = 0.001). Geographical DDRs (c,d) were 54.5% steeper for the active community than for the total community (p = 0.001). Warmer colours represent a greater density of data points. Analyses based on Bray–Curtis distance and Sørensen's distance produced qualitatively similar results (see electronic supplementary material). The red line is the DDR resulting from a null model whereby communities were randomly assigned to different locations.

Table 2.

Slopes and summary statistics associated with the distance–decay relationships (DDRs) based on environmental distance, geographical distance and three different similarity metrics (Bray–Curtis, Sørensen and Canberra). Slopes were derived from simple linear regression; p-values correspond with tests to determine whether DDR slopes from the active bacterial community (RNA) differed from the total bacterial community (DNA).

metric	DDR type	community	slope	% difference	p-value
Bray–Curtis	environmental	active	−0.326	25.2	0.001
		total	−0.253
	geographical	active	−0.182	31.8	0.015
		total	−0.132
Sørensen	environmental	active	−0.099	57.1	0.001
		total	−0.055
	geographical	active	−0.052	47.6	0.002
		total	−0.032
Canberra	environmental	active	−0.053	58.5	0.001
		total	−0.029
	geographical	active	−0.028	54.5	0.002
		total	−0.016

Table 3.

Intercepts and summary statistics associated with distance–decay relationships (DDRs) based on environmental distance, geographical distance and three different similarity metrics (Bray–Curtis, Sørensen and Canberra). Intercepts were derived from simple linear regression; p-values correspond with tests to determine whether DDR intercepts from the active bacterial community (RNA) differed from the total bacterial community (DNA).

metric	DDR type	community	intercept	% difference	p-value
Bray–Curtis	environmental	active	0.434	0.69	0.332
		total	0.437
	geographical	active	0.422	0.94	0.343
		total	0.426
Sørensen	environmental	active	0.319	21.5	0.001
		total	0.257
	geographical	active	0.314	20.7	0.001
		total	0.255
Canberra	environmental	active	0.106	26.7	0.001
		total	0.081
	geographical	active	0.103	25.1	0.001
		total	0.080

Beyond differences between DNA and RNA, slopes of environmental DDRs were more than 50% greater than their corresponding geographical DDRs regardless of the distance metric used (p = 0.001, table 4). By randomly permuting communities (i.e. rows) from the site-by-taxa matrices, we found that the slopes and y-intercepts of environmental DDRs differed from a null expectation that would result from disassociating communities from their environmental conditions while preserving their structure (i.e. relative abundances among taxa). By contrast, slopes of geographical DDRs only differed from a null expectation when community similarity emphasized dominant OTUs, i.e. Bray–Curtis metric (figure 2; electronic supplementary material, figures S4 and S5).

Table 4.

Slopes and summary statistics associated with distance–decay relationships (DDRs) based on environmental distance, geographical distance and three different similarity metrics (Bray–Curtis, Sørensen and Canberra). Slopes were derived from simple linear regression; p-values correspond with tests to determine whether DDR intercepts from the active bacterial community (RNA) differed from the total bacterial community (DNA).

metric	community	DDR type	slope	% difference	p-value
Bray–Curtis	active	environmental	−0.326	56.7	0.001
		geographical	−0.182
	total	environmental	−0.253	62.9	0.001
		geographical	−0.132
Sørensen	active	environmental	−0.099	62.3	0.001
		geographical	−0.052
	total	environmental	−0.055	52.9	0.001
		geographical	−0.032
Canberra	active	environmental	−0.053	61.7	0.001
		geographical	−0.028
	total	environmental	−0.029	57.8	0.001
		geographical	−0.016

(b). Mechanistic modelling

Models, whether simulation-based or not, are rarely challenged to reproduce more than one or two aspects of empirical data (e.g. the slope of a single DDR). However, all of our models reproduced at least 44 out of 50 aspects of our empirical data, with 41% reproducing all 50 (electronic supplementary material, figure S8). Constraining our analyses to only those simulations that reproduced all 50 aspects of our empirical results, we found that slopes for environmental and geographical DDRs were significantly different from 0, intercepts were significantly greater than 0, slopes of environmental DDRs were steeper than those of geographical DDRs, and DDRs for the active community were characterized by steeper slopes and greater y-intercepts than those of the total community, and each of these results held irrespective of the similarity metric (table 2).

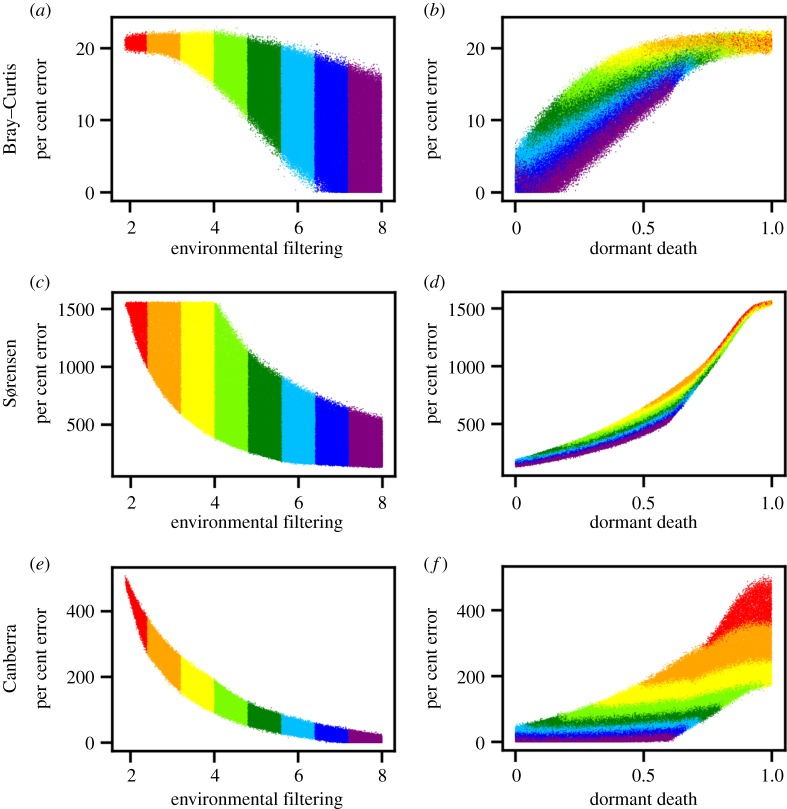
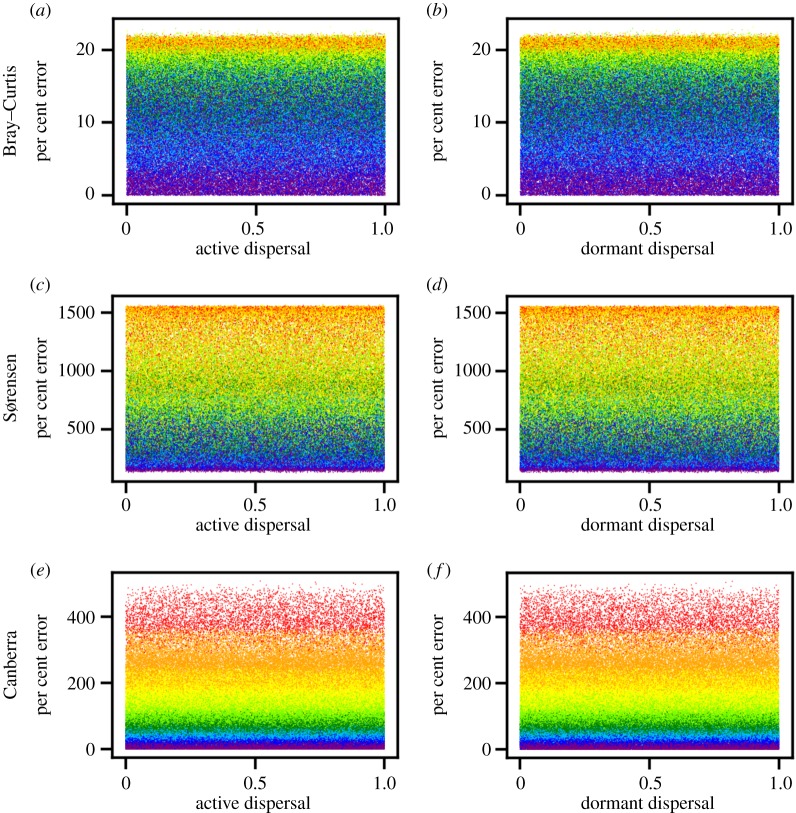
Among the subset of simulations that reproduced all 50 aspects of our empirical DDRs, more than 61% excluded dispersal. Models that excluded dispersal and that had the highest levels of environmental filtering and lowest levels of dormant death came within 0% error of our environmental DDR slopes (figure 3). By contrast, dispersal had little-to-no effect on how closely a given simulation approximated the slopes of our empirical DDRs (figure 4). The inclusion of dispersal actually caused our models to reproduce fewer aspects of our empirical data (electronic supplementary material, figure S8).

Figure 3.

Average per cent error between slopes of environmental distance–decay relationships (DDRs) from field surveys and slopes of environmental DDRs from simulated communities versus randomly drawn values of model parameters. Community similarity is based on the Bray–Curtis (a,b), Sørensen (c,d) and Canberra (e,f) metrics. Each point represents the result of a single model and is coloured according to the value of environmental filtering. Models with greater degrees of environmental filtering and lesser degrees of dormant death more closely approximated empirical DDRs to within 0% error.

Figure 4.

Average per cent error between slopes of environmental distance–decay relationships (DDRs) from the field survey and slopes of environmental DDRs from simulated communities versus randomly drawn values of active and dormant dispersal parameters. Community similarity is based on the Bray–Curtis (a,b), Sørensen (c,d), and Canberra (e,f) metrics. Each point represents the result of a single model and is coloured according to the value of environmental filtering.

4. Discussion

While numerous studies have demonstrated how dormancy maintains local diversity, few have explored how seed banks affect spatial patterns of biodiversity, including intensively studied biogeographic relationships such as the DDR. Our combination of empirical field surveys and mechanistic modelling supports recent theoretical claims that seed banks may have important but overlooked effects on the spatial patterns of biodiversity [2]. By contrast, we found little-to-no effect of dispersal in driving bacterial DDRs. In fact, the inclusion of dispersal between sites actually decreased the ability of models to approximate empirical results. Altogether, our complementary approaches suggest that dormancy dampened DDRs within our study system and that these DDRs were largely driven by environmental filtering and resilience of seed banks to extrinsic mortality.

(a). Overlooked role of dormancy on biogeography

For the past two decades, microbial studies have reached conflicting conclusions about the existence of biogeographic patterns among communities of bacteria, archaea, fungi and protists. These conclusions often speculate on the contrasting strengths of dispersal and selection, while usually providing direct evidence of neither. Our study suggests a potential unifying explanation for both idiosyncratic biogeographic patterns and the inconsistency of environmental variables in explaining compositional differences among microbial communities. Specifically, we found that dormancy dampened biogeographic patterns across spatial and environmental gradients (table 2 and figure 2). Had we relied solely on the total community (i.e. DNA), as is common in microbial surveys, we would have observed weaker environmental DDRs and weaker geographical DDRs.

The effect of dormancy and seed banks on biogeographic patterns may differ depending on the environmental conditions found among sites. For example, a study conducted across sites that support large seed banks might fail to demonstrate a meaningful relationship, while an analogous study conducted across sites that support relatively small seed banks might yield more detectable effects. Our findings suggest it may be possible to quantify the dampening (or amplifying) effect of dormancy on ecological patterns by simultaneously examining the active and total fractions of microbial communities. Specifically, differences in the forms of ecological or biogeographic patterns for total communities and their active portions could be compared, and the differences quantified using a measure of effect size. This approach would begin to quantify an important component of microbial communities that has largely only been speculated about in microbial ecology and biogeography [1].

(b). The influence of dormancy on commonness and rarity

Commonness and rarity have been increasingly studied in microbial ecology, often with consideration given to the potential influence of dormancy [53–55]. In our study, we found that environmental and geographical DDRs were strongest (steeper slopes, greater y-intercepts) when community similarity emphasized dominant taxa. However, differences in DDR slopes and intercepts between the active and total communities were greatest when similarity emphasized rare taxa or ignored abundance altogether. Together, these findings suggest that compositional similarity across distance is more strongly driven by dominant taxa, but also that the influence of dormancy in dampening DDRs is manifested in the compositional differences that dormancy produces among rare taxa. There is at least one straightforward reason for these observations. Specifically, the observed abundance and occurrence of rare (i.e. low abundance) taxa are more likely than those of dominant taxa to be affected by random variation in reproduction, death and empirical sampling efforts. This effect would explain the lower y-intercepts and shallower slopes of DDRs based on Canberra distance that were observed not only in our empirical data but also in our simulations, which, importantly, lacked the assumptions regarding the classification of a taxon's metabolic status based on molecular information. Together, our findings suggest that dormancy has an effect on the commonness and rarity of bacterial taxa with implications for local- and regional-scale patterns of diversity [14,53–55]. However, it is worth noting that we were agnostic as to how dormancy was distributed among taxa with respect to their relative abundance. For example, we did not assume that highly abundant (i.e. dominant) taxa were active or that rare taxa were disproportionately dormant. In fact, dominant taxa have been shown to be disproportionately dormant while rare taxa have been shown to be disproportionately active [14,56].

(c). Rethinking microbial dispersal

The role of dispersal in shaping the biogeography of microorganisms has fuelled decades of debate. In contrast with many DDR studies, the independence of environmental distance and geographical distance in our study should have allowed the signatures of dispersal and geographical distance to be more easily detected. And yet, we found no support for a role of dispersal between sites, whether aided by dormancy or not. We do not imply, however, that dispersal was altogether unimportant. There are several dispersal scenarios that we did not explore (e.g. strongly directional, regional pool immigration, homogenizing dispersal). However, bacterial community composition is bound to reflect repeated transitions between activity and dormancy that may overwhelm the signal of dispersal or dispersal limitation. These repeated, if not cyclic, transitions are probably driven by local-to-regional scale environmental changes as well as variation among individuals and microhabitats [9]. Consequently, even after dispersal occurs, the combination of dormancy and environmental filtering may dampen the signal of biogeographic processes. In particular, environmental filtering may decrease the homogenizing influence of unhindered dispersal, dormancy may decrease the influence of dispersal limitation, and both may operate simultaneously.

Our findings challenge commonly held assumptions about homogenizing dispersal and its effect on microbial biogeography. Homogenizing dispersal has often been invoked when biogeographic patterns fail to emerge from microbial datasets. Though rarely recognized, this reasoning assumes that dispersal is more or less directionally random and occurs frequently enough to swamp the effect of environmental filtering. This assumption is rarely justified or tested, especially with regard to spatial scale. For example, given the local-to-regional scale of our study, passive dispersal driven by forces such as weather could have been frequent and less consistently directional than analogous forces acting at larger scales (e.g. ocean and currents) [57,58]. Consequently, detecting the signal of dispersal may be a matter of understanding how the directionality of passive dispersal interacts with the stochasticity of dispersal and how this relates to spatial scale.

(d). Greater insight through mechanistic modelling

Increasingly, microbial ecologists are making use of the statistical models often used in macroecology [59]. In addition, mechanistic models may provide insight into ecological processes underlying phenomena that are difficult to directly observe or measure in microbial systems. For example, in our study, we used RNA and DNA sequencing to classify taxa in the total and active pools of an assemblage, respectively. While this approach has proven to be a useful proxy for metabolic status, it does not allow the direct identification of dormant organisms. To address this shortcoming, we developed a process-based modelling approach that allowed us to challenge our empirical conclusions through inferences about unobserved processes (e.g. dormancy, dispersal between sites, environmental filtering based on species optima) on the DDR. These models reproduced an uncommonly large set of empirical results and were free of methodological caveats associated with RNA–DNA comparisons and the idiosyncrasies of amplicon studies. Similar modelling approaches could be used to increase the confidence of conclusions surrounding the effects of unobserved mechanisms such as heterogeneity in active metabolism, ribosomal turnover, and cellular age, as well as the influence of host behaviour (e.g. migration) and weather on microbial dispersal. Finally, mechanistic modelling could yield insight into the role of deterministic and stochastic forces that influence dispersal, which too often is presumed without evidence to be entirely stochastic in microbial ecological studies.

5. Conclusion

Over the past decade, the study of microbial biogeography has matured from what was motivated by a century-old hypothesis of unhindered dispersal and cosmopolitan distributions to a body of literature that supports many of the core tenets of biogeography [29,58,60]. While dispersal limitation and environmental filtering are among the most general forces shaping biogeographic patterns, other ecological processes are important for understanding the assembly of communities in complex landscapes. In this study, we tested recent predictions that dormancy can have a strong effect on the biogeography and biodiversity of microbial communities [1,2,9,61]. By combining mechanistic modelling with a molecular-based survey of bacteria from a network of freshwater ponds, we demonstrated that the DDR was dampened by the accumulation of dormant individuals into a seed bank. Given that dormancy is a widespread life-history strategy, our findings may help to explain why patterns of microbial biogeography often appear weaker in comparison with what is reported for non-microbial communities [26]. If generalizable, our findings may also inform biogeographic studies of plant and animal systems [59].

Data accessibility

Data and code used in this manuscript can be found on GitHub (https://github.com/LennonLab/DormancyDecay), Zenodo (doi:10.5281/zenodo.3662441) and NCBI (BioProject PRJNA554375).

Authors' contributions

K.J.L. and J.T.L. conceived the study; K.J.L. and J.T.L. analysed and interpreted data; K.J.L. developed and executed simulation modelling; K.J.L. and J.T.L. wrote the manuscript; M.E.M., S.R.B. and M.L.L. generated data; J.T.L. and M.L.L. collected field samples; M.E.M. processed sequence data; S.E.J., S.R.B., M.E.M. and M.L.L. edited the manuscript; all authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

The study was supported by the National Science Foundation grant no. DEB-1442246 (J.T.L., K.J.L., S.E.J.) and the US Army Research Office grant no. W911NF-14-1-0411 (J.T.L.).