PUlasso: High-Dimensional Variable Selection With Presence-Only Data

Abstract

In various real-world problems, we are presented with classification problems with positive and unlabeled data, referred to as presence-only responses. In this article we study variable selection in the context of presence only responses where the number of features or covariates p is large. The combination of presence-only responses and high dimensionality presents both statistical and computational challenges. In this article, we develop the PUlasso algorithm for variable selection and classification with positive and unlabeled responses. Our algorithm involves using the majorization-minimization framework which is a generalization of the well-known expectation-maximization (EM) algorithm. In particular to make our algorithm scalable, we provide two computational speed-ups to the standard EM algorithm. We provide a theoretical guarantee where we first show that our algorithm converges to a stationary point, and then prove that any stationary point within a local neighborhood of the true parameter achieves the minimax optimal mean-squared error under both strict sparsity and group sparsity assumptions. We also demonstrate through simulations that our algorithm outperforms state-of-the-art algorithms in the moderate p settings in terms of classification performance. Finally, we demonstrate that our PUlasso algorithm performs well on a biochemistry example. Supplementary materials for this article are available online.

1. Introduction

In many classification problems, we are presented with the problem where it is either prohibitively expensive or impossible to obtain negative responses and we only have positive and unlabeled presence-only responses (see, e.g., Ward et al. 2009). For example, presence-only data are prevalent in geographic species distribution modeling in ecology where presences of species in specific locations are easily observed but absences are difficult to track (see, e.g., Ward et al. 2009), text mining (see, e.g., Liu et al. 2006), bioinformatics (see, e.g., Elkan and Noto 2008), and many other settings. Classification with presence-only data is sometimes referred to as PU-learning (see, e.g., Liu et al. 2006; Elkan and Noto 2008). In this article, we address the problem of variable selection with presence-only responses.

1.1. Motivating Application: Biotechnology

Although the theory and methodology we develop apply generally, a concrete application that motivates this work arises from biological systems engineering. In particular, recent high-throughput technologies generate millions of biological sequences from a library for a protein or enzyme of interest (see, e.g., Fowler and Fields 2014; Hietpas, Jensen, and Bolon 2011). In Section 5, the enzyme of interest is beta-glucosidase (BGL) which is used to decompose disaccharides into glucose which is an important step in the process of converting plant matter to biofuels (Romero, Tran, and Abate 2015). The performance of the BGL enzyme is measured by the concentration of glucose that is produced and a positive response arises when the disaccharide is decomposed to glucose and a negative response arises otherwise. Hence, there are two scientific goals: firstly to determine how the sequence structure influences the biochemical functionality; secondly, using this relationship to engineer and design BGL sequences with improved functionality.

Given these two scientific goals, we are interested in both the variable selection and classification problem since we want to determine which positions in the sequence most influence positive responses as well as classify which protein sequences are functional. Furthermore, the number of variables here is large since we need to model long and complex biological sequences. Hence, our variable selection problem is high-dimensional. In Section 5, we demonstrate the success of our algorithm in this application context.

1.2. Problem Setup

To state the problem formally, let $x\in {ℝ}^p$ be a p-dimensional covariate such that $x~{\mathbb{P}}_X$, y ∈ {0, 1} an associated response, and z ϵ {0, 1} an associated label. If a sample is labeled (z = 1), its associated outcome is positive (y = 1). On the other hand, if a sample is unlabeled (z = 0), it is assumed to be randomly drawn from the population with only covariates x not the response y being observed. Given n_ℓ labeled and n_u unlabeled samples, the goal is to draw inferences about the relationship between y and x. We model the relationship between the probability of a response y being positive and (x, θ) using the standard logistic regression model

$$\mathbb{P}(y=1|x;\theta )=\frac{e^{{\eta }_{\theta }(x)}}{1+e^{{\eta }_{\theta }(x)}},\hspace{1em}{\eta }_{\theta }(x)={\theta }^{T}x$$ (1)

and $y|x~\mathbb{P}(\cdot |x;{\theta }^{\ast })$ where ${\theta }^{\ast }\in {ℝ}^p$ refers to the unknown true parameter. Also, we assume the label z is assigned only based on the latent response y independent from x. Viewing z as a noisy observation of latent y, this assumption corresponds to a missing at random assumption, a classical assumption in latent variable problems.

Given such z, we select n_l labeled and n_u unlabeled samples from samples with z = 1 and z = 0, respectively. An important issue is how positive and unlabeled samples are selected. In this article, we adopt a case-control approach (e.g., McCullagh and Nelder 2006)which is suitable for our biotechnology application and many others. In particular, we introduce another binary random variable s ∈ {0, 1} representing whether a sample is selected (s = 1) or not (s = 0) to model different sampling rates in selecting labeled and unlabeled samples. Since there are n_ℓ labeled and n_u unlabeled samples, we have

$$\frac{\mathbb{P}(z=1|s=1)}{\mathbb{P}(z=0|s=1)}=\frac{n_{\mathcal{l}}}{n_u},$$

and we see only selected samples, ${(x_i,z_i,s_i=1)}_{i=1}^{n_{\mathcal{l}}+n_u}$. It is further assumed that the selection is only based on the label z, independent of x and y. We note that this case-control scheme (Lancaster and Imbens 1996;Wardet al. 2009), opposed to the single training sampling scheme (Elkan and Noto 2008) is needed to model the case where unlabeled samples are random draws from the original population, since positive samples have to be overrepresented in the dataset to satisfy such model assumption.

In our biotechnology application the case-control setting is appropriate since the high-throughput technology leads to the unlabeled samples being drawn randomly from the original population (see Romero, Tran, and Abate 2015 for details). As is displayed in Figure 1, sequences are selected randomly from a library and positive samples are generated through a screening step. Hence, the positive sequences are sampled randomly from the positive sequences while the unlabeled sequences are based on random sampling from the original sequence library. This experiment corresponds exactly to the case-control sampling scheme discussed.

Figure 1.

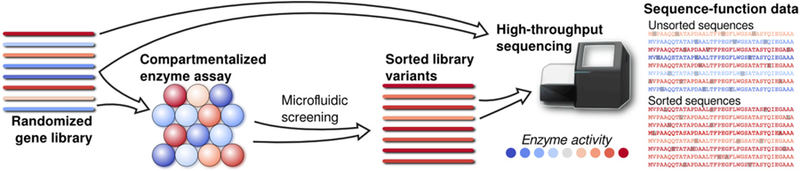
High-throughput sequencing diagram.

Furthermore, the true positive (TP) prevalence is

$$\pi :=\mathbb{P}(y=1)=\int \frac{e^{{\eta }_{{\theta }^{\ast }}(x)}}{1+e^{{\eta }_{{\theta }^{\ast }}(x)}}d{\mathbb{P}}_X(x)\in (0,1)$$? (2)

and π is assumed known. In our biotechnology application, π is estimated precisely using an alternative experiment (Romero, Tran, and Abate 2015).

In the biological sequence engineering example, ${(x_i)}_{i=1}^{n_{\mathcal{l}}+n_u}$ correspond to binary covariates of biological sequences. In the BGL example, for each of the d positions, there are M possible categories of amino acids. Therefore, the covariates correspond to the indicator of an amino acid appearing in a given position (p = O(dM)) as well as pairs of amino acids (p = O(d²M²)), and so on. Here d = O(1000) and M ≈ 20 make the problem high-dimensional.

High-dimensional PU-learning presents computational challenges since the standard logistic regression objective leads to a nonconvex likelihood when we have positive and unlabeled data. To address this challenge, we build on the expectation maximization (EM) procedure developed in Ward et al. (2009) and provide two computational speed-ups. In particular, we introduce the PUlasso for high-dimensional variable selection with positive and unlabeled data. Prior work that involves the EM algorithm in the low-dimensional setting in Ward et al. (2009) involves solving a logistic regression model at the M-step. To adapt to the high-dimensional setting and make the problem scalable, we include an ℓ₁-sparsity or ℓ₁/ℓ₂-group sparsity penalty and provide two speed-ups. First, we use a quadratic majorizer of the logistic regression objective, and secondly, we use techniques in linear algebra to exploit sparsity of the design matrix X which commonly arises in the applications we are dealing with. Our PUlasso algorithm fits into the majorization minimization (MM) framework (see, e.g., Lange, Hunter, and Yang 2000; Ortega and Rheinboldt 2000) for which the EM algorithm is a special case.

1.3. Our Contributions

In this article we make the following major contributions:

• Develop the PUlasso algorithm for doing variable selection and classification with presence-only data. In particular, we build on the existing EM algorithm developed in Ward et al. (2009) and add two computational speed-ups, quadratic majorization and exploiting sparse matrices. These two speed-ups improve speed by several orders of magnitude and allows our algorithm to scale to datasets with millions of samples and covariates.

• Provide theoretical guarantees for our algorithm. First we show that our algorithm converges to a stationary point of the nonconvex objective, and then show that any stationary point within a local neighborhood of θ* achieves the minimax optimal mean-squared error for sparse vectors. To provide statistical guarantees we extend the existing results of generalized linear model with a canonical link function (Negahban et al. 2012; Loh and Wainwright 2006) to a noncanonical link function and show optimality of stationary points of nonconvex objectives in high-dimensional statistics. To the best of our knowledge the PUlasso is the first algorithm where PUlearning is provably optimal in the high-dimensional setting.

• Demonstrate through a simulation study that our algorithm performs well in terms of classification compared to stateof-the-art PU-learning methods in Du Marthinus, Niu, and Sugiyama (2015), Elkan and Noto (2008), and Liu et al. (2006), both for low-dimensional and high-dimensional problems.

• Demonstrate that our PUlasso algorithmallows us to develop improved protein-engineering approaches. In particular, we applyour PUlassoalgorithmto sequencesofBGL enzymes to determine which sequences are functional. We demonstrate that sequences selected by our algorithm have a good predictive accuracy and we also provide a scientific experiment which shows that the variables selected lead to BGL proteins that are engineered with improved functionality.

The remainder of the article is organized as follows: in Section 2 we provide the background and introduce the PUlasso algorithm, including our two computational speed-ups and provide an algorithmic guarantee that our algorithm converges to a stationary point; in Section 3 we provide statistical meansquared error guarantees which show that our PUlasso algorithm achieves the minimax rate; Section 4 provides a comparison in terms of classification performance of our PUlasso algorithm to state-of-the-art PU-learning algorithms; finally in Section 5, we apply our PUlasso algorithm to the BGL data application and provide both a statistical validation and simple scientific validation for our selected variables.

Notation: For scalars a, $b\in ℝ$, we denote a ∧ b = min{a, b}, a ∨ b = max{a, b}. Also, we denote a ≳ b if there exists a universal constant c > 0 such that a ≥ cb. For $w\in {ℝ}^p$, we denote ℓ₁, ℓ₂, and ℓ_∞ norm as ${\Vert v\Vert }_1={\sum }_{i=1}^n\left|v_i\right|$, ${\Vert v\Vert }_2=\sqrt{v^{T}v}$, and ${\Vert v\Vert }_{\infty }={\sup }_j\left|v_j\right|$ and use $v\circ w\in {ℝ}^p$ to denote Hadamard product (entry-wise product) of v,w. For a set S, we use |S| to denote the cardinality of S. For any subset $S\subseteq \{1,\hspace{0.17em}\dots \hspace{0.17em},p\}$, $v_S\in {ℝ}^{\left|S\right|}$ denotes the subvector of the vector v by selecting the components with indices in S. Likewise for matrix $A\in {ℝ}^{n\times p}$, $A_S\in {ℝ}^{n\times \left|S\right|}$ denotes a submatrix by selecting columns with indices in S. For a group ℓ₁/ℓ₂ norm, the norm is characterized by a partition $\mathcal{G}:=(g_1,\hspace{0.17em}\dots \hspace{0.17em},g_J)$ of {1, … , p} and associated weights ${(w_j)}_1^J$. We let $\mathcal{G}:=(\mathcal{G},{(w_j)}_1^J)$ and define the ℓ₁/ℓ₂ norm as ${\Vert v\Vert }_{\mathcal{G},2,1}:={\sum }_j{w}_j{\Vert v_{g_j}\Vert }_2$. We often need a dual norm of ${\Vert \hspace{0.17em}\cdot \hspace{0.17em}\Vert }_{\mathcal{G},2,1}$. We use $\overline{\mathcal{G}}$ to denote $\overline{\mathcal{G}}:=(\mathcal{G},{(w_j^{-1})}_1^J)$ and write ${\Vert v\Vert }_{\overline{\mathcal{G}},2,\infty }={\max }_j{w}_j^{-1}{\Vert v_{g_j}\Vert }_2$. Finally, we write ${\mathbb{B}}_q(r,v)$ for an ℓ_q ball with radius r centered at $v\in {ℝ}^p$, and denote as ${\mathbb{B}}_q(r)$ if v = 0.

For a convex function $f:{ℝ}^p\to ℝ$, we use ∂f (x) to denote the set of subgradients at the point x and ∇f (x) to denote an element of ∂f (x). Also for a function f + g such that f is differentiable (but not necessarily convex) and g is convex, we define $\partial (f+g)(x)=\{\nabla f(x)+h\in {ℝ}^p;h\in \partial g(x)\}$ with a slight abuse of notation. Also, we say f (n) = O(g(n)), f (n) = Ω(g(n)), and f (n) = Θ(g(n)) if |f | is asymptotically bounded above, bounded below, and bounded above and below by g.

For a random variable $x\in ℝ$, we say x is a sub-Gaussian random variable with sub-Gaussian parameter σ_x > 0 if $E[\exp (t(x-E[x]))]\le \exp (t^2{\sigma }_x^2/2)$ for all $t\in ℝ$ and we denote as $x~\text{subG}({\sigma }_x^2)$ with a slight abuse of notation. Similarly, we say x is a sub-exponential random variable with sub-exponential parameter (ν, b) if E[exp(t(x − E[x]))] ≤ exp(t²ν²/2) for all |t| ≤ 1/b and we denote as x ∼ subExp(ν, b). A collection of random variables (x₁,…, x_n) is referred to as $x_1^n$.

2. PUlasso Algorithm

In this section, we introduce our PUlasso algorithm. First, we discuss the prior EM algorithm approach developed in Ward et al. (2009) and apply a simple regularization scheme. We then discuss our two computational speed-ups, the quadratic majorization for the M-step and exploiting sparse matrices. We prove that our algorithm has the descending property and converges to a stationary point, and show that our two speedups increase speed by several orders of magnitude.

2.1. Prior Approach: EM Algorithm With Regularization

First we use the prior result in Ward et al. (2009) to determine the observed log-likelihood (in terms of the z_is) and the full log-likelihood (in terms of the unobserved y_is and z_is). The following lemma, derived in Ward et al. (2009), gives the form of the observed and the full log-likelihood in the case-control sampling scheme.

Lemma 2.1 (Ward et al. 2009). The observed log-likelihood $\log L(\theta ;x_1^n,z_1^n)$ for our presence-only model in terms of ${(x_i,z_i,s_i=1)}_{i=1}^n$ is

$$\begin{gathered} \log L(\theta ;x_1^n,z_1^n)=\log \left(\prod _i{\mathbb{P}}_{\theta }(z_i|x_i,s_i=1)\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\sum _{i=1}^n\log {\left(\frac{\frac{n_l}{\pi n_u}{e}^{{\theta }^{T}x}}{1+(1+\frac{n_l}{\pi n_u})e^{{\theta }^{T}x}}\right)}^{z_i}\times {\left(\frac{1+e^{{\theta }^{T}x}}{1+(1+\frac{n_l}{\pi n_u})e^{{\theta }^{T}x}}\right)}^{1-z_i}. \end{gathered}$$ (3)

The full log-likelihood $L_f(\theta ;x_1^n,y_1^n,z_1^n)$ in terms of ${(x_i,y_i,z_i,s_i=1)}_{i=1}^n$ is

$$\begin{gathered} \log L_f(\theta ;x_1^n,y_1^n,z_1^n) \\ \hspace{1em}\hspace{0.17em}=\log \left(\prod _i{\mathbb{P}}_{\theta }(y_i,z_i|x_i,s_i=1)\right) \\ \hspace{1em}\hspace{0.17em}\propto \sum _{i=1}^n[y_i\left(x_i^T\theta +\log \frac{n_{\mathcal{l}}+\pi n_u}{\pi n_u}\right) \\ \hspace{1em}\hspace{0.17em}-\log \left(1+\exp \left(x_i^T\theta +\log \frac{n_{\mathcal{l}}+\pi n_u}{\pi n_u}\right)\right)], \end{gathered}$$ (4)

where n_ℓ, n_u are the number of positive and unlabeled observations, n = n_ℓ + n_u and π is defined in (2).

The proof can be found in Ward et al. (2009). Our goal is to estimate the parameter ${\theta }^{\ast }:=\arg {\min }_{\theta \in {ℝ}^p}E[-\log L(\theta ;x_1^n,z_1^n)]$, which we assume to be unique. In the setting where p is large, we add a regularization term. We are interested in cases when there exists or does not exist a group structure within covariates. To be general we use the group ℓ₁/ℓ₂-penalty for which ℓ₁ is a special case. Hence, our overall optimization problem is

$$\underset{\theta }{\text{minimize}}\hspace{1em}-\frac{1}{n}\sum _{i=1}^n\log L(\theta ;x_i,z_i)+P_{\lambda }(\theta ),$$ (5)

where log L(θ; x_i, z_i) is the observed log-likelihood. For a penalty term, we use the group sparsity regularizer

$$P_{\lambda }(\theta ):=\text{λ}{\Vert \theta \Vert }_{\mathcal{G},2,1}=\text{λ}\sum _{j=1}^J{w}_j{\Vert {\theta }_{g_j}\Vert }_2$$ (6)

with $\mathcal{G}=(\mathcal{G},{(w_j)}_{j=1}^J)$, such that $\mathcal{G}:=(g_1,\hspace{0.17em}\dots \hspace{0.17em},g_J)$ is a partition of (1,…, p) and w_j > 0.We note that ${\Vert \theta \Vert }_{\mathcal{G},2,1}={\Vert \theta \Vert }_1$ if J = p, g_j = {j} and w_j = 1, ∀j. For notational convenience we denote the overall objective ${\mathcal{F}}_n(\theta )$ as

$${\mathcal{F}}_n(\theta ):=-\frac{1}{n}\sum _{i=1}^n\log L(\theta ;x_i,z_i)+P_{\text{λ}}(\theta )={\mathcal{L}}_n(\theta )+P_{\text{λ}}(\theta ),$$ (7)

where we define the loss function ${\mathcal{L}}_n(\theta )$ as ${\mathcal{L}}_n(\theta )\hspace{1em}:=-n^{-1}{\sum }_{i=1}^n\log L(\theta ;x_i,z_i)$ and $P_{\text{λ}}(\theta )=\text{λ}{\Vert \theta \Vert }_{\mathcal{G},2,1}=\text{λ}{\sum }_{j=1}^J{w}_j{\Vert {\theta }_{g_j}\Vert }_2$.

In the original proposal of the group lasso, Yuan and Lin (2006) recommended to use (6) for orthonormal group matrices $X_{g_j}$, that is,$X_{g_j}^T{X}_{g_j}/n=I_{|g_j|\times |g_j|}$. If group matrices are not orthonormal, however, it is unclear whether we should orthonormalize group matrices prior to application of the group lasso. This question was addressed in Simon and Tibshirani (2012), and the authors provide a compelling argument that prior orthonormalization has both theoretical and computational advantages. In particular, Simon and Tibshirani (2012) demonstrated that the following orthonormalization procedure is intimately connected with the uniformly most powerful invariant testing for inclusion of a group. To describe this orthonormalization explicitly, we obtain standardized group matrices $Q_{g_j}\in {ℝ}^{n\times |g_j|}$ and scale matrices $R_{g_j}\in {ℝ}^{|g_j|\times |g_j|}$ for j ≥ 2 using the QR-decomposition such that

$$P_0{X}_{g_j}=Q_{g_j}{R}_{g_j}\hspace{1em}\text{and}\hspace{1em}{Q}_{g_j}^T{Q}_{g_j}=n{I}_{|g_j|\times |g_j|},$$ (8)

where $P_0=(I_{n\times n}-\frac{{\mathrm{𝟙}}_n{\mathrm{𝟙}}_n^T}{n})$ is the projection matrix onto the orthogonal space of ${\mathrm{𝟙}}_n$. Letting $Q:=[{\mathrm{𝟙}}_n,Q_{g_2},\hspace{0.17em}\dots \hspace{0.17em},Q_{g_J}]=[q_1^T,\hspace{0.17em}\dots \hspace{0.17em},q_n^T]$, the original optimization problem (5) can be expressed in terms of q_is and becomes

$$\underset{\nu }{\arg \min }\{-\frac{1}{n}\sum _{i=1}^n\log L(\nu ;q_i,z_i)+\text{λ}\sum _{j=1}^J{w}_j{\Vert {\nu }_{g_j}\Vert }_2\},$$ (9)

where we use the transformation θ to ν

$${\theta }_{g_j}=\{\begin{array}{ll}{\nu }_1-{\sum }_{j=2}^J\frac{{\mathrm{𝟙}}_n^T}{n}{X}_{g_j}{R}_{g_j}^{-1}{\nu }_{g_j}\hfill & j=1\hfill \\ R_{g_j}^{-1}{\nu }_{g_j}\hfill & j\ge 2.\hfill \end{array}$$ (10)

We note that this corresponds to the standard centering and scaling of the predictors in the case of standard lasso. For more discussion about group lasso and standardization (see, e.g., Huang, Breheny, and Ma 2012).

A standard approach to performing this minimization is to use the EM-algorithm approach developed in Ward et al. (2009). In particular, we treat $y_1^n$ as hidden variables and estimate them in the E-step. Then use estimated ${\widehat{y}}_1^n$ to obtain the full log-likelihood $\log L_f(\theta ;x_1^n,{\widehat{y}}_1^n,z_1^n)$ in the M-step.

The E-step follows from $E_{{\theta }^m}[y_i|z_i,x_i,s_i=1]={\left(\frac{e^{x_i^T{\theta }^m}}{1+e^{x_i^T{\theta }^m}}\right)}^{1-z_i}$ since z_i = 1 implies y_i = 1 and when z_i = 0, observations in the unlabeled data are random draws from the population. An initialization θ⁰ can be any ${ℝ}^p$ vector such that ${\mathcal{F}}_n({\theta }^0)\le {\mathcal{F}}_n({\theta }_{\text{null}})$ where θ_null is the parameter corresponding to the intercept-only model. If we are provided with no additional information, we may use θ_null for the initialization. We use θ⁰ = θ_null as the initialization for the remainder of the article. For the M-step, it was originally proposed to use a logistic regression solver. We can use a regularized logistic regression solver such as the glmnet R package to solve (12). We discuss a computationally more efficient way of solving (12) in the subsequent section.

2.2. PUlasso: A Quadratic Majorization for the M-Step

Now we develop our PUlasso algorithm which is a faster algorithm for solving (5) by using quadratic majorization for the M-step. The main computational bottleneck in algorithm 1 is the M-step which requires minimizing a regularized logistic regression loss at each step. This subproblem does not have a closed-form solution and needs to be solved iteratively, causing inefficiency in the algorithm. However, the most important property of the objective function in the M-step is that it is a surrogate function of the likelihood which ensures the descending property (see, e.g., Lange, Hunter, and Yang 2000). Hence, we replace a logistic loss function with a computationally faster quadratic surrogate function. In this aspect, our approach is an example of the more general MM framework (see, e.g., Lange, Hunter, and Yang 2000; Ortega and Rheinboldt 2000).

On the other hand, our loss function itself belongs to a generalized linear model family, as we will discuss in more detail in the subsequent section. A number of works have developed methods for efficiently solving regularized generalized linear model problems. A standard approach is to make a quadratic approximation of the log-likelihood and use solvers for a regularized least-square problem. Works include using an exact Hessian (Lee et al. 2006; Friedman, Hastie, and Tibshirani 2010), an approximate Hessian (Meier, Van De Geer, and Bühlmann 2008) or a Hessian bound (Krishnapuramet al. 2005; Simon and Tibshirani 2012; Breheny and Huang 2013) for the second-order term. Solving a second-order approximation problem amounts to taking a Newton step, thus convergence is not guaranteed without a step-size optimization (Lee et al. 2006;Meier, Van De Geer, and Bühlmann 2008), unless a global bound of the Hessian matrix is used. Our work can be viewed as in the line of these works where a quadratic approximation of the loss function is made and then an upper bound of the Hessian matrix is used to preserve a majorization property.

A coordinate descent (CD) algorithm (Wu and Lange 2008; Friedman, Hastie, and Tibshirani 2010) or a block coordinate descent (BCD) algorithm (Yuan and Lin 2006; Puig et al. 2011; Simon and Tibshirani 2012; Breheny and Huang 2013) has been a very efficient and standard way to solve a quadratic problem with ℓ₁ penalty or ℓ₁/ℓ₂ penalty and we also take this approach. When a feature matrix $X\in {ℝ}^{n\times p}$ is sparse, we can set up the algorithm to exploit such sparsity through a sparse linear algebra calculation. We discuss this implementation strategy in Section 2.2.1.

Now we discuss the PUlasso algorithm and the construction of quadratic surrogate functions in more details. Using the MM framework, we construct the set of majorization functions $-\overline{Q}(\theta ;{\theta }^m)$ with the following two properties

$$\overline{Q}({\theta }^m;{\theta }^m)=Q({\theta }^m;{\theta }^m),\hspace{1em}\overline{Q}(\theta ;{\theta }^m)\le Q(\theta ;{\theta }^m),\forall \theta ,$$ (13)

where our goal is to minimize −Q where $Q(\theta ;{\theta }^m)\hspace{1em}:=n^{-1}{E}_{{\theta }^m}[\log L_f(\theta )|z_1^n,x_1^n,s_1^n=1]$.

Using the Taylor expansion of Q(θ; θ^m) at θ = θ^m, we obtain Q(θ; θ^m)

$$\begin{gathered} =Q({\theta }^m;{\theta }^m)+\frac{1}{n}{[X^T(\widehat{y}({\theta }^m)-{\mu }^{\ast }({\theta }^m))]}^T{\Delta }_m-\frac{1}{2n}{\int }_0^1{\Delta }_m^T{X}^{T}W(\theta +s{\Delta }_m)X{\Delta }_{m}ds \\ \ge Q({\theta }^m;{\theta }^m)+\frac{1}{n}{\left(\widehat{y}({\theta }^m)-{\mu }^{\ast }({\theta }^m)\right)}^{T}X{\Delta }_m-\frac{1}{8n}{\Delta }_m^T{X}^{T}X{\Delta }_m, \end{gathered}$$

where we define ${\Delta }_m:=\theta -{\theta }^m$, ${\mu }^{\ast }{({\theta }^m)}_i:=\frac{e^{x_i^T{\theta }^m+b}}{1+e^{x_i^T{\theta }^m+b}}$, $b:=\log \frac{n_{\mathcal{l}}+\pi n_u}{\pi n_u}$ and $W\in {ℝ}^{n\times n}$ is a diagonal matrix with ${[W(\theta )]}_{ii}:={\mu }^{\ast }{(\theta )}_i(1-{\mu }^{\ast }{(\theta )}_i)$. The inequality follows from $W(\theta )\prec \frac{1}{4}{I}_{n\times n}$, ∀θ. Thus, setting $\overline{Q}$ as follows

$$\begin{gathered} \overline{Q}(\theta ;{\theta }^m):=Q({\theta }^m;{\theta }^m)+\frac{1}{n}{\left(\widehat{y}({\theta }^m)-{\mu }^{\ast }({\theta }^m)\right)}^T(X\theta -X{\theta }^m) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}-\frac{1}{8n}{\left(\theta -{\theta }^m\right)}^T{X}^{T}X(\theta -{\theta }^m), \end{gathered}$$

$\overline{Q}$ satisfies both conditions in (13). Also with some algebra, it follows that

$$\begin{gathered} \overline{Q}(\theta ;{\theta }^m)=-\frac{1}{8n}{\left(4(\widehat{y}({\theta }^m)-{\mu }^{\ast }({\theta }^m))+X{\theta }^m-X\theta \right)}^T(4(\widehat{y}({\theta }^m) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}-{\mu }^{\ast }({\theta }^m))+X{\theta }^m-X\theta )+c({\theta }^m) \end{gathered}$$

for some c(θ^m) which does not depend on θ. Hence, $-\overline{Q}$ acts as a quadratic surrogate function of−Q which replaces our M-step for the original EM algorithm. Therefore, our PUlasso algorithm can be represented as follows.

Now we state the following proposition to show that both the regularized EM and PUlasso algorithms have the desirable descending property and converge to a stationary point. For convenience we define the feasible region $\widetilde{{\Theta }_0}$, which contains all θ whose objective function value is better than that of the intercept-only model, defined as

$$\widetilde{{\mathrm{\Theta }}_0}:=\{\theta \in {ℝ}^p;{\mathcal{F}}_n(\theta )\le {\mathcal{F}}_n({\theta }_{\text{null}})\},$$ (17)

where ${\theta }_{\text{null}}={[\log \frac{\pi }{1-\pi },0,\hspace{0.17em}\dots \hspace{0.17em},0]}^T$, an estimate corresponding to the intercept-only model. We let $\mathcal{S}$ be the set of stationary points satisfying the first-order optimality condition, that is,

$$\begin{gathered} \mathcal{S}:=\{\theta ;\exists \nabla {\mathcal{F}}_n(\theta )\in \partial {\mathcal{F}}_n(\theta )\hspace{0.17em}\text{such}\hspace{0.17em}\text{that} \\ \nabla {\mathcal{F}}_n{\left(\theta \right)}^T(\theta \prime -\theta )\ge 0,\forall \theta \prime \in \widetilde{{\mathrm{\Theta }}_0}\}. \end{gathered}$$ (18)

One of the important conditions is to ensure that all iterates of our algorithm lie in $\widetilde{{\mathrm{\Theta }}_0}$ which is trivially satisfied if θ⁰ = θ_null.

Proposition 2.1. The sequence of estimates (θ^m) obtained by Algorithms 1 or 2 satisfies

1. ${\mathcal{F}}_n({\theta }^m)\ge {\mathcal{F}}_n({\theta }^{m+1})$, and ${\mathcal{F}}_n({\theta }^m)>{\mathcal{F}}_n({\theta }^{m+1})$ if ${\theta }^m\notin \mathcal{S}$.

2. All limit points of ${({\theta }^m)}_1^{\infty }$ are elements of the set $\mathcal{S}$, and ${\mathcal{F}}_n({\theta }^m)$ converges monotonically to ${\mathcal{F}}_n(\tilde{\theta })$ for some $\tilde{\theta }\in \mathcal{S}$.

3. The sequence (θ^m) has at least one limit point, which must be a stationary point of ${\mathcal{F}}_n(\theta )$ by (ii).

Proposition 2.1 shows that we obtain a stationary point of the objective (7) as an output of both the regularized EM algorithm and our PUlasso algorithm. The proof uses the standard arguments based on Jensen’s inequality, convergence of EM algorithm and MM algorithms and is deferred to the supplement S1.1.

2.2.1. Block Coordinate Descent Algorithm for M-Step and Sparse Calculation

In this section, we discuss the specifics of finding a minimizer for the M-step (16) for each iteration of our PUlasso algorithm. After preprocessing the design matrix as described in (9) and (10), we solve the following optimization problem using a standard block-wise coordinate descent algorithm.

$$\underset{\nu }{\arg \min }\left\{\frac{1}{2n}{\Vert u-Q\nu \Vert }_2^2+4\text{λ}\sum _{j=1}^J{w}_j{\Vert {\nu }_{g_j}\Vert }_2\right\}.$$ (19)

S(., λ) is the soft thresholding operator defined as follows

$$S(z,\text{λ}):=\{\begin{array}{ll}({\Vert z\Vert }_2-\text{λ})\frac{z}{{\Vert z\Vert }_2}\hfill & \text{if}{\Vert z\Vert }_2>\text{λ}\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

Note that we do not need to keep updating the intercept ν₁ since Q_gj, j ≥ 2 are orthogonal to $Q_{g_1}\equiv {\mathrm{𝟙}}_n$. For more details (see, e.g., Breheny and Huang 2013).

For our biochemistry example and many other examples, X is a sparse matrix since each entry is an indicator of whether an amino acid is in a position. In Algorithm 3, we do not exploit this sparsity since Q will not be sparse even when X is sparse. If we want to exploit sparse X we use the following algorithm.

To explain the changes to this algorithm, we modify (20) and (22) so that we directly use X rather than Q to exploit the sparsity of X. Using (8), we first substitute $Q_{g_j}$ with $P_0{X}_{g_j}{R}_{g_j}^{-1}$ to obtain

$$z_j=n^{-1}{R}_{g_j}^{-1}{X}_{g_j}^T{P}_{0}r+{\nu }_{g_j}$$ (28)

$$r\prime \leftarrow r+P_0{X}_{g_j}{R}_{g_j}^{-1}({\nu }_{g_j}-{\nu }_{g_j}^{\prime }).$$ (29)

However, carrying out (28) – (29) instead of (20) – (22) incurs a greater computational cost. Calculating $Q_{g_j}^{T}r$ requires n|g_j| operations. On the contrary, the minimal number of operations required to do a matrix multiplication of $R_{g_j}^{-1}{X}_{g_j}^T{P}_{0}r$ is $n^2+n|g_j|+{|g_j|}^2$, when it is parenthesized as $R_{g_j}^{-1}(X_{g_j}^T(P_{0}r))$. Inmany cases |g_j| is small (for standard lasso, |g_j| = 1, ∀j and for our biochemistry example, |g_j| is at most 20), but the additional increase in n can be very costly (especially in our example where n is over 4 million).

For a more efficient calculation, we first exploit the structure of $P_0=I_{n\times n}-\frac{{\mathrm{𝟙}}_n{\mathrm{𝟙}}_n^T}{n}$ when multiplying P₀ with a vector, which reduces the cost from n² operations to 2n operations. Also, we carry out calculations using $X_{g_j}$ instead of $P_0{X}_{g_j}$ when calculating residuals and do the corrections all at once.

Before going into detail about (23)–(26), we first discuss the computational complexity. Comparing (23) with (20), the first term only requires an additional |g_j|² operations. The second term $(X_{g_j}^T{\mathrm{𝟙}}_n)/n$ can be stored during the initial QR decomposition; thus the only potentially expensive operation is calculating an average of r which requires n operations. Comparing (25) with (22), only |g_j|² additional operations are needed when we parenthesize as $X_{g_j}(R_{g_j}^{-1}({\nu }_{g_j}-{\nu }_{g_j}^{\prime }))$. Note that if we had kept P₀, there would have been an additional 2n operations even though we had used the structure of P₀. In the calculation of (27), we note that n operations are involved in subtracting ${\sum }_{j=2}^J{a}_j$ from r because a_j are scalars. In summary, we essentially reduce additional computational cost from O(n²) to nJ per cycle by carrying out (23)–(26) instead of (28)–(29).

Now we derive/explain the formulas in Algorithm 4. To make quantities more explicit, we use r_j and $r_j^{\prime }$ to denote a residual vector before/after update at j using Algorithm 3 and ${\tilde{r}}_j$ and ${\tilde{r}}_j^{\prime }$ using Algorithm 4. By definition, $r_{j+1}=r_j^{\prime }$ and ${\tilde{r}}_{j+1}={\tilde{r}}_j^{\prime }$. Also we note that in the beginning of the cycle $r_2={\tilde{r}}_2$. Equation (23) can be obtained from (28) by replacing P₀ with $I_{n\times n}-\frac{{\mathrm{𝟙}}_n{\mathrm{𝟙}}_n^T}{n}$. Now we show that modified residuals still correctly update coefficient. Starting from j = 2, a calculated ${\tilde{r}}_j^{\prime }$ is a constant vector off from a correct residual $r_j^{\prime }$, as we see below

$$r_j^{\prime }=r_j+P_0{X}_{g_j}{R}_{g_j}^{-1}({\nu }_{g_j}-{\nu }_{g_j}^{\prime })$$ (30)

$$=r_j+X_{g_j}{R}_{g_j}^{-1}({\nu }_{g_j}-{\nu }_{g_j}^{\prime })-{\mathrm{𝟙}}_n\frac{{\mathrm{𝟙}}_n^T}{n}{X}_{g_j}{R}_{g_j}^{-1}({\nu }_{g_j}-{\nu }_{g_j}^{\prime })$$ (31)

$$={\tilde{r}}_j^{\prime }-{\mathrm{𝟙}}_n{a}_j,$$ (32)

where we recall that $a_j=\frac{{\mathrm{𝟙}}_n^T}{n}{X}_{g_j}{R}_{g_j}^{-1}({\nu }_{g_j}-{\nu }_{g_j}^{\prime })$. We note $P_0{r}_j^{\prime }=P_0{\tilde{r}}_j^{\prime }$ because $P_0{\mathrm{𝟙}}_n=0$. Then the next z_j+1, thus new ${\nu }_{g_{j+1}}$, are still correctly calculated since

$$\begin{gathered} z_{j+1}=n^{-1}{R}_{g_{j+1}}^{-1}{X}_{g_{j+1}}^T{P}_0{r}_{j+1}+{\nu }_{g_{j+1}} \\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=n^{-1}{R}_{g_{j+1}}^{-1}{X}_{g_{j+1}}^T{P}_0{\tilde{r}}_{j+1}+{\nu }_{g_{j+1}}. \end{gathered}$$ (33)

The next residual ${\tilde{r}}_{j+1}^{\prime }$ is again off by a constant from the correct residual ${\tilde{r}}_{j+1}^{\prime }$. To see this, ${\tilde{r}}_{j+1}^{\prime }=r_{j+1}+P_0{X}_{g_{j+1}}{R}_{g_{j+1}}^{-1}({\nu }_{g_{j+1}}-{\nu }_{g_{j+1}}^{\prime })={\tilde{r}}_{j+1}+P_0{X}_{g_{j+1}}{R}_{g_{j+1}}^{-1}({\nu }_{g_{j+1}}-{\nu }_{g_{j+1}}^{\prime })-a_j{\mathrm{𝟙}}_n$ by (29). Going through (30) – (32) with j being replaced by j + 1, we obtain

$$r_{j+1}^{\prime }={\tilde{r}}_{j+1}^{\prime }-(a_j+a_{j+1}){\mathrm{𝟙}}_n.$$

Inductively, we have correct z_j, thus ${\nu }_{g_j}$ for all j ≥ 2. At the end of the cycle, we correct the residual vector all at once by letting $r\leftarrow r-({\sum }_{j=2}^J{a}_j){\mathrm{𝟙}}_n$.

2.3. R Package Details

We provide a publicly available R implementation of our algorithm in the PUlasso package. For a fast and efficient implementation, all underlying computation is implemented in C++. The package uses warm start and strong rule (Friedman et al. 2007; Tibshirani et al. 2012), and a cross-validation function is provided as well for the selection of the regularization parameter λ. Our package supports a parallel computation through the R package parallel.

2.4. Run-Time Improvement

Now we illustrate the run-time improvements for our two speed-ups. Note that we only include p up to 100 so that we can compare to the original regularized EM algorithm. For our biochemistry application p = O(10⁴) and n = O(10⁶) which means the regularized EM algorithm is too slow to run efficiently. Hence, we use smaller values of n and p in our run-time comparison. It is clear from our results that the quadratic majorization step is several orders of magnitude faster than the original EM algorithm, and exploiting the sparsity of X provides a further 30% speed-up.

3. Statistical Guarantee

We now turn our attention to statistical guarantees for our PUlasso algorithm under the statistical model (1). In particular, we provide error bounds for any stationary point of the nonconvex optimization problem (5). Proposition 2.1 guarantees that we obtain a stationary point from our PUlasso algorithm.

We first note that the observed likelihood (3) is a generalized linear model (GLM) with a noncanonical link function. To see this, we rewrite the observed likelihood (3) as

$$L(\theta ;x_1^n,z_1^n)=\prod _{i=1}^n\exp (z_i{\eta }_i-A({\eta }_i))$$ (34)

after some algebraic manipulations, where we define ${\eta }_i\hspace{0.17em}\hspace{0.17em}:=\log ({\pi }_{\mathcal{l}}/\pi n_u)+x_i^T\theta -\log (1+e^{x_i^T\theta })$ and $A({\eta }_i):=\log (1+e^{{\eta }_i})$. Also, we let µ(η_i) := A′(η_i), which is the conditional mean of z_i given x_i, by the property of exponential families. For the convenience of the reader, we include the derivation from (3) to (34) in the supplementary materials (S2.1). The mean of z_i is related with θ^Tx_i via the link function g through g(µ(η_i)) = θ^Tx_i, where g satisfies ${(g\circ \mu )}^{-1}({\theta }^T{x}_i)=\log (n_{\mathcal{l}}/\pi n_u)+x_i^T\theta -\log (1+e^{x_i^T\theta })$. Because (g ○ µ)⁻¹ is not the identity function, the likelihood is not convex anymore. For a more detailed discussion about the GLM with noncanonical link (see, e.g., McCullagh and Nelder 2006; Fahrmeir and Kaufmann 1985).

A number of works have been devoted to sparse estimation for generalized linear models. A large number of previous works have focused on generalized linear models with convex loss functions (negative log-likelihood with a canonical link) plus ℓ₁ or ℓ₁/ℓ₂ penalties. Results with the ℓ₁ penalty include a risk consistency result (van de Geer 2008) and estimation consistency in ℓ₂ or ℓ₁ norms (Kakade et al. 2010). For a group-structured penalty, a probabilistic bound for the prediction error was given in Meier, Van De Geer, and Bühlmann (2008). An ℓ₂ estimation error bound in the case of the group lasso was given in Blazère, Loubes, and Gamboa (2014).

Negahban et al. (2012) rederived an ℓ₂ error bound of an ℓ₁-penalized GLM estimator under the unified framework for M-estimators with a convex loss function. This result about the regularized GLM was generalized in Loh and Wainwright (2006) where penalty functions are allowed to be nonconvex, while the same convex loss function was used. Since the overall objective function is nonconvex, authors discuss error bounds obtained for any stationary point, not a global minimum. In this aspect, our work closely follows this idea. However, our setting differs from Loh and Wainwright (2006) in two aspects: first, the loss function in our setting is nonconvex, in contrast with a convex loss function (a negative log-likelihood with a canonical link)with nonconvex regularizer in Loh andWainwright (2006). Also, an additive penalty function was used in the work of Loh and Wainwright (2006), but we consider a group-structured penalty.

After the initial draft of this article was written, we became aware of two recent papers (Elsener and van de Geer 2018; Mei, Bai, and Montanari 2018) which studied nonconvex M-estimation problems in various settings including binary linear classification, where the goal is to learn θ* such that $E[z_i|x_i]=\sigma (x_i^T{\theta }^{\ast })$ for a known σ(·). The proposed estimators are stationary points of the optimization problem: $\arg {\min }_{\theta }{n}^{-1}{\sum }_{i=1}^n{(z_i-\sigma (x_i^T\theta ))}^2+\text{λ}{\Vert \theta \Vert }_1$ in both papers. As the focus of our article is to learn a model with a structural contamination in responses, our choice of mean and loss functions differ from both papers. In particular, our choice of mean function is different from the sigmoid function, which was the representative example of σ(·) in both papers, and we use the negative log-likelihood loss in contrast to the squared loss. We establish error bounds by proving a modified restricted strong convexity condition, which will be discussed shortly, while error bounds of the same rates were established in Elsener and van de Geer (2018) through a sharp oracle inequality, and a uniform convergence result over population risk in Mei, Bai, and Montanari (2018).

Due to the nonconvexity in the observed log-likelihood, we limit the feasible region Θ₀ to

$${\mathrm{\Theta }}_0:=\{\theta \in {ℝ}^p;{\Vert \theta \Vert }_2\le r_0,{\Vert \theta \Vert }_{\mathcal{G},2,1}\le R_n\}$$ (35)

for theoretical convenience. Here r₀, R_n > 0 must be chosen appropriately and we discuss these choices later. Similar restriction is also assumed in Loh andWainwright (2006).

3.1. Assumptions

We impose the following assumptions. First, we define a sub-Gaussian tail condition for a random vector $x\in {ℝ}^p$; we say x has a sub-Gaussian tail with parameter ${\sigma }_x^2$, if for any fixed $\nu \in {ℝ}^p$, there exists σ_x > 0 such that $E[\exp (t{(x-E[x])}^T\nu )]\le \exp \left(t^2{\Vert \nu \Vert }_2^2{\sigma }_x^2/2\right)$ for any $t\in ℝ$. We recall that θ* is the true parameter vector, which minimizes the population loss.

Assumption 1. The rows $x_i\in {ℝ}^p$, i = 1,2, … , n of the design matrix are iid samples from a mean-zero distribution with sub-Gaussian tails with parameter ${\sigma }_x^2$. Moreover, ${\sum }_x:=E[x_i{x}_i^T]$ is a positive definite and with minimum eigenvalue λ_min(∑_x) ≥ K₀ where K₀ is a constant bounded away from 0.We further assume that ${(x_{ij})}_{j\in g_j}$ are independent for all j ∈ g_j and $g_j\in \mathcal{G}$.

Similar assumptions appear in, for example, Negahban et al. (2012). This restricted minimum eigenvalue condition (see, e.g., Raskutti, Wainwright, and Yu 2010 for details) is satisfied for weakly correlated design matrices. We further assume independence across covariates within groups since sub-Gaussian concentration bound assuming independence within groups is required.

Assumption 2. For any r > 0, there exists $K_1^r$ such that ${\max }_i\left|x_i^T\theta \right|\le K_1^r$ a.s. for all θ in the set $\{\theta \hspace{1em}:\hspace{1em}{\Vert \theta -{\theta }^{\ast }\Vert }_2\le r\hspace{0.17em}\cap \text{supp(}\theta -{\theta }^{\ast }\text{)}\subseteq g_j\hspace{0.17em}\text{for}\hspace{0.17em}\text{some}\hspace{0.17em}{g}_j\in \mathcal{G}\}$.

Assumption 2 ensures that $\left|x_i^T{\theta }^{\ast }\right|$ is bounded a.s., which guarantees that the underlying probability ${(1+e^{-x_i^T{\theta }^{\ast }})}^{-1}$ is between 0 and 1, and $\left|x_i^T\theta \right|$ is also bounded within a compact sparse neighborhood of θ* which ensures concentration to the population loss. Comparable assumptions are made in Elsener and van de Geer (2018); Mei, Bai, and Montanari (2018) where similar nonconvex M-estimation problems are investigated.

Assumption 3. The ratio of the number of labeled to unlabeled data, that is, n_ℓ/n_u is lower bounded away from 0 and upper bounded for all n = n_ℓ + n_u, as n → ∞. Equivalently, there is a constant K₂ such that $\left|\log (n_{\mathcal{l}}/\pi n_u)\right|\le K_2$ Assumption 3 ensures that the number of labeled samples n_ℓ is not too small or large relative to n. The reason why n_ℓ cannot be too large is that the labeled samples are only positives and we need a reasonable number of negative samples which are a part of the unlabeled samples.

Assumption 4 (Rate conditions). We assume a high-dimensional regime where both (n, p) → ∞ log p = o(n). For $\mathcal{G}=((g_1,\hspace{0.17em}\dots \hspace{0.17em},g_J),{(w_j)}_1^J))$ and $m:={\max }_j|g_j|$, we assume J = Ω(n^β) for some β > 0, m = o(n ∧ J), min_j w_j = Ω(1), and max_j w_j = o(n ∧ J).

Assumption 4 states standard rate conditions in a high-dimensional setting. In terms of the group structure, we assume that growth of p is not totally attributed to the expansion of a few groups; the number of groups J increases with n, and the maximum group size m is of small order of both n and J. Also we note that a typical choice of $w_j=\sqrt{|g_j|}$ satisfies Assumption 4 because min_j w_j ≥ 1, ${\max }_j{w}_j=\sqrt{m}$ and $\sqrt{m}/n$,$\sqrt{m}/J=o(1)$.

Finally, we define the restricted strong convexity assumption for a loss function following the definition in Loh and Wain-wright (2006).

Definition 3.1 (Restricted strong convexity). We say ${\mathcal{L}}_n$ satisfies a restricted strong convexity (RSC) condition with respect to θ* with curvature α > 0 and tolerance function τ over Θ₀ if the following inequality is satisfied for all θ ∈ Θ₀

$${\left(\mathrm{\Delta }{\mathcal{L}}_n(\theta )-\nabla {\mathcal{L}}_n({\theta }^{\ast })\right)}^T\mathrm{\Delta }\ge \alpha {\Vert \mathrm{\Delta }\Vert }_2^2-\tau ({\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1}),$$ (36)

where Δ:= θ – θ* and $\tau ({\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1})={\tau }_1{\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1}^2\frac{\log J+m}{n}+{\tau }_2{\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1}\sqrt{\frac{\log J+m}{n}}$.

In the special case where ${\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1}={\Vert \mathrm{\Delta }\Vert }_1$ and hence $\tau ({\Vert \mathrm{\Delta }\Vert }_1)={\tau }_1{\Vert \mathrm{\Delta }\Vert }_1^2\frac{\log p}{n}+{\tau }_2{\Vert \mathrm{\Delta }\Vert }_1\sqrt{\frac{\log p}{n}}$, similar RSC conditions were discussed in Negahban et al. (2012) and Loh and Wainwright (2006) with different τ and Θ₀. One of the important steps in our proof is to prove that RSC holds for the objective function ${\mathcal{L}}_n(\theta )$.

3.2. Guarantee

Under Assumptions 1 – 4, we will show in Theorem 3.2 that the RSC condition holds with high probability over $\{\theta ;{\Vert \theta \Vert }_2\le r_0\}$ and therefore over Θ₀, for Θ₀ defined in (35). Under the RSC assumption, the following proposition, which is a modification of Theorem1 in Loh and Wainwright (2006), provides ℓ₁/ℓ₂ and ℓ₂ bounds of an error vector $\widehat{\mathrm{\Delta }}:=\widehat{\theta }-{\theta }^{\ast }$. Recall that m = max_j |g_j| (the size of the largest group) and J is the number of groups.

Proposition 3.1. Suppose the empirical loss ${\mathcal{L}}_n$ satisfies the RSC condition (36) with $\tau ({\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1})={\tau }_1{\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1}^2\frac{\log J+m}{n}+{\tau }_2{\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1}\sqrt{\frac{\log J+m}{n}}$ over Θ₀ where Θ₀ is feasible region for the objective (5), as defined in (35), and the true parameter vector θ* is feasible, that is, θ* ∈ Θ₀. Consider λ such that

$$\begin{gathered} 4\max \{{\Vert \nabla {\mathcal{L}}_n({\theta }^{\ast })\Vert }_{\overline{\mathcal{G}},2,\infty }, \\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\left({\tau }_1\frac{2R_n(\log J+m)}{n}+{\tau }_2\sqrt{\frac{(\log J+m)}{n}}\right)\}\le \text{λ}. \end{gathered}$$ (37)

Let $\widehat{\theta }$ be a stationary point of (5). Then the following error bounds

$${\Vert \widehat{\mathrm{\Delta }}\Vert }_2\le (\underset{j\in \hspace{0.17em}S}{\max }{w}_j)\frac{3\sqrt{s}\text{λ}}{2\alpha }\hspace{1em}\text{and}\hspace{1em}{\Vert \widehat{\mathrm{\Delta }}\Vert }_{\mathcal{G},1,2}\le {(\underset{j\in \hspace{0.17em}S}{\max }{w}_j)}^2\frac{6s\text{λ}}{\alpha },$$ (38)

hold where $S:=\{j\in (1,\hspace{0.17em}\dots \hspace{0.17em},J);{\theta }_{g_j}^{\ast }\ne 0\}$ and s :=|S|.

The proof for Proposition 3.1 is deferred to the supplementary materials (S2.3). From (38), we note the squared ℓ₂-error to grow proportionally with s and λ². If θ* ∈ Θ₀ and the choice of $\text{λ}=\mathrm{\Theta }\left(\sqrt{\frac{\log J+m}{n}}\right)$ satisfies the inequality (37), we obtain squared ℓ₂ error which scales as $s\frac{\log J+m}{n}$, provided that the RSC condition holds over Θ₀. In the case of lasso we recover $\frac{s\log p}{n}$ parametric optimal rate since J = p, m = 1.

With the choice of $r_0\ge {\Vert {\theta }^{\ast }\Vert }_2$ and $R_n=\mathrm{\Theta }\left(\sqrt{\frac{n}{\log J+m}}\right)$¹, we ensure θ* is feasible and $\text{λ}=\mathrm{\Theta }\left(\sqrt{\frac{\log J+m}{n}}\right)$ satisfies the inequality (37) with high probability. Clearly $\left({\tau }_1\frac{2R_n(\log J+m)}{n}+{\tau }_2\sqrt{\frac{\log J+m}{n}}\right)$ is of the order $\sqrt{\frac{\log J+m}{n}}$ with the choice of $R_n=\mathrm{\Theta }\left(\sqrt{\frac{n}{\log J+m}}\right)$, and following Lemma 3.1, we have ${\Vert \nabla {\mathcal{L}}_n({\theta }^{\ast })\Vert }_{\overline{\mathcal{G}},2,\infty }=\mathcal{O}\left(\sqrt{\frac{\log J+m}{n}}\right)$ with high probability. Thus, inequality (37) is satisfied with $\text{λ}=\mathrm{\Theta }\left(\sqrt{\frac{\log J+m}{n}}\right)$ w.h.p. as well.

Lemma 3.1. Under Assumptions 1 – 4, for any given ϵ > 0, there is a positive constant c such that

$$\mathbb{P}\left({\Vert \nabla {\mathcal{L}}_n({\theta }^{\ast })\Vert }_{\overline{\mathcal{G}},2,\infty }\ge c\sqrt{\frac{\log J+m}{n}}\le ϵ\right)$$

given a sample size $n\gtrsim (\log p+m)\vee {(1/ϵ)}^{1/\beta }$.

The proof for Lemma 3.1 is provided in the supplement S2.4. Now we state them a in theorem of this section which shows that RSC condition holds uniformly over a neighborhood of the true parameter.

Theorem 3.2. For any given r > 0 and ϵ > 0, there exist strictly positive constants α, τ₁, and τ₂ depending on σ_x, K₀, $K_1^r$, and K₂ such that

$${\left(\nabla {\mathcal{L}}_n(\theta )-\nabla {\mathcal{L}}_n({\theta }^{\ast })\right)}^T\mathrm{\Delta }\ge \alpha {\Vert \mathrm{\Delta }\Vert }_2^2-{\tau }_1{\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1}^2\frac{\log J+m}{n}-{\Vert \mathrm{\Delta }\Vert }_{\mathcal{G},2,1}\sqrt{\frac{\log J+m}{n}}$$ (39)

holds for all θ such that ${\Vert \mathrm{\Delta }\Vert }_2:={\Vert \theta -{\theta }^{\ast }\Vert }_2\le r$ with probability at least 1 – ϵ, given (n, p) satisfying $n\gtrsim (\log J+m)\vee {(1/ϵ)}^{1/\beta }$.

The proof of Theorem3.2 is deferred to the supplement S2.5. There are a couple of notable remarks about Theorem 3.2 and Proposition 3.1.

• The application of the Proposition 3.1 requires for a RSC condition to hold over a feasible regionΘ₀. Setting r = 2r₀ in Theorem3.2, inequality (39) holds over $\{\theta ;{\Vert \theta -{\theta }^{\ast }\Vert }_2\le 2r_0\}$ w.h.p., therefore, over ${\mathrm{\Theta }}_0\subseteq \{\theta ;{\Vert \theta -{\theta }^{\ast }\Vert }_2\le 2r_0\}$.

• We discuss how underlying parameters r₀, σ_x, and constants K₀–K₂ in Assumptions 1–3 are related to the ℓ₂-error bound. From Proposition 3.1, we see that ℓ₂-error is proportional to τ₁/α and τ₂/α. The proof of Theorem3.2 reveals that ${\tau }_1/\alpha \lesssim {({\sigma }_x{K}_3/K_0)}^2$ and ${\tau }_2/\alpha \lesssim {\sigma }_x(1+K_1^{2r_0})/K_0{L}_0$, where L₀ and K₃ are also constants defined as $L_0:=\underset{\left|u\right|\le K_2+K_1^{2r_0}+2r_0{K}_3}{\inf }(e^u/{(1+e^u)}^2){(1+e^{K_1^{2r_0}+2r_0{K}_3})}^{-2}$ and $K_3\lesssim {\sigma }_x\log \hspace{0.17em}{({\sigma }_x^2/K_0)}^{1/2}$. As L₀ is inversely related to K₂ and r₀, ℓ₂-error is proportional to the r₀, σ_x, $K_1^{2r_0}$ and K₂ in Assumptions 2 and 3, but inversely related to the minimum eigenvalue bound K₀ in Assumption 1.

• The mean-squared error $\frac{s\log p}{n}$ in the case of J = p is verified below in Figure 2 and both the mean-squared error and ℓ₁ errors are minimax optimal for high-dimensional linear regression (Raskutti,Wainwright, and Yu 2011).

Figure 2.

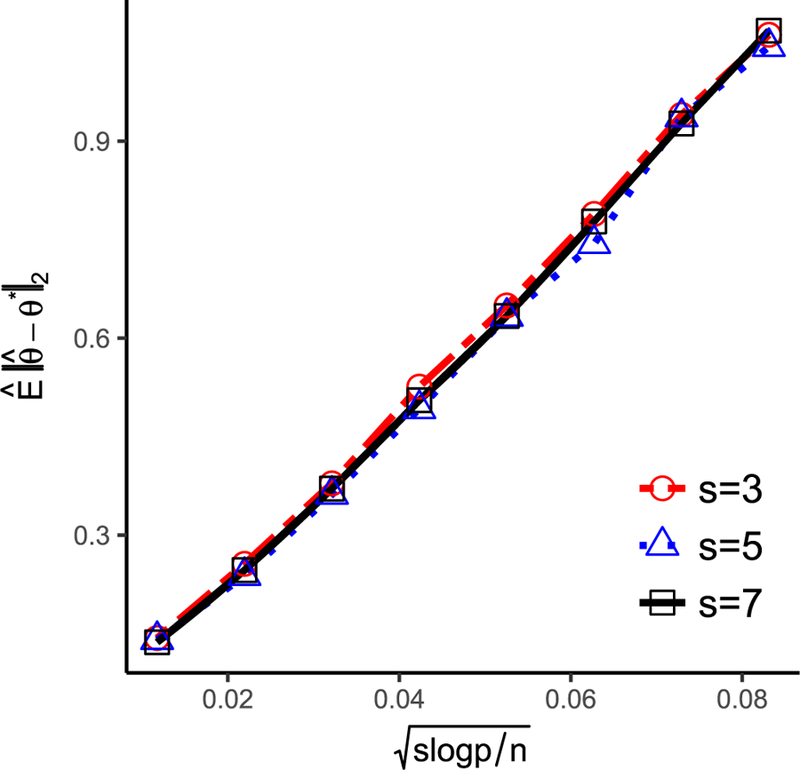
$\widehat{E}[{\Vert \widehat{\theta }-\theta \Vert }_2]$plotted against $\sqrt{s\log p/n}$ with fixed p = 500 and varying s and n.

To validate the mean-squared error upper bound of $\frac{s\log p}{n}$ in Section 3, a synthetic dataset was generated according to the logistic model (1) with p = 500 covariates and X ∼ N(0, I_500×500). Varying s and n were considered to study the rate of convergence of ${\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }_2$. The ratio n_ℓ/n_u was fixed to be 1. For each dataset, $\widehat{\theta }$ was obtained by applying PUlasso algorithm with a lambda sequence ${\text{λ}}_n:=c_s\sqrt{\frac{\log p}{n}}$ for a suitably chosen c_s for each s. We repeated the experiment 100 times and average ℓ₂-error was calculated. In Figure 2, we illustrate the rate of convergence of ${\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }_2$. In particular, ${\Vert \widehat{\theta }-{\theta }^{\ast }\Vert }_2$ against $\sqrt{\frac{s\log p}{n}}$ is plotted with varying s and n. The error appears to be linear in $\sqrt{\frac{s\log p}{n}}$, and thus we also empirically conclude that our algorithm achieves the optimal $\sqrt{\frac{s\log p}{n}}$ rate.

4. Simulation Study: Classification Performance

In this section, we provide a simulation study which validates the classification performance for PUlasso. In particular, we provide a comparison in terms of classification performance to state-of-the-art methods developed in Du Marthinus, Niu, and Sugiyama (2015), Elkan and Noto (2008), and Liu et al. (2006). The focus of this section is classification rather than variable selection since many of the state-of-the-artmethods we compare to are developed mainly for classification and are not developed for variable selection.

4.1. Comparison Methods

Our experiments compare six algorithms: (i) logistic regression model assuming we know the true responses (oracle estimator); (ii) our PUlasso algorithm; (iii) a bias-corrected logistic regression algorithm in Elkan and Noto (2008); (iv) a second algorithm from Elkan and Noto (2008) that is effectively a one step EM algorithm; (v) the biased SVM algorithm from Liu et al. (2006); and (vi) the PU-classification algorithm based on an asymmetric loss from Du Marthinus, Niu, and Sugiyama (2015).

The biased SVM from Liu et al. (2006) is based on the supported vector machine (SVM) classifier with two tuning parameters which parameterize misclassification costs of each kind. The first algorithm from Elkan and Noto (2008) estimates label probabilities $\mathbb{P}(z=1|x)$ and corrects the bias in the classifier via the estimation of $\mathbb{P}(z=1|y=1)$ under the assumption of a disjoint support between $\mathbb{P}(x|y=1)$ and $\mathbb{P}(x|y=0)$. Their secondmethod is amodification of the first method; a unit weight is assigned to each labeled sample, and each unlabeled example is treated as a combination of a positive and negative example with weight $\mathbb{P}(y=1|x,z=0)$ and $\mathbb{P}(y=0|x,z=0)$, respectively. Du Marthinus, Niu, and Sugiyama (2015) suggested using asymmetric loss functions with ℓ₂-penalty. Asymmetric loss function is considered to cancel the bias induced by separating positive and unlabeled samples rather than positive and negative samples. Any convex surrogate of 0–1 loss function can be used for the algorithm. There is a publicly available matlab implementation of the algorithm when a surrogate is the squared loss on the author’s webpage² and since we use their code and implementation, the squared loss is considered.

4.2. Setup

We consider a number of different simulation settings: (i) small and large p to distinguish the low and high-dimensional setting; (ii) weakly and strongly separated populations; (iii) weakly and highly correlated features; and (iv) correctly specified (logistic) or mis-specified model. Given dimensions (n, p), sparsity level s, predictor autocorrelation ρ, separation distance d, and model specification scheme (logistic, misspecified), our setup is the following

• Choose the active covariate set S ⊆ {1, 2,…, p} by taking s elements uniformly at random from(1, 2,…, p). We let true ${\theta }^{\ast }\in {ℝ}^p$ such that ${\theta }_j^{\ast }={\mathrm{𝟙}}_S(j)$.

• Draw samples $x\in {ℝ}^p$, iid from ${\mathbb{P}}_X=0.5{\mathbb{P}}_1+0.5{\mathbb{P}}_0$ where ${\mathbb{P}}_1:=\mathcal{N}({\mu }_1,{\Sigma }_{\rho })$,${\mathbb{P}}_0:=\mathcal{N}({\mu }_2,{\Sigma }_{\rho })$. More concretely, firstly draw u ∼ Ber(0.5). If u = 1, draw x from ${\mathbb{P}}_1$ and draw x from ${\mathbb{P}}_0$ otherwise.

  • Mean vectors µ₁, ${\mu }_2\in {ℝ}^p$ are chosen so that they are s-sparse, that is, $\text{supp}({\mu }_i)=S$, $E[{\Vert {\mu }_1-{\mu }_2\Vert }_2^2]=d^2$ and variance of μ_i does not depend on d. Specifically, we sample μ₁,μ₂ such that for j ∈ S, we let ${\mu }_{1_j}~\mathcal{N}(\sqrt{(2d^2-1)/8s},1/\sqrt{8s})$, μ_2j = −μ_1j, and for j ∉ S, μ_ij = 0 for i ∈ (1, 2).

  • A covariance matrix ${\Sigma }_{\rho }\in {ℝ}^{p\times p}$ is taken to be ${\Sigma }_{\rho ,ij}=K_{\rho }{\rho }^{\left|i-j\right|}$ where K_ρ is chosen so that ${\mathrm{𝟙}}_S^T{\Sigma }_{\rho }{\mathrm{𝟙}}_S=s$. This scaling of Σ_ρ is made to ensure that the signal strength $\mathrm{var}(x^T{\theta }^{\ast })={\mathrm{𝟙}}_S^T{\Sigma }_{\rho }{\mathrm{𝟙}}_S$ stays the same across ρ.

• Draw responses y ∈ {0, 1}. If scheme = logistic, we draw y such that $y~\text{Ber}({\mathbb{P}}_{{\theta }^{\ast }}(y=1|x))$ where ${\mathbb{P}}_{{\theta }^{\ast }}(y=1|x)=1/(1+\exp (-{\theta }^{\ast T}x))$. In contrast, if scheme = mis-specified, we let y = 1 if x was drawn from ${\mathbb{P}}_1$, and zero otherwise; that is,$y=\mathrm{𝟙}\{u=1\}$.

To compare performances both in low and high dimensional setting, we consider (p = 10, s = 5) and (p = 5000, s = 5). We set the sample size n_ℓ = n_u = 500 in both cases. Autocorrelation level ρ takes values in (0, 0.2, 0.4, 0.6, 0.8). In the high dimensional setting, we excluded algorithm (v), since (v) requires a grid search over two dimensions, which makes the computational cost prohibitive. For algorithms (i)–(iv), tuning parameters λ are chosen based on the 10-fold cross-validation.

4.3. Classification Comparison

We use two criteria, misclassification rate and F₁ score, to evaluate performances. F₁ is the harmonic mean of the precision and recall, which is calculated as $F_1\hspace{0.17em}\hspace{0.17em}:=\hspace{0.17em}\hspace{0.17em}2\cdot \frac{\text{precision}+\text{recall}}{\text{precision}\cdot \text{recall}}$. The F₁ score ranges from 0 to 1, where 1 corresponds to perfect precision and recall. Experiments are repeated 50 times and the average score and SEs are reported. The result for the misclassification rate under correct model specification is displayed in Figure 3.

Figure 3.

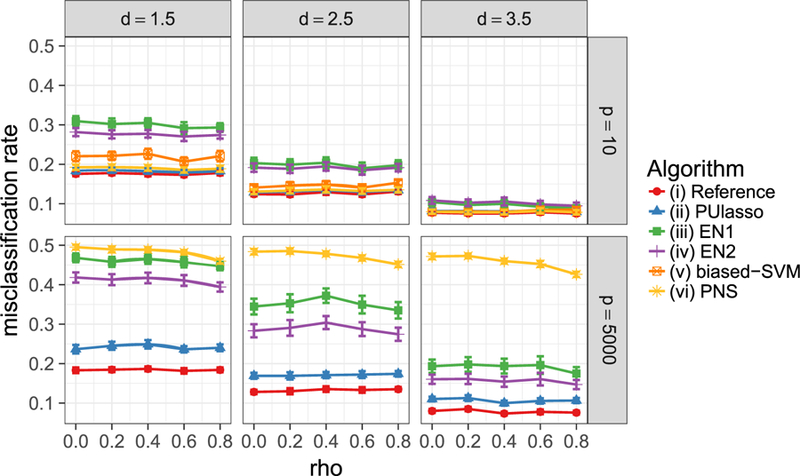
Misclassification rates of algorithms (i)–(vi) under correct (logistic) model specification. Each error bar represents two SEs of the mean.

Not surprisingly the oracle estimator has the best accuracy in all cases. PUlasso and algorithm (vi) performs almost as well as the oracle in the low-dimensional setting and better than remaining methods in most cases. It must be pointed out that both PUlasso and algorithm (vi) use additional knowledge π of the true prevalence in the unlabeled samples. PUlasso performs best in the high-dimensional setting while the performance of algorithm (vi) becomes significantly worse because estimation errors can be greatly reduced by imposing many 0s on the estimates in PUlasso due to the ℓ₁-penalty (compared to ℓ₂-penalty in algorithm (vi)). The performance of (iii)–(iv) is greatly improved when positive and negative samples are more separated (large d), because algorithms (iii)–(iv) assume disjoint support between two distributions. The algorithms showsimilar performancewhen evaluated with the F₁ scoremetric and in the mis-specified setting. Due to space constraints, we defer the full set of remaining results in the supplementarymaterials (Section S3).

5. Analysis of Beta-Glucosidase Sequence Data

Our original motivation for developing the PUlasso algorithm was to analyze a large-scale dataset with positive and unlabeled responses developed by the lab of Dr. Philip Romero (Romero, Tran, and Abate 2015). The prior EM algorithm approach of Ward et al. (2009) did not scale to the size of this dataset. In this section, we discuss the performance of our PUlasso algorithm on a dataset involving mutations of a natural BGL enzyme. To provide context, BGL is a hydrolytic enzyme involved in the deconstruction of biomass into fermentable sugars for biofuel production. Functionality of the BGL enzyme is measured in terms of whether the enzyme deconstructs disaccharides into glucose or not. Dr. Romero used a microfluidic screen to generate a BGL dataset containing millions of sequences (Romero, Tran, and Abate 2015).³

Main effects and two-way interaction models are fitted using our PUlasso algorithm with ℓ₁ and ℓ₁/ℓ₂ penalties (we discuss how the groups are chosen shortly) over a grid of λ values. We test stability of feature selection and classification performance using a modified ROC and AUC approach. Finally a scientific validation is performed based on a follow-up experiment conducted by the Romero lab. The variables selected by PUlasso were used to design a new BGL enzyme and the performance is compared to the original BGL enzyme.

5.1. Data Description

The dataset consists of n_ℓ = 2,647,877 labeled and functional sequences and n_u = 1,567,203 unlabeled sequences where each of the observation σ = (σ₁,…, σ₅₀₀) is a sequence of amino acids of length d = 500. Each of the position σ_j ∈ (A, R,…,V, *) takes one of M = 21 discrete values, which correspond to the 20 amino acids in the DNA code and an extra to include the possibility of a gap(*).

Another important aspect of the millions of sequences generated is that a “base wild-type BGL sequence” was considered and known to be functional (y = 1), and the millions of sequences were generated by mutating the base sequence. Single mutations (changing one position from the base sequence) and double mutations (changing two positions) from the base sequence were common but higher-order mutations were not prevalent using the deep mutational scanning approach in Romero, Tran, and Abate (2015). Hence, the sequences generated were not random samples across the entire enzyme sequence space, but rather very local sequences around the wild-type sequence. Hence, the number of possible mutations in each position and consequently the total number of observed sequences is also reduced dramatically. With this dataset, we want to determine which mutations should be applied to the wild-type BGL sequence.

Categorical variables σ are converted into indicator variables: $x={(\mathrm{𝟙}\{{\sigma }_j=l\})}_{j,l}$ where 1 ≤ j ≤ 500, $l\in (A,R,\hspace{0.17em}\dots \hspace{0.17em}\hspace{0.17em},V,\ast )\backslash ({\sigma }_l^{WT})$ for the main-effects model, $x={(\mathrm{𝟙}\{{\sigma }_j=l\},\mathrm{𝟙}\{{\sigma }_j=l,{\sigma }_k=m\})}_{j,k,l,m}$ where 1 ≤ j, k≤ 500, $j\ne k,l,m\in (A,R,\hspace{0.17em}\dots \hspace{0.17em},V,\ast )\backslash ({\sigma }_{l\hspace{0.17em}or\hspace{0.17em}m}^{WT})$ for the pairwise interaction models, where ${\sigma }_l^{WT}$ represents the amino acid of the wild-type sequence at the lth position. In other words, each variable corresponds to an indicator of mutation from the base sequence or interaction between mutations. Although there are in principle p ≈ d(M − 1) variables for a main-effects model and p ≈ d²(M − 1)² if we include main-effects and two-way interactions, there are many amino acids that never appear in any position or appear only a small number of times. For features corresponding to the main-effects $(\mathrm{𝟙}\{{\sigma }_j=l\}\text{for}\hspace{0.17em}\text{some}\hspace{0.17em}j\hspace{0.17em}\text{and}\hspace{0.17em}l)$, those sparse features are aggregated within each position until the number of mutations of the aggregated column reaches 100 or 1% of the total number of mutations in each position; accordingly, each aggregated column is an indicator of any mutations to those sparse amino acids. For two-way interactions features $(\mathrm{𝟙}\{{\sigma }_j=l,{\sigma }_k=m\}\text{for}\hspace{0.17em}\text{some}\hspace{0.17em}j,k,l,\hspace{0.17em}\text{and}\hspace{0.17em}m)$, sparse features (≤ 25 out of 4,215,080 samples) are simply removed from the feature space. Using this basic preprocessing we obtained only 3075 corresponding to single mutations and 930 binary variables corresponding to double mutations. They correspond to 500 unique positions and 820 two-way interactions between positions, respectively. As mentioned earlier, we consider both ℓ₁ and group ℓ₁/ℓ₂ penalties. We use the ℓ₁-penalty for the main-effects model and the ℓ₁/ℓ₂ for the two-way interaction models. For the two-way interaction model each group gj corresponds to a different position (500 total) and pair of positions (820 total) where mutations occur in the preprocessed design matrix and the group size |g_j| corresponds to the number of different observed mutations in each position or pair of mutations in pair of positions (for this dataset m = max_j |g_j| = 8). Higher-order interactions were not modeled as they did not frequently arise. Hence, the main-effects and two-way interaction model we consider have p = 3076 (1 + 3075) and p = 4006 (1 + 3075 + 930) and J = 1320 (500 + 820) groups, respectively. In summary, we consider the following two models and corresponding design matrices

$$\begin{gathered} X_{\text{main}}:=[\text{Intercept}(1)+\text{main}\hspace{0.17em}\text{effects}(3075)] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\in {\left\{0,1\right\}}^{4,215,080\times 3076} \end{gathered}$$

$$\begin{gathered} X_{\text{int}}:=[\text{Intercept}(1)+\text{main}\hspace{0.17em}\text{effects}(3075)] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}+\text{two}\hspace{0.17em}\text{way}\hspace{0.17em}\text{interactions(930)]}\in {\left\{0,1\right\}}^{4,215,080\times 4006} \end{gathered}$$

and the response vector z = [1, …, 1, 0,…, 0]^T ∈ {0, 1}^4,215,080.

5.2. Classification Validation and Model Stability

Next we validate the classification performance for both the main-effect and two-way interaction models. We fit models using 90% of the randomly selected samples both from the positive and unlabeled set and use area under the ROC curve (AUC) to evaluate the classification performance on the 10% of the hold-out set. Since positive and negative samples are mixed in the unlabeled test dataset this is a nontrivial task with presence-only responses. A naive approach is to treat unlabeled samples as negative and estimate AUC, but if we do so, the AUC is inevitably downward-biased because of the inflated false positive (FP) rate. We note that a TP rate can be estimated in an unbiased manner using positive samples. To adjust such bias, we follow the methodology suggested in Jain, White, and Radivojac (2017) and adjust FP rate and AUC value using the following equation

$${\text{FP}}^{\text{adj}}=\frac{{\text{FP}}^{\text{naive}}-\pi \text{TP}}{1-\pi },\hspace{1em}{\text{AUC}}^{\text{adj}}=\frac{{\text{AUC}}^{\text{naive}}-\pi /2}{1-\pi }$$

where π is the prevalence of positive samples.

As Figure 4 shows, we have a significant improvement in AUC over random assignment (AUC = 0.5) in both the main effect (AUC = 0.7933) and two-way interaction (AUC = 0.7938) models. The performances of the two models in terms of AUC values are very similar at their best λ values chosen by 10-fold cross-validation. This is not very surprising as only a small number of two-way interactions are observed in the experiments.

Figure 4.

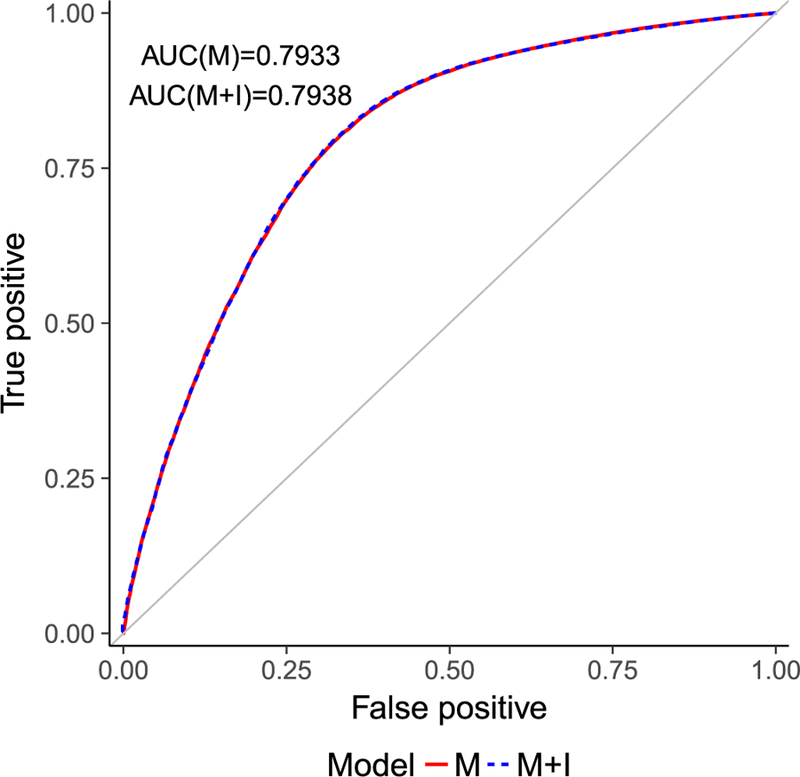
ROC curves of main effects (M) and two-way interaction model (M+I) with λ chosen based on 10-fold cross-validation.

We also examined the stability of the selected features for both models as the training data changes. Following the methodology of Kalousis, Prados, and Hilario (2007), we measure similarity between two subsets of features s, s′ using S_S(s, s′) defined as $S_S(s,s\prime ):=1-\frac{\left|s\right|+\left|s\prime \right|-2\left|s\cap s\prime \right|}{\left|s\right|+\left|s\prime \right|-\left|s\cap s\prime \right|}$. S_S takes values in [0, 1], where 0 means that there is no overlap between the two sets, and 1 that the two sets are identical. S_s is computed for each pair of two training folds (i.e., we have $\frac{9\cdot 10}{2}$ pairs) using selected features and computed values are finally averaged over all pairs. Feature selection turned out to be very stable across all tuning parameter λ values: on average we had about 95% overlap of selection in main effect model (M) and about 98% overlap in main effect+interaction model (M+I). Stability score is higher in the latter model since we do a feature selection on groups, whose number is much less than individual variables (1320 groups vs. 3076 individual variables).

5.3. Scientific Validation: Designed BGL Sequence

Finally, we provide a scientific validation of the mutations estimated by our PUlasso algorithm. In particular, we fit the model with the PUlasso algorithm and selected the best λ = 0.0001 based on the 10-fold cross-validation. We use the top 10 mutations based on the largest size of coefficients with positive signs from our PUlasso algorithm because we are interested in mutations that enhance the performance of the sequence. Dr. Romero’s lab designed the BGL sequence with the 10 positive mutations from Table 4. This sequence was synthesized, expressed, and assayed for its hydrolytic activity. Hence, the designed sequence has 10 mutations compared to the wild-type (base) BGL sequence.

Table 4.

Ten positive mutations.

	Base/position/mutated
T197P		E495G
K300P		A38G
G327A		S486P
A150D		T478S
D164E		D481N

Figure 5 shows firstly that the designed protein sequence folds which in itself is remarkable given that 10 positions are mutated. Secondly, Figure 5 shows that the designed sequence decomposes disaccharides into glucose more quickly than the wild-type sequence. These promising results suggest that our variable selection method is able to identify positions of the wild-type sequences with improved functionality.

Figure 5.

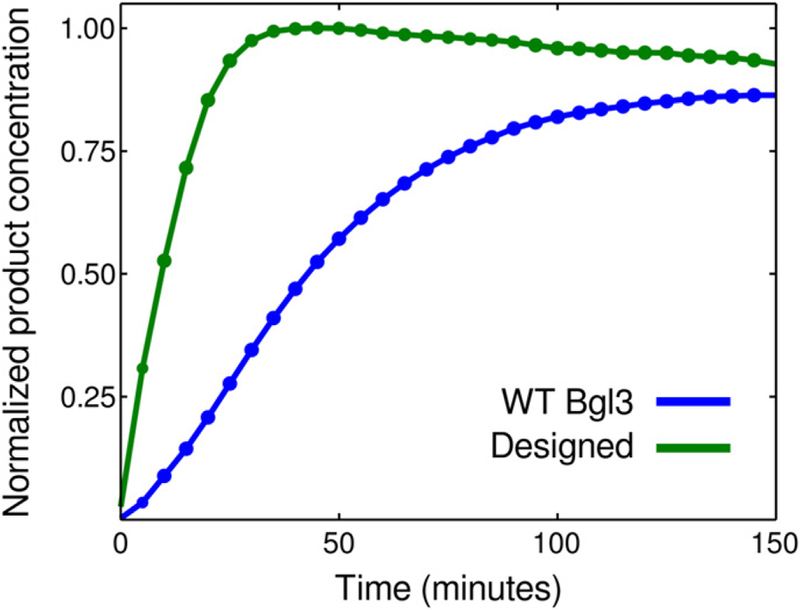
Kinetics 10 positive mutations used in the lab(base state/position/mutated state) and kinetics of designed BGL enzyme versus wild-type (WT) BGL sequence. The designed BGL enzyme based on mutations from Table 4 displays faster kinetics than the WT BGL sequence.

6. Conclusion

In this article, we developed the PUlasso algorithm for both variable selection and classification for high-dimensional classification with presence-only responses. Theoretically, we showed that our algorithm converges to a stationary point and every stationary point within a local neighborhood of θ* achieves an optimal mean squared error (up to constant). We also demonstrated that our algorithm performs well on both simulated and real data. In particular, our algorithm produces more accurate results than the existing techniques in simulations and performs well on a real biochemistry application.

Table 1.

Timings (in seconds).

	(n, p)	PUlasso	EM	Time reduction (%)
Dense matrix	n = 1000, p = 10	0.94	443.72	99.79
	n = 5000, p = 50	2.52	1844.98	99.86
	n = 10,000, p = 100	9.45	5066.86	99.81
Sparse matrix	n = 1000, p = 10	0.40	196.86	99.80
	n = 5000, p = 50	2.01	614.65	99.67
	n = 10,000, p = 100	4.29	1201.09	99.64

NOTE: Sparsity level in X = 0.95, n_ℓ/n_u = 0.5. Total time for 100 λ values, averaged over 3 runs.

Table 2.

Timings (in seconds) using sparse and dense calculation for fitting the same simulated data.

(n, p)	Sparse calculation	Dense calculation	Time reduction (%)
n = 10,000, p = 100	12.91	19.24	32.89
n = 30,000, p = 100	25.64	38.73	33.79
n = 50,000, p = 100	39.47	57.18	30.97

NOTE: Sparsity level in X = 0.95, n_ℓ/n_u = 0.5. Total time for 100 λ values, averaged over 3 runs.

Table 3.

Summary of stability scores across all tuning parameter λ values.

	1st Qu.	Median	Mean	3rd Qu.
M	93.3%	94.9%	94.9%	96.8%
M+I	97.9%	98.8%	98.4%	99.3%