Selection of nonlinear interactions by a forward stepwise algorithm: Application to identifying environmental chemical mixtures affecting health outcomes

Summary

Simultaneous exposure to multiple environmental pollutants could affect human health in a multitude of complex ways. For understanding the health effects of multiple environmental exposures, it is often important to identify and estimate complex interactions among exposures. However, this issue becomes analytically challenging in presence of potential nonlinearity in the outcome-exposure response surface and a set of correlated exposures. In this paper, we propose a stepwise forward selection algorithm for detecting effects of environmental exposures and their interactions that could potentially be nonlinear. Through simulation studies and analyses of test datasets that were simulated as a part of a data challenge in multipollutant modeling organized by the National Institute of Environmental Health Sciences (http://www.niehs.nih.gov/about/events/pastmtg/2015/statistical/), we illustrate the advantages of our proposed method in comparison with existing alternative approaches. A particular strength of our method is that it demonstrates very low false positives across empirical studies. Our method is also used to analyze a dataset that was released from the Health Outcomes and Measurement of the Environment (HOME) Study as a benchmark beta-tester dataset as a part of the same workshop.

1 |. INTRODUCTION

Studying the effects of chemical exposures and their interactions plays an important role in environmental research. Many toxicological and epidemiologic studies in animals and humans found evidence of health impacts due to exposure to a wide range of pollutants. Exposure to many pollutants can occur simultaneously, and multiple exposures have been linked to some of the same types of adverse health outcomes. These exposures may be acting through similar or differing mechanisms toward the same outcome, resulting in potential additive, synergistic, or antagonistic effects. For example, some of the well-known health effects found to be associated with environmental exposures include ambient air pollution with impaired cardiac function, ¹ cardiovascular events, ² and cancer risk. ³ Studies also reported the impact of air pollution on children’s health including raised incidence of respiratory symptoms in children, ⁴ preterm delivery and low birth weight. ⁵ Exposure to heavy metals has been well-documented to adversely impact neurological development and cognitive function in children and elderly has been well documented. ^6,7 Recent attention has been focused on the tens of thousands of synthetic chemicals that are in commerce today, many of which have been shown to disrupt endocrine function. Exposure to endocrine disrupting chemicals has been linked to reduced reproduction and fertility, increased child neurodevelopmental disorders, increased obesity and diabetes, endocrine-related cancers, and other effects. ⁸ Some health effects from endocrine disrupting chemicals have been shown to result when exposed to mixtures of chemicals but not the individual chemicals alone. ⁹ Endocrine disruptors have also been widely shown to demonstrate nonlinear dose-response relationships at low doses encountered in the environment. ¹⁰

While classical environmental epidemiology has focused on estimating the effect of one pollutant at a time, the reality is that we are exposed to multiple pollutants simultaneously. There has been a recent trend in the field to consider the “exposome” and obtain measurements on a large number of environmental contaminants and attempt to study their joint effects. To this end, exposure-wide association studies ¹¹ analogous to Genome wide association studies (GWAS) have been proposed. Modifications to the original exposure-wide association study that considered one exposure at a time to a multivariate setting have been proposed. ¹² Several advanced statistical and machine learning approaches have been utilized for analyzing and extracting information from multi-pollutant datasets including classification and regression tree (CART), ¹³ Bayesian kernel machine regression and Bayesian hierarchical modeling. ¹⁴ A review of existing statistical methods applicable in the context of multipollutant research is also available. ^15,16 While in principle many other machine learning algorithms such as ensemble methods or Gaussian process models can be used, they do not explicitly select the interaction effects.

Another way to incorporate interactions is to use regression based methods where interactions are modeled explicitly in the regression function. While nonlinearity in the exposure-outcome dose-response relationship has often been noted in multipollutant research ¹², a majority of the existing work on interaction selection and screening focused on modeling the main effects and/or interaction effects linearly. Recent work on modeling nonlinear effects using penalization including a variable selection method allowing for nonlinear main effects but without any interactions, ¹⁷ and methods for selection of both nonlinear main effects and nonlinear interactions. ^18,19 We review some of the existing interaction selection methods ^18,20,21,22 in more detail in Section 2.

We consider a specific aspect of multipollutant modeling, namely, identifying nonlinear exposure main effects and interactions. Nonlinearity in exposure-outcome dose-response relationship has often been noted. ^23,24 Non-linearity in the response surface is often expected in the modeling of exposures in the health effects evaluation and the sample dataset that was released as a beta-tester by NIEHS describes a highly non-linear dose-response function also demonstrates this. ^12,25 Several authors ^26,27 noted non-linear effects of pollutant profiles on term low birth weight and other indicators of poverty. Non-linear association between lead exposure and maternal stress among pregnant women has also been found. ²⁸ Several studies have demonstrated non-linear relationships between lead-concentrations and IQ. ^29,30 Numerous studies reported highly non-linear relationship between blood lead levels and quantity of soil lead ^31,32 while in addition non-linear association of age of a child with both the lead levels has also been reported. ³³ When the underlying associations are non-linear, not accounting for nonlinearity of the effects could lead to smoothing out the magnitude of such exposures, missing important variables, and selection of spurious interaction effects. ³⁴

In spite of the importance of modeling non-linearity of the effects, most of the recent work on interaction selection and screening based on a regression structure is focused on modeling the main effects and/or interaction effects linearly. Several linear interaction selection methods on environmental exposure datasets have been studied. ¹⁶ Two major classes of methods for interaction selection are penalization-based methods and forward (stepwise) selection methods. Penalization-based methods work by minimizing the usual objective function such as least squares together with a penalty term such as ℓ₁ penalty to induce sparsity and shrinkage ³⁵. While a majority of the penalty-based methods did not specifically consider interaction effects, penalty-based methods specifically targeted for models with linear interactions have been recently proposed. ^20,36,22 Forward selection algorithms provide useful alternatives to penalization approaches due to their scalability and easy interpretation and are commonly used in practice. In the context of interaction selection, forward step-wise algorithms have the advantage of not directly dealing with the expanded predictor space of all possible interactions. Moreover, an extensive empirical study ³⁷ suggests that the performance of forward selection is very similar to best subset selection. We refer to ^38,39,40 and the references therein for recent forward selection based approaches for linear models without interactions. Recently, forward selection methods that accommodate linear interactions have been proposed. ^41,21

In this paper, we propose a new stepwise forward selection based interaction identification method that accommodates the nonlinearity of both the main and interaction effects. In the step-wise forward selection space, we are not aware of any existing methods in the literature that account for nonlinear interactions. We call our newly proposed algorithm SNIF (Selection of Nonlinear Interactions by a Forward stepwise method). Our SNIF algorithm incorporates nonlinearity of the effects by introducing basis function expansions of the predictors and creates a forward selection path for main and interaction effects following the strong heredity principle (i.e. interactions are present only when both the corresponding main effects are present). In addition to adding the basis functions for each predictor to account for nonlinearity, SNIF retains the linear terms so that the basis functions for a predictor are used only when the linear term is not sufficient to explain its effect on the outcome.

The data challenge of National Institute of Environmental Health Sciences (NIEHS)’s Epidemiology- Statistics (Epi- Stats) workshop held on July 13 to 14, 2015 reinforced the need to develop statistical methods for assessing health effects of mixtures and multiple pollutants. NIEHS Epi-Stats conference invited scientists to evaluate different statistical methods for studying the effect of exposure to multiple pollutants in the environment. Two synthetic datasets emulating environmental exposures together with a real dataset from the Health Outcomes and Measurement of the Environment (HOME) study (Braun et al., 2016) were provided for comparing the performance of different statistical approaches. The overarching aim of the data analysis from HOME study was to examine the association between prenatal exposure to pollutants with children’s cognitive and behavioral development before the age of three. In our empirical work, we demonstrate the competitive performance of SNIF using different simulation settings as well as the NIEHS test datasets and the dataset from the HOME study.

The rest of the article is organized as follows. We provide a brief review of existing interaction selection methods in Section 2 and a detailed description of the proposed SNIF algorithm in Section 3. We compare SNIF with existing methods in a simulation study in Section 4. We investigate the performance of SNIF on the two synthetic datasets from NIEHS Epi-Stat workshop in Section 5. In Section 6, we present results provided by SNIF for detecting the effects of environmental exposures on child mental development based on the data from the HOME study.

2 |. EXISTING INTERACTION SELECTION METHODS

We first provide an overview of some of the existing methods for interaction selection to get a sense of the current landscape. We later use these methods for comparing the performance of our proposed SNIF algorithm. Let y denote the vector of response variables and let x₁, ⋯, x_p denote column vectors corresponding to the p predictors under consideration. We would like to learn about the functional relationship between the predictors and the mean of the response. In a general form, the response-predictor relationship can be written as

$$\mathit{y}=f\left(x_1,\cdots ,x_p\right)+\mathit{ϵ},$$ (1)

where ϵ is the error vector such that E(ϵ | x₁, ⋯, x_p) = 0 and E(y | x₁, ⋯, x_p) = f(x₁, ⋯, x_p). As the mean function f(·) in (1) may not be estimated feasibly in a fully nonparametric way using limited number of observations, approximations are often considered involving different orders of interactions between the predictors. The first order model containing only main-effects without any interactions can be written as

$$\mathit{y}=\sum _{j=1}^p{f}_j\left({\mathit{x}}_j\right)+\mathit{ϵ},$$ (2)

where f_j(·) is the main effect function for predictor j. In particular, if all the main effect functions f_j(·) are linear, we obtain the classical linear regression model:

$$E\left(\mathit{y}|{\mathit{x}}_1,\cdots ,{\mathit{x}}_p\right)=\alpha +\sum _{j=1}^p{\mathit{x}}_j{\beta }_j:={\mu }_L(\mathbf{\Theta }),$$ (3)

where α is the intercept, β_p×1 = (β₁, ⋯, β_p) is the vector of the main effect coeffcients, and the generic parameter Θ is used to denote all the parameters in the model. In Equation (3), μ_L(Θ) denotes the conditional mean function with only linear main effects.

To incorporate nonlinear main effects, basis functions such as cubic splines are often utilized. That is, for each covariate j, the n×M dimensional matrix X_j = {ψ₁(x_j), ⋯, ψ_M(x_j)} is considered as the new set of predictors, where ψ_j are basis functions of our choice and M is the number of basis functions. A model with nonlinear main effects is given by

$$E\left(\mathit{y}|{\mathit{x}}_1,\cdots ,{\mathit{x}}_P\right)=\alpha +\sum _{j=1}^p{\mathit{X}}_j{\mathit{\beta }}_j:={\mu }_N(\mathbf{\Theta }),$$ (4)

where for each j = 1, ⋯, p, β_j are M × 1 parameter vector corresponding to the j^th covariate. In this model, X_jβ_j approximates the nonlinear main effect function f_j(x_j).

A generic second order model incorporating pairwise interaction effects can be written as

$$\mathit{y}=\sum _{j=1}^p{f}_j\left({\mathit{x}}_j\right)+\sum _{1\le l<k\le p}{f}_{kl}\left({\mathit{x}}_k,{\mathit{x}}_l\right)+\mathit{ϵ},$$ (5)

where f_kl(·, ·) are the interaction effects. For a completely linear second order model assuming interaction effects also to be linear, the mean function can be written as

$$E\left(\mathit{y}|{\mathit{x}}_1,\cdots ,{\mathit{x}}_p\right)=\alpha +\sum _{j=1}^p{\mathit{x}}_j{\beta }_j+\sum _{k=2}^p\sum _{l=1}^{k-1}{\mathit{x}}_k\cdot {\mathit{x}}_l{\gamma }_{kl}:={\mu }_{LL}(\mathbf{\Theta }),$$ (6)

where γ_kl are the interaction effects, · denotes Hadamard product, and μ_LL denotes mean under both main effects and interaction effects being linear. A model with nonlinear main effects and linear interaction effects can be defined by replacing $\sum _{j=1}^p{\mathit{x}}_j{\beta }_j$ with $\sum _{j=1}^p{\mathit{X}}_j{\mathit{\beta }}_j$.

More generally, nonlinear interaction effects f_kl in Model (5) can be approximated using the product of the basis functions X_k and X_l (denoted by X_kl having dimension n × M²).

$$E\left(\mathit{y}|{\mathit{x}}_1,\cdots ,{\mathit{x}}_p\right)=\alpha +\sum _{j=1}^p{\mathit{X}}_j{\mathit{\beta }}_j+\sum _{k=2}^p\sum _{l=1}^{k-1}{\mathit{X}}_{kl}{\gamma }_{kl}:={\mu }_{NN}(\mathbf{\Theta }),$$ (7)

where γ_kl are the M² × 1 vector of interaction effects.

We shall now describe some of the existing methods that deal with models (6) and (7) that have pairwise interaction effects with different ways to impose the strong heredity principle.

1. GLinternet ²²: Glinternet is a linear interaction learning method which estimates the parameters in model (6) by utilizing a Group LASSO ⁴² penalization. The GLinternet objective function is,

   $$\frac{1}{2}{\Vert \mathit{y}-\alpha -\mathit{X}\mathit{\beta }-\sum _{k=2}^p\sum _{1=1}^{k-1}\left[{\mathit{x}}_k,{\mathit{x}}_l,{\mathit{x}}_k\cdot {\mathit{x}}_l\right]{\gamma }_{kl}^{*}\Vert }_2^2+{\lambda }_1\Vert \mathit{\beta }{\Vert }_1+\lambda \sum _{k=2}^p\sum _{1=1}^{k-1}{\Vert {\gamma }_{kl}^{*}\Vert }_2,$$

   where each ${\gamma }_{kl}^{*}$ is a three-dimensional vector with the third element corresponding to the interaction effect. The main effects appear twice in the least squares objective function above and create an overlap in the penalty terms (through β once and through ${\gamma }_{kl}^{*}$ again). The strong hierarchy is enforced through this overlapped group-LASSO penalty.
2. HIERNET ²⁰ is an ℓ₁ penalization-based method for model (6) that allows for linear main and interaction effects. HIERNET extends the the well-known LASSO ³⁵ method to allow for interaction effects under heredity constraints. More specifically, HIERNET minimizes the following objective function:

   $$\frac{1}{2}{\Vert \mathit{y}-\alpha -\mathit{X}\mathit{\beta }-\frac{1}{2}\sum _{k=1}^p\sum _{l=1}^p{\mathit{x}}_k\cdot {\mathit{x}}_l{\gamma }_{kl}\Vert }_2^2+{\lambda }_1\sum _{j=1}^p\left|{\beta }_j\right|+\frac{1}{2}{\lambda }_2\sum _{k=1}^p\sum _{l=1}^p\left|{\gamma }_{kl}\right|,$$

   subject to the constraints: ${\gamma }_{kl}={\gamma }_{lk}\forall 1\le k,l\le p;{\sum }_{l=1}^p\left|{\gamma }_{kl}\right|\le \left|{\beta }_k\right|$, for k = 1, ⋯, p. The second constraint here induces strong heredity.

3. IFORM ²¹ is a sequential interaction selection algorithm that also considers the linear main and interaction effects model (6). The SNIF algorithm we propose in the next section reduces to the IFORM algorithm if there are no nonlinear terms, and so we defer further discussion on this approach to the next section.

4. VANISH ¹⁸ method gives a general penalization-based framework for interaction selection allowing for nonlinear effects. In particular, VANISH provides a penalized objective function for the general model (7) given by:

   $$\begin{gathered} \frac{1}{2}{\Vert \mathit{y}-\alpha -\mathit{X}\mathit{\beta }-\sum _{k=2}^p\sum _{l=1}^{k-1}{\mathit{X}}_{kl}{\gamma }_{kl}\Vert }_2^2+{\lambda }_1\sum _{j=1}^p{({\Vert {\mathit{\beta }}_j\Vert }_2^2+\sum _{k=2}^p\sum _{l=1}^{k-1}{\Vert {\gamma }_{kl}\Vert }_2^2)}^{1/2} \\ +{\lambda }_2\sum _{k=2}^p\sum _{l=1}^{k-1}{\Vert {\gamma }_{kl}\Vert }_2. \end{gathered}$$

   Through this construction, both nonlinear main effects and nonlinear interaction effects are considered. In this framework, since ${\mathit{\beta }}_j^{\prime }\mathrm{s}$ and ${\gamma }_{kl}^{\prime }\mathrm{s}$ are combined together in the first penalty term through the square root of a L₂ norm, main effects and interaction effects are all zeros or all nonzeros similar to how group LASSO penalty works.

Table 1 provides a quick summary regarding the properties of each of the methods described here. GLinternet and HIERNET are penalty-based methods and IFORM is a forward selection method that considers only linear interactions. VANISH is a penalty-based method accommodating nonlinear interactions. We now provide a description of our proposed SNIF algorithm, which is a forward selection method accounting for nonlinear interactions.

TABLE 1.

Scope and categories of different methods considered (A ✓ under “Linear.Int” indicates methods considering linear interactions, under “Nonlinear.Int” is for those allowing for nonlinear interactions, “Penalty” for penalization-based methods, and “For.Sel” for methods using forward stepwise selection algorithms):

Method	Linear.Int	Nonlinear.Int	Penalty	For.Sel
GLinternet22	✓		✓
HIERNET20	✓		✓
IFORM21	✓			✓
VANISH18	✓	✓	✓
SNIF	✓	✓		✓

3 |. SNIF ALGORITHM

The proposed SNIF algorithm provides a forward stepwise algorithm to select nonlinear main effects and interaction effects for the second order model (5). SNIF sequentially includes one effect from all the main effects (possibly nonlinear) and all the interaction effects formed between the already selected main effects. SNIF accounts for nonlinear effects by using basis function expansions of the covariates similar to the model in (7). However, in addition to the basis function expansions X_j for each covariate, SNIF also considers the linear original terms x_j. By doing so, SNIF avoids the use of nonlinear basis functions when the true effect is linear and reduces the number of parameters involved in such cases thus enhancing the power of discovery of interactions. In other words, the basis function expansion terms are used only when they are necessary under the presence of nonlinear effects allowing for using a sparser linear term whenever possible. A concise outline of the SNIF Algorithm is provided in 1 and all the details of the algorithm are provided below.

Algorithm 1.

Outline of SNIF Algorithm

Input:

y: the n × 1 response vector, xj,: the n × 1 vector corresponding to jth covariate, number of basis functions M and number of iterations K

Step 0: Initialize the following index sets:

Set L0 = Ø (Index Set of Linear Main Effects Selected)

Set N0 =Ø (Index Set of Nonlinear Main Effects Selected)

Set I0 = Ø (Index Set of Interaction Effects Selected)

Set P0 = {1, ⋯, p} (Set of all Linear Main Effects)

Set N P0 = {1*, ⋯, p*} (Set of all Nonlinear Main Effects)

Set C0 = P0 ∪ N P0 (Set of Candidate Effects for Selection at the first step)

Step 1: Update the index sets Lt, Nt, It, Ct at iteration t (1 ≤ t ≤ K) as follows:

Select one effect st (can be linear main/nonlinear main/interaction effect) from the candidate set Ct–1 that maximizes the measure Mt(·) (see the detailed algorithm)

Update the index sets Lt, Nt and It by adding st to the relevant set

Update Ct by removing st, and when st is a main effect by adding interactions of st with the already selected linear and nonlinear main effects

Step 2: Solution Path {s1, ⋯, sK} of the selected effects is obtained by iterating Step 1. A final model is selected by applying BIC to this solution path.

Details of the SNIF algorithm:

We first define the following index sets:

L_t : set of all linear main effects selected until step t,

N_t: set of nonlinear main effects selected until step t,

I_t: set of interaction effects (both linear and nonlinear) selected until step t,

C_t: set of candidate effects from which one effect is to be selected at step t + 1,

P₀ = {1, ⋯, p} is the index set of all linear main effects, and

NP₀ = {1*, 2*, ⋯, p*} is the index set of all nonlinear main effects.

Before starting the SNIF algorithm (t = 0), the sets L_t, N_t, and C_t are initialized. We always initialize the SNIF algorithm to start from the null model. Other choices of initialization can also be used, and different initializations may not necessarily lead to the same selection path.

Step 0 (Initialization): The sets L₀ = Ø, N₀ = Ø, I₀ = Ø, and C₀ = P₀ ∪ NP₀.

Step 1 is the major step of the algorithm which sequentially selects one effect in a forward regression fashion. That is, at step t, one effect from C_t−1 is selected and added to the appropriate set L_t, N_t, or I_t followed by updating C_t. For example, in the first forward selection step with t = 1, one effect from the candidate set C₀ containing all the main effects is selected and added to either L₀ or N₀ depending on whether it is a linear main effect or nonlinear main effect, respectively.

Step 1 (Selection and Updating): In the t^th iteration (for t ≥ 1), given the index sets L_t−1, N_t−1, I_t−1 containing the already selected effects, forward regression is used to select one more effect from the potential set C_t−1. This could be a new linear main effect, a new nonlinear main effect, or an interaction effect.

To perform selection at this step using forward regression, we compute a “measure of value” added by an effect s ∈ C_t−1 on top of the already selected effects. This measure shall be denoted by M_t(s) (two choices for the measure are defined below), and select the effect s ∈ C_t−1 that has the largest M_t(s). That is, the effect selected at iteration t is:

$$s_t=\underset{s\in C_t}{\mathrm{argmax}}{M}_t(s).$$

We use the following BIC-based metric for M_t(s):

$$M_t(s)=-BIC\left(s\cup L_{t-1}\cup N_{t-1}\cup I_{t-1}\right),$$

where BIC(·) is the Bayesian Information Criterion value obtained by regressing all the input variables corresponding to the index set in the argument (using least squares regression). BIC criterion is model selection consistent and controls for multiple comparisons as long as the number of effects being considered is smaller than $\sqrt{n}$ in order. ⁴³ A more recently proposed version called the extended BIC ⁴³ can be alternatively used especially when the number of effects is very large. We note here that a less stringent criterion on interaction effects can be used in comparison with main effects by weighting the metric M_t(s) differently if s is an interaction effect. That is, one can define a new metric $M_t^{*}(s)$ as

$$M_t^{*}(s)=w(s)M_t(s),$$

where

$$w(s)=\{\begin{array}{ll}1,& \text{if}s\text{is}\text{a}\text{main}\text{effect}\\ w,& \text{if}s\text{is}\text{an}\text{interaction}\text{effect},\end{array}$$

for a pre-specified value w > 1. The larger w is the easier it would be to include interaction effects. In all our empirical results, we give equal weight to main effects and interaction effects by always using w = 1. This is our default recommended value unless there is a reason driven by the specific scientific context for giving more importance to interaction effects.

Based on the type of the selected effect s_t, the sets L_t, N_t, I_t, and C_t are updated as follows:

Case 1: s_t is a linear main effect: we add s_t to L_t (the index set for linear main effects) and update C_t (the set of candidate effects for future selection). More specifically, L_t = L_t−1 ∪ s_t, and C_t = {C_t−1 − s_t} ∪ {s_t × L_t−1} ∪ {s_t × N_t−1}, where s_t × L_t−1 denotes all interactions of s_t with variables in L_t−1 (similarly for N_t−1). That is, s_t is removed and all the interaction effects of s_t with the other existing effects are added to C_t. Finally, the index sets N_t = N_t−1, and I_t = I_t−1 remain unchanged.

Case 2: s_t is a nonlinear main effect: similar to Case 2, N_t and C_t are updated as follows. N_t = N_t−1 ∪ s_t, C_t = {C_t−1 − s_t} ∪ {s_t × L_t−1} ∪ {s_t × N_t−1}, I_t = I_t−1, and L_t = L_t−1.

Case 3: s_t is an interaction effect: in this case, s_t is simply added to I_t and excluded in C_t with the main effects unchanged. That is, I_t = I_t−1 ∪s_t, C_t = {C_t−1 − s_t}, N_t = N_t−1, and L_t = L_t−1. Recall that X_j is used to denote the basis functions corresponding to the predictor x_j. The selected interaction effect s_t can be of the form x_i×x_j or x_i×X_j or X_i×X_j for some covariates i and j whose main effects are already present in either of the selected sets L_t−1 or N_t−1. Since an interaction effect is added only when both the corresponding main effects are present, this step naturally induces the strong heredity principle.

Step 2 (Solution Path): The solution path consists of the sets {L_t, N_t, I_t}_0≤t≤K, obtained by iterating the selection in Step 1 for a specified length K. The final model is chosen by thresholding the model path using BIC on the sequence of models obtained.

Remark 1. SNIF algorithm follows the strong heredity principle in the sense that interactions are included only when both the corresponding main effects are included. The algorithm could be easily modified to follow the weak heredity principle which requires that for an active interaction effect at least one of its main effects to be active.

We illustrate SNIF with a simple example having p = 3 predictors.

Step 0 (Initialization): Set L₀ = N₀ = I₀ = Ø, and C₀ = {1, 2, 3, 1*, 2*, 3*} from which one effect shall be selected.

Step 1: Suppose the linear main effect 2 is selected at iteration 1, then L₁ = {2}, N₁ = I₁ = Ø, and C₁ = {1, 3, 1*, 2*, 3*}. At iteration 2, if 1* (nonlinear main effect for 1) is selected, then L₂ = {2}, N₂ = {1*}, I₂ = Ø, and C₂ = {1, 3, 2*, 3*, 1* × 2}. Now, if the interaction effect 1* × 2 is selected, I₃ = {1* × 2} will be updated.

Step 2: The sequence {2, 1*, 1* × 2} is the forward selection path from which the final model is selected by using BIC.

Remark 2. Computational complexity of SNIF. The worst case computational complexity of the SNIF algorithm (as a function of p and K) is in the order of qK + K³, where q = p(p + 1)/2 is the total number of effects. On the other hand, penalization methods such as GLinternet, HIERNET and VANSIH have a complexity in the order of q². Therefore, as long as the number of iterations K is smaller in order than q^2/3, SNIF is computationally more appealing. In our implementation, we use K = p which is smaller in order than q^2/3.

Remark 3. Flexibility of SNIF. SNIF algorithm is flexible and can be modified as per requirement. If certain effects are apriori known to be important, those effects can be included by always placing them in the selected sets L_t, N_t, or I_t. Likewise, if some variables are known to have no nonlinear (or interaction) effects, the corresponding effects can be excluded from the candidate set C_t. If none of the nonlinear interactions are considered in the SNIF algorithm, then we obtain a simpler algorithm that allows nonlinear main effects but only linear interactions. Similarly, if the interaction set I_t is never updated, then we obtain an algorithm used for multiple exposures under the generalized additive model (GAM). If only linear terms for both the main effects and interaction effects are considered, then it reduces to the IFORM algorithm of ²¹ for the linear model. One can easily specify certain predictors (such as binary predictors) to have only linear effects by not including them in N_t for nonlinear effects. In SNIF, it is also possible to group different covariates (such as compounds) by using contextual information such as their toxicological effect score. ⁴⁴

Remark 4. Assumptions for SNIF. There are a few assumptions required for the validity of our proposed SNIF approach. Due to the least squares regression used in SNIF, the standard Gauss-Markov assumptions on the errors are assumed: (i) constant error variance, (ii) (approximate) normality of the errors, and (iii) uncorrelation of the errors and the predictors. In addition, the true effects are assumed to satisfy the strong heredity principle.

4 |. SIMULATION STUDY

We now demonstrate the performance of SNIF for screening and selection of main and interaction effects in simulation studies. We present the results for HIERNET, IFORM, and VANISH as competing alternatives. We also use the regular LASSO by including all the pairwise linear interaction effects as covariates. We use the “lars” package to implement regular LASSO, and the R package “hierNet” to implement HIERNET. To implement VANISH, we use an R code provided by the authors which provides a path of nonlinear effects. SNIF is performed following the algorithm in Section 3 by using B-spline basis functions with K = 10 degrees of freedom for capturing the nonlinear effects. IFORM is performed exactly the same way as SNIF but with only linear main and interaction effects. For all these methods, the path of effects obtained for a sequence of penalty parameters is used to select a final model based on minimizing the BIC. Along with evaluating the different methods based on the final model they select, we also evaluate them in terms of their efficiency in screening the top effects of a specified number.

Simulation Setting

We consider the following setting for our simulation study to compare the different selection methods. Each simulated dataset contains n = 500 observations and p = 10 or p = 20 covariates. The regression model is

$$\mathit{y}=\mu \left({\mathit{x}}_1,\cdots ,{\mathit{x}}_p\right)+ϵ,$$

with ϵ ~ N (0, σ²). We note that even though the number of covariates p is not very large, the total number of resultant effects due to interactions, which is given by p(p + 1)/2, is large. Two values for the error variance are considered: σ² = 1 or σ² = 4. Several choices for the conditional mean function μ(·) are considered representing both first order and second order models with linear as well as nonlinear effects representing all the scenarios discussed in Section 2. In Table 2, the different conditional mean functions considered for μ(·) are presented. The covariate values for each observation are generated independently from a multivariate normal distribution with mean zero and unit variance and a correlation of ρ = 0.25 between all the covariates. That is, Cov(x) := Σ₁ = 0.75I_p +0.25J_p, where I_p and J_p are the p×p identity matrix and the p×p matrix of ones, respectively. In the latter part of this section, we also consider an additional simulation study using the covariates from the HOME study to represent more realistic scenarios for the correlations between covariates.

TABLE 2.

Conditional mean in simulation settings: in the Model column, “L” indicates presence of only linear main effects, “N” indicates only nonlinear main effects, “LL” indicates linear main and interaction effects, “NL” indicates nonlinear main effects and linear interactions, and “NN” where all effects are nonlinear. Models (a) - (n) satisfy the strong heredity principle while models (o) - (q) satisfy the weak heredity principle but not the strong heredity principle. True Effects column gives indices of the active main and interaction effects with “*” denoting the presence of nonlinearity. For brevity, we use numbers 1, 2, etc. to indicate the linear of effects X₁, X₂, etc. while 1*, 2* indicate the non-linear effects of $X_1^{*}$, $X_2^{*}$.

Model	Mean Function	True Effects
L	(a) ${\mu }_a(x)=2+\sum _{j=1}^5{x}_j$	1,2,3,4,5
N	(b) ${\mu }_b(x)=2+8{\left(\left|x_1\right|-1\right)}^2+||4x_2|-1|+\sum _{j=3}^5{x}_j$ (c) ${\mu }_c(x)=2+(\left|x_1\right|\ge 1.5\&\left|x_1\right|\le 2))+\mathbb{1}\left(\left|x_1\right|\le 0.5\right)+2\mathbb{1}\left(0.5\le \left|x_1\right|\le 1.5\right)+4||x_2|-1|+\sum _{j=3}^5{x}_j$ (d) ${\mu }_d(x)=2+2\left|x_1\right|\mathbb{1}\left(\left|x_1\right|<1\right)+2\mathbb{1}\left(\left|x_1\right|>1\right)+4\Vert x_2|-1|+\sum _{j=3}^5{x}_j$	1*,2*,3,4,5
LL	(e) ${\mu }_d(x)=2+\sum _{j=1}^5{x}_j+6x_4{x}_5$	1,2,3,4,5,(4×5)
NL	(f) μf (x) = μb(x) + 6x4x5 (g) μg(x) = μc(x) + 6x4x5 (h) μh(x) = μd(x) + 6x4x5	1*,2*,3,4,5,(4×5)
NN	(i) μi(x) = μb(x) + 8|x1|||x2| − 1| (j) μj(x) = μc(x) + 8|x1|||x2| − 1| (k) μk(x) = μd(x) + 8|x1|||x2| − 1|	1*,2*,3,4,5,(1* × 2*)
NN	(l) ${\mu }_l(x)={\mu }_i(x)+8x_3\sqrt{\left|x_2\right|}$ (m) ${\mu }_m(x)={\mu }_j(x)+8x_3\sqrt{\left|x_2\right|}$ (n) ${\mu }_n(x)={\mu }_k(x)+8x_3\sqrt{\left|x_2\right|}$	1*,2*,3,4,5,(1* × 2*),(2* × 3)
NN	(o) ${\mu }_o(x)=2+\mathbb{1}\left(1.5\le \left|x_1\right|\le 2\right)+\mathbb{1}\left(\left|x_1\right|\le 0.5\right)+2\mathbb{1}\left(0.5\le \left|x_1\right|\le 1.5\right)+\sum _{j=3}^5{x}_j+8\left|x_1\Vert x_2\right|-1|$ (p) ${\mu }_p(x)=2+\mathbb{1}\left(1.5\le \left|x_1\right|\le 2\right)+\mathbb{1}\left(\left|x_1\right|\le 0.5\right)+2\mathbb{1}\left(0.5\le \left|x_1\right|\le 1.5\right)+\sum _{j=3}^5{x}_j+8\left|x_1\right|||x_2|-1|$ (q) ${\mu }_q(x)=2+2\left|x_1\right|\mathbb{1}\left(\left|x_1\right|<1\right)+2\mathbb{1}\left(\left|x_1\right|>1\right)+\sum _{j=3}^5{x}_j+8\left|x_1\right|||x_2|-1|$	1*,3,4,5,(1* × 2*)

Simulation Results

We present our simulation results in terms of the following six evaluation metrics. In the following definitions, R is the total number of simulated datasets and T is the total number of active effects.

• Missed main effects (MME) = $\frac{1}{TR}\sum _{r=1}^R$ (# of active main effects missed in simulated dataset r).

• False main effects selected (FME) = $\frac{1}{TR}\sum _{r=1}^R$ (# of false main effects selected in simulated dataset r).

• Missed interaction effects (MIE) = $\frac{1}{TR}\sum _{r=1}^R$ (# of active interaction effects missed in simulated dataset r).

• False interaction effects selected (FIE) = $\frac{1}{TR}\sum _{r=1}^R$ (# of false interaction effects selected in simulated dataset r).

• Missed main effects among the top p effects (MME10 for p = 10 and MME20 for p = 20) = $\frac{1}{TR}\sum _{r=1}^R$ (# of missed main effects among the top p effects in simulated dataset r).

• Missed interaction effects among the top p effects (MIE10 or MIE20) = $\frac{1}{TR}\sum _{r=1}^R$ (# of missed interaction effects among the top p effects in simulated dataset r).

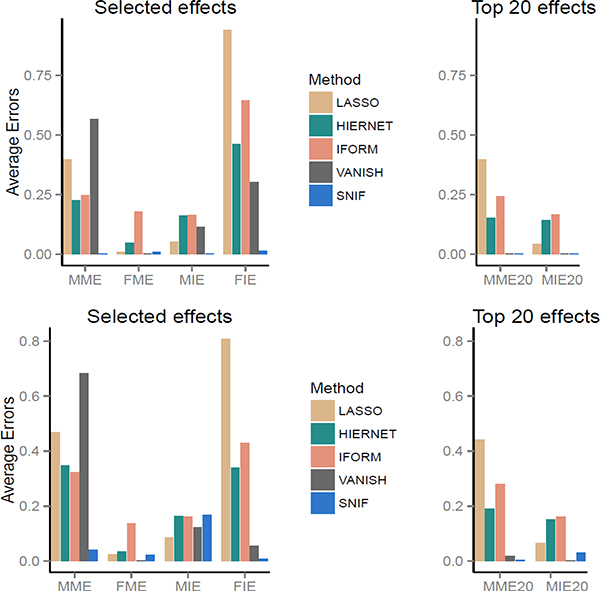
The first four measures demonstrate the quality of the effects selected for each method. The last two measures are based on the top p effects, which are the selected effects if the total number of effects (main and interaction effects together) to be selected is pre-specified to be p. For example, for SNIF the top p effects are all the effects selected within the first p iterations. For all the above measures, small values indicate good performance. Small values for the first four measures indicate effectiveness of the model selected and those for the last two measures indicate the effectiveness of screening based on top effects. In the main text of the paper, we present the results for the mean structure of Model (i) in Table 2, which has both nonlinear main effects and nonlinear interaction effects. The results for other mean structures will be provided in the Supplementary Material. The results in Figure 1 are when the number of predictors is p = 10 and those in Figure 2 when p = 20. Both these figures show results for two different levels of error variance (σ² = 1 and σ² = 4).

FIGURE 1.

Simulation results for Model (i) from Table 2 : n= 500, p = 10, σ² = 1 (top panel) and σ² = 4 (bottom panel). MME (MIE) stands for average main (interaction) effects missed and FME (FIE) for average false main (interaction) effects selected in the chosen model. MME10 and MIE10 stand for MME and MIE among the top 10 effects selected.

FIGURE 2.

Simulation results for Model (i) from Table 2 : n= 500, p = 20, σ² = 1 (top panel) and σ² = 4 (bottom panel). MME (MIE) stands for average main (interaction) effects missed and FME (FIE) for average false main (interaction) effects selected in the chosen model. MME20 and MIE20 stand for the corresponding quantities among the top 20 effects selected.

We now provide a summary of the simulation results from Figures 1 and 2 and the extended results in the Supplementary Material. For the high signal cases when σ² = 1 under Model (i), (corresponding to the top panels in Figures 1 –2), SNIF has nearly zero error according to all the six evaluation measures considered, whereas all the other methods have at least one of the six measures as large as 0.6. For instance, LASSO, HIERNET, IFORM and VANISH have MME ranging from 0.2 to 0.7 and FIE varying from 0.3 to 1 whereas these measures are nearly zero for SNIF.

Similar comparisons hold true for results from the other mean structures presented in the Supplementary Material except for the purely linear models (a) and (e). Not surprisingly, linear methods such as LASSO, HIERNET and IFORM have a slightly better performance for the linear models. However, it is worth noting that the performance loss for SNIF is not very high in spite of the motivation of SNIF for capturing nonlinear effects. For example, the largest values for FME and FIE for LASSO are between 0.05 to 0.1 whereas for SNIF they are between 0.1 to 0.2 in models (a) and (e) (see the Supplementary Material). This assures that SNIF does not overfit when the underlying model is a linear model.

For the cases with a weaker signal (σ² = 4), it becomes harder for every method to detect the interaction effects (bottom panels of Figures 1 and 2). The performance for SNIF is strictly better than all the competing methods based on MME, FME and FIE. MIE for SNIF ranges from 0 – 0.2 and is better or at least comparable with the other methods. Although the performance of VANISH is similar to that of SNIF in terms of interaction selection (based on MIE and FIE), VANISH has much larger values for MME with MME nearly as large as 0.7 whereas it is close to 0.02 for SNIF (bottom panels of Figures 1 and 2). An extensive empirical study ³⁷ suggests that the performance of forward selection for variable selection is quite competitive and is very similar to best subset selection. Both these methods perform particularly well when the signal is moderately strong. This is also the case with our simulation results.

The strong performance of SNIF for screening the effects across all the settings is worth mentioning. The measures MME10 and MIE10 (when p = 10) and MME20 and MIE20 (when p = 20) indicate the performance of the corresponding method for screening active effects among the top p effects. These measures are also free of the tuning used to select a final model. SNIF has nearly zero error in most settings based on these measures (except for mean structure (g) where MME20 is 0.02 which is the largest for SNIF based on screening measures - see Figure (g) for p = 20 in the Supplementary Material). In spite of VANISH performing better than other competitive methods, its performance is not close to that of SNIF. For instance, MME10 for VANISH is nearly as larger as 0.2 (compared to 0.02 at most for SNIF) in several cases (including for Model (i) in Figure 1).

To consider the performance of SNIF under a more realistic chemical exposure studies, we will use the data from the HOME study to generate simulated outcomes. There are p = 18 covariates corresponding to different chemical exposures in the HOME study (see Section 6 for details). We use these to generate outcomes Y in the following manner:

$$Y=-2X_1+4X_2-2X_3+2X_4+2{\left(\left|X_{16}\right|-1\right)}^2+2X_2{X}_4+2X_4\left(X_{16}^2+X_{16}\right)+ϵ,$$ (8)

with ϵ ~ N (0, σ²). Therefore, there are five main effects and two interaction effects with X₁₆ having both nonlinear main and interaction effects. We summarize the results for this setting in Figure 3 which shows the strong performance of SNIF also under the more realistic set-up for the correlations between the covariates. The pairwise correlations between the covariates ranged from −0.41 to 0.82 with several of them being larger than 0.7. In comparison to penalization methods such as the LASSO, forward selection methods such as SNIF are expected to perform better under high correlations between the predictors. ³⁷ In summary, the performance of SNIF algorithm is very competitive and often superior across all the settings and metrics considered. A particular strength of SNIF is that its identification of false effects (based on FME and FIE) is much smaller compared to the other methods. It also has better or comparable identification of true effects (both main and interaction effects based on MME and MIE). Furthermore, it performs very well in terms of screening the top ranked effects.

FIGURE 3.

Results for the Model given by Equation (8) using the covariates from the HOME study: n= 270, p = 18, σ² = 1 (top panel) and σ² = 4 (bottom panel). MME (MIE) stands for average main (interaction) effects missed and FME (FIE) for average false main (interaction) effects selected in the chosen model. MME18 and MIE18 stand for the corresponding quantities among the top p = 18 effects.

5 |. ANALYSES OF TEST DATASETS RELEASED BY NIEHS

The data challenge of National Institute of Environmental Health Sciences (NIEHS)’s Epidemiology- Statistics (Epi- Stats) workshop held on July 13 to 14, 2015 reinforced the need to develop statistical methods for assessing health effects of mixtures and multiple pollutants. NIEHS Epi-Stats conference invited scientists to evaluate different statistical methods for studying the effect of exposure to multiple pollutants in the environment. Two synthetic datasets emulating environmental exposures together with a real dataset from the Health Outcomes and Measurement of the Environment (HOME) study ⁴⁵ were provided for comparing the performance of different statistical approaches (we refer to ²⁵ for more details about the workshop). In this section, we analyze the synthetic datasets for studying the performance of SNIF.

5.1 |. NIEHS Test Dataset 1

This test dataset contains n = 500 observations and p = 8 input variables, seven of which are continuous variables (denoted by X₁, ⋯, X₇) representing exposures and the last one is a binary variable (denoted by Z) representing a demographic variable such as gender. The response Y is a continuous outcome. The data generating model used to obtain the response Y given the covariate values is

$$Y={\alpha }_0+\frac{{\alpha }_1\left(\frac{T}{K_T}+\frac{X_1}{K_1}+\frac{X_2}{K_2}\right)}{\left(\frac{T}{K_T}+\frac{X_1}{K_1}+\frac{X_2}{K_2}+\frac{X_4}{K_4}+\frac{X_5}{K_5}\right)}{R}_0\left(X_7\right)+\gamma Z+ϵ,$$

where $R_0\left(X_7\right)=R_{00}+\frac{\lambda X_7}{K_7+X_7}$. The values of all the constants α₀, α₁, K₁, ⋯ K₅, K_T, R₀₀, γ and the generation schemes for the covariates and errors are described in detail on the NIEHS conference website at https://www.niehs.nih.gov/about/events/pastmtg/2015/statistical/index.cfm.

Tables 3 describes the main effects and the interaction effects selected by different methods considered. All the penalized based methods LASSO, HIERNET, VANISH as well as the linear forward selection method IFORM select interaction effects spuriously whereas SNIF did not select any interaction effects consistent with the data generating model. As a drawback, SNIF did not identify X₂’s main effects. This can be attributed to the extremely high correlation between the covariates X₁ and X₂ (greater than 0.9).

TABLE 3.

NIEHS Test Dataset 1: Effects Selected by each of the methods considered (for SNIF, ✓* indicates nonlinearity of the corresponding effect; for VANISH all the selected effects are nonlinear). True active effects are shown in bold (that is, the covariates X₁, X₂, X₄, X₅, X₇, and Z have active effects.)

Main effects									Interaction effects
	X1	X2	X3	X4	X5	X6	X7	Z
LASSO	✓	✓		✓	✓		✓	✓	LASSO	X5 × X7	(X4, X5) × Z
HIERNET	✓	✓		✓	✓		✓	✓	HIERNET	X5 × X7	X5 × Z
VANISH	✓	✓			✓		✓	✓	VANISH	X5 × X7
IFORM	✓	✓		✓	✓		✓	✓	IFORM	X5 × X7	X1 × X2
SNIF	✓*			✓	✓		✓*	✓	SNIF

In Figure 4, we show the estimated marginal relationships between the response and the covariates X₁, X₄, X₅ and X₇. These relationships are estimated by refitting the model selected. The refitted model may not be used for performing inference about the significance of the coefficients due to the potential bias model selection incurs, and so we only use the refitted estimation for demonstrating how well it approximates the marginal relationship between the response and the covariates. As we can see from Figure 3, the marginal relationship (with all the other covariates set at their mean values) approximates the truth quite well. It only slightly misses the effect of X₅ at either of its boundaries due to the linear approximation.

FIGURE 4.

Estimated marginal relationships for NIEHS test dataset 1: the plots show the relationship between the conditional mean of the response as a function of the covariates, the true one in solid black and the estimated one in dashed blue. The remaining covariates are fixed at their mean values.

5.2. NIEHS Test Dataset 2

For the second dataset provided by NIEHS, there are n = 500 observations and p = 17 covariates. Three of those covariates represent poverty index ratio (Z₁), age (Z₂), and gender (Z₃), and the other covariates (X₁, ⋯, X₁₄) represent chemical concentrations of PCBs, dioxins and furans. Among the input variables, gender alone is binary. For the data generating model, the conditional mean of the outcome Y is different across gender, and is given as follows.

For Z₃ = 0, the conditional mean is

$$E\left(Y|X^{\prime }s,Z^{\prime }s\right)=3+0.05X_4+0.1X_6+0.1X_{11}+0.5X_{12}+0.1X_{14}+0.01Z_1+0.003Z_2,$$

and for Z₃ = 1,

$$E\left(Y|X^{\prime }s,Z^{\prime }s\right)=3+0.01X_1+0.05x_4+0.1X_{11}+0.1X_{14}+0.01Z_1+0.003Z_2-\mathrm{0.32.}$$

Therefore, when Z₃ = 0, X₄, X₆, X₁₁, X₁₂ and X₁₄ influence the mean of Y, while for Z₃ = 1, X₁, X₄, X₁₁ and X₁₄ are associated with the mean of Y. The correlations between X₃, X₄, X₅ are very high and are given by 0.95, 0.96, 0.99, and so it is expected to be difficult to distinguish between them. Due to the set-up, the true interaction effects are (Z₃ × X₁₂), (Z₃ × X₆), (Z₃ × X₁), which are all linear. No interactions between the chemical concentrations (the X covariates) are present.

It is worth noting that for this model, there are no nonlinear main or interaction effects. Therefore, we do not necessarily expect SNIF to perform better than all the linear methods. Table 4 provides the results of variable selection for all the different methods considered. It is remarkable to note that SNIF identified most of the selected effects to be linear. We, therefore, do not present the marginal relationship plots for this data example. It is satisfying to note that the performance of SNIF is still competitive with IFORM and not noticeably worse than HIERNET and LASSO in spite of using a more flexible model. SNIF has three false positives and five true positives (with FDR of 0.375 ) whereas LASSO has eight false positives and nine true positives (FDR of 0.471), HIERNET has nine false positives and nine true positives (FDR of 0.474), VANISH has six false positives and three true positives (FDR of 0.667), and IFORM has three false positives and six true positives (FDR of 0.333). This indicates that both IFORM and SNIF perform well although SNIF did not lose much even under the completely linear model. In terms of selecting the true effects, the performance of SNIF, in this case, is not as competitive as in other situations. This is partly because there are no non-linear effects in this case. SNIF performs much better than VANISH, which is the other method incorporating non-linear effects. This can be associated with the way SNIF only considers nonlinear effects when linear effects are not satisfactory, unlike VANISH which always considers nonlinear effects. The performance of SNIF is not superior in terms of all performance measures one can consider but seems reasonable at least in terms of having a low FDR.

TABLE 4.

NIEHS Test Dataset 2: Main effects selected by each of the methods considered (for SNIF, ✓* indicates nonlinearity of the corresponding effect; for VANISH all the selected effects are nonlinear). True active effects are shown in bold. For example, main effects of X₁, X₄, and interaction between X₁₂ and Z₃ are active.

Main Effects Selected

X1

X2

X3

X4

X5

X6

X7

X8

X9

X10

X11

X12

X13

X14

Z1

Z2

Z3

LASSO

✓

✓

✓

✓

✓

✓

✓

✓

✓

✓

✓

✓

✓

HIERNET

✓

✓

✓

✓

✓

✓

✓

✓

✓

✓

✓

✓

✓

✓

VANISH

✓

✓

✓

✓

IFORM

✓

✓

✓

✓

✓

✓

SNIF

✓

✓

✓

✓*

✓

✓

Interaction Effects Selected

LASSO

X10 × Z2

X12 × Z3

X7 × Z3

X2 × Z3

HIERNET

X10 × Z2

X12 × Z3

X7 × Z3

X2 × X13

VANISH

X12 × Z3

X2 × Z3

X2 × Z12

X2 × X13

X12 × X13

IFORM

X10 × Z2

X12 × Z3

X6 × Z3

SNIF

X10 × Z2

X12 × Z3

6 |. EXPOSURES AND MENTAL DEVELOPMENTAL INDEX IN CHILDREN

6.1 |. Data Description

We now consider a study on prospective pregnancy and birth cohort of mother-child pairs in the United States called the Health Outcomes and Measures of the Environment (HOME) study. HOME study is a longitudinal pregnancy and birth cohort study with the aim of examining the association between prenatal exposure to lead, tobacco smoke, mercury, polychlorinated biphenyl (PCB), and pesticides with children’s cognitive and behavioral development before the age of three. The HOME study enrolled pregnant women living in nine counties of Cincinnati, OH metropolitan area for participation in the study during the period of March 2003 to January 2006. Eligibility criteria for enrollment required the women to be older than 18 years, having less than 19 weeks in pregnancy, and living in a home (not a mobile or a trailer home) built during or before 1978.

The study collected extensive measurements of environmental chemical exposures, child health, and confounders in mothers and children. The study used standardized questionnaires to identify sources of exposures to pregnant women or children’s exposure to the different exposures considered. We provide below more details about the dataset.

Exposures and other covariates

Concentrations of polychlorinated biphenyl (PCB) congeners, polybrominated diphenyl ether (PBDE) congeners, and organochlorine pesticides are measured using gas chromatography - high resolution mass spectrometry (GC-HRMS) methods. ⁴⁶ The dataset includes concentrations of 14 PCBs, 4 PBDEs, and 4 organochlorine pesticides. Some of these exposures are mutually extremely correlated, and we will only use one each from such highly correlated groups. Demographic variables collected include child’s gender and maternal age at delivery, education, race, and smoking status during pregnancy. In total, there are p = 18 input variables in our analysis.

Outcome

The study used tests and surveys to assess neurobehavioral development domains in children. One of the major outcomes is a Mental Development Index (MDI) based on the Bayley Scale of Infant Development-II (BSID-II). ⁴⁷ This BSID-II is an age-standardized measure of children’s cognitive and language abilities and was administered by trained examiners to children at 1, 2, and 3 years of their age. BSID-II is our continuous outcome variable where higher scores indicate better cognitive and language abilities.

Sample Size

Among the 392 mothers who had a live birth, we consider n = 270 mother-child pairs which have no missing values for the outcome, exposures, or covariates. This is the same set of data as provided in the NIEHS Epi-Stats conference.

6.2 |. Results

In Table 5, we present the effects selected by the LASSO, HIERNET, IFORM and SNIF (we exclude VANISH as its implementation required a test dataset). IFORM and SNIF methods choose the same effects which are all linear. These effects are the main effect of child’s gender (gend), mother’s education (mom.edu), mother’s race (mom.race), PCB156 (pcb156), and the interaction effect of gender and PCB156. When we perform a linear regression analysis by including all the variables selected by different methods considered, the effects child.gend, mom.edu, mom.race, and the interaction between gender and PCB156 are significant but all the other effects are not significant.

TABLE 5.

HOME Study MDI Dataset: Selected Main and Interaction Effects (for SNIF, ✓* indicates nonlinearity of the corresponding effect)

	gend	mom.edu	mom.race	pcb156	pcb105	gend × pcb156	mom.race × pcb156	mom.race × mom.edu
LASSO		✓	✓					✓
HIERNET		✓	✓	✓			✓
IFORM	✓	✓	✓	✓		✓
SNIF	✓	✓	✓	✓		✓

It is possible that nonlinearities of some of the effects may not have been identified due to large error variance. We also present the top p = 18 effects screened by the methods in Tables 6 and 7. These results can be useful for future research on more comprehensive understanding of the effects of exposures on child developmental index. From the results, we note that SNIF algorithm suggests potential interactions between several congeners, particularly several interactions involving the PCB105 and PCB156 congeners. PCB 105 and PCB156 are moderately persistent dioxin-like congeners that have both been classified as potentially antiestrogenic and immunotoxic. ⁴⁸ The top effects screened by SNIF also suggest potential nonlinearity both in the main effects and the interaction effects involving the PCB105 congener. In general, the top effects screened by SNIF can be useful in designing further research studies.

TABLE 6.

HOME Study MDI Dataset: Main Effects among the Top p = 18 effects screened (for SNIF, ✓* indicates nonlinearity of the corresponding effect).

	gend	edu	race	pcb105	pcb156	PBDE47	pcb180	pcb199	oxychlor	hcb	PBDE153	pp.dde
LASSO	✓	✓	✓	✓
HIERNET	✓	✓	✓	✓	✓	✓	✓	✓	✓
IFORM	✓	✓	✓	✓	✓	✓	✓	✓		✓
SNIF	✓	✓	✓	✓*	✓	✓					✓*	✓

TABLE 7.

HOME Study MDI Dataset: Interaction Effects among the Top p = 18 effects screened (for SNIF, * indicates nonlinearity of the corresponding effect)

LASSO	race × (smoke, nonachlor, pcb74, pcb156)		pcb199 × (smoke, nonachlor)
HIERNET	race × (smoke, nonachlor, pcb74, pcb156)		pcb199 × (smoke, nonachlor)
	pcb74 × mom.edu	pcb156 × gend	PBDE47 × PBDE153
IFORM	race × (smoke, nonachlor, pcb74, pcb156)		pcb199 × (smoke, nonachlor)
	pcb74 × mom.edu	pcb156 × gend	PBDE47 × PBDE153
SNIF	race × (pcb156, PBDE153*)		pcb156 × (gend, PB47)
	pcb105 × (edu, PB47, pcb156)		pcb105* × pp.dde

7 |. DISCUSSION

In this article, we first provide a comprehensive overview of penalization and forward selection methods targeted towards interaction search. We propose a new method that can account for nonlinear main effects and interactions and compare it with existing approaches for interaction selection. By careful selection of nonlinear interaction terms when needed we improve the detection rates of true nonlinear interactions and are still able to maintain competitive power for selection of linear interactions when only linear interactions are present. In other words, SNIF algorithm reduces false positives by adequately modeling non-linearity. Extensive simulation studies and use of test datasets released as part of the mixtures modeling workshop by NIEHS strengthens the supporting evidence for SNIF as a new tool for searching interactions in the presence of nonlinearity. While we demonstrate SNIF and its usefulness for identifying chemical exposures, it is a general approach to select nonlinear effects which can be useful in many other applications.

The performance of forward selection based approaches may not be as strong when the signal is very weak. In particular, the performance of SNIF may be compromised if the main effects are very weak or if the (weak) heredity principle is violated. It might be of interest for applied researchers to estimate the magnitudes of the selected effects. While it is tempting to use the selected model directly for performing inference about the selected effects, one needs to be cautious of the bias it could introduce. ⁴⁹ There is a recent body of literature ^50,51 that attempts to address this issue which can possibly be adapted for SNIF.

We emphasize that the focus of the article and the main objective of the proposed SNIF method is selection of the effects and not prediction or estimation. Characterizing the effects of one pollutant/chemical on health outcome post-selection is an important direction to pursue. ⁵² tries to report the effect of one exposure for fixed quantiles of the other exposures in a two-pollutant context. Similar ideas can be adapted to a multipollutant context. Estimates of policy relevant quantities can be provided following the ideas of ¹⁴. A fully Bayes variable shrinkage and selection algorithm may be able to achieve both selection and estimation with the adequate propagation of uncertainty. These are important considerations but beyond the scope of the current paper.