Distinguishing cognitive effort and working memory load using scale-invariance and alpha suppression in EEG

Abstract

Despite being intuitive, cognitive effort has proven difficult to define quantitatively. Here, we proposed to study cognitive effort by investigating the degree to which the brain deviates from its default state, where brain activity is scale-invariant. Specifically, we measured such deviations by examining changes in scale-invariance of brain activity as a function of task difficulty and posited suppression of scale-invariance as a proxy for exertion of cognitive effort. While there is some fMRI evidence supporting this proposition, EEG investigations on the matter are scant, despite the EEG signal being more suitable for analysis of scale invariance (i.e., having a much broader frequency range). In the current study we validated the correspondence between scale-invariance (H) of cortical activity recorded by EEG and task load during two working memory (WM) experiments with varying set sizes. Then, we used this neural signature to disentangle cognitive effort from the number of items stored in WM within participants. Our results showed monotonic decreases in H with increased set size, even after set size exceeded WM capacity. This behavior of H contrasted with behavioral performance and an oscillatory indicator of WM load (i.e., alpha-band desynchronization), both of which showed a plateau at difficulty levels surpassing WM capacity. This is the first reported evidence for the suppression of scale-invariance in EEG due to task difficulty, and our work suggests that H suppression may be used to quantify changes in cognitive effort even when working memory load is at maximum capacity.

Introduction

Cognitive effort is a seemingly intuitive aspect of cognition, yet has proven difficult to quantify because of gaps in both its operationalization and theory. Regarding operationalization, researchers lack consensus on a neural signature of mental effort. As a result, different measurements such as response time, brain activity in regions including dorsal anterior cingulate cortex, or pupil diameter have been used as indicators of effort (see Westbrook & Braver, 2015 for a review).

From a theoretical perspective, some researchers, at least implicitly, equate mental effort with working memory load (Garbarino & Edell, 1997; Kitzbichler, Henson, Smith, Nathan, & Bullmore, 2011), whereas others see working memory load and effort as confounded measures that could, in theory, be separable (Vogel & Machizawa, 2004). For example, the decision making literature commonly defines effort as the set of processes that determine the level of performance that will be realized based on the characteristics of a given task and the individual’s available information processing capacity (e.g., working memory capacity) (Bonner & Sprinkle, 2002; Kahneman, 1973; Shenhav et al., 2017). The utility of effort, therefore, is to optimize the allocation of limited (or unlimited but shared) cognitive resources between different tasks based on the expected cost and value of exerting cognitive control. From this definition, it logically follows that if an individual is performing at their maximum ability level (e.g., at their working memory capacity limit), no more effort will be exerted for that specific task, because it is not judicious. To test whether individuals can exert seemingly “fruitless” cognitive effort—that is, whether it is possible to exert cognitive effort in the absence of behavioral performance gains— we propose a different view on cognitive effort and then apply it in conjunction with research on working memory capacity.

Effort as suppression of scale-free brain activity

In the current study we use a theoretical framework that operationalizes the amount of cognitive effort as the degree of deviations in current brain states from those more proximal to the default-mode brain states. In this framework, we assume the brain at rest is organized at a critical state (de Arcangelis, Perrone-Capano, & Herrmann, 2006; Kitzbichler, Smith, Christensen, & Bullmore, 2009), because such a state provides maximum dynamic range for a network (Gautam, Hoang, McClanahan, Grady, & Shew, 2015; Kinouchi & Copelli, 2006), and optimizes active information storage and transfer (Boedecker, Obst, Lizier, Mayer, & Asada, 2012; Shriki et al., 2013; Shriki & Yellin, 2016; Tanaka, Kaneko, & Aoyagi, 2008). However, as a task requires increasingly disproportionate allocation of resources due to its higher demands, the brain moves further away from criticality (i.e., departing further from the default state) as a trade-off for gaining specificity for the task at hand (Gollo, 2017). In order to measure these changes in brain state, we utilize the Hurst exponent (H), which is a common way of measuring large-scale critical dynamics in the brain and estimates the scale-invariance of brain activity signals. Scale-invariance in biological signals refers to a property of signals where all measured time scales contribute to a signal of interest, with no particular timescale having a dominant contribution. In summary, we propose that suppression of scale-invariance in brain activity (i.e., decreases in H) signals degree of departure from default brain states and can be used as a measure of cognitive effort.

Some supporting evidence for our hypothesis comes from fMRI research on scale-free dynamics of fMRI timeseries, which have demonstrated that global Blood Oxygenation Level Dependent (BOLD) activity of the brain becomes less scale-free (lower H) in the presence of cognitive tasks and other modulators of cognitive effort (Barnes, Bullmore, & Suckling, 2009; Churchill et al., 2016; He, 2011). Specifically, fMRI timeseries have lower H when individuals are: 1) performing hard vs. easy perceptual decision tasks, (Churchill et al., 2016), 2) performing a visual detection task vs. open-eyes rest (He, 2011), 3) performing an n-back task versus rest (Barnes et al., 2009), 4) performing novel tasks vs. more familiar tasks (Churchill et al., 2016), and 5) when participants were under physical and mental burden (Churchill et al., 2015). These findings suggest that suppression of H may be a generalizable neuroimaging marker of increased cognitive effort.

Working memory load and cognitive effort

Within the context of neuroimaging studies of working memory tasks, a core challenge for identifying a neural signal of effort involves disentangling effort signals from working memory storage signals. This is because, until working memory capacity is reached, exerting more effort often enables meeting larger working memory demands. EEG research on visual working memory points to a capacity limit (referred to as K) beyond which the individual cannot maintain any more mental representations of the presented items (i. e., working memory load is maximum). Specifically, recent research in visual working memory suggests a limit of 3-4 items for K (Adam, Vogel, & Awh, 2017; Fukuda, Awh, & Vogel, 2010; Luck & Vogel, 2013; Rouder et al., 2008), but see (Alvarez & Cavanagh, 2004)). Additionally, this research has suggested that the primary role of alpha band (8-12 Hz) oscillations (α) in the context of visual working memory is to maintain distinct working memory representations rather than to suppress irrelevant information (Foster & Awh, 2019). This indicates that as the number of relevant items in working memory increases, α will systematically decrease until working memory capacity (K) is reached (Adam, Robison, & Vogel, 2018; Fukuda, Kang, & Woodman, 2016; Fukuda, Mance, & Vogel, 2015) and will asymptote there.

Therefore, translating the fMRI work examining H and cognitive effort to EEG experiments on oscillatory activity and K can provide us with the framework needed to investigate the distinction between cognitive effort and working memory load. Pertinently, previous literature has shown that BOLD fMRI signal fluctuations are linked to scale-free fluctuations in EEG measurements of neural activity (Van de Ville, Britz, & Michel, 2010). As such, an effort-related suppression in scale-invariance, which is inherently a scale invariant measurement, would also be expected at the electrophysiological timescale. Additionally, studying these broadband effects with EEG will potentially be more fruitful than with fMRI since this method overcomes the limited range of timescales that can be examined for H in fMRI due to its slow sampling rate. To our knowledge, this relationship between suppression of H and cognitive effort beyond K has not yet been investigated using EEG, where it would provide a critical validation of the fMRI findings using a more direct measure of neural activity and a faster time-scale.

Experiments overview and hypotheses

In the current study, we analyzed two visual working memory EEG experiments including a ‘Remember N’ task (Experiment 1) and a Discrete Whole-Report task (Experiment 2)¹. In both experiments, a memory array was presented to participants while they maintained fixation on the center of the screen. Memory load was parametrically varied (N = 1, 2, 3, or 6 items)². We hypothesized that scale-invariance (H) of the EEG signal during the retention interval would decline parametrically with increasing task load, even beyond K (i.e., beyond 3-4 items). In contrast, α suppression has been shown to plateau for set sizes beyond K. As such, we further predicted that the pattern of H across set sizes would significantly diverge from the pattern of α across set sizes because α suppression would not continue to decrease beyond K. These predictions assume that cognitive effort is distinguishable from the amount of information held in working memory (i. e., working memory load). This does not mean that we are hypothesizing working memory load and cognitive effort signals to be independent, just that effort can continue passed one’s working memory capacity which distinguishes it from working memory load. In summary, we propose that (1) scale-invariance of cortical brain activity as recorded by EEG can be used as a metric of cognitive effort within individuals, and (2) this broad-band signal characteristic can dissociate visual working memory load from effort.

Methods

Experiment 1 Methods

Participants

Experiment 1 included 31 participants (18-35 years old; 17 female) from the University of Oregon and surrounding community (Mance, 2015). A total of 6 were excluded from analyses because of excessive EEG artifacts (see Artifact Rejection), leaving a final sample of 25 participants. Participants gave written informed consent, and experimental procedures were approved by the University of Oregon’s Committee for the Protection of Human Subjects (CPHS) and Institutional Review Board (IRB). All participants had normal or corrected-to-normal visual acuity and reported no history of neurological disorders.

Stimuli

Participants were seated ~100 cm from a 17-in. cathode ray tube monitor. Stimuli were rendered using the Psychophysics toolbox (Brainard, 1997; Pelli, 1997). Participants remembered colored squares presented on a medium gray background (RGB = 120 120 120) while maintaining fixation on a small white dot (0.2°). A pool of eight distinct colors: red (RGB = 255 0 0), green (0 255 0), blue (0 0 255), yellow (255 255 0), magenta (255 0 255), cyan (0 255 255), white (255 255 255), and black (1 1 1) were used to choose the colors from in each trial. Each square subtended 1°, and each square was placed at one of 32 locations on the screen (equally spaced grid of 4 x 8 locations, placed within a portion of the display subtending 8.1° to the left or right of fixation and 4.7° above or below fixation.

The Remember N Task

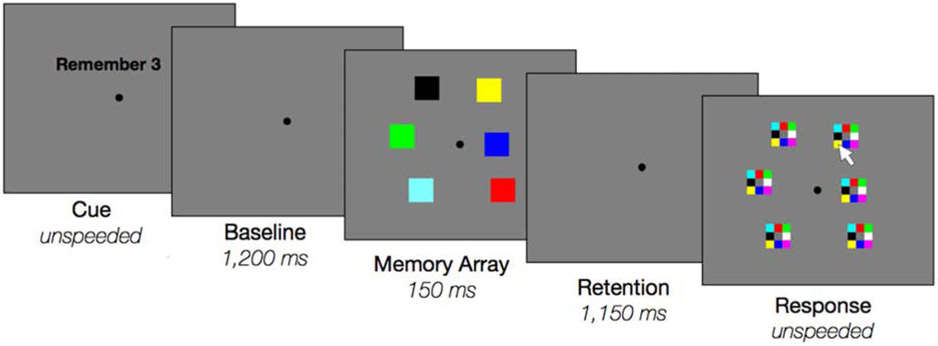
On each trial, participants were first given a cue which indicated how many items they should encode from the upcoming display (e.g., “Remember 3”) and pressed the spacebar to initiate the trial. The cue presentation was un-speeded but had a minimum duration of 600 ms. After a blank baseline (1,200 ms), participants briefly viewed six colored squares (150 ms) and remembered all or some of these squares across a delay (1,150 ms). Participants were instructed to try their best to only remember the cued number of items and to ignore the rest (Figure 1), but they were not instructed about which particular items to remember (they could freely choose). To respond, participants clicked the color in the response grid corresponding to the color remembered at that location. During the response, participants only had the option to respond to as many items as they were cued to remember (for example, if the cue was “Remember 1”, they could only make one response during the recall phase). After the participant had made all responses the cue for the next trial appeared after 500 ms. There were a total of 150 trials per set-size (30 blocks of 20 trials, ~2.5 hours).

Figure 1:

Experiment 1: “Remember N” task procedures. At the beginning of every trial, participants were cued about how many items to remember from the upcoming memory array. Memory arrays always contained six items shown in random locations. At response, participants only recalled as many items as they were asked to remember.

Data Acquisition and Analysis

Data were acquired with an SA Instrumentation amplifier with a band-pass of .01-80 Hz and digitized at 250 Hz in LabView 6.1. We measured EEG from 20 tin electrodes mounted in an elastic cap (Electrocap International, Eaton, OH) at International 10/20 sites F3, Fz, F4, T3, C3, Cz, C4, T4, P3, Pz, P4, T5, O1, and O2 and five nonstandard sites: OL midway between T5 and O1, OR midway between T6 and O2, PO3 midway between P3 and OL, PO4 midway between P4 and OR, and POz midway between PO3 and PO4 (Figure S1). All sites were recorded using a left-mastoid reference and re-referenced offline to the algebraic average of the left and right mastoids. The vertical electrooculogram (EOG) was recorded from an electrode placed ~1 cm below the right eye. The horizontal EOG was recorded from electrodes placed ~1 cm lateral to the external canthus of each eye. Electrode impedances were kept below 3 kΩ. Participants were instructed not to move their eyes or blink during the trial until the test array appeared on the screen. Trials including horizontal eye movements, blinks, blocking (amplifier saturation after drift), or excessive noise were excluded from analysis (mean = 16.8% of trials).

Artifact Rejection

For horizontal eye movement rejection, we used a split-half sliding window approach (window size = 150 ms, step size = 10 ms, threshold = 20 μV) on the HEOG signal, where a 150 ms time window was slid in steps of 10 ms from the beginning to the end of the trial. If the change in voltage from the first half to the second half of the window was greater than 20 μV, it was marked as an eye movement and rejected. We also used a sliding window step function to check for blinks in the VEOG (window size = 100 ms, step size = 10 ms, threshold = 40 μV). For blocking rejection, we slid a 200 ms time window in steps of 50 ms and excluded trials for blocking if any EEG electrode had at least 20 consecutive time-points (i.e. 80 ms) that were within 1 μV of each other. We excluded trials for excessive noise if any electrode had peak-to-peak amplitude greater than 200μV within a 15 ms time window. Data were visually inspected to confirm that rejection criteria were working as expected; some additional trials were manually rejected. Six participants were excluded for excessive artifacts (fewer than 70 good trials per condition on average, remaining n = 25). After rejection, included participants had an average of 110 trials per condition (SD = 22.5).

Estimation of α Power

To estimate alpha power (8-12 Hz), we first band-pass filtered the raw EEG signal for each trial and electrode using a two-way least-squares FIR filter, ‘eegfilt.m’, (Delorme & Makeig, 2004). We calculated instantaneous power with the MATLAB Hilbert transform (‘hilbert.m’). Because we were interested in event-related changes to alpha power as a function of memory load, we analyzed percent change in alpha power from +300 ms to +1150 ms interval in Experiment 1 and from +400 ms to +1300 ms in Experiment 2 (all with respect to onset of the memory array) compared to the baseline period (500 ms to 100 ms before the memory array onset). This means that the delay period included in the analysis for both experiments start 150 ms after the memory array is removed from the screen and end with the end of the retention interval. For each participant and electrode, we first averaged single-trial power across each load condition, then calculated the percent change in alpha power for each condition relative to a baseline period (500 ms to 100 ms before the memory array).

Estimation of Scale-Invariance (H)

Scaling analyses of temporal signals seek to determine whether all measured frequencies (or timescales) contribute to the signal of interest. Scale-invariance occurs when no particular frequency (or timescale) has a dominant contribution to the signal, implying that the signals have long-range temporal dependency. This dependency is indexed via the Hurst exponent H, where H ≤ 0.5 indicates short-range dependency, H=0.5 denotes an uncorrelated process, and H ≥ 0.5 indicates long-range dependency. The typical H values reported for fMRI rest and task data with very low frequency components (i. e., [0.01-0.1] Hz) are in the range of [0.7-1] (Churchill et al.,2015; 2016; 2007; He, 2011). H is directly related to the β exponent in P(f) ∝ f^−β, where P is the power of the signal as a function of frequency (f), such that H = (1+β)/2. The typical β values reported for EEG in healthy individuals are in the range of 1-2.5, which corresponds to H ~ 1-1.75 (Dehghani et al., 2010; Freeman, Holmes, Burke, & Vanhatalo, 2003).

While there exist many different methods to estimate H, the wavelet leader multifractal (WLMF) formalism has emerged as a powerful technique that is highly efficient and robust to signal non-stationarity (Jaffard, Lashermes, & Abry, 2007). We applied the WLMF method on the EEG signal during retention interval (after memory array and before response) to quantify the scale-invariance of the EEG signal during maintenance. The wavelet transform uses translated and dilated versions of a basis function Ψ([t – k]/a) to analyze the signal of interest at different delays and time scales. The wavelet coefficient d_x(a, k) measures signal energy present at delay k and time scale a by calculating the integral:

$$d_x(a,k)=\frac{1}{a}\int x(t)\Psi \left(\frac{t-k}{a}\right)dt$$

At a range of dyadic scales, i.e., a = 2^j for integer j. Wavelet leaders L_x(a, k) are subsequently calculated as the largest coefficient value ∣d_x (a′, k′)∣ within a narrow temporal neighbourhood of k, for any scale a′ ≤ a. Multifractal scaling is then defined by the function:

$$\frac{1}{K}{\sum }_k\mid L_x(2^j,k){\mid }^q=C_q{2}^{j\varsigma (q)}$$

Which describes wavelet power as a function of time scale, for a range of different scaling exponents q, in terms of a characteristic function ς(q). Typically parameterized as a polynomial expansion ς(q) = Σ_pc_p(q^p/p!), the log-cumulants c_p define the scaling behavior of the signal x(t).

The raw EEG signal was first band-pass filtered to 4-30 Hz and then WLMF was applied to the delay interval (same as alpha power analysis; starting 150 ms after the memory array is removed from the screen and end with the end of the retention interval). In this study, we focused on first-order cumulant c₁, which is closely linked to the monofractal scaling parameter H (Wendt, Abry, & Jaffard, 2007). An exploratory analysis of the higher-order cumulants (c₂ and c₃) did not show a relationship between them and the memory load in our two experiments. The band-pass filtering was done because 1) EEG components above 30 Hz could be contaminated with EMG signals, which could be driven by facial muscular signals of exerting effort and 2) components slower than 4 Hz are not well characterized in the signal due to the short length of the delay interval.

Canonical Correlation Analysis

In a canonical correlation analysis (CCA), two sets of variables are related together (as opposed to many variables to a single dependent variable) and the degree of relationship between the two sets of variables is assessed (Hotelling, 1936). An advantage of multivariate methods such as CCA over univariate methods is that they reveal the linear relationship between all spatial (every electrode) and task-related (every task load level) contrasts simultaneously without introducing multiple comparisons problem or requiring a-priori contrasts.

For two datasets X and Y, CCA identifies pairs of canonical weighting vectors w_x and w_y which produce corresponding linear latent variables l_x = Xw_x and l_y = Yw_y, such that correlation ρ_XY = corr(l_x, l_y) is maximized and orthogonal to any other latent variable pairs. We used CCA to find latent variables that relate either scale-invariance (H) of the 20 electrodes (bottom set of variables in Figure 2A) to the task loads (top set of variables in Figure 2A) or the alpha desynchronization of the 20 EEG electrodes (bottom set of variables in Figure 2B) to the task loads (top set of variables in Figure 2B). Each task load (i.e., set size) was dummy coded as a binary variable, so the number of total latent variables possible was N-1 (i.e., the rank of the smaller set of variables), where N is the number of levels of load in each experiment (N = 4 in experiment 1; N = 3 in experiment 2). Only the primary latent variables in the experiments are shown in the results because no secondary (or tertiary for Exp. 1) latent variables were large enough (ρ_XY > 0.25) in either experiment to be considered meaningful. Small effects, conventionally in the range of r = [0.15 0.25] (Kirk, 2012), are not of interest here because a biomarker with smaller than medium effect size (i. e., r = 0.25) (Kirk, 2012) will likely not have practical utility due to lack of sufficient sensitivity. Each electrode’s or task load’s contribution to the latent variable is represented by the canonical weight of the observed variable which is the Pearson correlation coefficient of that variable with the latent variable. The stability of the latent variables is evaluated by the error bars of the canonical weights on both left and right sets, which are the 95% confidence intervals calculated by bootstrapping the data (3000 samples with replacement) to create distributions for the canonical weights similar to (Kardan et al., 2017). The strength of the association between the two sets in a latent variable is represented by the correlation between the two sides (double sided arrows in Figure 2). As such, the relationship represented in a latent variable is considered strong and stable if the correlation is large (ρ_XY > 0.4) and there is at least one variable in each side (i.e., at least one electrode and one task load) whose weight reliably differs from zero across the bootstrapped samples (i. e., omnibus non-parametric p<0.05).

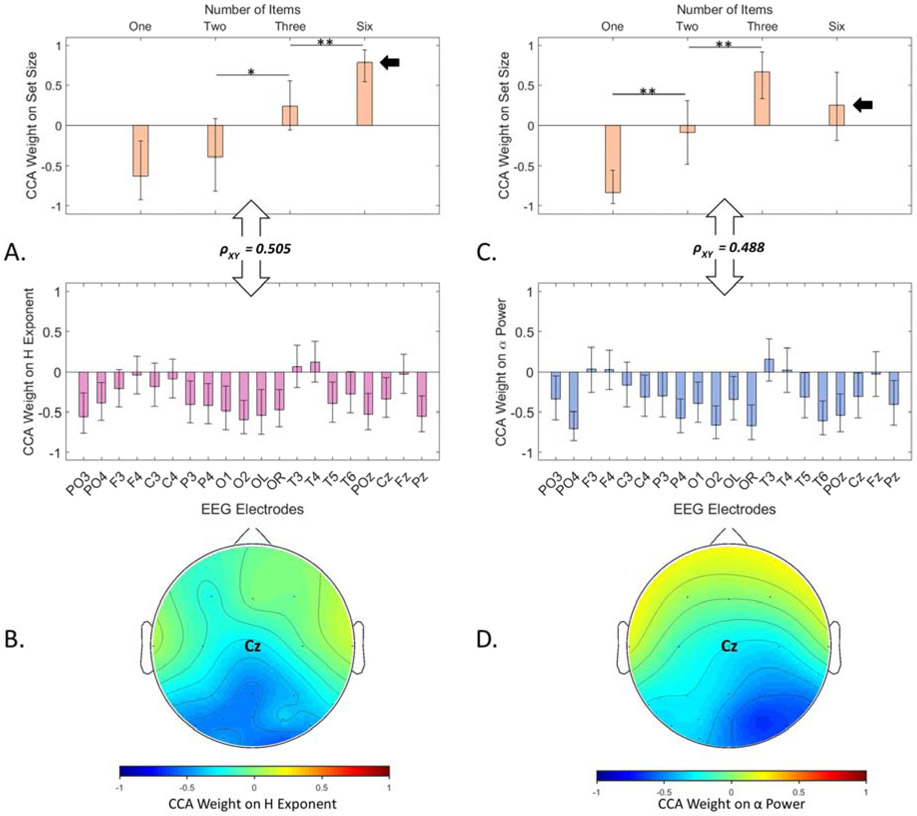
Figure 2.

The primary latent variables of the CCA analysis for the Remember N task in Experiment 1. (A) The primary relationship between scale-invariance (H) of the EEG electrodes during the retention period (pink) with the number of items to remember (orange). The double-headed arrows show the strength of the correlation between the bottom set (electrodes) and the top set (task loads). The vertical axis in each panel shows the contribution of an electrode (bottom) or a specific task load (top) to the latent variable as indicated by the size of its normalized CCA weight. The error bars show bootstrapped 95% confidence intervals around the means for the weights. The asterisks show statistical significance in the difference between weights of adjacent levels of task load (i.e., 1 item to 2 items, 2 items to 3 items, and 3 items to 6 items), *p < 0.05 and **p <0.01. (B) Topographic demonstration of the CCA weights on the H exponent. (C) The primary relationship between the desynchronization of α band power from baseline during the retention period (blue) with the number of items to remember (orange). One-sided arrows demonstrate difference in CCA weight for set size 6 in the relationship between task load and H versus task load and alpha power. (D) Topographic demonstration of the CCA weights on alpha power.

Both α power and H values were z-scored across all trials within each participant to remove baseline differences not related to task conditions in the CCA. Supplementary to the CCA, Tables S1 and S2 show global H values (i. e., average over all electrodes) in each condition before z-scoring for both experiments and provide all univariate pairwise comparisons for conditions using paired t-tests.

Statistical Power

Following our hypothesis regarding relationships between electrode data and set sizes, we simulated the CCA analysis to estimate statistical power for detecting a true correlation between electrodes’ data and a contrast delineating a set size from the other set sizes (e.g., contrast C = [−1 −1 +1 −1] delineates set size 3 in Experiment 1). This was done in 5 steps. First, we generated a random Gaussian variable Norm(0,1) for N levels of set size and 20 electrodes for n participants. Second, to create a true correlation between the generated electrodes data and a set size contrast, we introduced a bias (i. e., a uniformly distributed random variable with an expected value above zero) in the generated electrode data for one set size (chosen randomly). We did this by adding a β_bias * Unif(0,1) to the generated data for that set size and subtracting β_bias * Unif(0,1) from the other set sizes. This produces a difference of β_bias in the expected values of the electrode data for the biased set size compared to electrode data of other set sizes. Third, through trial and error iterations, we found that β_bias = 0.62 induced correlations that closely resembled the minimum effect size of interest (r = 0.25, see CCA analysis). This value of β_bias resulted in true correlations in the range of r = [0.24 0.26] between the set size contrast (i. e., dummy variables coding 1 for the biased set size and −1 for the other set sizes) and the generated electrodes data for Experiment 1. Fourth, we then applied the CCA procedure explained in the previous section³ to the generated data to determine whether the CCA weight for the biased set size in the primary latent variable was found to be significant at α = 0.05. Finally, we repeated step (4) 500 times, with N = 4 and n = 25 to simulate the final sample size for Experiment 1. Statistical power was estimated to be 0.78 by calculating the proportion of times in the 500 runs where the induced correlation was found to be significant in the simulated CCAs.

Experiment 1 Results

The average number of correctly reported items was 0.96 (SD = 0.03) items, 1.84 (SD = 0.13) items, 2.35 (SD = 0.35) items, and 2.29 (SD = 0.44) items for set sizes 1, 2, 3, and 6, respectively. This pattern of performance is consistent with our assumption that working memory capacity in this task would be limited to around 3 items; when the set size increased from 3 to 6 items, the number of correctly reported items did not increase (t = −0.545, p = 0.588, N.S.).

CCA Results for Scale-Invariance

In the Remember N task, the primary latent variable from the CCA showed a strong (R² = 0.254, p < 0.001) and stable relationship (see Figure 2A bottom panel) between the number of to-be-remembered items and the scale-invariance of the EEG signal during retention, where a global decrease in H (especially in occipital and parietal regions, see Figure 2B) tracked increases in task load. Importantly, the decrease in scale-invariance corresponded monotonically to task load, where each load level had a significantly larger canonical weight than the previous one (except for when going from load 1 to 2, perhaps due to both loads being relatively easy). The canonical weights were r₁ = −0.63, r₂ = −0.39, r₃ = 0.24, and r₆ = 0.78 for each set size, respectively. The significant increment from load 3 to 6 (one-sided arrow in Figure 2A top) follows our hypothesis that H is sensitive to the exerted cognitive effort rather than the capacity limits of visual working memory.

CCA Results for α Desynchronization

As shown in Figure 2C, the primary CCA latent variable relating change in α power during the retention period and task load showed a strong and stable relationship (R² = 0.239, p < 0.001) between the two sets of variables. As expected, lower α power in the posterior electrodes (occipital and parietal, see Figure 2D) corresponded to higher task load. The canonical weights were r₁ = −0.83, r₂ = −0.09, r₃ = 0.66, and r₆ = 0.25 for each set size, respectively. Importantly, the correspondence was not monotonic as indicated by the canonical weight for load 6 not being larger than canonical weight for load 3 (in fact it was marginally smaller; non-parametric p = 0.057). Thus, the relationship between alpha power and task load diverged from the monotonic correspondence between H and task load that we reported above. This bifurcation (see one-sided arrows in Figure 2A and C top panels) in the relationship between task load and H versus alpha was statistically significant (Fischer’s Z = 2.66, p = 0.008), supporting our hypothesis that posterior α desynchronization is sensitive to working memory load rather than cognitive effort. Together, the results from the first experiment suggest that working memory load and cognitive effort are distinguishable and can be tracked by alpha band desynchronization versus broad-band characteristics of the EEG signal (H).

Experiment 2 Methods

Participants

A group of 31 participants (ages between 18 to 35, 12 women) were recruited from the University of Oregon and surrounding community (Adam et al., 2018). All participants had self-reported normal or corrected-to-normal visual acuity and normal color vision. All participants gave informed consent and completed the 3-hr session for $30 in compensation. Four participants were excluded from analyses for having fewer than 70 trials per condition on average after artifact rejection (remaining n = 27). After rejection, included participants had an average of 148 trials per condition (SD = 39.5).

Stimuli

Stimuli and procedures were similar to Experiment 1. The key difference was that for this lateralized whole-report task, participants were cued to attend either the left- or right-half of the display before the onset of the memory array. They were asked to remember all items presented in the cued hemifield. The cue was a small pink and green diamond, approximately 0.2° tall by 0.4° wide and was presented 0.4° above the fixation cross. Participants remembered colored squares presented on a medium gray background (RGB = 127.5 127.5 127.5) while maintaining fixation on a small black dot (0.12°). A pool of nine distinct colors: red (RGB = 255 0 0), green (0 255 0), blue (0 0 255), yellow (255 255 0), magenta (255 0 255), cyan (0 255 255), orange (255 128 0), white (255 255 255), and black (1 1 1) were used to choose the colors from in each trial. Each square subtended 1.2° and they could appear anywhere within a portion of the display subtending 7.0° to the left or right of fixation and 5.2° above or below fixation as long as there was a minimum distance of at least 1.5 squares between the centroids of any two squares.

Discrete Whole-Report Task

Each trial began with a blank inter-trial interview (500 ms) followed by the spatial cue (1100 ms) which indicated which side of the screen to attend. After the cue period ended, a memory array containing an equal number of items on both sides of the screen (cued and uncued) was presented for 250 ms. The colors of squares in the memory array were chosen without replacement within each side (i.e., all cued colors were unique but might be repeated on the uncued side of the display). After encoding, participants remembered the items across a blank delay of 1300 ms. At test, a 3×3 matrix of the nine possible colors was presented at the location of each item on both the attended and unattended side. Similar to the Remember N task in Experiment 1, participants were instructed to click the color in each matrix corresponding to the color presented at the location (see Figure 3). The response period ended after participants made a response for all items on the attended side. Participants clicked the mouse to initiate the beginning of the next trial.

Figure 3.

Experiment 2 “Whole-Report” task procedures. At the beginning of every trial participants were given a cue indicating which side of the screen to remember from the upcoming memory array. Memory arrays could contain 1, 3, or 6 items shown in random locations on each side; at response participants only recalled items from the cued side.

Data Analysis and Statistical Methods

Artifact rejection, alpha power analysis, wavelet analysis for H, and the CCA analysis were the same as described in Experiment 1⁴. For statistical power, the parameters of the simulation were set at N = 3, n = 27, and β_bias = 0.60 for Experiment 2, which determined a statistical power of 0.72 for the analysis. The simulation showed that Experiment 2 would have sufficient power (conventionally 0.8) to detect effects only if they are equal to or larger than r = 0.29.

Experiment 2 Results

The average number of correctly reported items was 0.95 (SD = 0.04) for set size 1, 2.41 (SD = 0.33) for set size 3, and 2.53 (SD = 0.53) for set size 6. This, again, indicates that average K was still less than 3 even for 6 items, and was not significantly different from average K for set size 3 (t = 1.129, p = 0.264, N.S.).

CCA Results for Scale-invariance

Replicating the Remember N task, the primary latent variable from the CCA in the lateralized Whole-Report task showed a very strong (R² = 0.416, p < 0.001) and stable relationship between the number of presented items to be remembered in the task and the scale-invariance of the EEG signal during retention (Figure 4A). Again, a global decrease in H tracked increases in the task load. The canonical weights for each set size in this latent variable were r₁ = −0.78, r₃ = −0.13, and r₆ = 0.91, respectively. Importantly, the decrease in scale-invariance changed monotonically with task load, where the canonical weight for each load level was significantly larger than the previous one including from load 3 to 6. This follows our hypothesis that H is sensitive to the exerted cognitive effort in visual working memory tasks.

Figure 4.

The primary latent variables of the CCA analysis for the Whole-Report task in Experiment 2. (A) The primary relationship between the scale-invariance (H) of the EEG electrodes during retention period (pink) with the number of items to remember (orange). The double-headed arrows show the strength of the correlation between the bottom set (electrodes) and the top set (task loads). The vertical axis in each panel shows the contribution of an electrode (bottom) or a specific task load (top) to the latent variable as indicated by the size of its normalized CCA weight. The error bars show bootstrapped 95% confidence intervals around the means for the weights. The asterisks indicate statistical significance in the difference between weights of adjacent levels of task load (i.e., 1 item to 2 items, 2 items to 3 items, and 3 items to 6 items), where *p < 0.05 and **p <0.01. (B) Topographic demonstration of the CCA weights on the H exponent. (C) The primary relationship between the desynchronization of α band power from baseline during retention period (blue) with the number of items to remember (orange). (D) Topographic demonstration of the CCA weights on alpha power.

CCA Results for α Desynchronization

The primary CCA latent variable relating change in α power and task load was not stable, as the 95% confidence intervals for all of the electrodes contained zero (Figure 4C bottom). The task load levels were not significantly different from one another (Figure 4C top), although there was a numerical trend of suppression of α power for 6 items compared to 1 item. Thus, the relationship between task load and alpha power did not follow the pattern we observed in Experiment 1. However, since the latent variable was not stable, the canonical correspondence for α suppression in this experiment was not conclusive with regards to our hypothesis about distinguishing working memory load from cognitive effort.

Discussion

In this study we proposed a model for measuring cognitive effort via scale-invariance of brain activity. We conceptualized effort as the process of overcoming the cost of departure from automaticity or rest (Shenhav, 2017), and operationalized such departure as the degree of H suppression in EEG. H is a useful candidate for investigating effortful states because scale-free activity patterns are an emergent property of a network at a critical state. Therefore, we hypothesized that the degree of suppression of H signified the degree of departure from default-state criticality of the brain as the brain tunes to a specific (non-automatic) task. When H is not suppressed, small perturbations can lead to large changes in brain state (Chialvo, 2004), thereby enabling rapid adaptability to heterogeneous external demands (Gisiger, 2001). But when disproportionate allocation of resources to a specific cognitive task is required, this susceptibility is sacrificed as brain networks move further away from this critical state. In other words, a departure from criticality represents a change from a more flexible to a more engaged brain state. Our results supported this hypothesis, as we found a monotonic correspondence between H suppression and task load across two experiments. This is the first reported evidence for changes in scale-invariance due to task difficulty as measured with EEG (a relatively high frequency signal), complementing previous research relating H suppression of BOLD activity (a very low frequency signal) to task difficulty (Churchill et al., 2016).

To determine whether there is more to cognitive effort than working memory load (Heitz, Schrock, Payne, & Engle, 2008), we compared the relationship between H and task load to the relationship between α suppression and task load within individuals. We found that, whereas the number of recalled items and the degree of α suppression (indicating working memory load) hardly increased after intermediate task difficulty levels (in other words, both nearly plateaued after K), H continued to increase with task load beyond working memory capacity. This suggests that H is more sensitive to neural processes associated with task difficulty than with overt performance. Consequently, by showing a neurobiological dissociation between cognitive effort and the amount of information available for manipulation in working memory, our results support the theoretical account of cognitive effort that distinguishes it from information in working memory. In other words, there is a difference between effort and working memory load and individuals can exert seemingly “fruitless” cognitive effort.

Unlike α suppression, the differences in the task design of the two experiments did not change the behavior of H with regards to task load. Specifically, the differences in the experimental designs could test if certain aspects of the tasks such as: (1) the inhibition of the distracting information, (2) the number of internal representations, or (3) the perception of items or their iconic memory traces is responsible for the suppression of scale-invariance. In the Remember N experiment when participants were cued to only remember one item, the other five items on the screen were essentially distractors. If scale-invariance was primarily driven by inhibition of irrelevant information, the relationship between set size and H should have been in the opposite direction between the two experiments, since the greatest amount of suppression of irrelevant information is required in set-size 1 trials in Experiment 1 (five distractors) and set-size 6 in Experiment 2 (six distractors). If H was modulated by the number of internal representations, its behavior would be similar to α power (Foster et al., 2019), i.e., it would plateau beyond ~3 items. Finally, if H was modulated by the visual display imbalance between the different set sizes (or a form of iconic memory trace), then we should have only seen a correspondence between scale-invariance and set size in the whole-report task (Experiment 2) and not in Experiment 1 since the number of items on the screen was constant in Experiment 1(6 items were always shown).

Importantly, the scale-invariance of EEG signals in our experiments is a broad-band characteristic of the signal that is directly related to the proximity of the brain to a critical state and was not driven by changes in any particular narrow-band signals. Even though H is (anti)correlated with narrow-band oscillations such as theta, alpha, and beta band power of the EEG signal (see supplementary Figure S2), its relationship with task difficulty was not driven by any of these specific narrow-band oscillation correlates (regarding cognitive tasks modulating beta and theta oscillations see (Engel & Fries, 2010; Sederberg, Kahana, Howard, Donner, & Madsen, 2003). We demonstrated this by applying CCA to investigate the correspondence between theta (4-7 Hz) as well as beta (13-30 Hz) band powers of the electrodes with the set sizes in both experiments similar to the analyses done for α and H. Neither theta nor beta band powers mimicked H suppression’s relationship with set size (see supplementary results: CCA for theta and beta bands). Even though it is the case that one needs to examine the broad-band signal to get the effects in the CCA analyses presented in this study, it is important to make clear that we are not claiming that there are no narrow-band analyses that can track task load levels; we are only arguing that our H results here are not driven by a specific narrow band. We think it is important to show that because our theoretical framework is based on shifts in scale-invariance of brain activity and estimating changes in brain state; and not on theories related to particular oscillatory components.

While H is systematically reduced with task complexity, without a measure of subjective effort, it is not clear that H suppression reflects volitional effort. However, before moving on to discussion of alternative accounts and counter arguments for them, it should be noted that part of this work’s motivation is to argue for a different perspective on how we could conceptualize cognitive effort based on deviations from default scale-free brain states. In this view, we do not argue for loss of brain criticality (H suppression) as a way of approximating subjective effort ratings, rather we see H suppression and subjective effort rating as complementary ways of observing an effortful state. As such, we think that in the same way that physical effort or stress could be measured with self-reported ratings or by more objective estimates (e. g. muscle and cardiovascular load, and cortisol levels), cognitive effort as a latent variable could also be evaluated through complementary but not redundant measures including self-reported ratings of subjective effort and/or measures of criticality in brain networks as quantified with H. Nevertheless, it is highly important for future studies to examine the strength of relationship between subjective cognitive effort and H suppression of brain activity. For instance, previous studies have shown only modest correlations between subjective and objective estimates of physical exertion (Jakobson et al., 2013), or stress (Van Eck & Nicolson, 1994).

There are some limitations and caveats in our study that should be discussed. At the core of all of the limitations mentioned in the next three paragraphs is the fact that we interpreted task complexity as being directly related to cognitive effort in this dataset. While a more difficult task does not necessarily guarantee the exertion of more cognitive effort from participants, below we argue that it was likely the case in these studies that participants exerted more effort with increasing task load. However, future work, which includes subjective measures of effort will obviate the need for post-hoc arguments.

First, the current studies were not designed to ensure that participants were motivated to modulate their effort exertion as a function of task load (e.g., through monetary incentives). In particular, one could argue that participants did not behave differently between set size 3 and 6 trials as reflected by equivalent performance levels between the two conditions. To investigate this, we calculated the Hurst exponent from the ‘remember-3’ trials of the remember-N task in which participants were able to remember 3 items (i.e., participants had to remember 3 out of the 6 presented items and they successfully did so; we refer to these as 3/3 trials), and compared these with the Hurst exponent from ‘remember-6’ trials in which participants were able to remember 3 items (i.e., participants had to remember 6 out of the 6 presented items and they only succeeded in remembering 3; we refer to these as 3/6 trials). This analysis was performed to directly assess that participants were, at the very least, doing something different between remember 6 vs. remember 3 trials even when the amount of successfully maintained information was exactly equal within the same individual with equated visual stimulation (the number of presented items on screen is always 6 in this task). We found a significant global (averaged over all electrodes) decrease in H in the 3/6 trials (Mean = 1.00, SD = 0.151) compared to the 3/3 trials (Mean = 1.04, SD = 0.136) within participants (paired t-test, t(24) = −3.61, p<0.01), suggesting that trials with extra to-be-remembered items were treated differently by the participants in a manner that is detectable with H suppression. We interpret this difference in H as a cognitive effort signal, where participants were exerting more effort in the 3/6 trials compared to the 3/3 trials because they were trying to remember more items (i.e., they are supposed to remember all 6), but they were unable to. It is important to reiterate that in both cases participants stored the same amount of information, i.e., 3 items, and had the same amount of visual information on the screen, i.e., 6 items.

Second, H suppression could be explained by other factors that scale with task complexity but are not directly related to cognitive effort (i. e. only indirectly related to cognitive effort). These factors could include fear of failure or stress / anxiety (Cohen, 2011; Eysenck, 1985). First, since success in the whole-report and the remember-N tasks is not binary, fear of failure is less likely to be applicable to these tasks. For example, achieving a performance of 3 is still partial success in a remember-6 trial. In that sense, there are very few complete failures in the task (i.e., participants rarely get 0 correct). Second, we would argue that participants were likely neither underperforming due to stress nor giving up due to the extra task demands, since performance did not drop for the “remember 6” condition compared to the “remember 3” condition in either experiment (in both cases, people successfully recalled around 2.5 items). A potential caveat, however, is that there may be a cost-free form of stress such that the increased stress is not detrimental to performance but causes H suppression, hence H could be not scaling with effort but with a cost-free form of stress.

One final piece of evidence to support our argument that H suppression is related to cognitive effort as opposed to task difficulty or a benign form of stress comes from its relationship with performance when external task difficulty is held constant. We analyzed data from (Adam, Robison, & Vogel, 2018) in which participants performed the whole-report task (same as in Experiment 2) with the set size held constant at 6 items (see supplementary section Repeated set-size 6 whole-report task for details). This provided us with a larger sample size and enough trials to compare the Hurst exponent in ‘lower’ performance trials (fewer than 3 items remembered) with H in ‘higher’ performance trials (more than 3 items remembered) within the same task difficulty level (i.e., all load 6). We found that global H during the maintenance interval was lower for high performance trials (Mean = 1.02, SD = 0.158) compared to low performance trials (Mean = 1.16, SD = 0.185) within participants (paired t-test, t(33) = −5.27, p<0.01). This relationship between H suppression and performance within the same level of task difficulty suggests that decreased H is likely related to exerting beneficial cognitive effort rather than being a detrimental stress signal that we would hypothesize would either hurt performance or not affect it at all.

Because of the limitations discussed above, future work will be necessary to further delineate the relationship between subjective cognitive effort, external factors like stress and motivation, and cognitive load. Important future directions include: 1) having more levels of difficulty, 2) having other types of cognitive tasks, 3) recording self-report measures of subjective effort, and 4) manipulating levels of reward to alter motivation levels. Factors such as motivation, fatigue, stress, and arousal could interact with both subjective effort and successful task performance (Esterman & Rothlein, 2019), and it will be important in future work to independently manipulate the contribution of each factor to task performance and subjective cognitive effort. For example, higher levels of motivation and/or lower levels of fatigue could increase the participants’ tolerance for expending cognitive effort without greatly affecting working memory capacity (see Bonner & Sprinkle, 2002; Botvinick & Braver, 2015). Along these lines, previous research has shown that self-reported fatigue due to physical burdens, such as chemotherapy treatment and chemotherapy recovery, could disrupt brain function in a manner that is unrelated to objective working memory performance (Kardan et al., 2019). Moreover, such physical burdens in this cohort have been shown to alter the scaling properties (i. e., H) of fMRI timeseries (Churchill et al., 2015). To shed light on these issues, an experimental design with multiple levels of task loads both below and above working memory capacity could be fully crossed with low vs. high reward conditions. In such an experiment, participant’s subjective effort and motivation in some trials could be collected via infrequent experience sampling to be used in conjunction with the neural measures used here. With this experiment one could test if H suppression is 1) correlated with subjective effort and 2) tracks more levels of task load beyond capacity for the high reward condition compared to the low reward condition. In other words, if H suppression plateaus or decreases for high task loads when motivation is low but increases (i.e., more H suppression) with high task loads when motivation is high, that would mean that the H suppression model of effort is a robust indicator of effortful states and that the maximum tolerance for H suppression is dictated by motivation (unlike the maximum capacity of working memory).

In conclusion, we used the time scale-invariance characteristic of the EEG signal (H) to dissociate visual working memory load from the cognitive effort exerted for the task at hand. Our work further demonstrates the utility of H as a neuromarker of cognitive effort. These results have theoretical implications for research on motivation and cognitive fatigue, as they support our theoretical framework of modeling an effortful state as departures from the brain’s self-organized criticality at rest. Additionally, we ruled out interpretations of cognitive effort that equate it with the information in working memory by providing evidence that scale-invariant brain activity can be suppressed further than indicators of working memory load.