Simulating the SARS outbreak in Beijing with limited data

Abstract

We propose a mathematical model to simulate the SARS outbreak in Beijing. The model consists of six subpopulations, namely susceptible, exposed, quarantined, suspect, probable and removed, as China started to report SARS cases as suspect and probable separately from April 27 and cases transferred from suspect class to probable class from May 2. By simplifying the model to a two-compartment suspect-probable model and a single-compartment probable model and using limited data, we are able to simulate the SARS outbreak in Beijing. We estimate that the reproduction number varies from 1.0698 to 3.2524 and obtain certain important epidemiological parameters.

1. Introduction

Atypical pneumonia, called fei dian in Chinese, was first reported in Guangdong Province, China in November of 2002 (WHO, 2003a). As of February 11, 2003, there were 305 atypical pneumonia cases (105 were health workers) and five related deaths in Guandong Province.3 Despite the urgent announcements and warnings issued by the Health Department of the Guandong Province in late January,4 very quickly the emerging disease spread to some other regions in Mainland China as well as Hong Kong, Singapore, Vietnam, Canada, etc. In March of 2003, the World Health Organization, for the first time in its history, issued a globally warning about the disease (WHO, 2003a) and officially defined the disease as severe acute respiratory syndrome (SARS) (WHO, 2003d). In late June of 2003, the disease was under control globally, but it had spread to 32 countries and regions causing about 800 deaths and more than 8000 infections (WHO, 2003e).5

The first SARS cases in Beijing were reported in early March, 2003.6 Compared with the outbreaks in Hong Kong, Singapore, Vietnam and Toronto, in mid April the WHO Beijing team estimated that Beijing may have had as many as 200 cases of SARS, rather than the 37 officially reported cases (WHO, 2003c) and recommended that Beijing improve its reporting system. On April 20, the Health Minister of China and the Mayor of Beijing City were surprisingly removed from their posts.7 On April 21, China's State Council Information Office reported that Beijing had 339 confirmed (probable) and 402 suspected SARS cases.8 Since then China has reported public information about SARS cases on a daily and more accurate basis (Ministry of Health of P. R. China, 2003).

In late April and May, Beijing became the hardest hit city in the world with the most probable SARS cases. After a vigorous campaign to combat the spread of SARS, such as closing schools, theaters, Internet cafes and other recreational centers, creating the first SARS-only hospital, Beijing Xiaotangshan Hospital,9 and quarantining more than 30,000 exposed individuals,10 the outbreak of SARS in Beijing was under control in June. On June 24, Beijing was removed from the WHO SARS list. By then there had been 2521 probable cases and 191 deaths (WHO, 2003e; Ministry of Health of P. R. China, 2003).

It has been recognized that a coronavirus is responsible for SARS (Drosten et al., 2003; Ksiazek et al., 2003; Peiris et al., 2003; WHO, 2003b). Although its transmission modes are not completely known, droplets and contacts appear to be the predominant transmission modes. The cases at universities and hospitals in Beijing suggest that airborne transmission is also possible. Since there are no valid medicines or vaccine for SARS, measures to control the spread of SARS have taken two major forms: isolation of symptomatic individuals and quarantine and close observation of asymptomatic individuals (WHO, 2003f).

Mathematical models have recently been used to examine the transmission dynamics and model the control of SARS in Hong Kong (Chowell et al., 2003; Riley et al., 2003), Singapore (Chowell et al., 2003; Lipsitch et al., 2003) and Toronto (Chowell et al., 2003). The objective of this paper is to study the transmission dynamics of the spread of SARS in Beijing at the population level. As China started to report SARS cases as suspect and probable separately from April 27 (Ministry of Health of P. R. China, 2003) following the WHO definitions (WHO, 2003d), we classify the population of Beijing into six classes, namely susceptible (S(t)), exposed (E(t)), quarantined (Q(t)), suspect infective (I _s(t)), probable infective (I _p(t)) and removed (R(t)). It is assumed that individuals in the E class are exposed to SARS virus but not isolated from the community and individuals in the Q class are isolated from the community.

We first propose a deterministic model consisting of the six components, which is a system of six ordinary differential equations with various parameters modelling the feature of SARS transmission. However, unlike the SARS outbreaks in Hong Kong, Singapore and Toronto, which have been well studied and for which detailed data are available in the literature (see Donnelly et al., 2003; Lee et al., 2003; Tsang et al., 2003 for Hong Kong; Lipsitch et al., 2003 for Singapore; Booth et al., 2003; Poutanen et al., 2003 for Toronto) so that parameter values can be estimated from these reports, so far there have been few published reports about the SARS outbreak in Beijing. Moreover, the data about Beijing are very limited (Ministry of Health of P. R. China, 2003; WHO, 2003e), with only the daily suspect cases, probable cases (including number of cases transferred from previously reported suspect cases), cleared suspect cases, number of patients released from hospitals, and deaths given (see Table 1). Because of the limitation of the data, we simplify the general model to two simpler models. The first is a two-component model consisting of only the suspect infectives (I _s(t)) and the probable infectives (I _p(t)). The daily suspect and probable cases will be regarded as the inputs, the cleared suspect cases will be the output for I _s(t), the number of SARS patients released from hospitals plus the deaths will be the output for I _p(t). The model also include a term representing the cases transferred from I _s(t) to I _p(t). The second is a one-compartment model for the probable variable I _p(t) only. We will use the data in Table 1 to model the input, output and transmission terms. Then we use the mathematical models to make predictions of future incidence and to simulate the impact of additional control strategies.

Table 1.

Daily reported cases (Ministry of Health of P. R. China, 2003) of the suspect, probable (cumulative minus recovered and death), transfer from suspect to probable, cleared suspect, and removed probable (recovered plus death, numbers in brackets represent death) in Beijing from April 27 to June 10

Date	4/27	4/28	4/29	4/30	5/1	5/2	5/3	5/4	5/5
Suspect	1191	1275	1358	1408	1415	1468	1493	1537	1510
Probable	980	1062	1198	1275	1371	1436	1530	1585	1673
Transfer	50	37	49	31	40	48	48	26	58
Cleared						44	31	20	34
Removed	10(8)	3(3)	12(7)	16(9)	17(7)	18(9)	11(5)	7(4)	6(3)
Date	5/6	5/7	5/8	5/9	5/10	5/11	5/12	5/13	5/14
Suspect	1523	1514	1486	1425	1397	1411	1378	1338	1308
Probable	1719	1798	1872	1895	1936	1959	1972	1969	1979
Transfer	37	57	57	28	24	21	39	34	18
Cleared	30	49	51	87	49	16	42	41	63
Removed	17(4)	10(3)	13(2)	18(2)	9(2)	15(4)	26(9)	46(5)	13(5)
Date	5/15	5/16	5/17	5/18	5/19	5/20	5/21	5/22	5/23
Suspect	1317	1265	1250	1250	1249	1225	1221	1205	1179
Probable	1991	1991	1968	1955	1938	1895	1841	1770	1723
Transfer	12	22	13	8	4	10	7	11	14
Cleared	20	73	43	24	24	31	31	27	29
Removed	6(1)	17(1)	38(4)	27(2)	20(3)	50(4)	54(2)	83(2)	56(2)
Date	5/24	5/25	5/26	5/27	5/28	5/29	5/30	5/31	6/1
Suspect	1134	1105	1069	1005	941	803	760	747	739
Probable	1660	1628	1589	1512	1473	1413	1337	1253	1217
Transfer	24	10	4	7	0	3	5	1	1
Cleared	40	35	52	68	79	141	44	18	11
Removed	88(3)	41(4)	44(1)	85(4)	41(3)	63(1)	79(1)	85(4)	37(0)
Date	6/2	6/3	6/4	6/5	6/6	6/7	6/8	6/9	6/10
Suspect	734	724	718	716	713	668	550	451	351
Probable	1184	1152	1078	1020	936	893	795	685	591
Transfer	0	2	0	0	0	0	0	0	0
Cleared	11	10	8	3	5	47	118	99	100
Removed	33(0)	32(0)	74(0)	58(0)	84(2)	43(0)	98(1)	110(0)	94(2)

2. The general model

Let f _rs(I _s(t)) denote the removal rate of the suspected infective individuals at time t, fsp(Is(t)) the transition rate from suspect class to probable class at time t, f _rd(t,I _p(t)) the sum of the removal rate and the death rate of the probable infective individuals at time t. Statistics show that some individuals who are infectious are not quarantined at Beijing partially because some infective individuals in hospitals failed to report some of their close contacts for various reasons. These individuals are the sources for the spread of SARS outside the quarantined sites. Further, the data (Ministry of Health of P. R. China, 2003) show that the valid contact rate of SARS in Beijing depends on the numbers of infected individuals. One of the reasons is that the people in Beijing have been taking various protection measures such as reducing social activities, using mouth-masks, strengthening immune functions, etc.

Let λ(I _p) denote the valid contact rate of SARS at Beijing. Then the transition rate from the S compartment to the E compartment is f _se≔λ(I _p)(lI _p/(S+E+R+lI _p))S, where l is the fraction of probable infectives who can transmit the disease. The quarantine rate for the E class is q (see the flow diagram in Fig. 1). k ₀₁ and k ₀₂ are fractions of the transition rates from E to I _s and from E to I _p, respectively. k ₁ and k ₂ are fractions of the transition rates from Q to I _s and from Q to I _p, respectively. k ₃ is the fraction of the transition rate from Q to S. Using Fig. 1, we have the model

(2.1).

dSdt=−λ(Ip)lIpS+E+R+lIp S+k3Q+frs(t,Is),

dEdt=λ(Ip)lIpS+E+R+lIp S−(q+k01+k02)E,

dQdt=qE−(k1+k2+k3)Q,

dIsdt=k1Q+k01E−frs(t,Is)−fsp(t,Is),

dIpdt=k2Q+k02E+fsp(t,Is)−frd(t,Ip),

dRdt=frd(t,Ip).

Fig. 1.

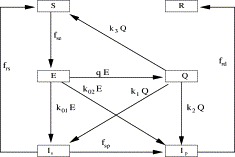
The schematic flow diagram for the general model consisting of susceptible (S), exposed (E), quarantine (Q), suspect (I_s), probable (I_p) and removed (R) classes.

3. The simplified models

In order to use valid data, we simplify (2.1) into two submodels. The first is a two-compartment model for I _s and I _p and the second is a scalar equation for I _p only.

3.1. The suspect-probable model

Our purpose is to consider the dynamics of suspect and probable cases. Note that the first two terms in the right-hand side of the fourth equation (i.e. the I _s equation) of (2.1) represent the net flow rate from the E and Q compartments to the I _s compartment (because of the I _p). Let us denote this input rate by f ₀. To fit this function and others, we set April 26, 2003 as time zero and take days as time units. Thus, April 27, 2003 is the first day, April 28, 2003 is the second day, etc. Then, we use the curve-fitting package (cftool) from Matlab 6.5, in which polynomial, exponential, power, rational, Weibull, Gaussian and Custom equations can be chosen and certain techniques can be used to fit data according to the mean-square error (MSE). By analysing the SARS data for Beijing from April 27 to June 10, 2003 (see Table 1), we can see that it can be approximated by a function a(I _p)I _p, where (see Fig. 2)

a(Ip)=−0.1257Ip(t)/980+0.2712if 1⩽t⩽17,0.0195(Ip(t)/1979)3.478if 18⩽t⩽45. (3.1)

Fig. 2.

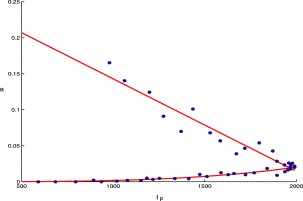
The graph of a(I_p) versus I_p, where the dots represent f₀/I_p specified by the data in Table 1.

For the transition rate from the I _s class to the I _p class, using the data from April 27 to June 10 of 2003 in Table 1, the rate can be approximated by b(t)I _s(t), where (see Fig. 3)

b(t)=0.04296 exp(−0.05858t). (3.2)

Fig. 3.

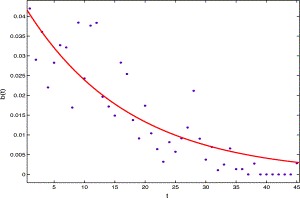
The per capita transition rate from I_s class to I_p class versus time t, the solid line is b(t) and the dots represent the data from Table 1.

Similarly, the clear rate f _rs of the suspect class can be approximated by a function e(t)I _s(t), where (see Fig. 4)

e(t)=0.03092,1⩽t⩽20,0.000853t2−0.0402t +0.4942,20⩽t⩽34,0.005946(t−34)2−0.0456t+1.63125,34⩽t. (3.3)

Fig. 4.

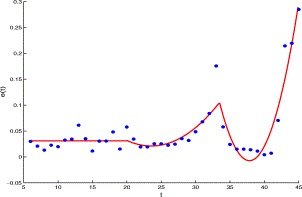
The per capita clear rate of the suspect versus time t, the solid line is made from e(t) and the dots represent the data from Table 1.

Let D denote the first two terms of the right-hand side in the fifth equation (i.e. the I _p equation) of (2.1). Then D represents the net flow rate at which individuals enter the I _p compartment directly from the E and Q compartments (which depends on I _p). By the curve-fitting method, we obtain (see Fig. 5)

D(Ip)=(−0.06881Ip(t)/980 +0.1461)Ip(t),1⩽t⩽17,5.678(Ip(t)/1979)6.644,18⩽t⩽45. (3.4)

Fig. 5.

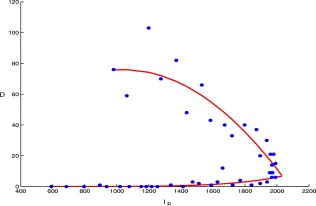
The direct transition rate from the E and Q compartments to I_p compartment versus I_p, the solid line is made from D(I_p) and the dots are plotted using the data in Table 1.

For the removal rate of the probable class (recovered plus death), using the data from April 27 to June 10 in Table 1, we can see that it can be approximated by a function c(t)I _p, where (see Fig. 6)

c(t)=0.00367(t/10)5−0.03791(t/10)4+0.1384(t/10)3−0.2063 (t/10)2+0.01156 t−0.007672, 1⩽t⩽45. (3.5)

Fig. 6.

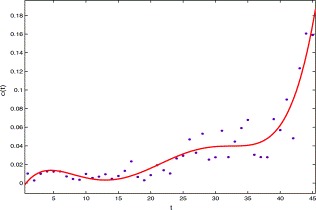
The graph of the per capita removal rate of probable class versus time t, the solid line is made from c(t) and the dots are made from the data in Table 1.

Summarizing the above discussions, we obtain the simplified two-compartment suspect-probable model

(3.6).

dIsdt=a(Ip)Ip−b(t)Is−e(t)Is,

dIpdt=D(Ip)+b(t)Is−c(t)Ip.

3.2. The probable model

First, note that the first three terms in the right-hand side of the I _p equation in (2.1) represent the net flow rate from the E, Q and I _s compartments to the I _p compartment (which caused by I _p). If we denote this input rate by u, by analysing the data in Table 1, we can see that it can be approximated by a function β(I _p)I _p, where

β(Ip(t))=−0.09589Ip(t)/980 +0.2164,1⩽t⩽19,0.01029(Ip(t)/1991)2.842,20⩽t⩽45, (3.7)

where April 27 is specified as t=1 (see Fig. 7).

Fig. 7.

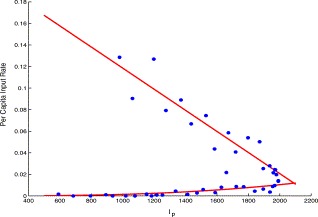
The per capita input rate of probable individuals to I_p compartment versus I_p, the solid lines represent β(I_p) and the dots are plotted using the data in Table 1.

The transmission rate β reflects the protection measures at two stages. At the first stage, people took protection measures such as reducing social activities, wearing mouth-masks, strengthening immune system, etc. The rate is a linear decreasing function of the number of infected individuals, because the more infectious individuals there are the more frightened the society is, so that more severe measures are taken. The second stage coincides with the period of keeping maximal protection measures. In this period, all the main protection measures have been performed, and its intensity stays invariant so that the rate mainly depends upon the number of infectious individuals. Furthermore, from Fig. 7 we can see that the values of β(I _p) is quite low at the second stage, which implies that the disease can be eradicated.

The rate of removal and death for the probable class is same as c(t)I _p (see Eq. (3.5) and Fig. 6). Hence, the I _p equation in (2.1) is reduced to

dIpdt=β(Ip)Ip−c(t)Ip, 1⩽t. (3.8)

4. Simulations

4.1. The suspect-probable model

Using the suspect-probable model (3.6) and choosing April 27 as an initial point (t=1), the computer simulations are given in Fig. 8 for suspect I _s.

Fig. 8.

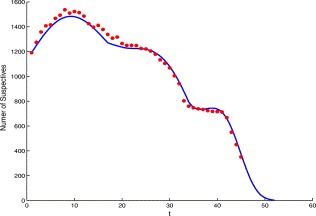
Comparison of the simulation result (solid curve) from the suspect-probable model (3.6) and the reported data (dotted curve) from Table 1 of the suspect SARS cases, I_s.

Let us now change the initial data from Is(1)=1191, Ip(1)=980 to Is(1)=0, Ip(1)=1, that is, we assume that Beijing was completely susceptible and only one probable member was introduced into on April 27. Then by keeping the parameter values in (3.6) unchanged, numerical calculations from (3.6) show that there will be 16 suspected individuals on the 17th day. Furthermore, if we let

a(Ip)=−0.1257Ip(t)/980+0.2712, 1⩽t,

D(Ip)=(−0.06881Ip(t)/980+0.1461)Ip(t), 1⩽t,

that is, we keep the per capita suspect input rate and the direct transition rate from the E and Q compartments to I _p compartment after the 17th day as the same as those before the 17th day. Basically, this means that intervention measures are not maintained. Now keep c(t), b(t) and e(t) unchanged and take I _s(1)=0,I _p(1)=1. Then there will be 418 suspect individuals when t=43. This indicates the importance of maintaining intervention measures.

4.2. The probable model

The probable model (3.8) fits the data well (see Fig. 9), where we fixed c(t)=0.1491 for t⩾45, which was obtained by fitting the data after 45 days.

Fig. 9.

Comparison of the simulation result (solid curve) using the probable model (3.8) and the reported data (dotted curve) from Table 1 of the probable SARS cases, I_p. Here I_p(1)=980.

We now consider the reproduction number for the SARS outbreak in Beijing. Since the exact infection period is not clear at this moment, which is crucial for the computation of the reproduction number, we look for an estimation. We claim that the mean infection duration of probable individuals varies from 5 to 16. The lower bound 5 is obtained from the study by Donnelly et al. (2003) in which it was reported that the mean time from the onset of clinical symptoms to the admission to hospitals is about 5 days. If there is no risk to transmit the disease by a probable individual quarantined in a hospital and the transmission occurs only in the time interval from the onset of clinical symptoms to the admission to a hospital, the five days can be used as a lower bound for the infection duration. The upper bound 16 is derived from Zhong (2003) in which it was reported that “few probable individuals are infectious at the onset of symptoms, the infectiousness of probable individuals increases as the infected process develops, the maximal infection force occurs with highest temperature and heavy coughing in the second week and then falls quickly as the temperature decreases”. Now assume that the infection force is equally distributed in the time interval from the onset of symptoms to the 16th day. From the expression of c(t), we can see that the expectation that an infective stays in I _p compartment is 4.9436 during the first 5 days and 15.0298 during the first 16 days. By the standard method for the calculation of the reproduction number (see, for example van den Driessche and Watmough, 2002), we can see that a reasonable estimation for the reproductive number is 1.0698⩽R ₀⩽3.2524.

Suppose that β(I _p) defined in (3.7) is valid for all t⩾1. If we take c(t) as defined in (3.5) for 1⩽t⩽45 and c(t)=0.1491 for t>45, which is the mean value of the per capita removal rate of probable individuals from April 23 to June 21, and choose an initial value as I _p(1)=1 in (3.8), then we have the dynamical behavior shown in the left picture of Fig. 10. From the figure, we can see that there will be 41 infective individuals when maximal control measures are taken if we introduce one infectious individual into a completely susceptible population in Beijing. Moreover, that figure shows that the number of infective individuals returns to 1 after 61 days and dies out as time evolves thereafter.

Fig. 10.

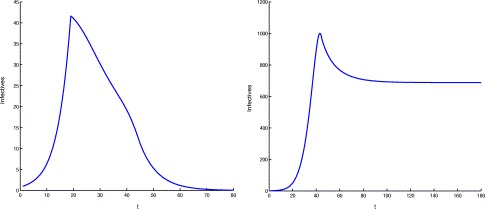
The computer simulations of probable cases when one infectious individual enters a completely susceptible population. The left figure shows the dynamics when protection measures are taken and the maximal control measures are maintained, while in the right one the maximal control measures were not maintained.

Now suppose that the infection force from the first stage always takes effect, i.e. we take β(I _p)=−0.09589I _p(t)/980+0.2164 for t⩾1. This means that the maximal control measures were not maintained. If we keep all others unchanged as the case in previous paragraph, then the disease can spread quickly (see the right graph in Fig. 10). In this case, the disease will be persistent at a level of 688 infective individuals and there will be 1000 infective individuals on the 43th day. Furthermore, if we replace the transmission rate by β(I _p)=−0.0958kI _p(t)/980+0.2164 for t⩾1, where k represents the intensity of protection measures, numerical calculations show that the disease can be persistent at a level of 14 infectives and there will be 35 infective individuals on the 36th day even though k=50. This indicates the necessity of maintaining the maximal control policies for a suitable period of time in order to eradicate the disease.

To learn more about the mechanism of controling the disease successfully in Beijing from the point of view of modelling, we suppose that the SARS disease can activate for a long time and take c(t) as its mean value 0.03349 in first the 45 days. Then, Eq. (3.8) can be partitioned into two equations

dIpdt=Ip(−0.09589Ip(t)/980+0.2164)−0.03349Ip (4.1)

and

dIpdt=0.01029(Ip(t)/1991)2.842Ip−0.03349Ip. (4.2)

Eq. (4.1) has an endemic equilibrium I _p=1869.35 which is globally stable. For Eq. (4.2), there is an endemic equilibrium Ip∗=3015.8 which is unstable. Furthermore, I _p(t) decreases to zero as t evolves if Ip(0)<Ip∗, and increases as t evolves if Ip(0)>Ip∗. If protection measures are merely used and the intervention policies are not adopted, then only (4.1) takes effect. It follows that the disease can be persistent at a level of 1869 probable individuals when t is large. Furthermore, if the intervention measures are implemented so late that the probable numbers are greater than 3016, then the above analysis shows that the disease will be persistent. This again shows that it is important to perform strong intervention measures before the number of infectives reaches Ip∗.

5. Discussion

There have been a few published reports on studying the transmission dynamics of SARS in Hong Kong, Singapore and Toronto (Chowell et al., 2003; Lipsitch et al., 2003; Riley et al., 2003), but so far there are few published scientific reports about the transmission dynamics in China (Wang and Zhao, 2003; Zhou et al., in press), where the virus was originally found. Beijing, the hardest hit city in the world with the most SARS cases, had already been removed from the WHO SARS list in June 2003. However, questions and mysteries about spread, reporting and treatment of SARS in Beijing remain. One of the fundamental questions is that how many of the reported suspect SARS cases were indeed probable cases and how the suspect individuals affect the transmission of the disease.

In this study, we proposed a mathematical model to simulate the SARS outbreak in Beijing. Differing from the SARS models in Chowell et al. (2003), Lipsitch et al. (2003) and Riley et al. (2003), our model consists of six subpopulations, namely susceptible, exposed, quarantined, suspect infectives, probable infectives and removed. By simplifying the model to a two-compartment suspect-probable model and a single-compartment probable model and using limited data, we are able to simulate the SARS outbreak in Beijing. We estimated that the reproduction number varies from 1.098 to 3.2524 and obtained certain important epidemiological parameters. The basic reproduction number R ₀ is defined as the expected number of secondary cases produced in a completely susceptible population by a typical infective individual. This quantity determines the potential for an infectious agent to start an outbreak (Anderson and May, 1991; Brauer and Castillo-Chavez, 2000; Diekmann and Heesterbeek, 2000). We found that the incidence rate has the characteristic of two stages. The first stage is the process of taking protection measures and quarantine policy and the second stage coincides with the process of maintaining control measures. Our study showed that it is necessary to implement the maximal control measures in the second stage for a certain period in order to eradicate the disease. Furthermore, the control measures in the second stage should be implemented before a threshold for the number of probable cases is reached.

The Chinese health professionals have substantial experience with a variety of anti-viruses, antibiotics, Chinese herbal medicines, and corticosteroids, and with using assisted ventilation in the treatment of SARS patients (Breiman et al., 2003; Zhong and Zeng, 2003). The SARS outbreak in Beijing shows that better and careful surveillance of suspected cases, rapid and accurate reporting of infected cases, transparent communication with the public about the disease, rigorous application of knowledge through public health measures are effective in fighting emerging infectious disease. Delaying reporting and implementation can result in disastrous public health consequences.

As more clinic and epidemiological data about the SARS outbreak in Beijing become available (Jiang et al., 2003; Liu et al., 2003; Xie et al., 2003), we expect that we would be able to estimate the parameter values in the general model (2.1) and would have a better understanding of the SARS transmission dynamics in Beijing by analysing the general system (2.1). Also, in modelling real diseases such as SARS, stochastic processes should be considered. We leave these for future study.