Abstract.
Purpose: Due to the high incidence and mortality rates of lung cancer worldwide, early detection of a precancerous lesion is essential. Low-dose computed tomography is a commonly used technique for screening, diagnosis, and prognosis of non-small-cell lung cancer. Recently, convolutional neural networks (CNN) had shown great potential in lung nodule classification. Clinical information (family history, gender, and smoking history) together with nodule size provide information about lung cancer risk. Large nodules have greater risk than small nodules.
Approach: A subset of cases from the National Lung Screening Trial was chosen as a dataset in our study. We divided the nodules into large and small nodules based on different clinical guideline thresholds and then analyzed the groups individually. Similarly, we also analyzed clinical features by dividing them into groups. CNNs were designed and trained over each of these groups individually. To our knowledge, this is the first study to incorporate nodule size and clinical features for classification using CNN. We further made a hybrid model using an ensemble with the CNN models of clinical and size information to enhance malignancy prediction.
Results: From our study, we obtained 0.9 AUC and 83.12% accuracy, which was a significant improvement over our previous best results.
Conclusions: In conclusion, we found that dividing the nodules by size and clinical information for building predictive models resulted in improved malignancy predictions. Our analysis also showed that appropriately integrating clinical information and size groups could further improve risk prediction.
Keywords: radiomics, non-small-cell lung cancer, National Lung Screening Trial, convolutional neural network, low-dose CT, ensemble
1. Introduction
Lung cancer is the most commonly diagnosed cancer and the leading cause of cancer-related mortality worldwide.1 In the United States, lung cancer is the second most commonly diagnosed cancer, accounting for 13% of all cancer diagnoses, and lung cancer is the leading cause of cancer-related deaths.2 Over the last several decades, there have been only small improvements in five-year survival rates among patients diagnosed with lung cancer. Part of the reason why lung cancer survival is dismal is because most patients with lung cancer are diagnosed in a late stage. To detect lung cancer at earlier stages, the National Cancer Institute (NCI) conducted the National Lung Screening Trial3 to compare low-dose CT (LDCT) screening versus chest radiography to reduce lung cancer mortality. The NLST was a randomized clinical trial conducted on 53,454 patients over 3 years (baseline and next 2 years’ follow-up scans) and revealed a 20% mortality reduction among individuals screened with LDCT. However, there are limitations with screening by LDCT, including false positives and detection of large numbers of indeterminate pulmonary nodules. As such, biomarkers that can discriminate between malignant and benign nodules would have direct translational significance.
Radiomics4 is an approach to extracting high-dimensional quantitative features from standard-of-care medical imaging (including LDCT) that can be analyzed for predictive and diagnostic analysis. Along with the quantitative radiomics features, deep learning approaches have been utilized recently for lung cancer early detection and classification.5–8 In this study, we utilized convolutional neural network (CNN) for analysis. In our previous study,9 we experimented with cropping (extracting a fixed region for every patient) and warping (extracting the exact tumor region for every patient) using transfer learning. In this study, we evaluated the performance for both warped and cropped nodules for training a CNN.
Nodule size, especially the longest diameter, provides important information on nodule malignancy. Cherezov et al.10 took the nodule size as a parameter to split the dataset into large (), medium ( and ), and small () nodules and then built individual radiomics models for each of those smaller subsets. He showed that by splitting lung nodules into size categories, overall malignancy prediction could be improved. Clinical information, such as family history, smoking history, and gender,11 are the epidemiologic risk factors for lung cancer. The stratified analysis by size and clinical covariates was to try to discover subgroups (e.g., male or former smoker) that would allow for better prediction of future risk. An overall model was created by combining predictions from these individual subgroups to enhance the malignancy prediction.
In this paper, we make the following contributions to obtain a better prediction of nodules that will become malignant.
-
I.
The distribution of nodule size differs between lung cancer and control cases. Changing the size threshold from 4 mm in the NLST study to 6 mm in the National Comprehensive Cancer Network (NCCN) and American College of Radiology (ACR) enabled the false positive rate to be reduced.12–14 Because of these reasons, we analyzed whether the classification result could be enhanced by dividing the nodules by size information. In this study, we used three different categorizations for splitting.
-
II.
Clinical features are epidemiological risk factors for lung cancer. So we utilized three different clinical features (family history, gender, and smoking history) to divide the cohorts.
-
III.
We designed an effective hybrid model by merging size and clinical information for malignancy prediction, as recommended by Ref. 15.
2. Materials and Methods
2.1. Convolutional Neural Network
A CNN16 is a feed forward network in the deep neural network family in which outputs generated from the previous layer pass as inputs to the next layer. CNNs usually consist of many layers, and a large quantity of training data is required as well. In our current dataset, we had 261 cases for training, which was very small to train a CNN from scratch. Data augmentation was applied to generate more training images. Three CNN architectures were built using Keras17 with Tensorflow.18 Experiments with larger and smaller size models and transfer learning were conducted, but the models discussed were most effective. The input image size for the CNN was (bicubic interpolation was used for resizing). RMSprop19 was used for gradient descent optimization, along with a constant learning rate of 0.0001 and 200 training epochs. A batch size of 16 was used during the training and validation. Dropout20 along with L2 regularization21 was applied before the classification layer to minimize overfitting for all three CNNs. Since we had two classes, binary cross entropy was used as the loss function.
CNN1 with 841,681 parameters had two convolution layers succeeded by two fully connected layers. CNN2 had two convolution layers succeeded by one fully connected layer and one long short-term memory (LSTM)22 layer. CNN2 had 845,033 parameters. CNN3 was a cascaded CNN architecture in which the images were fed to both the left branch and the right branch. We applied dropout to both the left and right branches to prevent overfitting. In the left branch, a max pooling operation () was applied to reduce the image size so that both left and right branches can be concatenated. After the concatenation, another convolution layer was used before the final classification layer. The main idea behind this architecture was to provide the classification layer a reduced version of the raw image and image feature information (features generated directly from original images in the left branch).23 CNN3 had 39,553 parameters, which is significantly fewer parameters than our other 2 CNN architectures. In our previous study,24 we experimented with different numbers of layers, learning rates, and convolution kernels and different amounts of regularization and evaluated the performance on the validation data. Based on the performance of validation data, the parameters for our CNNs are shown in Table 1. More detailed analysis about the CNN architectures can be found in Ref. 24.
Table 1.
CNN architectures.
| CNN1 | CNN2 | CNN3 | |||
|---|---|---|---|---|---|
| Layers | Parameters | Layers | Parameters | Layers | Parameters |
| Input image | Input image | Left branch: | |||
| Conv 1 | , pad 0, stride 1 | Conv 1 | , pad 0, stride 1 | Input image | |
| Max pool 1 | |||||
| Leaky ReLU 1 | Alpha = 0.01 | Leaky ReLU 1 | Alpha = 0.01 | Dropout | 0.1 |
| Max pool 1 | , stride 3, pad 0 | Max pool 1 | , stride 3, pad 0 | Right branch: Input image | |
| Conv 2 | , pad 0, stride 1 | Conv 2 | , pad 0, stride 1 | Conv 1 | , pad 0, stride 1 |
| Leaky ReLU 2 | Alpha = 0.01 | Leaky ReLU 2 | Alpha = 0.01 | Leaky ReLU 1 | Alpha = 0.01 |
| Max pool 2 | , stride 3, pad 0 | Max pool 2 | , stride 3, pad 0 | Max pool 2a | , stride 3, pad 0 |
| Conv 2 | , pad 0, stride 1 | ||||
| Dropout | 0.1 | Dropout | 0.1 | ||
| Fully connected | 128 | Fully connected | 128 | Leaky ReLU 2 | Alpha = 0.01 |
| 1 + ReLU | 1 + ReLU | Max pool 2b | , stride 3, pad 0 | ||
| Fully connected | 8 | LSTM 1 + ReLU | 8 | Dropout | 0.1 |
| 2 + ReLU | L2 regularizer | 0.01 | |||
| L2 regularizer | 0.01 | Dropout | 0.25 | ||
| Dropout | 0.25 | Fully connected 2 | 1 sigmoid | Merge left branch and right branch | |
| Fully connected 3 | 1 sigmoid | Conv 3 + ReLU | , pad 0, stride 1 | ||
| Max pool 3 | , stride 2, pad 0 | ||||
| L2 regularizer | 0.01 | ||||
| Dropout | 0.1 | ||||
| Fully connected 1 | 1 sigmoid | ||||
| Total parameters: 841,681 | Total parameters: 845,033 | Total parameters: 39,553 | |||
2.2. NLST Dataset
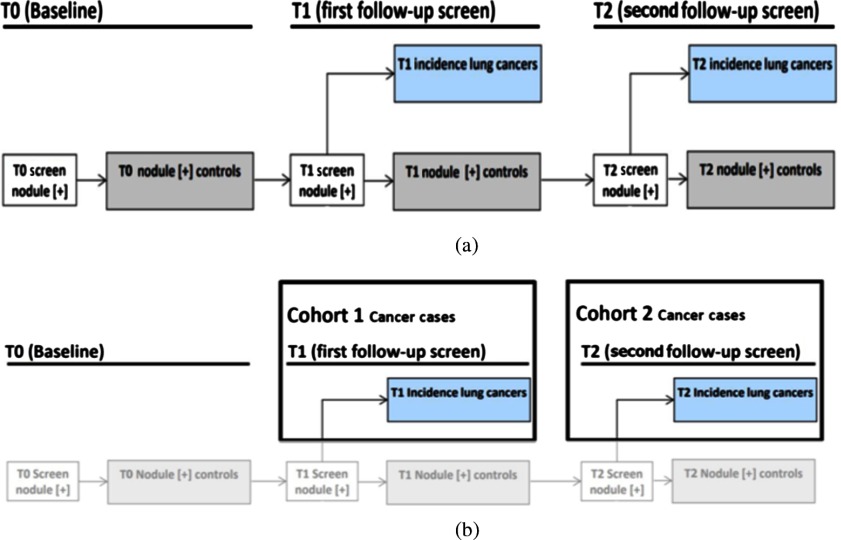
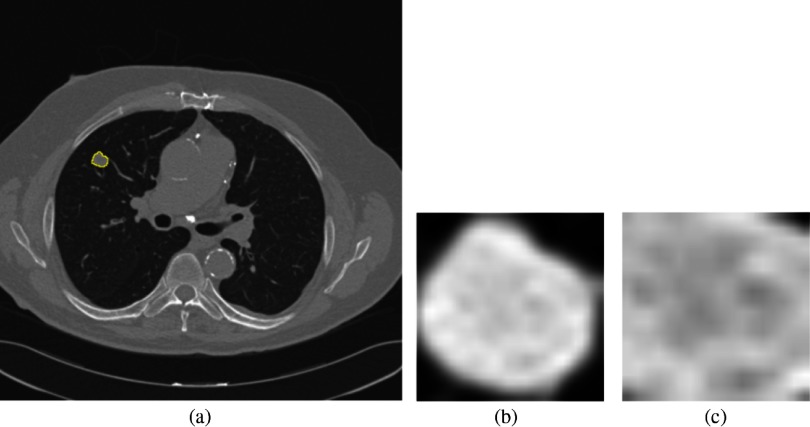
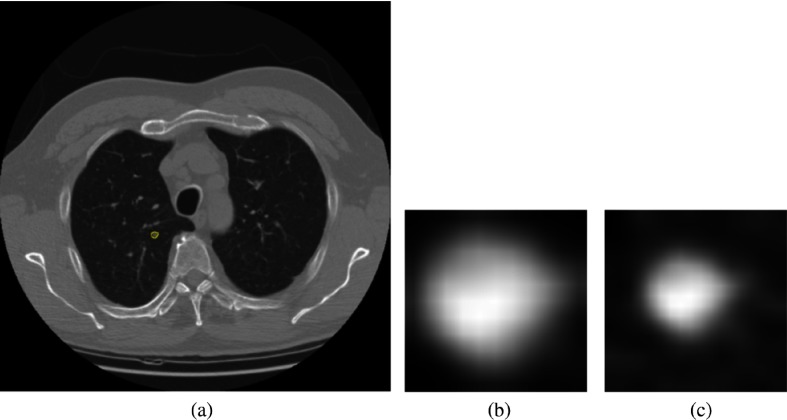
A subset of deidentified noncancer, nodule positive controls, and screen detected lung cancer cases3,25 from the LDCT arm of NLST was obtained from the Cancer Data Access System from the NCI. The multi-institutional NLST study spanned 3 years: baseline screening (T0) along with two follow-up screening intervals (T1 and T2) 1 year apart. The nodule positive controls and lung cancer cases all had a nodule identified at the T0 screen, but it was not diagnosed as lung cancer. The original selection of lung cancers and nodule positive controls was explained by Schabath et al.25 There were 170 screen-detected lung cancers identified, which had a positive screening at baseline (T0) and then the lung cancer was diagnosed as screen detected lung cancers at T1 (85 cases) and T2 (85 cases). Using a 2:1 nested case-control study, 328 nodule-positive controls had nodules (never diagnosed as cancer) that were followed from T0 to T2 and had similar demographics as those diagnosed as lung cancer. The nodule positive controls and lung cancer cases were divided into two cohorts: cohort 1 (for training) and cohort 2 (testing). Figure 1 presents how the cases were split into two cohorts. Cohort 1 contained the lung cancer cases that had a positively screened nodule in the baseline scan, and the positively screened nodules were diagnosed as lung cancer at the first follow-up scan (T1); whereas in cohort 2, the positively screened nodules during the baseline scan (T0) became malignant after 2 years (T2). Throughout this study, the nodule positive controls had never developed lung cancer. Cohort 1 contained 85 incident lung cancer cases and 176 control cases, whereas cohort 2 had 85 incident lung cancer and 152 control cases. From the LDCT scans, the nodules were segmented using the Definiens Software26 by a radiologist with more than 9 years of experience as described elsewhere.27 For the current analysis, we utilized a single image slice for each subject that had the largest nodule area. We then extracted only the nodule region by incorporating a rectangular region that completely contained the nodule region and called it a “warped” nodule. We also applied a fixed region size of (average height and width for all cohort 1 cases) to extract the nodule region and called it “cropped.” Some examples of cropped and warped nodules are shown in Figs. 2 and 3. In this case, some images would have area outside the nodule, and some images would partially cover a nodule.
Fig. 1.
(a) NLST study and (b) flowchart of selection of cohort 1 and cohort 2 from NLST study.
Fig. 2.
(a) Lung image with a small nodule inside outlined by yellow, (b) warped nodule, and (c) cropped nodule (the cropped size of was smaller than the warped nodule, hence, the cropped nodule image partially covers the nodule).
Fig. 3.
(a) Lung image with a very small nodule inside outlined by yellow, (b) warped nodule, and (c) cropped (the cropped size of was larger than the warped nodule, hence, the cropped nodule image has area outside the nodule).
2.3. Splitting Criterions for Training and Test Set
In this study, we analyzed the lung cancer cases and nodule positive controls by longest nodule diameter and clinical features (gender, smoking history, and family history). According to the NCCN and ACR, the positively screened nodule should have in diameter.28 Based on the longest diameter, we have divided both cohort 1 and cohort 2 into three subsets: (small nodules), and (intermediate nodules), and (large nodules).29 The number of cases for the large nodules () was small, so we merged the intermediate and large nodules into one class and continued our experiment with two classes: (small nodules) and (large nodules).
We also used the Fleischner criteria for solid nodules to split the dataset into three groups according to the size: , and , and (split by 6 and 8). Table 2 shows the number of cases in each subset after splitting using size.30 We also analyzed the cases and controls by three clinical covariates: gender (male and female), family history of lung cancer (yes and no), and smoking history (current and former). Table 3 shows the number of cases in each subset after splitting using various clinical criteria. For each subset, data augmentation was used to generate more images, and each of the three CNNs was trained separately.
Table 2.
Number of cases after splitting using various nodule size criteria.
| Splitting criteria | Cohort | Subset | Cancer | Noncancer | Total | Chi-square |
|---|---|---|---|---|---|---|
| Split by 6 and 16 | C1 | 14 | 43 | 57 | 76.172 | |
| and | 54 | 126 | 180 | |||
| 17 | 7 | 24 | ||||
| C2 | 23 | 21 | 44 | 87.265 | ||
| and | 43 | 123 | 166 | |||
| 19 | 8 | 27 | ||||
| Split by 6 | C1 | 14 | 43 | 57 | 155.37 | |
| 71 | 133 | 204 | ||||
| C2 | 23 | 21 | 44 | 134.35 | ||
| 62 | 131 | 193 | ||||
| Split by 6 and 8 | C1 | 14 | 43 | 57 | 35.92 | |
| and mm | 7 | 65 | 72 | |||
| 64 | 68 | 132 | ||||
| C2 | 23 | 21 | 44 | 27.51 | ||
| and | 19 | 64 | 83 | |||
| 43 | 67 | 110 |
Note: Chi-square analysis: For split by 6 and 16 mm and 6 and 8 mm, and , critical value is 5.991; for split by 6 mm only and , critical value is 3.84. Here none of them are significant.
Table 3.
Number of cases after splitting using various clinical criteria.
| Splitting criteria | Cohort | Subset | Cancer | Noncancer | Total | Chi-square |
|---|---|---|---|---|---|---|
| Gender | C1 | Male | 46 | 104 | 150 | 9.5824 |
| Female | 39 | 72 | 111 | |||
| C2 | Male | 48 | 88 | 136 | 6.9004 | |
| Female | 37 | 64 | 101 | |||
| Family history | C1 | Yes | 22 | 32 | 54 | 89.69 |
| No | 63 | 144 | 207 | |||
| C2 | Yes | 19 | 24 | 43 | 85.799 | |
| No | 66 | 128 | 194 | |||
| Smoking history | C1 | Current | 43 | 90 | 133 | 0.0957* |
| Former | 42 | 86 | 128 | |||
| C2 | Current | 46 | 85 | 131 | 4.60192 | |
| Former | 39 | 67 | 106 |
Note: Chi square analysis: Here and , critical value is 3.84. Smoking history cohort 1 is significant.
Statistical significance.
3. Experiments and Results
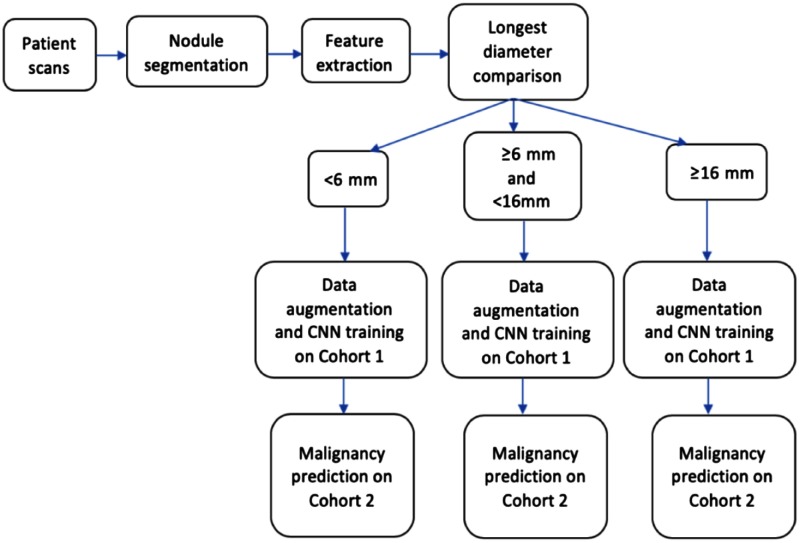
In our study, cohort 1 and cohort 2 were taken as the train and test set, respectively. Figures 4 and 5 show the workflow diagram of our study. Splitting the cohorts based on nodule longest diameter and clinical features provides multiple subgroups for training. For each subgroup, we trained a CNN on cohort 1 data and made a prediction on cohort 2. Cohort 1 and cohort 2 were divided using a chosen splitting criterion, and then for every criterion, 70% of the images from cohort 1 were chosen randomly for training, and the remaining 30% were used as a validation set.
Fig. 4.
Workflow diagram of our analysis.
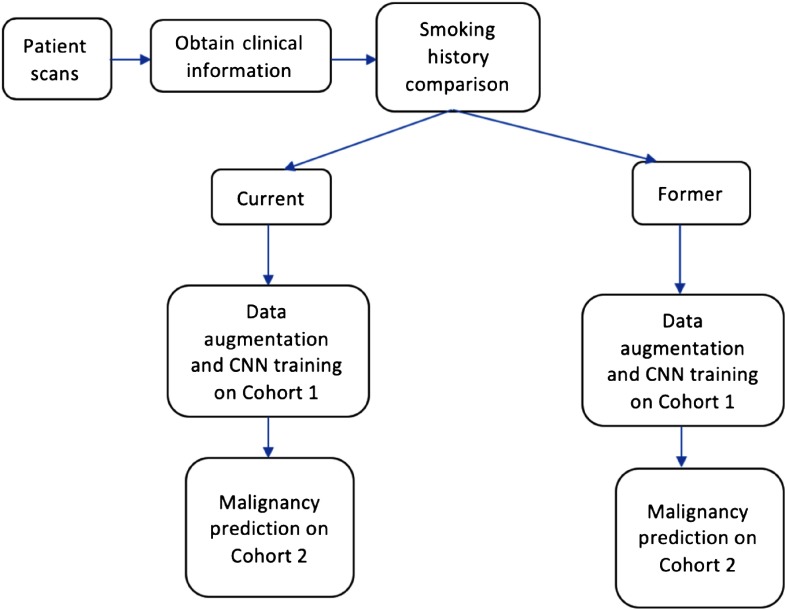
Fig. 5.
Workflow diagram of our analysis for clinical features.
Training a CNN from scratch requires hundreds of images for every class. Image augmentation was applied on cohort 1 by rotating each image 15 deg and then flipping vertically. Along with the rotation, elastic deformation (shifting each pixel value) was used to enhance the number of images for our training set further. Elastic deformation31,32 can be illustrated as
| (1) |
where is the new location of the original pixel after the shifting, is the original pixel, is the displacement vector, and is the strength of the displacement. To obtain an 85% similarity (structural similarity index) between elastic augmented image and original images, in our study, , , and were chosen empirically as 3. Elastic augmentation was performed on the original nodule images, and then rotation and flipping were performed on the elastic augmented images. Hence, our training set had original nodule images, rotated and flipped original images, and elastic augmented nodule images of the original nodule as well as rotated and flipped versions of them.
The completely separate cohort 2 was used to evaluate performance using area under the receiver operating characteristic (AUROC).33 Overall accuracy was computed by summarizing the confusion matrices of each size group and the pseudoprobabilities from each size group were merged to obtain overall AUROC.
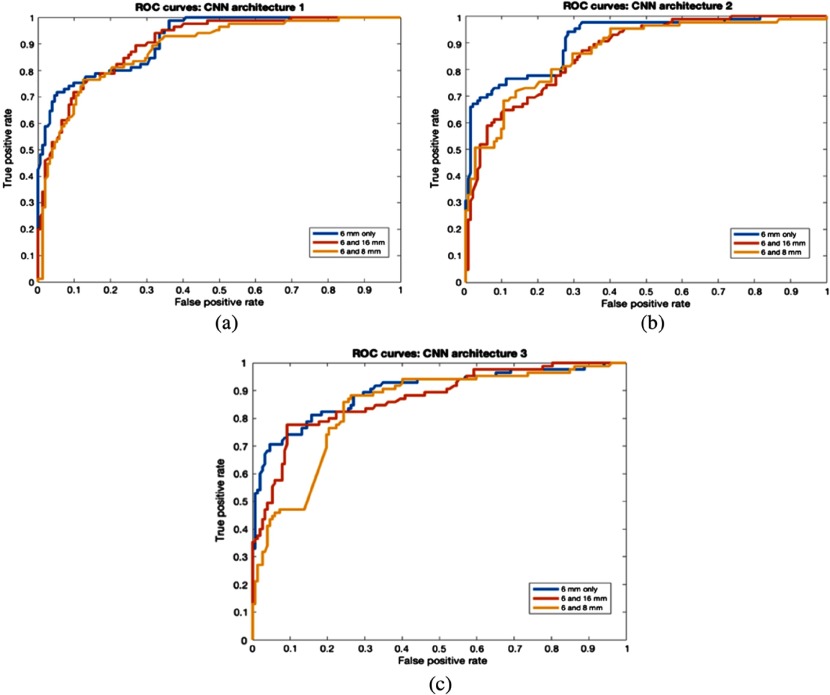
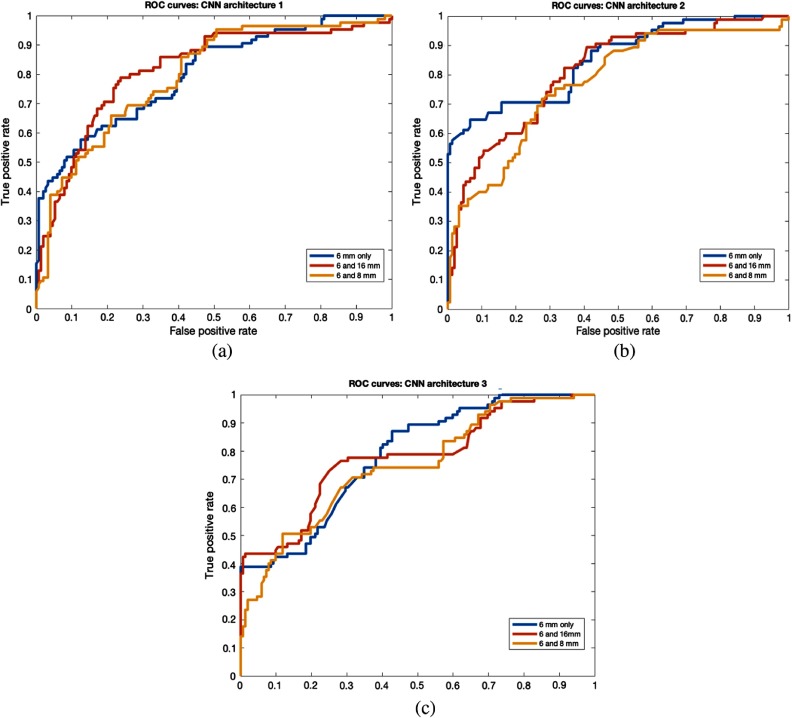
Where the data were split by nodule size, we observed that classification performance on large nodules () or () were better than on small nodules () for all 3 CNN architectures. We also found that warped nodules enabled better results than cropped nodules. For 6-mm and 16-mm split, CNN1 obtained 96.29% accuracy with 0.92 AUC for large nodules (). CNN1 also achieved 82.72% accuracy with 0.9 AUC for large nodules () in the 6- and 8-mm split. For small nodules (), 72.72% accuracy with 0.82 AUROC was obtained from CNN3. The overall best accuracy of 78.9% and AUC of 0.9 was obtained from CNN1 using 6- and 16-mm thresholds. Detailed results from warped and cropped tumors using size splits are shown in Tables 4 and 5, respectively. An overall AUCROC curve for each CNN is shown in Figs. 6 and 7.
Table 4.
Overall results using CNNs for nodule size (warp).
| CNN | 6 only | Overall 6 mm | 6 and 16 | Overall 6 and 16 mm | 6 and 8 | Overall 6 and 8 mm | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| and | and | ||||||||||
| CNN1 | 61.36 (0.78) | 79.27 (0.92) | 76 (0.89) | 61.36 (0.78) | 80.16 (0.91) | 96.29 (0.92) | 78.9 (0.9) | 61.36 (0.78) | 77.1 (0.89) | 82.7 (0.9) | 76.79 (0.88) |
| CNN2 | 61.36 (0.78) | 78.23 (0.9) | 75.1 (0.87) | 61.36 (0.78) | 78.29 (0.88) | 77.77 (0.87) | 75.1 (0.87) | 61.36 (0.78) | 77.1 (0.88) | 80 (0.9) | 75.5 (0.87) |
| CNN3 | 72.72 (0.82) | 79.79 (0.89) | 78.48 (0.89) | 72.72 (0.82) | 79.52 (0.85) | 77.77 (0.88) | 78.05 (0.87) | 72.72 (0.82) | 77.1 (0.88) | 80.9 (0.81) | 78.05 (0.83) |
Note: Accuracy and AUC in brackets obtained from each size group are shown in this table. An overall model was made by combining predictions of the individual subgroups.
Boldface signifies the best results obtained.
Table 5.
Overall results using CNNs for nodule size split (crop).
| CNN | 6 only | Overall 6 mm | 6 and 16 | Overall 6 and 16 mm | 6 and 8 | Overall 6 and 8 mm | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| and | and | ||||||||||
| CNN1 | 56.81 (0.66) | 71 (0.82) | 67.92 (0.79) | 56.81 (0.66) | 75.9 (0.87) | 74.07 (0.76) | 72.15 (0.82) | 56.81 (0.66) | 77.1 (0.88) | 66.36 (0.78) | 68.77 (0.8) |
| CNN2 | 52.27 (0.63) | 72.53 (0.83) | 67.92 (0.8) | 52.27 (0.63) | 76.5 (0.88) | 74.07 (0.76) | 71.3 (0.8) | 52.27 (0.63) | 77.1 (0.86) | 68.18 (0.79) | 68.35 (0.77) |
| CNN3 | 52.27 (0.63) | 71 (0.82) | 66.6 (0.78) | 52.27 (0.63) | 75.3 (0.81) | 74.07 (0.78) | 70.46 (0.77) | 52.27 (0.63) | 77.1 (0.83) | 66.36 (0.75) | 67.08 (0.75) |
Note: Accuracy and AUC in brackets obtained from each size group are shown in this table. An overall model was made by combining predictions of the individual subgroups.
Fig. 6.
ROC curves for nodule size (warp). (a) CNN1 architecture, (b) CNN2 architecture, and (c) CNN3 architecture.
Fig. 7.
ROC curves for various nodule size splits (crop). (a) CNN1 architecture, (b) CNN2 architecture, and (c) CNN3 architecture.
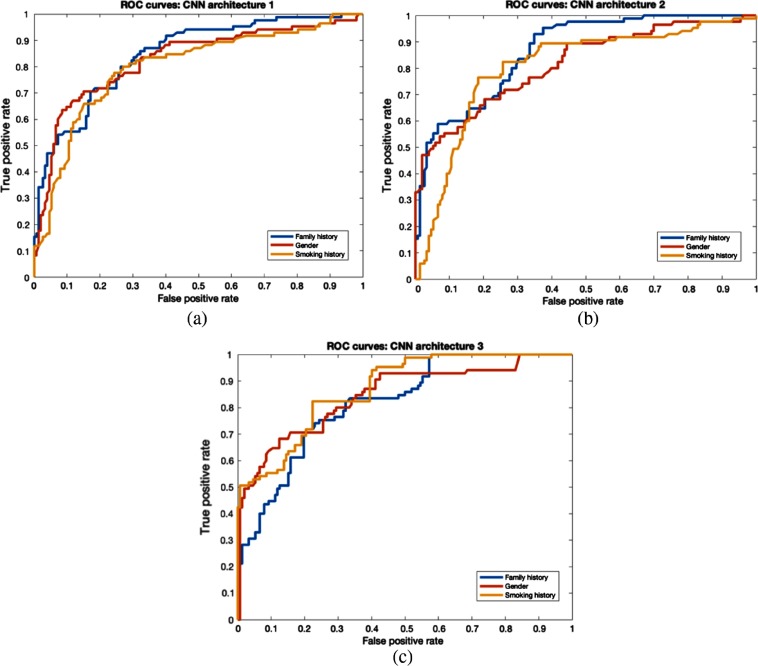
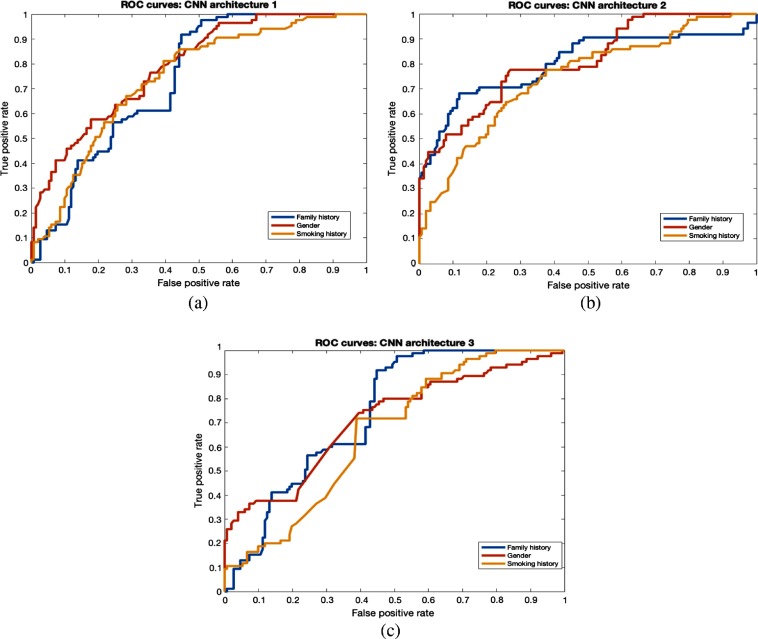
Clinical features (gender, family history, and smoking history) were also utilized to split the dataset. From our study, we found that by training using only female study participants, we generated 78.43% accuracy with 0.86 AUC from CNN1, which was better than for the male cases. In a study conducted by Pinsky et al.,34 lung cancer risk was reduced gradually over time for 30+ pack year former smokers. Former smokers’ risk can change with time, so it is perhaps harder to predict their risk, and good performance on that group will show the power of our approach. From CNN3, 78.3% accuracy and 0.86 AUC were achieved for former smokers. Family history, a clinical feature, is associated with lung cancer incidence. Most subjects had no family history of lung cancer. Our model was most accurate on the no family history group, with 76.3% accuracy (0.84 AUC) using CNN3. Classification performance of warped nodules was better than for cropped nodules for clinical features. The overall best accuracy of 76.79% and AUC of 0.88 was obtained using the CNN3 architecture with a smoking history threshold. Detailed results from warped and cropped tumors using clinical features to split examples are shown in Tables 6 and 7, respectively. The overall AUCROC curve for each CNN is shown in Figs. 8 and 9.
Table 6.
Overall results using CNNs for clinical features (warp).
| CNN | Family | Overall family | Gender | Overall gender | Smoke | Overall smoke | Ensemble | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Yes | No | Male | Female | Former | Current | Average | ||||
| CNN1 | 72.09 (0.81) | 74.74 (0.85) | 74.26 (0.84) | 72.05 (0.82) | 78.43 (0.86) | 75.1 (0.85) | 74.52 (0.8) | 75.57 (0.83) | 75.1 (0.81) | 80.16 (0.89) |
| CNN2 | 67.44 (0.76) | 74.74 (0.84) | 73.41 (0.82) | 70.58 (0.77) | 75.24 (0.83) | 72.5 (0.82) | 73.58 (0.8) | 75.57 (0.82) | 74.68 (0.82) | 77.21 (0.83) |
| CNN3 | 72.33 (0.8) | 76.3 (0.84) | 75.5 (0.82) | 73.5 (0.83) | 77.21 (0.86) | 75.1 (0.87) | 78.3 (0.86) | 75.57 (0.87) | 76.79 (0.88) | 81.01 (0.9) |
Note: Accuracy and AUC in brackets obtained from each clinical feature group are shown in this table. An overall model was made by combining predictions of the individual subgroups. Ensemble by averaging was the ensemble of all three clinical features for each CNN.
Boldface signifies the best results obtained.
Table 7.
Overall results using CNNs for clinical features (crop).
| CNN | Family | Overall family | Gender | Overall gender | Smoke | Overall smoke | Ensemble | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Yes | No | Male | Female | Former | Current | Average | ||||
| CNN1 | 65.11 (0.78) | 68.04 (0.78) | 67.5 (0.78) | 64.7 (0.77) | 69.3 (0.77) | 66.67 (0.77) | 70.75 (0.79) | 64.88 (0.72) | 67.5 (0.75) | 73 0.8 |
| CNN2 | 67.4 (0.76) | 67.52 (0.78) | 67.5 (0.77) | 67.64 (0.76) | 71.3 (0.8) | 69.19 (0.78) | 70.75 (0.79) | 65.56 (0.72) | 67.93 (0.75) | 73.83 0.81 |
| CNN3 | 62.79 (0.74) | 66.5 (0.74) | 65.8 (0.74) | 64.7 (0.76) | 65.34 (0.71) | 64.97 (0.72) | 64.15 (0.69) | 65.56 (0.66) | 64.97(0.66) | 72.15 0.76 |
Note: Accuracy and AUC in brackets obtained from each clinical feature group are shown in this table. An overall model was made by combining predictions of the individual subgroups. Ensemble by averaging was the ensemble of all three clinical features for each CNN.
Fig. 8.
ROC curves for clinical features (warp). (a) CNN1 architecture, (b) CNN2 architecture, and (c) CNN3 architecture.
Fig. 9.
ROC curves for clinical features split (crop). (a) CNN1 architecture, (b) CNN2 architecture, and (c) CNN3 architecture.
To integrate the three clinical features into a single model, an ensemble approach was chosen. For a given size split averaging, the pseudoprobabilities from the ensemble of three CNN clinical models (smoking history, gender, and family history) provided a new classifier. The overall best accuracy of 81% and AUC of 0.9 was obtained with CNN3 when using an ensemble of the three clinical features. Detailed results from warped and cropped tumors using clinical features to split the data are shown in Tables 6 and 7, respectively.
Since nodule size is also a risk factor for lung cancer incidence,10 we made an ensemble of all three clinical features and size categories to investigate if adding size and the clinical features would further improve the result. This means, e.g., with the 6-mm split, that there will be four CNNs used to create a prediction for and . Using this approach, we achieved 83.12% accuracy with 0.9 AUC from CNN1 using three clinical features and the 6- and 16-mm size threshold. Detailed results are shown in Tables 8 and 11 (Appendix). In our previous study24 without splitting, we achieved 75.1% (AUC 0.82), 75.5% (AUC 0.86), and 76% (AUC 0.87) from CNN1, CNN2, and CNN3, respectively. In a separate study27 using radiomics features, 76.79% accuracy with 0.81 AUC was achieved. We next discussed the improvement by splitting using different criteria from our previous studies.24,27 From this study, 78.9% accuracy with 0.9 AUC was achieved by splitting using 6- and 16-mm threshold using CNN1, which displayed an improvement of in accuracy and 0.08 in AUC. Similarly, splitting using smoking criteria showed an improvement of 0.79% in accuracy and 0.01 in AUC using CNN3.
Table 8.
Results using CNNs by ensemble of size and clinical features (warp).
| CNN | 6 mm only + clinical features | 6 and 16 mm + clinical features | 6 and 8 mm + clinical features |
|---|---|---|---|
| CNN1 | 81.89 (0.89) | 83.12 (0.9) | 81.89 (0.89) |
| CNN2 | 78.05 (0.87) | 78.48 (0.88) | 78.05 (0.87) |
| CNN3 | 82.27 (0.89) | 82.7 (0.9) | 82.7 (0.87) |
Table 11.
Results using CNNs by ensemble of size and clinical features (crop).
| CNN | 6 mm only + clinical features | 6 and 16 mm + clinical features | 6 and 8 mm + clinical features |
|---|---|---|---|
| CNN1 | 72.57 (0.8) | 74.68 (0.83) | 73.83 (0.81) |
| CNN2 | 73.83 (0.81) | 74.2 (0.82) | 74.2 (0.82) |
| CNN3 | 72.5 (0.78) | 73 (0.78) | 72.5 (0.77) |
After creating an ensemble, these results were further enhanced. The McNemar test and standard error were used to test significance improvement in accuracy and AUCROC, respectively. Detailed statistical analysis is shown in Tables 9 and 10.
Table 9.
Comparison of our current results with quantitative features19 for warped nodules.
| Significance test | AUROC (standard error) | Accuracy (McNemar) |
|---|---|---|
| Quantitative features27 versus CNN1 ensemble of 3 clinical features | 0.81 (SE: 0.0273) versus 0.89 (SE: 0.0205) | 76.79% versus 80.16% |
| Significant at | Not significant at | |
| Quantitative features27 versus CNN2 ensemble of 3 clinical features | 0.81 (SE: 0.0273) versus 0.83 (SE: 0.0258) | 76.79% versus 77.21% |
| Not significant at | Not significant at | |
| Quantitative features27 versus CNN3 ensemble of 3 clinical features | 0.81 (SE: 0.0273) versus 0.9 (SE: 0.0195) | 76.79% versus 80.01% |
| Significant at | Not significant at | |
| Quantitative features27 versus CNN1 ensemble of three clinical features + 6 mm size | 0.81 (SE: 0.0273) versus 0.89 (SE: 0.0205) | 76.79% versus 81.89% |
| Significant at | Not significant at | |
| Quantitative features27 versus CNN1 ensemble of 3 clinical features + 6 and 16 mm size | 0.81 (SE: 0.0273) versus 0.9 (SE: 0.0195) | 76.79% versus 83.12% |
| Significant at | Significant at | |
| Quantitative features27 versus CNN1 ensemble of 3 clinical features + 6 and 8 mm size | 0.81 (SE: 0.0273) versus 0.89 (SE: 0.0205) | 76.79% versus 81.89% |
| Significant at | Not significant at | |
| Quantitative features27 versus CNN2 ensemble of 3 clinical features + 6 mm size | 0.81 (SE: 0.0273) versus 0.87 (SE: 0.0224) | 76.79% versus 78.05% |
| Not significant at | Not significant at | |
| Quantitative features27 versus CNN2 ensemble of 3 clinical features + 6 and 16 mm size | 0.81 (SE: 0.0273) versus 0.88 (SE: 0.0215) | 76.79% versus 78.48% |
| Not significant at | Not significant at | |
| Quantitative features27 versus CNN2 ensemble of 3 clinical features + 6 and 8 mm size | 0.81 (SE: 0.0273) versus 0.87 (SE: 0.0224) | 76.79% versus 78.05% |
| Not significant at | Not significant at | |
| Quantitative features27 versus CNN3 ensemble of 3 clinical features + 6 mm size | 0.81 (SE: 0.0273) versus 0.89 (SE: 0.0205) | 76.79% versus 82.27% |
| Significant at | Not significant at | |
| Quantitative features27 versus CNN3 ensemble of 3 clinical features + 6 and 16 mm size | 0.81 (SE: 0.0273) versus 0.9 (SE: 0.0195) | 76.79% versus 82.7% |
| Significant at | Not significant at | |
| Quantitative features27 versus CNN3 ensemble of 3 clinical features + 6 and 8 mm size | 0.81 (SE: 0.0273) versus 0.87 (SE: 0.0224) | 76.79% versus 82.7% |
| Not significant at | Not significant at |
Abbreviation: SE, standard error.
Table 10.
Comparison of our current results with CNNs without splitting18 for warped nodules.
| Significance test | AUROC (standard error) | Accuracy (McNemar) |
|---|---|---|
| CNN1 versus CNN1 6 mm only | 0.82 (SE: 0.0266) versus 0.89 (SE: 0.0205) | 75.1 versus 76 |
| Significant at | Not significant at | |
| CNN1 versus CNN1 6 and 16 mm only | 0.82 (SE: 0.0266) versus 0.9 (SE: 0.0195) | 75.1 versus 78.9 |
| Not significant at | Not significant at | |
| CNN1 versus CNN1 6 and 8 mm only | 0.82 (SE: 0.0266) versus 0.88 (SE: 0.0215) | 75.1 versus 76.79 |
| Not significant at | Not significant at | |
| CNN2 versus CNN2 6 mm only | 0.86 (SE: 0.0233) versus 0.87 (SE: 0.0224) | 75.5 versus 75.1 |
| Not significant at | NA | |
| CNN2 versus CNN2 6 and 16 mm only | 0.86 (SE: 0.0233) versus 0.87 (SE: 0.0224) | 75.5 versus 75.1 |
| Not significant at | NA | |
| CNN2 versus CNN2 6 and 8 mm only | 0.86 (SE: 0.0233) versus 0.87 (SE: 0.0224) | 75.5 versus 75.5 |
| Not significant at | Not significant at | |
| CNN3 versus CNN3 6 mm only | 0.87 (SE: 0.0224) versus 0.9 (SE: 0.0195) | 76 versus 78.48 |
| Not significant at | Not significant at | |
| CNN3 versus CNN3 6 and 16 mm only | 0.87 (SE: 0.0224) versus 0.87 (SE: 0.0224) | 76 versus 78.05 |
| Not significant at | Not significant at | |
| CNN3 versus CNN3 6 and 8 mm only | 0.87 (SE: 0.0224) versus 0.83 (SE: 0.0258) | 76 versus 78.05 |
| NA | Not significant at | |
| CNN1 versus CNN1 ensemble of 3 clinical features | 0.82 (SE: 0.0266) versus 0.89 (SE: 0.0205) | 75.1% versus 80.16% |
| Significant at | Not significant at | |
| CNN2 versus CNN2 ensemble of 3 clinical features | 0.86 (SE: 0.0233) versus 0.83 (SE: 0.0258) | 75.5% versus 77.21% |
| NA | Not significant at | |
| CNN3 versus CNN3 ensemble of 3 clinical features | 0.87 (SE: 0.0224) versus 0.9 (SE: 0.0195) | 76.79% versus 80.01% |
| Significant at | Not significant at | |
| CNN1 versus CNN1 ensemble of 3 clinical features + 6 mm size | 0.82 (SE: 0.0266) versus 0.89 (SE: 0.0205) | 75.1% versus 81.89% |
| Significant at | Not significant at | |
| CNN1 versus CNN1 ensemble of 3 clinical features + 6 and 16 mm size | 0.82 (SE: 0.0266) versus 0.9 (SE: 0.0195) | 75.1% versus 83.12% |
| Significant at | Significant at | |
| CNN1 versus CNN1 ensemble of 3 clinical features + 6 and 8 mm size | 0.82 (SE: 0.0266) versus 0.89 (SE: 0.0205) | 75.1% versus 81.89% |
| Significant at | Not significant at | |
| CNN2 versus CNN2 ensemble of 3 clinical features + 6 mm size | 0.86 (SE: 0.0233) versus 0.87 (SE: 0.0224) | 75.5% versus 78.05% |
| Not significant at | Not significant at | |
| CNN2 versus CNN2 ensemble of 3 clinical features + 6 and 16 mm size | 0.86 (SE: 0.0233) versus 0.88 (SE: 0.0215) | 75.5% versus 78.48% |
| Not significant at | Not significant at | |
| CNN2 versus CNN2 ensemble of 3 clinical features + 6 and 8 mm size | 0.86 (SE: 0.0233) versus 0.87 (SE: 0.0224) | 75.5% versus 78.05% |
| Not significant at | Not significant at | |
| CNN3 versus CNN3 ensemble of 3 clinical features + 6 mm size | 0.87 (SE: 0.0224) versus 0.89 (SE: 0.0205) | 76% versus 82.27% |
| Not Significant at | Not significant at | |
| CNN3 versus CNN3 ensemble of 3 clinical features + 6 and 16 mm size | 0.87 (SE: 0.0224) versus 0.9 (SE: 0.0195) | 76% versus 82.7% |
| Not Significant at | Significant at | |
| CNN3 versus CNN3 ensemble of 3 clinical features + 6 and 8 mm size | 0.87 (SE: 0.0224) versus 0.87 (SE: 0.0224) | 76% versus 82.7% |
| Not significant at | Significant at |
4. Discussion and Conclusions
Clinically, LDCT scans are an early detection modality to detect nodules. Definitive diagnosis must be conducted via pathological assessment. Screening for lung cancer via LDCT can detect lung cancer in early stages, which has been shown to improve survival outcomes and lower medical expenses.35 Therefore, as a screening tool, a low-false negative rate for LDCT is crucial. However, current LDCT detects large numbers of indeterminate pulmonary nodules, of which only a fraction () are malignant. Thus there is a critical need to reduce the false positive rate using noninvasive approaches, such as radiomics and quantitative imaging. In this study, we divided both cohorts created from NLST data using different sizes and clinical features and analyzed each of these size (e.g., ) or clinical groups (e.g., female and male) individually using small CNNs. We found that splitting nodules into various groups enabled the CNNs to generate improved overall malignancy prediction.
Nodule size, especially the longest diameter, provides important information regarding nodule malignancy.36,37 Preliminary results from the NELSON trial38 reported that small nodules () had a 0.4% probability of lung cancer, large nodules () needed prompt diagnostic attention (15% probability of lung cancer), and intermediate nodules ( and ) had a lung cancer risk (1.3% lung cancer probability) and needed to be addressed via a screening procedure. Shi et al.39 analyzed the nodule sizes for solitary pulmonary nodules (SPN) in predicting malignancy. They found that large nodules () were more prone to have lobulation. had a higher risk factor for air cavity density. Chang-Zhang also correlated malignancy occurrence with respect to nodule sizes and found that larger lesions () tend to be malignant while smaller nodules () were generally benign lesions. Larici et al.15 studied various size parameters and clinical aspects of lung cancer and concluded that size information along with the clinical features (e.g., family history, smoking history, and age) would enhance the malignancy risk for pulmonary nodules.
In this work, we analyzed whether nodule size and clinical features could provide additional meaningful information to improve lung nodule malignancy prediction. We utilized the CNN architectures from our previous study24 to investigate whether a CNN could learn better after grouping cases for training by size and clinical information. Due to the inclusion of size and clinical information, the workflow of this study became slightly different; this is shown in Figs. 4 and 5. We split the nodules with respect to different sizes and clinical categories and trained a CNN for each of the size and clinical categories. Later, the models of these subgroups were combined into an ensemble of classifiers to provide an overall accuracy and AUC. To our knowledge, this is the first analysis using a CNN ensemble that considers clinical and nodule size information for malignancy prediction.
The malignant and control cases had varied distributions,10 which is why three different size (longest diameter) thresholds were chosen for our study: 6 mm only, 6 and 16 mm, and 6 and 8 mm. 6 and 16 mm were chosen based on the criteria of NCCN and ACR. Based on 6- and 16-mm thresholds, the nodules were separated into three groups: (small nodules), and (intermediate nodules), and (large nodules). We had a very small number of large nodules (), so we merged the large nodules with intermediate nodules using a single threshold of 6 mm: (small nodules) and (large nodules). Based on the Fleischner criteria, we also utilized 6 and 8 mm as thresholds to split the nodules into three groups: (small nodules), and (intermediate nodules), and (large nodules).
Large lung nodules are prone to malignancy, so it is important to find them early and provide an accurate diagnosis. CNN1 achieved 96% accuracy with 0.92 AUC using the lung nodules of . An 82.72% accuracy with 0.9 AUC was achieved by CNN1 for nodule . Even the nodules were predicted with accuracy and 0.89 AUC by CNN3. From the analysis, we found that for all three size thresholds used, models for large nodules were showing better predictive performance than those for small nodules (). From CNN3 72.72% accuracy was achieved for small nodules (), which showed that smaller nodules could be difficult to classify. They usually have less risk38 and could be identified by semantic or visual features (e.g., spiculation and lobulation).41,42 We did not include any semantic or visual features in the current study, but in future studies, we will incorporate visual findings for small nodules. We found the overall best accuracy of 78.9% and AUC 0.9 from the 6- and 16-mm threshold using CNN1 as shown in Table 4.
Family history, smoking history, and gender are epidemiological risk factors for lung cancer. Smoking is one of the major contributors to the lung cancer risk. Tindle et al.43 analyzed the association between mortality and smoking abstinence using the patients from NLST study. Kaplan-Meier survival curves were used to analyze survival differences. Current smokers had a lung cancer specific and all-cause mortality hazard ratio of (2.14 to 2.29) and (1.79 to 1.85), respectively, which was higher than the former smokers. They also concluded that former smokers with more than 7 years of cessation from smoking would have mortality reduced by 20%. The study by Remen et al.44 showed that the risk of lung cancer among current smokers is higher than a former heavy smoker and the risk would get lower within five years after quitting. But still, former smokers had three times greater risk of lung cancer than nonsmokers. Cannon-Albright et al.45 conducted a case-control study in Montreal to determine the association between risk of lung cancer and smoking history. The study was conducted between 1996 and 2000 and included 1203 lung cancer and 1513 control cases. They discovered that the odds ratio for nonsmoking versus smoking was 7.82 for males and 11.76 for females. They also found that 86% of lung cancer cases were associated with smoking and concluded that the lung cancer risk would increase with duration and intensity of smoking.
Yoshida et al.46 evaluated the involvement of family history of lung cancer with the risk of lung cancer. The study was conducted on 5048 lung cancer cases. They observed a significant relationship between lung cancer with the first-, second-, or third-degree relatives. The relative risk of lung cancers increased for each additional case of first degree relative (FDR) spanning from 2.57 relative risk for 1 or more FDR to 4.44 relative risk for 3 or more FDR. Novello et al.47 analyzed the associations between family history of cancer and the risk of lung cancer. The study included 1733 lung cancer and 6643 control cases. Among males, the lung cancer history in siblings was associated significantly with small cell carcinoma risk (2.28 odds ratio) and adenocarcinoma risk (2.25 odds ratio), whereas the parental lung cancer history increased the adenocarcinoma risk (odds ratio = 1.72) among females.
The development of lung cancer in men differs from that in women. Cherezov et al.48 analyzed the lung cancer risk on gender and smoking status. They concluded that the risk of adenocarcinoma was higher in female smokers than male and the risk of lung cancer was also higher in females than in males. In a recent study by Schabath and Cote,11 it was shown that the lung cancer incidence and mortality among males is more than among females in the USA. Due to these reasons, we also analyzed three different clinical features separately to analyze which of them could be useful for malignancy prediction and risk assessment.
From our study, we correctly predicted females (78.43% accuracy) and males (73.5% accuracy). We already know family history is a risk factor for lung cancer. We correctly predicted nodules would become malignant for 76.3% of patients with no family history and 72.33% patients with family history. In the set of current and former smokers, we predicted nodules becoming malignant correctly for 78.3% of former smokers and 75.57% of current smokers.
The clinical features are dependent on each other and could provide more predictive information if we combine them.48 They are certainly used in combination by physicians. So we made an ensemble of models using these three clinical features and achieved 81% accuracy (0.9 AUC). As size is also a lung cancer risk predictor, we also combined models built on different size nodules with the clinical features. Hence, we learned an ensemble of four models using the CNN1 architecture (for each model) and obtained 83.12% accuracy with 0.9 AUC as shown in Table 8. This is significantly better than our previous results.24,27 Detailed results including significance tests are shown in Tables 9 and 10
Multivariable analysis was performed to determine if the size and clinical features were statistically significant with respect to the class labels. Logistic regression was performed using R software (glm2 package). The clinical features (gender, smoking history, and family history) were not statistically significant, but all size thresholds (6 mm only, 6 and 16 mm, and 6 and 8 mm) were significant at . These suggest that the size is more important for malignancy prediction. The logistic regression models were not competitive for accuracy/AUC.
We also compared malignancy prediction between warped and cropped nodules. We found that warped nodules give better malignancy prediction than cropped nodules. Warped nodules will always contain the full nodule, but cropped nodules could have only part of the nodule or some excess area around the nodule, which could be the reason that models using cropped nodules perform worse. Results obtained from the cropped nodules are shown in Tables 5, 7, and 11 (in Appendix).
In Ref. 48, it was shown that a CNN can learn the size of an object even when an image is resized. This experiment was performed on the COCO49 and the NLST dataset.
There were some limitations to this study. For this study, we used 2-D slices instead of 3-D volumes. We experimented with 2-D slices to check the viability of providing size and clinical information to build a CNN model. We utilized a semiautomatic segmentation approach and analysis, which is a limitation for this study.
In conclusion, we found that dividing the nodules according to size and clinical information for building predictive models gave better malignancy prediction. An ensemble of models built on different size nodules and nodules from patients with different clinical features significantly enhances malignancy prediction.
5. Appendix
In this section, we show the results obtained from the cropped lung nodules. We found the overall best accuracy of 74.68% and AUC 0.83 from the 6- to 16-mm threshold and clinical features using CNN1, as shown in Table 11.
Acknowledgments
This research partially supported by the National Institute of Health under Grant Nos. NIH U01 CA143062, NIH U24 CA180927, and NIH U01 CA200464; the National Science Foundation under Award No. 1513126; and the State of Florida Department of Health under Grant No. 4KB17.
Biographies
Rahul Paul received his MS degree in computer science from the Indian Institute of Technology (ISM), Dhanbad, India, in 2015. He is pursuing his PhD at the University of South Florida, Tampa, Florida, USA. He has worked to improve the prediction of malignancy of pulmonary nodules from CT screening by utilizing deep features and quantitative CT features from the nodule. His areas of interest include pattern recognition, image processing, deep learning, data mining, and lung cancer.
Matthew B. Schabath received his PhD in epidemiology from the University of Texas in 2003. He is an associate member of the Department of Cancer Epidemiology in the H. Lee Moffitt Cancer Center and Research Institute, Tampa, Florida, USA. He has more than 18 years of experience studying tobacco-related diseases, including lung cancer, bladder cancer, chronic obstructive pulmonary disease, and heart disease.
Robert Gillies is the chair of Cancer Physiology Department, the director of the Center of Excellence in Cancer Imaging and Technology, and the vice chair of radiology research at the H. Lee Moffitt Cancer Center and Research Institute, Tampa, Florida, USA. His work is focused on defining and characterizing deregulated pathways with therapeutic relevance in subsets of human cancers. His colleagues have identified targetable cell surface receptors in pancreatic, melanoma, and breast cancers.
Lawrence O. Hall received his PhD in computer science from Florida State University. He is a professor in the Computer Science and Engineering Department, University of South Florida, Tampa, Florida, USA. He is a fellow of IEEE, IAPR, AAAS, and AIMBE. His research interests lie in distributed machine learning, extreme data mining, bioinformatics, pattern recognition, and integrating AI into image processing.
Dmitry B. Goldgof received his PhD in electrical engineering from the University of Illinois at Urbana-Champaign. He is a professor in the Computer Science and Engineering Department, University of South Florida, Tampa, Florida, USA. He is a fellow of IEEE, IAPR, AAAS, and AIMBE. His research interests are related to biomedical image analysis and machine learning with applications in MR, CT, positron emission tomography, and microscopy images, radiomics and bioinformatics, motion analysis with biometrics, face analysis, and surveillance applications.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
Contributor Information
Rahul Paul, Email: rahulp@mail.usf.edu.
Matthew B. Schabath, Email: Matthew. Schabath@moffitt.org.
Robert Gillies, Email: robert.gillies@moffitt.org.
Lawrence O. Hall, Email: lohall@mail.usf.edu.
Dmitry B. Goldgof, Email: goldgof@mail.usf.edu.
References
- 1.Fitzmaurice C., et al. , “The global burden of cancer 2013,” JAMA Oncol. 1(4), 505–527 (2015). 10.1001/jamaoncol.2015.0735 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Howlader N., et al. , “SEER cancer statistics factsheets: lung and bronchus cancer,” National Cancer Institute, Bethesda, Maryland, 2016, http://seer.cancer.gov/statfacts/html/lungb.html.
- 3.National Lung Screening Trial Research Team, “Reduced lung-cancer mortality with low-dose computed tomographic screening,” N. Engl. J. Med. 365, 395–409 (2011). 10.1056/NEJMoa1102873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lambin P., et al. , “Radiomics: extracting more information from medical images using advanced feature analysis,” Eur. J. Cancer 48(4), 441–446 (2012). 10.1016/j.ejca.2011.11.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nishio M., et al. , “Computer-aided diagnosis of lung nodule classification between benign nodule, primary lung cancer, and metastatic lung cancer at different image size using deep convolutional neural network with transfer learning,” PLoS One 13(7), e0200721 (2018). 10.1371/journal.pone.0200721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tsakok M., et al. , “Differential findings and use of convolutional neural network (CNN)-derived risk score on benign resolving and non-resolving pulmonary nodules,” Clin. Radiol. 73, e14–e15 (2018). 10.1016/j.crad.2018.07.164 [DOI] [Google Scholar]
- 7.Causey J. L., et al. , “Highly accurate model for prediction of lung nodule malignancy with CT scans,” Sci. Rep. 8(1), 9286 (2018). 10.1038/s41598-018-27569-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ardila D., et al. , “End-to-end lung cancer screening with three-dimensional deep learning on low-dose chest computed tomography,” Nat. Med. 25(6), 954–961 (2019). 10.1038/s41591-019-0447-x [DOI] [PubMed] [Google Scholar]
- 9.Paul R., et al. , “Deep feature transfer learning in combination with traditional features predicts survival among patients with lung adenocarcinoma,” Tomography 2(4), 388–395 (2016). 10.18383/j.tom.2016.00211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cherezov D., et al. , “Improving malignancy prediction through feature selection informed by nodule size ranges in NLST,” in IEEE Int. Conf. Syst. Man Cybern. (SMC), pp. 001939–001944 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schabath M. B., Cote M. L., “Cancer progress and priorities: lung cancer,” Cancer Epidemiol. Prev. Biomarkers 28(10), 1563–1579 (2019). 10.1158/1055-9965.EPI-19-0221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.McKee B. J., et al. , “Performance of ACR Lung-RADS in a clinical CT lung screening program,” J. Am. Coll. Radiol. 13(2), R25–R29 (2016). 10.1016/j.jacr.2015.12.009 [DOI] [PubMed] [Google Scholar]
- 13.Gierada D. S., et al. , “Projected outcomes using different nodule sizes to define a positive CT lung cancer screening examination,” J. Natl. Cancer Inst. 106(11), dju284 (2014). 10.1093/jnci/dju284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kazerooni E. A., et al. , “ACR-STR practice parameter for the performance and reporting of lung cancer screening thoracic computed tomography (CT): 2014 (resolution 4),” J. Thoracic Imaging 29(5), 310–316 (2014). 10.1097/RTI.0000000000000097 [DOI] [PubMed] [Google Scholar]
- 15.Larici A. R., et al. , “Lung nodules: size still matters,” Eur. Respir. Rev. 26(146), 170025 (2017). 10.1183/16000617.0025-2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zeiler M. D., Fergus R., “Visualizing and understanding convolutional networks,” in Eur. Conf. Comput. Vision, pp. 818–833 (2014). [Google Scholar]
- 17.Ketkar N., “Introduction to Keras,” in Deep Learning with Python, pp. 95–109, Apress, Berkeley, California: (2017). [Google Scholar]
- 18.Abadi M., et al. , “Tensorflow: large-scale machine learning on heterogeneous distributed systems,” arXiv:1603.04467 (2016).
- 19.Tieleman T., Hinton G., “Lecture 6.5-rmsprop: divide the gradient by a running average of its recent magnitude,” COURSERA: Neural Networks Mach. Learn. 4(2), 26–31 (2012). [Google Scholar]
- 20.Srivastava N., et al. , “Dropout: a simple way to prevent neural networks from overfitting,” J. Mach. Learn. Res. 15(1), 1929–1958 (2014). 10.5555/2627435.2670313 [DOI] [Google Scholar]
- 21.Ng A. Y., “Feature selection, L 1 vs. L 2 regularization, and rotational invariance,” in Proc. Twenty-First Int. Conf. on Mach. Learn. (2004). [Google Scholar]
- 22.Gers F. A., Schraudolph N. N., Schmidhuber J., “Learning precise timing with LSTM recurrent networks,” J. Mach. Learn. Res. 3, 115–143 (2002). 10.1162/153244303768966139 [DOI] [Google Scholar]
- 23.Li H., et al. , “A convolutional neural network cascade for face detection,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 5325–5334 (2015). 10.1109/CVPR.2015.7299170 [DOI] [Google Scholar]
- 24.Paul R., et al. , “Predicting malignant nodules by fusing deep features with classical radiomics features,” J. Med. Imaging 5(1), 011021 (2018). 10.1117/1.JMI.5.1.011021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schabath M. B., et al. , “Differences in patient outcomes of prevalence, interval, and screen-detected lung cancers in the CT arm of the national lung screening trial,” PLoS One 11(8), e0159880 (2016). 10.1371/journal.pone.0159880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Definiens AG. Developer XD 2.0. 4. Reference Book (2012).
- 27.Hawkins S., et al. , “Predicting malignant nodules from screening CT scans,” J. Thoracic Oncol. 11(12), 2120–2128 (2016). 10.1016/j.jtho.2016.07.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wood D. E., et al. , “Lung cancer screening, version 1.2015,” J. Natl. Compr. Cancer Network 13(1), 23–34 (2015). 10.6004/jnccn.2015.0006 [DOI] [PubMed] [Google Scholar]
- 29.Cherezov D., et al. , “Delta radiomic features improve prediction for lung cancer incidence: a nested case-control analysis of the National Lung Screening Trial,” Cancer Med. 7(12), 6340–6356 (2018). 10.1002/cam4.1852 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.MacMahon H., et al. , “Guidelines for management of incidental pulmonary nodules detected on CT images: from the Fleischner Society 2017,” Radiology 284, 228–243 (2017). 10.1148/radiol.2017161659 [DOI] [PubMed] [Google Scholar]
- 31.Sorokin D. V., et al. , “Non-rigid contour-based registration of cell nuclei in 2-D live cell microscopy images using a dynamic elasticity model,” IEEE Trans. Med. Imaging 37(1), 173–184 (2017). 10.1109/TMI.2017.2734169 [DOI] [PubMed] [Google Scholar]
- 32.Perez F., et al. , “Data augmentation for skin lesion analysis,” in OR 2.0 Context-Aware Operating Theaters, Computer Assisted Robotic Endoscopy, Clinical Image-Based Procedures, and Skin Image Analysis, pp. 303–311, Springer, Cham: (2018). [Google Scholar]
- 33.Hajian-Tilaki K., “Receiver operating characteristic (ROC) curve analysis for medical diagnostic test evaluation,” Caspian J. Intern. Med. 4(2), 627–635 (2013). [PMC free article] [PubMed] [Google Scholar]
- 34.Pinsky P.F., Zhu C. S., Kramer B. S., “Lung cancer risk by years since quitting in 30+ pack year smokers,” J. Med. Screening 22(3), 151–157 (2015). 10.1177/0969141315579119 [DOI] [PubMed] [Google Scholar]
- 35.Atwater T., Massion P. P., “Biomarkers of risk to develop lung cancer in the new screening era,” Ann. Transl. Med. 4(8), 158 (2016). 10.21037/atm.2016.03.46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gould M. K., et al. , “Evaluation of individuals with pulmonary nodules: when is it lung cancer?: diagnosis and management of lung cancer: American College of Chest Physicians evidence-based clinical practice guidelines,” Chest 143(5), e93S–e120S (2013). 10.1378/chest.12-2351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhang J., et al. , “Relationship between tumor size and survival in non-small-cell lung cancer (NSCLC): an analysis of the surveillance, epidemiology, and end results (SEER) registry,” J. Thoracic Oncol. 10(4), 682–690 (2015). 10.1097/JTO.0000000000000456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Horeweg N., et al. , “Lung cancer probability in patients with CT-detected pulmonary nodules: a prespecified analysis of data from the NELSON trial of low-dose CT screening,” Lancet Oncol. 15(12), 1332–1341 (2014). 10.1016/S1470-2045(14)70389-4 [DOI] [PubMed] [Google Scholar]
- 39.Shi C. Z., et al. , “Size of solitary pulmonary nodule was the risk factor of malignancy,” J. Thoracic Dis. 6(6), 668–676 (2014). 10.3978/j.issn.2072-1439.2014.06.22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang M., et al. , “Classification of lung nodules in CT images based on Wasserstein distance in differential geometry,” arXiv:1807.00094 (accessed 30 June 2018).
- 41.Furuya K., et al. , “New classification of small pulmonary nodules by margin characteristics on highresolution CT,” Acta Radiol. 40(5), 496–504 (1999). 10.3109/02841859909175574 [DOI] [PubMed] [Google Scholar]
- 42.Tanner N. T., et al. , “The association between smoking abstinence and mortality in the National Lung Screening Trial,” Am. J. Respir. Crit. Care Med. 193(5), 534–541 (2016). 10.1164/rccm.201507-1420OC [DOI] [PubMed] [Google Scholar]
- 43.Tindle H. A., et al. , “Lifetime smoking history and risk of lung cancer: results from the Framingham Heart Study,” J. Natl. Cancer Inst. 110(11), 1201–1207 (2018). 10.1093/jnci/djy041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Remen T., et al. , “Risk of lung cancer in relation to various metrics of smoking history: a case-control study in Montreal,” BMC Cancer 18(1), 1275 (2018). 10.1186/s12885-018-5144-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Cannon-Albright L. A., Carr S. R., Akerley W., “Population-based relative risks for lung cancer based on complete family history of lung cancer,” J. Thoracic Oncol. 14, 1184–1191 (2019). 10.1016/j.jtho.2019.04.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yoshida K., et al. , “Association between family history of cancer and lung cancer risk among Japanese men and women,” Tohoku J. Exp. Med. 247(2), 99–110 (2019). 10.1620/tjem.247.99 [DOI] [PubMed] [Google Scholar]
- 47.Novello S., Stabile L. P., Siegfried J. M., “Gender-related differences in lung cancer,” in IASLC Thoracic Oncol., pp. 30–45 (2018). [Google Scholar]
- 48.Cherezov D., et al. , “Lung nodule size are encoded when scaling CT image for CNN’s,” USF Computer Science and Engineering, Technical Report ISL-1-20, www.cse.usf.edu/~lohall/TR-ISL-1-20.pdf (2020). [DOI] [PMC free article] [PubMed]
- 49.Lin T. Y., et al. , “Microsoft coco: common objects in context,” in Eur. Conf. Comput. Vision, Springer, Cham, pp. 740–755 (2014). [Google Scholar]