The Architecture of Working Memory: Features from Multiple Remembered Objects Produce Parallel, Coactive Guidance of Attention in Visual Search

Abstract

Theories of working memory (WM) differ in their claims about the number of items that can be maintained in a state that directly interacts with other, ongoing cognitive operations (termed the focus of attention). A similar debate has arisen in the literature on visual working memory (VWM), focused on the number of items that can simultaneously interact with attentional priority. In three experiments, we used a redundancy-gain paradigm to provide a comprehensive test of the latter question. Participants searched for two cued features (e.g., a color and a shape) within a search array. The cued feature values changed on a trial-by-trial basis, requiring VWM. The target (when present) could match one of the cued features (single-target trials) or both cued features (redundant-target trials). We tested whether response time distributions contained a substantial proportion of trials with redundant-target responses that were faster than predicted by two independent guidance processes operating in parallel (i.e., violations of the race-model inequality). Violations are consistent with a coactive architecture in which both cued values guide attention in parallel and sum on the priority map. Robust violations were observed in all cases predicted by the hypothesis that multiple items in VWM can guide attention simultaneously, and these results were inconsistent with the hypothesis that guidance is limited to a single item simultaneously. When considered in the larger context of the literature on VWM and attention, the present results are consistent with a model of WM architecture in which the focus of attention can maintain multiple, independent representations.

Working memory (WM) describes mechanisms that make representations accessible in the service of ongoing tasks. Functional models of WM (e.g., Cowan, 1999; Oberauer, 2002) propose an embedded set of processes, in which different “layers” are distinguished by relative accessibility, from the vast store of latent representations in long-term memory to the highly active representations available for direct report and for participation in ongoing cognitive operations. In Cowan’s embedded process model (Cowan, 1988, 1999, 2005), a small set of representations is maintained in the latter, online state – termed the focus of attention – with the capacity of the focus of attention constituting the overall capacity of WM. In contrast, the concentric activation model proposed by Oberauer (2002; 2009; for a related view, see McElree, 2001, 2006) divides WM into two functionally different states: a direct access component (corresponding to the overall capacity of WM) and a more restricted focus of attention that operates over the direct access component and is limited to a single item or chunk. In this latter view, most representations in the direct access component are maintained in an offline but highly accessible state. Only the single, attended item is maintained in a state that can directly interact with other, ongoing cognitive operations. Thus, current models of WM differ in their claims about WM architecture, specifically the capacity of the component supporting the very most active representation(s).

A closely related debate has developed in the literature on visual working memory (VWM), attention, and visual search. Here, the issue is whether multiple representations in VWM can be maintained in an active state to simultaneously guide attention. For example, when searching a complex scene for an apple that might be either red or green, can VWM representations of both red and green interact simultaneously with attentional priority maps to bias attention and gaze toward both red and green objects? As with the larger architectural debate over WM, two competing views have emerged: a multiple-item-template hypothesis (Bahle, Beck, & Hollingworth, 2018; Beck, Hollingworth, & Luck, 2012), holding that multiple VWM items can guide attention simultaneously, and a single-item-template hypothesis (Olivers, Peters, Houtkamp, & Roelfsema, 2011; van Moorselaar, Theeuwes, & Olivers, 2014), holding that the active, template state is limited to a single item. Evidence to discriminate between these views has come, largely, from the presence or absence of switch costs when alternating guidance between two different feature values (Beck et al., 2012; Ort, Fahrenfort, & Olivers, 2017) and from attentional capture by stimuli that match the content of VWM when multiple items are maintained in VWM (Bahle et al., 2018; Hollingworth & Beck, 2016; van Moorselaar et al., 2014). However, we will argue that switch costs do not necessarily distinguish between the competing theories, and evidence from capture is limited to automatic processes, potentially underestimating the strength of multiple-item guidance under more typical conditions. In the present study, we sought to address this question in a novel paradigm that 1) generates clear competing predictions from the single- and multiple-item hypotheses and 2) probes the central construct of interest: simultaneous, strategic guidance of attention by multiple items maintained in VWM. In addition, by examining the effects of VWM representations on other, ongoing operations—rather than testing explicit access to WM representations, as in most studies in the general WM literature—we sought to shed new light on the broad question of WM architecture, establishing an empirical and theoretical bridge between the literature on WM in general and that on VWM in particular.

Review of Extant Evidence

Evidence concerning the span of the focus of attention in the general WM literature has typically involved assessing the timing of explicit access to individual items, either through overt report or through strategic use in higher-level cognitive tasks. For example, response times (RTs) to memory probes tend to be more rapid for the last item in a list (Oberauer, 2006; Verhaeghen & Basak, 2005) and, under manipulated time constraint, the rate of improvement in accuracy is higher for the last item (McElree, 2001; McElree & Dosher, 1989). These data have been interpreted as indicating qualitatively different WM states, with the most accessible state limited to a single item/chunk, and access to other items requiring a shift of the focus of attention. Converging evidence has come from studies requiring participants to update representations in WM, e.g., by having to conduct arithmetical operations on multiple running totals (Garavan, 1998; Oberauer, 2002). The typical finding is of switch costs in RT when switching the particular total to be updated, consistent with the idea that a unitary focus of attention must be redirected in order to access and operate upon individual WM representations.

Although these results are difficult to reconcile with a multiple-item focus of attention account in which all items are equally accessible, they do not necessarily rule out versions of this theory that allow for different absolute levels of activation within a multiple-item focus of attention (for extended discussion, see Cowan, 2011; Sewell, Lilburn, & Smith, 2016). That is, multiple items could be maintained simultaneously in a manner that can interact directly with other, ongoing cognitive processes, but with different relative strength, generating both differential efficiency of access and switch costs when the task requires a change in relative strength (i.e., selection). Further, two papers suggest that the focus of attention can be expanded to encompass at least two items when operations over elements in WM are minimally confusable (Gilchrist & Cowan, 2011; Oberauer & Bialkova, 2011), such as numerical updating and spatial updating. Such data suggest when a highly restricted focus of attention is observed, this may not be a structural feature of WM but rather a functional constraint to avoid crosstalk between tasks (Oberauer & Bialkova, 2011), with the representations for one task maintained in the focus of attention and the representations for the other maintained an offline, but highly accessible, state (e.g., the direct access component in the concentric activation model). Finally, because all of these studies have examined various modes of explicit access—either report/confirmation or strategic use in a complex cognitive task—it is possible that strong capacity limitations are introduced in the processes that support explicit access, rather than reflecting the inherent capability of multiple items to be maintained in an active state that can interact with, or even control, other cognitive operations.

Similarly to the general WM literature, competing theories of architecture have been tested in the VWM literature by probing for costs when attentional guidance must be changed from one feature value to another. The multiple-item-template hypothesis, which holds that multiple items can be maintained in an active state that interacts with attentional selection, predicts minimal or no switch costs. The single-item-template hypothesis holds that one item is maintained in the active template state; other items in VWM are in an accessory state that is inert with respect to attentional guidance (i.e., they do not interact with attentional priority maps to influence selection). Thus, if guidance must switch from one remembered feature value to another, this will introduce a switch cost reflecting the time necessary to promote an accessory item to the template state. This has typically been measured by saccade latency when switching from overt selection of items containing a particular target color to items of a different target color. Tests of these predictions have generally, though not unambiguously, supported the multiple-item hypothesis. Switch costs have either been absent or minimal in several studies (Beck et al., 2012; Grubert, Carlisle, & Eimer, 2016; Johannesson, Thornton, Smith, Chetverikov, & Kristjansson, 2016). Other studies have found moderate switch costs in this type of paradigm, but only under limited conditions (Ort et al., 2017; Ort, Fahrenfort, & Olivers, 2018). For example, Ort et al. (2017) observed ~50 ms switch cost in a two-color search task, but limited to a condition where only one target color was present in each of a series of search displays with the same two cued colors.

Ultimately, however, switch costs are not an ideal means to distinguish between theories, for the same reason as discussed in the general WM literature (Cowan, 2011; Sewell et al., 2016). Robust evidence for the absence of switch costs provides support for the multiple-item hypothesis (at least for the models as they are currently instantiated). However, the presence of relatively small switch costs can be accounted for by both theories. It is plausible that, even if multiple items are maintained in state that interacts with attention, there will be differences in their absolute level of activity (or priority), particularly if one feature value has been used to guide attention over several recent selections. A switch cost could plausibly arise in the course of modifying this activity, so that a different feature value is now of higher relative priority. In this view, priority for guidance would be a matter of relative activity among VWM representations that are each already providing some level of control over attention, as opposed to a model, such as the single-item hypothesis, in which there are discrete transitions between priority states. Switch costs could plausibly arise in either model.

The issue of single- versus multiple-item attentional guidance has also been studied extensively in the context of attention capture paradigms (for a review, see Bahle et al., 2018). In the general method, a remembered feature value, never an attribute of the target of the central search task, is introduced as a distractor into a search array; capture is assessed by the extent to which attention is directed toward the matching item, indexed either by search RT or by the probability of distractor fixation. Two studies illustrate the current state of this literature. First, in Hollingworth and Beck (2016), participants searched for a static target (box with gap on left or right) on each trial and remembered either one or two colors for a concurrent memory task. In the search array, two colored distractors appeared, with neither, one, or both matching a color held in VWM. Substantial capture by matching distractors was observed on search RT when participants remembered more than one color (cf., van Moorselaar et al., 2014). In addition, capture was significantly greater when there were two memory items and two color matches compared with one memory item and one color match, suggesting that attention was guided by both items in the former case. These effects have been replicated in several subsequent studies (Chen & Du, 2017; Fan et al., 2019; Fratescu, van Moorselaar, & Mathot, 2018). Second, in Bahle et al. (2018) participants searched for a different target feature (e.g., shape) on every trial (requiring a VWM template representation) and simultaneously remembered a feature value on a different feature dimension (e.g., color) for a memory task. Under the single-item hypothesis, the unitary template state should have been occupied by the search target, leaving the memory item in an accessory state that was inert with respect to guidance. Yet, memory-matching distractors reliably captured attention, observed both on manual search RT and on the probability of distractor fixation (see also B. Zhang, S. Liu, M. Doro, & G. Galfano, 2018).

Although capture effects provide support for the multiple-item hypothesis, there are limitations to this method. Capture effects might significantly underestimate the capabilities of strategic guidance by multiple items because they reflect the automatic influence of VWM representations on attentional orienting when participants have incentive to avoid attending to memory-matching items. Additionally, capture effects often provide little information about the frequency or strength of the guidance by multiple items. Although such data can be estimated using direct measures of capture, such as fixation probability (Bahle et al., 2018; B. Zhang, S. H. Liu, M. Doro, & G. Galfano, 2018), the large majority of studies have inferred capture from mean manual RT. In these studies, one cannot eliminate the possibility that episodes of capture were rare, perhaps reflecting lapses in control over the template representation (see discussion in Bahle et al., 2018).

Present Study

In the present study, we developed an approach that allowed us to conduct the most direct and rigorous tests of the single-item and multiple-item hypotheses to date, probing the central question of interest: whether attention can be strategically guided by multiple items in VWM simultaneously. To do this, we modified a redundancy gains paradigm originally developed in the literature on decision-making and response-activation in simple target-detection tasks (Miller, 1982; Mordkoff & Yantis, 1991; Raab, 1962; see also Krummenacher, Müller, & Heller, 2002). The logic of the method is explained in the following sections. First, we discuss the structure of the task. Second, we discuss the assumptions of the competing theoretical models (single- and multiple-item hypotheses) within the context of the task. Finally, we discuss the analytical approach that allowed us to discriminate between model predictions.

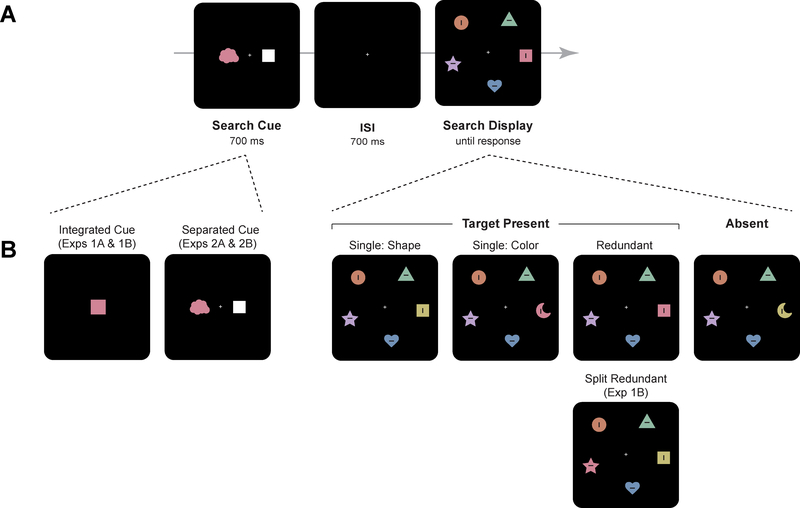
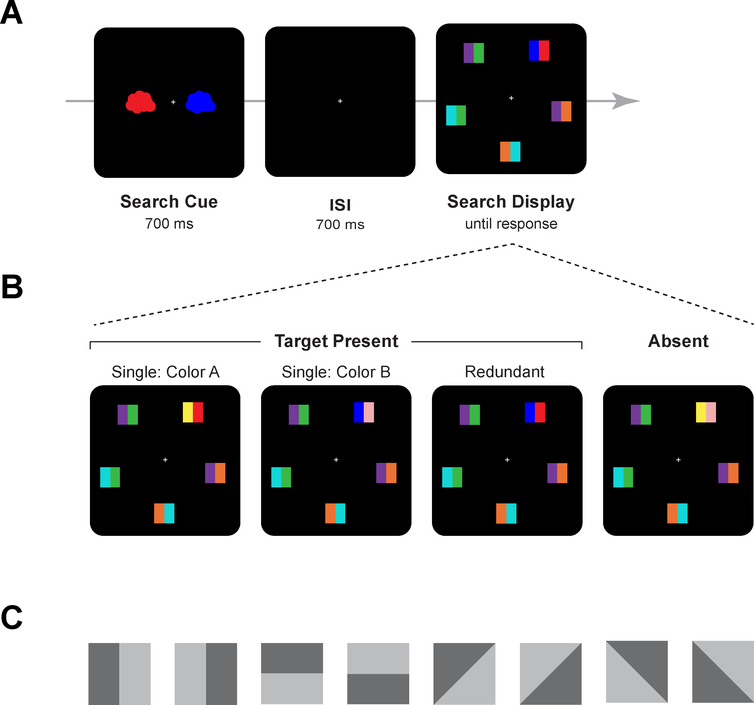
In the basic method (Figure 1), participants first saw two cued features values (e.g., a color and a shape) that defined the properties of a target in a subsequent search array. The specific value of on each feature dimension changed randomly from trial to trial, which required participants to maintain the two cued features in VWM.¹ The search task was present/absent (except in Experiment 2B). Participants searched for the presence of either or both of the two cued features. For example, in the trial illustrated in Figure 1, participants searched for the presence of either a red item in the search array or a square item. On target-absent trials, neither cued feature was present in the array. Critically, there were three different types of target-present trials. On color-match trials, the target matched the cued color but not the cued shape. On shape-match trials, the target matched the cued shape but not the cued color. (Collectively, these two are termed single-target trials.) Finally, on redundant-target trials, the target matched both cued features.

Figure 1.

A) Sequence of events in a trial of Experiments 1 and 2. Participants first saw a search cue consisting of two feature values (a color and a shape) that randomly changed on a trial-by-trial basis. Next, they searched for a target object in the search array that matched either of the two cued feature values. The search task was present/absent, except in Experiment 2B (internal bar orientation report). Note that the embedded horizontal or vertical bars were present in all sub-experiments but were task relevant only in Experiment 2B. B) Search conditions and other manipulations. The right side of Panel B illustrates the main search conditions. There were three target-present conditions. In the two single-target conditions, the target object matched one of the two cued feature values but not the other. In the redundant-target condition, the target matched both feature values. Finally, on target-absent trials, neither feature value was present (there were no target-absent trials in Experiment 2B). Note that in Experiment 1A, 2A, and 2B, when redundant target features were present, they were associated with the same object in the search array. In Experiment 1B, they were associated with different objects in the search array. Finally, the left side of Panel B illustrates the cue manipulation. In Experiment 1 the two cued feature values were presented as part of a single object (integrated cue). In Experiment 2, these values were presented as parts of two separate objects (separated cue).

A comparison of RT distributions from the single- and redundant-target conditions can be used to discriminate between various models of the architecture underlying the interaction between VWM and attentional guidance. Here, we considered three possible classes of architecture. The first, a serial model, holds that attention can be controlled by only one feature at a time and thus that the two cued values would need to be searched sequentially. This is consistent with a relatively strong formulation of the single-item hypothesis where an “item” is equivalent to a feature. (Later, in Experiments 2 and 3, we consider a formulation of the single-item hypothesis in which an “item” can span multiple feature values chunked into a single object.) We also considered two parallel guidance models that would be consistent with the multiple-item hypothesis. In the first, a parallel, separate-activations model or race-model, the two features are assumed to control attention simultaneously but independently; on redundant-target trials, the two guidance operations would unfold in parallel, and the faster of the two would determine response time for that trial. In the second, a parallel-coactive model, guidance from the two cued values is combined (e.g., by pooling or direct summation) to influence attentional allocation.

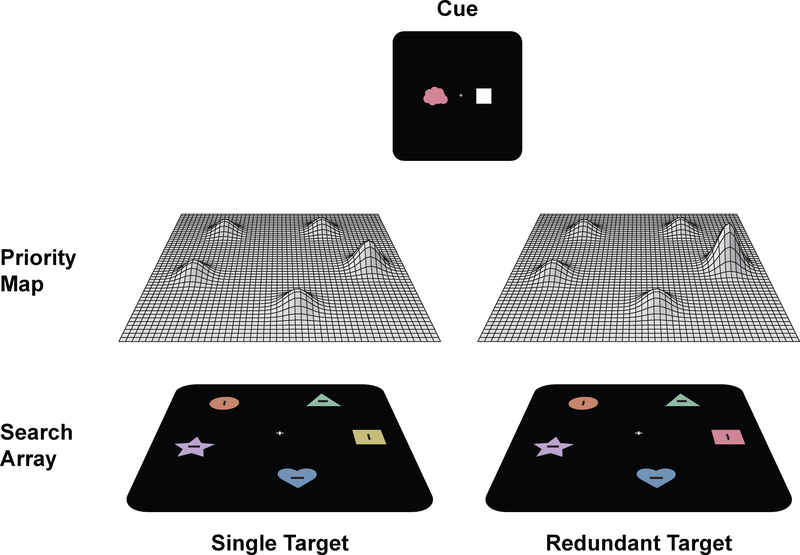
To make this last model explicit, consider activity on a spatially organized neural map coding the priority of currently visible objects as targets of spatial attention and gaze (for a review, see Zelinsky & Bisley, 2015). Top-down control from VWM would be applied broadly to the priority map, resulting in increased activity at locations containing matching features. On redundant-target trials (right-side of Figure 2), the two sources of guidance from VWM would sum on the priority map (i.e., coactivate), generating a larger signal at the target location compared with single-target trials (left-side of Figure 2). We consider this type of coactive architecture the most plausible implementation of the multiple-item hypothesis given that convergent guidance, either from bottom-up or top-down sources, is a core assumption of most models of attention and visual search (e.g., Wolfe, 1994). However, these assumptions have never been tested before in the context of guidance from multiple different items in VWM.² Thus, our primary goal was to either confirm or disconfirm a coactive architecture of guidance from multiple representations in VWM on the priority map used to guide attention.

Figure 2.

An illustration of the possible implementation of coactive guidance from multiple items in VWM on the priority map used to guide attention. The left-side of the figure illustrates guidance on single-target trials. When searching for a red item or a square item, a green square in the display will generate a larger salience signal than other items given its match to the cued shape, allowing attention to be oriented to the target location. The right-side of the figure illustrates guidance on redundant-target trials. A redundantly matching red square will create a salience signal that is larger than could have been generated by any single-feature match, because top-down guidance from the two feature values sum at the target location, allowing more efficient orientating to the target than could have been generated in the single-target condition. In other words, guidance from the two feature values coactivate at the target location.

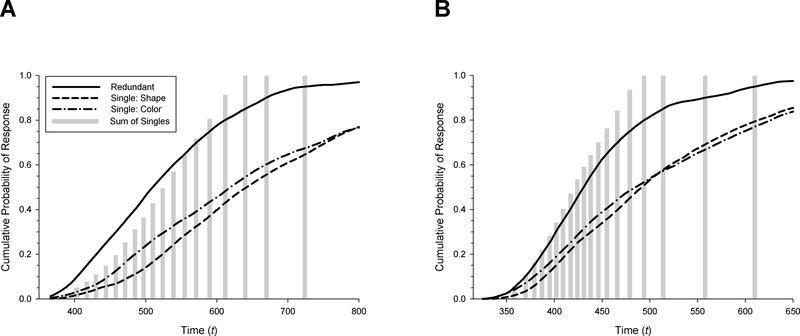
In the current paradigm, all three models predict redundancy gains in central-tendency measures of RT (i.e., faster mean RT on redundant-target than on single-target trials, see, e.g., Raab, 1962). However, well-developed analytic techniques exist for testing between the distributional predictions of models that involve coactivation and those that do not (Miller, 1982; Mordkoff & Yantis, 1991). The details of this analysis are discussed in the methods of Experiment 1; however, we provide an overview here. At the broadest level of description, we tested for the presence of redundant-target trials with RTs that were too fast to have been generated by a separate-activation model (including both parallel, separate activation models and serial models, such as the single-item hypothesis). Such trials are consistent with coactivation in the guidance of attention. Specifically, we tested for the presence of trials in the redundant-target condition with RTs that were faster than could have been generated by the faster of two independent processes operating in parallel. To illustrate this test, consider the sample distributions shown in Figure 3A. These cumulative distribution functions (CDFs) reflect the observed probability of generating a response in the search task by a particular time, t. (Note that the steeper rise in the redundant-target condition, compared with the single-target conditions, indicates a redundancy gain.) The parallel, separate-activations model (or race model) holds that the two guidance processes each constitute an independent opportunity to observe a response by a particular value of t, with these probabilities estimated from the single-target conditions. Thus, under this model, the sum of the probabilities observed in the single-target conditions places an upper bound on the response probabilities that should be observed in the redundant-target condition. This is termed the race model inequality (RMI; Miller, 1982; Mordkoff & Yantis, 1991). Summed probabilities for the single-target conditions are illustrated as gray bars in Figure 3A for values of t that correspond to the 5^th to the 95^th percentile of the redundant-target distribution. Observe that, in Figure 3A, response probability in the redundant-target condition consistently exceeds the sum of the single-target probabilities for the faster responses in the distribution. This constitutes a violation of the RMI, indicating that there were a substantial proportion of trials with RTs faster than could have been generated by the faster of two independent guidance processes operating in parallel. In contrast, Figure 3B illustrates a situation in which there is a redundancy gain but no violations of the RMI (i.e., the probability of a response in the redundant-target condition never exceeds the sum of the single-target probabilities). As discussed above, violations of the RMI falsify all separate activation models—including all serial models and all parallel, separate-activation models—and provide support for multiple-item models that involve coactivation.

Figure 3.

A) Hypothetical cumulative distribution functions (CDFs) illustrating a data pattern the violates the race model inequality (RMI). Lines indicate the cumulative probability of response by a particular time, t, for the three target-present conditions. Gray bars indicate the sum of the single-target probabilities for values of t corresponding to the 5^th to the 95^th percentile of the redundant target distribution. Violations of the RMI (i.e., higher probability of response for the redundant target condition than the sum of the single-target probabilities) are present for lower percentiles (i.e., faster trials). B) Hypothetical CDFs illustrating a data pattern that does not violate the RMI. Note that at no point does the probability of response in the redundant target condition exceed the sum of the single-target probabilities.

In addition to testing for parallel, coactive guidance from multiple items in VWM by probing for violations of the RMI, we had two secondary goals. First, we tested the single-item and multiple-item hypotheses using a method that probed the direct interaction between VWM representations and ongoing cognitive operations, without the need for explicit memory access or report: that is, we examined the effects of WM representations rather than access to WM representations. Thus, the present method has the potential to provide novel evidence relevant to the larger debate over WM architecture, focused specifically on the question of whether WM can maintain multiple representations that are “active” in the sense of controlling other on-going cognitive processes (here, the allocation of attention). ³ Second, we probed the nature of the structural units in VWM that organize guidance (i.e., what constitutes an “item” in VWM). This issue has not received a great deal of attention in the VWM-guidance literature, as researchers have either been agnostic on this issue or have simply assumed that features associated with different perceptual objects are maintained as individual representations in VWM (i.e., that the object is the structural unit). However, in the general WM literature, a key consideration when evaluating theories concerns whether information associated with discrete stimuli can be integrated or chunked into composite representations (Gilchrist & Cowan, 2011; Oberauer & Bialkova, 2009, 2011). In the present study, we addressed this issue in two ways. First, we examined whether multiple-feature guidance from VWM is coactive when the two features have been encoded from the same cue object (Experiment 1) versus two different cue objects (Experiment 2). The former possibility is consistent with the multiple-item hypothesis and a formulation of the single-item hypothesis in which an item can contain multiple features from the same cue object; the latter is consistent with only the multiple-item hypothesis. Second, we probed the possible role of chunking in guidance by modifying the paradigm (Experiment 3) to minimize the possibility that participants could integrate multiple cued features from separate objects into a unitary template representation.

To preview the results, we observed robust evidence of coactivation in all experiments where they were predicted to occur under the multiple-item hypothesis, including several cases for which the single-item hypothesis was inconsistent with the results. Further, violations of the RMI were observed both when the two cued features were attributes of the same object in the cue display and when they were attributes of different cue objects, again consistent with the multiple-item hypothesis, but not the single-item hypothesis. Moreover, we observed violations in a paradigm that required shifts of attention to the target rather than depending on a simple target present/absent decision, expanding the current findings beyond the extant redundancy gains literature. Finally, evidence of coactivation was observed even under conditions that strongly limited the possibility of integration/chunking, ruling out certain modified versions of the single-item hypothesis. Together, the results provide strong evidence in favor of the multiple-item hypothesis, and, more broadly, support a view of WM in which multiple items—whether defined as a collection of features or objects—can be active simultaneously within the focus of attention.

Experiment 1A and 1B

The primary goal of Experiments 1A and 1B was to assess the extent to which two features can guide attentional priority in a coactive manner. In both experiments, participants searched for the presence of either of two features (a color and a shape) among a heterogeneous display of colored shapes (see Figure 1). The cued feature values on each dimension changed randomly on a trial-by-trial basis, requiring VWM. In the cue display, the two features were presented as part of an integrated object (integrated cue). To implement the redundancy gains method, there were three different types of target-present displays. On color-match displays, the cued color was present in the display, but the cued shape was not. On shape-match displays, the cued shape was present in the display, but the cued color was not. Together, these two conditions are referred to as single-target trials. Finally, on redundant-target trials, both cued features were present in the display. If we observed coactivation in this latter condition, it would provide strong evidence that multiple features can guide attention simultaneously.

In addition to Experiment 1’s primary goal, we also probed whether coactivation (if present) depended on whether the cued features on redundant-target trials were associated with one or two target objects in the search display. Specifically, on the redundant-target trials of Experiment 1A, both cued features were present in the same object in the search display. In contrast, on the redundant-target trials of Experiments 1B, both cued features were present but in two separate search-array items, both of which were targets. That is, one search-array item matched the cued color (but not the cued shape) and another matched the cued shape (but not the cued color). Thus, Experiment 1B served as a test of model assumptions: violations of the RMI should be observed only when the relevant features occur at the same object location (Experiment 1A), as only this situation would lead to summing of activation within the spatially-organized priority map (Figure 2).

Method

Participants

Twenty-four participants completed each of the sub-experiments. All human subjects’ procedures were approved by the University of Iowa Institutional Review Board. A given participant completed only one experiment. The participants were recruited from the University of Iowa community, were between the ages of 18 and 30, were naïve with respect to the hypotheses under investigation, and received course credit for their participation. An N of 24 was chosen based on the typical finding of a standardized effect size of at least .333 when violations of the RMI are both predicted and observed (Mordkoff & Danek, 2011; Mordkoff & Yantis, 1991). We replaced participants with false-alarm or miss rates greater than 20%. Seven subjects were replaced in Experiment 1A and six in Experiment 1B. Of the final 24 participants in each sub-experiment, the number of female participants was 12 in Experiment 1A and 10 in Experiment 1B.

Apparatus

The apparatus was the same for all Experiments reported. The stimuli were presented on an LCD monitor (resolution: 1280 × 960 pixels) with a refresh rate of 100 Hz at a viewing distance of 77 cm, maintained by a chin and forehead rest. Manual responses to both the search and memory test were collected with a USB response pad. The experiment was controlled by E-prime software (Schneider, Eschmann, & Zuccolotto, 2002).

Stimuli

All stimuli were presented against a black background with a white central fixation cross subtending 0.61° × 0.61° visual angle. There were six possible shape values, (square, star, triangle, circle, heart, and crescent). There were also six possible color values, each from a different color category: red (x = 0.36, y = 0.29, 72.1 cd/m²), orange (x = 0.42, y = 0.38, 71.0 cd/m²), yellow (x = 0.35, y = 0.40, 135.7 cd/m²), blue (x = 0.23, y = 0.22, 64.2 cd/m²), green (x = 0.29, y = 0.35, 104.2 cd/m²), and purple (x = 0.26, y = 0.19, 76.1 cd/m²). Note that we used a relatively desaturated set of colors (see Figure 1). These were chosen based on pilot testing to produce broadly equivalent distributions of RT for the two types of single-target trials (shape-target and color-target). The objects used in the cue and search displays were combinations of one feature from each dimension, subtending 2.06° × 2.06° on average.

For the cue display, a color and a shape were randomly chosen on each trial to be the search target features for that trial. A target was defined by the presence of either feature. For example, if the target features were chosen to be blue and circle, the task would be to search for the presence of any blue item or any circular item. The cued color and shape were presented centrally as a single object before the onset of the search array (e.g., a blue circle).

For the search array, each item had a unique color and a unique shape. The array consisted of five search items, evenly arrayed around a virtual circle with a radius of 4.12°. To vary the absolute positions of objects, the array was randomly offset on each trial by an angular value between 0 and 71 degrees. On target-present trials, the search display contained one item that matched one of the cued features (color-target or shape-target; collectively termed single-target trials), or the search display contained both cued features (redundant-target trials). On the redundant-target trials of Experiments 1A, the two matching features were attributes of the same search object. On the redundant-target trials of Experiment 1B, the two matching features were attributes of different search objects. On target-absent trials, none of the items in the display possessed either of the cued features. Finally, each search item had an internal, black line (1.03° × 21°) that was oriented horizontally or vertically (randomly chosen for each object). Line orientation was irrelevant to the present/absent task in Experiments 1A and 1B but was relevant to the task in Experiment 2B. It was included in Experiments 1A, 1B, and 2A to equate stimuli across Experiments 1 and 2, which were designed as a group.

Procedure

The trial event sequence is illustrated in Figure 1. Each trial began with a presentation of a central fixation cross for 500 ms, followed by the cue display for 700 ms, another 700-ms fixation cross, and finally the search array, which remained visible until manual button response regarding the presence/absence of the cued features. On incorrect trials, feedback was provided (“Incorrect!” in white, Arial font, 1000 ms duration). After correct response or incorrect feedback, there was 500 ms blank inter-trial-interval before the fixation cross for the next trial appeared.

Upon arriving for the experimental session and providing informed consent, participants were given oral and written instructions. They then completed a practice block of 24 trials. Finally, they completed 30 experimental blocks of 24 trials each. The 24 trials in each block were divided evenly between four conditions: color-target, shape-target, redundant-target, and target absent. Trials from the various conditions were randomly intermixed within each block. Participants were required to take at least a seven second break between blocks, though they were able to rest for as long as desired. The entire experiment lasted approximately 55 minutes.

Data Analysis

The primary analysis concerned tests of the rule that all separate-activations models—including single-template, serial models—must obey. In the context of target-detection tasks, this rule is known as the race-model inequality (RMI; Miller, 1982; Mordkoff & Yantis, 1991), and the same label will be used here. The RMI uses the data from the single-target conditions to set an upper bound for the redundant-target condition on the assumption that each feature match (between cue and display object) constitutes an independent opportunity for at least one match to be detected. Thus, the rule must be obeyed by both serial models and parallel models under which coactivation does not occur. In contrast, parallel models with coactivation, such as a multiple-template model with activation summation on the priority map, do not need to obey the RMI.

As written, the RMI concerns the cumulative distribution functions (CDFs) for the redundant-target condition and each of the two single-target conditions. In what follows, a redundant-target trial will be denoted by “Ts & Tc” which, for present purposes, stands for target that matches the cued shape and target that matches the cued color, whereas the two single-target trials will be “Ts only” and “Tc only.” Using this standard notation (Miller, 1982; Mordkoff & Yantis, 1991), the RMI is:

$$p(RT<t|Ts\&Tc)\le p(RT<t|Ts)+p(RT<t|Tc)$$

where the left side of the equation is the CDF for the redundant-targets condition and the right side is the sum of the two single-target CDFs.

In practice, tests of the RMI do not involve entire CDFs; instead, the rule is tested at each of many quantiles. Here, we tested the 5^th through 95^th percentiles in 5% steps (see Figure 3). Note, however, that even when the underlying system involves coactivation, violations of the RMI are only expected in the faster end of the distribution (i.e., the lower percentiles), because the left side of the RMI has a maximum value of 1, whereas the right side continues to 2 (which makes violation impossible for slower responses). Put another way, the test is not only one-sided (as implied by the inequality), but highly conservative, such that a significant violation of the RMI provides strong evidence that both cued features are playing a role in guiding attention on redundant-target trials. In addition, violations (when observed) are often smaller or even absent at the very lowest percentiles, as these can be influenced by rapid, anticipatory responses that do not reflect condition-specific processes (Mordkoff, 1992).

The way that tests of the RMI are conducted involves several steps. First, separately for each subject, the values of RT that correspond to the 5^th through 95^th percentiles of the redundant-target condition are found (see Figure 3). These will be the values of t at which the RMI will be tested for this particular subject. In the second step, still separately for each subject, obedience to the RMI is evaluated at each of the calculated values of t by subtracting the sum of the two cumulative probabilities of RT for the single-target conditions from the cumulative probability for the redundant-targets condition⁴. (Only a positive value is an actual violation of the RMI, but the specific signed value is always retained, such that a hypothesis test can next be conducted.) In other words, by some simple algebra, the RMI is tested via:

$$p(RT<t|Tc\&Ts)-[p(RT<t|Tc)+p(RT<t|Ts)]\le 0$$

where any positive value produced by the left side is a “violation” of the RMI.

In the last step, at each of the quantiles, the mean violation (across subjects) of the RMI is tested against zero using a one-sided, one-tailed, t-test (i.e., only positive mean violations are tested). Note how this last step involves matching the data across subjects in terms of percentile (i.e., the t-tests are conducted at the 5^th through 95^th percentiles) and not matching in terms of values of t. This is a form of “Vincentizing” (see Ratcliff, 1979), and it is done to both preserve the shape of the individual subject CDFs and to ensure that every subject plays a role in each of the tests. If matching were done using values of t, instead of percentile, then the CDFs would be “smeared” (with an onset equal to the onset of the fastest subject and an offset equal to the offset of the slowest subject) and only the fastest subjects would play a role in the critical tests of the RMI, which all occur at lower percentiles (because violations become impossible at the higher percentiles).

Prior to analysis, trials were removed for the following reasons: 1) the first 10 blocks of the experiment to eliminate practice effects (Mordkoff & Miller, 1993), 2) the first two trials from the remaining blocks, as these served as warm-up trials, 3) incorrect trials, and 4) trials after incorrect responses, to remove recovery effects (Rabbitt, 1966).

Results

In this section, we first report analyses over mean RT to assess the presence of redundancy gains. Note again that the mere presence of redundancy gains is predicted by all competing models. Second, we report the critical analysis of violations of the RMI, which can provide evidence in favor of a parallel-coactive model of multiple-feature guidance.

Redundancy Gains

Mean RT on the redundant-target trials were compared with mean RT on single-target trials, collapsing across shape target and color target. Reliable redundancy gains were observed in both sub-experiments: Experiment 1A [redundancy gain= 135 ms, with redundant-target mean = 528 ms and single-target mean = 663 ms, t(23) = 6.86, p < .001], and Experiment 1B [redundancy gain of 82 ms, with redundant-target mean = 561 ms and single-target mean = 643 ms, t(23) = 12.56, p < .001].

Violations of the RMI

The results for Experiment 1A and 1B are plotted in Figure 4. In addition to the critical violation plots, we also plot aggregate CDFs to show the relationships among contributing distributions. The individual subject CDFs, used to calculate the differences scores aggregated in the violation plots, are reported in the supplementary materials for each of the experiments in this study.

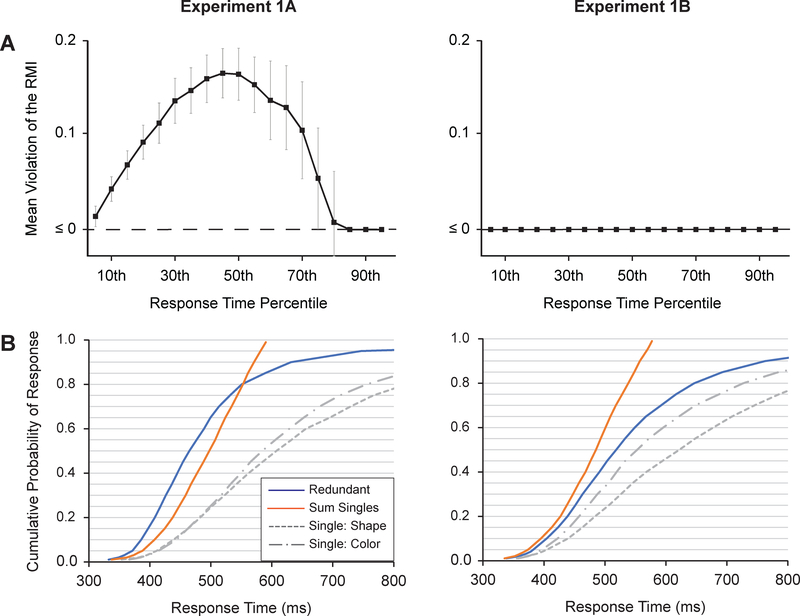
Figure 4.

A) Violation plots for Experiment 1. Mean violations of the race model inequality for the integrated-cue condition as a function of whether the redundant-target features were associated with the same search target object (Experiment 1A) or with two, separate search target objects (Experiment 1B). Error bars are condition-specific, within-subject 95% confidence intervals (Morey, 2008). Note that negative mean differences scores (as observed across the range of response percentiles in Experiment 1B) are plotted as ≤ 0, since tests of the RMI are inherently one sided. B) Aggregate cumulative distribution functions (CDFs) for the single-target conditions and the redundant-target condition. The orange line shows the sum of the two single-target CDFs. For this plot, participant RT values were averaged across corresponding percentiles in the participants’ RT distributions (i.e., Vincentized). In the violation plots in Panel A, difference scores were first calculated for each participant and then averaged. Thus, there may be subtle variations between the CDFs reported in Panel B and the mean difference scores reported in Panel A. The individual participant CDFs, from which the difference scores in the violation plots were calculated, are reported in supplementary materials.

In Experiment 1A, reliable violations of the RMI were observed from the 5^th to the 75^th percentile, all t’s > 2.20, all p’s < .02. In contrast, no violations were observed in Experiment 1B (all difference scores were negative, plotted at ≤ 0 in Figure 4), and thus no tests of the RMI were required.

Discussion

In Experiment 1A (integrated cue, and cued features integrated in a single target object) we observed robust violations of the RMI, consistent with a parallel-coactive architecture of multiple-feature guidance. This provides strong evidence against a single-item hypothesis formulation in which guidance is limited to a single feature at a time. Additionally, this evidence of coactivation was entirely absent in Experiment 1B, when the two cued features were attributes of different target objects in the search display on redundant-target trials. Thus, and consistent with the proposed effect of multiple features on attentional priority, violations occurred only when guidance by the two features could sum at a common object location within the priority map.

Experiment 2A and 2B

Although Experiment 1A provided evidence of coactivation from multiple feature guidance when the features were cued as an integrated object, it is possible that such coactive guidance would be eliminated if the cued features came from separate objects. Thus, in Experiment 2, we probed the issue of whether guidance depended on the number of objects maintained in VWM from the cue display. Specifically, in Experiment 2, the cue was split into two separate objects presented to the left and right of central fixation (separated-cue condition). One cued object was a relatively colorless (white) shape, and the other cued object was a relatively shapeless (cloud) color. In this separated-cue experiment, we assumed that participants would maintain two separate representations of the two objects in VWM (an assumption tested further in Experiment 3). Evidence of coactivation would then provide strong support for the multiple-item hypothesis (and rule out a formulation of the single-item hypothesis in which multiple feature guidance is only possible when the features are integrated in the same object), as it would suggest that two object representations in VWM can guide attention simultaneously.

In addition to the primary goal of Experiment 2, we also probed whether the coactivation observed in Experiment 1A reflected summed activation at a decision or response-activation stage rather than summed activation in the guidance of spatial attention to a target location. The former possibility is a plausible alternative explanation, as participants responded to the presence of the cued features in the search display in Experiment 1. Note that the lack of violations in Experiment 1B (split target) provides little or no evidence against this possibility because the same pattern of results – i.e., violations when both cued features are parts of one target object and no violations when the cued features are parts of different target objects – has been observed in the target-detection literature (Mordkoff & Danek, 2011). Thus, to provide a direct test, we modified the method of Experiment 2A such that participants were required to report a secondary feature of the search target. Specifically, Experiment 2B was identical to Experiment 2A, except all trials were target-present trials, and participants reported the orientation of a line superimposed over the target object (horizontal or vertical). This method required attention to be allocated to the target location. In addition, the method probed whether the results from Experiment 2A would generalize to a task where the reported value was orthogonal to the cued dimensions guiding search (shape and color). We note, however, that adding any source of variability after the hypothesized coactive stage can severely limit the ability to detect violations (Mordkoff, 1992). Thus, we expected the additional line discrimination and response selection operations in Experiment 2B to reduce our sensitivity to violations of the RMI, at least to some extent.

Method

Participants

Twenty-four new participants completed each sub-experiment in Experiment 2. The participants were recruited from the University of Iowa community, were between the ages of 18 and 30, were naïve with respect to the hypotheses under investigation, and received course credit for their participation. We replaced participants with false alarm or miss rates greater than 20%. Five subjects were replaced in Experiment 2A and one in Experiment 2B. Of the final 24 participants in each sub-experiment, the number of female participants was nine in Experiment 2A and 19 in Experiment 2B.

Stimuli and Procedure

The stimuli and procedure of Experiment 2A were identical to Experiment 1A, except that the cued color and shape were presented as two separate objects, 3.08 degrees to the left and right of central fixation. The color cue was presented as a part of a relatively shapeless object (cloud), and the shape cue was presented as part of a relatively colorless object (white). Of course, cloud was not a possible cued shape, and white was not a possible cued color. The size of the two cue objects was the same as in Experiment 1. The left/right locations of the color and shape cues were determined randomly on each trial. The method of Experiment 2B was identical to Experiment 2A, except that the 24 trials in each block were divided evenly between the two single-target conditions and the redundant-target condition. Moreover, in Experiment 2B, participants reported the orientation of the line embedded within the target object, pressing the left button to indicate horizontal and the right button to indicate vertical.

Results

Redundancy Gains

Reliable redundancy gains were observed in both Experiment 2A [redundancy gain = 195 ms, with redundant-target mean = 577 ms and single-target mean = 772 ms, t(23) = 19.1, p < .001] and Experiment 2B [redundancy gain = 257 ms, redundant-target mean = 798 ms and single-target mean = 1055 ms, t(23) = 22.5, p < .001].

Violations of the RMI

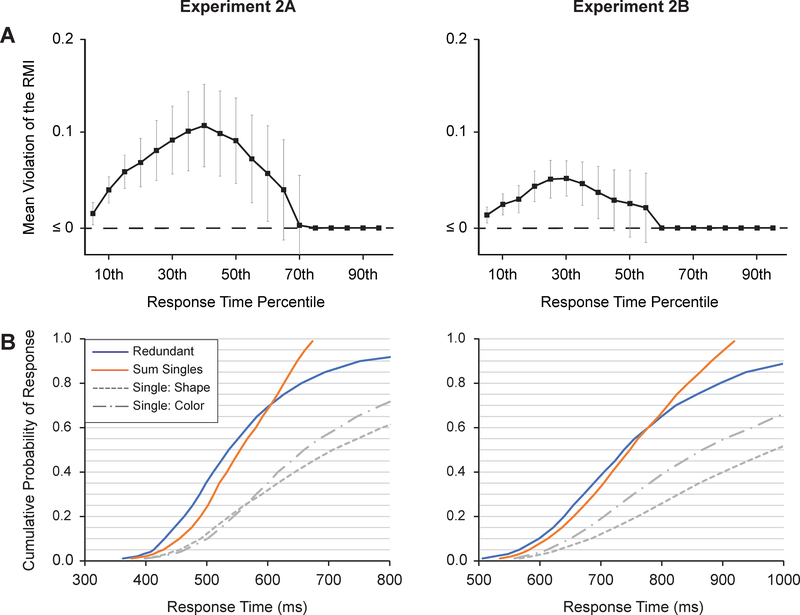
Reliable violations were observed in Experiment 2A from the 5^th to the 60^th percentile, all t’s > 1.95, all p’s < .04 and in Experiment 2B from the 5^th to the 40^th percentile, all t’s > 2.33, all p’s < .02 (Figure 5). Note that the absolute magnitudes of the violations were smaller in Experiment 2B compared with Experiment 2A, which was likely caused by the additional sources of variance (line discrimination and response selection) that limit the ability to detect violations (Mordkoff, 1992).

Figure 5.

A) Violation plots for Experiment 2. Mean violations of the race model inequality for the separated cue condition as a function of whether the response was a present/absent decision (Experiment 2A) or report of a secondary feature of the target object (Experiment 2B). Error bars are condition-specific, within-subject 95% confidence intervals (Morey, 2008). B) Aggregate cumulative distribution functions (CDFs) for the single-target conditions and the redundant-target condition. The orange line shows the sum of the two single-target CDFs. Given differences in the method of aggregation, there may be subtle variations between the CDFs reported in Panel B and the mean difference scores reported in Panel A.

Discussion

Robust violations of the RMI were observed when the features to be maintained in VWM were attributes of different objects in the cue display. In this condition, it is likely that the cued features were represented as two discrete objects in VWM, indicating that multiple object representations in VWM can guide attention in a parallel, coactive manner, thus supporting the multiple-item hypothesis and ruling out a formulation of the single-item hypothesis in which the item of guidance is a single, multiple-feature object. These violations were also present when the task required a shift of attention to the target object (Experiment 2B) to report a secondary feature value, consistent with simultaneous guidance of attention to the target location by multiple items in VWM. This demonstrates that coactivation is unlikely to be occurring solely at the level of decision or response-activation, as violations were observed when the reported feature value was orthogonal to the dimensions relevant for target detection and localization.

Experiment 3

In Experiment 2, we observed robust violations of the RMI when the two cued feature values were associated with different objects in the cue display, suggesting parallel, coactive guidance by multiple object representations in VWM. However, it is possible that participants extracted the relevant features from each of the two cue objects and combined them into a single VWM representation (e.g., converting the representation of a blue cloud and a white circle to a single representation in VWM of a blue circle; for a similar explanation in the general WM literature, see Oberauer & Bialkova, 2011). That is, they may have chunked shape and color into a single, multiple-feature template representation.

In Experiment 3, rather than having participants search for a color and a shape simultaneously, we had them search for two colors simultaneously among a heterogeneous display of two-colored objects (see Figure 6A). The two colors were presented separately in the cue display. In the search display, the search shapes were squares that had two colored regions. Importantly, there were eight possible configurations of the two-colored regions (see Figure 6B), and the specific configuration was randomly selected on each trial, so that participants could not predict (and thus could not prepare for) the configuration of colors in the target item.

Figure 6.

A) Illustration of the sequence of events in Experiment 3. B) Illustration of the three target-present conditions and the target-absent condition for this example trial. C) Possible configurations of colors within the two-color objects in the search display.

We considered two possible mechanisms by which two colors could be integrated into a unitary VWM representation, and the design was intended to eliminate them as plausible accounts of the predicted coactivation results. First, participants might combine two colors by representing an intermediate color in color space or by representing a broad region of color space that contains both colors. For this strategy to work, the two cued colors would need to be linearly separable from the colors of the distractors. By using a large set of colors (eight), we ensured that there would be extremely few trials on which the cued colors were linearly separable from the distractor colors, precluding such a strategy. Second, it is possible that the two colors could be integrated into a single object representation by representing them as discrete sub-regions of a single object. Note that this type of integration would potentially violate the core assumptions of the single-item-template hypothesis, as it would constitute the maintenance of multiple discrete representations of color in the template state. Nevertheless, we made the particular configuration of colors in the search array unpredictable, so that participants could not reliably prepare a unitary template representation that would correspond to the configuration of colors in the search array, nor could they search for a particular edge boundary between the two colors, as the type of edge between the two colors changed randomly on a trial-by-trial basis.⁵ Thus, violations of the RMI in this experiment would provide strong converging evidence that the two features generating parallel, coactive guidance were associated with distinct representations in VWM.

Method

Participants

Twenty-four new participants from the University of Iowa completed the experiment for course credit. Seven participants were replaced for high false alarm rates. Of the final 24, 18 were female.

Stimuli

There were eight possible color values for the search cue and items in the display, each from a different color category: red (x = 0.63, y = 0.33, 50.3 cd/m²), orange (x = 0.55, y = 0.39, 66.9 cd/m²), yellow (x = 0.39, y = 0.49, 160.0 cd/m²), pink (x = 0.44, y = 0.24, 62.4 cd/m²), blue (x = 0.15, y = 0.05, 25.3 cd/m²), green (x = 0.31, y = 0.61, 79.8 cd/m²), purple (x = 0.21, y = 0.08, 32.3 cd/m²), and cyan (x = 0.22, y = 0.31, 114.9 cd/m²). On each trial, two colors were chosen randomly to be the cued colors for the present trial (e.g., blue and red). In the cue display, one color “cloud” was presented to the left of fixation and the other to the right of fixation. The search array was composed five squares, arrayed in the same manner as in Experiment 1. The squares were composed of two, equally-sized color regions, divided either on the vertical dimension, the horizontal dimension, or one of the two diagonals. All items in the search array had the same basic configuration, and configuration type was selected randomly from the eight options on each trial (Figure 6B).

In all conditions, one item in the search display was chosen to have two unique colors within the array. On redundant-target trials, these two colors were the two cued colors. On single-target trials, one of the colors matched one of the cued colors, and the other did not. On target-absent trials, neither color in this item was a cued color. Thus, the conditions were equated for the presence of exactly one search item that possessed two unique colors in the array. This design feature was conservative: any property (e.g., uniqueness) that is correlated with the target equally in all conditions works against observing violations of the RMI. On target-absent trials, this left four of the eight colors available to be used in the remaining four distractors (since the two cued colors could not appear in the search array). To equate the composition of distractors, in all conditions, exactly four of the available colors were used to construct the four remaining distractors. The was done by cycling colors through distractors in the following way, where letters stand for colors: AB, BC, CD, DA. This method ensured that each of the four color combinations was unique. Specific colors were assigned within this structure randomly, and the locations of all search elements was also determined randomly. See Figure 6A for an illustration of an example search display.

As in previous experiments, there were 30 blocks of 24 trials each. On 18 trials in each block, one item in the search display matched at least one of the cued features. These trials were split evenly between color-match to the color presented to the left of fixation in the cue display, color-match to the color presented to the right of fixation in the cue display, and redundant-target trials that matched both colors. The remaining 6 trials were target-absent trials, in which none of the items in the display possessed either of the cued colors.

Procedure

To maximize sensitivity to potential violations of the RMI, we used the present/absent task used in all previous experiments (except Experiment 2B). Specifically, the task was identical to Experiment 1A, 1B, and 2A, except that participants searched for any object that contained a cued color. The trial event sequence and block structure were also the same as in these previous experiments

Results

Redundancy Gains

As in previous experiments, there was a large redundancy gain of 218 ms, with mean RTs of 594 ms and 812 ms for the redundant-target and mean of the two single-target conditions, respectively, t(23) = 16.3, p < .001.

Violations of the RMI

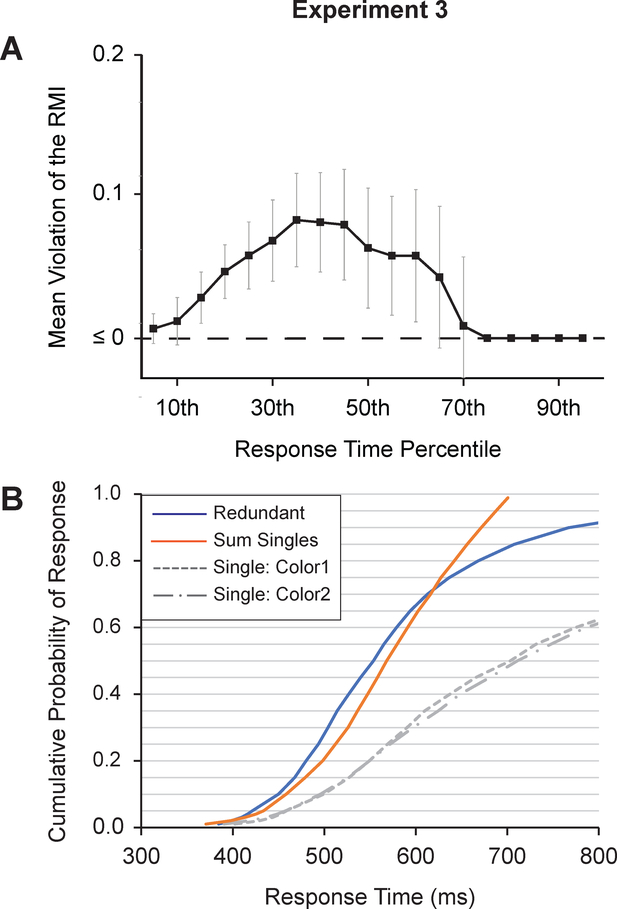
As illustrated in Figure 7, there were robust violations of the RMI from the 15^th to the 60^th percentile, all t’s > 2.13, all p’s < .03.

Figure 7.

A) Mean violations of the race model inequality for the two-color search task of Experiment 3. Error bars are condition-specific, within-subject 95% confidence intervals (Morey, 2008). B) Aggregate cumulative distribution functions (CDFs) for the single-target conditions and the redundant-target condition. The orange line shows the sum of the two single-target CDFs. Given differences in the method of aggregation, there may be subtle variations between the CDFs reported in Panel B and the mean difference scores reported in Panel A.

Discussion

Participants were able to simultaneously (and coactively) search for two colors maintained in VWM. This result, along with Experiment 1 and 2, provides strong evidence in favor of the multiple-item hypothesis, and, more broadly, a conceptualization of the focus of attention as spanning multiple representations that are not chunked into a single unit.

General Discussion

In the present study, our goal was to investigate the architecture of interaction between WM representations and ongoing cognitive operations. In particular, we probed whether multiple representations in VWM can simultaneously guide attention by implementing a redundancy-gain paradigm in which participants searched for the presence of either of two cued features in a search array: a color and a shape (Experiments 1 and 2) or two colors (Experiment 3), which changed on a trial-by-trial basis. We then tested for coactive guidance from the two cued features by assessing whether the distribution of RT on redundant-target trials contained a substantial proportion of responses faster than could have been generated by two independent guidance processes operating in parallel, i.e., violations of the race model inequality (RMI). Experiment 1 provided evidence that multiple features can guide attention simultaneously and in a coactive manner, and this coactivation was limited to the case that the two cued features were attributes of the same target object. Experiment 2 provided evidence that features from two different objects can guide attention simultaneously and in a coactive manner, and this coactivation was still observed when the task required attention to be directed to the target object. Finally, Experiment 3 demonstrated that multiple-feature, coactive guidance is observed even when the two guiding features are on the same dimension (color) and cannot be integrated into a single template representation. Together, the findings provide strong evidence that multiple representations in VWM can guide attention simultaneously.

In addition to providing key evidence to resolve the debate between the single-item template hypothesis and the multiple-item template hypothesis, the present results also mediate between competing theories of general WM architecture. These are distinguished on two, logically separable, issues. The first is whether limited capacity performance in WM tasks reflects a single functional state (the focus of attention in the embedded processes model, Cowan, 1999) or multiple states (a direct access component plus a more restricted focus of attention in the concentric activation model, Oberauer, 2002; see also Olivers et al., 2011). The second is whether the focus of attention—the state making representations available for report or for interaction with other, ongoing cognitive operations—is limited to a single item/chunk (McElree, 2001; Oberauer, 2002; van Moorselaar et al., 2014) or can span multiple items/chunks (Beck et al., 2012; Gilchrist & Cowan, 2011). The present data inform the second issue, providing support for the claim that the focus of attention can span multiple items that are not chunked into a single representation.

One major difference between previous work cited in favor of a single-item focus of attention (Garavan, 1998; McElree, 2001; McElree & Dosher, 1989; Oberauer, 2002, 2006; Verhaeghen & Basak, 2005) and the present study is that the former tasks required explicit access to WM representations (to support report, confirmation, or use in complex tasks), whereas the present tasks examined the effects of WM representations on the guidance of attention. Within the field of VWM, there is growing evidence that access to VWM representations involves processes that diverge structurally from the processes supporting VWM-based control of attention. In the work most closely related to the present study, Saiki (2016) used a redundancy gains method to examine feature binding and object structure in a VWM recognition task. Participants remembered two objects on each trial, each a combination of shape and color. In the test display, they saw a single object and reported a match to any of the remembered features. When two matching features were present, Saiki observed violations of the RMI, indicating coactivation in the operations supporting recognition and/or response selection. Moreover, this effect was observed when the redundant test object matched two features of a single remembered object but not when it matched two features associated with different remembered objects. The latter effect contrasts with the present finding of coactive attentional guidance from multiple features associated with different objects in VWM (particularly, Experiment 2A and 2B). Although there are significant differences in method between the two studies that preclude strong conclusions, the results are consistent with other evidence suggesting a dissociation between recognition processes and the guidance of attention: whereas recognition processes are quite strongly influenced by object structure in VWM, the guidance of attention from VWM is implemented in manner that appears largely independent of object structure (Hollingworth & Bahle, in press; Thayer, Bahle, & Hollingworth, 2019).

The present findings are consistent with other studies that have observed a multiple-item focus of attention in the general WM literature (Gilchrist & Cowan, 2011; Oberauer & Bialkova, 2011). However, these earlier findings depended on the use of dissimilar memoranda, whereas here we observed a multiple-item focus of attention for two similar stimuli (two colors in Experiment 3). This empirical difference may reflect differences in task demands and the potential for crosstalk. The tasks of Gilchrist and Cohen and Oberauer and Bialkova involved iterative updating of multiple items, and a multiple-item focus of attention may have been implemented because dissimilar items minimized the possibility for crosstalk. For example, in the Oberauer and Bialkova method involving spatial and numerical updating, spatial updating could not easily have been applied to a number, and numerical updating could not easily have been applied to a location. In contrast, a more restricted focus of attention is likely to be implemented when there is a strong possibility for crosstalk (e.g., when updating two different numbers or two different locations, Oberauer & Bialkova, 2011). In the present experiments, we implemented a single task (visual search), and not only was there no possibility for crosstalk between guidance from the two items, simultaneous guidance benefited performance. Thus, the present results are consistent with a view in which the span of the focus of attention is flexible (Cowan et al., 2005; Oberauer & Bialkova, 2011), with the capability to maintain multiple items when this is consistent with the structure of the task.

Integral to the concept of a flexible focus of attention or template state is the idea not all items maintained in VWM need necessarily interact simultaneously with attention. Indeed, the VWM literature generally supports a multiple-state account (Oberauer, 2002; Olivers et al., 2011). Specifically, when given strong incentive to prioritize only one of multiple items encoded into VWM, two studies indicate that the active or template state can be limited to a single item (Hollingworth & Hwang, 2013; van Moorselaar et al., 2014). In Hollingworth & Hwang, participants remembered two colors on each trial and received a retention-interval cue (a retro cue) that indicated the color most likely to be tested at the end of the trial (80% probability), allowing them to prioritize the cued item for retention. Following the cue but before the memory test, participants completed a search task in which a single colored distractor could be present that either matched or mismatched one of the memory colors for that trial. Distractors that matched the prioritized color reliably captured attention; distractors that matched the deprioritized color did not. This latter effect was observed even when the continuous report test at the end of the trial indicated that the deprioritized color had been retained precisely, indicating that performance in VWM tasks can be driven by relatively precise representations of perceptual features that are maintained in a state that does not interact directly with attentional priority. Thus, considered broadly, the literature on VWM and attentional priority support a hybrid model of WM architecture and VWM interaction with attentional guidance (see also Bahle et al., 2018; Hollingworth & Beck, 2016). VWM appears to be composed of states that do and do not interact with attentional priority. In addition, the template state, or focus of attention, can be flexibly configured to maintain one or multiple items.

In the present study, we have used the following terms interchangeably: active state, template state, and focus of attention. We have defined these terms functionally, as a state of VWM that allows for direct interaction with other, ongoing cognitive operations (specifically, the guidance of attention). This naturally leads to consideration of the extent to which an active state in VWM overlaps with an active neural representation, defined by sustained firing activity of subpopulations of neurons coding feature values (e.g., Goldman-Rakic, 1995). Such neural representation can be distinguished from both short-term changes in synaptic weights (i.e., activity-silent WM) and longer-term learning (for reviews, see Postle, 2015; Stokes, 2015). We make no strong claims about the overlap between our functional definition of active and the neurophysiological sense of active, especially as our data cannot speak directly to that topic. However, we believe it is plausible that there exists substantial overlap between these two constructs. As reviewed above, items that have been de-prioritized within VWM, yet remembered accurately, have minimal effect on attentional guidance (Hollingworth & Hwang, 2013; van Moorselaar et al., 2014). In addition, de-prioritized items in VWM transition from a neurally active state to an activity-silent state (LaRocque, Lewis-Peacock, Drysdale, Oberauer, & Postle, 2013; Lewis-Peacock, Drysdale, Oberauer, & Postle, 2012; Rose et al., 2016; Sprague, Ester, & Serences, 2016; Wolff, Jochim, Akyurek, & Stokes, 2017). Together, these finding suggest there may be a direct relationship between neural state and functional state vis-a-vis attentional guidance, with only neurally active VWM representations exerting substantial control over attentional orienting. Again, we stress that this is a hypothesis to be tested by future research and not a conclusion from the present data.

The present results also have implications for understanding the mechanisms by which multiple top-down feature cues interact to influence activity on attentional priority maps. Priority maps are winner-take-all mechanisms of attentional selection, with spatially-organized activity in the map representing the extent to which a location is prioritized for attentional selection (Zelinsky & Bisley, 2015). Ultimately, the priority map allows for competition among locations for selection, with one location winning control of motor behavior (e.g., a saccade), so as to complete coherent, goal-directed action. The topography of the priority map derives from both bottom-up and top-down sources of information. The bottom-up information is typically conceptualized as a saliency computation on incoming sensory input: those regions of the visual scene that have greatest local feature contrast have highest priority. However, these activations can be modulated by top-down control, as the transmission of sensory information to the priority map is filtered by top-down expectations of likely target features (Desimone & Duncan, 1995; Wolfe, 1994). This filtering process is typically implemented through the maintenance of a target template representation in VWM. Thus, the present results suggest that top-down guidance can be simultaneously implemented by multiple representations in VWM. Moreover, when features at a location in the priority map match multiple values in VWM, the boost in priority is coactive, leading to a higher priority than would be possible from any single feature match.

These findings for top-down guidance are broadly consistent with theories that posit convergent guidance from multiple feature dimension in the top-down control of priority (Bundesen, 1990; Wolfe, 1994). In Guided Search, priority can be influenced coactively by multiple task-relevant features (for example, when searching for a conjunction target). However, Guided Search and similar models were developed in the context of paradigms in which the top-down cues were static throughout an entire experiment and were likely to have been driven by long-term mechanisms of priority (Carlisle et al., 2011) rather than by online guidance based on rapidly changing VWM representations. The present results indicate that cue information maintained in VWM also leads to summation on the priority map in a coactive manner. Moreover, we demonstrate that coactive guidance from VWM does not depend centrally on whether the relevant features are associated with one object or multiple object representations. Finally, the present results are inconsistent with one key claim in Guided Search: namely, that only one feature from each feature dimension can contribute to the simultaneous guidance of attention. Under this assumption, coactive guidance can be implemented only across different dimensions: activity should sum for, say, combinations of color and shape but not for combinations of two colors. However, the results of Experiment 3 demonstrate that within-dimension cues also coactivate on the priority map. This is consistent with other, recent studies using static cues that have also demonstrated simultaneous guidance of attention by multiple colors (Grubert & Eimer, 2015; Irons, Folk, & Remington, 2012; Stroud, Menneer, Cave, & Donnelly, 2012).

Here, we found coactive guidance by multiple between- and within-dimension features, associated either with a single item or with multiple items in VWM. Does a similar architecture apply to the bottom-up computation of salience? Classic theories of visual attention (Treisman & Gelade, 1980; Wolfe, 1994) posit that feature dimensions are first processed independently but eventually summate on the master priority map. Krummenacher and colleagues tested these claims using a redundancy gains paradigm in several pop-out visual search tasks (e.g., Krummenacher et al., 2002). In one of the original versions of their task, participants searched for the presence of a target singleton that could differ from distractors in either color, orientation, or both. They observed violations of the RMI, and these violations were observed only when the redundant-target features appeared in the same object in the search display (cf. our Experiment 1A and 1B). Thus, there is evidence that bottom-up signals to the priority map sum in a coactive manner across dimensions in the same manner as observed for top-down guidance in the present experiments. However, it should be noted that target features in the Krummenacher et al. studies were always static. For example, the pop-out target was always a red or blue item among green distractors and/or a non-vertical item among vertical distractors. This could have allowed participants to learn the target- and distractor-defining properties over the course of the experiment and develop a strategic set for those feature values, generating top-down effects of coactivation similar to those observed here. Thus, although present evidence is consistent with the possibility that bottom-up activity from multiple features coactivates to guide attention, the extant data are not necessarily definitive.

The present findings and conclusions are also consistent with and extend previous work in the literature on decision-making and response-activation in simple target-detection tasks. To see this, it is important to note that performance in a typical redundant-targets detection task could easily involve the use of a top-down template for the target, as participants are asked to respond to pre-specified feature values, such as a particular color and a particular shape, and the targets do not “pop out” from the distractors. The main difference is that target-detection displays usually contain only one or two perceptual objects (Miller, 1982; Mordkoff, Miller, & Roch, 1996; Mordkoff & Yantis, 1991, 1993) such that locating the target(s), when present, is not what limits response speed. Viewed in this way, the present results extend the previous findings by demonstrating that attentional guidance, in additional to decision-making and response activation, also involves some form of coactivation.

At a more detailed level, the results from Experiments 1A and 1B, which showed that evidence of coactivation is only observed when redundant cued features (or targets) are parts of the same search-display object, matches what has been previously found for mere target detection (see, e.g., Feintuch & Cohen, 2002; Mordkoff & Danek, 2011). In the case of search that is being guided by matches to representations in VWM (i.e., the present results), this is argued to be due to the requirement that the redundant targets cause increases in activation at the same location within a spatially organized priority map. In the case of target detection (e.g., Mordkoff & Danek, 2011) the parallel pattern of results is argued to be due to the requirement that both targets be processed at the same time in order for their activations to have a chance to coactivate a target-present response.

Conclusion

In sum, the coactive guidance of attention by representations in VWM can occur for 1) multiple features encoded from one perceptual object, 2) multiple features encoded from separate perceptual objects, and 3) multiple features from separate perceptual objects that could not be chunked into a single representation. These findings provide strong evidence in favor of the multiple-item hypothesis. Taken together with the larger literature on VWM guidance, the results suggest a model of WM architecture in which there are qualitatively different functional states, and a focus of attention, or template state, that has the capability to span multiple discrete items.