Coexistence of Lipid Phases Stabilizes Interstitial Water in the Outer Layer of Mammalian Skin

Abstract

The lipid matrix in the outer layer of mammalian skin, the stratum corneum, has been previously investigated by multiple biophysical techniques aimed at identifying hydrophilic and lipophilic pathways of permeation. Although consensus is developing over the microscopic structure of the lipid matrix, no molecular-resolution model describes the permeability of all chemical species simultaneously. Using molecular dynamics simulations of a model mixture of skin lipids, the self-assembly of the lipid matrix lamellae has been studied. At higher humidity, the resulting lamellar phase is maintained by partitioning excess water into isolated droplets of controlled size and spatial distribution. The droplets may fuse together to form intralamellar water channels, thereby providing a pathway for the permeation of hydrophilic species. These results reconcile competing data on the outer skin’s structure and broaden the scope of molecular-based methods to improve the safety of topical products and to advance transdermal drug delivery.

Significance

Permeation of biologically active substances through the skin can cause human diseases while also providing mechanisms for their treatment. Connecting the permeability of chemical species to the molecular-level structure of skin is thus of scientific and medical importance; however, such connections remain elusive, especially in the case of hydrophilic species. Molecular simulation, which is employed to probe the phase behavior of the skin lipid matrix at the molecular level, reveals the existence of interstitial water droplets, whose coalescence can lead to channels that provide a hydrophilic permeation pathway. Therefore, the mobility of macromolecular drugs, so far understood only empirically, can be rationalized from the molecular properties of the skin’s lipids.

Introduction

The stratum corneum (SC) of mammalian skin provides the outermost and primary barrier against harmful chemicals and pathogens (1). Circumventing its function in a controlled manner has allowed for the transdermal delivery of drugs to treat a broad range of medical conditions (2). There is a demonstrated need to further understand how chemical species permeate through skin, which can be measured quantitatively (3) but has yet to be spatially resolved at the molecular level. Cells in the SC, called corneocytes, are almost entirely made up of a solid keratin mesh, within which the average water concentration amounts to less than 50% of the protein’s weight (4). A lipid matrix made up of a varying number of lipid lamellae envelops the stacked corneocytes and fills the narrow regions between them (5). The lipid matrix has been the object of many studies using biophysical methods, including electron microscopy (6,7), infrared spectroscopy (8,9), x-ray or neutron diffraction (10, 11, 12, 13), and molecular dynamics (MD) simulations (14, 15, 16, 17, 18, 19).

Unlike the plasma membranes of viable cells, the SC’s lipid matrix must minimize permeability (20) but also adapt to the mechanical strain and the changes in humidity and pH associated with epidermal growth. Such changes are particularly significant closest to the corneocytes’ surface, where keratin-bound lipids dictate the structure of the lipid matrix (21). Plasticity and low permeability are achieved by a mixture of lipid species, whose primary constituents are ceramides, cholesterol, and free fatty acids (FFAs) in comparable proportions. Because of the absence of electron-dense phosphate groups and the very low humidity of the lipid matrix, biophysical detection methods are limited in resolution, and significant uncertainty remains. The most widely accepted fact is that the lipid matrix is made up of multiple lamellae, lying parallel to the nearest corneocyte’s surface (6).

A single bilayer of skin lipids forms the so-called short-periodicity phase (SPP), ∼5.4 nm in thickness (22). However, the typical thickness of the lipid lamellae in extracted skin samples is ∼13 nm (6), consistent with the long-periodicity phase (LPP) observed in mixtures of skin lipids (23). The LPP and the SPP are often detected in coexistence with each other, but the relative stability of the two is not established universally (24), nor is that of other phases reported by diffraction of skin lipids (13).

To explain the LPP, a multilayer model has been proposed (12,25,26), wherein two ordered leaflets enclose partially disordered central layers, through which permeation is more likely. NMR experiments have also shown that the skin's lipids are in equilibrium between “solid” and “liquid” states, with the “solid” state being dominant (3). Because of the long times required for the LPP to emerge even when synthetic samples rich in the critically important long-chain ceramides are prepared in the laboratory, it is currently not possible to use computation to quantify the relative stability of each phase.

Aside from lamellae, bicontinuous cubic and other negative-curvature phases have also been reported by cryo-microscopy imaging (27) and MD simulations (14). These results correlate well with the intrinsic preference of ceramides for negative curvature (28), and it has been suggested that the skin lipids only form lamellar phases when confined between the rigid corneocytes (14). According to this hypothesis, lamellar phases would be obtained in vitro only through the use of a heating process targeted at reproducing the in vivo structure (23).

The aforementioned models of the organization of skin lipids do not explain all available experimental permeability data. For small lipophilic molecules, permeability measurements from skin samples led to the development of empirical models (29) whose accuracy is comparable to atomistic computations (30). However, hydrophilic molecules and macromolecules are found to permeate through the skin many orders of magnitude more quickly than through lipid bilayers (31). It has been hypothesized by an increasing number of researchers that these molecules exploit an alternative hydrophilic pathway, formed by sporadic water channels of microscopic diameter running through the SC’s lipid matrix (31, 32, 33, 34). Although evidence exists that permeation of water is inhomogeneous through the SC (33), it is unclear if such nanometer-size channels can be sustained through the lipid matrix.

This work uses a combination of coarse-grained (CG) and atomistic MD simulations to show that several of the lipid phases described above can coexist at close distance. Bilayers of a skin lipid mixture rich in long-chain ceramides are shown to contain a central disordered region, a property that is shared with the more complex LPP. Permeation across such an interface yields accurate predictions of the permeability of lipophilic molecules through the skin. Stable lamellae with LPP thickness are also formed via the spontaneous demixing of individual lipids, which follow with good approximation the distributions modeled from neutron diffraction (25,26). Such comparison is free from bias because the measured properties of skin lipids were not used to parameterize the CG intermolecular force field (18) or to prepare the initial simulation conditions (19).

Also shown in this study is that when water is allowed to diffuse into the lamellae, it aggregates into inverse-micellar droplets surrounded by lipid headgroups; despite significant humidity in the outer water buffer, these droplets account for only a 1.7 water/lipid ratio in the lamellar interior. The size and shape of the droplets are quantitatively described by a mechanical model based on experimental measurements of skin permeability (35). The same model predicts the formation of channels as a rare event, with activation energy well within the range that can be supplied by permeation enhancers. These results show that the ability of the skin’s lipids to appear in both lamellar and nonlamellar states explains the simultaneous presence of different permeability pathways for distinct chemical species.

Methods

MD simulation force fields for skin lipids

Forces between skin lipids in MD simulations were computed with atomistic and CG levels of resolution. Atomistic simulation parameters were taken from the CHARMM36 force field (36,37) for all lipids, CGENFF (38) for small molecules and ions, and TIP3P (39) for water. CG force field parameters for acyl chains, ester groups, hydroxyl groups, cholesterol, and water are from published work (40,41). Parameters for amides and the protonated carboxyl group were also derived from experimental properties of the corresponding liquids (see Supporting Materials and Methods).

MD simulation protocols

The programs NAMD (42) and LAMMPS (43) were employed to carry out MD simulations at the atomic and CG resolutions, respectively. Short-ranged Coulomb and Lennard-Jones terms were cut off at 1.2 nm for atomistic and 1.5 nm for CG simulations, with particle mesh Ewald (44) applied to long-ranged terms. Temperature (45,46) and pressure couplings (47,48) were used with a target temperature of 30°C and pressure of 1 atm unless otherwise noted. For each simulation, the pressure coupling was isotropic (NPT ensemble) until the density of the system reached equilibrium (typically less than 1 ns) and anisotropic (NP_xP_yP_zT ensemble) thereafter. Simulations with semi-anisotropic pressure couplings (P_y and P_z coupled) are specifically indicated in the Results. Integration steps were 2 and 10 fs for atomistic and CG simulations, respectively.

Preparation of initial structures for atomistic and CG simulations

Unless otherwise noted in the Results, CG simulations were initialized as fully randomized mixtures of lipids and water. Atomistic bilayers were prepared by assembling a monolayer system containing 32 molecules each of CER[NS], cholesterol, and behenic acid. Atoms were added to the fatty acid chains of 16 CER[NS] molecules to form CER[EOS] molecules, with the linoleic acid tails initially lying parallel to the monolayer’s plane. Each monolayer was replicated and rotated by 180° to give a symmetric bilayer, which was then solvated with water and neutralized by the addition of Na⁺ ions in the water phase in systems that contained unprotonated FFAs. The resulting 16,000-atom model (4 × 4 nm² bilayer area) was then equilibrated and replicated multiple times along the bilayer’s midplane and four times orthogonal to the bilayer. An additional 1.5 μs simulation of the hydrated bilayer was carried out to verify its stability at atomistic detail and mutual agreement with the self-assembled CG bilayers (Fig. S5). Conversion of CG models to atomistic resolution was done by placing atoms at randomized positions within the radius of the respective CG particle, followed by 20 ns of equilibration at constant volume. Coordinate manipulation and visualization were performed with VMD (70).

Potential of mean force and permeability calculations

For potential of mean force (PMF) calculations, each small molecule was inserted in a pre-equilibrated 4 × 4 nm² bilayer at different depths and the surrounding lipids re-equilibrated before sampling to minimize the emergence of spurious barriers associated with nonequilibrium work (15,16). Lipid molecules with atoms within a 2 nm radius from the small molecule in the initial structure were translated along the bilayer away from the small molecule; the length of the translation was defined so as to remove all clashes for the nearest lipid neighbors and linearly decreased to 0 for the lipids beyond 2 nm from the small molecule.

40 replicas for each system were simulated with NAMD, each covering a 0.4 nm interval around the initial depth. Sampling was enhanced by the adaptive biasing force method (49,50) as implemented in the Colvars module (51), with free energies computed via projection onto the collective variable of the internal atomic forces. Uniform coverage was achieved by using half-harmonic boundary restraints (often also called a flat-bottom potential) outside the interval; boundary forces were not included in the PMF. The centers of consecutive intervals were spaced by 0.1 nm, ensuring large overlap between neighboring windows and allowing to reduce hysteresis (49). After minimization and equilibration in the NP_xP_yP_zT (fully isotropic) ensemble for 0.3 μs, each PMF calculation was carried out for a total sampling time of 1 μs for each molecule (including all replicas) and integrated to produce the PMFs shown in Fig. S8. Diffusion coefficient profiles D(z) were obtained from the simulation trajectory after subtracting the time-dependent biasing force (52).

The positions and heights of the local maxima and minima of each PMF were defined by fitting quadratic curves. The permeability of the outer bilayer leaflet was defined as

$${k_P}^{\left[leaflet\right]}={\left(\int \frac{\text{exp}\left(\frac{G\left(z\right)}{k_{\text{B}}T}\right)}{D\left(z\right)}\text{d}z\right)}^{-1}\approx \text{exp}\left(-\frac{G^{\ast }}{k_{\text{B}}T}\right)D.$$ (1)

This approximation is justified by the occurrence of a single free-energy barrier of height G^∗ in each PMF, the exponential dependence of the expression on the free energy, and the fact that each diffusion coefficient D(z) is approximately constant along the bilayer’s normal. The simplified expression is used directly in Eq. 2 for clarity. As indicated in the Results, a single diffusion pathlength λ₀ was derived for all lipophilic molecules by linear regression of the expression above against the experimental skin permeabilities.

Hexatic order calculations

The hexatic order of model bilayers was calculated by mapping the positions of sphingosine and fatty acid chains separately, as well as cholesterol molecules, using the third aliphatic CG particle from the headgroup. Based on the lateral positions of each tail’s six nearest neighbors, its local hexatic order (|ѱ₆|) was then estimated by taking the norm of the bond orientation parameter (ѱ₆) introduced by Halperin and Nelson (53). Cholesterol molecules were treated as nearest neighbors when calculating the |ѱ₆| values for the ceramide tails: however, the averages in Fig. S4 are based solely on the |ѱ₆| values of the ceramide tails and do not include |ѱ₆| values of the cholesterol molecules for consistency across compositions.

Water exchange events and droplet cluster analysis

The water exchange data in Tables 1 and 2 and related droplet sizes were obtained by performing cluster analysis on the water particles in the configurations from the corresponding CG and AA simulations. For the CG simulations, the cluster analysis was performed using a distance of 0.66 nm to extract nearest-neighbor water particles. Note that 0.66 nm corresponds to the first minimum in the radial distribution function for the CG water particles (54). In turn, CG water particles separated by less than 0.66 nm were labeled as part of the same cluster. For atomistic water, a distance cutoff of 0.35 nm was instead used to establish adjacent (i.e., connected) water molecules. Isolated water particles and clusters containing fewer than 10 CG water beads (i.e., 30 water molecules) were labeled as “free” water; this ensured that small transient clusters were not misidentified as droplets. Note that the smallest droplet size observed in the two lamellae CG simulation corresponded to 52 CG water beads (i.e., 156 water molecules). The water layers were easily identified by their much larger size compared to the water droplets. In turn, water exchange events were detected by comparing a simulation’s successive configurations and monitoring the movement of water particles between droplets, layers, and free states.

Table 1.

Lamellar-Phase Simulations of Simple Ceramide Mixtures and Skin Lipid Mixtures

	Water/Lipid Ratios	Model System Dimensions	Initial Conditions	Model
CER[NS], 1:1 CER[NS]/CHOL (Fig. S1)	5:1	15 × 17 × 21 nm3	fully randomized	CG
		18 × 17 × 14 nm3
CER[EOS], 1:1 CER[EOS]/CHOL (Fig. S1)	5:1	43 × 39 × 39 nm3	fully randomized	CG
		42 × 28 × 39 nm3
1:0, 9:1, 8:2, 7:3, 6:4, and 1:1	5:1, 20:1	∼9 × 9 × 6 nm3	bilayer	AA, CG
CER[NS]/CHOL (Figs. S2 and S4)		∼9 × 9 × 8 nm3
1:0, 9:1, 8:2, 7:3, 6:4, and 1:1	5:1, 20:1	∼10 × 10 × 8 nm3	bilayer	AA, CG
CER[EOS]/CHOL (Figs. S3 and S6)		∼10 × 10 × 10 nm3
1:1:1 CER[NS]/CER[EOS]/CHOL (Fig. S7)	5:1	55 × 55 × 69 nm3	partially randomized	CG
1:1:2:2 CER[NS]/CER[EOS]/CHOL/FFA (Fig. 1)	5:1, 20:1	∼6 × 6 × 8 nm3	bilayer	AA, CG

First five rows, simple ceramide mixtures; last row, skin lipid mixture used in this work. Approximate system dimensions are taken from the final simulation snapshots.

Table 2.

Atomistic Simulations of Multi-Bilayer Systems Subject to Heating

Water/Lipid Ratio	Model System Dimensions	Protonated/Unprotonated FFA Ratio	Heating Period (95°C)	Relaxation Period (30°C)
5:1	16 × 16 × 32 nm3	1:1	0.25 μs	1.8 μs
5:1	16 × 16 × 32 nm3	1:0	0.25 μs	–
2:1	16 × 16 × 32 nm3	1:1	0.25 μs	–
5:1	24 × 24 × 32 nm3	1:1	0.25 μs	–
2:1	24 × 24 × 32 nm3	1:1	0.25 μs	–

The composition is 1:1:2:2 CER[NS]/CER[EOS]/CHOL/FFA.

Results

The first three Results sections examine the properties of skin lipids in the bilayer phase: 1) self-assembled models from CG simulations are validated against atomistic simulation and experimental data, 2) permeabilities of small neutral molecules across the SPP bilayer model are computed, and 3) it is demonstrated that heating of hydrated SPP bilayers induces the confinement of water into droplets or channels. In the following sections, multilayer lamellae are generated by self-assembly and shown to contain water droplets formed by the spontaneous aggregation of individual molecules at physiological temperature. As a control, the formation of dehydrated lamellae is also simulated and compared to experimental data for dry skin lipid samples. Lastly, the size and shape distributions of the droplets and their propensity to form continuous channels are analyzed.

Self-assembly of ceramide-cholesterol mixtures

Before conducting extensive CG simulations of skin lipid self-assembly, we first tested the CG model’s ability to reproduce properties of skin lipid systems (Table 1). Two ceramide species were considered based on the availability of experimental data for each using consistent preparation methods: these are the “long-chain” CER[EOS] with a C30:0 fatty acid chain that is ester linked to a C18:2 linoleic acid chain and the “intermediate-chain” CER[NS] with a C24:0 fatty acid chain. The CG simulation model was tested on simple mixtures of the two ceramides by characterizing the self-assembly of models of different sizes from randomized initial conditions (Table 1). A 5:1 water/lipid ratio was used, which is higher than the 1:1 or 2:1 water/lipid ratios inferred from neutron diffraction (13,55). Such conditions ensured that results are transferable between atomistic simulations, which treat water molecules independently, and CG simulations, which treat three water molecules as a single CG particle that does not form ordered hydrogen networks.

Mixtures of ceramides, cholesterol, and water self-assembled consistently into lamellar phases within hundreds of nanoseconds of CG MD simulation (Fig. S1). Partly because of the periodic boundaries, the direction of the lamellar repeats is homogeneous even at compositions at which a macroscopic lamellar phase is difficult to form, such as pure CER[NS] (22). Bilayers were also simulated in atomistic and CG resolution, and both were compared with experimental data. Simulations of CER[NS] exhibit gel or liquid lamellar phases depending on the computational model used and give rise to distinct spacings (Fig. S2) that correspond to diffraction peaks measured for a ceramide mixture with CER[NS] as the primary component (22).

In the presence of cholesterol, the atomistic and CG computational models of both CER[EOS] and CER[NS] deliver very similar bilayer thickness, hexatic order parameter, and lipid distribution (Figs. S2–S5). Thicknesses are in agreement with diffraction measurements: ∼7.5 nm for CER[EOS]:CHOL vs. 7.7 nm (56) and ∼5.4 nm for CER[NS]:CHOL vs. 5.36 nm of a mixture with predominantly CER[NS] (55).

In all simulations, the ceramide headgroups are in contact with the water layer; the sphingosine chain, the fatty acid chain of CER[NS] (C24:0), and the saturated portion (C30:0) of the CER[EOS] fatty acids chains are highly ordered (Fig. S6). Instead, the ester-linked unsaturated chains (C18:2) of CER[EOS] are in a liquid-disordered isotropic configuration with a significant fraction of “hooked” conformations, similar to what is measured in multicomponent lipid mixtures by NMR (57). Cholesterol molecules may remain aligned with the saturated chains or position near the disordered linoleic acid segments of CER[EOS]. Consistent with neutron diffraction studies of lipid mixtures rich in CER[EOS] (58), the relative probability of the latter state increases at lower humidity (Fig. S6).

Although the use of relatively small periodic unit cells favors the bilayer structure, it is clear from Fig. S1 that larger model systems do not always form homogeneous multilamellar domains. However, as was proposed earlier (14), the assembly of skin lipids into large multilamellar structures is facilitated by the presence of a template (Fig. S7).

Skin lipid bilayers rich in long-chain ceramides show an order-disorder interface

In samples of extracted skin lipids (23) as well as synthetic mixtures, the SPP is competitive with the LPP; however, the relative abundance of the SPP can be artificially decreased by using high concentrations of CER[EOS] in synthetic mixtures (26). A similar model mixture of CER[EOS], CER[NS], cholesterol, and FFAs in a 1:1:2:2 ratio was used here as a simplified model for the lipid matrix (Table 1, last row). The FFA distribution was modeled using behenic acid (C22:0), which is at the peak of the FFA chain length distribution in the SC (59). Bilayers of this mixture are examined in this section, whereas lamellae with LPP thickness are discussed later.

Fig. 1, A–D show snapshots of the bilayer structure for the lipid mixture examined. During 1.5 μs of atomistic simulation at 1 bar and 30°C, all ceramides and fatty acids remain embedded in the respective leaflets, whereas some cholesterol molecules are exchanged between the outer leaflets and the central layer (Fig. 1 C). In the corresponding CG simulation, lipid diffusion is enhanced, resulting in both cholesterol and fatty acid molecules exchanging between the outer leaflets: however, the steady-state distributions of each lipid species are very similar to those from the atomistic model (Fig. S5).

Figure 1.

Structure and permeability of skin lipid model bilayers. (A)–(D) show a simulation snapshot of a skin lipid bilayer in atomistic detail; individual lipid species of the same snapshot are shown separately, with hydrogen atoms hidden. CER[EOS] (A), CER[NS] (B), cholesterol (C), and behenic acid (D) are colored in gray, blue, pink, and cyan, respectively; to the right of each snapshot is one molecule of the same species, with a schematic of its coarse-grained (CG) representation. (E) shows the electron density profiles of the bilayer (black) and of terminal methyl groups (blue); the orange line is the boundary between ordered and disordered regions. (F) shows the computed skin permeability k_P (blue) and empirical estimates from the Potts-Guy equation (red) plotted against experimental values; squares indicate values for mannitol. Root mean-squared errors on log(k_P) are 0.73 and 0.72 for the computed and empirical values, respectively. To see this figure in color, go online.

The outer leaflets exhibit high orientational order, particularly for the ceramides, and slow lateral diffusion (less than 0.2 nm²/μs), suggesting an ordered phase. The region near the bilayer midplane, which is mostly composed by the linoleic acid segments of CER[EOS] with a small fraction of cholesterol, is instead in a liquid-disordered phase. The boundary between the two regions can be defined by the inflection point of the computed electron density profile, located at z = 1.25 nm above the SPP bilayer’s midplane, a value that also delimits the distribution of the terminal methyl groups of the alkyl chains (Fig. 1 E).

Permeation of small lipophilic molecules is controlled by the order-disorder interface

Permeability computations were performed using the bilayer model described above by computing PMFs for the permeation of eight molecules that are moderately soluble in lipids (octanol-water partition coefficients K_ow ranging from 0.2 to 5000) and one molecule with poor solubility in lipids (mannitol, K_ow = 8 × 10⁻⁴). All have a molecular weight below 300 Da and small anisotropy and internal flexibility, thus being amenable to PMF computations using the center-of-mass position along the bilayer’s normal (see Methods).

The PMFs computed across the hydrated SPP bilayer with atomistic detail span the interval from z = 0 (bilayer’s midplane) to z = 4 nm (bulk water phase) (Fig. S8). Near the lipid-water interface (z = 2.7 nm), no deep free-energy minima characteristic of stable adsorption can be observed because of the mild or absent amphiphilicity of the molecules examined and the tight lipid packing in the L_o outer leaflet. For each PMF, the largest free-energy barrier is located near the order-disorder boundary (Fig. 1 E). It is reasonable to attribute this barrier to the entropic cost of disentangling chain segments around the small molecule, whose movement as it progresses into the disordered region is constrained laterally by the saturated lipid chains. This effect is, however, only thermodynamic because the computed diffusion coefficient is constant across the bilayer and particularly across the order-disorder boundary (Fig. S9).

Given the structure of the SC, viable diffusion pathways are not distributed homogeneously in three dimensions but follow the intrinsically two-dimensional lipid matrix. Accordingly, the diffusion pathlength λ₀ does not necessarily represent a straight path through the lipid matrix (31) and must be accounted for empirically. Unlike in other permeability calculations by MD simulation (19,30), the value of λ₀ is not assumed a priori but is obtained by regression between computed and measured data for multiple molecules as follows.

Similarly to the Potts-Guy equation (29), k_P is parameterized as a function of the mean diffusion coefficient D and of the probability P_liq that the molecule reaches the more permeable liquid portion of the lipid matrix:

$$k_P=D/{\lambda }_0{P}_{liq}.$$ (2)

The main difference with the original equation (29) is that P_liq measures the solubility of the molecule not in the entire lipid matrix, but only the permeable liquid-disordered portion of it. P_liq is then estimated by the Boltzmann factor exp(−ΔG_o/d), where ΔG_o/d is the free-energy difference (19) between the lowest-lying state in the L_o layer and the free-energy barrier associated to the transition into the more permeable disordered layer (Fig. 1 E). The diffusion coefficients D computed for several molecules are very similar to the volume-based empirical estimate from the Potts-Guy equation (29): D ∼ exp(−0.0061 × MW) where MW is the molecular weight (Fig. S9), confirming that steric hindrance is the main factor in determining diffusion for small neutral molecules and allowing us to treat diffusivity and lipophilicity as independent factors (31).

A linear regression of (log(P_liq) + log(D)) against the experimental log(k_P) yields a slope of 1.03 (r² = 0.89) and an intercept of −0.96, validating the use of Eq. 2. Based on these parameters, the theoretical maximum of k_P is ∼8.9 cm/h, corresponding to a particle with zero volume and 100% probability to reach the disordered region. By comparing the computed diffusion coefficients D and those modeled empirically in the Potts-Guy equation (29), the theoretical diffusion coefficient for the same idealized molecule can be estimated as D₀ = 0.052 cm²/h, which gives an estimate of λ₀ ≈ 59 μm for the diffusion pathlength. This value is significantly shorter than what is used in most empirical permeability models (31) because the probability of accessing a viable diffusion pathway is not factored implicitly into λ₀ but is estimated more directly by P_liq. At the same time, the value of λ₀ here obtained exceeds the typical thickness of the SC (∼25 μm) by less than an order of magnitude, consistent with a permeation model following the boundaries between corneocyte cells rather than a straight path.

Although the computed values of k_P agree well with measured ones for all lipophilic molecules (Fig. 1 F), the permeability of a strongly hydrophilic species such as mannitol using the above parameters is strongly underestimated (1.6 × 10⁻⁷ cm/h vs. 3.7 × 10⁻⁵ cm/h). Such discrepancy is in line with similar computations across other model skin lipid systems (30) and is a known limitation of models based on homogeneous lipid lamellae (31). There is, in fact, an increasing consensus that the permeability of hydrophilic molecules is explained by a distinct pathway from the lamellar phase (31, 32, 33, 34).

Bilayers fuse easily at high temperature: Water reorganizes into droplets or channels

The formation of the LPP in synthetic models is a slow process, and a heating protocol is often applied near the range of melting temperatures of the ceramides to accelerate mixing, followed by equilibration into an ordered lipid phase (23). It is therefore useful to identify any metastable states produced by heating of skin lipids, particularly in the presence of water; part of this goal can be achieved by simulating the heating of SPP bilayers.

Stacks of four hydrated bilayers were prepared with the same composition discussed above and two model sizes of 16 × 16 × 32 nm³ and 24 × 24 × 32 nm³ (Fig. 2). For the smaller system size, two distinct pH conditions were modeled using fully protonated FFAs (low pH) and an equal mixture of protonated and unprotonated FFAs (intermediate pH). For both systems, 2:1 as well as 5:1 water/lipid ratios were considered (Table 2).

Figure 2.

Skin lipid bilayers subject to heat reach a hemifused state with interstitial water confined into droplets or channels. (A) shows the initial snapshot of the 5:1 water/lipid 16 × 16 × 32 nm³ atomistic model and (B) the same system after heating at 95°C for 0.2 μs, followed by annealing 30°C for 1.8 μs; small crystalline domains are formed during the latter stage. (C) shows the final snapshot of the 2:1 water/lipid model after heating. Lipid molecules are colored as in Fig. 1, water in white and Na⁺ ions in yellow. (D) shows the final snapshot of the 16 × 16 × 32 nm³ 2:1 water/lipid model, showing the distribution of interstitial water as clusters shown in distinct colors. To see this figure in color, go online.

Atomistic simulations at 30°C for ∼0.5 μs did not reveal significant changes in the multi-bilayer structure. A short heating cycle was then applied to each model system (0.25 μs at 95°C, well above the melting temperatures of most ceramides) to enhance the rate of structural changes. The large temperature promoted the hemifusion between bilayers at multiple contact points (Fig. 2, B and C) and the reorganization into an inverse-hexagonal structure. Mixing of lipids from the fused bilayers further consolidated this structure (Fig. 2 B).

The hemifused lipid regions contain a significantly increased proportion of CER[EOS] in extended form (Fig. S11), similar to the LPP structure. This transition is concurrent with lipid mixing and resembles a widely used model for the early stages of phospholipid membrane fusion (60). After hemifusion, water is organized as continuous channels in the 16 × 16 × 32 nm³ model at 5:1 water/lipid (Fig. 2 B) and as a combination of channels and droplets in the 2:1 water/lipid model and the larger 24 × 24 × 32 nm³ models (Fig. 2, C and D).

After heating, the temperature was brought down to 30°C to investigate any metastable structures. The resulting structures maintained the overall geometry assumed during heating; however, exact hexagonal spacing in the 16 × 16 × 32 nm³ models is prevented by the uneven thicknesses of the lipid regions surrounding the water channels. Because of the limited simulation timescale, the hemifused regions retain significant double-bilayer structure and do not progress toward a multilayer structure like the LPP. This configuration was also found to be metastable in recent CG simulations of comparable length, in which a lateral compression was applied to the lipids to enhance lipid order (18); this compression was not used here, and each unit cell vector was pressure controlled independently at 1 atm.

Skin lipids self-assemble into lamellae of thickness compatible with the LPP

To model skin lipid lamellae with thickness above the SPP, 20-nm-thick lipid slabs were prepared and allowed to reach an equilibrium structure via CG simulation (Table 3). A water buffer was used to allow anisotropic transformations in the simulation unit cell without artifacts imposed by the periodic boundary conditions. The lipid-water interfaces were initialized based on two hydrated lipid bilayer leaflets (Fig. 1), whereas the inner lipids (a total of ∼15 nm thickness) were set up in randomized conditions (Fig. 3 A; Video S1). After equilibration, excess water was removed to generate multilamellar stacks (Fig. 3 H), as discussed below.

Table 3.

CG Simulations of Hydrated Skin Lipid Lamellae

Simulation Number	Hydrated Interior	Water/Lipid Ratio	Initial Conditions	Simulation Period	Final System Dimensions
I (Fig. 3G)	Yes	10:1	randomized slab	5 μs	∼37 × 43 × 13 nm3
II (Fig. 3, C, D, and F)	Yes	10:1	randomized slab	2 μs	∼35 × 45 × 13 nm3
III (Fig. 3B)	No	10:1	randomized slab	2 μs	∼33 × 38 × 16 nm3
IV (Fig. 4)	Yes	5:1	simulation I (lamella with one droplet)	25 μs	∼10 × 7 × 14 nm3
V (Fig. 3H)	Yes	5:1	simulation IV (4 × 4 × 2 copies)	2 μs	∼40 × 28 × 28 nm3
VI (Fig. 6)	Yes	10:1	simulation I (1 × 1 × 2 copies)	2 μs	∼37 × 43 × 26 nm3
VII (Fig. S16)	Yes	10:1	simulation III	1.2 μs	∼33 × 38 × 16 nm3

Indexed by Roman numerals. Simulations IV–VII were initialized based on snapshots of simulations I or III.

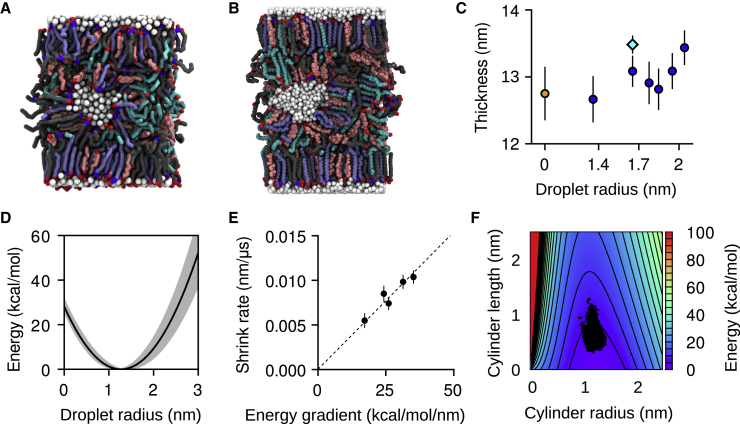
Figure 3.

Self-assembled ∼13 nm lamellae with and without interstitial water droplets. Initially randomized lipids (A) reorganize into dehydrated lamellae with homogeneous thickness (B) or hydrated lamellae with inhomogeneous thickness (C). Hydrated lamellae contain water droplets (D) formed by nucleation and growth of water molecules (E); (F) and (G) show the final distributions of droplets (seen from above the lamellar plane) for two independent runs. Multilamellar models were also simulated (H). For the hydrated lamellae, the number and the median, maximum, and minimum of the droplets’ radii are shown in (E) as a function of simulated time. To see this figure in color, go online.

Video S1. Initially Randomized Lipids Reorganize into Hydrated Lamellae with Inhomogeneous Thickness

Related to Fig. 3.

Two lipid slabs (Table 3, simulations I and II) were simulated: no restrictions were placed on the movement of water, and these models are referred to as “hydrated” models. Physiological pressure was maintained with fully anisotropic and semi-anisotropic couplings, respectively; no significant differences between the results of the two were observed, suggesting no bias from the periodic boundaries along the lamellar plane. A third slab (simulation III) was also simulated with an additional repulsive potential applied selectively to the water particles, preventing them from entering the region within ±6 nm from the midplane; this model is hereafter called “dehydrated,” reflecting the lack of water in the lamellar interior regardless of the water buffer.

Lipid molecules progressively diffuse over 0.5 μs from the randomized inner layer to the surface of the lamella, decreasing its thickness and increasing its total surface area by up to 60% (Fig. 3, B and C). Within 2 μs, the unit cell dimensions of each system converge in all simulations. For the “dehydrated” system (simulation III), the final lamellar thickness is ∼13 nm and is determined by interplay between intermolecular forces and the boundary potential acting on the water particles (Fig. 3 B).

The two “hydrated” lamellae (simulations I and II) reach an equilibrium structure with two apparent coexisting thicknesses of ∼11 and ∼6 nm, respectively (Fig. 3 C). In the thick regions, the transformation is accompanied by the aggregation of water molecules into small droplets in the lamellar interior (Fig. 3 D). Although appearing as containing significant water, the droplets themselves account for only 1.7 water molecules for every lipid molecule that is not part of the outer leaflets and thus represent a level of local humidity compatible with the SC’s lipid matrix.

Homogeneous lamellae were obtained by extracting an 8 × 8 nm² section of one of the thick regions and removing all water in excess of 5:1 water/lipid; one droplet was retained in the model and counted as part of the 5:1 ratio. This section was then equilibrated for 25 μs (Table 3, simulation IV) with periodic boundary conditions and anisotropic pressure coupling, reaching a thickness of ∼13 nm. The resulting snapshot was replicated 4 × 4 times parallel to the plane and two times orthogonally (simulation V) and equilibrated for 2 μs, yielding the multilamellar structure shown in Fig. 3 H.

The resulting lipid distribution of the ∼13 nm thick lamellae is symmetric around the midplane, consistent with the structure factors measured by x-ray and neutron diffraction (25,61). The interior exhibits a partially demixed lipid distribution characteristic of the LPP (12,25,26), with a higher concentration of ceramides in the outer leaflets (±4 to ±6 nm), cholesterol in the regions immediately below the outer leaflets (±2 to ±4 nm), and fatty acids in the central region (−2 to +2 nm) (Figs. 4 and S14). This demixing is caused by the selective migration of lipids during equilibration and was not determined by the initial conditions. Nonetheless, because of the use of a water buffer, the two ceramides remain in a homogeneous mixture with each other, unlike in skin lipid diffraction studies that show a preference in the outer leaflets for CER[EOS] molecules (25), which extend across multiple adjacent lamellae (58).

Figure 4.

Distributions of individual lipids in the ∼13 nm lamellae. (A)–(D) show the distribution of lipid headgroups for the dehydrated lamella shown in Fig. 3B (dotted lines) and the hydrated lamellae shown in Fig. 3, C and D (dashed lines). Profiles for CER[EOS], CER[NS], cholesterol, and behenic acid electron density profiles are colored in gray, blue, pink, and cyan, respectively. To see this figure in color, go online.

In all models, the computed electron density profile (Fig. S14) shows well-defined peaks at the outer edges of the lamella and a broader region of high density near its core; the magnitude of the latter depends on the presence of interstitial water (“hydrated” versus “dehydrated” models). The low-density regions are located approximately at ±4 nm, consistent with x-ray diffraction (61). The unsaturated segments of CER[EOS] (both for molecules in the outer leaflets and in the inner core) often exhibit the “hooked” conformation (Fig. 4 A) measured in the LPP near ±4 nm (57,58).

The distribution of lipid headgroups (Fig. 4) shows the lipids in the central region as either relatively isotropic in the dehydrated lamella (simulation III), or spherically arranged around the droplets in the hydrated models (simulations I and II). This is in contrast with the structural models derived from x-ray and neutron diffraction (25,61), which indicate the presence of inner peaks at ±2 nm, less intense than the outer peaks yet sufficiently narrow to produce diffraction. It is possible that the difference may be caused by the CG model lacking the ability to form ordered hydrogen bonds between the headgroups or the CG water particles accounting for three water molecules each and preventing isolated water molecules from acting as an intermediate between headgroups. Because of this discrepancy, the dehydrated structure shown in Fig. 3 B is only an approximation to the LPP.

In the hydrated lamellae, the ceramides’ headgroups are exposed to water from either the outer layer or from the droplet; such hydrated interfaces are well described by the CG model, suggesting that the corresponding structure is metastable in the skin’s lipid matrix. Nonetheless, the possibility of a more subtle bias by the CG lipid model toward inverse-micellar phases was investigated by constructing hexagonally packed lattices of droplets and simulating them at CG resolution (Fig. S15): this structure was unstable and within 10 μs evolved into a coexistence of inverse-micellar and lamellar phases.

The final snapshot after 25 μs of a 8 × 8 nm² periodic lamellae containing a 1.6 nm droplet (Fig. 5 A) was also used to initialize an atomistic simulation (Fig. 5 B). Despite significant diffusion of water molecules between the droplet and its periodic images (Fig. S17) and of the lipids surrounding the droplet (Fig. S18) over 2 μs, the net transfer of water between the droplet and the outer layer is almost zero (Table 4), and the droplet does not dissolve within this timescale. Furthermore, the droplet retains its near-spherical shape (Fig. 5 B) and does not transition to a water layer. Data from this atomistic simulation are also used to compute the electron densities shown in Fig. S14. These results indicate that interstitial water droplets in the interior of skin lipid lamellae are relatively long-lived.

Figure 5.

Water droplets are metastable within a lamellar core. (A) shows a CG simulation snapshot after 25 μs and (B) a snapshot from a 2 μs atomistic simulation. (C) shows the estimated thicknesses of the dehydrated CG lamella (orange circle), the hydrated CG lamellae (blue circles), and the hydrated atomistic lamella (cyan diamond). (D) shows the energy as a function of the droplet radius from Eq. 3; the shaded area reflects the uncertainty in the interfacial tension estimate. (E) shows the estimated rate of shrinkage of the larger droplets as a function of the gradient of Eq. 3 with respect to the droplet’s radius. (F) shows the energy landscape for a droplet shaped as a cylindrical capsule; dots indicate the radii and lengths distribution for self-assembled droplets (Fig. 3E). Error bars are standard deviations. To see this figure in color, go online.

Table 4.

Water Transfer Statistics for a Single Lamella with One Water Droplet and One Water Layer from CG and Atomistic Simulations

	CG Data (∼7.5 μs)		Atomistic Data (∼2 μs)
	Layer-Droplet	Droplet-Layer	Layer-Droplet	Droplet-Layer
Number of transfers	2037	2058	0	1
Exchange rate (ns−1)	0.273	0.267	0	0.0008
Mean displacement ± standard error (nm)	6.6 ± 0.1	6.4 ± 0.1	N/A	4.93

Rates are computed over the entire atomistic trajectory and a CG trajectory segment in which no significant changes in the droplet size were observed (as confirmed by equal transfer rates to and from the water layer). The column headings follow the convention that the first label indicates where the water particle started from, and the second label indicates where it went. Transfers of water molecules between the single droplet and its periodic images, though occurring in both simulations in significant numbers, were excluded from the analysis because of the ambiguity in the duration of their travel time.

Excess water aggregates into interstitial droplets of controlled size

After nucleation, droplets grow exponentially up to a radius of r^∗ = 1.3 nm (Fig. 3 E); 19 and 20 droplets are formed in each hydrated lamella, positioned along a quasihexagonal two-dimensional lattice (Fig. 3, F and G) and separated from each other by lipid regions of thickness comparable with a lipid bilayer (SPP). No long-range positional order can be observed in the lateral distribution of the droplets.

The size distribution of the self-assembled droplets also agrees well with the lower end of the distribution of droplets or channels resulting from atomistic simulations with heating (Figs. 2 and S19). Atomistic distributions of droplets above 1.3 nm could not be compared because they were determined by the initial water content of those atomistic simulations. A model energy function for the droplets’ size was thus defined as follows. The free energy of the surface S of a water droplet was modeled as the sum of the interfacial tension with the lipid phase and the elastic bending energy of the surrounding lipid layer (62):

$$F\left(S\right)=\underset{S}{\int }\left[\gamma +\frac{K_c}{2}{\left(c–c_0\right)}^2\right]d{A}_S,$$ (3)

where γ is the tension of the water/lipid interface, c = r_x⁻¹ + r_y⁻¹ and c₀ = r₀⁻¹ are the total and spontaneous curvatures of the lipids, K_c is their bending modulus, and dA_S is the surface area element. Lacking specific measurements, the interfacial tension between water and 1-octanol (γ ≈ 8.5 mN/m) was used and, for simplicity, assumed not to change with the curvature c. Based on the distribution of interfacial tension values of fatty alcohols, 2 mN/m was used as the uncertainty (Fig. 5 D).

The radius of spontaneous curvature r₀ could be obtained at conditions of high local humidity, in which all lipid headgroups are exposed to water and the interfacial tension term in Eq. 3 is constant. Currently, no direct measurements of r₀ are available. Based on the permeabilities of many hydrophilic species across skin samples, a probability distribution of the radii of water channels through the SC has previously been derived: P(r) ∼ exp(−0.045 × r²). The mean of this distribution is ∼2.7 nm (35). This number is also compatible with the range of the radii of ceramide-lined channels in phospholipid membranes, 0.8–11 nm (63), and was used here as the radius of spontaneous curvature r₀. To estimate K_c for the skin lipid mixture, the computed area compressibility modulus of the SPP bilayer (K_A = 273 ± 35 mN/m) was used with the polymer-brush model (64) to obtain K_c = 9.5 ± 1.2 kcal/mol.

For a spherical droplet, the free energy estimated by Eq. 3 has a minimum at a radius of approximately r^∗ = 1.3 nm (Fig. 5 D), consistent with the target radius of the self-assembled droplets (Fig. 3 E). Equation 3 was then also tested by constructing additional copies of the single-droplet model (Fig. 5 A), each with an increased number of water particles up to six times the original droplet. One of the copies was also simulated atomistically (Fig. 5 B). After minimization and equilibration with semi-anisotropic pressure coupling, all of the larger droplets gradually lose water, shrinking with an approximately exponential decay (Fig. S20). The rates of shrinkage are proportional to the free-energy gradient dF(r)/dr calculated at the corresponding radii (Fig. 5 E), confirming the validity of the model to describe the dynamics of the droplets.

The decay time constants range between ∼75 and 100 μs (Fig. 5 E) with a mean of ∼90 μs, much longer than the initial nucleation and growth of the droplets (Fig. 3 E). Because the exchange rates of individual water particles are relatively high in the CG model (Table 5), such long decay times are not water limited. Rather, lipid movements control droplet decay times because the surface area of a droplet, and hence its size, is limited by the movement of the lipid headgroups surrounding it.

Table 5.

Water Exchange Events in a System with Multiple Droplets at CG Resolution

	Layer-Layer	Layer-Droplet	Droplet-Layer	Droplet-Droplet
Number of transfers	32,733	59,091	57,231	129,342
Exchange rate (ns−1)	6.547	11.818	11.446	25.868
Relative exchange rate (with respect to droplet-droplet rate)	0.25	0.46	0.44	1.00
Mean displacement ± standard error (nm)	8.44 ± 0.03	6.13 ± 0.02	6.10 ± 0.02	4.42 ± 0.01

These results are based on 5 μs of CG simulation with two lamellae and 38 droplets initially (shown in Fig. 6A) and were determined using the same approach as for Table 4. Because of the limited sampling of merging events, it is not possible to directly compute the net water transfer rates between individual droplets. Based on a decay rate of 90 μs evaluated with the single-droplet system (Fig. 5E) and the 45% ratio between droplet-layer and droplet-droplet water exchange rates estimated here, a decay time of 40 μs is estimated for droplet-droplet net water transfer. Because diffusion times of CG lipids are shorter than atomistic lipids by about an order of magnitude (Fig. S18), this value is probably underestimated.

Elongation of water droplets into channels is more favorable than isotropic growth

The above data indicate that the formation of continuous water channels is a rare event that may be promoted by external factors. To estimate the energy cost of such an event, the free energy of a model cylindrical capsule was computed using the model from Eq. 3 (Figs. 5 F and S21). Using the leading eigenvalue of each droplet’s inertia tensor to parameterize the length L and the mean of the other two eigenvalues for the radius r, the shape fluctuations of self-assembled droplets were compared to the energy landscape. All droplets are distributed near the minimum of the free energy F (r, L), located at r^∗ = 1.3 nm and L^∗ = 0 (Fig. 5 F). Because of the thermal fluctuations of the droplet’s shape, the smallest cylindrical length explored is, however, not zero but L_min ≈ 0.3 nm, i.e., the approximate radius of a water molecule. The largest length explored is L_max ≈ 1.2 nm, corresponding to droplets that are ∼50% longer along one axis than the other two axes. The distribution of individual droplets exhibits tails that appear to follow the constant-volume contour lines (Fig. S21) but remain within 8 kcal/mol from the free-energy minimum. Therefore, the two-dimensional model is a simplified but reasonably accurate description of droplet anisotropy.

Assuming a droplet with optimal initial radius r = 1.3 nm, the elongation required to cover the typical distance with the nearest droplets is L ≈ 6 nm. If the transformation occurs at constant volume (i.e., a fixed size for the droplet), ∼43 kcal/mol of energy would be required (Fig. 5 F). If changes in the droplet’s volume are allowed by addition of water, this activation energy is reduced to 33 kcal/mol. Both values are sufficiently high to justify a low probability of water channels at equilibrium conditions (35). At the same time, corrugations induced by the local surface of the corneocytes (6), as well as the use of transdermal delivery enhancement methods, could offset at least part of this energy cost, greatly increasing the probability of formation of water channels.

The coalescence of water droplets is affected by interactions between lamellae

Although a multilamellar model with embedded droplets is metastable, with homogeneous lamellae and flat equilibrium structure (Fig. 3 H), it is useful to investigate the dynamics of interstitial water in the presence of corrugations. A simple test of this effect was constructed by replicating one of the snapshots at 2 μs shown in Fig. 3 along the direction normal to the lamella (Fig. 6 A; Table 3, simulation VI). Within 1 μs, the thick regions of the two lamellae move such that the thickness of the water layers becomes homogeneous throughout the unit cell, thus adapting to the irregular lamellar profile (Fig. 6 B).

Figure 6.

Relative movements of the lipid lamellae promote droplet coalescence. (A) shows the initial condition and (B) the final snapshot after 5 μs. (C) shows the total number of droplets and radii distribution in the two lamellae; the solid line is the median and the shaded area the size range. Note the sudden jump at ∼0.3 μs, reflecting the first merging event. To see this figure in color, go online.

Although the thick regions of each lamella maintain their pre-existing thickness, their area along the lamellar plane decreases by ∼25–30% (visual inspection). This change is accompanied by the merger of several droplets, starting at 38 droplets in each lamella and reaching 30 droplets after 5 μs (Fig. 6 C). Despite the decrease in the number of droplets, the total amount of water contained in the droplets increases by ∼15%, and the median droplet radius saturates near 1.3 nm after ripening and merging of individual droplets (Fig. 6 C). Therefore, the coalescence between preformed water droplets, although unfavorable, appears to be promoted easily while obeying the same parameters that control the aggregation of droplets from individual water molecules.

Discussion

The results presented here demonstrate a direct connection between the coexistence of multiple lipid phases (Fig. 7) and the ability of skin lipids to sustain interstitial water, which is essential in controlling the skin’s permeability to water-soluble substances. Among the phases investigated are bilayers (Fig. 1), inverse-hexagonal and inverse-micellar structures (Fig. 2), and lamellae with thickness equal to the LPP (Fig. 3). A lamella self-assembled without interstitial water bears a structure similar to the LPP but with significant disorder in its interior because the intralamellar “peaks” of the headgroup distributions (Fig. 4) are ∼3 nm wide compared with the ∼1 nm suggested by x-ray- and neutron-diffraction-based models (25,61).

Figure 7.

Summary of the stable and metastable skin lipid phases relevant to interstitial water. The structures simulated in this study (A–D) are compared to the LPP (E). Lipids are drawn schematically and colored in gray where the local composition equals the global composition, purple where locally enriched in ceramides, and orange where locally depleted in ceramides. Ordered water-lipid or lipid-lipid interfaces are highlighted with black lines. Splayed ceramides, although important to the cohesion of the dry lamellar phases, and chemical differences between the lipids are not drawn for clarity. Transitions from bilayers (A) to inverse-hexagonal and inverse-micellar phases (B and C) were observed as a result of heat (Fig. 2). Thick lamellae were also obtained by self-assembly (Fig. 3) in the hydrated state (C) and dehydrated state (D), with partial transitions between the two as a result of water diffusion. Permeability of hydrophilic molecules through the skin is thought to be nonvanishing only in the presence of metastable water channels (B). To see this figure in color, go online.

Because self-assembly simulations of skin lipids cannot be carried out at atomistic detail, it is difficult to attribute this discrepancy to the CG force field. Recent atomistic simulations (19) initialized using the LPP model proposed by the Bouwstra laboratory (25,26) yielded three-dimensional structures metastable on the microsecond timescale at 5:1 water/lipid but unstable at 2:1 water/lipid. It is unclear if this result is due to limited experimental resolution in the measurements used to estimate the water content or the inability of simulation models to sustain a dehydrated phase of the skin lipids. It is possible that CG models based on machine learning of atomistic simulations (18) could help elucidate the matter.

In hydrated lamellae, the spontaneous formation of water droplets (Fig. 3) allows for the lipid headgroups to interact with water, a physical state that is well described by the CG force field used. Atomistic simulations confirmed that lamellae containing droplets are metastable over microsecond timescales (Fig. 6 B), raising the possibility that they could be measured given suitable experimental conditions. For example, specific lipid compositions may positively stabilize such nonmicellar structures (for example, by addition of oleic acid, which has a negative intrinsic curvature).

The two-dimensional arrangement of the simulated droplets exhibits locally hexagonal packing but lacks long-range positional order (Fig. 3, F and G), and the droplets’ shape is not always spherical (Fig. 5 F). Both factors may significantly hinder experimental detection of droplets at physiological conditions. Comparison with x-ray diffraction data of a three-dimensional inverse-micellar phospholipid phase (65) suggests that even if the droplets followed a perfect hexagonal lattice, their characteristic peaks may not be intense enough to be detected in x-ray or neutron diffraction: the nearest neighbors of each droplet (100 and 010 lattice vectors) are at a distance comparable to the SPP, and the peaks associated with the 110 and similar vectors are likely to be much weaker (65). Lastly, the synthetic lipid mixtures used to obtain the highest-resolution diffraction measurements are typically exposed to water for times much shorter than the turnover times of the SC (66) and are probably less likely to accumulate excess water.

High-resolution cryo-electron microscopy of extracted skin sections shows in some images a series of intralamellar spots of the same size and spacing of the simulated droplets, with the majority of images showing a purely lamellar structure (7). This is consistent with inverse-micellar droplets being a metastable state of the skin’s lamellae. Beyond structural data, the permeabilities of hydrophilic substances have already been used to model the distribution of radii of water channels (35), and such radii quantitatively describe the self-assembled water droplets as well (Eq. 3). Coalescence of water droplets is then estimated to be a rare event (Fig. 5 F), but its probability may be increased at certain conditions (for example, under external strain (Fig. 6)) to promote the formation of hydrophilic permeation channels.

Besides allowing hydrophilic permeability, another possible role of intralamellar droplets could be facilitating the relative movement of the lamella’s outer leaflets under shear. Such a role would be useful only while humidity is changing across the SC; accordingly, at low humidity, the skin lipid lamellae have little to no interstitial water (Fig. 7). Observing the complete dissolution of water droplets under a humidity gradient probably exceeds available simulation timescales (Fig. S20). However, the slower rate of water exchange across the lamellae than between droplets (Fig. S16; Table 5) supports the hypothesis that the water layers between lamellae evaporate first, whereas the more stable droplets within them evaporate at a later stage. Consistent with this hypothesis is also the multistate mechanism of skin homeostasis proposed from studies of evaporation from amphiphiles/water mixtures (67). The steep increase in water permeability of the SC above >80% relative humidity (68) can also be explained by the formation of continuous channels that are further stabilized by the resulting swelling of the corneocytes’ keratin mesh (68).

Other factors that may promote the formation of water channels are mechanical forces. For example, the 20 kHz frequency of the ultrasound vibrations used to enhance hydrophilic permeability (69) is at the order of magnitude of net droplet-droplet water transfer (τ ≈ 40 μs, Table 5). The previously suggested activation energy of 43 kcal/mol per droplet gives an upper bound of about ∼1.9 × 10⁻⁴ J/cm² of energy density (assuming 15 lipid lamellae per corneocyte and 15 corneocytes across the SC). The energy density supplied by permeability-enhancing ultrasound vibrations over the course of several hours is >100 J/cm² on the entire epidermis (69), of which >3 J/cm² is apportioned to the SC’s lipid matrix based on its volume. Although much of this energy would be lost by thermal dissipation, its total is more than 50,000 times higher than the activation energy required to overcome the energy barrier. This comparison is consistent with the coalescence between water droplets as a mechanism for hydrophilic permeability.

In conclusion, the results presented here demonstrate that the multiplicity of phases of the skin lipids, rather than being an artifact of different experimental conditions, directly explains the presence of hydrophilic pathways of permeation. The skin’s homeostasis and the modulation of barrier function can thus be described by the relative abundance of stable and metastable structures, of which only the latter can provide continuous water channels through the skin.

Author Contributions

Initial planning for the project was carried out by R.H.D. and G.F.; simulations were designed by G.F. using force-field parameters derived by C.M.M. and carried out by C.M.M. and G.F. Simulation results were analyzed by G.F., K.W.H., and C.M.M.; G.F., K.W.H., and M.L.K. wrote the manuscript.

Editor: Tommy Nylander.