Endothelial Glycocalyx Layer Properties and Its Ability to Limit Leukocyte Adhesion

Abstract

The endothelial glycocalyx layer (EGL), which consists of long proteoglycans protruding from the endothelium, acts as a regulator of inflammation by preventing leukocyte engagement with adhesion molecules on the endothelial surface. The amount of resistance to adhesive events the EGL provides is the result of two properties: EGL thickness and stiffness. To determine these, we used an atomic force microscope to indent the surfaces of cultured endothelial cells with a glass bead and evaluated two different approaches for interpreting the resulting force-indentation curves. In one, we treat the EGL as a molecular brush, and in the other, we treat it as a thin elastic layer on an elastic half-space. The latter approach proved more robust in our hands and yielded a thickness of 110 nm and a modulus of 0.025 kPa. Neither value showed significant dependence on indentation rate. The brush model indicated a larger layer thickness (∼350 nm) but tended to result in larger uncertainties in the fitted parameters. The modulus of the endothelial cell was determined to be 3.0–6.5 kPa (1.5–2.5 kPa for the brush model), with a significant increase in modulus with increasing indentation rates. For forces and leukocyte properties in the physiological range, a model of a leukocyte interacting with the endothelium predicts that the number of molecules within bonding range should decrease by an order of magnitude because of the presence of a 110-nm-thick layer and even further for a glycocalyx with larger thickness. Consistent with these predictions, neutrophil adhesion increased for endothelial cells with reduced EGL thickness because they were grown in the absence of fluid shear stress. These studies establish a framework for understanding how glycocalyx layers with different thickness and stiffness limit adhesive events under homeostatic conditions and how glycocalyx damage or removal will increase leukocyte adhesion potential during inflammation.

Significance

We present an analytical framework for assessing the physical properties of the endothelial glycocalyx layer (EGL) and understanding how its properties affect the ability of leukocytes to adhere to endothelium, a critical step in the immune response. Atomic force microscopy (AFM) indentation measurements are shown to match two descriptions of the EGL, one a molecular brush and one a thin elastic layer. The approach eliminates arbitrary assumptions made in some prior analyses and provides a more accurate and consistent determination of properties. We demonstrate a reduction in EGL thickness in cells grown at low shear stress that correlates with increases in neutrophil capture, and we present a predictive model for how bond formation will be affected by layers of different thickness and stiffness.

Introduction

The endothelial glycocalyx layer (EGL) is a complex surface layer composed of proteins, glycolipids, glycoproteins, and proteoglycans (1). It is thought that there is a tightly bound protein layer extending on the order of tens of nanometers from the cell surface with a much larger, loosely bound proteoglycan layer that includes heparan sulfate, chondroitin sulfate, and hyaluronic acid and may extend (depending on the tissue) up to 1 μm from the cell surface (2). The thickness and structure of the EGL have been studied primarily using electron microscopy (3) and fluorescence microscopy (4, 5, 6), but these imaging modalities vary in the values they report for the thickness of the EGL. These differences are likely due in part to the measurement approaches, but it is important to recognize that the EGL is sensitive to a number of environmental factors. For example, it is known that there is a significant active remodeling of the cell’s actin cortex and an associated upregulation of hyaluronic acid on the endothelial cell surface after a 24-h exposure to shear stresses on the order of 15 dyn/cm² (7). There are also significant differences in reported values for the EGL thickness for different tissues or culture conditions (2,3).

Functionally, the EGL is thought to play a role in regulating both leukocyte adhesion and endothelial permeability. The regulation of adhesion may be particularly relevant in the lung during sepsis (8). When mice were exposed to septic conditions, the pulmonary EGL was significantly reduced in thickness, as indicated by fluorescence labeling. Although there was an increase in the number of adherent neutrophils in the capillaries and surrounding pulmonary tissue, there was not an upregulation of adhesion molecules on the endothelial surface, indicating that the increased adhesion was a result of increased molecular accessibility. This increase in adhesion was also observed when the EGL was degraded enzymatically using heparanase, and a return to normal cell adhesion was observed when EGL components, notably heparan sulfate, were injected into the mouse at the same time as the heparanase or inflammatory stimulus, suggesting that the function of the EGL can be quickly restored.

To understand the role of the EGL as a physical barrier, imaging approaches alone are not adequate. Several groups have used AFM to test endothelial cell surface properties. Early tests of endothelial surface properties employed standard AFM tips with tip dimensions on the order of tens of nanometers. The stresses imposed by such small cross sections are far too large to detect the extremely soft resistance of the EGL to indentation, and those earlier applications focused primarily on the properties of the endothelial cell cytoskeleton (9, 10, 11). New approaches using several-micron-sized beads attached to cantilever tips to provide a large contact area have more recently been used to detect contributions from the EGL. Methods for interpreting the AFM force-indentation curves have varied, however, from group to group. Some have attempted to identify different linear regions in the force-indentation curves (12,13). However, most force-indentation data, at least in our hands, show a continuous, smooth curve without obvious breaks where a change in slope can be identified. Others have used a modified Hertz theory to calculate an elastic modulus as a function of indentation depth (14). They then attribute the properties of the EGL to the outermost regions of the indentation. Another approach has been to superimpose the Hertz theory for an elastic half-space with a model of the EGL as a polymer brush (15, 16, 17). We have previously introduced an alternative approach based on an analytical approximation to finite element modeling of a thin, soft elastic layer on top of an elastic half-space developed by Clifford and Seah (18,19). In this case, the EGL thickness, the EGL modulus, and the elastic modulus of the cell appear as parameters in a single expression that can be fit to the data to extract these important properties. In this report, we compare the results for the elastic layer model of the EGL with predictions based on the brush model, and we explore the rate dependence of the properties we derive. We then use these values to model indentation of the EGL by leukocyte microvilli to assess the effectiveness of the EGL as a physical barrier to leukocyte adhesion.

Materials and Methods

Cell culture and seeding flow chambers

Human umbilical vein endothelial cells (HUVECs) and growth medium were purchased from Vec Technologies (Rensselaer, NY). Cells were grown to confluence in a T25 flask. The growth medium was removed from the flask, and the monolayer of cells was washed with 1 mL of sterile phosphate-buffered saline and then released from the flask with 1 mL of 2.5% trypsin. Once the cells were in solution, the trypsinization was quenched with the addition of 1 mL of cell culture medium to the flask. The suspension was centrifuged for 5 min to form the cells into a pellet, and the supernatant was removed. The cells were resuspended in 1 mL of cell culture medium for injection into the flow chamber (20). A seeding density of ∼1 × 10⁶ cells/mL was used for all experiments. Cells were grown to confluence (typically 48 h) with or without shear stress. Human pulmonary microvasculature endothelial cells (HPMECs) and growth media were purchased from Promo Cell (Heidelberg, Germany). Cells were seeded in a similar manner to HUVECs. After 24 h of static growth, HPMECs were condition with 24 h of 5 dyn/cm² shear stress and then flowed for 24 h under a shear stress of 10 dyn/cm². On the day of experiment, the top of the flow channel was lifted off, and the cells were placed directly onto the stage of the AFM system for measurement.

Neutrophil capture experiments

Whole-blood samples were obtained from healthy, consented donors under a protocol approved by the Institutional Review Board at the University of Rochester. Neutrophils were isolated from the blood using one-step polymorphs (Accurate Chemical and Scientific, Westbury, NY). HUVECs were grown to confluence in microslides (flattened glass channels) (20,21) under high (10 dyn/cm²) or low (<0.5 dyn/cm²) shear stress. Neutrophils were infused into the microslides at controlled flow rates and observed using video microscopy. After 5 min of flow, nonadhered cells were washed away at the same shear rate for 2 min, and then flow was stopped, and the number of adherent neutrophils in a 3-mm² area was counted.

Atomic force microscopy measurements on confluent cell layers

Tipless AFM cantilevers (NanoWorld, Neuchâtel, Switzerland) with spring constants in the range of 30 pN/μm were attached to a 6-μm-diameter glass bead using Norland 68 optical adhesive and then calibrated using the thermal noise fitting protocol built into the Asylum MFP3D software. In a typical cell indentation, a cell was identified under bright-field illumination in the microscope, and the glass bead was positioned over the perinuclear region of the cell. The cell was indented 10 times in the same location at the given loading rate to a maximal indentation force of 5 nN. The cantilever was retracted far from the cell surface so that any adhesions of the bead to the cell surface were broken, and the cell was given ∼10 s to recover before the next indentation. Cells were treated with Heparinase III (MilliporeSigma, St. Louis, MO) and Hyaluronidase (MilliporeSigma, St. Louis, MO) to enzymatically remove some of the EGL structure. The flow channel above the cells was removed, and 1 U/mL of Heparinase III was incubated with the cells for 1 h at room temperature. For treatment with hyaluronidase, HUVEC monolayers were treated with 10 U/mL hyaluronidase for 2 h at room temperature and then indented.

Elastic layer model

The Hertz model is commonly used to determine the moduli of simple elastic materials from indentation measurements, but the study of the mechanical properties of cells using atomic force microscopy has necessitated the development of more-complex mathematical models. Hertz theory of indentation into elastic materials serves as a basic framework and has been applied to different biological systems for interpretation of atomic force microscopy measurements. For a spherical indenter with radius R, the force applied can be described using Hertz theory, in which the force of indentation, F_cell, is given by the equation

$$F_{cell}=\frac{4}{3}{E}^{\ast }{R}^{\frac{1}{2}}{\delta }_c^{\frac{3}{2}},$$ (1)

where ${\delta }_c$ is the indentation depth into the material, and E^∗ is the reduced modulus of the material under test. In the case of an infinitely stiff indenter impinging a uniform elastic half-space, E^∗ is given by the equation

$$E^{\ast }=\frac{E}{1-v^2},$$ (2)

where E is the elastic modulus, and ν is the Poisson ratio of the material. For our current application, we seek to identify the properties of the EGL, a thin layer on the surface of the cell. Currently, there are no analytical solutions for the deformation of a thin film with a deformable underlying substrate. Recent work using finite elements to model thin polymer films has yielded an elastic layer model for determining the modulus and thickness of thin films (18,19). The authors used experimental data and finite element modeling to calculate the stiffness of both the thin film layer and the underlying material. We applied their model treating the EGL as a uniform thin soft film on the surface of the cell body. With this approach, the reduced modulus of the system becomes

$$E^{\ast }=E_{GL}+\left(E_{Cell}-E_{GL}\right)\left(\frac{P{\xi }^n}{1+P{\xi }^n}\right),$$ (3)

where E_GL is the modulus of the EGL, E_cell is the modulus of the cell body, P and n are constants that have been empirically determined from the fits to the finite element results, and ξ is given by the equation

$$\xi =\frac{\sqrt{R\delta }}{t}{\left(\frac{E_{GL}}{E_{Cell}}\right)}^m\left(\frac{1-B_s{\nu }_s^2}{1-B_L{v}_L^2}\right),$$ (4)

where t is the thickness of the EGL layer; $v_G$ is the Poisson ratio of the glycocalyx; $v_C$ is the Poisson ratio of the cell; and m, $B_s$, and $B_L$ are constants determined from the finite element fits. We used these relationships (the “elastic layer model”) to fit the raw indentation curves and determine the properties of the glycocalyx. Experimental force curves were fit using a least-squares regression in MATLAB (The MathWorks, Natick, MA) to calculate values of the stiffness of the glycocalyx, stiffness of the cell body, and the thickness of the glycocalyx.

Brush model

An alternative description for the properties of the EGL is that of a molecular brush (17,22, 23, 24). Theories for interactions of polymers irreversibly grafted on a surface have been described by de Gennes (25). When two polymer-coated surfaces come into contact with each other, there are two contributions to the force of interaction: the osmotic pressure inside the brush and the elastic force or contraction of the brush. The repulsive pressure of the interaction for grafted polymers on a surface is

$$P\left(h\right)=\frac{k_{b}T}{s^3}\left({\left(\frac{L}{h}\right)}^{\frac{9}{4}}-{\left(\frac{h}{L}\right)}^{\frac{3}{4}}\right)forh<L,$$ (5)

where L is the resting brush height, $h$ is the instantaneous brush height, s is the separation distance between the elements of the brush, $k_b$ is the Boltzmann constant, and T is the absolute temperature. The first term describes the osmotic repulsion between the brushes, and the second term is the elastic stretch energy of the brush. We apply this to the case of a large bead indenting a surface brush. To obtain the total force required for the indentation, we integrate Eq. 5 over the contact region between the brush and a spherical indenter (see Supporting Material for details).

$$F_{brush}=\frac{2\pi kT}{s^3}\left[\frac{2}{5}R{h}_{br}\left[{\left(\frac{h_{br}}{L}\right)}^{\frac{5}{4}}-1\right]-\frac{2}{7}\left[R{h}_{br}-h_{br}{\left(\frac{L}{h_{br}}\right)}^{\frac{3}{4}}\right]\right]$$ (6)

The relationship between the brush height at the center of the indentation and the total indentation distance measured in the experiment is complicated by the fact that the surface of the cell is also being displaced (indented) in response to the applied force. We use the fact that the force on the cell and the force on the EGL must be equal. For a given force, the cell indentation is determined from the Hertz equation, and the EGL indentation is determined by Eq. 6. As described in the Supporting Material, the instantaneous brush height for a given measured indentation δ_tot is obtained by finding the root to the following equation:

$$0=\frac{4}{3}\frac{E}{1-{\nu }^2}\sqrt{r}{\left({\delta }_{tot}+L-h_{br}\right))}^{\frac{3}{2}}-2\pi \frac{kT}{s^3}\left[\frac{2}{5}R{h}_{br}\left[{\left(\frac{h_{br}}{L}\right)}^{\frac{5}{4}}-1\right]-\frac{2}{7}\left[R{h}_{br}-h_{br}{\left(\frac{L}{h_{br}}\right)}^{\frac{3}{4}}\right]\right].$$ (7)

To obtain $h_{br}$ we find the roots of Eq. 7 at each indentation point along the force-indentation curve.

Data analysis

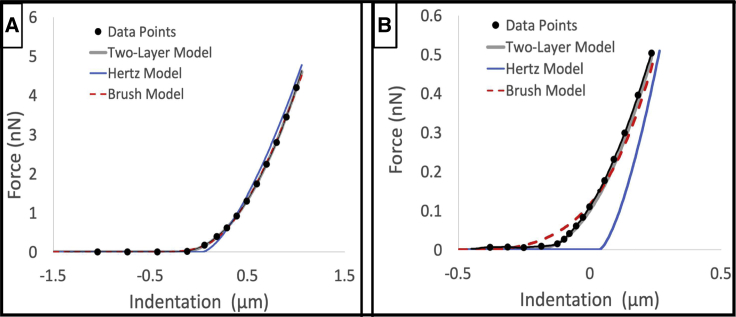
In a typical experiment, 10 force-versus-distance curves were obtained from a region of the cell near but not over the nucleus. These curves were superimposed and averaged (see Supporting Material) to obtain a single averaged indentation-versus-force curve. One of the more problematic aspects of interpreting AFM measurements on soft materials is determining exactly where the initial point of contact is between the indenter and the material. In our case, we rationalize that the EGL is much softer than the cell, so it contributes little to the indentation at high forces. Therefore, we follow the procedures of Simon et al. (26) and extrapolated data obtained at high forces (in our case, F > 2 nN) using a simple Hertz model to identify the location of the cell surface. This zero-point location was held constant for the least-squares regressions of the different theoretical relationships to the averaged curves. For the model regressions, there were three free parameters. For the brush model, these were the brush coefficient (kT/s³), the glycocalyx thickness, and the modulus of the cell. For the elastic layer model, these were t, the thickness of the glycocalyx layer; $E_{GC}$, the modulus of the glycocalyx; and $E_{cell}$, the modulus of the cell body. We experimented with different values for the Poisson ratios for the EGL $\left(v_G\right)$ and the cell $\left(v_C\right)$ (see Supporting Material). The sensitivity of the fits to these parameters was not large, but a value of 0.3 for both $v_G$ and $v_C$ seemed to provide the greatest fidelity with the measured curves. Therefore, the Poisson ratio for each of the layers was fixed at 0.3. The values of the remaining parameters in the two-layer model were taken from the original modeling of Clifford and Seah (19): p = 2.25, n = 1.5, m = 2/3, B_L = 1.92, and B_s = 0.22. An example of the fitted curves is shown in Fig. 1.

Figure 1.

Results of the elastic layer model, the brush model, and Hertz model fits for a representative force-indentation curve. (A) Shown is the entire range of interaction from 0 to a maximum of 5 nN indentation force. (B) Shown is a portion of the indentation curve from 0 to 0.5 nN to focus on the initial interaction between the bead and the surface. Note that the dots represent a small fraction (∼1/30) of the measured data pairs, which follow the thin black line connecting the dots. The single modulus Hertz indentation theory matches the data well in the high-force regime where the cantilever has compressed the soft EGL layer and the slope of the indentation curve is dominated by the modulus of the cell body. The elastic-layer model fits the raw indentation curve data with high fidelity throughout the range of indentation forces as compared to the other two models. To see this figure in color, go online.

Data inclusion criteria

For the set of 10 averaged curves at each measurement location, we calculated the three best-fit parameters and the coefficient of variation for each parameter. To avoid including erroneous values because of anomalies in the force-indentation measurements, we required that the coefficient of variation be less than 10% for each of the fitted parameters for the data to be included in the results. A comparison of included and excluded curves is given in the Supporting Material. The percentage of excluded measurements varied with indentation rate and which model was being used for the fit. These are summarized in the Results.

Leukocyte indentation model

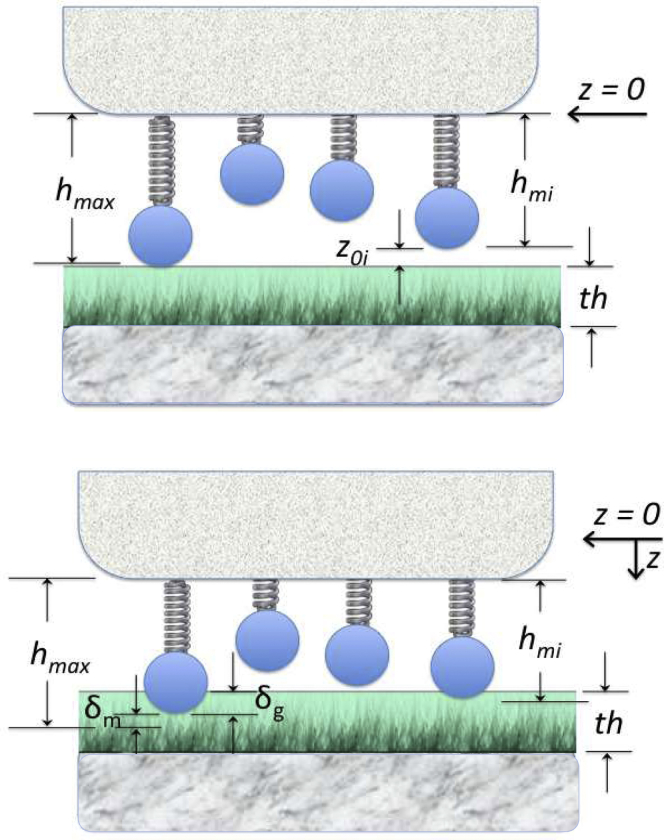
To assess what role the EGL plays in limiting leukocyte adhesion, we adapt a model of the leukocyte surface developed in previous publications (27,28). An overview of the modeling procedure is given here, and details are provided in the Supporting Material. For the purposes of the indentation analysis, we treat the individual microvilli as springs with spherical caps that are pressed into the EGL. The microvilli have different lengths that are assumed to be distributed log-normally. As the cell approaches the EGL, the longest microvilli interact with the EGL first, and more and more microvilli are engaged as the impingement force increases (Fig. 2).

Figure 2.

Schematic of leukocyte microvilli penetrating the EGL. A microvillus on the surface of the leukocyte has a height h_Mi, and its tip is approximated as a sphere with radius R_M. The maximal microvillus length is h_max. We use our measured values of the thickness of the EGL (labeled th) and the modulus of the EGL. As the microvillus is pressed into the EGL, we calculate the compression of the microvillus δ_M and the penetration depth into the EGL δ_g as functions of the indenting force to estimate how much force is needed to bring integrin molecules located near the base of the microvillus into bonding range with ligands on the endothelial cell surface. To see this figure in color, go online.

A previous analysis of the cell impinging on a smooth rigid surface has shown that as the cell is pressed against the substrate, there is an initial phase in which the primary effect is to compress the microvilli (27). A point is reached, however, at which the stiffness of the leukocyte is not sufficient to compress the microvilli further, at which point a flat interface between the cell and the substrate begins to grow at a constant separation distance between the cell and the surface (27) (see Supporting Material). It is at this point that the indentation of the microvilli into the EGL would be maximized. The modulus of the endothelial cell is significantly greater than the stiffness of a typical leukocyte, allowing us to treat the endothelial cell as a rigid substrate in the model. As the microvilli are pressed into the EGL, both the microvilli and the EGL are compressed. An approximation to the Hertz model is used to determine the force for a given depth of penetration into the EGL, and the corresponding compression of the microvillus is estimated from a linear spring approximation. The total force of impingement for a given indentation is determined by summing over the microvilli with lengths contacting the EGL weighted by the frequency of occurrence of that length on the cell surface.

To determine the number of adhesion molecules in range of bonding for a given indentation, we use the results of our previous experiments (27), in which total internal reflectance fluorescence microscopy (TIRFM) measurements were used to determine the distributions of different molecules relative to the cell surface topography. In keeping with those studies, the distribution of integrins along the microvillus length was modeled as a β-distribution, and coefficients that were determined in those studies were used here (27, 28, 29). Integrins within 40 nm of the endothelial surface (the approximate combined lengths of ICAM-1 and LFA-1) are taken to be within bonding range, and the fraction of integrins on the microvilli within 40 nm of the endothelial cell surface can be calculated as a function of the impingement force.

Results

Comparison of the two EGL models

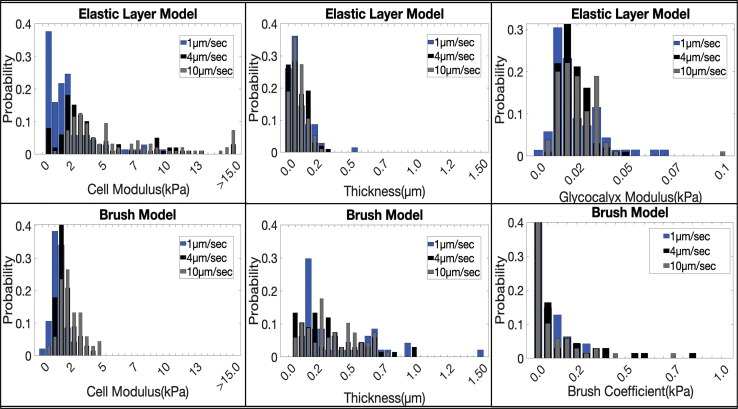
Endothelial cells were tested at three different indentation rates. Approximately 350 different cells were tested on five different days of experiments for each indentation rate. The percentage of cells that met the criterion that the coefficients of variation for all three fitted parameters were less than 10% depended on the model used and the rate of indentation. These percentages are shown in Table 1, along with the number of cells tested/kept for each case. Examples of kept and discarded fits are given in the Supporting Material. The percentage of “good fits” was higher for the two-layer model than for the brush model except at the lowest indentation rate, at which both models had difficulty fitting the data. We speculate that the slowest indentation rate data were problematic because the cells may be actively responding to contact over this time frame. It would take only a small fluctuation of the cell surface location to introduce large uncertainties in the determination of EGL properties. We also note that there is a set of data for which we could not find a solution using the brush model. These numbers are included in the percentages in Table 1. Histograms showing the distribution of values obtained with the two models are shown in Fig. 3.

Table 1.

Percentage of Cells that Were Considered Valid Fits for Both of the Models

Indentation Rate $\left(\frac{\mu \mathrm{m}}{\mathrm{s}}\right)$	Brush Model (Percent Retained) (Nkept/Ntested)	Elastic Layer Model (Percent Retained) (Nkept/Ntested)
1	36% (46/127)	54% (68/127)
4	57% (66/115)	85% (98/115)
10	63% (67/105)	89% (93/105)

Curve fits were considered valid if the coefficient of variation was less than 10% for the three fitted parameters.

Figure 3.

Histograms of the distribution of the three fitted parameters for both the brush model and the elastic layer model. To see this figure in color, go online.

Effect of indentation rate on endothelial glycocalyx properties

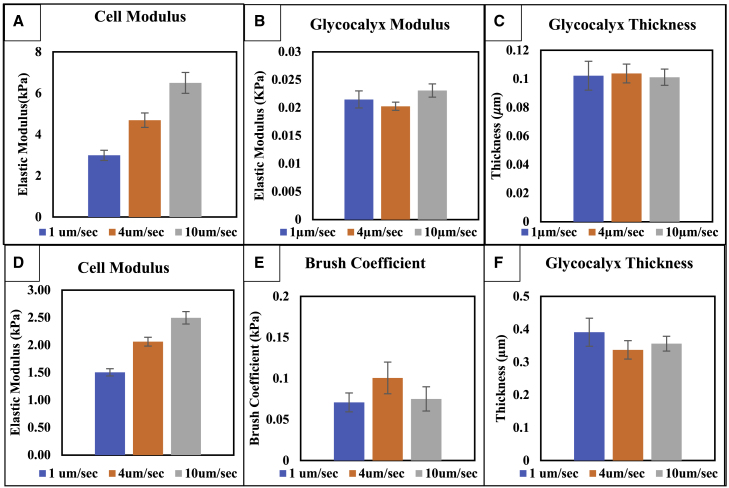
Based on a general understanding that cells are viscoelastic, we expected there to be an effect of indentation rate on the three fitted parameters, and we were interested to see if our model could capture this phenomenon. There was a clear dependence of the cell modulus on indentation rate, with the apparent modulus increasing with rate of deformation for both of the models (Fig. 4). Surprisingly, we did not see a rate dependence for the EGL thickness or modulus using either the brush model or the elastic layer model.

Figure 4.

Effect of indentation rate on cell properties: brush model and elastic layer model. The apparent Young’s modulus of the endothelial cell is significantly increased with faster indentation rates for both the elastic layer (A) and brush model (D). Indentation rate had no significant effect on the thickness (B and E) or modulus (C and F) of the EGL for either of the models (ANOVA, p < 0.05). Error bars represent the standard error of the mean. To see this figure in color, go online.

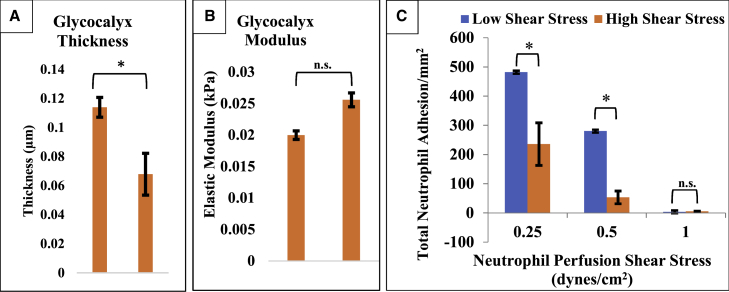
Effects of shear stress on EGL properties and cell capture

To test the effects of the EGL on cell capture, we grew endothelial cells under different shear stresses so that they would produce EGLs with different properties. Differences that occur in the endothelium as a result of changes in shear rate are well-documented, and some reports have shown that cells grown at high shear should produce a more robust glycocalyx (30). We confirm this finding. A comparison of AFM measured properties of HUVECs grown at high (10 dyn/cm²) and low (0.5 dyn/cm²) shear stress is shown in Fig. 5. Cells grown at high shear stress had a significantly thicker EGL, although there was no significant difference in the stiffness of the EGL between the two groups. Interestingly, this was also reflected in the capture of neutrophils flowing over HUVECs grown under these same conditions (Fig. 5 C). Cells cultured at low shear stress show significant increases in neutrophil adhesion with respect to cells cultured at physiological shear stress. Fluorescence labeling with an antibody against ICAM-1 showed no difference in ICAM-1 expression for cells grown at different shear rates (data not shown). This result is consistent with the idea that the EGL provides a physical barrier to cell adhesion, and when the barrier is thinner, more cell capture is observed. Note that cell capture was not robust and was only observed at very low perfusion rates (0.25–0.5 dyn/cm²). Typically, neutrophil capture studies in vitro are performed under shear stresses of 1.0 dyn/cm². At that stress, differences in capture are not observed because very few cells adhered.

Figure 5.

(A and B) Shown are AFM data for low and high shear stress glycocalyx properties. Cells that were cultured under static conditions showed a significant decrease in thickness. There was no significant difference for the glycocalyx modulus for cells cultured. (C) Flow adhesion assay results are shown. Neutrophils were perfused over endothelial cells at physiological shear stress (0.25–0.5 dyn/cm²) for 5 min, and the number of adhering leukocytes was counted. Neutrophil capture depends on the shear rate at which they interact with the endothelium, which decreases with increasing shear stress. Cells cultured at low shear stress show significant increases in neutrophil adhesion with respect to cells cultured at 10 dyn/cm². Error bars represent standard error. ANOVA was used to test for significance, p < 0.05. To see this figure in color, go online.

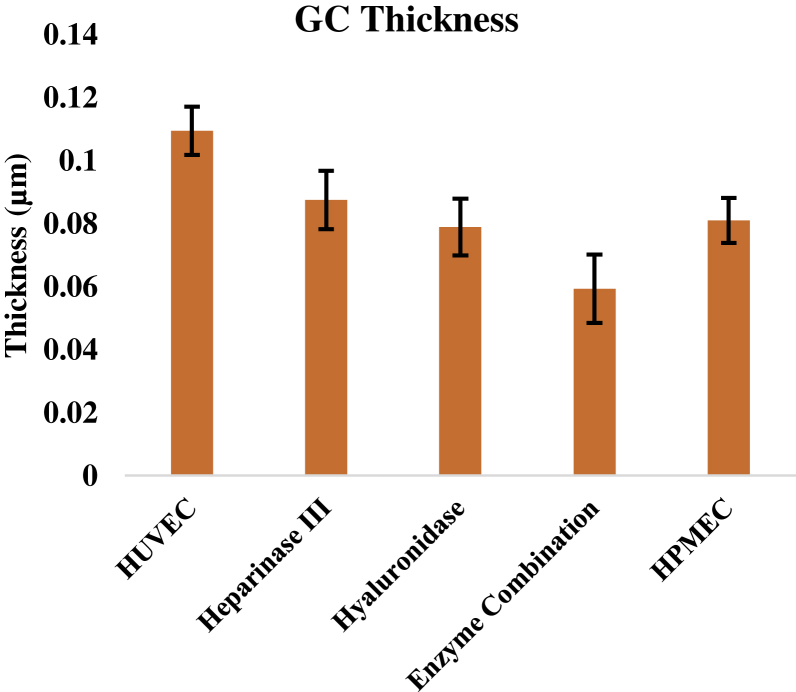
Alteration of EGL properties by enzymatic degradation and between cell types

To further illustrate the capability of our approach to detect differences in EGL properties, we tested the effects of enzymatic degradation on the properties of the EGL, and we tested the properties of the EGL on HPMECs. The results are summarized in Fig. 6. The EGL thickness was substantially reduced by enzymatic digestion. Both Heparinase III, which degrades heparan sulfate (31), and hyaluronidase, which degrades hyaluronic acid, caused significant reductions in EGL thickness, and even greater reductions were observed when the two were used in combination. EGL moduli and cell moduli were not found to be different. Measurements on HPMECs revealed that these cells have a thinner EGL than HUVECs, confirming a previous report (13).

Figure 6.

AFM data for enzymatic treatment of HUVECS and pulmonary endothelial cell glycocalyx thickness. Cells that were enzymatically treated with either Heparinase III or hyaluronidase showed a significant decrease in thickness compared to untreated HUVEC. A combination of heparanase and hyaluronidase provided the largest measured effects for decreases in thickness. Pulmonary endothelial cells also had a significantly smaller glycocalyx than HUVECs. Error bars represent standard error. ANOVA was used to test for significance, p < 0.05. To see this figure in color, go online.

Modeling results

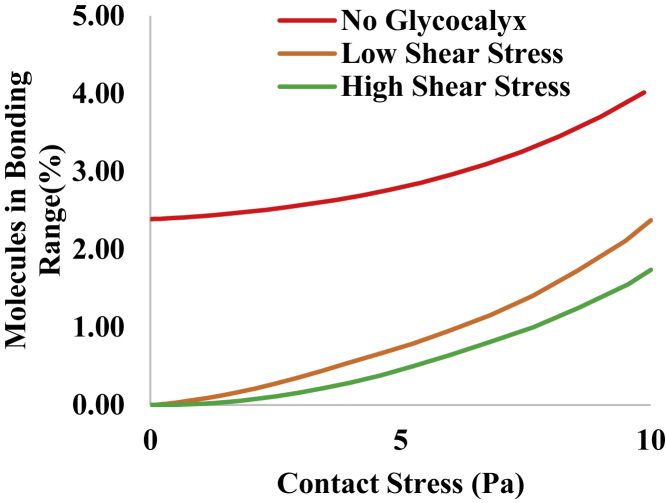
To predict how the presence of the EGL will affect bond formation between neutrophils and the endothelium, we performed calculations of the percentage of molecules on the surface in range of bonding. The extended length of LFA-1 from the surface is estimated to be ∼26 nm, and the extended length of its receptor ICAM-1 is estimated to be 16 nm, making the range of interaction suitable for bonding ∼40 nm (32,33). In Fig. 7 we show how the percentage of molecules on the cell surface in range of bonding increases as the impingement pressure between the cell and the endothelium increases. Note that in the absence of the EGL, roughly 2% of the molecules are available for bonding when the cell is resting on the surface without compression. Even the EGL cultured at low shear offers protection against bonding for small contact forces, and the EGL grown at high shear stress offers even more protection.

Figure 7.

Percentage of integrins on the cell surface that fall within 40 nm of the endothelial cell surface as a function of contact stress for the three conditions given in Table 1 (high shear stress, green curve; low shear stress, orange curve; and the case in which no EGL is present, red curve). Note that the maximal contact stress that can be exerted by a neutrophil with typical cortical tension (20 pN/μm) is 10 Pa. To see this figure in color, go online.

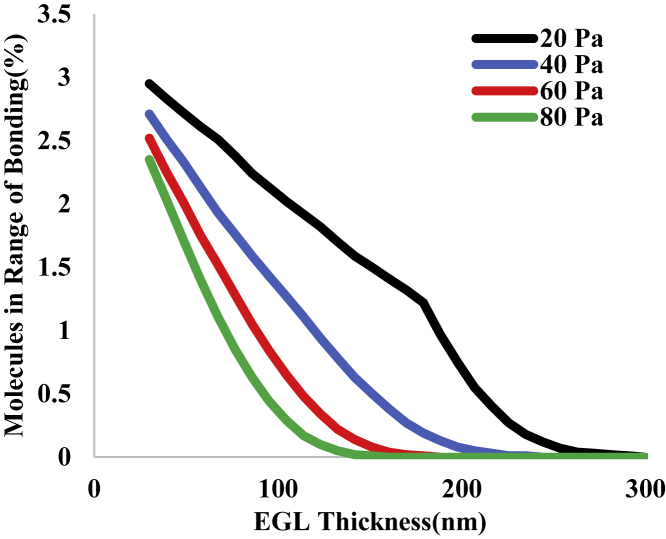
Values for the percentage of molecules on the surface within bonding range of the endothelium (40 nm) at the maximal contact stress (∼10 Pa) depend on both the thickness and stiffness of the glycocalyx layer. This dependence is illustrated in Fig. 8. The “knee” in the curves occurs where the cell body contacted the outer boundary of the EGL. For EGL thicknesses smaller than this point, successive decreases in EGL thickness result in changes in the relative compression of the microvilli, so the distance of the cell membrane from the endothelium depends both on the properties of the microvilli and on the EGL thickness. For EGL thicknesses greater than this point, the compression of the microvilli remains the same at the point where the cell body contacts the EGL, and the distance to the surface depends only on the total thickness of the EGL.

Figure 8.

The percentage of integrins on the neutrophil surface in range of bonding (<40 nm) as a function of EGL thickness for EGLs with different moduli: top curve, 20 Pa; next curve, 40 Pa; next curve, 60 Pa; and bottom curve, 80 Pa. The knee in the top curve (softest EGL) occurs where the leukocyte cell body contacts the surface of the EGL and no further compression of the microvilli occurs (see Supporting Material). To see this figure in color, go online.

Discussion

EGL mechanics

AFM indentation has been used to directly measure the modulus and thickness of the endothelial glycocalyx in living cells using a method that explicitly separates contributions from the EGL from contributions of the underlying cell. Comparing our values for the EGL with values for EGL stiffness reported previously is difficult because of the different methods used to interpret the measurements. Two groups, Oberleithner et al. (12) and Wiesinger et al. (13), used a simple spring constant (rather than an elastic modulus) to characterize EGL resistance to indentation. Both obtained spring constants in the range of 0.1–0.4 pN/nm. Unfortunately, these values are not directly comparable to elastic moduli. O’Callaghan et al. (14) and Bai and Wang (34) used different versions of Hertz theory to look for changes in the apparent modulus either with depth of penetration or over time as the EGL developed. Both then extrapolated to estimate a modulus for the EGL as opposed to the cell itself. Both of these groups report values of 250–300 Pa. Although these moduli are consistent with each other, they are much larger than what we have determined in this study. We believe that this is due to the different methods of calculation, but we cannot rule out real differences in the physical properties of the EGLs tested in the different studies. Early reports from our laboratory using the elastic layer method also indicated a much larger EGL modulus than we are reporting here, but we have since discovered that those larger values were likely erroneous because of flaws (since corrected) in the measurement apparatus. Values for the cell modulus are more easily compared across different studies and generally show good agreement. Both O’Callaghan et al. (14) and Bai and Wang (34) reported values of ∼3 kPa for endothelial cells, which are consistent with our own findings, particularly at lower indentation rates. Reports for values of the glycocalyx thickness are much more variable and are almost certainly model/method dependent. Even in our own study, the estimated thickness based on the brush model (∼350 nm) is much larger than the value obtained using the elastic layer model (∼100 nm). Wiesinger et al. (13) provides a thorough discussion of the wide-ranging variability in estimates of EGL thickness, which range from a few tens of nanometers to nearly 1.0 μm. The values we obtain using the elastic layer approach are on the low end of this range and may be due to our relatively short duration for culture, as well as the nature of the model itself, which reflects a thickness over which there is significant mechanical resistance.

Another approach to dealing with the outer surface coat of cells in general is to treat the outermost layer of the cell as a molecular brush (35). In a careful study of different analytical approaches for interpreting AFM data on cervical epithelial cells, Guz et al. demonstrated that standard Hertz models of the cell using a single elastic modulus yield a depth-dependent modulus, contradicting the basic assumption of this approach. They also showed that the addition of a resistance due to the presence of a molecular brush on the surface of the cell yields consistent, depth-independent elastic moduli (35). Our approach, in which we treat the cell as having a thin, soft elastic layer on its surface, also provides a match of the indentation data using a constant value for both the cell and EGL moduli over the full range of indentation depths we have accessed in our studies. Both approaches demonstrate the need to treat the cell surface layer as having different mechanical properties than the cell interior, and it appears from our current results that treating the surface layer either as a brush or as a thin elastic layer provides equally valid descriptions of the mechanical response of the cell during indentation under the conditions of our experiments. Interestingly, the brush coefficient we measure (100 Pa) corresponds to a brush molecular density of ∼800/μm², which is in excellent agreement with reports from Sokolov et al. (15), who reported values ranging from 300 to 1000/μm² for epithelial cells. Other more-complex models of the EGL are certainly possible and may provide more realistic descriptions of its properties. For example, it may be possible to extend the polymer brush model to account for the highly charged character of its constituent molecules by treating the EGL as a polyelectrolyte brush (36), building on recent approximations of polyelectrolyte brush behavior (37). Alternatively, one might consider more-complex mechanical models that consider anisotropy or develop more exact descriptions of the EGL based on poroelastic or triphasic theories of glycosaminoglycan compression. However, given experimental limitations, it will be difficult to document the capability of more-complex models to improve predictions of the EGL response.

We note that all these approaches make the assumption that, at least in the micron-sized regions being tested, the glycocalyx is a uniform structure. We recognize that in living systems, the EGL may vary in properties both with depth and laterally across the cell surface. To the extent that our results are consistent with theoretical predictions assuming that properties do not change with depth, this assumption appears justified. Our ability to assess variations in properties in different regions of the cell surface is limited because endothelial cells are very thin, and contributions from the substrate likely have greater impact in regions farther from the nucleus, where the cell is thinner, complicating interpretation. We have not observed a systematic difference in properties from location to location within the perinuclear region sampled in these experiments, but we cannot rule out the possibility that the EGL may have different properties in different regions of the cell. It seems unlikely, however, that these variations are larger than the substantial differences we have observed among different cells in our studies. We also cannot rule out the possibility that indentation may cause lateral migration of the EGL away from the contact zone. Such a possibility is not accounted for in our theories and could lead to underestimation of the intrinsic EGL modulus. However, given that other indenters would likely cause similar reorganizations, our measurements should still provide reliable estimates of the resistance of the EGL to penetration.

Rate dependencies

A potentially important aspect of the EGL properties that, to our knowledge, has not been explored in endothelial cells to date is the possibility that EGL properties are rate dependent. Indeed, extracellular matrix materials typically exhibit poroelastic character, and it seemed likely that the EGL will also (38). The indentation rates used in AFM studies (1–10 μm/s (12, 13, 14,35,39)) are comparable to indentation rates that might occur in vivo as leukocytes roll along the endothelium. Our estimation is based on observations that cells in close contact with the endothelium typically roll at a velocity of 27 μm/s (40), which means that a point 1.0 μm from the point of closest contact will become the point of closest contact 37 ms later (see Supporting Material). As the cell rotates forward, the distance of this point from the surface goes from ∼250 nm to zero (in 37 ms), for an average penetration rate of ∼6.7 μm/s, a value consistent with the indentation rates imposed experimentally. Values reported by Simon et al., using the brush model to analyze indentations using similar-sized beads and similar rates of indentation as in our studies, reported values for the cell body modulus to be around 0.40 $\pm 0.30\mathrm{k}\mathrm{P}\mathrm{a}$ for cancer cells, with reported values of the length of a brush to be 1020 $\pm$ 600 nm (16). In contrast to our results, however, they found that the EGL layer accounted for much if not all of the rate dependence they observed in the indentation data. There is no obvious explanation for these differences, except that the two cell types serve markedly different functions in vivo and may have very different properties. It is also the case, however, that the majority of the current literature indicates that living cells behave as viscoelastic materials (41, 42, 43, 44, 45, 46), and it is surprising that the neuronal cells being tested did not.

Indentation rate and indenter size are both expected to affect the apparent properties of a poroelastic material, and future studies should examine this in greater detail. Interestingly, most of the studies published so far have used similarly sized beads for indentation and roughly similar rates of indentation: 6-μm diameter, 1.0–10.0 μm/s, this study; 17-μm diameter, 10 μm/s (14); 5-μm diameter, 10μm/s (35); 10-μm diameter, 1.0 μm/s (13); and 1.0-μm diameter, 0.4 μm/s (12), with only the last having a substantially smaller bead and slower indentation rate. We do not observe significant differences in measured properties of the EGL for indentation rates of 1.0, 4.0, and 10 μm/s. Although the bead size and indentation rates are similar, the differences in analytical approach, cell type, and growth conditions make it difficult to draw clear comparisons among existing studies. Nevertheless, we do note that groups using similar methods of interpretation with widely different indenter sizes often report similar measures of stiffness, arguing against a strong dependence of apparent modulus on indenter size (12, 13, 14,34).

Implications for leukocyte-endothelial interactions

Knowledge of the modulus and stiffness of the EGL gives us an opportunity to make predictions about the effects of the presence of the EGL on molecular ligation between leukocytes and endothelium. A quasistatic force balance on a rolling neutrophil reveals that a neutrophil rolling on the endothelium at a wall shear stress of 6 dyn/cm² is subjected to a reaction force at the trailing edge of ∼375 pN and a contact pressure at the forward region of the cell on the order of 10 pN/μm² (47). Our modeling calculations provide insight into the consequences of such forces on penetration of microvilli into the EGL and consequent effects on bond formation. In constructing our model, we took advantage of our former work characterizing the surface topography and distribution of molecules on the surface of a neutrophil. Using TIRFM, we confirmed earlier reports that principal adhesion molecules (and chemokine receptors) are distributed nonuniformly relative to cell surface topography, with L-selectin localized to the microvillus tips and integrins and chemokine receptors preferentially located in the valleys between the microvilli (27, 28, 29). Moreover, we developed mathematical descriptions of the relative probability of finding different molecules at different distances from the microvillus tips and obtained coefficients for those relationships that were consistent with TIRFM measurements (27,29). We also discovered the importance of accounting for the fact that microvilli are different sizes and developed descriptions of the distribution of microvillus heights that are consistent with experimental observation. Finally, we showed how the proximity of different adhesion molecules to a contacting substrate increases with impingement force (29).

A thick glycocalyx will make it much more difficult for the circulating leukocyte to interact with the endothelial cell surface. The molecules required for leukocyte adhesion are typically much smaller than the glycocalyx. The cell must compress the glycocalyx to access the adhesion molecules that are present on the surface of the endothelial cells. Interestingly, even in the absence of a protecting EGL layer, a surprisingly small fraction of integrins or chemokine receptors fall within range of bond formation with a substrate when passive neutrophils contact a surface, even under mechanical impingement (28). Although this might seem surprising, there is evidence that ligation of only a few molecules may be sufficient to be physiologically significant. For example, model calculations of the response of a neutrophil to contact with chemokine immobilized onto a bead surface indicate that occupation of fewer than 10 chemokine receptors is sufficient to initiate a spreading response in the cell, leading to significant increases in the occupation of receptors and the subsequent release of intracellular calcium stores (48). Another observation supporting this comes from measurements showing that neutrophils, with integrins activated by divalent cations interacting with beads coated with ICAM-1, exhibit bond formation rates on the order of 0.05 bonds/μm²/s (47,49), whereas the total number of LFA-1 molecules on the neutrophil surface is ∼100/μm². In our analysis, we show that the presence of the EGL further decreases the likelihood of bond formation. We predict that the number of molecules within bonding range should decrease by an order of magnitude for the 110-nm-thick layer we observed in our control experiments and even further for an EGL with larger thickness. A prior analysis of microvillus penetration of the EGL used a substantially different approach to the problem (50). Like our approach, a heterogeneous distribution of microvillus heights was assumed, but in their case, the microvilli were treated as rigid spikes, and the EGL was treated as a fluid, in which the penetration velocity was proportional to force and independent of depth. These assumptions are inconsistent with AFM experiments (including the experiment presented here), all of which indicate an elastic resistance to indentation for physiologically relevant indentation rates.

Conclusion

To assess the role of the EGL in limiting the interaction of adhesive molecules on leukocytes with the endothelial surface, we performed model calculations of the percentage of molecules on a neutrophil surface in sufficient proximity to the endothelial cell surface to form a bond. Our calculations indicate that at physiologically relevant force ranges, an EGL with a thickness of 110 nm causes an order of magnitude decrease in the availability of integrins for bond formation compared with a surface having no EGL. Thus, we provide a quantitative basis for understating prior qualitative observations of increased leukocyte-endothelial engagement when the EGL is damaged or removed (8,51). Our results emphasize the view that the degradation of the EGL by the endothelial cell is an active mechanism by which the cell can enhance integrin accessibility and upregulate leukocyte adhesion under inflammatory conditions.

Author Contributions

L.F.D. performed the published AFM experimental results, performed the numerical analysis of the data, prepared most of the figures and cowrote the final manuscript. R.E.W. and L.F.D. worked together to develop the analytical approach used here for the brush model. G.A.M. adapted the thin elastic layer model for analyzing experiments and developed the impingement model for estimation of bond formation in the presence of the EGL. He also cowrote an earlier draft of the manuscript. R.E.W. worked with L.F.D. to develop MATLAB code to analyze the data and with G.A.M. in developing and L.F.D. in implementing the leukocyte impingement model. He cowrote both the original draft (with G.A.M.) and final draft (with L.F.D.) of the manuscript and developed some of the figures.

Editor: Philip LeDuc.

Supporting Citations

References (52, 53, 54, 55) appear in the Supporting Material.