Choice of Force Field for Proteins Containing Structured and Intrinsically Disordered Regions

Abstract

Biomolecular force fields optimized for globular proteins fail to properly reproduce properties of intrinsically disordered proteins. In particular, parameters of the water model need to be modified to improve applicability of the force fields to both ordered and disordered proteins. Here, we compared performance of force fields recommended for intrinsically disordered proteins in molecular dynamics simulations of three proteins differing in the content of ordered and disordered regions (two proteins consisting of a well-structured domain and of a disordered region with and without a transient helical motif and one disordered protein containing a region of increased helical propensity). The obtained molecular dynamics trajectories were used to predict measurable parameters, including radii of gyration of the proteins and chemical shifts, residual dipolar couplings, paramagnetic relaxation enhancement, and NMR relaxation data of their individual residues. The predicted quantities were compared with experimental data obtained within this study or published previously. The results showed that the NMR relaxation parameters, rarely used for benchmarking, are particularly sensitive to the choice of force-field parameters, especially those defining the water model. Interestingly, the TIP3P water model, leading to an artificial structural collapse, also resulted in unrealistic relaxation properties. The TIP4P-D water model, combined with three biomolecular force-field parameters for the protein part, significantly improved reliability of the simulations. Additional analysis revealed only one particular force field capable of retaining the transient helical motif observed in NMR experiments. The benchmarking protocol used in our study, being more sensitive to imperfections than the commonly used tests, is well suited to evaluate the performance of newly developed force fields.

Significance

We compared the performance of several force fields in molecular dynamics simulations of three proteins differing in the content of ordered and disordered regions. From the obtained trajectories, we predicted a set of measurable quantities and compared them with their experimental values. Among the predicted parameters, NMR relaxation data were particularly sensitive to the choice of force field parameters, especially those defining the water model. The presented benchmarking protocol will help to select force fields that reliably simulate properties of physiologically important intrinsically disordered proteins.

Introduction

The fact that many proteins of biological relevance contain considerably large intrinsically disordered regions (IDRs), contradicting the classical structure-function paradigm, has been accepted by the structural biology community during the past two decades (1, 2, 3). Intrinsically disordered proteins (IDPs) represent a relatively diverse class of molecules differing in their biophysical properties. One polypeptide chain often contains fully structured domains together with IDRs. Moreover, IDRs are not random polymer chains but exhibit various degree of partial ordering. They typically contain a short segment with an increased propensity to form secondary transient structures, described in the literature as prestructured motifs (4), preformed structural elements (5), or molecular recognition features (6). Such hybrid systems present methodological challenges because an IDR tethered to a well-ordered domain is a molecule consisting of regions with highly diverse dynamics. As a result, it is difficult for experimental and computational methods to accurately capture both types of behavior in these systems.

NMR represents a method of choice for studies of proteins with IDRs at atomic resolution, as disordered systems are difficult to investigate using single-crystal x-ray diffraction or single-particle reconstruction of cryo-electron microscopic images. Currently available NMR methods provide sufficient resolution to overcome the narrow distribution of chemical shifts of IDPs (7,8). However, it should be noted that the resolution improvement of IDP-targeted NMR experiments relies on the slow relaxation of IDRs. Therefore, the sensitivity of such experiments is often too low for the rapidly relaxing signals of amino acids in the well-ordered regions of hybrid proteins.

Molecular dynamics (MD) simulations could, in principle, serve as an ideal tool to study behavior of hybrid proteins at an atomic level. Moreover, most of the NMR parameters can be reliably predicted from structural models, which allows for direct comparison of MD results with experimental data. In practice, several problems complicate MD simulations of IDPs. The energy landscapes of IDRs are expected to be weakly funneled such that the search for a specific functionally competent conformation could be extremely inefficient (9). In this study, we examined the applicability of MD simulations to hybrid proteins and assessed their reliability by predicting several measurable parameters from the obtained trajectories and comparing them with experimental data. Moreover, we provide an example of prediction of measurable parameters as a guide to select optimal setup for future experiments, such as positions with paramagnetic relaxation enhancement (PRE) labels. We tested the currently available force fields Amber99SB-ILDN (A99), CHARMM22^∗ (C22^∗), and CHARMM36m (C36m) in combination with explicit solvent models TIP3P, TIPS3P, and TIP4P-D. Chemical shift, residual dipolar coupling (RDC), PRE, relaxation rate, and small-angle x-ray scattering (SAXS) experimental data were used for validation. It should be pointed out that our goal was not to describe the properties of the studied proteins as faithfully as possible but to look for features that would distinguish the performance of various force fields in MD simulations of a microsecond time range. The hybrid proteins investigated in this study included 1) δ subunit of RNA polymerase from Bacillus subtilis (δRNAP), 2) regulatory domain of human tyrosine hydroxylase (RD-hTH), and 3) a fragment consisting of residues 159–254 of rat microtubule-associated protein 2c (MAP2c^159–254). δRNAP makes RNA polymerase sensitive to the concentration of initiating nucleoside triphosphates, which is important for rapid changes in gene expression (10). It consists of two domains of a similar size. The N-terminal half of δRNAP folds into a well-ordered, mostly α-helical domain, whereas the C-terminal half is disordered and highly negatively charged, with the exception of a lysine-rich motif ⁹⁶KAKKKKAKK¹⁰⁴ and C-terminal Lys173 (11). Experimental data showed that the lysine stretch makes transient electrostatic contacts with various residues in the acidic C-terminal region (1). No sign of formation of transient α-helical structures was observed in the C-terminal domain, which prefers extended backbone conformations, presumably because of the electrostatic repulsion of the acidic side chains. RD-hTH catalyzes hydroxylation of L-tyrosine to L-3,4-dihydroxyphenylalanine (L-DOPA) and is a key and rate-limiting enzyme in biosynthesis of important catecholamine neurotransmitters (12,13). Its N-terminal region (∼40% of its sequence) is disordered but contains a segment with ∼80% propensity to form four turns of α-helix (14). MAP2c^159–254 corresponds to the central region of MAP2c, where proteins regulating the microtubule-stabilizing activity of MAP2c bind in a phosphorylation-dependent manner (15,16). MAP2c^159–254 is mostly disordered but exhibits an ∼20% propensity to form four turns of an α-helix presumably important for intermolecular interactions (16,17).

Materials and Methods

NMR spectroscopy

NMR assignments of δRNAP and of the disordered part of RD-hTH were published previously (14,18). MAP2c^159–254 was assigned as described for full-length MAP2c (19). PRE data of δRNAP were published previously (11). RDCs were calculated as a difference between splitting observed in in-phase/anti-phase (IPAP) spectra (20) obtained for proteins in stretched 5% polyacrylamide gel and in isotropic medium. The RD-hTH data were acquired at 20°C on a 600 and 850 MHz Bruker Avance III spectrometer (Bruker, Billerica, MA), and the MAP2c^159–254 data were acquired at 27°C on a 600 MHz Bruker Avance III spectrometer. The backbone amide ¹⁵N relaxation data were published previously for δRNAP (21) and measured using standard pulse sequences (22) for 1.0 mM [¹⁵N]-RD-hTH and 0.34 mM [¹⁵N]-MAP2c^159–254 at 27°C on 850 and 950 MHz Bruker Avance III spectrometers, respectively. The interscan delays were set to 1.5, 2, 6, and 25 s for R₁, R₂, and steady-state heteronuclear Overhauser effect (ssNOE) measurements without and with ssNOE transfer, respectively. The relaxation delays for the R₁ experiment were 11.2, 16.8, 28.0, 44.8, 61.6, 95.2, 196, and 308 ms, and the delays for the R₂ experiment were 0, 14.4, 28.8, 43.2, 57.6, 86.4, and 129.6 ms. R₁ and R₂ data were fitted using a two-parameter exponential. The errors were obtained using the bootstrap procedure (23). The ssNOE values were calculated as a ratio between signal intensities obtained from spectra with or without ¹H saturation. The errors were derived from background noise levels in each individual spectrum.

SAXS

The SAXS data sets were collected using a BioSAXS-1000 (Rigaku, Tokyo, Japan) instrument with an x-ray beam wavelength of 1.54 Å at 27°C. The distance between the sample and the detector (PILATUS 100K; Dectris, Baden-Daettwil, Switzerland) was 0.48 m, covering a scattering vector (q = 4πsin(θ)/λ) range from 0.009 to 0.65 Å⁻¹. For solvent and sample, one two-dimensional image was collected with 1 h exposure time per image. Radial averaging of two-dimensional scattering images and the solvent subtractions were performed using SAXSLab3.0.0r1 (Rigaku). All data sets were truncated to a maximal scattering vector of 0.3 Å⁻¹ for further analysis. Radii of gyration were determined using PRIMUS from ATSAS v2.7.2 (24) with Guinier analysis (implemented in the PRIMUS Guinier Wizard) in the range 2–52 for δRNAP and in the range 9–30 for MAP2c^159–254; the globular particle type was used for both proteins. The molecular form factor analysis (25) was performed online at http://sosnick.uchicago.edu/SAXSonIDPs.

Computational details

The MD simulations were performed using Amber99SB-ILDN (26), CHARMM22^∗ (27), and CHARMM36m (28) force-field parameters for the protein atoms and the TIP3P, TIPS3P (29,30), or TIP4P-D (31) water models. The proteins were solvated using a rhombic dodecahedral box of waters with a minimal distance between the box walls and solute of 2 nm. The charge of the system was neutralized by adding Cl⁻ and Na⁺ ions, and the concentration of salt was adjusted to 100 mM. All simulations were performed under periodic boundary conditions. Before the MD runs, in vacuo and solvent energy minimizations with the steepest descent algorithm were carried out. The lengths of bonds with hydrogen atoms were constrained using the LINCS algorithm (32). An integration time step of 2 fs was used. A cutoff of 1.0 nm was applied for the Lennard-Jones interactions and short-range electrostatic interactions. Long-range electrostatic interactions were calculated by particle mesh Ewald summation with a grid spacing of 0.12 nm and a fourth-order interpolation (33). The four-step 8-ns-long equilibration protocol consisted of the following parts: 1) 2-ns relaxation of water molecules at 300 K during the NVT equilibration with restrained (1000 kJ mol⁻¹ nm⁻²) solute coordinates, 2) 2-ns NVT (300 K) run with restrained (1000 kJ mol⁻¹ nm⁻²) backbone atom coordinates, 3) 2-ns NpT (300 K, 1 atm) run with restrained (1000 kJ mol⁻¹ nm⁻²) backbone atom coordinates, and 4) 2 ns of unrestrained NpT simulation (300 K, 1 atm). The length of the follow-up production NpT simulations (300 K, 1 atm) was 200 ns. The simulations using the TIP4P-D water model were further prolonged to 1 μs, and additional independent simulations (500 ns for δRNAP and MAP2c^159–254, 400 ns for RD-hTH) starting from different initial conditions were run for all listed force fields and protein systems. The temperature and pressure were maintained using the Berendsen coupling scheme (34) during the equilibration steps; the production NpT simulations were performed using the velocity rescaling thermostat with a stochastic term (35) and the Parrinello-Rahman barostat algorithms (36). Atomic coordinates were recorded every 1 ps.

Predictions of NMR parameters

Chemical shifts were calculated using the prediction algorithm SPARTA+ (37) for each structure, and averaged secondary chemical shifts (SCSs) were calculated by subtracting the random-coil values (38). RDC calculations using a local alignment window were performed. For calculations using a local alignment window, the RDC, calculated using the program PALES (39), for the central amino acid of the local 15-amino-acid segment was calculated for each conformer (40). The resulting RDC profile along the primary sequence was calculated by averaging each value over the whole trajectory and multiplying by the corresponding scaled absolute value of the generic baseline to account for long-range effects (41). The scale was chosen so that the lowest root mean-square deviations (RMSDs) from the experimental values were obtained in the disordered regions. PRE was calculated for the spin label used in the experiments, i.e., for thiol-reactive methanethiosulfonate (MTSL) attached to a side chain of cysteine introduced by site-directed mutagenesis. Sterically allowed MTSL side-chain conformations were sampled using previously published rotameric distributions (42) and built explicitly for each spin-label site of each individual structure backbone. 600 side-chain conformers were calculated, and the sterically allowed conformers were retained. Relaxation effects were averaged over these conformers as described by Salmon et al. (41).

The strategy described previously (43) was used to calculate relaxation rates. The autocorrelation function C_i(τ) was calculated from subtrajectories of each simulation, probing two timescales (τ_max ≤ 5 or 50 ns). Each trajectory was thus divided into the blocks of 10 and 100 ns, respectively, and averaged. For each averaged block, C_i(τ) was described as a sum of N = 512 exponentials ${\text{e}}^{-\tau /{\tau }_{c,i}}$ whose amplitudes A_i were obtained using a Tikhonov regularization procedure (44). For each averaged block, the spectral densities are then defined as

$$J_i\left(\omega \right)=\sum _{i=1}^N\frac{A_i{\tau }_{c,i}}{1+{\omega }^2{\tau }_{c,i}^2}$$ (1)

and used to predict spin relaxation rates.

Results and Discussion

Impact of selected water model

Our first goal was to examine the performance of various models of water in simulations of three hybrid proteins used as test molecules in this study. It is well described in the literature (31) that the water models typically used in MD simulations (e.g., TIP3P) significantly underestimate London dispersion interactions. To prevent this problem, TIPS3P and TIP4P-D water models were also tested, and the reliability of the behavior of IDPs or the IDRs was analyzed. Modified TIP3P containing nonzero van der Waals parameters was introduced originally in 1998 (30) and shown to provide more realistic results for IDPs when combined with C36m (28). Simulations using this model typically result in extended states when other models of water tend to produce ensembles that are structurally too compact relative to experiments (31).

Our preliminary 200-ns MD runs, using the TIP3P water model in combination with A99 (26), confirmed the artificial behavior of TIP3P.

The inferior performance of TIP3P was manifested most clearly by the calculated radius of gyration (R_g) of MAP2c^159–254. All simulations started with conformations having R_g close to the experimental value of 2.5 nm obtained from SAXS. During the initial 100 ns of simulations with TIP3P, R_g dropped to ∼1.5 nm regardless of the protein force field used (Fig. 1 b). This result confirms that attractive interactions leading to formation of compact structures are unnaturally enhanced when TIP3P is used, as was also reported previously in (31,45). We also ran 200-ns simulations with the TIPS3P model (30) in combination with the C22^∗ (26) and C36m (28) force fields. Remarkably, TIPS3P did not prevent the artificial compaction of MAP2c^159–254 (Fig. 1 b; a comparison of trajectories calculated using C36m with TIP3P and TIPS3P is presented in Fig. S1). A similar trend was observed also for RD-hTH (Fig. 1 c), although a direct comparison with the experiment was not possible because of the RD-hTH dimerization in real samples.

Figure 1.

Simulated R_g of δRNAP (a and d), MAP2c^159–254 (b and e), and RD-hTH (c and f) obtained using the TIP3P (TIPS3P in the case of C22^∗ and C36m) water model (a–c) and TIP4P-D water model (d–f). Experimental data are shown in gold, and values calculated using A99, C22^∗, and C36m are shown in green, red, and blue, respectively. To see this figure in color, go online.

Finally, we performed MD simulations with the TIP4P-D water model combined with A99, C22^∗, and C36m. In agreement with the literature (31) and in a sharp contrast with the simulations run with TIP3P and TIPS3P, R_g of MAP2c^159–254 did not drop below the value calculated from the SAXS data (Fig. 1 e). In the case of RD-hTH, TIP4P-D also prevented unexpected compaction but only in combination with C36m (see the discussion of the impact of the protein force field parameters in the following section).

Interestingly, the water model influenced simulated R_g of δRNAP less than R_g of MAP2c^159–254 and RD-hTH. We observed the artificial collapsed structure only rarely in simulations of δRNAP with TIP3P or TIPS3P (see A99 data in Fig. 1 a). The most likely explanation is that the C-terminal IDR of δRNAP is very strongly negatively charged, preventing its collapsed structure regardless of applied water model (Fig. S2). To examine the influence of water models in the simulations of δRNAP more closely, we also calculated NMR relaxation parameters from the MD trajectories. As discussed below in more details, the prediction of relaxation parameters is a challenging task. Therefore, we hoped that a comparison of calculated and experimental relaxation parameters might reveal more subtle effects. Indeed, we observed much lower predicted values of ssNOE for residues 134–173 of δRNAP (Fig. 2 a). Such values indicate an artificially high disorder of the highly acidic region further than 30 residues from the positively charged lysine stretch (residues 96–104). Importantly, this effect was observed not only for the original TIP3P model but also for the modified version TIPS3P (red and blue traces in Fig. 2 a). Limitations of TIPS3P were already noticed by Huang et al., who reported that this model with C36m provided correct R_g for the arginine-serine but underestimated the R_g of the Thermotoga maritima cold-shock protein and of the N-terminal domain of HIV-1 integrase (28). A further modification of TIPS3P improved the R_g prediction for the cold-shock proteins but worsened the agreement for the other two proteins (28).

Figure 2.

ssNOE (a and d) and relaxation rates Γ_x (b and e) and R₁ (c and f) of the C-terminal IDR of δRNAP obtained with the 5-ns sliding window using the TIP3P (TIPS3P in the case of C22^∗ and C36m) water model (a–c) and TIP4P-D water model (d–f). Experimental data are shown in gold, and values calculated using A99, C22^∗, and C36m are shown in green, red, and blue, respectively. To see this figure in color, go online.

In conclusion, significant differences between water models were already observed during the first 200 ns of the simulations. Considering the results for TIP3P, TIPS3P, and TIP4P-D, we continued our study only with the TIP4P-D model, extending the MD simulations to the microsecond range.

Impact of force fields on global shape of proteins

We first examined the global shape of studied proteins in terms of R_g and SAXS curves. The R_g-values calculated from 1-μs (Fig. 1) and 0.5-μs (Figs. S3 and S4) A99, C22^∗, and C36m trajectories of δRNAP (simulated using TIP4P-D) oscillated between 3 and 6 nm. The experimental R_g-value, obtained by the Guinier analysis of the SAXS curve, was (3.45 ± 0.3) nm. The R_g alone did not reveal any systematic difference among the force fields, except for an extending event observed around 550 ns in the C36m simulation.

The R_g-values calculated from MD trajectories of MAP2c^159–254 oscillated between 2 and 4.5 nm, close to the experimental value of (2.5 ± 0.3) nm (Fig. 1 e).

Figs. S5 and S6 show the comparisons between the predicted and measured SAXS profiles for δRNAP and MAP2c^159–254 and for individual force fields. The lowest Q-factors, indicating the best fit (Table 1), were obtained for the C22^∗ force field. Inspection of individual SAXS profiles revealed that C36m and A99 overestimated SAXS intensities for MAP2c^159–254 and underestimated SAXS intensities for δRNAP in the medium- and low-q region (0.1 nm⁻¹ < q < 1 nm⁻¹; see Table 1), whereas C22^∗ predicted the medium- and low-q SAXS intensities well.

Table 1.

Comparison of Calculated RMSD from Experimental Values and Normalized scores

Metric	δRNAP			RD-hTH			MAP2c159–254
	A99	C22∗	C36m	A99	C22∗	C36m	A99	C22∗	C36m
RMSD:
ΔδCα/ppm	0.92	0.88	0.82	0.92	0.84	0.64	0.74	0.44	0.55
ΔδCβ/ppm	0.86	0.78	0.79	0.63	0.52	0.43	0.45	0.45	0.41
ΔδC(O)/ppm	0.74	0.67	0.62	0.96	0.90	0.56	0.84	0.55	0.65
ΔδN/ppm	1.71	1.92	1.67	3.55	3.40	2.88	1.54	1.90	1.07
Q for D(NHN)	0.30	0.33	0.33	1.21	1.12	0.89	0.76	0.69	0.74
Local PREa by MTSL at L110C	0.25	0.41	0.26	n.d.b	n.d.	n.d.	n.d.	n.d.	n.d.
Local PRE by MTSL at L132C	0.07	0.17	0.16	n.d.	n.d.	n.d.	n.d.	n.d.	n.d.
Local PRE by MTSL at L151C	0.12	0.13	0.14	n.d.	n.d.	n.d.	n.d.	n.d.	n.d.
Local PRE by MTSL at L168C	0.06	0.06	0.07	n.d.	n.d.	n.d.	n.d.	n.d.	n.d.
PRE (all data)	0.08	0.10	0.09	n.d.	n.d.	n.d.	n.d.	n.d.	n.d.
ssNOE	0.15	0.17	0.20	0.11	0.38	0.25	0.15	0.20	0.16
R2 or Γx/s−1	1.50	1.56	2.46	2.62	2.32	0.93	1.13	1.32	1.09
R1/s−1	0.12	0.15	0.14	0.19	0.24	0.13	0.21	0.19	0.23
Q for SAXS (0.1 nm−1 < q < 1 nm−1)	0.057	0.040	0.084	n.d.	n.d.	n.d.	0.070	0.048	0.075
Q for SAXS (all data)	0.060	0.045	0.085	n.d.	n.d.	n.d.	0.084	0.066	0.083
Score:
sCS	1.11	1.08	1.00	1.46	1.32	1.00	1.42	1.22	1.11
sRDC	1.00	1.09	1.08	1.33	1.20	1.00	1.06	1.00	1.36
sPRE (all data)	1.00	1.25	1.11	n.d.	n.d.	n.d.	n.d.	n.d.	n.d.
srelax	1.00	1.13	1.37	1.74	2.57	1.44	1.04	1.16	1.07
sNMR	1.00	1.13	1.44	1.54	1.89	1.22	1.06	1.12	1.07
sSAXS (all data)	1.32	1.00	1.87	n.d.	n.d.	n.d.	1.28	1.00	1.26
sall	1.08	1.08	1.21	1.55	1.78	1.17	1.24	1.15	1.11
Rg/nm	4.13	4.03	4.66	n.d.	n.d.	n.d.	2.60	2.94	2.78
Rg penalty	0.13	0.10	0.28	n.d.	n.d.	n.d.	0	0.06	0
scombined	1.21	1.18	1.49	1.55	1.78	1.17	1.24	1.21	1.11

^aCalculated for PRE of residues 84–104 because of the indicated spin label.

^bInput experimental data not determined.

We also fitted the experimental and predicted SAXS profiles to molecular form factors (MFFs) developed by Riback et al. (25). Fitting the experimental MAP2c^159–254 data to an MFF provided R_g = (2.87 ± 0.3) nm and a value of the Flory exponent typical for a fully unfolded polypeptide (ν = 0.59 ± 0.02). Very similar values were obtained by fitting the profile simulated by C22^∗, R_g = (2.952 ± 0.003) nm and ν = 0.603 ± 0.001. As expected, the MFF did not fit well the SAXS profile of δRNAP, containing a large well-ordered domain.

The effect of a force field on the global conformations of RD-hTH was examined as well (Fig. 1 f). Compact structures with R_g ≈ 2 nm were formed after 500 ns in simulations with A99 and C22^∗ force fields but not with C36m. Therefore, it seems that CH36m in combination with TIP4P-D most efficiently prevents the collapse of structures of RD-hTH and MAP2c, representing proteins not exhibiting extraordinary electrostatic repulsion.

Impact of force fields on long-range contacts

After evaluating the effect of different force-field parameters on the global shapes of the studied proteins, we compared the ability of the force fields to properly reproduce contacts between residues further apart in the sequence. We started by inspecting δRNAP as a test system for which long-range contacts are observed experimentally, yet no transient helicity is observed in the C-terminal IDR.

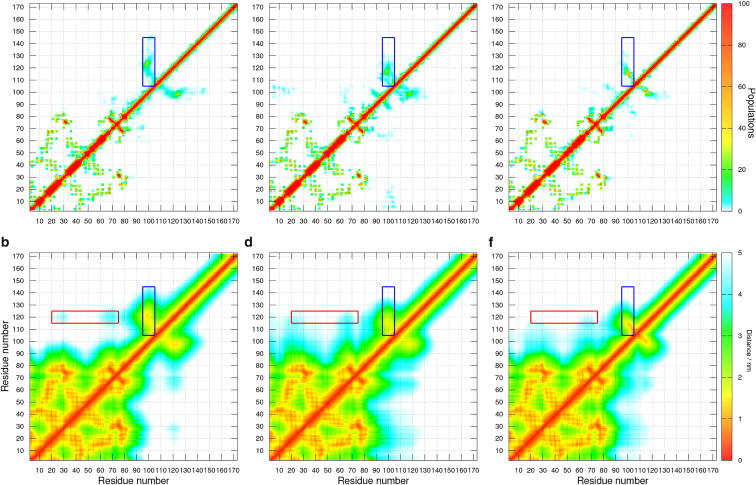
Residue pairwise distance maps represent an efficient way to evaluate contacts formed during individual MD runs. Rectangular boxes in the maps presented in Fig. 3 highlight distances 1) between the lysine-rich stretch ⁹⁶KAKKKKAKK¹⁰⁴ and highly acidic residues in the C-terminal region and 2) between the ordered N-terminal and disordered C-terminal domains. Differences between distances represented by colors document that the relative average distances varied depending on the force field used. For example, the lysine tract interacted with the residues in the vicinity of Glu120 more strongly in the A99 simulation than in the runs with the C22^∗ and C36m force fields (blue rectangles in Fig. 3). The average distances between the N-terminal domain and vicinity of Glu120 (red rectangles in Fig. 3) also differed. We want to emphasize that the reliability of distance maps is influenced not only by the capabilities of individual force fields applied for the δRNAP in combination with the TIP4P-D water model but also by limited sampling within the trajectories of the cumulative length of 1.5 μs.

Figure 3.

Maps describing the distances between residue pairs of δRNAP simulated using A99 (a and b), C22^∗ (c and d), and C36m (e and f) force fields in combination with TIP4P-D. The scales shown at the right indicate color coding of mean inter-residue C^α-C^α distances (lower row) and of populations of events when the distance between any pair of residue atoms was shorter than 0.4 nm (upper row). To see this figure in color, go online.

To directly compare the contacts observed during the MD calculations with the experimental data, we simulated PRE of individual residues of δRNAP for a series of spin-label positions examined in a previous experimental study (11). The results showed that A99 realistically reproduced experimentally observed contacts of the lysine stretch ⁹⁶KAKKKKAKK¹⁰⁴ with labels placed at L110C and L132C in the highly acidic C-terminal sequence (Fig. 4, a and b). The experimentally detected contact with L151C was also predicted. In agreement with the distance map, C22^∗ overestimated contacts of the lysines with the closest label at L110C and underestimated contacts with more distant labels, including L132C. C36m did not overestimate contacts with the label at L110C but underestimated contacts with the label at L132C similarly to C22^∗ and A99 (see RMSD for PRE in the lysine stretch for individual spin labels, listed in Table 1).

Figure 4.

Simulated PRE of δRNAP with the spin label at L110C (a), L132C (b), L151C (c), and E168C (d). Experimental data are shown in gold, and values calculated from MD simulations using the TIP4P-D water model combined with the A99, C22^∗, and C36m force fields are shown in green, red, and blue, respectively. To see this figure in color, go online.

In conclusion, correct prediction of electrostatic contacts between residues apart in the sequence is a challenging task. In the case of δRNAP, A99 with TIP4P-D performed best, being able to predict reliably distances between amino acids separated by up to 50 residues in the sequence.

Impact of protein force-field parameters on local conformations

In the next step, we analyzed the accuracy of description of local backbone conformations of δRNAP in the simulations. For this purpose, we compared experimental values of several NMR parameters reflecting the local backbone conformation with the values calculated from snapshots of the MD simulations. First, we checked values of RDC. In principle, RDCs depend both on local conformation and on the overall shape of the molecule, determining the distribution of orientations of the molecule in a partially aligned environment (20). However, it is very demanding to achieve a good sampling of conformations and orientations to faithfully reproduce experimental data without any prior information. Therefore, we used the knowledge of long-range electrostatic contacts in the δRNAP molecule, obtained experimentally as PRE, and applied the local averaging window (40) to predict RDC values. The predicted RDC values are plotted in Fig. 5 a. The prediction varied especially in the vicinity of the lysine stretch, in which A99 and C36m achieved better agreement with the experiment than C22^∗.

Figure 5.

Values of RDC (a, f, and k) and SCS (b–e, g–j, and l–o) in C-terminal IDR (residues 85–173) of δRNAP (a–e), N-terminal IDR (residues 1–65) of RD-hTH (f–j), and MAP2c^159–254 (k–o) simulated with the TIP4P-D water model. Experimental data are shown in gold, and values calculated using A99, C22^∗, and C36m are shown in green, red, and blue, respectively. The random-coil limits are shown in gray. The MD simulations started from structures with α-helices modeled for residues 40–53 of RD-hTH and 200–216 of MAP2c^159–254. For the sake of clarity, the statistical errors are not displayed here but separately in Figs. S7–S9. To see this figure in color, go online.

The second examined NMR parameter reflecting local conformation was the chemical shift. In comparison with RDC, the chemical shifts are measured with higher precision, and their prediction does not require a prior knowledge of molecular orientation. SCSs (deviations of predicted chemical shifts from their random-coil values (38)) are compared with the experimental data in Fig. 5, b–e. Values provided by all force fields agree well with the experimental chemical shifts, except for some mismatch of data predicted by C22^∗ for the lysine stretch.

In summary, all force fields predicted local conformation of the extended disordered region of δRNA reasonably well. The slightly worse prediction in the lysine-rich motif by C22^∗ most likely reflects less accurate description of electrostatic contacts by the force field.

Simulation of transient helical regions

In the next step, we tested how different force fields describe transient α-helical elements in (partially) disordered proteins. A propensity to adopt α-helical secondary structure represents another level of complexity of IDP conformations not present in the mostly extended C-terminal domain of δRNAP. To explore its effect on the simulations, we inspected MD trajectories of RD-hTH and MAP2c^159–254. These proteins were chosen so that they differ in α-helical propensity.

Experimental values of chemical shifts (17,19) indicate that RD-hTH and MAP2c^159–254 form α-helices in the regions 40–53 and 200–216 with ∼80 and 20% propensity, respectively (cf. Fig. 5). We performed a set of simulations with different force fields, starting from structures containing ideal α-helices in the experimentally identified α-helical regions, and observed the stability of the helices (Figs. S10–S12). During MD simulations using A99 and C22^∗ force fields, the initially present α-helix unfolded in less than 80 ns (Fig. S12). Huang et al. (28) reported that C36m optimized with TIPS3P 1) correctly simulated transient α-helices and 2) provided correct R_g for the arginine-serine peptide but not for other two tested IDPs. Therefore, we were curious whether C36m would keep its ability to maintain the transient α-helices with TIP4P-D. For RD-hTH, C36m with TIP4P-D maintained the α-helical conformation in the whole 1-μs trajectory and for 220 ns in an independent 400-ns run (Fig. S13). In the case of MAP2c^159–254, the transient α-helix unfolded after ∼35, 85, and 830 ns in three independent runs starting from conformations including the helix at the beginning (Fig. S9). The lower stability of the MAP2c^159–254 helix in simulations is in agreement with its low (20%) population observed experimentally. Formation of the well-defined helix was not observed in the remaining 465, 415, and 170 ns of the trajectories or during two 0.5-μs runs started from conformations without the helix. However, temporary formation of the helix (for ∼50 ns) was observed in simulations of MAP2c^159–254 using C22^∗ (Document S1. Figs. S1–S15 and Tables S1–S6, Document S2. Article plus Supporting Material a) and A99 (Fig. S12 d). It should be emphasized that the calculated trajectories do not fully sample the equilibrium canonical ensembles. Therefore, we do not expect to observe quantitative agreement between the experimental and simulated populations of transient α helices.

The ability of the force fields to reliably describe transient α-helices was directly reflected by the predicted SCS values (Fig. 5). Outside of the helical region, a good agreement of the predicted and experimental chemical shifts was obtained for all force fields tested. Deviations from the experimental values were observed for the A99 and C22^∗ simulations in the region where the originally present α-helix unfolded. For the C36m simulations, SCSs typical for α-helices were obtained in the regions where the α-helix was modeled (Fig. 5, g–i and l–n). Quantitatively, the values of predicted versus SCSs corresponded to 87% populations of the helix in the simulations vs. ∼80% population in the real sample of RD-hTH. In the case of MAP2c^159–254, data from all trajectories were combined in a ratio corresponding to the experimentally estimated 20% population of the helix.

In conclusion, the ability of C36m and TIP4P-D to keep the transient α-helices during the simulation and to prevent the artificial collapse of IDR structures suggests that this combination is most robust for our studied proteins. This is noteworthy considering that C36m was not optimized in combination with TIP4P-D, but with TIPS3P and its variants (28). We believe that the C36m and TIP4P-D combination is a promising candidate for a benchmarking on a wider range of proteins, as was done, e.g., by Robustelli et al. (45).

It should be noted that the tests discussed so far utilize a limited set of the most readily available experimental values. We already discussed that NMR relaxation data distinguished the performance of TIP3P and TIP4P-D water models better than R_g in the A99 and C36m simulations of δRNAP (details are presented in the section Impact of Selected Water Model). In the next section, we examine whether extending the benchmarking to NMR relaxation helps to discriminate the ability of force fields to describe dynamic properties of hybrid proteins.

Simulation of NMR relaxation data

To test the examined force fields within the MD framework more thoroughly, we compared their abilities to reproduce NMR relaxation rates. The NMR signal relaxes because of the local magnetic fields that fluctuate as a result of stochastic molecular motions. The stochastic reorientation of vectors describing the interactions contributing to relaxation is described by the correlation function. In real samples, large numbers of molecules with an almost isotropic distribution of orientations are measured. Consequently, the correlation functions have a simple analytical form (series of exponential functions). In simulations, the sufficient sampling of the orientations is difficult to achieve (in principle, data of large sets of independent trajectories should be averaged), which deteriorates the calculated correlation function regardless of the force field employed. In our analyses of limited numbers of trajectories, the ensemble averaging was approximated by calculating averages of correlation functions of different regions of the trajectories. The simulations should be also sufficiently long because the correlation function reflects only the effects of motions on the timescale covered by the simulation. The obtained predictions must be interpreted carefully to not confuse the artifacts of the force fields with the effects of the sampling scheme used.

The δRNAP molecule is particularly well suited to test the ability of force fields to predict relaxation rates because its domains greatly differ in their stochastic motions. Dynamics of the well-ordered N-terminal domain is dominated by overall tumbling and probes the ability of the force fields to reproduce hydrodynamic properties. In contrast, internal motions contribute most significantly to the relaxation rates of residues in the disordered C-terminal domain. Analysis of the simulated trajectories showed that correlation functions calculated for 5-ns sliding time windows (solid lines in Fig. 6, a–c) describe relaxation in the C-terminal IDR sufficiently well but fail to match the experimental data in the well-ordered region, where slower motions, most notably the overall tumbling, dominate the dynamics. Smooth profiles of the calculated NMR relaxation parameters, resembling the experimental profiles in the IDR, document that the use of a short sliding window allowed us to average a sufficient number of correlation functions and to capture most important modes of motion.

Figure 6.

ssNOE (a, d, and g) and relaxation rates Γ_x (b), R₂ (e and h), and R₁ (c, f, and i) of δRNAP (a–c), N-terminal IDR (residues 1–65) of RD-hTH (d–f), and MAP2c^159–254 (g–i). Experimental data are shown in gold, and values calculated using A99, C22^∗, and C36m are shown in green, red, and blue, respectively. Solid and dashed lines indicate data obtained from correlation functions calculated using 5- and 50-ns windows, respectively. For the sake of clarity, the statistical errors are not displayed here but separately in Figs. S13–S15. To see this figure in color, go online.

To obtain relaxation rates close to the experimental values also in the well-ordered N-terminal region, the time window was extended to 50 ns, and averages of 12 correlation functions were calculated (dashed lines in Fig. 6, a–c). Prediction of the cross-correlated Γ_x rate, which is most sensitive to slow motions, was most informative (Γ_x was used to monitor the slow motions instead of the more frequently measured R₂ rates because Γ_x could be obtained with a higher accuracy than R₂ for δRNAP, which has an extremely poor dispersion of chemical shifts in its C-terminal IDR (21)). Predicted and experimental values were comparable for tested force fields, albeit scattered for individual residues because of the contribution of slow motions that were not sufficiently averaged in the small set of the 30 independent correlation functions. The match of the experimental and (average) simulated Γ_x-values is in the line with the fact that TIP4P-D reproduces the water diffusion coefficient more reliably than the TIP3P model (31).

The general agreement was also good in the disordered region for all three force field, but significant differences were observed when different regions of the δRNAP sequence were compared. The trend of ssNOE values, most sensitive to fast motions, was best reproduced by A99 (green line in Fig. 6 a). Also, the predictions by CHARMM force fields reflected their abilities to predict long-range contacts. Somewhat higher ssNOE values (and elevated Γ_x) in the vicinity of residues 100 and 125 indicated that C36m slightly overestimated partial ordering in the most rigid regions of the C-terminal domain, where long-range contacts were predicted (see the section Impact of the Force Fields on Long-Range Contacts). This is in agreement with the difficulty of predicting contacts between residues far in the sequence, as discussed above. C22^∗ overestimated ssNOE around residues 115 and 90, in agreement with its tendency to prefer contacts of the lysine stretch with residues closer in the sequence.

In conclusion, we calculated NMR relaxation rates from MD trajectories using two time windows (50 and 5 ns) to cover different timescales of motions in the ordered and disordered regions, respectively. The results independently confirmed the observed moderate differences in predicting long-range contacts and showed that all force fields describe well the hydrodynamic properties for the TIP4P-D water model. For δRNAP with a well-ordered domain and highly charged disordered domains not forming transient helical structures, A99 performed best. The C36m force field described long-range electrostatic contacts slightly worse, but its accuracy was acceptable. C22^∗ somewhat overestimated electrostatic contacts between residues close in the sequence, which resulted in noticeable, but not dramatic, deviations of simulated NMR parameters from the experiment.

NMR relaxation data were also predicted for RD-hTH and MAP2c^159–254. In the case of RD-hTH, the comparison was possible only in the N-terminal IDR because the protein dimerizes in real samples. As a consequence, relaxation of the well-ordered portion of RD-hTH is incomparable (faster) with that simulated for the monomer. Moreover, broadening of the peaks of the well-ordered region did not allow us to obtain sufficiently sensitive NMR spectra under the conditions used. Comparison of the simulated and experimental relaxation rates in the N-terminal IDR of RD-hTH (Fig. 6, d–f) and MAP2c^159–254 (Fig. 6, g–i) led to the same general conclusions as for δRNAP. However, the simulation of RD-hTH allowed us to address a particular feature not manifested by δRNAP, namely the effect of formation of the transient α-helix on the calculated relaxation rates. In the experimental data, the propensity to form an α-helix is reflected by elevated R₂ values. Comparison of the relaxation rates calculated from the C36m trajectories (in which the helix was present during most of the simulation time) with those obtained from the A99 and C22^∗ runs (in which the helix quickly unfolded) revealed that the presence of the α-helix in the simulated structures is needed to reproduce the values of R₂ (Fig. 6). The 5-ns sliding window was sufficient to match the experimental R₂ profile in the C36m simulations, indicating that the dynamics of the IDR of RD-hTH is dominated by relatively short correlation times. Less frequent conformational changes occurring in the α-helical region were not sampled sufficiently and resulted in high standard deviations of R₂. Outside of the transient α-helix, the data obtained with the 50-ns window matched the experimental profile well.

In the case of MAP2c^159–254, which has a much lower α-helical propensity, the increase of R₂ is hardly visible in the experimental data. Similarly to RD-hTH, relaxation data predicted using the 5-ns window matched the experimental values reasonably well.

Quantitative comparison of the force-field reliability

To express the discussed differences of the force field performance quantitatively, we applied the metrics developed by Robustelli et al. (45) and calculated normalized force-field scores based on the RMSDs of the experimentally obtained parameters from the corresponding values predicted from the simulations (Table 1). The calculated combined force-field scores (s_combined) show that none of the tested force fields provided superior prediction of all parameters for all proteins.

In the case of δRNAP with a highly charged IDR forming no transient α-helices, relative accuracy of predicting experimental data varied for different parameters. Predicted chemical shifts, reflecting the local backbone conformation, was similar for all force fields (best for C36m). A99 best reproduced NMR data sensitive to long-range intramolecular interactions (RDC, PRE, and relaxation data, described by s_NMR). The chemical shift RMSD values are within the reported standard deviation of the SPARTA+ predictor (2.45, 1.09, 0.94, and 1.14 ppm for backbone N, C(O), C^α, and C^β nuclei (37)). The quality factor Q of RDC is comparable with typical RMSDs of data predicted from x-ray structures with 2-Å resolution (46). PRE and relaxation data deviated from the experimental ranges by less than 10%, with the exception of Γ_x, which is particularly difficult to predict, as discussed above. C22^∗ provided the best prediction of parameters describing the overall shape of δRNAP (R_g and SAXS profiles), with the Q-factor of SAXS data equal to 5%. If the individual scores are averaged with the same weights, the overall scores s_all are better for C22^∗ and A99 than for C36m.

In the case of RD-hTH, with the experimentally determined 80% propensity to form an α-helix in its IDR, C36m predicted all experimental data much better than A99 or C22^∗. The superior performance of C36m, reflected by low s_all, can be clearly attributed to its ability to maintain the experimentally observed transient α-helix. The quantitative parameters showed that C36m predicted the experimental data well (compared with the reference values discussed above), with the exception of RDC.

In the case of MAP2c^159–254, which lacks a well-ordered domain and exhibits only ∼20% propensity to form an α-helix, all force fields predicted the experimental data with similar accuracy, reflected by small differences between their scores. It documents that the ability of C36m to maintain transient α-helices loses its significance if the populations of the helical structures are low. The performance of all force fields was good, based on comparison with the reference values discussed in the details of the δRNAP simulations.

In conclusion, the quantitative comparison confirmed the superior performance of C36m in the case when a transient α-helix was present. A99 predicted most accurately parameters influenced by long-range electrostatic interactions (s_NMR = 1 for δRNAP).

Prediction of suitable spin-label positions

Calculation of already measured experimental parameters is important for benchmarking of the simulations as illustrated above. However, prediction of so far unknown measurable values is also very useful because it can facilitate experimental design. Selection of residues for placement of paramagnetic labels can serve as an example. Preparation of paramagnetically labeled samples is a time-consuming procedure, including site-directed mutagenesis, expression, purification, and paramagnetic spin labeling of the protein before the NMR PRE measurements. A choice of the label position not providing information about long-range contacts thus represents a considerable waste of time and sources. Reliable MD simulations can be used for in silico prediction how much structural information a label in a certain position can provide and how much such labeling perturbs the native structural ensemble. An example of such prediction for all solvent accessible positions within the RD-hTH is presented in Fig. 7.

Figure 7.

Predicted preferential positions of spin labels in RD-hTH (a) and simulated PRE profiles for four selected spin-label positions (b–e). To see this figure in color, go online.

Based on the simulations using C36m and TIP4P-D, we calculated PRE profiles for all possible positions. To localize solvent accessible positions reporting on long-range contacts with the disordered region, we defined the following score. Integrals of the areas between PRE profiles and a threshold of 0.8 were summed in the disordered region (residues 1–70), except for ±10 residues in the vicinity of the spin label. In addition, the score was set to zero for residues with solvent accessibility lower than 0.6 according to Fraczkiewicz and Braun (47) because the label should be freely accessible on the surface of protein and should not interfere with any protein conformation. The analysis presented in Fig. 7 a indicates four to five areas well suited for attachment of spin labels for future PRE experiments. Predicted PRE profiles for labels placed in the centers of the suggested areas are presented in Fig. 7, b–e.

Conclusions

The goal of our study was to assess the applicability of currently available MD approaches to hybrid proteins consisting of ordered and disordered regions. We tested the performance of the A99, C22^∗, and C36m force fields in combination with the TIP3P and TIP4P-D water models. The performance was examined for mostly disordered MAP2c^159–254 containing a low population of prestructured α-helix, for δRNAP consisting of comparably large well-ordered and disordered domains without transient α-helices, and for RD-hTH consisting of ordered and disordered domains with a highly populated α-helical prestructured motif. Considering the functional importance of transient helical elements, we paid particular attention to the ability to preserve the α-helix during the simulation. The generated structural ensembles were used for predicting a variety of NMR and SAXS parameters and subsequently compared with the experimental data.

The TIP4P-D water model performed substantially better than TIP3P or TIPS3P. The differences between force fields were less distinct. The optimal (most universal) combination was CHARMM36m with the TIP4P-D water model, which most efficiently prevented artificial collapse of disordered regions and retained transient α-helical structure elements within the disordered regions. The study also showed that the performance of different force fields and models can vary depending on the actual physical properties of investigated IDRs.

Considering the fast pace of force-field development (45,48), the major value of this study is not identification of the best force field available at the time of testing but presentation of a generally applicable benchmarking approach, including NMR relaxation rates. An important feature of the approach is the combination of checked parameters that report on abilities of the force fields to reproduce a broad range of physical properties of the studied molecules.

Author Contributions

J.H. and L.Ž. designed the research. V.Z., A.M., P.L., A.L., E.N., and V.K. carried out calculations, performed the experiment, and analyzed the data. Z.J., M.M., and K.M. prepared the samples and performed the experiment. V.Z., A.M., P.L., J.H., and L.Ž. wrote the article, and all authors reviewed the manuscript.

Editor: Rohit Pappu.