Stochastic Model of T Cell Repolarization during Target Elimination I

Abstract

Cytotoxic T lymphocytes (T) and natural killer cells are the main cytotoxic killer cells of the human body to eliminate pathogen-infected or tumorigenic cells (i.e., target cells). Once a natural killer or T cell has identified a target cell, they form a tight contact zone, the immunological synapse (IS). One then observes a repolarization of the cell involving the rotation of the microtubule (MT) cytoskeleton and a movement of the MT organizing center (MTOC) to a position that is just underneath the plasma membrane at the center of the IS. Concomitantly, a massive relocation of organelles attached to MTs is observed, including the Golgi apparatus, lytic granules, and mitochondria. Because the mechanism of this relocation is still elusive, we devise a theoretical model for the molecular-motor-driven motion of the MT cytoskeleton confined between plasma membrane and nucleus during T cell polarization. We analyze different scenarios currently discussed in the literature, the cortical sliding and capture-shrinkage mechanisms, and compare quantitative predictions about the spatiotemporal evolution of MTOC position and MT cytoskeleton morphology with experimental observations. The model predicts the experimentally observed biphasic nature of the repositioning due to an interplay between MT cytoskeleton geometry and motor forces and confirms the dominance of the capture-shrinkage over the cortical sliding mechanism when the MTOC and IS are initially diametrically opposed. We also find that the two mechanisms act synergistically, thereby reducing the resources necessary for repositioning. Moreover, it turns out that the localization of dyneins in the peripheral supramolecular activation cluster facilitates their interaction with the MTs. Our model also opens a way to infer details of the dynein distribution from the experimentally observed features of the MT cytoskeleton dynamics. In a subsequent publication, we will address the issue of general initial configurations and situations in which the T cell established two ISs.

Significance

Cytotoxic T lymphocytes are the main cytotoxic killer cells of the human body to eliminate target cells. The microtubule (MT) organizing center repositioning plays a key role in the killing process, and two underlying mechanisms are discussed: cortical sliding and capture-shrinkage. We devise a theoretical model for the molecular-motor-driven motion of the MT cytoskeleton confined between the membrane and the nucleus during T cell polarization and make quantitative predictions about the spatiotemporal evolution of the MT organizing center position and the MT cytoskeleton morphology comparable with experiments. It reveals the mechanism underlying the experimentally observed biphasic behavior and a remarkable synergy between capture-shrinkage and cortical sliding mechanisms. It also opens a way to infer dynein distribution from details of MT cytoskeleton dynamics.

Introduction

Cytotoxic T lymphocytes and natural killer (NK) cells have a key role in our immune system by finding and destruction of virus-infected and tumor cells, parasites, and foreign invaders. Once a T cell leaves the thymus, it circulates through the organism in search of a target cell. The directional killing of a target cell is completed in three subsequent steps. First, T cell receptors bind to antigens on the surface of the target cell presented by the major histocompatibility complex (1, 2, 3, 4, 5, 6), leading to the creation of a tight contact zone called the immunological synapse (IS) (7, 8, 9) composed of multiple supramolecular activation clusters (9, 10, 11). In the second step, the cell repolarizes by relocating the microtubule organizing center (MTOC) toward the IS (12, 13, 14, 15, 16, 17, 18) under the influence of forces exerted on MTs. Moreover, because mitochondria, the Golgi apparatus, and the endoplasmic reticulum are attached to MTs, these organelles are dragged along with the MT cytoskeleton (16,19, 20, 21, 22, 23, 24). Consequently, the repolarization process involves massive rearrangements of the internal, MT-associated structure of the cell. In the third step, the T cell releases at the IS the cytotoxic material (e.g., the pore-forming protein perforin and the apoptosis-inducing granzyme) from vesicles, the lytic granules (25, 26, 27, 28, 29), toward the target cell, leading to its destruction (29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39). Although the lytic granule secretion can take place without MTOC repolarization (40) or before it (41), the MTOC-accompanied granule secretion may be required for the killing of resistant cells such as tumor cells.

The IS is partitioned into several supramolecular activation clusters (SMACs) including the distal SMAC, peripheral SMAC (pSMAC), and the central SMAC (cSMAC) (7,9,11,42,43), in which T cell receptors (cSMAC) and adhesion molecules are organized. Moreover, the engagement with the target cell results in the formation of actin and actomyosin networks at the IS (44). Dynein, a minus-end-directed (toward the MTOC) molecular motor protein anchored at the cell cortex, is absolutely necessary for the repolarization to take place, as was experimentally demonstrated with knock-out experiments (45) analogous to dynein exerting forces against anchor proteins fixed at the cell cortex during mitosis (46, 47, 48, 49).

Once the T cell is activated, the adaptor protein ADAP forms a ring at the periphery of the IS with which dynein colocalizes (50,51). Concerning the underlying mechanism, it was proposed that the repolarization is driven by the cortical sliding mechanism (50,52), in which dyneins anchored at the cell cortex step on the MT toward the minus end and thus pull the MTOC toward the IS. The first experimental indications for cortical sliding came from observation of cytoskeleton movement using polarization light microscopy (17). Subsequent experiments indicate that the IS periphery, in particular the ring-shaped pSMAC, is the region where dyneins attach to and pull on MTs (17,50).

The repositioning was observed in various experiments. Focused activation of the photoactivable peptide-MHC on the glass surface was used in (53). In (16), the repositioning was observed alongside with the rotation of the mitochondria, which provided evidence that the mitochondria are dragged with the MT cytoskeleton. Detailed observations were made by Yi et al. (14), providing new insight into the mechanism of the repolarization. In (14), an optical trap was used to place a target cell so that the initial point of contact is in diametrical opposition to the current position of the MTOC, which allowed for dynamical imagining in a quantitative fashion. During the experiment, the deformations and changes in MT structures were observed and the position of the MTOC was tracked. First of all, Yi et al. (14) provided strong experimental evidence against the cortical sliding mechanism. Instead, the observations indicate that the MTOC is driven by a capture-shrinkage mechanism (54) localized in a narrow central region of the IS. The capture-shrinkage mechanism involves dynein interacting in an end-on fashion with the plus end of a MT, which is fixed in a position on the membrane of the cell where the MT depolymerizes. The MT shrinkage part happens plausibly because dynein pulls the MT plus end against the cell membrane, which increases the force-dependent MT depolymerization rate (54).

In sequences of microscope pictures, (14) showed that MTs reach from the MTOC to the IS and bend alongside the cell membrane. Subsequently, MTs form a narrow stalk connecting the MTOC with the center of the IS. The plus end of MTs in the stalk, while captured in the center of the IS, straighten (probably under tension due to the dynein pulling at the plus end) and shrink by depolymerization at the capture point. Consequently, the MTOC is dragged toward the center of IS, which invaginates into the cell, further proving the location of the main pulling force. When the MT depolymerization was inhibited by taxol, the MTOC repositioning slowed down substantially. These observations supported the hypothesis that the capture-shrinkage mechanism plays a major role. However, the velocity of the MTOC repositioning is not always an advantage because time is necessarily for the killing of target cells in hostile environments (55) and might be beneficial for slower killing processes (56). Additionally, Yi et al. (14) reported that the repositioning is biphasic and that the two phases differ in the velocity of the MTOC and the orientation of its movement. In the first, so-called polarization phase, the MTOC travels quickly around the nucleus of the cell in a circular manner. The polarization phase ends when the MTOC is approximately 2 μm from the center of the IS. Subsequently, during the second, “docking” phase, the MTOC travels directly toward the IS with a substantially decreased velocity.

The cortical sliding mechanism alone was previously analyzed with a deterministic mechanical model (57), in which it was demonstrated that mechanism is capable of reorienting the MTOC into a position under the IS underneath certain conditions. Furthermore, oscillations between two ISs were studied in different situations. Nevertheless, the forces in the model were deterministic, neglecting the stochastic nature of dynein attachment, detachment, and stepping, leaving various experimental observations unexplained such as, for instance, the preferential attachment of MTs to a dynein anchored in the periphery of the IS.

Sarkar et al. (58) hypothesized that dynamic MTs find the central region of the IS, where they can be captured by a dynein by growing from the MTOC in random directions, analogous to the search and capture mechanism during the formation of the mitotic MT cytoskeleton. Once MTs attach to the dynein in the central region of the IS, the relocation of the MTOC starts, which is the process that is analyzed in this work.

Despite these detailed experimental observations, many aspects of the internal mechanisms driving the relocation of the MTOC during the T cell repolarization remain poorly understood, like the cause of the transition from the polarization to the docking phase. Yi et al. argue that a resistive force emerges when the MTOC-IS distance is around 2 μm, leading to a reduction in the MTOC’s velocity. The potential causes are physical impediments to the MTOC’s translation or a reduced attachment or a force development of molecular motors. Moreover, the experiments of Yi et al. were performed with specific initial positions of the IS and the MTOC being diametrically opposed. The question arises whether the observed dominance of the capture-shrinkage mechanism would be robust in other naturally occurring situations in which the initial position of the MTOC is not in diametrical opposition to the IS. If capture-shrinkage is the truly dominant mechanism, what is the role of cortical sliding? Finally, why are cortically sliding MTs caught just on the periphery of the IS (17), and is it caused purely by the colocalization of dyneins with the ADAP ring (50)? The answers to these questions are still elusive, and in this work, we analyze them in the framework of a quantitative theoretical model for the relocation of the MTOC after the IS formation. Although this study focuses on the T cell, NK cells display the same kind of phenomenology: IS formation, MTOC relocation, and the release of lytic granules.

We distribute our analysis into two consecutive publications. In this first publication, we describe the theoretical model we use and present our results focusing on the experiments described in (14,17,50) and on an analysis of the two mechanisms: cortical sliding and capture-shrinkage. This comprises the setup in which the T cell has one IS and the initial positions of the IS and the MTOC are diametrically opposed to each other.

A subsequent, second, publication will focus on quantitative predictions of our model for situations that have not yet been analyzed experimentally. There, we will focus on the repolarization after initial configurations not realized in (43), which will also provide additional insight into the different effects of the two mechanisms, cortical sliding and capture-shrinkage. Moreover, we will analyze the eventually oscillating MT/MTOC movement with two ISs.

Methods

Computational model

The cell and its nucleus are modeled as two concentric spheres of the radius 5 and 3.8 μm, respectively. The model of the cytoskeleton consists of MTs and the MTOC; see Fig. 1. MTs are thin filaments with a diameter of ∼25 nm (59, 60, 61). The measured values of the flexural rigidity vary between experiments (62,63); in our model, we take 2.2 × 10⁻²³ nm² (64), yielding a persistence length larger than 5 mm that exceeds the size of the cell by three orders of magnitude. A single MT is represented by a bead-rod model (65). Because repolarization occurs on a timescale of seconds, the growth of MTs is neglected. The beads move under the influence of forces to be described below (and defined in detail in the Supporting Materials and Methods: bending, drag, molecular motor, and stochastic forces). Assuming zero longitudinal elasticity of the MTs, we use constrained Langevin dynamics to model the motion of the MTs; see the Supporting Materials and Methods. Repulsive forces acting on the MT segments confine the cytoskeleton between the nucleus and the cell membrane.

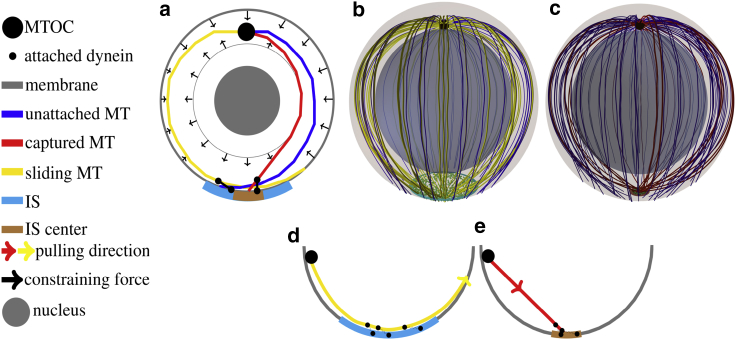
Figure 1.

(a–c) Sketch of the model. (a) A two-dimensional cross-section of the model is shown. MTs sprout from the MTOC, and their movement is confined by constraining forces from the cell membrane and the nucleus. MTs are attached to dynein motors in the IS, and they are pulled by the capture-shrinkage or the cortical sliding mechanism. (b and c) A three-dimensional sketch of the cell model is given. The outer transparent and inner spheres represent the cell membrane and the nucleus of the cell, respectively. (b) The blue disk represents the IS, where cortical sliding dynein is anchored. Small green dots in the IS represent randomly distributed dynein. (c) The brown disk represents the central region of the IS where the capture-shrinkage dynein is anchored. (d and e) A sketch of the cortical sliding mechanism (d) and the capture-shrinkage mechanism (e) is shown. Small black dots on the membrane: dynein anchor points, small black dots on the MTs: attachment points. Note that MTs depolymerize when pulled by capture-shrinkage dynein toward the membrane. To see this figure in color, go online.

The MTOC is a large protein complex that has a complex structure composed of mother and daughter centrioles (66, 67, 68, 69) embedded in the pericentriolar material (70, 71, 72). MTs nucleate from γ-tubulin-containing ring structures within the pericentriolar material mainly at the appendages of the mother centriole (66,73). MTs can sprout from the MTOC in all directions. MTs whose original direction is approximately parallel to the membrane of the cell will continue to grow to the cell periphery. Other MTs will soon hit the wall of the cell or its nucleus. Such MTs can either bend and assume a new direction parallel to the cell membrane or undergo the MT catastrophe. Therefore, long MTs are seemingly always sprouting from the MTOC in one plane, as can be seen in (14). Consequently, we model the MTOC as a planar, rigid polygon structure (Fig. S3) from which MTs emanate in random directions by fixing the positions and directions of their first segment (Fig. S4). MTs sprout from the MTOC to the cell periphery; see Fig. 1 a.

Unattached dynein is represented just with one point on the surface of the cell. If the dynein is closer to the MT than L₀, protein attaches with a probability p_a. Dynein motors are distributed randomly in specific, spatially varying concentrations on the cell boundary. Attached dynein is represented by a fixed anchor point located on the cell boundary and an attachment point located on an MT, both being connected by an elastic stalk of a length L₀ (74,75). The force exerted on an MT F_i^Dynein depends on the stalk’s elastic modulus k_Dynein and its prolongation. The dynein stepping depends on the magnitude of the force and its orientation. If the force is parallel to the preferred direction of the stepping, the attachment point moves one step to the MT minus end (toward the MTOC) with a constant probability p₋. If the orientation of the force is opposite and its magnitude smaller than a stall force F_S, dynein makes one step toward the minus end with a force-dependent probability. If |F_i^Dynein| > F_S and the force has a unfavorable direction, the dynein makes one step to the plus end with a constant probability p₊. The steps of the dynein have varying lengths (75), but for simplicity, we set it to the most frequently measured value of d_step = 8 nm. The probability of detachment, p_detach, increases with the force.

Experimentally, two mechanisms by which the dynein act on MTs have been identified: cortical sliding (17), in which MTs under the effect of dynein move tangentially along the membrane, and capture-shrinkage (14), by which MTs under the effect of dynein are reeled in toward the membrane and concomitantly depolymerized (sketched in Fig. 1, d and e).

The IS is divided into two regions: the center, where dyneins act on MTs via the capture-shrinkage mechanism (14), and the complete IS, where dyneins act via the cortical sliding mechanism. Each region is modeled as an intersection of the cell sphere with a cylinder, 1, with radius R_IS = 2 μm for the complete IS and R_CIS = 0.4 μm for the central region. Dyneins are distributed randomly with uniform area density ρ_IS in the small central region, denoted as capture-shrinkage dynein, and density ${\tilde{\rho }}_{\text{IS}}$ in the larger region of the whole IS, denoted as cortical sliding dynein.

Results

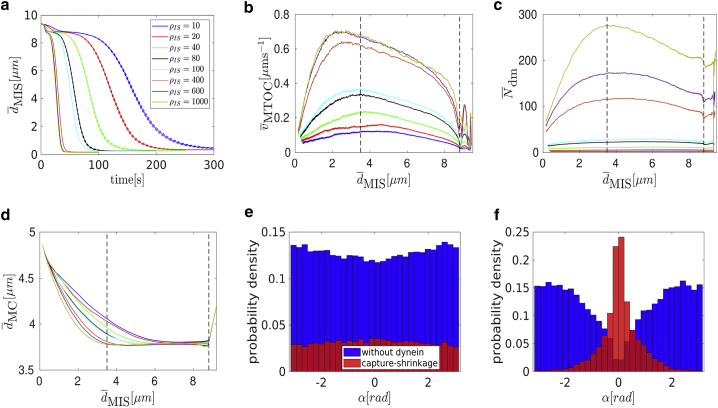
We analyzed the role of the cortical sliding and capture-shrinkage mechanisms and their combined effect during the repolarization by computer simulations of the model defined in the previous section. The density of dyneins anchored at the IS, ${\tilde{\rho }}_{IS}$, and the central region of the IS, ρ_IS, are unknown model parameters, which we therefore vary over a broad range between 0 (no anchored dynein) and 1000 μm⁻² (the maximal number of anchored dynein because of the lateral size of dyneins; see Supporting Materials and Methods, Section S1.1.5). During the integration of the equation of motion, various quantities are calculated: the distance between the center of the MTOC and the IS, d_MIS; the number of dyneins attached to the MTs, N_dm; the velocity of the MTOC, v_MTOC; and the distance between the MTOC and the center of the cell, d_MC. For each point in the parameter space, these quantities were averaged over 500 simulation runs. Each simulation run is initialized with the mechanical equilibrium (minimal elastic energy) configuration of the MT/MTOC-system and all dyneins being detached. Results are shown with the standard deviation as error bars only when they are larger than the symbol size.

Capture-shrinkage mechanism

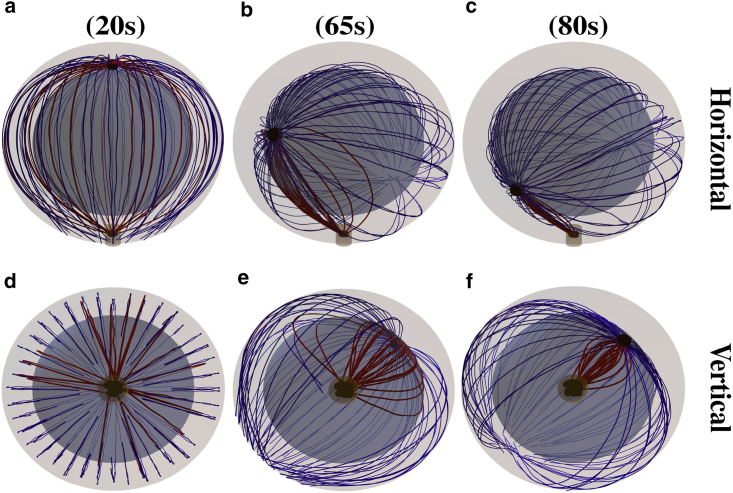
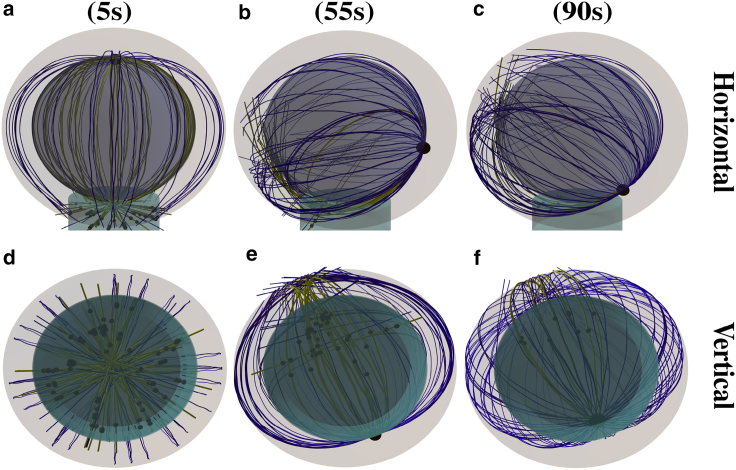
The repositioning process under the effect of the capture-shrinkage mechanism is visualized in Fig. 2. In Fig. 2, a and d, it can be seen that initially, the attached MTs aim from the MTOC in all directions. Subsequently, the stalk of MTs is almost formed in the middle phase of the repositioning (Fig. 2, b and e), and it is fully formed as the MTOC approaches the IS; see Fig. 2, c and f and Video S1 showing the time evolution of the MT cytoskeleton configuration under the effect of the capture-shrinkage mechanism with 100 MTs and the dynein density ρ_IS = 100 μm⁻².

Figure 2.

Snapshots from the time evolution of the MT cytoskeleton configuration under the effect of the capture-shrinkage mechanism alone (dynein density ρ_IS = 100 μm⁻²). MTs are connected to the MTOC indicated by the large black sphere. Blue and red curves are unattached and attached MTs. Small black spheres in the IS represent dyneins. The brown cylinder indicates the center of the IS, where the capture-shrinkage dyneins are located. (a and d) d_MIS = 9 μm. Initially, the attached MTs sprout from the MTOC in all directions. (b and e) d_MIS = 6 μm. As time progresses, MTs form a stalk connecting the MTOC and the IS. (c and f) d_MIS = 2.5 μm. The stalk is fully formed, and it shortens as the MTOC approaches the IS. To see this figure in color, go online.

Video S1

Capture-Shrinkage Repositioning

The process can be divided into three phases based on the time evolution of the MTOC velocity; see Fig. 3 b. In the first phase, when the distance between the MTOC and the center of the IS is ${\overline{d}}_{\text{MIS}}$ > 8.8 μm, the velocity changes rapidly in the first seconds of the process and then falls to a local minimum. In the second phase, the velocity continually increases to a maximum, and then in the third phase, it decreases again. By comparison of Fig. 3, b and c, it can be seen that the time evolution of the velocity corresponds to the time evolution of the number of dyneins acting on MTs. The evolution of the number of attached dyneins during the first phase can be understood from an analysis of Figs. 2, a and b and 3 d. At the beginning of the simulations, a substantial number of MTs intersects the IS (visually demonstrated in Fig. 2, a and d), resulting in a fast increase of the number of attached dyneins. Because the MTs attached to dynein sprout from the MTOC in every direction (cf. Fig. 3 e), the MTOC moves toward the IS and, simultaneously, to the nucleus of the cell (see Fig. 3 d). As the MTOC approaches the nucleus of the cell, the nucleus starts to oppose the movement by repelling the MTs and, at the end of the first phase, the MTOC. Therefore, as the pulling force of the dyneins is opposed by the nucleus, the dyneins detach because the detachment rate is force dependent.

Figure 3.

Capture-shrinkage mechanism: (a) the dependence of the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. (b–d) Dependencies of the average MTOC velocity ${\overline{v}}_{\text{MTOC}}$ (b), the number of dyneins acting on microtubules ${\overline{N}}_{\text{dm}}$ (c), and the MTOC-center distance ${\overline{d}}_{\text{MC}}$ (d) on the average MTOC-IS distance are shown. Black dashed lines denote transitions between different phases of the repositioning process. (e and f) Probability distributions of the angles between the first MT segments and the direction of the MTOC movement for a dynein density ρ_IS = 100 μm⁻² (e), t = 1 s, ${\overline{d}}_{\text{MIS}}$ ∼ 9 μm are given. (f) t = 60 s, ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm. To see this figure in color, go online.

The increase of the number of attached dyneins ${\overline{N}}_{\text{dm}}$ in the second phase can be explained by considering the fact that the MTOC slides over the surface of the nucleus and the MT stalk forms. At the beginning, the nucleus presents an obstacle between the MTOC and the IS; see Fig. 2 a. The opposing force from the nucleus decreases with the approach of the MTOC toward the IS. At the end of the repositioning, the nucleus no longer stands between the two objects; see Fig. 2, c and f. Therefore, the opposing force from the nucleus contributing to dynein detachment decreases. More importantly, attached MTs form the MT stalk. The angle α between the first segment of the MT and the direction of the MTOC movement is used to describe the deformation of the cytoskeleton structure and the stalk formation. At the beginning of the simulation (the first phase and the beginning of the second), attached MTs aim in every direction (see Fig. 3 e, visualized in Fig. 2, a and d). Therefore, the dyneins pull in multiple directions, which makes them oppose each other, leading to dynein detachment. After a few seconds, the MTOC travels in the direction of the biggest pulling force. Consequently, the attached MTs form a stalk as the simulation progresses, and dyneins act in alignment; see Figs. 2, b and e and 3 f. They no longer oppose each other but share the load from opposing forces. Consequently, the detachment probability of dynein decreases with the opposing force, and the number of attached dyneins increases.

The number of dyneins decreases in the final phase when ${\overline{d}}_{\text{MIS}}$ < 3.5 μm; see Fig. 3 c. Unattached MTs in the IS are pushed backward by viscous drag as the MTOC moves to the IS. As a result, one observes an “opening” of the MT cytoskeleton; cf. Figs. 2, c and f and 3 e. Unattached MTs do not intersect the IS (see Fig. 3 f) and cannot attach to dyneins. The attached MTs shorten because of the depolymerization, further lowering the probability of dynein attachment. Moreover, an opposing force arises from the cytoskeleton being dragged from the nucleus to the membrane (see Fig. 3 d), causing the detachment of dyneins because the detachment rate is force dependent.

To summarize, the trajectory of the MTOC toward the IS displays three phases, in which the two longer phases have also been reported in experiment (14), but not the short initial phase. First, the MTOC descends to the nucleus (see Fig. 3, a and d); then it moves to the IS quickly and slows down during the last 2 μm (see Fig. 3 b). Once the MTOC bypasses the nucleus, it moves away, switching from a purely circular to partially radial movement (see Fig. 3 d). The variation of the MTOC velocity, its modulus, and its direction are clearly visible in Video S2, showing a simulation with a smaller nucleus radius r_N = 3.3 μm. Note that the duration of the complete repositioning process in the experiments is ∼60–90 s, which our model predicts to be achieved by a dynein density of 80–200 μm⁻².

Video S2

Capture-Shrinkage Repositioning with Smaller Nucleus

Cortical sliding mechanism

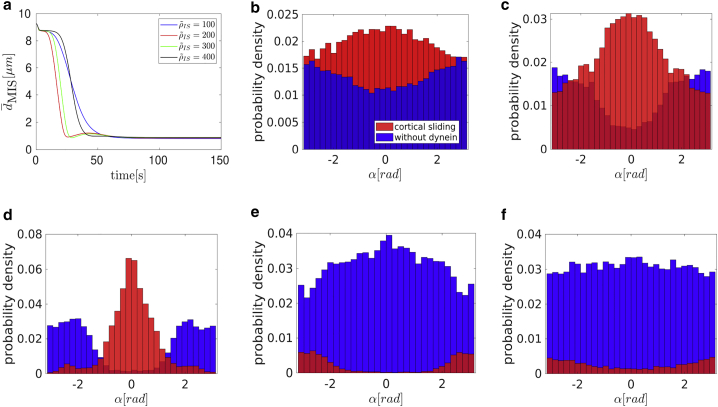
For low, medium, and high densities, one observes for each a different characteristic behavior. In the regime of low dynein densities (${\tilde{\rho }}_{\text{IS}}$ < 100 μm⁻²), the repolarization velocity increases with the dynein density, and the MTOC moves directly to the IS; see Fig. 5 a. For medium dynein densities (100 μm⁻² ≤ ${\tilde{\rho }}_{\text{IS}}$ < 500 μm⁻²), the MTOC movement is more complex; see Fig. 7 a. For high dynein densities (${\tilde{\rho }}_{\text{IS}}$ > 500 μm⁻²), the repolarization velocity surprisingly decreases with ${\tilde{\rho }}_{\text{IS}}$; see Fig. 8 a.

Figure 5.

Cortical sliding with low dynein densities ${\tilde{\rho }}_{\text{IS}}$. (a) The dependence of the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time is shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. (b–d) Dependencies of the average MTOC velocity ${\overline{v}}_{\text{MTOC}}$ (b), number of dyneins acting on MTs ${\overline{N}}_{\text{dm}}$ (c), and the MTOC-center distance ${\overline{d}}_{\text{MC}}$ (d) on the average MTOC-IS distance are shown. (e and f) Probability distributions of the angles α between the first MT segment and the MTOC motion, ${\tilde{\rho }}_{\text{IS}}$ = 60 μm⁻², are shown. (e) t = 5 s, ${\overline{d}}_{\text{MIS}}$ ∼ 9 μm. (f) t = 65 s, ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm. To see this figure in color, go online.

Figure 7.

Cortical sliding mechanism with medium dynein densities ${\tilde{\rho }}_{\text{IS}}$. (a) The dependence of the MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time is shown. Probability distributions of the angles α between the first MT segment and the MTOC motion, ${\tilde{\rho }}_{\text{IS}}$ = 200 μm⁻², are shown. (b) t = 5 s, ${\overline{d}}_{\text{MIS}}$ ∼ 9 μm. (c) t = 15 s, ${\overline{d}}_{\text{MIS}}$ ∼ 6 μm. (d) t = 20 s, ${\overline{d}}_{\text{MIS}}$ ∼ 2.5 μm. (e) t = 25 s, ${\overline{d}}_{\text{MIS}}$ ∼ 1.5 μm, other side of IS. (f) t = 60 s, ${\overline{d}}_{\text{MIS}}$ ∼ 0.8 μm. To see this figure in color, go online.

Figure 8.

Cortical sliding with high dynein densities ${\tilde{\rho }}_{\text{IS}}$. (a) The dependence of the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time is shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. (b) The dependence of the average number of dyneins ${\overline{N}}_{\text{dm}}$ on the MTOC-IS distance is shown. (c) Probability distribution of the angle α between the first MT segment of attached MTs and the direction of the MTOC motion, ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm, is shown. (d) The probability distribution of the distance of attached dynein anchor points from the axis of the IS r_IS when ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm is shown. (e and f) The two-dimensional probability density of attached dyneins in the IS, ${\overline{d}}_{\text{MIS}}$ = 5 μm, is shown. (e) Area density of cortical sliding dyneins ${\tilde{\rho }}_{\text{IS}}$ = 500 μm⁻². (f) ${\tilde{\rho }}_{\text{IS}}$ = 1000 μm⁻². To see this figure in color, go online.

Cortical sliding with low dynein densities

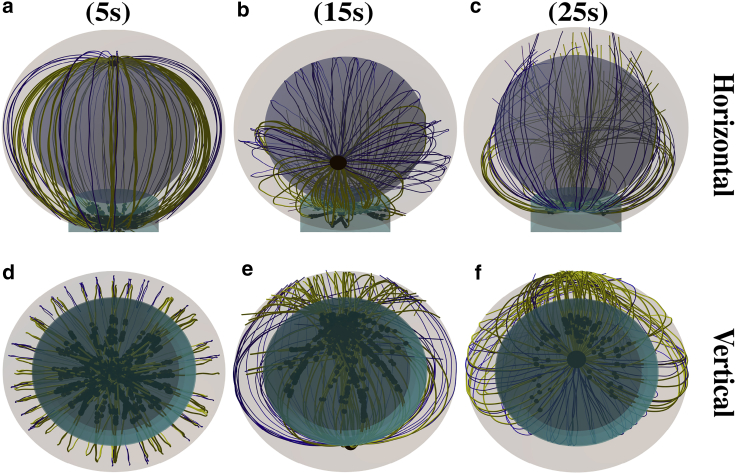
Video S3 shows MTOC repositioning under the effect of the cortical sliding mechanism with ${\tilde{\rho }}_{\text{IS}}$ = 60 μm⁻². It shows MTs sprouting in all directions in the initial stage, the subsequent stalk formation, and the final slowing down of the MTOC. In Fig. 5 b, the dependence of the MTOC velocity on the MTOC-IS distance is shown. As in the case of the capture-shrinkage mechanism, the time evolution of the MTOC velocity can be divided into three phases. However, the transition points between the second and the third phase depend on the density ${\tilde{\rho }}_{\text{IS}}$. Similarly to the case of the capture-shrinkage mechanism, the behavior in the first phase can be explained by the interplay of fast-attaching dyneins and forces from the nucleus. In the second phase, the velocity of the MTOC increases despite a continuously decreasing number of attached dyneins (see Fig. 5, b and c), which is due to the alignment of the MTs. Initially, attached MTs aim in all directions (see Fig. 5 e), as for the capture-shrinkage mechanism (cf. Fig. 4, a and d). Consequently, MTs whose original orientation does not correspond to the movement of the MTOC detach from dynein (see Figs. 4, b and e and 5 f). The probability density in the intermediate state of the repositioning (${\overline{d}}_{\text{MIS}}$ ∼ 5 μm) shows that attached MTs are aligned and less in numbers. The MTOC does not significantly recede from the nucleus at the end of the repositioning (see Fig. 5 d), which implies that the MTs do not follow the cell membrane (with the capture-shrinkage mechanism, MTs always touch the membrane); see Fig. 4, c and f. Consequently, the attachment probability is lower and leads to the decrease in velocity in the third phase.

Figure 4.

Snapshots from the time evolution of the MT cytoskeleton configuration under the effect of cortical sliding mechanism with a low dynein density, ${\tilde{\rho }}_{\text{IS}}$ = 60 μm⁻². The cyan cylinder indicates the IS area. Blue and yellow lines are unattached and attached MTs, respectively. The black spheres in the IS are the positions of dyneins attached to MTs. (a and d) ${\overline{d}}_{\text{MIS}}$ = 9 μm. Originally, the attached MTs aim from the MTOC in every direction. (b and e) ${\overline{d}}_{\text{MIS}}$ = 4.5 μm. MTs attached to dynein aim predominantly in one direction. (c and f) ${\overline{d}}_{\text{MIS}}$ = 1.5 μm. Just a few MTs remain under the actions of cortical sliding, and they rarely touch the surface of the cell in the IS. To see this figure in color, go online.

Video S3

Cortical Sliding Repositioning with Small Dynein Density

Cortical sliding with medium dynein densities

The differences between the behavior with low and medium dynein densities for the cortical sliding mechanism are analyzed in this section. Video S4 shows the repositioning with ${\tilde{\rho }}_{\text{IS}}$ = 200 μm⁻². The repositioning is very fast, and the MT cytoskeleton is considerably deformed. Moreover, the MTOC passes the IS and subsequently returns to the center of IS. 5 s after the initialization, MTs in all directions are attached (see Fig. 6, a and d), but the direction of the MTOC motion is already established (see Fig. 7 b). Contrary to the case of low densities, the dynein forces are sufficiently strong to hold attached MTs. Subsequently, some MTs do not detach but take a direction partially aligned to the MTOC movement (see Fig. 7, c and d). Moreover, almost all MTs aligned with the MTOC motion are attached to dyneins (compare Figure 5, Figure 7 d). Consequently, the large majority of MTs are aligned with the direction of movement of the MTOC movement, causing a substantial increase of the MTOC velocity. By comparing the temporal evolution of the MTOC-IS distance ${\overline{d}}_{IS\left(t\right)}$ for small, medium, and large dynein densities (Figs. 5 a, 7 a, and 8 a), one observes that the velocity of the MTOC is maximal for medium densities of cortical sliding dyneins (see also Fig. 9, a and b below). Moreover, by comparing the configuration snapshots for low and high densities (Fig. 4, b and e and 6, b and e), one observes that the strong forces exerted at high dynein densities cause large deformations of the MT cytoskeleton.

Figure 6.

Snapshots from the time evolution of the MT cytoskeleton configuration under the effect of cortical sliding alone, with a medium area density of the dynein ${\tilde{\rho }}_{\text{IS}}$ = 200 μm⁻²) from two perspectives. (a and c) ${\overline{d}}_{\text{MIS}}$ = 9 μm. MTs sprout from the MTOC in all directions. (b and d) ${\overline{d}}_{\text{MIS}}$ = 5 μm. The majority of MTs are attached, and the MT cytoskeleton is deformed. (c and e) ${\overline{d}}_{\text{MIS}}$ = 1 μm. At the end of the repositioning, the MTOC passed the center of the IS, and attached MTs aim in all directions. To see this figure in color, go online.

Figure 9.

Comparison of the capture-shrinkage and the cortical sliding mechanisms in terms of the average MTOC velocity in both phases ${\overline{V}}_{\text{MTOC}}$, times of repositioning, and the final MTOC-IS distance ${\overline{d}}_{\text{MIS}}$. (a) The MTOC velocity in the first and the second phase is shown. (b) Repositioning times are shown. Final MTOC-IS distances are shown in the inset. (c) The dependence of the average distance ${\overline{r}}_{\text{IS}}$ of attached dynein motors from the axis of the IS on dynein area density ${\tilde{\rho }}_{\text{IS}}$ for the case of sole cortical sliding is shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. To see this figure in color, go online.

Video S4

Cortical Sliding Repositioning with Medium Dynein Density

Because of the deformation of the cytoskeleton, a large number of MTs are attached to dynein at the end of the repositioning (see Fig. 7 d), and dyneins are predominantly found at the opposite side of the IS (compared to the MTOC). Because of the attachment, the MTOC passes the center of the IS (see Fig. 7 a) and the anchor points of certain dynein motors (see Fig. 6, c and f). The MTs are attached to anchor points, so the probability density of α changes, and the majority of MTs are behind the MTOC (see Fig. 7 e). When the MTOC returns to the IS, the probability density levels (see Fig. 7 f), and dynein detaches.

Cortical sliding with high dynein densities

An example for repositioning under the effect of cortical sliding with a high dynein density ${\tilde{\rho }}_{\text{IS}}$ = 1000 μm⁻² is shown in Video S5. As the area density ${\tilde{\rho }}_{\text{IS}}$ rises, the MTs are more and more attached at the periphery (see Fig. 8 d). This is further demonstrated by Fig. 8, e and f (the center of the IS is almost depopulated when ${\tilde{\rho }}_{\text{IS}}$ = 1000 μm⁻²). The reason is that there are a sufficient number of dyneins to firmly catch the MTs passing just the periphery of the IS. The higher number of MTs also logically means bigger pulling forces on MTs. In a spherical cell, dyneins act in competition, which leads to dynein detachment. The bigger the competition is, the more frequent the detachment, as can be seen in Fig. 8 b, in which the highest number of attached dyneins corresponds to the lowest area density.

Video S5

Cortical Sliding Repositioning with High Dynein Density

Constantly attaching and detaching dyneins does not allow MTs to align with the direction of the MTOC movement. Subsequently, the MTOC “lingers” behind the nucleus before it moves to the IS as the dominant orientation of attached MTs forms slowly. The duration of this inactivity rises with ${\tilde{\rho }}_{\text{IS}}$ (see Fig. 8 a). Even when the dominant direction is established, MTs are still attached in every direction, slowing down the movement (see Fig. 8 c). Therefore, the slowing in the third section (cf. Fig. 8 a) is caused by two effects: first, the misalignment of MTs, resulting in contradictory pulling forces and a lower number of attached dyneins; second, the increasing probability of attachment at the periphery, resulting in MTs being pulled to different places and increasingly contradicting each other as the MTOC approaches the IS.

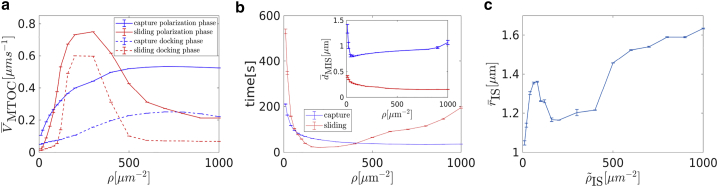
Comparison of cortical sliding and capture-shrinkage

In this section, two mechanisms are compared in terms of MTOC velocity: times and final MTOC-IS distances. The biological motivation is that the velocity (times) indicates the efficiency of transmission of the force of dynein on the cytoskeleton, and the final distance determines the completion of the repositioning. In the previous sections, the repositioning was divided into three phases based on the MTOC velocity (see Figs. 3 and 5), which enabled the analysis of the dynamics based on the attached dyneins and deformations of the cytoskeleton structure.

To analyze average velocity, the repositioning is divided into three phases based on the MTOC-IS distance: the activation, the first, and the second phase. This approach will later enable a comparison with experimental results. The activation phase ends when d_MIS ≤ 8.2 μm (identical with the first phase based on the MTOC velocity). Although the activation phase is important for the observation of the influence of dynein motors (see Figs. 3 c, 5 c, and 8 b), the phase lacks experimental analogy because in reality, the IS, along with a high dynein area density, is not created instantly. Therefore, it will not be further analyzed. In the first phase, the MTOC-IS distance 8.2 μm > d_MIS > d_f + 1 μm, where d_f is the final MTOC-IS distance, which depends on the area density and mechanism. The second phase comprises the last micrometer of the MTOC journey.

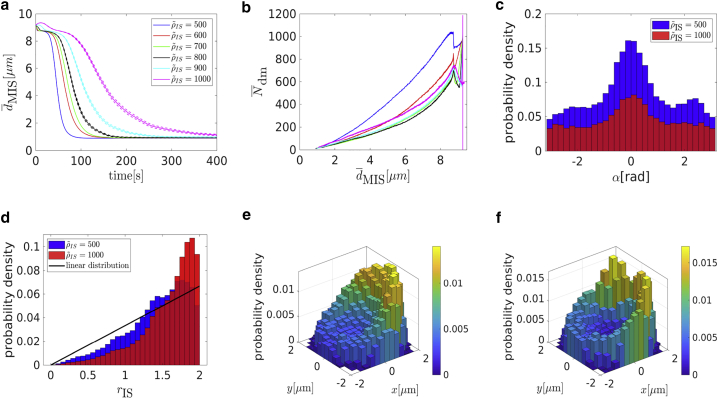
The MTOC velocity in the capture-shrinkage repositioning increases with the area density of dyneins for both phases (see Fig. 9 a). The development of the average MTOC velocity of the cortical sliding repolarization is more difficult because it rises to its maximum (middle densities) (see Fig. 9 a) and then falls sharply. The velocity of the cortical sliding repositionings is lower except when considering middle area densities of the cortical sliding dynein. Moreover, for the low and high densities, the velocity of capture-shrinkage is more than two times the velocity of cortical sliding (see Fig. 9 a). The times of repositioning evolve accordingly (see Fig. 9 c). Times are longer for the case of capture-shrinkage only when ρ corresponds to the middle densities of cortical sliding (see Fig. 9 a).

The final MTOC-IS distance decreases with the rising ρ in the case of sole capture-shrinkage (see Fig. 9 b). In the case of cortical sliding, the situation is more complicated because of the lack of an anchor point. The large final distances at low area densities are caused by the insufficient pulling force. The shortest distance is at the end of low area densities ρ = 80 μm⁻², which is caused by the fact that the formation of the narrow MT stalk, in which MTs pull in alignment, is limited just to low densities (see Figs. 5 e, 7 c, and 8 c). Then, we can observe a steady rise in final distances caused by the growing attachment of MTs at the peripheries as ${\tilde{\rho }}_{\text{IS}}$ causes the increasing competition of pulling forces in the final stages of the polarization.

Fig. 9 c explains the lower MTOC velocity for cortical sliding. First of all, let us notice that the three regimes of the cortical sliding behavior are visible in Fig. 9 c. We can see that the increasing ${\tilde{\rho }}_{\text{IS}}$ causes MT attachment on the periphery of the IS, as was already suggested by Fig. 8, d–f. Moreover, the attached dynein is always predominantly at the periphery because the average distance for the uniform distribution of dynein is ${\overline{r}}_{\text{IS}}=\left(1/2\right)$R_IS = 1 μm. Therefore, as the MTOC approaches the IS, MTs are pulled to different locations, and the forces of dynein oppose each other and cause the dynein detachment.

The capture-shrinkage mechanism is faster, with the relatively narrow exception of the middle area densities. Cortical sliding never achieves shorter distances in comparison to capture-shrinkage; moreover, in the case of high or low densities, the final distances differ substantially. Fig. 9 shows the dependencies on area density. Nevertheless, in the case of capture-shrinkage, we consider just the density in the center of the IS. We should remind the reader that the radii of the center and the entire IS are R_CIS = 0.4 μm and R_IS = 2 μm. Because the number of dyneins depends on the area, the number of dyneins in the IS N_IS = 25 × N_CIS, where N_CIS is the number of dyneins in the center of the IS. Consequently, Fig. 9 confirms that the capture-shrinkage mechanism is the main driving force of the repositioning because this mechanism produces bigger or comparable velocities with just 4% of the dynein motors of cortical sliding. Moreover, the MTOC comes closer to the IS, meaning that the capture-shrinkage mechanism is more likely to finish repositioning. To summarize, considering the lower number of dyneins, the capture-shrinkage mechanism is largely superior in the considered setup. The most important difference between the two mechanisms is the firm, narrow anchor point in case of the capture-shrinkage mechanism. It assures a firm attachment of the MTs (see Fig. 3 f) and a geometrical alignment of the pulling forces in all stages of repositioning. The capture-shrinkage mechanism was identified as the main driving force of the repositioning (14), and our model fully supports this statement. In the next section, we will scrutinize the role of cortical sliding.

Combination of capture-shrinkage and cortical sliding

In this section, the interplay between the two mechanisms is analyzed. A comparison of Video S6 (capture-shrinkage, with ρ_IS = 60 μm⁻², ${\tilde{\rho }}_{\text{IS}}$ = 0 μm⁻²) and Video S7 (both mechanisms combined, ${\tilde{\rho }}_{\text{IS}}$ = ρ_IS = 60 μm⁻²) demonstrates the difference between the MT cytoskeleton dynamics under the effect of capture-shrinkage alone and under the effect of both mechanisms combined. The videos show the first few seconds of the process. In the case of sole capture-shrinkage, only long enough MTs attach to the center of the IS. One clearly sees in Video S7 that MTs intersecting the IS and attached to cortical sliding dynein are passed to the center of the IS, where they are captured by cortical sliding dynein. Video S8 shows the complete repositioning of the MTOC under the effect of both mechanisms combined (${\tilde{\rho }}_{\text{IS}}$ = ρ_IS = 60 μm⁻²).

Video S6

First Seconds of Capture-Shrinkage Repositioning

Video S7

First Seconds of Repositioning with Both Mechanisms

Video S8

Repositioning Under the Influence of Both Mechanism

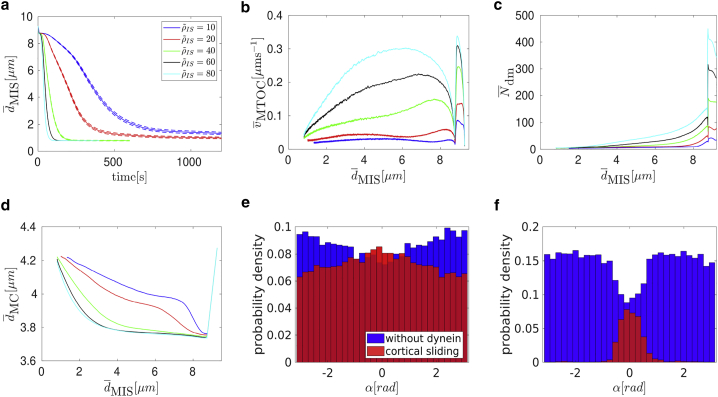
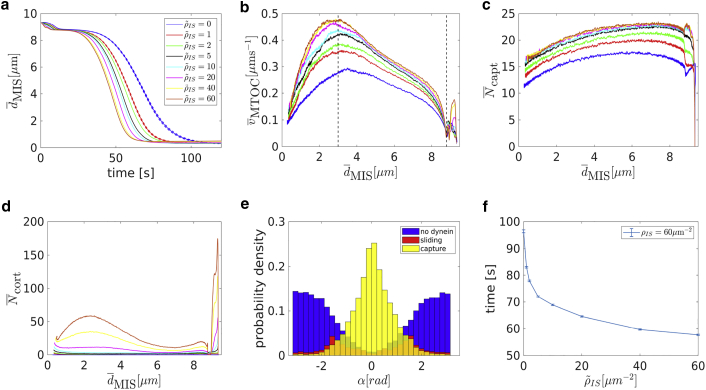
A quantitative analysis in Fig. 10, a and b shows that the repolarization velocity increases with the cortical sliding density ${\tilde{\rho }}_{\text{IS}}$ as expected. Quite unexpectedly, it turns out that the average number of attached capture-shrinkage dyneins depends on the density of cortical sliding dyneins ${\tilde{\rho }}_{\text{IS}}$ and increases with it, as demonstrated by Fig. 10 c.

Figure 10.

Combination of capture-shrinkage and cortical sliding: (a) dependence of the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time. Dependence of the average MTOC velocity ${\overline{v}}_{\text{MTOC}}$ (b), the average number of attached capture-shrinkage dyneins ${\overline{N}}_{\text{capt}}$ (c), and the average number of attached cortical sliding dyneins ${\overline{N}}_{\text{cort}}$ (d) on the average MTOC-IS distance is shown (cortical sliding densities corresponding to different line colors in b–d are the same as in a). (e) The probability density of the angles α between the first MT segment and the direction of the MTOC motion is shown; t = 50 s, ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm, ${\tilde{\rho }}_{\text{IS}}$ = ρ_IS = 60 μm⁻². (f) Dependence of times of repositioning on cortical sliding area density ${\tilde{\rho }}_{\text{IS}}$ is shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. To see this figure in color, go online.

This finding indicates a synergy of the two mechanisms, capture-shrinkage and cortical sliding, and can be explained by the alignment of the MTs during repositioning. The MTs attached to the cortical sliding dyneins tend to align with the MTOC movement, as demonstrated by Fig. 10 e, in which the dominant central peak in direction α = 0 is caused by capture-shrinkage dyneins, and cortical sliding dyneins provide only two small peaks from angles toward the periphery of the IS. As MTs align with the MTOC movement, they are captured by the capture-shrinkage dyneins in the central region of the IS, and the number of cortical sliding dyneins drops dramatically, as shown in Fig. 10 d.

A comparison of the probability densities shown in Fig. 3 f for capture-shrinkage alone and Fig. 5 f for cortical sliding alone reveals the mechanism by which cortical sliding supports capture-shrinkage. Fig. 3 f shows that the unattached MTs are pushed back by friction forces, which leads to the opening of the MT cytoskeleton such that MTs cannot intersect the narrow center of the IS anymore (visualized in Fig. 2 f). Attached MTs align with the MTOC movement in the case of cortical sliding (cf. Fig. 5 f). Therefore, when both mechanisms are combined, MTs attached by the cortical sliding dyneins are not pushed back by friction, they align with the MTOC movement, and the attachment probability of the capture-shrinkage dynein increases. Comparing the probability density of the angle α for cortical sliding alone (Fig. 5 f) with the one for the combined mechanisms (Fig. 10 e) demonstrates impressively that most MTs attached to cortical sliding dyneins have detached and attached to capture-shrinkage dyneins.

These observations suggest an answer to the question about the role of the cortical sliding: it passes the MTs to the more efficient capture-shrinkage mechanism. Additionally, it provides a bigger pulling force than for cortical sliding alone because of the fact that the capture-shrinkage mechanism also supports cortical sliding. By comparison of Figs. 5 c and 8 b with Fig. 10 d, one realizes that the dependencies of the number of cortical sliding dyneins on the MTOC-IS distance are very different. As the MTOC approaches the IS, the number of dyneins acting on MTs decreases in the case of sole cortical sliding (cf. Figs. 5 c and 8 b) but rises for the case of the combined mechanisms (cf. Fig. 10 d). The reason lies in the firm anchoring of MTs in the center of the IS and the emergence of the remarkable “arc” formations of attached dynein (cf. Fig. 11, b and c).

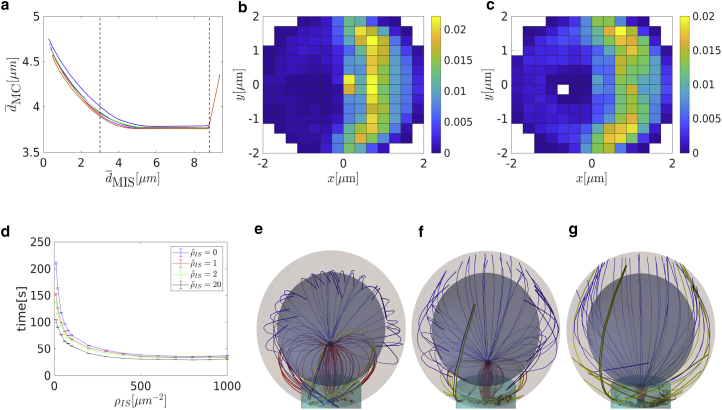
Figure 11.

Combination of capture-shrinkage and cortical sliding. (a) Dependence of the average distance between the center of the cell and the MTOC ${\overline{d}}_{\text{MC}}$ on the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ is shown. (b and c) A probability density plot for the spatial distribution of attached dynein is given. (b) t = 50 s, ${\overline{d}}_{\text{MIS}}$ ∼ 4.5 μm. (c) t = 60 s, ${\overline{d}}_{\text{MIS}}$ ∼ 1.5 μm. (d) Repositioning times as a function of the density of capture-shrinkage dynein ρ_IS for four different values of the cortical sliding area density ${\tilde{\rho }}_{\text{IS}}$ are shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. (e–g) Snapshots from simulation are given. The blue, red, and bold yellow curves correspond to MTs without dynein and with capture-shrinkage and cortical sliding, respectively. Black dots depict positions of attached dynein motors. (e) d_MIS = 4.5 μm, (f) d_MIS = 2.5 μm, and (g) d_MIS = 1 μm. To see this figure in color, go online.

The velocity of the capture-shrinkage processes explains this surprising finding. The capture-shrinkage mechanism is more efficient because the MTs shorten because of depolymerization, align with the MTOC movement, and are pulled to the same place. Slower stepping in the cortical sliding mechanism will result in MT lengths between the MTOC and the IS far longer than the direct distance. Therefore, MTs have to bend (see Fig. 11, e–g), which explains the “arc” patterns of attached dyneins in the IS. In other words, firm anchoring of capture-shrinkage pushes the cortical sliding MTs against the IS, causing further attachment. By comparison of Fig. 5 d and Fig. 11 a, one observes that the MTOC approaches the IS more closely in the case of combined mechanisms than in the case of cortical sliding, which is another proof of the pulling of the MTOC toward the center of the IS. We conclude that the cortical sliding mechanism supports the dominant capture-shrinkage mechanism by “passing” the MTs, and the capture-shrinkage mechanism supports the cortical sliding mechanism by providing the anchoring and pushing the MTs against the IS.

This synergy is also indicated by Fig. 11 d, which shows the total repositioning times as a function of the density of capture-shrinkage dynein for various fixed values of the cortical sliding dynein. Although the repositioning time does not decrease further for large values of the capture-shrinkage dynein density (ρ_IS > 600 μm⁻²), it can actually be decreased further by increasing cortical sliding dynein. Consequently, the combination of the two mechanisms with relatively low area densities is faster than the dominant mechanism alone with maximal area density (compare cases ρ_IS = 200 μm⁻² with various ${\tilde{\rho }}_{\text{IS}}$ with the case of ρ_IS = 1000 μm⁻² in Fig. 11 d). Further parameter variations supporting this result can be found in the Supporting Materials and Methods, Section S3.3.3. The effect is certainly advantageous for the cell because the cortical sliding mechanism is not as efficient as the capture-shrinkage mechanism, considering the large amount of dynein required.

Discussion

We have analyzed the experiments of (14) with a mechanistic model for the relocation of the MTOC in T cells. By using biologically realistic values for the model parameters such as the number and the stiffness of MTs, dynein pulling forces and detachment probabilities, and cytosol viscosity, we can recapitulate for a wide range of dynein densities the experimental observations of (14). In particular, the timescale for the completion of the relocation process, as well as the MTOC velocities predicted by the model, agrees well with the experimental results.

Our model predicts that the cytoskeleton deforms substantially during the MTOC-repositioning process because of the combined effects of the capture-shrinkage mechanism and friction forces. The captured MTs form a narrow stalk between the MTOC and the IS, straightening under the tension caused by dynein motors acting on it and causing the rotation of the whole MT cytoskeleton toward it. Concomitantly, unattached MTs are pushed backward by the emerging viscous drag “opening” the MT cytoskeleton (cf. Fig. 2, e and f). Thus, our model provides a mechanistic explanation of the MT cytoskeleton opening that is also clearly visible in the experiments, as, for instance, in Fig. 5 A of (14). The opening can also be seen in the case of combined mechanisms, although for partially different reasons (Fig. 11, e–g).

The MT cytoskeleton opening might have interesting consequences for the distribution of Ca²⁺ in the cell, which is highly relevant for cell function. As the cytoskeleton rotates, the mitochondria are dragged with it (16) until they approach the IS. Because of the MT cytoskeleton opening, the mitochondria are positioned asymmetrically around the IS, resulting in an asymmetric absorption and redistribution of Ca²⁺ by the mitochondria. Consequently, an asymmetric distribution of Ca²⁺ arises around the IS, the function of which might deserve further investigation.

The detailed analysis of the MT cytoskeleton arrangement for the cortical sliding mechanism revealed three different deformation characteristics depending on three regimes for the dynein density (Cortical-Sliding Mechanism). This observation opens an interesting experimental perspective to estimate the dynein distribution from the MT cytoskeleton deformation during the MTOC repositioning.

Moreover, our model also predicts a biphasic behavior of the relocation process, as reported for the experiments in (14). Figs. 3 a and 10 a bear a clear resemblance to Fig. 3 D of (14). We showed that after a short initial period in which MTs start to attach to the dynein, the first phase observed experimentally corresponds in our model to the circular motion of the MTOC around the nucleus and the second phase to the last 1 μm of the MTOC movement, when it detaches from the nucleus and moves more or less straight to the IS with a substantially reduced velocity for both mechanisms (capture-shrinkage and cortical sliding) and a large range of dynein densities. During the latter phase, the MTOC increases its distance from the cell center by approximately 1 μm ∼ 0.2 × R_Cell, which is close to the value reported in (14).

It was hypothesized in (14) that a resistive force emerges at the transition point between the phases, causing slowing down of the MTOC. Our model shows that the assumption of a resistive force is not necessary to explain the biphasic behavior: the velocity of the MTOC is only determined by the number of motors pulling on the MTs and on MT alignment (Figs. 3, 5 a, and 8). The reason for the slowing down is therefore simply the decrease of the number of dyneins attached to the MTs, which again is a consequence of the changing geometry and forces during the movement of the MTOC, i.e., a consequence of the interplay between the MT cytoskeleton and motors.

Experimentally, it was also observed that a treatment with taxol substantially reduced the velocity of the repositioning. Taxol impedes depolymerization of the MTs, which we could mimic in our model by reducing the capture-shrinkage efficiency. With this modification, our model reproduces the experimental observation (Fig. S10, a and b).

An interesting prediction of our model is that the two mechanisms, capture-shrinkage and cortical sliding, appear to act in remarkable synergy (Combination of Capture Shrinkage and Cortical Sliding), which provides an answer to the question about the role of cortical sliding (14). Cortical sliding passes the MTs to the more efficient capture-shrinkage mechanism, which in return provides a firm anchor point. Therefore, cortical sliding is useful even in the configuration when capture-shrinkage is dominant. The synergy has a very practical effect because the combination of mechanisms with relatively low area densities can be faster than only the dominant mechanism with much higher area density Fig. 11 d. Therefore, the synergy of the two mechanisms can substantially reduce the area densities necessary for an effective repositioning and reduces the necessary resources (dynein). In our model, the cytoskeleton does not have to force its way through multiple organelles with complex structure, and the synergy manifests itself mainly in the velocity of the repositioning process. But one could speculate that in the real cell, the synergy can actually make the difference between completed and no repositioning.

It was proven in (50) that dyneins colocalize with the ADAP ring in the pSMAC. Moreover, in (17) it was hypothesized that the MTs are part of the reason why the pSMAC takes the form of a ring. Additionally, (17) reported the sharp turns in MTs upon interaction with the pSMAC and that the MTs do not project directly to the cSMAC. In our model, the cortical sliding dynein is homogeneously distributed over the entire IS; nevertheless, we observe that dyneins attach to MTs predominantly at the periphery of the IS (cf. Fig. 8, d–f). If both mechanisms are present, attached cortical sliding dyneins are even completely absent in the central region (cf. Fig. 11). We therefore conclude, like (17), that cortical sliding MTs do not project directly into the cSMAC and identify the periphery of the IS as the region where cortical sliding MTs are anchored. In agreement with the experiments (17), we observe that cortical sliding MTs turn upon contact with the periphery (Fig. 11, e–g), twist, and contribute to the formations of dynein “arcs.” Because the dynein in the central region of the IS does not contribute to the MTOC repositioning via cortical sliding, one could hypothesize that the pSMAC takes the shape of a ring to facilitate interaction with MTs (17).

We presented a numerical analysis of the repositioning in the case in which the MTOC and the IS are initially at the opposite sides of the cell. Even a case so restricted brought interesting results, enabling comparison with experiments and a proposed explanation for the experimental observable. We found that the cell performs the repositioning with great efficiency. The dyneins are placed only at the peripheries of the IS (pSMAC), which is the place where they are used the most, evacuating less-used regions. Moreover, we introduced a synergy of two mechanisms that minimizes the necessary area density of dynein.

In this work, we presented the results of our theoretical analysis of the MTOC repositioning that are relevant for the experimental setup in (14), in which the IS and the initial position of the MTOC are diametrically opposed. Here, it turned out that even if both mechanisms (capture-shrinkage and cortical sliding) are at work, capture-shrinkage is always dominant, as reported in (14). In a second part of this work (unpublished data), we will examine other initial positions of the MTOC and the IS that will naturally occur in biologically relevant situations, and we will investigate under which circumstances cortical sliding will become the dominant mechanism over capture-shrinkage. Moreover, we will further demonstrate the synergy of two mechanisms introduced in this work and prove that it has more far-reaching effects in other initial configurations than the one studied here. Also, in the situation in which the T cell establishes two ISs, interesting dynamical behavior of the MTOC can be expected and will be analyzed in detail. In the end, we will see that in T cells the two mechanisms (capture-shrinkage and cortical sliding) and the spatial distribution of dynein are combined so as to minimize the number of dyneins necessary for polarization and to minimize the damage of the MT cytoskeleton.

Author Contributions

H.R. designed the research. I.H. performed calculations, prepared figures, and analyzed the data. I.H. and H.R. wrote the manuscript.

Editor: Kevin Janes.

Supporting Citations

References (76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130) appear in the Supporting Material.