Abstract
In this study, we developed a dynamic mathematical model of E. coli cell-free protein synthesis (CFPS). Model parameters were estimated from a dataset consisting of glucose, organic acids, energy species, amino acids, and protein product, chloramphenicol acetyltransferase (CAT) measurements. The model was successfully trained to simulate these measurements, especially those of the central carbon metabolism. We then used the trained model to evaluate the performance, e.g., the yield and rates of protein production. CAT was produced with an energy efficiency of 12%, suggesting that the process could be further optimized. Reaction group knockouts showed that protein productivity was most sensitive to the oxidative phosphorylation and glycolysis/gluconeogenesis pathways. Amino acid biosynthesis was also important for productivity, while overflow metabolism and TCA cycle affected the overall system state. In addition, translation was more important to productivity than transcription. Finally, CAT production was robust to allosteric control, as were most of the predicted metabolite concentrations; the exceptions to this were the concentrations of succinate and malate, and to a lesser extent pyruvate and acetate, which varied from the measured values when allosteric control was removed. This study is the first to use kinetic modeling to predict dynamic protein production in a cell-free E. coli system, and could provide a foundation for genome scale, dynamic modeling of cell-free E. coli protein synthesis.
Keywords: Biochemical engineering, Cell-free protein synthesis, Kinetic modeling
Highlights
-
•
Protein production is biphasic, powered initially by glucose and later by pyruvate.
-
•
Protein is produced with an energy efficiency of only 12%.
-
•
Protein productivity is most sensitive to oxidative phosphorylation and glycolysis.
-
•
Protein production is robust to allosteric control.
Nomenclature.
| GLC | alpha-D-Glucose |
|---|---|
| G6P | Glucose 6-phosphate |
| F6P | Fructose 6-phosphate |
| FBP | Fructose 1,6-diphosphate |
| T3P | Dihydroxyacetone phosphate |
| 13DPG | 1,3-bis-Phosphoglycerate |
| 3PG | 3-Phosphoglycerate |
| 2PG | 2-Phosphoglycerate |
| PEP | Phosphoenolpyruvate |
| PYR | Pyruvate |
| LAC | D-Lactate |
| 6PG | 6-Phospho-D-glucono-1,5-lactone; 6-Phospho-D-gluconate |
| RU5P | D-Ribulose 5-phosphate |
| XU5P | D-Xylulose 5-phosphate |
| R5P | Ribose 5-phosphate |
| S7P | sedo-Heptulose 7-phosphate |
| G3P | Glyceraldehyde 3-phosphate |
| E4P | Erythrose 4-phosphate |
| 2DDG6P | 2-Dehydro-3-deoxy-D-gluconate 6-phosphate |
| COA | Coenzyme A |
| ACCOA | Acetyl coenzyme A |
| AC | Acetate |
| CIT | Citrate |
| ICIT | Isocitrate |
| AKG | alpha-Ketoglutarate |
| SUCCOA | Succinyl coenzyme A |
| SUCC | Succinate |
| FUM | Fumarate |
| MAL | Malate |
| OAA | Oxaloacetate |
| FOR | Formate |
| PROP | Propanoate |
| ALA | Alanine |
| ARG | Arginine |
| ASP | Aspartate |
| ASN | Asparagine |
| CYS | Cysteine |
| GLU | Glutamate |
| GLN | Glutamine |
| GLY | Glycine |
| HIS | Histidine |
| ILE | Isoleucine |
| LEU | Leucine |
| LYS | L-Lysine |
| MET | Methionine |
| PHE | Phenylalanine |
| PRO | Proline |
| SER | Serine |
| THR | Threonine |
| TRP | Tryptophan |
| TYR | Tyrosine |
| VAL | Valine |
| AA | Amino acid |
| AA tRNA | Aminoacyl tRNA |
| ATP | Adenosine triphosphate |
| ADP | Adenosine diphosphate |
| AMP | Adenosine monophosphate |
| CTP | Cytidine triphosphate |
| CDP | Cytidine diphosphate |
| CMP | Cytidine monophosphate |
| GTP | Guanosine triphosphate |
| GDP | Guanosine diphosphate |
| GMP | Guanosine monophosphate |
| UTP | Uridine triphosphate |
| UDP | Uridine diphosphate |
| UMP | Uridine monophosphate |
| CAT | Chloramphenicol acetyltransferase |
1. Introduction
Cell-free protein expression is a widely used tool in systems and synthetic biology, and a promising technology for personalized point of use biotechnology (Pardee et al., 2016). Cell-free systems offer many advantages for the study, manipulation and modeling of metabolism compared to in vivo processes. Central amongst these advantages is direct access to metabolites and the biosynthetic machinery without the interference of a cell wall, or the complications associated with cell growth. Thus, we can interrogate (and potentially manipulate) the chemical microenvironment while the biosynthetic machinery is operating, possibly at a fine time resolution. Cell-free protein synthesis (CFPS) is arguably the most prominent example of a cell-free system used today (Jewett et al., 2008). However, CFPS is not new; CFPS in crude E. coli extracts has been used since the 1960s to explore fundamental biological mechanisms. For example, Matthaei and Nirenberg used E. coli cell-free extracts in ground-breaking experiments to decipher the sequencing of the genetic code (Matthaei and Nirenberg, 1961; Nirenberg and Matthaei, 1961). Spirin and coworkers later improved protein production in cell-free extracts by continuously exchanging reactants and products; however, while these extracts could run for tens of hours, they could only synthesize a single product and were energy limited (Spirin et al., 1988). More recently, energy and cofactor regeneration in CFPS has been significantly improved; for example, ATP can be regenerated using substrate-level phosphorylation (Kim and Swartz, 2001) or even oxidative phosphorylation (Jewett et al., 2008). While it was once debated whether oxidative phosphorylation occurred in cell-free systems, Jewett and coworkers demonstrated its existence definitively in the Cytomim system by inhibiting it using electron transport chain and F1FO-ATPase inhibitors, as well as membrane gradient uncouplers, and observing a significantly lower protein yield (Jewett et al., 2008). They hypothesized respiration was occurring in inverted membrane vesicles created during cell lysis. Today, cell-free systems are used in a variety of applications ranging from therapeutic protein production (Lu et al., 2014) to synthetic biology (Hodgman and Jewett, 2012; Hu et al., 2015; Pardee et al., 2016). Moreover, there are also several CFPS technology platforms, such as the PANOx-SP and Cytomim platforms developed by Swartz and coworkers (Jewett and Swartz, 2004a; Jewett et al., 2008), the TXTL platform of Noireaux (Garamella et al., 2016) or the PURE system developed by Shimizu et al. (2001). However, for point of use cell-free manufacturing to become a mainstream technology, we must first understand the system performance, and eventually optimize important metrics such as yield and productivity. A critical tool towards this goal is mathematical modeling. We previously developed a constraint-based model of CFPS which integrated the expression of the protein product with the supply of metabolic precursors and energy (Vilkhovoy et al., 2018).
Dynamic mathematical modeling has long contributed to our understanding of metabolism (Wayman and Varner, 2013). Decades before the genomics revolution, mechanistically structured metabolic models arose from the desire to predict microbial phenotypes resulting from changes in intracellular or extracellular states (Fredrickson, 1976). The single cell E. coli models of Shuler and coworkers pioneered the construction of large-scale, dynamic metabolic models that incorporated multiple regulated catabolic and anabolic pathways constrained by experimentally determined kinetic parameters (Domach et al., 1984). Shuler and coworkers generated many single cell kinetic models, including single cell models of eukaryotes (Steinmeyer and Shuler, 1989; Wu et al., 1992), minimal cell architectures (Castellanos et al., 2004), and DNA sequence based whole-cell models of E. coli (Atlas et al., 2008). More recent studies have extended the approach, from integrating disparate models of cellular processes in M. genitalium (Karr et al., 2012), to describing dozens of mutant strains in E. coli with a single partially kinetic model (Khodayari and Maranas, 2016), to identifying industrially useful target enzymes in E. coli for improved 1,4-butanediol production (Andreozzi et al., 2016). Taken together, mathematical modeling of metabolism has proven useful for applications across systems biology. However, dynamic metabolic model development is often time consuming, and model identification and validation requires significant experimental information.
Parameter identification is a challenge to the development of predictive dynamic metabolic models. Sethna identified parameter sloppiness as a common feature of systems biology models; the eigenvalues of the network sensitivity were distributed across wide ranges, and were not generally aligned with single parameters (Brown and Sethna, 2003; Gutenkunst et al., 2007). This leads to parameter values being unknown despite comprehensive metabolite information. Furthermore, if direct parameter measurements were attempted, they had to be precise and exhaustive to yield reliable model predictions. Surprisingly, despite this, models often still accurately predict multiple phenotypes via collective parameter fitting. Liao and coworkers constructed an ensemble of models across a wide range of kinetic parameters that satisfied thermodynamic constraints and steady state flux distributions, and selected from within the ensemble those models that described enzyme overexpression datasets (Tran et al., 2008). In this way, specific parameter identification was bypassed, and multiple relevant phenotypes could be described. Meanwhile, Hatzimanikatis and coworkers employed machine learning to simplify the parameter estimation problem (Andreozzi et al., 2007). They segregated the feasible-solution parameter space into N-dimensional boxes, via a binary decision tree which determined the values of parameters. This subsequently allowed for uniform, non-asymptotic sampling within the subregions; a convenient byproduct of this approach was a simple estimation of the volume of the solution space. Taken together, large-scale, descriptive models of prokaryotic metabolism can be constructed and trained to predict diverse biological behaviors with uncertain parameter information.
In this study, we developed an ensemble of kinetic cell-free protein synthesis (CFPS) models using dynamic metabolite measurements from an early glucose powered Cytomim E. coli cell-free extract. While cell-free technology has evolved considerably since this data set was generated, developing a model using a previous generation CFPS platform offers several unique opportunities. First and foremost, is the ability to directly compare the different improvements established by purely experimental means, to those estimated using a dynamic mathematical model. The CFPS model equations were formulated using the hybrid cell-free modeling framework of Wayman and coworkers (Wayman et al., 2015), which integrates traditional kinetic modeling with a logical rule-based description of allosteric regulation. Model parameters were estimated from measurements of glucose, organic acids, energy species, amino acids, and the protein product, chloramphenicol acetyltransferase (CAT) over the course of a 3 h protein synthesis reaction. A constrained Markov Chain Monte Carlo (MCMC) approach was used to minimize the squared difference between model simulations and experimental measurements, where a plausible range for each kinetic parameter was established from BioNumbers (Milo et al., 2009). The ensemble of parameter sets described the training data with a median cost greater than two orders of magnitude smaller than a population of random parameter sets constructed using the same literature parameter constraints. We then used the ensemble of kinetic models to analyze the performance of the CFPS system, and to estimate the pathways most important to protein production. We calculated that CAT was produced with an energy efficiency of 12%, suggesting that much of the energy resources for protein synthesis were diverted to non-productive pathways. By simulating the knockout of metabolic enzyme groups (this was not actually done experimentally), we showed that metabolism and protein production in particular depended upon oxidative phosphorylation and glycolysis/gluconeogenesis. In addition, translation was more important to productivity than transcription. Lastly, CAT production was robust to allosteric control, as was most of the network, with the exception of the organic acid trajectories in central carbon metabolism. Taken together, this study provides a foundation for sequence specific genome scale, dynamic modeling of cell-free E. coli protein synthesis.
2. Results
The cell-free E. coli metabolic network was constructed by removing growth-associated reactions from the iAF1260 reconstruction of K-12 MG1655 E. coli (Feist et al., 2007), and by adding reactions describing chloramphenicol acetyltransferase (CAT) biosynthesis (Fig. 1). In addition, reactions that were knocked out in the host strain used to prepare the extract were removed from the network (speA, tnaA, sdaA, sdaB, gshA, tonA, endA). Lastly, we added transcription and translation processes for the synthesis of the CAT protein. These processes were based on the transcription and translation template reactions from the earlier work done of Allen and Palsson (2003) and more recently Vilkhovoy et al. (2018). The metabolic network, which contained 148 metabolites and 204 reactions, is available in the supplemental materials. Model equations followed the hybrid modeling framework of Wayman and coworkers (Wayman et al., 2015), combining multiple saturation kinetics with a rule-based model of allosteric regulation. An ensemble of 100 model parameter sets was estimated from measurements of glucose, CAT, organic acids, energy species, and 18 of the 20 proteinogenic amino acids (Vilkhovoy et al., 2018) using a constrained Markov Chain Monte Carlo (MCMC) approach. The organic acids measured included pyruvate, lactate, acetate, succinate, and malate. The energy species included three phosphorylation states each of the four ribonucleosides: ATP, ADP, AMP, GTP, GDP, GMP, CTP, CDP, CMP, UTP, UDP, and UMP. Nicotinamide adenine dinucleotide (NAD(H)) and nicotinamide adenine dinucleotide phosphate (NADP(H)), while present in the model, were not measured in the dataset. The model equations and parameter sets, as well as the experimental dataset, are available under an MIT open source software license from the Varnerlab website (Varnerlab).
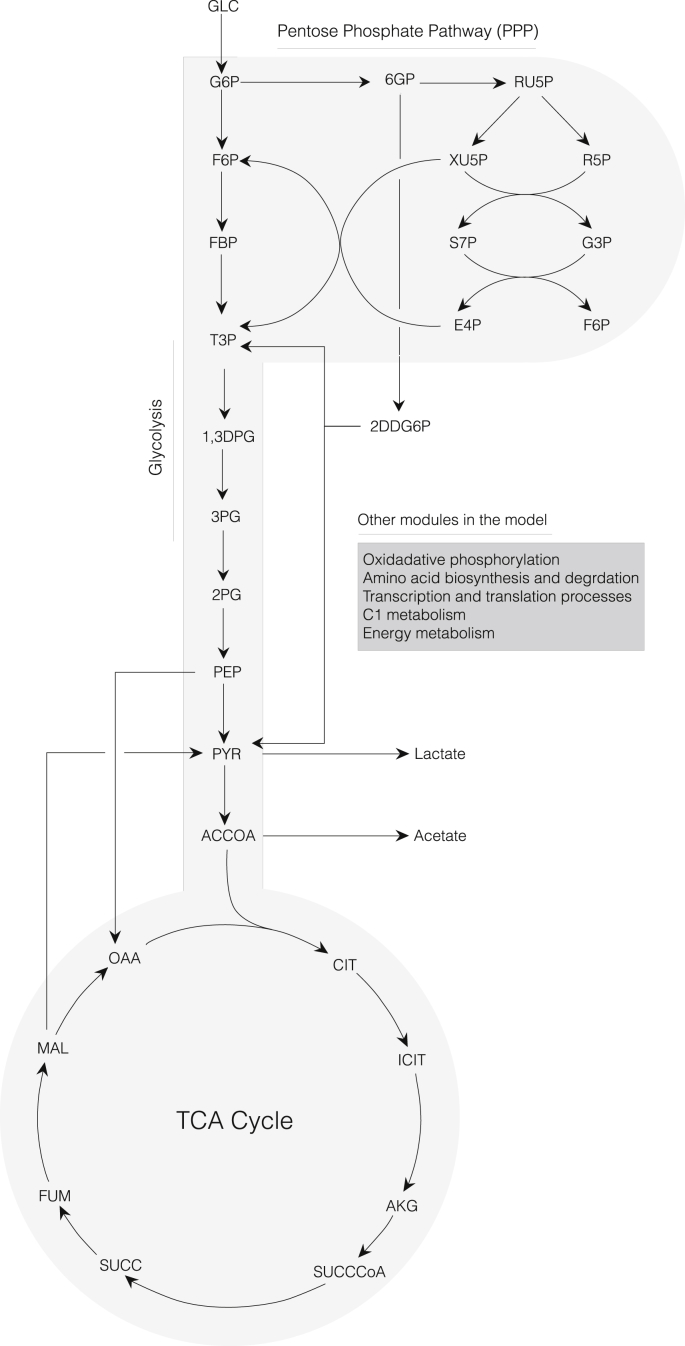
Fig. 1.
Schematic of the core portion of the cell-free E. coli metabolic network. Metabolites of glycolysis, pentose phosphate pathway, Entner-Doudoroff pathway, and TCA cycle are shown. Metabolites of oxidative phosphorylation, amino acid biosynthesis and degradation, transcription/translation, chorismate metabolism, and energy metabolism are not shown.
The MCMC algorithm minimized the squared difference (residual) between the training data and model simulations starting from an initial parameter set assembled from literature and inspection. Bounds on permissible parameter values were established using studies from the BioNumbers database (Milo et al., 2009). For each newly generated parameter set, the balance equations were re-solved and the cost function re-calculated; all sets with a lower cost (and some with higher cost) were accepted into the ensemble. Parameter sets were also required to meet strict ordinary differential equation solver tolerances, to ensure numerical stability. Approximately 3000 parameter sets were accepted into an initial ensemble; each set contained 204 maximum reaction rates, 204 enzyme activity decay constants, 548 saturation constants, and 34 control parameters, for a total of 815 parameters in each set. Of these 3000 accepted parameter sets, we selected a final ensemble of 100 sets (based upon training error) for the model analysis studies. The final ensemble (despite being close in overall error) had a mean Pearson correlation coefficient of 0.78; this suggested parameter sets were not over-sampled in the region of a local minimum. The median maximum reaction rate () across the ensemble was 11.6 mM/h, assuming a total cell-free enzyme concentration of approximately 170 nM. This , which corresponded to a median catalytic rate of 19 s−1 across the ensemble, was in relative agreement with the 13.7 s−1 median catalytic rate found by Milo and coworkers (Bar-Even et al., 2011). The median enzyme activity decay constant was 0.0045 h−1, corresponding to an enzyme activity half life of approximately 6 days. The median saturation constant was 1.0 mM; this was within one order of magnitude of the 130 μM reported by Milo and coworkers. Lastly, both the median control gain and order parameters, which appeared in the allosteric control functions, were on order 1. While the maximum reaction rates of the ensemble were distributed evenly across the allowed range (Fig. S1A), the saturation constants were clustered around the upper and lower bounds (Fig. S1B) of the parameter search. Taken together, the constrained MCMC approach estimated a numerically stable ensemble of model parameters that was on aggregate consistent with literature values. Next, we examined the model fit to the experimental training data.
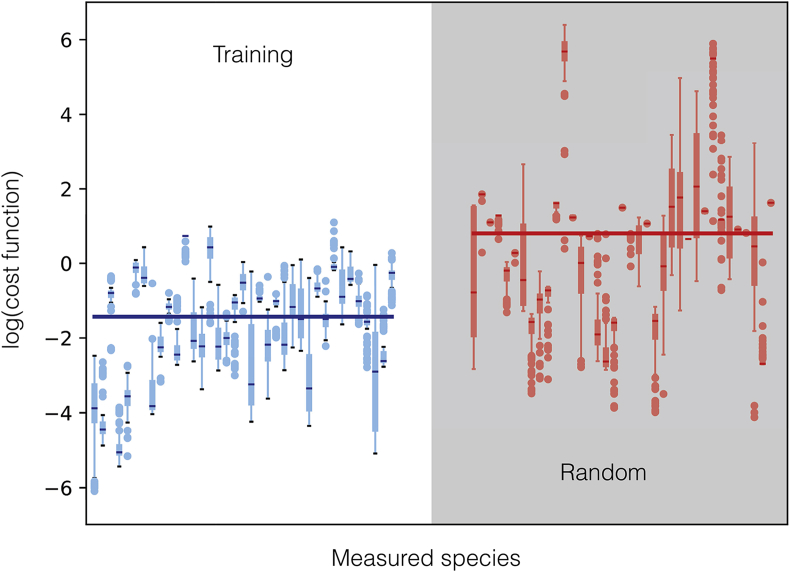
The ensemble of kinetic CFPS models captured the time evolution of protein biosynthesis, and the consumption and production of organic acid, amino acid and energy species. The time evolution of central carbon metabolites (Fig. 2, top), amino acids (Fig. 3), and energy species (Fig. 4) were captured by the ensemble and the best-fit parameter set. The constrained MCMC approach estimated parameter sets with a median error more than two orders of magnitude less than random parameter sets generated within the same parameter bounds established from literature (Fig. 5). For 29 of the 37 measurements in the training dataset, the mean Akaike information criterion (AIC) of the predicted ensemble was lower than that of the random sets, signifying a better fit of the data (Table 3). For the remaining eight measurements, the AIC score of the random ensemble was lower than that of the predicted ensemble, but the difference was within the standard deviation of the AIC score (with the exception of isoleucine: = 4.8, = 5.0). Taken together, these results suggested that the predicted ensemble modeled cell-free metabolism and protein production, significantly better than the random ensemble, not just overall but for the majority of individual metabolite and protein measurements. Next, we analyzed the important features of the cell-free protein synthesis timecourse.
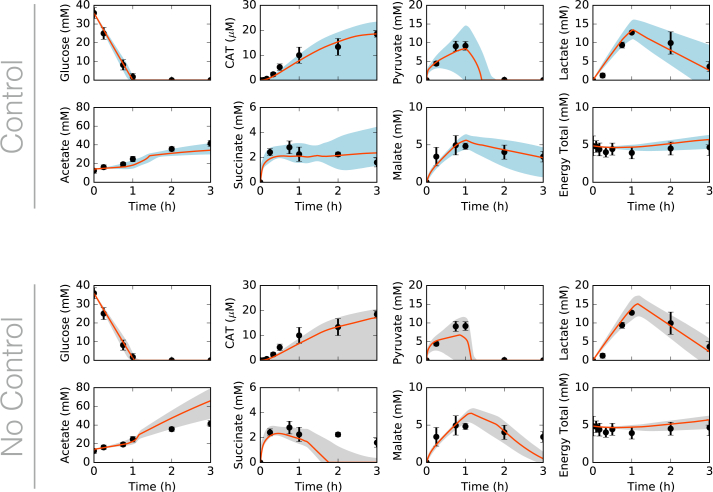
Fig. 2.
Central carbon metabolism in the presence (top) and absence (bottom) of allosteric control, including glucose (substrate), CAT (product), and intermediates, as well as total concentration of energy species. Best-fit parameter set (orange line) versus experimental data (points). 95% confidence interval (blue or gray shaded region) over the ensemble of 100 sets. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
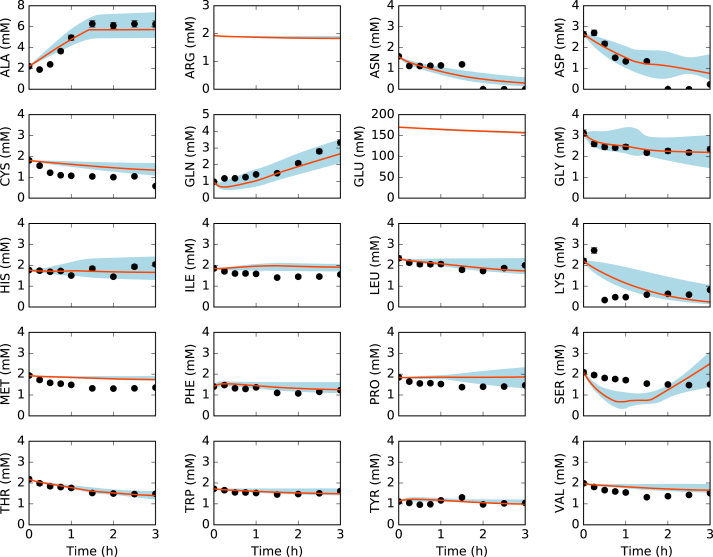
Fig. 3.
Amino acids in the presence of allosteric control. Best-fit parameter set (orange line) versus experimental data (points). 95% confidence interval (blue shaded region) over the ensemble of 100 sets. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
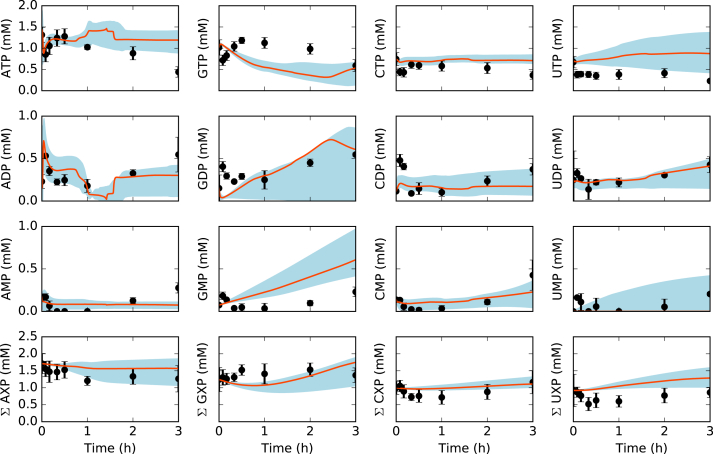
Fig. 4.
Energy species and energy totals by base in the presence of allosteric control. Best-fit parameter set (orange line) versus experimental data (points). 95% confidence interval (blue shaded region) over the ensemble of 100 sets. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Fig. 5.
Log of cost function (residual between training data and model simulations) across 37 datasets for data-trained ensemble (blue) and randomly generated ensemble (red, gray background). Median (bars), interquartile range (boxes), range excluding outliers (thin lines), and outliers (circles) for each dataset. Median across all datasets (large bar overlaid). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Table 3.
Mean and standard deviation of Akaike information criterion (AIC), by measurement, for the ensemble and random ensemble.
| Measurement | |||||
|---|---|---|---|---|---|
| GLC | 65.4 | 2.1 | 103.9 | 0.6 | 38.5 |
| CAT | −23.0 | 10.5 | −5.2 | 0.1 | 17.8 |
| PYR | 64.8 | 10.3 | 84.7 | 0.7 | 19.9 |
| LAC | 70.7 | 4.5 | 88.9 | 0.1 | 18.2 |
| AC | 79.4 | 6.0 | 96 | 2.1 | 16.6 |
| SUCC | 59.6 | 3.4 | 55.5 | 4.1 | −4.1 |
| MAL | 60.8 | 4.1 | 71.6 | 6.3 | 10.8 |
| ATP | 51.1 | 3.3 | 69.1 | 0.1 | 18.0 |
| ADP | 39.8 | 3.7 | 53.2 | 4.7 | 13.4 |
| AMP | 32.9 | 1.5 | 75.1 | 5.7 | 42.2 |
| GTP | 53.4 | 1.6 | 68.2 | 0.1 | 14.8 |
| GDP | 45.7 | 2.9 | 43.6 | 9.5 | −2.1 |
| GMP | 46.5 | 4.2 | 46.1 | 12.5 | −0.4 |
| CTP | 44.9 | 2.6 | 58.5 | 0.1 | 13.7 |
| CDP | 38.8 | 1.6 | 50.7 | 8.2 | 11.8 |
| CMP | 32.1 | 4.0 | 51.9 | 9.1 | 19.8 |
| UTP | 55.6 | 5.2 | 53 | 0.1 | −2.7 |
| UDP | 28.2 | 4.6 | 51.9 | 11.5 | 23.6 |
| UMP | 35.3 | 3.3 | 72.3 | 7.3 | 36.9 |
| ALA | 66.4 | 4.4 | 100.5 | 1.1 | 34.1 |
| ASN | 53.7 | 1.5 | 67.6 | 3.8 | 13.8 |
| ASP | 65.9 | 2.5 | 79.5 | 0.1 | 13.6 |
| CYS | 60.5 | 3.1 | 74 | 0.1 | 13.5 |
| GLN | 54.3 | 5.6 | 84.7 | 0.1 | 30.4 |
| GLY | 47.2 | 12.7 | 75.5 | 11.7 | 28.3 |
| HIS | 46.3 | 6.2 | 43.2 | 3.2 | −3.2 |
| ILE | 53.3 | 3.8 | 48.4 | 4.8 | −5.0 |
| LEU | 41.5 | 6.5 | 52.5 | 4.6 | 10.9 |
| LYS | 68.4 | 2.0 | 73.9 | 0.2 | 5.5 |
| MET | 55.9 | 1.0 | 57.4 | 4 | 1.5 |
| PHE | 43.4 | 5.9 | 57.7 | 8.3 | 14.3 |
| PRO | 54.4 | 2.8 | 47.9 | 6.7 | −6.5 |
| SER | 65.9 | 4.1 | 81.4 | 0.1 | 15.6 |
| THR | 28.2 | 5.5 | 63.2 | 14.9 | 35.0 |
| TRP | 31.2 | 5.7 | 79.9 | 1.4 | 48.6 |
| TYR | 39.3 | 2.0 | 36.7 | 5.4 | −2.6 |
| VAL | 51.3 | 3.1 | 55.5 | 4.6 | 4.1 |
The predicted ensemble of models captured the biphasic time course of CAT production. During the first hour, glucose powered protein production, and CAT was produced at 8 μM/h; subsequently, pyruvate and lactate reserves were consumed to power metabolism, and CAT was produced at 5 μM/h. Allosteric control was important to central carbon metabolism, especially for pyruvate, acetate, and succinate (Fig. 2, bottom). However, CAT production was robust to the removal of allosteric control. The difference between the allosteric control and no-control cases was mostly seen in the second (pyruvate-driven) phase of CAT production, following glucose exhaustion. Specifically, pyruvate, succinate, and malate consumption and acetate accumulation increased with the removal of allosteric control. The rate of acetate accumulation increased by 172%, while the rates of malate, pyruvate, and lactate consumption increased by 146%, 82%, and 9%, respectively. Succinate went from accumulating slightly in the second phase, in the presence of allosteric control, to being fully consumed. While ATP generation varied when allosteric control was removed, ATP expenditure toward CAT production did not. Most of the fluxes that differed between the two cases involved PEP and pyruvate, which directly participated in many of the reactions modulated by allosteric control. Taken together, the ensemble of kinetic models was consistent with time series measurements of the cell-free production of a model protein. Although the ensemble described the experimental data, it was unclear which kinetic parameters and pathways most influenced metabolism and CAT production. To explore this question, we performed reaction group knockout analysis.
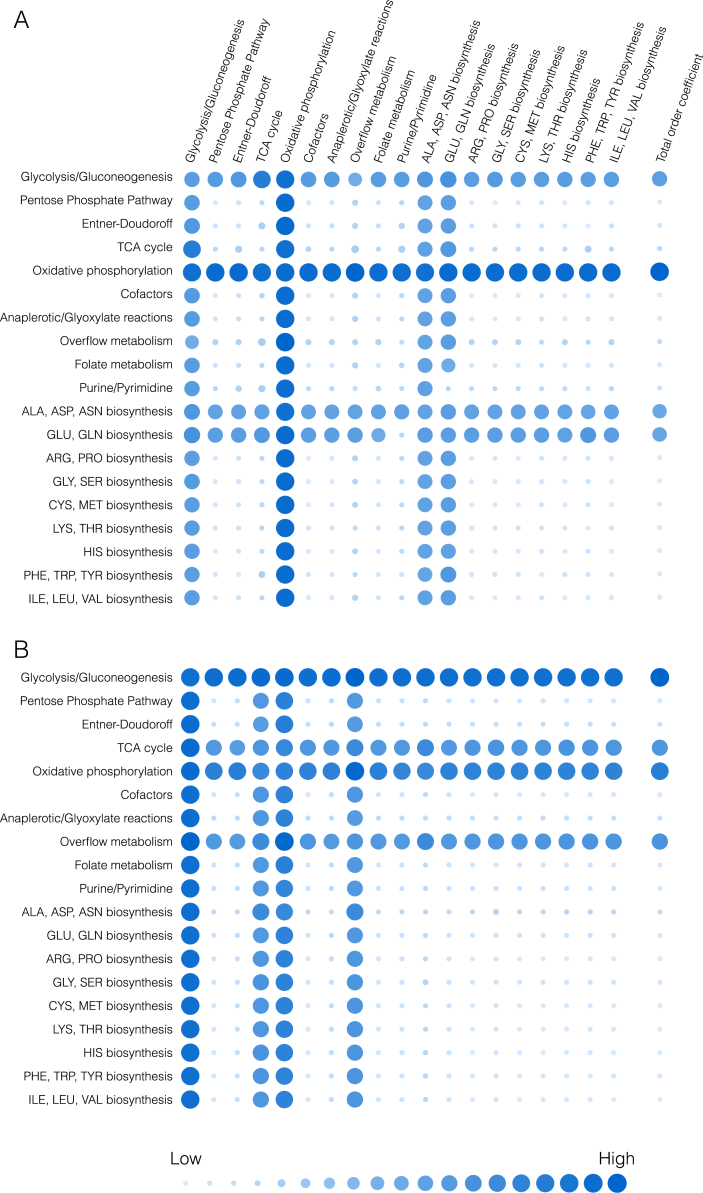
The importance of CFPS pathways was estimated using pathway group knockout analysis (Fig. 7). The metabolic network was divided into 19 reaction groups, spanning central carbon metabolism, energetics, and amino acid biosynthesis. Group knockout analysis was used to estimate the influence of broadly defined network functions on protein synthesis. While this approach is not directly transferable to experimental investigation, deleting groups of reactions avoids under-predicting the sensitivity of reactions that exist in parallel with others e.g., isozymes. It also gives a global picture of the robust and fragile elements of the network in terms of the functional groups. The response in the productivity (Fig. 7A) and overall system state (Fig. 7B) was calculated for single and pairwise deletion of each of these reaction groups. Lastly, the overall effect of the deletion of a pathway was estimated by summing the single and pairwise effects (summation across the columns of the response array). Glycolysis/gluconeogenesis and oxidative phosphorylation had the greatest effect on both productivity and system state. This supports previous studies that have suggested oxidative phosphorylation is occurring in a cell-free system (Jewett et al., 2008); Jewett and coworkers observed a decrease in CAT yield, ranging from 1.5-fold to 4-fold, when inhibiting oxidative phosphorylation reactions in the Cytomim cell-free platform, using both pyruvate and glutamate as substrates. CAT productivity was also affected by two sectors of amino acid biosynthesis: alanine/aspartate/asparagine, and glutamate/glutamine biosynthesis. Aspartate, glutamate, and glutamine are key reactants in the biosynthesis of many other amino acids, all of which are required for CAT synthesis. Meanwhile, the TCA cycle and overflow metabolism (which included acetyl-coA/acetate reactions and the interconversion of pyruvate and lactate) also had a significant effect on the system state. These reactions directly impacted key system species: succinate and malate in the TCA cycle, and acetate, pyruvate, and lactate in the overflow metabolism. In addition, the relative influence of transcription and translation parameters was interrogated by global sensitivity analysis (Sobol, 2001). Productivity was sensitive to the maximum reaction rate of transcription (coefficient of 0.43 0.06), but was more sensitive to variations in the maximum reaction rate of translation (0.66 0.08). Thus, translation appeared to be the limiting step of cell-free protein synthesis.
Fig. 7.
Effect of group knockouts on system. A. Change in CAT productivity when one (diagonal) or two (off-diagonal) reaction groups are turned off. B. Change in system state (only species for which data exist) when one (diagonal) or two (off-diagonal) reaction groups are turned off. Total-order effect for each group calculated as the sum of first-order effect and all pairwise effects. Larger and darker circles represent greater effects.
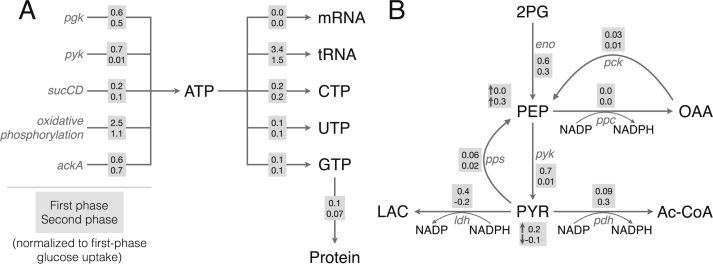
The energy efficiency of CAT production, as well as the sources of energy generation and consumption, were tracked for the best-fit set. Energy efficiency was calculated as the ratio of transcription and translation rates (weighted by the associated ATP costs of each step) to the amount of ATP generated by all sources. During the first phase of protein production, with glucose as the substrate, CAT was produced with a productivity of 8 μM/h and an energy efficiency of 10%. The organic acids that accumulated in the first phase (with the exception of acetate) were then utilized as substrates in the second phase, once glucose was depleted. We assumed the second phase of CAT production was powered largely by pyruvate; although malate was also consumed in the second phase, it accounted for only 11% of substrate consumption. Lactate accounted for a significant amount of substrate consumption, but was connected in the stoichiometry only to pyruvate. Thus, we considered the second phase as pyruvate-driven production. Interestingly, while this mode of protein production was slower (5 μM/h), it exhibited a higher energy efficiency (14%). Of the ATP generated, about half was observed to come from oxidative phosphorylation (R_atp) in each of the two phases of production (Fig. 6A, Table 1). Another 30% was generated by glycolysis during the first phase (R_pgk,R_pyk), which decreased to approximately 20% following glucose exhaustion. However, glycolysis was also amongst the largest consumers of ATP during first phase of production (R_glk_atp, R_pfk) (Table 2). The TCA cycle (R_sucCD) contributed 3% to the overall rate of ATP generation in the first phase and 5% in the second. The hypothesis that pyruvate drives the second phase explains this; stores of accumulated pyruvate can be converted to acetyl-CoA, as well as OAA (via PEP), and thus power the TCA cycle just as when glucose was available. Interestingly, ATP generation through acetate metabolism (R_ackA) increased from 12% in the first phase to 28% in the second. The switch from glycolysis in the first phase, to consumption of organic acid reserves and increased acetate accumulation in the second phase, can also be seen in the reaction fluxes surrounding PEP and pyruvate (Fig. 6B). Lastly, amino acid degradation contributed a negligible amount to energy production. Taken together, while the efficiency of production was higher for the pyruvate-driven phase, it was still relatively low, suggesting that there is room for platform optimization. This strengthens the importance of glycolysis and oxidative phosphorylation, and presents a trade-off between productivity and energy efficiency in CFPS.
Fig. 6.
Key reaction fluxes of the network, in the first (gray boxes, top row) and second (gray boxes, bottom row) phases of metabolism. A. Fluxes of ATP generation and consumption, and GTP consumption toward protein synthesis. B. Fluxes of glycolysis and lactate and acetate metabolism. Fluxes are normalized to the first-phase glucose uptake rate. For PEP and pyruvate, accumulation (normalized to glucose uptake) is also shown.
Table 1.
Breakdown of ATP generation. Flux through ATP-generating pathways in the first and second phases as percentages of total ATP generation in that phase.
| Name | Index | Reaction | Phase 1 | Phase 2 |
|---|---|---|---|---|
| R_pgk | 12 | 13DPG + ADP 3PG + ATP | 14% | 21% |
| R_pyk | 18 | ADP + PEP ATP + PYR | 16% | 1% |
| R_sucCD | 45 | ADP + Pi + SUCCOA ATP + COA + SUCC | 3% | 5% |
| R_atp | 55 | ADP + Pi + 4 He ATP + 4 H + H2O | 54% | 46% |
| R_ackA | 68 | ACTP + ADP AC + ATP | 12% | 28% |
| R_asn_deg | 102 | ASN + AMP + PPi NH3 + ASP + ATP | 1% | 1% |
| R_thr_deg3 | 109 | THR + Pi + ADP NH3 + FOR + ATP + PROP | 1% | 1% |
Table 2.
Breakdown of ATP consumption. Flux through ATP-consuming pathways in the first and second phases as percentages of total ATP consumption in that phase.
| Name | Index | Reaction | Phase 1 | Phase 2 |
|---|---|---|---|---|
| R_glk_atp | 1 | ATP + GLC ADP + G6P + H | 22% | 1% |
| R_pfk | 4 | ATP + F6P ADP + FBP | 24% | 1% |
| R_pps | 22 | ATP + H2O + PYR AMP + PEP + Pi | 1% | 1% |
| R_acs | 70 | AC + ATP + COA ACCOA + AMP + PPi | 8% | 19% |
| R_glnA | 86 | GLU + ATP + NH3 GLN + ADP + Pi | 1% | 2% |
| R_atp_amp | 152 | ATP + H2O AMP + PPi | 6% | 13% |
| R_udp_utp | 160 | UDP + ATP UTP + ADP | 3% | 6% |
| R_cdp_ctp | 161 | CDP + ATP CTP + ADP | 4% | 8% |
| R_gdp_gtp | 162 | GDP + ATP GTP + ADP | 3% | 4% |
| R_atp_ump | 163 | ATP + UMP ADP + UDP | 1% | 3% |
| R_atp_cmp | 164 | ATP + CMP ADP + CDP | 2% | 3% |
| R_adk_atp | 166 | AMP + ATP 2 ADP | 18% | 35% |
| tRNA charging | 185–204 | AA + tRNA + ATP + H2O AA tRNA + AMP + PPi | 2% | 2% |
| Other | 4% | 4% |
3. Discussion
In this study, an ensemble of kinetic cell-free protein synthesis (CFPS) models was developed using dynamic metabolite measurements from an early glucose powered Cytomim E. coli cell-free extract. The hybrid cell-free modeling approach of Wayman and coworkers, (Wayman et al., 2015), which integrates traditional kinetic modeling with a logic-based description of allosteric regulation, was employed to describe the time evolution of the CFPS reaction. The ensemble captured dynamic metabolite measurements over two orders of magnitude better than random parameter sets generated in the same region of parameter space. The ensemble captured the biphasic time course of CAT production, relying on glucose during the first hour and pyruvate and lactate following glucose exhaustion. Allosteric control was essential to the description of the organic acid trajectories; without allosteric control, pyruvate, lactate, succinate, and malate were predicted to be consumed more quickly following glucose exhaustion, to power CAT synthesis. However, CAT production was robust to the removal of allosteric control because the amino acids and energy species that are reactants for CAT synthesis were also not affected by allosteric control. The ensemble of kinetic models was then used to analyze the performance of the CFPS system, and to estimate the pathways most important to protein production. CAT was produced with an approximate aggregate energy efficiency of 12%, suggesting that much of the energy resources for protein synthesis were diverted to non-productive pathways. By knocking out metabolic enzymes in groups, it was shown that metabolism and protein production in particular depended upon oxidative phosphorylation and glycolysis/gluconeogenesis. Lastly, global sensitivity analysis suggested that the translation rate was more important to protein productivity than transcription. Taken together, this study provides a foundation for sequence-specific genome scale, dynamic modeling of cell-free E. coli protein synthesis that could be adapted to model the production of other proteins and synthetic circuits.
The ensemble of models could serve as a surrogate to rationally design cell-free production processes to optimize production rate and energy efficiency. In analyzing the effect of reaction groups on CAT production and the system state, the regions of metabolism associated with substrate utilization and energy generation were the most important. Oxidative phosphorylation was vital, since it provided most of the energetic needs of CFPS. While it is unknown how active oxidative phosphorylation is compared to that of in vivo systems, this study suggested it was critical to CFPS performance. However, the biphasic operation of CFPS highlights the ability of the system to respond to an absence of glucose. During the first phase, central carbon metabolites accumulated with the majority of flux going toward acetate and some toward pyruvate, lactate, succinate and malate. While acetate continued to accumulate as a byproduct, the other organic acids were consumed as secondary substrates after glucose was no longer available. Glutamate also served as a substrate throughout both phases, powering amino acid synthesis. These results confirmed experimental findings that CAT production can be sustained by other substrates in the absence of glucose, providing alternative strategies to optimize CFPS performance. While CAT synthesis can be powered by other substrates, the productivity was lower (5 μM/h, as opposed to 8 μM/h). This is in accordance with literature, where pyruvate provided a relatively slow but continuous supply of ATP (Swartz, 2001). Taken together, this shows CFPS can be designed towards a specified application, either requiring a slow stable energy source or faster production.
Presented herein is the first dynamic model of E. coli cell-free protein synthesis. A hybrid modeling framework was applied to describe an experimental dataset for production of a model protein (Vilkhovoy et al., 2018) and identified system limitations and areas of improvement for production efficiency. Having captured the system dynamics, areas of improvement for CFPS performance were investigated. The model predicted CAT production with an energy efficiency of 10% under glucose consumption and 14% under pyruvate consumption. The accumulation of glycolytic intermediates and byproducts such as acetate and carbon dioxide was responsible for this sub-optimal performance. If fluxes could be balanced such that intermediates were fully utilized, CAT production would increase. Theoretical estimations of the energy efficiency of an in vivo system can be as high as 80%, as found by our group (Vilkhovoy et al., 2018) and others (Maitra and Dill, 2015). However, the corresponding experimental values are much lower; 16% in the case of our experimentally-constrained sequence-specific model (Vilkhovoy et al., 2018). While the efficiency is lower, and the ATP produced per unit glucose consumed is also likely lower, the demand for ATP in a cell free system is significantly less. Previously, we estimated that approximately 120–160 mM ATP/h was produced in a cell free system powered by glucose, in contrast to 12–84 mM ATP/h for optimal protein production estimated by a constraint based model (Vilkhovoy et al., 2018). Thus, despite being less efficient, the cell free system may not be energy limited as it overproduced ATP relative to the demand from protein synthesis. Knocking out sections of network metabolism revealed that glycolysis/gluconeogenesis and oxidative phosphorylation were the most important to CAT production and the system as a whole. Productivity was also heavily dependent on the synthesis reactions of alanine, aspartate, asparagine, glutamate, and glutamine, while TCA cycle and overflow reactions affected the system state. These findings represent the first dynamic model of E. coli cell-free protein synthesis, an important step toward a functional genome scale description of cell-free systems. This work could be extended through further experimentation to gain a deeper understanding of system performance under a variety of conditions. Specifically, CAT production performed in the absence of amino acids could inform the system’s ability to synthesize them, while experimentation in the absence of glucose or oxygen could shed light on the importance of those substrates. Another extension of this study would be to apply its insights to other protein applications. CAT is only a test protein used for model identification; the modeling framework, and to some extent the parameter values, should be protein agnostic. However, it should be noted that the fully kinetic approach resulted in a model that was computationally expensive to solve, difficult to characterize, and arduous to interrogate. Future applications may benefit from alternate modeling strategies. For example, our group also employed a dynamic constraint-based approach to model CFPS (Dai et al., 2018). This involved constraining the problem to hundreds of different combinations of measurements, and solving the model for each. That approach also captured the dynamics, and allowed the question of which measurements might best characterize a system to be explored. Approaching that question using the fully kinetic approach would have been untenable. However, constraint-based approaches depend on the accuracy of the measurements to which they are constrained. A kinetic approach can theoretically predict dynamics in the absence of data, if parameters are well identified. Taken together, the dynamics of multiphasic metabolism and protein synthesis in CFPS were accurately captured, and the importance of various pathways was interrogated toward improvement of production; however, other modeling approaches have advantages that make them well suited for future endeavors.
4. Materials and Methods
4.1. Cell-free protein synthesis and measurement
The protein synthesis reaction was conducted using a modified version of the PANOxSP protocol (Jewett and Swartz, 2004b). Briefly, the protein synthesis reaction was performed using the S30 extract in 1.5-mL Eppendorf tubes (working volume of 15 μL) and incubated in a humidified incubator at 37 °C. Plasmid pK7CAT was used as the DNA template for chloramphenical acetyl transferase (CAT) expression by placing the cat gene between the T7 promoter and the T7 terminator (Kigawa et al., 1995). The plasmid was isolated and purified using a Plasmid Maxi Kit (Qiagen, Valencia CA). Cell-free reaction samples were quenched at specific timepoints with equal volumes of ice-cold 150 mM sulfuric acid to precipitate proteins. Protein synthesis of CAT was determined from the total amount of 14C-leucine-labeled product by trichloroacetic acid precipitation followed by scintillation counting as described previously (Calhoun and Swartz, 2005). Samples were centrifuged for 10 min at 12,000 g and 4 °C. The supernatant was collected for high performance liquid chromatography (HPLC) analysis. HPLC analysis (Agilent 1100 HPLC, Palo Alto CA) was used to separate nucleotides and organic acids, including glucose. Compounds were identified and quantified by comparison to known standards for retention time and UV absorbance (260 nm for nucleotides and 210 nm for organic acids) as described previously (Calhoun and Swartz, 2005). The standard compounds quantified with a refractive index detector included inorganic phosphate, glucose, and acetate. Pyruvate, malate, succinate, and lactate were quantified with the UV detector. The stability of the amino acids in the cell extract was determined using a Dionex Amino Acid Analysis (AAA) HPLC System (Sunnyvale, CA) that separates amino acids by gradient anion exchange (AminoPac PA10 column). Compounds were identified with pulsed amperometric electrochemical detection and by comparison to known standards. More details are available in the Materials and Methods section of Vilkhovoy et al. (2018).
4.2. Formulation and solution of the model equations
Cell-free protein synthesis was modeled using ordinary differential equations (ODEs) to estimate the time evolution of metabolite (), scaled enzyme activity (), transcription (m) and translation () in an E. coli cell-free metabolic network:
| (1) |
| (2) |
| (3) |
| (4) |
The quantity denotes the number of metabolic reactions, denotes the number of metabolites and denotes the number of metabolic enzymes in the model. The quantity denotes the rate of reaction j. Typically, reaction j is a non-linear function of metabolite and enzyme abundance, as well as unknown kinetic parameters (). The quantity denotes the stoichiometric coefficient for species i in reaction j. If , metabolite i is produced by reaction j. Conversely, if , metabolite i is consumed by reaction j, while indicates metabolite i is not connected with reaction j. Lastly, denotes the scaled enzyme activity decay constant. The system material balances were subject to the initial conditions and (initially we have 100% cell-free enzyme activity).
Metabolic reaction rates were written as the product of a kinetic term () and a control term (), . We used multiple saturation kinetics to model the reaction term :
| (5) |
where denotes the maximum rate for reaction j, denotes the scaled enzyme activity which catalyzes reaction j, denotes the saturation constant for species s in reaction j, and denotes the set of reactants for reaction j.
The control term depended upon the combination of factors which influenced rate process j. For each rate, we used a rule-based approach to select from competing control factors. If rate j was influenced by factors, we modeled this relationship as where denotes a transfer function quantifying the influence of factor i on rate j. The function is an integration rule which maps the output of regulatory transfer functions to a control variable. We used Hill-like transfer functions and in this study (Wayman et al., 2015). We included 17 allosteric regulation terms, taken from literature, in the CFPS model. PEP was modeled as an inhibitor for phosphofructokinase (Kotte et al., 2010; Cabrera et al., 2011), PEP carboxykinase (Kotte et al., 2010), PEP synthetase (Kotte et al., 2010; Chulavatnatol and Atkinson, 1973), isocitrate dehydrogenase (Kotte et al., 2010; Ogawa et al., 2007), and isocitrate lyase/malate synthase (Kotte et al., 2010; Ogawa et al., 2007; MacKintosh and Nimmo, 1988), and as an activator for fructose-biphosphatase (Kotte et al., 2010; Donahue et al., 2000; Hines et al., 2006, 2007). AKG was modeled as an inhibitor for citrate synthase (Kotte et al., 2010; Pereira et al., 1994; Robinson et al., 1983) and isocitrate lyase/malate synthase (Kotte et al., 2010; MacKintosh and Nimmo, 1988). 3PG was modeled as an inhibitor for isocitrate lyase/malate synthase (Kotte et al., 2010; MacKintosh and Nimmo, 1988). FDP was modeled as an activator for pyruvate kinase (Kotte et al., 2010; Zhu et al., 2010) and PEP carboxylase (Kotte et al., 2010; Wohl and Markus, 1972). Pyruvate was modeled as an inhibitor for pyruvate dehydrogenase (Kotte et al., 2010; Kale et al., 2007; Arjunan et al., 2002) and as an activator for lactate dehydrogenase (Okino et al., 2008). Acetyl-CoA was modeled as an inhibitor for malate dehydrogenase (Kotte et al., 2010).
The symbol denotes the transcription rate, u denotes a promoter specific activation model, and denotes the transcript degradation rate. The transcription rate was modeled as:
| (6) |
where denotes the maximum transcription rate, denotes the RNA polymerase concentration, denotes the gene concentration, denotes the gene saturation constant, denotes the saturation constant for species s, and denotes the set of reactants for transcription: ATP, GTP, CTP, UTP, and water. In this study, we considered only the T7 promoter; we have previously estimated 0.95 for T7 (Vilkhovoy et al., 2018). Transcription was modeled as saturating with respect to gene concentration and directly proportional to the concentration of RNA polymerase. Transcript degradation was modeled as first-order in transcript:
| (7) |
where denotes the transcript degradation rate constant.
The symbol denotes the translation rate, which was modeled as:
| (8) |
where denotes the maximum translation rate, denotes the ribosome concentration, m denotes the transcript concentration, denotes the transcript saturation constant, denotes the saturation constant for species s, and denotes the set of reactants for translation: GTP, water, and the 20 species representing tRNA charged with amino acids. Translation was modeled as saturating with respect to transcript concentration and directly proportional to the concentration of ribosomes (Table 6).
Table 6.
Reference values for transcription, translation, and mRNA degradation from literature. Transcription rate calculated from elongation rate, mRNA length, and promoter activity level. Translation rate calculated from elongation rate, protein length, and polysome amplification constant. mRNA degradation rate calculated from mRNA degradation time.
| Description | Parameter | Value | Units | Reference |
|---|---|---|---|---|
| T7 RNA polymerase concentration | 1.0 | μM | ||
| Ribosome concentration | 2 | μM | Garamella et al. (2016) | |
| Transcription saturation coefficient | 100 | nM | estimated | |
| Translation saturation coefficient | 45 | μM | estimated | |
| Transcription elongation rate | 25 | nt/s | Garamella et al. (2016) | |
| CAT mRNA length | 660 | nt | Kigawa et al. (1995) | |
| Promoter activity level | u | 0.9 | estimated | |
| Transcription rate | 123 | h−1 | calculated | |
| Translation elongation rate | 1.5 | aa/s | Garamella et al. (2016) | |
| CAT protein length | 219 | aa | Kigawa et al. (1995) | |
| Polysome amplification constant | 10 | estimated | ||
| Translation rate | 247 | h−1 | calculated | |
| mRNA degradation time | 8 | min | BNID 106253 | |
| mRNA degradation rate | 5.2 | h−1 | calculated | |
| ATP transcription coefficient | 176 | calculated | ||
| CTP transcription coefficient | 144 | calculated | ||
| GTP transcription coefficient | 151 | calculated | ||
| UTP transcription coefficient | 189 | calculated | ||
| ATP tRNA charging coefficient | 219 | calculated | ||
| GTP translation coefficient | 438 | calculated |
4.3. Estimation of kinetic model parameters
We estimated an ensemble of kinetic parameter sets using a constrained Markov Chain Monte Carlo (MCMC) random walk strategy. We have used this technique previously to estimate numerically stable low-error parameter sets for signal transduction models (Tasseff et al., 2010, 2011). Starting from a small number of parameter sets estimated by inspection and literature, we calculated the cost function, equal to the sum-squared-error between experimental data and model predictions:
| (9) |
where denotes the number of datasets ( = 37), denotes the weight of the dataset, denotes the number of timepoints in the dataset, denotes the timepoint, denotes the measurement value of the dataset at the timepoint, and denotes the simulated value of the metabolite corresponding to the dataset, interpolated to the timepoint. Lastly, the cost function was scaled by the maximum experimental value in the dataset, . We then perturbed each model parameter between an upper and lower bound that varied by parameter type:
| (10) |
where denotes the number of parameters ( = 815), which includes 204 maximum reaction rates (), 204 enzyme activity decay constants, 548 saturation constants (), and 34 control parameters, denotes the new value of the parameter, denotes the current value of the parameter, a denotes a distribution variance, denotes a random sample from the normal distribution, denotes the lower bound for that parameter type, and denotes the upper bound for that parameter type. Model parameters were constrained by literature collected using the BioNumbers database (Milo et al., 2009). Transcription, translation, and mRNA degradation were bounded within a factor of two of their reference values. A characteristic cell-free enzyme concentration of 170 nM was calculated by diluting the one-tenth maximal concentration of lacZ (5 μM, BNID 100735) by a cell-free dilution factor of 30. This enzyme level was then used to calculate rate maxima from turnover numbers for various enzymes from BioNumbers (Table 4). Enzyme levels calculated from the rate maxima of select reaction fluxes in the best-fit set and catalytic rates reported in the MOMENT study of Shlomi and coworkers (Adadi et al., 2012) (Table 5) had a median value of 202 nM, well in agreement with this characteristic value. Rate maxima were bounded within one order of magnitude of the reference value where available; all other rate maxima were bounded within two orders of magnitude of the geometric mean of the available values. Enzyme activity decay constants were bounded between 0 and 1 h−1, corresponding to half lives of infinity and 42 min, respectively. Saturation constants were bounded between 0.0001 and 10 mM. Control gain parameters were bounded between 0.05 and 10 (dimensionless), while order parameters were bounded between 0.02 and 10 (dimensionless) (see Table 6).
Table 4.
Reference values for reaction rate maxima () from BioNumbers. values calculated from turnover numbers () from BioNumbers, and a characteristic enzyme concentration of 170 nM. Characteristic rate maximum for all other reactions calculated as geometric mean of calculated rate maxima.
| Enzyme | Reaction | (min−1) | (mM/h) | BNID# |
|---|---|---|---|---|
| Serine dehydrase | R_ser_deg | 10400 | 104 | 101119 |
| Isocitrate dehydrogenase | R_icd | 11900 | 119 | 101152 |
| Lactate dehydrogenase | R_ldh | 5800 | 58 | 101036 |
| Aspartate transaminase | R_aspC R_tyr R_phe | 25800 | 258 | 101108 |
| Enolase | R_eno | 13200 | 132 | 101028 |
| Pyruvate kinase | R_pyk | 25000 | 250 | 101029 101030 |
| Malic enzyme | R_maeA R_maeB | 35400 | 354 | 101167 |
| Phosphofructokinase | R_pfk | 554400 | 5544 | 104955 |
| Malate dehydrogenase | R_mdh | 33000 | 330 | 101163 |
| Citrate Synthase | R_gltA | 42000 | 420 | 101149 |
| 6PG dehydrogenase | R_zwf R_pgl R_gnd | 3200 | 32 | 101048 |
| Succinate dehydrogenase | R_sdh | 121 | 1.21 | 101162 |
| Succinyl-coA synthetase | R_sucCD | 4700 | 47 | 101158 |
| 3PGA dehydrogenase | R_gpm | 1100 | 11 | 101135 |
| PEP carboxylase | R_ppc | 35400 | 354 | 101139 |
| 3PGA kinase | R_pgk | 4300 | 43 | 101016 |
| Characteristic | 110 |
Table 5.
Enzyme levels for key reaction fluxes, calculated from enzyme turnover numbers 58 and rate maxima from the best-fit set.
| Enzyme | Reaction | (min−1), MOMENT | (mM/h), best-fit set | Enzyme Level (nM), calculated |
|---|---|---|---|---|
| Isocitrate dehydrogenase | R_icd | 1700 | 37 | 356 |
| Lactate dehydrogenase | R_ldh | 52500 | 35 | 11 |
| Aspartate transaminase | R_aspC | 4900 | 39 | 130 |
| Pyruvate kinase | R_pyk | 8100 | 610 | 1250 |
| Malic enzyme | R_maeA | 8100 | 46 | 96 |
| Malic enzyme | R_maeB | 4000 | 66 | 274 |
| Phosphofructokinase | R_pfk | 5000 | 15600 | 51800 |
| Malate dehydrogenase | R_mdh | 43700 | 33 | 13 |
| Succinate dehydrogenase | R_sdh | 10000 | 4.9 | 8.2 |
| Succinyl-coA synthetase | R_sucCD | 1500 | 250 | 2690 |
| Median | 202 |
For each newly generated parameter set, we re-solved the balance equations and calculated the cost function. All sets with a lower cost were accepted into the ensemble. Sets with a higher cost were also accepted into the ensemble, if they satisfied the acceptance constraint:
| (11) |
where denotes a random number taken from a uniform distribution between 0 and 1, cost denotes the cost of the current parameter set, costnew denotes the cost of the new parameter set, and α denotes a tunable parameter to control the tolerance to high-error sets. A total of 3875 sets were accepted into the initial ensemble, from which we selected N = 100 with minimal error for the final ensemble.
Lastly, a random ensemble of 100 parameter sets was generated within the same parameter bounds as the trained ensemble. The randomized parameter sets were generated using a Monte Carlo approach: each parameter was taken from a uniform distribution constructed between its upper and lower bounds. The model equations were then solved and the cost function and the Akaike information criterion (AIC) were calculated for each of the 37 separate experimental datasets (Table 6).
4.4. Reaction group knockouts
The metabolic network was divided into 19 reaction groups: glycolysis/gluconeogenesis, pentose phosphate, Entner-Doudoroff, TCA cycle, oxidative phosphorylation, cofactor reactions, anaplerotic/glyoxylate reactions, overflow metabolism, folate synthesis, purine/pyrimidine reactions, alanine/aspartate/asparagine synthesis, glutamate/glutamine synthesis, arginine/proline synthesis, glycine/serine synthesis, cysteine/methionine synthesis, threonine/lysine synthesis, histidine synthesis, tyrosine/tryptophan/phenylalanine synthesis, and valine/leucine/isoleucine synthesis. Each reaction group and pair of reaction groups were removed and the model was re-solved; the CAT productivity was then calculated and subtracted from that of the base case (no knockouts):
| (12) |
| (13) |
| (14) |
where denotes the first-order productivity knockout effect for reaction group i, denotes the pairwise productivity knockout effect for reaction groups i and j, denotes the total-order productivity knockout effect for reaction group i, denotes the base case CAT productivity, denotes the CAT productivity when reaction group i is knocked out, denotes the CAT productivity when reaction groups i and j are knocked out, and denotes the absolute value of x. The system state, defined as the model predictions for all species for which experimental data exists, was also recorded for each knockout and compared to the base case:
| (15) |
| (16) |
| (17) |
where denotes the first-order system state knockout effect for reaction group i, denotes the pairwise system state knockout effect for reaction groups i and j, denotes the total-order system state knockout effect for reaction group i, denotes the base-case system state, denotes the system state when reaction group i is knocked out, denotes the system state when reaction groups i and j are knocked out, and denotes the norm of x. In order to not dominate the colorbar, the total-order knockout effects were normalized to the same ranges as the main arrays (first-order and pairwise effects).
4.5. Sensitivity of CAT productivity to transcription and translation
The catalytic rates of transcription and translation were sampled within one order of magnitude on each side from the best-fit values. The parameter bounds were set as the base-10 logarithms of the upper and lower bound for each rate; then, 10 was taken to the power of each parameter sample to obtain the catalytic rates:
| (18) |
| (19) |
| (20) |
where denotes the sample of the transcription catalytic rate, denotes the sample of the translation catalytic rate, denotes the best-fit value of the transcription catalytic rate, and denotes the best-fit value of the translation catalytic rate. The sampling was performed using the Sensitivity Analysis Library in Python (Numpy) with 3000 samples (Herman).
4.6. Calculation of energy efficiency
Energy efficiency was calculated as the ratio of transcription and translation (weighted by the appropriate energy species coefficients) to ATP generation:
| (21) |
| (22) |
| (23) |
where denotes the net accumulation of mRNA in phase τ (first, second, or overall), denotes the net accumulation of protein in phase τ, denotes the energy cost of transcription, denotes the energy cost of translation, denotes the set of ATP-producing reactions, and denotes the ATP coefficient for reaction j. , , , denote the stoichiometric coefficients of each energy species for transcription, and , denote the stoichiometric coefficients of ATP and GTP for translation. During transcription and tRNA charging, triphosphate molecules are consumed with monophosphates as byproducts; this is the reason for the factors of 2 on , , , , and .
5. Availability of model code
The cell-free model equations and the parameter estimation procedure were implemented in the Julia programming language (Bezanson et al., 2017). The model equations were solved using the CVODE solver of the SUNDIALS suite (Hindmarsh et al., 2005), with an absolute tolerance and relative tolerance of 1e−9; any parameter sets exhibiting CVODE errors were discarded. Thus, the numerical stability of all parameter sets in the ensemble was ensured. The model code and parameter ensemble is freely available under an MIT software license and can be downloaded from the Varnerlab website (Varnerlab).
Author’s contributions
J.V directed the modeling study. K.C and J.S conducted the cell-free protein synthesis experiments. J.V, J.W, and N.H developed the cell-free protein synthesis mathematical model and parameter ensemble. The manuscript was prepared and edited for publication by J.S, N.H, M.V, J.W and J.V.
Funding
This study was supported by a National Science Foundation Graduate Research Fellowship (DGE-1333468) to N.H. Research reported in this publication was also supported by the Systems Biology Coagulopathy of Trauma Program with support from the US Army Medical Research and Materiel Command under award number W911NF-10-1-0376.
Declaration of competing interest
The authors declare that they have no competing interests.
Acknowledgements
We gratefully acknowledge the suggestions from the anonymous reviewers to improve this manuscript.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.mec.2019.e00113.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
Histograms of model parameters, across the ensemble of 100 sets. A. Histogram of rate maxima. B. Histogram of saturation constants.
References
- Adadi R., Volkmer B., Milo R., Heinemann M., Shlomi T. Prediction of microbial growth rate versus biomass yield by a metabolic network with kinetic parameters. PLoS Comput. Biol. 2012;8 doi: 10.1371/journal.pcbi.1002575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen T.E., Palsson B.Ø. Sequence-based analysis of metabolic demands for protein synthesis in prokaryotes. J. Theor. Biol. 2003;220:1–18. doi: 10.1006/jtbi.2003.3087. [DOI] [PubMed] [Google Scholar]
- Andreozzi S., Miskovic L., Hatzimanikatis V. iSCHRUNK – in silico approach to characterization and reduction of uncertainty in the kinetic models of genome-scale metabolic networks. Metab. Eng. 2007;33:158–168. doi: 10.1016/j.ymben.2015.10.002. [DOI] [PubMed] [Google Scholar]
- Andreozzi S., Chakrabarti A., Soh K.C., Burgard A., Yang T.H., Van Dien S., Miskovic L., Hatzimanikatis V. Identification of metabolic engineering targets for the enhancement of 1,4-butanediol production in recombinant E. coli using large-scale kinetic models. Metab. Eng. 2016;35:148–159. doi: 10.1016/j.ymben.2016.01.009. [DOI] [PubMed] [Google Scholar]
- Arjunan P., Nemeria N., Brunskill A., Chandrasekhar K., Sax M., Yan Y., Jordan F., Guest J.R., Furey W. Structure of the pyruvate dehydrogenase multienzyme complex E1 component from Escherichia coli at 1.85 Å resolution. Biochemistry. 2002;41:5213–5221. doi: 10.1021/bi0118557. [DOI] [PubMed] [Google Scholar]
- Atlas J.C., Nikolaev E.V., Browning S.T., Shuler M.L. Incorporating genome-wide DNA sequence information into a dynamic whole-cell model of Escherichia coli: application to DNA replication. IET Syst. Biol. 2008;2:369–382. doi: 10.1049/iet-syb:20070079. [DOI] [PubMed] [Google Scholar]
- Bar-Even A., Noor E., Savir Y., Liebermeister W., Davidi D., Tawfik D.S., Milo R. The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry. 2011;50 doi: 10.1021/bi2002289. [DOI] [PubMed] [Google Scholar]
- Bezanson J., Edelman A., Karpinski S., Shah V. Julia: a fresh approach to numerical computing. SIAM Rev. 2017;59:65–98. [Google Scholar]
- Brown K.S., Sethna J.P. Statistical mechanical approaches to models with many poorly known parameters. Phys. Rev. E - Stat. Nonlinear Soft Matter Phys. 2003;68 doi: 10.1103/PhysRevE.68.021904. [DOI] [PubMed] [Google Scholar]
- Cabrera R., Baez M., Pereira H.M., Caniuguir A., Garratt R.C., Babul J. The crystal complex of phosphofructokinase-2 of Escherichia coli with fructose-6-phosphate: kinetic and structural analysis of the allosteric ATP inhibition. J. Biol. Chem. 2011;286:5774–5783. doi: 10.1074/jbc.M110.163162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun K.A., Swartz J.R. An economical method for cell-free protein synthesis using glucose and nucleoside monophosphates. Biotechnol. Prog. 2005;21:1146–1153. doi: 10.1021/bp050052y. [DOI] [PubMed] [Google Scholar]
- Castellanos M., Wilson D.B., Shuler M.L. A modular minimal cell model: purine and pyrimidine transport and metabolism. Proc. Natl. Acad. Sci. U. S. A. 2004;101:6681–6686. doi: 10.1073/pnas.0400962101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chulavatnatol M., Atkinson D.E. Phosphoenolpyruvate synthetase from Escherichia coli. Effects of adenylate energy charge and modifier concentrations. J. Biol. Chem. 1973;248:2712–2715. [PubMed] [Google Scholar]
- Dai D., Horvath N., Varner J.D. Dynamic sequence specific constraint-based modeling of cell-free protein synthesis. Processes. 2018;6:132. [Google Scholar]
- Domach M.M., Leung S.K., Cahn R.E., Cocks G.G., Shuler M.L. Computer model for glucose-limited growth of a single cell of Escherichia coli B/r-A. Biotechnol. Bioeng. 1984;26:203–216. doi: 10.1002/bit.260260303. [DOI] [PubMed] [Google Scholar]
- Donahue J.L., Bownas J.L., Niehaus W.G., Larson T.J. Purification and characterization of glpX-encoded fructose 1, 6-bisphosphatase, a new enzyme of the glycerol 3-phosphate regulon of Escherichia coli. J. Bacteriol. 2000;182:5624–5627. doi: 10.1128/jb.182.19.5624-5627.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feist A.M., Henry C.S., Reed J.L., Krummenacker M., Joyce A.R., Karp P.D., Broadbelt L.J., Hatzimanikatis V., Palsson B.Ø. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007;3:121. doi: 10.1038/msb4100155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fredrickson A.G. Formulation of structured growth models. Biotechnol. Bioeng. 1976;18:1481–1486. doi: 10.1002/bit.260181016. [DOI] [PubMed] [Google Scholar]
- Garamella J., Marshall R., Rustad M., Noireaux V. The all E. coli TX-TL toolbox 2.0: a platform for cell-free synthetic biology. ACS Synth. Biol. 2016;5:344–355. doi: 10.1021/acssynbio.5b00296. [DOI] [PubMed] [Google Scholar]
- Gutenkunst R.N., Waterfall J.J., Casey F.P., Brown K.S., Myers C.R., Sethna J.P. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 2007;3:e189. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- J. D. Herman, Sensitivity analysis library in Python (Numpy) http://jdherman.github.io/SALib/.
- Hindmarsh A.C., Brown P.N., Grant K.E., Lee S.L., Serban R., Shumaker D.E., Woodward C.S. SUNDIALS: suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math Software. 2005;31:363–396. [Google Scholar]
- Hines J.K., Fromm H.J., Honzatko R.B. Novel allosteric activation site in Escherichia coli fructose-1,6-bisphosphatase. J. Biol. Chem. 2006;281:18386–18393. doi: 10.1074/jbc.M602553200. [DOI] [PubMed] [Google Scholar]
- Hines J.K., Fromm H.J., Honzatko R.B. Structures of activated fructose-1,6-bisphosphatase from Escherichia coli. Coordinate regulation of bacterial metabolism and the conservation of the R-state. J. Biol. Chem. 2007;282:11696–11704. doi: 10.1074/jbc.M611104200. [DOI] [PubMed] [Google Scholar]
- Hodgman C.E., Jewett M.C. Cell-free synthetic biology: thinking outside the cell. Metab. Eng. 2012;14:261–269. doi: 10.1016/j.ymben.2011.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu C.Y., Varner J.D., Lucks J.B. Generating effective models and parameters for rna genetic circuits. ACS Synth. Biol. 2015;4:914–926. doi: 10.1021/acssynbio.5b00077. [DOI] [PubMed] [Google Scholar]
- Jewett M.C., Swartz J.R. Mimicking the Escherichia coli cytoplasmic environment activates long-lived and efficient cell-free protein synthesis. Biotechnol. Bioeng. 2004;86:19–26. doi: 10.1002/bit.20026. [DOI] [PubMed] [Google Scholar]
- Jewett M.C., Swartz J.R. Mimicking the Escherichia coli cytoplasmic environment activates long-lived and efficient cell-free protein synthesis. Biotechnol. Bioeng. 2004;86:19–26. doi: 10.1002/bit.20026. [DOI] [PubMed] [Google Scholar]
- Jewett M.C., Calhoun K.A., Voloshin A., Wuu J.J., Swartz J.R. An integrated cell-free metabolic platform for protein production and synthetic biology. Mol. Syst. Biol. 2008;4:220. doi: 10.1038/msb.2008.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kale S., Arjunan P., Furey W., Jordan F. A dynamic loop at the active center of the Escherichia coli pyruvate dehydrogenase complex E1 component modulates substrate utilization and chemical communication with the E2 component. J. Biol. Chem. 2007;282:28106–28116. doi: 10.1074/jbc.M704326200. [DOI] [PubMed] [Google Scholar]
- Karr J.R., Sanghvi J.C., Macklin D.N., Gutschow M.V., Jacobs J.M., Bolival B., Assad-Garcia N., Glass J.I., Covert M.W. A whole-cell computational model predicts phenotype from genotype. Cell. 2012;150:389–401. doi: 10.1016/j.cell.2012.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khodayari A., Maranas C.D. A genome-scale Escherichia coli kinetic metabolic model k-ecoli457 satisfying flux data for multiple mutant strains. Nat. Commun. 2016;7:13806. doi: 10.1038/ncomms13806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kigawa T., Muto Y., Yokoyama S. Cell-free synthesis and amino acid-selective stable isotope labeling of proteins for NMR analysis. J. Biomol. NMR. 1995;6:129–134. doi: 10.1007/BF00211776. [DOI] [PubMed] [Google Scholar]
- Kim D.-M., Swartz J.R. Regeneration of adenosine triphosphate from glycolytic intermediates for cell-free protein synthesis. Biotechnol. Bioeng. 2001;74:309–316. [PubMed] [Google Scholar]
- Kotte O., Zaugg J.B., Heinemann M. Bacterial adaptation through distributed sensing of metabolic fluxes. Mol. Syst. Biol. 2010;6:355. doi: 10.1038/msb.2010.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Y., Welsh J.P., Swartz J.R. Production and stabilization of the trimeric influenza hemagglutinin stem domain for potentially broadly protective influenza vaccines. Proc. Natl. Acad. Sci. U. S. A. 2014;111:125–130. doi: 10.1073/pnas.1308701110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKintosh C., Nimmo H.G. Purification and regulatory properties of isocitrate lyase from Escherichia coli ML308. Biochem. J. 1988;250:25–31. doi: 10.1042/bj2500025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maitra A., Dill K.A. Bacterial growth laws reflect the evolutionary importance of energy efficiency. Proc. Natl. Acad. Sci. U. S. A. 2015;112:406–411. doi: 10.1073/pnas.1421138111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthaei J.H., Nirenberg M.W. Characteristics and stabilization of DNAase-sensitive protein synthesis in E. coli extracts. Proc. Natl. Acad. Sci. U. S. A. 1961;47:1580–1588. doi: 10.1073/pnas.47.10.1580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milo R., Jorgensen P., Moran U., Weber G., Springer M. BioNumbers–the database of key numbers in molecular and cell biology. Nucleic Acids Res. 2009;38:750–753. doi: 10.1093/nar/gkp889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nirenberg M.W., Matthaei J.H. The dependence of cell-free protein synthesis in E. coli upon naturally occurring or synthetic polyribonucleotides. Proc. Natl. Acad. Sci. U. S. A. 1961;47:1588–1602. doi: 10.1073/pnas.47.10.1588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa T., Murakami K., Mori H., Ishii N., Tomita M., Yoshin M. Role of phosphoenolpyruvate in the NADP-isocitrate dehydrogenase and isocitrate lyase reaction in Escherichia coli. J. Bacteriol. 2007;189:1176–1178. doi: 10.1128/JB.01628-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okino S., Suda M., Fujikura K., Inui M., Yukawa H. Production of D-lactic acid by Corynebacterium glutamicum under oxygen deprivation. Appl. Microbiol. Biotechnol. 2008;78:449–454. doi: 10.1007/s00253-007-1336-7. [DOI] [PubMed] [Google Scholar]
- Pardee K., Slomovic S., Nguyen P.Q., Lee J.W., Donghia N., Burrill D., Ferrante T., McSorley F.R., Furuta Y., Vernet A., Lewandowski M., Boddy C.N., Joshi N.S., Collins J.J. Portable, on-demand biomolecular manufacturing. Cell. 2016;167 doi: 10.1016/j.cell.2016.09.013. 248–59.e12. [DOI] [PubMed] [Google Scholar]
- Pereira D.S., Donald L.J., Hosfield D.J., Duckworth H.W. Active site mutants of Escherichia coli citrate synthase. Effects of mutations on catalytic and allosteric properties. J. Biol. Chem. 1994;269:412–417. [PubMed] [Google Scholar]
- Robinson M.S., Easom R.A., Danson M.J., Weitzman P.D. Citrate synthase of Escherichia coli. Characterisation of the enzyme from a plasmid-cloned gene and amplification of the intracellular levels. FEBS Lett. 1983;154:51–54. doi: 10.1016/0014-5793(83)80873-4. [DOI] [PubMed] [Google Scholar]
- Shimizu Y., Inoue A., Tomari Y., Suzuki T., Yokogawa T., Nishikawa K., Ueda T. Cell-free translation reconstituted with purified components. Nat. Biotechnol. 2001;19:751–755. doi: 10.1038/90802. [DOI] [PubMed] [Google Scholar]
- Sobol I. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simulat. 2001;55:271–280. [Google Scholar]
- Spirin A., Baranov V., Ryabova L., Ovodov S., Alakhov Y. A continuous cell-free translation system capable of producing polypeptides in high yield. Science. 1988;242:1162–1164. doi: 10.1126/science.3055301. [DOI] [PubMed] [Google Scholar]
- Steinmeyer D., Shuler M. Structured model for Saccharomyces cerevisiae. Chem. Eng. Sci. 1989;44:2017–2030. [Google Scholar]
- Swartz J. A pure approach to constructive biology. Nat. Biotechnol. 2001;19:732–733. doi: 10.1038/90773. [DOI] [PubMed] [Google Scholar]
- Tasseff R., Nayak S., Salim S., Kaushik P., Rizvi N., Varner J.D. Analysis of the molecular networks in androgen dependent and independent prostate cancer revealed fragile and robust subsystems. PLoS One. 2010;5 doi: 10.1371/journal.pone.0008864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tasseff R., Nayak S., Song S.O., Yen A., Varner J.D. Modeling and analysis of retinoic acid induced differentiation of uncommitted precursor cells. Integr. Biol. 2011;3:578–591. doi: 10.1039/c0ib00141d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran L.M., Rizk M.L., Liao J.C. Ensemble modeling of metabolic networks. Biophys. J. 2008;95:5606–5617. doi: 10.1529/biophysj.108.135442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varnerlab, http://www.varnerlab.org/downloads/.
- Vilkhovoy M., Horvath N., Shih C.-H., Wayman J.A., Calhoun K., Swartz J., Varner J.D. Sequence specific modeling of e. coli cell-free protein synthesis. ACS Synth. Biol. 2018;7:1844–1857. doi: 10.1021/acssynbio.7b00465. [DOI] [PubMed] [Google Scholar]
- Wayman J.A., Varner J.D. Biological systems modeling of metabolic and signaling networks. Curr. Opin. Chem. Eng. 2013;2 [Google Scholar]
- Wayman J.A., Sagar A., Varner J.D. Dynamic modeling of cell-free biochemical networks using effective kinetic models. Processes. 2015;3:138. [Google Scholar]
- Wohl R.C., Markus G. Phosphoenolpyruvate carboxylase of Escherichia coli. Purification and some properties. J. Biol. Chem. 1972;247:5785–5792. [PubMed] [Google Scholar]
- Wu P., Ray N.G., Shuler M.L. A single-cell model for CHO cells. Ann. N. Y. Acad. Sci. 1992;665:152–187. doi: 10.1111/j.1749-6632.1992.tb42583.x. [DOI] [PubMed] [Google Scholar]
- Zhu T., Bailey M.F., Angley L.M., Cooper T.F., Dobson R.C. The quaternary structure of pyruvate kinase type 1 from Escherichia coli at low nanomolar concentrations. Biochimie. 2010;92:116–120. doi: 10.1016/j.biochi.2009.09.016. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Histograms of model parameters, across the ensemble of 100 sets. A. Histogram of rate maxima. B. Histogram of saturation constants.