A pharmacodynamic model of clinical synergy in multiple myeloma

Abstract

Background

Multiagent therapies, due to their ability to delay or overcome resistance, are a hallmark of treatment in multiple myeloma (MM). The growing number of therapeutic options in MM requires high-throughput combination screening tools to better allocate treatment, and facilitate personalized therapy.

Methods

A second-order drug response model was employed to fit patient-specific ex vivo responses of 203 MM patients to single-agent models. A novel pharmacodynamic model, developed to account for two-way combination effects, was tested with 130 two-drug combinations. We have demonstrated that this model is sufficiently parameterized by single-agent and fixed-ratio combination responses, by validating model estimates with ex vivo combination responses for different concentration ratios, using a checkerboard assay. This new model reconciles ex vivo observations from both Loewe and BLISS synergy models, by accounting for the dimension of time, as opposed to focusing on arbitrary time-points or drug effect. Clinical outcomes of patients were simulated by coupling patient-specific drug combination models with pharmacokinetic data.

Findings

Combination screening showed 1 in 5 combinations (21.43% by LD50, 18.42% by AUC) were synergistic ex vivo with statistical significance (P < 0.05), but clinical synergy was predicted for only 1 in 10 combinations (8.69%), which was attributed to the role of pharmacokinetics and dosing schedules.

Interpretation

The proposed framework can inform clinical decisions from ex vivo observations, thus providing a path toward personalized therapy using combination regimens.

Funding

This research was funded by the H. Lee Moffitt Cancer Center Physical Sciences in Oncology (PSOC) Grant (1U54CA193489-01A1) and by H. Lee Moffitt Cancer Center's Team Science Grant. This work has been supported in part by the PSOC Pilot Project Award (5U54CA193489-04), the Translational Research Core Facility at the H. Lee Moffitt Cancer Center & Research Institute, an NCI-designated Comprehensive Cancer Center (P30-CA076292), the Pentecost Family Foundation, and Miles for Moffitt Foundation.

Research in Context.

Evidence before this study

Multiple myeloma (MM), a cancer of bone marrow-resident plasma cells, remains incurable, despite successful approval of multiple therapeutic agents. MM therapy often involves combinations of three or more agents, with the rationale that combining drugs with different mechanisms of action could maximize efficacy by targeting several subpopulations of cancer cells simultaneously. Currently, there are two approaches employed to quantify combination drug effects: (a) phase-III, two-arm clinical trials seek to assess the clinical benefit of adding an experimental drug to a standard-of-care regimen, by comparing response rates, progression free survival and overall survival between two arms; (b) pre-clinical drug sensitivity assays generate dose-response curves for two single agents and combinations, and combination indices (CI) are computed to quantify synergistic effect in homogeneous cell lines. To date, synergy remains difficult to investigate and, in turn, translate into clinical utility. This is because, although clinical trials account for inter-patient heterogeneity, tumor microenvironment, and drug pharmacokinetics, it is impossible to investigate synergy (irrespective of the definition of additivity) in patients. Conversely, the pre-clinical platforms used to quantify synergy don't account for heterogeneity, tumor microenvironment, and the effect of pharmacokinetics, thus their predictions cannot be translated to clinical outcome or benefit.

Added value of this study

In order to address this translational need, we developed a novel framework involving co-cultured myeloma cells from patient samples in an ex vivo reconstruction of the bone marrow, to test the efficacy of single drugs and combinations. This framework features a pharmacodynamic model to capture the two-way synergistic effect between pairs of drugs, using patient-derived tumor-specific ex vivo drug sensitivity. The patient-specific model parameters capture the effect of inter-patient heterogeneity, intra-tumoral heterogeneity, and tumor microenvironment. Pharmacokinetic data from phase-I clinical trials are coupled with model parameters to simulate clinical response to a therapeutic regimen. This framework computes additive (from single agent ex vivo responses) and combination clinical responses, thereby making quantification of clinical synergistic effect possible. 203 MM patient-derived tumor specimens were tested with 130 two-drug combinations, which resulted in high-throughput combination screening based on pre-clinical data (LD50/AUC) and clinical predictions. This analysis demonstrated that only half of the combinations synergistic ex vivo also synergize clinically, emphasizing the need to develop drug combination effect models that account for pharmacokinetics and dosing schedules.

Implication of all the available evidence

This high-throughput combination screening framework identified drug combinations that are putatively clinically synergistic, and thus could potentially be used to screen for combinations that are likely candidates for a phase-III clinical trial. This could greatly benefit patients enroling in these trials by improving the response on the experimental arm. The combinations shown to be most synergistic could be investigated to identify molecular pathways that govern this interaction.

Alt-text: Unlabelled box

1. Introduction

In the field of clinical pharmacology, there are multiple definitions for drug additivity. Bliss, for example, assumes statistical independence in the action of the drugs in a given combination [1], whereas Loewe defines it as a scenario where the reduction in dose of one drug proportionally complements the dose reduction achieved due to the second drug [2]. In this manuscript, we will use the definition of synergy as a benefit over an additive response as it better matches the reality of the clinic: a physician will not reduce the dosing of drugs to achieve the same outcome, but would rather seek a tolerable combination with most improvement over its independent effects. The pursuit for synergistic drug combinations arises from the myriad of advantages of combination therapy, such as maximizing efficacy [3], reducing toxicity [4], and addressing interpatient variability [5], as well as delaying [6] and/or overcoming [7] innate or acquired resistance.

Innate or acquired resistance poses a major hurdle in effectively treating many cancers. Resistance to a drug arise as a consequence of enhanced degradation of the drug, increased expression of the drug target, alteration of the target, clonal evolution, microenvironmental factors [8], or intratumoral heterogeneity [9]. Thus, combination effect could be improved either by combining a drug that disrupts the mechanism of resistance of a second drug, or by combining drugs that target different subpopulations in the tumor.

In spite of the advantages seen in combination therapies, there is also the potential for adverse drug-drug interactions translating to increased toxicities for patients [10]. Furthermore, a combination proven to be statistically beneficial for a cohort of patients may not be the most promising option for each individual patient in the cohort, some patients could be further benefited by combinations tailored to their particularities and needs. However, absolute personalization of therapy cannot be inferred solely on a patient's clinical history and clinical literature. Accordingly, we propose to screen therapeutic regimens using clinical decision support tools backed by experiments conducted using the patient's own biopsy samples to identify therapies that yield better outcomes and complement a physician's clinical acumen [11,12].

We chose to study combination effects in multiple myeloma (MM), a treatable yet incurable cancer of bone marrow–resident plasma cells, for several reasons. MM provides access to rich patient specimens from bone marrow biopsies. Due to inter– and intra-tumoral heterogeneity in MM, we anticipate that a priori knowledge of drug effects may markedly improve clinical outcomes [11]. Multiagent therapy is the cornerstone of treatment in MM [12]. MM patients often respond well to initial therapy, but eventually relapse, and subsequent lines of therapy are characterized by ever-shortening responses followed by relapses, ultimately leading to multidrug resistance [13], [14], [15], [16], [17]. Recent advances in clinical outcomes for MM patients are derived from the combination of novel agents [18], [19], [20], [21], [22], [23], [24], [25], [26]. The common rationale is that these drugs potentiate each other's effects; however, there are no available tools to estimate clinical synergy (better than additive) or clinical benefit (better than either single agent) of combination therapy in MM or other malignancies. To this end, MM is serves as an ideal cancer to examine novel tools to quantify patient drug combination activity and predict clinical response.

Using tumor cells from MM patients, we developed the Ex vivo Mathematical Malignancy Advisor (EMMA) [11,27,28], a mathematical framework that estimates tumor-specific drug sensitivity from patient-derived primary MM cells in an ex vivo reconstruction of the bone marrow microenvironment. EMMA relies on a drug-agnostic mechanistic model comprised of a dose–effect relationship at the pharmacodynamic level and a cumulative effect–response relationship to estimate the percent tumor burden within a clinically actionable time frame (6 days). However, in its previous form, EMMA lacked the ability to capture combination effects for combination therapies. Instead, it assumed the effect to be additive, as defined by the Bliss independence model [1]. To address this, we developed a synergy-augmented model (SAM), which captures interactions between drugs ex vivo and translates combination effects from fixed ex vivo drug concentrations to clinically relevant time-varying concentrations modeled from pharmacokinetic data. By incorporating SAM into our high-throughput testing of drugs on fresh primary MM cells, we show how this new drug-agnostic synergy-modeling framework could serve as an effective tool in identifying the most viable combination at a given point in each patient's treatment history.

2. Materials and methods

2.1. Ex vivo assay

An ex vivo assay was used to quantify the chemosensitivity of primary MM cells. Fresh bone marrow aspirate cells were enriched for CD138⁺expression using Miltenyi (Bergisch Gladbach, Germany) 130-051-301 antibody-conjugated magnetic beads. MM cells (CD138⁺) were seeded in Corning (Corning, NY) CellBIND 384 well plates with collagen I and previously established human-derived stroma to a total volume of 8 mL, containing approximately 4000 MM cells and 1000 stromal cells. Each well was filled with 80 μL of Roswell Park Memorial Institute (RPMI) 1640 media supplemented with fetal bovine serum (FBS, heat inactivated), penicillin/streptomycin, and patient-derived plasma (10%, freshly obtained from patient's own aspirate, filtered) and left overnight for adhesion of stroma. The next day, drugs were added using a robotic plate handler so that every drug/combination was tested at 5 (fixed concentration ratio, for combinations) concentrations (1:3 serial dilution) in two replicates. Negative controls (supplemented growth media with and without the vehicle control dimethyl sulfoxide [DMSO]) were included, as well as positive controls for each drug (cell line MM1.S at highest drug concentration). A plot of percent viability across time for negative control of Pt415, a 65 year-old female early relapsed/refractory MM patient, is shown in Supplemental Information S11a. A marginal border effect amounting to a 10% increase in cellularity can be noticed in the plot during the first and last 6 h of the experiment. This is an artefact of the image processing algorithm and hence, ex vivo responses of all drugged wells are normalized with primary MM control responses. A grouped bar plot shows a histogram of primary MM cellularity after 24, 48, 72, and 96 h across 203 MM patients is presented in Supplemental Information S11b. The histogram indicates the range of cellularity for majority of patients lies between 100 and 120 percent of initial value, while some specimens show a gradual decay up to 70%, others show a gradual increase up to 160% over 96 h. These indicate that primary MM cells cultured ex vivo using the proposed approach survive for the duration of the experiment. Plates were placed in a motorized stage microscope (EVOS Auto FL, Life Technologies, Carlsbad, CA) equipped with an incubator and maintained at 5% CO₂ and 37 °C. Each well was imaged every 30 min for a total duration of up to 6 days.

2.2. Digital image analysis

A digital image analysis algorithm [27] was implemented to determine changes in viability of each well longitudinally across the 96-hour interval. This algorithm computes differences in sequential images and identifies live cells with continuous membrane deformations resulting from their interaction with the surrounding extracellular matrix. These interactions cease upon cell death. By applying this operation to all 288 images acquired for each well, we quantified non-destructively, and without the need to separate the stroma and myeloma, the effect of drugs as a function of concentration and exposure time.

2.3. Model fitting

There are two mathematical models that were fitted to the ex vivo data: EMMA for single agents and SAM for combinations. Both the models have distinct sets of equations, as described in Fig. 1. MATLAB's lsqcurvefit function from the Optimization toolbox was used to fit the ex vivo tumor burden measurements to these models, and parameters that govern tumor-drug/combination specific behavior were estimated. The optimization algorithm used for minimizing the sum of squares of the error between the model estimates and the actual data is called the trust-region–reflective method [29]. This approach uses a quadratic form to restrict the step size of iterations when the initial guess is too far from the solution. This leads to a more reliable convergence to minima. The single-agent EMMA model involved four submodels that have a longitudinal variation in phenotypic heterogeneity, where the tumor is assumed to be a homogenous population, two homogeneous subpopulations, a normal distribution of subpopulations with varying thresholds to drug sensitivity, or two normal distributions of subpopulations [11]. The convergence of the fitting was progressively improved for more complex models (models with a greater number of parameters) by using the converged solution of the less complex model as an initial guess. For example, the initial guess for one normal distribution of subpopulations could be the converged solution of the homogeneous population parameters with a negligible standard deviation. This allows lsqcurvefit to look for solutions in the neighborhood of the simpler model, thus providing insight into the need for complexity. Similarly, the SAM model has two submodels: monotonic SAM and non-monotonic SAM, where the converged solution of the monotonic SAM is used as the initial guess for the non-monotonic SAM. This approach improved the reliability of the convergence and ensured that the solutions to the more complex models are closer to the simpler ones.

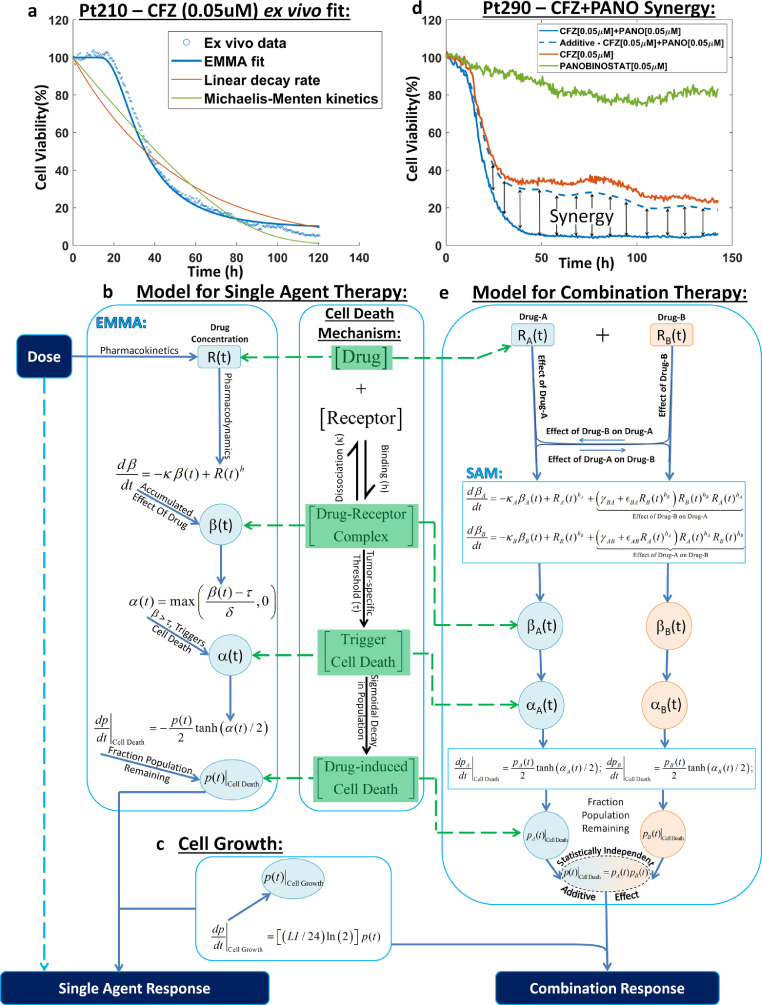
Fig. 1.

Overview of the modelling framework. a, Response to therapy modelled as a second-order function of drug exposure: Pt210's ex vivo response to 0.05 μM of carfilzomib (blue scatter plot) was fit to a second-order sigmoidal function that accounts for tumour drug-specific threshold modelled as a precursor to cell death (EMMA, solid blue line). The EMMA model fit is compared to linear decay rate model (red solid line) and first-order Michaelis-Menten kinetic model (solid green line) to show that it is necessary to account for exposure-driven threshold that traditional models ignore. b, Illustration of the drug-agnostic mechanism of response to single agent therapy: The drug-agnostic mechanism of cell death is based on drug occupancy theory, where the interaction of a drug with a receptor is governed by a reaction-kinetic equation that results in a drug-receptor complex (β), which initiates cell death beyond a clonal-specific threshold (τ) via cell death trigger (α). c, Tumour growth model: A simple doubling time equation is used to estimate tumour growth, where 1% to 3% (LI) of the population is assumed to double every 24 hours. d, Synergy is a dynamic phenomenon: Pt290's ex vivo response to 0.05 μM of carfilzomib (solid red line), 0.05 μM of panobinostat (solid green line), their combination (solid blue line), and the theoretical additive response (dashed blue line) computed from the two single agent response curves assuming Bliss independence are shown. The synergistic effect is measured as the difference in response between theoretical additive and the actual combination. It can be seen that synergistic interaction is a dynamic phenomenon and requires quantification using finely spaced temporal response data. e, Illustration of the two-way pharmacodynamic modelling framework: The path from dose to response for a two-drug combination obeys the same mechanism of cell death as the single agent model but accounts for the two-way combination effect at the pharmacodynamic level by augmenting the reaction-kinetic equations used in computing the drug-receptor complex (β_A and β_B) for single agents with a nonlinear combination effect term (β_BA and β_AB) as shown in the differential equations for β_A and β_B. The combination response is computed from the fraction population remaining estimates for the two drugs as if they were statistically independent. Abbreviations: CFZ, carfilzomib; EMMA, Ex Vivo Mathematical Malignancy Advisor; h/h_A/h_B, stoichiometric coefficient of the pharmacodynamic equation; LI, Labelling Index; M, Molar; Pt, Patient; p/p_A/p_B, predicted tumour burden; R/R_A/R_B, drug concentration; t, time; α/α_A/α_B, cell death trigger; β/β_A/β_B, drug-induced damage; δ, drug-specific factor; ε_AB/ε_BA, combination effect quadratic coefficient; γ_AB/γ_BA, combination effect linear coefficient; κ/κ_A/κ_B, cell dissociation coefficient in the pharmacodynamics equation; τ, tumour-specific threshold.

2.4. Model selection

The single-agent EMMA model has 4 candidate submodels, each quantifying the phenotypic heterogeneity in a different manner. The choice of the best model cannot be purely based on the lowest sum of squares of residual (difference between the actual data and its corresponding model estimates), as noisy data seldom fits more complex models better than the simple ones due to the added degrees of freedom. Hence, we wish to fit data to the model but also avoid fitting through noise at the same time. The statistical model identification tool AIC was used to offset the goodness of fit with the complexity of the model (measured in terms of the number of parameters) [30]. Originally, AIC was developed to suit data obtained from a single experiment, but in the case of choosing between the 2 SAM models, the data comes from 3 different experiments: the 2 single agents’ and the combinations’ ex vivo assays. A modified AIC for a composite experiment was derived from first principles in Supplemental Information S1, where the maximum log-likelihood function that minimizes the variance in the measurement noise was assumed to be for the composite experiment as a whole and not for individual experiments. This assumption facilitates the derivation of a maximum log-likelihood function to be used in the modified AIC that minimizes the variance in the measurement noise for the entire composite experiment. Matlab codes used for model fitting and model selection, along with a user guide can be found here DOI: 10.7303/syn20698242. The ex vivo patient data folders can be found here DOI: 10.7303/syn9758131.

2.5. Statistical analysis

Due to variability in combination effect between patients, it is essential that a high-throughput combination screening tool account for combination effect using statistical means. A volcano plot is employed to graphically depict the extent of combination effect along x-axis and the likelihood of combination effect along y-axis. This presents an overview of the nature of benefit in combining a given pair of drugs. The y-axis for Figs. 3b, d, 5a, and b represent –log₁₀(p-value) of a two-tailed paired t-test between the additive response (LD50, AUC, clinical prediction) and the combination response. The threshold for a significant change in means between the two groups (additive and combination) is chosen to be a p-value greater than 0.05, which corresponds to likelihood greater than 95% for the null hypothesis to be false.

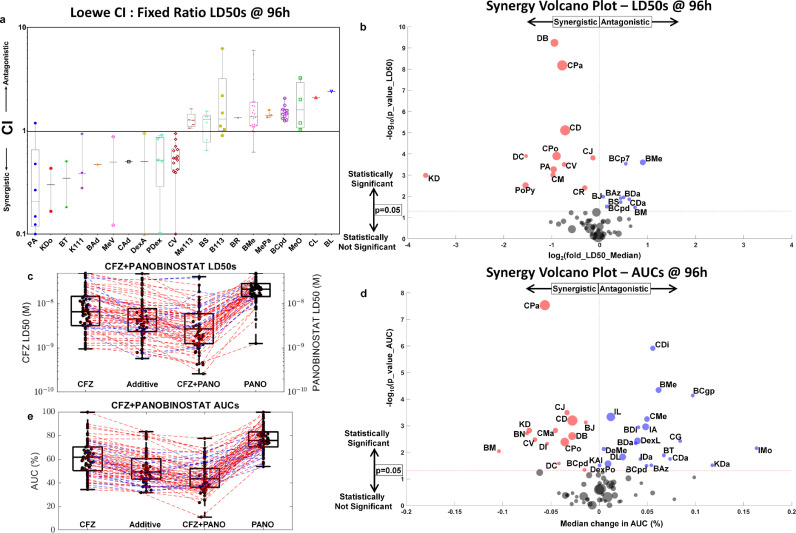
Fig. 3.

High-throughput combination screening based on ex vivo response measurements using CI, and a novel use of volcano plot to show statistical significance in synergy by LD50s and AUCs to demonstrate the relative merits and demerits of each method. a, CIs presented as whisker box plots: CIs are shown as box-and-whisker plots for 20 combinations (the 10 most synergistic and antagonistic by median CI; the rest can be found in Supplemental Information S5, which features 62 combinations) tested ex vivo, where the CI values are computed at LD50, 50% effect (cell kill), at 96 hours, estimated using EMMA and SAM models that capture tumour heterogeneity in a patient-specific manner. b, High-throughput combination screening by LD50: High-throughput combination screenings for 56 combinations were tested using at least 10 patients' specimens each via a volcano plot. Each disc is a two-drug combination with an x-coordinate that represents the log2 fold-change in LD50 at 96 hours for the median patient to signify the extent of combination effect, and the y-axis represents the -log10 p-value (for a two-tailed paired t-test) comparing the computed (from the two single-agent responses) additive responses (BLISS) to the combination responses to signify the statistical significance of the combination effect. Many combinations in A have sparse CI data, despite having ex vivo data from several patients (like BL and CL, which had 76 and 74 patients tested ex vivo), only one patient had a response, where both the single agents reached LD50. The volcano plot is a better approach to screen for synergistic combinations when using patient samples in diseases like MM as the combination response is compared to the additive response, which is computed from the response surfaces of the two single agents. This helps to consider combinations involving drugs that aren't equipotent in the high-throughput screen. c, Carfilzomib and panobinostat synergy by LD50 shown using a box-and-whisker plot: A box-and-whisker plot of LD50s for 60 MM patient samples treated ex vivo with carfilzomib (column 1), panobinostat (column 4), and their combination (column 3) is shown. The combination LD50s are compared to the additive LD50s (column 2) estimated from the additive response surface, which is the pointwise product of fraction population remaining at 96 hours for each of the two drugs. The red dashed lines indicate patients exhibiting synergy ex vivo for the combination, and the blue dashed lines indicate patients showing antagonism ex vivo. d, Carfilzomib and panobinostat synergy by AUC using a box-and-whisker plot: Similar to c, the additive response whisker box plot is compared to the combination response for the same 60 MM patients to estimate the P value for a two-tailed paired t test. e, High-throughput combination screening by AUC: Similar to b, a high-throughput combination screen is presented for 76 combinations, where the P value (of the two-tailed paired t test), estimated by comparing the additive and combination AUCs in d, is plotted along the y-coordinate and the x-coordinate shows the median change in AUC (%) between the additive and combination responses. The number of combinations and the criteria for studying them in a, b, and e is presented in Supplemental Information S9. Abbreviations: B113, bortezomib and 113; BAd, bortezomib and adavosertib; BAz, bortezomib and AZ-628; BCgp, bortezomib and CGP-60474; BCp7, bortezomib and CP-724714; BCpd, bortezomib and CPD22; BDa, bortezomib and dabrafenib; BJ, bortezomib and JNK-IN-8; BL, bortezomib and lenalidomide; BM, bortezomib and MARK-INHIBITOR; BMe, bortezomib and melphalan; BN, bortezomib and NU-7441; BR, bortezomib and R406; BS, bortezomib and silmitasertib; BT, bortezomib and TAI-1; CAd, carfilzomib and adavosertib; CDa, carfilzomib and dabrafenib; CD, carfilzomib and dexamethasone; CDi, carfilzomib and dinaciclib; CG, carfilzomib and GDC-0980; CJ, carfilzomib and JNK-IN-8; CL, carfilzomib and lenalidomide; CM, carfilzomib and MARK-INHIBITOR; CMe, carfilzomib and melphalan; CPa, carfilzomib and panobinostat; CPo, carfilzomib and pomalidomide; CR, carfilzomib and R406; CV, carfilzomib and volasertib; DB, daratumumab and bortezomib; DC, daratumumab and carfilzomib; DI, daratumumab and ixazomib; DL, daratumumab and lenalidomide; DeMe, defactinib and melphalan; DexA, dexamethasone and ABT-199; DexL, dexamethasone and lenalidomide; DexPo, dexamethasone and pomalidomide; IA, ixazomib and ABT-199; IMo, ixazomib and motesanib; K111, selinexor and 111; KAl, selinexor and alisertib; KDa, selinexor and dabrafenib; KDo, selinexor and doxorubicin; Me113, melphalan and 113; MePa, melphalan and panobinostat; MeV, melphalan and VS4718; MeO, melphalan and ONX; PA, panobinostat and ABT-199; PDex, panobinostat and dexamethasone; PoPy, pomalidomide and pyrvinium; LD50, the dose that achieves 50% cell kill; AUC, average area under the dose-response curve over all time points; CI, Loewe's Combination Index; CFZ, carfilzomib; PANO, panobinostat; h, hours; M, molar.

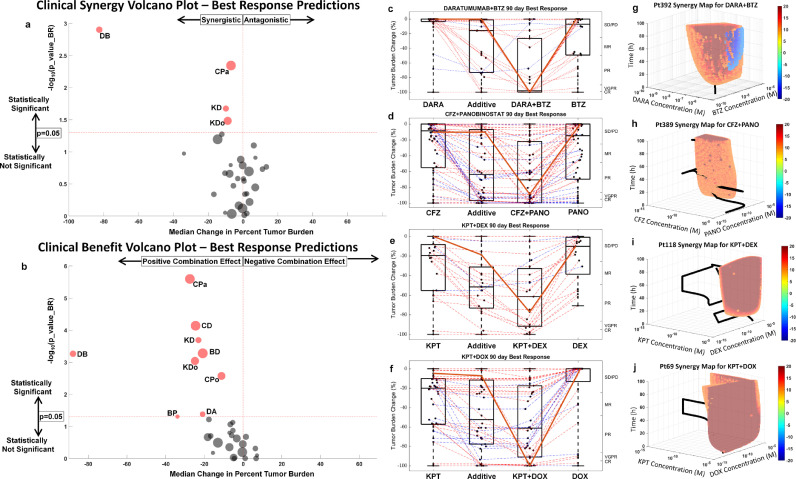
Fig. 5.

High-throughput combination screens of clinically synergistic and clinically beneficial combinations. a, Clinical synergy via volcano plot: A volcano plot featuring 46 two-drug combination best response predictions computed from ex vivo experiments conducted across a cohort of 203 MM patients' specimens to screen for synergistic/antagonistic combinations that pass a two-tailed paired t test between the combination clinical best response predictions and theoretical additive is shown. The theoretical additive response is the pointwise product of fraction cells surviving therapy (viability) for the two drugs as single agents. Further, best response is defined as the lowest percent population surviving therapy for 90 days. In contrast to LD50 and AUC, best response is a prediction of the clinical response from the model parameters (EMMA/SAM) estimated from ex vivo response data coupled with pharmacokinetic data from phase I clinical trials. The drugs that show clinically relevant synergy are shown as red discs. b, Clinical benefit via volcano plot: Similarly, the combination clinical best response was compared to the more viable single agent to obtain the p-values (two-tailed paired t-test) and the median change in percent tumour burden. The more viable single agent response prediction is merely the best response of the drug that achieves greater percent cell kill. c, Daratumumab and bortezomib clinical synergy: The combination daratumumab and bortezomib are shown to be the most synergistic combination both by extent of synergism along the x-axis and by the likelihood of synergism on the y-axis. A whisker box plot is shown comparing the best response clinical predictions over a 90-day treatment period for the two single agents, the theoretical additive response prediction, and the combination. Red lines indicate synergism and blue lines indicate antagonism. The solid red line shows the patient with the most improvement over additive. d, Whisker box plots for carfilzomib and panobinostat; e, Whisker box plot for selinexor and dexamethasone; f, Whisker box plot for selinexor and liposomal doxorubicin. The solid red line in each of C-F is the patient with the most clinically-relevant predicted synergistic effect. g–j, Ex vivo synergy maps: Heat maps are used to show regions of ex vivo synergy/antagonism. Regions of red indicate synergy, blue denote antagonism, and empty spaces represent additivity for the four statistically significant combinations shown in a. The criteria for studying the 46 combinations featured in a and b is presented in Supplemental Information S9. Abbreviations: BD, Bortezomib and Dexamethasone; BP, bortezomib and pomalidomide; CD, carfilzomib and dexamethasone; CPa, carfilzomib and panobinostat; CPo, carfilzomib and pomalidomide; DA, dexamethasone and ABT-199; DB, daratumumab and bortezomib; KD, KPT-330 and dexamethasone; KDo, KPT-330 and doxorubicin; BR, best response; DARA, daratumumab; BTZ, bortezomib; CFZ, carfilzomib; PANO, panobinostat; KPT, selinexor; DEX, dexamethasone; DOX, doxorubicin; h, hours; M, molar.

2.6. Combination matrix (checkerboard assay)

A combination matrix experiment was implemented on a 384-well plate using the approach described above, where CD138⁺ cells are seeded with collagen I and bone marrow stromal cells in media and the patient's plasma. The purpose of this assay was to show that the model predictions made using parameters estimated from fitting fixed concentration ratio ex vivo combination responses at various concentration magnitudes and ratios correlate well with experimental results. This was done by treating each well of the multi-well plate with a two-drug combination, where five serially (1:3) diluted concentrations of each drug were combined in 25 ways, best represented by a 5×5 matrix of concentration duplets. The concentration of one drug progresses from highest to lowest along rows and the second drug's concentration varies across columns, resulting in a constant concentration ratio along the diagonal. The five constant concentration ratio ex vivo responses (along the diagonal) are fit to SAM, and the model predictions at all the off-diagonal concentrations are compared with ex vivo responses.

2.7. Primary cancer cells

We investigated the ex vivo responses of cancer cells from 203 MM patients, demographic data can be found in Supplemental Information S8. Investigators obtained signed informed consent from all patients who were enrolled in the clinical trials MCC14745, MCC14690, and MCC18608 conducted at the H. Lee Moffitt Cancer Center and Research Institute, as approved by the Institutional Review Board. To this end, patient samples were used in accordance with the Declaration of Helsinki, International Ethical Guidelines for Biomedical Research Involving Human Subjects (CIOMS), Belmont Report, and U.S. Common Rule. The medical records were deidentified, and only the following clinically relevant information was reviewed: (A) the treatment administered (therapeutic agents, doses, and schedule) prior to biopsy, (B) cytogenetics, and (C) serum and urine electrophoresis results.

3. Results

3.1. Modeling tumor-specific single-agent sensitivity ex vivo using EMMA

EMMA is a mathematical modeling framework powered by a high-throughput novel ex vivo assay [27], where primary MM cells treated with 31 drugs/combinations are imaged every 30 min for up to 6 days in an ex vivo reconstruction of the tumor microenvironment. At the center of this mathematical framework rests the concept that drug-induced damage drives the rate of cell death when the damage exceeds a tumor-specific threshold [11,27,28]. Fig. 1a depicts drug-induced decrease in cell viability (in percent, normalized by viability at time = 0 hours) for one patient's (patient 210′s) primary MM cells treated ex vivo with 0.05 μM of the proteasome inhibitor carfilzomib for an interval of 120 hours. Linear decay and Michaelis–Menten models can fit the late dynamics of drug-induced cell killing, but, unlike EMMA, they are unable to describe an approximate 30-hour delay between start of treatment and initiation of cell death. This delay is further magnified at lower concentrations, where increasing intervals of drug exposure are required to initiate cell death. This limitation results from a direct functional dependence of cell death rates on drug concentration in these models [31], [32], [33], [34], [35], [36]. EMMA, on the other hand, is a second-order model that requires accumulation of drug-induced damage beyond a certain threshold before the observed cell death can occur.

The dose–effect relationship for a single agent is governed by a reversible reaction kinetic equation (Fig. 1b) where: R(t) is the concentration of the drug at time t; β(t) represents drug-induced accumulated damage, or the "effect" in the dose–effect relationship; κ is the tumor-specific cell damage reduction, or repair rate; and h is an empirical exponent that couples the stoichiometry of drug concentration to the damage effect in the cell. Drug-induced damage (β) accumulates with drug exposure and decreases with cell repair. Cell death only initiates after β crosses a tumor-specific threshold (τ) and proceeds at a rate governed by a sigmoidal function.

3.2. Modeling patient's clinical response to combination therapy assuming additivity

We have previously demonstrated the accuracy and reproducibility of EMMA's clinical predictions in a cohort of 52 MM patients treated with different combination regimens, assuming additivity [11]. In order to simulate the clinical responses of MM patients, we have included a tumor growth model (Fig. 1c), as previously described [11]. Briefly, it is a doubling time equation, where LI is the labeling index, or percentage of replicating cells, assumed to vary between 1% and 3%, and p(t) is the tumor burden at time t, in hours. Intratumoral heterogeneity of sensitivity to single agents was estimated by fitting ex vivo drug sensitivity data to models of increasing complexity, where the entire tumor was described by one or two subpopulations, each subpopulation being either clonal or represented by a normal distribution [11]. Akaike information criterion (AIC) was used to choose the model that best represents the data [11]. Tumor drug–specific parameters of the best-ranked AIC model were coupled with pharmacokinetic data from phase I clinical trials to simulate patient/drug-specific clinical response. EMMA-based clinical predictions of combination regimens assumed additivity. Here, we advance this framework to model the potential combination effect between agents.

3.3. Modeling tumor-specific two-drug combination interactions ex vivo using SAM

Fig. 1d depicts the ex vivo drug response of primary MM cells of a patient (patient 290) to the combination of 0.05 μM carfilzomib and 0.05 μM panobinostat (solid blue line), as well as single-agent responses (carfilzomib in red and panobinostat in green). The "additive" response (dashed blue line) was computed as a pointwise product of the fractional viability of the 2 single agents, as per the Bliss independence model [1], assuming statistical independence between the effects of each drug. In this example, the actual combination of the 2 drugs is more effective in killing MM cells than the predicted additive effect, and thus is considered synergistic. The combination effect, however, is dynamic, varying with exposure time, drug concentrations, and the tumor cells being tested. Thus, similar to the modeling approach employed to estimate tumor-specific parameters governing the single-agent response, we have developed a model for the combination effect accounting for these different variables (Fig. 1e).

Assume a sample is simultaneously treated with 2 drugs: A and B. The EMMA framework was extended to account for the two-way combination effect by incorporating into the pharmacodynamic equation of the first drug (Drug A) a term that represents the effect of the second drug (Drug B) on the first: effect of Drug B on Drug A. Conversely, the same was done for Drug B. The action of Drug A (R_A in Eq. (1)) as a single agent causes the damage β_A in Eq. (1),

$${\beta }_{{}_A}\left(t\right)=\underset{0}{\overset{t}{\int }}exp(-{\kappa }_A(t-\tilde{t}))R_A{\left(\tilde{t}\right)}^{h_A}d\tilde{t},$$ (1)

where κ_A and h_A are estimated from single-agent EMMA model for Drug A. Similarly, Drug B's single-agent damage, β_B, is described by Eq. (2):

$${\beta }_B\left(t\right)=\underset{0}{\overset{t}{\int }}exp(-{\kappa }_B(t-\tilde{t}))R_B{\left(\tilde{t}\right)}^{h_B}d\tilde{t}.$$ (2)

Eqs. (1) and (2) are closed-form solutions of the single-agent pharmacodynamic equation shown in Fig. 1B. When combined, in addition to the effects of the 2 drugs acting alone, there are two combination effects due to the interaction of the 2 drugs. For example, the effect of Drug B on Drug A, β_BA, is described in Eq. (3),

$${\beta }_{BA}\left(t\right)=\underset{0}{\overset{t}{\int }}exp(-{\kappa }_A(t-\tilde{t}))f_{BA}\left(R_A{\left(\tilde{t}\right)}^{h_A},R_B{\left(\tilde{t}\right)}^{h_B};{\lambda }_{BA}\right)d\tilde{t},$$ (3)

where λ_BA represents a parameter set and f_BA is the function that defines the combination effect between Drug A and Drug B such that $f_{BA}({R_A}^{h_A},{R_B}^{h_B})=0,\forall R_A=0,\text{or}{\mathrm{R}}_B=0.$ The simplest mathematical expression that satisfies the above condition is the bilinear function $f_{BA}({R_A}^{h_A},{R_B}^{h_B})={\gamma }_{BA}{R}_A^{h_A}{R}_B^{h_B},$ where γ_BA is an undetermined coefficient to be estimated using the fixed-ratio combination ex vivo sensitivity data. Similarly, the effect of Drug A on Drug B, β_AB, is given by Eq. (4):

$${\beta }_{AB}\left(t\right)=\underset{0}{\overset{t}{\int }}exp(-{\kappa }_B(t-\tilde{t}))f_{AB}\left(R_A{\left(\tilde{t}\right)}^{h_A},R_B{\left(\tilde{t}\right)}^{h_B};{\lambda }_{AB}\right)d\tilde{t}.$$ (4)

Thus, damage caused by R_A in the presence of R_B is β_Α/_Α+Β = β_A+ β_BA and damage caused by R_B in the presence of R_A is β_Β/_Α+Β = β_B+ β_AB. Estimated from the single-agent models and fixed-ratio ex vivo combination, damages β_Α/_Α+Β and β_Β/_Α+Β accumulate over time, and cell death initiates when either exceeds the tumor-specific thresholds τ_A or τ_B, respectively. The accumulated damages β_A and β_B result in changes in the viability, given by dp_A(t)/dt and dp_B(t)/dt, respectively. Viability of the two-drug combination, p(t), is given by the product between p_A(t) and p_B(t), assuming statistical independence, since the interaction between R_A and R_B was already accounted for by β_BA and β_AB. This modeling framework, capturing the two-way combination effect from patient-specific ex vivo response measurements, is SAM.

This first version of SAM assumes monotonicity of the combination effects between the 2 drugs. However, combination studies often show that a non-monotonic relationship may exist where particular concentrations, or “sweet spots,” of either or both drugs yields the maximum combination effect. In order to allow the model to account for such an effect, a second-order polynomial was chosen to describe the functional dependence between the combination effect (f_BA) and the concentration of the aiding drug (R_B) which required additional parameters (ε_BA) for each of the 2 drugs (Eq. (5)). In every two-drug combination in this work, we have calculated both monotonic and non-monotonic SAM models and applied a modified AIC (derivation in Supplemental Information S1) to choose the simplest model for a composite experiment that best fits the data over noise (additive model, monotonic, or non-monotonic SAM).

$$f_{ji}(R_i^{h_i},R_j^{h_j})=R_i^{h_i}\left({\gamma }_{ji}+{\epsilon }_{ji}{R}_j^{h_j}\right)R_j^{h_j},\forall \left(i,j\right)=\left\{\left(A,B\right),\left(B,A\right)\right\}$$ (5)

3.4. Validation of SAM ex vivo

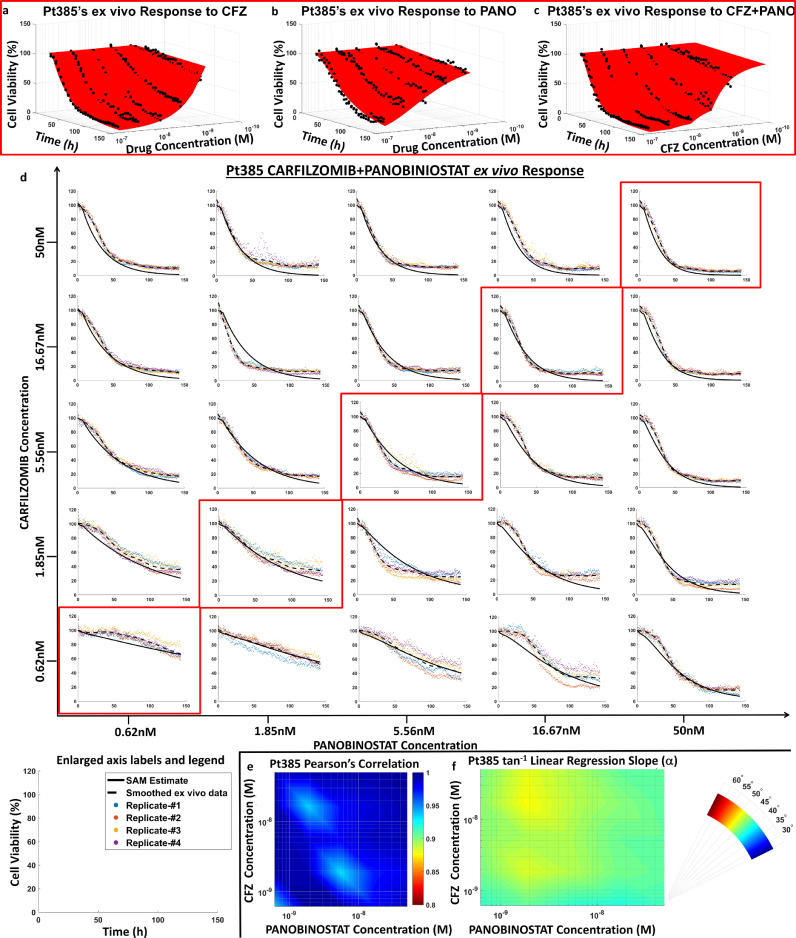
We have tested whether SAM could be parameterized exclusively by single-agent EMMA parameters and fixed-ratio combination ex vivo data by comparing SAM's model predictions with ex vivo results from an actual drug combination matrix (checkerboard assay). In every experiment, each drug was tested in 5 different concentrations following a 1:3 dilution, in duplicates, except for the combination matrix, where quadruplicates were used. Figs. 2a–c depict the ex vivo response of primary MM cells (derived from patient 385) to single-agent carfilzomib and panobinostat, as well as to the combination of both drugs at a fixed concentration-ratio (1:1), respectively. The results from the combination matrix are presented in Fig. 2d, where the plots highlighted in red are the fixed-ratio concentrations used for estimating SAM parameters. Each plot in Fig. 2d depicts the data points for measured cell viability (colored dots for different replicates), a smoothed (locally weighted scatter plot smoothing [LOWESS] algorithm) curve of the ex vivo cell viability data (dashed black line), and the SAM model prediction (solid line).

Fig. 2.

Ex vivo validation of synergy augmented model (SAM). a-c, EMMA and SAM model parameters estimated from single agent and fixed concentration-ratio combination ex vivo response data: Pt385's ex vivo responses to carfilzomib (maximum concentration 0.05 μM) and panobinostat (maximum concentration 0.05 μM) as single agents is fit using EMMA as shown in a and b to estimate parameters that quantify the extent of response and tumour drug-specific heterogeneity. These parameters are used in conjunction with the combination response data (scatter plot) shown in C to estimate parameters that define the combination effect term in SAM. d, Chequered board assay response: A two-dimensional chequered board combination experiment is conducted to use the fixed concentration-ratio data to estimate SAM parameters and compare ex vivo model predictions with experimental results. Five three-fold serially diluted concentrations of each drug are combined yielding a 5×5 matrix of ex vivo combination response data with 4 replicates (shown as coloured scatter plots) for each two-drug concentration duplet. The mean response of the four replicates is smoothed using LOWESS to estimate the smoothed ex vivo response data (black dashed line). The solid lines in the plots signify SAM model predictions. Enlarged axes labels and a legend are provided for each of the subplots in the chequered board assay. e, SAM Validation - Pearson's correlation coefficients: Pearson's correlation coefficients (r) for each of the 25 two-drug concentration duplets are plotted on a log-log heat map, where the x and y axes show panobinostat and carfilzomib concentration, respectively, on log scales, and the colour represents the r value. The model correlates very well with the data, with r values ranging from 0.93 to 1. f, SAM Validation – Linear Regression: Similarly, a log-log heat map of the arc tangent of linear regression slope (α) for the 25 concentration duplets is shown to range from 45° to 50°, which implies that the model predictions agree very well with the ex vivo experimental combination response data. Abbreviations: CFZ, carfilzomib; h, hours; LOWESS, Locally Weighted Scatter Plot Smoothing; M, molar; PANO, panobinostat; Pt, patient; SAM, Synergy Augmented Model.

Fig. 2e depicts Pearson's correlation coefficient (r) between SAM's model predictions and smoothed ex vivo response for each of the 25 two-drug combination concentration pairs, showing high linear correlation between model predictions and experimental measurements (r  >  0.93). Similarly, Fig. 2f shows the angle of the slope (α) of the linear regression, ranging between 45° (green) and 50° (yellow), where an α value of 45° and r = 1 represent a perfect linear correlation. Additional comparisons with a second sample (patient 390) and 2 other pairs of drugs (carfilzomib/dexamethasone and carfilzomib/panobinostat) are provided as Supplemental Information S2-S4.

3.5. SAM as a tool to study combination effect of drugs in primary samples ex vivo

We calculated the Loewe Combination Index (CI) of 130 drug combinations tested with primary MM samples in EMMA, according to Chou–Talalay's method [37] using the median lethal dose (LD50, defined as the drug concentration that reduces cell viability to 50% of initial measurement) and 96-hour time point as metrics. By definition, this method requires that both drugs reach the cell-kill effect (LD50) at the time point of CI calculation (96 h), which reduced the number of drug combinations with CI down to 62. Fig. 3a depicts the 10 drug combinations with the lowest (most synergistic) and highest (most antagonistic) values of median CI (the entire set is available in Supplemental Information S5). The wide range of ex vivo cell-kill effects of MM-relevant classes of drugs significantly limited the application of this method; while proteasome inhibitors (e.g., bortezomib) or chemotherapeutic agents (e.g., melphalan) can induce LD50 in less than 48 h; immunomodulators (e.g., pomalidomide), steroids (e.g., dexamethasone), or immunologics (e.g., daratumumab) required over 96 h to reduce cell viability to 30% of initial measurements, even at maximum solubility levels. In addition, because of inherent interpatient tumor heterogeneity, the calculation of the combination effect between 2 drugs should be performed using group statistics in a cohort of samples.

Fig. 3b depicts a novel combination effect analysis to address these limitations. In this volcano plot, the horizontal axis represents the log₂ fold-change in median LD50 between the actual ex vivo two-drug combination, and the theoretically computed additive response, which was calculated assuming statistical independence between the cell-kill effects of both drugs: the single-agent ex vivo dose–time–response surfaces of each drug in the combination (e.g., Fig. 2a–b) were multiplied pointwise to generate the theoretical additive response curve, from which LD50 was computed at 96 h. The vertical axis represents the –log₁₀ P value for a two-tailed paired t-test conducted between the theoretical additive and the actual LD50-at-96-hours values for all samples tested with the combination. Fig. 3c exemplifies this test for the combination of carfilzomib and panobinostat, a combination that is consistently synergistic, as evidenced by the overwhelming number of samples where the LD50 of the combination was lower than predicted by additivity. Thus, to use this approach, it is sufficient that the actual ex vivo combination, and theoretical additive combination, reached LD50, instead of both single agents. In addition, Fig. 3b provides a statistical measurement of magnitude and heterogeneity of the combination effect in the group of samples.

We have further extended this combination effect analysis by introducing a second measure of ex vivo drug resistance: the average area under the curve (AUC) of the 5 concentrations from the beginning of the experiment until the final time point (e.g., 96 h). The benefit of this second metric is that it is not bound to an arbitrary minimum cell-kill effect, thus allowing direct comparisons among drugs and combinations with significantly different cell-kill dynamics. Fig. 3d–e reflects the same analyses as Fig. 3b–c, except that they compare the actual versus theoretical additive values of the AUC.

Importantly, the most synergistic ex vivo combinations identified by this approach are part of clinical combination regimens in MM: carfilzomib/panobinostat; daratumumab/bortezomib; carfilzomib/dexamethasone; carfilzomib/pomalidomide; and selinexor/dexamethasone, recently approved to treat refractory MM [38].

3.6. Estimation of clinical synergy

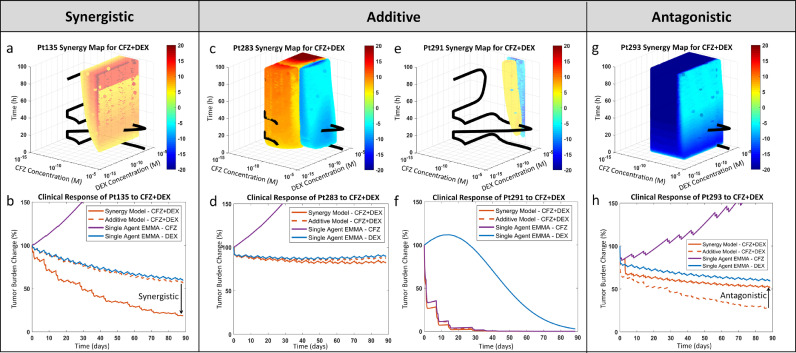
Summary metrics such as LD50 and AUC, while useful for preclinical studies, are unable to account for the complex pharmacokinetic/pharmacodynamic interactions of actual clinical regimens. Since the magnitude of drug combination effects vary with exposure time and drug concentrations, it is imperative to use models that can analyze combination effects in clinically relevant concentrations while also accounting for drug-specific pharmacokinetics. To this effect, we have parameterized patient-specific SAM models with drug-specific phase I pharmacokinetic data to estimate magnitude and interpatient heterogeneity of the clinical combination effects of drug regimens in MM. Fig. 4 contains 4 synergy maps, which define regions of synergy and antagonism of 2 drugs (carfilzomib/dexamethasone) as a function of drug concentrations and exposure time in primary MM samples ex vivo. Fig. 4a presents the synergy map for one MM patient's (patient 135s) primary cell ex vivo response to carfilzomib and dexamethasone, where red-yellow (hot) regions denote synergy and blue-cyan (cold) represent antagonism. The combination effects for each point in the 3D space were calculated as the difference between the viability of the actual ex vivo combination, as predicted by SAM, and the theoretical additive viability, computed as previously described (Fig. 3). Also part of the synergy map is a pharmacokinetic trajectory (black ribbon), representing the varying concentrations of both drugs during the first 96 h of the combination regimen. Fig. 4b represents the simulation of treatment of the same patient (patient 135) with either of the single agents, as well as the theoretical additive combination and the clinical prediction, based on SAM data. In this simulation, the patient would be resistant to carfilzomib but sensitive to dexamethasone, reaching approximately 50% tumor reduction after 3 months of treatment, based on the additive model. However, when the combination effect is considered, the predicted clinical response is 75% tumor burden reduction, and thus clinically synergistic.

Fig. 4.

Interpatient heterogeneity in combination effect and clinical relevance of synergy. a, Synergy map for Pt135's response to carfilzomib and dexamethasone: The theoretical additive response is estimated from the single agents' models (EMMA) and subtracted from the combination model (SAM) estimated ex vivo response for the first 96 hours over a wide range of concentrations/concentration ratios. The difference is presented as a heat map, where a benefit over additive (synergy) is indicated as ‘hot’ (yellow-red) and a loss in percent viability is marked as ‘cold’ (cyan-blue). The synergy map also features the pharmacokinetic curve of the standard of care therapeutic regimen for this combination. The relative residence period of the pharmacokinetic curve in the hot/cold regions qualitatively shows the extent of clinically relevant synergistic/antagonistic effect. b, Pt135's predicted clinical response to carfilzomib and dexamethasone: The two single agent clinical response simulations (via EMMA), along with additive and combination response simulations (via SAM), are shown. The residence of the pharmacokinetic curve in the synergistic region is reflected in the clinical prediction. This analysis is repeated in c and d for Pt283, e and f for Pt291, and g and h for Pt293. These four patients were classified as early relapse/refractory at the time of their biopsy. In spite of their similar classification, the synergy maps and the clinical response simulations show significant variation. Abbreviations: CFZ, carfilzomib; DEX, dexamethasone; Pt, patient; h, hours; M, molar.

In this particular patient/drug combination, the pharmacokinetic trajectory of treatment was confined to synergistic or additive regions (Fig. 4a), which explains the clinical synergy of the model predictions. However, when the pharmacokinetic trajectory crosses regions of both synergy and antagonism (Fig. 4c) or mainly additivity (Fig. 4e), the resulting clinical effect is additive (Fig. 4d and f), and incidentally, when the pharmacokinetic trajectory is located in regions of antagonism (Fig. 4g), the predicted clinical outcome is antagonistic (Fig. 4h).

3.7. SAM as a tool to estimate the clinical combination effect and clinical benefit of drug combinations

Patient-specific SAM parameters, estimated by fitting ex vivo drug/combination sensitivity data for 203 patients, were coupled with pharmacokinetic data from phase I clinical trials to estimate the combination effect and clinical benefit of 46 (out of 130) two-drug combinations (Fig. 5), which have publically available pharmacokinetic data. In this context, the combination effect is considered synergistic if the minimum tumor burden, as estimated by SAM, is lower than the theoretical additive (as described in Fig. 4) and is considered antagonistic if the opposite is true. Clinical benefit was defined as the improvement in clinical response of the SAM-estimated combination compared to the clinical response of the best single agent.

Fig. 5a's volcano plot depicts the clinical drug combination effect, showing on the vertical axis the –log₁₀ (P value) from the two-tailed paired t-test between theoretical additive and SAM-estimated best response predictions, the horizontal axis represents the median percent tumor burden change between theoretical additive and SAM-estimated combination. among the 46 combinations tested, 4 were classified as clinically synergistic: daratumumab/bortezomib, carfilzomib/panobinostat, selinexor/dexamethasone, and selinexor/doxorubicin. Figs. 5c–f represent these 4 combinations, where the first and fourth columns show simulated best responses for each single agent, the second column represents theoretical additive best response, and the third column represents the SAM-calculated best response of the combination. The best response for a therapeutic option is defined as the lowest tumor burden observed over a treatment period (90 days). The left vertical axis represents the tumor burden reduction from the start of treatment (with 0% corresponding to no response and 100% corresponding to total tumor eradication). The right vertical axis represents tumor burden reduction according to International Myeloma Working Group's classification of the depth of response [39]. The values of the 4 columns corresponding to each patient are linked by a dashed line, lines for patients with synergistic combinations are red and antagonistic combinations are blue. The solid red lines in Fig. 5c–f highlight the most synergistic patient within each drug combination. The synergy maps for each of these patients are shown in Fig. 5g–j and confirm that the pharmacokinetic trajectories of these drug combinations are confined to regions of synergy in all 4 patients. Conversely, Supplemental Information S6 highlights in solid blue lines the most antagonistic patient responses for each of the 4 drug combinations, and their corresponding synergy maps confirm that the pharmacokinetic trajectories are confined by regions of antagonism.

Clinical trials, however, do not assess combination effect, but clinical benefits [40]. For example, phase III trials quantify the clinical benefit of a new agent by treating patients in one arm with the standard of care therapy, while patients in the experimental arm are treated with a combination of the standard of care and the new agent. A trial is considered successful if, in addition to meeting safety and toxicity standards, the experimental arm patients have a better outcome than the standard of care arm. Fig. 5b reflects this concept in a volcano plot where SAM-predicted combination clinical responses are compared to the predicted responses of the more efficacious of the 2 single agents. Similar to Fig. 5a, in Fig. 5b a two-tailed paired t-test was used to compute the P value (vertical axis) and the difference in the medians (horizontal axis) for each drug pair. In addition to the 4 clinically synergistic drug combinations identified in Fig. 5a, five new ones were predicted to perform better than either single agent did independently: carfilzomib/dexamethasone, bortezomib/dexamethasone, carfilzomib/pomalidomide, bortezomib/pomalidomide, and dexamethasone/venetoclax.

4. Discussion

Multidrug combination therapies have been instrumental in improving patient outcomes in the treatment of MM. However, inter– and intra-patient heterogeneity of tumor sensitivity to single agents leads to variability in the combination effects of therapy. We have previously described a high-throughput assay designed to test the chemosensitivity of primary MM cells cultured in an ex vivo reconstruction of the bone marrow microenvironment, and, ultimately, to predict clinical response to therapies. This model (EMMA), however, relies solely on additive effects of individual agents [11]. Here, we have successfully extended this platform. Using fixed-ratio ex vivo two-drug combination response data with a high sampling rate, we fit a novel pharmacodynamic model (SAM) capable of capturing the two-way synergistic effect found in two-drug combinations. This improvement further increases the original model's ability to estimate clinical response by accounting for the potential synergistic effects of combination regimens.

As a preliminary validation of SAM's ability to estimate combination effect, a checkerboard assay was used to measure the ex vivo response of two primary samples to 3 pairs of drug combinations in a 5×5 concentration combination matrix. We have shown that, when parameterized with the single agent and fixed-ratio combination, SAM accurately estimates ex vivo drug response to other drug concentration combinations, confirming that this reduced dataset is sufficient to parameterize this combination effect model.

We have computed the CI for a comprehensive panel of two-drug combinations tested in a cohort of primary MM samples, and we have described how SAM can extend this well-established model of synergy to classes of drugs with significant differences in potency as well as account for intertumor heterogeneity. In this process, we have identified a list of ex vivo synergistic drugs, including a number of combinations that are currently approved for MM therapy.

In order to investigate synergy in clinical regimens, we have used patient-specific SAM models to simulate clinical response to combination regimens by parameterizing these models with clinical pharmacokinetic data. Using a graphical representation of combination effect as a function of drug concentrations and exposure time, we have demonstrated how the pharmacokinetic trajectory of drug concentrations crosses regions of synergy and antagonism during a cycle of a regimen, defining if the clinical response will be synergistic or antagonistic.

An analysis of 46 drug pairs with pharmacokinetic data from clinical trials revealed 4 clinically synergistic combinations: daratumumab/bortezomib, carfilzomib/panobinostat, selinexor/dexamethasone, and selinexor/doxorubicin. This is consistent with a recent study [5] that compared Kaplan–Meier curves from various phase II and phase III clinical trials in melanoma, ovarian, colorectal, pancreatic, and breast cancer patients treated with targeted therapies, immunotherapies, chemotherapies, etc., as single agents and combinations. The study revealed that the benefit of combinations over monotherapy is primarily due to independent drug action, reiterating that synergism observed preclinically did not necessarily translate in to the clinic for most of the combinations. The authors showcased a study in PDX (patient-derived xenograft) patients, where testing 33 combinations across 6 tumor types revealed only four synergistic combinations [5].

Next, we simulated phase II/III clinical trials by assessing clinical benefit of a combination of 2 drugs over the best response of the more efficacious drug, identifying 5 additional combinations. These results were consistent with recent clinical studies in relapsed and refractory MM: the combination of daratumumab/bortezomib/dexamethasone was shown to be superior to the combination of bortezomib/dexamethasone in a phase III two-arm clinical trial [41]. The efficacy of carfilzomib/panobinostat was studied in a phase I/II clinical trial setting and shown to be beneficial for relapsed/refractory MM patients [42]. The combination of selinexor/dexamethasone has recently shown encouraging activity in a phase II trial involving highly refractory MM patients, leading to its FDA approval [43]. Further, adding liposomal doxorubicin to the combination of selinexor/dexamethasone for relapsed and refractory MM patients is being currently studied as a phase I trial [44]. Thus, the 4 combinations predicted to be clinically synergistic (Fig. 5a) have been shown to be at least clinically beneficial in clinical trials. In addition to these, the 5 other combinations identified as clinically beneficial have shown improved efficacy in multiagent clinical trials—carfilzomib/dexamethasone [45], bortezomib/dexamethasone [46], carfilzomib/pomalidomide [47], bortezomib/pomalidomide [48], and dexamethasone/venetoclax [49]. We expect that these data will represent critical steps toward the clinical translation of the proposed modeling framework.

Of note, our results also suggest that, at least in this cohort, a number of drug pairs do not have synergistic activity (or even clinical benefit) across the majority of sample tested, but may be synergistic, or at least clinically beneficial, on a patient-by-patient bases. These observations further highlight the importance of accounting for interpatient heterogeneity and the need for personalized tools to improve clinical decisions as depicted in Fig. 5a, where a bird's-eye-view of 46 drug combinations can be 'zoomed into' single-drug pairs (Fig. 5c), and, finally, into specific pharmacokinetic/pharmacodynamic interactions in individual patient samples (Fig. 5g).

Combination therapy in MM typically involves combining two, three, or more drugs to maximize efficacy and time to relapse. The conclusions made from studying two-drug combinations can be extended to three-drug (or more) combinations by assuming that higher-order synergistic effects are negligible as shown in the literature [50,51]. The approach used to compute three-drug combination response from two-drug responses is described in Supplemental Information S7. The three-drug ex vivo combination response computed using this approach can be used to estimate AUC, as well as synergy, for any three-drug combination therapy received by a patient in the clinic. Supplemental Information S12 depicts how these ex vivo measurements could be used to predict patients’ clinical response. Using Receiver Operating Characteristic (ROC) curves, we show that ex vivo combination AUC serves as an excellent classifier of patients’ clinical response between IMWG response stratifications of CR/VGPR (complete response/very good partial response), and partial response (PR) or worse with an area under the ROC curve of 0.9804 and a p-value of 0.0006 (for a t-test with the null hypothesis that the area under ROC is 0.5), while ex vivo synergy (ΔAUC Synergy), was the better classifier between PR/MR (minimal response/partial response) and SD/PD (stable disease/progressive disease) patients, with an area under the ROC curve of 0.8167 and a statistically significant p-value of 0.0452 (for a t-test with the null hypothesis that the area under ROC is 0.5). Furthermore, the proposed modeling framework could potentially be used to modulate doses and schedules (within clinically viable limits) to maximize clinical synergy, and identify regimens that would lead to significant improvement over the standard of care dosing for each patient.