Predicting Inpatient Length of Stay After Brain Tumor Surgery: Developing Machine Learning Ensembles to Improve Predictive Performance

Abstract

BACKGROUND

Current outcomes prediction tools are largely based on and limited by regression methods. Utilization of machine learning (ML) methods that can handle multiple diverse inputs could strengthen predictive abilities and improve patient outcomes. Inpatient length of stay (LOS) is one such outcome that serves as a surrogate for patient disease severity and resource utilization.

OBJECTIVE

To develop a novel method to systematically rank, select, and combine ML algorithms to build a model that predicts LOS following craniotomy for brain tumor.

METHODS

A training dataset of 41 222 patients who underwent craniotomy for brain tumor was created from the National Inpatient Sample. Twenty-nine ML algorithms were trained on 26 preoperative variables to predict LOS. Trained algorithms were ranked by calculating the root mean square logarithmic error (RMSLE) and top performing algorithms combined to form an ensemble. The ensemble was externally validated using a dataset of 4592 patients from the National Surgical Quality Improvement Program. Additional analyses identified variables that most strongly influence the ensemble model predictions.

RESULTS

The ensemble model predicted LOS with RMSLE of .555 (95% confidence interval, .553-.557) on internal validation and .631 on external validation. Nonelective surgery, preoperative pneumonia, sodium abnormality, or weight loss, and non-White race were the strongest predictors of increased LOS.

CONCLUSION

An ML ensemble model predicts LOS with good performance on internal and external validation, and yields clinical insights that may potentially improve patient outcomes. This systematic ML method can be applied to a broad range of clinical problems to improve patient care.

ABBREVIATIONS

CI

confidence intervals

LOS

length of stay

ML

machine learning

NIS

National Inpatient Sample

NSQIP

National Surgical Quality Improvement Program

RMSLE

root mean square logarithmic error

Machine learning (ML) is a powerful analytic tool that uses computer algorithms to recognize patterns in data that are not explicitly programmed.¹ Historically, regression-based algorithms have dominated predictive modeling in medicine.² These algorithms assume certain relationships between variable coefficients and outcomes and that variables function independently to influence outcomes. Given the complexity of human disease, these assumptions may not hold. Increasing emphasis is being placed on the potential of nonregression ML algorithms to improve outcomes research.^3-4 Many of these algorithms can handle and combine vast numbers of variables in complex and nonlinear ways to generate sophisticated predictions.⁴ Predictive models based on these techniques may therefore help providers identify clinically significant risk in patients whose constellation of risk factors may otherwise have been missed, or identify novel and unexpected predictors of risk.^5-7 Although used extensively in medical imaging and genomics, the use of nonregression ML algorithms to model clinical outcomes is less well-established.^8-12

Nonregression ML has been used in clinical medicine, including predicting survival in glioma patients following surgery using support vector machines¹³ and diagnosing diabetic retinopathy from retinal fundus photographs using neural networks.¹⁴ A variety of ML techniques have been described. Often a particular ML algorithm is selected a priori and thus may not necessarily arrive at the optimal solution. Although certain ML algorithms have theoretical advantages over others, the only way to know with certainty which algorithm will produce the best predictions is by direct comparison of the predictive power of different algorithms.

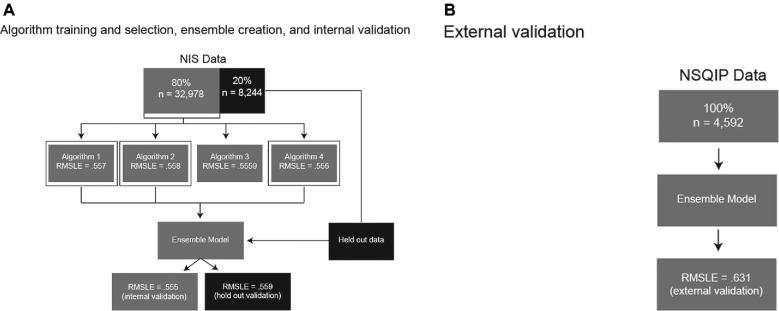
Here, we propose a unique technique for predicting patient outcomes that leverages the power of many types of ML: to guide algorithm selection, we evaluate and rank the predictive abilities of a broad range of ML algorithms before combining the best performers into an ensemble, allowing us to take advantage of the complementary strengths of multiple algorithms.¹⁵ In this proof-of-concept study, we build and internally validate a guided ML ensemble to predict length of stay (LOS)in hospital of patients following craniotomy for brain tumor from preoperative patient variables recorded in the National Inpatient Sample (NIS). We then externally validate the ensemble using the American College of Surgeons National Surgical Quality Improvement Program (NSQIP) database. Finally, we use permutation importance analyses and partial dependence plots to understand the independent impact of variables that the ensemble deems important in order to glean clinical insights (Figure 1).

FIGURE 1.

Methods overview. A, Description of algorithm training and validation (using RMSLE as validation metric), selection of the top three performing algorithms (the three algorithms with validation RMSLE closest to 0), combination of these algorithms into a separate, ensemble model, and internal and holdout validation. B, External validation of the ensemble model using an entirely separate database derived from the NSQIP. RMSLE, root mean square logarithmic error; NIS, National Inpatient Sample; NSQIP, National Surgical Quality Improvement Project.

We chose to model LOS in part because it has been identified as a primary driver of increasing cost for craniotomy for brain tumor.¹⁶ Accurate modeling of this outcome can help providers identify risk factors for, and potentially cut down on, unnecessary hospital days after craniotomy for brain tumor, decreasing waste and potentially improving care for these patients.

METHODS

Training Database

We used the NIS database from 2002 to 2011 to train and internally validate the ensemble. The NIS is the largest publicly available all-payer inpatient database in the United States, representing roughly 8 million hospital stays from ∼1000 hospitals. The database is built to approximate a 20% stratified sample of nonfederal US hospitals (The Agency for Healthcare Research and Quality, Rockville, Maryland).¹⁷

External Validation Database

For external validation, we used data from the NSQIP from 2012 to 2013. The NSQIP, which is administered by the American College of Surgeons, is a multi-institutional program that prospectively collects data on randomly selected surgical patients from over 400 academic and private hospitals across the United States.¹⁸ We selected years outside of the range included in the training database to ensure no overlap between the training and validation databases.

Both the NIS and NSQIP are publicly available, deidentified databases, and were considered exempt from Institutional Review Board review.

Patient Selection

We screened each of 79 742 743 admissions registered in the NIS from 2002 to 2011 for inclusion in the training dataset, and each of 1195 375 admissions registered in the NSQIP between 2012 and 2013 for inclusion in the external validation dataset. Eligible admissions were identified by International Classification of Diseases (ICD)9 diagnosis codes for brain tumor (225.0-225.4, 225.8, 225.9, 199.1, and 191.0-191.9) and ICD9 procedure codes matching craniotomy in the NIS dataset (01.20-01.29, 01.31, 01.32, 01.39, and 01.59), or Current Procedural Terminology (CPT) codes for craniotomy in the NSQIP dataset (61 510, 61 512, 61 518-61 521, 61 526, and61 530). Only patients 18 yr or older were included. In total, 41 222 admissions met criteria for inclusion in the training dataset, and 4592 admissions met criteria for inclusion in the external validation dataset.

Variable Selection and Primary Outcomes

A variety of preoperative patient characteristics were collected that are available in both the NIS training and the NSQIP validation datasets, including age, race, sex, specific neurosurgical diagnosis, preoperative comorbidities, admission quarter (within the year of hospitalization), and emergent vs nonemergent surgery. In total, 26 different variables were considered (see Table, Supplemental Digital Content 1 for listed variables).

Data Preprocessing

Missing numerical data were imputed using the median value for the given variable, and a new binary variable created to denote the imputation.^19,20 Some algorithms (decision tree-based models in particular) are well suited to detect and leverage variable interactions in ways that linear models are not, while at the same time being unable to function (algorithmically) in the presence of missing data. Using this approach to handling missing data allows the greatest number of algorithms to train while still permitting those that can leverage imputation to do so.

Each column of numeric data was standardized by subtracting the mean value of the column and then dividing by its standard deviation. For linear algorithms, one-hot encoding was used to transform categorical data into multiple binary columns. Missing categorical values were treated as their own category and got their own column. For tree-based algorithms, categorical data was encoded using randomly assigned integers.

Algorithm Selection and Ensemble Validation

Prior to training, 20% of the training dataset was randomly selected as the holdout and excluded from training.^19,20 The remaining data was divided into 5 mutually exclusive folds, For each of 29 algorithms training was performed 5 times, with each fold used once for validation and the remaining 4 used together as training.²¹ In choosing a 5-fold (as opposed to a higher fold) validation, we made a tradeoff between algorithm training run time and additional estimates of ensemble generalizability on cross-validation. To offset this tradeoff, we evaluated the final model against an entirely separate database, the NSQIP, which is the ultimate measure of the ensemble's ability to generalize to new data.

Model hyperparameters were optimized within each fold by creating an additional sub-fold training/validation split. Each combination of hyperparameters was tested within this sub-fold training/validation setup to determine optimal hyperparameters. The algorithm was then retrained using these hyperparameters.

We calculated cross-validation scores by taking the root mean square logarithmic error (RMSLE) of the 5 possible validation folds (the closer to 0 the RMSLE value, the more accurate the model, with a RMSLE = 0 denoting zero error). We chose RMSLE as our validation metric because it penalizes large error less when both predicted and actual LOS are very large than when predicted and actual LOS are small. RMSLE can be interpreted as the standard deviation of the log of unexplained variance (eg, error). A less-than-technical treatment would be: “the model's prediction is usually within e to the power of the calculated RMSE times the true value.” The algorithms with the highest cross-validation scores were identified and combined with an elastic net to form an ensemble.

The ensemble model was trained and cross-validated in the same manner as the individual algorithms. As additional internal validation, the RMSLE was calculated for predictions made on the never-before-seen holdout dataset. Following internal validation, the ensemble was trained on 100% of the NIS database. The fully trained model was then externally validated with the NSQIP database (Figure 1). The NIS holdout and the NSQIP dataset were taken to be one sample of data with a single RMSLE and so no confidence intervals (CI) were calculated. ML software from DataRobot, Inc was used for model training and validation (DataRobot ver 3.0, Boston, Massachusetts).

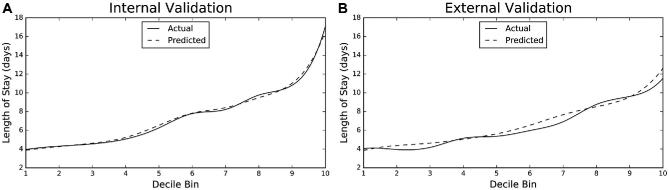
We generated lift charts in order to visualize how accurately each ensemble model predicts LOS. To generate these charts, we ranked and divided the ensemble predictions into 10 “bins” and calculated the average predicted LOS for each bin. We then calculated the average actual LOS for each decile and plotted the average predicted values against the average actual values.

Permutation Importance

We used permutation importance to compute the relative importance of a variable to the final ensemble.^19,20,22 The ensemble was retrained on a version of the data in which all values for the variable in question are randomly permuted, which removes any predictive value of the variable while maintaining its distribution. We then compared the difference in RMSLE between the original model and the model built with the permuted variable. By calculating the change in model performance for each permuted variable, we can rank the relative importance of each variable to the model, with more important variables yielding greater losses in model performance.

Partial Dependence

Partial dependence plots allow one to visualize how a model reacts to changes in a single variable.^19,20,23 To generate these plots, a random subset of the training data is selected. For each variable, all the values for the variable are replaced with one of many constant test values. Predictions are made using the test values and the mean value of the predictions calculated. The mean prediction is plotted over the test values to generate a visual representation of the model's response to changes in the variable. For categorical variables, we tested each value seen in the training data. For numerical values, we tested values over regularly spaced intervals between the maximum and the minimum observed value.

Other Statistical Methods

Additional statistical analysis was performed to describe selected patient and hospital characteristics. We compared continuous variables using the Mann–Whitney U test and categorical variables using Pearson's χ² test. All analyses were performed with open source tools available from SciPy (SciPy ver 0.17, http://www.scipy.org/).

RESULTS

Patient Characteristics

A total of 41 222 admissions for craniotomy for brain tumor were reviewed for analysis. Average LOS was 7.8 d (standard deviation = 8.7 d). One admission was excluded from the study because it had no recorded LOS. Patients who are male (P = .02), non-White (P < .001), have nonelective surgery (P < .001), and have comorbidities (P < .001) tend to have longer hospitalizations (Table 1). The NIS and NSQIP patient populations differed significantly from each other in a variety of ways (Table, Supplemental Digital Content 2).

TABLE 1.

Characteristics of Patients Used for Algorithm Training

		Average LOS (SD),
Variable	Total	d	P valuea
Total admissions	41 221		–
Sex n, (%)
Female	19 604 (47.6)	7.7 (8.6)	.02
Male	21 617 (52.4)	7.9 (8.9)
Age at surgery, mean (SD), y	54.4 (15.9)	–
Race n, (%)
White	25 747 (62.5)	7.3 (7.9)	<.001
Hispanic	2720 (6.6)	10.0 (11.6)
Black or African American	2186 (5.3)	10.8 (13.2)
Other/Not reported	988 (2.4)	9.7 (9.4)
Asian	763 (1.9)	9.7 (11.5)
American Indian/Alaska native	142 (0.3)	9.3 (11.7)
Missing	8675 (21.0)	7.4 (7.2)
Elective surgery, n (%)
Yes	23 544 (57.1)	5.7 (7.1)	<.001
No	17 616 (42.7)	10.6 (9.8)
Missing	61 (0.2)	8.8 (6.4)
Admission quarter, n (%)
1	9531 (23.1)	7.7 (8.3)	.28
2	9423 (22.9)	7.6 (8.4)
3	9546 (23.2)	7.7 (8.6)
4	9321 (22.6)	7.9 (9.0)
Missing	3400 (8.2)
COMORBIDITIES
Diabetes, n (%)
Yes	5140 (12.5)	9.5 (10.0)	<.001
No	35 663 (86.5)	7.5 (8.5)
Missing	418 (1.0)	7.9 (11.1)
Congestive heart failure, n (%)
Yes	731 (1.8)	12.8 (10.9)	<.001
No	40 072 (97.2)	7.7 (8.6)
Missing	418 (1.0)	7.9 (11.1)
Hypertension, n (%)
Yes	16 213 (39.3)	8.4 (8.2)	<.001
No	24 590 (59.7)	7.4 (9.0)
Missing	418 (1.0)	7.9 (11.1)
Metastatic cancer, n (%)
Yes	2070 (5.0)	8.5 (7.3)	<.001
No	38 733 (94.0)	7.8 (8.8)
Missing	418 (1.0)	7.9 (11.1)
Weight loss, n (%)
Yes	735 (1.8)	20.8 (18.4)	<.001
No	40 068 (97.2)	7.6 (8.2)
Missing	418 (1.0)	7.9 (11.1)
Sodium abnormality, n (%)
Yes	2852 (6.9)	14.8 (14.2)	<.001
No	38 369 (93.1)	7.3 (7.9)
Missing	0 (0)	–
Alcohol abuse, n (%)
Yes	615 (1.5)	10.7 (10.6)	<.001
No	40 606 (98.5)	7.8 (8.7)
Missing	0 (0)	–
Pneumonia, n (%)
Yes	696 (1.7)	23.7 (20.5)	<.001
No	40 525 (98.3)	7.5 (8.1)
Missing	0 (0)	–
Esophageal varices, n (%)
Yes	5 (0.01)	9.4 (6.0)	.19
No	41 216 (99.99)	7.8 (8.7)
Missing	0 (0)	–
Previous PCI, n (%)
Yes	673 (1.6)	7.1 (5.8)	.40
No	40 548 (98.4)	7.8 (8.8)
Missing	0 (0)	–
Previous cardiac surgery, n (%)
Yes	736 (1.8)	7.76 (6.9)	.001
No	40 485 (98.2)	7.80 (8.8)
Missing	0 (0.0)	–
History of TIA or stroke n (%)
Yes	423 (1.0)	11.4 (11.5)	<.001
No	40 798 (99.0)	7.8 (8.7)
Missing	0 (0)	–
Pregnant at time of surgery, n (%)
Yes	0 (0)	–	–
No	41 221 (100)	7.8 (8.7)
Missing	0 (0)	–
Smoker at time of surgery, n (%)
Yes	4727 (11.5)	6.8 (6.3)	<.001
No	36 494 (88.5)	7.9 (9.0)
Missing	0 (0)	–
History of COPD, n (%)			<.001
Yes	2000 (4.9)	9.5 (9.4)
No	39 221 (95.1)	7.7 (8.7)
Missing	0 (0)	–
History of ascites, n (%)
Yes	0 (0)	–	–
No	41 214 (99.98)	7.8 (8.7)
Missing	7 (.02)	15.3 (6.3)
Dialysis at time of surgery, n (%)
Yes	5 (0.01)	11.6 (8.6)	.15
No	41 216 (99.99)	7.8 (8.7)
Missing	0 (0)	–
History of bleeding disorders, n (%)
Yes	1470 (3.6)	12.1 (12.4)	<.001
No	39 751 (96.4)	7.6 (8.5)
Missing	0 (0)	–
Any comorbidities, n (%)
Yes	24 167 (58.6)	8.9 (9.6)	<.001
No	17 054 (41.4)	6.3 (7.0)
Missing	0 (0)	–
Comorbidity counts, n (%)
0	17 054 (41.4)	6.3 (7.0)	<.001
1	13 301 (32.3)	7.7 (8.3)
2-4	10 225 (24.8)	10.3 (10.8)
5+	641 (1.5)	9.4 (11.0)

^aMann–Whitney U test and 1-way ANOVA test for significant difference between groups.

LOS, length of stay; SD, standard deviation; y, years; d, days; PCI, percutaneous coronary intervention; TIA, transient ischemic attack; COPD, chronic obstructive pulmonary disease.

Algorithm Leaderboard

Twenty-nine ML algorithms, including tree-based models, linear classifiers, support vector machines, RuleFit, neural networks, and naïve Bayes classifiers, were trained to predict the primary outcomes. The top performing algorithms were 2 gradient boosted trees and a Nystroem kernel support vector machine. These were combined with an elastic net to create an ensemble model.

RMSLE and Lift Chart for the Ensemble Model

The ensemble model had a RMSLE of .555 (95% CI, 0.553-0.557) on internal validation, a RMSLE of 0.559 for the holdout, and a RMSLE of 0.631 on external validation. Lift charts for both the internal and external validation are shown below (Figure 2, Table 2).

FIGURE 2.

Lift charts. Lift charts demonstrating graphically the accuracy of predicted LOS relative to actual LOS for the ensemble model on A, internal and B, external validation. Predicted LOS is divided into 10 equal bins, or deciles. Mean predicted LOS and mean actual LOS are calculated and plotted for each decile bin. Note that the lift charts reflect the fact that the average LOS in the NSQIP is shorter than the average LOS in the NIS. Solid line denotes actual LOS; dashed line denotes predicted LOS. LOS, length of stay.

TABLE 2.

Lift Chart Metrics

Internal validation (NIS)
Decile	1	2	3	4	5	6	7	8	9	10
Predicted mean LOS, d	4.1	4.5	4.8	5.5	6.7	7.8	8.3	9.3	10.9	16.2
Actual mean LOS, d	4.2	4.3	4.6	5.0	6.8	7.6	8.5	9.8	11.0	16.7
% difference	1.4	4.6	4.3	9.1	1.9	2.2	1.8	4.8	1.1	3.2
External validation (NSQIP)
Decile	1	2	3	4	5	6	7	8	9	10
Predicted mean LOS, d	3.8	4.4	4.6	5.0	5.6	6.5	7.7	8.5	9.6	12.6
Actual mean LOS, d	4.0	3.9	4.2	5.1	5.4	6.0	6.9	8.8	9.6	11.5
% difference	5.3	10.7	11.0	2.0	4.8	9.5	10.8	2.8	0.5	9.4

Description of lift chart metrics. The predicted length of stay for the internal and external validation are divided into deciles and the means calculated. This is compared to the mean for actual length of stay. LOS, length of stay; d, days.

Permutation Importance and Partial Dependence

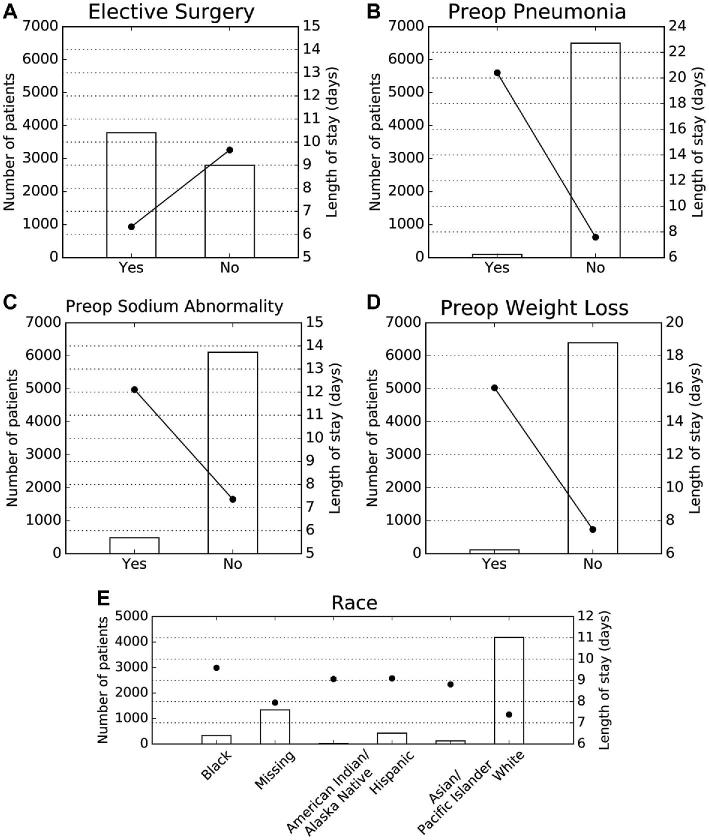
The variables that most strongly influence LOS are as follows: nonelective craniotomy, preoperative pneumonia, preoperative sodium abnormality, preoperative weight loss, and non-White race (Figure 3). Nonelective surgery independently increased predicted LOS from 6.3 to 9.7 d; pneumonia (defined as new or recently diagnosed) independently increased predicted LOS from 7.6 to 20.4 d; preoperative sodium abnormality independently increased predicted LOS from 7.4 to 12.1 d; and preoperative weight loss (defined as > 10% decrease in body weight in the 6 mo prior to surgery) independently increased predicted LOS from 7.5 to 16.1 d. Identifying as African American (9.6 d), Hispanic (9.1 d), Asian (8.8 d), American Indian or Alaska Native (9.1 d) conferred a longer LOS than identification as White (7.4 d; Figure 4). Patients with multiple risk factors had higher predicted LOS, though risk was not necessarily additive; for example, an African American patient with pneumonia and a nonelective surgery was predicted to have a LOS of 24 d (actual LOS = 30 d).

FIGURE 3.

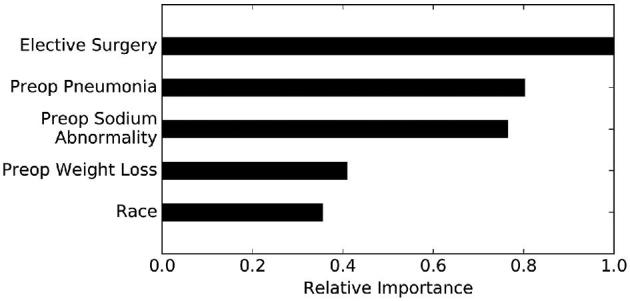
Permutation importance. Permutation importance analyses demonstrating the relative importance of the five most influential variables on the predictions of the ensemble. The most important variable is assigned the value “1.0” and all other variables are assigned numerical values based on their importance relative to the most important variable.

FIGURE 4.

Partial dependence plots. Partial dependence plots demonstrating the independent impact of A, elective surgery, B, preoperative pneumonia, C, preoperative sodium abnormalities, D, preoperative weight loss, and E, patient race on the ensemble model. Left Y-axis represents patient incidence for each patient group and corresponds to bars. Right Y-axis represents predicted LOS and corresponds to round heads. LOS, length of stay.

DISCUSSION

Models that accurately predict postoperative outcomes can be leveraged to improve patient care. Such models could be incorporated into and run in the background of clinical data systems or EMRs to automatically return predicted outcomes in a point-of-care setting. Ideally, our ensemble would be used to predict LOS prior to admission to aid in decision-making, including surgery scheduling. Importantly, potentially reversible predictors of LOS, such as sodium abnormalities, could be addressed prior to surgery. The ensemble also provides patients and families with information to aid in planning for work absences or postdischarge care, while also better enabling them to provide informed consent. Predictions could prove useful to nonclinicians, as well. For instance, bed managers could ensure that adequate numbers of beds are available in intensive care units for postoperative patients. Ancillary services, such as case management or social work, could also be mobilized at times that minimize delays in discharge. Although we do not study the relative accuracy of the model compared to clinician estimates of LOS, we imagine the ensemble being used as a “check” of provider intuition.

The ensemble could also be used to guide quality improvement initiatives. LOS indices, which compare expected to observed LOS, have been proposed as markers of efficiency and hospital performance. Using patient-specific predicted LOS to measure expected LOS may improve the accuracy of such indices, allowing hospitals to generate more representative quality metrics and, in reimbursement schemes that incentivize quality care, avoid punishment for taking on higher risk patients.²⁴

Improving Modeling Methods

Our technique of algorithm selection and ensemble creation circumvents important limitations of traditional, regression-based modeling. First, we overcome biases associated with algorithm selection through direct comparison of a panel of ML algorithms, enabling empiric identification of the most predictive algorithms. A table describing some of the most common ML algorithms is included below (Table 3). Second, we take advantage of complementarity between classes of ML algorithms by creating an ensemble model from the most predictive algorithms, allowing us to generate the most accurate predictions for a given dataset.

TABLE 3.

Common ML Algorithms

Model	Description	Advantages	Disadvantages
Support vector machines	Inputsa are represented as vectors in higher dimensional space, with each axis corresponding to a different variable. The algorithm then calculates a plane that separates the inputs into 2 different classes. New inputs are then assigned to a class based on which side of the plane they fall on.	Can model complex, nonlinear relationships between inputs and outputsRobust to noiseFast to predict	Requires significant processing powerSlow to trainKernel selection requires expertise
Artificial neural networks	Designed as a series of layers of artificial neurons, with weights assigned to every variable. Individual neurons will “fire” and propogate the signal to later layers if the weighted sum of its inputs (variables or previous neurons in the network) passes a threshold. Neural networks have been shown to be able to recognize meaningful, complex interactions in data as the number of layers increases.	Can model complex, nonlinear relationships between inputs and outputs	Difficult to interpret the underlying mechanisms driving predictions (a black box)Requires significant processing powerSlow to train
K nearest neighbors	Inputs are represented as vectors in multidimensional space, with each axis corresponding to a different variable. Prediction outputs are based on the values of the k nearest training examples according to a specified distance metric.	Simple and easy to interpretCan be used to discriminate between many different classes, eg, tagging textNo training is involved, so new training examples can be easily added. This makes the model quickly adaptable new inputs.	Slow—can take a long time to calculate nearest neighbors in large datasets.Need to know that the distance function is clinically meaningful
Generalized Additive models	Variables are fed into individual smooth functions, summed, then transformed by some (potentially nonlinear) link function into a final output.	Can more accurately represent outcomes that are not normally distributed.	Requires expertise and care in selecting appropriate link function.Effective use requires some foreknowledge of the training data.
Tree-based models
Decision tree	Uses decision rules to classify data. Large trees may have many decision rules. Every input will be classified into 1 output value.	Easy to interpret	Prone to overfitting.Not built to maximize any objective metric.
Random forest	An ensemble of many decision trees, the output of which is determined by the mean prediction of the individual trees. The use of many trees effectively combats overfitting.	Corrects for overfitting in decision trees.Observed to perform well in a wide variety of contexts.	Optimum performance depends on tuning several important parameters.
Gradientboosted Trees	An ensemble of weak decision trees built in a stagewise manner. Subsequent trees are added according their ability to improve the model.	Observed to perform well in a wide variety of contexts.	Optimum performance depends on turning several important parameters.
Linear models
Ordinary leastSquares(logisticand linearregression)	The traditional regression technique. Finds the coefficients of a linear model that minimize the Mean Squared Error.	Easy to interpretFor classification, output can be interpreted as a probabilityFast to train	Assumes independently acting predictors that influence the outcome in a linear fashion.
Regularizedlinear andregularizedlogisticregression	Regression that employ mechanisms to minimize overfitting by shrinking or eliminating large regression coefficients. Examples include ridge regularization, lasso regularization, and elastic net regularization (which combines ridge and lasso regularizations).	Robust to noiseEasy to interpretFor classification, output can be interpreted as a probabilityFast to train	Assumes independently acting predictors that influence the outcome in a linear fashion.
Stochasticgradientdescent	Linear model that initially assigns each variable a random coefficient. The error function of the model is then calculated, and coefficient values updated in the direction that minimizes the error function. This process continues in a stepwise manner until minimization is achieved.	Robust to noiseCan be used in online-learning contexts	Susceptible to converge to suboptimal local minima
Naïve bayes	Given a training dataset, assigns probabilities that the value of a given variable is associated with the outcome of interest. Inputs are classified based on the probabilities assigned to the values of their individual variables.	Easy to understand	Assumes independently acting predictorsSusceptible to outsized effects for infrequently observed data.If the frequency of classes is unbalanced in the training dataset, can have classification skewed toward the more common outcome.

^aInputs refers to individual patients, each of which is defined by the various variables attributable to that patient.

We demonstrated that this guided ML ensemble technique can be used to predict LOS from preoperative patient characteristics with good accuracy on internal (RMSLE = .555, 95% CI, .553-.557) and external (RMSLE = .631) validation, demonstrating generalizability to never-before-seen data. Although we chose to predict LOS, this technique is broadly generalizable, and guided ML ensembles can be built to predict any number of medical outcomes.

Clinical Insights from ML Models

A common misconception of nonregression ML algorithms is that their underlying mechanisms are difficult to understand, making them less useful or easy to interpret than regression models. In this study, however, we demonstrate well-established ML techniques that provide comparable, if not more informative, clinical insights. For example, we used permutation importance analysis to identify which of the myriad risk factors identified in univariate analysis is most important in determining extended LOS.

Partial dependence plots graphically depict the independent impact of a variable on model predictions. Plots are constructed by graphing the partial dependence “coefficient” across the entire range of values for a variable. As such, these analyses are more dynamic than regression coefficients, which remain static across the range.

Strengths and Limitations

ML techniques are often criticized for overfitting. A major strength of our study lies in the techniques we use to ensure that our ensemble predictions are not overly tailored to training data. First, we internally validate our data using five nonoverlapping cross-validation folds, generating 5 independent estimates of the ability of the ensemble to generalize to unseen data. Second, we demonstrate generalizability to a holdout dataset never used in algorithm training. Finally, we validate the ensemble on an entirely separate database, the NSQIP.

Internal validation alone can yield overly optimistic results as testing and validation data are often very similar.⁵ Demonstration of generalizability to an external dataset is therefore the gold standard for model validation, though it is rarely reported in outcomes literature.^25-26 Importantly, the populations represented in our training (NIS) and validation (NSQIP) datasets are significantly different in many respects, demonstrating that the NSQIP dataset is truly external to the NIS dataset (Table, Supplemental Digital Content 2). For example, average LOS is significantly shorter in the NSQIP than the NIS (6.5 vs 7.8 d P < .001). It is thus particularly remarkable that the NIS-trained ensemble can make accurate predictions from the NSQIP database with only a modest loss in performance (RMSLE = .631 vs .555). Future directions for this work include validating the ensemble on a larger external dataset, with more years represented, and validating the ensemble in a prospective fashion. It will also be important to build and validate an ensemble built from a single institution's data, allowing for tailoring of the ensemble to the specific practice milieu of the neurosurgeon(s) using the ensemble's predictions.¹⁹

Although our study has many advantages, it also has important limitations. First, because we trained our ensemble only using variables present in both the NIS and NSQIP database, there is the potential to miss important predictors that were present in only 1 of the datasets. For example, no hospital characteristics are captured in the NSQIP, a significant limitation given the importance of hospital geography as a predictor of LOS.²⁰ Furthermore, these datasets do not capture neurosurgery-specific variables, such as tumor characteristics. Building large, neurosurgery-specific databases will further enhance the utility of this technology in the neurosurgical sphere. Finally, our ML strategy is novel and will require further study and validation. We hope, however, that this work will encourage researchers to utilize ML in predictive modeling.

CONCLUSION

ML is a powerful, albeit underutilized, tool in clinical medicine with direct relevance to neurosurgical outcomes research. In this proof-of-concept study, we build an internally and externally validated ML ensemble model that predicts LOS following craniotomy for brain tumor. We show that clinical insights can be derived from these ML algorithms, including identification of important risk factors for extended LOS. This technique can be applied broadly to various outcomes, potentially translating into improved care for patients.

Disclosures

Mr Akagi is a data scientist employed at DataRobot Inc. Ms Muhlestein is married to Mr Akagi. Ms Muhlestein received financial support from the Vanderbilt Medical Scholars Program and the UL1 RR 024975 NIH CTSA grant. The other authors have no personal, financial, or institutional interest in any of the drugs, materials, or devices described in this article.

Supplemental Digital Content 1. Table. Variables included in ensemble training and external validation.

Supplemental Digital Content 2. Table. Patient characteristics for training and validation databases.

COMMENTS

In the early 1990s, the gene for Huntington's Disease was discovered, and a highly accurate test for it was developed. More than 2 decades later, most people will probably still decline to take the tests today. Why? The answer, as we all know, is a common clinical dictum: Why test for things that you cannot do something about?

One of the attractions of artificial intelligence is the ability to develop highly accurate prediction models. However, this high accuracy may not be as useful as computer scientists would make us think. They have a risk of becoming the modern-day version of genetic testing.

To make sure these new tools are actually contributing to patient care, AI projects need to incorporate concepts of modifiability in their search for predictors. But computers don’t know what is modifiable and what is not. The best way (and probably the only way) to do this is to engage clinicians and health services researchers in the process. The expectation that computers can completely automate the process is unrealistic, and will likely lead to “interesting” results that may only be of interest to computer scientists, but not for clinicians taking care of patients.

There is still no substitute (yet) for the human common sense.

David Chang

Boston, Massachusetts

The authors have conducted a machine learning algorithm to help predict length of stay (LOS) in patients undergoing brain tumor surgery. Machine learning in predictive modelling is underutilized in medicine. Using the National Inpatient Sample (NIS) to train a variety of models and the National Surgical Quality Improvement Program (NSQIP) database for validation, the authors attain good prediction and identify several dichotomous risk factors increasing LOS, including non-elective surgery, pneumonia, sodium abnormalities, weight loss, and non-white race.

Strengths of this interesting study include the use of the NIS: predictive models generalize best when trained on large, representative datasets. External validation is the gold standard for reducing bias and overfitting; nevertheless, the authors should perform a more extensive, prospective validation going forward. While better LOS prognosticating may result in efficiency gains for hospital systems, it is unclear how these findings may be clinically meaningful.

Put to useful ends, machine learning algorithms progressively improve performance on specific tasks using specific datasets; they are beholden to the quality and generalizability of their data. Machine learning in medicine will result in large efficiency gains in detecting empirical relationships that can facilitate prediction of certain parameters.

There are many areas within neurosurgery that could benefit from better predictive modelling: in addition to providing a more accurate LOS prognosis as in this paper, machine learning algorithms could better predict rare but devastating events which are poorly suited to traditional statistical modelling - such as which aneurysms are bound to rupture; or they could assist in surgical risk assessment, or complication avoidance.

Christopher Carr

Peter S. Amenta

Aaron S. Dumont

New Orleans, Louisiana