Transdiagnostic Brain Mapping in Developmental Disorders

Summary

Childhood learning difficulties and developmental disorders are common, but progress toward understanding their underlying brain mechanisms has been slow. Structural neuroimaging, cognitive, and learning data were collected from 479 children (299 boys, ranging in age from 62 to 223 months), 337 of whom had been referred to the study on the basis of learning-related cognitive problems. Machine learning identified different cognitive profiles within the sample, and hold-out cross-validation showed that these profiles were significantly associated with children’s learning ability. The same machine learning approach was applied to cortical morphology data to identify different brain profiles. Hold-out cross-validation demonstrated that these were significantly associated with children’s cognitive profiles. Crucially, these mappings were not one-to-one. The same neural profile could be associated with different cognitive impairments across different children. One possibility is that the organization of some children’s brains is less susceptible to local deficits. This was tested by using diffusion-weighted imaging (DWI) to construct whole-brain white-matter connectomes. A simulated attack on each child’s connectome revealed that some brain networks were strongly organized around highly connected hubs. Children with these networks had only selective cognitive impairments or no cognitive impairments at all. By contrast, the same attacks had a significantly different impact on some children’s networks, because their brain efficiency was less critically dependent on hubs. These children had the most widespread and severe cognitive impairments. On this basis, we propose a new framework in which the nature and mechanisms of brain-to-cognition relationships are moderated by the organizational context of the overall network.

Highlights

• •Machine learning identified cognitive profiles across developmental disorders
• •These profiles could be partially predicted by regional brain differences
• •But crucially there were no one-to-one brain-to-cognition correspondences
• •The connectedness of neural hubs instead strongly predicted cognitive differences

Different brain structures are inconsistently associated with different developmental disorders. Siugzdate et al. instead show that the connectedness of neural hubs is a strong transdiagnostic predictor of children’s cognitive profiles.

Introduction

Between 14%–30% of children and adolescents worldwide are living with a learning-related problem sufficiently severe enough to require additional support (https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/729208/SEN_2018_Text.pdf; https://nces.ed.gov/programs/coe/indicator_cgg.asp). Their difficulties vary widely in scope and severity and are often associated with cognitive and/or behavioral problems. In some cases, children who are struggling at school receive a formal diagnosis of a specific learning difficulty, such as dyslexia, dyscalculia, or developmental language disorder (DLD). Others may receive a diagnosis of a related neurodevelopmental disorder commonly associated with learning problems such as attention deficit and hyperactivity disorder (ADHD), dyspraxia, or autism spectrum disorder (ASD). However, in many cases, children who are struggling have either no diagnosis or receive multiple diagnoses (http://embracingcomplexity.org.uk/assets/documents/Embracing-Complexity-in-Diagnosis.pdf; [1]).

But how does the developing brain give rise to these difficulties? The answers to this question have been remarkably inconsistent, and a wide range of neurological bases have been linked to individual disorders. One reason for this is study variability. Sample size and composition varies across studies, and the selection of comparison groups and analytic approaches differ widely. But even when broadly similar designs and analysis approaches are taken, there are substantial differences in the results. For example, take ADHD—this disorder has been associated with differences in gray matter within the anterior cingulate cortex [2, 3], caudate nucleus [4, 5, 6], pallidum [7, 8], striatum [9], cerebellum [10, 11], prefrontal cortex [12, 13], the premotor cortex [14], and most parts of the parietal lobe [15].

One likely reason for this inconsistency is that these diagnostic groups are highly heterogeneous and overlapping. Symptoms vary widely within diagnostic categories [16, 17] and can be shared across children with different or no diagnoses [18, 19, 20, 21, 22, 23, 24]. In short, the apparent “purity” of developmental disorders has been overstated. To remedy this, many scientists now advocate a transdiagnostic approach. Emerging first in adult psychiatry [25, 26, 27], this approach focuses on identifying underlying symptom dimensions that likely span multiple diagnoses [28, 29, 30]. Within the field of learning difficulties, the primary focus has been on identifying cognitive symptoms that underpin learning [28, 31, 32, 33, 34, 35, 36, 37, 38].

A second possible reason for why consistent brain-to-cognition mappings have been so elusive is because they do not exist. A key assumption of canonical voxel-wise neuroimaging methods is that there is a consistent spatial correspondence between a cognitive deficit and brain structure or function. However, this assumption may not be valid. There could be many possible neural routes to the same cognitive profile or disorder, as our review of ADHD above suggests (see also [39]). This is sometimes referred to as equifinality. Complex cognitive processes or deficits may have multiple different contributing factors. Conversely, the same local neural deficit could result in multiple different cognitive symptoms across individuals (see [40] for early ideas around this). This is sometimes referred to as multifinality. The complexity of the developing neural system makes it highly likely that there is some degree of compensation; the same neural deficit has different functional consequences across different children. While concepts of equifinality and multifinality have been present within developmental theory for some time, these concepts have not been translated into analytic approaches. The traditional voxel-wise logic means that most cognitive symptoms associated with developmental disorders are thought to reflect a specific set of underlying neural correlates (for recent reviews, see [41, 42, 43]).

The purpose of this study was to take a transdiagnostic approach to establish how brain differences relate to cognitive difficulties in childhood. Data were collected from children referred by professionals in children’s educational and/or clinical services (n = 812, of which 337 also underwent MRI scanning) and from a large group of children not referred (n = 181, from which 142 underwent MRI scanning). Cognitive data from all 479 scanned children—including all those with and without diagnoses—were entered into an unsupervised machine learning algorithm called an artificial neural network. Unlike other data reduction techniques (e.g., principal component analysis), this artificial neural network does not group variables or identify latent factors but, instead, preserves information about profiles within the dataset, can capture non-linear relationships, and allows for measures to be differentially related across the sample [44]. This makes it ideal for use with a transdiagnostic cohort. Hold-out cross-validation revealed that the profiles learned using the artificial neural network generalized to unseen data and were significantly predictive of childrens’ learning difficulties.

To test how brain profiles relate to cognitive profiles the same artificial neural network was applied to whole-brain cortical morphology data. The algorithm learned the different brain profiles within the sample. Hold-out cross-validation showed that these brain profiles generalized to unseen data and that a child’s age-corrected brain profile was significantly predictive of their age-normed cognitive profile. But crucially, there were no one-to-one mappings, and the overall strength of the relationship was small. One brain profile could be associated with multiple cognitive profiles and vice versa.

How can the same pattern of neural deficits result in different cognitive profiles across children? Finally, the data show that some children’s brains are highly organized around a hub network. Using diffusion-weighted neuroimaging, we created whole-brain white-matter connectomes. We then simulated an attack on each child’s connectome by systematically disconnecting its hubs. Drops in efficiency and the embeddedness of learning-related areas highlighted the key role of these hubs. The more central the hubs to a child’s brain organization, the milder or more specific the cognitive impairments. By contrast, where these hubs were less well embedded, children showed the more severe cognitive symptoms and learning difficulties.

Results

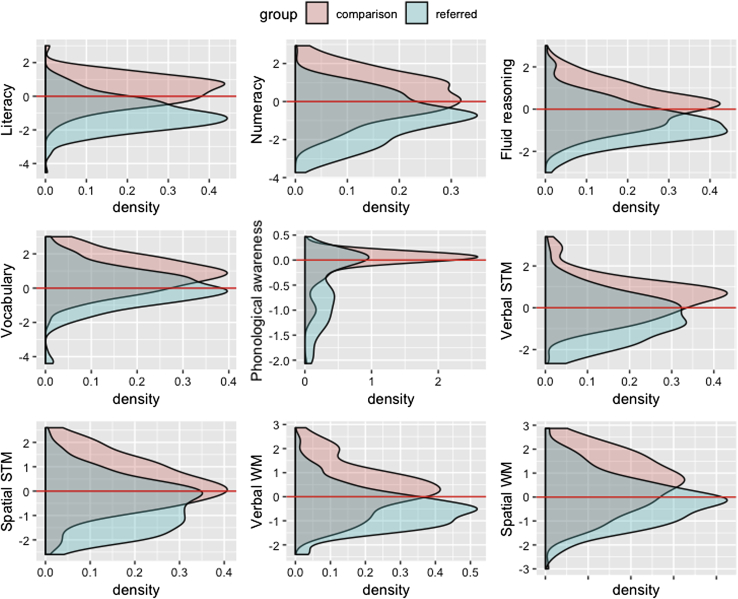
The large subset of children referred by children’s specialist educational and/or clinical services performed very poorly on measures of learning ability (literacy: t(477) = 15.79, p < 2.2 × 10⁻¹⁶, d = 1.58; and numeracy: (t(477) = 10.037, p < 2.2 × 10⁻¹⁶, d = 1.00)) relative to the non-referred comparison group. They also performed more poorly on measures of fluid reasoning (t(477) = 8.34, p = 7.9 × 10⁻¹⁶, d = 0.83), vocabulary (t(477) = 8.11, p = 4.31 × 10⁻¹⁵, d = 0.81), phonological awareness (t(477) = 7.93, p = 1.5 × 10⁻¹⁴, d = 0.79), spatial short-term (t(477) = 8.4, p = 5.5 × 10⁻¹⁶, d = 0.84), spatial working memory (t(477) = 9.3, p < 2.2 × 10⁻¹⁶, d = 0.93), verbal short-term (t(477) = 8.6, p < 2.2 × 10⁻¹⁶, d = 0.86), and verbal working memory (t(477) = 7.3, p = 1.0 × 10⁻¹², d = 0.73). Distributions on all of these measures can be seen in Figure 1, and descriptive statistics of our sample can be found in the STAR Methods.

Figure 1.

Distribution of Normalized Cognitive Scores per Group

Z scores correspond to age-normalized expected levels using the standardization data and, accordingly, a score of zero is age-expected. The specific tests used to assess each domain can be found in the table in the STAR Methods.

Mapping Cognitive Symptoms and Learning Ability

The cognitive data were introduced to the simple artificial neural network as Z scores, using the age standardization mean and standard deviation from each assessment. Thus, a score of zero will correspond with age-expected performance and −1 to a standard deviation below age-expected levels. The learning measures (literacy and numeracy) were held-out because these would be used in a subsequent cross-validation exercise. We intentionally did not control for ability level—the severity of any deficit is crucial information for understanding any associated neural correlates [45].

The specific type of network used was a self-organizing map (SOM; [46]). This algorithm represents multidimensional datasets as a two-dimensional (2D) map. Once trained, this map is a model of the original input data, where individual measures are represented as weight planes. The algorithm was modified from its original implementation such that it could adapt its size to best match the dimensionality of the input data and represent hierarchical information within the input data [47]. It does this by growing additional nodes to represent the input data optimally and can spawn subordinate layers of nodes to capture hierarchical relationships.

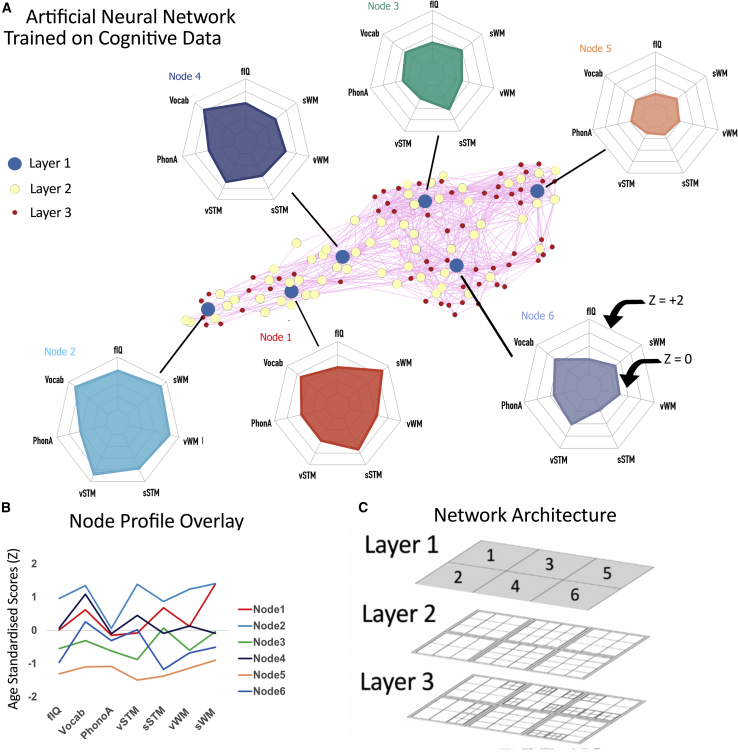
A three-layer representation was learned by the artificial neural network. One way of showing this in pictoral form is to take the weights for each node and calculate the Euclidean distance to all other nodes. Using a Force Atlas, layout these nodes can then be plotted in 2D space [48]. The closer the nodes are to each other, the more similar the weights. This is depicted in Figure 2A. Each layer of the network provides an increasingly granular account of the original dataset. The top layer explains an average of 52%, the top two layers explain 78%, and all three layers explain an average of 83% of the variance in the original cognitive variables. To provide a comparison, a three-factor PCA solution explains 73% of the variance.

Figure 2.

Cognitive Profiles Defined by Neural Network and Their Descriptives

(A) Graphical representation of the three-layer representation, using Euclidean distance and a Force Atlas layout in Gephi toolkit (gephi.org). The blue nodes correspond to the top layer of nodes, and the radar plots show the profiles of those nodes (ranging from Z = −2 to +2). Related to Table S6 and Figure S3.

(B) The profiles of the top layer of nodes overlayed. Related to Table S7.

(C) The network architecture produced by the hierarchical growing, self-organizing map.

A good way to depict the different cognitive profiles learned by the algorithm is to plot the weight profiles for the different nodes in the first (top) layer. These can be seen in the radar plots in Figure 2A. The network learned that there were children with broadly age-appropriate performance (Node 1), high-ability children (Node 2), children who perform poorly on tasks requiring phonological awareness (alliteration and forward and backward digit span; Node 3), broad but relatively moderate cognitive impairments (Node 4), widespread and severe cognitive impairments (Node 5), and children with particularly poor performance on executive function measures (spatial short-term memory, working memory, and fluid reasoning; Node 6). For ease of comparison, the weight profiles of the top layer of nodes are overlaid in Figure 2B. Bootstrapping with 500 samples allowed us to test the consistency of the node allocations in this top layer. Across the boostraps, children ranged from two to ten times more likely to be allocated to the same top-layer best maching unit (BMU) than any other, with a modal value of 4.16 times more likely.

Identifying each child’s best matching node (typically termed their BMU) provides another way of capturing the different characteristics of these nodes. The nodes very strongly distinguish between referred and non-referred children. For example, Nodes 3, 4, 5, and 6 are the BMUs for the majority of children referred by clinicans or special education (80%, 60%, 80%, and 97% referred, respectively; see Table S6). Children not referred for a learning difficulty were more likely to be associated with Nodes 1 and 2 (50% and 69%, non-referred, respectively). Gender did not differ significantly across the 6 cognitive profiles (χ² (5, N = 479) = 5.8951, p = 0.3166; Node 1 = 72% boys, Node 2 = 62% boys, Node 3 = 63% boys, Node 4 = 62% boys, Node 5 = 52% boys, and Node 6 = 61% boys). Mean age was not significantly different across the six nodes (F(5,478) = 0.52, p = 0.7617; Node 1 = 117 months, Node 2 = 122 months, Node 3 = 116 months, Node 4 = 116 months, Node 5 = 118 months, and Node 6 = 118 months).

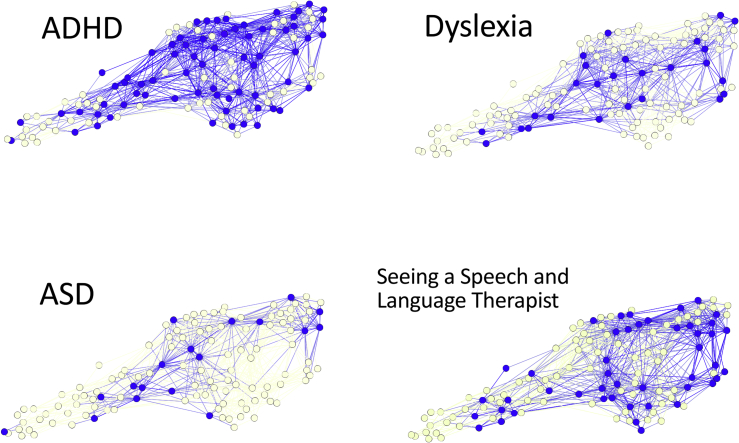
The heterogeneity of cognitive profiles within diagnostic categories can be depicted pictorally by identifying the BMUs (using Euclidean distance) of children with different diagnoses. This was done for ADHD, dyslexia, ASD, and children under the care of a speech and language therapist (Figure 3). If these categories are predictive of a child’s cognitive profile, then these nodes should be grouped together within the network; however, if these diagnostic labels are unrelated to cognitive profile, then they should be randomly scattered within the network. None of these categories are associated with a discrete set of cognitive profiles.

Figure 3.

The Locations of Nodes by Diagnosis Type

Graphical representation of the network archictecture using Euclidean distance and a Force Atlas layout, where BMUs of different diagnoses highlighted in blue.

Cross-Validation: Cognitive Profiles Predict Learning Ability

Cognitive profiles are robustly related to children’s learning ability [34], so a good test of whether the network can reliably represent individual differences in cognition is to test whether it will generalize to unseen data and predict children’s learning scores. We used a 5-fold hold-out cross-validation to test whether the cognitive profiles predict learning scores. The network was trained from scratch on 80% of the sample, randomly selected. The BMU (which could come from any of the three layers) for each individual in the remaining 20% of the sample was then identified using the minimum Euclidean distance. We then used children sharing this BMU from the training set to make a prediction about the held-out child’s performance on the learning measures (literacy and numeracy). Then, we calculated Euclidean distance between the predicted performance and the actual performance. This provides a measure for the accuracy of the prediction; the smaller the value, the closer the prediction was to the actual learning scores. Next, we created a null distribution by repeating the process but shuffling the held-out learning measures. This process was repeated until all children had appeared in the held-out 20%. We could then compare these two distributions—the genuine prediction accuracy versus the accuracy within the shuffled data—using a t test. The network made significantly accurate predictions about a child’s learning ability, relative to the null distribution (t(477) = 10.44, p = 2.95 × 10⁻²⁴, Cohen’s d = 0.47). This is a particularly strong test of the generalizability of our model. It accurately classifies unseen individuals, and this extends to measures that were unseen during the original training. The spread of the prediction accuracy can be seen in Figure S3.

Mapping Brain Profiles

The machine learning process was repeated for the structural neuroimaging data. Whole-brain cortical morphology metrics (cortical thickness, gyrification, sulci depth) were calculated for each child across a 68 parcel brain decomposition [49].

We performed feature selection before the machine learning to reduce the risk of over-fitting with so many measures. LASSO regression reduced the number of indices down to 21 distinct measures, across 19 of the 68 parcels (see Supplemental Information, Figure S2 for details). The regions selected were the bank of left superior temporal sulcus, left cuneus, left entorhinal cortex, left fusiform, right fusiform, left inferior parietal, right lateral occipital, right medial orbito frontal, right middle temporal, left paracentral, left pars orbitalis, right pars triangularis, left posterior cingulate, right posterior cingulate, right rostral anterior cingulate, left superior parietal, right superior temporal, left supramarginal, and the left frontal pole.

An analysis of age effects was conducted on the cortical morphology data. We modeled age as a second order polynomial function and tested whether our 19 parcels were significantly associated with age in months. Twelve of them were significant and three survived family-wise error correction. Next, we used a regression in which we modeled the degree of learning difficulty, age in months, and the interaction between these two factors. This was to test whether there were differential developmental trajectories within the sample, according to children’s learning difficulty. Two parcels show the significant interaction term, but neither survive family-wise error correction. This is because while the overall age range of this cohort is large, the vast marjority (over 69%) are aged between 7 and 11 years—the peak age at which developmental disorders and cooccurring learning difficulties are first identified. The end result was that we controlled for age in our analysis by first regressing it from the parcel values, but we did not include age itself in the machine learning analysis.

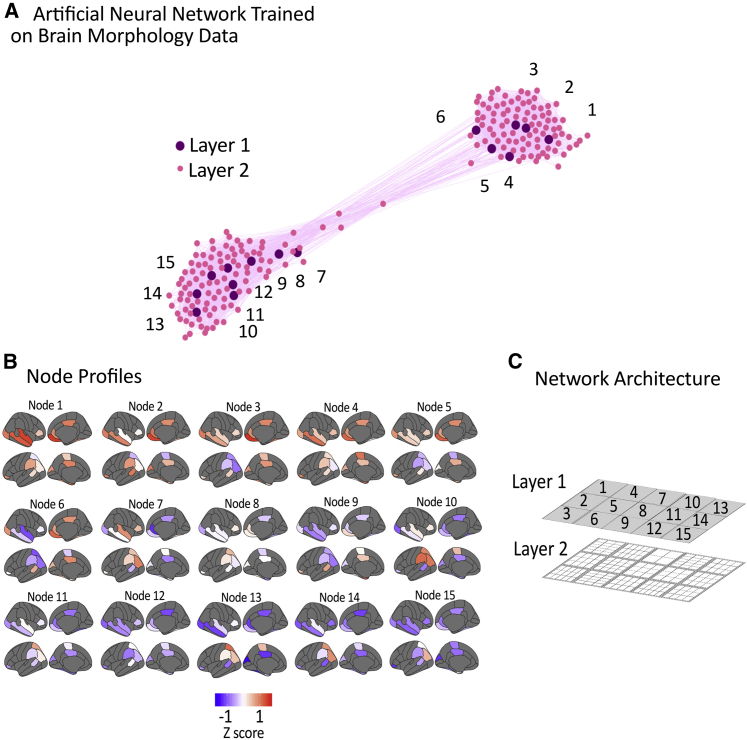
The neural network learned a two-layer structure with a top layer of 15 nodes. This can be depicted in the same way as the cognitive data, by using Euclidean distance to position the nodes in a 2D plane according to the similarity of their weights (Figure 4A). The top layer explains an average of 49% of the variance and, together, both layers explain 73% of the variance. By comparison, a two factor PCA solution explains 49% of the variance. The weight profiles of each of the 15 nodes within the top layer can be seen in Figure 4B, and the formal network architecture can be seen in Figure 4C.

Figure 4.

Brain Morpholgical Profiles Defined by Neural Network and Their Weighted Representation on the Cortical Surface

(A) Graphical representation of the network archictecture using Euclidean distance and a Force Atlas layout. The purple nodes correspond to the top layer.

(B) The cortical morphology profiles of the top layer of 15 nodes.

(C) The network architecture learnt by the hierarchical growing self-organizing map.

Cross-Validation: Children’s Brain Profiles Predict Their Cognitive Profile

The extent to which the different brain profiles identified by artificial neural network can predict children’s cognitive profiles was tested next using a 5-fold hold-out cross-validation. Using 80% of the sample, the artificial neural network was trained from scratch. Then, taking each child from the hold-out 20%, their BMU (across any layer) was idenitifed, using Euclidean distance. Children occupying this BMU from the training set were then used to predict the held-out child’s cognitive profile. The Euclidean distance between this prediction and the child’s actual profile was then compared with a null distribution derived by shuffling the held-out cognitive data. The genuine predictions were then compared with the null distribution using a t test. The network was able to make significantly accurate predictions about a child’s cognitive profile, given their brain profile, relative to the shuffled null distribution (t(478) = −3.14, p = 0.0017). Again, this is a strong test of generalizability because it requires an accurate prediction about both unseen individuals and unseen outcome measures. But, here, the effect size is substantially lower—only Cohen’s d = 0.15. In other words, knowing a child’s regional brain profile makes the prediction of their cognitive profile around 4% more accurate than it would have been by chance. And the accuracy of this prediction drops even further if you take a child’s second best matching unit [t(478) = −0.7377, p = 0.4609], indicating that there is some granularity to the mapping within the brain data.

So far, a child’s cognitive profile is significantly related to their learning difficulties, and these cognitive symptoms can be significantly predicted by their structural brain profile across 19 learning-related cortical parcels. Crucially, this brain-cognition relationship is not nearly as strong as might be predicted from far smaller studies [50].

Mapping Brain Profiles to Cognitive Profiles

An alternative way to show that children’s brain profiles are significantly associated with their cognitive profiles is to perform a χ² test. Using the top layers of the cognitive and brain networks as a simple represention of the data, we could test whether there was a significant relationship between these two types of data. A child’s BMU in the top layer of the cognitive network and their BMU in the top layer of the structural brain network were significantly associated (χ²(70, N = 479) = 130.59, p = 1.5 × 10⁻⁵). This corroborates the result of the cross-validation—there is a significant relationship between a child’s structural brain profile and their cognitive profile.

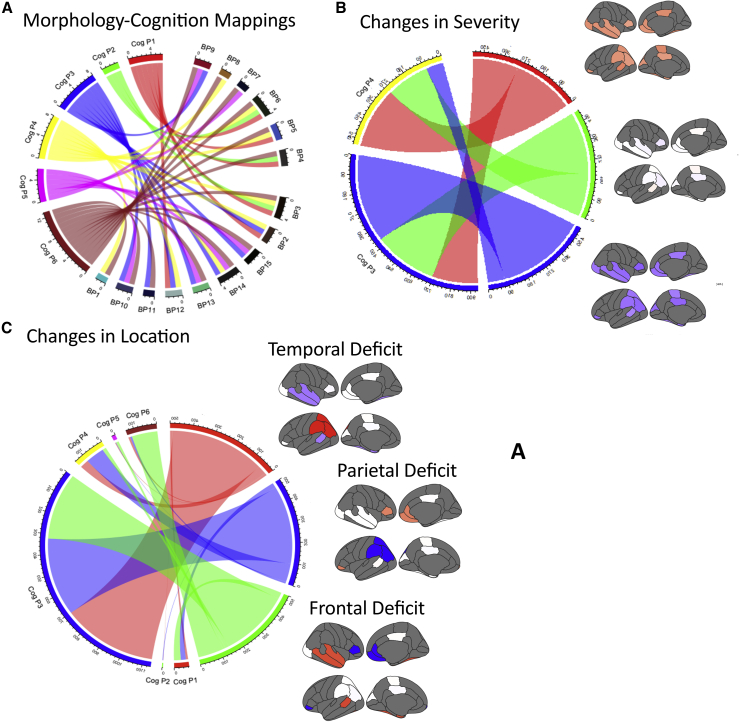
However, this is not because specific brain profiles predict particular cognitive profiles, and this may explain why the overall effect size of the brain-cognition relationship is relatively low. Figure 5A shows the correspondence between each cognitive node and brain nodes. A child can arrive at a particular cognitive profile from multiple different brain profiles, and vice versa.

Figure 5.

Correspondence between Cognitive Profiles and Brain Profiles

(A) The correspondence between cognitive (Cog P1-Cog P6) and brain profiles (BP1- BP15) within the sample. Related to Table S3.

(B) Simulated differences in the overall severity of the brain profile and the corresponding cognitive profiles as learned by the artificial neural network. Related to Table S4.

(C) Simulated differences in temporal, parietal and frontal regions and the corresponding cognitive profiles as learned by the artificial neural network. Related to Table S5.

What Is the Artificial Neural Network Learning?

Next, we asked whether the artificial neural network had primarily learned about the “severity” of a particular set of brain values, or whether it had learnt to identify peaks and troughs in the individual profiles. To do, this we used simulations. To be clear, these simulations are not intended to be an accurate reflection of the underlying basis for learning difficulties or developmental disorders. Instead, the simulations are designed to test what the artificial neural network is learning about the differences between children.

Brain profiles were simulated using the correlation structure of the original datasets. First, 1,500 profiles were simulated, with an overall mean of 0 and a standard deviation of 1. For 500 simulated profiles. an additional 0.5 standard deviation was added to each parcel value. For 500 simulated profiles, 0.5 standard deviation was subtracted from each parcel. Thus, across the 1,500 simulations, there were three sub-groups that varied systematically across 1 standard deviation, but there were no systemtic sub-group differences in the peaks and troughs of the profiles. The same cross-validation exercise was repeated for the real data, but using the real data as the “train” set and with these simulations acting as our “test” set. If the machine learning process is sensitive to the overall severity of the profile, then the systematic severity manipulation should change the cognitive profiles that are predicted. We grouped the predicted cognitive profiles according to the six top-level cognitive profiles present in the original data. Indeed, controlling all differences in profile but systematically manipulating just the overall severity did significantly change the predicted cognitive profile (χ²(2, N = 1500) = 185.4669, p = 5.33 × 10⁻⁴¹; Figure 5B). The machine learning is sensitive to the severity of child’s overall brain deficit.

Next, another 1,500 profiles were simulated using the same procedure. This time sub-groups (each of N = 500) were created that were matched for overall severity but had peaks or troughs of the temporal lobe parcels (left bank of the superior temporal cortex, the left enthorinal, left and right fusiform, right middle temporal, and right superior temporal cortex), the parietal lobe parcels (left inferior parietal, left superior parietal, and left supramarginal cortex), or the frontal lobe parcels (right medial orbital frontal cortex, right pars orbitalis, right pars triangularis, right rostral anterior cingulate, and the left frontal pole). The overall severity of these simulated deficits was adjusted such that the overall profiles within each sub-group all summed to zero. If the machine learning is also sensitive to the location of peaks or troughs, irrespective of overall severity, then these three sub-groups should be probablistically linked with different cognitive profiles. Controlling for overall differences in severity by systematically varying the location of the deficit does indeed significantly change the predicted cognitive profile (χ²(10, N = 1500) = 270.6562, p = 2.43 × 10⁻⁵²; Figure 5C). In short, the machine learning is sensitive to both the overall severity of the neural profile and the locations of the peaks and troughs.

It’s a Small World? Structural Connectomic Analysis

How can the same neural deficit result in multiple cognitive outcomes? One possibility is that the overall organization of a child’s brain has important consequences for the relationship between any particular area and cognition. For a representative portion of the sample (N = 205), diffusion-weigthed imaging (DWI) data were available. These data could be used to identify white-matter connections, and whole-brain connectomes were constructed for each child (Figure 6A). Graph theory provides a mathematical framework that captures the organizational properties of complex networks. In particular, global efficiency describes the overall information exchange possible within the network. Network efficiency was compared across the 6 cognitive groupings from our original mapping of the cognitive data. There were no significant differences (F(5,202) = 0.74, p = 0.595).

Figure 6.

White-Matter Structural Connectomics

(A) Connectogram based on a weighted degree between 68 ROIs

(B) Degree (Dj) of parcels in the group‐average connectome. Parcels shown in red are considered hubs with a degree that is one standard deviation above the mean across parcels.

(C) Reductions in network global efficiency (E_G) as 8 hub areas are disconnected versus 8 peripheral areas. Cognitive profiles 1 and 2 were the most sensitive to the simulated attack

(D) Reductions in local clustering coefficient (C_j) of 19 parcels as 8 hub areas are disconnected. Cognitive profiles 1 and 2 were the most sensitive to the simulated attack

A prevalent theory in network science is that “small-worldness” is the optimal organization for a complex system [51, 52]. A small-world network is a mathematical graph in which most brain areas are not directly connected but instead organized around a small number of hub regions [52, 53], sometimes called “the rich club” [54]. This organizational principle has been identified in social networks [55], gene networks [56, 57], and, more recently, the adult human brain [52, 58]. Hubs allow for the sharing of information within the network while minimizing the wiring cost. One possibility is that the same regional neural deficit can be associated with different cognitive profiles because of individual differences in the way brain regions are integrated via hubs.

We identified the rich club within our sample (Figure 6B—defined as parcels with a connection degree [number of connections] more than a standard deviation greater than the mean [59]). We then simulated an attack on these rich club areas by downgrading their connections to the minimum possible value (deleting the connection altogether does not work because many graph-theory measures also take into account the number of connections). To clarify, we calculated structural connectomes with real data for each child, and then experimentally altered the data to effectively remove the connections from each hub region in sequence. The sequence of hubs was randomized across participants. With each knockdown, global efficiency was recalculated, and the corresponding drop in network efficiency was measured. As the hubs were removed, efficiency dropped, but this was not consistent across children—the efficiency of some children’s brains strongly relied on hubs, others less so. Importantly, the impact of this simulated knockdown was strongly associated with children’s cognitive profile. We tested this by comparing the overall drop in efficiency resulting from the simulated knockdown across the six top-layer cognitive groupings idenitified in the original mapping process (mean ± SEM; Node 1 = −0.0819 ± 0.0006, Node 2 = −0.0876 ± 0.0007, Node 3 = −0.0761 ± 0.001, Node 4 = −0.0824 ± 0.0009, Node 5 = −0.0715 ± 0.004, and Node 6 = −0.0788 ± 0.0008). Cognitive grouping had a large effect on the impact of this simulated knockdown (Cohen’s f = 0.4461; F(5,202) = 5.29, p = 1.38 × 10⁻⁴; Figure 6C). For children with the most widespread and severe cognitive impairment, network efficiency was least dependent on the rich club. By contrast, network efficiency for children with high cognitive performance was the most reduced by the knockdown.

This process was then repeated for the same number of randomly selected peripheral brain areas (i.e., non-hub brain areas). There was no significant group difference in the non-hub knockdown effect (F(5,202) = 1.14, p = 0.3431), confirming that the difference across groups is specific to the reliance on hubs. We suspect that these differences only emerge with the simulated attack because of statistical power—with only 68 cortical parcels in our connectomes, the relative importance of hubs in determining whole-network efficiency may only emerge robustly once hubs are gradually removed.

Next, we looked specifically at the impact of the hub knockdown on the 19 parcels previously implicated in learning. We calculated the clustering coefficient for each of the 19 parcels previously implicated in learning. This coefficient provides a measure of the embeddness of that brain area within the network. The systematic rich club knockdown was then repeated, and each of the 19 parcel’s clustering coefficeint was recalculated after each attack. We could then establish the embeddeness of the 19 parcels with the hubs by tracking their mean drop in clustering coefficient with each attack (Figure 6D). Again, averaged across the 19 parcels, the same attack had different consequences according to a child’s cognitive grouping (F(5,202) = 3.53, p = 0.0045). Children with the most widespread and severe cognitive impairments had the least well-integrated parcels. Children with the highest cognitive abilities had the highest degree of embeddness with the hubs.

In short, properties of different connectomes respond differently to the same attack, thereby revealing different underlying organizational principles. Some children’s connectomes are strongly organized around hubs, and these children also have either no cognitive impariments at all or more selective deficits.

Discussion

The different cognitive profiles of children with developmental disorders cannot be well predicted from regional differences in gray matter. The same structural brain profile can result in a different set of cognitive symptoms across children. One important determinant of these relationships is the organization of a child’s whole-brain network. Some children’s brains are organized critically around hub regions, and areas implicated in learning are well embedded within these hubs. In these children, cognitive difficulties are restricted or non-existent. By contrast, the efficiency of some children’s brains is less reliant on hubs—these children are more likely to show widespread cognitive problems.

Children referred by educational and clinical services had deficits in phonological awareness, verbal and spatial short-term memory, complex span working memory tasks, vocabulary, and fluid reasoning. Four cognitive profiles were closely associated with these referrals relative to the non-referred comparison sample: broad impairments of a (1) relatively moderate or (2) severe nature and (3) more selective impairments in phonologically based tasks or (4) impairments in executive tasks including working memory. This is consistent with a transdiagnostic approach to understanding developmental disorders—cognitive strengths and weaknesses cut across disorders and difficulties [26, 27, 36]. This stands in contrast to theories that specify a particular cognitive impairment as being the route to a particular diagnosed learning problem [60] but is consistent with earlier ideas that developmental difficulties reflect complex patterns of associations rather than highly selective deficits [40].

Unsupervised machine learning techniques are rarely used with cognitive or neural data, but they are well suited to modeling highly complex multi-dimensional data, like this trandiagnostic cohort. They capture non-linear relationships [61], identify sub-populations [62, 63], and reveal underlying organizational principles not captured by linear data reduction methods [64]. An artificial neural network applied to both cognitive and cortical morphology data resulted in very different network architectures. The cognitive data produced a three-layer structure with six nodes in the top layer. The structural brain data, with higher dimensionality, produced a much flatter two-layer structure with 15 nodes in the top layer. These two different structures are significantly related, but not strongly—specific brain structures were not associated with particular cognitive profiles. Even simulated profiles that controlled for severity but with peaks and troughs in different locations could converge on very similar cognitive profiles. There are some demonstrations of this “equifinality” in the literature already [65, 66, 67, 68, 69, 70], but the demonstration of “multifinality” is more surprising and theoretically challenging. It is particularly challenging to accounts that posit some core underlying cognitive deficit with an associated specific neuro-anatomical substrate [71]. It is compelling evidence that unlike the impact of acquired brain damage in adulthood, neurodevelopmental disorders are unlikely to reflect spatially overlapping neural effects. Instead, these findings fit better with theoretical accounts that allow for the dynamic interaction between different brain systems across the course of development [72].

We propose that the relationship between a local neural effect and cognitive symptoms in childhood can only be understood when taking into account wider organizational brain properties [72, 73, 74]. Something that is still unclear is the causal relationship between these observations. For example, do local differences cause this greater integration to develop as a means of dynamic compensation over developmental time, or, does this integration vary across children regardless, making some more succeptable to the ongoing underdevelopment of specific regions? Within the current dataset, because of the referred nature of our sample and its age distribution, we controlled for age effects. However, future longitundinal data will be vital to disentangle these potentially separate accounts.

Hub organization appears to be present early, even prenatally, and gets refined by preferential attachment [75, 76, 77]. Preferential attachment describes how likely a new node will connect to an existing node in a network, given some statistical property of the existing node. Typically, preferential attachment refers to the notion that the more connected a node is, the more likely it is to receive new connections. But it is likely that multiple factors will drive individual differences in this organization, and dynamically so over developmental time. Individual variation in hub organization arises gradually, resulting from temporally dynamic interaction between brain regions. Differences in both genetics and experience could give rise to different parameterized geometrical and non-geometrical rules that underpin the growth of these networks [78]. Genes with relatively specific regional expression profiles, and with moderate neuronal excitability or efficiency, may play a causal role in regionally specific variations in neuronal development. For example, genes that are highly expressed in language and rolandic areas may be strongly predictive of the common developmental phenotype of language impairments and rolandic seizure activity [79, 80, 81, 82]. By contrast, genes that are highly expressed within multi-modal hub regions will likely play a key role in determining the overall properties of the network [83]. The interplay between these two pathways could determine a large amount of variance in the scope and severity of a child’s cognitive difficulties. This is yet another reason why longitudinal data will be vital in establishing changes in connectomic organization and how this varies according to gene expression and experience.

There are important limitations inherent in these data and our approach. First, while these gray-matter measures are used widely, they may not be specific enough regional brain data to establish links with cognition. The feature selection constrained the analysis to 19 parcels; these data pass through multiple processing steps (e.g., regressing out age effects, training the artificial neural network) that could remove crucial information. Furthmore, there could be regional microstructural differences that correspond to specific cognitive difficulties, not captured by the current neuroimaging methods. In short, spatially specific neural differences could be associated with different childhood cognitive difficulties, but they are lost in the analysis or not captured at all. Second, by focusing on transdiagnostic cognitive groupings, we are not able to examine the links between “pure” diagnoses and specific brain structures. This was intentional, but nonetheless, we have not tested whether more rarified diagnoses are significantly associated with particular brain structures. Third, controlling for age is an important limitation. The relationship between brain and cognition will likely change over development. For example, the neural processes associated with phonological difficulties in a 5 year old may be very different to those of a 10 year old. And finally, we only characterize the cognitive and learning impairments of the sample and not their social, environmental, or behavioral profiles. Other highly relevant domains, like home and school life, social processing, and behavior ratings [29], are more challenging to assess reliably and have psychometric properties that are difficult to model. For example, a child’s experiences (environmental interactions, nutrition, education) influence brain development [84] and cognitive test performance [85], but these factors are not measured in the current study.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
MATLAB	Mathworks	RRID: SCR_001622
K nearest-neighbor algorithm	MATLAB 2015a	Knnimpute function
R	RStudio 1.1.46	RRID: SCR_000432
DiPy	Python v.0.11 [86]	RRID: SCR_000029
ANTs	[87]	v1.9
A Computational Anatomy Toolbox for SPM (CAT12)	http://www.neuro.uni-jena.de/cat/	N/A
Statistical Parametric Mapping software (SPM12)	http://www.fil.ion.ucl.ac.uk/spm/software/spm12/)	RRID: SCR_007037
FreeSurfer v.5.3	http://surfer.nmr.mgh.harvard.edu	RRID: SCR_001847
LASSO regression, aka algorithm	Matlab2015a [88]	lasso function
GHSOM	https://github.com/DuncanAstle/DAstle	N/A
Brain Connectivity Toolbox (BCT)	Matlab2015a, BCT version 1.1.1.0 [73]	RRID: SCR_004841
FSL eddy tool	https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/eddy	N/A

Lead Contact and Materials Availability

Requests for resources should be directed to and will be fulfilled by the Lead Contact, Duncan Astle (duncan.astle@mrc-cbu.cam.ac.uk). This study did not generate new unique reagents.

Experimental Model and Subject Details

The largest portion of our sample was made up of children who were referred by practitioners working in specialist educational or clinical services to the Centre for Attention Learning and Memory (CALM), a research clinic at the MRC Cognition and Brain Sciences Unit, University of Cambridge. Referrers were asked to identify children with cognitive problems related to learning, with primary referral reasons including difficulties ongoing problems in “language,” “attention,” “memory,” or “learning / poor school progress.” Exclusion criteria were uncorrected problems in vision or hearing, English as a second language, or a causative genetic diagnosis. Children could have single, multiple or no formally diagnosed learning difficulty or neurodevelopmental disorder. Eight hundred and twelve children were recruited and tested. A consort diagram of the recruitment process can be found in Supplementary material, Figure S1. But only 337 from the referred sample were used in the current analysis, because they also had MRI scans. The 337 (117.1 months; 68.8% boys; Reading = −1.08; Maths = −0.86) were representative of the wider 812 referred to CALM (113.76 months; 69% boys; Reading = −0.87; Maths = −1.01). The prevalence of diagnoses were: ASD = 21, 6.3%; dyslexia = 31, 9.3%; obsessive compulsive disorder (OCD) = 4, 1.2%. Twenty‐four percent of the sample had a diagnosis of ADD or ADHD, and further 24 (7%) were under assessment for ADHD (on an ADHD clinic waiting list for a likely diagnosis of ADD or ADHD). Finally, 63 (19%) of the sample had received support from a Speech and Language Therapist (SLT) within the past 2 years, but in the UK these children are typically not given diagnoses of Specific Language Impairment or Developmental Language Disorder. These data were collected under the permission of the local NHS Research Ethics Committee (reference: 13/EE/0157).

We also included n = 142 children who had not been referred (mean age 119.08, range 81-189, 47.1% boys). These were recruited from surrounding schools in Cambridgeshire. These data were collected under the permission of the Cambridge Psychology Research Ethics Committee (references: Pre.2013.34; Pre.2015.11; Pre.2018.53). For all data, parents/legal guardians provided written informed consent and all children provided verbal assent.

In total four hundred and seventy nine of them underwent MRI scanning. These children were included in the main analysis (mean age 117, age range 62-223 months, 232 (68.4%) boys). Despite the increased likelihood of boys being referred for learning difficulties, gender was not significantly associated with the average performance across our cognitive measures [t(477) = −0.5858, p = 0.5583].

The 205 children who were included in the connectomics analysis were representative of the overall sample used for the rest of our analysis. They include 58% boys (versus 62.4% in the wider sample), mean age was 115.2 months (versus 117.9), age range was 66-215 (versus 62-223), and 33% came from the non-referred comparison sample (versus 30% in the overall sample). Full demographic information about the groups of participants are in Supplementary material, Tables S1–S2.

Method Details

Cognitive and Learning Assessments

A large battery of cognitive, learning, and behavioral measures were administered in the CALM clinic (see [30] for full protocol). Seven cognitive tasks meeting the following criteria were used in the current paper: (a) data were available for almost all children; (b) accuracy was the outcome variable; and (c) age standardized norms were available. For all measures, age-standardized scores were converted Z-scores using the mean and standard deviation from the respective normative samples to put all measures on a common scale (original age norms were a mix of scaled, t, and standard scores). The following measures of fluid and crystallized reasoning were included: Matrix Reasoning, a measure of fluid intelligence (Wechsler Abbreviated Scale of Intelligence [WASI] [89];); Peabody Picture Vocabulary Test (PPVT [90];). Phonological processing was assessed using the Alliteration subtest of the Phonological Awareness Battery (PhAB [91];). Important to note is that there is an obvious ceiling effect in this measure – it is only sensitive for younger children or those with phonological difficulties. Verbal and visuo‐spatial short‐term and working memory were measured using Digit Recall, Dot Matrix, Backward Digit Recall, and Mr X subtests from the Automated Working Memory Assessment (AWMA [92, 93];). These same measures were also used in the children not recruited via the CALM clinic.

	Non-referred Mean ± SEM	Referred Mean ± SEM	t test	P	Effect size Cohen’s d
Matrix Reasoning	0.14 ± 0.08	−0.64 ± 0.05	8.34	7.9x10−16	0.83
Vocabulary	0.85 ± 0.08	−0.02 ± 0.06	8.11	4.31x10−15	0.81
Alliteration	−0.08 ± 0.03	−0.54 ± 0.03	7.93	1.5x10−14	0.79
Forward Digit	0.43 ± 0.08	−0.45 ± 0.06	8.4	5.5x10−16	0.84
Dot Matrix	0.30 ± 0.08	−0.56 ± 0.05	8.6	2.2x10−16	0.86
Backward Span	0.31 ± 0.09	−0.51 ± 0.04	9.3	2.2x10−16	0.93
Mister X	0.57 ± 0.09	−0.18 ± 0.05	7.3	1.0x1012	0.73
Literacy	0.33 ± 0.07	−1.08 ± 0.05	15.79	2.2x10−16	1.58
Numeracy	0.31 ± 0.09	−0.86 ± 0.06	10.037	2.2x10−16	1

Mean and standard errors for referred and non-referred samples. All scores are given as z scores, relative to the age standardized normative sample for each test.

Learning measures (literacy and numeracy) were taken from the Wechler Individual Achievement Test II (WIAT II [94],) and the Wechler Objectove Numerical Dimensions (WOND [95],), save for 85 of the comparison children for which we used multiple subtests (reading fluency, single-word reading, passage comprehension, maths fluency and calculations) from the Woodcock Johnson Tests of Acheivement [96]. All learning scores were converted to z scores before analysis, using the mean and standard deviation from their respective standardization samples. Within the wider 812 referred sample we had an initial small group of 60 who did the Woodcock Johnson measures, but their scores do not differ significantly from the subsequent 60 referrals who undertook the WIAT measures. This gives us confidence that these two sets of learning measures are broadly as sensitive as each other to detect maths and reading difficulties.

We had almost complete data on all of these measures (ranging from 93% to 99% across the nine measures). Missing data were imputed using the K nearest-neighbor algorithm in MATLAB 2015a (MATLAB 2015a, The MathWorks, Natick, 2015), using the weighted average of the 20 nearest neighbors.

MRI Acquisition

Magnetic resonance imaging data were acquired at the MRC Cognition and Brain Sciences Unit, Cambridge UK. All scans were obtained on the Siemens 3 T Tim Trio system (Siemens Healthcare, Erlangen, Germany), using a 32‐channel quadrature head coil. T1‐weighted volume scans were acquired using a whole brain coverage 3D Magnetization Prepared Rapid Acquisition Gradient Echo (MP‐RAGE) sequence acquired using 1 mm isometric image resolution. Echo time was 2.98 ms, and repetition time was 2250 ms.

For 205 participants we also acquired diffusion weighted imaging data (DWI). Diffusion scans were acquired using echo‐planar diffusion‐weighted images with an isotropic set of 60 non‐collinear directions, using a weighting factor of b = 1000s^∗mm‐2, interleaved with a T2‐weighted (b = 0) volume. Whole brain coverage was obtained with 60 contiguous axial slices and isometric image resolution of 2 mm. Echo time was 90 ms and repetition time was 8400 ms.

Morphological Data Preprocessing and Analysis

Anatomical images were pre-processed using the computational anatomy toolbox (CAT12: http://www.neuro.uni-jena.de/cat/) for SPM 12 (Statistical Parametric Mapping software, http://www.fil.ion.ucl.ac.uk/spm/software/spm12/) in MATLAB 2018a in order to gather cortical thickness, gyrification and sulcus depth estimates. Initially, a non-linear deformation field was estimated that best overlaid the tissue probability maps on the individual subjects’ images. Then, we segmented these images into gray matter (GM), white matter (WM) and cerebral spinal fluid (CSF). Using these three tissue components, we calculated the overall tissue volume and total intracranial volume in the native space. All of the native-space tissue segments were registered to the standard Montreal Neurological Institute (MNI) template using the affine registration algorithm. Finally to refine inter-subject registration we modulated GM tissues using a non-linear deformation approach to compare the relative GM volume adjusted for individual brain size. In the same step, reconstruction of central surface and cortical thickness estimation based on the projection-based thickness (PBT) method [97] for ROI analysis was performed. In the next step, additional surface parameters, namely gyrification index and sulcus depth were calculated. Finally, data were visually inspected and we used the index of quality rating (IQR) from the CAT12 toolbox in SPM12, in which a score of over 60% is considered sufficient quality (in terms of noise, bias and resolution) for inclusion in subsequent analyses. All of our scans passed this threshold. Four hundered and thirty five of our participants scored between 80%–90%, a further 38 scored between 70%–80% and a further 6 scored between 60%–70%. The mean values for all three estimates were extracted for 68 ROIs defined by the Desikan‐Killiany atlas [49]. The estimated mean values of cortical thickness, gyrification and sulcus depth for each ROI were stored in separate files for further analysis.

Feature Selection

Feature selection is a common step in machine learning. It is generally considered to reduce overfitting, improve generalisability and aid interpretability [98]. Prior to the machine learning we used a a least absolute shrinkage and selection operator algorithm, aka. LASSO [88] regression, with a 10-fold hold out cross validation, regularising to the learning measures. Age in months was regressed from the raw parcel-wise values before they were entered to the LASSO algorithm. From the total cortical morphology measures (204), 21 were selected for the subsequent machine learning (Figure S2, Supplemental Information).

Growing Hierarchical Self-Organizing Maps

A Self-Organizing Map (SOM) is a simple artificial neural network [46]. They provide a means of representing multidimensional datasets as a 2D map. Once trained, this map is a model of the original input data, with individual measures represented as individual weight planes (or layers). Each node corresponds to a weight vector with the same dimensionality as the input data. I.e., once trained the map acts like a model of the original data, and each node is like a data point with the same number of values as the original input data. For example, if you have ten cognitive tasks, then the model will have 10 layers, with the node weights in each layer corresponding to each task.

A conventional SOM uses a flat 2D plane of nodes to represent the input data [28, 44]. There are two limitations of this: i) it is unclear how large the layer of nodes should be; and ii) the flat plane cannot capture hierarchical relationships, which may well be expected in data like these [99], necessitating some form of clustering to extract a higher order structure. In the current manuscript a variant of the traditional SOM algorithm was used, termed a Growing Hierarchical Self-Organizing Map (GHSOM). A full description can be found at [47], but what follows is a brief overview of their description.

The initial map contains just a single node and is initialised as the mean of all input vectors – i.e., the first node is just group mean across the tasks. The mean quantitization error (mqe) for this node is calculated. This is the mean distance between the original data points and this node. In other words, how good a job does this first node do of representing the data? The node-wise mqe value is important because it provides the basic mechanism by which the network grows over subsequent training steps. In the next step a new layer of four nodes is spawned, beneath the initial layer. This layer is then trained just as a standard SOM would be, and following the training the mqe for each node is calculated. If this exceeds a specified boundary then new nodes will need to be added, such that the input space can be better represented. The unit with the highest mqe will be the one that expands. To determine where the extra nodes should go the Euclidean distance between the existing nodes is calculated, surrounding the node with the highest mqe. Where the biggest gap exists a new row or column of nodes will be inserted, to decrease the distance between the node and its neighbors, and thereby reduce the node’s mqe are the next iteration. This process continues until the maps mean mqe reaches a particular fraction (Ʈ¹) of the unit in the original layer. This parameter, Ʈ¹, will determine the degree to which each subsequent map has to represent the information mapped onto its base unit.

The stopping criteria for the training process is MQE_m < Ʈ¹ ⋅ mqe_u, where MQE_m is the average mqe of the map being grown, and mqe_u is effectively the overall dissimilarity of the input items represented on the parent node.

As the training process continues additional layers can be added to further refine how data are represented by their parent units. If once the training process has finished a unit is representing too diverse a set of input vectors then a new map in the next layer is spawned. This threshold for this is determined by Ʈ². This defines the granularity requirement for each unit – i.e., the minimum quality of data representation required for each unit, defined as a fraction of the dissimilarity of all the input data. Once a new map is spawned it will be grown until it reaches the stopping criteria described above. The process of adding new layers continues until this stopping rule is reached: mqe_i < Ʈ² ⋅ mqe_0. Where mqe₀ reflects the mqe of the original layer – i.e., the single unit layer – and mqe_i represents the mqe of the nodes in the new layer. Thus this stopping rule reflects the minimum quality of representation for the lowest layer of each branch.

The GHSOM will automatically add nodes to guarantee the quality of data representation, within the constraints of these two parameters. In the current analysis we used Ʈ¹ = 0.7 and Ʈ² = 0.01, and this broadly reflects parameters used in previous GHSOM papers. Changing these parameters will affect the overall granularity of the network created. Crucially the same parameters were used for the MRI and cognitive data, so differences in network structure reflect differences in the nature of the input data rather than parameter choices for the learning algorithm.

Diffusion Weighted Imaging (DWI) Data Preprocessing

The DWI data (see Supplementary material, Table S1 for demographic information) were first converted DICOM images into NIfTI‐1 format, then we applied correction for motion, eddy currents, and field inhomogeneities was applied using FSL eddy tool (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/eddy) (see Supplementary, Figure S4). Next, non‐local means de‐noising [100] was applied using the Diffusion Imaging in Python (DiPy) v0.11 package [86] to boost signal‐to‐noise ratio. For ROI definition, T1‐weighted images were submitted to nonlocal means denoizing in DiPy, robust brain extraction using ANTs v1.9 [87], and reconstruction in FreeSurfer v5.3 (http://surfer.nmr.mgh.harvard.edu). Regions of interests were based on the Desikan‐Killiany parcellation of the MNI template [49]. The cortical parcellation was expanded by 2 mm into the subcortical white matter. The parcellation was moved to diffusion space using FreeSurfer tools.

Connectome Construction

We used diffusion weighted imaging data to construct the white matter connectome. After standard steps of preprocessing that are explained above, the general procedure of estimating the most probable white matter connections for each individual followed. Then, we obtained measures of fractional anisotropy (FA). For each pairwise combination of ROIs, the number of streamlines intersecting both ROIs was estimated and transformed to a density map. The weight of the connection matrices was based on fractional anisotropy (FA). In summary, the connectomes presented in the main analysis represent the FA value of white matter connections between cortical regions of interest (Figure 6A). To remove potentially spurious connections, for each individual connectome the bottom 10% of edges by FA were removed. This was done individually thereby controlling for connection density while allowing the absolute threshold to vary from individual to individual [101].

Quantification and Statistical analysis

Graph Theory Measures To Evaluate Simulated Attacks

The current analysis focused on global efficiency (E_G) and the local clustering coefficient (C_j). We calculated global efficiency for weighted undirected networks as described in the Brain Connectivity Toolbox [73]. These were calculated for each individual child. We then simulated an attack on each child’s connectome by randomly choosing one of 8 hub regions and setting its connection strengths to the minimum value observed in the data. We then recalculated global efficiency and substracted the value pervious to the attack to identify the relative drop in efficiency. This was repeated for the next hub region, and so on. This process was repeated across all 205 children. We then tested whether the overall drop in efficiency as a result of the attack was significantly different according to the child’s cognitive profile, using a one-way ANOVA. The same approach was taken for calculating the local clustering coefficient for each of the 19 parcels implicated in learning. The average drop across all 19 was calculated and compared using a one-way ANOVA.

Data and Code Availability

The code generated during this study is available at https://github.com/DuncanAstle/DAstle. The datasets supporting the current study have not been deposited in a public repository because of restrictions imposed by NHS ethical approval, but are available from the corresponding author on request.

Published: February 27, 2020