Abstract
This study investigates the propagation power and effects of the coronavirus disease 2019 (COVID-19) in light of published data. We examine the factors affecting COVID-19 together with the spatial effects, and use spatial panel data models to determine the relationship among the variables including their spatial effects. Using spatial panel models, we analyse the relationship between confirmed cases of COVID-19, deaths thereof, and recovered cases due to treatment. We accordingly determine and include the spatial effects in this examination after establishing the appropriate model for COVID-19. The most efficient and consistent model is interpreted with direct and indirect spatial effects.
Keywords: COVID-19, Spatial effects, Spatial panel data models
1. Introduction
Twenty-seven cases of pneumonia of unidentified aetiology were discovered in Wuhan city, Hubei province of China on 31 December 2019. Wuhan city is the most densely populated city in central China, with more than 11 million residents. In the 27 cases, most patients were admitted into hospitals with clinical symptoms of fever, dry cough, dyspnoea, and bilateral lung infiltrates as seen on imaging. All incidents were correlated to the city’s Huanan Seafood Wholesale Market which predominantly sells a diversity of fish as well as live animals such as marmots, bats, poultry, and snakes (Lu et al., 2020). The causative agent was detected from throat swab samples of patients, taken by the Chinese Centre for Disease Control and Prevention (CCDC) on 7 January 2020. The coronavirus disease 2019 (COVID-19), as labelled by the World Health Organization (WHO), was declared to cause Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) (WHO Director-General’s remarks at the media briefing on 2019-nCoV on 11 February 2020, 2020 February 11).
To date, most patients with SARS-CoV-2 have had developed mild symptoms, such as sore throat, dry cough, and fever. Many cases have been unexpectedly determined. However, a minority of patients have been known to develop fatal complications, such as septic shock, organ failure, severe pneumonia, pulmonary oedema, and acute respiratory distress syndrome.
As per recent statistics, 54.3% of those diagnosed with SARS-CoV-2 were male with a median age of 56 years. Patients who required intensive care help were, on average, older and/or were previously diagnosed with comorbidities, such as cerebrovascular, cardiovascular, digestive, endocrine, and chronic respiratory disease.
Those in intensive care were also more likely to report abdominal pain, dizziness, dyspnoea, and anorexia (Wang et al., 2020).
Efforts directed toward interpreting the pathophysiology of COVID-19 have led to the EU mobilizing €10,000,000 into research that would “contribute to more efficient clinical management of patients infected with the virus, as well as public health preparedness and response” (Coronavirus: EU mobilises €10 million for research, 2020 January 31). Further, US-based corporations such as Co-Diagnostics and the Novacyt’s molecular diagnostics division Primerdesign have been developing COVID-19 testing kits for use in the research setting (Primerdesign launches molecular test for new coronavirus, 2020 January 31). The UK government has also sanctioned £20,000,000 to support the development of a COVID-19 vaccine (Coronavirus: UK donates £20 m to speed up vaccine, 2020 February 3). Given the nature of the pandemic, COVID-19 has been a subject of intense discussion since the beginning of 2020. As the pandemic spreads exponentially, healthcare enterprises and non-profit organizations have already begun work to counter it.
In this study, we investigate the propagation power and effects of COVID-19 in light of published data. Thus, the factors affecting COVID-19 are examined together with spatial effects, and spatial panel data models are used to determine the relationship among the variables (factors) with spatial effects. Using spatial panel models, we analyse the relationship between the rate of confirmed cases () of COVID-19, the rate of deaths (), the rate of recovered cases () due to treatment, with spatial and temporal effects.
2. Methodology
We first estimate a standard linear panel data model devoid of spatial effects. This model can be used as a reference for the estimation results of spatial panel data models as well as to check the robustness of these estimation results (Yang et al., 2017). The formulation of a standard linear regression model (SLM) is as follows (Baum and Christopher, 2006, Tatoglu, 2012):
| (1) |
where is the explained variable, denotes the individuals, and constitutes the regions (). is the dimension of the time series, that is, from 22 January 2020 to 10 March 2020. is the vector of observations of the explanatory variables and is the vector of undetermined coefficients. is an individual effect that cannot be directly observed and quantified and is a disturbance term that varies with the individual and time. If is related to , the panel data model is a fixed effects model; otherwise, it is a random effects model (Fotheringham and Rogerson, 2008).
Spatial panel data models include the spatial autoregression model (SAR), spatial error model (SEM), spatial autocorrelation model (SAC), and spatial Durbin model (SDM). These models consider the spatial effects based on the SLM and they are estimated using the maximum likelihood principle. Among them, the SAR model considers the spatial spillover effect of the dependent variable. Hence, its formula includes the spatial lag term of the dependent variable, which can be expressed as follows:
| (2) |
where is the spatial lag of the dependent variable and is the contiguity based on the weighted Rook matrix. is the spatial autoregression coefficient. If has statistical significance, it demonstrates the existence of a significant spatial dependence among the dependent variables. That is, a confirmed case in a region depends on the contiguous regions. The value of reflects the degree of the spatial dependence (Gelfand et al., 2010).
The SEM discovers the effects of the omitted variables on the observation of the determined (dependent) variable in a provincial area, which contains a spatial error term. A spatial autocorrelation among residuals is thus practical and the SEM can be formulated as follows:
| (3) |
| (4) |
where is the spatial error term, is the autoregressive factor, and is a random error term that is usually assumed to be independent and identically distributed (i.i.d.). We can confirm the existence of hidden independent variables with spatial autocorrelation if is statistically significant, which results in the trend of a noticeable spatial autocorrelation in the residuals. The SAC model is a combination of the SAR models and SEMs; it consists of the dependent variable spatial lag and a spatial error term, which can be expressed as follows:
| (5) |
In the above equation, corresponding to various research functions and needs, SWM W1 and SWM W2 (spatial weight matrix) can be the same or different (LeSage, 2008, Yang et al., 2017). In this study, we used the same SWM to estimate the model, that is, , and the residual terms are the same as those revealed above.
The SDM includes the dependent variable spatial lags and explanatory variables. It uses the marginal effects of the explanatory variables from the nearby regions/state based on the SAR model. The common specification for the SDM is as follows:
| (6) |
where is the explanatory variables’ spatial lag, is the constant independent variable matrix, and is the vector of the parameters that determine the marginal effects of the independent variables from nearby observations on , the dependent variable.
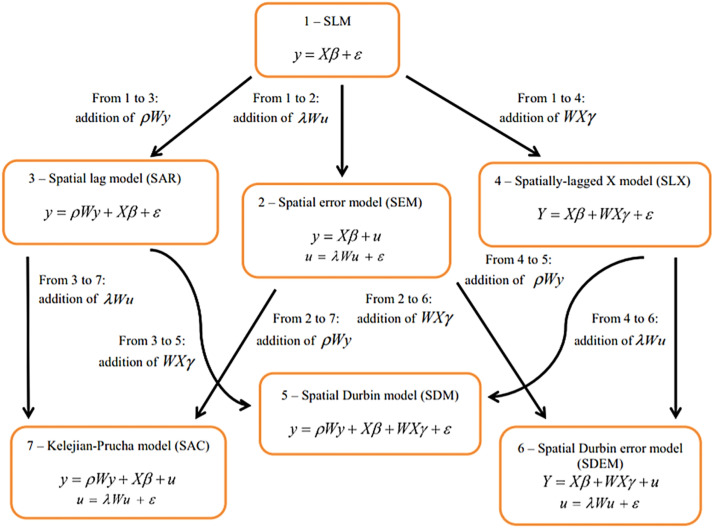
Fig. 1, which is similar to a part of the figure presented in Elhorst (2010), illustrates the relationships among the previously stated spatial panel models. First, we examine the SLM estimated by ordinary least squares. We start with this model, as it is the simplest and most common. Though it is a non-spatial effect model, it is frequently used as a diagnostic tool for model specification and is a benchmark for comparisons with spatial models.
Fig. 1.
Relationships among spatial panel models .
Source: Some Spatial Models (Golgher and Voss, 2016).
We also represent the SEM, as the interpretation of the coefficients is similar to that of an SLM. The SAR is introduced in Section 3. Because of endogenous spatial dependence in this model, it is more challenging to interpret the coefficients. This section also examines the SAC model (Kelejian and Prucha, 1998), which is characteristically close to the SAR model. In Section 4, we present two regression models with spatial lags only in the independent variables—the spatially-lagged X model (SLX) other than the spatial Durbin error model, both of which include exogenous spatial dependence. In Section 5, we consider he interpretation of coefficients for an SDM, which includes both exogenous and endogenous spatial dependencies, consequently complicating the interpretation more than for the preceding models (Golgher and Voss, 2016).
3. Data and empirical results
3.1. Dataset and descriptive statistics
For the purpose of our objective, we include sampling data from 22 January 2020 to 10 March 2020 for the 311 regions in Mainland China. The data are collected from the COVID-2019 situation reports2 by WHO. We analyse the relationship between the rate of confirmed cases () of COVID-19, the rate of deaths (), and the rate of recovered cases (), with spatial and temporal effects. The rates are calculated classifying each variable by the population in the province. Population statistics for each province is collected from the National Bureau of Statistics of China.3 The statistics of the rate of confirmed deaths and recovered cases on 10 March 2020 and average statistics are presented in Table A.1.
Table A.1.
COVID-19 descriptive statistics in Mainland China.
| Region | 10 March 2020 |
Mean |
||||
|---|---|---|---|---|---|---|
| Hubei | 10.7147 | 7.5495 | 7.5495 | 6.4980 | 2.1258 | 0.2406 |
| Guangdong | 0.2139 | 0.2015 | 0.2015 | 0.1586 | 0.0784 | 0.0005 |
| Henan | 0.2011 | 0.1972 | 0.1972 | 0.1461 | 0.0839 | 0.0018 |
| Zhejiang | 0.1921 | 0.1883 | 0.1883 | 0.1460 | 0.0788 | 0.0001 |
| Hunan | 0.1610 | 0.1565 | 0.1565 | 0.1195 | 0.0692 | 0.0003 |
| Anhui | 0.1565 | 0.1556 | 0.1556 | 0.1122 | 0.0610 | 0.0006 |
| Jiangxi | 0.1478 | 0.1466 | 0.1466 | 0.1066 | 0.0577 | 0.0001 |
| Shandong | 0.1199 | 0.1137 | 0.1137 | 0.0765 | 0.0352 | 0.0004 |
| Jiangsu | 0.0998 | 0.0991 | 0.0991 | 0.0712 | 0.0402 | 0.0000 |
| Chongqing | 0.0911 | 0.0865 | 0.0865 | 0.0683 | 0.0342 | 0.0006 |
| Sichuan | 0.0852 | 0.0756 | 0.0756 | 0.0603 | 0.0279 | 0.0003 |
| Heilongjiang | 0.0761 | 0.0686 | 0.0686 | 0.0507 | 0.0223 | 0.0013 |
| Beijing | 0.0678 | 0.0506 | 0.0506 | 0.0481 | 0.0201 | 0.0006 |
| Shanghai | 0.0544 | 0.0504 | 0.0504 | 0.0409 | 0.0223 | 0.0003 |
| Hebei | 0.0503 | 0.0485 | 0.0485 | 0.0343 | 0.0207 | 0.0005 |
| Fujian | 0.0468 | 0.0466 | 0.0466 | 0.0356 | 0.0177 | 0.0001 |
| Guangxi | 0.0398 | 0.0370 | 0.0370 | 0.0293 | 0.0129 | 0.0002 |
| Shaanxi | 0.0387 | 0.0359 | 0.0359 | 0.0289 | 0.0149 | 0.0001 |
| Yunnan | 0.0275 | 0.0269 | 0.0269 | 0.0211 | 0.0110 | 0.0001 |
| Hainan | 0.0266 | 0.0251 | 0.0251 | 0.0196 | 0.0105 | 0.0005 |
| Guizhou | 0.0231 | 0.0204 | 0.0204 | 0.0160 | 0.0083 | 0.0002 |
| Tianjin | 0.0215 | 0.0207 | 0.0207 | 0.0151 | 0.0078 | 0.0003 |
| Shanxi | 0.0210 | 0.0207 | 0.0207 | 0.0157 | 0.0088 | 0.0000 |
| Gansu | 0.0198 | 0.0139 | 0.0139 | 0.0115 | 0.0069 | 0.0002 |
| Liaoning | 0.0198 | 0.0176 | 0.0176 | 0.0150 | 0.0072 | 0.0001 |
| Jilin | 0.0147 | 0.0144 | 0.0144 | 0.0104 | 0.0057 | 0.0001 |
| Xinjiang | 0.0120 | 0.0115 | 0.0115 | 0.0082 | 0.0037 | 0.0002 |
| Inner Mongolia | 0.0119 | 0.0111 | 0.0111 | 0.0085 | 0.0034 | 0.0000 |
| Ningxia | 0.0119 | 0.0112 | 0.0112 | 0.0081 | 0.0052 | 0.0000 |
| Qinghai | 0.0028 | 0.0028 | 0.0028 | 0.0023 | 0.0016 | 0.0000 |
| Tibet | 0.0002 | 0.0002 | 0.0002 | 0.0001 | 0.0001 | 0.0000 |
Note: The rates are multiplied by 100,000.
Table A.1 shows that Hubei had the highest concentration of the rate of confirmed cases (10.714 cases per 100,000 people), followed by Guangdong (0.214 cases per 100,000 people) and Henan (0.201 cases per 100,000 people). The least rate of confirmed cases was from Ningxia, Qinghai, and Tibet. These data are up to 10 March 2020. In Hubei, an average of 6.498 out of 100,000 people tested positive for COVID-19, 2.126 out of 100,000 patients recovered, and 0.241 out of 100,000 people lost their lives. For Guangdong, these statistics are 0.159, 2.126, and 0.241, respectively.
3.2. Comparison of Spatial Panel Models estimation
Before fitting spatial panel models, we require an SWM matrix. An SWM characterizes the spatial relationships among variables in a dataset (Fotheringham and Rogerson, 2008, Zeren, 2010). The in this research was 31 × 31, row-standardized with zero diagonal factors and developed via the conceptualization of spatial relations of the polygon rook contiguity in Stata 16. Formally,
| (7) |
| (8) |
| (9) |
This form is then transformed into a suitable format for Stata 16.0 and is used in spatial panel regression.
To manage the spatial autocorrelation effect of the dependent variable and correctly analyse the affecting factors and their spatial spillover effects, spatial panel data models can be used. Compared with standard linear panel data models, spatial panel data models take on spatial effects, such as the spatial dependence and spillover effects. Further, compared with the spatial model built on cross-sectional data, the spatial panel data model can grasp the individual heterogeneity of spatial units – that is, individual effects – and can escape missing variables and estimation errors more efficiently (Elhorst, 2014)
Before estimating spatial panel data models, we need to test for cross-sectional dependence. The primary issue when confronted with spatially referenced data is to determine whether spatial dependence exists, that is, whether “nearby” cases are more correlated than distant ones. A flexible way of assessing whether dependence in the cross-section of a panel dataset is spatially related is the particularization of the Pesaran (2004) test for general cross-sectional dependence (Croissant and Millo, 2019, Tatoğlu, 2013).
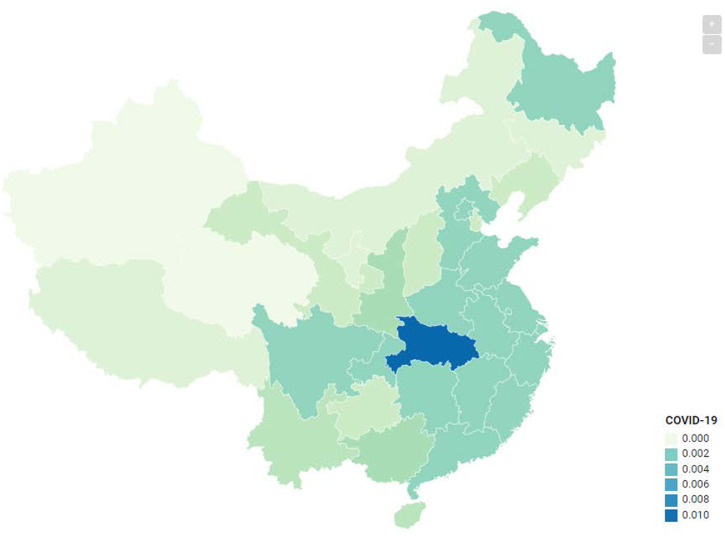
Table 1 shows the cross-sectional dependence test reports; we can reject that the null hypothesis errors are i.i.d. This is not surprising given our hit map visual (Fig. 2) appraisal of confirmed COVID-19 cases. Consequently, we require spatial panel models.
Table 1.
Spatial panel models for COVID-19 in China.
| Spatial panel models |
|||||||
|---|---|---|---|---|---|---|---|
| Variables | SLM | SAR (1) | SEM (2) | SAC (3) | SLX (4) | SDM (5) | SDEM (6) |
| −0.729 | −0.734*** | −0.729*** | −0.734*** | −0.734*** | −0.734*** | −0.734*** | |
| 32.378 | 32.467*** | 32.391*** | 32.472*** | 32.486*** | 32.498*** | 32.487*** | |
| cons | 0.001 | 0.067*** | 0.068*** | 0.067*** | 0.067*** | 0.067*** | 0.067*** |
| 0.052*** | 0.059*** | −0.048 | |||||
| −0.033 | −0.117** | −0.067 | |||||
| lag.r | −0.127** | −0.060 | −0.024 | ||||
| lag.d | 1.719*** | 3.290*** | 1.717*** | ||||
| Temporal effects | Table A.2 | ||||||
| Statistics | |||||||
| F-stat / LR stat | 1564*** | 82731*** | 78735*** | 84297*** | 85972*** | 83092*** | 83649*** |
| R2 /Pseudo R2 | 0.9905 | 0.9910 | 0.9905 | 0.9914 | 0.9916 | 0.9911 | 0.9913 |
| LM test of common spatial terms | 31.627*** | 0.600 | 40.590*** | 41.853*** | 38.282*** | 40.328*** | |
| AICc | −3802.08 | −3720.996 | −3690.331 | −3724.130 | −3725.134 | −3723.516 | −3724.639 |
| BIC | −3530.47 | −3444.054 | −3413.389 | −3413.862 | −3445.866 | −3435.922 | −3437.045 |
Peseran-CD test stat 21.791 prob<0.01
SLX model Hausman Test chi (49) 25.18 (prob<0.001)
SLX Model LM test chi (1) 4.02 (prob<0.050)
SLX Model LM chi (1) 11.94 (prob<0.001)
* ; ** ; *** .
Fig. 2.
Spread of COVID-19 in Mainland China on 10 March 2020.
The estimation results for the SLM and the six spatial panel data models are shown in Table 1. The parameters of the spatial panel models are estimated using the quasi-maximum likelihood estimator derived by Lee and Yu (2010) and the -value is calculated using the robust standard error. All of spatial panel data models include two-way effects: individual (cross) and temporal (time) effects. Temporal effects for each spatial panel model are shown in Table A.2.
Table A.2.
Temporal effects of spatial panel model.
| Spatial panel models |
|||||||
|---|---|---|---|---|---|---|---|
| Temporal effects | SLM | SAR(1) | SEM(2) | SAC(3) | SLX(4) | SDM(5) | SDEM(6) |
| Ref. | |||||||
| 0.0006 | 0.0006 | 0.0006 | 0.0005 | 0.0006 | 0.0006 | 0.0006 | |
| 0.0013 | 0.0012 | 0.0013 | 0.0012 | 0.0013 | 0.0013 | 0.0012 | |
| 0.0026 | 0.0023 | 0.0026 | 0.0022 | 0.0024 | 0.0025 | 0.0024 | |
| 0.0043 | 0.0039 | 0.0043 | 0.0037 | 0.0041 | 0.0042 | 0.0040 | |
| 0.0050 | 0.0044 | 0.0051 | 0.0043 | 0.0046 | 0.0049 | 0.0046 | |
| 0.0105 | 0.0093 | 0.0105 | 0.0092 | 0.0098 | 0.0103 | 0.0098 | |
| 0.0138 | 0.0124 | 0.0138 | 0.0122 | 0.0131 | 0.0137 | 0.0131 | |
| 0.0187 | 0.0168 | 0.0187 | 0.0166 | 0.0177 | 0.0186 | 0.0178 | |
| 0.0225 | 0.0202 | 0.0225 | 0.0199 | 0.0213 | 0.0224 | 0.0213 | |
| 0.0275 | 0.0246 | 0.0274* | 0.0242 | 0.0260 | 0.0272 | 0.026 | |
| 0.0351** | 0.0313* | 0.0351** | 0.0308** | 0.0330* | 0.0346** | 0.0330** | |
| 0.0418** | 0.0373** | 0.0417** | 0.0366** | 0.0393** | 0.0412** | 0.0393** | |
| 0.0516*** | 0.0463*** | 0.0516*** | 0.0455*** | 0.0488*** | 0.0512*** | 0.0487*** | |
| 0.0594*** | 0.0534*** | 0.0594*** | 0.0524*** | 0.0562*** | 0.0589*** | 0.0561*** | |
| 0.0660*** | 0.0593*** | 0.0659*** | 0.0582*** | 0.0624*** | 0.0654*** | 0.0622*** | |
| 0.0716*** | 0.0641*** | 0.0715*** | 0.0631*** | 0.0675*** | 0.0708*** | 0.0674*** | |
| 0.0743*** | 0.0663*** | 0.0743*** | 0.0651*** | 0.0698*** | 0.0731*** | 0.0697*** | |
| 0.0756*** | 0.0669*** | 0.0756*** | 0.0659*** | 0.0705*** | 0.0740*** | 0.0705*** | |
| 0.0759*** | 0.0667*** | 0.0759*** | 0.0655*** | 0.0702*** | 0.0737*** | 0.0702*** | |
| 0.0747*** | 0.0651*** | 0.0747*** | 0.0638*** | 0.0685*** | 0.0719*** | 0.0684*** | |
| 0.0782*** | 0.0684*** | 0.0782*** | 0.0672*** | 0.0720*** | 0.0756*** | 0.0720*** | |
| 0.1051*** | 0.0926*** | 0.1051*** | 0.0911*** | 0.0975*** | 0.1023*** | 0.0975*** | |
| 0.1161*** | 0.1025*** | 0.1161*** | 0.1008*** | 0.1078*** | 0.1131*** | 0.1078*** | |
| 0.1127*** | 0.0987*** | 0.1127*** | 0.0969*** | 0.1037*** | 0.1088*** | 0.1036*** | |
| 0.1135*** | 0.0990*** | 0.1134*** | 0.0971*** | 0.1040*** | 0.1091*** | 0.1038*** | |
| 0.1150*** | 0.1002*** | 0.1150*** | 0.0982*** | 0.1051*** | 0.1103*** | 0.1050*** | |
| 0.1120*** | 0.0968*** | 0.1119*** | 0.0946*** | 0.1014*** | 0.1064*** | 0.1012*** | |
| 0.1067*** | 0.0915*** | 0.1066*** | 0.0892*** | 0.0957*** | 0.1004*** | 0.0954*** | |
| 0.1008*** | 0.0855*** | 0.1007*** | 0.0831*** | 0.0893*** | 0.0937*** | 0.0889*** | |
| 0.1058*** | 0.0905*** | 0.1057*** | 0.0880*** | 0.0944*** | 0.0991*** | 0.0940*** | |
| 0.0990*** | 0.0834*** | 0.0988*** | 0.0809*** | 0.0868*** | 0.0911*** | 0.0863*** | |
| 0.1005*** | 0.0849*** | 0.1004*** | 0.0826*** | 0.0884*** | 0.0928*** | 0.0880*** | |
| 0.0905*** | 0.0749*** | 0.0904*** | 0.0724*** | 0.0778*** | 0.0817*** | 0.0773*** | |
| 0.0924*** | 0.0767*** | 0.0923*** | 0.0742*** | 0.0796*** | 0.0835*** | 0.0790*** | |
| 0.0952*** | 0.0794*** | 0.0950*** | 0.0769*** | 0.0823*** | 0.0864*** | 0.0817*** | |
| 0.1012*** | 0.0855*** | 0.1011*** | 0.0830*** | 0.0885*** | 0.0929*** | 0.0880*** | |
| 0.1056*** | 0.0898*** | 0.1055*** | 0.0874*** | 0.0930*** | 0.0975*** | 0.0924*** | |
| 0.1102*** | 0.0943*** | 0.1100*** | 0.0918*** | 0.0976*** | 0.1023*** | 0.0970*** | |
| 0.1159*** | 0.1000*** | 0.1158*** | 0.0975*** | 0.1035*** | 0.1084*** | 0.1028*** | |
| 0.1194*** | 0.1034*** | 0.1192*** | 0.1010*** | 0.1070*** | 0.1121*** | 0.1063*** | |
| 0.1230*** | 0.1071*** | 0.1229*** | 0.1046*** | 0.1107*** | 0.1160*** | 0.1100*** | |
| 0.1264*** | 0.1105*** | 0.1263*** | 0.1080*** | 0.1141*** | 0.1196*** | 0.1134*** | |
| 0.1285*** | 0.1126*** | 0.1285*** | 0.1104*** | 0.1163*** | 0.1219*** | 0.1157*** | |
| 0.1305*** | 0.1146*** | 0.1305*** | 0.1123*** | 0.1183*** | 0.1240*** | 0.1177*** | |
| 0.1320*** | 0.1161*** | 0.1320*** | 0.1138*** | 0.1198*** | 0.1255*** | 0.1192*** | |
| 0.1340*** | 0.1181*** | 0.1340*** | 0.1159*** | 0.1219*** | 0.1277*** | 0.1213*** | |
| 0.1355*** | 0.1196*** | 0.1354*** | 0.1173*** | 0.1234*** | 0.1292*** | 0.1227*** | |
| 0.1375*** | 0.1216*** | 0.1374*** | 0.1193*** | 0.1254*** | 0.1314*** | 0.1248*** | |
Note: The values of the coefficient are multiplied by 100,000
* ; ** ; *** .
Firstly, we eliminated SEM (2), SDM (5) and SDEM (6) models since there was spatial effect no statistically significant at %5 level. Following, we had to choose from models such as SAR (1), SAC (3) and SLX (4). The estimated coefficient of the spatially lagged independent variables (LM and LM) in the SLX (spatially-lagged X) model was statistically significant at the %5 level. That is, the rate of confirmed COVID-19 cases for provinces in China is spatially correlated. This further suggests that it is necessary to construct spatial panel data models rather than SLMs, which do not consider spatial effects, if our objective is to explore the influencing factors of the rate of confirmed cases and their spatial spillover effects.
The pseudo-R2 (99.16), likelihood ratio-stat (LR-stat) (85972), and Lagrange multiplier (LM) test of common spatial terms stat (41.853) for the SLX are higher than SAR (1) and SAC (2) models. Its value of the corrected Akaike information criterion (AICc) (−3725.134), which is calculated for small samples, and Bayesian information criterion (BIC) (−3725.134) is also lower than the SAR and SAC models. The LM, and LM test statistics for the SLX are significant at the %5 level, and, hence, spatial effects of explanatory variables (LM, LM) are different from zero. Hausman test statistics is 21.791 for SLX; further, the fixed effects SLX is more consistent in comparison with the random effects SLX (prob<0.001). Consequently, the SLX can be considered a better-fitting spatial panel regression model. Therefore, we mainly interpret the influencing factors based on the estimation results of the SLX in the following analysis.
3.3. Analysis of spatial effects
The average direct, indirect, and total effects of these explanatory variables are presented in Table 2. The direct effect expresses the marginal effect of the change in the independent variable of one percent on the dependent variable of the same unit. The indirect effect is the marginal effect of the change in the independent variable in one percent on the dependent variable value of all neighbouring units. The total effect is the sum of both effects. The average direct effects of the rate of recovered cases and the rate of deaths are 32.485 (prob<0.001) and −0.734 (prob<0.001), respectively, indicating that one-percent increase in the rate of deaths (example, in Hubei) leads to 32% positive change in the rate of confirmed cases (in Hubei) and a one-percent increase in the rate of recovered cases leads to 0.7% negative change in the ratio of confirmed cases (in Hubei), respectively.
Table 2.
Spatial effects of independent variables of the SLX.
| Independent variables |
dy/dx | Delta-Method Std. Err. | Prob | 95% Confidence interval |
|
|---|---|---|---|---|---|
| Lower | Higher | ||||
| Direct spatial effects | |||||
| 32.485 | 0.185 | <0.001 | 32.122 | 33.849 | |
| −0.734 | 0.013 | <0.001 | −0.759 | −0.708 | |
| Indirect spatial effects | |||||
| 1.663 | 0.481 | <0.001 | 0.720 | 2.607 | |
| −0.025 | 0.033 | 0.436 | −0.091 | 0.039 | |
| Total spatial effects | |||||
| 34.150 | 0.536 | <0.001 | 33.099 | 35.199 | |
| −0.759 | 0.036 | <0.001 | −0.831 | −0.688 | |
Compared with the average direct effects and the estimated coefficients, the average indirect effects can more comprehensively reflect the actual effect of the influencing factors. The indirect effects of the rate of recovered cases are measured at 1.663 (prob<0.001), indicating that a one-percent increase in the rate of deaths (in Hubei) leads to 1.7% positive change in the rate of confirmed cases (in neighbouring regions of Hubei, namely, Henan, Anhui etc.). However, the indirect effect of the rate of recovered cases is not significant at the 5% level (prob>0.05).
Table A.2 shows temporal effects of SLX model. We consider that the rate of confirmed cases in the first days increased slightly and it was not statistically significant at %5 level. However, for the SLX model, after 3 February 2020 date, the rate of confirmed case increases had become statistically significant. The increase in the rate of confirmed cases since the beginning of March 2020 has become dramatic. So, we contemplate that the confirmed cases on 10 March 2020 compared to 22 January 2020 date increased by 0.1254 cases in 100,000 people.
4. Conclusion
Built on the spatial panel data of 31 regions in China from 22 January 2020 to 10 March 2020, we investigated the influencing variables (the rate of deaths and recovered cases) and their spatial spillover effects of COVID-19. Before we built and compared the spatial panel data models, we tested the cross-sectional dependence using the Pesaran test. We thus found cross-sectional dependence between the units.
Among the panel data regression models estimated to capture spatial effects, the most efficient and consistent model was determined according to the maximum pseudo-R2, LR-test, LM-test statistics, and minimum AICc and BIC values. The results of the model comparison allowed us to select the SLX from the predicted spatial panel data models for interpretation.
In the SLX model, the spatial effects of the dependent and independent variables were examined separately. Specifically, the independent variables effects were split into the total, indirect (spatial spillover effects), and direct effects in order to improve the identification of the actual impacts and spatial interactions of the factor components on COVID-19.
We thus draw the following conclusions:
-
•
As per the total effect, the rate of deaths has significant positive effects, while the rate of recovered cases has significant negative effects on COVID-19.
-
•
As per the direct effect, the rate of deaths has significant positive effects on COVID-19. That is, a one-percent increase in the rate of deaths leads to 32% the rate of confirmed positive changes. In addition, the recovered cases have significant negative effects on COVID-19. That is, a one-percent increases in the rate of recovered cases leads to 0.7% confirmed negative changes.
-
•
As per the indirect effect, the rate of deaths has significant positive effects on COVID-19 in the neighbouring region. That is, a one-percent increase in the rate of deaths leads to 1.7% confirmed positive changes in the neighbouring regions. However, the rate of recovered cases did not have significant negative effects on COVID-19.
-
•
As a result of the temporal effect analysis, the rate of confirmed cases is increasing day by day. We compared the date of 22 January 2020 with the date of 10 March 2020, the confirmed cases had increased nearly by 0.13 cases per 100,000 people, in other word, 13 cases per 10,000,000 people.
Some limitations need to be addressed while discussing the results of the present study. We cannot model the rate of deaths because of the presence of high proportion of zeros. In addition, we consider that the time period is short. Future research can be examined with a big dataset.
In general, this study had provided researchers with information about the effects of the spread of the COVID-19 virus. Therefore, the effects of the spread of the virus have been addressed both spatially and temporally, and efforts have been made to produce information that would be useful to all humanity.
Footnotes
Anhui, Beijing, Chongqing, Fujian, Gansu, Guangdong, Guangxi, Guizhou, Hainan, Hebei, Heilongjiang, Henan, Hubei, Hunan, Inner Mongolia, Jiangsu, Jiangxi, Jilin, Liaoning, Ningxia, Qinghai, Shaanxi, Shandong, Shanghai, Shanxi, Sichuan, Tianjin, Xinjiang, Tibet, Yunnan, and Zhejiang.
Appendix.
References
- Baum C.F., Christopher F. 2006. An introduction to modern econometrics using stata. stata press. [Google Scholar]
- Coronavirus: EU mobilises €10 million for research, 2020 January 31. Retrieved from https://ec.europa.eu/info/news/coronavirus-eu-mobilises-eur10-million-for-research-2020-jan-31_en.
- Coronavirus: UK donates £20 m to speed up vaccine, 2020 February 3. Retrieved from https://www.bbc.com/news/health-51352952.
- Croissant Y., Millo G. Wiley Online Library; 2019. Panel Data Econometrics with R. [Google Scholar]
- Elhorst, J.P., 2010. Applied spatial econometrics: raising the bar. 5(1), 9–28.
- Elhorst J.P. Spatial Econometrics: From Cross-Sectional Data to Spatial Panels. Springer; Berlin, Heidelberg: 2014. Spatial panel data models; pp. 37–93. [Google Scholar]
- Fotheringham A.S., Rogerson P.A. Sage; 2008. The SAGE Handbook of Spatial Analysis. [Google Scholar]
- Gelfand A.E., Diggle P., Guttorp P., Fuentes M. CRC press; 2010. Handbook of Spatial Statistics. [Google Scholar]
- Golgher, A.B., Voss, P.R.J.S.D., 2016. How to interpret the coefficients of spatial models: Spillovers, direct and indirect effects. 4(3), 175–205.
- Kelejian H.H., Prucha I.R. A generalized spatial two-stage least squares procedure for estimating a spatial autoregressive model with autoregressive disturbances. J. Real Estate Finance Econ. 1998;17:99–121. [Google Scholar]
- Lee, L.-f., Yu, J., 2010. Estimation of spatial autoregressive panel data models with fixed effects. 154(2), 165–185.
- LeSage, J.P., 2008. An introduction to spatial econometrics. (123), 19–44.
- Lu H., Stratton C.W., Tang Y.W. 2020. Outbreak of Pneumonia of Unknown Etiology in Wuhan China: The Mystery and the Miracle. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesaran M.H. 2004. General diagnostic tests for cross section dependence in panels. [Google Scholar]
- Primerdesign launches molecular test for new coronavirus, 2020 January 31. Retrieved from https://www.medicaldevice-network.com/news/primerdesign-molecular-test-coronavirus/.
- Tatoglu F.Y. 2012. Panel veri ekonometrisi. [Google Scholar]
- Tatoğlu Y. 2013. İleri panel veri analizi stata uygulamal. [Google Scholar]
- Wang D., Hu B., Hu C., Zhu F., Liu X., Zhang J. Clinical characteristics of 138 hospitalized patients with 2019 Novel Coronavirus–Infected Pneumonia in Wuhan, China. JAMA. 2020;323(11):1061–1069. doi: 10.1001/jama.2020.1585%JJAMA. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO Director-General’s remarks at the media briefing on 2019-nCoV on 11 February 2020. Retrieved from https://www.who.int/dg/speeches/detail/who-director-general-s-remarks-at-the-media-briefing-on-2019-ncov-on-11-february-2020.
- Yang, W., Chen, B.Y., Cao, X., Li, T., Li, P., 2017. The spatial characteristics and influencing factors of modal accessibility gaps: A case study for Guangzhou, China. 60, 21–32.
- Zeren, F., 2010. Mekansal etkileşim analizi. (12), 18–39.