Abstract
During epithelium tissue maintenance, lineages of cells differentiate and proliferate in a coordinated way to provide the desirable size and spatial organization of different types of cells. While mathematical models through deterministic description have been used to dissect role of feedback regulations on tissue layer size and stratification, how the stochastic effects influence tissue maintenance remains largely unknown. Here we present a stochastic continuum model for cell lineages to investigate how both layer thickness and layer stratification are affected by noise. We find that the cell-intrinsic noise often causes reduction and oscillation of layer size whereas the cell-extrinsic noise increases the thickness, and sometimes, leads to uncontrollable growth of the tissue layer. The layer stratification usually deteriorates as the noise level increases in the cell lineage systems. Interestingly, the morphogen noise, which mixes both cell-intrinsic noise and cell-extrinsic noise, can lead to larger size of layer with little impact on the layer stratification. By investigating different combinations of the three types of noise, we find the layer thickness variability is reduced when cell-extrinsic noise level is high or morphogen noise level is low. Interestingly, there exists a tradeoff between low thickness variability and strong layer stratification due to competition among the three types of noise, suggesting robust layer homeostasis requires balanced levels of different types of noise in the cell lineage systems.
Keywords: Stem cell, noise, tissue size, morphogen, feedback
1. Introduction.
In multicellular organisms, homeostasis is critical to tissues and organs for their functions. Multistage cell lineages, generally consisting of stem cells, transit-amplifying (TA) cells and terminally differentiated (TD) cells, serve as fundamental units for tissue and organ development, maintenance and regeneration.
Growth factors, one type of diffusive morphogen that is secreted by cells, play an important role by regulating multiple cellular processes to control the cell populations in the lineage [20]. Growth factors are often found to be important in regulating organ regeneration, as observed in liver [32], mouse olfactory epithelium [46], muscles [30], and hematopoietic system [48]. In such systems, different types of cells are located at spatial locations in the tissues for different functions. For examples, the stem cell niche, a spatial region with concentrated level of stem cells, often provides protective support for environmental variability [33, 24, 22], as seen in intestinal epithelia [47], neurons [8] and tumors [6]. In particular, the epithelium tissue is a great system to study the stratified layers of different types of cells that contain the stem cell niche [43].
Several mathematical modeling approaches have been employed to study the tissue growth and patterning, for example, on digits of limb [38], melanoblast [27], feather [23, 25] and stripe in mammalian palate [10]. Regarding the tissue size, analysis and computation of non-spatial cell lineage models suggest that the negative feedback is critical to regulating growth in epithelium [21, 26] and blood [18, 28]. For spatial models, continuum and discrete models have been used to study formation of stratified structure and stem cell niche in tissue. A one-dimensional continuum model [7] shows that the spatial morphogen gradient contributes to the tissue stratification. Studies of two-dimensional models suggest sources for distorted tissue morphologies [34, 35]. Through studying a discrete cell model, the selective cell adhesion is found to be a key factor for layer formation and tissue stratification [9].
Recently, stochastic effects, such as noise in gene expressions [11, 29, 17, 14], stochastic gene-state switching [1, 13], noise in cell divisions [15] and cell migration [41], are found to be important in biological functions [37, 40]. In many cases, noise is detrimental to biological functions, and noise attenuation mechanisms are critical in signal transduction [4, 2, 44]. Interestingly, noise is also found to be beneficial, such as improved signal transmission facilitated by stochastic resonance [12, 31], enhanced fitness to the environmental fluctuations by gene expression noise [5, 3, 42], and sharpening patterning boundaries through gene expression noise [49, 45, 36].
While noise effect and tissue maintenance have been extensively studied individually, how noise affects tissue growth and maintenance remains elusive. Based on the one-dimensional deterministic cell lineage model for epithelium growth [7], here we develop a stochastic cell lineage model that include three different types of noise. In particular, we use the multiplicative noise in the cell lineage equations to model the cell-intrinsic noise, the additive noise in the same equations for the cell-extrinsic noise, and multiplicative noise in the equation of diffusive molecules for morphogen noise. First, we study the effects of those three types of noise individually on layer thickness and stratification. Then we look into some specific combinations according to the opposite individual effects, more particularly, the combination of cell-intrinsic noise and cell-extrinsic noise, and the combination of cell-intrinsic noise and morphogen noise. Finally we combine all three types of noise to investigate the range of noise levels under which the homeostatic thickness and stratification can be maintained.
2. A stochastic spatial cell lineage model and quantifications of layer thickness and stratification.
2.1. A deterministic model.
Previously a one-dimensional deterministic model was developed to study the stratification of epithelium development and maintenance [7]. In the model there are three cell stages in the main lineage consisting of stem cells, transient amplifying (TA) cells, and terminally differentiated (TD) cells, with each cell type densities represented by C0, C1 and C2 (Figure 1), respectively. The cell lineage equations are given by:
| (1) |
Figure 1. A schematic diagram of a main cell lineage in epithelium.
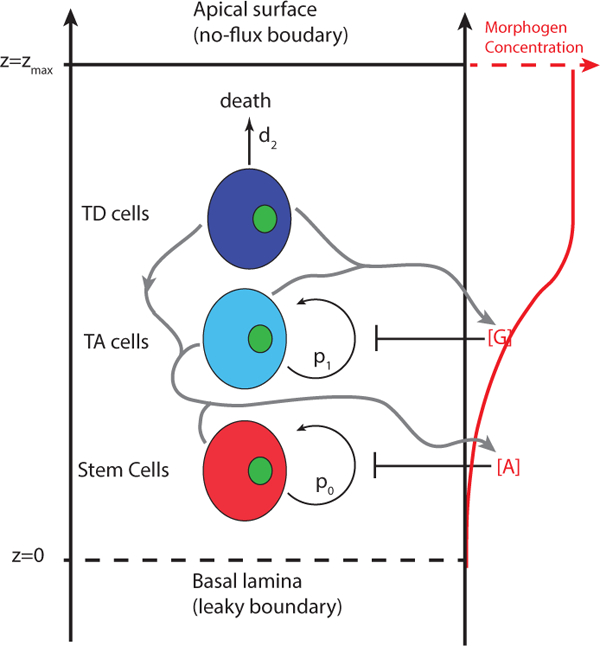
Stem cells and TA cells proliferate with probabilities p0 and pi and differentiate with probabilities 1 — p0 and 1 — p1. TD cells undergo cell death with rate d2. All three types of cells can secrete molecule A that inhibits self-renewal probability p0. TD and TA cells secrete molecule G that inhibits self-renewal probability p1. Molecules A and G are diffusive in the epithelium. The apical surface is moving with the dynamic position zmax and no-flux boundary condition is imposed. On the other hand, leaky boundary condition is imposed at the basal lamina with its position fixed.
Here V (z, t) is the layer growth velocity driven by cell proliferation and differentiation of cells. For ith cell type, pi denotes self-renewal probability, 1 — pi is then the differentiated probability, di is the death rate, and vi is ln2 over cell cycle length. With the assumption that the total cell density remains as a constant, we then normalize the constant with C0 + C1 + C2 = 1. Adding all equations in Eq. (1) leads to
| (2) |
The dynamic layer thickness zmax is governed by
| (3) |
The molecules secreted by cells inhibit the cell self-renewal rates (Figure 1). Two types of morphogen A and G are considered in this system. The proliferative probabilities p0 and p1 are modeled by the Hill functions:
| (4) |
where and are the maximal self-renewal probabilities, respectively; and are the reciprocal of EC50, and m and n are the Hill coefficients.
The diffusive morphogens are modeled by the advection-diffusion equations,
| (5) |
where Da and DG are diffusion coefficients, adeg and gdeg are degradation rates of A and G, A and G are produced by the cell type Ci at rates and respectively. The permeable basal lamina and a closed boundary at apical surface could give rise to heterogeneous distribution of A and G, contributing to the formation of layer stratification. We take the leaky boundary conditions at z = 0 basal lamina and no-flux boundary conditions at z = zmax (t) for apical surface:
| (6) |
where αA and αG are the corresponding coefficients of permeability.
2.2. A stochastic model on cell lineages and morphogens.
Next we add stochastic fluctuations to both equations of cell distributions and mophogens. For simplicity, we model three kinds of noise in the system: cell-intrinsic noise, cell-extrinsic noise, and morphogen noise. The cell-intrinsic noise is modeled by multiplicative noise in the cell lineage equations to mimic fluctuations on the cell density that arise due to stochastic effects associated with cell cycle, cell proliferation, or cell differentiation and so on. The cell-extrinsic noise is modeled by additive noise to mimic environmental fluctuations that may affect the overall dynamics of cell lineages, which is usually independent of the cell density level. To avoid solving stochastic differential equations for the morphogen, which is at a fast time scale, we add a multiplicative noise term to the deterministic quasi-steady state solution of the morphgens to model the noisy morphogen dynamics.
We model the cell-intrinsic and cell-extrinsic noise by adding both a term for multiplicative noise and a term for additive noise to the deterministic Eq. (1):
| (7) |
The density C2 is obtained by the normalized equation C0 + C1 + C2 = 1. The multiplicative white noise, (i = 0, 1), mimics cell-intrinsic noise. The additive white noise, (i = 0, 1), mimics cell-extrinsic noise.
Because the time scale of molecular diffusion is much faster than the time scale of cells divisions, we solve quasi-steady state (see Method) for Eq. (5) to obtain [A]ss (z, t) and [G]ss (z, t) [7]. To model the morphogen noise in the stochastic model, we add fluctuations to the quasi-steady-state at time t:
| (8) |
where is a standard normally-distributed random variable at space z and time t, and independent of both spatial and temporal variables. Such multiplicative noise can maintain mean concentrations on morphogens.
2.3. Quantification of layer thickness, variability and stratification.
To systematically explore the three major properties of the tissue layer, we quantify each of them using one measurement. Due to stochastic effect, the tissue layer may not reach a constant thickness, and we define its average thickness by
| (9) |
where T is the final time of the simulation. With a large T, TH will have a limiting behavior and can describe the long-term behavior of the thickness.
To measure the variability of the layer thickness, we use the coefficient of variation (CV) relative to its mean thickness:
| (10) |
A large CV can reflect either strong oscillations or rapid growth. One case with oscillations will be shown in Section 3.1, and the other case with rapid growth will be shown in Section 3.2
A stratification factor [7] was defined to measure the level of stratification for cell type i at time t:
| (11) |
where θ (t) is defined by the following equation:
| (12) |
To measure the long-time average level of the tissue stratification, we define the stratification factor for cell type i as the following.
| (13) |
The value of sf and SF are between 0 and 1. The value 0 corresponds to homogeneous distribution of cell type i and the value 1 corresponds to the extreme polarization at the basal lamina.
2.4. A baseline simulation.
First we present a simulation for the model in which all the three types of noise are involved by setting ε0 = ε1 = ε, σ0 = σ1 = σ and We show the spatial distributions of cells and morphogens at different time points, and dynamics of layer thickness and stratification (Figure 2).
Figure 2. A baseline simulation for the system containing all three kinds of noise.
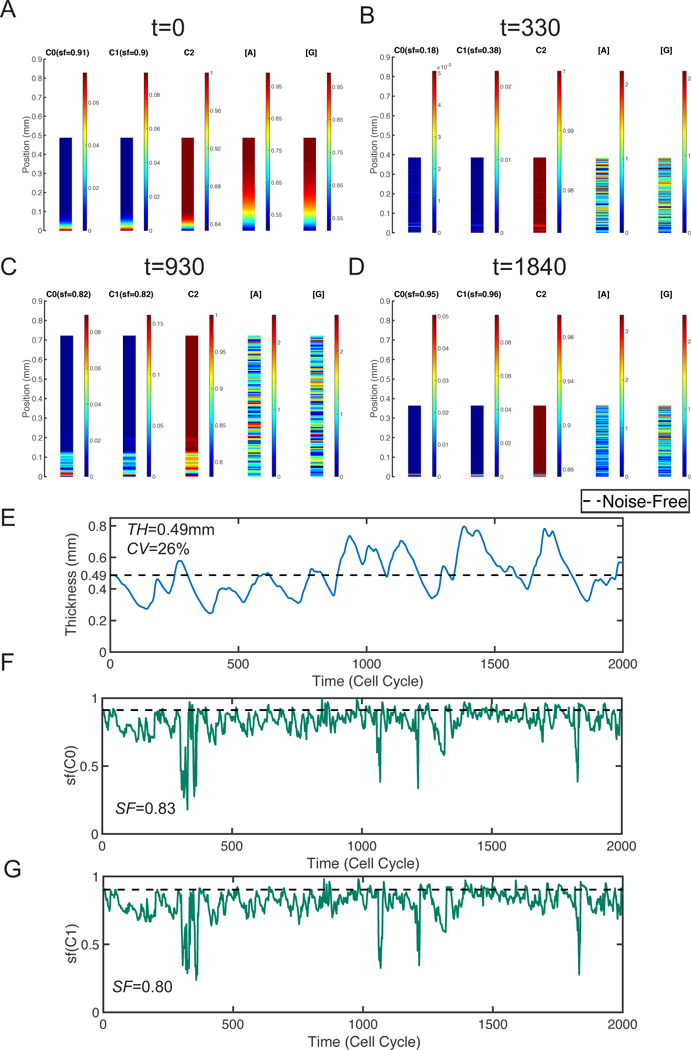
The spatial distribution of three types of cells and different mophogens at four different time points: A. t=0; B. t=330; C. t=860; D. t=1200. E. Layer thickness in one particular stochastic simulation. F. Stratification factor of stem cells (sf(C0)). G. Stratification factor of TA cells (sf(C1)). In E-G, the black dash line is the steady-state value for corresponding quantities in the deterministic system. The noise levels used are ε0 = ε1 = 0.6, σ0 = σ1 = 10−4, and
To study the layer maintenance, it is natural to take the steady state in the deterministic system as the initial condition for this stochastic simulation. We use the same initial condition in simulations presented in this work. To investigate the long-time behavior of the layer regarding its thickness, variability and stratification, we test different final time T in one simulation until the TH, CV and SF have no significant relative change in time. We find T = 2000 cell cycles allows a consistent long time behavior of the layer for all simulations presented below.
Initially, the stem cells are mainly located near the basal lamina and the mor- phogen concentration are higher in the region close to the apical surface, leading to a well-stratified layer which is similar to the deterministic case (Figure 2A). With the noise, the layer first shrinks and the morphogen gradient becomes less obvious at t = 330 (Figure 2B). As the time increases, the layer becomes thicker (Figure 2C) and, interestingly, later the layer shrinks again (Figure 2D). Clearly, by looking at the thickness as a function of time (Figure 2E), one observes an oscillatory behavior. The mean thickness of this layer, TH, is identical to the homeostatic thickness SS = 0.49mm. The variability of the layer thickness is quantified by CV = 26%.
On the other hand, noise affects the stratified structure of tissues. At t = 330, the distribution of stem cells is nearly uniform everywhere and the extremely low stratification factor is consistent with our observation (Figure 2B). At t = 930, stem cells mainly locate in a small region next to the basal lamina (Figure 2C). This region with high stem cell density is slightly wider than the one at initial stage, leading to a minor reduction of stratification factor. At t = 1840, while the distribution of stem cells looks uniform, the stem cells highly concentrate in a very narrow region close to the basal lamina and the stratification factor is larger than the initial one (Figure 2D). Overall, the stratification factor is able to capture stratified level appropriately (Figure 2A–2D). As time increases, we observe four drops in the stratification factor and, interestingly it always returns to the average level quickly (Figure 2F). Overall, the layer has well-stratified stem cells in average with SF = 0.83 while the TA cells have an average SF = 0.80 (Figure 2G).
Together, this simulation suggests that noise affect both thickness and stratification, leading to an oscillation of the tissue thickness during tissue maintenance. To dissect the role of each type of noise, we next scrutinize each noise type one by one.
3. The effects of single type of noise.
In the stochastic model, there are three types of noise: cell-intrinsic noise, cell-extrinsic noise and morphogen noise. In this section, we discuss the effects of each type of noise individually. For example, for the cell-intrinsic noise, we set and discuss the layer behaviors with different cell-intrinsic noise levels ε. We show the statistical quantities TH, CV and SF. The number of simulations has been chosen such that all these quantities become stable in the mean sense. In particular, in this study, we run 20 simulations for each scenario.
3.1. Cell-intrinsic noise causes reduction and oscillations of tissue layer size.
For the system containing only cell-intrinsic noise we first present the layer thickness as a function of time for three different noise levels (Figure 3A). The layer fluctuates around the homeostasis when the noise level is small such as ε = 0.2. As the noise level increases, such as ε = 0.6 or 1, the layer oscillates below its thickness at homeostasis. Especially, the oscillation exhibits a clear pattern with a period around 400 cell cycles at e = 1 (Figure 3A).
Figure 3. Simulations with only cell-intrinsic noise.
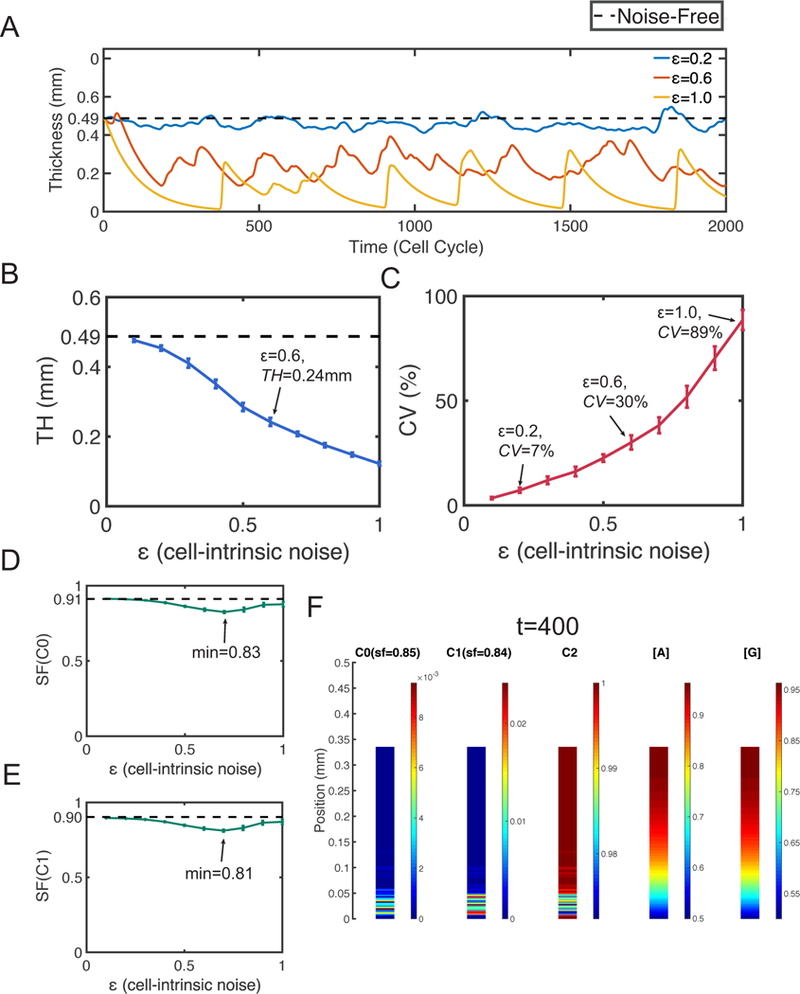
Dash lines represent the corresponding quantities at homeostasis. A. Layer thickness in three simulations with ε = 0.2, 0.6 and 1. B. The mean TH. The error bars show the standard deviation. C. The mean CV. The error bars show the standard deviation of CV. The mean SF of D. stem cells and E. TA cells. The error bars show the standard deviation. F. Distribution of cells and morphogens in a specific simulation with ε = 0.6 at time t = 400. In (B-E), all statistical quantities are captured based on 20 simulations, and the standard deviations (error bars) are negligible compared to the means.
Next we look into the statistical behaviors of the mean and variability of the layer thickness TH and CV, respectively (Figure 3B and 3C). As e increases, TH decreases and a 50% reduction can be observed at ε = 0.6 with TH = 0.24mm. The thickness variability (CV) increases as e increases. At ε = 0.2, CV = 7% and a 3-fold increase on CV can be observed at ε = 0.6. Interestingly, when the thickness variability is high, the high value quantity CV seems to reflect the oscillation amplitude of the layer. Especially, at ε = 1, the strongly oscillatory layer (Figure 3A) results in a high variability with CV = 89% (Figure 3C).
Then we look into the tissue stratification for both stem cells and TA cells (Figure 3D and 3E). Although the SFs have minor reduction when noise is induced, any SF above 0.8 still indicates a well-stratified structure for both stem cells and TA cells. One specific example of the cells distribution displays the well-stratified tissue structure (Figure 3F).
Therefore, the cell-intrinsic noise usually causes reduction of layer thickness and leads to oscillations on the thickness. The oscillations exhibit a periodic pattern when the noise level is high. While the noise may cause a minor reduction in stratification, the layers remain well stratified when the cell-intrinsic noise is presented only.
3.2. Cell-extrinsic noise causes rapid growth, and deteriorates layer stratification.
For the system containing only cell-extrinsic noise we first study the layer thickness as a function of time for three different noise levels (Figure 4A). All layers grow monotonically in time and their growth rates have positive correlation with the level of noise σ. The layer grows slowly at early time and then stops growing when the noise level is low such as σ = 1 × 10–3 and σ = 2 × 10–3. The unbounded growth can be observed when the noise level is large such as σ = 4 × 10–3 (Figure 4A).
Figure 4. Simulations with only cell-extrinsic noise.
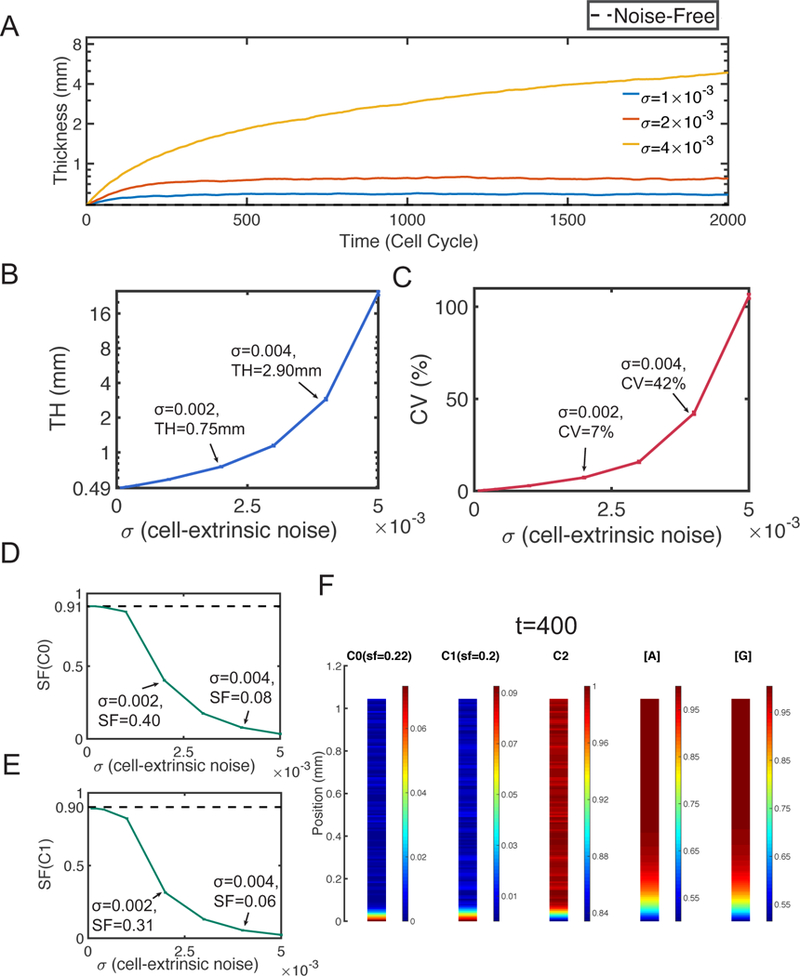
Dash lines represent the corresponding quantities at homeostasis. A. Layer thickness in three simulations with σ = 1 × 10–3, 2 × 10–3 and 4 × 10–3. B. The mean TH. The error bars show the standard deviation. C. The mean CV. The error bars show the standard deviation of CV. The mean SF of D. stem cells and E. TA cells. The error bars show the standard deviation. F. Distribution of cells and morphogens in a specific simulation with σ = 3 × 10−3 at time t = 400. In (B-E), all statistical quantities are captured based on 20 simulations, and the standard deviations (error bars) are negligible compared to the means.
Next we look into statistical behaviors of the mean and variability of the layer thickness TH and CV, respectively Figure 4B and 4C). As a increases, the average TH shows an exponential growth. A 6-fold increase (2.90mm) can be observed at σ = 4 × 10−3, the TH is even over 10mm at σ = 5 × 10−3 (Figure 4B). Also the layer thickness variability quantified by CV grows exponentially as a function of σ. When σ < 3 × 10–3, CV is still lower than 10%. At σ = 4 × 10–3, we observe CV = 42%, and at σ = 5 × 10−3 CV is as high as 106% (Figure 4C).
On the tissue stratification (Figure 4D and 4E), the SFs decrease quickly as a function of σ. The stratification level of stem cells is already small at σ = 2 × 10–3 with SF = 0.4. The stem cells distribute nearly uniformly at σ = 4 × 10–3 with SF = 0.08 (Figure 4D). The stratification of TA cells behaves similarly as the stem cells (Figure 4E). As also seen in a typical simulation of the cell distribution (Figure 4F), the stem cells and TA cells locate in narrow regions close to the basal lamina with highest densities. Outside of those regions, the distribution of cells is nearly uniform with non-negligible densities, resulting in a low stratification level near sf = 0.2.
It is clear from the simulations that the cell-extrinsic noise increases layer thickness and hinders the stratification. Such noise can lead to unbounded growth of the layer when the noise level is high.
3.3. Noise in morphogens increases layer size without affecting tissue stratification.
For the system containing only noise on morphogen (ε = σ = 0), we first present layer thickness as a function of time for three different noise levels (Figure 5A). The layer thickness is increased within a short time and the layer fluctuates slightly later. As the noise level increases, the layer fluctuates around a higher size.
Figure 5. Simulations with only morphogens noise.
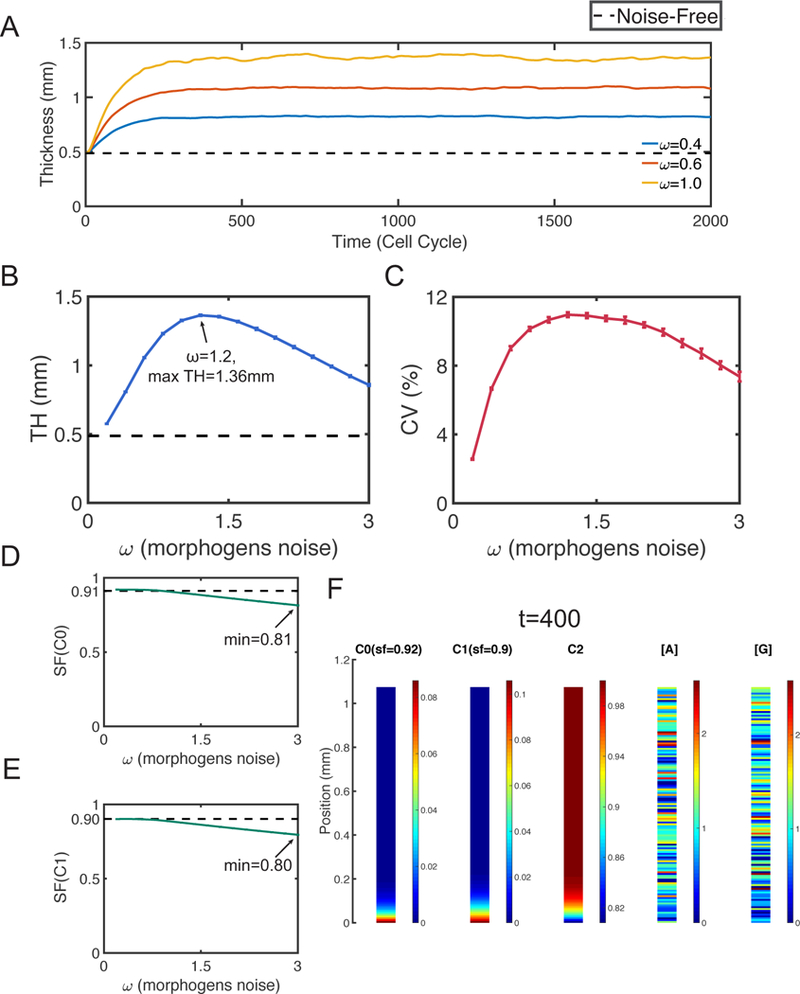
Dash lines represent the corresponding quantities at homeostasis. A. Layer thickness in three simulations with = 0.4, 0.6 and 1. B. The mean TH. The error bars show the standard deviation. C. The mean CV. The error bars show the standard deviation of CV. The mean SF of D. stem cells and E. TA cells. The error bars show the standard deviation. F. Distribution of cells and morphogens in a specific simulation with = 0.6 at time t = 400. In (B-E), all statistical quantities are captured based on 20 simulations, and the standard deviations (error bars) are negligible compared to the means.
Interestingly, the average TH has an inverted U-shape with a maximum 1.36mm at = 1.2 (Figure 5B). Unlike the unbounded growth caused by cell-extrinsic noise, the morphogen noise can only induce an increase up to 3-fold (Figure 5B). The layer thickness variability is low with CV < 12% (Figure 5C), neither strong oscillation nor rapid growth is observed.
By looking at the average SF of stem cells or TA cells (Figure 5D and 5E), we see the average SF decreases slowly as the noise level w increases. The minimums of SFs are larger than 0.8, indicating the layers remain well stratified. An example of the simulation shows the layer has a clear stratification despite morphogens are very noisy (Figure 5F).
We observe that the morphogen noise can increase the layer thickness up to a limited level and the thickness remains bounded. The tissue stratification is preserved when the morphogen noise is present only. Although such noise often causes minor reduction of stratification, the layers remain well stratified.
4. The effects of two different combinations of two types of noise.
We have studied the effects of single noise in Section 3. Here we combine two types of noise that have shown opposite effects on layer thickness individually, and investigate the layer thickness and stratification under such noise combination. For convenience, from now on, the stratification factor presented below is only for stem cells as the similar stratification pattern are observed for the stem cells and TA cells.
4.1. Cell-extrinsic noise reduces the variability of the layer thickness caused by cell-intrinsic noise but with less stratified layer.
For the system containing both cell-intrinsic noise and cell-extrinsic noise (= 0), we first plot layer thickness and stratification factor as functions of time in several stochastic simulations (Figure 6). With small noise levels, the layer thickness and stratification both fluctuates slightly around homeostasis (Figure 6A). As the cell-extrinsic noise level σ increases, the mean thickness increases regardless of the levels of cell-intrinsic noise ε (Figure 6A–C, Figure 6D–F, and Figure 6G–I). For the thickness variability, it has little changes when the cell-intrinsic noise is small, but interestingly, with a larger cell-intrinsic noise level, the thickness variability actually decreases as σ increases (Figure 6D–F, and Figure 6G–I). On the other hand, the mean thickness decreases as the cell-intrinsic noise level e increases (Figure 6 ADG, Figure 6 BEH, Figure 6 CFI). For the thickness variability, there are little changes as ε increases, except a clear increase when the noise is small (Figure 6AD). For the stratification, the mean of stratification factor decreases as either a function of the cell-intrinsic noise level ε or cell-extrinsic noise level σ.
Figure 6. Simulations with both cell-intrinsic noise and cell-extrinsic noise.
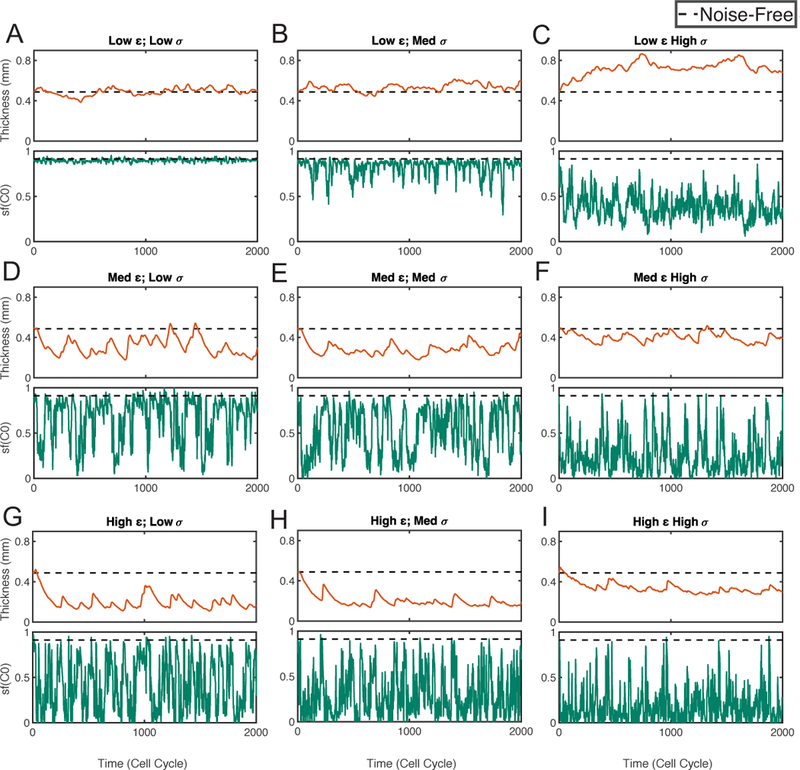
Simulations with different noise levels are shown in (A-I). In each subfigure, the panel on the top shows the dynamics of layer thickness, the panel on the bottom shows the dynamics of layer stratification of stem cells (sf (C0)). The dash line represents for the corresponding quantity at homeostasis. Three different levels are chosen for each type of noise. For cell- intrinsic noise level ε: 0.2 (Low), 0.6 (Medium), 1 (High). For cell-extrinsic noise level σ: 5 × 10–4 (Low), 1 × 10–3 (Medium), 2 × 10–3 (High).
The statistical quantities of TH, CV and SF (Table 1) show the behaviors of the layer thickness and stratification are consistent with the individual stochastic simulations (Figure 6). With low cell-intrinsic noise levels, such as ε = 0.2, CV is an increasing function of the cell-extrinsic noise level σ but the values of CV are always small (CV < 10%). With high cell-intrinsic noise levels, such as ε = 0.6 and 1, CV is a decreasing function of σ. Especially, the decreasing rate is high when the cell-extrinsic noise is near zero. For example, CV decreases from 89% to 36% as σ increases from 0 to 5 × 10–4 at ε = 1. Interestingly, CV is always below 20% when σ = 2 × 10−3 regardless of the value of e. On the other hand, as a function of ε, CV is an increasing function with small increasing rate.
Table 1. The statistics of TH, CV and SF(C0) with combined cell-intrinsic (ε) and cell-extrinsic (σ) noise.
All quantities are captured based on 20 simulations.
| ε╲σ | 0 | 5 × 10−4 | 1 × 10−3 | 2 × 10−3 | |
|---|---|---|---|---|---|
| 0 | TH | 0.49mm | 0.53mm | 0.58mm | 0.75mm |
| CV | 0% | 1% | 3% | 7% | |
| SF | 0.91 | 0.90 | 0.88 | 0.40 | |
| 0.2 | TH | 0.45mm | 0.49mm | 0.54mm | 0.69mm |
| CV | 7% | 7% | 7% | 8% | |
| SF | 0.91 | 0.90 | 0.82 | 0.39 | |
| 0.6 | TH | 0.24mm | 0.28mm | 0.30mm | 0.44mm |
| CV | 30% | 25% | 23% | 17% | |
| SF | 0.84 | 0.69 | 0.52 | 0.27 | |
| 1 | TH | 0.12mm | 0.19mm | 0.22mm | 0.38mm |
| CV | 89% | 36% | 32% | 19% | |
| SF | 0.88 | 0.42 | 0.32 | 0.18 | |
In summary, with the combination of cell-intrinsic noise and cell-extrinsic noise, the cell-intrinsic noise causes reduction of layer thickness and the cell-extrinsic noise causes increase of layer thickness. These observations are similar to the observations when each of the two types of noise appears individually. For the thickness variability, we surprisingly observe that the cell-extrinsic noise can actually suppress thickness variability below a low level (CV < 20%). For the stratification factor, these two types of noise have accumulative effects on reducing stratification.
4.2. Combination of cell-intrinsic noise and morphogen noise.
For the system containing the cell-intrinsic noise and the morphogen noise (σ = 0), we first study the layer thickness and the stratification factor as functions of time in several stochastic simulations (Figure 7). With small noise, the layer thickness and stratification both fluctuates slightly around homeostasis (Figure 7A). As the morphogen noise level increases, both the mean thickness and the thickness variability increase regardless of the levels of cell-intrinsic noise ε (Figure 7A–C, Figure 7D–F, and Figure 7G–I). The mean stratification factor changes little as increases. On the other hand, as the cell-intrinsic noise level ε increases, the mean of the layer thickness decreases. Also oscillation becomes more obvious and the thickness variability increases as ε increases. For the stratification, as ε increases, the stratification factor (sf (C0)) shows short-time corruption in its long-time dynamics but its mean seldom changes (Figure 7ADG, Figure 7BEH, and Figure 7CFI).
Figure 7. Simulations with both cell-intrinsic noise and morphogen noise.
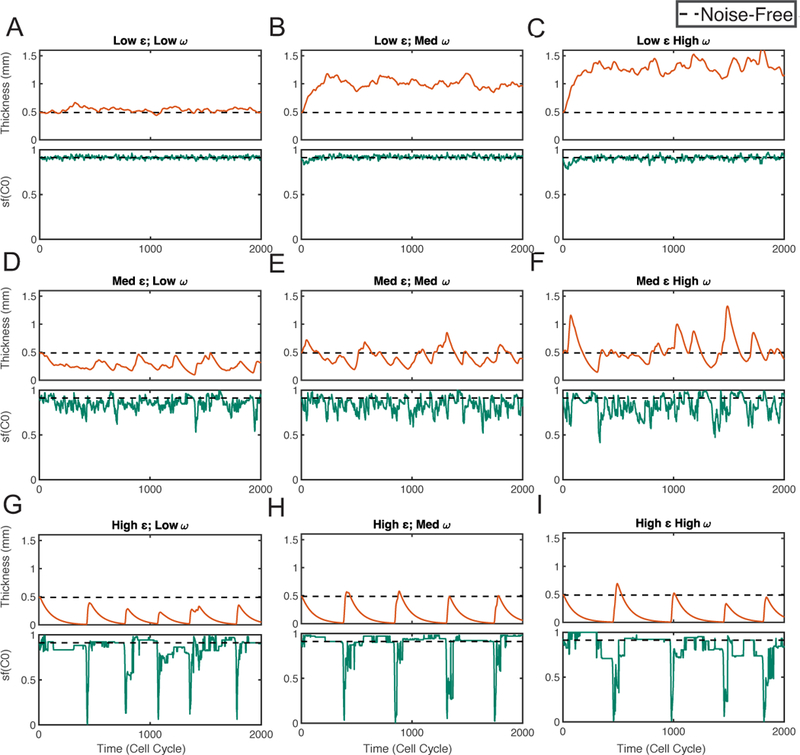
Simulations with different noise levels are shown in (A-I). In each subfigure, the panel on the top shows the dynamics of layer thickness, the panel on the bottom shows the dynamics of layer stratification of stem cells (sf(C0)). The dash line represents for the corresponding quantity at homeostasis. Three different levels are chosen for each type of noise. For cell- intrinsic noise level ε: 0.2 (Low), 0.6 (Medium), 1 (High). For morphogen noise level : 0.2 (Low), 0.6 (Medium), 1 (High).
As seen through the statistical quantities of TH, CV and SF (Table 2), the behaviors of layer thickness, variability and stratification are all consistent with the individual stochastic simulations (Figure 7). In particular, CV increases as a function of both cell-intrinsic noise level ε and morphogen noise level Its increasing rate with respect to ε is higher than that regarding The layers always have well-stratified structure where SF is always above 0.80.
Table 2. The statistics of TH, CV and SF(C0) with combined cell-intrinsic (ε) and morphogen () noise.
All quantities are captured based on 20 simulations.
| ε╲ω | 0 | 0.2 | 0.6 | 1 | |
|---|---|---|---|---|---|
| 0 | TH | 0.49mm | 0.58mm | 1.06mm | 1.33mm |
| CV | 0% | 3% | 9% | 11% | |
| SF | 0.91 | 0.92 | 0.92 | 0.91 | |
| 0.2 | TH | 0.45mm | 0.54mm | 0.98mm | 1.23mm |
| CV | 7% | 7% | 11% | 13% | |
| SF | 0.91 | 0.91 | 0.92 | 0.90 | |
| 0.6 | TH | 0.24mm | 0.26mm | 0.43mm | 0.52mm |
| CV | 30% | 29% | 30% | 33% | |
| SF | 0.84 | 0.83 | 0.84 | 0.81 | |
| 1 | TH | 0.12mm | 0.13mm | 0.15mm | 0.16mm |
| CV | 89% | 87% | 97% | 108% | |
| SF | 0.88 | 0.88 | 0.87 | 0.84 | |
In summary, with the combination of the cell-intrinsic noise and the morphogen noise, the cell-intrinsic noise causes reduction of layer thickness and the morphogen noise causes increase of layer thickness. These observations are similar to the observations when each of the two types of noise appears individually. With a higher level of cell-intrinsic noise level, the layers show higher thickness variability. The variability becomes even higher when the morphogen noise level increases. On the other hand, such combination of noise has little impact on the stratification.
5. The combination of three types of noise during homeostasis: Tradeoff between low layer thickness variability and strong layer stratification.
From the above study, either the cell-extrinsic noise or the morphogen noise alone results in an increase of layer size away from the homeostasis. However, by adding the cell-intrinsic noise to either one of them, the layer thickness decreases compared to the case with only cell-extrinsic noise or morphogen noise. Next we include all three types of noise to explore the conditions under which the homeostasis is maintained.
With the homeostasis maintained, the cell-extrinsic noise level σ and the morphogen noise level exhibit a negative correlation when the cell-intrinsic noise level e is fixed (Figure 8A). The plane is divided into stabilized (region I-IV) and non-stabilized region (region V). As long as the levels of cell-extrinsic noise and morphogen noise are located in the stabilized region, the homeostasis can be maintained with a proper cell-intrinsic noise level ε. Particularly, the curves with ε = 0.6, 0.8 and 1 are located in a region with narrow width at σ direction. This indicates even a small change in the cell-extrinsic noise level σ requires a large change in the cell-intrinsic noise level ε to maintain the homeostasis. Therefore, it suggests that the balance between the cell-intrinsic noise and cell-extrinsic noise plays a key role during the homeostasis maintenance regardless of the morphogen noise. On the other hand, inside non-stabilized region, the layer is unable to maintain homeostasis for any value of ε.
Figure 8. Simulations for maintaining homeostasis (SS=0.49mm) with different combinations of three types of noise.
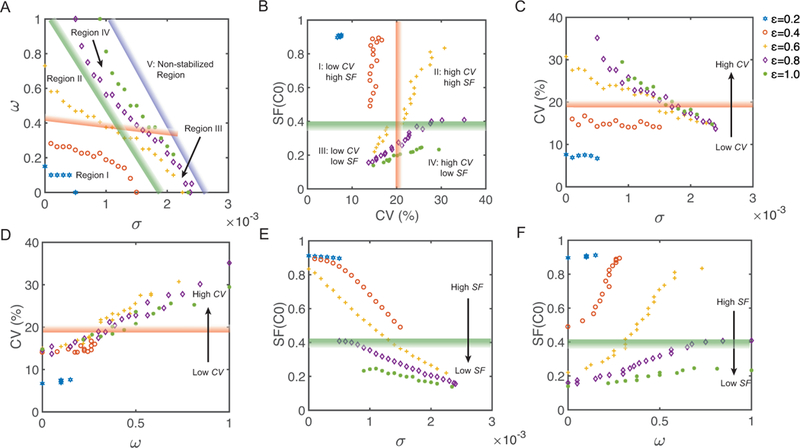
Points with the same color and the same marker represent for simulations with the same cell-intrinsic noise level ε, where ε = 0.2, 0.4, 0.6, 0.8 and 1 respectively. The strips, filled with color gradient, roughly divide the plane into several regions. Data points located in the region next to dark/light color of an individual strip have more/less desirable properties. A. The relation between the cell-extrinsic noise level σ and the morphogen noise level The blue strip sketches the green points with maximal cell-intrinsic noise level ε = 1. It divides this plane into stabilized region (region I-IV) and non-stabilized region (region V). The stabilized region is divided into four parts (region I-IV) by a red strip and a green strip. These regions will be introduced next. B. The relation between layer thickness variability (CV) and layer stratification factor of stem cells (SF(C0)). The red strip with CV= 20% divides this plane into two regions with low CV or high CV. Also the green strip with SF(C0) = 0.4 divides the plane into two regions with high SF or low SF. The red and the green strips together divide the stabilized region into four regions (Region I: low CV and high SF; Region II: high CV and high SF; Region III: low CV and low SF; Region IV: high CV and low SF). C. The relation between σ and CV. D. The relation between and CV. E. The relation between σ and SF (C0). F. The relation between and SF (C0).
The stabilized region can be divided into two parts either with respect to CV by a red strip with CV = 20% (Figure 8A–D), or with respect to SF by a green strip with SF = 0.4 (Figure 8A–B and 8E–F). Together, the stabilized region can be divided into four regions based on the thickness variability and the stratification level (Figure 8A–B): low-CV and high-SF region (region I); high-CV and high-SF region (region II); low-CV and low-SF region (region III) and high-CV and low-SF region (region IV).
The CV can be considered as a three-variable function in terms of noise levels With fixed cell-intrinsic noise level ε, the CV is a decreasing function of the cell-extrinsic noise level σ (Figure 8C) and an increasing function of the morphogen noise level (Figure 8D). It increases slowly when and then increases linearly. Interestingly, as a function of CV looks independent of ε and σ where all data points are located in a narrow region in the plane (Figure 8D), which suggests that the layer thickness variability is mainly adjusted by morphogen noise.
The SF can also be considered as a three-variable function in terms of noise levels With fixed cell-intrinsic noise level e, the SF is a decreasing function of σ (Figure 8E) and an increasing function of (Figure 8F). Its value also highly depends on ε. Therefore, all three types of noise play important roles in layer stratification.
There exists a clear tradeoff between low variability and strong stratification (Figure 8A and 8B). With low cell-intrinsic noise levels all data points are contained in region I. But a high morphogen noise level w improves layer stratification without affecting the thickness variability. With medium cell-intrinsic noise levels data points move from region III to region II as the morphogen noise level w increases. The layer can only have either low thickness variability or high stratification. The morphogen noise improves stratification but increases variability. In the other word, the cell-extrinsic noise improves thickness variability but deteriorate stratification. With high cell-intrinsic noise level, such as the data points move from region III to region IV as w increases. In this case, the low morphogen noise level w results in low thickness variability. Although the stratification factor is still an increasing function of w, the layer stratification is always in the undesirable range due to the high value of regardless of the value of For the homeostasis maintenance, the balance between cell-intrinsic noise and cell-extrinsic noise is dominant in the combination of three types of noise. The morphogen noise can adjust the layer thickness variability, and plays a complementary role by adjusting the balance between layer thickness variability and stratification.
6. Method.
All simulations are conducted in MATLAB 2015b. The numerical methods are described as below.
6.1. Solving morphogen gradient equations by using quasi-steady state.
The time scale of cell cycle lengths is days, whereas the time scale of molecule interactions is hours. The morphogen system can reach the steady state quickly compared to the cell cycle. Therefore, in the deterministic system, we calculate the quasi-steady state of Eq. (5) at each computational time step:
| (14) |
A second order central difference method is carried out to approximate Laplacian operators in Eq. (14). The resulting linear systems are solved by the MATLAB’s built-in backslash function
In the stochastic system, we also acquire the same quasi-steady state and then add fluctuations according to Eq. (8).
6.2. Solving stochastic cell lineage equations.
To solve the cell lineage equations Eq. (2, 3, 4, 7), we first transform the spatial domain to a unit domain [0,1] by a transformation [34]:
| (15) |
By applying Eq. (3), we have the transformed derivatives:
| (16) |
Using Eq. (2), we obtain the transformed equations of Eq. (7) in the new coordinate system
| (17) |
The transformed Eq. (2) and (3) are given as the following: dV
| (18) |
All equations in the new coordinate are included in Eq. (17) and Eq. (18). To discretize them in space, we use a uniform grid with N + 1 grid points In Eq. (17), the advection term is discretized by the second order upwind method. The infinite-dimensional noise term [16], where are independent of different The trapezoidal rule is used to discretize in Eq. (18).
For temporal discretization, we apply Euler-Maruyama method [19] with time step Δt. To ensure we make the following adjustments to the numerical solution at each computational time step:
| (19) |
6.3. Noise combination during tissue homeostasis.
In Section 5, we search for the combination of all three types of noise where the homeostasis is maintained. We solve the equation TH — SS in the average sense for noise levels By fixed and we solve w by using bisection method with tolerance 3% of the homeostasis (SS). The mean TH is captured based on 20 simulations. The noise level e and a are chosen to satisfy
6.4. Parameters and computational setup.
In this study, only noise levels ε, σ and are varied. The parameters used in Eq. (2) to Eq. (7) are listed in Table 3. The noise levels in Eq. (7) and (8) used in different figures are listed in Table 4. For the initial conditions in the stochastic simulations, we take the steady state solutions of the deterministic system, with its initial thickness being SS = 0.49mm.
Table 3.
| Parameters | Values | Units |
|---|---|---|
| 1 | ln2*(cell cycle)−1 | |
| 0.01 | ln2*(cell cycle)−1 | |
| 10−5 | mm2s−1 | |
| 10−3 | ||
| 10−3 | s−1 | |
| 10 | mm−1 | |
| 0.95 | - | |
| 0.5 | - | |
| 1.6 | ||
| 2 |
Table 4.
In all simulations, we choose N = 128 as the number of grid points and the time step Δt = 0.002. Numerical tests have been performed with different grid sizes and time steps to assure the convergence of the numerical solutions.
7. Discussion and conclusions.
Here we have explored noise effects on the epithelium layer maintenance on its thickness and stratification. We have found that the cell-intrinsic noise causes reduction and oscillation of layer on its thickness. The cell-extrinsic noise or the morphogen noise introduces an increase in the layer thickness. The cell-extrinsic noise can reduce the layer thickness variability introduced by the cell-intrinsic noise, but resulting in weaker stratification. To study layer homeostasis, we explore different combinations of three types of noise. The cell- extrinsic noise level and morphogen noise level display a negative correlation under a fixed cell-intrinsic noise level. With the low cell-intrinsic noise levels, the high morphogen noise levels actually improve layer stratification. With the medium cell- intrinsic noise levels, there exists a tradeoff between low layer thickness variability and strong stratification, and the high morphogen noise levels lead to better stratification whereas the low morphogen noise levels lead to lower thickness variability. However, with the high cell-intrinsic noise level, the layer stratification becomes weaker, but the layer thickness variability can be reduced through low morphogen noise levels.
The randomness in morphogen dynamics can come from multiple biological processes with both cell-intrinsic and cell-extrinsic sources: noise in the downstream gene expression, randomness in diffusion, and stochastic bindings between morphogen and their receptors. It is not surprising that our study finds the morphogen noise has both effects similar to the cell-extrinsic noise on increasing layer thickness, and to the cell-intrinsic noise on increasing layer thickness variability without damaging stratification. Morphogen noise exhibits properties of a mixture of cell- intrinsic noise and cell-extrinsic noise.
In this study, the stochastic simulations have been performed on a very long time scale with 2000 cell cycles in order to study noise effects on homeostasis. The biological relevant span for regeneration or development is much shorter in a range of 50 cell cycles, corresponding to a few weeks in real time. During the homeostasis study, one layer oscillates with a time window shorter than 50 cell cycles (e.g. Figure 2E). The long time dynamics in the simulation allows us to check if the layer really approaches to a stable state or only exhibits short time transient properties.
To the best of our knowledge, our study is the first work to include noise dynamics to the cell lineage models. In stochastic gene expression modeling, the internal (or intrinsic) noise and external (or extrinsic) noise in stochastic gene expression systems are modeled in a similar way, respectively [14]. In particular, the internal noise alters the transcription rate, and is modeled by multiplicative noise, and the external noise alters the background production of gene expressions, and is then modeled by additive noise [14].
In our model, different types of noise in cell lineage equations affect the layer growth velocity through cell densities. Such stochastic effects consequently affect the layer thickness. It would be interesting to explore how other types of stochastic effects may also affect layer growth by adding noise directly to the equations for growth velocity or/and layer thickness. Biological identities in the environment not included in our current model, such as cells in the dermal, may be modeled through the boundary conditions. Study the stochastic dynamics of those quantities requires new approaches of including noise in the boundary conditions, which is computationally challenging.
Rather than using the generic noise considered in this model, one may include more specific types of noise in the system. For example, noise on cell cycle, noise on cell death and noise on morphogen synthesis rate may be modeled in an explicit way. Complex tissue morphology in two or three dimensions may also have synergistic effect with noise. Simulations for noise in PDEs (e.g. through the two-dimensional model [35]) in two or three dimensions are usually much more challenging than the one-dimensional system studied in this work.
The morphogen is the only factor considered for regulation of stratification in our work. There are many other important factors that may also affect stratification. The selective cell-adhesion, one type of intercellular mechanical force, is another mechanism that can improve the stratification [9]. In order for the tissue to control the layer thickness variability, mechanical forces may play important role [39], for which discrete cell model may provide a convenient framework [9]. Gene regulatory networks in the downstream of the morphogens are neglected in this work. In many cases, the network structure and dynamics are critical to attenuate noise [44] and sometimes, noise in gene expression actually benefits spatial organization of cells [49, 45].
In summary, our study suggests the cell-intrinsic noise can battle the stochastic uncertainty in cell population size caused by cell-extrinsic noise. While the morphogen noise has properties of both types of noise, it can be utilized through its regulation of the downstream gene expressions to adjust the cell-intrinsic component of the stochastic effects to regulate the variability and stratification, consequently improving tissue homeostasis.
Acknowledgments
This work is supported by the NIH grants U01AR073159, R01GM107264, and R01NS095355; a grant from the Simons Foundation (594598, QN), and the NSF grant DMS1763272, DMS1562176, and DMS1762063.
Footnotes
2010 Mathematics Subject Classification. Primary: 92B05, 60H15; Secondary: 65C30.
Contributor Information
Yuchi Qiu, Department of Mathematics, University of California, Irvine Irvine, CA 92697, USA.
Weitao Chen, Department of Mathematics, University of California, Riverside Riverside, CA 92507, USA.
Qing Nie, Department of Mathematics, Department of Developmental and Cell Biology, University of California, Irvine, Irvine, CA 92697, USA.
REFERENCES
- [1].Acar M, Mettetal JT and Van Oudenaarden A, Stochastic switching as a survival strategy in fluctuating environments, Nature genetics, 40 (2008), 471. [DOI] [PubMed] [Google Scholar]
- [2].Austin D, Allen M, McCollum J, Dar R, Wilgus J, Sayler G, Samatova N, Cox C and Simpson M, Gene network shaping of inherent noise spectra, Nature, 439(2006), 608. [DOI] [PubMed] [Google Scholar]
- [3].Avery SV, Microbial cell individuality and the underlying sources of heterogeneity, Nature Reviews Microbiology, 4 (2006), 577. [DOI] [PubMed] [Google Scholar]
- [4].Becskei A and Serrano L, Engineering stability in gene networks by autoregulation, Nature, 405 (2000), 590. [DOI] [PubMed] [Google Scholar]
- [5].Blake WJ, Balaázsi G, Kohanski MA, Isaacs FJ, Murphy KF, Kuang Y, Cantor CR, Walt DR and Collins JJ, Phenotypic consequences of promoter-mediated transcriptional noise, Molecular Cell, 24 (2006), 853–865. [DOI] [PubMed] [Google Scholar]
- [6].Borovski T, Felipe De Sousa EM, Vermeulen L and Medema JP, Cancer stem cell niche: The place to be, Cancer Research, 71 (2011), 634–639. [DOI] [PubMed] [Google Scholar]
- [7].Chou C-S, Lo W-C, Gokoffski KK, Zhang Y-T, Wan FY, Lander AD, Calof AL and Nie Q, Spatial dynamics of multistage cell lineages in tissue stratification, Biophysical Journal, 99 (2010), 3145–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Doetsch F, A niche for adult neural stem cells. Current Opinion in Genetics & Development, 13 (2003), 543–550. [DOI] [PubMed] [Google Scholar]
- [9].Du H, Wang Y, Haensel D, Lee B, Dai X and Nie Q, Multiscale modeling of layer formation in epidermis, PLoS Computational Biology, 14 (2018), e1006006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Economou AD, Ohazama A, Porntaveetus T, Sharpe PT, Kondo S, Basson MA, Gritli-Linde A, Cobourne MT and Green JB, Periodic stripe formation by a Turing mechanism operating at growth zones in the mammalian palate, Nature Genetics, 44 (2012), 348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Elowitz MB, Levine AJ, Siggia ED and Swain PS, Stochastic gene expression in a single cell, Science, 297 (2002), 1183–1186. [DOI] [PubMed] [Google Scholar]
- [12].Gammaitoni L, Haanggi P, Jung P and Marchesoni F, Stochastic resonance, Reviews of Modern Physics, 70 (1998), 223. [Google Scholar]
- [13].Ge H, Qian H and Xie XS, Stochastic phenotype transition of a single cell in an intermediate region of gene state switching, Physical Review Letters, 114 (2015), 078101. [DOI] [PubMed] [Google Scholar]
- [14].Hasty J, Pradines J, Dolnik M and Collins JJ, Noise-based switches and amplifiers for gene expression. Proceedings of the National Academy of Sciences, 97 (2000), 2075–2080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Huh D and Paulsson J, Non-genetic heterogeneity from stochastic partitioning at cell division, Nature Genetics, 43 (2011), 95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Jentzen A and Kloeden PE, Taylor Approximations for Stochastic Partial Differential Equations, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2011. [Google Scholar]
- [17].Kaern M, Elston TC, Blake WJ and Collins JJ, Stochasticity in gene expression: From theories to phenotypes, Nature Reviews Genetics, 6 (2005), 451. [DOI] [PubMed] [Google Scholar]
- [18].Kirouac DC, Madlambayan GJ, Yu M, Sykes EA, Ito C and Zandstra PW, Cell-cell interaction networks regulate blood stem and progenitor cell fate, Molecular Systems Biology, 5 (2009), 293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Kloeden PE, The Numerical Solution of Stochastic Differenttial Equations, Springer-Verlag, Berlin, 1992. [Google Scholar]
- [20].Lander AD, Pattern, growth, and control, Cell, 144 (2011), 955–969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Lander AD, Gokoffski KK, Wan FY, Nie Q and Calof AL, Cell lineages and the logic of proliferative control, PLoS Biology, 7 (2009), e1000015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Lander AD, Kimble J, Clevers H, Fuchs E, Montarras D, Buckingham M, Calof AL, Trumpp A and Oskarsson T, What does the concept of the stem cell niche really mean today?, BMC Biology, 10 (2012), 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Li A, Figueroa S, Jiang T-X, Wu P, Widelitz R, Nie Q and Chuong C-M, Diverse feather shape evolution enabled by coupling anisotropic signalling modules with self organizing branching programme, Nature Communications, 8 (2017), ncomms14139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Li L and Xie T, Stem cell niche: Structure and function, Annu. Rev. Cell Dev. Biol, 21 (2005), 605–631. [DOI] [PubMed] [Google Scholar]
- [25].Lin C-M, Jiang TX, Baker RE, Maini PK, Widelitz RB and Chuong C-M, Spots and stripes: pleomorphic patterning of stem cells via p-ERK-dependent cell chemotaxis shown by feather morphogenesis and mathematical simulation, Developmental Biology, 334 (2009), 369–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Lo W-C, Chou C-S, Gokoffski KK, Wan FY-M, Lander AD, Calofand Q AL. Nie, Feedback regulation in multistage cell lineages, Mathematical Biosciences and Engineering: MBE, 6 (2009), 59–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Luciani F, Champeval D, Herbette A, Denat L, Aylaj B, Martinozzi S, Ballotti R, Kemler R, Goding CR and De Vuyst F, Biological and mathematical modeling of melanocyte development, Development, 138 (2011), 3943–3954. [DOI] [PubMed] [Google Scholar]
- [28].Marciniak-Czochra A, Stiehl T, Ho AD, Jaager W and Wagner W, Modeling of asymmetric cell division in hematopoietic stem cells-regulation of self-renewal is essential for efficient repopulation, Stem Cells and Development, 18 (2009), 377–386. [DOI] [PubMed] [Google Scholar]
- [29].McAdams HH and Arkin A, Stochastic mechanisms in gene expression, Proceedings of the National Academy of Sciences, 94 (1997), 814–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].McCroskery S, Thomas M, Maxwell L, Sharma M and Kambadur R, Myostatin negatively regulates satellite cell activation and self-renewal, The Journal of Cell Biology, 162 (2003), 1135–1147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].McDonnell MD and Abbott D, What is stochastic resonance? Definitions, misconceptions, debates, and its relevance to biology, PLoS Computational Biology, 5 (2009), e1000348, 9pp. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Moolten FL and Bucher NL, Regeneration of rat liver: Transfer of humoral agent by cross circulation, Science, 158 (1967), 272–274. [DOI] [PubMed] [Google Scholar]
- [33].Moore KA and Lemischka IR, Stem cells and their niches, Science, 311 (2006), 1880–1885. [DOI] [PubMed] [Google Scholar]
- [34].Ovadia J and Nie Q, Numerical Methods for Two-Dimensional Stem Cell Tissue Growth, Journal of Scientific Computing, 58 (2014), 149–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Ovadia J and Nie Q, Stem cell niche structure as an inherent cause of undulating epithelial morphologies. Biophysical Journal, 104 (2013), 237–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Rackauckas C, Schilling T and Nie Q, Mean-independent noise control of cell fates via intermediate states, iScience, 3 (2018), 11–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Rao CV, Wolf DM and Arkin AP, Control, exploitation and tolerance of intracellular noise, Nature, 420 (2002), 231. [DOI] [PubMed] [Google Scholar]
- [38].Raspopovic J, Marcon L, Russo L and Sharpe J, Digit patterning is controlled by a Bmp- Sox9-Wnt Turing network modulated by morphogen gradients, Science, 345 (2014), 566–570. [DOI] [PubMed] [Google Scholar]
- [39].Ruiz-Herrero T, Alessandri K, Gurchenkov BV, Nassoy P and Mahadevan L, Organ size control via hydraulically gated oscillations, Development, 144 (2017), 4422–4427. [DOI] [PubMed] [Google Scholar]
- [40].Simpson ML, Cox CD, Allen MS, McCollum JM, Dar RD, Karig DK and Cooke JF, Noise in biological circuits, Wiley Interdisciplinary Reviews: Nanomedicine and Nanobiotechnology, 1 (2009), 214–225. [DOI] [PubMed] [Google Scholar]
- [41].Stokes CL, Lauffenburger DA and Williams SK, Migration of individual microvessel endothelial cells: stochastic model and parameter measurement, Journal of Cell Science, 99 (1991), 419–430. [DOI] [PubMed] [Google Scholar]
- [42].Thattai M and Van Oudenaarden A, Stochastic gene expression in fluctuating environments, Genetics, 167 (2004), 523–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Tumbar T, Guasch G, Greco V, Blanpain C, Lowry WE, Rendl M and Fuchs E, Defining the epithelial stem cell niche in skin, Science, 303 (2004), 359–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Wang L, Xin J and Nie Q, A critical quantity for noise attenuation in feedback systems, PLoS Computational Biology, 6 (2010), e1000764, 17pp. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Wang Q, Holmes WR, Sosnik J, Schilling T and Nie Q, Cell sorting and noise-induced cell plasticity coordinate to sharpen boundaries between gene expression domains, PLoS Computational Biology, 13 (2017), e1005307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Wu H-H, Ivkovic S, Murray RC, Jaramillo S, Lyons KM, Johnson JE and Calof AL, Autoregulation of neurogenesis by GDF11, Neuron, 37 (2003), 197–207. [DOI] [PubMed] [Google Scholar]
- [47].Yen T-H and Wright NA, The gastrointestinal tract stem cell niche, Stem Cell Reviews, 2 (2006), 203–212. [DOI] [PubMed] [Google Scholar]
- [48].Zhang J, Niu C, Ye L, Huang H, He X, Tong W-G, Ross J, Haug J, Johnson T and Feng JQ, Identification of the haematopoietic stem cell niche and control of the niche size. Nature, 425(2003), 836. [DOI] [PubMed] [Google Scholar]
- [49].Zhang L, Radtke K, Zheng L, Cai AQ, Schilling TF and Nie Q, Noise drives sharpening of gene expression boundaries in the zebrafish hindbrain, Molecular Systems Biology, 8 (2012), 613. [DOI] [PMC free article] [PubMed] [Google Scholar]


