Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS

Abstract

The purpose of this paper is to reveal the spread rules of the three pneumonia: COVID-19, SARS and MERS. We compare the new spread characteristics of COVID-19 with those of SARS and MERS. By considering the growth rate and inhibition constant of infectious diseases, their propagation growth model is established. The parameters of the three coronavirus transmission growth models are obtained by nonlinear fitting. Parametric analysis shows that the growth rate of COVID-19 is about twice that of the SARS and MERS, and the COVID-19 doubling cycle is two to three days, suggesting that the number of COVID-19 patients would double in two to three days without human intervention. The infection inhibition constant in Hubei is two orders of magnitude lower than in other regions, which reasonably explains the situation of the COVID-19 outbreak in Hubei.

Highlights

• •The growth rate of SARS-CoV-2 is about twice that of the SARS and MERS viruses.
• •Doubling cycle for the cases of COVID-19 is two to three days if without intervention.
• •The infection inhibition constant in Hubei is two orders of magnitude lower than in other regions.

1. Introduction

In December 2019, patients with pneumonia of unknown cause appeared in some medical institutions in Hubei province, China. A new coronavirus, initially named 2019-ncov, was identified as the causative agent of pneumonia. The World Health Organization (WHO) named the pneumonia caused by the new coronavirus “COVID-19.” At the same time, the International Committee on Taxonomy of Viruses announced that it was calling the new coronavirus severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Medical researchers believe that SARS-CoV-2 is probably closely related to the coronavirus carried by the Chinese horseshoe bat, but the intermediate host has not been confirmed.

SARS-CoV-2 is a coronavirus similar to SARS-CoV and MERS-CoV. SARS-CoV first occurred from November 2002 to June 2003 in Guangdong, China, and spread to many parts of the world. MERS-CoV was found in 2012 in Saudi Arabia. Its main outbreak areas were in the Middle East and South Korea, and it occurred occasionally elsewhere.

The dynamics of SARS and MERS have made some progress. At present, there are two main mathematical models of epidemiological dynamics: the deterministic model and the stochastic model. Donnelly et al. (2003) measured associations between the estimated case fatality rate and patients'age and the time from onset to admission. They estimated that the mean incubation period of the disease was 6.4 days, and that the mean time from onset of clinical symptoms to admission to hospital varied between 3 and 5 days, with longer times earlier in the epidemic. Lipsitch et al. (2003) estimated that a single infectious case of SARS would infect about three secondary cases in a population that had not yet instituted control measures. Public-health efforts to reduce transmission were expected to have a substantial impact on reducing the size of the epidemic. Riley et al. (2003) analyzed the first 10 weeks of the severe acute respiratory syndrome (SARS) epidemic in Hong Kong, and presented that the epidemic was characterized by two large clusters initiated by two separate super-spread events (SSEs) and by ongoing community transmission. Excluding SSEs, they also estimated that 2.7 secondary infections were generated per case on average at the start of the epidemic, with a substantial contribution from hospital transmission. Li et al. (2004) used a logistic deterministic growth model to fit the data of some countries and regions, and some provinces and cities in mainland China, revealing the uneven infectious force of SARS in various regions, along with differences in prevention and control measures. Tan et al. (2003) established the SEIR epidemic model of SARS and a parameter identification system with incubation period and lifelong immunity, and demonstrated the main mathematical properties of the control model and the flow invariance and weak invariance of the system. Li et al. (2013) researched the problem of epidemic spreading dynamics on a multi-relationship network, proposed a kind of dual relationship network model (work-friends network), and studied the effect of multi-relationships on epidemic spread dynamics behavior. They also studied the outbreak threshold of epidemic spreading dynamics on complex networks (Li et al., 2016), and summarized the similarities and differences of outbreak thresholds between the susceptible–infected–recovered (SIR) and susceptible-infected-susceptible (SIS) models. Kim and Jung (2018)) studied the dynamic development of MERS in the inter-organizational public health emergency management network, and mapped the communication and response network patterns during the outbreak of MERS. Through retrospective epidemiological analysis, Nishiura et al. (2016)) studied the determinants of the heterogeneous transmission dynamics of the MERS outbreak in South Korea in 2015. They used the transmission tree to identify the super spenders and estimated the reproduction number of different types of hosts, i.e., the average number of secondary cases generated by a single major case, and its changes over time. To identify super spreaders in a complex network, Chen et al. (2019)) proposed a fusion index, called the degree of extension center, by extracting and synthesizing topology feature information of traditional centrality indices and spreading influence to identify nodes, and conducted simulation experiments on four real networks and node removal to verify the accuracy of the proposed centricity. The classical SIR model describes the transmission of infection. People's response to epidemics affects transmission, thus information transmission is also considered often in the literature. Lu and Liu (2019)) analyzed how the operation of information transmission affects infected individuals and the transmission conditions of epidemics and proposed a susceptibility-recovery-activity (SIR-A) model that maps infection and information transmission to a two-layer network based on the hypothesis that community size and individual consciousness may have an impact on infection rates. Ning et al. (2020)) used an evolutionary game model of complex networks to study the process of epidemic transmission. Ning et al. selected strategies by assuming that individuals would compare their own benefits with those of neighboring individuals in the process of disease transmission, updated strategies using four simulation principles, analyzed counterintuitive phenomena, and found that simulation principles will affect the scope and severity of counterintuitive phenomena. Through epidemiological SIS investigation involving independent disseminators, Ding et al. (2019)) explained that complex systems in which the dynamics of diffusion occur often have many underlying relationships that can facilitate the process of infectious disease transmission. Huang et al. (2019)) studied the impact of human behavior and contact heterogeneity on the spread of infectious diseases. Based on the consideration of fear levels of individuals with different potential contact times with others, a network-based SIRS epidemic model with a general feedback mechanism was proposed. Zhang et al. (2018)) proposed a novel susceptible–infected–susceptible–recovered–susceptible virus transmission model based on partial immunity and immune inefficiency in complex networks and studied the epidemic dynamics behavior of this model in unified networks and scale-free networks based on mean field theory. Liu et al. (2018)) simulated an infection transmission process on multiplex contact networks accounting for the natural history of influenza and found that the classical concept of the basic reproduction number was untenable in realistic populations, and it did not provide any conceptual understanding of the epidemic evolution. Based on the complex network theory, Fan et al. (2020)) established the SEIR dynamic model of 2019-ncov epidemic with incubation period, and predicted the epidemic inflection point through model parameter simulation.Based on Wuhan migration data, Yang et al. (2020)) estimated the number of people infected with SARS-CoV-2 in Wuhan by the number of confirmed people and found that the rate of confirmed patients in 15 cities in Hubei province was lower than that in 35 cities outside the province in terms of the mean and median. Lombardi et al.'s research (Lombardi et al., 2020) showed that isolation of those affected and the use of personal protective equipment (PPE) were the mainstay to block transmission of this pathogen, which was presumed through respiratory droplets. A 14 days quarantine was applied to subjects coming from endemic areas or who had contact with confirmed cases. Fanelli and Piazza (2020)) analyze the temporal dynamics of the coronavirus disease 2019 outbreak in China, Italy and France in the time window 22/01–15/03/2020. A first analysis of simple day-lag maps points to some universality in the epidemic spreading, suggesting that simple mean-field models can be meaningfully used to gather a quantitative picture of the epidemic spreading, and notably the height and time of the peak of confirmed infected individuals. These scholars studied the propagation rules of SARS and MERS from the aspects of deterministic models, stochastic models, and complex network propagation dynamics, but the propagation research of COVID-19 is just beginning.

As a new infectious disease, the transmission mechanism of COVID-19 is not yet clear. Although SARS-CoV-2 is a kind of coronavirus similar to SARS-CoV and MERS-CoV, there are still many questions to be studied about its infectious characteristics.

2. Propagation process modelling

2.1. Model hypothesis

We analyze the number of people infected with infectious diseases. The number of infectious cases is a function of time, expressed as N(t) at time t. When a new coronavirus occurs, people lack full understanding of its origin and route of transmission, which may lead to insufficient recognition of its prevention and control. Therefore, at the beginning, the growth rate of infections can be regarded as a constant r ₀. However, when the number of infected cases reaches a certain level, people will gradually devote increased attention to the epidemic disease and take measures such as disinfection and isolation. At this point, the growth rate of infected people decreases with the increase of their number N, i.e., the growth rate can be expressed as a monotonically decreasing function r(N). For simplicity, let us assume the growth rate r(N) is a linear function of the number of infected people N, r(N) = r ₀ − sN, where r ₀ is a constant indicating the growth rate of people doing nothing and letting the virus spread at will, and s is the infection inhibition constant, which reflects the effect of prevention and control measures taken to suppress infectious diseases. The larger s is, the more effective the prevention and control measures are. Moreover, it is assumed that under the combined effect of viral infectivity and prevention and control measures, the maximum number of infected cases is N _max, i.e., when N = N _max, the growth rate r(N _max) = 0. At this point, the infection inhibition constant s = r ₀/N _max can be obtained.

Notations: N(t) or N denotes the number of infectious cases at time t, while N _max is the maximum number of N(t), i.e., the limit of N(t). r(N) is the growth rate of infected cases with N, and r ₀ is the growth rate at the beginning with no measure taken. s denotes the infection inhibition constant. The multiplication cycle with no measure taken is denoted by T ₀ and T denotes the multiplication cycle varied with the number of infected cases N, which has measures taken with N increasing.

2.2. Mathematical modelling of infected cases

According to the hypothesis of the model, under the continuous setting, the number of newly infected persons ΔN within the time Δt can be expressed as the product of the growth rate r(N) and N, and the number of infected persons at t ₀ is N ₀, so we can obtain the initial value problem of the differential equation of infected persons,

$$\left\{\begin{array}{l}\frac{\mathit{dN}}{\mathit{dt}}=r_0\left(1-\frac{N}{N_{\max }}\right)N,\\ N\left(t_0\right)=N_0.\end{array}\right)$$ (1)

The first term, r ₀ N, of differential equation (1) expresses the natural epidemic trend of infectious diseases in the absence of any prevention and control measures, while the second term, −r ₀ N ²/N _max, shows the effect of prevention and control measures for communicable diseases. At the beginning of an epidemic of an infectious disease, due to the lack of strong prevention and control measures, the evolution of the epidemic law is mainly affected by the spreading characteristics of the virus itself, and the first term plays a leading role. At this moment, one can consider that −r ₀ N ²/N _max = 0, and in this setting, the solution of the differential equation is

$$N=N_0{e}^{r_0\left(t-t_0\right)}.$$ (2)

This solution implies that the virus can spread freely without human intervention, and the number of infected people increases exponentially over multiple generations. In the outbreak of an infectious disease, the role of the second term gradually begins to assume a dominant position, the number of new cases gradually decreases and approaches zero, and the disease is finally under control.

Eq. (1) is an initial-value problem of variable-separable differential equations, which can be solved by

$$N\left(t\right)=\frac{N_{\max }}{1+\left(\frac{N_{\max }}{N_0}-1\right)e^{-r_0\left(t-t_0\right)}}.$$ (3)

According to differential equation (1), the second derivative of N(t) is

$$\frac{d^{2}N}{{\mathit{dt}}^2}=r_0^2\left(1-\frac{N}{N_{\max }}\right)\left(1-\frac{2N}{N_{\max }}\right)N.$$ (4)

From the second derivative (4), it can be known that the change rate of infected persons dN/dt reaches its maximum when N = N _max/2, i.e., the period of accelerated growth occurs when the number of infected persons reaches half of the limit value. Therefore, the moment corresponding to N = N _max/2 can be called the inflection point of the number of new infections.

2.3. Multiplication cycle

The time span in which the number of infections increases from N to 2N is called a multiplication cycle. If there is no human intervention, it can be obtained from Eq. (2) that the multiplication cycle is T ₀ =  ln 2/r ₀. The multiplication cycle depends only on the rate of infection r ₀ without human intervention.

With human intervention, such as protective measures, the multiplication cycle will not depend only on r ₀. From Eq. (3), we can obtain

$$t=\frac{1}{-r_0}ln\left(\frac{N_{\max }-N}{N}/\frac{N_{\max }-N_0}{N_0}\right)+t_0.$$ (5)

Suppose that the number of infections is N at moment t ₁ and 2N at moment t ₂. Then, the multiplication cycle can be obtained as

$$T=t_2-t_1=\frac{1}{-r_0}ln\left[\frac{N_{\max }-2N}{2\left(N_{\max }-N\right)}\right].$$ (6)

T is a function of the number of infected people N, with N _max − 2N > 0. This inequality holds because when N approaches N _max/2, the multiplication cycle will approach to infinity. The derivative of T is

$$\frac{\mathit{dT}}{\mathit{dN}}=\frac{N_{\max }}{r_0\left(N_{\max }-N\right)\left(N_{\max }-2N\right)}.$$

Thus, we know that T is a monotonically increasing function, T → T ₀ when N → 0, while T →  + ∞ when N → N _max/2. This shows that when the inflection point occurs, the doubling of the number of infected people no longer occurs.

3. Data and mathematical methods

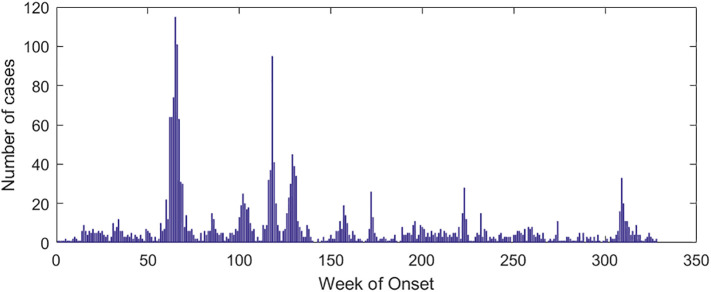
The data used in this paper are from the WHO (http://www.who.int) and the National Health Commission of the People's Republic of China (http://www.nhc.gov.cn/). The National Health Commission publishes data of accumulated and newly confirmed cases of COVID-19 from January 20, 2020, from which the data from January 21 to March 18 were selected. The regions selected were Hubei (HB), Guangdong (GD), Zhejiang (ZJ), and Henan (HN). The data of confirmed SARS cases were selected from April 21, 2003, to June 30, 2003. The selected countries or regions were China (excluding Hong Kong, Macau, and Taiwan) (Nat), Guangdong (GD), Beijing (BJ), and Hong Kong (HK). Saudi Arabia's MERS case data were selected for analysis. Fig. 1 shows the number of weekly infections in Saudi Arabia from the 12th week of 2012 to the 24th week of 2019. As can be seen from Fig. 1, Saudi Arabia experienced four significant MERS outbreaks, from week 7 to week 23 in 2014, week 1 to week 12 in 2015, week 15 to week 26 in 2015, and week 28 to week 39 in 2015. These four outbreak cycles are recorded as C#1, C#2, C#3, and C#4, respectively. We selected these four cycles of MERS cases for analysis. The software 1stOpt and its Levenberg-Marquardt optimization algorithm (Bi and Liang, 2018; Liang and Clay, 2019) were used to fit Eq. (3).

Fig. 1.

Cases of MERS in Saudi Arabia.

4. Analysis and discussion of parameters

4.1. Fitting results

The number of cases of COVID-19, SARS, and MERS in each region was fitted using model (3), and the fitting effect was significant. Table 1 shows the results, where the correlation coefficient measures the degree of linear correlation between N and t, and the determination coefficient reflects the reliability of the regression function N(t). The values of the correlation coefficient and the determination coefficient both go from 0 to 1. According to Table 1, the minimum values of the correlation coefficient and determination coefficient are 0.9822 and 0.9647, respectively. For the number of COVID-19 cases of Hubei, the values of N _max are fairly close to the real cases, and the absolute value of the average relative error is less than 3%. The true number of confirmed COVID-19 cases on March 18, 2020, is 67,800, close to its simulation value 67,680.39 (Table 1).

Table 1.

Simulation result.

Disease	Region	Correlation coefficient	Determination coefficient	Nmax/cases	Real cases/cases	Average relative error (%)
COVID-19	HB	0.9981	0.9962	67,680.395	67,800	−0.18
	GD	0.9995	0.9988	1347.647	1369	−1.56
	ZJ	0.9982	0.9960	1203.305	1232	−2.33
	HN	0.9996	0.9990	1270.729	1272	−0.10
SARS	Nat	0.9984	0.9967	5355.991	5327	0.54
	GD	0.9822	0.9647	1516.151	1512	0.27
	BJ	0.9997	0.9994	2520.522	2521	−0.02
	HK	0.9986	0.9972	1755.788	1755	0.04
MERS	C#1	0.9996	0.9992	632.762	629	0.6
	C#2	0.9997	0.9994	161.823	157	3.07
	C#3	0.9981	0.9957	269.475	267	0.93
	C#4	0.9997	0.9994	228.499	227	0.66

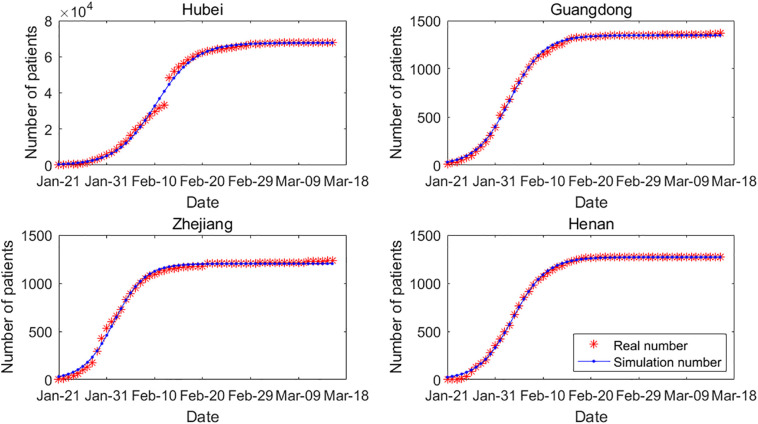
To fit the model for COVID-19, we selected four provinces with severe epidemics: Hubei, Guangdong, Zhejiang, and Henan. The statistical profile changed on February 13 when the method of establishing confirmed cases was changed from diagnosis of COVID-19 by nucleic acid test to clinical diagnosis, which resulted in a jump in the number of confirmed cases. A total of 14,840 new cases were confirmed in Hubei on February 13. Therefore, Fig. 2 shows a jump in the cumulative number of cases on February 13. In general, the model fitting effect of the four provinces is significant.

Fig. 2.

Real cases and simulation result for COVID-19. The sample sizes for Hubei, Guangdong, Zhejiang and Henan are all 58, Chi-Squares are 3158.95, 36.94, 110.97, 135.22, and F-Statistics are 14525.04, 54763.65, 15502.61, 69710.64, respectively.

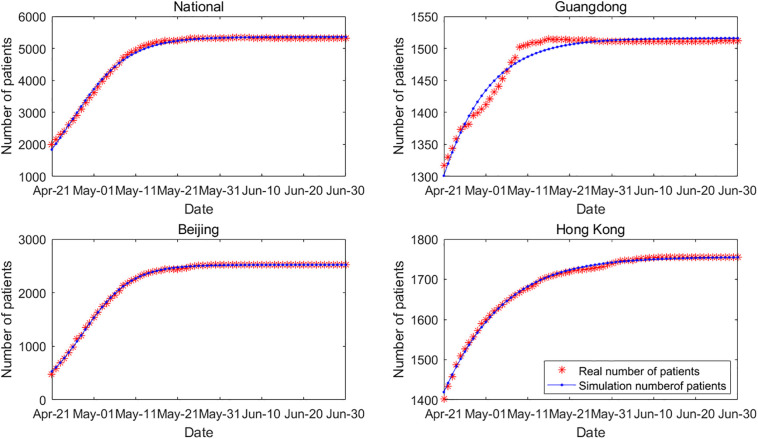
The incidence of SARS cases in China is different from that of COVID-19. By March 18, 2020, a total of 80,894 cases of COVID-19 had occurred in China (data exclude Hong Kong, Macau, and Taiwan), including 67,800 cases in Hubei, whose cumulative cases account for the majority of those in China. In 2003, SARS occurred in China, and there was no significant difference in the number of cases among the most severely affected provinces. Therefore, on a regional basis, we selected the number of cases in China (national data), Guangdong, Beijing, and Hong Kong. The fitting results are shown in Fig. 3 , and the fitting effect is also significant.

Fig. 3.

Real cases and simulation result for SARS. The sample sizes for national, Guangdong, Beijing and Hong Kong are all 71, Chi-Squares are 30.92, 2.38, 5.72, 0.47, and F-Statistics are 21136.76, 1883.17, 124221.70, 24350.03, respectively.

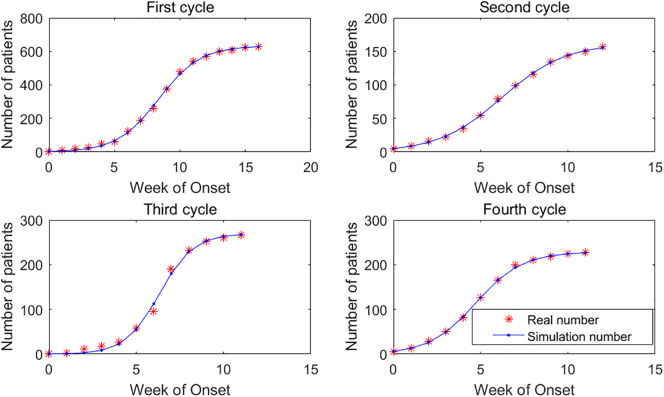
Saudi Arabia experienced four distinct cycles of MERS outbreaks. The model fitting of MERS cases in these four cycles is shown in Fig. 4 . The largest average relative error of the four cycles is in the second cycle (3.07%), and the overall fitting effect is reasonable.

Fig. 4.

Real cases and simulation result for MERS.The sample sizes for C#1, C#2, C#3, and C#4 are 17， 13， 12， 12， Chi-Squares are 7.52, 0.28, 10.74, 0.26, and F-Statistics are 19345.43, 17782.60, 2624.14, 18312.06, respectively.

5. Growth rate and multiplication cycle

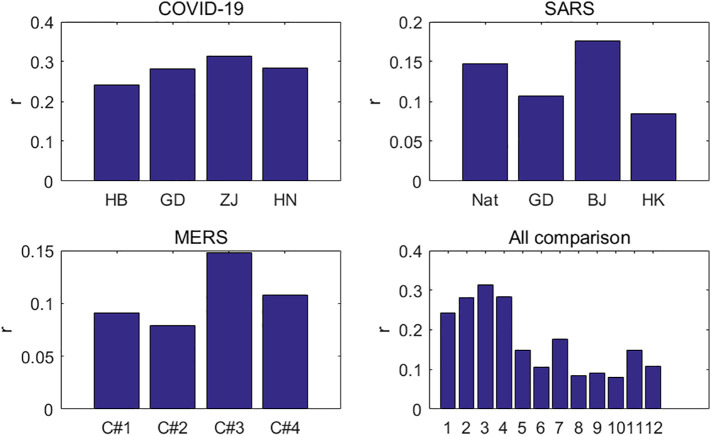
The growth rate r ₀ mainly reflects the natural transmission of an infectious disease, which is affected by a number of factors, including the infectivity of the virus itself, population flow, and public health quality. Although population density can also affect the spread of infectious diseases, its influence is not very obvious. For the growth rate r ₀ of COVID-19, it can be seen from the first graph of Fig. 5 that the growth rates of Hubei, Guangdong, Zhejiang, and Henan are between 0.2 and 0.32, with an average of 0.281. The differences among them are not very obvious. In the case of SARS, the second graph of Fig. 5 shows that the growth rate of Beijing is about twice that of Hong Kong. The growth rates of the MERS virus in the four cycles in Saudi Arabia were not significantly different, with an average of 0.106, as shown in the third graph of Fig. 5. The fourth graph of Fig. 5 compares the transmissibility of the three coronaviruses. The growth rate of COVID-19 is significantly higher than those of SARS and MERS, and is about twice that of SARS, indicating that SARS-CoV-2 is much more infectious than SARS-CoV and MERS-CoV. That is why the COVID-19 outbreak is growing much faster than the SARS and MERS outbreaks.

Fig. 5.

Growth rate for COVID-19, SARS and MERS.

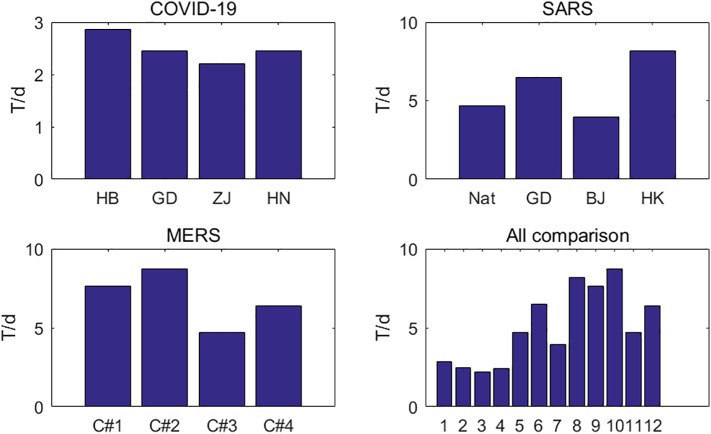
It can be seen from Fig. 6 that the multiplication cycles of SARS and MERS are similar, ranging from 5 to 10 days. For SARS, this is consistent with a culture cycle of 2 to 7 days for the SARS. The multiplication cycle of COVID-19 is only two to three days, and the number of cases of COVID-19 will increase rapidly under the effect of exponential growth.

Fig. 6.

Multiplication cycle for COVID-19, SARS and MERS.

5.1. Infection inhibition constant

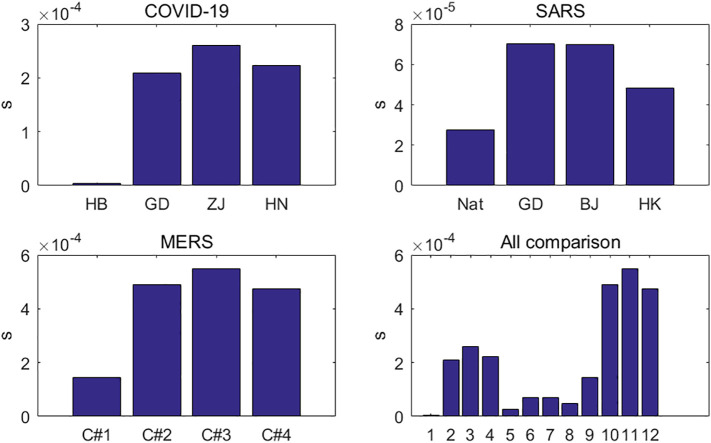
The infection inhibition constant s is related to some human intervention factors, mainly including the isolation of infected people, the isolation of confirmed and suspected cases, the public's attention to infectious diseases, and the cleaning and disinfection of epidemic areas. These human intervention measures are closely related to the measures taken by local governments and medical institutions after the outbreak, and they reflect the emergency management capabilities of government departments and medical and health departments. In principle, vaccines are part of the human intervention, but there is no vaccine for any of the three coronaviruses. The larger the infection suppression constant s, the timelier and more effective are human intervention measures, and the easier it is to control the outbreak in a short time. Otherwise, the outbreak is more likely to get out of control.

The three pneumonias, COVID-19, SARS, and MERS, show significant differences in infection inhibition constants (Fig. 7 ). For SARS, the differences of the infection inhibition constants among the Chinese mainland, Guangdong, Beijing, and Hong Kong are not significant, and their infection inhibition constants are all on the order of 10⁻⁵. The constants of Guangdong and Beijing are almost the same, about twice that of mainland China. The infectious inhibition constant of MERS is an order of magnitude higher than that of SARS, at 10⁻⁴, and the constants for the first to fourth cycle are almost gradually increasing, indicating that Saudi Arabia took stronger emergency intervention measures in subsequent outbreak cycles to stop the transmission of the MERS virus. In Guangdong, Zhejiang, and Henan, the infection inhibition constants of COVID-19 have the same order of magnitude as those of MERS. In Hubei, however, the infection inhibition constant of COVID-19 is 3.58 × 10⁻⁶, two orders of magnitude lower than in Guangdong, Zhejiang, and Henan. That is why COVID-19 grew out of control in Hubei in the early stage. Of course, Guangdong, Zhejiang, and Henan have much higher infection inhibition constants than Hubei, thanks to the strong closure measures taken by Hubei. At the beginning of 2020, Guangdong, Zhejiang, and Henan launched a first-level response to public health emergencies, causing government authorities, health authorities, and the public to take more active measures. The vast majority of Chinese provinces and cities finally started the first-level response to public health emergencies, requiring people to stay in quarantine at home, to wear masks outside, and to improve personal hygiene. As for Hubei province, due to the large number of patients in the early stage, medical institutions could not cope with the shortage of hospital beds, equipment, medicine, masks, protective clothing, and other materials, resulting in the inability to effectively isolate patients, which led to a significantly higher infection inhibition constant in Hubei province. Later, Hubei province adopted more stringent control measures, such as that two AD hoc hospitals were established for the treatment of COVID-19, several cabin hospitals were established for the treatment of mild or asymptomatic patients, and communities were closed.

Fig. 7.

Infection inhibition constant for COVID-19, SARS and MERS.

6. Conclusion

In this paper, a dynamic mathematical model of infectious diseases was established, and the model was used to analyze the epidemic characteristics of COVID-19, SARS, and MERS. The growth rate of infectious diseases determines their prevalence in the early stage, and the infection inhibition constant depends on the prevention and control measures adopted by different regions. The parameter analysis of the three coronavirus dynamics models reasonably explains the characteristics of their transmission and the measures taken in different places during the outbreak. The growth rate of COVID-19 is much higher than that of SARS and MERS, with a doubling period about half of theirs. The infection inhibition constant of COVID-19 in Hubei is two orders of magnitude lower than in other regions, making the outbreak situation of Hubei much more severe.

Author contributions

All the contributions of this manuscript, including conceptualization, modelling, software, data analysis, figure drawing, writing, editing, are finished by Kaihao Liang.

Declaration of Competing Interest

The authors declared that they have no conflicts of interest to this work.