Online education platforms scale college STEM instruction with equivalent learning outcomes at lower cost

Online platforms are an affordable and effective solution to expand STEM education.

Abstract

Meeting global demand for growing the science, technology, engineering, and mathematics (STEM) workforce requires solutions for the shortage of qualified instructors. We propose and evaluate a model for scaling up affordable access to effective STEM education through national online education platforms. These platforms allow resource-constrained higher education institutions to adopt online courses produced by the country’s top universities and departments. A multisite randomized controlled trial tested this model with fully online and blended instruction modalities in Russia’s online education platform. We find that online and blended instruction produce similar student learning outcomes as traditional in-person instruction at substantially lower costs. Adopting this model at scale reduces faculty compensation costs that can fund increases in STEM enrollment.

INTRODUCTION

A shortage of professionals in science, technology, engineering, and mathematics (STEM) fields is slowing down growth and innovation in the global knowledge economy (1–2). Developed and developing countries alike have introduced multibillion-dollar programs to increase the supply of STEM graduates (3–5). However, institutions of higher education face a need to curb the rising costs associated with attracting qualified instructors and serving more graduates as STEM degree programs cost more to run than most other majors (6). The largest global producers of STEM graduates—China, India, Russia, and the United States—are actively seeking policy alternatives to increase the cost-effectiveness of STEM education at scale (5). We present an affordable approach to addressing this global challenge and demonstrate its efficacy in a randomized field experiment.

Experts in education and economics have touted blended or fully online content delivery as a vehicle for expanding access to higher education (7). Experimental or quasi-experimental evidence indicates that online and blended approaches to content delivery can produce similar or somewhat lower academic achievement compared with in-person programs (8–12). These findings are based on comparisons between the modality of course delivery within the same university or the same course taught by one instructor. Yet, scaling up affordable access to STEM education requires a concerted effort across multiple universities and instructors at the national level.

We propose a model relying on national online education platforms that were recently established in many countries, including China (XuetangX, WEMOOC, and CNMOOC), India (Swayam), and Russia [National Platform of Open Education (OpenEdu)] to address challenges associated with the shortage of qualified instructors and growing demand for higher education. National online education platforms allow resource-constrained institutions that struggle with attracting and retaining qualified instructors to include online courses produced by the country’s highest ranked departments or universities into their traditional degree programs. In addition to reducing costs, the integration of online courses into the curriculum can potentially enable resource-constrained universities to enrich student learning by leveraging the expertise of the instructors from top departments or universities.

Russia’s OpenEdu is a nonprofit organization that offers full-scale online university courses to the public. It was established in 2015 by eight top Russian universities with support from the Ministry of Higher Education and Science (MHES). These universities established OpenEdu to address growing concerns about the quality of higher education (13) and to improve the cost-effectiveness of the massified higher education system during an economic recession. Russian higher education institutions can integrate any of the 350+ courses from the OpenEdu platform into their curricula by paying a small fee to the university that produced the course. Students at the purchasing institution can take the course for credit with either fully online or blended instruction—an online course augmented with in-person discussion sections.

If the country’s highest ranked universities or departments can deliver online STEM courses at resource-constrained institutions without substantial declines in student learning outcomes, then the OpenEdu model could alleviate strains on hiring qualified instructors at resource-constrained institutions and become an affordable alternative to traditional STEM instruction. We conducted a multisite randomized controlled trial (RCT) to test the effectiveness of the OpenEdu model, including testing the effect of instruction modality (fully online instruction, blended instruction, and in-person instruction) on student learning and calculating cost savings that the model could bring to the higher education system.

In the 2017–2018 academic year, we selected two required semester-long STEM courses [Engineering Mechanics (EM) and Construction Materials Technology (CMT)] at three participating, resource-constrained higher education institutions in Russia. These courses were available in-person at the student’s home institution and alternatively online through OpenEdu. We randomly assigned students to one of three conditions: (i) taking the course in-person with lectures and discussion groups with the instructor who usually teaches the course at the university, (ii) taking the same course in the blended format with online lectures and in-person discussion groups with the same instructor as in the in-person modality, and (iii) taking the course fully online.

The course content (learning outcomes, course topics, required literature, and assignments) was identical for all students. A feature of Russia’s higher education system, also found in other countries, is that the content of required courses at all state-accredited universities must comply with Federal State Education Standards (FSES). FSES sets the requirements for both student learning outcomes and the topics that should be covered within academic programs (with limited discretion for the instructor) and most online courses on OpenEdu comply with the FSES. To further minimize variation in course materials between courses, we worked with course instructors before the experiment to ensure that all students received the same assignments and required reading. We also surveyed course instructors and collected information about their sociodemographic characteristics, research, and teaching experience. As expected, the online course instructors from one of the country’s top engineering school had better educational backgrounds, more research publications, and more years of teaching experience than the in-person instructors.

Before the start of the course, students under all three conditions attended an in-person meeting at their home university with the instructor and the research team, where they were informed about the experiment and given the opportunity to opt out without consequences (5 of 330 students opted out). During the meeting, students took a knowledge pretest assessing their mastery of the course content. They also completed a survey questionnaire asking about their sociodemographic characteristics and prior learning experiences. At the end of the course, all students took a standardized final exam assessing their mastery of the course content and completed a questionnaire about their course experience and satisfaction; both were administered by course instructors and the research team on-site at each university.

In total, 325 second-year college students from three universities were randomly assigned to one of three experimental conditions: 101 in-person, 100 blended, and 124 online. The distribution across conditions was uneven by design. Nearly, the entire cohort of mechanical engineering majors at University 1 (U1; n = 98) and civic engineering majors at U2 (n = 140) took the five-credit EM course. At U3, the entire cohort of mechanical engineering majors (n = 87) took the four-credit course on CMT. Random assignment successfully created three groups of students with balanced sociodemographic characteristics (F = 1.12, P = 0.31). We verified using attendance sheets that students remained in their assigned instruction modality. At the end of the courses, 294 participants (90%; attrition was independent of condition) took the final examination, which was developed by the online course instructors and independently evaluated for alignment with FSES learning outcomes.

We consider three student outcomes: (i) students’ final exam score, (ii) their average grade across all course assessments, and (iii) their self-reported satisfaction with the course. Students received the same exam and weekly assessment materials under all conditions, except that online students were permitted three attempts instead of a single attempt on the weekly assessments but not on the final exam. We analyze the data with and without covariate adjustment using ordinary least squares (OLS) regression with fixed effects for university, pooling multiple imputations to address missing values (see Materials and Methods for model details).

RESULTS

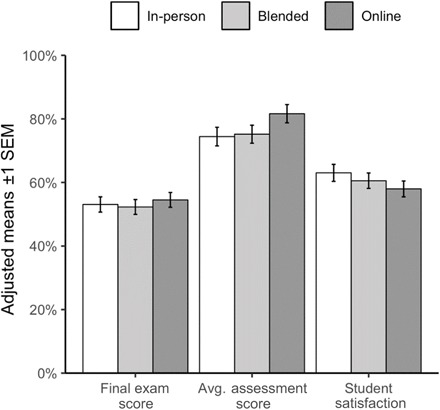
We find minimal evidence that final exam scores differ by condition (F = 0.26, P = 0.77) (Fig. 1). The average assessment score varied significantly by condition (F = 3.24, P = 0.039): Students under the in-person and blended conditions have similar average assessment scores (t = 0.26, P = 0.80), but those under the online condition scored 7.2 percentage points higher (t = 2.52, P = 0.012). This effect is likely an artifact of the more lenient assessment submission policy for online students, who were permitted three attempts on the weekly assignments. Nevertheless, despite the difference in assessments scores, we find minimal evidence that student satisfaction differs by condition (F = 2.22, P = 0.109). Online students were slightly less satisfied with their course experience than in-person students (t = −1.88, P = 0.062), while blended and in-person students reported similar levels of satisfaction (t = −0.91, P = 0.36). Results with covariate adjustment, as reported and illustrated in Fig. 1, are qualitatively similar without adjustment.

Fig. 1. Average student outcomes under each condition from covariate-adjusted regression models for three outcome measures: final exam score, average assessment score, and self-reported student satisfaction.

National online education platforms have the potential to address the shortage of resources and qualified STEM instructors by bringing cost savings for the economically distressed higher education institutions. The existing supply of instructors is expected to decline sharply as 41% of STEM faculty in Russia today are older than 60. Given looming shortages of faculty and growing demand from students, national online platforms can mitigate budget constraints as the supply of qualified instructors puts upward pressure on faculty compensation. To demonstrate the cost efficacy, we estimate whether the introduction of blended or fully online instruction of EM and CMT scaled to all state-funded resource-constrained higher education institutions in Russia would allow these institutions to enroll more STEM students at the same or lower cost for the national system.

There are 129 state-run institutions of higher education that receive only basic funding from Russia’s Ministry of Higher Education and Science and that admitted students who were required to take EM and/or CMT as part of their major. In 2018, these universities admitted 29,992 freshmen students who were required to take EM and 72,516 freshmen students who were required to take CMT. Tuition for these students is paid by the Ministry: Each university receives an annual subsidy per student that covers both instructor compensation and all other costs (e.g., staff and management salaries, buildings maintenance and utilities, and study equipment). In our model, we assume that part of the state subsidy for each resource-constrained university will go to the country’s highest ranked universities for the production, delivery, and proctoring of an online version of EM and CMT (see Materials and Methods for model details). However, blended and online instruction will reduce instructor compensation expenses and enable resource-constrained universities to enroll more students with the same state subsidy.

On the basis of university-level data on instructor salaries and the number of enrolled students per year at these 129 universities, we calculate instructor compensation per student for each course when offered in-person, blended, or fully online. Our estimates are based on the same teaching model that was used by the universities in the experiment: All students attend a common lecture (no more than 300 students) and are then assigned to discussion sections in groups of no more than 30 students. Our estimates for blended and online modalities account for the cost of production (media production and faculty and staff compensation), support, and proctoring of online courses. Compared to the instructor compensation cost of in-person instruction, blended instruction lowers the per-student cost by 19.2% for EM and 15.4% for CMT; online instruction lowers it by 80.9% for EM and 79.1% for CMT (Fig. 2).

Fig. 2. Average instructor compensation per 1000 students with in-person, blended, and online instruction for EM and CMT courses at 129 Russian higher education institutions.

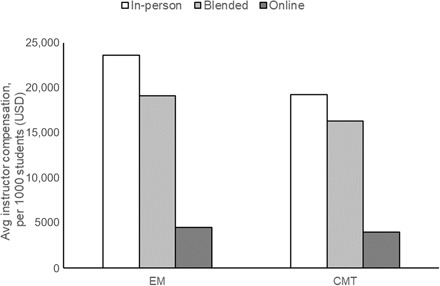
USD, U.S. dollars.

These cost savings can fund increases in STEM enrollment with the same state funding. Conservatively assuming that all other costs per student besides instructor compensation at each university remain constant, resource-constrained universities could teach 3.4% more students in EM and 2.5% more students in CMT if they adopted blended instruction. If universities relied on online instruction, then they could teach 18.2% more students in EM and 15.0% more students in CMT.

DISCUSSION

This study demonstrates the potential of national online education platforms for scaling up affordable access to STEM education. In the model we propose, national online education platforms license online courses created by top universities to resource-constraint universities with a shortage of qualified instructors. The platform not only provides information technology infrastructure for hosting online courses but also supports universities with the design, production, and delivery of online courses. For each course, the learning outcomes, topics, required reading, and assignments are standardized with iterative quality assurance from domain experts and psychometric evaluators. Resource-constrained universities can offer the licensed courses for credit either fully online or in a blended format. Blended instruction is facilitated by providing instructors at resource-constrained universities with a set of teaching materials (lecture slides, assigned reading, and problem sets).

There are challenges and limitations associated with using a national online education platform to expand STEM education. First, there are substantial start-up costs for the platform itself, for faculty professional development programs to improve online teaching and for the introduction of new models of instruction at universities. These costs can be covered by the state or by a consortium of universities that will become course providers on the platform. Second, these platforms will be more efficient in settings where academic programs are synchronized both in terms of student learning outcomes and academic calendars. State or private accreditation boards and professional associations could play a more active role in harmonizing curricula across universities. Cross-country variation in the impact of online education platforms on student learning and the cost of instruction warrants further investigation. Third, more research is needed on how combining different instruction modalities in degree programs affect learning and career outcomes for students with diverse backgrounds. Policy makers and course designers need to experiment with new approaches that can improve student outcomes relative to traditional forms of instruction.

To achieve tight control between the three instruction modalities, the online learning approach tested in this study did not include novel learning activities available in modern online learning platforms. Automated formative assessment, just-in-time learning, and interactive learning materials with immediate feedback can provide learning benefits similar to one-on-one tutoring at a lower cost (14–15). Our estimates of the online learning benefits may therefore be conservative, and models that make better use of the online affordances might show benefits for learning outcomes and efficiency that offset the higher up-front development cost (8). A centralized national model for STEM education can also provide an unprecedented opportunity for systematic research into improving learning resources and pedagogy with national student samples, fine-grained longitudinal outcome measures, and experimental control over the learning environment.

At a time when both developed and developing countries experience a shortage of resources and qualified instructors to expand STEM education, national or accredited online education platforms can provide a feasible alternative to traditional models of instruction. Our study shows that universities can use these platforms to increase enrollments without spending more resources on instructor compensation and without losses in student learning outcomes. While students’ satisfaction may fall, the decline in satisfaction pales in comparison to the potential cost savings. A cost-effective expansion of STEM programs will allow countries facing instructor shortages and rising costs to be more competitive in the global knowledge economy.

MATERIALS AND METHODS

Study context

The study was conducted in the 2017–2018 academic year in Russia as part of a larger feasibility study on the integration of online courses from Russia’s National Platform of OpenEdu into traditional degree programs at Russian universities (16). OpenEdu is Russia’s largest national online education platform, which was established in 2015 by eight leading Russian universities with the support from the Ministry of Higher Education and Science. OpenEdu was developed using an open source platform Open edX. OpenEdu is administered as a nonprofit organization and, as of April 2019, offered more than 350 online courses from the best Russian universities.

Most of the courses at OpenEdu are full-scale university courses that comply with Russian FSES. FSES are detailed requirements to student learning outcomes, structure of academic programs, and required resources (staffing, financial resources, and physical infrastructure) within a particular academic field. All state-accredited higher education institutions must design their academic programs and courses as compliant to the FSES, or otherwise, their accreditation will be terminated. FSES are developed by interuniversity curricular boards in each academic field. Universities can include online courses from other universities at OpenEdu in their accredited academic programs because course content is aligned with FSES. OpenEdu relies on the evaluations from content-matter experts to assess the alignment of a particular course with FSES before launch.

The merits of such a coordinated system are not part of the discussion in this paper. However, the fact that the content of both online courses offered by OpenEdu and traditional in-person courses at state-accredited universities complies with FSES created an opportunity to investigate the impact of replacing in-person courses at resource-constrained institutions with online course produced by the country’s best universities and departments.

Data collection

Data were collected during an RCT at three universities. The RCT included two courses, one on EM and another on CMT. Data collection was organized in six stages, as detailed below.

Selection of universities

At the first stage, we selected universities for the study based on the list of 12 higher education institutions provided by OpenEdu. These higher education institutions either already collaborated with OpenEdu integrating online courses in their academic programs or had inquired with OpenEdu about the possibility of doing so. We then excluded seven universities that either had a prestigious designation of Federal University, National Research University, Special Status, or “Project 5-100” university (meaning they also receive additional funding from the state) or were not located in the European part of Russia. Location in the European part of Russia was important so that the research team is able to travel no more than 10 hours from Moscow to conduct organizational meetings and proctor examinations. We then sent invitations to the five selected institutions to participate in the study. There were several conditions for participation:

The university has STEM academic programs and is willing to replace one of the in-person courses with an online course from OpenEdu.

The university has a cohort of second-year students majoring in one of the STEM subjects, and this cohort is larger than 75 students. We have chosen second-year students because we wanted to include in our study a foundational STEM course that is required for the whole cohort of students. These courses are most common during the first and the second year of study. We chose the second-year students because they have already adapted to the university environment. We needed a cohort of 75 students to have the size of control and experimental groups no less than 25 students. Cohorts of 100 students and smaller per major are typical for Russian higher education because majors (especially in engineering) tend to reflect narrow specializations (17). In Russia, similar to most universities outside of the United States, students choose their major upon admission to the university and the cohort admitted to the same major study together. Lectures are organized for the entire cohort, and discussion groups and labs convene in groups of 20 to 30 students assigned by the administration.

The university can provide a field coordinator (who cannot be the course instructor) to work with the research team on the implementation of the experiment.

Three universities agreed to participate in the study under these conditions. U1 is a polytechnic university with an enrollment of 10,000 students and located in a city with a population of more than 250,000 people in the European part of Russia. In the 2017 national ranking by selectivity of admission, U1 was ranked in the bottom half of 458 higher education institutions. A cohort of 103 second-year students majoring in Mechanical Engineering at U1 was selected to participate in the experiment.

U2 is also a polytechnic university with an enrollment of 15,000 students located in a city of more than 1 million people in the European part of Russia. In 2017 national ranking by selectivity of admission, U2 was also ranked in the bottom half of 458 higher education institutions. The cohort of 140 second-year students majoring in Civil Engineering at U2 was selected to participate in the experiment.

U3 is a comprehensive (former polytechnic) university with an enrollment of 25,000 students located in a city of more than 500,000 people in the European part of Russia. In 2017 national ranking by selectivity of admission, the university was ranked in the bottom half of 458 higher education institutions. The cohort of 87 second-year students majoring in Mechanical Engineering was selected to participate in the experiment.

Selection of courses

At the second stage, we selected online courses for the experiment. The courses were selected on the basis of the following criteria:

An online course should comply with Russia’s FSES.

An online course should have an equivalent in-person course at one of the selected universities and majors. The equivalent in-person course should be a required course for second-year students in the selected majors.

An online course at OpenEdu should start during the same time as the equivalent in-person course (i.e., September 2017).

As a result, two online courses were selected for the study: EM (at U1 and U2) and CMT (at U3). The online course on EM (18) was taught on OpenEdu during the fall semester of the 2017–2018 academic year (18 weeks, from 11 September 2017 to 15 February 2018). The course counts for five credit units. To successfully master the course, students must have a high school–level knowledge of physics, mathematics, and descriptive geometry. The syllabus includes 17 topics divided into three sections: statics, kinematics, and dynamics. The required literature includes four textbooks and problem sets. The learning outcomes of the EM course emphasize the ability to design and apply mechanic and mathematical models to describe various mechanical phenomena. Course learning outcomes are assessed with in-class multiple-choice quizzes, homework problems for each topic, a comprehensive course project, and a final exam.

The online course on EM was produced and delivered by Ural Federal University, which has an enrollment of 33,000 students and is located in Yekaterinburg (population more than 1.3 million people). Ural Federal University is one of the best Russian universities (it is one of 10 federal universities and a Project “5-100” universities that receive additional funding to become world-class universities). In the 2017 national ranking by selectivity of admission, Ural Federal University was ranked in the top 25% of 458 higher education institutions. It was also ranked in the top 10 of Russian universities by selectivity of admissions in both Mechanical Engineering and Civil Engineering.

The instructors of the online course have a better education background, more years of teaching experience, eight times more publications indexed by Scopus or Web of Science citation databases than instructors at the U1 and U2 combined (see Table 1). In addition, instructors of the online course are authors of two textbooks on EM.

Table 1. Characteristics of instructors.

Notes: (i) Only publications in journals indexed by Web of Science and Scopus were included; (ii) Russia has a two-level system of doctoral qualifications. The first level—Candidate of Sciences—is equivalent to PhD or similar degrees. The second level—Doctor of Sciences—is an additional qualification that allows obtaining an academic rank of full professor (similar to “Habilitation” in Germany and other European countries).

Course	Instructor	Academic degree	Place of graduation	Academic rank	Years of teaching	Publications
EM	Instructor A, online	PhD (Habilitation)	Elite university	Professor	46	39
	Instructor B, online	PhD (Habilitation)	Elite university	Associate professor	24	20
	Instructor A, U1	PhD	Non-elite university	Associate professor	17	–
	Instructor B, U1	PhD	Non-elite university	Associate professor	20	1
	Instructor A, U2	PhD	Non-elite university	Associate professor	35	1
	Instructor B, U2	–	Non-elite university	Senior lecturer	12	5
CMT	Instructor A, online	PhD	Elite university	Associate professor	31	–
	Instructor B, online	PhD	Elite university	Associate professor	43	–
	Instructor C, online	PhD	Elite university	Associate professor	47	–
	Instructor D, online	PhD	Elite university	Associate professor	51	–
	Instructor A, U3	–	Non-elite university	Senior lecturer	11	–

The online course on CMT (19) was taught on OpenEdu during the fall semester of the 2017–2018 academic year (18 weeks, from 11 September 2017 to 15 February 2018). Course workload is four credit units. To successfully master the course, students must have a high school–level knowledge of physics, mathematics, and chemistry. The syllabus includes 16 topics focused on the characteristics of construction materials, methods of their production, and manufacturing of component blanks and machine parts from these materials. The required literature includes three textbooks and problem sets. The learning outcomes of the CMT course emphasize the ability to design technologies and mathematical models and select appropriate materials for construction. Course learning outcomes are assessed with in-class multiple-choice quizzes, homework problems for each topic, and a final exam.

The online course on CMT was produced and delivered by Ural Federal University (same as the online course on EM). The instructors of this online course also have a better education background and more years of teaching experience compared to the instructor at the university (see Table 1).

Standardizing course content

At the third stage, we worked with course instructors to make sure that the content of the online courses and in-person courses was identical. Although both in-person courses and online courses complied with FSES, some assignments and required literature were different. Instructors from participating universities were provided a set of teaching materials (lecture slides, assigned reading, and problem sets) to update their programs. Learning outcomes, course topics, required literature, and assignments for every topic were identical in all modalities of instruction (online, blended, and in-person). The typical weekly class in the in-person modality included an in-person lecture on the certain topic, followed by an in-person discussion section group with in-class quiz and the discussion of the homework assignment. The typical weekly class in the blended modality included an online lecture on the certain topic, followed by an in-person discussion section group with in-class quiz and the discussion of the homework assignment. The typical weekly class in the online modality included an online lecture on the certain topic, followed by an online quiz and an online homework assignment. We also surveyed course instructors and collected information about their sociodemographic characteristics and teaching experience.

Random assignment

At the fourth stage, the research team obtained the list of students from each university and randomly assigned them to one of three experimental conditions. Students assigned to the in-person condition took the course in the traditional instructional modality (lectures and discussion groups) with the instructor who usually teaches the course at this university. Students assigned to the blended condition watched lectures from the online course and then attended in-person discussion groups with the instructor who usually teaches this course at this university. Last, students assigned to the online condition watched lectures online and completed course assignments online after the end of each lecture; they did not have access to in-person discussion groups.

After the random assignment was complete, we conducted on-site organizational meetings with students before the start of the courses. Students were told about the context of the study, the experimental procedures, and practical considerations of taking courses in blended or fully online formats. At the meeting, students took a pretest aimed at assessing the level of their preparation to course content. The pretest included eight assignments on mathematics, physics, and engineering drawing. Students also completed a survey questionnaire asking about their sociodemographic characteristics and learning experience. Only after they completed all of this, students were told which experimental condition they had been assigned to. At this point, students had the opportunity to opt out of the experiment. Those who agreed to participate signed an informed consent form to participate in the study. Students were not incentivized to participate in the experiment.

Of 103 students from U1, 98 agreed to participate in the experiment (95%). All students from U2 (140 students) and U3 (87 students) agreed to participate in the experiment. The experiment included 325 students in total: 101 under the in-person condition, 100 under the blended condition, and 124 under the online condition. The distribution across treatment status was uneven by design. U1 requested an accommodation for scheduling the in-person class during the study, and thus, 50% of students were assigned to the online condition, 25% to in-person, and 25% to blended instruction. Students at U2 and U3 were assigned to conditions with equal probability (one-third per condition). Student characteristics by each group are in Table 2.

Table 2. Student level summary statistics in each condition.

Note: GPA, grade point average.

Covariate	In-person condition			Blended condition			Online condition
	N	Means	SD	N	Means	SD	N	Means	SD
Female	101	0.32	0.47	100	0.40	0.49	124	0.27	0.44
Age	97	18.90	0.90	97	18.96	1.14	110	18.92	0.97
Had online learning experience	93	0.28	0.45	94	0.22	0.42	99	0.25	0.44
Pretest score	96	31.38	18.14	96	32.16	19.26	110	27.61	18.24
College entrance exam score, Russian	97	75.43	12.08	97	74.58	12.58	111	74.46	13.45
College entrance exam score, math	96	58.72	13.42	97	59.96	13.57	111	57.87	13.89
College entrance exam score, physics	96	54.87	9.55	95	55.76	11.39	109	53.95	10.44
Cumulative college GPA	97	3.87	0.47	97	3.86	0.50	111	3.88	0.51
Intrinsic motivation index (α = 0.73)	80	3.79	1.57	73	4.23	1.56	93	4.28	1.44
Extrinsic motivation index (α = 0.72)	84	4.67	1.17	85	4.86	1.18	101	4.76	1.03
Self-efficacy in learning index (α = 0.71)	58	0.13	1.15	64	−0.02	0.91	76	−0.08	0.95
Interaction with instructors index (α = 0.70)	81	0.07	1.09	84	0.11	1.02	98	−0.15	0.88

Students take courses

At the fifth stage, students took the course in the assigned instructional modality. The research group collected information about their attendance and course performance through instructors and OpenEdu.

Posttest and Interviews

At the sixth stage, all three groups of students took a posttest—a final examination assessing their mastery in course topics. The content of posttest assessments was identical to the final exams in the online versions of EM and CMT on the OpenEdu platform. Both courses comply with FSES as required by the OpenEdu platform. FSES does not provide standardized assessments for each course, but it provides some guidance how assessments should be designed and conducted. The authors of the online courses used guidance from FSES to create question banks that measure learning outcomes as required by FSES. Each item was created to measure one or several learning outcomes. Question items include multiple choice and open-ended questions. Before courses were launched on OpenEdu, the test-item banks underwent a formative evaluation by the experts in the corresponding subject areas for alignment with FSES learning outcomes. When a student takes the online course for credit, the proctored exam has the same number of items randomly selected from the question bank as posttest assessment. For the EM course, the question bank comprised 177 items across 10 sections, and the posttest assessment is constructed by selecting one item from each section. For the CMT course, the question bank comprised 623 items across 30 sections, and the posttest assessment is constructed by selecting one item from each section. Internal consistency of the question banks in terms of Cronbach’s alpha is 0.82 (95% confidence interval, 0.78 to 0.86) for the CMT course and 0.71 (95% confidence interval, 0.67 to 0.75) for the EM course. According to Bland and Altman (20), alpha values of 0.7 to 0.8 are regarded as satisfactory for research tools to compare groups.

All students in the experiment who took final examination received the same set of test items. The exam was administered on-site by the research team and course instructors for all three student groups simultaneously. For the EM course, 216 (91%) students took the exam (60 min, 10 test assignments); for the CMT course, 78 (90%) students took the exam (40 min, 30 test assignments). Student attrition was independent of condition.

Students completed a survey questionnaire asking them about their course experience and satisfaction. The research team also conducted several in-depth interviews and focus groups with students.

Covariate measures

Before the start of the course, we collected data on student characteristics that we used as covariates. Prior research showed that student performance in online courses is associated with sociodemographic characteristics (21), motivation (22, 23), self-efficacy (24), and interaction with instructors (25). In the survey after the pretest, we asked students about their gender and age, prior experience in taking online courses either independently or as part of their university’s curriculum, academic motivation, self-efficacy in learning, and frequency of interactions with instructors. In addition, universities provided administrative data on student first-year cumulative grade point average (GPA) and their national college entrance exam scores in physics, math, and Russian language. Russia’s national college entrance exam—Unified State Exam—is a series of subject-specific standardized tests in Russia that students pass at the end of high school to graduate both from high school and enter higher education institutions. Each exam is measured from 0 to 100. See student-level summary statistics across three conditions in Table 2.

After self-determination theory (26), we measured two types of motivation—intrinsic and extrinsic—using the shortened version of academic motivation questionnaire by Vallerand et al. (27) later translated in Russian and validated by Gordeeva et al. (28). Students were asked to evaluate to what extent eight statements about their homework assignments correspond to them: Two statements measured intrinsic motivation (items 1 and 2 below), and six statements measured extrinsic motivation [items 3 to 8 below; two statements per identified regulation (items 3 and 4), introjected regulation (items 5 and 6), and external regulation (items 7 and 8) components of extrinsic motivation]. These statements were then combined into two indices.

I do my homework because… [seven-point scale from “does not correspond at all” (1) to “corresponds exactly” (7)]:

1) I experience pleasure and satisfaction while learning new things.

2) My studies allow me to continue to learn about many things that interest me.

3) It will help me to broaden my knowledge and skills that I need in the future.

4) It will help me make a better choice regarding my future career.

5) My classmates do it.

6) I would be embarrassed if I do not do it.

7) I want to avoid problems with instructors.

8) I want to get a high grade.

We measured self-efficacy in learning by relying on the questionnaire of self-regulated learning developed by Zimmerman (29) and adapted for online learning by Littlejohn et al. (22). Students were asked to evaluate their agreement or disagreement with four statements related to the way they learn at the university [four-point scale from “strongly disagree” (1) to “strongly agree” (4)]:

1) I can cope with learning new things because I can rely on my abilities.

2) My past experiences prepare me well for new learning challenges.

3) When confronted with a challenge, I can think of different ways to overcome it.

4) I feel that whatever I am asked to learn, I can handle it.

These statements were then combined into the measure of self-efficacy using principal components analysis. We measured frequency of interactions with instructors using survey two items (1 and 2 below) from Student Experience in the Research University undergraduate student survey (30) and two items (3 and 4 below) from Maloshonok and Terentev (31). Students were asked to evaluate four statements on various aspects of interaction with instructors in the past academic year [five-point scale from “never” (1) to “very often” (5)]:

1) Talked with the instructor outside of class about issues and concepts derived from a course.

2) Worked with a faculty member on an activity other than coursework (e.g., student organization, campus committee, and cultural activity).

3) Talked with the instructor about your grades and course tasks.

4) Received feedback on your work from the instructor.

We used principal components analysis to create the index of interactions with instructors.

Outcome measures

We consider three outcomes in this study to measure final learning outcomes, academic achievement during the course, and satisfaction in the course. First, the final learning outcomes are assessed using the official final exam score (between 0 and 100%). Second, academic achievement during the course is assessed by the average score across all course assignments (between 0 and 100%). Third, satisfaction was assessed using a survey question on the exit survey. The question was “Please rate your level of satisfaction with the course,” and students could respond on a four-point scale from “completely dissatisfied” to “very satisfied.”

We check convergent and divergent validity by computing correlations between students’ final exam scores and other scores that should be either statistically related or unrelated. The final exam score is significantly correlated with both their average assessment score (Pearson correlation = 0.35, P < 0.001) and their pretest score (Pearson correlation = 0.16, P = 0.008) but uncorrelated with their overall GPA (Pearson correlation = 0.07, P = 0.27) and high-school exam scores (Pearson correlation < 0.1, P > 0.11). This provides evidence that the final exam measures not only general student ability but also specifically knowledge and skills related to the course objectives. The average assessment score and satisfaction correlate at r = 0.35; the final exam score and satisfaction correlate at r = 0.095.

Analytical approach

Missing values were imputed 50 times using predictive mean matching. OLS regression estimates are pooled across the 50 imputations using Barnard-Rubin adjusted degrees of freedom (32). SEs and P values are adjusted for the increase in variance due to nonresponse. The covariate balance test combines the result from Zellner’s (33) seemingly unrelated regression models test for the 50 imputations using a chi-square approximation.

We compare results from the adjusted and unadjusted models predicting the three outcome measures. The unadjusted OLS regression models take the following form with the in-person modality condition coded as the reference group

$$Y_i=b_0+b_1\times {\text{ModalityBlended}}_i+b_2\times {\text{ModalityOnline}}_i+b_3\times \mathrm{U} 2_i+b_4\times \mathrm{U} 3_i+e_i$$ (1)

The covariate-adjusted OLS regression models add the following pretreatment covariates as defined above: knowledge pretest score; gender; age; prior experience in taking online courses; cumulative GPA; national college entrance exam scores in physics, math, and Russian language; academic motivation; self-efficacy in learning; and interactions with instructors. Unadjusted and covariate-adjusted regression results are presented in Table 3.

Table 3. Unadjusted and covariate-adjusted regression estimates for three outcome measures: final exam score, average assessment score, and self-reported student satisfaction.

Note: SEs in parentheses.

	Outcome: Final exam score		Outcome: Average assessment score		Outcome: Student satisfaction
	1a. Unadjusted	1b. Covariate- adjusted	2a. Unadjusted	2b. Covariate- adjusted	3a. Unadjusted	3b. Covariate- adjusted
Condition = online	0.589 (2.21)	1.442 (2.28)	7.22** (3.06)	7.19** (2.85)	−5.01** (2.54)	−5.05* (2.69)
Condition = blended	−1.081 (2.31)	−0.791 (2.35)	1.28 (3.19)	0.744 (2.92)	−2.03 (2.69)	−2.48 (2.71)
Intercept	52.089*** (2.26)	53.074*** (2.41)	70.74*** (3.05)	74.436*** (2.92)	64.12*** (2.55)	63.02*** (2.67)
University fixed effect	True	True	True	True	True	True
Addl. covariates	False	True	False	True	False	True
R2	14.0%	18.4%	57.8%	68.1%	19.9%	29.5%

***P < 0.01, **P < 0.05, and *P < 0.1

Cost-savings analysis

Our analysis of cost savings associated with the introduction of blended or online instruction has two steps. First, we calculate and compare costs of instructor compensation for in-person, blended, and fully online modalities for EM and CMT courses at all MHES-funded universities that do not have a prestigious designation of National Research University, Federal University, Special Status, or Project 5-100 university (and do not receive additional state funding for this status) and that require these courses. Second, we calculate how many students these universities can enroll in EM and CMT courses if they adopt the blended or online model with the amount of funding that is currently available to them. Our calculations are based on four assumptions.

First, our analysis focuses on resource-constrained state universities that do not have the prestigious designation of National Research University, Federal University, Special Status, or Project 5-100 university. There are 203 such universities that enroll 61% of state-funded students in STEM majors that require EM or CMT as part of their curriculum. We analyze university-level data from 129 of these universities that receive funding through the Ministry of Higher Education and Science. Other 74 universities receive funding through the Ministry of Agriculture or the Ministry of Transport of Russian Federation. For these 74 universities, we had only instructor compensation data but not the data on other costs per student. Cost savings on instructor compensation in blended and online instruction are several percentage points higher if these universities were included in the sample. The data include average instructor compensation and all other costs per student per credit for in-person instruction at each university. These 129 universities account for 45% of all state-funded enrollment in STEM majors that require EM or CMT as part of their curriculum. All universities that participated in the RCT belong to this group.

Second, we calculate cost savings in public spending on higher education in STEM fields. More than 80% of Russia’s STEM enrollment is fully funded by the state. Currently, each university receives an annual subsidy per student that covers both instructor compensation and all other costs (e.g., staff and management salaries, buildings maintenance and utilities, and study equipment). The amount of subsidy per university varies and depends on geographical location and specialization. On average, instructor compensation accounts for 24.7% of all costs per student, based on university-level data on the amount of state subsidies and instructor compensation at 129 MHES-funded non-elite universities.

In a scaled-up version of this program, part of state subsidy for each of non-elite university would likely be spent on production, delivery, and proctoring of an online version of EM and CMT at one of the top universities. Resource-constrained universities can then reduce instructor compensation costs using blended or online instruction and enroll more students with the same state subsidy. Our model assumes that all 129 universities will introduce either online or blended instruction.

Third, our calculations are made for the same teaching model that was used in the experiment. For in-person instruction, we assume that all students attend a common lecture (no more than 300 students) and are assigned to discussion sections of no more than 30 students. The EM course lasts 18 weeks with two academic hours (one academic hour = 40 min) of lectures per week and two academic hours of discussion sections per week. The CMT course lasts 16 weeks with two academic hours of lectures per week and two academic hours of discussion sections per week. We calculate the cost of the in-person modality (Eq. 2) separately for EM and CMT based on university-level instructor salary data from 129 universities and the number of hours the instructor spends on each course.

$${\text{CP}}_a=\frac{{\displaystyle {\sum }_{i=1}^n}(C_i\times 2\times {\text{LG}}_{\mathit{ai}}\times {\text{LH}}_a+{\mathrm{C}}_i\times {\text{SG}}_{\mathit{ai}}\times {\text{SH}}_a)}{{\displaystyle {\sum }_{i=1}^n}{N}_{\mathit{ai}}}$$ (2)

where CP_a is the cost of instructor compensation per student in the in-person modality for the course a and C_i is the average instructor compensation (before taxes) per academic hour at the university i. Compensation for a lecture is twice as higher compared to the discussion section. LG_ai is the number of lecture groups at the university i for the course a, LH_a is the number of lecture academic hours for the course a, SG_ai is the number of discussion section groups at the university i for the course a, SH_a is the number of discussion section academic hours for the course a, and N_ai is the number of students at university i for the course a.

For blended instruction, students watch lectures online and then attend the same discussion sections as the in-person group. We calculate the cost of the blended modality (Eq. 3) separately for EM and CMT by accounting for the compensation of instructors who lead in-person discussion sections and the cost of developing online courses (video production and faculty and staff compensation) and supporting the online delivery (maintenance and communication with students via discussion boards or email). Our estimates of the cost of developing and supporting online courses are based on the actual costs of the Ural Federal University to develop and support EM and CMT courses for OpenEdu.

$${\text{CB}}_{\mathrm{a}}=\frac{{\displaystyle {\sum }_{i=1}^n}(C_i\times {\text{SG}}_{\mathit{ai}}\times {\text{SH}}_a)+{\text{PC}}_a}{{\displaystyle {\sum }_{i=1}^n}{N}_{\mathit{ai}}}+{\text{SC}}_a$$ (3)

where CB_a is the cost of instructor compensation per student in the blended modality for the course a, C_i is the average instructor compensation (before taxes) per academic hour at the university i, SG_ai is the number of discussion section groups at the university i for the course a, SH_a is the number of discussion section academic hours for the course a, PC_a is the total production costs of the online version of the course a (video production and instructor compensation), N_ai is the number of students at university i for the course a, and SC_a is the student support costs per student for the course a (calculated on the basis of 2017 data for the course a).

For online instruction, students watch lectures, communicate with instructors, and complete assignments online. We calculate the cost of the online modality (Eq. 4) separately for EM and CMT by accounting for the costs of developing and supporting online courses and the cost of proctoring of the final exam at the end of the course via a specialized service unit. The cost of proctoring per student was also provided by the Ural Federal University.

$${\text{CO}}_a=\frac{{\text{PC}}_a}{{\displaystyle {\sum }_{i=1}^n}{N}_{\mathit{ai}}}+{\text{SC}}_a+\text{PC}$$ (4)

where CO_a is the cost of online modality per student in the fully online modality for the course a, PC_a is the total production costs for the course a (video production and instructor compensation), N_ai is the number of students at university i for the course a, SC_a is student support costs per student for the course a (calculated on the basis of 2017 data for the course a), and PC is cost of proctoring per student.

Fourth, when we calculate increases in enrollment in the blended or online modalities, we assume that all the costs besides instructor compensation will remain the same. This assumption leads to a rather conservative estimation in the increase in the number of students, especially in the online modality. In reality, other costs will also go down because blended or online instruction will require less spending on, for example, building maintenance and utilities and hiring instructors. However, these changes are much harder to estimate, and thus, we assume here that they will stay the same. We estimate the number of students in the courses with the blended and online modalities using Eqs. 5 and 6

In blended

$${\text{SE}}_{\mathrm{b}a}={\displaystyle {\sum }_{i=1}^n}\frac{S_{\mathit{ai}}}{{\text{CB}}_{\mathit{ai}}+{\text{OC}}_{\mathit{ai}}}$$ (5)

where SE_ba is the student enrollment for the course a with blended instruction modality, S_ai is the state subsidy for the course a at the university i, CB_ai is the cost of instructor compensation per student in the blended modality for the course a at the university i, and OC_ai is all other costs per student for the course a at the university i.

In online

$${\text{SE}}_{\mathrm{o}a}={\displaystyle {\sum }_{i=1}^n}\frac{S_{\mathit{ai}}}{{\text{CO}}_{\mathit{ai}}+{\text{OC}}_{\mathit{ai}}}$$ (6)

where SE_oa is the student enrollment for the course a with online instruction modality, S_ai is the state subsidy for the course a at the university i, CO_ai is the cost of instructor compensation per student in the online modality for the course a at the university i, and OC_ai is all other costs per student for the course a at the university i. Summary statistics and the results of cost savings analysis are shown in Table 4.

Table 4. Cost-savings summary statistics.

Note: SD in parentheses.

Course	Overall student enrollment, in-person per year	Student enrollment per year per institution	Average instructor compensation, per 1000 students (USD)		Cost of the online course per 1000 students (USD)*	Savings on instructor compensation (%)		Increase in student enrollment per year
			In-person	Blended		Blended/ in-person	Online/ in-person	Blended	Online
EM	29,992	233 (225)	23,670 (12,170)	19,130 (6810)	4520	19.2%	80.9%	1005	5457
CMT	72,516	562 (475)	19,270 (7170)	16,310 (5630)	4030	15.4%	79.1%	1825	10,865

*Cost of the online course includes production, delivery, and proctoring