Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2019 Nov 20;36(7):2113–2118. doi: 10.1093/bioinformatics/btz870

Protein docking model evaluation by 3D deep convolutional neural networks

Xiao Wang 1, Genki Terashi 2, Charles W Christoffer 1, Mengmeng Zhu 2, Daisuke Kihara 1,2,✉
Editor: Yann Ponty
PMCID: PMC7141855  PMID: 31746961

Abstract

Motivation

Many important cellular processes involve physical interactions of proteins. Therefore, determining protein quaternary structures provide critical insights for understanding molecular mechanisms of functions of the complexes. To complement experimental methods, many computational methods have been developed to predict structures of protein complexes. One of the challenges in computational protein complex structure prediction is to identify near-native models from a large pool of generated models.

Results

We developed a convolutional deep neural network-based approach named DOcking decoy selection with Voxel-based deep neural nEtwork (DOVE) for evaluating protein docking models. To evaluate a protein docking model, DOVE scans the protein–protein interface of the model with a 3D voxel and considers atomic interaction types and their energetic contributions as input features applied to the neural network. The deep learning models were trained and validated on docking models available in the ZDock and DockGround databases. Among the different combinations of features tested, almost all outperformed existing scoring functions.

Availability and implementation

Codes available at http://github.com/kiharalab/DOVE, http://kiharalab.org/dove/.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The three-dimensional (3D) structure of a protein complex provides fundamental information about the physicochemical nature of the protein complex, which facilitates a better understanding of the molecular mechanisms of its biological function in a biological pathway. Although the experimental structural biology community, now with increasingly powerful techniques in cryo-electron microscopy (cryo-EM), has determined protein complex structures at a steady pace, the structures of many important protein interactions have not yet been determined. To aid the experimental efforts, computational modeling approaches for protein complex structures, often called protein docking methods, have been actively developed over the past two decades.

Protein docking methods are roughly classified into two categories, template-based modeling methods, which use known global (Anishchenko et al., 2015) or local (Tuncbag et al., 2011) complex structures, and ab initio methods, which assemble two individual protein structures without referring to known complex structures. Many ab initio methods exist, the details of which vary greatly: Protein structure representations used include molecular surface-based (Venkatraman et al., 2009) and voxel-based (Pierce et al., 2011). For docking pose search, Fast Fourier Transform (Katchalski-Katzir et al., 1992; Padhorny et al., 2016) is a popular choice; other methods, e.g. geometric hashing (Fischer et al., 1995; Venkatraman et al., 2009) and particle swarm optimization (Moal and Bates, 2010) have also been successful. To take protein flexibility into account, normal mode analysis (Oliwa and Shen, 2015) and protein dynamics simulation (Gray et al., 2003) have been applied. Methods have also been developed that extend conventional pairwise docking, such as multiple-chain docking (Esquivel-Rodriguez et al., 2012; Ritchie and Grudinin, 2016; Schneidman-Duhovny et al., 2005), peptide-protein docking (Alam et al., 2017; Kurcinski et al., 2015), docking with disordered proteins (Peterson et al., 2017), docking order prediction (Peterson et al., 2018a, b) and docking modeling for cryo-EM maps (Esquivel-Rodriguez and Kihara, 2012; van Zundert et al., 2015).

Although substantial improvements have been achieved in ab initio protein docking, there are still unsolved shortcomings in existing methods. One of the foremost shortcomings is the scoring of docking models (decoys) (Moal et al., 2013). Since a typical ab initio method produces a large decoy set that only includes a small number of near-native models (hits), an accurate scoring function for selecting hits critically influences the performance of docking. Recognizing the importance of the scoring, the Critical Assessment of Prediction of Interactions (CAPRI), the community-wide docking prediction experiment (Lensink et al., 2018), has a specific category for evaluating scoring methods, where participants are asked to select 10 plausible decoys from over thousands of decoys provided by the organizers.

Approaches that have been applied for scoring decoys include physics-based potentials (Gray et al., 2003; Kingsley et al., 2016), interface shape-based scores (Venkatraman et al., 2009), knowledge-based statistical potentials (Huang and Zou, 2008; Lu et al., 2003) and machine learning methods (Fink et al., 2011) and evolutionary profiles of interface residues (Nadaradjane et al., 2018).

In this work, we applied a 3D convolutional neural network (CNN) to the problem of distinguishing near-native decoys from incorrect decoys. CNNs have been very successful in 2D (Krizhevsky et al., 2012) and 3D (Maturana and Scherer, 2015; Subramaniya et al., 2019) image recognition tasks (LeCun et al., 2015), which motivated us to apply it to docking decoy hit recognition. In the bioinformatics field, 3D CNNs have been applied to drug-protein interaction scoring (Ragoza et al., 2017), protein functional site analysis (Torng and Altman, 2017), quality assessment of single protein structure models (Derevyanko et al., 2018; Pages et al., 2019) and secondary structure detection in cryo-EM maps (Subramaniya et al., 2019). To the best of our knowledge, this is the first work to apply CNNs to the protein docking problem. Our method, DOcking decoy selection with Voxel-based deep neural nEtwork (DOVE), takes a docking decoy structure as input, maps the structure into a 3D grid, scans the protein–protein interface with a 3D cube, examines inter-atom interaction patterns and their energetic contributions, and judges if the decoy is close to the native structure or not. Compared to popular scoring functions used for selecting docking decoys, DOVE showed substantially better performance.

2 Materials and methods

We first explain the datasets used for training and testing DOVE, as well as the statistical potentials used as input features of DOVE. Subsequently, we describe the network architecture and the training process of DOVE.

2.1 Datasets

The primary dataset used was based on the ZDOCK benchmark dataset ver. 4.0 (Hwang et al., 2010). For each of the 178 protein complexes in the dataset, there are on average 53 999 decoys (minimum: 53 962; maximum: 54 000). For each decoy, we computed the root-mean square deviation (RMSD) of the interface residues (iRMSD, interface residues are defined as those within 10.0 Å of any residue of the other protein), ligand RMSD (lRMSD, RMSD of ligands when receptors are superimposed) and the fraction of the native contacting residue pairs (fnat; residue pairs with any heavy atom within 5.0 Å) to the native structure as well as two statistical potential values, GOAP (Zhou and Skolnick, 2011) and ITScore (Huang and Zou, 2008), both of which were used as features to characterize decoys. A protein complex and all its decoys were discarded if computing GOAP or ITScore failed or iRMSD, lRMSD or fnat could not be computed due to inconsistency of the sequence in the structures provided in the ZDOCK dataset from the native complex structure in PDB (Berman et al., 2000), or if. After the removal of complexes, 120 complexes remained.

For each protein complex in ZDOCK benchmark, the numbers of correct decoys, defined as decoys of acceptable quality or better as defined by the CAPRI criteria using iRMSD, fnat and lRMSD of decoys (Lensink et al., 2018) and incorrect decoys are highly imbalanced, which makes training the network model difficult. Thus, we augmented the number of correct decoys by placing each of them in 24 orientations on a grid with 90 degree rotations around the Z-axis of the original coordinates in the PDB file (thus 4 orientations) and with each of the 6 faces that was put upwards. With this augmentation, each of 120 complexes has now on average 8909.4 correct decoys with the minimum 264 and the maximum 60 192. Then, we sampled an equal number of incorrect models to the correct models for each complex. This augmented decoy set was only used in the training. For testing, we report the accuracy using the original number of correct models with the same number of incorrect models as used in the training. In total, the training dataset of the 120 complexes include 1 069 128 correct and incorrect decoys, respectively. For testing, the number of correct decoys was 44 547.

To remove redundancy, we grouped the 120 complexes using TM-Score (Zhang and Skolnick, 2004). Two complexes were put in the same group if at least 1 pair of proteins from the 2 complexes had a TM-score of over 0.5 and sequence identity of 30% or higher. This resulted in 63 groups (Supplementary Table S1). These groups were split into four subgroups to perform 4-fold cross validation (Supplementary Table S2). Three subsets were used for training while remaining one subset was used for testing. Thus, for each feature combination, we have four different models. Of the training set, 80% of the decoys were used for training parameters under a given hyper-parameter setting and the remaining 20% were used as the validation set, which was used to determine the best hyper-parameter set for the training set.

In addition to the ZDOCK dataset, we also used the DockGround benchmark dataset (Liu et al., 2008) for testing. Since we found decoys in the dataset often have residue pairs that are too close, we relaxed all the structures by Rosetta (Conway et al., 2014). DockGround includes 58 target complexes each with on average 9.83 correct and 98.5 incorrect decoys.

2.2 Knowledge-based statistical contact potentials

We used two distance-dependent contact potentials, GOAP and ITScore, to characterize energetic contributions of atoms at the docking interfaces of decoys. Both potentials were derived from statistics of atom pairs in known protein structures but using different ideas. GOAP considers angles as well as the distances of side-chains of interacting residues while ITScore was numerically optimized to be able to distinguish native structures from incorrect decoys. We chose these two potentials because they perform well in selecting docking decoys (Peterson et al., 2018a, b).

We modified the original codes of GOAP and ITScore so that they output the binding energy of each atom, which is the sum of the interaction energy between the atom and all other atoms within 30 Å in the decoy. Using this modified output, we mapped the atom-wise interaction energy to each position of interface atoms of a decoy. Interface atoms are defined as those in residues which locate within 10 Å of any residues of the other protein in the complex.

2.3 Network architecture of DOVE

DOVE uses the CNNs to capture features of protein interactions in decoys. Figure 1 shows the architecture of the network.

Fig. 1.

Fig. 1.

Open in a new tab

The network architecture of DOVE. DOVE takes atom positions and potentials in a 20*20*20 input cube that is placed at the docking interface of a decoy and predicts if the decoy is in the CAPRI acceptable quality or not. The number of filters in each layer were 100, 200, 200, 400, 400; 20, 18, 16, 8, 6, 3 are the output cube size of each layer; 10 800, 1000, 100 denotes the number of neurons for FC layer. Block means 3D convolutional operation block that outputs data in 3D cube; Flat is to make a 1D vector from a 3D cube; Pool is a max-pooling operation and FC is fully-connected network. Dropout of 0.3 was applied to FC

DOVE takes a docking decoy as an input and judges if the decoy has an acceptable quality or not based on the CAPRI criteria (Lensink et al., 2018). The actual input data for a decoy is atom positions and atom-wise statistical potential values within a 203 Å3 or 403 Å3 size cube that is placed at the protein–protein docking interface. The cubes are centered on the interface, where the interface is defined as the set of heavy atoms that locate within 10.0 Å to any heavy atoms of the other protein in the complex. We considered positions of carbon, oxygen, nitrogen and other atoms at the interface separately in four different channels (the left part of the network in Fig. 1). For a channel of an atom type, the number of the atoms of the type is counted and stored in each voxel of a size of 13 Å3 within the cube of 203 Å3 or voxels of 23 Å3 within the cube of 403 Å3 (thus the input data size is always 203). The deep learning models that use the 203 Å3 or the 403 Å3 cube are referred as DOVE-Atom20 or -Atom40, respectively.

Furthermore, as described in the previous section, we used the contact potentials, GOAP and ITScore, as input features. Figure 2 illustrates how the GOAP potential mapped to atoms distribute on a protein surface. We visualized GOAP mapped on atoms in a ligand protein in the correct (the pose on the left in Fig. 2A and B) and in an incorrect pose (the pose on the right in Fig. 2A and C). As shown in the color scale, in the correct bound form binding energies of atoms at the interface become more favorable upon docking (blue), while interface atoms in the incorrect pose have more unfavorable energy.

Fig. 2.

Fig. 2.

Open in a new tab

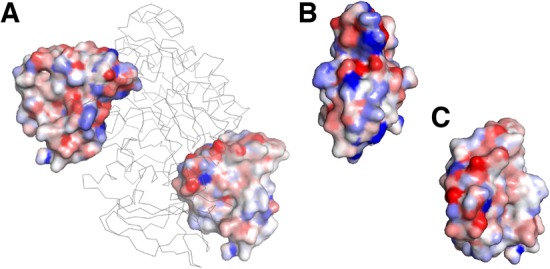
Example of atom-wise contact potential mapped on protein surface. GOAP was mapped to a ligand protein (ones with the surface representation) when it is in the isolated state and in a bound state, and the difference between the two states was visualized in a color scale. Blue shows the atoms have more preferable binding energy in the bound form relative to the isolated form while red shows the binding energy went worse in the bound form. The complex used is pancreatic a-amylase complexed with an inhibitor, tendamistat (PDB ID: 1bvn). (A) The receptor, a-amylase, is shown in the ribbon representation in gray. The inhibitor is shown in the surface representation in two poses: On the left, the inhibitor in the acceptable bound pose (iRMSD: 1.27 Å; fnat: 0.71); right, in an incorrect pose (iRMSD: 20.6 Å; fnat: 0.0). (B) The binding interface surface (facing toward us) of the inhibitor in the acceptable pose. (C) The interface in the incorrect pose

Similar to how the atom-based features were represented, the atom-wise energy of atoms within each voxel are summed and assigned as a feature value of the voxel in the cube. The deep learning models using GOAP and ITScore are referred to as DOVE-GOAP and DOVE-ITScore, respectively. For using the contact potentials, we used the cube of 403 Å3. We also tested models with two features, a combination of Atom40 and GOAP (DOVE-Atom40+GOAP), Atom40 and ITScore (DOVE-Atom40+ITScore) and GOAP and ITScore (DOVE-GOAP+ITScore). Finally, we also tested with all the features, DOVE-Atom40+GOAP+ITScore. Values of a feature (i.e. channel) are normalized so that the distribution is zero-centered by considering maximum and minimum values of the feature in the training dataset.

As shown in Figure 1, the input channels are connected to two convolutional layers with the output size of 183 and 163, respectively, each of which has 100 and 200 filters of the size of 3*3*3. The CNN layers were connected to a max pooling layer, followed by another set of convolutional layers followed by a max pooling layer. Then, the outputs from these layers are fed to fully connected (FC) layers followed by a sigmoid function, which finally outputs the probability that the input decoy has an acceptable model quality. The overall architecture is similar to the one used in an earlier work of local protein structure analysis by Torng and Altman (2017). DOVE was implemented using the Keras (Chollet, 2018) and Tensorflow (Abadi et al., 2016) packages.

2.4 Training the deep learning models

For training, we used cross entropy (Goodman, 2001) as the loss function. Nadam (Dozat, 2016) with an adaptive learning rate and the default decay rate of 0.004 was used for optimizing the weights. Weights were initialized using the glorot-uniform (Glorot and Bengio, 2010) to have a zero-centered distribution for each network layer. Bias was initialized to 0 for all layers (Glorot and Bengio, 2010). Dropout (Srivastava et al., 2014) of 0.3 and L2 regularization was used for the FC layers.

As described in the Section 2.1, we performed 4-fold cross validation. The resulting hyper-parameter combinations are provided in Supplementary Table S3. Since a decoy set of a protein complex contains many more incorrect models than acceptable models, we balanced the data of the two classes by choosing the same number of acceptable quality models as incorrect models in every batch for training. The batch size was set to 128. Usually the training converged in around 10 epochs.

3 Results

We tested DOVE first on the ZDOCK benchmark dataset with the 4-fold cross validation. Then, the trained model was further tested on the DockGround benchmark dataset.

3.1 Performance on the ZDOCK benchmark dataset

We compared the performance of DOVE with eight different feature combinations on the test set in comparison with five existing scoring functions, GOAP, ITScore, ZRANK (Pierce and Weng, 2007), ZRANK2 (Pierce and Weng, 2008) and IRAD (Vreven et al., 2011). During the cross-validation process, DOVE’ accuracies were consistent over the four training and validation subsets (Supplementary Fig. S1). The average SD of the accuracy of the four training sets and the validation sets were 0.0298 and 0.0300, respectively. Determined hyper-parameter values were also very consistent across the 4-fold validation (Supplementary Table S3). Thus, throughout the training process results of accuracy and identified parameters were very consistent and stable.

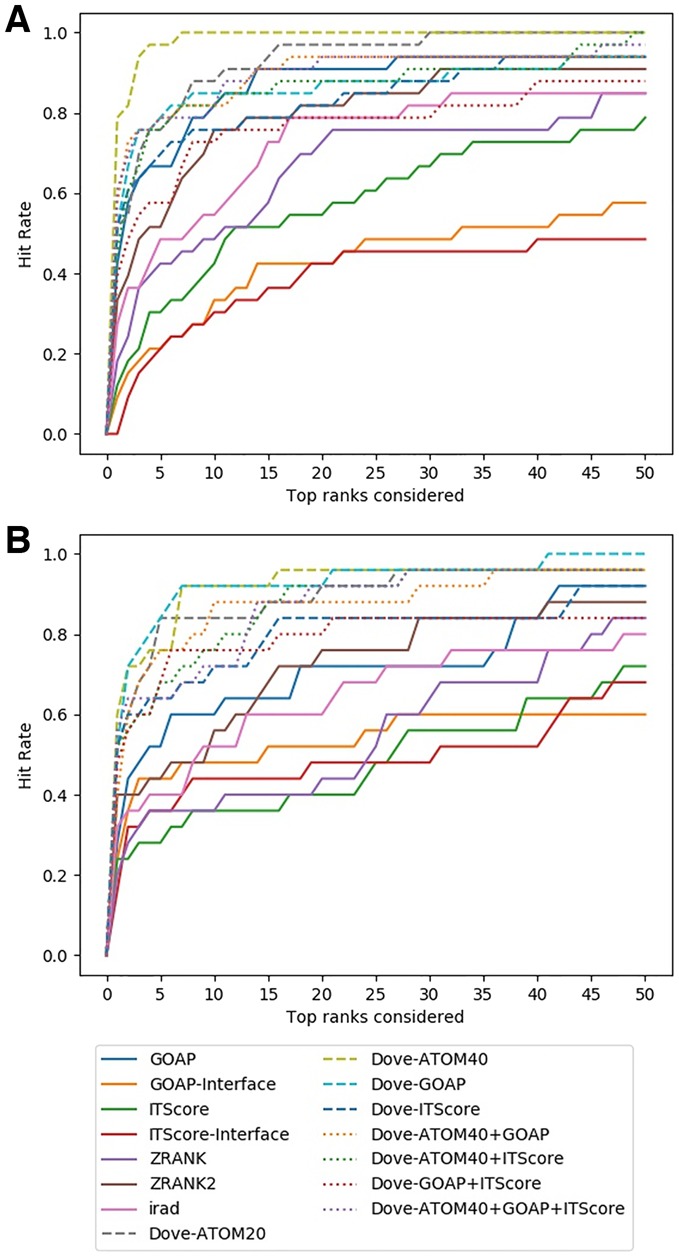
Figure 3 shows the fraction of target complexes in the ZDOCK dataset for which a method produced at least one correct (i.e. CAPRI acceptable) model within top k rank. GOAP and ITScore were run in two different ways; one as originally designed and the other by taking interaction scores only from interface regions that are within 10.0 Å of interacting protein (GOAP/ITScore-Interface). Thus, in total there were seven existing reference methods DOVE was compared against.

Fig. 3.

Fig. 3.

Open in a new tab

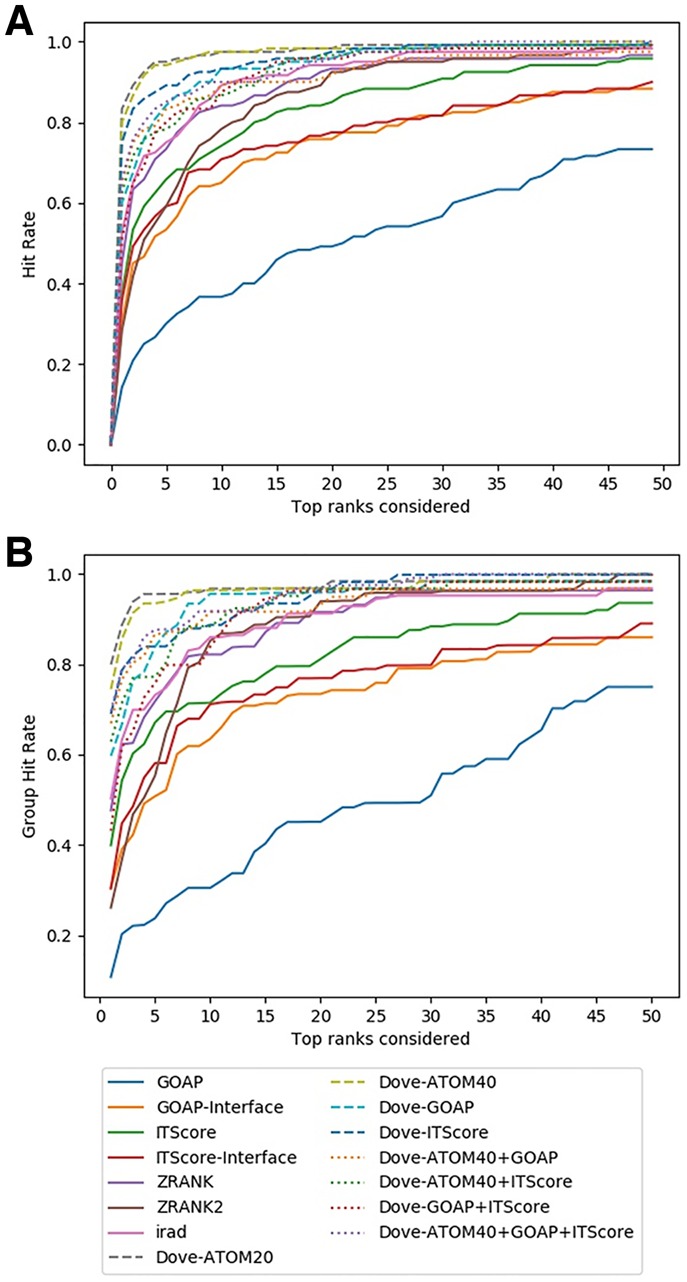
Comparison on the ZDOCK Benchmark dataset. (A) The fraction complexes among the 120 complexes in the benchmark set for which each method selected at least 1 acceptable model (within top x scored models) was shown. Results shown are from test sets. In addition to DOVE with eight different feature combinations, performance of GOAP, GOAP-Interface, ITScore, ITScore-Interface, ZRANK, ZRANK2 and IRAD are shown. (B) Considering the similar complexes that were grouped into 63 groups (Supplementary Table S1), the hit rates for complexes in each group were averaged and re-averaged over the 63 groups for each x

Overall, DOVE (dashed lines) was more successful than the existing methods in ranking correct models within earlier ranks in many target complexes. For example, at the top 10 (x = 10), 6 out of 8 feature combinations of DOVE had a higher hit rate than any of the existing scores (Fig. 3A). The remaining two combinations (DOVE-Atom40-ITScore and DOVE-GOAP-ITScore) were better than all the existing scores except IRAD. The results were almost the same when the 63 groups of target complexes rather than individual 120 complexes were considered to compute the hit rate (Fig. 3B). In general, the DOVE variations showed higher hit rate than existing scoring functions. DOVE-Atom20 and DOVE-Atom40 were consistently the two best scores in both Figure 3A and B. Among the existing scores, IRAD performed the best and GOAP showed the lowest accuracy.

We also examined the hit rates of models of medium quality, a better quality class than the acceptable quality in the CAPRI criteria (Supplementary Fig. S2). An issue when using medium quality models is that they constitute a small fraction, 11.3% (5046 out of 44 547), of acceptable quality models. Among the 120 complexes in the dataset, 21 of them had 0 medium quality models; these targets were excluded in the evaluation. Overall hit rate of medium models (Supplementary Fig. S2) was lower than the hit rate for acceptable models, which probably occurred due to the small number of medium quality models in decoy sets. Relative performance of the methods were similar with Figure 3 except that IRAD, ZRANK and ITScore came among top in performance. When top 10 models were considered, the highest hit rate was marked by DOVE-ITScore, followed by IRAD, DOVE-ATOM40, DOVE-ATOM20 and ZRANK in this order. Results for DOVE would improve if it is trained to distinguish medium quality models from incorrect models, but the current dataset includes a too small number of medium quality models for training.

We have also computed the enrichment factor (EF) as the evaluation measure of decoy selection (Fig. 4). The EF is defined as the fraction of correct hits within the models up to the score rank x that is currently considered relative to the total fraction of the correct models in the entire decoys of the target complex. Thus, the EF reduces the bias to the evaluation by using the hit rate (Fig. 3) that is caused by the difference of the number of correct decoys in the decoy set of each target. As shown by the plots (Figs 3 and 4), essentially the consistent results in the relative performance of the scoring functions was observed in terms of the EF. Quantitatively, the margin actually increased between the top feature combinations, DOVE-Atom40, DOVE-Atom20 and DOVE-ITScore and scores that follow them.

Fig. 4.

Fig. 4.

Open in a new tab

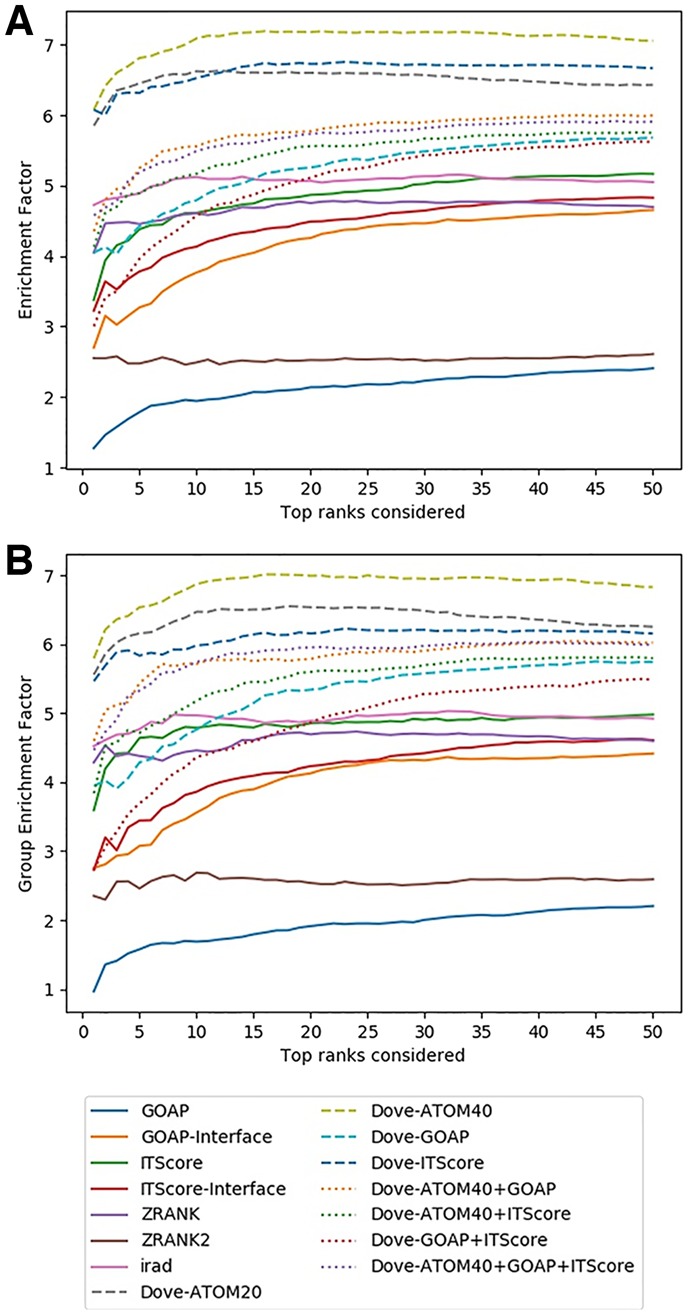
Comparison of the EF on the ZDOCK Benchmark dataset. (A) For each method, the average EF over the 120 complexes in the benchmark set were plotted considering the top x ranks. (B) The EFs of complexes in the same group was averaged, which was further averaged over the 63 groups

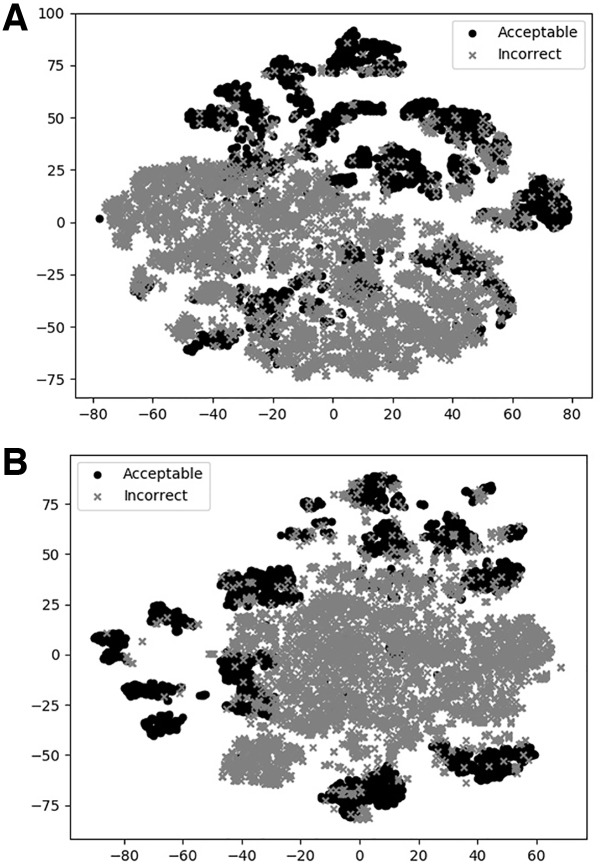
To illustrate how DOVE classifies decoys, we used t-SNE to visualize DOVE’s encoding of decoys (Fig. 5). Two features, DOVE-Atom40 and DOVE-GOAP, which performed relatively well among other feature sets (Figs 2 and 3) were used for this illustration. In both plots, most of the acceptable models (black circles) are clearly separated from a large cluster of incorrect models (crosses), indicating that the networks have successfully distinguished the two decoy groups.

Fig. 5.

Fig. 5.

Open in a new tab

t-SNE plots of decoy selection. Decoys from five target complexes, 1US7, 1BKD, 1HE1, 2OT3, 2CFH, which include 817 acceptable models (solid circles) and 1087 incorrect models (crosses) were used. Encoded features of the decoys taken from the output of the FC network (a vector of 100 elements) in Figure 1 were projected into a 2D space using t-SNE. (A) DOVE-Atom40 was used for the feature set. (B) DOVE-GOAP

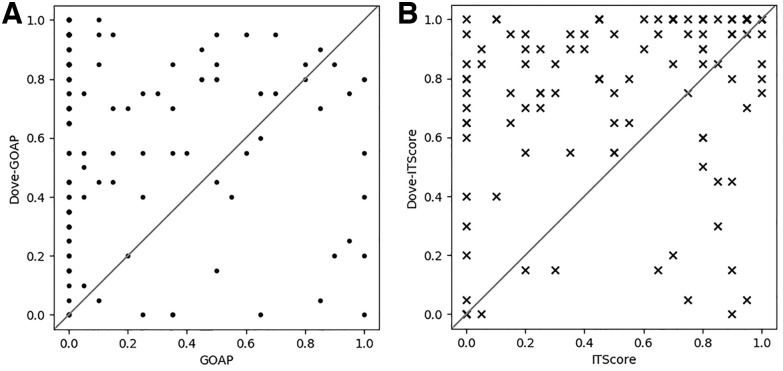
Since GOAP and ITScore were used as original independent scores and also as atom-based features of DOVE, we compared performance of these two schemes in Figure 6. For each target complex, the fraction of correct models within the top 20 models ranked by GOAP/ITscore and Dove-GOAP/DOVE-ITScore were plotted on the x- and y-axis, respectively. DOVE selected more correct models than GOAP and ITScore for 93 and 85 targets, respectively, out of 120 target complexes. Both GOAP and ITScore evaluate a structure model by the sum of pairwise interaction energies of atoms while DOVE convolves atom-wise energy mapped at the docking interface by CNNs. Therefore, the results imply that DOVE is capturing multi-body interaction energy patterns at the interfaces of correct and incorrect decoys.

Fig. 6.

Fig. 6.

Open in a new tab

Comparison of the fraction of correct models within top 20 ranked models by GOAP/ITScore and DOVE-GOAP/DOVE-ITScore. Each data point represents a target complex from the 120 complexes in the ZDOCK dataset. Since top 20 models were considered, the fractions of correct models have discrete values from 0 to 1.0 with 0.05 = 1/20 as a scale interval (A) Comparison between GOAP (x-axis) and DOVE-GOAP (y-axis). DOVE-GOAP was better than GOAP for 93 cases, tied for 5 cases and worse in 22 cases. (B) Comparison between ITScore (x-axis) and DOVE-ITScore (y-axis). DOVE-ITScore was better than ITScore for 85 cases, tied for 14 cases and worse for 21 cases. Comparison on top 10 and top 50 ranked decoys are shown in Supplementary Figure S3

On the other hand, there are cases where DOVE made results worse than GOAP and ITscore (data points at bottom right of Fig. 6A and B). Although it is not easy to understand why a deep learning method worked or did not work on particular input data, we observed that DOVE scores for the top 20 scoring decoys were higher and more consistent for cases that DOVE-GOAP/-ITscore showed better performance (i.e. top left in the plots) than cases where DOVE deteriorated (bottom right). The average and the SD of the top 20 scores by DOVE-GOAP/-ITscore when DOVE showed substantial improvement (x ≤ 0.3 and y ≥ 0.7) were avg: 0.78/0.79, std: 0.04/0.04 (Fig. 6A and B) whereas the values were avg: 0.72/0.69, std: 0.11/0.06 (Fig. 6A and B) when DOVE did not work (x ≥ 0.7 and y ≤ 0.3). Thus, DOVE was less confident (smaller average) and less consistent (larger SD) when it did not work well.

3.2 Testing on the DockGround benchmark dataset

We further tested DOVE on another dataset, DockGround (Liu et al., 2008). From the 4-fold cross validation on the ZDOCK dataset, we have four deep learning models for each feature combination. Thus, here, for evaluating a decoy we considered the average probability of the four models. The accuracies of the four models do not vary much as shown in Supplementary Figure S3. The average SD of the top 10 hit rates by the 8 feature combinations was 0.03.

In Figure 7, the hit rate results were shown in two panels, panel A reporting results for 33 target complexes which are independent from the ZDOCK set while panel B shows results on the remaining 25 targets that are grouped to at least 1 target in the ZDOCK set (i.e. at least 1 pair of proteins from the 2 complexes had a TM-score of over 0.5 and sequence identity of 30% or higher). In both panels, DOVE performed consistently better than the existing scores as we observed on the ZDOCK benchmark dataset. Particularly, consistent with the results on the ZDOCK dataset (Figs 2 and 3), DOVE with Atom40 showed the top performance on the independent dataset (Fig. 7A). On this dataset, DOVE-Atom40 showed an outstanding hit rate at early ranks relative to other scoring functions (Fig. 7A). At the rank 5, DOVE-Atom40 had a hit rate of 66.7%, and reached a 1.0 rate at the rank of 7. On the dataset of complexes that are similar to ZDOCK, Atom40 was among top performing feature combinations together with DOVE-GOAP and DOVE-Atom20.

Fig. 7.

Fig. 7.

Open in a new tab

Decoy selection performance on the DockGround dataset. (A) Thirty-three target complexes that are independent from the ZDOCK benchmark dataset. (B) Twenty-five targets that have structural similarity to any of the complexes in ZDOCK set

4 Discussion

In this work, we developed DOVE for docking decoy selection, which uses CNN to capture multi-body physical and energetic interactions patterns that are observed at protein docking interface. In protein structure prediction, the importance of considering multi-body (atom or residues) interactions has been long discussed and often actually shown to be effective in selecting native-like protein structure models (Gniewek et al., 2011; Kim and Kihara, 2014, 2016; Olechnovic and Venclovas, 2017). Each such method used an original idea to capture multiplicity of interactions. When it comes to capturing interaction multiplicity in molecular structures, 3D CNN is very natural and easy to use as we did in this work. Therefore, 3D CNN will continue to be actively applied to various tasks of protein structural bioinformatics for several more years. We have made the source code available on GitHub (https://github.com/kiharalab/DOVE), and a webserver of DOVE is available at http://kiharalab.org/dove/. Among the feature combinations we tested, we recommend users to use the top-performing features in Figures 3–5, which include DOVE-Atom20 and DOVE-Atom40. The source code also allows users to add new input features of decoys.

The current version of DOVE uses essentially two types of features, atom types and their locations and the atom-wise statistical potentials. It is expected that other structural features, such as sequence conservation and flexibility of atoms from molecular dynamics simulation etc. can further improve the performance. Also, a different network architecture, such as ResNet (He et al., 2016), may also contribute to exhibit a higher accuracy.

Funding

This work was partly supported by the National Institutes of Health (R01GM123055), the National Science Foundation (DMS1614777, CMMI1825941 and MCB1925643). C.C. is supported by predoctoral fellowship from the National Institutes of Health (T32GM132024).

Conflict of Interest: none declared.

Supplementary Material

btz870_Supplementary_Data
Click here for additional data file. (264.5KB, pdf)

References

  1. Abadi M. et al. (2016) Tensorflow: large-scale machine learning on heterogeneous distributed systems. arXiv Preprint arXiv: 1603.04467. [Google Scholar]
  2. Alam N. et al. (2017) High-resolution global peptide-protein docking using fragments-based PIPER-FlexPepDock. PLoS Comput. Biol., 13, e1005905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Anishchenko I. et al. (2015) Structural templates for comparative protein docking. Proteins, 83, 1563–1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Berman H.M. et al. (2000) The protein data bank. Nucleic Acids Res., 28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chollet F. (2018) Keras: The Python Deep Learning Library. Astrophysics Source Code Library.
  6. Conway P. et al. (2014) Relaxation of backbone bond geometry improves protein energy landscape modeling. Protein Sci., 23, 47–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Derevyanko G. et al. (2018) Deep convolutional networks for quality assessment of protein folds. Bioinformatics, 34, 4046–4053. [DOI] [PubMed] [Google Scholar]
  8. Dozat T. (2016) Incorporating nesterov momentum into adam. In: International Conference on Learning Representations (ICLR) 2016 Workshop, San Juan, Puerto Rico.
  9. Esquivel-Rodriguez J., Kihara D. (2012) Fitting multimeric protein complexes into electron microscopy maps using 3D Zernike descriptors. J. Phys. Chem. B, 116, 6854–6861. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Esquivel-Rodriguez J. et al. (2012) Multi-LZerD: multiple protein docking for asymmetric complexes. Proteins, 80, 1818–1833. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fink F. et al. (2011) PROCOS: computational analysis of protein-protein complexes. J. Comput. Chem., 32, 2575–2586. [DOI] [PubMed] [Google Scholar]
  12. Fischer D. et al. (1995) A geometry-based suite of molecular docking processes. J. Mol. Biol., 248, 459–477. [DOI] [PubMed] [Google Scholar]
  13. Glorot X., Bengio Y. (2010) Understanding the difficulty of training deep feedforward neural networks. In: Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Proceedings of Machine Learning Research, 9: 249–256.
  14. Gniewek P. et al. (2011) Multibody coarse-grained potentials for native structure recognition and quality assessment of protein models. Proteins, 79, 1923–1929. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Goodman J. (2001) Classes for fast maximum entropy training. In: 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP'01), 2001, Utah, pp. 561–564.
  16. Gray J.J. et al. (2003) Protein-protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J. Mol. Biol., 331, 281–299. [DOI] [PubMed] [Google Scholar]
  17. He K. et al. (2016) Deep residual learning for image recognition. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, pp. 770–778.
  18. Huang S.Y., Zou X. (2008) An iterative knowledge-based scoring function for protein-protein recognition. Proteins, 72, 557–579. [DOI] [PubMed] [Google Scholar]
  19. Hwang H. et al. (2010) Protein-protein docking benchmark version 4.0. Proteins, 78, 3111–3114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Katchalski-Katzir E. et al. (1992) Molecular surface recognition: determination of geometric fit between proteins and their ligands by correlation techniques. Proc. Natl. Acad. Sci. USA, 89, 2195–2199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kim H., Kihara D. (2014) Detecting local residue environment similarity for recognizing near-native structure models. Proteins, 82, 3255–3272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kim H., Kihara D. (2016) Protein structure prediction using residue- and fragment-environment potentials in CASP11. Proteins, 84(Suppl. 1), 105–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kingsley L.J. et al. (2016) Ranking protein-protein docking results using steered molecular dynamics and potential of mean force calculations. J. Comput. Chem., 37, 1861–1865. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Krizhevsky A. et al. (2012) Imagenet classification with deep convolutional neural networks. Adv. Neural Inform. Process. Syst., 1, 1097–1105. [Google Scholar]
  25. Kurcinski M. et al. (2015) CABS-dock web server for the flexible docking of peptides to proteins without prior knowledge of the binding site. Nucleic Acids Res., 43, W419–W424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. LeCun Y. et al. (2015) Deep learning. Nature, 521, 436–444. [DOI] [PubMed] [Google Scholar]
  27. Lensink M.F. et al. (2018) The challenge of modeling protein assemblies: the CASP12-CAPRI experiment. Proteins, 86(Suppl. 1), 257–273. [DOI] [PubMed] [Google Scholar]
  28. Liu S. et al. (2008) Dockground protein–protein docking decoy set. Bioinformatics, 24, 2634–2635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lu H. et al. (2003) Development of unified statistical potentials describing protein-protein interactions. Biophys. J., 84, 1895–1901. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Maturana D., Scherer S. (2015) VoxNet: a 3D convolutional neural network for real-time object recognition. In: IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, pp. 922–928.
  31. Moal I.H., Bates P.A. (2010) SwarmDock and the use of normal modes in protein-protein docking. Int. J. Mol. Sci., 11, 3623–3648. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Moal I.H. et al. (2013) The scoring of poses in protein-protein docking: current capabilities and future directions. BMC Bioinformatics, 14, 286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Nadaradjane A.A. et al. (2018) Protein-protein docking using evolutionary information. Methods Mol. Biol., 1764, 429–447. [DOI] [PubMed] [Google Scholar]
  34. Olechnovic K., Venclovas C. (2017) VoroMQA: assessment of protein structure quality using interatomic contact areas. Proteins, 85, 1131–1145. [DOI] [PubMed] [Google Scholar]
  35. Oliwa T., Shen Y. (2015) cNMA: a framework of encounter complex-based normal mode analysis to model conformational changes in protein interactions. Bioinformatics, 31, i151–i160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Padhorny D. et al. (2016) Protein-protein docking by fast generalized Fourier transforms on 5D rotational manifolds. Proc. Natl. Acad. Sci. USA, 113, E4286–E4293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Pages G. et al. (2019) Protein model quality assessment using 3D oriented convolutional neural networks. Bioinformatics, 35, 3313–3319. [DOI] [PubMed] [Google Scholar]
  38. Peterson L.X. et al. (2017) Modeling disordered protein interactions from biophysical principles. PLoS Comput. Biol., 13, e1005485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Peterson L.X. et al. (2018a) Improved performance in CAPRI round 37 using LZerD docking and template-based modeling with combined scoring functions. Proteins, 86(Suppl. 1), 311–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Peterson L.X. et al. (2018b) Modeling the assembly order of multimeric heteroprotein complexes. PLoS Comput. Biol., 14, e1005937. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Pierce B., Weng Z. (2007) ZRANK: reranking protein docking predictions with an optimized energy function. Proteins, 67, 1078. [DOI] [PubMed] [Google Scholar]
  42. Pierce B., Weng Z. (2008) A combination of rescoring and refinement significantly improves protein docking performance. Prot. Struct. Funct. Bioinform., 72, 270–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Pierce B.G. et al. (2011) Accelerating protein docking in ZDOCK using an advanced 3D convolution library. PLoS One, 6, e24657. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Ragoza M. et al. (2017) Protein-ligand scoring with convolutional neural networks. J. Chem. Inf. Model., 57, 942–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Ritchie D.W., Grudinin S. (2016) Spherical polar Fourier assembly of protein complexes with arbitrary point group symmetry. J. Appl. Crystallogr., 49, 158–167. [Google Scholar]
  46. Schneidman-Duhovny D. et al. (2005) Geometry-based flexible and symmetric protein docking. Proteins, 60, 224–231. [DOI] [PubMed] [Google Scholar]
  47. Srivastava N. et al. (2014) Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res., 15, 1929–1958. [Google Scholar]
  48. Subramaniya S.R.M.V. et al. (2019) Protein secondary structure detection in intermediate resolution cryo-EM maps using deep learning. Nat. Methods, 16, 911–917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Torng W., Altman R.B. (2017) 3D deep convolutional neural networks for amino acid environment similarity analysis. BMC Bioinformatics, 18, 302. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Tuncbag N. et al. (2011) Predicting protein-protein interactions on a proteome scale by matching evolutionary and structural similarities at interfaces using PRISM. Nat. Protoc., 6, 1341–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. van Zundert G.C.P. et al. (2015) Integrative modeling of biomolecular complexes: HADDOCKing with cryo-electron microscopy data. Structure, 23, 949–960. [DOI] [PubMed] [Google Scholar]
  52. Venkatraman V. et al. (2009) Protein-protein docking using region-based 3D Zernike descriptors. BMC Bioinformatics, 10, 407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Vreven T. et al. (2011) Integrating atom-based and residue-based scoring functions for protein-protein docking. Protein Sci., 20, 1576–1586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Zhang Y., Skolnick J. (2004) Scoring function for automated assessment of protein structure template quality. Prot. Struct. Funct. Bioinform., 57, 702. [DOI] [PubMed] [Google Scholar]
  55. Zhou H., Skolnick J. (2011) GOAP: a generalized orientation-dependent, all-atom statistical potential for protein structure prediction. Biophys. J., 101, 2043–2052. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

btz870_Supplementary_Data
Click here for additional data file. (264.5KB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES