Ultra-high-resolution fMRI of Human Ventral Temporal Cortex Reveals Differential Representation of Categories and Domains

Human ventral temporal cortex (VTC) is critical for visual recognition. It is thought that this ability is supported by large-scale patterns of activity across VTC that contain information about visual categories. However, it is unknown how category representations in VTC are organized at the submillimeter scale and across cortical depths.

Abstract

Human ventral temporal cortex (VTC) is critical for visual recognition. It is thought that this ability is supported by large-scale patterns of activity across VTC that contain information about visual categories. However, it is unknown how category representations in VTC are organized at the submillimeter scale and across cortical depths. To fill this gap in knowledge, we measured BOLD responses in medial and lateral VTC to images spanning 10 categories from five domains (written characters, bodies, faces, places, and objects) at an ultra-high spatial resolution of 0.8 mm using 7 Tesla fMRI in both male and female participants. Representations in lateral VTC were organized most strongly at the general level of domains (e.g., places), whereas medial VTC was also organized at the level of specific categories (e.g., corridors and houses within the domain of places). In both lateral and medial VTC, domain-level and category-level structure decreased with cortical depth, and downsampling our data to standard resolution (2.4 mm) did not reverse differences in representations between lateral and medial VTC. The functional diversity of representations across VTC partitions may allow downstream regions to read out information in a flexible manner according to task demands. These results bridge an important gap between electrophysiological recordings in single neurons at the micron scale in nonhuman primates and standard-resolution fMRI in humans by elucidating distributed responses at the submillimeter scale with ultra-high-resolution fMRI in humans.

SIGNIFICANCE STATEMENT Visual recognition is a fundamental ability supported by human ventral temporal cortex (VTC). However, the nature of fine-scale, submillimeter distributed representations in VTC is unknown. Using ultra-high-resolution fMRI of human VTC, we found differential distributed visual representations across lateral and medial VTC. Domain representations (e.g., faces, bodies, places, characters) were most salient in lateral VTC, whereas category representations (e.g., corridors/houses within the domain of places) were equally salient in medial VTC. These results bridge an important gap between electrophysiological recordings in single neurons at a micron scale and fMRI measurements at a millimeter scale.

Introduction

Human ventral temporal cortex (VTC) plays a central role in visual recognition (Tong et al., 1998; Grill-Spector et al., 2000, 2004; Moutoussis and Zeki, 2002; Gaillard et al., 2006; Parvizi et al., 2012; Rangarajan et al., 2014). Studies of VTC have shown that ecological domains of objects, faces, body parts, characters, and places elicit clustered responses in predictable anatomical locations within VTC (Malach et al., 1995; Kanwisher et al., 1997; Aguirre et al., 1998; Epstein and Kanwisher, 1998; Grill-Spector et al., 1999; Cohen et al., 2000; Peelen and Downing, 2005; Weiner et al., 2014). In parallel with the ecological domain framework, studies have demonstrated that different object categories elicit distinct and reliable patterns of activity across VTC (Haxby et al., 2001; Cox and Savoy, 2003; Kriegeskorte et al., 2008b; Huth et al., 2012). These distributed representations have a hierarchical organization whereby more abstract categorical distinctions are represented at a larger scale than more specific distinctions. For example, the representation of animate stimuli spans multiple centimeters across lateral VTC, and nested within it are clustered responses to faces and body parts (∼1 cm in scale). Similarly, the representation of inanimate stimuli spans medial VTC, and within it are clustered responses to places (Grill-Spector and Weiner, 2014).

Despite the evidence for both theoretical frameworks, the relationship between representations of categories and ecological domains in VTC remains elusive for several reasons. First, ecological domains differ in the variability of visual features of their exemplars; for example, faces are similar in their features and configurations, but body parts, such as limbs and torsos, are visually dissimilar. Second, domains vary with respect to their classically defined level of abstraction (superordinate, basic, and subordinate) (Rosch et al., 1976); for example, places are a superordinate category, but faces are a basic-level category. Third, it is unknown whether the proposed spatial hierarchy of representations extends from the level of domains to categories within a domain (e.g., limbs and headless bodies within the domain of body parts).

Prior studies have evaluated representations across voxels each spanning between 1 mm (McGugin et al., 2012, 2014) and several millimeters on a side, leaving unknown the nature of distributed representations in VTC when measured with submillimeter voxels. With higher spatial resolution, functionally heterogeneous neural populations that would be grouped within a standard fMRI voxel are divided into separate voxels, giving us an opportunity to assess more detailed representations. Recent advances in ultra-high-field (7T) fMRI have enabled such submillimeter measurements (Koopmans et al., 2010; De Martino et al., 2018; Dumoulin et al., 2018). 7T fMRI studies have generally focused on early visual cortex and have revealed fine-scale structure: ocular dominance (Cheng et al., 2001) and orientation columns in V1 (Yacoub et al., 2008), disparity- and color-selective stripes in V2 and V3 (Nasr et al., 2016), and motion-direction columns in hMT+ (Schneider et al., 2019). However, ultra-high-resolution investigations of object category representations in VTC have not been systematically conducted. Further, as VTC in adults is 1.5- to 3-mm-thick (Sowell et al., 2003; Natu et al., 2019), submillimeter fMRI offers the potential to investigate the variability of object representations across cortical depths (Fujita et al., 1992; Tanaka, 1996; Wang et al., 1996; Tsunoda et al., 2001; Maass et al., 2014).

To fill these gaps in knowledge, we conducted an ultra-high-resolution (0.8 mm) fMRI experiment at 7T in which 7 participants viewed images from five ecological domains with two visual categories per domain (Fig. 1A). Critically, we designed stimuli such that each visual category contained exemplars with similar parts and configuration (Grill-Spector et al., 2004; Grill-Spector and Kanwisher, 2005; Weiner and Grill-Spector, 2010; Stigliani et al., 2015). We measured distributed responses to domains and categories in each participant and tested how this information is represented in lateral and medial VTC as well as across cortical depths. Finally, we compared ultra-high-resolution data with simulated standard-resolution data to determine the necessity of ultra-high-resolution fMRI for revealing the nature of VTC representations.

Figure 1.

Experimental design. A, Stimuli. Images were drawn from five ecological domains: characters, body parts, faces, objects, and places (columns). Each domain contained two visual categories (rows). Exemplars of each category had the same parts and configurations (see sample stimuli). B, Experimental design schematic. Each 4 s trial consisted of 8 different images drawn from the same visual category, presented for 500 ms each. Images of phase-scrambled backgrounds with no foreground item (“oddball” images) could appear within a trial, as schematized with magenta boundaries. Color represents the image category (same as border of the sample stimuli in A).

Materials and Methods

Participants

Seven participants (3 males; a participant, S1, was an author [K.N.K.]) participated in this study. All participants had normal or corrected-to-normal visual acuity. The experimental protocol was approved by the University of Minnesota Institutional Review Board. Informed written consent was obtained from all participants.

Stimulus presentation

Stimuli were presented using a Cambridge Research Systems BOLDscreen 32 LCD monitor positioned at the head of the 7T scanner bed (resolution 1920 × 1080 at 120 Hz; viewing distance 189.5 cm). Participants viewed the monitor via a mirror mounted on the RF coil. A Mac Pro computer was used to control stimulus presentation using code based on Psychophysics Toolbox. Behavioral responses were recorded using a button box.

Experimental design and task

Participants viewed grayscale images drawn from five domains, with two visual categories per domain: characters (pseudowords and numbers), bodies (headless bodies and limbs), faces (adult and child), places (corridors and houses), and objects (cars and string instruments) (Fig. 1A). Following conventions established in prior work on visual representations in humans, we define a visual category as a set of exemplars sharing the same parts and configuration (Grill-Spector and Kanwisher, 2005; Weiner and Grill-Spector, 2010; Weiner et al., 2010; Stigliani et al., 2015). For example, limb exemplars all have five digits protruding from a cylindrical object. A domain is defined according to Kanwisher (2000, 2010) as a grouping of items from one or more categories by ecological validity (regardless of whether they share visual features), which are hypothesized to require specialized cortical processing (Kanwisher, 2000, 2010). For example, limbs and headless bodies are visually dissimilar categories within the domain of body parts. Each exemplar was presented on a phase-scrambled background, randomly generated from one of the images in the database. Items from each category were randomly jittered in their size, position, and orientation. Stimuli of each visual category were controlled for low-level features, including luminance, contrast, and pixelwise similarity as well as cognitive factors, such as familiarity (Stigliani et al., 2015; Nordt et al., 2019). We note that ecological domains differ in their visual variability; for example, images of children and adult faces from the face domain are visually more similar to each other than images of houses and corridors from the place domain.

Each run contained 48 randomly selected exemplars of a possible 144 unique exemplars from each of the 10 categories. The stimuli (with background) occupied a square region with dimensions 10° × 10°. In each run, stimuli from each visual category were presented in 4 s trials, each consisting of 8 images from a given category presented for 500 ms each (Fig. 1B). On a randomly selected one-third of trials, 1 of the 8 images consisted of a background phase-scrambled image with no foreground exemplar. Each run contained 6 trials of each category with different stimuli, as well as blank trials in which a gray screen was presented, for a total of 312 s per run. Images were not repeated within a run. Participants were instructed to fixate on a centrally presented red dot and to report via button press when a background phase-scrambled image (the “oddball”) appeared without a superimposed, intact exemplar. Each participant completed 12 runs in a single scanning session. We excluded one run for Participant S2 and two runs for Participant S6 due to poor visually evoked responses. The order of blocks was pseudorandomized for each run.

MRI data acquisition

Data acquisition procedures are identical to those described in a previous publication (Kay et al., 2019). A summary of these procedures is provided below, and we refer the reader to the previous publication for further details.

MRI data were collected at the Center for Magnetic Resonance Research at the University of Minnesota. Anatomical data were collected using a 3T Siemens scanner at 0.8 mm isotropic resolution. To ensure high signal-to-noise ratio (SNR), we acquired several repetitions of each type of anatomical volume. For each participant, we typically collected 8 scans of a whole-brain T1-weighted MPRAGE sequence (TR 2400 ms, TE 2.22 ms, TI 1000 ms, flip angle 8°) and 2 scans of a whole-brain T2-weighted SPACE sequence (TR 3200 ms, TE 563 ms). We used the prescan-normalized version of the T1 and T2 volumes, which corrects for receive-coil inhomogeneities. Functional data were collected at 7T using a Siemens Magnetom scanner and a custom 4-channel-transmit, 32-channel-receive RF head coil. We used gradient-echo EPI at 0.8 mm isotropic resolution with partial-brain coverage: 84 oblique slices covering occipitotemporal cortex, slice thickness: 0.8 mm, slice gap: 0 mm, FOV: 160 mm (FE) × 129.6 mm (PE), phase-encode direction: inferior-superior, matrix size: 200 × 162, TR: 2.2 s, TE: 22.4 ms, flip angle: 80°, partial Fourier: 6/8, in-plane acceleration factor: 3, and a slice acceleration factor: 2. Gradient-echo fieldmaps were also acquired for post hoc correction of EPI spatial distortion (same prescription as the EPI data, resolution: 2 mm × 2 mm × 2.4 mm, TE1 = 4.59 ms, TE2 = 5.61 ms). Fieldmaps were periodically acquired over the course of each scan session to track changes in the magnetic field (before and after the functional runs as well as approximately every 20 min interspersed between the runs).

Data analysis

Data analysis was performed using a combination of custom MATLAB, Python, and R code and includes tools from FreeSurfer, SPM, and FSL (specific instances are noted below). Routines developed for preprocessing and visualization of data are available online (http://github.com/kendrickkay/).

Anatomical preprocessing

Preparation of anatomical volumes.

T1- and T2-weighted anatomical volumes were corrected for gradient nonlinearities based on scanner calibration measurements. T1 volumes were coregistered (rigid-body transformation estimated using a 3D ellipse that focuses the cost metric on cortical voxels; cubic interpolation) and averaged to improve SNR, and the same was done to the T2 volumes. Each volume was inspected for image artifacts and rejected from the averaging procedure if deemed of poor quality. The FSL tool FLIRT was then used to coregister the averaged T2 volume to the averaged T1 volume (rigid-body transformation; sinc interpolation). We henceforth refer to the averaged and coregistered T1 and T2 volumes as simply the T1 and T2 volumes.

Generation of cortical surface representations.

The T1 volume (0.8 mm resolution) was processed using FreeSurfer version 6 beta (build-stamp 20161007) with the -hires option. Manual edits of tissue segmentation were performed to maximize accuracy of the resulting cortical surface representations. Several additional processing steps were performed. Using mris_expand, we generated cortical surfaces positioned at different depths of the gray matter. Specifically, we constructed six surfaces spaced equally between 10% and 90% of the distance between the pial surface and the boundary between gray and white matter. We also increased the density of surface vertices using mris_mesh_subdivide. This bisected each edge and resulted in a doubling of the number of vertices. For all analyses in this paper, we averaged GLM estimates between depths 1 and 2, 3, and 4, as well as 5 and 6 to effectively create three cortical surfaces: a superficial, middle, and deep surface. Finally, to reduce computational burden, we truncated the surfaces to include posterior portions of the occipital, temporal, and parietal lobes (since this is where functional measurements were made).

Functional preprocessing

Preparation of fieldmaps.

Fieldmaps acquired in each session were phase-unwrapped using the FSL utility prelude. We then regularized the fieldmaps by performing 3D local linear regression using an Epanechnikov kernel (Epanechnikov, 2005) with radius 5 mm; we used values in the magnitude component of the fieldmap as weights in the regression to improve robustness of the field estimates. This regularization procedure removes noise from the fieldmaps and induces some degree of spatial smoothness. Finally, we linearly interpolated the fieldmaps over time, producing an estimate of the field strength for each functional volume acquired.

Volume-based preprocessing.

We performed both temporal and spatial preprocessing of the fMRI data. First, cubic interpolation was performed on each voxel's time-series data to correct for differences in slice acquisition times and to obtain an integer sampling rate (2.0 s). This can be viewed as a temporal correction step. Next, the regularized time-interpolated fieldmap estimates were used to correct EPI spatial distortion (Jezzard and Balaban, 1995). Rigid-body motion parameters were then estimated from the undistorted EPI volumes using the SPM5 utility spm_realign. Finally, cubic interpolation was performed on each slice-time-corrected volume to compensate for the combined effects of EPI spatial distortion and motion. This can be viewed as a spatial correction step.

Coregistration to anatomy.

We coregistered the average of the preprocessed functional volumes obtained in a scan session to the T2 volume (affine transformation estimated using a 3D ellipsoid that focuses the cost metric on cortical ROIs). This resulted in a transformation that maps the EPI data to the participant-native brain anatomy volume.

Surface-based preprocessing.

With the anatomical coregistration complete, the functional data were reanalyzed using surface-based preprocessing. The exact same procedures associated with volume-based preprocessing were performed, except that the final spatial interpolation was performed at the locations of the vertices of the six depth-dependent surfaces. Thus, the only difference between volume- and surface-based preprocessing is that the data are prepared either on a regular 3D grid (volume) or an irregular manifold of densely spaced vertices (surface). The use of simple interpolation to map volumetric data onto surface representations helps maximize spatial resolution and avoids making strong assumptions about cortical topology.

Anatomical definition of VTC partitions and early visual cortex

In each participant's native anatomical space, we defined three nonoverlapping ROIs according to anatomical landmarks that have been used in prior work (Weiner and Grill-Spector, 2010; Weiner et al., 2010, 2014; Bugatus et al., 2017; Nordt et al., 2019) (Fig. 2B): lateral VTC, medial VTC, and human occipital cytoarchitectonic area 1 (hOc1), which closely matches functionally defined primary visual area V1 (Hinds et al., 2008; Rosenke et al., 2018). Lateral and medial VTC are separated by the mid-fusiform sulcus (MFS), which identifies transitions in both anatomical and functional properties (Grill-Spector and Weiner, 2014; Weiner et al., 2014; Weiner, 2019). The posterior end of both VTC ROIs was the posterior transverse collateral sulcus; the anterior end of these ROIs was the anterior tip of the MFS. The posterior transverse collateral sulcus is also the separating anatomical landmark between the occipital and temporal lobes, and additionally serves as a boundary marking the transition between hV4 and VO1 (Witthoft et al., 2014). The lateral VTC was laterally bounded by the occipitotemporal sulcus and medially by the MFS. Medial VTC was laterally bounded by the MFS and medially by the collateral sulcus. Whenever possible, the full extent of these bounding sulci was included; for example, the medial VTC includes all of the occipital portion of the collateral sulcus within the anterior and posterior bounds. The hOc1 ROI is defined on the FreeSurfer (https://surfer.nmr.mgh.harvard.edu) average surface (Dale et al., 1999; Fischl et al., 1999) and was projected onto each participant's cortical surface using cortex based alignment. All ROIs were defined bilaterally and data from both hemispheres were concatenated before analysis. In the remainder of the paper, we refer to the hOc1 ROI as “V1” for simplicity.

Figure 2.

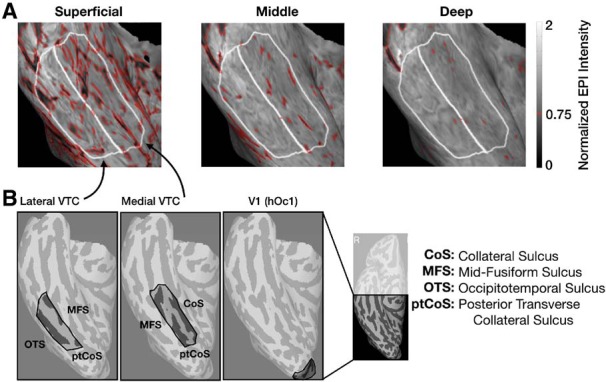
Visualization of likely veins and ROI definitions on the cortical surface of a representative participant's right-hemisphere VTC. A, Time-averaged normalized EPI intensities in a zoomed-in view of an example participants' right-hemisphere ventral temporal cortex (VTC) shown at each cortical depth. White lines indicate the boundaries of the lateral VTC and medial VTC ROIs for this participant. Red outlines indicate values < 0.75, designated as likely veins. The data at the corresponding surface locations were removed at all depths from subsequent analyses. B, Example ROI definitions in the right hemisphere of a representative participant for lateral VTC (left), medial VTC (middle), and V1 (right). Far right inset, The posterior region of the right hemisphere to which data acquisition was restricted.

Masking of potential venous artifacts

The effects of draining veins in superficial cortical layers colocalize with increased signal change, signal variability estimates, and t values (Vu and Gallant, 2015; Kay et al., 2019). While the influence of large veins on the measured BOLD response cannot be completely mitigated with presently available techniques, we implemented an approach to limit their contribution to the effects described here. One of the advantages of ultra-high-resolution fMRI is that it enables identifying likely veins by their low mean EPI intensity (Koopmans et al., 2010; Kay et al., 2019). While EPI intensities can be used as an anatomical marker of the location of venous effects, they are influenced by inhomogeneities in the transmit and receive profiles of the RF coil. To reduce these biases, we estimate the measurement bias map and then correct the measured raw values by the bias map. Bias correction of EPI intensities is used only to help identify venous effects; the additional analyses described below are performed on the preprocessed functional data without bias correction.

Vertices exhibiting low bias-corrected EPI intensity (<75% of the median EPI intensity) at any cortical depth were removed from all cortical depths at that surface location for further analyses (e.g., Fig. 2A, red outlines). This procedure led to the removal of 27 ± 1% of likely vein vertices across participants. To ensure that our results do not depend on this vein-removal procedure, all analyses were repeated without this preprocessing step.

Surface visualization.

To visualize surface-based data, we used a tool (cvnlookupimages: https://github.com/kendrickkay/cvncode) that orthographically projects the vertices of a surface onto the image plane and then uses nearest-neighbor interpolation to assign values from vertices to pixels. To summarize the various transformations from fMRI data to surface visualizations: (1) we acquire fMRI data with 0.8 mm voxels, (2) these voxels are resampled via cubic interpolation onto densely packed surface vertices with 0.4 mm resolution, and (3) these surface vertices are visualized using a nearest-neighbor mapping to image pixels. For the figures generated here, we restrict visualized vertices to those included in an anatomically defined VTC mask.

Computation of temporal SNR (tSNR)

Before GLM analysis of the functional data, tSNR was computed on the raw BOLD time-series for each vertex in each participant as the ratio of the time-series mean to its standard deviation (SD). We averaged over all vertices in a given partition and depth for each participant, yielding nine values per participant (3 depths × 3 ROIs) for comparison.

General Linear Model (GLM)

Preprocessed functional data were analyzed using GLMdenoise software (Kay et al., 2013). However, we chose to disable the denoising option to provide a closer comparison to conventional data analysis methods. Thus, the GLM consisted of experimental regressors (constructed by convolving the design matrix with a canonical hemodynamic response function) and polynomial regressors that characterize the baseline signal level in each run. GLMs were run separately for two splits of the data: odd runs and even runs. The standard error (SE) of the GLM β estimates was computed by bootstrapping 100 times over the runs present for the given data split. On each bootstrap iteration, N runs were sampled with replacement and the β estimate was computed for those runs, where N is the number of runs present for the data split.

The GLM was fit to the time-series data in each vertex of the six depth surfaces generated, then averaged across each pair of adjacent depths to form the three surfaces we analyzed (superficial, middle, and deep). While prior descriptions of these data describe all six surfaces (Kay et al., 2019), we chose to present data across three depths for two reasons. First, given a voxel size of 0.8 mm and an estimated cortical thickness ranging between 1.5 and 3 mm (Sowell et al., 2003; Natu et al., 2019), the functional data projected onto six equidistant surfaces would be similar between adjacent depths, whereas dividing cortex into three depths reduces (but does not necessarily eliminate) this dependence. Second, we found that describing differences between depths in terms of a superficial, middle, and deep depth lent itself to conceptually simpler interpretation. Beta weights from the GLM (reflecting BOLD response amplitudes to the experimental conditions) were converted from raw image units to units of percent BOLD signal change by dividing the signal in each vertex by its mean signal and multiplying by 100. We also computed the variance explained by the GLM (R²) for each vertex.

Metrics to evaluate distributed responses patterns.

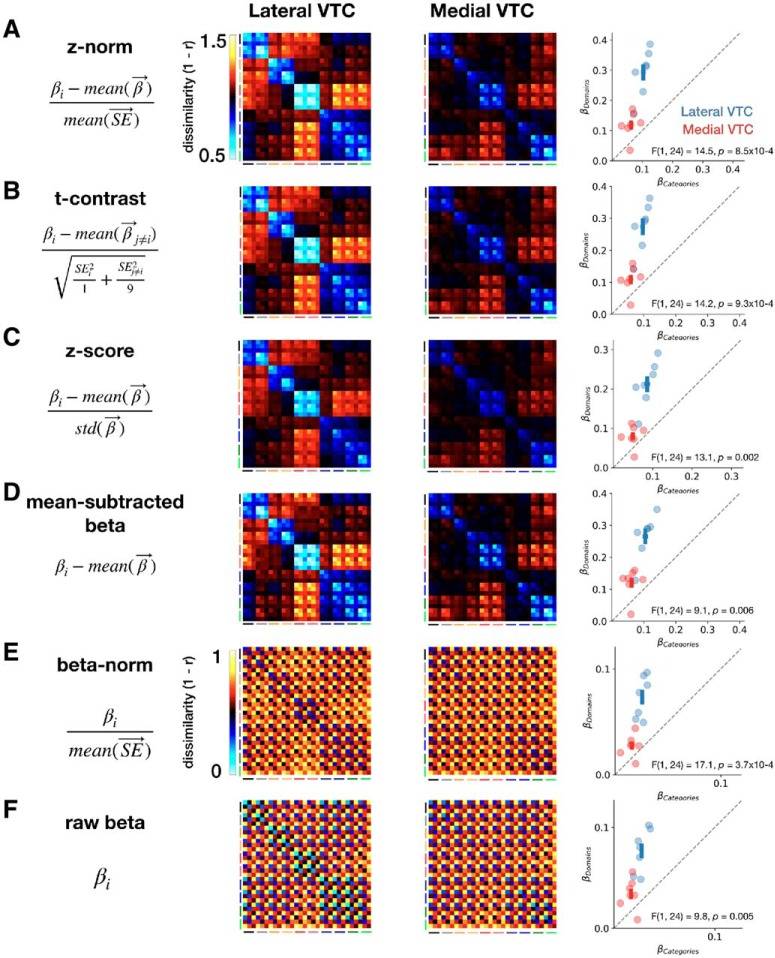
For each participant, we calculated six metrics of distributed responses for each split of the data (odd runs and even runs), described in detail in Table 1. Of these, the primary metric for which we report results is the z-norm metric. To remove the effects of mean signal differences between vertices due to incidental factors that are not of interest (e.g., proximity to a draining vein) and to down-weight vertices with poor GLM fits, we computed the z-norm metric of each vertex's responses to each of the 10 categories by (1) subtracting the mean response for that vertex and (2) dividing by the mean SE of β estimates across the 10 categories. For the MATLAB code provided in Table 1, we define the following commonly used variables, where i and j index groups of one or more categories: response_i: mean response to group i; response_j: mean response to group j; mean_across_conditions: mean response across all 10 categories; se_across_conditions: mean SE of response estimate across all 10 categories; std_across_conditions: SD of responses across all 10 categories; se_i: mean SE of response estimate for group i; se_j: mean SE of response estimate for group j; n_i: number of categories in group i; n_j: number of categories in group j.

Table 1.

Metric names and MATLAB code for each of the six metrics computed

Metric name	MATLAB code
z norm	(response_i - mean_across_conditions)./ se_across_conditions
t contrast	(response_i - response_j) ./ sqrt((se_i2 / n_i) + (se_j2 / n_j))
z score	(response_i - mean_across_conditions)./ std_across_conditions
Mean-subtracted β	response_i - mean_across_conditions
β norm	response_i ./ se_across_conditions
Raw β	response_i

Representational dissimilarity matrices (RDMs).

RDMs (Kriegeskorte et al., 2008a) were computed to illustrate the pairwise dissimilarity between distributed responses to different categories at different cortical depths across odd and even splits of the data. z-norm response maps from each combination of categories and cortical depths from one-half of the data were correlated with maps from each combination in the other half of the data (i.e., data from odd runs were compared with data from even runs). Each cell in the RDM reflects the dissimilarity (one minus correlation) between the distributed responses to pairs of categories, across odd and even splits of the data.

Given 10 stimulus types and three cortical depths, each RDM is a 30 × 30 matrix. RDMs were computed separately for each participant and each anatomical partition (lateral VTC, medial VTC, and V1). The RDM is arranged by stimulus type (domain, then category) and depth (superficial, then middle, then deep); thus, starting from the top left (see, e.g., Fig. 3), each 3 × 3 square indicates the dissimilarity between the same pairs of categories across the three depths, and each 6 × 6 square indicates the dissimilarities between the same pairs of domains across categories and depths. We also generated 10 × 10 RDMs for each cortical depth (superficial, middle, and deep; see Fig. 9) by selecting the corresponding cells from the full 30 × 30 RDM. These 10 × 10 RDMs contain the pairwise dissimilarities between distributed responses to different categories within a given cortical depth. To enable RDMs to be used as distance matrices for the construction of multidimensional scaling (MDS) embeddings, we symmetrized the matrices by averaging the upper and lower triangles and duplicating the result on either side of the diagonal, which remained unchanged. In the main analyses, RDMs are shown for data excluding likely veins (see Masking of potential venous artifacts). Control analyses include all vertices.

Figure 3.

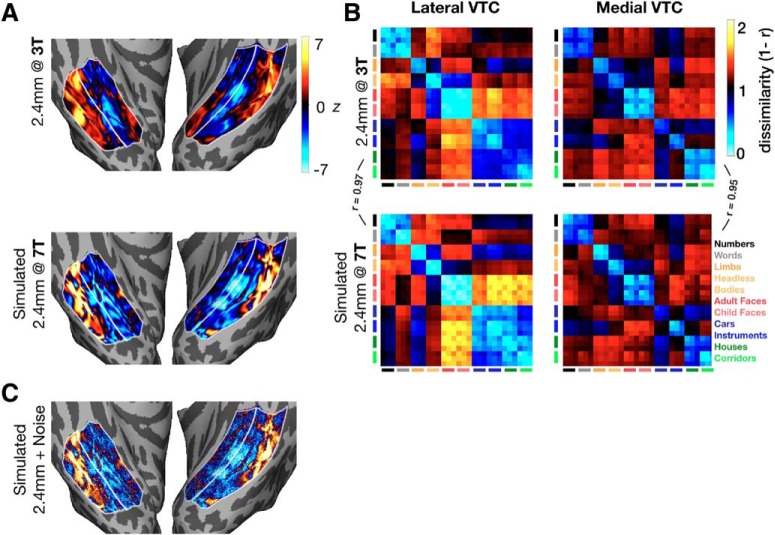
Validation of the Fourier-based smoothing method for simulating 2.4 mm acquisitions. A, z-normed response maps for an example category (child faces) are shown for Participant S1. The 2.4 mm data acquired at 3T (top) resemble the simulated 2.4 mm data acquired at 7T (bottom). B, RDMs in lateral VTC (left column) and medial VTC (right column) for the 2.4 mm (top) and the simulated 2.4 mm data (bottom). Bottom right, Legend indicates mapping between categories and the colors of the bars indexing rows and columns of RDMs. C, z-normed responses to child faces for simulated 2.4 mm data with Gaussian noise added.

Figure 9.

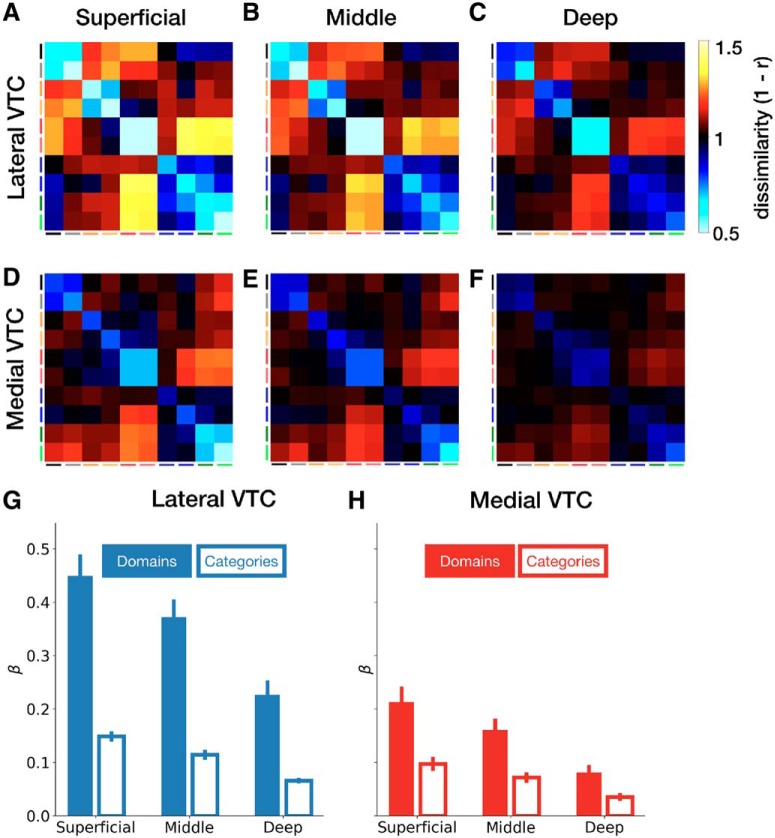
Representational structure in VTC partitions across cortical depths. Group-averaged RDM for lateral VTC (A–C) and medial VTC (D–F) at each cortical depth. Average domain and category weights for lateral VTC (G) and medial VTC (H) across depths. Error bars indicate SEM across participants. Category order matches Figure 6.

Modeling RDMs.

To evaluate the amount of domain-level, category-level, and depth-level structure in the measured RDMs for each partition and each participant, we fit each RDM as a weighted sum of idealized model RDMs (Khaligh-Razavi and Kriegeskorte, 2014) for the three levels of interest (domain, category, and depth) and an intercept term. Because the RDMs and regressors are symmetric, we simplified the model by retaining only the lower triangle (and diagonal) of each matrix used in the regression analysis. After vectorizing the target RDM and predictors, we used linear least squares regression to determine the contribution (β weights) of each regressor (derived from the 3 model RDMs) so that the total contribution minimized the sum squared differences between the measured and predicted RDMs. When modeling depth-specific RDMs, the same procedure was used but without depth as a regressor.

MDS.

To better visualize the representational structure from high-dimensional RDMs, we performed multidimensional scaling (MDS) (Kruskal, 1964) of the RDM. MDS embeds the representation of each combination of stimulus type and cortical depth into lower dimensional space (here, two dimensions). The 2D embeddings afford an intuitive understanding of the representational structure; for example, if the point representing cars at the superficial depth is close to the point representing cars at the middle depth, we can infer that the response maps for cars from these two depths are positively correlated. However, because information is necessarily lost in the dimensionality reduction, the MDS embeddings are used only for visualization and statistical tests are based on the full-dimensionality RDMs. Finally, to facilitate comparison of embeddings across partitions, participants, and depths, all embeddings were aligned via a Procrustes transformation (Gower, 1975) to a common space (the embedding from Participant S1's lateral VTC).

Controlling for anatomical differences in GLM variance explained.

To control for potential differences in the quality of the GLM fit between lateral and medial VTC partitions, we created a variant of the dataset in which groups of vertices that matched in number and mean variance explained (R²) were subsampled from the entire population of vertices in the anatomically defined VTC ROIs. We note that it is effectively impossible to select a subset of the data that is matched in R² across depths, given that superficial depths have higher BOLD signal magnitudes that translate to higher R² values (Kay et al., 2019). Thus, this control dataset is used strictly to evaluate the dependence of partition differences on R².

For the deepest cortical depth, we first sorted all vertices by their R² value, then identified the partition with the fewest total vertices, and selected the 70% of vertices from that partition with the highest R². From the larger partition, we again sorted vertices by their R² value, then computed all possible windows of sorted vertices containing the same number of vertices as selected from the smaller partition. The subset of vertices whose mean R² matched the target value from the smaller partition was used, such that we selected a group of vertices of exactly the same number and mean R² value in both partitions. These vertices, selected to match R² between lateral and medial VTC in the deepest depth, were then fixed to be in the same positions at the other two depths. This procedure was performed separately for each participant. Across participants, the mean difference in percentage of variance explained between lateral and medial VTC was <0.01% in the deepest depth and <0.5% in the middle (0.14 ± 0.08%) and superficial (0.29 ± 0.17%) depths. These differences were statistically indistinguishable from 0 for all depths (all t values < 1.8, all p values > 0.13), indicating that, separately at each depth, this procedure was successful in matching the variance explained between partitions.

Simulation of standard-resolution fMRI data.

One comparison of interest is between ultra-high-resolution (submillimeter) data and standard resolution (2.4 mm) data. This comparison was done by simulating the acquisition of standard-resolution data by spatially smoothing the preprocessed functional volumes using an ideal Fourier filter (10th-order low-pass Butterworth filter). Similar approaches have been implemented by other groups (Zaretskaya et al., 2018). In both the ultra-high-resolution and simulated standard-resolution cases, the data were subsequently analyzed using the same methods as the original ultra-high-resolution data (surface-based preprocessing, GLM analysis, etc.). Simulating the 2.4 mm data from the 0.8 mm data enabled us to control for factors that may change across sessions, including the scanner and coil, respiration, fatigue, attention, and performance. For consistency with other analyses, the same vertices designated as likely veins (and thus, removed from main analyses) were removed from both the ultra-high-resolution data and the simulated standard-resolution data.

To validate the simulated 2.4 mm data, we obtained functional data for Participant S1 at 2.4 mm in a separate scan session on a 3T scanner. We then compared the simulated standard-resolution data with the true standard-resolution data by computing RDMs as described above and computing the correlation coefficient between lower triangles of the RDMs. A sample category preference map (Fig. 3A) and RDMs (Fig. 3B) are shown for both the measured and simulated 2.4 mm data to demonstrate the similarity between simulated and actual 2.4 mm data. Due to higher SNR at lower resolution, RDM magnitudes (defined as the mean dissimilarity across all cells) were lower for the simulated 2.4 mm than 0.8 mm data. To control for this difference, we added noise to the simulated 2.4 mm data to make the RDM magnitudes more comparable with those in the 0.8 mm data. To generate this dataset, referred to as “simulated 2.4 mm + noise,” we added white Gaussian noise to the category preference maps. We used different magnitudes of noise and report results with noise normally distributed around 0 with a SD of 2.5. The SD of the Gaussian was selected such that the resultant data produced RDM magnitudes that were statistically indistinguishable from those in the original data.

Statistical analyses

When data from two conditions (e.g., lateral VTC vs medial VTC) were directly compared, we used paired t tests, in which each pair consists of the two values obtained for each participant. When data consisted of multiple factors, we used repeated-measures ANOVAs, with participant number as a random effect and other factors as fixed effects. Where cortical depth is included as an independent variable, it is coded as a continuous regressor, as opposed to a multilevel factor, thus making the analysis an ANCOVA. Effect sizes are reported as η², the proportion of variance in the dependent variable that is explained by the term or interaction of terms specified. Post hoc tests were done by computing Tukey's Honest Significant Difference where the familywise confidence level is set at 0.95. p values reported from these post hoc tests are thus corrected for multiple comparisons.

Statistics were computed using the scipy package for Python (https://www.scipy.org/) and the nlme and sjstats package for scripts in R (https://cran.r-project.org/web/packages/nlme/nlme.pdf; https://cran.r-project.org/web/packages/sjstats/index.html).

Results

During an ultra-high-resolution fMRI experiment, participants performed an oddball detection task while viewing images of exemplars from five domains (characters, bodies, faces, objects, and places). Each domain was composed of two categories, where exemplars of each category had similar parts and configuration (Fig. 1). We estimated the response magnitude to each category using a GLM (see Materials and Methods) at each vertex in lateral and medial VTC, the two anatomically defined partitions examined in this study. As VTC anatomy (Glasser and Van Essen, 2011; Saygin et al., 2011, 2016; Caspers et al., 2013; Weiner et al., 2014; Lorenz et al., 2017) and function (Martin et al., 1996; Levy et al., 2001; Hasson et al., 2002; Nasr et al., 2011; Connolly et al., 2012; Weiner et al., 2014) vary across a lateral-medial axis, we examined visual representations in these two partitions separately (see Materials and Methods). To examine distributed responses across each anatomical partition, we computed z-normed (see Materials and Methods) response maps within each partition and visualized the distributed responses to each category across VTC (Fig. 4).

Figure 4.

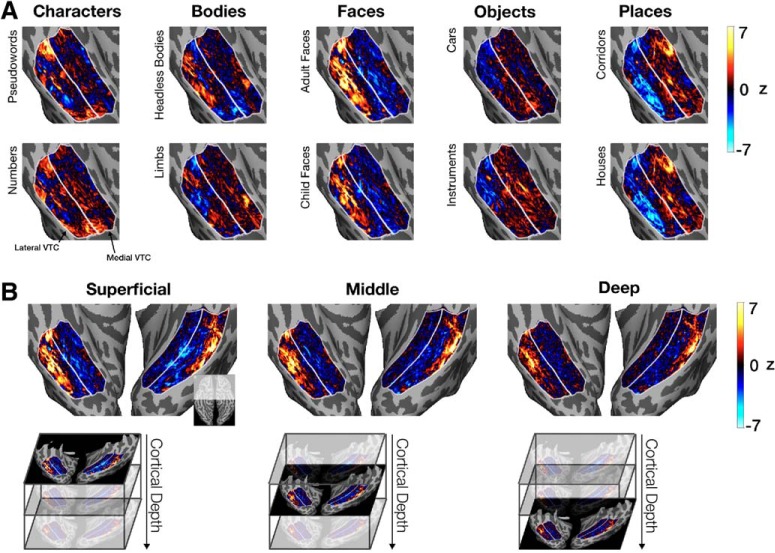
Response maps in VTC shown on the inflated cortical surface of Participant S1. A, The z-normed response map for each category is shown for the right hemisphere VTC of a representative participant (S1) at the superficial cortical depth. White lines indicate the lateral and medial VTC partitions. B, Maps of z-normed responses for adult faces in both hemispheres of Participant S1 shown across cortical depths: superficial, middle, and deep. Top left inset, The cortical region being visualized with respect to the entire ventral cortical surface.

Visualizations of response maps on the cortical surface show fine-scale structure in VTC that is largely consistent with prior characterizations of its functional architecture (Fig. 4A) (Haxby et al., 2001; Grill-Spector and Weiner, 2014). Ultra-high-resolution acquisition also allowed us to not only investigate differences in responses across lateral and medial VTC, but also across different cortical depths (Fig. 4B). Response maps to each of the categories from three cortical depths (superficial, middle, and deep) suggest both consistency between the spatial profile of category responses across cortical depth (e.g., face-responsive vertices are found in the lateral fusiform gyrus at all depths) as well as differences across depths (e.g., the number of face-responsive vertices decreases between the superficial and deep depths; Fig. 4B).

An advantage of ultra-high-resolution fMRI is that it allows identification of likely veins as vertices with low mean signal, which are more prevalent in superficial cortical depths (Fig. 2A). Thus, in subsequent analyses, we examined response maps, excluding vertices that were identified as likely veins (see Masking of potential venous artifacts).

How reliable are distributed responses measured at ultra-high-resolution?

Given the novelty of ultra-high-resolution measurements throughout human VTC, we sought to establish the split-half reliability of distributed response maps used in our analyses. Here, reliability refers to the correlation of distributed responses from independent halves of the data in which participants viewed randomly selected images from each category. Thus, this measure can be thought of as an estimate of the generalizability of distributed responses across different images from these categories. We computed reliability separately for each category at each depth and then averaged across categories and depths in each participant. The reliability of distributed responses is significantly >0 in both lateral VTC (r = 0.38 ± 0.04, mean ± SEM, across participants; t₍₆₎ = 11.4, p = 2.7 × 10⁻⁵) and medial VTC (r = 0.18 ± 0.02, t₍₆₎ = 9.2, p = 9.5 × 10⁻⁵), indicating that distributed responses in both partitions are reliable and generalize across exemplars of a category.

What is the nature of representations in lateral and medial VTC?

To examine distributed VTC representations across partitions and depths, we computed RDMs (Kriegeskorte et al., 2008a). RDMs quantify the dissimilarity between distributed response maps computed at different depths and to different stimuli. Each cell in the RDM indicates the dissimilarity (1 − correlation) between a given pair of response maps across independent halves of the data. Because 10 categories and three depths are compared from each half of the data, each RDM consists of 900 cells.

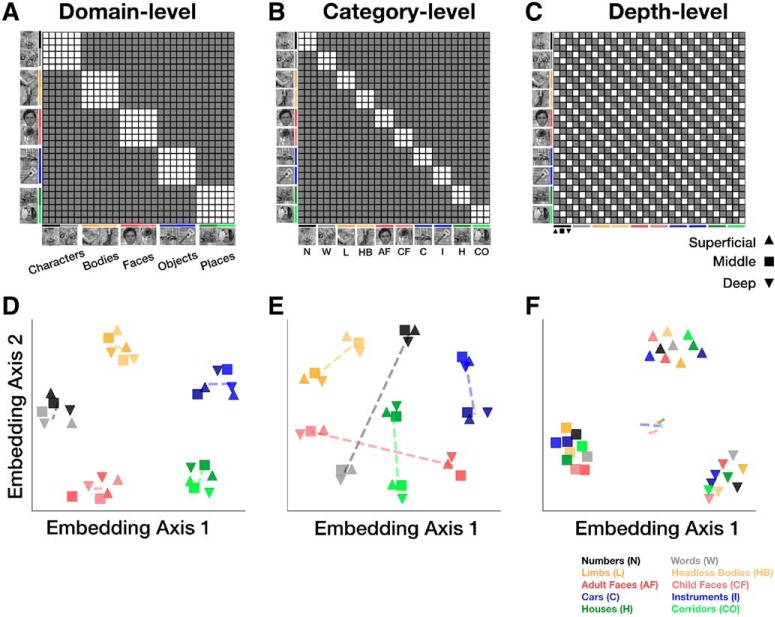
We considered several possible representational structures in VTC. Schematized RDMs reflecting hypotheses consistent with domain-level, category-level, or depth-level similarity are illustrated in Figure 5A,B, and C, respectively. Other possible representational structures can be described by a combination of these hypothetical RDMs. We tested which of these hypothesized representational structures (Fig. 5) might be consistent with the measured ultra-high-resolution fMRI data. To more intuitively visualize these 900-cell RDMs, we also computed 2D embeddings of the same hypothetical representational structures using MDS (Fig. 5D–F; see Materials and Methods).

Figure 5.

Hypothetical representational structures. Expected representational dissimilarity matrix (RDM) structure for (A) domain-level, (B) category-level, and (C) depth-level distributed representations. Filled (gray) cells represent higher dissimilarities than empty (white) cells. Each RDM is arranged by stimulus type (domain, then category) and depth (from superficial to deep). Thus, starting from the top left, each 3 × 3 square represents the similarity among items from the same category across the 3 depths, and each 6 × 6 square represents the similarity among items from the same domain across categories and depths. D–F, 2D MDS embeddings of the RDMs (in A–C) after adding white noise to the RDMs to prevent points from being perfectly overlapping. Colors represent the categories (same as in A–C). Shapes represent depths as follows: upward triangle represents superficial; square represents middle; downward triangle represents deep. Dashed lines connect the centroids of each pair of categories from a domain.

We found that RDMs are strikingly similar across participants: the mean correlation between the lower triangle of RDMs (excluding the diagonal) from different participants is 0.88 ± 0.01 in lateral VTC and 0.78 ± 0.02 in medial VTC (mean ± SEM). By removing the diagonal, the common difference between low on-diagonal and high off-diagonal dissimilarities no longer dominates the correlation coefficient; rather, it is the similarity among pairs of patterns across participants that is being compared (Ritchie et al., 2017). Given the similarity of RDMs from different participants, data in subsequent Figures 6 and 9 show group-averaged RDMs. The group-averaged RDMs are only used for visualization, and all statistical analyses are based on individual participant data.

Figure 6.

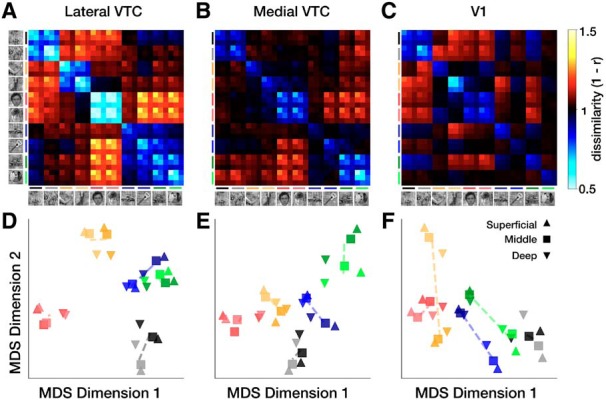
Representational structure in lateral and medial VTC. Group-averaged RDMs in (A) lateral VTC, (B) medial VTC, and (C) V1. Color of each cell represents pairwise dissimilarity between distributed representations across independent halves of the data. D, 2D MDS embeddings of the RDMs for lateral VTC, (E) medial VTC, and (F) V1. Colors represent categories as follows: black represents numbers; gray represents words; dark yellow represents limbs; yellow represents bodies; dark red represents adult faces; red represents child faces; dark blue represents cars; blue represents string instruments; dark green represents houses; green represents corridors. Shapes represent depths as follows: upward triangle represents superficial; square represents middle; downward triangle represents deep. Dashed lines connect the centroids of each pair of categories from a domain.

The group-averaged RDM from lateral VTC shown in Figure 6A appears largely consistent with the domain-level representation illustrated in Figure 5A. This is particularly evident for faces, bodies, characters, and places, but less so for objects, which also have low representational dissimilarity to places. In contrast, category-level representations appear stronger in medial VTC as shown in Figure 6B, which is more consistent with the predictions illustrated in Figure 5B. Neither VTC partition demonstrates representations that are modulated only by depth, as schematized in Figure 5C. Instead, we observe similarity among distributed representations for items of the same category and the same domain (especially in lateral VTC) across cortical depths.

Two-dimensional MDS embeddings of the group-averaged RDMs clarify the mixture of domain-level and category-level representations in each VTC partition. In lateral VTC, we observe a hierarchical structure to the embedding: with the exception of objects (cars and instruments), stimuli from a common domain are clustered, with some additional separation of categories within the domain and across depths (Fig. 6D–F). For example, the domain of characters forms a cluster; and its two constituent categories, pseudowords (black) and numbers (gray), are additionally separable within the cluster. Additionally, the deep layer (downward triangles) seems further separated from the others. In medial VTC, on the other hand, domain-level clusters are less clear, as the separation between categories and domains is similar (Fig. 6E). For example, the separation between bodies and faces is similar to the separation between bodies and limbs.

An important question is whether the representational structure evident in VTC is simply inherited from early retinotopic areas. To examine this question, we defined a V1 ROI on the basis of cytoarchitectonic boundaries (human occipital cytoarchitectonic area 1) (Hinds et al., 2008; Rosenke et al., 2018). We reasoned that finding similar RDMs across V1 and VTC partitions would indicate that the representational structure is inherited from earlier visual stages. While we observe low representational dissimilarity between images of the same category (3 × 3 on-diagonal blocks), even in V1 (Fig. 6C), the RDM structure is different between V1 and VTC partitions. The highest dissimilarity in V1 is between categories whose typical visual field extent differed; E.g., representations of bodies (which tend to extend vertically), are most dissimilar from representations of cars, houses, and characters (which tend to extend horizontally). In contrast, in both medial and lateral VTC, the largest dissimilarities are between representations of faces and of the inanimate categories cars, houses, and corridors. To more thoroughly quantify the similarity of RDMs from different regions, we computed correlations between the lower triangles (excluding the diagonal) between the V1, lateral VTC, and medial VTC RDMs in each participant. We found that the correlation between the V1 RDM and the RDMs of either lateral (average across participants = 0.56 ± 0.02) or medial VTC (r = 0.44 ± 0.05) is lower than the correlation between the lateral and medial VTC RDMs (r = 0.70 ± 0.03; both two-sample t tests, t values > 4.5, both p values < 0.01). Together, these analyses demonstrate that domain and category structure in VTC does not simply mirror differences among stimuli that are already present in V1.

We next quantified the amount of domain-level, category-level, and depth-level structure in the RDMs by using a regression analysis in which each participant's RDM is predicted from a linear combination of idealized model RDMs (Fig. 7A). This approach allows us to jointly estimate the degree to which each model RDM contributes to the structure in the measured RDMs. Our goal was not to perform an exhaustive search over candidate models to identify which best fits the data reported here; instead, we sought to test the specific hypotheses that relate to the hierarchical nature of the stimulus set used in this experiment.

Figure 7.

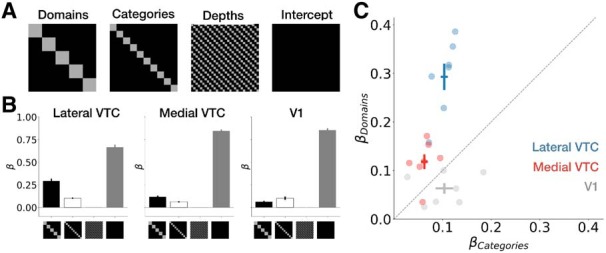
Regression analysis of RDM structure. A, Diagram indicating the model RDMs that were linearly combined to fit measured RDMs. Black represents 1; gray represents 0. B, Average weights ± SEM across participants in each ROI. C, Individual participants' weights for the domain and category regressors. Each dot represents a single participant; cross represents mean across participants ±1 SEM along each axis; dashed line represents unity line; color represents ROI.

The contributions of domain, category, and depth to RDM structure are summarized in Figure 7B. In general, across all participants and ROIs, the weights estimated for the depth regressor are close to 0 (lateral VTC: 0.005 ± 0.0005, mean ± SEM across participants; medial VTC: 0.003 ± 0.0003; V1: 0.001 ± 0.002), suggesting that the within-depth similarity hypothesis (Fig. 5C) does not describe our data well. Weights fit to the domain, and category regressors are substantially larger and significantly differ across ROIs: a two-way ANOVA on weights with factors of ROI (lateral VTC/medical VTC/V1) and regressor (domain/category/depth) reveals a main effect of partition (F_(2,54) = 29.1, p = 2.7 × 10⁻⁹, η² = 0.15), a main effect of ROI (F_(2,54) = 92.6, p = 3.6 × 10⁻¹⁸, η² = 0.47), and a significant ROI × regressor interaction (F_(4,54) = 23.8, p = 2.3 × 10⁻¹¹, η² = 0.24). This interaction remains significant when disregarding the low-magnitude depth weights; that is, including only weights fit to the domain and category regressors (F_(2,36) = 22.8, p = 4.1 × 10⁻⁷, η² = 0.28), and when removing the control ROI (V1) from the analyses (F_(1,24) = 14.5, p = 0.001, η² = 0.12). These analyses provide further support for differential representational structure across VTC partitions.

The regression analysis shows that both category and domain information contribute to the RDM structure in the VTC ROIs. Notably, domain-level structure is more pronounced than category-level structure in lateral VTC: a post hoc test (Tukey's honest significant difference) on the two-way ANOVA described above shows that domain weights are significantly larger than category weights in lateral VTC (p = 4.2 × 10⁻⁷). In medial VTC, however, domain-level structure and category-level structure are statistically indistinguishable in magnitude (p = 0.14). Indeed, a scatter plot of the contribution of domain and category structure to the RDMs in each participant (Fig. 7C) demonstrates that the contribution of domain was larger than category in both partitions, but more so in lateral VTC than medial VTC for each of the individual participants.

These results held (all significant effects remained significant and all nonsignificant effects remained nonsignificant) for data that were not subject to the vein-removal procedure. In particular, the regressor × partition interaction remains significant (F_(1,24) = 14.9, p = 0.001, η² = 0.12).

To facilitate comparison with prior research and verify the robustness of our results, we also recomputed these metrics after reconstructing the RDMs from five other commonly used metrics, including raw betas and category-preference maps (Table 1). Representational structure for the other metrics is shown in Figure 8. For metrics that do not subtract the responses of other categories (i.e., β-norm and raw β), the weight fit to the depth regressor ranged between 0.23 and 0.32. For the remaining four metrics, the range of the depth weight was 0.002–0.007, which includes the z-norm metric we primarily use. Critically, we found that, for all six metrics, there is a significant interaction between VTC partition and regressor: all F values > 9.0, all p values < 0.01, all η² values > 0.08 (Fig. 8), indicating that there is differential domain and category information across lateral and medial VTC.

Figure 8.

RDMs and regression analysis fits of the RDM for multiple metrics. In each row: leftmost column, metric; middle columns, RDMs for lateral and medial VTC, respectively; rightmost column, β weights of category and domain contributions to the RDM (see regressors in Fig. 7A). Colors represent ROI, crosses represent mean across participants ± 1 SEM along each axis. A, z-norm metric. B, t-contrast metric. C, z-score metric. D, Mean-subtracted β metric. E, β-norm metric. F, Raw β metric.

Does representational structure in VTC vary with cortical depth?

While the depth-specific model RDM does not fit our measured RDMs well, the relative contributions of domains and categories might still vary across cortical depth. Recent fMRI studies of early visual cortex have identified heterogeneity in function across cortical depths (Muckli et al., 2015; Fracasso et al., 2016; Klein et al., 2018), prompting us to test whether the differences we found between lateral and medial VTC might also depend on cortical depth. Thus, we examined visual representations separately for each cortical depth in both VTC partitions.

We split each RDM into three depth-specific RDMs: one for each of the superficial, middle, and deep depths (Fig. 9A–C, lateral VTC; and Fig. 9D–F, medial VTC). Examination of the RDMs in Figure 9 reveals that category and domain distinctions are more prominent in superficial than deep layers: within-domain and within-category dissimilarities are lower (cyan) in the superficial than deep layers, whereas between-category and between-domain dissimilarities are higher (yellow) in the superficial than deep layers.

We quantified the contribution of domain and category structure for each depth and partition using a regression analysis in which each RDM is predicted as a weighted sum of idealized domain-level and category-level RDMs. In both lateral (Fig. 9G) and medial VTC (Fig. 9H), weights for the domain-level predictor are larger than category-level weights, and both domain and category weights decrease with depth. Notably, the difference between domain-level and category-level structure is largest in superficial lateral VTC and smallest in deep medial VTC. In contrast, deep lateral VTC and superficial medial VTC are well matched in domain-level and category-level structure (compare Fig. 9G, deep, with Fig. 9H, superficial). However, this structure is driven by different representational distinctions. For example, in deep lateral VTC (Fig. 9C), words and numbers are dissimilar from faces and bodies; but in superficial medial VTC, words and numbers are most dissimilar from places (Fig. 9D).

To quantify the effect of depth on representational structure in each VTC partition, we conducted a three-way ANCOVA on regression weights with partition (lateral VTC/medial VTC) and regressor (domain/category) as factors and depth as a continuous covariate. We found a main effect of depth (F_(1,76) = 60.8, p = 2.7 × 10⁻¹¹, η² = 0.14), whereby fit β weights decrease by 0.04 per unit depth (e.g., from superficial to middle). Consistent with the previous analysis that aggregated across depths, we also found a main effect of partition (F_(1,76) = 83.8, p = 6.8 × 10⁻¹⁴, η² = 0.2), a main effect of regressor (F_(1,76) = 152.9, p = 7.0 × 10⁻²⁰, η² = 0.36), and a partition × regressor interaction (F_(1,76) = 35.7, p = 6.9 × 10⁻⁸, η² = 0.08). Finally, we found a regressor × depth interaction (F_(1,76) = 10.8, p = 0.002, η² = 0.03), suggesting that domain and category weights decrease at different rates. We did not find a partition × regressor × depth interaction (F_(1,76) = 1.2, p = 0.28), indicating that this decrease is similar in both lateral and medial VTC.

Does representational structure in VTC vary across domains?

The results presented thus far summarize representational structure across all 10 categories and 5 domains. However, as there are differences across domains in visual similarity (e.g., child and adult faces are visually similar, but cars and guitars are visually dissimilar) and abstraction level (e.g., faces can be considered a basic-level category, and places a superordinate one), we further quantified representational structure separately by domain. For each domain, we extracted the dissimilarities between representations of exemplars within the same category and domain (e.g., different houses) as well as the dissimilarities between representations of exemplars from different categories within the same domain (e.g., houses vs corridors). The dissimilarities were calculated across independent split halves of the data, separately for each domain and depth (Fig. 10).

Figure 10.

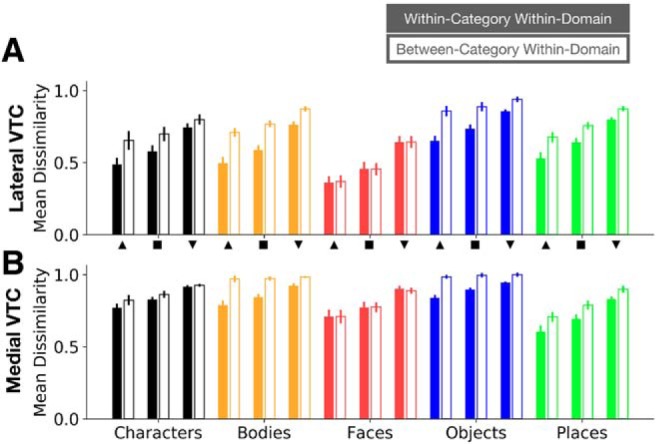
Within-category/within-domain and between-category/within-domain representational dissimilarities in VTC. Mean representational dissimilarity across participants in lateral VTC (A) and medial VTC (B) for each domain and each depth. Error bars indicate SEM across participants. Filled bars represent mean within-category/within-domain dissimilarity; hollow bars represent mean between-category/within-domain dissimilarity. Dissimilarities are plotted for each depth. Upward triangle represents superficial depth; square represents middle depth; downward triangle represents deep depth. Colors and x-axis labels represent domains.

We observe three main effects: (1) across domains and partitions, both within-category/within-domain (Fig. 10, filled bars) and between-category/within-domain (Fig. 10, empty bars) representational dissimilarities are lowest in superficial VTC and highest in deep VTC; (2) with the exception of faces (Fig. 10, red bars), between-category/within-domain dissimilarities are larger than within-category/within-domain dissimilarities across depths; and (3) dissimilarities vary across domains and partitions. We quantified these observations using a four-way ANCOVA with factors of partition (lateral/medial VTC), domain (characters/bodies/faces/objects/places), and dissimilarity type (within-category/between-category), with depth as a continuous covariate. In support of our observations, we found: (1) a main effect of depth (F_(1,380) = 227.7, p = 1.2 × 10⁻⁴⁰, η² = 0.13), whereby dissimilarity increases by 0.05 per unit depth, (2) a significant interaction between domain and within- versus between-category dissimilarity (F_(4,380) = 12.0, p = 3.2 × 10⁻⁹, η² = 0.03), and (3) both a main effect of domain (F_(4,380) = 81.5, p = 6.9 × 10⁻⁵⁰, η² = 0.18) and a significant domain × partition interaction (F_(4,380) = 35.4, p = 4.1 × 10⁻²⁵, η² = 0.08), indicating that the representational dissimilarities for these five domains differ between partitions. Together, these results provide evidence that depth effects are consistent across domains, categories, and partitions, but representational structure varies across domains and VTC partitions.

Can differences in measurement quality explain differences between partitions and depths?

As veins are more prevalent in superficial than deeper cortical depths (Fig. 2A) (Duvernoy et al., 1981; Lauwers et al., 2008; Polimeni et al., 2010; Siero et al., 2011; Goense et al., 2016; Kay et al., 2019), it is important to consider how our results may depend on cortical vasculature. In this section, we consider whether measurement quality, which is affected by draining veins, impacts the results. To determine whether measurement differences across depths and partitions can explain the data, we compared two additional metrics in each VTC partition and depth: (1) the mean time-series tSNR, which is insensitive to specification of the GLM used to estimate responses, and (2) the mean variance explained (R²) by the GLM. Further, we also computed the mean response amplitude to each stimulus type to characterize potential differences in mean response magnitude across each ROI. We reasoned that, if any of these measurements could be explained by an interaction between (1) partition and depth or (2) partition and category, we should further test whether these factors account for our results.

Across partitions and cortical depths, the mean tSNR across participants ranges between 12.7 and 15.7 (Fig. 11A), consistent with prior reports at similar voxel volumes (Triantafyllou et al., 2005). A two-way ANCOVA with partition (lateral/medial VTC) and depth as a continuous covariate indicated no significant effect of depth on tSNR (F_(1,38) = 1.46, p = 0.23) and no partition × depth interaction (F_(1,38) = 0.016, p = 0.90). This analysis suggests that tSNR cannot explain differences in representations across cortical depths or partitions. A similar analysis (two-way ANCOVA with partition and depth as a continuous covariate) on variance explained by the GLM (R²; Fig. 11B) revealed a main effect of partition (F_(1,38) = 42.5, p = 1.1 × 10⁻⁷, η² = 0.30), a main effect of depth (F_(1,38) = 56.7, p = 4.8 × 10⁻⁹, η² = 0.39), and a significant interaction between partition and depth (F_(1,38) = 6.6, p = 0.01, η² = 0.05). As we found differences in representational structure across lateral and medial VTC, we tested whether our results hold after reexamining domain-level and category-level structure in a subset of our data that was closely matched in mean R² across partitions (see Material and Methods). Recomputing domain and category weights for RDMs generated from these R²-matched data replicate our results: we observe a significant regressor (domain/category) × partition (lateral/medial VTC) interaction (F_(1,24) = 15.1, p = 7.1 × 10⁻⁴, η² = 0.12), whereby domain-level structure exceeds category level structure in lateral, but not medial, VTC. Thus, differences between representations across partitions are likely not driven by differences in R².

Figure 11.

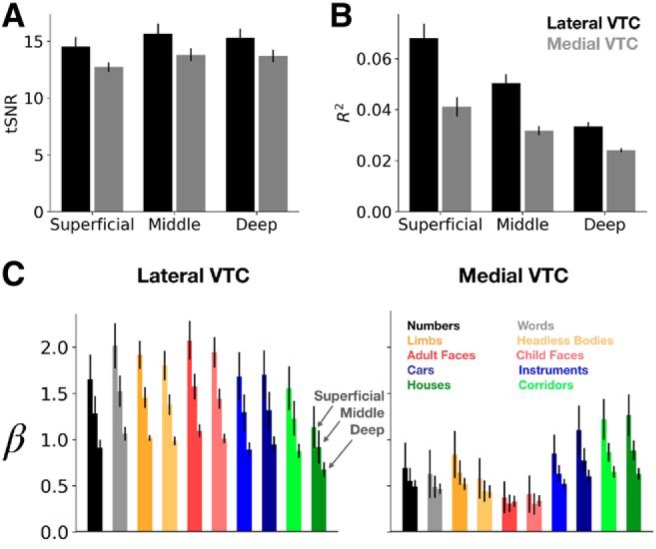
tSNR, variance explained, and response amplitude across cortical depth. Each metric was calculated at each vertex and then averaged across vertices of the ROI. tSNR (A) and variance explained by the GLM (B) in lateral and medial VTC at the three cortical depths examined in this study. C, Mean response amplitudes to the 10 stimulus categories in lateral and medial VTC. Normed amplitudes were averaged first across vertices in an ROI and then across participants. Error bars indicate SEM across participants. Bar colors represent stimulus category (see legend at right). Each triplet of bars sharing a color proceed through depth (superficial, middle, and deep) from left to right.

Inspection of GLM betas (% BOLD signal change) by category, depth, and partition (Fig. 11C) reveals that, as previously reported (Polimeni et al., 2010; Kay et al., 2019), response amplitudes decrease across cortical depth. A three-way ANCOVA on the average % BOLD signal change (averaged across all vertices in the partition of interest) with category and partition (lateral VTC/medial VTC) as factors and depth as a continuous covariate revealed a main effect of depth (F_(1,380) = 106.7, p = 3.2 × 10⁻²², η² = 0.12), and of partition (lower amplitudes in medial than lateral VTC, F_(1,380) = 273.8, p = 1.1 × 10⁻⁴⁶, η² = 0.31). There is no main effect of category (F_(9,380) = 0.93, p = 0.50), and no category × depth interaction (F_(9,380) = 0.12, p > 0.99), indicating that response amplitude was well matched across conditions and decreased with depth evenly across all conditions. We also found a significant category × partition interaction (F_(9,380) = 7.795, p = 1.47 × 10⁻¹⁰, η² = 0.08), which is driven by higher responses to inanimate (cars, guitars, houses, and corridor) than animate stimuli in medial, but not lateral, VTC (Fig. 11C). However, this overall higher mean response to inanimate versus inanimate categories in medial VTC does not explain the categorical structure in medial VTC, as distributed responses to houses, guitars, and cars are dissimilar from one another (Fig. 6B), even as their mean responses are similar. Together, these analyses suggest that differential category and domain structure across medial and lateral VTC cannot be explained by tSNR, variance explained by the GLM, or mean response amplitudes to certain categories. However, depth effects are coupled with lower variance explained and lower signals in deeper than superficial layers.

Is ultra-high-resolution necessary to reveal these representations?

The differences between anatomical partitions and cortical depths described thus far have been derived from submillimeter resolution data. We tested whether these findings of differential representations across depths and partitions require ultra-high-resolution acquisition, or whether the same findings would be accessible to more standard fMRI measurements at 2.4 mm resolution. Some features of these data, such as depth-dependent effects, will clearly depend on ultra-high-resolution acquisition; if the voxel size matches the thickness of the cortical sheet (between 2 and 3 mm) (Fischl and Dale, 2000), functional differences at different cortical depths would be challenging, if not impossible, to identify with 2.4 mm resolution. The differences between lateral and medial VTC in the level of abstraction of their representations, however, may be apparent at lower spatial resolutions as well.

To investigate differences between visual representations at ultra-high-resolution (0.8 mm voxels) and standard-resolution (2.4 mm voxels), we downsampled each participant's functional data to 2.4 mm using a Fourier-space smoothing method (see Materials and Methods). Downsampling a fixed set of data, as opposed to collecting a separate dataset, has the advantage of controlling for session-to-session variability in attention, fatigue, and performance (Peelen and Downing, 2005; Weiner et al., 2016; Zaretskaya et al., 2018). The simulated 2.4 mm data were projected onto the same FreeSurfer surfaces as the high-resolution data to facilitate comparison. Additionally, the entire experiment was repeated at 3T to validate this downsampling method in Participant S1 (Fig. 3).

How closely do the simulated 2.4 mm data match data acquired natively at 2.4 mm? The simulated and measured 2.4 mm maps have similar spatial structure, mean absolute RDM magnitude (the average dissimilarity in the RDM), and RDM structure (Fig. 3). Indeed, the correlation between the lower triangles (excluding the diagonal) of RDMs computed from Participant S1's measured 3T data and downsampled 7T data is r = 0.97 in lateral VTC and r = 0.95 in medial VTC, indicating high consistency in the representational structure across resolutions. This comparison for Participant S1 suggests that the downsampled data in the remaining 6 participants are an appropriate approximation of the data one may observe in an experiment done with 2.4 mm data acquired at 3T.

Comparing the ultra-high-resolution 0.8 mm and simulated standard-resolution 2.4 mm data revealed two key results. First, the representational dissimilarities are lower overall in the simulated 2.4 mm data than in the 0.8 mm data (Fig. 12A,B and Fig. 12D,E). A two-way ANOVA on the RDM magnitudes with anatomical partition (lateral/medial) and data resolution (0.8 mm/2.4 mm) as factors revealed a main effect of resolution (F_(1,24) = 54.7, p = 1.2 × 10⁻⁷, η² = 0.48), a main effect of partition (F_(1,24) = 32.2, p = 7.7 × 10⁻⁶, η² = 0.28), but no interaction between data resolution and partition (F_(1,24) = 2.4, p = 0.13). To account for the difference in overall magnitude of representational dissimilarities between the data at each resolution, we simulated another variant of the 2.4 mm data in which we added Gaussian noise to the simulated 2.4 mm preference maps (see Materials and Methods; Fig. 12C,F). Comparison of the mean RDM magnitude for the 0.8 mm data with the 2.4 mm + noise data preserved the main effect of anatomical partition (F_(1,24) = 37.6, p = 2.5 × 10⁻⁶, η² = 0.61); critically, however, there was no effect of dataset (0.8 mm/2.4 mm + noise; F_(1,24) = 0.04, p = 0.85). Thus, in subsequent comparisons in which we also used the simulated 2.4 mm + noise data, RDM magnitude is appropriately controlled across resolutions.

Figure 12.

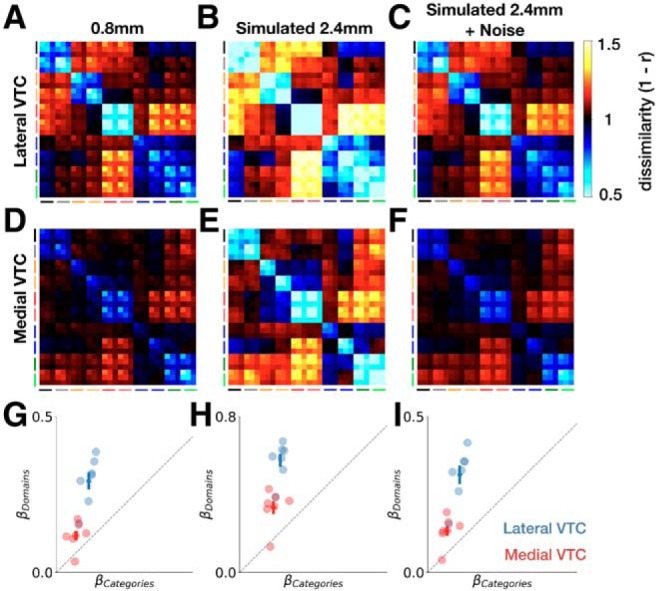
Effects of spatial resolution on representational structure. Group-averaged RDM for lateral VTC at (A) 0.8 mm, (B) simulated 2.4 mm, and (C) simulated 2.4 mm with added Gaussian noise. D–F, Same as in A–C, but for medial VTC. Model RDM fits for domains and categories for lateral VTC (blue) and medial VTC (red) at (G) 0.8 mm, (H) simulated 2.4 mm, and (I) simulated 2.4 mm with added Gaussian noise. Crosses represent ±1 SEM across participants.

Second, we found that, while RDM magnitude differs between spatial resolutions, the representational structure was largely similar. Regression analyses using the domain, category, and depth predictors (as in Fig. 7A) revealed that, in all three data preparations (0.8 mm, simulated 2.4 mm, and simulated 2.4 mm with added noise), domain weights exceed category weights more strongly in lateral than medial VTC (Fig. 12G–I). As in the 0.8 mm data, a two-way ANOVA on the regression weights with regressor (domain/category) and partition (lateral/medial VTC) as factors indicated a significant interaction when using the simulated 2.4 mm data (F_(1,24) = 14.9, p = 7.4 × 10⁻⁴, η² = 0.09). This result held with the stimulated 2.4 mm + noise data (F_(1,24) = 13.4, p = 0.001, η² = 0.11).

To further investigate the effect of spatial resolution on representational structure, we directly compared weights for the domain-level and category-level regressors for each data preparation. A three-way ANOVA with partition (lateral VTC/medial VTC), data resolution (0.8 mm/2.4 mm), and regressor (domain/category) indicated main effects of all three factors, as expected from prior analyses (all p values < 1 × 10⁻⁹). Critically, we found no evidence for a three-way interaction (F_(1,48) = 1.3, p = 0.26), which would have suggested that the regressor × partition interaction reported here varies with data resolution. Adding noise to the simulated 2.4 mm data yields the same results: the three-way interaction remained nonsignificant (F_(1,48) = 0.01, p = 0.92). Together, these analyses demonstrate that representational differences of categories and domains across lateral and medial VTC are robust across resolutions from 0.8 to 2.4 mm.

Discussion

Using ultra-high-resolution fMRI, we measured responses in VTC to a hierarchically structured stimulus set of five domains, each consisting of two categories. These measurements allowed us to compare submillimeter representations both parallel to the cortical surface and through cortical depth, revealing three novel results. First, we find that anatomically distinct lateral and medial partitions of VTC represent the visual input at multiple levels of abstraction: there was both domain structure and more granular category structure in each VTC partition. However, domain-level representations were stronger in lateral VTC than in medial VTC. Second, both domain-level and category-level structure decreased with cortical depth. Third, downsampling the data to 2.4 mm mirrored the differential representational structure across VTC partitions that we observed with ultra-high-resolution. In the sections below, we discuss the utility of ultra-high-resolution fMRI for measuring category representations, relate our findings to prior research, and discuss the theoretical implications of our findings.

The strength, but not nature, of VTC representations varies with cortical depth

Submillimeter resolution enabled us to test the structure of visual representations across cortical depths in human VTC for the first time. We found a quantitative, but not qualitative, change in VTC representations across depths: while domain- and category-level structure both decrease with cortical depth, their relative contributions are similar across depths. Future studies will be needed to examine whether other factors, such as cortical thickness and curvature, might also affect representations across depths.

The stability of representations across cortical depth is consistent with findings by Tanaka, Tanifuji, and colleagues (Fujita et al., 1992; Tanaka, 1996; Wang et al., 1996; Tsunoda et al., 2001) who reported a columnar structure in macaque IT (which is thought to be homologous to human VTC). Using optical imaging and electrophysiology, they found that neurons with similar functional properties were clustered across cortical depths. More recent ultra-high-resolution fMRI studies of early visual cortex have reported that attentional modulation of population receptive fields in V1 varies by cortical depth and is highest in deeper layers (Klein et al., 2018). Such findings suggest the possibility that tasks with higher top-down load than the present oddball task may differentially modulate VTC representations across cortical depths.

The quantitative effect of depth, which is evinced by stronger domain and category structure in superficial than deep cortical depths, is coupled with stronger response amplitudes and higher variance explained by the GLM in the superficial cortical depth. This raises the possibility that differences across depths may be explained by the underlying vasculature; that is, stronger responses in the superficial layers may be a consequence of draining veins in superficial cortex (Koopmans et al., 2010; Vu and Gallant, 2015; Kay et al., 2019). While we took care to exclude cortical vertices that are likely veins in our data, we may not have excluded all venous effects. Nonetheless, representations measured from deep cortical depths, which are predominantly free of the influence of large draining veins, resemble those from the superficial and middle depths. Thus, one important insight from our data is that the domain-level and category-level structure of VTC representations is not driven by draining veins but is a functional property of the underlying representations.

Ultra-high-resolution fMRI reveals consistency of category and domain representations across spatial resolutions

We found that the differences in representational structure between lateral and medial VTC are apparent even when downsampling our submillimeter data to a standard fMRI resolution of 2.4 mm. This direct comparison of 0.8-mm-resolution data to 2.4-mm-resolution data suggests that distributed representations in VTC studied with standard resolution fMRI are consistent with representations probed with measurements at a finer scale. This finding is hardly trivial. It suggests that the vast literature on domain and category information in human VTC (Malach et al., 1995; Kanwisher et al., 1997; Aguirre et al., 1998; Epstein and Kanwisher, 1998; Cohen et al., 2000; Haxby et al., 2001; Cox and Savoy, 2003; Peelen and Downing, 2005; Kriegeskorte et al., 2008b; Huth et al., 2012; Weiner et al., 2014) is unlikely to be a strict artifact of spatial smoothing by voxels that are several millimeters on a side. Instead, our 0.8 mm measurements validate that domain and category representations are an inherent functional property of VTC representations.

We note, however, that other aspects of VTC representations, including semantic information and visual features (Bracci and Op de Beeck, 2016; Jozwik et al., 2016; Proklova et al., 2016; Bracci et al., 2019), environmental regularities (Peelen and Downing, 2017; Kaiser et al., 2019), typical size (Konkle and Oliva, 2012), and eccentricity (Levy et al., 2001; Hasson et al., 2002; Gomez et al., 2019) might differ when examined with ultra-high-resolution fMRI. For example, we have not tested finer categorical distinctions at the subordinate scale (e.g., different types of string instruments) or exemplar-level representations (e.g., face identity across views). It is also possible that representations of object parts and features, which have been found in macaque IT with electrophysiology (Fujita et al., 1992; Tsunoda et al., 2001; Issa et al., 2013) may only be apparent with ultra-high-resolution fMRI. These hypotheses can be tested in future research.

Different visual representations across VTC partitions

Our finding that distributed representations in medial VTC differ from those in lateral VTC adds to a large body of work on anatomical and functional differences between these partitions. Anatomically, medial and lateral VTC differ in their cytoarchitectonic properties (Weiner et al., 2014, 2017; Gomez et al., 2017; Lorenz et al., 2017) and connectivity fingerprint (Saygin et al., 2011, 2016; Osher et al., 2016). Functionally, they differ in (1) eccentricity preference (Levy et al., 2001; Hasson et al., 2002; Weiner et al., 2014), (2) real-world object size preference (Konkle and Oliva, 2012), (3) stimulus animacy preference (Martin et al., 1996; Connolly et al., 2012), and (4) the domains they represent: clustered representations for faces (Kanwisher et al., 1997), words (Cohen et al., 2000; Nordt et al., 2019), and bodies (Downing et al., 2001; Weiner and Grill-Spector, 2010) are in lateral VTC, whereas clustered representations for places are in medial VTC (Aguirre et al., 1998; Epstein and Kanwisher, 1998).

Our use of a hierarchical stimulus set consisting of five domains and two categories per domain allowed us to investigate whether ecological domain (Kanwisher, 2000, 2010) or category (Haxby et al., 2001) is the dominant organizing principle of VTC. We found that both domain and category structure contribute to VTC representations and that these representations are not merely inherited from early visual areas. Critically, however, we discovered that these representations are not uniform across VTC: domain representations are more prominent than category representations in lateral VTC, but domain and category structure similarly contribute to medial VTC representations.

Differential representations across VTC partitions and depths form a functional-architectural foundation for flexible readout

What might be the utility for this difference in the granularity of representations across VTC partitions? Central to our understanding of the functional architecture of VTC are theories that link the neuroanatomical and functional implementational features of the visual system to information processing (Zeki and Shipp, 1988; Van Essen et al., 1992; Malach, 1994; Grill-Spector and Weiner, 2014). According to these frameworks, the functional divergence of representations across lateral and medial VTC may produce a diversity of representations that can be used by downstream regions for different tasks in a flexible manner. One inference from our findings is that representations in lateral VTC are better suited toward readouts that favor more abstract domain distinctions, whereas representations in medial VTC are better suited for reading out categorical distinctions. For example, finding a face in a hallway may rely on a representation that discriminates domains (faces vs places), which is prominent in lateral VTC. However, deciding whether that place is a hallway at work or a corridor in your house may depend on a representation that discriminates among place categories, such as those in medial VTC.

We note that, because we used categories and domains that have been typically used in prior research and are associated with ecological constructs, the domains are not controlled for visual similarity or level of abstraction. For example, the face domain contains child and adult faces, which, being important social categories, are both the most visually homogeneous and most specific in terms of level of abstraction compared with the other four domains. Future experiments using carefully controlled stimuli (Jozwik et al., 2016; Proklova et al., 2016; see, e.g., recent elegant work by Bracci and Op de Beeck, 2016; Bracci et al., 2019) can further examine the role of visual similarity and conceptual knowledge on both domain and category representations.

In conclusion, ultra-high-resolution measurements allowed us to compare representational structure across cortical depths and partitions of human high-level visual cortex. We show that anatomically distinct partitions of VTC exhibit different representational structure and that the strength of both domain and category-level representations varies with cortical depth.