Commutative Properties of Head Direction Cells during Locomotion in 3D: Are All Routes Equal?

Navigation often requires movement in three-dimensional (3D) space. Recent studies have postulated two different models for how head direction (HD) cells encode 3D space: the rotational plane hypothesis and the dual-axis model. To distinguish these models, we recorded HD cells in female rats while they traveled different routes along both horizontal and vertical surfaces from an elevated platform to the top of a cuboidal apparatus.

Abstract

Navigation often requires movement in three-dimensional (3D) space. Recent studies have postulated two different models for how head direction (HD) cells encode 3D space: the rotational plane hypothesis and the dual-axis model. To distinguish these models, we recorded HD cells in female rats while they traveled different routes along both horizontal and vertical surfaces from an elevated platform to the top of a cuboidal apparatus. We compared HD cell preferred firing directions (PFDs) in different planes and addressed the issue of whether HD cell firing is commutative—does the order of the animal's route affect the final outcome of the cell's PFD? Rats locomoted a direct or indirect route from the floor to the cube top via one, two, or three vertical walls. Whereas the rotational plane hypothesis accounted for PFD shifts when the animal traversed horizontal corners, the cell's PFD was better explained by the dual-axis model when the animal traversed vertical corners. Responses also followed the dual-axis model (1) under dark conditions, (2) for passive movement of the rat, (3) following apparatus rotation, (4) for movement around inside vertical corners, and (5) across a 45° outside vertical corner. The order in which the animal traversed the different planes did not affect the outcome of the cell's PFD, indicating that responses were commutative. HD cell peak firing rates were generally equivalent along each surface. These findings indicate that the animal's orientation with respect to gravity plays an important role in determining a cell's PFD, and that vestibular and proprioceptive cues drive these computations.

SIGNIFICANCE STATEMENT Navigating in a three-dimensional (3D) world is a complex task that requires one to maintain a proper sense of orientation relative to both local and global cues. Rodent head direction (HD) cells have been suggested to subserve this sense of orientation, but most HD cell studies have focused on navigation in 2D environments. We investigated the responses of HD cells as rats moved between multiple vertically and horizontally oriented planar surfaces, demonstrating that HD cells align their directional representations to both local (current plane of locomotion) and global (gravity) cues across several experimental conditions, including darkness and passive movement. These findings offer critical insights into the processing of 3D space in the mammalian brain.

Introduction

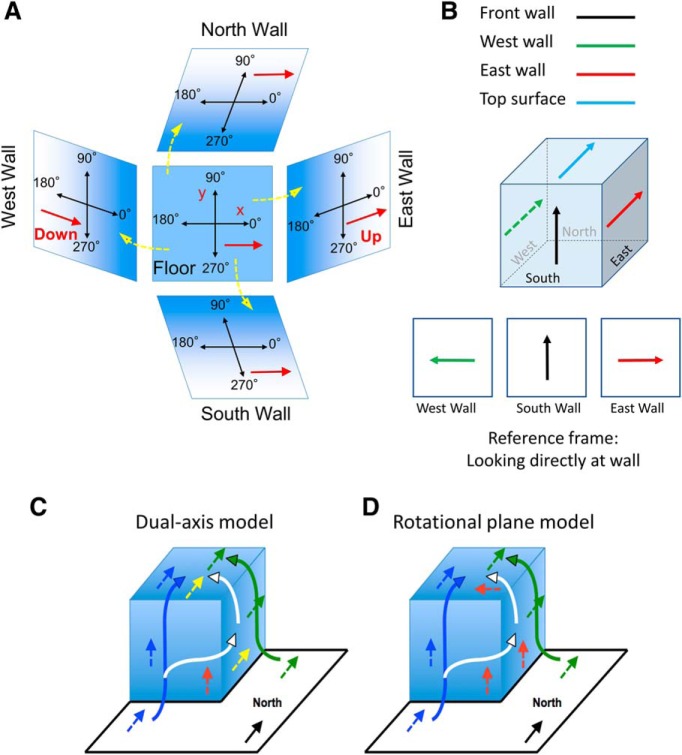
The vast majority of studies on spatial cells have explored their responses when animals locomote along a two-dimensional surface in the horizontal plane. Many animals, however, inhabit and navigate in a more three-dimensional (3D) world—traveling between different horizontal surfaces that differ in height or climbing in a vertical plane. Head direction (HD) cells are neurons that fire as a function of the animal's directional heading in the horizontal plane (Taube et al., 1990a; Taube, 1995). Two models have emerged to account for how HD cells fire across vertical planes: the rotational plane hypothesis and the dual-axis model. Initial studies monitored HD cell responses as a rat locomoted from a horizontal surface onto a vertical wall and found that HD cell discharge was maintained in the vertical plane, and that the cell's preferred firing direction (PFD) could be predicted based on the cell's PFD in the horizontal plane (Stackman et al., 2000; Calton and Taube, 2005). Specifically, as the rat moved from the horizontal to the vertical surface, the cell would transform its frame of reference to its current plane of locomotion by rotating the horizontal plane by 90° into the vertical plane (Fig. 1A). This finding led to the hypothesis that HD cells may define their reference frame based on the animal's plane of locomotion.

Figure 1.

A, Rotational plane hypothesis. Central image shows x–y coordinate system on the floor and how it rotates (yellow arrows) onto the different walls. Red arrow on the floor shows a hypothetical cell tuned toward the east wall (0°) and how its PFD is oriented on each wall. B, Dual-axis model. Top, Orientation of a cell's PFD tuned to “up” on the south wall and its orientation on the west and east walls and on the top surface. Bottom, View of each wall looking directly at it. Note that the cell's PFD rotates CW when the animal traverses a vertical corner to the right and rotates 90° CCW when traversing a vertical corner to the left. Thus, the cell's PFDs are 180° opposite as viewed directly looking at the wall. C, D, Routes from the floor to the top surface on the cube. Dual-axis model (C) and rotational plane model (D) predictions based on direct (one-wall) or indirect (two-wall) routes. See text for details.

This view was extended to account for firing on any change of planar surface—the animal simply rotates its current horizontal reference frame into the new plane. Note that the horizontal semicircular canals, which are best activated during an upright yaw turn, are also activated when the animal turns its head in the vertical plane, although a different otolith signal is generated on the two surfaces. Recent experiments which enabled the rat to sample all 360° in the vertical plane along different walls further tested this hypothesis, and the findings were consistent with the view that a cell's PFD could be accounted for by considering the orientation of the PFD in the horizontal plane and then rotating its vector around any corner with the animal (Taube et al., 2013). Thus, the cell would update its orientation by treating the vertical plane as an extension of the floor, where the animal shifts its reference frame to align with its current plane of locomotion (Fig. 1A). This scheme was referred to as the rotational plane hypothesis.

Two recent modeling studies have challenged the rotational plane hypothesis (Page et al., 2018; Laurens and Angelaki, 2019). In the Page et al. study, preliminary data showed that HD cell PFDs shifted between two opposing walls of a cuboidal surface such that their orientations were 180° opposite of one another (as viewed by an observer facing each wall; Fig. 1B). These authors postulated that there were two axes/planes to consider when accounting for cell firing in 3D. The first axis was the animal's yaw rotation around its dorsal—ventral (D–V) axis (the vertical axis when the animal is upright). The second axis was how the rat's D-V axis was oriented relative to the gravity vector. Together, the two components accounted for a cell's PFD in any plane, and an equation was formulated to express these properties. This model was referred to as the dual-axis model. The model predicts that there is a 90° clockwise (CW) rotation of a cell's PFD when going around right vertical corners and a 90° counter-clockwise (CCW) rotation when going around left vertical corners. In contrast, the rotational plane hypothesis predicts no shift in the cell's PFD when traveling around vertical corners because the cell's PFD follows the animal's plane of motion.

Here, we tested these two models against one another as rats navigated around different types of corners of a cuboidal apparatus. We also determined whether HD cell firing is commutative in 3D and asked the following question: does the route the animal travels between two locations affect the HD cell's PFD at the final destination? (Commutativity is the property whereby changing the order of how items are processed does not change the result; e.g., 3 + 4 = 4 + 3 = 7.) Our experiments tested HD cell responses under different conditions, including (1) light or dark conditions, (2) active versus passive displacement of the animal, (3) rotation of the apparatus with the animal on it, (4) traversing an inside vertical corner, and (5) traversing a 45° outside vertical corner instead of a 90° corner. Finally, recent studies have challenged the view that cell firing rates are similar between the horizontal and vertical planes (Laurens and Angelaki, 2019), and the experiments on the cube provided another opportunity to examine this issue.

Materials and Methods

Subjects

Subjects were 17 female Long–Evans rats aged 3–11 months and weighing 224–400 g before surgery. Rats were individually housed in Plexiglas cages and maintained on a 12 h light/dark cycle. Food and water were provided ad libitum. All experimental procedures involving the rats were performed in compliance with institutional standards as set forth by the National Institutes of Health Guide for the Care and Use of Laboratory Animals and approved by the Dartmouth Institutional Animal Care and Use Committee.

Behavioral training

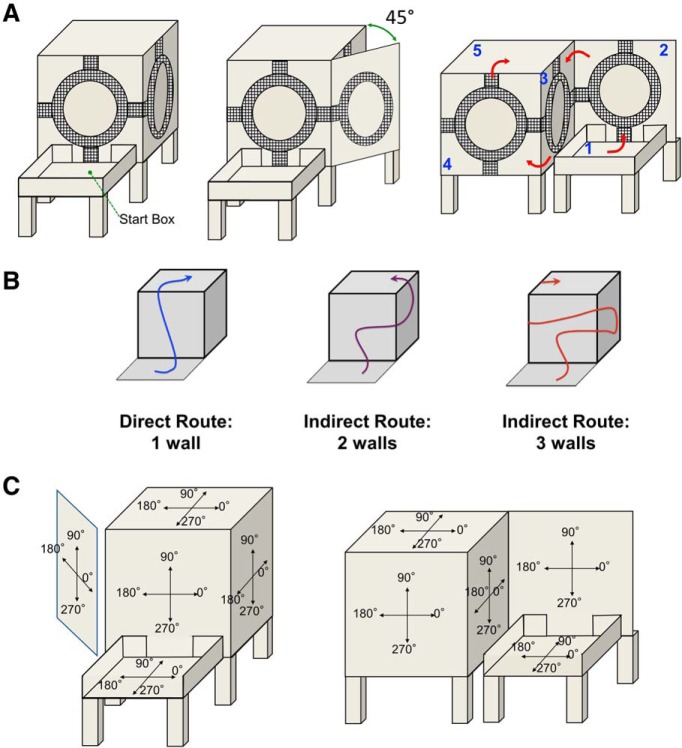
To test cell responses in different planes and around different types of vertical corners, rats were trained to navigate different routes around a cuboidal apparatus (Fig. 2). Different routes could be set up that entailed traversals around outside or inside vertical corners, as well as routes that traversed horizontal corners that went from a horizontal surface to a vertical one or vice versa.

Figure 2.

Experimental apparatus and configurations. A, Left, Wooden cube apparatus with elevated start box leading to front vertical wall. Middle, Configuration of apparatus used for testing a 45° outside vertical corner. Right, Configuration of apparatus used for traversal of an inside vertical corner. Route follows numerical order from 1 to 5. B, Different routes for one-wall, two-wall, and three-wall paradigms. The three-wall paradigm involved travel along four walls between the start box and the cube top—first from the front wall to one of the adjacent walls, followed by a return to the front wall, and then travel to the other adjacent wall. For clarity, start box is shown positioned on the floor, but in fact it was elevated as shown in A. C, Left, Coordinate system used for each of the surfaces for all sessions except for the session involving an inside vertical corner. Right, Coordinate systems used for the session involving an inside vertical corner.

Before surgery, rats were trained to locomote on a vertical surface that was covered in wire mesh. Rats were first allowed to walk on a horizontal training surface covered in wire mesh, and over the course of 1–3 weeks the horizontal surface was slowly inclined until it was completely vertical. Subsequent training took place on the main apparatus used for this experiment, which was a wooden cube with side lengths of 94 cm (Fig. 2A, left). The front, left, and right vertical faces of the cube were covered in wire mesh, which was itself covered in plastic sheeting cut to expose a circle of mesh (48 cm in diameter, 10 cm wide) on each face such that animals could walk in a circle in the corresponding vertical plane and accordingly sample all possible HDs on each vertical face of the cube. The plastic sheeting was also cut such that the animals could locomote from one vertical face to another, or from any vertical face to the top of the apparatus. These passages were usually blocked by additional plastic sheeting, which could be removed by the experimenter to enable the animals to move from one surface to another. Once rats could comfortably locomote on the vertical surface, they were trained to climb from an elevated (∼0.5 m) horizontal starting surface (start box) onto the front face of the cube. The start box was a wooden, gray, rectangular enclosure that measured 56 × 61 × 15 cm. It had an opening along one wall that was placed adjacent to the front face of the cuboidal apparatus, such that the animal could locomote from the start box onto the front vertical face of the cube. After sufficient directional sampling on the front face (two revolutions around the mesh circle), they were subsequently allowed to move either directly onto the top of the cube or onto an adjacent wall (where two revolutions were also required) before climbing to the top. The rats fully rotated their bodies as they made their revolutions around the mesh circles, sampling all 360° of possible head directions. For example, if a rat were moving counterclockwise around the mesh circle, it would be facing left at the top of the circle, down on the left side of the circle, right at the bottom of the circle, and up on the right side of the circle. However, it should be noted that the rats preferred to face up instead of down on the vertical surfaces; thus, to help aid the rats from falling off the apparatus, they were supported during downward head directions by an experimenter gently holding the base of the animal's tail. This directional facing preference led to higher sampling of up directions than down directions on the vertical surfaces (i.e., more time spent looking at 90° than 270°; Fig. 2C left), though the bias did not appear to influence the PFDs of recorded HD cells (data not shown). Recording sessions were only included in the analysis if the animal sampled all HDs on each visited face of the cube. Getting to the top of the apparatus served as the only motivation for the rats to traverse the maze. The experimental room was completely open and visible to the animals during traversal, which provided several orienting visual landmark cues. These cues included several posters on the walls, a doorway, and a black curtain that hung along the back side of the cube against a white-wall background. Animals were also allowed to freely explore a cylindrical enclosure (76 cm diameter, 51 cm height) that contained a sheet of white cardboard along one wall (subtending ∼100° of arc), which served as an orienting cue. This cylinder was used to “screen” for HD cells (discussed later).

Electrode construction

Following initial training, all animals were implanted with a moveable microdrive consisting of a bundle of eight stereotrodes targeting the anterodorsal thalamic nucleus (ADN). The stereotrodes were constructed by twisting together two strands of 17 μm nichrome wire. These twisted strands were subsequently threaded through a single 26-gauge stainless steel cannula, and the end of each wire was connected to a single pin of a Mill-Max connector. The two center pins of the connector were attached to the cannula, which acted as an animal ground. Three drive screws were secured around the connector using dental acrylic, making the electrode drivable in the D-V plane.

Electrode implantation

Animals were anesthetized with isoflurane. They were subsequently placed in a stereotaxic frame, and an incision was made in the scalp to expose the skull. A single hole was drilled into the skull, and the electrode was implanted 1.3 mm posterior to bregma, 1.5 mm lateral to bregma, and 3.7 mm ventral to the cortical surface. These coordinates placed the microelectrodes just above the ADN. The microelectrode array was secured to the skull using dental acrylic.

Recording of neural data

Animals were allowed to recover for at least 7 d following surgery. Over the course of several weeks, the stereotrodes were “screened” for cells as the animals freely locomoted in the cylinder. Electrical signals were preamplified using unity-gain operational amplifiers on an HS-18-MM headstage (Neuralynx). Signals from each stereotrode wire were then differentially referenced against a quiet channel from a separate stereotrode and bandpass filtered (600 Hz to 6 kHz) using a Cheetah 32 Data Acquisition System (Neuralynx). If signals on a given stereotrode crossed a predefined amplitude threshold (30–50 μV), they were time stamped and digitized at 32 kHz for 1 ms. The headstage was also equipped with red and green light-emitting diodes (LEDs) spaced ∼6 cm apart over the head and back of the animal, respectively. A color video camera positioned over the arena captured video frames with a sampling rate of 30 Hz, and an automated video tracker extracted the x-position and y-position of the LEDs as well as their angle (i.e., the animal's head direction). The tracking frames were time stamped so they could be matched up to the neural data. If clearly isolated waveforms were visually apparent, we recorded an 8 min baseline session in the cylinder. Otherwise, stereotrodes were advanced ∼50–100 μm and screened again at least 2 h later or the next day.

Spike sorting

Spike sorting was conducted offline. Spikes collected from a recording session were first automatically sorted into clusters using the automated clustering program Kilosort (Pachitaru et al., 2016), after which manual “cleanup” was performed using the manual clustering program SpikeSort 3D (Neuralynx). For the manual step, waveform features including peak, valley, height, width, and principal components were used to visualize the characteristics of individual spikes across both wires of a stereotrode simultaneously as a 3D scatter plot. Cleanup of automatically sorted clusters, which was not always required, was performed by drawing a polygon around the visually apparent boundaries of each cluster. Single-unit isolation was assessed using metrics such as L-ratio and isolation distance. For each well isolated cluster, we saved the time stamps for each spike and then analyzed and matched them to the tracking data.

Experimental design and behavioral testing

If an HD cell was isolated following a screening session in the cylinder (classification discussed later), the cell was subsequently recorded as the animal traversed one of several versions of the 3D cuboidal apparatus.

Standard cube sessions

Several different types of sessions were conducted. Each session began with a 4 min session in the start box (Table 1) and ended with a 4 min session on the top surface. In between these two sessions, the animal moved across one, two, or three vertical walls (Fig. 2B).

Table 1.

Firing properties of all recorded HD cells in the start box

	Mean	SEM	Range
Peak firing rate (spikes/s)	36.64	2.32	4.86–103.06
Background firing rate (spikes/s)	1.70	0.17	0.049–8.07
Directional firing range (degrees)	95.90	2.86	53.12–181.96
Mean vector length	0.72	0.015	0.44–0.95

One-wall session.

Following recording in the start box, the animal was allowed to move onto the front vertical face of the cube. Once the animal had made at least two revolutions around the mesh circle on the front face (i.e., had adequately sampled all possible head directions), it was allowed to locomote to the top of the apparatus. In summary, start box→front wall→top (Fig. 2B, left).

Two-wall session.

This session included the same start box and front wall periods as the one-wall session, but after recording on the front face of the apparatus, the animal was allowed to locomote to either the left or right vertical face of the apparatus (left or right sessions). Once the animal had made at least two revolutions around the mesh circle on this face, it was allowed to locomote to the top of the apparatus. In summary, start box→front wall→left or right wall→top (Fig. 2B, middle).

Three-wall session.

This session included the same start box, front wall, and side wall periods as the two-wall session, but after recording on the left or right face of the apparatus, the animal was allowed to locomote back to the front face of the apparatus. After at least two revolutions about the mesh circle, the animal was required to locomote to the side face opposite the one it had previously been on (“left first” or “right first” sessions). After at least two revolutions on this face, the animal was allowed to move to the top of the apparatus. In summary, start box→front wall→left or right wall→front wall→right or left wall→top (Fig. 2B, right).

Final box session.

Following this series of recordings, the animal was passively moved from the top of the cube to the start box for a final 4 min recording session.

Dark sessions

Dark sessions were identical to the aforementioned standard sessions, except the lights were extinguished following the start of recording in the start box for each session. Thus, the animal had to traverse the faces of the cuboidal apparatus without the aid of visual cues. All surfaces of the cube were additionally wiped down with 70% alcohol between sessions, and for one-wall and two-wall sessions, the cube was rotated pseudorandomly 90° CW or CCW so that the front wall differed from session to session. These measures were meant to reduce the rats' use of olfactory or tactile cues left behind from previous recording sessions.

Passive sessions

Three different types of passive sessions were conducted.

Two-wall passive session.

These sessions were identical to the standard two-wall session, except the rat was passively moved by an experimenter from the front wall to either the left or right wall (left or right sessions). In summary, start box→front wall→passively moved to left or right wall→top.

Box-to-wall passive session.

These sessions were identical to the two-wall passive session, except the front wall recording was omitted and the rat was passively moved by an experimenter directly from the start box to either the left or right wall (left or right sessions). In summary, start box→passively moved to left or right wall→top.

Passive rotation session.

These sessions were identical to the two-wall passive session, except instead of passively moving the rat from the front wall to a side wall, the entire apparatus was rotated 90° while the rat was on the apparatus. For example, instead of the animal physically moving from the front wall to the left wall, the entire apparatus was rotated 90° CW. Thus, the animal remained on the same physical side of the cube between the “front wall” and “side wall” recordings, but the apparatus was rotated such that the animal's plane of locomotion rotated by 90°, as if the animal had moved across a vertical corner. In summary, start box→front wall→90° leftward or rightward rotation→top.

45° Corner session

The 45° corner session started with a 4 min recording in the start box, after which the animal was allowed to move onto the front face of the apparatus where recording took place. Following this session, the animal was allowed to locomote to the right face, which had been opened up partially such that movement across the vertical corner resulted in a 45° shift in the animal's place of locomotion instead of the usual 90° (Fig. 2A, middle). In summary, start box→front wall→45° side wall. No session was conducted on the cube top for this series because the angle of the side wall did not allow the animal to reach the top surface.

Inside vertical corner session

For this session, an additional traversable wall (inside wall) was placed abutting the right vertical corner of the front face of the apparatus, oriented perpendicular to the front face (Fig. 2A, right). Thus, movement from the inside wall to the front face of the apparatus, across an inside vertical corner as opposed to the usual outside corners, resulted in a 90° CCW shift in the rat's plane of locomotion. The rat moved directly from the start box to the inside wall for recording in a manner similar to other sessions. The rat then moved from the inside wall across the inside vertical corner to the front face of the apparatus where recording took place, after which it moved to the left face of the apparatus for recording (an outside corner), and finally moved to the top of the apparatus. In summary, start box→inside wall→front wall→left wall→top. For some sessions, this manipulation was also performed in darkness.

Video recordings

A color video camera mounted on the ceiling was used to track the animal's movements and head direction during locomotion in the start box and on the top of the apparatus. Additional cameras mounted on tripods were positioned squarely facing each traversable vertical face of the apparatus for tracking on those surfaces. A video camera switching board was used to manually switch between cameras as the animal moved from one surface to another, and switching the camera sent a transistor–transistor logic pulse to the recording system to indicate which camera was newly active. These signals were time stamped and saved so that they could be matched with the spike and tracking data.

Depending on the orientation of the video camera, the x–y coordinate frame had to be shifted sometimes to align the reference frame across the different surfaces. Figure 2C left, shows the x–y coordinate frame for all of the standard cube and the 45° vertical corner experiments (see Figs. 3–8). Figure 2C, right, shows the coordinate frame used for the inside vertical corner experiment (see Fig. 9).

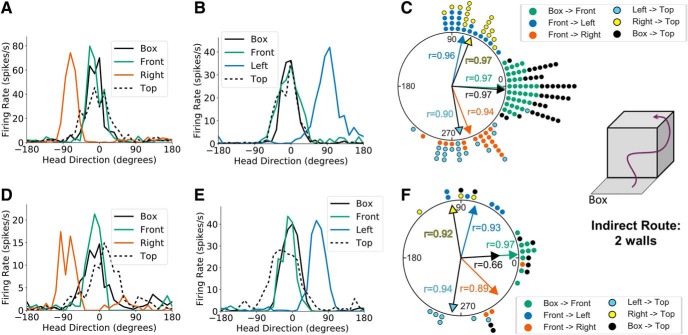
Figure 3.

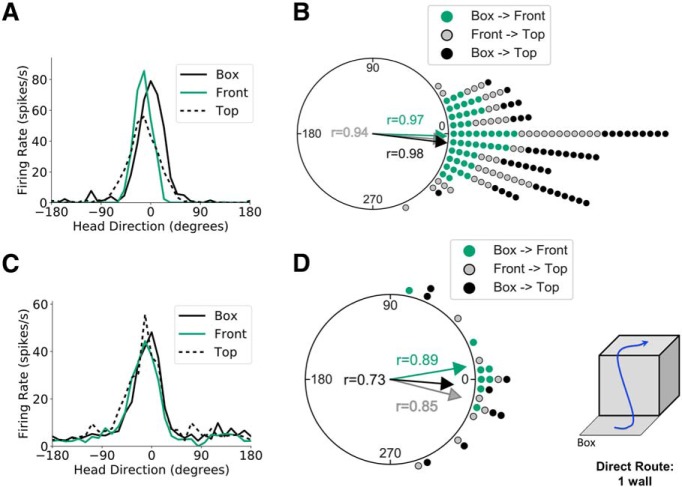
One-wall sessions. A, Head direction tuning curves for a representative HD cell recorded during a one-wall session (front wall) in light conditions. Head direction is measured relative to the cell's PFD in the start box. B, A polar dot plot showing PFD shifts between relevant planes of locomotion for all one-wall sessions recorded in light conditions. Each dot represents one recording session. C, D, Same as A and B but for recording sessions in darkness. For clarity, the box depicted in the schematic of the apparatus is shown without walls and not elevated here and in Figures 4 and 5.

Figure 8.

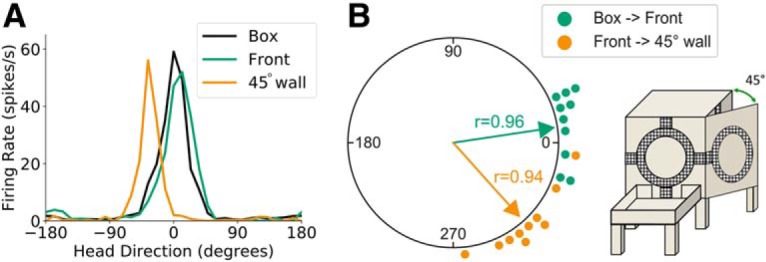
Open wall sessions (45°). A, Head direction tuning curves for a representative HD cell recorded during an open wall session in light conditions. Head direction is measured relative to the cell's PFD in the start box. B, A polar dot plot showing PFD shifts between relevant planes of locomotion for all open wall sessions recorded in light conditions. Each dot represents one recording session. Note that the cells' PFDs shifted ∼45° CW for rightward outside 45° vertical corners.

Figure 9.

Inside corner sessions. A, Head direction tuning curves for a representative HD cell recorded during an inside corner session in light conditions. Head direction is measured relative to the cell's PFD in the start box. B, A polar dot plot showing PFD shifts between relevant planes of locomotion for all inside corner sessions recorded in light conditions. Each dot represents one recording session. C, D, Same as A and B but for recording sessions in darkness. Note that the cells' PFDs shifted ∼90° CW for leftward inside vertical corners.

Histology

Once recordings were complete, animals were deeply anesthetized with sodium pentobarbital, and small marking lesions were made at the stereotrode tips by passing a small anodal current (15 μA, 15–20 s) through two active wires from separate stereotrodes. Animals were then intracardially perfused with saline followed by 10% formalin solution, after which the brains were removed from the skull and postfixed in 10% formalin solution with 2% potassium ferrocyanide for at least 24 h. The brains were then transferred to 20% sucrose solution for at least 24 h, after which they were frozen and sliced coronally (30 μm sections) using a cryostat. Sections were mounted on glass microscope slides and stained with thionin, after which the sections were examined using a light microscope. Electrode tracks were identified, and the locations of recorded cells were determined by measuring backwards from the most ventral location of the marking lesions or, if marking lesions were not visible, the electrode tracks.

Data analysis

Head direction tuning curves

HD tuning curves were created using 12° bins, rather than the typically used 6° bins, due to lower sampling on the apparatus walls. For each cell, we calculated the amount of time that each bin was sampled and the number of spikes fired per bin over the course of a session. The cell's tuning curve was computed by dividing the number of spikes per bin by the amount of sampling time per bin. We then determined the mean vector length and mean angle for each cell to indicate tuning strength and preferred firing direction, respectively (discussed in the next section).

Classification and analysis of HD cells

A cell was only analyzed for a given recording session if it had a mean vector length >0.4 for all portions of that session (i.e., on each wall of the apparatus). If a cell was recorded across multiple sessions of the same type (e.g., multiple two-wall left sessions), it was only included in analyses for the first recorded session. Because HD cells tend to shift their preferred firing directions in register with each other (Taube et al., 1990b; Knierim et al., 1995; Yoganarasimha et al., 2006), if multiple HD cells were recorded during the same session, PFD shifts between different planes of locomotion were calculated as the average of the PFD shifts across all included HD cells, such that each session had a single PFD shift associated with each change of plane. In the current study, we recorded 34 HD cell pairs across all experiments, 11 triplets, and 3 quadruplets. Corecorded HD cells largely shifted their PFDs in register with each other, such that the PFD shifts of simultaneously recorded cells differed by <45° in 272 of 293 total cell pairings across all corner traversals. The remaining 21 discrepancies were scattered across animals and conditions and did not appear to be a result of poor clustering or contamination from neighboring HD cells.

Analysis of HD cell firing properties focused on several established measures: (1) PFD, the direction at which a cell has its maximum firing rate; (2) mean vector length, used to assess tuning strength; (3) peak firing rate (PFR), the firing rate at the cell's PFD; (4) directional firing range, the angular spread of the cell's elevated tuning; and (5) background firing rate, the cell's firing rate outside of its directional firing range. A cell's mean vector length (r) was computed by first computing a weighted mean of the cell's polar tuning curve along Cartesian x and y components (r_x and r_y) and then computing the length of the resultant vector:

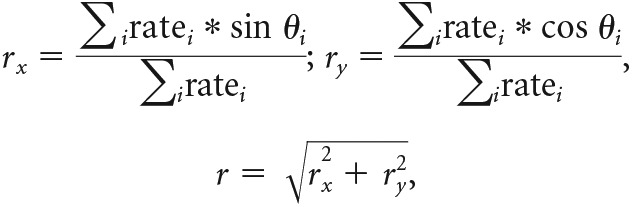where i indexes across bins in the tuning curve, rate_i is the firing rate in bin i, and θ_i is the angle represented by bin i. The cell's PFD was computed as the direction (mean angle) of the resultant vector:

PFD shifts between different planes of locomotion were calculated as the difference between the cell's mean angles on each surface. The concentration of PFD shifts across sessions was assessed using the Rayleigh statistic (r), which was used to calculate an angular deviation score (Batschelet, 1981):

This value was presented along with the mean PFD shifts (not including absolute shifts) in the same way that an SD would typically be used for nonangular data. Nonangular means (e.g., PFR, directional firing range, background firing rate) were presented with SDs.

The cell's PFR was calculated by extracting the maximum firing rate from the cell's tuning curve (i.e., the firing rate at the cell's PFD). Directional firing range was calculated by first fitting a triangle to the cell's tuning curve using a least-squares method (Taube et al., 1990a; Mehlman et al., 2019) and then calculating the angular spread encompassed by the triangle. The cell's baseline firing rate was calculated as the mean firing rate in all bins >12° to the left and right of the base of the triangular fit.

Statistical analyses

Statistical analyses were performed using custom Python code. All tests were two-sided and used an α level of 0.05. A circular V test was used to test for concentration of PFD shifts around a predicted value, whereas the Rayleigh statistic was used to assess general clustering of angular shifts (Batschelet, 1981). Differences in the angular variance of PFD shifts between two or more conditions were assessed by testing for equality of their concentration parameters (κ; Batschelet, 1981; Mardia and Jupp, 2000). Between-group and within-group nonangular comparisons were assessed using one-way ANOVA and one-way repeated-measures ANOVA. If samples violated sphericity (assessed using Mauchly's test), we applied a Greenhouse–Geisser correction. Post hoc pairwise comparisons were performed using Bonferroni-corrected paired t tests.

Results

Testing for commutative properties

For the cuboidal surface depicted in Figure 1C,D, there are two possible routes from the floor to the top surface: a direct route via one vertical wall (blue or green pathways) or an indirect route using either of the two adjacent vertical walls (white-arrow pathway). If HD cell firing properties are commutative, then it should not matter which route the animal takes to the top surface. Importantly, the rotational plane and dual-axis models each make different predictions as to the commutative properties of the cells, as well as the orientation of the cell's PFD on the top surface. If the rat takes a direct route to the top surface using one wall (blue or green paths in Fig. 1C,D), the cell's PFD should rotate with the animal's plane of locomotion from the floor onto the wall and then again from the wall to the top surface. Thus, the cell's PFD will maintain the same orientation on the top surface as on the floor. Both the rotational plane and dual-axis models make the same predictions for this direct route. In contrast, if the rat traveled the indirect route from the floor to the wall and then locomoted over to an adjacent wall before continuing onto the top surface (white path in Fig. 1C,D), the rotational plane model and the dual-axis model make different predictions about the orientation of the cell's PFD on the top surface. In the dual-axis scheme, the model postulates that there is a 90° rotation of the cell's PFD when the animal goes around the vertical corner. Thus, for the indirect route (white-arrow pathway), the cell's PFD will rotate 90° CW (Fig. 1C, red to yellow arrows) as the animal traverses the vertical corner and then will keep this orientation (yellow arrow on top surface) as it traverses the horizontal corner onto the top surface. In this case, the cell's PFD on the top surface will be the same as on the floor (blue and yellow arrows on top surface), and the cell's properties can be considered commutative. In contrast, the rotational plane model suggests that the cell's PFD will not shift when the animal traverses a vertical corner (Fig. 1D, white-arrow pathway, red arrow on side wall) because the PFD will remain aligned to the animal's body orientation and will rotate this orientation onto the new surface. Importantly, however, the cell's PFD on this second vertical surface would differ from that if the animal had traveled directly onto this vertical surface from the floor (green pathway; Fig. 1D, green vs red arrow on side wall). Further, when the animal then travels onto the top surface, the orientation of the cell's PFD would differ from that when traveling the direct route from the floor (Fig. 1D, blue vs red arrows on top surface). In this case, the cell's responses would not be commutative. In sum, the two models make different predictions for the cell's PFD that are 90° apart on the top surface.

HD cell properties following traversal of horizontal corners

Across all manipulations, we recorded a total of 80 HD cells from 17 rats (firing properties summarized in Table 1). Previous studies (Stackman et al., 2000; Calton and Taube, 2005; Taube et al., 2013) have demonstrated that, following traversal of horizontal corners (e.g., from the floor to a vertical wall or vice versa), HD cells update their PFDs based on yaw rotations within the animal's current plane of locomotion. According to the rotational plane hypothesis, the vector of the cell's PFD in the horizontal plane is rotated into the vertical plane of interest. Thus, a cell that fires preferentially on the floor when the animal faces the vertical wall would fire on the vertical wall when the animal faces upward and would fire downward on a 180° opposing vertical wall (Fig. 1A). Similarly, when the animal locomotes from the floor onto either of the adjacent walls, the vector representing the cell's PFD points in the same direction as it did on the floor. Viewing each plane of locomotion using a local reference frame (i.e., with a video camera pointed at the vertical surface and viewing the animal's back as it locomotes), there would appear to be no shift in an HD cell's PFD between the horizontal and vertical planes, as if the vertical plane was simply an extension of the floor. Because there is no rotation of the animal's D–V axis about the gravity vector during such a manipulation, both the dual-axis and rotational plane hypotheses agree regarding these results.

To assess this response in the present study, we recorded from 58 HD cells across 47 sessions as rats (n = 16) moved from a horizontal plane (start box) across an “inside” (concave) horizontal corner to a vertical plane (front face of the cube apparatus), and finally, across an “outside” (convex) horizontal corner at the top of the front vertical face to the top horizontal face of the cube (start box→front face→top; Fig. 2A, left). Because one animal showed inconsistent results compared with all other animals in terms of HD cell firing properties during this and all subsequent manipulations, this animal's data have been excluded from the regular statistical analysis and instead are analyzed separately at the end of the Results section. As predicted by both models, a circular V test revealed a 0° shift in the PFD between the start box and the front face (u = 9.38, n = 47, p < 0.001; mean shift: −1.92 ± 0.25°), between the front face and the top surface (u = 9.08, n = 47, p < 0.001; mean shift: −4.73 ± 0.35°), and between the start box and the top of the apparatus (u = 9.40, n = 47, p < 0.001; mean shift: −6.84 ± 0.22°; Fig. 3A,B), suggesting that HD cells maintained their PFDs according to yaw rotations within the animal's current plane of locomotion.

To test whether the animals relied upon visual cues to orient themselves during the task, or whether other cues (e.g., self-motion, proprioceptive, vestibular) were sufficient, we repeated the procedure with the room lights turned off. Twelve HD cells were recorded from six rats using this procedure across eight recording sessions. Again, a V test revealed that PFD shifts between the start box and front face (u = 3.51, n = 8, p < 0.001; mean shift: 9.22 ± 0.47°), between the front face and top surface (u = 3.31, n = 8, p < 0.001; mean shift: −13.22 ± 0.55°), and between the start box and top of the apparatus (u = 2.91, n = 8, p < 0.01; mean shift: −4.74 ± 0.74°) were significantly clustered around 0° (Fig. 3C,D). These results suggest that HD cells can use nonvisual cues to update their firing properties with respect to the current plane of locomotion during movement across horizontal corners. However, it is possible that the PFD shifts were more variable in the dark condition than in the light condition, which is suggested by the lower mean vector lengths for shifts in darkness compared to PFD shifts in the light (Fig. 3B vs Fig. 3D). To assess this possibility, we tested for differences in shift concentration parameters (κ) between the two conditions. Whereas concentrations were always lower in the dark sessions than in the light sessions (i.e., higher variance), only the shift between the start box and the top of the apparatus reached significance (F_(7,46) = 12.87, p < 0.01; κ_dark = 2.20, κ_light = 21.22). This result suggests that visual cues may be helpful in stabilizing PFD shifts during traversal of horizontal corners.

HD cell properties following traversal of vertical and horizontal corners

Although a recent study (Page et al., 2018) demonstrated that HD cells adopt 180° opposing PFDs during locomotion on opposite vertical faces of a cube when viewed within a local reference frame (i.e., viewer looking directly at vertical surface), it has not been demonstrated how HD cells shift their PFDs during locomotion across a single vertical corner. As described earlier, the rotational plane hypothesis and dual-axis model make different predictions. The rotational plane hypothesis predicts that an HD cell's firing properties should shift along with the rat's plane of locomotion, resulting in the same apparent PFD when each vertical plane is viewed in a local reference frame. In contrast, the dual-axis hypothesis predicts a 90° shift in the cell's PFD.

We conducted two experiments to determine how HD cells shift their PFDs on adjacent and opposing vertical planes. The first experiment, which only tested PFD shifts across adjacent planes, required animals to first locomote from the start box across an inside 90° horizontal corner to the front face of the apparatus, then across an outside 90° vertical corner onto either the left or right vertical face (left or right sessions), and finally across an outside 90° horizontal corner to the top of the apparatus (start box→front face→left or right face→top; Fig. 2B, middle). We recorded 22 HD cells in 19 left sessions and 23 HD cells in 17 right sessions, amounting to 29 unique HD cells recorded across 36 two-wall sessions (n = 11 rats). A V test revealed that the PFD shift between the start box and front face of the cube was significantly concentrated around 0° (u = 8.26, n = 36, p < 0.001; mean shift: −2.29 ± 0.23°), replicating our results described earlier. However, movement from the front face across an outside 90° vertical corner to the left face of the cube resulted in a 77.81 ± 0.30° (CCW) PFD shift that was significantly concentrated around 90° (V test, u = 5.76, n = 19, p < 0.001), whereas movement from the front face to the right face resulted in a −68.99 ± 0.35° (CW) shift that was concentrated around −90° (V test, u = 5.10, n = 17, p < 0.001). These results agree with the dual-axis hypothesis, as the animal's plane of locomotion rotated ±90° about the gravity vector during locomotion across the vertical corner and resulted in a corresponding ±90° shift in the PFDs of HD cells. Movement from the left face across a horizontal corner to the top of the cube resulted in a −80.28 ± 0.44° (CW) PFD shift that was concentrated around −90° (V test, u = 5.48, n = 19, p < 0.001), whereas movement from the right face to the top resulted in a 68.48 ± 0.26° shift that was concentrated around 90° (V test, u = 5.25, n = 17, p < 0.001). These final shifts from the vertical side walls of the cube to the top surface realigned the PFDs with those of the start box (V test, u = 8.28, n = 36, p < 0.001; mean shift: −3.91 ± 0.21°), demonstrating that HD cell firing properties are commutative and can maintain global consistency (Fig. 4A–C).

Figure 4.

Two-wall sessions. A, Head direction tuning curves for a representative HD cell recorded during a two-wall session (front and adjacent walls) in light conditions where the animal moved onto the right face of the cube apparatus before moving to the top. Head direction is measured relative to the cell's PFD in the start box. B, Same as A but for a session in which the animal moved onto the left face of the cube apparatus before moving to the top. C, A polar dot plot showing PFD shifts between relevant planes of locomotion for all two-wall sessions recorded in light conditions. Each dot represents one recording session. D–F, Same as A–C but for recording sessions in darkness. Note that the cells' PFDs shifted ∼90° CW for rightward outside vertical corners and ∼90° CCW for leftward outside vertical corners.

Note that these shift values makes it appear that the cell's PFD shifted ∼90° when the rat moved from the adjacent vertical face to the top of the cube. These apparent shifts, however, occur because of how the overhead video camera is oriented relative to the video camera that is pointing at the wall (Fig. 2C left). In actuality, the PFD vector on the wall is simply rotated with the plane's surface to the top of the cube apparatus. This planar rotation is similar to the rotational plane hypothesis process of traversing horizontally oriented corners, such as moving from the start box to the front wall. Thus, for example, when moving from the front wall to the adjacent right wall, the cell's PFD first shifts 90° CW, but then shifts 90° the opposite way, CCW, when moving from the right wall to the top of the cube. This process is necessary in order to keep the cell's PFD similar between the two horizontal surfaces (start box and top of cube).

We repeated these experiments in darkness, including 10 HD cells in six left sessions and four HD cells in three right sessions, amounting to 14 unique HD cells recorded during nine two-wall sessions (n = 5 rats). A V test revealed an ∼0° PFD shift between start box and front face (u = 4.12, n = 9, p < 0.001; mean shift: 2.55 ± 0.24°) and between start box and top (u = 2.76, n = 9, p < 0.01; mean shift: 3.12 ± 0.83°), but a 75.31 ± 0.36° (CCW) shift following movement from the front face to the left face of the cube that was concentrated around 90° (V test, u = 3.13, n = 6, p < 0.001). Subsequent movement from the left face to the top of the cube across a horizontal corner resulted in a −99.03 ± 0.35° (CW) shift that was concentrated around −90° (V test, u = 3.21, n = 6, p < 0.001). During the three right sessions, a −47.21 ± 0.46° (CW) shift was observed following movement from the front to the right face of the cube. This shift, however, only approached significance for concentration near −90°, which would be expected from the dual-axis model (V test, u = 1.97, n = 3, p = 0.05). This discrepancy could be due to either small sample size or potential PFD under-rotation in darkness. However, movement from the right face to the top resulted in a 100.59 ± 0.39° (CCW) PFD shift that was concentrated around 90° (V test, u = 2.23, n = 3, p < 0.05; Fig. 4D–F). Thus, neither HD cell tuning in the animal's current plane of locomotion nor its orientation with respect to the Earth's reference frame require visual cues.

It is possible that PFD shifts had more angular variance in the dark condition compared with the light. When testing for differences in shift concentration parameters between the two conditions, as with the one-wall sessions, only the shift between the start box and top of the cube showed significantly greater variance in the dark condition than in the light (F_(8,35) = 2.22, p < 0.05; κ_dark = 1.74, κ_light = 22.29). Therefore, it seems likely that visual cues aid in stabilizing PFD shifts across horizontal and vertical corners, though correct shifts (according to the dual-axis rule) are generally preserved in their absence.

The second experiment required animals to locomote on both adjacent and opposing faces of the cube apparatus. Animals first moved across an inside 90° horizontal corner from the start box to the front face of the apparatus, followed by movement across an outside 90° vertical corner to either the left or right vertical face (left first or right first sessions). This route was followed by movement back across the same vertical corner to the front of the cube, then across the previously uncrossed outside 90° vertical corner to the unvisited (left or right) face of the cube, followed by movement across a final outside 90° horizontal corner to the top of the cube (start box→front face→left or right face→front face→right or left face→top; Fig. 2B, right). This route allowed us to observe PFD shifts between adjacent vertical planes (e.g., front and left cube faces) as well as opposing planes (left and right cube faces), all of which required a rotation of the animal's D–V axis about the gravity vector.

Twelve HD cells were recorded across eight sessions in the left first condition, whereas 15 HD cells were recorded across 10 sessions in the right first condition, resulting in 24 unique HD cells being recorded across 18 three-wall sessions (n = 8 rats). As with previous results, a V test showed that PFD shifts between the start box and the first visit to the front face of the cube were strongly concentrated around 0° (u = 5.78, n = 18, p < 0.001; mean shift: −3.42 ± 0.27°). Movement across a vertical corner from the front to the left face of the cube resulted in a 91.68 ± 0.36° (CCW) PFD shift that was strongly concentrated around 90° (V test, u = 5.60, n = 18, p < 0.001), whereas movement from the front to the right vertical face resulted in a −80.16 ± 0.30° (CW) PFD shift relative to the start box that was concentrated around −90° (u = 5.65, n = 18, p < 0.001). As shown previously (Page et al., 2018) and predicted by the dual-axis model, HD cell PFDs during locomotion on the left and right (opposing) faces of the cube were offset by ∼180° (V test, u = 4.06, n = 18, p < 0.001; mean shift: 166.89 ± 0.78°). Movement from the left face across a horizontal corner to the top of the apparatus resulted in a −94.13 ± 0.49° (CW) PFD shift that was concentrated around −90° (V test, u = 3.93, n = 10, p < 0.001), whereas movement from the right face to the top was accompanied by a 76.92 ± 0.35° (CCW) PFD shift that was concentrated around 90° (V test, u = 3.65, n = 8, p < 0.001). These shifts realigned the PFDs at the top of the cube with those in the start box (V test, u = 5.90, n = 18, p < 0.001; mean shift: −4.48 ± 0.17°; Fig. 5). Thus, as with the two-wall sessions, the results of the three-wall sessions demonstrated that HD cells respond to an animal's head orientation relative to both the current plane of locomotion and the gravity vector, and their responses are commutative during 3D navigation.

Figure 5.

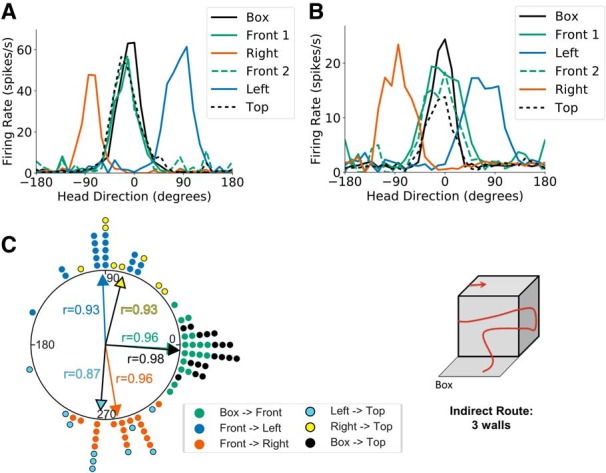
Three-wall sessions. A, Head direction tuning curves for a representative HD cell recorded during a three-wall session in light conditions where the animal moved onto the right face of the cube apparatus before the left face. Head direction is measured relative to the cell's PFD in the start box. B, Same as A but for a session where the animal first moved onto the left face of the cube apparatus before the right face. C, A polar dot plot showing PFD shifts between relevant planes of locomotion for all three wall sessions recorded in light conditions. Each dot represents one recording session. Note that the cells' PFDs shifted ∼90° CW for rightward outside vertical corners and ∼90° CCW for leftward outside vertical corners.

HD cell properties following passive movement across vertical and horizontal corners

We next sought to determine whether the PFD shifts observed in HD cells following locomotion across vertical corners were dependent upon active locomotion. Observing HD cell firing properties during passive movement across 3D planes would help us to determine whether visual, vestibular, and proprioceptive cues alone could support accurate updating of the HD signal in the absence of motor cues.

In the first passive experiment, the animal was allowed to actively locomote from the start box to the front face of the apparatus, after which it was moved by an experimenter across a 90° vertical corner to either the left or right vertical face (left or right sessions). The animal was then required to actively locomote across the final horizontal corner to the top of the cube (start box→front face→left or right face→top). Twelve HD cells across eight left sessions and 18 HD cells across 11 right sessions were recorded, resulting in a total of 21 unique HD cells recorded across 19 passive movement sessions (n = 5 rats). As in previous experiments, the PFD shifts between the start box and front face of the cube were strongly concentrated around 0° (V test, u = 6.02, n = 19, p < 0.001; mean shift: 1.84 ± 0.21°). Despite the lack of active locomotion across the vertical corner between the front and side faces, we observed an 80.74 ± 0.36° (CCW) PFD shift following passive movement of the animal from the front to the left face that was concentrated around 90° (V test, u = 3.70, n = 8, p < 0.001) and a corresponding −75.63 ± 0.23° (CW) PFD shift following passive movement from the front to the right face that was concentrated around −90° (V test, u = 4.42, n = 11, p < 0.001). These results suggest that active movement across a vertical corner is not necessary for appropriate updating of the HD signal, and that nonmotor (e.g., visual, optic flow, vestibular, and proprioceptive) cues are sufficient for this purpose. Movement from the left face to the top of the cube resulted in a −93.07 ± 0.41° (CCW) PFD shift that was concentrated around −90° (V test, u = 3.66, n = 8, p < 0.001), whereas movement from the right face to the cube top was accompanied by a 77.69 ± 0.19° shift that was concentrated around 90° (V test, u = 4.50, n = 11, p < 0.001), aligning the PFDs on the top of the cube with those from the start box (V test, u = 6.02, n = 19, p < 0.001; mean shift: −2.03 ± 0.21°; Fig. 6A–C).

Figure 6.

Two-wall and box-to-wall passive sessions. A, Head direction tuning curves for a representative HD cell recorded during a two-wall passive session in light conditions where the animal was passively moved from the front to the right face of the cube. Head direction is measured relative to the cell's PFD in the start box. B, Same as A but for a session in which the animal was passively moved from the front onto the left face of the cube apparatus. C, A polar dot plot showing PFD shifts between relevant planes of locomotion for all two-wall passive sessions recorded in light conditions. Each dot represents one recording session. Note that the cells' PFDs shifted ∼90° CW for rightward passive movements around the vertical corner and ∼90° CCW for leftward passive movements around the vertical corner. D, Head direction tuning curves for a representative HD cell recorded during a box-to-wall passive session in light conditions where the animal was passively moved from the start box to the right face of the cube. Head direction is measured relative to the cell's PFD in the start box. E, Same as D but for a session in which the animal was passively moved onto the left face of the cube apparatus. F, A polar dot plot showing PFD shifts between relevant planes of locomotion for all box-to-wall passive sessions recorded in light conditions. Each dot represents one recording session.

In the second passive experiment, the animal was passively moved directly from the start box to either the left or right vertical face of the cube (left or right sessions), after which it was allowed to actively move across a horizontal corner to the top of the apparatus (start box→left or right face→top). Thus, to correctly shift the PFDs of HD cells in accordance with (a) the change in the animal's plane of locomotion and (b) the change in the animal's D–V orientation with respect to the gravity vector, visual, vestibular, and proprioceptive cues would need to be used by the HD cells to accurately process movement across both a horizontal and a vertical corner without the help of motor cues. Thirteen HD cells were recorded across nine left trials, whereas 17 HD cells were recorded across 12 right trials, resulting in a total of 20 unique HD cells recorded across 21 passive movement sessions (n = 5 rats). We observed a 96.51 ± 0.22° (CCW) shift following passive movement from the start box to the left vertical face of the apparatus that was concentrated around 90° (V test, u = 4.12, n = 9, p < 0.001) and a −80.97 ± 0.27° (CW) shift following passive movement from the start box to the right vertical face that was concentrated around −90° (V test, u = 4.66, n = 12, p < 0.001). Movement from the left vertical face to the top of the cube resulted in a −100.28 ± 0.21° (CW) PFD shift that was concentrated around −90° (V test, u = 4.08, n = 9, p < 0.001), whereas movement from the right vertical face to the top resulted in a PFD shift of 77.61 ± 0.17° that was concentrated near 90° (V test, u = 4.72, n = 12, p < 0.001). These shifts aligned the PFDs at the top of the apparatus with those in the start box (V test, u = 6.38, n = 21, p < 0.001; mean shift: −3.59 ± 0.17°; Fig. 6D–F). These results suggest that HD cells can correctly update their firing properties following passive movement simultaneously across a horizontal and vertical corner.

The third passive experiment tested whether HD cells could correctly update their firing properties without explicit movement of the animal across planes of locomotion. Animals were first required to actively locomote from the floor to the front face of the apparatus, after which the apparatus was rotated 90° CW or CCW (leftward or rightward rotation sessions, respectively), such that the animal's plane of locomotion and D–V orientation relative to the gravity vector shifted by 90°, whereas its physical placement on the cube remained unchanged (start box→front face→leftward or rightward rotation→top). Twelve HD cells were recorded across nine leftward rotation sessions, whereas 14 HD cells were recorded across 11 rightward rotation sessions, resulting in 17 unique HD cells recorded across 20 passive rotation sessions (n = 5 rats). As in previous experiments, we observed a 0° PFD shift between the start box and front face of the apparatus (V test, u = 6.00, n = 20, p < 0.001; mean shift: 6.86 ± 0.30°). In contrast, there was a 56.88 ± 0.58° (CCW) PFD shift following CW rotation of the apparatus (such that the animal ended up on the left side of the cube) that was concentrated near 90° (V test, u = 2.97, n = 9, p < 0.01) and a −53.87 ± 0.26° (CW) PFD shift following CCW rotation that was concentrated near −90° (V test, u = 3.66, n = 11, p < 0.01). Although these shifts appeared smaller than those observed in previous vertical corner traversals (∼55° vs ∼80–90°; e.g., active or other passive movement sessions; see above), a one-way ANOVA showed that the absolute PFD shifts following vertical corner traversal were not significantly different across these manipulations (F_(3,180) = 1.11, p > 0.05). Movement from the left vertical face to the cube top resulted in a −76.84 ± 0.75° (CW) PFD shift that was concentrated around −90° (V test, u = 2.98, n = 9, p < 0.01), whereas movement from the right vertical face to the cube top was accompanied by a 51.27 ± 0.30° (CCW) shift that was concentrated near 90° (V test, u = 3.49, n = 11, p < 0.001). Thus, these final shifts realigned the PFDs at the top of the cube with those in the start box (V test, u = 6.08, n = 20, p < 0.001; mean shift: −6.06 ± 0.26°; Fig. 7). These results support the dual-axis model and demonstrate that HD cells are able to update their representations in response to shifts in the animal's plane of locomotion and D–V orientation relative to the gravity vector without an explicit change in the animal's location on the apparatus. In addition, there was no difference in concentration parameters for vertical corner traversals across the three passive conditions (χ₍₂₎² = 4.38, p > 0.05), indicating that traversals in the three conditions are processed similarly by the HD system.

Figure 7.

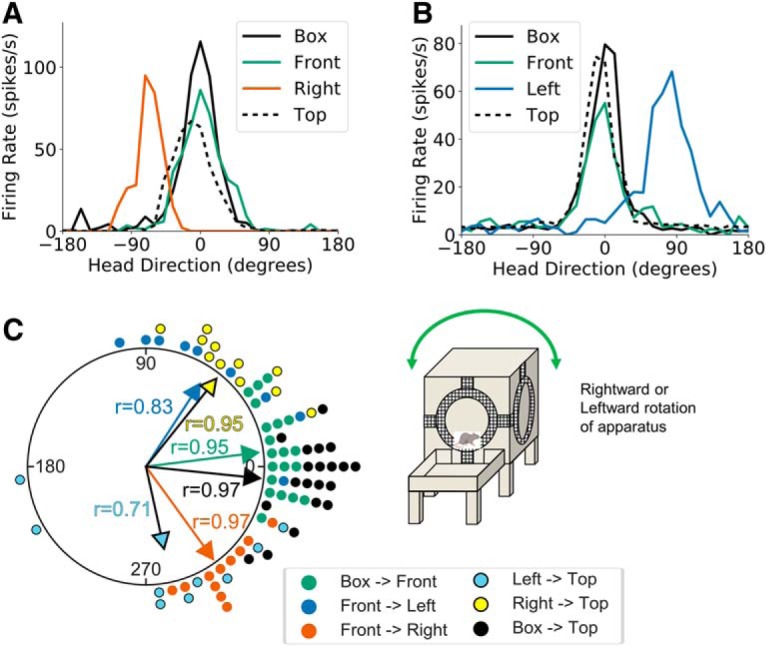
Two-wall rotation sessions. A, Head direction tuning curves for a representative HD cell recorded during a two-wall rotation session in light conditions where the apparatus was rotated to the right. Head direction is measured relative to the cell's PFD in the start box. B, Same as A but for a session in which the apparatus was rotated to the left. C, A polar dot plot showing PFD shifts between relevant planes of locomotion for all two-wall rotation sessions recorded in light conditions. Each dot represents one recording session. Note that the cells' PFDs generally shifted ∼90° CW or CCW for rightward and leftward cube rotations, respectively.

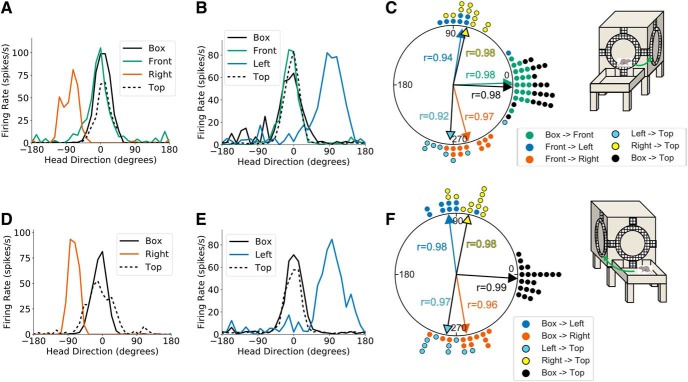
HD cell properties following traversal of a 45° vertical corner

We next sought to investigate the response of HD cells to locomotion across an outside vertical corner that involved a traversal of 45° instead of the previously investigated 90° traversals. Because the animal's D-V axis rotates CCW by 45° in this condition with respect to the gravity vector, the dual-axis hypothesis predicts a corresponding 45° CW shift in the PFDs of HD cells, measured using a local reference frame. The rotational plane hypothesis would predict no change in the cells' PFDs.

Animals (n = 4) were required to locomote from the floor onto the front vertical face of the cube, after which they moved rightward across a 45° vertical corner onto the right wall of the cube that had been opened to a 45° angle (start box→front face→45° face; Fig. 2A, middle). We recorded 14 HD cells across 10 sessions using this procedure. Whereas we observed an ∼0° shift in HD cell PFDs between the start box and the front face of the apparatus (V test, u = 4.24, p < 0.001; mean shift: 7.79 ± 0.29°), there was a −47.96 ± 0.35° (CW) PFD shift following movement from the front face across the 45° vertical corner that was concentrated around 45° (V test, u = 4.19, p < 0.001; Fig. 8). HD cells therefore adjust their PFDs following locomotion across a 45° vertical corner in a manner consistent with the dual-axis rule.

HD cell properties following traversal of an inside vertical corner

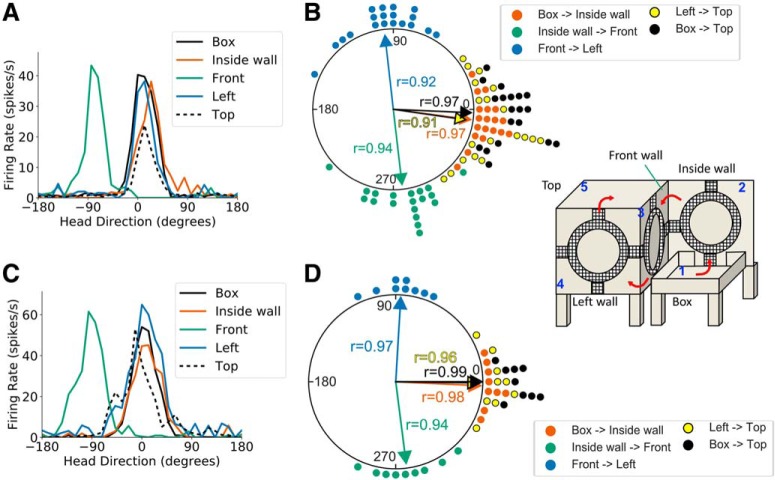
All of the vertical corners investigated thus far have been “outside” corners, which are convex. Movement from the front vertical face of the cube apparatus to the left face across an outside corner, for example, led to a 90° CW rotation of the animal's plane of locomotion (as viewed from above) about the gravity vector. If the animal instead moved to the left across an “inside” or concave vertical corner, its plane of locomotion would rotate 90° in the CCW direction. Given this situation, movement across inside and outside vertical corners should result in opposite shifts in an HD cell's PFD according to the dual-axis model because the animal's D-V axis is now rotating in the opposite direction around the gravity axis when traversing an inside vertical corner compared with traversing an outside vertical corner. Thus, traversal of an inside vertical corner to the right should lead to a 90° CCW shift of the cell's PFD and a 90° CW PFD shift for traversals around a left inside vertical corner.

To test this hypothesis, we first had animals (n = 4) locomote across a horizontal corner onto a new wall (referred to as the inside wall) that was placed perpendicular to the front vertical face of the cube apparatus, abutting its right edge to form a 90° inside corner (Fig. 2A, right). Movement from the start box onto the inside wall was not expected to lead to an apparent PFD shift between the two surfaces because it only involved traversal of a horizontal corner. Following this traversal, the animal was required to move across the 90° inside corner from the inside wall to the front face of the apparatus, where we expected a 90° CW shift in the cell's PFD (within the reference frame of a video camera pointed at each of the vertical walls), according to the dual-axis model. From the front wall, the animal then locomoted across an outside corner to the left vertical face and, finally, across a horizontal corner to the top of the apparatus (start box→inside wall→front face→left face→top). We recorded 27 HD cells across 19 sessions using this procedure. PFD shifts between the start box and the inside wall were strongly concentrated around 0° (V test, u = 5.92, n = 19, p < 0.001; mean shift: −7.87 ± 0.25°). Movement from the inside wall across an inside vertical corner to the front face of the apparatus resulted in a −82.73 ± 0.35° (CW) PFD shift that was concentrated around −90° (V test, u = 5.75, n = 19, p < 0.001). This shift was the opposite of the 90° (CCW) PFD shift that could be expected for traversal of an outside vertical corner. Traversal of a second vertical corner onto the left face of the cube (left outside corner) resulted in a 95.98 ± 0.38° (CCW) PFD shift that was concentrated around 90° (V test, u = 5.68, n = 19, p < 0.001). Movement across a final outside horizontal corner to the top of the cube resulted in a PFD shift concentrated near 0° (V test, u = 5.57, n = 19, p < 0.001; mean shift: −7.63 ± 0.42°). PFDs on top of the apparatus were similar to the PFDs from the start box (V test, u = 5.97, n = 19, p < 0.001; mean shift: −2.13 ± 0.24°; Fig. 9A–B). Thus, HD cells shift their PFDs following traversal of inside vertical corners in a direction opposite of their shift following traversal of outside vertical corners. In addition, we found no differences in concentration parameters among PFD shifts following active locomotion across outside 90° corners, inside 90° corners, and the 45° corner in light conditions (χ₍₂₎²: 0.11, p > 0.05), indicating that the HD system processes all of these transitions similarly.

This experiment was also run in the dark to determine whether HD cell PFD shifts across an inside vertical corner are dependent upon visual cues. This involved 11 unique HD cells recorded across nine sessions (n = 4 rats). As in the light session, there was an ∼0° PFD shift between the start box and the inside wall (V test, u = 4.15, n = 9, p < 0.001; mean shift: −2.65 ± 0.20°). Subsequent movement across the inside vertical corner to the front face of the cube resulted in a −83.06 ± 0.33° (CW) PFD shift that was concentrated around −90° (V test, u = 3.98, n = 9, p < 0.001). Movement across an outside vertical corner to the left face of the apparatus was accompanied by an 86.66 ± 0.25° (CCW) PFD shift that was concentrated around 90° (V test, u = 4.10, n = 9, p < 0.001), whereas traversal of the final horizontal corner to the top of the cube resulted in a −1.08 ± 0.28° (CW) PFD shift that was concentrated around 0° (V test, u = 4.07, n = 9, p < 0.001). PFDs on top of the box were in alignment with the PFDs in the start box (V test, u = 4.20, n = 9, p < 0.001; mean shift: 0.01 ± 0.14°; Fig. 9C,D). These results suggest that visual cues are not necessary for properly updating HD cell firing properties following traversal of an inside vertical corner. Unlike the one-wall and two-wall sessions, there was no significant difference in concentration parameters between light and dark conditions during any corner traversal, suggesting that HD cell responses during this experiment were robust to the absence of visual cues.

Influence of transition orientation on HD cell PFD shifts

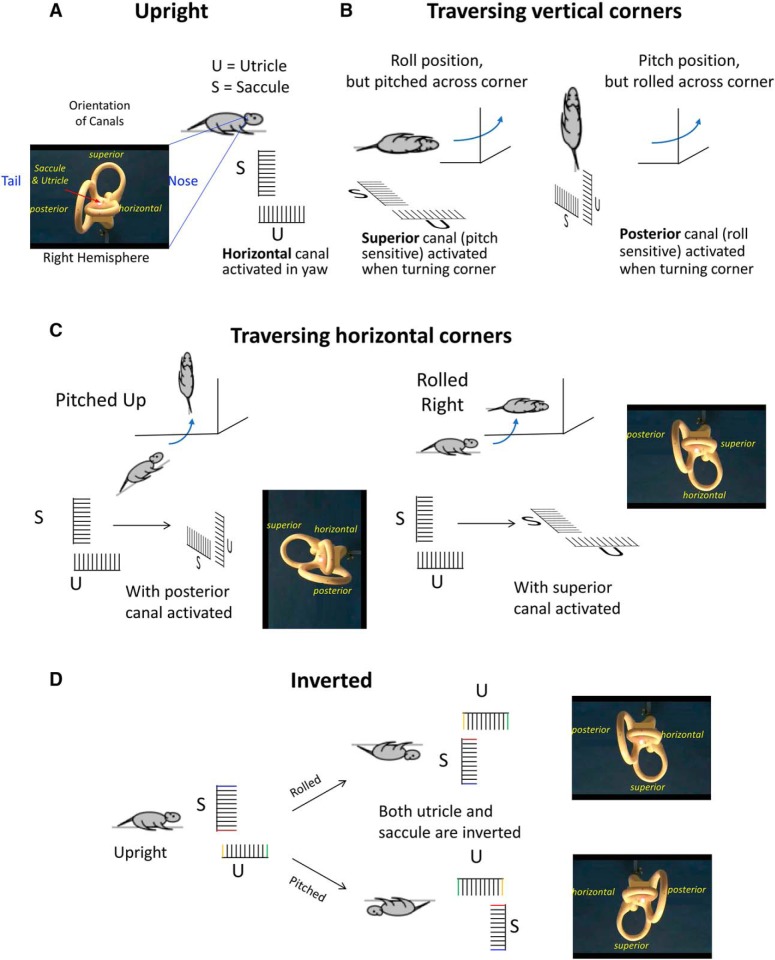
We next considered the impact of an animal's orientation as it traverses a vertical corner. The rats in the current study tended to move across corners between adjacent vertical surfaces using one of two techniques: (1) pitching, or maintaining an Earth-horizontal orientation during the transition; and (2) rolling, or maintaining an Earth-vertical orientation during the transition. Pitching across a corner would require the rats to tilt themselves forward onto the adjacent vertical surface, which should preferentially activate the superior semicircular canals. Alternately, rolling across a corner would require the rats to tilt themselves sideways (left for leftward movement and right for rightward movement), preferentially activating the posterior semicircular canals. Differences in HD PFD shifts following either pitch or roll transitions could suggest that one set of canals is better equipped to detect the traversal of horizontal corners. To address this question, we compared absolute PFD shifts across all active 90° vertical corner traversals according to whether the traversal was accomplished by pitching or rolling. Although animals sometimes used combinations of pitch and roll during their corner traversals, one was usually dominant, and as such, a “pitch” or “roll” designation could be assigned to 121 separate corner traversals. Of these, 96 were pitch transitions (mean absolute PFD shift: 85.70 ± 21.32°) and 25 were roll transitions (mean absolute PFD shift: 77.29 ± 19.12°). There was no significant difference in absolute PFD shifts between the two types of transitions (Welch's t test, t₍₁₁₉₎ = 1.88, p > 0.05), suggesting that both sets of semicircular canals are equally capable of processing vertical corner traversals.

Individual differences among animals

One rat consistently showed HD cell PFD shifts that were not aligned with those of the other 16 animals, with no straightforward way to relate the properties of this animal's HD cells to either the dual-axis or rotational plane hypothesis. One major inconsistency is that, although there was never a significant PFD shift for this rat's HD cells between the start box and the front face of the cube [one-wall sessions (n = 7), mean shift: −22.38 ± 0.29°, r = 0.96; two-wall sessions (n = 8), mean shift: −13.88 ± 0.20°, r = 0.98; three-wall sessions (n = 3), mean shift: −5.30 ± 0.06°, r = 1.00; two-wall passive sessions (n = 5), mean shift: −5.68 ± 0.21°, r = 0.98; two-wall rotation sessions (n = 5), mean shift: −14.28 ± 0.29°, r = 0.96], a shift always occurred following traversal of the final horizontal corner onto the top of the cube that caused the PFDs on top of the cube to be rotated ∼−90° (CW) relative to the PFDs in the start box [one-wall sessions (n = 7), mean shift: −70.56 ± 0.64°, r = 0.80; two-wall sessions (n = 8), mean shift: −80.38 ± 0.22°, r = 0.98; three-wall sessions (n = 3), mean shift: −82.68 ± 0.19°, r = 0.98; two-wall passive sessions (n = 5), mean shift: −84.65 ± 0.27°, r = 0.96; two-wall rotation sessions (n = 5), mean shift: −78.43 ± 0.25°, r = 0.97; box-to-wall passive sessions (n = 4), mean shift: −74.54 ± 0.11°, r = 0.99]. These responses suggest that the animal was misoriented when it was on the cube top compared with when it was in the start box. In addition, for this same rat, movement across a 90° vertical corner to the left consistently led to substantial under-rotation (i.e., CCW shifts <90°) of the HD cells' PFDs [two-wall left sessions (n = 4), mean shift: 33.61 ± 0.24°, r = 0.97; three-wall sessions (n = 3), mean shift: 35.70 ± 0.16°, r = 0.99; two-wall passive left sessions (n = 2), mean shift: 39.62 ± 0.04°, r = 1.00; two-wall leftward rotation sessions (n = 2), mean shift: 11.48 ± 0.11°, r = 0.99; box-to-wall passive left sessions (n = 2), mean shift: 31.74 ± 0.22°, r = 0.98], whereas movement across a 90° vertical corner to the right generally led to an over-rotation (i.e., CW shifts >90°) of the HD cells' PFDs [two-wall right sessions (n = 4), mean shift: −99.38 ± 0.41°, r = 0.92; three-wall sessions (n = 3), mean shift: −106.43 ± 0.10°, r = 0.99; two-wall passive right sessions (n = 3), mean shift: −128.35 ± 0.17°, r = 0.98; two-wall rightward rotation sessions (n = 2), mean shift: −82.47 ± 0.28°, r = 0.96; box-to-wall passive right sessions (n = 2), mean shift: −114.00 ± 0.02°, r = 1.00]. Overall, there seems to have been over-rotation during CW rotations and under-rotation during CCW rotations, in addition to the aberrant 90° CW PFD shift on the top surface of the cube, none of which is readily explained by either model of HD cell firing.

HD cells from other animals generally followed the dual-axis hypothesis across all corner traversals, though there were occasionally aberrant shifts, particularly in the dark. For example, in the one-wall dark sessions, three cells displayed PFD shifts >45° between the start box and top of the cube (Fig. 3D). These same three cells showed similar >45° PFD shifts between the start box and top of the cube in two-wall sessions in the dark (Fig. 4F). Importantly, these cells did not shift their PFDs between the start box and the top of the cube during either one-wall or two-wall sessions under light conditions (Figs. 3B, 4C), suggesting that the lack of visual cues during dark sessions caused these animals to become misoriented upon reaching the top of the cube, and that at least in some cases, visual cues are important for correctly integrating horizontal and vertical rotations of an animal's plane of locomotion during traversal of 3D paths.

Additional HD cell properties

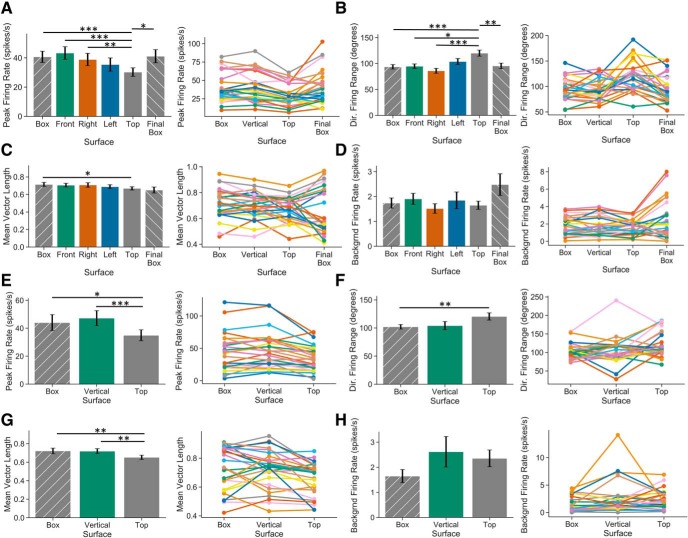
We next asked how other HD cell firing properties are influenced by navigation in 3D, focusing on three major questions: (1) whether HD cells show different firing properties on vertical and horizontal surfaces (i.e., tilt tuning); (2) whether HD cells show different firing properties on vertical surfaces oriented differently in the Earth-horizontal plane (i.e., left vs right vs front wall); and (3) whether HD cells show different firing properties on horizontal surfaces at different elevations (i.e., start box vs top of cube). We analyzed four separate firing properties of HD cells to address these issues: (1) PFR, or the firing rate of the HD cell at its PFD; (2) directional firing range, or the angular range over which the cell's firing rate was elevated above its background firing rate; (3) background firing rate, or the HD cell's firing rate outside of its directional firing range; and (4) mean vector length, a measure of the HD cell's tuning strength. We compared each of these firing properties across the start box, front wall, left wall, right wall, top of the apparatus, and final start box recordings, only including cells recorded on all six surfaces under light conditions so that paired comparisons could be made. This analysis included 26 unique HD cells and is summarized in Figure 10. Because each HD cell could be recorded multiple times on each surface, we took the average value of each firing property for each surface, such that each cell had only one value (e.g., one PFR) for each surface.

Figure 10.

Additional firing properties of HD cells during 3D locomotion. A, Bar plot and individual cell plots showing peak firing rates for HD cells recorded during locomotion on horizontal and vertical planes under light conditions. Values were generally lower on the top of the cube apparatus compared with the other surfaces. B, Same as A but for directional firing range. Tuning ranges were generally wider on the top of the cube compared with the other surfaces. C, Same as A but for mean vector lengths. Mean vector lengths were higher in the start box than the top of the cube. D, Same as A but for background firing rate. E–H, Same as A–D but in dark sessions. Error bars show SEM. ***p < 0.001; **p < 0.01; *p < 0.05.

A repeated-measures ANOVA demonstrated that PFRs differed across planes of locomotion (F_(5,125) = 5.10, p < 0.01). Importantly, however, post hoc analyses revealed no differences in PFR between the start box and any of the vertical faces (Fig. 10A). In contrast, there was a significant decrease in PFR on the top of the cube (mean PFR: 30.28 ± 14.52 spikes/s) compared with the start box (paired t test, t₍₂₅₎ = −6.83, p < 0.001, d = −0.61; mean start box PFR: 40.69 ± 19.24 spikes/s), the front vertical face of the cube (paired t test, t₍₂₅₎ = −7.30, p < 0.001, d = −0.71; mean front PFR: 43.30 ± 21.65 spikes/s), and the right vertical face (paired t test, t₍₂₅₎ = −4.20, p < 0.01, d = −0.47; mean right PFR: 38.86 ± 21.15 spikes/s). There was not a significant difference between the left face of the cube (mean left PFR: 35.43 ± 22.66 spikes/s) and the top. Importantly, PFRs increased relative to the top of the cube when the animals were placed back into the start box for a final recording session (paired t test, t₍₂₅₎ = 3.31, p < 0.05, d = 0.58; mean final box PFR: 41.12 ± 22.43 spikes/s), and there was no significant difference in PFRs between the start box and final box sessions (paired t test, t₍₂₅₎ = −0.14, p > 0.05), suggesting that the reduced firing rates on top of the cube were not due to reduced cell isolation over time. Of 26 cells, 24 showed reduced PFRs on top of the cube compared with the initial start box session, with PFRs for all cells decreasing by 24.79 ± 14.63%. Overall, these differences suggest that, whereas HD cells tend to show consistent PFRs from a low horizontal plane to several vertical planes, they decrease their PFRs during locomotion on an elevated horizontal plane.

Similar results were found regarding directional firing range (Fig. 10B), with a repeated-measures ANOVA showing a significant difference across planes (F_(5,125) = 9.22, p < 0.001). Post hoc analyses revealed no difference between the start box and vertical faces, or among the vertical faces themselves. However, there was a significant increase in directional firing range on top of the apparatus (mean firing range: 120.03 ± 29.29°) compared with the start box (paired t test, t₍₂₅₎ = 5.46, p < 0.001, d = 1.02; mean start box firing range: 93.65 ± 21.30°), the front vertical face of the cube (paired t test, t₍₂₅₎ = 3.43, p < 0.05, d = 0.96; mean front firing range: 94.78 ± 22.10°), and the right vertical face (paired t test, t₍₂₅₎ = 5.31, p < 0.001, d = 1.25; mean right firing range: 85.93 ± 24.09°). There was not a significant difference between the left face (mean firing range: 103.75 ± 29.54°) and the top of the cube. Firing ranges narrowed in the final box session compared with the top (paired t test, t₍₂₅₎ = 4.28, p < 0.01, d = 0.86; mean final box firing range: 95.40 ± 26.88°) and were not different from those in the initial start box session (paired t test, t₍₂₅₎ = 0.536, p > 0.05). Of 26 cells, 22 showed increased firing ranges on the top compared with the initial start box session. Overall, these data suggest that HD cell directional firing ranges were widened on top of the apparatus compared with the lower start box and the vertical cube faces. This result may explain the reduced PFR on the cube top if the cells were firing over a wider range of HDs. Further, the combination of a wider directional firing range with a decrease in PFR on top of the cube suggests that there could be weaker tuning (and therefore lower mean vector lengths) on top of the cube compared with the other planes of locomotion. In agreement with this, a repeated-measures ANOVA revealed significant differences in mean vector length among the planes of locomotion (F_(5,125) = 2.69, p < 0.05; Fig. 10C). However, mean vector lengths were only found to be decreased on top of the cube (mean vector length: 0.67 ± 0.09) compared with the start box (paired t test, t₍₂₅₎ = −3.67, p < 0.05, d = 0.42; start box mean vector length: 0.71 ± 0.11). A repeated-measures ANOVA also suggested that background firing rates differed across planes (F_(5,125) = 3.46, p < 0.05), but post hoc testing revealed no significant pairwise differences (Fig. 10D).

Similar results were found for dark sessions. Because there were few HD cells recorded on all surfaces in darkness, and because final box sessions were only recorded under light conditions, we limited the dark analyses to comparing the firing properties among the start box, pooled vertical surfaces, and the top of the cube. This analysis used data from 26 separate HD cells. As with light conditions, a repeated-measures ANOVA showed a significant difference in PFR among the different surfaces (F_(2,50) = 12.06, p < 0.001; Fig. 10E). Post hoc analyses revealed no difference between the start box and vertical surfaces, but PFRs were significantly decreased on the cube top compared with the start box (paired t test, t₍₂₅₎ = 3.16, p < 0.05, d = 0.37; mean start box PFR: 44.02 ± 28.71 spikes/s; mean cube top PFR: 34.94 ± 19.63 spikes/s), as well as the vertical faces (paired t test, t₍₂₅₎ = 4.21, p < 0.001, d = 0.51; mean vertical PFR: 47.19 ± 27.32 spikes/s). Differences were also found for directional firing range (repeated-measures ANOVA, F_(2,50) = 4.21, p < 0.05), although the firing range was only widened on top of the cube compared with the start box (paired t test, t₍₂₅₎ = −3.56, p < 0.01, d = −0.68; mean start box firing range: 102.10 ± 20.31°; mean top firing range: 120.42 ± 32.67°) but not the vertical faces (mean vertical firing range: 104.08 ± 36.93°; Fig. 10F). Differences were also found regarding mean vector length (repeated-measures ANOVA, F_(2,50) = 8.30, p < 0.001), with a decrease on top of the cube compared with the start box (paired t test, t₍₂₅₎ = 3.78, p < 0.01, d = 0.52; start box mean vector length: 0.72 ± 0.15; cube top mean vector length: 0.65 ± 0.11) as well as the vertical surfaces (paired t test, t₍₂₅₎ = 3.67, p < 0.01, d = 0.52; vertical mean vector length: 0.72 ± 0.15), but with no difference between the start box and vertical surfaces (Fig. 10G). No significant differences were found among the different surfaces in terms of background firing rate (Fig. 10H). These results are generally consistent with those found under light conditions, suggesting that the observed differences were not a result of different visual stimuli available on top of the cube compared with the other surfaces. The reason for the reduced PFR is unclear, although it could be attributed to less accurate directional tuning (PFD), which would be consistent with an increase in the directional firing range and an overall decrease in mean vector length.

Discussion

The results of our study provide strong evidence for the dual-axis model of HD cell firing (Page et al., 2018), such that HD cells shift their PFDs in response to both (a) azimuthal changes in the animal's plane of locomotion (yaw rotations) and (b) changes in the orientation of the animal's D–V axis relative to the gravity vector. Whereas locomotion across a horizontal corner results in HD cell firing that could appear to depend upon yaw rotations only (i.e., the rotational plane hypothesis), movement across a vertical corner results in a PFD shift that unambiguously depends upon the animal's orientation with respect to gravity. On a cuboidal apparatus with 90° vertical corners, locomotion between adjacent (perpendicular) walls results in a corresponding 90° shift in the PFDs of HD cells (in a local reference frame), whereas a 180° difference in PFDs can be observed during locomotion on opposite vertical faces. These shifts can also be observed during locomotion in darkness, suggesting that visual cues are not necessary for updating the HD cell representation of the animal's orientation in Earth azimuth. Motor information is also not required, as passive movement across vertical and horizontal corners as well as rotation of the entire local environment still result in an appropriate shift in HD cell PFDs according to the animal's orientation in the Earth-horizontal plane. Locomotion across an inside vertical corner and a 45° vertical corner both resulted in predictable PFD shifts that can be explained by the dual-axis model.

Dual-axis versus rotational plane models: local and global reference frames

The current study adds to previous investigations of HD cell firing in 3D (Stackman et al., 2000; Calton and Taube, 2005; Taube et al., 2013; Page et al., 2018) by demonstrating how HD cells update their PFDs during active locomotion across multiple adjacent horizontal and vertical planes, particularly traversal of vertical corners. The PFD shift observed following vertical corner traversal corresponded directly to a rotation of the animal's D–V axis about the gravity vector, suggesting that HD cells not only respond to yaw rotations within the local plane of locomotion but also keep track of the animal's orientation relative to the global gravity signal. HD cells therefore reference both local and global reference frames in establishing and shifting their directional representations, providing support for the dual-axis model as opposed to the rotational plane hypothesis. The dual-axis model accurately predicted PFD shifts across all types of vertical corner traversals, including active locomotion across 90° outside corners, 90° inside corners, and 45° outside corners, as well as multiple types of passive movement across 90° outside corners. The rotational plane hypothesis would not have predicted any PFD shifts following these traversals and, therefore, does not accurately fit the results of this study. These shifts were not purely visually driven, as locomotion in the dark resulted in comparable PFD shifts to locomotion in the light, and they were not fully reliant upon motor cues, as passive movement across both vertical and horizontal corners (as well as rotation of the entire cube apparatus) resulted in similar PFD shifts. These findings point to a vestibular, as well as proprioceptive, basis for computing an animal's current orientation in the Earth-horizontal plane.

It remains an open question exactly how or where these computations take place in the rat brain, although cells tuned to an animal's orientation relative to the gravity vector have been described in the primate cerebellum (Yakusheva et al., 2007; Laurens et al., 2013) and anterior thalamus (Laurens et al., 2016), whereas tilt tuning has been observed among cells in the bat presubiculum (Finkelstein et al., 2015). Tilt tuning in the latter two studies was restricted mostly to pitch, with few roll-modulated neurons observed. Some pitch tuning has also been observed in the rat lateral mammillary nucleus (Stackman and Taube, 1998), which is thought to convey vestibular signals to the ADN that are necessary for maintenance of the HD signal (Blair et al., 1998; Bassett et al., 2007). However, it seems unlikely that the ADN HD cells recorded in our study possessed tuning to tilt, as their firing rates were similar during locomotion on the vertical walls compared with the start box. Whereas the current study focused on HD cell responses during locomotion on horizontally and vertically oriented planar surfaces, further experiments will be necessary to elucidate the firing properties of HD cells during movement through volumetric space, as recently investigated in hippocampal place cells (Grieves et al., 2020).

Vestibular processing of 3D orientation

Based on the dual-axis rule, cells shift their PFDs when traversing vertical corners, but not horizontal corners. How does the brain determine whether an animal is traversing a horizontal or vertical corner? The yaw-based (local plane) HD signal is thought to rely upon the activity of hair cells in the horizontal semicircular canals, which are particularly sensitive to yaw rotations regardless of an animal's orientation in 3D space (Shinder and Taube, 2019). However, changes in orientation relative to the gravity vector are thought to be detected directly through inputs from the otolith organs (Angelaki, 1992), through a combination of otolith and semicircular canal signals (Angelaki et al., 1999), or through a full internally generated model of orientation in 3D space that integrates multiple self-motion cues (Laurens et al., 2011). The use of otolith signals alone would seem to introduce ambiguities during vertical corner traversal in the current study, as the orientations of the otolith organs with respect to the gravity vector should not change as the animal moves between differently oriented Earth-vertical planes (Fig. 11A). It has been demonstrated in macaques that semicircular canal activity can be used to correct for similar otolith ambiguities (Angelaki et al., 1999). Applied to the current study, if an animal pitches across the vertical corner to the adjacent wall, hair cells in the superior semicircular canals are primarily activated, whereas rolling across the vertical corner would cause activation primarily in the posterior semicircular canals (Blanks and Torigoe, 1989). In both cases, there is no accompanying change in the otolith signal. Nonyaw rotation at an angle oblique to pure pitch or roll will cause a unique combination of activation in these canals. Thus, whereas pure otolith signals might be ambiguous during movement across vertical corners, inputs from the semicircular canals might help to resolve the confusion and correctly update the HD cell system. In contrast, movement across a horizontal corner should cause simultaneous changes in both otolith and canal signals that are unambiguous (Fig. 11B). This difference in whether an activated canal signal is accompanied by a change in the otolith signal (in the case of traversing horizontal corners, but not vertical corners) would aid in distinguishing the corner type the animal is traversing (vertical vs horizontal). In the situation where the animal is inverted (Fig. 11C), both otoliths are inverted and together generate a much different signal than when the animal is upright or goes around corners. This condition may account for the findings that the HD signal loses its direction-specific firing when the animal is inverted (Calton and Taube, 2005; Gibson et al., 2013).

Figure 11.

Distinguishing horizontal versus vertical corners. A, Upright position showing orientations of utricle, saccule, and semicircular canals. B, Traversing vertical corners. Left, Rat is shown in an upright position with associated orientations for the utricle and saccule. Middle, Right, Rat traversing vertical corner from pitch (middle) or roll (right) orientations. In the former condition only, primarily the superior semicircular canal is activated, whereas in the latter condition, primarily the posterior semicircular canal is activated when traversing the corner. In both conditions, there is no change in the orientation of either the utricle or saccule. C, Traversing horizontal corners. When traversing the corner from a pitch orientation (left), the posterior canal is activated, whereas traversing the corner from the roll orientation (right) activates the superior canal. Note that in contrast to traversing vertical corners, in both situations the canal activation is accompanied by a change in otolith orientation. D, Inverted condition. In this situation, the orientation of both the utricle and the saccule are changed compared with the upright orientation. The precise orientation of the otoliths depends on whether the rat pitched or rolled into the inverted orientation. However, for both situations, not only does the utricle become inverted, but the orientation of the saccule is also reversed—in the upright position, gravity would pull the blue hair cell cilia toward the red hair cell, whereas in the inverted condition, gravity would pull the red hair cell cilia toward the blue hair cell.

Commutativity of HD cell responses

A major issue addressed by this study is that of commutativity in HD cell properties. Rotations in three dimensions are not commutative (e.g., a pitch, roll, and yaw rotation in a certain sequence will produce a different final orientation if that sequence is reordered; Tweed et al., 1999; Jeffery et al., 2015). Likewise, a rat's movement from the floor to the top of the cube apparatus, assuming no yaw rotations during locomotion, will result in the rat being at different orientations in the Earth-horizontal plane at the top of the cube, depending on the route it took to the top. For example, the blue route in Figure 1C,D would result in the animal looking north at the top of the cube, whereas the white route would result in the animal looking west. If HD cells followed the same rules that 3D rotations do in physical space (i.e., if HD cells rotated their PFDs along with the plane of locomotion and did not maintain a reference to Earth azimuth), then they would have different PFDs at the top of the cube, depending on the animal's route. Thus, HD cell PFDs would be globally inconsistent. If this were the case, HD cells could do one of two things upon reaching the top of the cube from different trajectories: (1) maintain their shifted PFDs and ignore their original Earth-horizontal orientation preferences, or (2) “snap” back to their original PFDs relative to the gravity vector. The first explanation seems unlikely because it would cause inconsistencies in the HD system and potentially be detrimental to navigation in the global environment (e.g., the animal might think it is rotated 90° from its actual orientation). The second explanation also seems unlikely, as a continuous attractor, such as the one thought to generate the HD signal (Skaggs et al., 1995; Zhang, 1996; Redish et al., 1996), is not well equipped for sudden jumps. A dual-axis explanation is attractive because it solves both problems, keeping the HD signal globally consistent and commutative while avoiding sudden jumps in the attractor. Our results demonstrate that maintaining a constant reference to gravity ensures that the HD signal is commutative during 3D navigation.

Passive movement

One area where our results differ from previous studies is in the passive movement paradigm. The current study demonstrated that passive movement from the start box to a side wall of the cube, passive movement from the front wall to the side wall of the cube, and rotation of the entire cube 90° about the gravity axis all caused a corresponding 90° shift in HD cell PFDs that kept their responses anchored to the Earth-horizontal plane. In contrast, in the previously discussed Taube et al. (2013) study, passive movement of the animal onto a vertical wall resulted in HD cells adopting a local reference frame (the vertical platform itself) regardless of the position of the wall in the room. For example, a cell that fired preferentially on the wall when the animal looked up would always fire up when the animal was passively placed onto the wall, even if the wall was moved to the opposite side of the room and rotated 180° about the gravity vector, essentially ignoring this rotation. This response suggests a potential cognitive or task-related component to the use of local or global reference frames by HD cells where the global 3D reference frame can be over-ridden by local landmark cues. Differences in the training protocols between these two studies may contribute to which reference frame was used. In this case, the task at hand or salient features of the local environment, such as geometric, tactile, or visual cues associated with the vertical platform, over-rode information derived from the internally based system to update HD cell representations. The results of the current study contrast with these previous results, as a dual-axis updating rule was always used by the animals' HD cells, regardless of active or passive movement across corners.

Summary

Overall, this study demonstrates that HD cells maintain a constant reference to both gravity and the current plane of locomotion in determining their PFDs. Remaining anchored to gravity allows HD cells to maintain global consistency and commutativity in their representations, whereas responding to yaw rotations allows them to provide navigationally relevant directional information in situations where an animal's orientation in the Earth-horizontal plane is less useful (i.e., locomotion on an Earth-vertical plane). Vestibular and proprioceptive cues are likely to drive these computations, though the precise neural underpinnings of these interactions remain to be elucidated. Nonetheless, it is clear that the gravity vector plays a critical role in shaping a cell's PFD, and that the dual-axis model accounts for how HD cell PFDs respond in 3D when activity is not being over-ridden by a local reference frame. This process equips the head direction system to support complex 3D navigation. Finally, the invariant nature of peak firing rates across the different surfaces indicates that it is unlikely that tilt orientation modulates the firing rates of ADN HD cells.