A transition of ω-Fe₃C → ω′-Fe₃C → θ′-Fe₃C in Fe-C martensite

Abstract

Carbon steel is strong primarily because of carbides with the most well-known one being θ-Fe₃C type cementite. However, the formation mechanism of cementite remains unclear. In this study, a new metastable carbide formation mechanism was proposed as ω-Fe₃C → ω′-Fe₃C → θ′-Fe₃C based on the transmission electron microscopy (TEM) observation. Results shown that in quenched high-carbon binary alloys, hexagonal ω-Fe₃C fine particles are distributed in the martensite twinning boundary alone, while two metastable carbides (ω′ and θ′) coexist in the quenched pearlite. These two carbides both possess orthorhombic crystal structure with different lattice parameters (a_θ′ = a_ω′ = a_ω = $\sqrt{2}$a_α-Fe = 4.033 Å, b_θ′ = 2 × b_ω′ = 2 × c_ω = $\sqrt{3}$a_α-Fe = 4.94 Å, and c_θ′ = c_ω′ = $\sqrt{3}$a_ω = 6.986 Å for a_α-Fe = 2.852 Å). The θ′ unit cell can be constructed simply by merging two ω′ unit cells together along its b_ω′ axis. Thus, the θ′ unit cell contains 12 Fe atoms and 4 C atoms, which in turn matches the composition and atomic number of the θ-Fe₃C cementite unit cell. The proposed theory in combination with experimental results gives a new insight into the carbide formation mechanism in Fe-C martensite.

Introduction

The main phase constituents in carbon steels are ferrites (α-Fe) and carbides according to the equilibrium binary Fe-C phase diagram. Therefore carbides have long been considered as a critical phase in strengthening carbon steels. Among all the carbides, the most well-known one is θ-type Fe₃C cementite, which possesses orthorhombic crystal structure (space group Pnma) with its lattice parameter being a_θ = 4.524 Å, b_θ = 5.088 Å and c_θ = 6.741 Å^1,2. Although the θ-Fe₃C cementite has been studied extensively due to its importance and popularity in carbon steels^3–16, its formation mechanism remains unclear. This is particularly true for the θ-Fe₃C formation during martensitic transformation. One possible reason for this is its ultra-fine particle size, which makes it difficult for the normal characterization techniques to detect the earlier stage of the carbide formation.

Thus far, several types of carbides, which are thought to be the precursors of cementite, have been investigated^17–25. However, detailed crystal structural relationship between these carbides has not been explained yet. To explain the formation mechanism of the cementite in martensitic structure, a martensite decomposition mechanism (martensite → ε-Fe carbide → cementite) has been proposed previously during tempering at low temperature around 200 °C^23,26–29. However, most of the alloys used for studying carbide formation were ternary (such as Fe-Ni-C) alloys or other complex alloy systems, which may complicate the analysis and interpretation of carbide formation mechanism. In order to study the fundamental formation mechanism of cementite, the simple binary Fe-C is more appropriate.

Each unit cell of the θ-Fe₃C cementite with the formula Fe₃C contains 12 Fe atoms and 4 C atoms, leading to a ratio of Fe to C being 3^1,2,30. Interestingly, a recently discovered ω-Fe phase located in the martensite twin boundary has three iron atoms in its unit cell as well^31,32. If one interstitial carbon atom were to join this ω-Fe unit cell, the product would have the formula ω-Fe₃C. The possibility that there exists certain relationship between the ω-Fe₃C and θ-Fe₃C stimulates the investigation into the possible unknown carbides formed earlier than θ-Fe₃C cementite in the binary Fe-C system.

Metastable hexagonal ω-Fe₃C phase particles, which are 1 to 2 nm big in size, distribute only at the body-centered cubic (BCC) {112}<111>-type twinning boundary region in twinned high-carbon Fe-C martensite^33–40. It was observed by in-situ heating transmission electron microscopy (TEM) that these twinning boundary ω-Fe₃C particles eventually transformed into θ-Fe₃C carbides^41–44. However, the ω → θ transition speed is too fast for any details to be recorded. Thus, indirect approach is needed to figure out the formation mechanism of these metastable carbides that might exist in the quenched high carbon Fe-C alloys in which several types of ultra-fine carbides with pearlite-like structures have been observed^45,46. Furthermore, as mentioned above, it is difficult to characterize the crystal structures of ultra-fine carbides via tilting TEM specimens since their particle size is approximately 1–2 nm. Another difficulty comes from the co-existence of several types of fine carbides in localized region. This situation often causes superimposition of relevant selected area electron diffraction (SAED) patterns from several carbide phases.

Therefore, in this paper, we study the metastable carbides by comparative analysis of theoretical and experimental TEM data. The structural models of new carbides were built based on the hexagonal ω-Fe structure and their electron diffraction patterns were simulated using the commercial software, which is designed to simulate the crystal structure, including electron and X-ray diffraction patterns. Then, the calculated diffraction patterns were compared with the observed experimental results. It was confirmed that new kind of metastable carbide, θ′-Fe(C) with 12 Fe atoms and 4 C or less C atoms in its unit cell, existed in the quenched high carbon Fe-C alloys. This carbide has a quite similar crystal structure and the same chemical composition with that of the well-known cementite (θ-Fe₃C). Thus, understanding the formation mechanism of the θ′-Fe(C) will help us to explore the nature of θ-Fe₃C cementite.

Materials and experiment

A Fe-1.6 C (wt.%) binary ingot was prepared in Ar atmosphere within a high-vacuum induction furnace. The ingot was hot-forged into 20 mm-thick plates. Thin plates (approximately 10 mm × 10 mm × 1.0 mm) were then mechanically cut from the hot-forged plates and austenitized at 1150 °C for 30 mins under flowing Ar atmosphere, followed by quenching in water. TEM specimens were prepared from the water-quenched thin plates. The specimens were mechanically ground, polished, and finally ion-milled at room temperature. An ion-mill device (Fischione Model 1050 TEM Mill) was used to prepare the specimens at 4 kV. Sample microstructure was observed using a JEM 2000FX TEM operated at 200 kV. Electron diffraction patterns were calculated using the commercial CrystalMaker software. All electron diffraction patterns shown in the present work were calculated such that the spot intensity saturation was 100 in the software.

Results and discussion

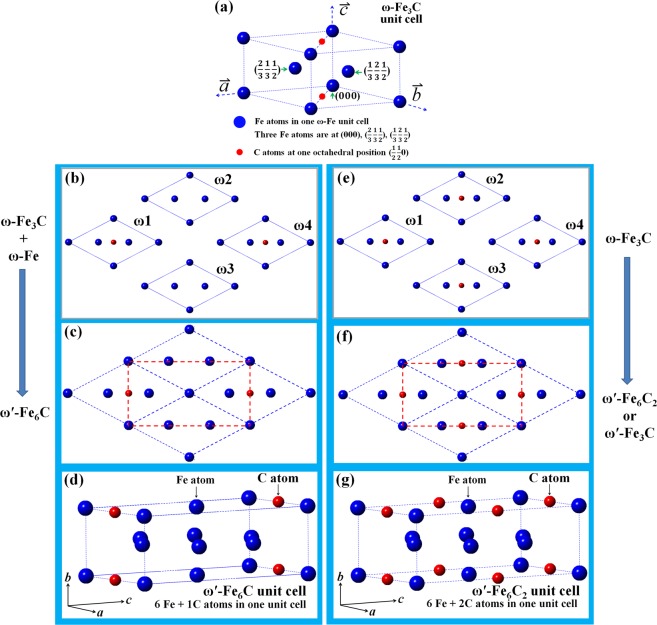
TEM observations revealed that ultra-fine ω-Fe₃C particles exist at twinning boundary region in twinned Fe-C martensite, and the ω-Fe₃C has a hexagonal crystal structure with lattice parameters of a = a_ω = $\sqrt{2}$a_α-Fe = 4.033 Å, c_ω = 1/2 × $\sqrt{3}$a_α-Fe = 2.47 Å for a_α-Fe = 2.852 Å^{31,33,35–38}. The ω-Fe₃C unit cell structure can be seen from Fig. 1(a).

Figure 1.

Atomic structure of various carbides. (a) Unit cell of ω-Fe₃C crystal structure. (b) Two ω-Fe₃C and two ω-Fe unit cells projected along their c axes. (c) Coarsening of the four unit cells of the ω-Fe₃C and ω-Fe in (b) results in the formation of new carbide (ω′-Fe₆C) outlined by red dashed lines. (d) The ω′-Fe₆C unit cell can have an orthorhombic structure and lattice parameters (a_ω′ = 4.033 Å, b_ω′ = 2.47 Å, and c_ω′ = 6.986 Å for a_α-Fe = 2.852 Å), and C atom at (0.5 0 0). (e) Four ω-Fe₃C unit cells. (f) Coarsening of the four ω-Fe₃C unit cell in (e) results in the formation of a new carbide (ω′-Fe₆C₂ or ω′-Fe₃C) with the same crystal structure and lattice parameters as the ω′-Fe₆C. (g) The ω′-Fe₆C₂ atomic structure in one unit cell.

ω′-variants

As an interstitial atom, the position of carbon atoms in crystals determines carbide structure. Two different coarsening behaviors of the ultra-fine ω-Fe₃C particles are illustrated in Fig. 1. Figure 1(a) shows the atomic structure of one ω-Fe₃C unit cell. The coarsening route (Fig. 1(b)) will generate a new kind of carbide, with its unit cell outlined by red dashed lines in Fig. 1(c). Its corresponding three-dimensional (3D) atomic structure is shown in Fig. 1(d). There are six iron atoms and one carbon interstitial atom in this unit cell, which has been designated as ω′-Fe₆C in our previous study⁴⁶. On the other hand, if the positions of two ω-Fe₃C (ω1, ω4) and two ω-Fe (ω2, ω3) in Fig. 1b exchange, the ω′-Fe₆C will has the carbon atom at (0 0 0.5) as shown in Fig. 2a. Obviously, ω′-Fe₆C has two forms because of the different carbon atom position as shown in Figs. 1d and 2a.

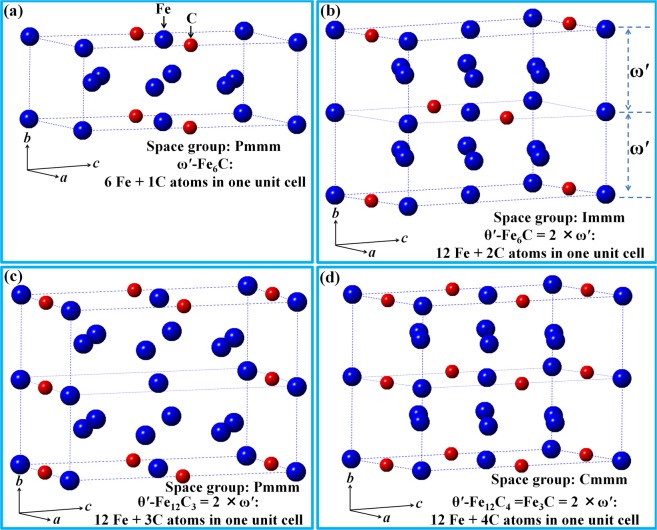
Figure 2.

Atomic structure of various carbides. (a) Unit cell of one ω′-Fe₆C variant with one C atom at (0 0 0.5). (b) New θ′ variant (θ′-Fe₁₂C₂ or θ′-Fe₆C) formed by merging the ω′-Fe₆C variant with one C atom at (0.5 0 0) (Fig. 1(d)) and the ω′-Fe₆C variant with one C atom at (0 0 0.5) in (a) along b axis. (c) New θ′ (θ′-Fe₁₂C₃ or θ′-Fe₄C) variant. (d) New θ′ variant of θ′-Fe₁₂C₄ or θ′-Fe₃C formed by doubling the ω′-Fe₆C₂ in Fig. 1(f) along b axis. All θ′ have an orthorhombic unit cell with lattice parameters of a_θ′ = 4.033 Å, b_θ′ = 2 × 2.47 Å = 4.94 Å, and c_θ′ = 6.986 Å for a_α-Fe = 2.852 Å).

When the coarsening of the ultra-fine ω-Fe₃C particles follows the route shown in Fig. 1(e–g), new carbide consisting of six iron atoms and two carbon atoms in its unit cell will form as shown in Fig. 1(g), with its formula being ω′-Fe₆C₂ or ω′-Fe₃C. There is no any difference in the calculated electron diffraction patterns between the ω′-Fe₆C₂ and ω-Fe₃C carbides since both carbide crystals have the exact same atomic positions. As can be seen in Fig. 1, the transformation of the ω-Fe₃C hexagonal structure to an orthorhombic structure depends on the carbon content and/or positons alone. Once the ordering of carbon atoms occurs, the orthorhombic structure can form in a spontaneous way. The electron diffraction spots associated with such an ordering has been observed in the ω′-Fe₆C carbide⁴⁶.

Since there is no obvious difference in the calculated electron diffraction patterns between ω-Fe₃C carbide and ω-Fe phase⁴⁵, the three phases (ω-Fe, ω-Fe₃C, ω′-Fe₆C₂ (ω′-Fe₃C)) would have similar electron diffraction patterns, which may cause difficulty in charactering the carbides experimentally. Simply speaking, there are three phases (hexagonal ω-Fe, orthorhombic ω-Fe₃C and ω′-Fe₆C₂ (ω′-Fe₃C)) present theoretically. However, it is difficult to distinguish among them since they show similar electron diffraction pattern experimentally. Formation of this new ω′-Fe₃C carbide can actually explain why the ultra-fine ω-Fe₃C particles never grow big in real materials. The ω-Fe₃C particle size is just only 1–2 nm.

The carbide coarsening can be achieved via the several fine ω-Fe₃C particles merged together. The driving force for the movement of fine ω-Fe₃C particles comes from the recrystallization of ultra-fine α-Fe matrix grains. There are two crystalline phases, namely fine α-Fe as a matrix grain and fine ω-Fe₃C particles at the α-Fe twinning boundaries that co-exist in the twinned martensitic structure. Thus, the coarsening behavior is actually controlled by the recrystallization process of the α-Fe matrix grains upon tempering. The α-Fe recrystallization results in a movement of the α-Fe grain boundaries and/or twinning boundaries, which promotes the ω-Fe₃C particles at the boundaries to move and meet other ω-Fe₃C particles. The coarsening behavior of the fine ω-Fe₃C particles and the recrystallization process of the ultra-fine α-Fe grains have been experimentally confirmed and explained in our previous work^{35,40,42–44}.

θ′-variants

Following the same coarsening mechanism explained in Fig. 1, new carbide, here designated as θ′, can be formed by combining two variants of ω′. The atomic structures of possible θ′ variants are shown in Fig. 2. Figure 2(a) shows one of the ω′ variants, while the other two ω′ variants are shown in Fig. 1(d,g). After two variants of ω′ merge together along its b axis, three θ′ variants (θ′-Fe₁₂C₂ or θ′-Fe₆C (Fig. 2(b)), θ′-Fe₁₂C₃ or θ′-Fe₄C (Fig. 2(c)), θ′-Fe₁₂C₄ or θ′-Fe₃C (Fig. 2(d))) can be formed. Thus, the θ′ carbides possess lattice parameter of a_θ′ = 4.033 Å, b_θ′ = 2 × 2.47 Å = 4.94 Å, and c_θ′ = 6.986 Å and retain an orthorhombic crystal structure. During the coarsening of fine ω′ particles, one ω′ particle with the crystal structure in Fig. 1(g) may combine with another ω′ particle with the same crystal structure along its b_ω′ axis. When this occurs, it is possible for a θ′-Fe₃C carbide particle to form.

The formation of θ′-Fe₁₂C₄ or θ′-Fe₃C variant involves merging two ω′-Fe₆C₂ or ω′-Fe₃C carbide particles together alone without any atomic movement or variation in carbon content. It can be seen from Figs. 1 and 2 that the position of both Fe and C atoms during the ω → ω′ → θ′ transition are kept unchanged, meaning that this transition depends completely on the size of the ω-Fe₃C carbide particle. The atomic positions of Fe and C atoms in the ω-Fe₃C, ω′-Fe₃C and θ′-Fe₃C unit cells have been listed in the Tables 1–3, respectively.

Table 2.

The fraction coordination of six Fe atoms and two C atom of ω′-Fe₃C in orthorhombic structure with the lattice parameters of a_ω′ = $\sqrt{2}$a_α-Fe = 4.033 Å_, b_{ω′ =} $\frac{\sqrt{3}}{2}$a_{α-Fe =} 2.47 _Å, c_ω′ = $\sqrt{6}$a_α-Fe = 6.986 Å for a_α-Fe = 2.852 Å. New variant of the ω′ carbide can be formed depending on the carbon concentration and positions.

Atoms	aω′	bω′	cω′
Fe1	0	0	0
Fe2	1/2	0	1/2
Fe3	1/2	1/2	1/6
Fe4	1/2	1/2	5/6
Fe5	0	1/2	1/3
Fe6	0	1/2	2/3
C1	1/2	0	0
C2	0	0	1/2

Table 1.

The fraction coordination of three Fe atoms and one C atom of ω-Fe₃C in hexagonal structure with the lattice parameters of a_ω = $\sqrt{2}$a_α-Fe = 4.033 Å_, c_{ω =} $\frac{\sqrt{3}}{2}$a_α-Fe = 2_.47 Å for a_α-Fe = 2.852 Å.

Atoms	aω	bω	cω
Fe1	0	0	0
Fe2	2/3	1/3	1/2
Fe3	1/3	2/3	1/2
C	1/2	1/2	0

Table 3.

The fraction coordination of twelve Fe atoms and four C atom of θ′-Fe₃C in orthorhombic structure with the lattice parameters of a_θ′ = $\sqrt{2}$a_α-Fe = 4.033 Å_, b_{θ′ =} $\sqrt{3}$a_α-Fe = 4.94 _Å, c_θ′ = $\sqrt{6}$a_α-Fe = 6.986 Å for a_α-Fe = 2.852 Å. Various variants are formed depending on the position and concentration of the intestinal carbon atoms.

Atoms	aθ′	bθ′	cθ′
Fe1	0	0	0
Fe2	1/2	0	1/2
Fe3	0	1/2	0
Fe4	1/2	1/2	1/2
Fe5	1/2	1/4	1/6
Fe6	1/2	1/4	5/6
Fe7	0	1/4	1/3
Fe8	0	1/4	2/3
Fe9	1/2	3/4	1/6
Fe10	1/2	3/4	5/6
Fe11	0	3/4	1/3
Fe12	0	3/4	2/3
C1	0	0	1/2
C2	1/2	0	0
C3	0	1/2	1/2
C4	1/2	1/2	0

As explained in Figs. 1 and 2, ω′ and θ′ can have other variants with lower carbon content than that in the ω′-Fe₆C₂ (ω′-Fe₃C) and θ′-Fe₁₂C₄ (θ′-Fe₃C) unit cells. The ω′ variant (ω′-Fe₆C) has been experimentally observed previously.⁴⁶ Fig. 3 shows the evidence that there exist other type θ′ variants in the quenched high carbon Fe-C alloys. Simulated electron diffraction pattern of the θ′-Fe₁₂C₃ carbide with its [100] zone axis parallel to the electron beam is shown in Fig. 3(a), while the corresponding experimental electron diffraction pattern is shown in Fig. 3(b). The experimental diffraction pattern is composed of two sets of diffraction spots. One set is from [011] α-Fe zone axis and the other is from the [100] zone axis of the θ′-Fe₁₂C₃ carbide as shown in Fig. 3(a). The mixed electron diffraction patterns of α-Fe and fine carbides are frequently observed in the quenched Fe-C alloy with pearlite structure since both phases have ultra-fine particles (the region selected for experimental observations depends on the selected aperture size in TEM equipment, the smallest diameter size of the aperture is about 250 nm).

Figure 3.

Electron diffraction patterns of the θ′ variants: (a) Simulated [100] zone axis pattern of the θ′-Fe₁₂C₃ carbide. (b) Experimental pattern consisting of the diffraction spots from the [011] α-Fe zone axis and [100] θ′-Fe₁₂C₃ carbide. (c) Experimental pattern consisting of three sets of diffraction spots: [011] α-Fe zone axis, [100] θ′-Fe₁₂C₃ carbide and [100] zone axis of [100] θ′-Fe₁₂C₂ carbide. (d) Simulated [100] zone axis pattern of the θ′-Fe₁₂C₂ carbide. (e) Simulated [110] zone axis pattern of the θ′-Fe₁₂C₃ carbide. (f) Experimental electron diffraction patterns consisting of the spots from the [012] α-Fe zone axis and [110] θ′-Fe₁₂C₃ carbide.

Figure 3(c) shows a particular experimental pattern, which is composed of three sets of diffraction spots: (1) the strong spots from [011] α-Fe zone axis as outlined by the yellow dashed lines, (2) the spots shown in Fig. 3(a), which is from [100] zone axis of the θ′-Fe₁₂C₃ carbide, and (3) the spots [100] zone axis of the θ′-Fe₁₂C₂ carbide as shown in Fig. 3(d). Experimental diffraction patterns are usually obtained from an area of several hundreds of nanometers in diameter. Thus, the diffraction pattern is composed of several sets of diffraction spots, which come from various carbides present in the pearlite-like region. Figure 3(e) shows the simulated electron diffraction patterns of the θ′-Fe₁₂C₃ carbide along its [110] zone axis. This pattern can also be observed experimentally along the α-Fe [012] zone axis as shown in Fig. 3(f).

The results in Fig. 3 reveal that various θ′ variants can co-exist in the quenched sample, and the formation of different type of variants is dependent on carbon concentration and positions. The possible variants of both θ′ carbides and ω′ carbides are summarized and listed in Table 4. Both ω′ and θ′ carbides possess orthorhombic crystal structure. The unit cell of θ′ carbides is composed of two ω′ unit cells merged along its b axis. The formation mechanism of θ′ carbides is the variation in carbon atoms or concentration on different atomic planes, which causes an ordering structure of ω-Fe. Since the carbon atoms or concentration are the same in (001) planes of ω′-Fe₆C₂ (ω′-Fe₃C) and θ′-Fe₁₂C₄ (θ′-Fe₃C) and the electron diffraction patterns of ω-Fe₃C, ω′-Fe₆C₂ (ω′-Fe₃C) and θ′-Fe₁₂C₄ (θ′-Fe₃C) are similar, no carbon-ordering diffraction spots could be observed. However, that is not to say the ω′-Fe₆C₂ (ω′-Fe₃C) or θ′-Fe₁₂C₄ (θ′-Fe₃C) does not exist in the sample.

Table 4.

The structural parameters and chemical composition of possible variants of the ω′ and θ′ carbides. The electron diffraction patterns of the ω′-Fe₆C₂ (ω′-Fe₃C) and θ′-Fe₁₂C₄ (θ′-Fe₃C) are the same with that of the ω-Fe₃C.

Metastable carbide	Variant composition	Notes
ω′, orthorhombic aω′ = 4.033 Å, bω′= 2.47 Å, cω′ = 6.986 Å	ω′-Fe6C	C atoms at different (001) atomic planes
	ω′-Fe6C
	ω′-Fe6C2 (ω′-Fe3C)
θ′, orthorhombic aθ′ = 4.033 Å, bθ′= 4.94 Å, cθ′ = 6.986 Å	θ′-Fe12C2 (θ′-Fe6C)	C concentration varies at different (001) atomic planes
	θ′-Fe12C3 (θ′-Fe4C)
	θ′-Fe12C4 (θ′-Fe3C)

θ-Fe₃C cementite

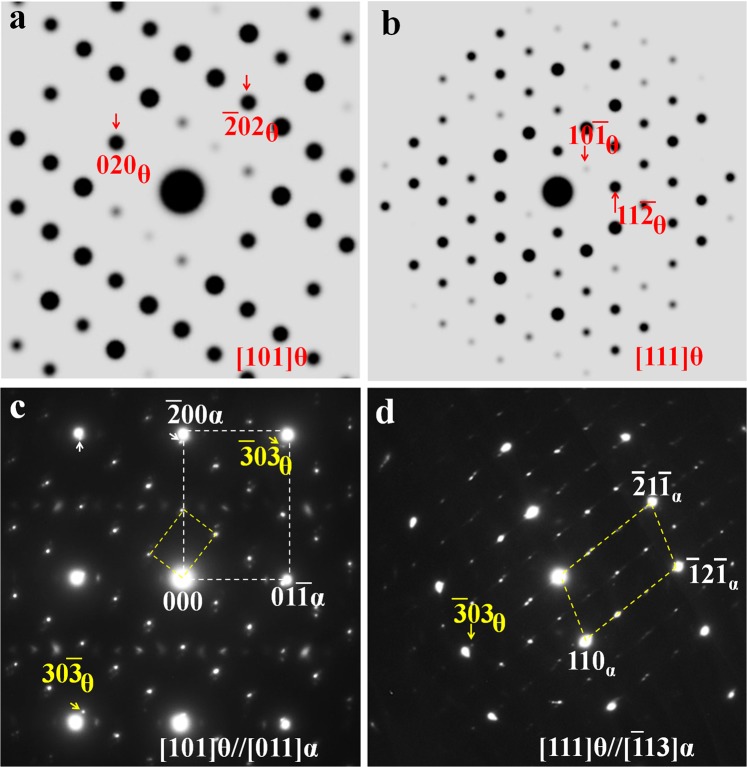
The diffraction patterns of θ-Fe₃C cementite from two different zone axes ([101]_θ in Fig. 4(a) and [111]_θ in Fig. 4(b)) are shown here in comparison with that of previous carbides (ω-Fe₃C, ω′-Fe₆C₂ (ω′-Fe₃C) or ω′-Fe₆C and various θ′-variants). It can be seen from Fig. 4(c), the experimental $\overline{3}$03_θ spot is completely separated from the α-Fe $\overline{2}$1 $\overline{1}$ spot, unlike the corresponding ω and ω′ or θ′ spots, which overlap perfectly with the corresponding α-Fe spots. This kind of separation can also be clearly observed in other direction as shown in Fig. 4(d). The results shown in Fig. 4 explain that the carbide with the well-known cementite structure has lost the perfect overlapping in diffraction spots compared with other carbides mentioned earlier.

Figure 4.

Simulated θ-Fe₃C electron diffraction patterns: (a) [101]θ and (b) [111]θ. The corresponding experimental patterns observed along the zone axes of (c) [011]α and (d) [113]α.

The electron diffraction patterns of ω-related carbide structures (ω, ω′, θ′ and θ) in quenched high-carbon binary Fe-C alloys are illustrated in Fig. 5. Figure 5(a–d) show the schematics of diffraction patterns based on the experimental results.^45,46 All these patterns are obtained from the same α-Fe [011] zone axis. The pattern shown in Fig. 5(a) can only be observed within twinned martensite (Fig. 5(e)). The pattern (Fig. 5(a)) reveals a complete overlapping between the 211 α and the 330 ω spots. In Fig. 5(b), the ω-Fe₃C diffraction pattern is converted into ω′-Fe₆C with an ordering pattern and the original three spots (1 $\overline{1}$0_ω, 2 $\overline{2}$0_ω and 3 $\overline{3}$0_ω) turn out to be six spots between the transmitted (central) and the 211 α diffraction spots. When two ω′-Fe₆C unit cells merge together to form a θ′-Fe₁₂C₃ variant with its b_θ′ = 2 bω_′, an extra row of diffraction spots would occur in reciprocal space as shown in Fig. 5(c). The corresponding diffraction pattern from θ-Fe₃C is shown in Fig. 5(d) for a comparison with that of the ω-Fe₃C-related carbides to show a crystal structural similarity among these carbides. The patterns shown in Fig. 5(b–d) are normally observed in quenched pearlite-like microstructure like that shown in Fig. 5(f). Not only can ω′ carbides be observed in the pearlite-like microstructure, but θ′ and θ fine carbides can also be observed in the same pearlite-like region. Nevertheless, it is difficult to differentiate these carbides based on particle size or morphology alone since all of them are several nanometers in size.

Figure 5.

Schematic electron diffraction patterns between α-Fe and the (a) ω, (b) ω′, (c) θ′, and (d) the θ-Fe₃C carbides. All patterns are along the [011]_α zone axis.(e) Dark field TEM image revealing the twinned structure, which corresponds to the ω existing region. (f) TEM bright field image showing the pearlite-like structure corresponding to the existing region of the ω′, θ′, and θ fine carbide region.

In experimental TEM observations, these three carbides (ω, ω′ and θ′) can be identified easily based on the superimposition of certain diffraction spots on 211 α-Fe. Once these carbides start to transform into the well-known θ-Fe₃C cementite, the separation of the 303 θ diffraction spots from 211 α-Fe spots can be clearly seen as shown in Fig. 5(d). Such a separation will produce complex diffraction patterns and cause difficulty in carbide characterization.

Conclusion

Ultra-fine carbides formed in quenched Fe-C alloys were investigated by comparing experimental results with simulated electron diffraction patterns.

1. Based on the unit cells of the ω′-Fe₃C and its variants, an orthorhombic θ′ carbide structure with lattice parameter of a = 4.033 Å, b = 4.94 Å, and c = 6.986 Å was constructed and experimentally confirmed. The θ′ carbide can be: θ′-Fe₁₂C₂ (or θ′-Fe₆C), θ′-Fe₁₂C₃ (or θ′-Fe₄C) and θ′-Fe₁₂C₄ (or θ′-Fe₃C) compounds.

2. A transition route (ω → ω′→ θ′) has been proposed during the coarsening of ultra-fine ω-Fe₃C particles to explain the formation mechanism of the θ′ carbide with various variants. The transition occurs accompanying the variation in the position and concentration of carbon atoms, while the position of Fe atoms is kept unchanged.

3. It was observed that the ω′, θ′ and θ metastable carbides with ultra-fine particle size co-existed in the pearlite-like microstructure of quenched high carbon Fe-C alloys.

Author contributions

D.H.P. contributed to the experimental work, the result analysis and manuscript writing. H.P.X. and H.C. contributed to the simulation work, L.L.G., K.Gao, and X.L. contributed to the sample preparation and discussion.

Competing interests

The authors declare no competing interests.