Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Mar 26;5(13):7182–7192. doi: 10.1021/acsomega.9b03623

Influence of Diesel Fuel Viscosity on Cavitating Throttle Flow Simulations under Erosive Operation Conditions

Marco Cristofaro †,‡,*, Wilfried Edelbauer †, Phoevos Koukouvinis ‡, Manolis Gavaises ‡
PMCID: PMC7143437  PMID: 32280858

Abstract

graphic file with name ao9b03623_0017.jpg

This work investigates the effect of liquid fuel viscosity, as specific by the European Committee for Standardization 2009 (European Norm) for all automotive fuels, on the predicted cavitating flow in micro-orifice flows. The wide range of viscosities allowed leads to a significant variation in orifice nominal Reynolds numbers for the same pressure drop across the orifice. This in turn, is found to affect flow detachment and the formation of large-scale vortices and microscale turbulence. A pressure-based compressible solver is used on the filtered Navier–Stokes equations using the multifluid approach; separate velocity fields are solved for each phase, which share a common pressure. The rates of evaporation and condensation are evaluated with a simplified model based on the Rayleigh–Plesset equation; the coherent structure model is adopted for the subgrid scale modeling in the momentum conservation equation. The test case simulated is a well-reported benchmark throttled flow channel geometry, referred to as “I-channel”; this has allowed for easy optical access for which flow visualization and laser-induced fluorescence measurements allowed for validation of the developed methodology. Despite its simplicity, the I-channel geometry is found to reproduce the most characteristic flow features prevailing in high-speed flows realized in cavitating fuel injectors. Subsequently, the effect of liquid viscosity on integral mass flow, velocity profiles, vapor cavity distribution, and pressure peaks indicating locations prone to cavitation erosion is reported.

Introduction

Significant efforts have been made in the last two decades to develop models able to predict the appearance of cavitation erosion in fuel injection equipment.1−4 The complexity of the phenomenon, in terms of both geometrical parameters and operation conditions, makes its prediction a nontrivial task. Experiments on simplified geometries are then of crucial importance to understand the underlying physical phenomena and to provide validation data for numerical models. The wide range of numerical models available in the literature is mainly validated against measurements obtained in enlarged injectors or simplified real-size nozzles operating at lower pressures.5−57 Numerical models based on multiphase computational fluid dynamics (CFD) are able to predict the phase-change process and the hydrodynamic phenomena occurring in cavitating flows and provide useful information with regard to cavitation erosion. Bark et al.12,13 developed a model based on the experimental observation of the dynamics of collapsing vapor cavities close to a solid surface. The model described in ref (14) is instead based on two efficiency values that model the energy transfer from the collapsing cloud to the nearby walls. The review article of Van Terwisga et al.15 summarized some of the most promising models, together with a description of the relevant physical mechanisms. Various more recent attempts to define the flow aggressiveness and erosion risk have been presented in refs.16−20 A cavitation aggressiveness index was defined by Koukouvinis et al.,4,21 considering the Lagrangian derivative of pressure and the collapsing time scales for a single bubble and for the whole vapor cavity. Bergeles et al.22 instead used the acoustic pressure computed from the single bubble collapse to compute an erosion aggressiveness index and validated the model on a real eroded injector geometry. State-of-the-art compressible multiphase CFD simulations are capable to reproduce the interaction between pressure waves and the vapor dynamics, including the peak pressure values at the latest stages of a collapsing cavity. The 2D inviscid density-based solver used in ref (16) for a microthrottle flow was proved to be able to simulate the pressure wave pattern and the related pressure peak values. In ref (23), a 3D density-based solver with the single-fluid approach in combination with large eddy simulation (LES) was utilized on the same geometry and it detected similar pressure peaks occurring during bubble collapse. A similar solver was also used by Mihatsch et al. in ref (20); a grid dependency study of pressure wave intensity was performed and a scaling law was defined to fit the pressure peak rate to the one recorded during the experiments. In ref (24), the pressure peak values on the walls were recorded during the simulation using a pressure-based solver with a single-fluid LES approach for both, a microchannel flow and a real diesel injector. Additional fluid dynamics simulations relating pressures with locations indicative of erosion as well as quantitative X-ray measurements of the volume cavitation vapor volume fraction in diesel injector orifices were investigated by the authors in refs (4, 22, 25, and 26).

In addition to cavitation erosion studies, the effect of fuel properties on internal nozzle flows has also been broadly investigated in recent years. The differences resulting in the flow distribution inside a diesel injector were investigated using two values of fuel viscosity in ref (27). The usage of constant and variable fluid properties in a nozzle flow, including the effect of increased temperature due to viscous heating, has also been studied numerically.28,29 More recently, different state-of-the-art equation of states were used to compute fluid properties of different surrogate diesel types, showing a good agreement with the experimental measurements even under extreme operating conditions.30 The connection between fluid properties and cavitation erosion was also previously investigated but for applications not related to diesel injection systems. A variable composition of glycerol/water has been used to study the effect of viscosity changes on cavitation erosion in an ultrasonic vibratory test rig.31 Lubricants with different properties were analyzed in terms of cavitation and cavitation erosion risks in hydraulic components.32 In ref (33), the effect of liquid properties was instead studied experimentally for cavitation erosion in liquid metals. However, most of the studies conducted until now are based on cavitation erosion phenomena induced by a vibratory apparatus and no studies exist investigating the effect of fluid properties on the flow field and the consequent cavitation erosion patterns in nozzle-like geometries.

The work presented in this paper employs the pressure-based solver implemented in the CFD code AVL FIRE; it aims to resolve the cavitating flow in a microthrottle flow channel, referred to as I-channel. Measurements using commercially available diesel were presented in ref (34). Following the multifluid approach, two momentum conservation equations are solved for the liquid and vapor phases that are coupled with a momentum exchange term.35 Thus, the developed model predicts the slip velocity between the phases and the relative magnitude can be analyzed. Turbulence is resolved using LES with the coherent structure model;36 recent studies from the authors have shown that it is able to capture most of the turbulent scales of the flow, strictly correlated with cavitation phenomena.37 The contribution of the present work is the investigation of the effect of different diesel viscosity values within the range defined by the European norm38 for commercial diesel fuels on cavitation erosion phenomena. Previous studies from the authors25 considered variable viscosity values depending on the local pressure distribution. Furthermore, most of the previously presented studies use variable properties with pressure and temperature but do not consider possible differences under the same conditions. In this study, instead, the significant uncertainty about the viscosity value of commercially available diesel is analyzed. This reflects the actual properties of all diesels available in the EU; thus, they represent a more realistic scenario compared to that of the standard diesel fuel typically employed for testing purposes. The wide range of viscosities allowed by the norm leads to the fact that even under the same operation condition, completely different nominal Reynolds numbers can be realized. Significant differences can then appear in the flow and vapor cavity behavior, leading to completely different cavitation erosion patterns.

Numerical Model

The Navier–Stokes equations describing iso-thermal compressible two-phase cavitating flows are numerically solved on a 3D domain following the finite volume discretization method; the convergence of the system of equations is obtained with the semi-implicit method for pressure-linked equations (SIMPLE) algorithm.39,40 In the applied methodology, the phases share the same pressure but have different velocities; this is also known as a multifluid model.41 The vapor phase is then treated as a second continuous phase interpenetrating the liquid phase. The volume fraction, αk, of each phase is computed with a separate mass conservation equation. The subscript k is used to indicate a quantity related to a generic phase. The letters l and v are instead used to denote the liquid and vapor phases, respectively. A joined continuity equation is used to obtain the common pressure, p, and two momentum conservation equations are solved to find the velocity fields, v̅k, of the two phases, while their densities, ρk, are computed from the corresponding equations of state. The interaction between the phases is included in the equations in the form of mass and momentum exchange source terms. In the present methodology, these terms are modeled considering the monodispersed hypothesis for a bubbly flow.40 The full set of governing equations for a two-phase system, including two volume fractions, one continuity, and six momentum conservation equations, was presented in ref (25), and it is not reported in the present work for brevity. The difference between the liquid and the vapor velocities (v®r = v®v – v®l) causes a drag force opposite to the relative motion; the interfacial momentum exchange is modeled considering the drag forces acting on each vapor bubble. Equation 1 presents the sum of the drag forces acting on the vapor bubbles in the monodispersed bubbly flow

graphic file with name ao9b03623_m001.jpg 1

The vapor bubble number density corresponds to the one used by the cavitation model with the value of 1 μm–3.25 The drag coefficient, Cd, depends on the flow regime around the bubbles and it is a function of the Reynolds number, Rev = ρl|v®r|2R/μl. The model from Ishii and Mishima.40,42 can provide the formulation for Cd, as shown in eq 2

graphic file with name ao9b03623_m002.jpg 2

The validation of the used algorithm to solve compressible multiphase flows is presented in the Appendix for the shock tube 1D case.

Geometrical Model and Simulation Setup

The computational domain is replicating the experimental test case shown in ref (34). The channel, with dimensions of 0.993 × 0.295 × 0.3 (L × H × D) mm3, is attached to two volumes with size 24 × 3 × 0.3 mm3. Considering the local hydraulic diameter, Dh, the region upstream the channel presents an L/Dh = 44, while the channel is characterized by an L/Dh = 3.338. Various meshes are generated with different refinement levels, but all of them are formed by structured blocks composed of hexahedral cells. The geometry dimensions and an example of the mesh at the channel corner are presented in Figure 1. The figure given above shows the whole simulation domain together with a zoomed view of the channel section; characteristic dimensions in millimeters and inlet and outlet boundary conditions are included in the figure. The figure given below presents a detailed view of the mesh at the channel inlet corner. The boundary conditions applied to the simulations are summarized in Table 1. The used computational grids are all block-structured volume meshes. Different refinement levels have been applied in the proximity of the throttle, starting from an initial characteristic cell size of 24 μm that is also maintained in the coarsest region. The Taylor length scale of the flow, computed as 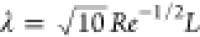Inline graphic, is estimated to be of the order of 7 μm. All adopted grids, described in Table 2, have characteristic cell sizes smaller than the Taylor length scale; thus, only the dissipative range of the turbulent spectrum is left to LES subgrid scale modeling, while the bigger structures are resolved. 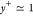In order to model appropriately the boundary layer, the same wall refinement technique is applied to all the used grids: the first cell layer height next to the walls is set to 0.44 μm (corresponding to Inline graphic) and the following five layers are within a distance of 4.8 μm. This wall treatment is applied only on the throttle walls to limit the cell count. Because cavitation is an inertial driven phenomenon, thermal effects are ignored to simplify the problem. The flow is then assumed to be isothermal with a fixed temperature of 40 °C. Following Iben et al.,43,44 the liquid diesel density is modeled with a linearized equation of state, as described in eq 3

graphic file with name ao9b03623_m005.jpg 3

Figure 1.

Figure 1

Open in a new tab

Mesh views: whole geometry with dimensions in millimeter (top) and the detailed view at the channel corner (bottom).

Table 1. Boundary Condition Summary with Reference to Figure 1.

location boundary condition type
inlet (blue) pIN, αl = 1
outlet (red) pOUT
walls (white) no-slip velocity
Open in a new tab

Table 2. Summary of Three Setups with Increasing Mesh Resolutiona.

mesh coarse mid fine
cell number [×106] 4.6 7.6 14.7
cell size [μm] 4.6 3.1 2
time step [ns] 7.5 5 2.5
total CPU time [h] 1680 4536 17,592
mass flow rate [g/s] 12.91 12.73 12.51
Δ [%] +3.20 +1.76  
nozzle αv [%] 21.79 4.93 4.06
Δ [%] +436.7 +21.2  
Open in a new tab
a

Time-averaged results with a relative difference to the fine mesh.

A reference density, ρref, of 820 kg/m3 is considered for the reference condition corresponding to pref = 1 bar and Tref = 40 °C. Density changes due to pressure are linearized with the speed of sound, cref = 1313 m/s. In the current approach, this value is considered constant. The diesel viscosity of 2.87 mPa s is used as the reference value, but the sensitivity to different viscosities is investigated in the following sections. The diesel vapor is instead assumed incompressible with properties computed under the saturation condition (psat = 4500 Pa at Tref = 40 °C): a viscosity of 4.6 μPa s and a density of 0.31 kg/m3. Because evaporation and condensation processes are the dominant effects on mixture compressibility,24,45 vapor density was considered constant to reduce the complexity of the model without losing its accuracy.

Results and Discussion

Mesh Sensitivity

The effect of mesh resolution is analyzed comparing the results of three simulations with increasing refinement levels. Table 2 presents the differences in the computational setup and CPU time for all three meshes in order to simulate 0.2 ms. The considered operating condition corresponds to 300 bar at the inlet and 120 bar at the outlet, while the liquid viscosity is taken as 2.87 mPa s. The characteristic cell size is computed as the mean value of the cubic root of the cell volume in the throttle region. In the same table, the resulting values of the time-averaged mass flow rate and total vapor volume fraction in the nozzle are presented together with their relative difference, Δ, to the fine mesh results. The relative difference in the mass flow rate between all meshes is below 3.2%. The amount of vapor in the channel of the coarse mesh is instead significantly bigger compared to the other two meshes. The near-wall average velocity profiles inside the channel for the three meshes are presented in Figure 2. The coarse mesh profile is significantly different compared to the other two meshes because the higher numerical diffusion caused by the poorer spatial discretization leads to a change in the flow regime, similarly to what is presented in the next sections. The two “valleys” appearing in the profile correspond to the locations of the vapor tubes that carry high momentum from the inner part of the channel to the side walls.

Figure 2.

Figure 2

Open in a new tab

Near-wall time-averaged velocity profiles at x = 603 μm for different mesh resolutions.

Because no significant difference exists between the mid and the fine meshes for both macroscopic flow data and velocity profiles, the mid one has been used for the analyses in the following sections.

Mass Flow Trend

A comparison between experiments and simulations for the mass flow rate is shown in Figure 3. Different pressure drops are considered for the same inlet pressure of 300 bar. The objective of this analysis is to verify the capability of the solver to correctly capture the cavitation critical point (CCP). This operation point coincides with the sudden change in the mass flow rate trend: from growing (as predicted by the Bernoulli equation) to constant. This generally corresponds to the operating point with the highest noise and fastest cavitation erosion rate.34 For higher pressure drops, the mass flow rate does not vary significantly and the flow is denoted as chocked. Both, simulations and experiments, indicate the CCP at a pressure drop close to 180 bar. The percentage of the vapor volume fraction in the nozzle shows that the nonlinearity in the mass flow trend is caused by the sudden increase in vapor volume fraction at the pressure drop corresponding to the CCP. For flow regimes with pressure drops higher than the CCP, simulations predicted a slightly smaller mass flow rate compared to the experiments. This can be attributed either to the dissipation of the numerical model or to an underestimation of the vapor cavity size because of inevitable small differences relative to the real geometry. The mass flow rate shows however a good agreement between experiments and simulations, as the relative error is below 6% for all operation points. For the following analysis, the operating condition of the CCP is considered: 300 bar at the inlet and 120 bar at the outlet; this corresponds to a cavitation number CN = (pIN – pOUT)/(pOUT – psat) ≃ (pIN – pOUT)/pOUT = 1.5. The CCP is also influenced by the magnitude of the mass transfer rate: reducing it translates into a higher pressure drop for the CCP, while increasing it makes the model converging toward thermodynamic equilibrium, thus reaching a minimum value of critical pressure. Because a significant displacement of the CCP can be reached only for relatively low mass transfer rates that also cause thermodynamic states questionably far from thermodynamic equilibrium (i.e., high negative pressure values and vapor existing above the saturation pressure), results are not included in this work.

Figure 3.

Figure 3

Open in a new tab

Mass flow rate at different pressure drops with a constant inlet pressure of 300 bar. Experiments from ref (34) (red continuous line), simulation time-averaged value (blue long stashed line with circles), and percentage of the vapor volume in the nozzle (gray short dashed line with x marks).

Viscosity Sensitivity

The European norm EN 59038 defines the physical properties that all automotive diesel fuel must meet if sold in the European Union. Table 3 reports density and kinematic viscosity limit values for diesel in temperate (class A) and arctic (class 4) climatic zones,38 together with the corresponding Reynolds numbers for the analyzed cases. These are based on the characteristic length of 3 × 10–4 m and a Bernoulli velocity (Inline graphic) of 210 m/s. Even though the norm defines the range for the density, its effect on the Reynolds number is included with the usage of the kinematic viscosity. It is also worth to mention that the viscosity range corresponds to Reynolds numbers’ relative variations above 300%, while the different densities would modify it by a factor below 10%. The reference temperature of 40 °C corresponds to the experimental temperature.34 For a pressure drop of 180 bar, an increase up to 7 °C was measured in the temperature because of viscous heating effects.34 Viscosity values then decrease along the channel of a factor that can be estimated to lay around 10%.46 Because these differences would consistently shift all simulation results toward a lower viscosity case but retaining the relative difference between them, thermal effects are neglected in the present work. For high-pressure diesel injectors, thermal effects have been investigated in refs (28) and (29). The effect of pressure on the viscosity is also neglected because no experimental measurements are available. At the inlet pressure of 300 bar, the viscosity can be expected to be around 30% higher relative to the value at the reference pressure of 1 bar;46 however, this would again consistently affect all solutions, uniformly moving the simulation results to different conditions but maintaining the differences between the cases. The viscosity furthest limits values of Table 3, highlighted in bold, are then analyzed together with the value used in Morozov and Iben in ref (34). Table 4 summarizes the three cases that have been taken into account. The same values for the linearized equation of state are used for defining the density of the compressible liquid of all cases. Time-averaged results in terms of mass flow rate and vapor volumetric content in the channel are also included with their standard deviation. The results show that both mass flow rate and volumetric vapor content in the nozzle increase with lower viscosities. However, while the variation of mass flow is relatively small, the amount of vapor in the nozzle in the lowest viscosity case is sensibly more compared to the other two cases. The mass flow rate measured during the experiments was 12.7 g/s,34 which is within the range of the simulation results.

Table 3. Diesel Kinematic Viscosity Range Defined in the European Norm EN 59038 with the Corresponding Reynolds Numbers.

diesel temperate arctic
ρ [kg/m3] at 15 °C 820 ÷ 860 800 ÷ 840
ν [mm2/s] at 40 °C 2 ÷ 4.5 1.2 ÷ 4
Re 31,500 ÷ 14,000 52,500 ÷ 15,750
Open in a new tab

Table 4. Cases with Selected Viscosity Values, Corresponding Reynolds Numbers, and Resulting Average Mass Flow and Vapor Content in the Nozzle.

  case A case B case C
ν [mm2/s] 4.5 3.5 1.2
μ [mPa s] 3.72 2.87 0.99
Re 14,000 18,000 52,500
mass flow rate [g/s] 12.40 12.73 12.87
  ±0.18 ±0.19 ±0.24
vapor volume 2.73 4.93 24.15
in nozzle [%] ±0.57 ±2.84 ±1.68
Open in a new tab

Flow Regimes

Figure 4 presents the internal time-averaged LES results for the three cases. The isosurface at 50% vapor volume fraction along the throttle is shown together with four longitudinal cuts colored by the velocity value and overlapped by vectors representing the velocity components perpendicular to the main flow direction. As already shown in ref (23), four counter-rotating corner vortices are visible along the channel for all cases. The differences in the amount of vapor in the nozzle presented in Table 4 can then be explained because of the longer vapor cavities filling the recirculation area and the cavitation inception in the four vortex cores. Two very different vapor distribution patterns can then be obtained with different viscosity values. Some common features between all regimes can however be detected: the recirculation zones starting from the channel inlet causes the boundary layer separation from the throttle walls and a free shear layer exists between the core flow and the recirculation region. In correspondence with the channel inlet, four counter-rotating corner vortices are also formed because of the interaction of the boundary layer on the side walls and the flow velocity y-component, vy, induced by the sudden flow contraction. A vorticity component longitudinal to the channel is then generated, wx = ∂vz/∂y – ∂vy/∂z ≃ −∂vy/∂z (being the z velocity component negligible compared to the one along y: vz ≪ vy). At one-fourth of the channel length, the recirculation zones reach their maximum thickness and the core flow has the smallest available section, leading to the highest velocity and lowest pressure. This is then the location where the vortices start to cavitate. Downstream of this region, two possible flow patterns can be distinguished: one with unstable cavity detachment and one with stable cavitating tubes (case C). In the flow regime with unstable cavity detachment, the liquid core flow expands and fills the entire channel section, causing a flow deceleration. The positive pressure gradient at the free shear layer promotes the transition from laminar to turbulent regimes, causing the rupture of the vapor sheet into smaller cavities. The high-pressure fluctuations in this region prevent the formation of stable vapor vortex tubes. This flow regime is highly unstable and it is characterized by cavities shedding the collapsing cloud further downstream. The flow is then strongly affected by the interaction of pressure waves and vapor cavities, with re-entrant jets occurring in the recirculation zone. A different flow pattern is instead detected when the cavitating vortical structures extend longer along the channel. In this case, the vapor generated in the vortex cores is convected downstream. This causes the effective passage section for the core liquid flow to remain confined and thus the liquid to keep its high velocity. The pressure is not recovering but remains in the same range until downstream of the half of the channel length. The shear layer instabilities are then damped, the laminar to turbulent transition is postponed, and the attached cavity sheet extends until after half of the channel length. Six stable vapor structures can then be identified inside the channel: two attached sheet cavities between the shear layers and the upper and lower channel walls and four cavitating corner vortices. After 3/4 of the channel length, the flow becomes turbulent and the cavitating structures break into smaller cavities that detach and collapse after being convected further downstream. The effect of these two different patterns can be detected in Table 4, by the higher vapor content in the nozzle and slightly higher mass flow for the second regime.

Figure 4.

Figure 4

Open in a new tab

Time-averaged flow fields on four longitudinal cuts (x = {0.05, 0.35, 0.65, and 0.95} mm) of the three cases. The isosurface of 50% vapor volume fraction with the velocity vectors perpendicular to the main flow direction.

Figure 5 presents the time-averaged velocity profile on the mid-depth plane of the channel for three longitudinal positions and all the three cases were simulated. The smaller deceleration of the core liquid flow in the case C postpones the shear–layer transition to turbulent. Furthermore, the boundary layer is re-attached to the wall in cases A and B at the location x = 500 μm, while this is still not happening for case C.

Figure 5.

Figure 5

Open in a new tab

Mid-depth time-averaged velocity profiles at x = {200, 500, and 800} μm (system of reference defined in Figure 1).

Figure 6 shows the time-averaged velocity difference between the liquid and vapor phases for case B. The highest values were measured in correspondence to the shear layer location, for which a relative difference in the velocity up to 75% was recorded. The slip velocity in this region is related to the very high velocity field gradient that appears to be less sharp for the vapor phase. The vapor bubble sizes in this study are in the order of 0.005–0.5 μm (corresponding to a bubble number density of 1 μm–3) and they lay in the range of previously reported values in the literature.47−49 The usage of a higher value for the vapor bubble number density would result in a relatively higher drag term. However, because of the relatively small magnitude of slip velocity compared to the main flow velocity and the low density ratio between vapor and liquid, differences in the slip velocity can be expected to lead to negligible effects on the main flow.

Figure 6.

Figure 6

Open in a new tab

Time-averaged slip velocity between liquid and vapor phases at the mid-depth of the channel for case B. Positive values correspond to the faster vapor phase.

Vapor Volume Fraction Distribution

Figure 7 presents the vapor volume fraction field inside the channel. The experimental visualization from ref (34) was obtained by averaging 50 light transmission images, each of them recorded with an exposure time of 100 ns. Similar to the averaging process used in the experimental study, a series of 40 light transmission images were generated. A threshold corresponding to 20% vapor volume fraction in the cell was considered to absorb all the passing light; then, for each x–y location, if any cell along the z-axis had more than 20% vapor volume fraction, the area was considered in shadow (black), otherwise it was taken as illuminated (white). The sequential images were then averaged to obtain an equivalent numerical picture. Because of the lack of experimental quantification of the scale of the obtained image, a 20% threshold was obtained as the best fitting to the experiments. A detailed description of the post-processing procedure is presented in ref (11).

Figure 7.

Figure 7

Open in a new tab

Average vapor volume fraction distribution comparison between experiments34 (top) and the simulation results corresponding to case B conditions.

Velocity Profiles Close to the Wall

In order to obtain velocity profiles comparable with the experiments presented in ref (34), a weighted integral average operation is applied to mimic the light absorption phenomenon. The time-averaged velocity is then integrated along the z-direction following eq 4

graphic file with name ao9b03623_m007.jpg 4

The value zM is the maximum distance from the glass considered for the numerical averaging procedure. The weight function, w(z), represents the spatial decays of the laser-induced fluorescence (LIF) signal used for the measurements. An exponential decay with the maximum intensity at the glass wall and penetration half width, zh, of 15 μm is adopted as described in ref 34.34Equation 5 shows the weight function

graphic file with name ao9b03623_m008.jpg 5

A maximum averaging depth of 50 μm was considered in the current work that corresponds to 90% of the weighting function unlimited integral.

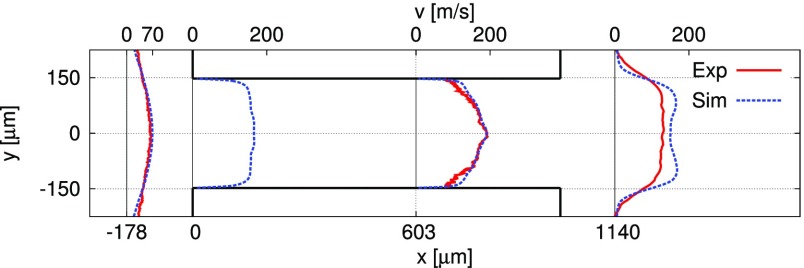
In Figure 8, the near-wall velocity profiles from the experiments are compared with the simulations of case B. The simulation results are in good agreement with the experimental curves.

Figure 8.

Figure 8

Open in a new tab

Experimental measurements and simulation results of near-wall time-averaged velocity profiles at different locations (x = {−178, 0, 603, and 1140} μm) for the medium case (system of reference defined in Figure 1).

The velocity profile analyses can also prove the existence of the four counter-rotating vortices in the experiments. A higher average velocity in the simulation is detected at the inlet location (x = 0 μm) close to the channel mid-line and for an extension of one-third of the channel height. This can be explained by the presence of the vortices that transport low momentum from the recirculation regions toward the middle of the channel. This causes a decrease in the velocity along the side walls. At the channel center, the counter-rotating vortex effect is instead canceled and the velocity is then higher. A similar pattern, but less extended, is also recorded by both experiments and simulation at x = 603 μm. The smaller extension of the region with higher velocity is due to the smaller distance between the vortex core locations.

Cavitation Erosion Predictions

The maximum pressure values on the channel top and bottom walls were recorded during the simulation time of 0.2 ms and overlapped for visualization purposes. These high values of pressure are generated because of the collapse of vapor cavities that initiate pressure waves impacting on the nearby walls. The mesh resolution effect on the recorded pressure peaks is shown in Figure 9. Even though the same qualitative results are obtained for all simulations, for example, similar pressure peak locations, very different magnitudes were recorded depending on the mesh resolution. This result is in apparent disagreement with the negligible mesh dependency of pressure peak values because of vapor bubble cloud collapse shown in ref (50); however, differences in the collapsing cavity size and location must be considered to analyze the peak intensity.

Figure 9.

Figure 9

Open in a new tab

Mesh sensitivity on accumulated pressure peaks on top and bottom walls of the channel.

Figure 10 shows a quantitative representation of the results presented in Figure 9. The percentage of the channel area covered by pressure peaks is shown using a semilogarithmic scale. Similarly to ref (20), a power law is detected for all simulations, leading to a linear trend of the logarithm of the area covered by pressure peaks as a function of the considered pressure range. Increasing the mesh resolution, a larger area is consistently covered by pressure peaks of all magnitudes, causing a vertical shift of the trends.

Figure 10.

Figure 10

Open in a new tab

Statistical results of the mesh resolution effect on pressure peak surface coverage.

The instantaneous maximum internal pressure values over the entire domain are then investigated. Different from the collapse detector that was applied in previous studies,20,51 in this work, only the maximum value of pressure in the domain is recorded at each time step. This drastically reduces the memory requirements and cancels the need of further modeling but only the strongest event is recorded in the case of simultaneous collapses. Following the approach presented in refs (20) and (50), the maximum pressure values are corrected considering the grid resolution: pmax* = pmax·lmesh/lref, lmesh and lref being the characteristic cell size of the mesh and an arbitrary reference length, respectively. Figure 11 presents the effect of the pressure correction on the probability of reaching the corresponding maximum pressure values in the domain at any time. After correction, the results from all three meshes are almost overlapping, thus removing the effect of mesh resolution on the obtained results. The effect of different lref is also included; however, this value could not be defined univocally because of the lack of further experimental measurements.

Figure 11.

Figure 11

Open in a new tab

Probability of the maximum pressure in the domain for different mesh resolutions. Pressure value correction considering the mesh resolution with two lref values. Original trends are included for comparison.

Considering Figure 9, a similar pressure peak location was detected on all three mesh resolutions at x ≃ 500 μm and z ≃ 250 μm. The single event is then investigated by detecting the internal flow peak pressure that caused it, pmax, and the corresponding time, t(pmax). Furthermore, the distance at which this peak was recorded is evaluated as d* ≃ lmesh·pmax/pw following ref (50), pw being the corresponding peak pressure recorded at the wall. The results presented in Table 5 show that all three peaks were recorded in a similar time not far from the start of the simulation and thus they may be caused by a similar vapor cavity structure. The results show that the collapsing distance from the wall decreases for finer meshes, causing a higher intensity peak to be recorded on the wall.

Table 5. Single Pressure Peak Comparison between Different Mesh Resolutions.

  coarse mid fine
pmax [bar] 1000 1500 4000
t(pmax) [μs] 7.30 5.84 5.76
pw [bar] 590 860 1750
d* [μm] 7.8 5.4 4.5
Open in a new tab

Figure 12 shows the pressure peaks of the simulation obtained with different viscosity values. Differences between the cases are visible in the location, intensity, and number of peaks: higher viscosity values lead to more pressure peaks compared to the case with the lowest viscosity (case C). This can be explained by the formation of the elongated vapor cavities inside the channel for case C that lead to quasi-steady flow conditions, thus reducing the number of collapsing cavities. Similarly to Figure 10, Figure 13 aims to provide a quantification of the recorded pressure peaks for the presented cases. Less than 0.1% of the total area is covered by pressure values above 300 bar in case C. Both the other two cases present a larger distribution of peak pressure values on the surface, with case B being the one with the highest bars and thus the estimated highest erosion risk. Opposite to the mesh resolution results, for which a linear behavior exists between the bar height and the mesh resolutions, in this case, a nonlinear behavior is detected: the cavitation erosion risk grows with the Reynolds number until a value close to 18,000 is reached and then start decreasing, causing case C to present the lowest risk. The so-called CCP is then detected close to case B conditions.

Figure 12.

Figure 12

Open in a new tab

Viscosity effect on accumulated pressure peaks on top and bottom walls of the channel.

Figure 13.

Figure 13

Open in a new tab

Statistical results of the viscosity effect on pressure peak surface coverage.

The probability of the maximum pressure in the entire domain is presented in Figure 14. Different from the mesh resolution analyses, no grid resolution correction has been applied to the data because the identical mesh was used for all simulations. Comparing case B and case C, it is possible to notice that the difference between the two cases shown in Figure 13 is reduced in the results of the internal maximum pressure (Figure 14). The pressure peak wall coverage results show a ratio close to 2 between the results of case B and case C for pressure ranges above 300 bar. The ratio is instead reduced to values below 1.5 for the probability of the maximum internal pressure above 400 bar. This may lead to the conclusion that the stronger recorded peak pressure on the wall of case B compared to that of case C is caused only partially by a reduction of the collapse event intensity and a larger distance of these events from the wall is expected to contribute to the difference as well. A similar conclusion can be made comparing case C with case B; however, the amount of recorded collapse events is much lower and thus statistically less accurate.

Figure 14.

Figure 14

Open in a new tab

Probability of the maximum pressure in the domain for different viscosities.

Conclusions

A microthrottle case was used to investigate the effect of diesel viscosity on cavitation development. Results of a two-phase shock tube are also included in the appendix, as validation of the compressible pressure-based solver capabilities. The simulation methodology is validated in a range of operation conditions of the I-channel case; the mass flow rate trends at different pressure drops from the simulation show a good agreement with the measurements. The mesh resolution is selected considering the flow field obtained from three meshes with different refinement levels. The effect of different liquid viscosities taken accordingly to the range specified by the European norm for automotive diesel fuel and changing the flow Reynolds number was then investigated. This results in different flow regimes to develop within the nozzle, with sensible differences in the vapor distribution and total vapor quantity inside the throttle. Slip velocity between the phases at the channel mid-depth shows the highest value in correspondence to the shear layer locations. Near-wall velocity profiles are then extracted from the simulation results with the vapor distribution most similar to the light transmission images and compared with the experimental measurements. The effect of space and time resolution on the recorded pressure peaks on the surfaces was then presented, showing a bigger number and higher intensity of peak values for the simulation with the finest computational grid. The distinguished flow regimes appearing at different viscosities lead to differences in the distribution of pressure peaks, demonstrating the sensibility of the model on the diesel viscosity value regarding the assessment of cavitation erosion risk. The similarities in the recorded pressure peak results for different mesh resolutions can provide confidence in the results obtained with the present model for real-life cases even for relatively coarse grids. For the considered fluid, diesel, the main model application is injection system components as pumps, valves, and injectors. The model can be also further extended to different applications affected by cavitation erosion as turbines, propellers, and internal combustion engine liners. A future extension of the model is to include the solid material response to the pressure peaks in order to evaluate material removal rates.

Acknowledgments

Financial support from the MSCA-ITN-ETN of the European Union Horizon 2020 programme under REA grant agreement number 642536 is acknowledged.

Appendix

An inexpensive but relevant test case to verify the ability of a compressible CFD solver to correctly resolve pressure waves, namely, shocks and expansion fans, is the shock tube. The considered fluid properties and operation conditions are taken consistently with refs (52) and (53). The problem is initialized as a 1 m long tube with liquid at high pressure on the left side and gas at low pressure on the right side. The two nonreacting fluids are initially separated by a membrane and velocity is zero everywhere. Figure 15 shows the characteristic flow field generated after the membrane is suddenly removed, as extensively described in refs (54) and (55).

Figure 15.

Figure 15

Open in a new tab

Flow configuration of a shock tube.

The initial conditions for the considered test case are

  • left: liquid dodecane at 1000 bar and 687 K (ρl = 500 kg/m3)

  • right: vapor dodecane at 1 bar and 1022 K (ρv = 2 kg/m3)

The stiffened gas equation of state (SG-EOS), shown in eq 6, is used for the computation of both liquid and vapor densities

graphic file with name ao9b03623_m009.jpg 6

The constant π is empirically determined and it models the effect of molecular attraction in the liquid state. The liquid density behaves then as an ideal gas that is already under a pressure equal to π.

The SG-EOS parameters and the specific heat capacity, Cp, are taken as constants and they are presented in Table 6. The equations are solved on a one-dimensional mesh of 10,000 equidistant cells. The selected time step of 0.2 μs corresponds to a convective CFL number of 0.3 and an acoustic CFL number of 3 for the liquid. The total enthalpy conservation equation is solved along with continuity and momentum transport equations. The equations are defined to compute one pressure and one velocity field, common for both phases. No mass or heat transfers are included in the model. Pressure boundary conditions are imposed on the extremities and symmetry on the other external faces along the tube. The solution is obtained proceeding in time with the first order accuracy and the spatial discretization was based on the Roe’s MINMOD scheme.56 The results presented in Figure 16 are in good agreement with the solution obtained from a Riemann solver. The results are presented at 4.73 μs after the simulation started (corresponding to the instant of removal of the membrane). The simulation results show the same wave configuration as predicted by the Riemann solution: a fast expansion fan in the liquid on the left, the shock in the vapor on the right, and the contact surface between the liquid and the vapor closer to the center. The pressure wave speed in both liquid and vapor is also correctly predicted, showing an overall satisfactory matching between simulation results and the Riemann solution.

Table 6. SG-EOS Parameters for Liquid and Vapor Dodecane52.

phase γ π [Pa] Cv [J/kg K] Cp [J/kg K]
vapor 1.025 0 1956 2005
liquid 2.35 4 × 108 1077 2534
Open in a new tab

Figure 16.

Figure 16

Open in a new tab

Liquid/vapor dodecane shock tube at 1000/1 bar with SG-EOS: Riemann solution (red line) and simulation results (blue circles). Graphs show the values along the tube of pressure (top left), pressure in logarithmic scale (top right), velocity (bottom left), and mixture density (bottom right).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b03623.

  • Animation of the vapor cloud dynamics in the channel and the pressure peak formation due to the collapse of a vapor cavity close to a wall (MPG)

The authors declare no competing financial interest.

Supplementary Material

ao9b03623_si_001.mpg (1.6MB, mpg)

References

  1. Van Basshuysen R.; Schäfer F.. Internal Combustion Engine Handbook—Basics, Components, Systems and Perspectives; SAE International, 2004; Vol. 345. [Google Scholar]
  2. Robert Bosch GmbH . In Automotive Handbook, 7th ed.; GmbH, Robert Bosch, Ed.; John Wiley & Sons, 2007. [Google Scholar]
  3. Egler W.; Giersch R. J.; Boecking F.; Hammer J.; Hlousek J.; Mattes P.; Projahn U.; Urner W.; Janetzky B. In Handbook of Diesel Engines; Mollenhauer K., Tschoeke H., Eds.; Springer–Verlag Berlin Heidelberg, 2010. [Google Scholar]
  4. Brunhart M.; Soteriou C.; Daveau C.; Gavaises M.; Koukouvinis P.; Winterbourn M. Cavitation erosion risk indicators for a thin gap within a diesel fuel pump. Wear 2020, 442–443, 203024. 10.1016/j.wear.2019.203024. [DOI] [Google Scholar]
  5. Grogger H. A.; Alajbegović A.. Calculation of The Cavitating Flow In Venturi Geometries Using Two Fluid Model. ASME Fluids Engineering Division Summer Meeting: Washington, D.C., USA, 1998.
  6. Arcoumanis C.; Flora H.; Gavaises M.; Badami M.. Cavitation in real–size multi–hole diesel injector nozzles. SAE Technical Paper 2000, 01, 10.4271/2000-01-1249. [DOI] [Google Scholar]
  7. Roth H.; Gavaises M.; Arcoumanis C.. Cavitation initiation, its development and link with flow turbulence in diesel injector nozzles. SAE Technical Paper 2002, 01, 10.4271/2002-01-0214. [DOI] [Google Scholar]
  8. Roth H.; Giannadakis E.; Gavaises M.; Arcoumanis C.; Omae K.; Sakata I.; Nakamura M.; Yanagihara H. Effect of multi–injection strategy on cavitation development in diesel injector nozzle holes. SAE Trans. 2005, 114, 1029–1045. [Google Scholar]
  9. Reid B. A.; Hargrave G. K.; Garner C. P.; Wigley G. An investigation of string cavitation in a true–scale fuel injector flow geometry at high pressure. Phys. Fluids 2010, 22, 031703. 10.1063/1.3372174. [DOI] [Google Scholar]
  10. Mitroglou N.; Gavaises M.. Cavitation inside real–size fully transparent fuel injector nozzles and its effect on near–nozzle spray formation. DIPSI Workshop on Droplet Impact Phenomena and Spray Investigations; University of Bergamo: Italy, 2011.
  11. Gavaises M.; Villa F.; Koukouvinis P.; Marengo M.; Franc J.-P. Visualisation and LES simulation of cavitation cloud formation and collapse in an axisymmetric geometry. Int. J. Multiphase Flow 2015, 68, 14–26. 10.1016/j.ijmultiphaseflow.2014.09.008. [DOI] [Google Scholar]
  12. Lorenzi M.; Mitroglou N.; Santini M.; Gavaises M. Novel experimental technique for 3D investigation of high-speed cavitating diesel fuel flows by X-ray micro computed tomography. Rev. Sci. Instrum. 2017, 88, 033706. 10.1063/1.4978795. [DOI] [PubMed] [Google Scholar]
  13. Bark G.; Berchiche N.; Grekula M.. Application of Principles for Observation and Analysis of Eroding Cavitation—The EROCAV Observation Handbook, 3.1 ed.; Chalmers University of Technology, 2004. [Google Scholar]
  14. Grekula M.; Bark G.. Analysis of video data for assessment of the risk of cavitation erosion. 1st International Conference on Advanced Model Measurement Technology for the EU Maritime Industry: Nantes, France, 2009.
  15. Fortes-Patella R.; Reboud J. L.; Briancon-Marjollet L.. A Phenomenological and Numerical Model for Scaling the Flow Agressiveness in Cavitation Erosion. EROCAV Workshop: Val de Reuil, F, 2006.
  16. Van Terwisga T. J. C.; Fitzsimmons P. A.; Ziru L.; Foeth E. J.. Cavitation Erosion—A review of physical mechanisms and erosion risk models. 7th International Symposium on Cavitation: Ann Arbor, Michigan, USA, 2009.
  17. Skoda R.; Iben U.; Mozorov A.; Mihatsch M.; Schmidt S. J.; Adams N. A.. Numerical Simulation of Collapse Induced Shock Dynamics for the Prediction of the Geometry, Pressure and Temperature Impact on the Cavitation Erosion in Micro Channels. WIMRC, 3rd International Cavitation Forum; University of Warwick, 2011.
  18. Skoda R.; Iben U.; Güntner M.; Schilling R.. Comparison of compressible explicit density–based and implicit pressure–based CFD methods for the simulation of cavitating flows. 8th International Symposium on Cavitation: Singapore, 2012.
  19. Fortes-Patella R.; Archer A.; Flageul C.. Numerical and experimental investigations on cavitation erosion. 26th IAHR Symposium on Hydraulic Machinery and Systems, 2012.
  20. Pöhl F.; Mottyll S.; Skoda R.; Huth S. Evaluation of cavitation–induced pressure loads applied to material surfaces by finite–element–assisted pit analysis and numerical investigation of the elasto–plastic deformation of metallic materials. Wear 2015, 330–331, 618–628. 10.1016/j.wear.2014.12.048. [DOI] [Google Scholar]
  21. Mihatsch M. S.; Schmidt S. J.; Adams N. A. Cavitation erosion prediction based on analysis of flow dynamics and impact load spectra. Phys. Fluids 2015, 27, 103302. 10.1063/1.4932175. [DOI] [Google Scholar]
  22. Koukouvinis P.; Bergeles G.; Gavaises M. A cavitation aggressiveness index within the Reynolds averaged Navier Stokes methodology for cavitating flows. J. Hydrodyn. 2015, 27, 579–586. 10.1016/S1001-6058(15)60519-4. [DOI] [Google Scholar]
  23. Bergeles G.; Li J.; Wang L.; Koukouvinis F.; Gavaises M. An Erosion Aggressiveness Index (EAI) Based on Pressure Load Estimation Due to Bubble Collapse in Cavitating Flows Within the RANS Solvers. SAE Int. J. Engines 2015, 8, 2276. 10.4271/2015-24-2465. [DOI] [Google Scholar]
  24. Egerer C. P.; Hickel S.; Schmidt S. J.; Adams N. A. Large–eddy simulation of turbulent cavitating flow in a micro channel. Phys. Fluids 2014, 26, 085102. 10.1063/1.4891325. [DOI] [Google Scholar]
  25. Koukouvinis P.; Gavaises M.; Li J.; Wang L. Large Eddy Simulation of Diesel injector including cavitation effects and correlation to erosion damage. Fuel 2016, 175, 26–39. 10.1016/j.fuel.2016.02.037. [DOI] [Google Scholar]
  26. Cristofaro M.; Edelbauer W.; Koukouvinis P.; Gavaises M. A numerical study on the effect of cavitation erosion in a diesel injector. Appl. Math. Model. 2020, 78, 200–216. 10.1016/j.apm.2019.09.002. [DOI] [Google Scholar]
  27. Koukouvinis P.; Mitroglou N.; Gavaises M.; Lorenzi M.; Santini M. Quantitative predictions of cavitation presence and erosion–prone locations in a high–pressure cavitation test rig. J. Fluid Mech. 2017, 819, 21–57. 10.1017/jfm.2017.156. [DOI] [Google Scholar]
  28. Giannadakis E.; Papoulias D.; Gavaises M.; Arcoumanis C.; Soteriou C.; Tang W.. Evaluation of the predictive capability of diesel nozzle cavitation models. SAE Technical Paper 2007–01–0245, 2007.
  29. Theodorakakos A.; Strotos G.; Mitroglou N.; Atkin C.; Gavaises M. Friction–induced heating in nozzle hole micro–channels under extreme fuel pressurisation. Fuel 2014, 123, 143–150. 10.1016/j.fuel.2014.01.050. [DOI] [Google Scholar]
  30. Strotos G.; Koukouvinis P.; Theodorakakos A.; Gavaises M.; Bergeles G. Transient heating effects in high pressure Diesel injector nozzles. Int. J. Heat Fluid Flow 2015, 51, 257–267. 10.1016/j.ijheatfluidflow.2014.10.010. [DOI] [Google Scholar]
  31. Vidal A.; Rodriguez C.; Koukouvinis P.; Gavaises M.; McHugh M. A. Modelling of Diesel fuel properties through its surrogates using Perturbed–Chain, Statistical Associating Fluid Theory. Int. J. Engine Res. 2018, 1–16, 1468087418801712. 10.1177/1468087418801712. [DOI] [Google Scholar]
  32. Saleh B.; Ezz El-Deen A.; Ahmed S. M. Effect Of Liquid Viscosity On Cavitation Damage Based On Analysis Of Erosion Particles. J. Eng. Sci. 2011, 39, 327–336. [Google Scholar]
  33. Meged Y.; Venner C. H.; ten Napel W. E. Classification of lubricants according to cavitation criteria. Wear 1995, 186–187, 444–453. 10.1016/0043-1648(95)07135-0. [DOI] [Google Scholar]
  34. Hattori S.; Inoue F.; Watashi K.; Hashimoto T. Effect of liquid properties on cavitation erosion in liquid metals. Wear 2008, 265, 1649–1654. 10.1016/j.wear.2008.04.007. [DOI] [Google Scholar]
  35. Morozov A.; Iben U.. Experimental Analysis and Simulation of Cavitating Throttle Flow. HEFAT, 6th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics: Pretoria, South Africa, 2008.
  36. Cristofaro M.; Edelbauer W.; Gavaises M.; Koukouvinis P.. Numerical simulation of compressible cavitating two–phase flows with a pressure–based solver. ILASS–Europe, 28th Conference on Liquid Atomization and Spray Systems: Valencia, Spain, 2017.
  37. Kobayashi H. The subgrid–scale models based on coherent structures for rotating homogeneous turbulence and turbulent channel flow. Phys. Fluids 2005, 17, 045104. 10.1063/1.1874212. [DOI] [Google Scholar]
  38. Edelbauer W.; Strucl J.; Morozov A.. Large Eddy Simulation of Cavitating Throttle Flow. Advances in Hydroinformatics. SimHydro: Modelling of Rapid Transitory Flows; Springer: Sophia Antipolis, F, 2014. [Google Scholar]
  39. European Committee for Standardization . EN-590: Automotive Fuels–Diesel–Requirements and Test Methods, 2009.
  40. Patankar S. V.; Spalding D. B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transfer 1972, 15, 1787–1806. 10.1016/0017-9310(72)90054-3. [DOI] [Google Scholar]
  41. Software User Manual. AVL FIRETM, 2018.
  42. Brennen C. E.Fundamentals of Multiphase Flows; Cambridge University Press, 2005. [Google Scholar]
  43. Ishii M.; Mishima K. Two–fluid model and hydrodynamic constitutive relations. Nucl. Eng. Des. 1984, 82, 107–126. 10.1016/0029-5493(84)90207-3. [DOI] [Google Scholar]
  44. Iben U.; Mozorov A.; Winklhofer E.; Skoda R.. Optical investigations of cavitating flow phenomena in micro Channels using a nano second resolution. WIMRC, 3rd International Cavitation Forum; University of Warwick, 2011.
  45. Iben U.; Morozov A.; Winklhofer E.; Wolf F. Laser–pulse interferometry applied to high–pressure fluid flow in micro channels. Exp. Fluids 2011, 50, 597–611. 10.1007/s00348-010-0950-9. [DOI] [Google Scholar]
  46. Franc J. P.; Michel J. M.. Fundamentals of cavitation; Springer Science & Business Media, 2005; Vol. 76. [Google Scholar]
  47. Schaschke C.; Fletcher I.; Glen N. Density and viscosity measurement of diesel fuels at combined high pressure and elevated temperature. Processes 2013, 1, 30–48. 10.3390/pr1020030. [DOI] [Google Scholar]
  48. Giannadakis E.; Gavaises M.; Arcoumanis C. Modelling of cavitation in Diesel injector nozzles. J. Fluid Mech. 2008, 616, 153–193. 10.1017/S0022112008003777. [DOI] [Google Scholar]
  49. Liu Z.; Brennen C. E. Cavitation Nuclei Population and Event Rates. J. Fluids Eng. 1998, 120, 728–737. 10.1115/1.2820730. [DOI] [Google Scholar]
  50. Mørch K. A. Reflections on cavitation nuclei in water. Phys. Fluids 2007, 19, 072104. 10.1063/1.2747210. [DOI] [Google Scholar]
  51. Schmidt S. J.; Mihatsch M.; Thalhamer M.; Adams N. A.. Assessment of the Prediction Capability of a Thermodynamic Cavitation Model for the Collapse Characteristics of a Vapor–Bubble Cloud. WIMRC, 3rd International Cavitation Forum; University of Warwick, 2011.
  52. Schreiner F.; Mottyll S.; Skoda R.. A Method For The Coupling Of Compressible 3d Flow Simulations With A Cavitation Erosion Model For Ductile Materials And Assessment Of The Incubation Time. VIII International Conference on Computational Methods in Marine Engineering; Göteborg: Sweden, 2019.
  53. Saurel R.; Petitpas F.; Abgrall R. Modelling phase transition in metastable liquids: application to cavitating and flashing flows. J. Fluid Mech. 2008, 607, 313–350. 10.1017/S0022112008002061. [DOI] [Google Scholar]
  54. Zein A.; Hantke M.; Warnecke G. Modeling phase transition for compressible two–phase flows applied to metastable liquids. J. Comput. Phys. 2010, 229, 2964–2998. 10.1016/j.jcp.2009.12.026. [DOI] [Google Scholar]
  55. Sod G. A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 1978, 27, 1–31. 10.1016/0021-9991(78)90023-2. [DOI] [Google Scholar]
  56. Anderson J. D.Modern Compressible Flow; Elsevier, 1983. [Google Scholar]
  57. Sweby P. K. High resolution schemes using flux limiters for hyperbolic conservation laws. SIAM J. Numer. Anal. 1984, 21, 995–1011. 10.1137/0721062. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b03623_si_001.mpg (1.6MB, mpg)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES