Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Mar 23;5(13):7348–7360. doi: 10.1021/acsomega.9b04259

Microfluidic Study of the Electrocoalescence of Aqueous Droplets in Crude Oil

Thomas Leary †, Mohsen Yeganeh ‡, Charles Maldarelli †,*
PMCID: PMC7144161  PMID: 32280876

Abstract

graphic file with name ao9b04259_0002.jpg

In electrocoalescence, an electric field is applied to a dispersion of conducting water droplets in a poorly conducting oil to force the droplets to merge in the direction of the field. Electrocoalescence is used in petroleum refining to separate water from crude oil and in droplet-based microfluidics to combine droplets of water in oil and to break emulsions. Using a microfluidic design to generate a two-dimensional (2D) emulsion, we demonstrate that electrocoalescence in an opaque crude oil can be visualized with optical microscopy and studied on an individual droplet basis in a chamber whose height is small enough to make the dispersions two dimensional and transparent. From reconstructions of images of the 2D electrocoalescence, the electrostatic forces driving the droplet merging are calculated in a numerically exact manner and used to predict observed coalescence events. Hence, the direct simulation of the electrocoalescence-driven breakdown of 2D emulsions in microfluidic devices can be envisioned.

1. Introduction

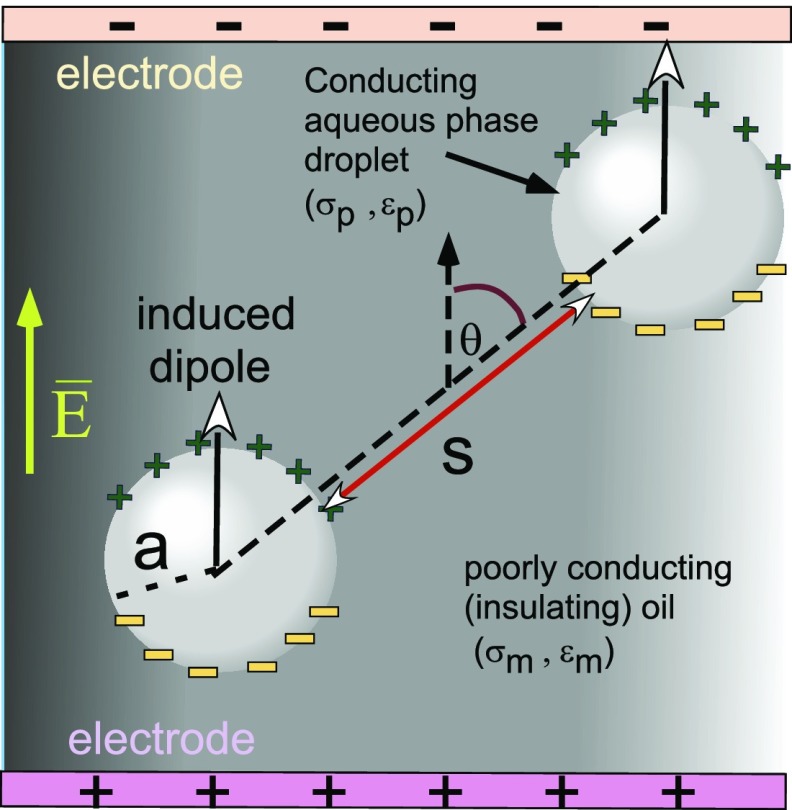
Electric field-mediated coalescence of conducting water droplets dispersed in a continuous, poorly conducting dielectric oil phase (Figure 1) is a long-standing technology in the petroleum refining industry. This technology has been used to remove emulsion droplets of water in crude oil,1−7 particularly in the context of the desalting operation of electrocoalescers. In this operation, fresh water is first introduced into the crude at the inlet to the electrocoalescer to remove organic salts by transferring into the water phase. The introduction of the water creates an emulsion of the water in oil, which is passed between electrodes. The electric field between the electrodes coalesces the salt-laden droplets in the direction of the field. Successive coalescence events between droplets produce progressively larger droplets that settle under gravity into a bulk water phase that can be easily removed. Generally, these water in crude oil emulsions are strongly stabilized against coalescence by the adsorption onto the water/oil interface of surface-active components from the oil, particularly the alkylated, polyaromatic asphaltenes (for reviews, see Mullins et al.8−10). Asphaltenes adsorb onto the interface to form interfacial layers, which in time age and give rise to highly elastic skins that resist droplet coalescence under typical conditions (for reviews, see refs (11, 12) and the studies13−18). In an electrocoalescer, these highly stabilized droplets are forced to merge at sufficiently high electric field strengths. Despite the importance of the electrocoalescence process in the refining industry, the fundamentals of this phenomenon are still evolving. This is in part due to the difficulty of examination of electrocoalescence in crudes because of the oil opacity. Therefore, many studies thus far substitute oil with a clean, transparent fluid that may not reproduce the crude oil environment, e.g., refs (19−23).

Figure 1.

Figure 1

Open in a new tab

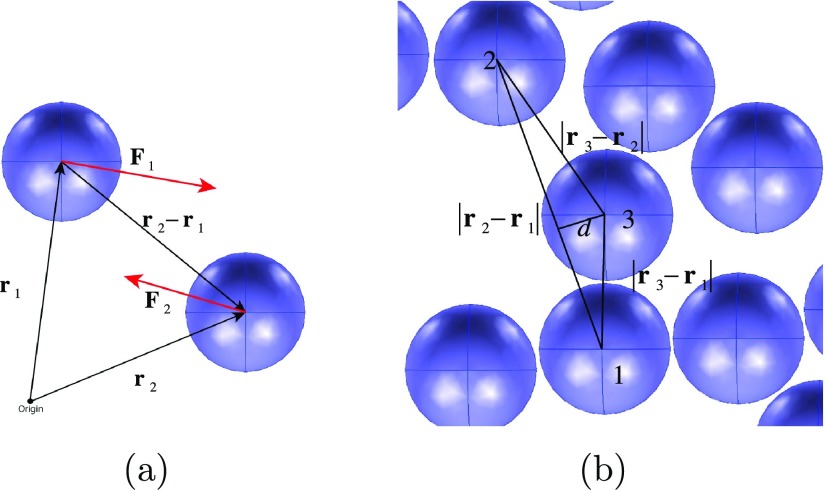
Induced dipole formation on the surfaces of a pair of spherical conducting aqueous droplets in a poorly conducting oil phase due to an imposed uniform electric field E̅ and the dipole–dipole interaction between the droplets, which creates an interdroplet attractive force.

Microfluidics can enable a direct visualization of electrocoalescence in crudes by generating emulsions in which the droplets are arranged in a single layer with a small depth transparent to optical microscopy, e.g., refs (24, 25). Microfluidics also offers the ability to form emulsions of controlled and uniform size (e.g., through the use of “T” junctions, flow-focusing orifices, and capillary tips).26−29 The first goal of this study is to demonstrate these unique fluid handling and visualization capabilities of microfluidics using crude oil to demonstrate how the electrocoalesence process in crudes can be examined in situ using microfluidics.

More recently, interest in electrocoalesence has focused on lab on chip devices30−40 in which two-dimensional (2D) water-in-oil emulsions are used for chemical or biological assays, extractions, and separations. In this context, electrocoalescence has drawn interest as a means for combining droplets and breaking water-in-oil emulsions to complete the chip operations (see for example41−50). As explained below, the model problem of the electrocoalescence of droplet pairs has been theoretically and experimentally examined as in Figure 1. However, few studies have examined theoretically the dynamics of electrocoalescence of emulsions in which the breakdown process is determined by multiple attractive and repulsive forces exerted on each droplet. This multidroplet process underlies the breakdown of water-in-crude oil emulsions and the combining of droplets and the breakdown of emulsions on lab on-chip processes. The second goal of this study is to obtain theoretical solutions for the electric field in the continuous phase of a microfluidically generated uniform 2D emulsion to predict electrocoalescence forces and coalescence events and to compare these predictions with the experiments.

In this study, we use a microfluidic arrangement to generate a train of water droplets in a continuous crude oil phase in a channel. The train is directed to a wide chamber in which the droplets are arranged in a single layer lubricated from above and below by very thin layers of oil. We term this freely moving, two-dimensional assembly a “2D emulsion”. We apply an electric field along the layer to cause the droplets to merge and the emulsion to breakdown. Numerical configurations of droplet arrangements in this 2D emulsion are reconstructed from images of electrocoalescence experiments in a microfluidic chamber. The electrical forces exerted on the droplets are computed to predict merging events. These predictions coincide with the merging events observed in the experiment, suggesting the breakdown can be simulated and potentially programmed, and this is the second motivation of our study.

We begin with a brief review. Electrocoalescence of an isolated pair of droplets of water in a continuous oil under a uniform applied electric field, Figure 1, has been studied theoretically22,51−68 and experimentally.19−22,62,68−77 The electrohydrodynamic forces, which cause the droplets to merge in the direction of the field, have been described by the field-induced charge distribution on the surface of the droplets. For an isolated spherical water droplet of radius a placed in a uniform oscillating field (E̅ eiωt where E̅ is the amplitude, t is the time, and ω is the frequency), mobile ions in the water and possibly oil phases are conducted in the field direction. In electrocoalesence, the conductivities and dielectric constants of the droplet phase, σp and εp, are larger than those of the oil continuous phase, σm and εm. Therefore, free and bound positive (negative) charges accumulate at the side of the droplet facing (opposite) to the direction of the electric field. To leading order, an oscillating electric dipole aligned with the field, 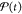Inline graphic, is induced as given by78−81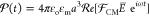Inline graphic. 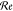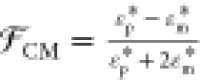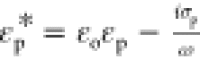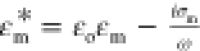Here, Inline graphic denotes the real part of the bracketed expression, Inline graphic is the Clausius Mossotti factor defined in terms of the complex dielectric constants of the oil and water phases with Inline graphic and Inline graphic, and εo is the permittivity of free space. 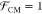Typically, σp ≫ σm and εp ≫ εm, and hence, Inline graphic. For a droplet pair, interaction forces arise principally because the dipole induced on each of the droplets falls within the dipole electric field created by its neighbor. For spherical droplets, the interaction depends on the angle of orientation of the droplet pair axis with the field, θ, and the edge-to-edge separation distance, s (Figure 1). If the electric field acting on each droplet is approximated by the far field dipole field of its neighbor, then the time average pairwise interaction force along the centerline is19−21,82

1. 1

where E̅RMS, the root mean square of the oscillating field, is equal to E̅/√2. The dipole field of the neighbor and correspondingly the force on the droplet intensify as the droplets approach one another. When the droplets are aligned with the field, θ = 0, the force is attractive as dipoles line-up end-to-end. Whereas, when the droplets are alongside each other, θ = π/2, the force is repulsive as the dipoles are parallel. Exact solutions for the interaction force between spherical conductors in a perfectly insulating dielectric (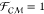Inline graphic) subject to a uniform electric field are obtained by Davis83 using bispherical coordinates. 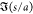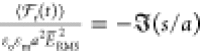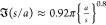For θ = 0, the interaction force is written in terms of the nondimensional function Inline graphic, i.e., Inline graphic. The bispherical exact solution for the force demonstrates that the dipole approximation is valid for s/a > 1, but the exact solution increases much more rapidly than the dipole approximation for s/a < 1. 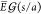For 10–3 < s/a < 10–1, a numerical fit22 is Inline graphic. For θ = 0, the bispherical solution shows that the maximum value of the electric field is at the poles of the droplets facing each other and is given by Inline graphic. This can be approximated as22,59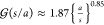Inline graphic for 10–3 < s/a < 10–1.

For a single aqueous droplet in oil subject to a uniform field (e.g., refs (53, 84−86)), the applied field exerts an electrical normal traction (Maxwell stress) on the induced free or bound surface charge. This, in turn, causes the droplets to deform in the field direction as prolate figures, which adopt conical tips (“Taylor” cones) at higher field strengths before bursting. This deformation scales as the electrocapillary number 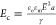Inline graphic where γ is the interfacial tension. For isolated droplet pairs approaching each other due to dipolar attraction and small Ec ≪ 1, the droplets remain spherical for s/a > 1. Assuming spherical shapes (Ec ≪ 1) and balancing the dipolar interaction force and viscous resistance with the lubrication theory for close enough separations (typically inertial forces are negligible), Eow et al.19 and Chiesa et al.20,21 compute trajectories starting from large separation distances s/a > 1 and up to coalescence. Their results agree well with corresponding experimental trajectories. More recent studies58,60−62,66,67,77 account for interface deformation and again map successfully theoretical predictions with experimental results on the trajectories of droplet pairs driven together by electrocoalescence.

The details of the final stages of electrocoalescence as the droplets approach to within a few tenths of a radius of each other and merge are more complicated. The merging process takes place on time scales of tens of milliseconds, which are typically much shorter than the time scale for the approach of droplets. As relatively spherical droplets approach (Ec ≪ 1) one another, the electric field exerted on the facing poles intensifies, and pronounced opposing prolate deformations develop that precede coalescence. These deformations have been examined theoretically by accounting for interface deformation in continuum computational simulations61−66 and molecular dynamics simulations.68

The final stages in the electrocoalescence process have also been visualized in small fluidic cells or microfluidic arrangements in which, in a continuous oil phase, an electric field is applied across free aqueous droplet pairs along their line of centers70−74 or anchored droplets at a fixed potential difference are arranged to face one another.75,87−94 The dynamics are visualized over a time interval of hundreds of milliseconds from an initial separation distance so/a. Three regimes are recognized: (i) no coalescence due to a large gap distance or a too small field strength, (ii) coalescence at large enough field strengths, or (iii) partial coalescence and repulsion at typically larger field strengths than necessary for coalescence. Coalescence is observed as a liquid bridge forms between the droplets from their individual prolate deformations. The liquid bridge then grows in radius to the order of the droplet radii bringing the droplets together into one fluid mass. In partial coalescence, the facing droplet interfaces are deformed into cones that connect to form a narrow bridge that becomes unstable, breaks, and drives a recoil. In the case of coalescence, which is of interest here, for anchored droplets at fixed potentials, Atten et al.89 measured the critical potential difference Vcrit at which the droplet faces merge. They correlated their results as the critical electrical capillary number 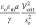Inline graphic as a function of so/a < 1 and find critical capillary numbers in the range of 0.2–0.4. These values agreed with their numerical calculations and are in the range of other theoretical calculations of anchored or suspended droplets in close proximity (so/a < 1), e.g., Latham and Roxburgh,51 Taylor,52 and Atten.59

The dynamics of electrocoalescence of multiple water droplets in water-in-oil emulsions has only been examined recently by Garstecki et al.95 They generated a 2D emulsion with flow focusing of water and hexadecane in a microfluidic cell and observed electrocoalescence across the emulsion under an AC field. They find a critical field strength necessary for electrocoalescence, which decreases with decreasing ω and increasing σp. This suggests that the faster the free charge relaxation in the water droplet phase (time scale 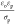Inline graphic) relative to the AC oscillation (1/ω), the greater is the charge separation (dipole strength) for an applied field. This is due to a redistribution of more free charge on the surface and higher droplet polarization, resulting in a greater dipolar attraction.

2. Results and Discussion

2.1. Visualization of Electrocoalesence in Crudes in a Microfluidic Cell

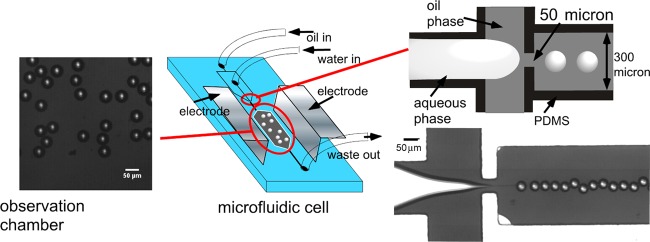
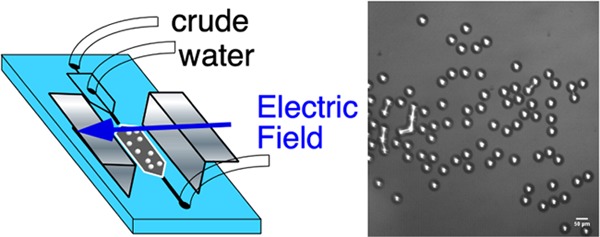
Our microfluidic experiments on the visualization of electrocoalescence of water droplets in an opaque petroleum crude are undertaken in a polydimethylsiloxane (PDMS) transparent cell using flow focusing at an orifice to form water droplets in the crude in a channel as a droplet train and directing the train to a wide chamber in which an AC field is applied to the 2D emulsion, which forms cf. Figure 2. (The fabrication of the cell, the material properties of the crude (including the dynamic oil/water tension), and the details of the applied field and frequency are described in the Experimental Section.) Figure 2 shows the flow-focusing production of the water droplets in oil at the orifice and the 2D emulsion of the droplets in the chamber prior to the application of the field. As is clear from the images, the droplets in the crude (which appears opaque and black in a 10 mL test tube) are readily visualized in the microfluidic cell due to the small thickness of the optical slice (60 μm). The droplets are monodisperse in size with a diameter of 2a = 36–48 μm. The assembled 2D emulsion presents interdroplet distances s, which vary from under one droplet diameter to several diameters. The separation distances are quantified when the droplet configuration is rendered for numerical calculation of the electric field and interdroplet forces. Under most circumstances in the flow-focusing generation of water drops in oil, surfactants are required in the oil phase to reduce the oil/water tension. This is necessary so that the water phase, drawn into a thread in the orifice, breaks into droplets.96 Here, the surface-active molecules native to the crude (e.g., asphaltenes) serve this role, and importantly, electrocoalescence of water droplets in crude can be examined in situ without any additional surfactants. The naturally reduced interfacial tensions of crudes against water (here 28 mN/m, Figure 8 in Experimental Section) allow a large deformability of the interface, ensuring that the water is easily segmented into drops at the flow-focusing orifice.

Figure 2.

Figure 2

Open in a new tab

Schematic of the microfluidic cell including the arrangement of the flow-focusing orifice to form individual droplets and the chamber in which the droplets assemble into a 2D emulsion and the electric field is applied. Shown also are images of the drop generation at the orifice (the schematic and the frame from the video) and the 2D emulsion in the chamber (the frame from the video). The scale bars are 50 μm.

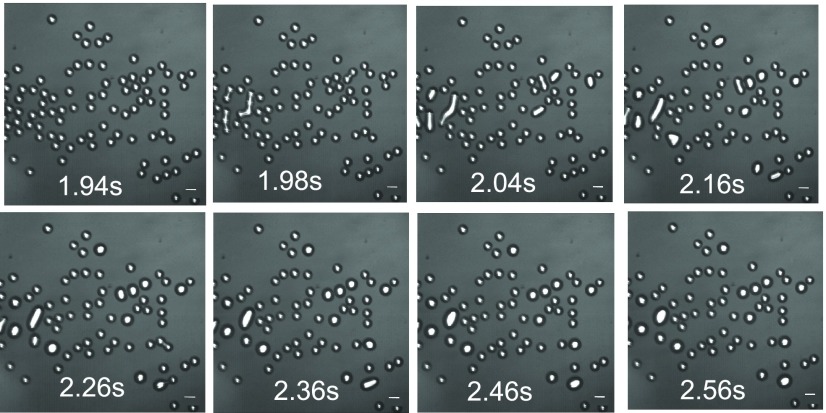
Figure 3 shows an illustrative sequence of images of electrocoalescence events in the chamber, over a period of approximately 1/2 s, for a field strength 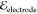Inline graphic = 250 V/mm. The images are a bird’s eye view of the 2D emulsion, with the field applied top-to-bottom, and with the assigned times relative to the moment the field is energized (the video is available in the Supporting Information.) For the first image shown in the sequence, no coalescence events have occurred. The sequence in Figure 3 includes droplet pairs coalescing, as well as events in which groups of three and four droplets coalesce. Also evident (the lower right-hand side of the figure) is a cascading event where two droplets merge, and the combined drop merges with a neighbor brought closer due to the prior electrocoalescence event as also observed by Garstecki et al.95 The coalescence events are clearly between droplets close enough so that they are a few tenths of a radius apart. Typically, coalescing droplets are aligned closely with the field. For an isolated pair of droplets, the dipole interaction force predicts an attractive force for 0 < θ < θc where θc is given by 3 cos2 θc – 1 =0, cf. eq (1), and is equal to 54.8°. For all of the coalescence events in Figure 3, the angle between the field and the line of centers between the droplet pair falls between 0 and approximately 55° in agreement with the dipole force approximation. Droplet pairs with angles larger than approximately 55° do not coalesce, even at close separation distance. Isolated droplet pairs that merge follow a common pattern in which they deform toward each other to create a joining liquid bridge (Figure 3). The faces of each drop, which are opposite to the bridging thread, remain more spherical as the field has not intensified on those surfaces away from the region between the drops. The connecting thread increases in radius until the drops merge and readopt a spherical configuration. While the coalescence process itself takes place on a time scale of milliseconds, the equilibration to a spherical shape takes place on a time scale of hundreds of milliseconds to 1 s. The triple droplet and quadruple droplet merging evident in the sequence of Figure 3 appear as simultaneous events between the multiple droplets. In these cases, connecting liquid threads form between adjoining pairs to form a merged cylinder that eventually relaxes to a spherical shape. Qualitatively, over the time frame studied, the coalescence events appear without noticeable movement of the droplets toward each other. Critical fields required for the coalescence of droplets a few tenths of a radius close to one another appear to be reached, and the droplets coalesce in place.

Figure 3.

Figure 3

Open in a new tab

Image sequence of the electrocoalescence of droplets in the chamber at times of 1.94–2.56 s, referenced from the moment (t = 0) the field is energized. In the first configuration, at 1.94 s, no droplets have yet coalesced. The scale bar is 50 μm. The field is applied top-to-bottom with 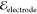Inline graphic = 250 V/mm.

2.2. Theoretical Calculation of Electric Field in the 2D Emulsion

Figure 3 makes clear that, upon application of the electric field, the electrocoalescence events in the crude oil can be recognized, cataloged, and sequenced. We demonstrate that these events can also be predicted by first computing the electric field distribution in the emulsion and then evaluating the field at the surfaces of the droplets to calculate the interdroplet forces and identify pairwise attractive interactions leading to the merging of droplet pairs. For a given droplet in the emulsion, the electric field that is experienced is determined by the imposed far field and by the droplets around them, and therefore the computation of the field is a mulitibody calculation. We use COMSOL Multiphysics 4.2 to obtain a numerical finite element solution for the electric field in the continuous oil phase. We start with an image captured at the beginning of an experiment in which the field has been turned on, but no coalescence has occurred (e.g., the first image of Figure 3). We render the two-dimensional images, representing the instantaneous configuration of uncoalesced droplets, into a three-dimensional (3D) COMSOL computational domain. This is intended to reproduce the observation chamber and the arrangements of droplets in the chamber. The droplets are modeled as fluid spheres and positioned in the computational domain at their exact locations in the image. The locations of the perimeters of the droplets in the 2D images are obtained by edge detection. The intensity range of each pixel is 0–255, and the perimeter is located by identifying the change in pixel intensity from bright (within the droplets) to dark (the exterior crude oil) along directions approximately perpendicular to the perimeter. The change occurs over the order of a few pixels, and the perimeter is demarcated as a set of points at which the area under the intensity vs pixel position on either side of a given point (relative to the asymptotic values on either side) is equal. Using this algorithm, the edge is located to an error of approximately one-half of a pixel or half a micron. The points are then fit to a circle with a radius, which is assigned to the radius of the droplet at that point. The center of the circle is assigned the center location of the droplet. A sphere is constructed from that center with the assigned radius and positioned halfway between the top and bottom of the chamber. 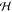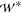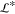The domain height is set equal to the chamber height Inline graphic = 60 μm, and the domain width (Inline graphic = 1 mm) and length (Inline graphic=1 mm section) are set equal to the width of the chamber and the length observed in the captured image. 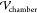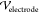The top and bottom are maintained at a potential difference Inline graphic, which is computed from the driving potential difference applied across the electrodes inserted into the PDMS (Inline graphic). Values of the dielectric constant of the cured PDMS elastomer (2.0)97 are approximately equal to the measured dielectric constant of the crude (2.5). 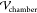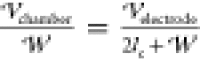Hence, for the purposes of the calculation of Inline graphic, the PDMS and crude in the chamber are considered as perfect dielectrics in capacitive series, leading to Inline graphic, which in the experiments is equal to 250 V/mm. Although the droplets settle downward during their residence time in the chamber, the approximation that they are at the center of the chamber for the electrostatic calculation is valid because the dielectric constants of the PDMS and oil are nearly equal. 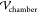The applied potential is 0 V on the bottom, −250 V = Inline graphic on the top. This is corresponding to the experimental gradient of 250 V/mm with the electric field directed from top to bottom. As the potentials are fixed, the calculations are undertaken assuming a static DC field is applied. As we demonstrate below, the equations and solutions for the electric field are all quasi-static. Hence from these solutions, to obtain the forces on the droplets to compare to the AC experiments, the square of the DC field strength used in the force calculations (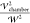Inline graphic) is replaced by 1/2 the square of the field, corresponding to the time average of the 250 V/mm AC field in the experiments.

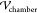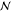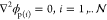To calculate the electric field, the crude, a poor conductor, is modeled as a “leaky dielectric”98 with zero volume charge density. This satisfies ∇2ϕm = 0, where ϕm is the oil electrostatic potential (made dimensionless with Inline graphic) and formulated in COMSOL’s cartesian coordinate representation of the computational domain. Each of the Inline graphic spheres in the computation domain is modeled as ohmic conductors in which the volume free charge relaxes quickly relative to 1/ω (i.e., Ω > 1). 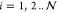Therefore, the potential field in the spheres is quasi-static and satisfies Inline graphic where ϕp(i) is the nondimensional electrostatic potential within drop i. 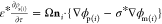The boundary conditions on the surface of each of the spheres are continuity of the electric potential, ϕm = ϕp(i), (Inline graphic) and the surface charge density conditions, Inline graphic (charge balance) and ε*ρs(i) = ni ·{ε*∇ϕm – ∇ϕp(i)} (Gauss’s law). 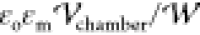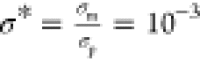Here, ni is the unit outward normal to the sphere i and τ is the time nondimensionalized by 1/ω and ρs(i) is the surface charge density on droplet i nondimensionalized by Inline graphic. 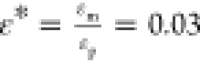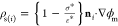Inline graphic and Inline graphic are, respectively, the ratios of the conductivities and dielectric constants of the continuous crude oil to the aqueous droplet phase. For Ω large and ϵ* small, the surface charge balance becomes quasi-static: ni·∇ϕp(i) = σ*ni·∇ϕm. We use this quasi-static formulation for the charge balance to obtain the potential fields, which are thereby quasi-static. 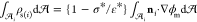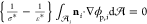In fact, since σ* ≪ 1, this quasi-static balance reduces to ni·∇ϕp(i) ≈ 0, which requires the electrostatic field in each of the droplets to be equal to zero and the droplets to be at uniform (though different) nondimensional potentials Inline graphic. The problem could be solved by computing the potential in the oil outside of the droplets subject to these constant potential conditions, but the potentials would have to be obtained by requiring zero charge on each of the droplets. Here, we retain the quasi-static surface charge balance at the droplet interfaces, using the measured values of the conductivities and dielectric constants for the simulation, and solve for the potentials within each drop as well as in the oil. 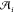In this way, the surface charge density can later be computed from Inline graphic. This charge density would automatically satisfy zero net charge on each droplet interface since from the charge balance Inline graphic = Inline graphic. Here, Inline graphic is the nondimensional area of droplet i scaled by a2 and the last equality follows because the droplet potential fields satisfy Laplace’s equation. The three-dimensional simulation domain is then closed by side walls in which the potential in the oil has assumed to relax. We also require nw·∇ϕm = 0 where nw is the unit outward normal to the side walls. To validate the calculations, we first compute the electric field and the electrocoalescence force between a droplet pair aligned with the field, see the Theoretical Calculation of Electric Field in the 2D Emulsion Section.

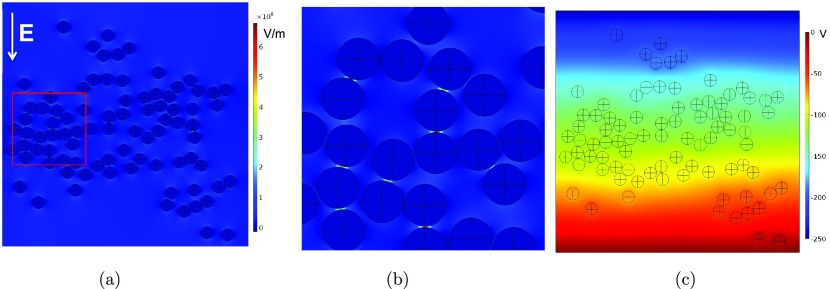
Figure 4a shows the COMSOL computational domain reproducing the configuration of the droplets in the 2D emulsion in Figure 3 for a time of 1.94 s, which is prior to any coalescence events. The figure also shows an overlay of a color map of the magnitude of the electric field in the droplets and continuous oil phase in the direction of the applied field. Although the field details are course, the enhanced electric fields between close droplet pairs whose center-to-center axes are approximately aligned with the applied field are clear. In comparison, the fields between droplet pairs aligned perpendicular to the field, even when they are very close together, are not as intensified. This can be understood if we consider, to a first approximation, the electric field between the droplets to be a superposition of the uniform far field and the dipolar fields generated by the dipoles created on the two droplets of the pair by the uniform field. Again to a first approximation, the droplet dipoles (Figure 1) lie in the uniform field direction. Each dipole field is strongest at the poles and weakest at the equator, and hence, the electric field is much larger in gaps between droplet pairs aligned with the uniform field. The electric fields within the droplets are zero. More details are provided in Figure 4b, which shows the electric field in the smaller region of the emulsion boxed in red in Figure 4a and in Figure 4c, which shows the electric potential of the larger region. Figure 4b clearly indicates the intensification of field strength between droplets aligned with the field. Note from the color map that the field is of order 5.0–7.5 × 106 V/m between the closest droplets aligned with the field. This is approximately 20–30 times the applied gradient of 2.5 × 105 V/m. The potential distribution, however, indicates that, for a given droplet pair, the dipolar fields generated from the assemblage of neighboring droplets also affect the field between the pair. The droplets are at uniform (though different) potentials as is clear from the color map of Figure 4c. Consequently, groups of droplets with uniform potentials within their interiors attenuate the up-down potential gradient imposed by the electrodes. This is clearly evident in the transverse zones of nearly uniform color in Figure 4c that widen as they envelop groups of droplets. If the conductivities of the droplets were equal to that of the oil, the applied potential gradient would be unattenuated, and the potential field would consist of straight, parallel stripes transversing the domain. The attenuation of the applied field and the local change in the gradient of the potential from the strictly up-down direction imposed by the electrodes affect the polarization of the droplets and the intensity and orientation of the dipoles induced on the droplets. Changes in dipolar intensity and direction affect the interdroplet forces and the pattern of droplet electrocoalescence.

Figure 4.

Figure 4

Open in a new tab

(a) Rendering of the COMSOL computational domain for the configuration of droplets in the 2D emulsion subject to a uniform field (up-to-down) as depicted in the image of Figure 2 at 1.94 s, prior to electrocoalescence events. Also shown is a superposition of the magnitude of the electric field (in the uniform field direction) in the oil and droplet phases. (b) Color map of the magnitude of the electric field for the inset region shown in (a). (c) Color map of the electrostatic potential around the droplets for the scale as in (a).

2.3. Theoretical Calculation of Electrocoalescence Forces

From the finite element simulations of the quasi-static electric field around the droplets in their arrangement in the 2D emulsion, the electrical forces on each of the droplets can be computed. This provides a detailed understanding and prediction of the coalescence events. We consider precoalescence arrangements at 1.94 s (i.e., Figure 3) and predict the merging events for t > 1.94 s. Excepting coalescence events, the fluids in the continuous and droplet phases are relatively static. The hydrodynamic stresses due to the flow recirculation move droplets relative to one another. However, Figure 3 indicates that this drifting does not move the droplets appreciably over the half-second of the duration of the sequence. (As the drift velocity is of order 20 μm/s, this short time period would correspond to (1/2) of a radius in movement.) In our consideration of the coalescence events, we only examine a window of 100 ms from an observed configuration prior to any coalescence (e.g., the first three snapshots in Figure 3). We therefore neglect the slow flow as the integrated effects of the hydrodynamic drift forces are negligible. 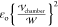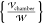For the static arrangement, the oil phase is only subject to the nondimensional pressure pm, scaled by Inline graphic, and the force of the field on the polarization charge Pm·∇Em = (1/2)(εm – 1)∇{|Em|2}. 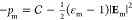Here, Em = −∇ϕm is the nondimensional electric field scaled by Inline graphic and Pm is the nondimensional polarization in the oil. 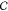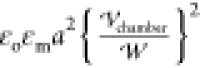The pressure is given by Inline graphic where Inline graphic is a constant. The dimensionless force on droplet i, Fi, scaled by Inline graphic, is the integration of the dimensionless Maxwell tension, Tm = εmEmEm – (1/2)|Em|2I, and the pressure, where I is the unit tensor. 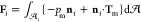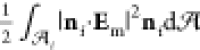Thus, Inline graphic = Inline graphic where the contribution of the tangential component of the electric field is neglected due to the high conductivity of the aqueous phase relative to the oil.

For a pairwise set of droplets (i, j) we compute the nondimensional interdroplet interaction force as Fi,j = r̂i,j·{Fj – Fi}. Here, r̂i,j is the unit vector extending from droplet i to droplet j in the field. As shown in Figure 5a, for droplets “1” and “2” with dimensionless position vectors r1 and r2 (scaled by a) from an origin and forces F1 and F2, 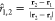Inline graphic. With this definition, negative values of Fi,j indicate attraction between the pair along their line of centers and positive values repulsion. Each droplet only has a certain number of nearest neighbors, which block its potential coalescence with other droplets. Therefore, an algorithm is employed to identify which droplet pairs are not obstructed by a third droplet and are potentially able to coalescence. For example (Figure 5b), droplet 2 is an accessible neighbor of droplet 1 if the distance d from droplet “3” center to the line of centers from droplet 1 to droplet 2 is greater than the radius of droplet 3.

Figure 5.

Figure 5

Open in a new tab

(a) Position and force vectors for defining the interdroplet force and (b) algorithm for identifying accessible neighbors.

Using these calculations, in Figure 6, the instantaneous normalized, nondimensional force F̃i,j between pairs of droplets (i, j) of accessible neighbors acquired from captured images is plotted as a function of the pair separation distance, s/a. Circles denote the fate of the pair over the following 100 ms, i.e., coalescence (red) or noncoalescence (blue). Figure 6 displays the results of six sets of experiments, of which Figure 3 represents one set, with approximately 60–80 droplets in each set, and with all drops considered in the simulation. The total number of droplet pairs accessible for coalescence, which are reported in Figure 6, is 288 with 84 pairs coalescing. 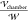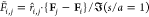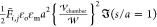In Figure 6, the nondimensional force is scaled by the force between two isolated droplets, which are subject to, and aligned with, a uniform field (Inline graphic) at one radius of separation as computed by Davis;83 thus Inline graphic. The dimensional interdroplet force is therefore given by Inline graphic. The factor of 1/2 accounting for the AC applied field.

Figure 6.

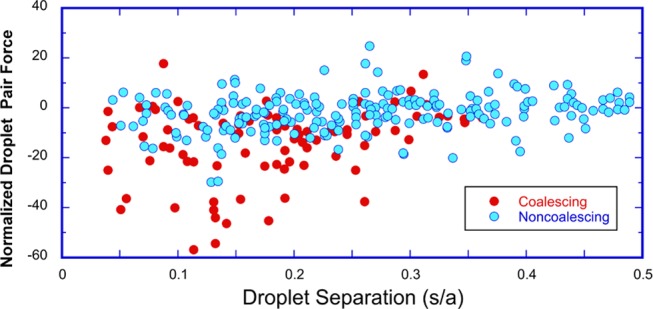
Figure 6

Open in a new tab

Plot of instantaneous normalized nondimensional electrostatic force, F̃i,j calculated between droplet pairs in 2D emulsion configurations as obtained from captured images taken prior to any coalescence. The nondimensional force F̃i,j is scaled by the Davis83 calculation of the force between a droplet pair aligned with the field and at one radius separation, i.e., 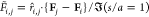Inline graphic. Filled red (blue) circles indicate droplet pairs that coalesce (do not coalesce) over an interval of 100 ms from the time that the image configuration on which the forces are computed is taken.

The interdroplet separation distances s/a plotted in Figure 6 are between 0.05 and 0.5. Separation distances s/a from 0.5 to about 2 are observed, but these typically correspond to pairs in which coalescence is not possible because of intervening neighbors (Figure 5b). For separations larger than approximately two with no intervening neighbors are present, but they are too far to coalesce in the 100 ms of observation from the frame capture. We also note that the shortest edge-to-edge separation distance observed in the plot is 0.05, which approaches the limit of the accuracy in the detection of the droplet edge (0.025).

Figure 6 makes clear that large normalized, nondimensional attractive forces, from −20 to −40, develop between the droplets for separation s/a < 0.25. This is as expected, since for the two-droplet problem, drops aligned with the field can, for 0.05 < s/a < 0.25, develop attractive forces 10 to 100 times the force at one radius of separation (the normalizing value in Figure 6). (See Figure 9 and the Atten et al.22 fit 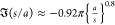Inline graphic for the two-droplet forces.) For larger values of the separation distance (0.5 > s/a > 0.25), the attractive forces drop off dramatically to the range of −10< F̃i,j < 0. This is also expected due to the significant reduction in the dipolar force (Figure 9a). Repulsive forces (F̃i,j > 0) are small over the entire range of separation distances, of order 1–10. This is also in agreement with the repulsive interaction force between two droplets aligned perpendicular to the field, where the repulsive force in magnitude is 0.1.83 The calculated larger repulsive values are due to the attractive interaction forces of neighboring droplets on the droplet pair, which act to push the droplets away from each other.

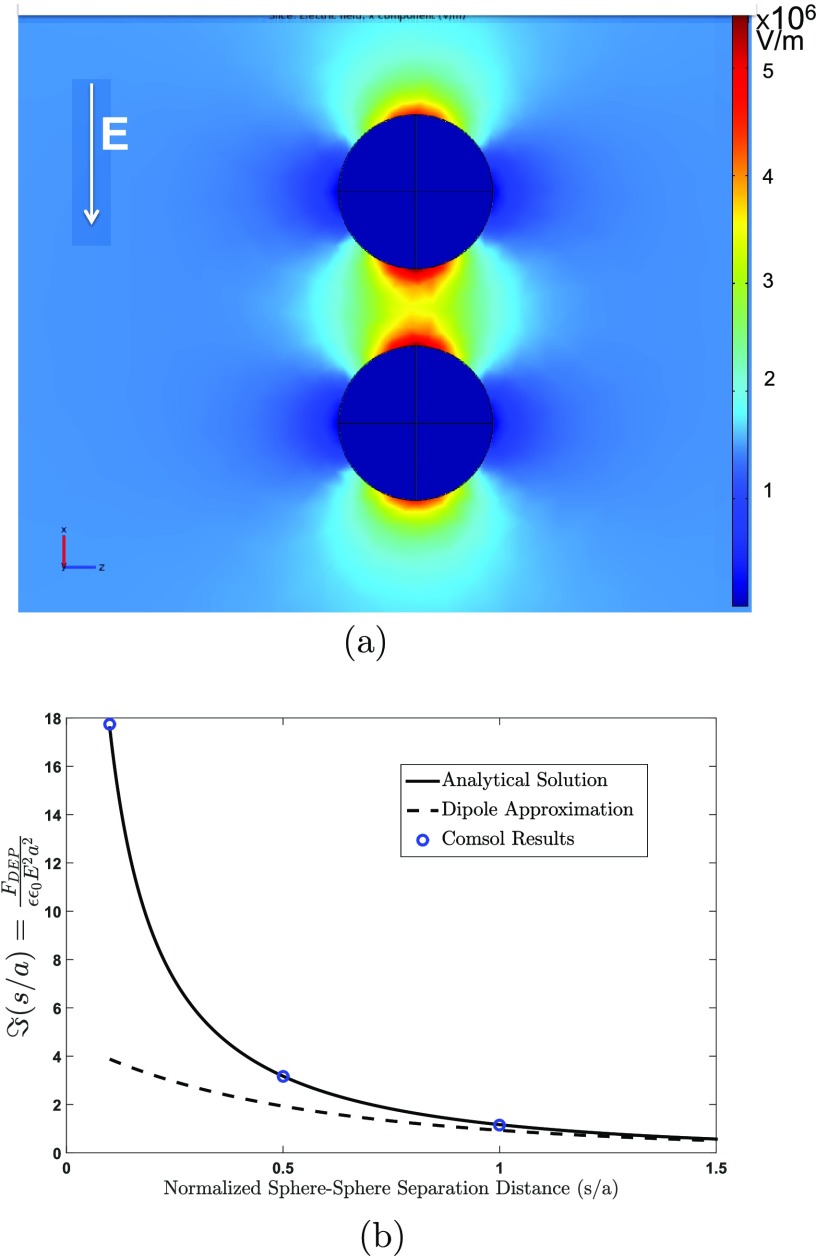
Figure 9.

Figure 9

Open in a new tab

(a) Pair of isolated droplets aligned with a uniform electric field applied far away (up-to-down) and a color map of the electric field in the uniform field direction as computed numerically (COMSOL). (b) The nondimensionalized attractive force 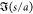Inline graphic exerted on each of the pairs as a function of the edge-to-edge separation s/a as computed from the COMSOL simulation and the bispherical analytical solution83 and compared to the dipole approximation.

From Figure 6, an assessment can be made on whether droplet pairs, which are calculated to be attractive in the instantaneous configuration in the images, do in fact coalesce in the 100 ms following the image capture. The figure indicates that almost all of the droplets with the largest attraction, |F̃i,j| > 20, which fall in the range s/a < 0.25, do coalesce. This is made clearer in a histogram plot, Figure 7a, of the count of the number of pairs, which coalesce (or do not coalesce), binned as a function of the normalized droplet pair force, |F̃i,j| > 20. The reason that the few pairs (3, cf. Figure 7a) that do not coalesce is the fact that one member of the pair coalesced with a member of another pair. However, less than half of the droplet pairs with smaller computed attractive forces, |F̃i,j| < 20, coalesces, even when the distance of separation is small (0.05 < s/a < 0.35). Pairs with even smaller attractions (|F̃i,j| < 10) and greater separations (0.35 < s/a < 0.5) do not coalesce at all.

Figure 7.

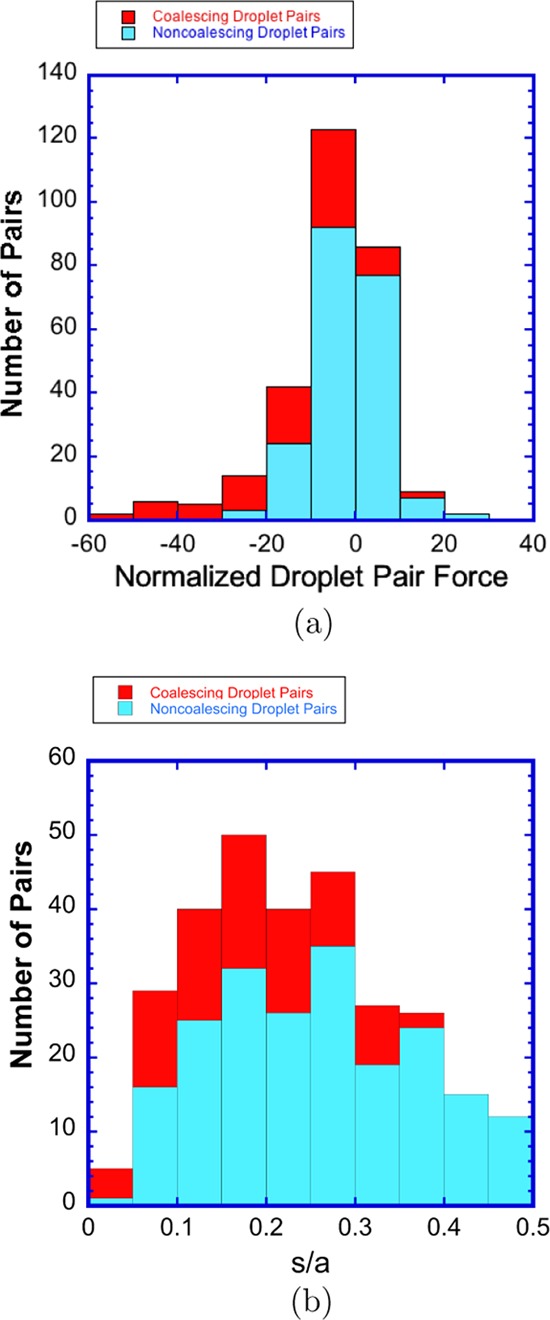
Figure 7

Open in a new tab

Histograms of the number of droplet pairs that coalesce or do not coalesce binned as a function of (a) normalized pairwise force F̃i,j and (b) separation distance s/a.

To understand these results, we note that a coalescence event occurs as droplet pairs approach to a critical distance where the field strength is large enough that droplets deform significantly and join through a liquid bridge, as seen in Figure 3. For the instantaneous configurations on which the normalized attractive and repulsive forces are calculated, the measured separation distances that are plotted are small (0.05 < so/a < 0.5). Coalescence is achieved as long as the droplet pair, either initially or within the 100 ms of observation, comes to a separation distance such that the critical field strength (which is a function of the dipoles of its neighbors) for coalescence is reached. To predict coalescence, we can use the results on the merging of anchored droplets. As reviewed in the introduction, in these studies (Atten et al.89), anchored, facing droplets are held at a fixed potential difference V and positioned at initial separation distances 10–3 < so/a < 1. The droplets deform and are found to merge when the imposed potential difference V exceeds a critical value Vcrit. The merging occurs at a critical distance, scrit/a, which is approximately 0.6 so/a. At this critical distance, the Maxwell tensions exerted by the normal electric field strengths at the facing poles are large enough that equilibrium solutions for prolate shapes no longer exist and droplets merge. This critical potential difference is correlated in terms of a critical electrocapillary number, which can be defined in terms of the electric field strength at the facing poles of the droplet pair at the coalescence point, i.e., 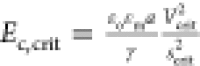Inline graphic. This is equal to 0.2–0.4, depending on the initial separation and the size of the capillary tips anchoring the droplets to the droplet radii.

With the above as context, consider first the droplet pairs with a large net attractive force, |F̃i,j| > 20 (so/a < 0.25). By examining the droplet pairs in this class, we observe that in most cases, the pair is aligned along the field (or close to this orientation) and at a short enough separation distance, so that the electric field at the facing poles is large. In addition, in these cases, the neighbors are either located at a far enough distance that they do not interact with the pair in the calculation of the interdroplet force or are arranged around the droplet pair perpendicular to the field so that only small repulsive forces are exerted. In these cases, the field at the poles is large enough that the critical capillary number is exceeded and the droplets coalesce. From the color map in Figure 4b as an example and using the exact calculations, we find that the droplets with large net attractive force (|F̃i,j| > 20) have electric fields at their facing poles, which are 20–30 terms larger than the applied field strength. The electrocapillary number corresponding to the applied field strength of 250 V/mm and γ = 28 mN/m (the value of the dynamic tension at the residence time for the droplets in the wide chamber) is equal to 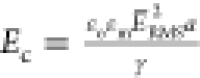Inline graphic= 5 × 10–4 (using the RMS value for the field). The droplets with large attractive force |F̃i,j| > 20 (separations s/a < 0.25 and electric field amplification of 20–30 the applied strength) have electrocapillary numbers in the range of 0.2–0.45. This is in the interval for coalescence and explains why they coalesce. It is also important to note that the electrocapillary numbers, at the point of coalescence with amplification of the fields, are still relatively small. Therefore, the droplets remain spherical until the point of coalescence, as is evident in the images of Figure 3a,b, and this is true in all of the remaining cases discussed below. The classes of droplets in Figure 6 with very small mutual attraction forces |F̃i,j| < 10 and large separations 0.35 < s/a < 0.5, on examination, have electric field values at their poles less than 10 times the applied strength. This leads to electrocapillary numbers no greater than 0.05, insufficient for coalescence.

In the class of droplets in Figure 6 with small attractive forces |F̃i,j| <20 for s/a < 0.35, some merge and some do not. An examination of the pairs in this category shows that the ones that do not merge have field amplification at the poles, which are smaller than 10, and hence electrocapillary numbers below the range required for coalescence. The ones that do merge have the requisite amplification, though, interestingly their attractive force is not as large as the droplets in the class where |F̃i,j| > 20. Case by case examination shows the coalescing pairs have neighbors in the field direction, which are close enough to exert attractive forces that reduce the net attractive interdroplet force between the pair. Thus, droplets can merge even if the attraction is not large. For this same reason, the few droplets pairs with net repulsion, which do merge in Figure 6 on examination, have bounding neighbors in the field direction that exert strong attractions on the pair members. This provides a resulting net repulsion between the members, even though the field on the facing surfaces of the droplets of the pair is large enough for coalescence. The above analysis of the criteria for electrocoalescence does not take into account the effect of the asphaltene film on the droplet interface on the coalescence. When an asphaltene film is present with a large surface elasticity, the elastic forces contribute to the restoring effects. This phenomenon acts against the Maxwell stress, and thus the restoring forces due to the tension are not the only surface restoring forces. The dynamics of the interface for this case has not been studied in detail, but a starting point would be to assume an equation of state for the tension, which would include the elastic effect due to the stretching of the asphaltene film. 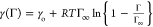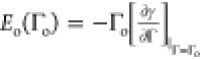Following Rane et al.,17 we could start with their supposition that the Langmuir equation of state is valid, Inline graphic where Γ is the surface concentration of the asphaltene, Γ∞ is the maximum packing concentration of the asphaltene, and γo is the tension in the absence of asphaltenes. As the area of the interface changes during electrocoalescence, the surface concentration changes. If we assume no additional adsorption during the time scale of the electrocoalescence process, then the surface concentration is given by the conservation equation, and the area expansion represents the strain on the film. 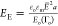For this case, the elasticity of the layer, which would account for the surface film, is Inline graphic where Γo is the asphaltene concentration at the point in which the field is applied. Following in this way, two nondimensional groups would appear. The first group is the electrocapillary number and a second group (Inline graphic) corresponding to the ratio of the Maxwell stress to the film elasticity. Note that in this formulation, the surface concentration Γo is directly related to the aging. For electrocoalesence, these ratios should exceed critical values. We note that other elastomechanical expressions could be formulated instead of the Langmuir equation of state, but in all cases, a second group would appear representing a value for the characteristic Maxwell stress to the characteristic film elasticity. Rane et al.17 undertake measurements of the film elasticity by oscillating a pendant drop and find that Eo increases with the age of the drop, with values between 0 and 30 mN/m for aging between 0 and 120 min. Hence, the elasticity is of the order of the tension. In our analysis, we base our criteria for electrocoalescence on the values of Ec, stating that when Ec is large enough, electrocoalescence occurs as the Mawell stresses are sufficiently larger than the tension. Since the elasticity is the same order as the tension, if Maxwell stresses are sufficiently large to exceed the restoring force of tension, the same should be true for the restoring force of elasticity. If the interfacial tension is extremely low (<1mN/m), then the dominant effect would be the elastic resistance. Alternatively, if the droplets are only aged a short amount of time, the elasticity is very low and the dominant effect is the tension.

3. Conclusions

This study has examined the process of electrocoalescence in a 2D emulsion of conducting water droplets in an insulating oil phase, which is generated in a microfluidic cell. An electric field applied across the emulsion induces charge separation and dipole formation in the conducting water droplets. The polarized droplets attract each other through dipolar forces, which intensify as the droplets approach to within a few tenths of a radius of each other. Petroleum crude is used for the oil because of the important applications of electrocoalescence to the removal of water from the crude. However, current interest is focused on the “droplet-based” microfluidic lab on chip applications that use electrocoalescence to combine droplets and break emulsions. Our microfluidic design uses flow focusing of water in oil to generate water droplets of uniform size, which are guided downstream as a single layer into a wide observation chamber. The 2D emulsion forms as the droplets collect in the chamber and an electric field is applied across the chamber to induce electrocoalescence. Our study provides two unique contributions: We demonstrate that our microfluidic design enables the electrocoalescence process in an opaque continuous phase to be visualized on the scale of the droplets with optical microscopy because the narrow chamber height allows the emulsion to become transparent. Electrocoalescence events are observed on an individual droplet basis, allowing an in situ examination of the merging process. Our study also demonstrates that the droplet scale data can be modeled to identify critical conditions for electrocoalescence using a local electrocapillary number. Numerical simulations for the electric field around the droplets in 2D configurations rendered directly from frame captures of microscopy images are obtained and used to compute the forces on the droplets. From the calculated forces, the mutual forces of attraction (or repulsion) between droplet pairs in the rendered images are examined as a function of the pair separation distance. These calculations are correlated with whether the droplet pair coalesced in the short (100 ms) time interval that followed from the captured frame on which the force calculation was based. Large mutual attractive forces at small separations (a few tenths of a droplet radius) correlated to electrocoalescence of the pair as the electric field between the droplets exceeded the value necessary for coalescence. Larger separations (approximately one-half of a radius) and very small attractive (or repulsive) forces correlated to noncoalescing droplets as the electric field strengths are too low. Almost all droplet pairs with repulsive interactions did not coalesce. For droplet pairs at close separation (a few tenths of a droplet radius) and intermediate values for mutual attraction, some pairs coalesced and some did not. An examination of the electric field on the droplet surfaces showed that for droplet pairs in this class that did coalesce the field strength between the droplets became large enough for coalescence. However, the net forces on each of the droplets (and hence the mutual force of attraction) were reduced because of the attractive interactions with neighboring droplets. Our demonstration that the electric field in a 2D emulsion can be computed exactly from rendered images and used to correlate coalescence events allows for a more in-depth study of the factors affecting electrocoalesence. This can open the possibility of programming the electrocoalesence process by manipulation of the applied electric field. Our approach of simulating directly the multiple droplet electrocoalescence to identify critical field strengths is also applicable to a three-dimensional study, although the visualization of the droplets in 3D would require other techniques such as pulsed field gradient (PFG) NMR since the 3D crude would be opaque in a microfluidic arrangement in which the channel height was larger to accommodate a 3D dispersion of droplets. The use of PFG-NMR to study water in crude oil emulsions has been undertaken by Sjoblom et al.99−101

4. Experimental Section

A petroleum crude (ExxonMobil) with εm = 2.5 and σm = 1.1 × 10–8 S/m (measured by an impedance analyzer, Agilent), viscosity μm = 0.023 kg m–1 s–1 (cone and plate viscometer), and density ρm = 8.75 × 102 kg/m3 is used, and the aqueous droplet phase is DI water with an assumed εp of 80, a measured σp of 1.2 × 10–5 S/m (conductivity meter), and ρp = 1.0 × 103 kg/m3. The crude oil/DI water dynamic interfacial tension, γ, is measured using a pendant drop tensiometer (Kruss) and is shown in Figure 8. (All data at 20 °C, the temperature of experiments). The asphaltene content of the crude was obtained by extraction of the asphaltene with heptane (see e.g., ref (9) ASTM 863-69 standard), and the asphaltene content was 0.5 percent by weight and visually the crude appeared opaque.

Figure 8.

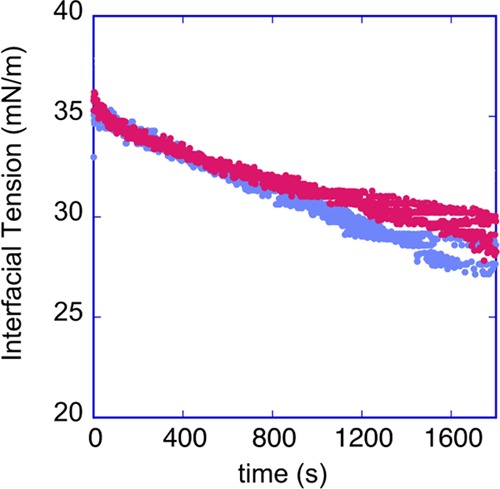
Figure 8

Open in a new tab

Dynamic interfacial tension between a crude oil droplet and DI water over a period of 2000 s; the graph shows three realizations.

The microfluidic cell is made using soft lithography102 and fabrication of two layers of polymerized and cured PDMS. One layer containing the open fluidic channels and chamber inscribed on one face is molded by curing PDMS (Sylgard 184, Dow Corning) over a negative epoxy master of the fluidic features. The second is a flat layer to seal the channel. The two layers are bonded together following exposure to an oxygen plasma and mounted on a standard glass microscope slide. Access ports cored into the top layer using a biopsy punch allow the introduction of the oil and aqueous streams via polyethylene tubing (1.5 mm OD) inserted into the ports and connected to syringe pumps (Harvard Apparatus PHD). The exit port allows the emulsion to exit through inserted tubing. A monodisperse train of water droplets suspended in the crude is generated by flow-focusing streams of crude and water through separate channels from entry ports to an orifice where the droplets are formed. 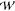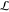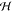The train is directed through a feeding channel to a holding chamber (width Inline graphic = 3 mm and length Inline graphic = 10 mm) in which the droplets arrange themselves in an arbitrary configuration to form the 2D emulsion, and in which the electric field is applied. Droplets leave the chamber through an exiting channel ending in an exit port. 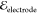Feeding and exit channel widths to the chamber are 300 μm and 2 mm long, and the height of the channels and chamber is Inline graphic = 60 μm, which (see below) is small enough for the crude to be transparent. The flow-focusing orifice is 50 μm in width, and at the flow rates of oil and water used (qm = 0.2 μL/min and qp = 0.02 μL/min, respectively), droplets approximately 40 μm in diameter are generated. The droplets move through the feeding channel and the chamber as a single layer. 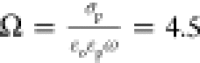For the field generation, planar electrodes of aluminum are inserted through the cell, perpendicular to its lateral plane, and sited parallel to the chamber at a distance Inline graphic. The electrodes were connected to an amplifier (TeK) controlled by a frequency generator (Agilent), which applied a potential Inline graphic across the electrodes. To prevent accumulation of charge and reduction of field strength, a sinusoidal AC rather than a DC driving potential is applied across the electrodes. The applied field is oscillated at a frequency ω = 500 Hz so that Inline graphic and the free volume charge in the conducting aqueous phase relaxes quickly relative to the inverse of the frequency. Droplet coalescence events in the chamber are visualized by optical microscopy using a microscope (Nikon) in the bright-field mode and recorded with a high-speed camera (Redlake, 50 frames/s) with a 10×, N.A. 1.4 (air) objective. The sensor has a pixel area of 1280 × 1024, and the field of view in the observation cell was 1 mm × 1 mm or a resolution of approximately 1 μm per pixel.

The experiments are undertaken in a continuous flow-through mode. The width of the chamber in the microfluidics device is much larger than the width of the microchannel, which feeds the droplets into the chamber. Therefore, the droplet movement in the chamber is relatively slow, and the droplets appear to drift very slowly across the field of view. At the oil flow rate qm used, the characteristic velocity of the droplets in the channel is 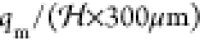Inline graphic ≈ 200 μm/s and in the chamber is ⟨v⟩ = 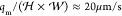Inline graphic. In the absence of an applied field, a steady state is established, the field is then energized for a few seconds, and a video of the coalescence dynamics in the chamber is recorded from the moment the potential is applied. The field is then turned off, and the slow flow in the chamber flushes the coalesced drops out. The experiment is then repeated after microscopy observation reveals there are no coalesced droplets in the chamber. 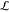Thus, for the droplets observed in the chamber during an experiment, the approximate time between their formation at the orifice and the initiation of the field is approximately 500 s (Inline graphic/⟨v⟩) as the residence time of the droplets in the channel feeding the chamber is only approximately 10 s (2 × 103 μm/200 μm/s). This 500 s time represents the approximate “aging time” of the droplets from their formation at the flow-focusing orifice. This time is important in applying the results of this microfluidic electrocoalescence study to the operation of field electrocoalescers. The residence time of the droplets in the electrocoalescer from their point of formation is important as it determines how long asphaltenes (and other surface-active material in the oil) have been allowed to adsorb from the oil onto the droplet surface. As we noted in the introduction, the greater this aging time the more elastic the interfacial layer and the more difficult it becomes for the droplets to merge. Conventional coalescers operate with a residences time of 30–40 min103 to deliver production rates of tens to hundreds of kilobarrales of oil/day. Newer compact designs, which have improved the efficiency of the electrocoalescence process, operate with lower holding volumes that have reduced this residence time.6,7 The residence times of 10 min in our experiments are of the order of the times for more compact electrocoalescers, so our study reflects realistic conditions. More importantly, the aging time can be increased (or adjusted to a desired value) within our microfluidic chip design by using longer, serpentine-shaped channels feeding into the chamber as undertaken by Nowbahar et al.24

5. Computational Methods

To validate the COMSOL calculation of the electrostatic field in the 2D emulsion of multiple water droplets in oil and the calculations of the forces on the droplets, we first simulate the electric field between two equally sized spherical droplets (radius a = 20 μm). The simulation is carried out for droplets in our computational chamber with the center-to-center axis between the droplets perpendicular to the top and bottom walls on which the potential difference 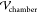Inline graphic is applied. 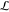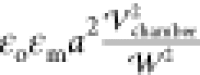The bounding surfaces of the chamber are set to be far from the droplet pair (Inline graphic = Inline graphic= Inline graphic = 10a). This represents the condition of a uniform electric field applied at infinity to two isolated drops, as solved by Davis83 analytically using bispherical coordinates. In Figure 9, we provide a color map of the field strength in a slice perpendicular to the top and bottom of the chamber. It contains the equatorial planes of both droplets for the conductivity and viscosity ratios of our multidroplet water-in-oil simulations (σ* = 10–3, ε* = 0.03). Since the droplets are so much more conductive than the oil, their electric fields are essentially zero in the droplets, as evident from the map. The intensification of the field between the droplets, which is the driving force of the electrocoalescence, is apparent with the highest field strengths at the poles of the facing droplets. Quantitatively, we obtain the attractive electrical force between the droplets, scaled by Inline graphic, (denoted by 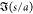Inline graphic as in the introduction) through the integration of the normal electric field on the surface of the droplets. This force is compared in Figure 9 with the exact analytical solution obtained by Davis.83 The agreement is excellent, demonstrating that because of the very low conductivity ratio of the oil to the water droplet phase, the field is essentially that of a continuous phase. The agreement also provides confidence in our COMSOL solutions for the multidroplet simulations. We also note that the dipole–dipole approximation for the force is satisfactory for interdroplet separations s/a larger than one.

Acknowledgments

This work was partially supported by an NSF grant to the Center for the Exploitation of Nanostructures in Sensors and Energy Systems (CENSES), an Army Research Office grant ARO W911NF-11-1-0161, the Donors of the American Chemical Society Petroleum Research Fund, and ExxonMobil Research and Engineering Co.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b04259.

  • AVI video of electrocoalesence corresponding to Figure 3 (AVI)

The authors declare no competing financial interest.

Supplementary Material

ao9b04259_si_001.avi (22.7MB, avi)

References

  1. Waterman L. Electrocoalescers. Chem. Eng. Prog. 1965, 61, 51–57. [Google Scholar]
  2. Galvin C. Design principles for electrocoalescers. IChemE Symp. Ser. 1986, 88, 101–113. [Google Scholar]
  3. Eow J.; Ghadiri M.; Sharif A.; Williams T. Electrostatic enhancement of coalecence of water droplets in oil: A review of the current understanding. Chem. Eng. J. 2001, 84, 173–192. 10.1016/S1385-8947(00)00386-7. [DOI] [Google Scholar]
  4. Eow J.; Gadhiri M. Electrostatic enhancement of coalescence of water droplets in oil: a review of the technology. Chem. Eng. J. 2002, 85, 357–368. 10.1016/S1385-8947(01)00250-9. [DOI] [Google Scholar]
  5. Lundgaard L.; Berg G.; Ingebrigtsen S.; Atten P.. Emulsions and Emulsion Stability; Sjoblom J., Ed.; Taylor and Francis, 2006; pp 549–592. [Google Scholar]
  6. Less S.; Vilagines R. The electrocoalescers’ technology: Advances, strengths and limitations for crude oil separation. J. Pet. Sci. Eng. 2012, 81, 57–63. 10.1016/j.petrol.2011.12.003. [DOI] [Google Scholar]
  7. Mhatre S.; Vivacquaa V.; Ghadiri M.; Abdullaha A.; Al-Marri M.; Hassanpour A.; Hewakandamby B.; Azzopardi B.; Kermani B. Electrostatic phase separation: a review. Chem. Eng. Res. Des. 2015, 96, 177–195. 10.1016/j.cherd.2015.02.012. [DOI] [Google Scholar]
  8. Mullins O. C. Review of the molecular structure and aggregation of asphaltenes and petroleomics. SPE J. 2008, 13, 48–57. 10.2118/95801-PA. [DOI] [Google Scholar]
  9. Mullins O. C. The asphaltenes. Ann. Rev. Anal. Chem. 2011, 4, 393–418. 10.1146/annurev-anchem-061010-113849. [DOI] [PubMed] [Google Scholar]
  10. Mullins O. C.; Sabbah H.; Eyssautier J.; Pomerantz A. E.; Barré L.; Andrews A. B.; Ruiz-Morales Y.; Mostowfi F.; McFarlane R.; Goual L. Advances in asphaltene science and the Yen-Mullins model. Energy Fuels 2012, 26, 3986–4003. 10.1021/ef300185p. [DOI] [Google Scholar]
  11. McLean J. D.; Spiecker P. M.; Sullivan A. P.; Kilpatrick P. K.. Structures and Dynamics of Asphaltenes; Springer, 1998; pp 377–422. [Google Scholar]
  12. Kilpatrick P. K. Water-in-crude oil emulsion stabilization: Review and unanswered questions. Energy Fuels 2012, 26, 4017–4026. 10.1021/ef3003262. [DOI] [Google Scholar]
  13. Ese M.-H.; Sjoblom J.; Fordedal H.; Urdahl O.; Ronningsen H. P. Ageing of interfacially active components and its effect on emulsion stability as studied by means of high voltage dielectric spectroscopy measurements. Colloids Surf., A 1997, 123, 225–232. 10.1016/S0927-7757(97)03963-0. [DOI] [Google Scholar]
  14. Yarranton H. W.; Hussein H.; Masliyah J. H. Water-in-hydrocarbon emulsions stabilized by asphaltenes at low concentrations. J. Colloid Interface Sci. 2000, 228, 52–63. 10.1006/jcis.2000.6938. [DOI] [PubMed] [Google Scholar]
  15. Verruto V. J.; Le R. K.; Kilpatrick P. K. Adsorption and molecular rearrangement of amphoteric species at oil- water interfaces. J. Phys. Chem. B 2009, 113, 13788–13799. 10.1021/jp902923j. [DOI] [PubMed] [Google Scholar]
  16. Pauchard V.; Rane J. P.; Zarkar S.; Couzis A.; Banerjee S. Long-term adsorption kinetics of asphaltenes at the oil-water interface: A random sequential adsorption perspective. Langmuir 2014, 30, 8381–8390. 10.1021/la500384r. [DOI] [PubMed] [Google Scholar]
  17. Rane J. P.; Zarkar S.; Pauchard V.; Mullins O. C.; Christie D.; Andrews A. B.; Pomerantz A. E.; Banerjee S. Applicability of the Langmuir equation of state for asphaltene adsorption at the oil-water interface: Coal-derived, petroleum, and synthetic asphaltenes. Energy Fuels 2015, 29, 3584–3590. 10.1021/acs.energyfuels.5b00179. [DOI] [Google Scholar]
  18. Qiao P.; Harbottle D.; Tchoukov P.; Masliyah J.; Sjoblom J.; Liu Q.; Xu Z. Fractionation of asphaltenes in understanding their role in petroleum emulsion stability and fouling. Energy Fuels 2017, 31, 3330–3337. 10.1021/acs.energyfuels.6b02401. [DOI] [Google Scholar]
  19. Eow J.; Ghadiri M. Drop-drop Coalescence in an electric field: The effects of applied electric field and electrode geometry. Colloids Surf., A 2003, 219, 253–279. 10.1016/S0927-7757(03)00051-7. [DOI] [Google Scholar]
  20. Chiesa M.; Melheim J.; Pedersen A.; Ingebrigtsen S.; Berg G. Forces acting on water droplets falling in oil under the influence of an electric field: numerical predictions versus experimental observations. Eur. J. Mech. B-Fluids 2006, 24, 717–732. 10.1016/j.euromechflu.2005.03.005. [DOI] [Google Scholar]
  21. Chiesa M.; Ingebrigtsen S.; Melheim J.; Hemmingsen P.; Hansen E.; Hestad O. Investigation of the role of viscosity on electrocoalescence of water droplets in oil. Sep. Purif. Technol. 2006, 50, 267–277. 10.1016/j.seppur.2005.12.003. [DOI] [Google Scholar]
  22. Atten P. Electrohydrodynamics of dispersed drops of conducting liquid: From drop deformation and interaction to emulsion evolution. Int. J. Plasma Environ. Sci. Technol. 2013, 7, 2–12. [Google Scholar]
  23. Yeganeh M.; Hegner J.; Lewandowski E.; Mohan A.; Lake L. W.; Cherney D.; Jusufi A.; Jaishankar A. In Capillary Desaturation Curve Fundamentals, SPE improved oil recovery conference. Tulsa, Oklahoma, USA, 2016.
  24. Nowbahar A.; Whitaker K. A.; Schmitt A. K.; Kuo T.-C. Mechanistic study of water droplet coalescence and flocculation in diluted bitumen emulsions with additives using microfluidics. Energy Fuels 2017, 31, 10555–10565. 10.1021/acs.energyfuels.7b01619. [DOI] [Google Scholar]
  25. Lin Y.-J.; Perrard A.; Biswal S. L.; Hill R. M.; Trabelsi S. Microfluidic investigation of asphaltenes-stabilized water-in-oil emulsions. Energy Fuels 2018, 32, 4903–4910. 10.1021/acs.energyfuels.8b00249. [DOI] [Google Scholar]
  26. Baroud C. N.; Gallaire F.; Dangla R. Dynamics of microfluidic droplets. Lab Chip 2010, 10, 2032–2045. 10.1039/c001191f. [DOI] [PubMed] [Google Scholar]
  27. Gu H.; Duits M.; Mugele F. Droplets formation and merging in two-phase flow microfluidics. Int. J. Mol. Sci. 2011, 122, 2572–2597. 10.3390/ijms12042572. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Bremond N.; Bibette J. Exploring emulsion science with microfluidics. Soft Matter 2012, 8, 10549. 10.1039/c2sm25923k. [DOI] [Google Scholar]
  29. Huerre A.; Miralles V.; Jullien M. Bubbles and foams in microfluidics. Soft Matter 2014, 10, 6888–6902. 10.1039/C4SM00595C. [DOI] [PubMed] [Google Scholar]
  30. Theberge A. B.; Courtois F.; Schaerli Y.; Fischlechner M.; Abell C.; Hollfelder F.; Huck W. T. S. Microdroplets in microfluidics: An evolving platform for discoveries in chemistry and biology. Angew. Chem., Int. Ed. 2005, 49, 5846–5868. 10.1002/anie.200906653. [DOI] [PubMed] [Google Scholar]
  31. Urbanski J. P.; Thies W.; Rhodes C.; Amarasinghe S.; Thorsen T. Digital microfluidics using soft lithography. Lab Chip 2006, 6, 96–104. 10.1039/B510127A. [DOI] [PubMed] [Google Scholar]
  32. Huebner A.; Sharma S.; Srisa-Art M.; Hollfelder F.; Edel J. B.; deMello A. J. Microdroplets: A sea of applications. Lab Chip 2008, 8, 1244–1254. 10.1039/b806405a. [DOI] [PubMed] [Google Scholar]
  33. Teh S.-Y.; Lin R.; Hung L.-H.; Lee A. P. Droplet microfluidics. Lab Chip 2008, 8, 198–220. 10.1039/b715524g. [DOI] [PubMed] [Google Scholar]
  34. Chiu D.; Lorenz R.; Jeffries G. Droplets for ultra small-volume analysis. Anal. Chem. 2009, 81, 5111–5118. 10.1021/ac900306q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. i Solvas X. C.; deMello A. Droplet microfluidics: recent developments and future applications. Chem. Commun. 2010, 47, 1936–1942. 10.1039/C0CC02474K. [DOI] [PubMed] [Google Scholar]
  36. Joensson H. N.; Andersson-Svahn H. Droplet microfluidics-a tool for protein engineering and analysis. Lab Chip 2011, 11, 4144–4147. 10.1039/c1lc90102h. [DOI] [PubMed] [Google Scholar]
  37. Joensson H. N.; Andersson Svahn H. Droplet microfluidics a tool for single-cell analysis. Angew. Chem., Int. Ed. 2012, 51, 12176–12192. 10.1002/anie.201200460. [DOI] [PubMed] [Google Scholar]
  38. Guo M. T.; Rotem A.; Heyman J. A.; Weitz D. A. Droplet microfluidics for high-throughput biological assays. Lab Chip 2012, 12, 2146–2155. 10.1039/c2lc21147e. [DOI] [PubMed] [Google Scholar]
  39. Seemann R.; Brinkmann M.; Pfohl T.; Herminghaus S. Droplet based microfluidics. Rep. Prog. Phys. 2012, 75, 016601 10.1088/0034-4885/75/1/016601. [DOI] [PubMed] [Google Scholar]
  40. Sesen M.; Alan T.; Neild A. Droplet control technologies for microfluidic high throughput screening (micro HTS). Lab Chip 2017, 17, 2372–2394. 10.1039/C7LC00005G. [DOI] [PubMed] [Google Scholar]
  41. Schwartz J. A.; Vykoukal J. V.; Gascoyne P. R. C. Droplet-based chemistry on a programmable micro-chip. Lab Chip 2004, 4, 11–17. 10.1039/b310285h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Kralj J.; Schmidt M.; Jensen K. Surfactant enhanced liquid-liquid Extraction in microfluidic channels with inline electric field enhanced coalescence. Lab Chip 2005, 5, 531–535. 10.1039/b418815b. [DOI] [PubMed] [Google Scholar]
  43. Ahn K.; Agresti J.; Chong H.; Marquez M.; Weitz D. A. Electrocoalescence of drops synchronized by size-dependent flow in microfluidic channels. Appl. Phys. Lett. 2006, 88, 264105–3. 10.1063/1.2218058. [DOI] [Google Scholar]
  44. Wang W.; Yang C.; Li C. Efficient on-demand compound droplet formation: From microfluidics to microdroplets as miniaturized laboratories. Small 2009, 5, 1149–1152. 10.1002/smll.200801598. [DOI] [PubMed] [Google Scholar]
  45. Niu X.; Gielen F.; deMello A. J.; Edel J. B. Electro-coalescence of digitally controlled droplets. Anal. Chem. 2009, 81, 7321–7325. 10.1021/ac901188n. [DOI] [PubMed] [Google Scholar]
  46. Zagnoni M.; Cooper J. M. On-chip electrocoalescence of microdroplets as a function of voltage, frequency and droplet size. Lab Chip 2009, 9, 2652–2658. 10.1039/b906298j. [DOI] [PubMed] [Google Scholar]
  47. Zagnoni M.; Lain G. L.; Cooper J. Electrocoalescence mechanisms of microdroplets using localized electric fields in microfluidic channels. Langmuir 2010, 26, 1443–14449. 10.1021/la101517t. [DOI] [PubMed] [Google Scholar]
  48. Gu H.; Murade C.; Duits M.; Mugele F. A microfluidic platform for on-demand formation and merging of microdroplets Using Electric Control. Biomicrofluidics 2011, 5, 011101 10.1063/1.3570666. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Chokkalingam V.; Ma Y.; Thiele J.; Schalk W.; Tei J.; Huck W. An Electro-coalescence chip for effective emulsion breaking in droplet microfluidics. Lab Chip 2014, 14, 2398–2402. 10.1039/C4LC00365A. [DOI] [PubMed] [Google Scholar]
  50. Bhattacharjee B.; Vanapalli S. Electrocoalescence based serial dilution of microfluidic droplets. Biomicrofluidics 2014, 8, 044111 10.1063/1.4891775. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Latham J.; Roxburgh I. Disintegration of pairs of water drops in an electric field. Proc. R. Soc. London, Ser. A 1966, 295, 84–97. 10.1098/rspa.1966.0227. [DOI] [Google Scholar]
  52. Taylor G. The coalescence of closely spaced drops when they are at different electric potentials. Proc. R. Soc. London, Ser. A 1968, 306, 423. 10.1098/rspa.1968.0159. [DOI] [Google Scholar]
  53. Brazier-Smith P.; Latham J. Numerical computations of the dynamics of disintegration of a drop Situated in an Electric Field. Proc. R. Soc. London, Ser. A 1969, 312, 277–289. 10.1098/rspa.1969.0153. [DOI] [Google Scholar]
  54. Brazier-Smith P.; Jennings S.; Latham J. An investigation of the behavior of drops and drop-pairs subjected to strong electrical forces. Proc. R. Soc. London, Ser. A 1971, 325, 363–366. 10.1098/rspa.1971.0174. [DOI] [Google Scholar]
  55. Atten P. Electrocoalescence of water drops in an insulating liquid. J. Electrost. 1993, 30, 259–270. 10.1016/0304-3886(93)90080-Q. [DOI] [Google Scholar]
  56. Zhang X.; Basaran O.; Wham R. Theoretical prediction of electric field enhanced coalescence of spherical drops. AIChE J. 1995, 41, 1629–1639. 10.1002/aic.690410704. [DOI] [Google Scholar]
  57. Baygents J.; Rivette N.; Stone H. Electrohydrodynamic Deformation and interaction of drop pairs. J. Fluid Mech. 1998, 368, 359–375. 10.1017/S0022112098001797. [DOI] [Google Scholar]
  58. Adamiak K. Interaction of two dielectric or conducting droplets aligned in the uniform electric field. J. Electrost. 2001, 51, 578–584. 10.1016/S0304-3886(01)00059-6. [DOI] [Google Scholar]
  59. Atten P.; Lundgaard L.; Berg G. A simplified model of electrocoalescence of two close water droplets in oil. J. Electrost. 2006, 64, 550–554. 10.1016/j.elstat.2005.10.009. [DOI] [Google Scholar]
  60. Mohammadi M.; Shahhosseini S.; Bayat M. Numerical study of the collision and coalescence of water droplets in an electric field. Chem. Eng. Technol. 2014, 37, 27–35. 10.1002/ceat.201200479. [DOI] [Google Scholar]
  61. Mohammadi M. Numerical and experimental study on electric field driven coalescence of binary falling droplets in oil. Sep. Purif. Technol. 2017, 176, 262–276. 10.1016/j.seppur.2016.12.015. [DOI] [Google Scholar]
  62. Mhatre S.; Deshmukh S.; Thaokar R. M. Electrocoalescence of a drop pair. Phys. Fluids 2015, 27, 092106 10.1063/1.4931592. [DOI] [Google Scholar]
  63. Bartlett C. T.; Généro G. A.; Bird J. C. Coalescence and break-up of nearly inviscid conical droplets. J. Fluid Mech. 2015, 763, 369–385. 10.1017/jfm.2014.664. [DOI] [Google Scholar]
  64. Lu J.; Fang S.; Corvalan C. M. Coalescence dynamics of viscous conical drops. Phys. Rev. E 2016, 93, 023111 10.1103/PhysRevE.93.023111. [DOI] [PubMed] [Google Scholar]
  65. Garzon M.; Gray L.; Sethian J. Electrohydrodynamic coalescence of droplets using an embedded potential flow model. Phys. Rev. E 2018, 97, 033112 10.1103/PhysRevE.97.033112. [DOI] [PubMed] [Google Scholar]
  66. Anand V.; Roy S.; Naik V. M.; Juvekar V. A.; Thaokar R. M. Electrocoalescence of a pair of conducting drops in an insulating oil. J. Fluid Mech. 2019, 859, 839–850. 10.1017/jfm.2018.849. [DOI] [Google Scholar]
  67. Anand V.; Patel R.; Naik V. M.; Juvekar V. A.; Thaokar R. M. Modelling and particle based simulation of electro-coalescence of a water-in-oil emulsion. Comput. Chem. Eng. 2019, 121, 608–617. 10.1016/j.compchemeng.2018.12.003. [DOI] [Google Scholar]
  68. Zhou Y.; Dong H.; Liu Y.-H.; Yang Z.-J.; Liu T.; Li M. Molecular dynamics simulations of the electrocoalescence behaviors of two unequally sized conducting droplets. Langmuir 2019, 35, 6578–6584. 10.1021/acs.langmuir.9b00744. [DOI] [PubMed] [Google Scholar]
  69. Allan R.; Mason S. Particle motions in sheared suspensions. XIV. Coalescence of liquid drops in electric and shear fields. J. Colloid Sci. 1962, 17, 383–408. 10.1016/0095-8522(62)90016-8. [DOI] [Google Scholar]
  70. Chabert M.; Dorfman K.; Viovy J. Droplet Fusion by Alternating Current (AC) Field Electrocoalescence in microchannels. Electrophoresis 2005, 26, 3706–3715. 10.1002/elps.200500109. [DOI] [PubMed] [Google Scholar]
  71. Thiam A. R.; Bremond N.; Bibette J. Breaking of an emulsion under an ac electric field. Phys. Rev. Lett. 2009, 102, 188304 10.1103/PhysRevLett.102.188304. [DOI] [PubMed] [Google Scholar]
  72. Priest C.; Herminghaus S.; Seemann R. Controlled electrocoalescence in microfluidics: Targeting a single lamella. Appl. Phys. Lett. 2006, 89, 134101–3. 10.1063/1.2357039. [DOI] [Google Scholar]
  73. Luo X.; Yin H.; Yan H.; Huang X.; Yang D.; He L. The electrocoalescence behavior of surfactant-laden droplet pairs in oil under a DC electric field. Chem. Eng. Sci. 2018, 191, 350–357. 10.1016/j.ces.2018.07.002. [DOI] [Google Scholar]
  74. Luo X.; Yin H.; Ren J.; Yan H.; Lü Y.; He L. Electrocoalescence criterion of conducting droplets suspended in a viscous fluid. J. Phys. Chem. C 2019, 123, 19588–19595. 10.1021/acs.jpcc.9b04357. [DOI] [Google Scholar]
  75. Bird J.; Ristenpart W.; Belmonte A.; Stone H. Critical Angle for Electrically driven coalescence of two conical droplets. Phys. Rev. Lett. 2009, 103, 164502 10.1103/PhysRevLett.103.164502. [DOI] [PubMed] [Google Scholar]
  76. Mohammadi M.; Shahhosseini S.; Bayat M. Electrocoalescence of binary water droplets falling in oil: Experimental study. Chem. Eng. Res. Des. 2014, 92, 2694–2704. 10.1016/j.cherd.2014.01.019. [DOI] [Google Scholar]
  77. Xia Y.; Reboud J.-L. Hydrodynamic and electrostatic interactions of water droplet pairs in oil and electrocoalescence. Chem. Eng. Res. Des. 2019, 144, 472–482. 10.1016/j.cherd.2019.02.012. [DOI] [Google Scholar]
  78. Jones T. B.; Jones T. B.. Electromechanics of Particles; Cambridge University Press, 2005. [Google Scholar]
  79. Pethig R. Review Article—Dielectrophoresis: Status of the the theory, technology and applications. Biomicrofluidics 2010, 4, 022811 10.1063/1.3456626. [DOI] [PMC free article] [PubMed] [Google Scholar]
  80. Kirby B. J.Micro-and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices; Cambridge University Press, 2010. [Google Scholar]
  81. Pethig R. R.Dielectrophoresis: Theory, Methodology and Biological Applications; John Wiley & Sons, 2017. [Google Scholar]
  82. Eow J.; Ghadiri M.; Sharif A. Experimental studies of deformation and break-up of aqueous drops in high electric fields. Colloids Surf., A 2003, 225, 193–210. 10.1016/S0927-7757(03)00330-3. [DOI] [Google Scholar]
  83. Davis M. H. Two charged spherical conductors in a unifrom electric field: forces and field strength. Q. J. Mech. Appl. Math. 1964, 17, 499–511. 10.1093/qjmam/17.4.499. [DOI] [Google Scholar]
  84. Taylor G. Disintegration of water drops in am electric field. Proc. R. Soc. London, Ser. A 1964, 280, 383–397. 10.1098/rspa.1964.0151. [DOI] [Google Scholar]
  85. Stone H.; Lister J.; Brenner M. Drops with conical ends in electric and magnetic fields. Proc. R. Soc. London, Ser. A 1999, 455, 329–347. 10.1098/rspa.1999.0316. [DOI] [Google Scholar]
  86. Rhodes A.; Yariv E. The elongated shape of a dielectric drop deformed by a strong electric field. J. Fluid Mech. 2010, 664, 286–296. 10.1017/S0022112010004581. [DOI] [Google Scholar]
  87. Ristenpart W.; Bird J.; Belmonte A.; Dollar F.; Stone H. Non-Coalescence of oppositely charged drops. Nat. Lett. 2009, 461, 377–380. 10.1038/nature08294. [DOI] [PubMed] [Google Scholar]
  88. Hamlin B.; Creasey J.; Ristenpart W. Electrically tunable partial coalescence of oppositely charged drops. Phys. Rev. Lett. 2012, 109, 094501 10.1103/PhysRevLett.109.094501. [DOI] [PubMed] [Google Scholar]
  89. Raisin J.; Reboud J.; Atten P. Electrically induced deformations of water-air and water-oil interfaces in relation to electrocoalescence. J. Electrost. 2011, 69, 275–283. 10.1016/j.elstat.2011.03.017. [DOI] [Google Scholar]
  90. Wang J.; Wang B.; Qiu H. Coalescence and breakup of oppositely charged droplets. Sci. Rep. 2014, 4, 7123 10.1038/srep07123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  91. Liu Z.; Wyss H. M.; Fernandez-Nieves A.; Shum H. C. Dynamics of oppositely charged emulsion droplets. Phys. Fluids 2015, 27, 082003 10.1063/1.4928854. [DOI] [Google Scholar]
  92. Liu Z.; Chan S. T.; Faizi H. A.; Roberts R. C.; Shum H. C. Droplet-based electro-coalescence for probing threshold disjoining pressure. Lab Chip 2015, 15, 2018–2024. 10.1039/C5LC00177C. [DOI] [PubMed] [Google Scholar]
  93. Anand V.; Juvekar V. A.; Thaokar R. M. Modes of coalescence of aqueous anchored drops in insulating oils under an electric field. Colloids Surf., A 2019, 568, 294–300. 10.1016/j.colsurfa.2019.02.002. [DOI] [Google Scholar]
  94. Chen X.; Liu P.; Qi C.; Wang T.; Liu Z.; Kong T. Non-coalescence of oppositely charged droplets in viscous oils. Appl. Phys. Lett. 2019, 115, 023701 10.1063/1.5109181. [DOI] [Google Scholar]
  95. Szymborski T.; Korczyk P.; Holyst R.; Garstecki P. Ion Polarization of liquid-liquid interfaces; Dynamic control of the rate of electro-coalescence. Appl. Phys. Lett. 2011, 99, 094101 10.1063/1.3629783. [DOI] [Google Scholar]
  96. Baret J.-C. Surfactants in droplet-based microfluidics. Lab Chip 2011, 12, 422–433. 10.1039/C1LC20582J. [DOI] [PubMed] [Google Scholar]
  97. Gaiser P.; Binz J.; Gompf B.; Berrier A.; Dressel M. Tuning the dielectric properties of metallic-nanoparticle/elastomer composites by strain. Nanoscale 2015, 7, 4566–4571. 10.1039/C4NR06690A. [DOI] [PubMed] [Google Scholar]
  98. Saville D. A. Electrohydrodynamics: The Taylor-Melcher leaky dielectric model. Annu. Rev. Fluid Mech. 1997, 29, 27–64. 10.1146/annurev.fluid.29.1.27. [DOI] [Google Scholar]
  99. Balinov B.; Urdahl O.; Soderman O.; Sjoblom J. Characterization of water-in-crude oil emulsions by the NMR self-diffusion technique. Colloids Surf., A 1994, 82, 173–181. 10.1016/0927-7757(93)02618-O. [DOI] [Google Scholar]
  100. Hjartnes T. N.; Mhatre S.; Gao B.; Sørland G. H.; Simon S.; Sjöblom J. Demulsification of crude oil emulsions tracked by pulsed field gradient NMR. Part II: Influence of chemical demulsifiers in external AC electric field. Colloids Surf., A 2019, 586, 124188 10.1016/j.colsurfa.2019.124188. [DOI] [Google Scholar]
  101. Hjartnes T. N.; Sørland G. H.; Simon S.; Sjöblom J. Demulsification of Crude Oil Emulsions Tracked by Pulsed Field Gradient (PFG) Nuclear Magnetic Resonance (NMR). Part I: chemical demulsification. Ind. Eng. Chem. Res. 2019, 58, 2310–2323. 10.1021/acs.iecr.8b05165. [DOI] [Google Scholar]
  102. McDonald J. C.; Duffy D. C.; Anderson J. R.; Chiu D. T.; Wu H. K.; Schueller O. J. A.; Whitesides G. M. Fabrication of microfluidic systems in poly(dimethylsiloxane). Electrophoresis 2000, 21, 27–40. . [DOI] [PubMed] [Google Scholar]
  103. Urdahl O.; Wayth N. I.; Fórdedal H.; Williams T. J.; Bailey A. G.. Encyclopedic Handbook of Emulsion Technology; CRC Press, 2001; pp 678–693. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b04259_si_001.avi (22.7MB, avi)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES