Robust Perpendicular Skyrmions and Their Surface Confinement

Abstract

Magnetic skyrmions are two-dimensional magnetization swirls that stack in the form of tubes in the third dimension and which are proposed as prospective information carriers for nonvolatile memory devices due to their unique topological properties. From resonant elastic X-ray scattering measurements on Cu₂OSeO₃ with an in-plane magnetic field, we find that a state of perpendicularly ordered skyrmions forms, in stark contrast to the well-studied bulk state. The surface state is stable over a wide temperature range, unlike the bulk state in out-of-plane fields which is confined to a narrow region of the temperature-field phase diagram. In contrast to ordinary skyrmions found in the bulk, the surface state skyrmions result from the presence of magnetic interactions unique to the surface which stabilize them against external perturbations. The surface guiding makes the robust state particular interesting for racetracklike devices, ultimately allowing for much higher storage densities due to the smaller lateral footprint of the perpendicular skyrmions.

Nonvolatile memory technology is currently key to information processing and storage. One of the main issues when scaling these devices down is the thermal stability of the magnetic information. In terms of scaling, the discovery of perpendicular magnetic anisotropy in thin films¹ revolutionized magnetic storage by going from planar to perpendicular bits and led to both a much higher than predicted increase in storage density and an enhancement in data stability. Recently, magnetic skyrmions have been proposed as binary information carrier replacements since their spin configuration is topologically entangled, making them more stable yet easier to manipulate.²⁻⁷

Magnetic skyrmions were first discovered in chiral magnets, which are governed by the bulk-type Dzyaloshinskii–Moriya interaction (DMI), forming long-range-ordered skyrmion lattices.² These skyrmions are Bloch-type vortices with a fixed chirality.⁸ On the other hand, at surfaces or interfaces of thin film materials, a DMI can be induced by the natural breaking of inversion symmetry at the terminating surfaces, giving rise to both isolated skyrmions and skyrmion lattices (SkLs) of Néel-type vortices.^5,6,9 Racetrack memory making use of planar skyrmions has been proposed,⁵⁻⁷ as illustrated in Figure 1a. The skyrmions are usually induced by a magnetic field that is out of plane, and the bits can be moved along the racetrack. The stability of the encoded information is thus based on a constant distance between the individual skyrmions, which is a challenging task.¹⁰ First, their positions fluctuate over time due to random noise stemming from magnons or thermal perturbations.¹¹⁻¹³ Moreover, edge effects in a typical racetrack geometry,⁵ as well as surface defects,¹⁴ can be detrimental to free skyrmion motion, making the precise control of the skyrmion position challenging. Second, as the surface anisotropy is usually of the easy-plane type, the ordered skyrmion lattice is not locked along a fixed direction, resulting in the formation of a multidomain state.^15,16 The recently discovered room-temperature skyrmion lattice state in the chiral magnet CoZnMn makes these types of high-temperature skyrmion-carrying materials promising candidates for practical memory devices.¹⁷ Nevertheless, keeping the material in the equilibrium skyrmion phase is a rather demanding technical task as the skyrmion pocket in the magnetic phase diagram is generally rather narrow.²

Figure 1.

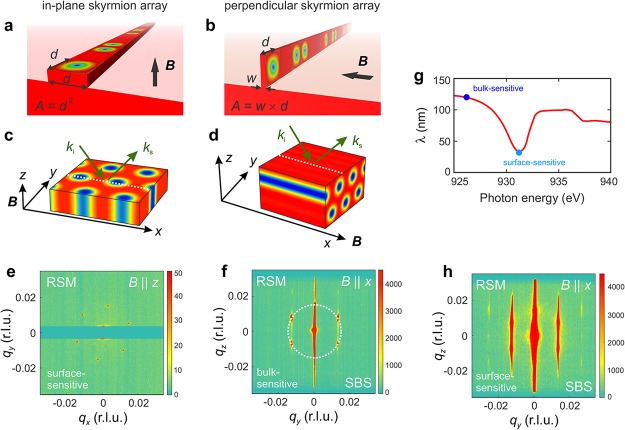
In-plane and perpendicular skyrmion states and their REXS observation in Cu₂OSeO₃. (a) Planar skyrmion racetrack memory (magnetic field out of plane) with a lateral bit size area of A = d², where d is the skyrmion diameter. (b) Perpendicular skyrmion racetrack memory (field in plane) with a lateral footprint of A = wd, where w is the width of the skyrmion fin. (c, d) Scattering geometry for the in-plane and perpendicular skyrmion lattices, respectively. k_i and k_s are the incident and scattered X-ray wavevectors, respectively. The surface normal of the [001]-oriented crystal is along the z direction, and [110] is along the x direction. The field is applied out of plane along z for the in-plane SkL and in plane along x for the perpendicular SkL. (e) Reciprocal space map of the (q_x, q_y, 1) plane showing the six diffraction peaks from the in-plane SkL phase (56 K, B_z = 20 mT), surrounding the (001) charge peak. (f) Bulk-sensitive RSM in the (0, q_y, q_z) plane showing again a 6-fold-symmetric diffraction pattern, now indicative of a hexagonally ordered in-plane SkL, the skyrmion bulk state (SBS). The dotted white circle has a radius of 0.015 r.l.u., corresponding to 59.5 nm in real space. (g) The probing depth can be varied by tuning the photon energy. The REXS penetration length λ (1/e drop in intensity) is shown as a function of photon energy. The blue dots represent the energies used in (e), (h), and (f), which represent surface-sensitive (931.2 eV) and bulk-sensitive (926.2 eV) conditions. (h) In the surface-sensitive condition, streaks dominate the RSM, indicative of pronounced 2D scattering behavior.

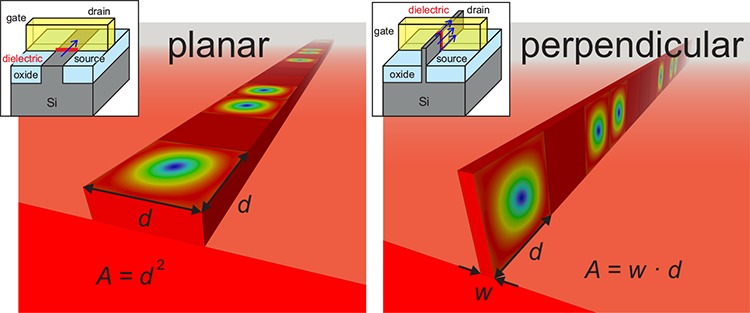
In this Letter, we show that by using an in-plane magnetic field a state of perpendicularly ordered skyrmions forms. Most interestingly, surface effects lead to the unexpected formation of a robust surface-bound state whose properties are significantly different from those of the well-studied skyrmion bulk state. The illustration of a perpendicular skyrmion racetrack structure is shown in Figure 1b and is reminiscent of the transition from planar field effect transistors (FETs) to FinFETs. The most striking advantage of this geometry is that the surface footprint of a single bit in the racetrack is greatly reduced from the square of the skyrmion diameter d to the product of d and the very scalable width of the skyrmion’s fin.

We study the skyrmion surface state in prototypical chiral magnet Cu₂OSeO₃ by resonant elastic X-ray scattering (REXS) in reflection geometry, which is the ideal tool for characterizing magnetic structures on a near-surface level.¹⁸⁻²⁰ The single-crystalline Cu₂OSeO₃ bulk samples were grown by the chemical vapor transport method and characterized by X-ray diffraction, magnetometry, and electron backscattering diffraction to confirm the correct structural and magnetic monochiral phase. For the REXS experiments, the samples were cut and the (001) surface was mechanically polished to a mirror finish. The samples typically measure 2 × 2 × 0.5 mm³ (in x, y, and z). The experiments were carried out on the SEXTANTS beamline at SOLEIL synchrotron (Gif-sur-Yvette, France) and on beamline I10 at the Diamond Light Source (U.K.). For 3d magnetic elements in resonance with the L₃ absorption edge, the magnetic scattering cross section strongly increases, making it comparable in size to charge scattering.¹⁸ Moreover, by tuning the photon energy around the Cu L₃ edge, largely different attenuation lengths are obtained,²¹ allowing for an adjustable probing depth which makes REXS an ideal tool for characterizing magnetic structures at and near surfaces.^19,20 In this way, the surface state can be distinguished from the bulk state. The calculation of the REXS penetration depth λ (1/e drop in intensity) is shown in Figure 1g. When the photon energy is tuned to the Cu L₃ edge at 931.2 eV, the probing depth is very shallow with a value of 31 nm (surface-sensitive). By changing the photon energy to a more off-edge value of 926.2 eV, the probing depth increases to 120 nm (bulk-sensitive).

Figure 1c,d shows the scattering geometries for the in-plane and perpendicular SkLs in which the field is applied perpendicular to the sample and in-plane along the x direction ([110] direction), respectively. (The y direction is along [1̅10].) Reciprocal space mapping (RSM)¹⁸ is performed by measuring a series of CCD images in which incident and scattered wave vectors k_i and k_s are systematically scanned. In this way, a 3D reciprocal space volume around the charge peak is probed.¹⁵Figure 1e shows the scattering from an in-plane SkL at 56 K for which a field of 16 mT is applied along the [001] surface normal direction (z), characterized by six magnetic satellites surrounding a charge peak.¹⁵ For the RSM in the (q_x, q_y, 1) plane, the magnetic peaks lie on a circle and the corresponding SkL constant is 59.5 nm. This bulk skyrmion state exists only in the temperature range from 55 to 57 K and at moderate magnetic fields.^15,22

When applying the field in-plane, the 6-fold-symmetric diffraction pattern can be observed only in the q_y–q_z plane for q_x = 0 (Figure 1f), representative of the perpendicular skyrmion bulk state (SBS) shown in Figure 1d. The corresponding SkL constant is identical to that in the in-plane SkL case. Note that for this bulk-sensitive measurement both the central charge peak and the magnetic peaks are elongated along the q_z direction, i.e., along the surface normal. This is a clear signature of surface diffraction (2D diffraction) in which diffraction streaks appear instead of the spots that are a signature of 3D diffraction.²³ In other words, the finite 2D long-range-ordered atomic lattice relaxes the Bragg condition along the q_z direction. If the magnetic structure is well-ordered at the surface level, then magnetic 2D diffraction can be clearly observed.²⁴ Consequently, when probing closer to the surface the magnetic features in the q_y–q_z plane become more pronounced with visible higher-order diffraction peaks, strongly suggesting an extended hexagonal skyrmion crystal. For surface-sensitive probing (Figure 1h), all magnetic peaks have completely transformed into rods, typical of 2D diffraction.

Figure 2a shows the temperature-field phase diagram mapped by REXS in which the skyrmion bulk state (SBS, red region) can be identified by its characteristic diffraction pattern (Figure 1e). This is consistent with magnetometry measurements shown in Figure 2b and in refs (22) and (25) as well as REXS measurements for the out-of-plane field geometry (B_z),¹⁵ in which the SkL phase exists only in a narrow temperature region (55 to 57 K). Upon cooling the system to below 55 K, the SkL phase surprisingly remains intact in the field in-plane geometry (B_x), down to the lowest accessible temperature of 25 K (yellow region in Figure 2a). For surface-sensitive mapping (at 55 K), the magnetic rods are clearly visible in Figure 2c. Despite the bulk-sensitive probing, Figure 2d shows obvious features of 2D diffraction, suggesting that the skyrmion state is confined to the surface, as illustrated in Figure 2e.

Figure 2.

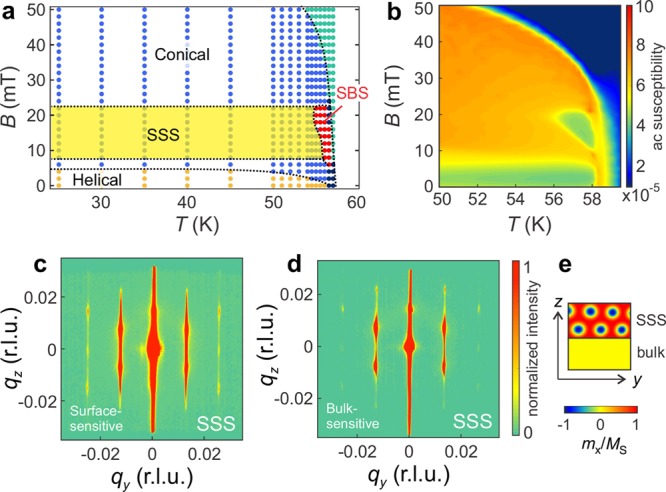
REXS measurements on surface and bulk skyrmions in Cu₂OSeO₃. (a) Temperature-field phase diagram mapped by REXS. The dots represent measured data points. The skyrmion bulk state (SBS) region, defined by the characteristic REXS pattern as shown in Figure 1(f), is marked in red. The bulk phase boundary is consistent with the ac susceptibility measurements for both field-cooled and zero-field-cooled protocols. The skyrmion surface state (SSS) region is marked in yellow. (b) Magnetic phase diagram showing the ac susceptibility plot (real component χ′) obtained using the same protocol as for the REXS plot in (a), i.e., field cooling from above T_C. (c, d) Reciprocal space maps of the surface state measured under surface-sensitive (931.2 eV) and bulk-sensitive (926.2 eV) conditions, respectively. (e) Illustration of the skyrmion surface state.

To study pinning of the skyrmion surface state (SSS), we tilted the magnetic field away from high-symmetry directions, both in the plane and perpendicular to it. Figure 3a,c shows the tilt-scan geometry in which the angle ϕ describes the azimuthal rotation of the magnetic field B in the x–y plane and γ is the elevation angle within the x–z plane. The SkL plane (surface normal n) is shown in red. The measurement was performed at 40 K with a constant field amplitude of 16 mT. For the standard bulk skyrmion lattice state, there are three possible scenarios for how the SkL can respond to field tilting: (i) The SkL plane could always remain perpendicular to the applied field, independent of the crystallographic direction. In this scenario, the SkL plane normal n should strictly follow the field angle ϕ_B, i.e., ϕ_n = ϕ_B. (ii) For a field rotation within the SkL plane, the skyrmion peaks may rotate azimuthally when overcoming the locking provided by the cubic anisotropy.² (iii) When tilting the field away from the substrate normal, a multidomain SkL may form, giving rise to a multitude of 6-fold-symmetric REXS patterns.¹⁵Figure 3b shows the experimental results for the SSS for in-plane field rotations in the x–y plane. Indeed, the SkL plane directly follows the field direction. When tilting the field toward the poles, i.e., performing an altitude scan in the x–z plane, γ_n was found to be completely pinned along x, regardless of the tilting field (Figure 3d). Moreover, the hexagonal lattice orientation in the SkL remains fully locked to the surface plane. These facts directly suggest that the surface plays the major role in pinning in-plane SkLs, dominating perturbations from either oblique fields or the cubic anisotropy. As a consequence, the surface state always favors hexagonal close packing configurations along the surface, as sketched in the insets to Figure 3b,d, highlighting the particle nature of the skyrmions.

Figure 3.

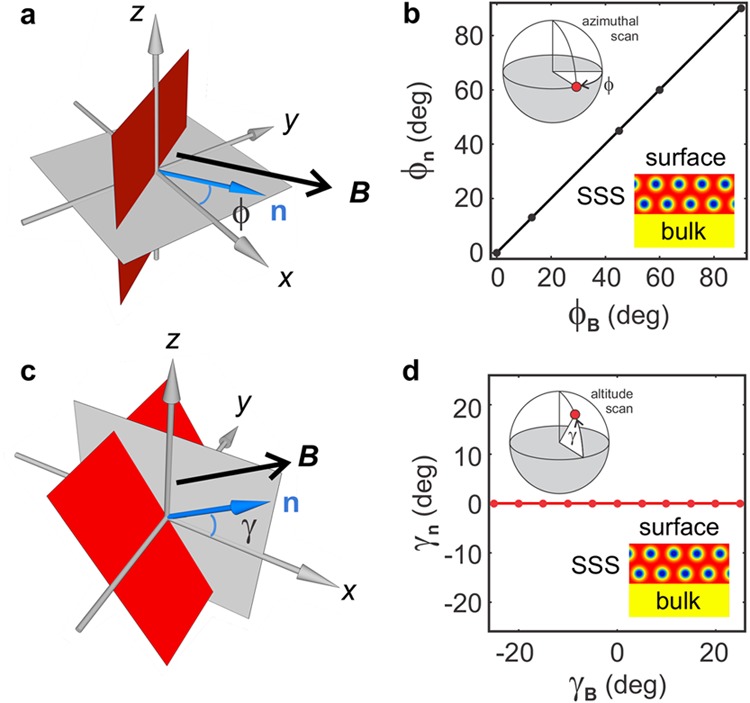
Study of surface-state pinning. (a) Orientation of the applied azimuthal tilting field. The coordinate system is the same as in Figure 1. The field amplitude is kept at 16 mT, and the field orientation is varied within the x–y plane (gray) by an angle ϕ_B with respect to the x axis. The SkL plane (red, surface normal n) orientation is described by ϕ_n. ϕ = 0° corresponds to the +x direction. (b) Plot of the measured linear ϕ_n–ϕ_B relationship in which the SkL plane strictly follows the applied field direction. (c, d) Complementary altitude field tilting scan about the y axis in the x–z plane (gray), described by the tilt angle γ_B. γ = 0° corresponds to the +x direction. Here, the skyrmion tilt angle γ_n is always 0°, i.e., constant and independent of the field tilt angle γ_B. This means that the SSS is always pinned to the surface, as depicted in Figure 2e, independent of the applied magnetic field direction.

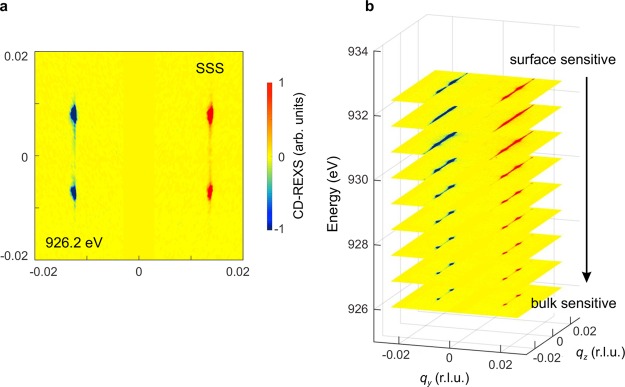
In order to reveal the physical origin of the SSS, we studied the in-plane surface state using circularly polarized light. The circular dichroism (CD) effect in REXS is a powerful technique for retrieving the detailed magnetic structure in chiral magnets.^19,20 The CD-REXS signal is obtained by carrying out two diffraction experiments with left and right circularly polarized soft X-rays and taking the difference (for the same magnetic peaks). In this way, ordered noncollinear spin structures can be fully determined. (For details, see refs (18−20).) Figure 4a shows the CD-REXS pattern using a photon energy of 926.2 eV (off resonance and thus bulk-sensitive) with the field applied along x. Note that in this field configuration two of the six expected CD-REXS skyrmion peaks (along q_y = 0) are extinct. The chirality of the skyrmion is fixed. We further performed a systematic study of the depth dependence of the CD-REXS pattern for the surface state by varying the energy of the incident X-rays (Figure 4b). The characteristic contrast remains the same throughout the probed thickness, and in particular, the two peaks at q_y = 0 remain extinct (the spin motif remains the same). This finding suggests that the surface state uniformly arranges in a close-packed hexagonal SkL. Note that the observed surface state is distinctly different from the metastable bulk states reported in other skyrmion materials.^26,27

Figure 4.

Depth dependence of the skyrmion surface state. (a) Experimental CD-REXS pattern of the SSS showing that the skyrmion has a fixed chirality. (b) Energy-dependent, and thus depth-dependent, CD-REXS patterns showing the same characteristic contrast throughout the probed depth.

The existence of a surface state in the field in-plane as well as the field out-of-plane²⁸ configuration indicates that another mechanism has to be added to the well-established SkL model.² In recent theoretical work, surface boundary confinement effects have been taken into account, leading to twisted skyrmion motifs that transform between Bloch-type and Néel-type skyrmions.^10,29 This coexistence of different skyrmion states has also been observed using electron holography³⁰ and REXS.³¹ Nevertheless, pure boundary confinement is not sufficient to explain our robust and uniform skyrmion surface state. The most likely origin is a DMI, induced by the broken inversion symmetry at the surface. Moreover, the surface anisotropy clearly is the dominating anisotropy term, which strongly pins the orientation of the in-plane SkL.

In summary, we discovered robust surface skyrmions coexisting with an underlying conical state in a much extended region of the magnetic phase diagram. Their existence points toward the presence of additional magnetic interactions which have not been included in the established skyrmion models. Their presence, however, should be universal for all noncentrosymmetric bulk DMI systems given their remarkable similarities,² including the recently discovered room-temperature SkL materials.¹⁷ From an application point of view, the skyrmion surface state in the perpendicular geometry is very promising as the surface is in fact stabilizing the skyrmion phase against external perturbations instead of being detrimental to the skyrmion dynamics.⁵ This surface guidance could be particular useful for racetracklike device schemes, ultimately allowing for much higher storage densities due to a smaller lateral footprint.

Author Contributions

S.Z., N.J., J.-Y.C., D.M.B., G.v.d.L., and T.H. performed the experiments; A.A.H. grew the samples; and Y.L. and W.W. carried out the supporting simulations. S.Z. and T.H. wrote the manuscript with input from all authors. All authors discussed the results and reviewed the manuscript.

S.Z. and T.H. acknowledge financial support from the Semiconductor Research Corporation (SRC) and EPSRC (EP/N032128/1), and S.Z. is grateful for a starting grant from ShanghaiTech University.

The authors declare no competing financial interest.