Electron–Electron Dipolar Interaction Poses a Challenge to the Radical Pair Mechanism of Magnetoreception

Abstract

A visual magnetic sense in migratory birds has been hypothesized to rely on a radical pair reaction in the protein cryptochrome. In this model, magnetic sensitivity originates from coherent spin dynamics, as the radicals couple to magnetic nuclei via hyperfine interactions. Prior studies have often neglected the electron–electron dipolar (EED) coupling from this hypothesis. We show that EED interactions suppress the anisotropic response to the geomagnetic field by the radical pair mechanism in cryptochrome and that this attenuation is unlikely to be mitigated by mutual cancellation of the EED and electronic exchange coupling, as previously suggested. We then demonstrate that this limitation may be overcome by extending the conventional model to include a third, nonreacting radical. We predict that hyperfine effects could work in concert with three-radical dipolar interactions to tailor a superior magnetic response, thereby providing a new principle for magnetosensitivity with applications for sensing, navigation, and the assessment of biological magnetic field effects.

Many animals are known to employ the Earth’s magnetic field as a pervasive source of navigational information.¹⁻³ In birds and some other species, an axial magnetic sense is believed to be facilitated by the coherent spin dynamics of paired radicals.⁴⁻⁹ This hypothesis relies on the radical pair mechanism (RPM), according to which the nonequilibrium electron spin configurations of the radical pair acquire magnetosensitivity via interactions with nearby nuclear spins when undergoing a spin-selective recombination reaction.⁴ The chemical model of avian magnetoreception is supported by findings that reception (1) relies on an inclination compass that is insensitive to field polarity, (2) depends on light of certain intensities and spectral properties, (3) has a narrow (but adjustable) magnetic-field-intensity window of operation, and (4) can be scrambled by weak oscillating magnetic fields.⁴ A complementary magnetic sense may employ biogenic magnetite.¹⁰

In the RPM model of the avian compass, the strength and direction of an applied field influence the relative yield of a structural signaling state to enable magnetosensation.^4,9,11 The only native biomolecules known to exhibit a magnetic field effect (MFE) of this kind are from the cryptochrome/photolyase family of proteins (Figure 1).^11,12In vitro, a photogenerated radical pair comprising flavin adenine dinucleotide (FAD) and tryptophan (W) can produce significant MFEs in cryptochrome¹²⁻¹⁵ and photolyase.^16,17In vivo, gene knockout experiments have shown that fruit flies (Drosophila melanogaster) rely on cryptochrome to mediate their magnetic sense.¹⁸⁻²² Likewise, cryptochrome-associated plant (Arabidopsis thaliana) growth responses to blue light were enhanced in the presence of magnetic fields.²³⁻²⁶ However, the exact role of the photogenerated FAD/W radical pair in magnetoreception remains unclear, as we elaborate further below.^9,26,27

Figure 1.

(a) Depiction of cryptochrome from D. melanogaster (PDB ID 4GU5) showing active-site residues and the FAD cofactor with atoms coded by color. (b) Schematic depiction of relevant radicals and the electron transfer chain (tryptophan tetrad) near the active site. The putative electron transfer pathway is shown with light-blue arrows, whereas the EED coupling interactions are represented in green using solid curves (for the primary pair involving either superoxide or a tryptophan radical cation; these two variants are shown simultaneously) or dashed curves (for the bystander radical). The FAD^•–/W_C^•+ radical pair has been implicated with magnetosensitivity in vitro.¹³ The alternative superoxide-containing radical pair has recently gained new support.^9,26

The RPM-mediated MFEs emerge from anisotropic hyperfine interactions between the radicals’ electron spins and associated nuclei.^11,28 These interactions can govern the spin dynamics when inter-radical interactions, such as the dipolar and exchange interactions, are small²⁹ or mutually balanced.³⁰ Radical–radical couplings generally inhibit magnetosensitivity at low fields by lifting the zero-field degeneracy of singlet and triplet states, thereby impeding field-dependent singlet–triplet conversion, and also by inducing spin relaxation.^31,32 Furthermore, recent calculations show that electron–electron dipolar (EED) interactions can abolish the “quantum needle”, a sharp feature in the directional MFE that was predicted to boost the acuity of the compass,^29,33 and may nullify the Larmor resonance,^33,34 a phenomenon observed in some behavioral studies employing radiofrequency (rf) magnetic fields to test for the RPM.³⁵ Nonetheless, the majority of past theoretical works on cryptochrome magnetoreception have omitted EED coupling to facilitate calculations on spin systems too large to be treated otherwise, instead focusing on hyperfine-induced effects as the sine qua non of low-field MFEs.^29,36

In a seminal study addressing the role of inter-radical interactions in weak fields, Efimova and Hore showed how dipolar and exchange coupling could compensate for each other if one of two matching conditions were met: 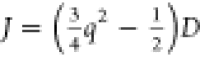, where q ∈ {0, ±1} and J and D are the exchange and dipolar coupling constants (defined in the Supporting Information).³⁰ This fortuitous coincidence, which became known as J/D cancellation, allows the zero-field degeneracy of singlet (S) and triplet states (T_q) to be partially restored. Although they demonstrated the effect of J/D cancellation on anisotropic MFEs in a significant fraction of cases of radical pairs with randomly chosen hyperfine interaction parameters, the feasibility of the effect in cryptochrome was not itself elucidated. It should also be noted that exchange (J) and dipolar (D) couplings emerge from characteristically different effects. Whereas exchange coupling may in principle be reduced by tuning the intervening media (i.e., coupling matrix elements) or individual excitation energies, the EED coupling between well-separated radicals is fixed by the electrons’ magnetic moments and their separation. Thus, EED interactions form the geometrical basis for long-range distance measurements in macromolecules by EPR spectroscopy.^37,38 Ranging from 10 to 23 MHz at distances of 15 to 20 Å, EED interactions constitute intrinsic characteristics of realistic RPM compass systems and are not arbitrary.³⁹

Surprisingly, the effects of EED interactions need not be detrimental per se. Rather, dipolarly coupled three-radical systems can generate considerable MFEs at geomagnetic sensitivity levels.⁴⁰ For example, triads of peroxyl radicals were shown to generate significant MFEs in weak magnetic fields, even where the recombining radicals exhibit a large exchange interaction and the third radical is far away.⁴¹ These effects rely on the singlet–triplet interconversion induced in a radical pair by EED coupling with an additional “bystander” radical.⁴⁰ This finding raises the prospect that the detrimental effects of hyperfine/EED interference on magnetoreception may be overshadowed by gains in magnetosensitivity if we allow a third radical to enter the picture. Here we sought to assess the extent to which magnetosensory MFEs can be generated in cryptochrome by an Earth-like (50 μT) magnetic field via coupling to a third, nonreactive “bystander” radical.

In cryptochrome-based models of magnetoreception, a radical pair has been assumed to be generated by photoreduction, giving rise to a flavin anion radical (FAD^•–) and an oxidized tryptophan radical (W^•+) after electron transfer along a chain of three or four W residues (see Figure 1).⁴ Experiments on cryptochromes isolated from the plant A. thaliana and the fly D. melanogaster indicated that magnetosensitivity is conferred by the radical pair comprising FAD^•– and the third tryptophan, W_C^•+ (Scheme 1).^12,13 However, a growing body of work has challenged this model of chemical magnetoreception.^9,19,26,42In vivo, “flicker” experiments have demonstrated magnetoreception in intermittent darkness,^9,26 suggesting a magnetoreceptive step involving the chemical reoxidation of FAD from its fully reduced state.^9,42 This finding has renewed interest in an alternative candidate comprising the flavin semiquinone and superoxide,⁴³ resulting from the presumed reoxidation by molecular oxygen (Scheme 1b).²⁷ While this model is limited by free superoxide’s fast spin relaxation, which ought to abolish putative MFEs,⁴⁴ this problem may be circumvented by adapting the superoxide model to three radicals in systems making use of the chemical Zeno effect.⁴⁵⁻⁴⁷

Scheme 1. RPM Model Reaction Mechanisms.

For the purpose of our analysis, we define a general system containing a total of m magnetic radicals, wherein the ith radical contains n_i magnetic nuclei. We define an electronic and nuclear spin density operator ρ̂(t) evolving in time t under the system Hamiltonian Ĥ and subject to nonunitary forward (escape) and back (recombination) reaction channels:

1

where the constants k_b and k_f define the respective rates at which the pair recombines into a closed-shell singlet or reacts forward to form a structural signaling state via a spin-independent structural change (Schemes 1 and 2). The singlet state is associated with the singlet projector P̂_S. The Hamiltonian Ĥ comprises Zeeman, EED, hyperfine, and exchange effects. The brackets [x, y] and braces {x, y} denote commutators and anticommutators, respectively. Additional details are provided in the Supporting Information. For each two- or three-radical configuration studied, we integrated the Liouville–von Neumann equation (eq 1), wherein the reaction coefficients were chosen to satisfy k_b = k_f = k. This allowed us to predict the relative yields of the forward and back reaction channels, 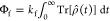and Φ_b = k_b∫₀^∞ Tr[P̂_Sρ̂(t)] dt, over a representative set of magnetic field directions Ω (each with 50 μT intensity) to assess the relative magnetic anisotropy Γ of the signaling reaction:

2

Scheme 2. R3M Model Reaction Mechanisms with Bystander B^•.

We carried out simulations of model radical pairs: [FAD^•–/W_C^•+], [FAD^•–/W_D], and [FADH^•/Z^•], where Z^• is a radical devoid of magnetic nuclei (i.e., it resembles O₂^•– except for its slow spin relaxation). The [FAD^•–/W^•+] pairs were initialized in the singlet state, 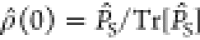, whereas those containing the superoxide-like Z^• radical were assumed to be generated in the triplet state (from the reaction of FADH^– with molecular oxygen; see Scheme 1). For the [FADH^•/Z^•] pair, we considered two different placements of the Z^• radical. One was motivated by a study of stable superoxide binding configurations in cryptochrome,⁴⁸ and the other was chosen at the largest distance from FAD (and thus the smallest EED coupling) for which the electron back-transfer could occur on a time scale of k_b^–1 = 3 μs (see eq S5 in the Supporting Information). Our models of cryptochrome were based on structures inferred from animals believed to exhibit cryptochrome-dependent magnetoreception, namely, fruit flies (DmCry, PDB ID 4GU5)⁴⁹ and birds (Columba livia cryptochrome (ClCry, PDB ID 6PU0).⁵⁰ The third (W_C) and fourth (W_D) tryptophan residues in the electron transfer chain correspond to Trp342 and Trp394 in DmCry⁴⁹ and Trp318 and Trp369 in ClCry, respectively.⁵⁰

For the [FAD^•–/W_C^•+] RPM model (m = 2; Scheme 1) without exchange or EED, a sharp directional response in the signaling yield—the “quantum needle”²⁹—is evident in Figure 2a (red line), where k^–1 = 10 μs has been used to emphasize the spiky feature (see Figure S1b for simulations with k^–1 = 3 μs). For the [FADH^•/Z^•] model without inter-radical interactions, a broad but large anisotropy is realized (Figure 2b, red line, k^–1 = 3 μs). The anisotropic MFEs of this system (Γ = 5%) markedly exceed those for the tryptophan-containing pairs, which may be attributed to the optimal “reference-probe” configuration,^51,52 wherein all of the hyperfine interactions are localized to one radical. For [FAD^•–/W_D], representative simulations are summarized in the Supporting Information (see Figure S2). The results resemble those for [FAD^•–/W_C^•+], except for the absence of the pronounced spike.

Figure 2.

a) Angular dependence of the signaling yield with respect to the magnetic field orientation in the yz plane of the flavin (defined in Figure 1) for the [FAD^•–/W_C^•+] RPM model with k_f^–1 = k_b^–1 = 10 μs without exchange or EED coupling (red), with EED (blue), and with EED and exchange such that D = −4J (purple) or D = 2J (yellow). (b) Angular dependence of the signaling yield for the [FADH^•/Z^•] RPM model with distant Z^• and k_f^–1 = k_b^–1 = 3 μs. The same color scheme as for (a) applies. (c) Relative anisotropy Γ in the yz plane for the [FAD^•–/W_C] RPM model from (a) as a function of the exchange coupling constant J = J₁₂, in comparison with the case without EED or exchange (red line; inset), or on its own. (d) Relative anisotropy Γ for the [FADH^•/Z^•] RPM model from (b) as a function of the exchange coupling constant J = J₁₂. The following hyperfine interactions have been considered here: N₅, N₁₀, and H₆ for FAD^•–; N₁, H₁, H₄, H_β, and H₇ for W^•+; N₅, N₁₀, H₅, and H₆ for FADH^•.

When EED interactions were introduced, the anisotropy of the MFE was strongly attenuated for all of the RPM models that we studied. For [FAD^•–/W_C^•+] (Figure 2a,c) and [FADH^•/Z^•] with Z^• in a remote location (Figure 2b,d), this anisotropy was reduced by nearly a factor of 10. For the [FADH^•/Z^•] model with Z^• at a short distance from FAD, MFEs were essentially abolished (Γ ≈ 10^–7; Figure S3). Can J/D compensation help recover the anisotropies of the hypothetical scenario without inter-radical interactions? We found that exchange interactions matching the J/D cancellation conditions did not restore the MFEs to levels significantly exceeding those in the presence of EED coupling alone. In particular, the “quantum needle”³⁴ was not restored (Figure 2a), nor did the [FADH^•/Z^•] recover its desired sensitivity (Figure 2b). For the [FAD^•–/W_C] model, the effect of the exchange coupling was actually to decrease the anisotropy below the EED-only scenario. Only for Z^• in the close configuration (Figures S3, S4) were the relative anisotropies markedly enhanced under the cancellation conditions; however, they remained insignificant (i.e., below 6 × 10^–5).

In the interest of establishing whether a J/D cancellation effect could be recovered at some arbitrary value(s) of J, we systematically varied the exchange coupling strength from −50 to 50 MHz. Although we found a complex dependence of the MFEs on the exchange coefficient J = J₁₂ of the primary radical pair, in no case could we re-establish the level of anisotropy characteristic of the pair with inter-radical interactions absent (Figures 2c,d; also see the Supporting Information). The same J/D cancellation inefficacy is observed for the W_D-containing radical pairs (Figure S5). Thus, J/D compensation is inefficient not only for the predicted crossing conditions but for all values of J tested for the primary radical pair. This is in part consistent with previous authors’ findings that J/D cancellation is rarely effective in systems with nuclear hyperfine interactions equally distributed across both members of the primary radical pair, but here it also pertains to [FADH^•/Z^•].³⁰ The maximum attainable anisotropies were typically 10 times smaller than those of the idealized scenario of negligible inter-radical coupling. Finally, it is notable that the experimental |J| values are too small to meet the cancellation condition.³⁸ We conclude that J/D cancellation may not be effective (for any J) in cryptochromes for proposed radical combinations at their expected relative positions in the protein.

Can the inadequacies of the RPM model be alleviated by extending it to include a third radical? To address the question of whether a three-radical mechanism (R3M) (m = 3; Scheme 2) could deliver a sharp compass signal, we characterized bystander-mediated MFEs by way of an exploration of possible bystander locations around the primary pair. We tested placements of a third radical on virtual spherical shells centered around the flavin, evaluating Γ at each one. Considering hyperfine-free (“D3M”^40,41) cases as a benchmark, we found substantial MFEs mediated by EED interactions alone. Evaluating the maximal MFE with respect to the bystander distance from the flavin, we observed broad maxima. For the DmCry [FAD^•–/W_C^•+] system in the absence of hyperfine interactions, anisotropies of up to 6% were predicted for a bystander radical placed at a distance 20 Å < R < 40 Å from the FAD cofactor (as can be seen in Figure 3a). We also discovered large anisotropic MFEs (of nearly 15%) for many bystander placements around the [FAD^•–/W_D] pair, where the radial distribution of maximum MFEs was well-approximated by an asymmetric “flat top” Gaussian distribution with a plateau region spanning from 40 to 60 Å away from the FAD (see Figures S7 and S8). Although hypothetical, these hyperfine-free calculations validate the basic idea behind the R3M model: three radicals can enable large low-field effects like those of the RPM, but based on three EED-coupled spins instead of hyperfine-coupled nuclei.^32,40 The large spatial extent of the effect also reveals how the presence of a free radical in the general vicinity of a radical pair could in principle produce unexpected effects on the relevant spin dynamics if not mitigated.

Figure 3.

For DmCry (PDB ID 4GU5), we show (a) the maximum relative anisotropy (max_θ,ϕ[Γ(θ, ϕ, R)]) for the pair [FAD^•–/W_C^•+] plus a bystander radical, where R is the radial distance from the bystander to the FAD center of spin density, for J₁₂ = {+80, 0, –80} kHz (top, middle, bottom) and neglecting hyperfine interactions, with a spherical plot of Γ(θ, ϕ, R)|_R=28 for J₁₂ = 0 in the inset; (b) max_θ,ϕ[Γ(θ, ϕ, R)] for the [FAD^•–/W_C] model with four hyperfine interactions, with Γ(θ, ϕ, R)|_R=18 shown in the inset; (c) max_θ,ϕ[Γ(θ, ϕ, R)] for the [FAD^•–/W_D^•+] model with four hyperfine interactions, with Γ(θ, ϕ, R)|_R=18 shown in the inset; and (d) max_θ,ϕ[Γ(θ, ϕ, R)]_R for the [FADH^•/Z^•] model with distant Z^• and three hyperfine interactions, with the associated Γ(θ, ϕ, R)|_R=3 shown in the inset. Red diamonds indicate locations where the bystander radical is found within the protein; blue squares mark outside bystander locations. For all of the plots, k_f^–1 = k_b^–1 = 3 μs.

More realistic simulations of model systems containing EED coupling and four hyperfine interactions (two at FAD and two at W) revealed potentially advantageous features of the R3M model. Unlike the broad optima of the D3M-only models (Figure 3a), we found sharp enhancements at specific bystander sites (Figure 3b–d): In the DmCry [FAD^•–/W_C^•+] case, we found a significant MFE (Γ = 2.2%) for a bystander radical placed proximally to W_D (Figure 3b), just inside the cryptochrome (nestled into a protein loop between W_C and W_D; Figure 4, top inset). Likewise, in the DmCry [FAD^•–/W_D] case, a markedly enhanced MFE (2.8%) emerged where a bystander was located near W_D on the protein surface (Figure 3c). In that case, the maximum R3M MFE exceeded the RPM MFE (in the presence of EED) by a factor of 20.

Figure 4.

Representation of DmCry (PDB ID 4GU5) as in Figure 1a, with colored orbs added at the sites of optimal radical bystander positions: Γ = 2.9%, [FAD^•–/W_D^•+] (four hyperfine interactions, J₁₂ = +430 kHz, pink); Γ = 2.3%, [FAD^•–/W_D] (four hyperfine interactions, J₁₂ = −430 kHz, lavender); Γ = 2.2%, [FAD^•–/W_C^•+] (four hyperfine interactions, all tested J₁₂, mauve); Γ = 1.4%, [FADH^•/Z^•] (three hyperfine interactions, no exchange, purple); Γ = 1.2%, [FADH^•/Z^•] (three hyperfine interactions, no exchange, plum). The insets show close-ups of the semitransparent protein surface superimposed on the proposed bystander binding site at W_D (top) and docking sites around and within the protein cavity housing the non-covalently bound FAD cofactor (bottom).

We found that the inclusion of a small, experimentally derived exchange coupling of |J₁₂| = 0.08 MHz³⁸ could either enhance or attenuate the MFE (Figure 3a) in the DmCry [FAD^•–/W_C^•+] model without hyperfine interactions, depending on the sign of J₁₂. In the presence of hyperfine interactions, this small exchange did not alter the MFEs to a marked extent. In particular, neither the size of the MFE nor the optimal bystander location substantially changed from the exchange-free prediction. For DmCry [FAD^•–/W_D], we used |J₁₂| = 0.43 MHz.³⁸ With the positive (enhancing) value of J₁₂, the anticipated docking site shifted closer toward W_D. The results of simulations employing the ClCry structure (Figure S9) revealed the same qualitative features as for DmCry as well as quantitative similarities: We found sharply peaked maxima in the bystander-dependent MFE anisotropies at distinct locations around the cryptochrome. In the ClCry [FAD^•–/W^•+] models, optima were found at the protein surface or inside the protein cavity, colocalized near one of the radical centers, just as for DmCry.

To expand on the possibilities of our model, we also explored the optimization of the bystander with respect to location and the exchange constants J_ij, where i, j ∈ {1, 2, 3}, for DmCry [FAD^•–/W_D^•+]. Using a search procedure employing a genetic algorithm, we found a location for the third radical close to W_D (distance: 7.7 Å) where we could boost the relative anisotropy by up to 4.8% by tuning the exchange integrals (Table S1). The optimum exchange parameters were J₁₂ = 1.8 MHz, J₂₃ = −24.9 MHz, and J₁₃ = −4.4 MHz, consistent with a simplistic picture in which nearby radicals exhibit greater exchange than those far apart.

For the [FADH^•/Z^•] model with Z^• at the distant position, there is a sharp peak in the MFE as the bystander moves to a position 3 Å away from the FAD cofactor (Figure 3d), which in DmCry is in close contact with Arg381. In addition, the R3M model predicted two distinct peaks at larger distance. For the three maxima at 3, 22, and 30 Å from the FAD, relative anisotropies of 1.4%, 1.2%, and 1.0% were found, respectively, corresponding to enhancements of 3.7, 3.2, and 2.8 times that of the RPM-only scenario—a moderate enhancement relative to the RPM. Much larger enhancements are found for the [FADH^•/Z^•] model with Z^• at the close position, for which the anisotropy spikes at a distance of 6 Å, as shown in Figure S10. However, Γ is still minute for this close arrangement of radicals.

In summary, we have reported results of numerical simulations of a model cryptochrome system incorporating Zeeman, dipolar, hyperfine, and exchange interactions. Our findings do not support the idea of a sensitive RPM-based chemical compass in cryptochrome. Rather, EED couplings strongly suppress the anisotropies of the conventional RPM, such that it seems implausible that such a compass could deliver the remarkable acuity proposed. In particular, our findings call into question the operation of previously considered [FAD^•–/W_C^•+] and [FADH^•/Z^•] radical pair systems on a “moonless night”, as these models do not provide the minimum effect size needed in the presence of EED coupling based on a recently established, purely information-theoretic bound.⁵³ Any anisotropic MFEs mediated by [FAD^•/W^•+]-type model radical pairs would be reduced with the inclusion of more nuclei in more realistic models. On the other hand, EED interactions in R3M model systems produce sizable enhancements over “bare” RPM-mediated MFEs, while EED–hyperfine interference effects “carve out” specific magnetically optimized sites around the protein surface that could act preferentially as radical binding or docking sites (Figure 4 insets).

For the DmCry [FAD^•–/W_D^•+] radical pair, two optimal bystander locations were found at the protein surface (depending on the exchange interaction), indicating the possibility of a radical docking site at the end of the tryptophan chain. This finding could have fundamental implications for magnetosensation, as it may designate a binding site for a free electron donor species or a docking location for a paramagnetic bystander species functioning as a magnetosensory switch to (dis)engage reception by (un)binding a third radical. In these scenarios, where the Hamiltonian defines strong EED couplings between two adjacent radicals (W^•+ and B^•) coupled weakly to a third, distant radical (FAD^•–), the system eigenstates will be superpositions of singlet and triplet states of the primary pair, which will develop marked magnetosensitivity in cases where those states are nearly degenerate. It is noteworthy to point out that in the avian cryptochrome 4, a tyrosine (Y319) is found in the immediate vicinity of W_C and W_D, which could form a long-lived radical (e.g., during primary photoreduction) to act as an enhancer for subsequent reaction cycles via the R3M. This indicates a need for experimental work to test for the possibility of an intrinsic radical site or a radical binding site at the end of the Trp chain, in close proximity to the nearby C-terminal tail. These conclusions have been obtained for negligible exchange with the bystander. Apart from the dependence of the MFE on a few features at low exchange values, this approximation is justifiable, insofar as the MFE is sustained and independent of J₂₃ for large exchange couplings (Figure S11). Even an enormous J₂₃ has no effect on the magnetic anisotropy of the radical, thereby showing that neglecting exchange, even for close bystander positions, does not invalidate our model. More generally, the exchange coupling J(r) has a complex dependence on the electronic properties of the radicals as well as their separation and relative orientation and the nature of the intervening medium. Governed by orbital symmetry, they may be small even for nearby radicals (as has been documented for nitroxide biradicals).^54,55 While this variability makes a general assessment difficult, our model is robust toward large exchange interactions and tunable for small ones, and thus, it is fully applicable to bystander radicals at close distance.

The highly localized effects found in the [FAD^•–/W_C^•+] and [FAD^•–/W_D] models with respect to optimal bystander sites hold promise for the synergistic effect of concerted actions of multiple radicals in cryptochrome to enhance magnetosensivity beyond the limits of the conventional RPM, which is a natural extension to this study. It will also be relevant to see whether these findings are robust in the presence of dephasing and relaxation, as it will be to assess the impact of replacing the bystander with a reactive “scavenging” radical (i.e., the chemical Zeno effect^46,47). Conversely, the spatial extent of the EED coupling itself suggests that encounters between magnetosensitive radical pairs and free radicals could have strong effects on the sensitivity of radical-pair-mediated reactions. In particular, this prospect may have bearing on the processes that govern electron transfer and catalysis for sensing and metabolism.⁴¹ We hope these predictions may direct future endeavors toward a comprehensive theory of biomagnetism as well as efficient organomagnetic sensor design.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c00370.

• Detailed specification of the model and parameters used and additional simulation results for two- and three-radical systems (PDF)

The authors declare no competing financial interest.