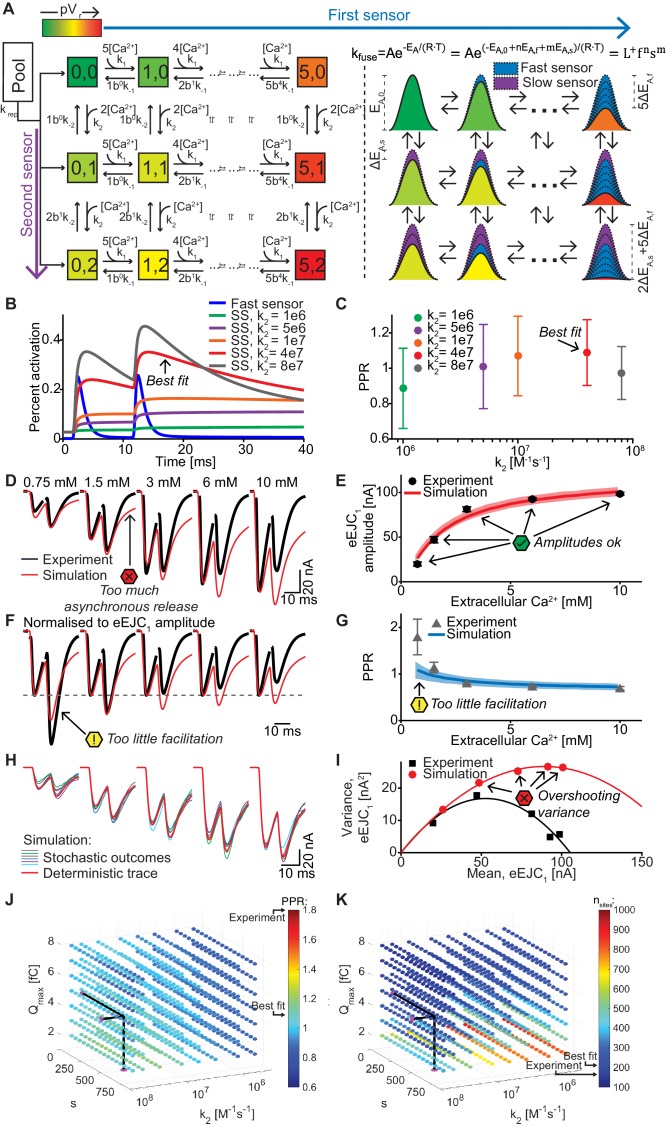
Figure 6. A dual fusion-sensor model of Ca²⁺ sensors cooperating for SV fusion improves STP behavior, but suffers from too little STF, asynchronous release and too much variance.

(A) Diagram of the dual fusion-sensor model (left). A second Ca²⁺ sensor for fusion with slower kinetics can increase pV_r (indicated by color of each Ca²⁺ binding state). The second fusion sensor is assumed to act on the energy barrier in a similar way as the first sensor (right). The top right equation shows the relation between the fusion constant, k_fuse, and energy barrier modulation with n and m being the number of Ca²⁺ bound to the first and second Ca²⁺ sensor, respectively. Ca²⁺ binding to the second sensor is described by similar equations as for the first sensor, but with different rate constants and impact on the energy barrier. (B) Simulation of Ca²⁺ binding to the fast (blue) and slow (other colors) Ca²⁺ sensor in simulations at 0.75 mM extracellular Ca²⁺ with different k₂ values but with constant affinity (i.e. fixed ratio of k_-2/k₂). The binding is normalized to the maximal number of bound Ca²⁺ to each sensor (5 and 2, respectively). For illustration purposes in this graph the fusion rate was set to 0 (because otherwise the fast sensor (blue line) would be consumed by SV fusion). k₂ = 4e7 M^-1s^-1 (red trace) illustrates the situation for the optimal performance of the model (approximately best fit value). (C) PPR values in stochastic simulations with the same parameter choices as in (B) but allowing fusion. (D) Experimental eEJC traces (black) together with average simulated traces (red). Simulations show too much asynchronous release compared to experiments. (E) eEJC₁ amplitudes of experiment (black) and simulation (red). Error bars and colored bands show standard deviations of data and simulations, respectively. Simulations reproduce eEJC₁ amplitudes well. (F) Average, normalized eEJC traces of experiment (black) and simulation (red). Simulations show too little facilitation compared to experiment. (G) PPR values of experiment (gray) and simulation (blue). Error bars and colored bands show standard deviation. Simulations show too little facilitation compared to experiment. (H) Average simulated traces (red) and examples of different outcomes of the stochastic simulation (colors). (I) Plot of the mean synaptic variance vs. the mean eEJC₁ values, both from the experiment (black) and the simulations (red). Curves are the best fitted parabolas with forced intercept at (0,0) (simulation: Var = −0.0034*<eEJC₁>²+0.5992 nA*<eEJC₁>, corresponding to n_sites = 294 and q = 0.60 nA when assuming a classical binomial model (Clements and Silver, 2000), see Materials and methods). Simulations lead to too much variance at the highest Ca²⁺ concentrations. (J) Parameter exploration of the second sensor varying the parameters Q_max, k₂, and s. Each ball represents a choice of parameters and the color indicates the average PPR value in stochastic simulations with 0.75 mM extracellular Ca²⁺. None of the PPR values match the experiment (indicated by the black arrow). Black lines show the best fit parameters. (K) Same parameter choices as in (I). The colors indicate the number of RRP SVs in order to fit the eEJC₁ amplitudes at the five different experimental Ca²⁺ concentrations. Black lines show the best fit parameters, and arrows show the experimental and best fit simulation values. Note that the best fit predicted more release sites than fluctuation analysis revealed in the experiment. Experimental data (example traces and means) depicted in panels D-G,I are replotted from Figure 2A–D,F. Parameters used for simulations can be found in Tables 1–3. Simulation scripts can be found in Source code 1. Results from simulations (means and SDs) can be found in the accompanying source data file (Figure 6—source data 1). Simulations of the dual fusion-sensor model with cooperativity 5 are summarized in Figure 6—figure supplement 1.

Figure 6—figure supplement 1. The dual fusion-sensor sensor model with cooperativity 5 (allowing the binding of 5 Ca²⁺ to the second fusion sensor).

(A) Average, experimental eEJC₁ traces (black) together with average simulated traces (red). The higher cooperativity increases the PPR compared to cooperativity 2 (Figure 6), but introduces massive asynchronous release resulting in distorted eEJC shapes. (B) eEJC₁ amplitudes of experiment (black) and simulation (red). Error bars and colored bands show standard deviation. Like with the three models described in the main text, simulations of this model reproduces eEJC₁ amplitudes well, but the variance at the higher extracellular Ca²⁺ concentrations is too large. (C) Average, normalized eEJC traces of experiment (black) and simulation (red). Like in (A) the wrong shape of the eEJC is evident. (D) PPR values of experiment (gray) and simulation (blue). Error bars and colored bands show standard deviation. Despite the increase in PPR compared to the dual fusion-sensor model with cooperativity 2, the PPR is still too low. (E) Plot of the mean synaptic variance vs. the mean eEJC₁ values, both from the experiment (black) and the simulation (red). The curves show the best fitted parabolas with forced intercept at (0,0) (simulation: Var = −0.00089*< eEJC₁>²+0.6728 nA*< eEJC₁>, corresponding to n_sites = 1124 and q = 0.67 nA when assuming a classical binomial model (Clements and Silver, 2000), see Materials and methods). This model leads to an even larger overshoot of the variance than the dual fusion-sensor model with cooperativity 2 (Figure 6). Experimental data (example traces and means) depicted in panels A-E are replotted from Figure 2A–D,F. Parameter values used for simulations can be found in Tables 1–3. Simulation scripts can be found in Source code 1. Results from simulations (means and SDs) can be found in the accompanying source data file (Figure 6—source data 1).