Elastic ripening and inhibition of liquid-liquid phase separation

Abstract

Phase separation is a central concept of materials physics [1–3] and has recently emerged as an important route to compartmentalization within living cells [4–6]. Biological phase separation features activity [7], complex compositions [8], and elasticity [9], which reveal important gaps in our understanding of this universal physical phenomenon. Here, we explore the impact of elasticity on phase separation in synthetic polymer networks. We show that compressive stresses in a polymer network can suppress phase separation of the solvent that swells it, stabilizing mixtures well beyond the liquid-liquid phase separation boundary. Network stresses also drive a new form of ripening, driven by transport of solute down stiffness gradients. This elastic ripening can be much faster than conventional surface tension driven Ostwald ripening.

Recent experiments have shown that network elasticity can dramatically impact liquid-liquid phase separation in swollen synthetic polymer networks. In a homogeneous network, droplets grow to a fixed size, controlled by the network stiffness [9]. When the network has an anisotropic state of stress, droplets grow with scale-independent ellipsoidal shapes [10].

In the nucleus of living cells, artificial phase separating domains formed preferentially in chromatin-poor regions [11]. After drops were triggered to grow in chromatin-rich regions, they migrated toward chromatin-poor regions. Theory and simulation suggest that these observations could be driven by gradients in network stiffness [9, 11]. However, these exciting observations are not sufficient to establish the role of network elasticity in droplet nucleation and migration. There are two main challenges. First, the heterogeneous mechanical properties of the nucleus remain unquantified. Second, the nucleoplasm is a multicomponent mixture, and the chemical solubility of one component (i.e. chromatin) can dramatically effect the solubility of other components (see e.g. the phase diagrams of three-component mixtures [12, 13]).

Here, we reveal the impact of network mechanics on droplet nucleation and ripening with experiments in a synthetic polymer system, where mechanical properties and chemical solubility can be tuned independently [9]. We find that network elasticity can fully suppress droplet nucleation deep inside the thermodynamically immiscible region, thus mechanically stabilizing supersaturated mixtures. The long-term stability of droplets is strongly affected by network elasticity. While we observe no ripening in homogeneous networks, in a mechanically heterogeneous network, solute moves from stiff to soft regions by diffusive transport through the dilute phase. Superficially resembling surface tension driven Ostwald ripening, this elastic ripening can be much faster and is driven by gradients of network elasticity.

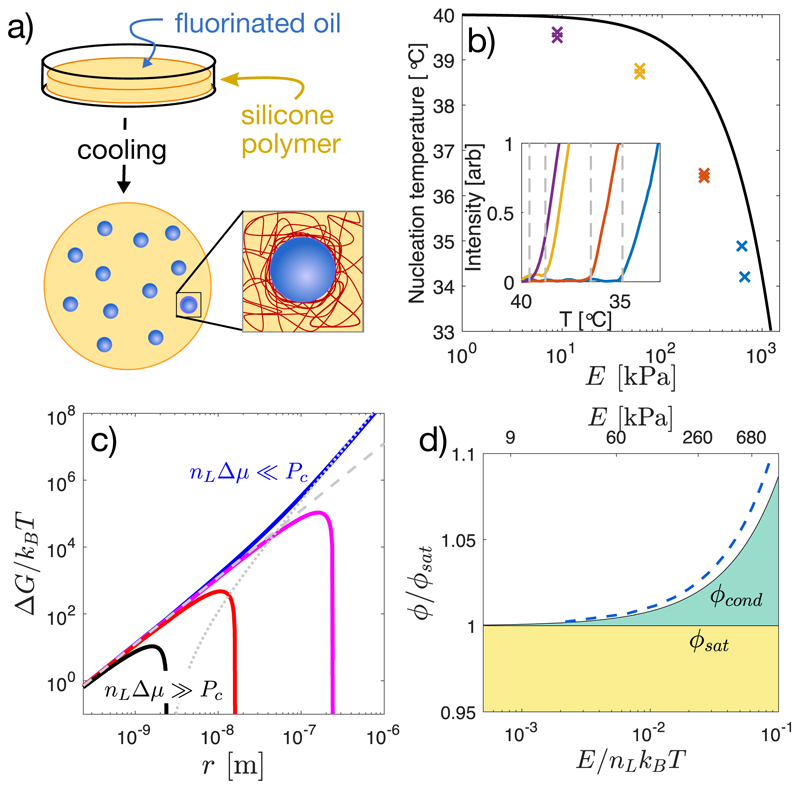
To investigate the impact of network elasticity on nucleation, we drove phase separation in silicone gels (Gelest). First, we saturated them in a bath of fluorinated oil (Fluorinert FC-770) at T_sat = 40°C [9]. After several hours, the volume fraction of oil saturated at ϕ_sat ≈ 0.036, independent of Young’s modulus, E, as shown in Figures S3,S4. Then, we quenched samples in a temperature controlled microscope stage (TSA12Gi, Instec), while recording bright-field images with a 20X NA 0.5 objective. With sufficient undercooling, droplets nucleate and grow, shown schematically in Figure 1a. Nucleation events were identified by quantifying the average pixel-wise intensity difference from a reference image at each temperature, which grows rapidly at the point of nucleation, as shown in the inset panel of Figure 1b. At quench rates below 1 °C/min, the nucleation temperature, T_nuc, has no significant dependence on the quench rate (Fig. S5). Thus we used a quench rate of 0.2 °C/min to measure the droplet nucleation temperature as a function of network stiffness from 9 kPa to 680 kPa. The nucleation temperature depends strongly on the network stiffness. In flexible networks, E = 9 kPa, droplets nucleated at only 0.5°C below T_sat. In stiff networks, E = 680 kPa, droplets did not appear until the sample was cooled about 6°C below T_sat (Fig. 1b).

Fig. 1. Network stiffness controls droplet nucleation.

(a) Schematic diagram of the method for nucleating and growing droplets in a polymer network. (b) Measured nucleation temperature for samples saturated at T_sat = 40°C and cooled down at 0.2°C /min, as a function of Young’s modulus, E. Inset shows the intensity signal used to identify the nucleation temperature. (c) Free energy landscape of a growing droplet, as given by Eq. 1. Here, E is set at 300 kPa, r_m ≈ 2.4 nm, γ = 4mN/m [10] and the driving pressure n_LΔμ is varied from 50 kPa (blue line) to 5 MPa (black line). Contributions from surface tension and elasticity are shown as dashed and dotted lines, respectively. (d) Fixed-temperature phase diagram showing the stability of the mixture with concentration and network stiffness. Mixtures are stable in the yellow region, unstable in the white region, and stable against droplet growth but unstable to demixing at the boundaries in the green region. The solid black curve for ϕ_cond is given by Eq.2, assuming elastic cavitation and dilute solution approximation for Δμ. The dashed blue line shows a non-dilute version of the theory with ϕ_sat = 0.036, as described in the Supplement.

These results suggest that network elasticity may constrain droplet nucleation. When the radius of the droplet exceeds the network mesh size, r_m ≈ (k_BT/E)^1/3 [14], the network can squeeze the growing droplet. However, as long as the pressure within a droplet exceeds a critical value, P_C, it can overcome elastic stresses and continue to grow [10, 15, 16]. We assume here that P_C = 5E/6, a classic result for nonlinear-elastic solids [15], which is a good approximation for many polymer networks [16]. This mechanical resistance is readily incorporated into classical nucleation theory, which considers the free energy, ΔG, of a droplet as a function of its radius, r,

$$\Delta G=-\frac{4\pi }{3}{r}^3{n}_L\Delta \mu +4\pi r^2\gamma +\frac{4\pi }{3}\Theta \left(r-r_m\right)(r^3-r_m^3)P_c.$$ (1)

Here, as in simple condensation, nucleation is driven by the chemical potential difference between the dilute and condensed phases, Δμ, and resisted by interfacial energy, γ. The number density of molecules in the condensed phase is n_L, and Θ(r) is the Heaviside step function. The product n_LΔμ is equivalent to the stall pressure, P_st, the maximum pressure a growing droplet can exert against its surroundings [9]. The last term is a simple approximation of the mechanical work required to expand the cavity beyond the scale of the network mesh, [15]. It can have a dramatic impact on the free energy landscape governing droplet growth. Figure 1c shows the predicted size dependence of the droplet free energy for four different supersaturation levels in a 300 kPa sample. At the highest supersaturations (n_LΔμ = 5 MPa, black curve), elasticity has no impact on the free energy landscape and droplets can nucleate and grow normally. At lowest supersaturation (n_LΔμ = 50 kPa, blue curve), the droplet free energy monotonically increases with radius, completely forbidding droplet growth.

Droplet nucleation is thus allowed only when n_LΔμ > P_c. Assuming the ideal form of the chemical potential of the dilute phase, Δμ = k_BT ln (ϕ/ϕ_sat), we identify a minimal volume fraction of solute needed for condensation,

$${\varphi }_{\mathit{\text{cond}}}={\varphi }_{\mathit{\text{sat}}}\text{exp}\left(P_C/n_L{k}_{B}T\right)\approx {\varphi }_{\mathit{\text{sat}}}\text{exp}\left(5E/6n_L{k}_{B}T\right).$$ (2)

The ratio E/n_Lk_BT thus plays a central role. As it increases beyond one, the supersaturation required for droplet nucleation diverges exponentially. In these experiments, n_Lk_BT = 11 MPa, and ϕ_cond/ϕ_sat reaches about 1.05, as shown in Figure 1d.

We identify three regimes of stability. When ϕ < ϕ_sat (shaded yellow in Figure 1d), the mixture is stable, independent of elasticity. When ϕ > ϕ_cond (shaded white), the mixture is unstable. When ϕ_sat < ϕ < ϕ_cond (shaded green) the supersaturated system is stable against nucleation and growth of droplets, but can demix by expelling solute beyond the boundaries of the polymer network. In this regime, compositions that would be unstable in the absence of elasticity are completely stable in the limit of infinite system size (i.e the thermodynamic limit).

To compare these predictions to our nucleation data, we determined T_cond, the temperature where Eq. 2 is satisfied, i.e. ϕ_sat(T_sat) = ϕ_sat(T_cond) exp(P_C/n_Lk_BT_cond). Using independently measured values of ϕ_sat(T) (Fig. S4), this yields the solid line in Figure 1b.

As expected, the stiffness dependence of T_cond follows the measured trend of T_nuc, but at a consistently higher temperature, likely reflecting kinetic limitations to nucleation. To further test our hypothesis that the supersaturated state is stable to nucleation of droplets, we cooled a 700 kPa sample to T = 38°C, where T_cond < T < T_sat. At this undercooling, softer samples nucleate and grow droplets in a matter of seconds. However, we fixed the temperature at this value for > 60 minutes, and found no evidence of nucleation in the stiffer sample.

Thus, elastic forces hinder nucleation and stabilize the supersaturated mixed state. Similarly, we expect the dilute phase to remain supersaturated even after droplet growth is completed. Consider a system quenched to ϕ > ϕ_cond, driving droplet nucleation. As droplets grow, they deplete solute from the dilute phase, and n_LΔμ decreases. When n_LΔμ = P_c, the free energy liberated by condensation is just sufficient to overcome the mechanical work needed to deform the polymer network, and droplet growth is arrested. At this point, ϕ = ϕ_cond, and the concentration in the dilute phase is stably supersaturated.

Since ϕ_cond increases with network stiffness, stiffness gradients should result in gradients of supersaturation, and transport of solute from stiff to soft regions [17]. This simple physical picture rationalizes transport down stiffness gradients observed in simulations [11].

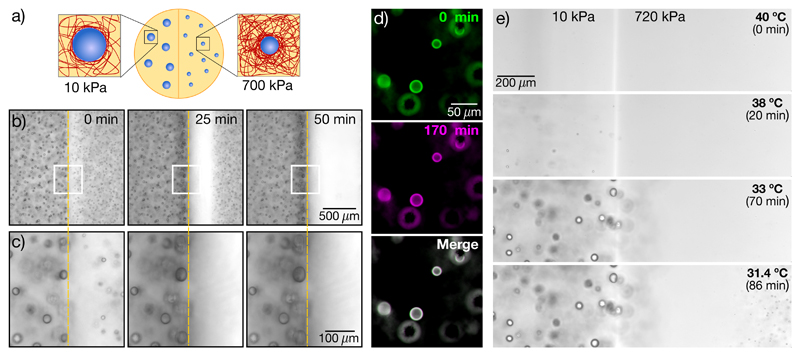
To test this hypothesis, we nucleated and grew droplets in samples with stiffness gradients, shown schematically in Figure 2a. Samples were saturated with oil at T_sat = 40°C to establish a uniform concentration ϕ_sat(T_sat), and quenched quickly so that both sides nucleated and grew droplets. Experimental data with a side-by-side step change in stiffness from 10 kPa to 700 kPa are shown in Figure 2b,c. As expected [9], we found larger droplets on the soft side than the stiff side. While droplets far from the interface were stable (Fig. S9 and Movies S1,S2), droplets on the stiff side, adjacent to the interface, started to dissolve soon after growth. Over time, more droplets dissolved on the stiff side, leaving a growing band of clear gel adjacent to the interface (Fig. 2b, Movie S3). Simultaneously, the droplets on the soft side, immediately adjacent to the interface, grew (Fig. 2c). This experiment reveals significant solute transport down the stiffness gradient, supporting our hypothesis that the solute is still supersaturated when droplet growth is arrested.

Fig. 2. Stiffness gradients drive solute transport and ripening.

(a) Schematic showing liquid droplets generated in a stiffness gradient. (b)-(c) Time-lapse bright-field images (10X NA 0.3) showing dissolution of droplets on the stiff side (E = 700kPa) and growth of droplets on the soft side (E = 10kPa). White boxes in (b) are shown at higher magnification in (c). (d) False color images of bi-disperse droplets grown in a homogeneous network with E = 80 kPa. Green(magenta) panels show the sample at the 0(170) minute time point. The merged image shows almost complete overlay of the two channels (seen as white) (e) Side-by-side gradient samples of stiff (E = 720kPa) and soft (E = 10kPa) cooled down at a rate of 0.1°C /min. Orange dashed lines in (b),(c) indicate the interface between stiff and soft sides.

This phenomenon resembles conventional surface tension driven Ostwald ripening [18], as small droplets shrink to feed the growth of larger droplets. To rule this out, we performed two experiments. First, we tested if Ostwald ripening occurs between droplets in a homogeneous silicone network. We produced a bi-dispersed droplet size distribution in a homogeneous 80kPa sample by making a sudden change in the quench rate during droplet growth, described in the Supplement. This method allowed us to produce droplets with radii of about 12 and 9.5 μm, with a typical spacing of about 90 μm. We monitored the size of the droplets for 170 minutes after the end of growth, and found no change in size (Fig. 2d, Movie S4). Compare this to the 140 kPa gradient sample in Figure S10, with droplets of 12 and 10 μm juxtaposed across the interface. In this case, smaller droplets more than 100 μm from the larger ones are dissolved completely within 100 minutes.

Second, we repeated the experiment with a side-by-side stiffness gradient, as in Figure 2 b, but with slow and controlled cooling, at 0.1°C/min. As expected from our data on nucleation in homogeneous samples (Fig. 1), droplets appeared at higher temperatures on the soft side than on the stiff side (Fig. 2e). Additionally, droplets never appeared near the stiff side of the interface. This indicates that stiffness-driven gradients of supersaturation depleted solute from the stiff side even before droplets could form there. While this is consistent with our proposed mechanism, it is not consistent with surface tension driven Ostwald ripening, which requires droplets of different sizes.

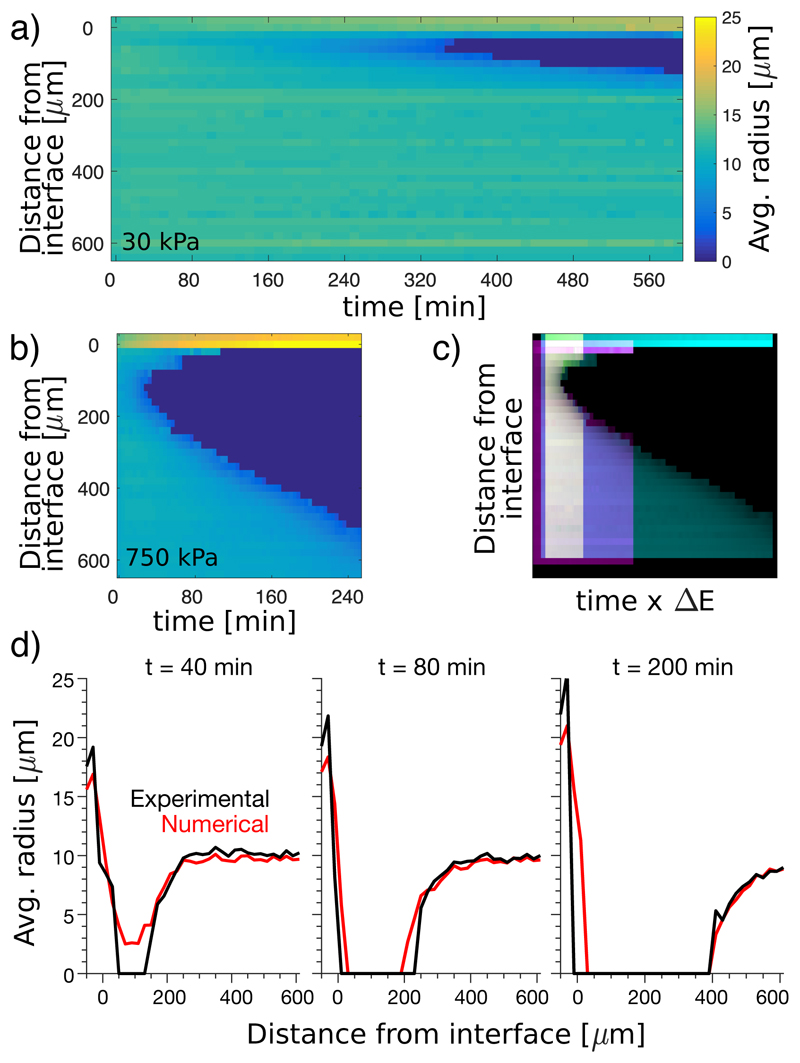
Having ruled out surface tension as a driving force for ripening, we now quantify the effect of stiffness gradients. We measured the average droplet size as a function of time and distance from the soft-stiff interface, visualized as a kymograph in Figure 3a,b. Keeping the stiffness at z < 0 fixed at 7 kPa, we varied the stiffness for z > 0 from 30 to 750 kPa. Results for the extremes are shown in Figure 3a,b, the rest in the Supplement. In all cases, droplets on the stiff side disappear near the interface after a delay, and a dissolution front invades the stiff side. The dissolution front appears sooner, and moves faster, in stronger stiffness gradients. In Figure 3c, we stretch these kymographs by an amount proportional to the stiffness difference, ΔE, and superimpose them. Intriguingly, with a small shift in starting time and starting position, the shapes of the dissolution fronts match (Fig. 3c). The rate of advance of the dissolution front therefore increases with ΔE.

Fig. 3. Rate of ripening increases with stiffness difference.

(a),(b) Kymographs showing average radius over time of droplets at different distances from the soft-stiff interface. The ‘soft’ sides (z < 0μm) have E = 7 kPa. ‘Stiff’ sides (z > 0μm) vary from E = 30 kPa in (a) to E = 750 kPa in (b) (further data Fig S10). (c) Superimposed kymographs with stiff sides of E = 140kPa (yellow), E = 330kPa (magenta), and E = 750kPa (cyan), where the time-scale is multiplied by the elastic modulus difference across the interface, and shifted so that the starting points are aligned. (d) Numerical simulation of 750kPa sample, shown with experimental data (see Movie S5 for further time points). Here, the simulation is based on simple diffusion in the dilute phase with the internal droplet pressure set by the stiffness of the gel.

A simple model of solute transport captures the essential features of these results. It is based on diffusion in the dilute phase, where the concentration is pinned to ϕ_cond ≈ ϕ_sat exp(P_C/n_Lk_BT) at the surface of the droplets (see Supplement). This model shows quantitative agreement for large ΔE, as shown in Fig. 3d (and Movie S5). It overestimates the delay before front formation for smaller stiffness differences, as shown in Fig. S10.

In general, both elasticity and surface tension could drive ripening. In Ostwald ripening, the driving force is given by the difference in Laplace pressure. For a narrow size distribution, this is roughly 2γΔR/R². In elastic ripening, the driving force is of order ΔE. The relative strength of the driving forces for Ostwald and elastic ripening is therefore given by the ratio 𝒦 = γΔR/R²ΔE. In the current experiments, this ratio is much smaller than one, and elastic forces dominate.

We have shown that a host polymer network can dramatically alter the nucleation and ripening of phase-separated liquid droplets. In classic liquid-liquid phase separation, these processes are controlled by interfacial energy. Here, the structure of the polymer network introduces a new term into the free energy, reflecting that droplets can grow only when their internal pressure exceeds a critical pressure, of order Young’s modulus. This splits the conventional phase boundary in two. One curve, ϕ_sat, determines the saturation equilibrium of a system in contact with a reservoir of solute. Another, ϕ_cond, determines the limit of stability of the mixture against droplet nucleation and growth.

These phenomena suggest that living cells might regulate the localization of membraneless organelles through gradients of their mechanical properties. Alternatively, recent physical modelling of the localization of phase-separated domains has focused on the role of activity gradients, [4, 7, 19, 20]. For membraneless organelles, reported values of γ vary from 10⁻⁷ – 10⁻⁴ N/m [4, 21–23], and R from 1 – 10 μm [4, 22]. Cytoskeletal shear moduli are of the order 10 Pa, [24–26]. Assuming ΔE/E ≈ ΔR/R ≈ 1, we find an enormous range of 𝒦 values from 𝒪(10⁻³) to 𝒪(10), suggesting that both elastic and Ostwald ripening could be relevant to cells. Thus, quantification of the heterogeneous mechanical properties of the cell interior and the size distribution and surface tension of droplets are required to assess the relative contributions of surface tension and elasticity in a specific cellular context. Furthermore, we should note that the current work is limited to static networks with relatively simple rheology. New phenomena are anticipated in living cells where the timescale of phase separation can be comparable to the viscoelastic relaxation timescale [3] or the remodelling timescale of active networks [27, 28].

I. Methods

A. Preparation of silicone gels

Silicone gels are made following the recipe in [29]. In brief, we mix divinyl-terminated polydimethylsiloxane (DMS-V31, Gelest), a cross-linker (HMS-301, Gelest) and a catalyst (SIP6831.2, Gelest). The mixture is thoroughly degassed, and then cured in an oven at 40°C for at least 24 hours. The gels’ Young moduli, E, are tuned by changing the ratio of divinyl-terminated chains to cross-linker in the mixture, while keeping the concentration of catalyst at 0.0019% by volume. The stiffness of the gels are measured by indentation experiments (e.g. [9]). Other mechanical properties of the gels are demonstrated in the Supplemental information.

B. Preparation of stiffness-gradient samples

Side-by-side stiffness gradients: ’Stiff’ gels of a thickness between 3mm and 5mm were cured in a 35 mm petri dish (Greiner) overnight at 40°C. These were cut in half and pulled off the dish, then placed in half of a new 35 mm glass-bottomed dish (MatTek). ’Soft’ gels were poured in the other side next to it, and again cured overnight at 40°C. Top-bottom stiffness gradients: ‘Stiff’ gels, about 900 μm - 1mm thick, with Young’s moduli from 30kPa to 750kPa were cured in a 35 mm glass-bottomed dish (MatTek). After curing, ‘soft’ gels with moduli of 7kPa were deposited on top and cured. For further characterization of these gradients, see the Supplemental information.

C. Polydisperse droplet sizes

Gels were soaked in fluorinated oil for more than 24 hours at 40°C, as described. To cool our samples we used a computer controlled apparatus, as described in [9]. We preheated the chamber to 40°C, inserted the sample inside and waited for the temperature to equilibrate. The sample was cooled at a fixed rate of 0.5°C/min for 16 minutes, during which time large droplets started appearing. The cooling rate was then increased to 2°C/min until room temperature was reached, and smaller droplets nucleated and grew. The samples were taken out of the chamber and placed on the microscope for imaging.

D. Dependence of Ripening on Stiffness Difference

We observed the rate of ripening for a series of samples with different top-down stiffness gradients. ‘Soft’ gels with moduli of 7 kPa were cured on top of ‘stiff’ gels with Young’s moduli from 30kPa to 750kPa. Samples were saturated by fluorinated oil at T_sat = 40°C for several days and cooled passively to room temperature to nucleate and grow droplets. Dissolution fronts were observed over time using a 20x, NA 0.5 objective. At each timepoint, the focal plane of the objective was varied over 1 mm in steps of 20 μm, generating a stack of images. In each image, we used standard particle location algorithms to locate each droplet and measure its radius. Thus, we are able to calculate the average droplet radius as a function of time and distance from the soft-stiff interface.

E. Numerical simulation of ripening

To develop a simple theoretical description of elastic ripening, we make two crucial assumption: First, we assume that droplets are far apart from each other, so they do not interact directly, but just by exchanging monomers via the dilute phase. Second, we assume that the growth dynamics are slow compared to the relaxation of the dilute phase, so the concentration field in the surrounding of each droplet relaxes quickly to a stationary state. These assumptions are identical to the ones made in the seminal Lifshitz-Slyozov paper describing Ostwald ripening [30]. However, in contrast to this paper, we here consider a spatially resolved theory where N droplets, each described by a radius R_i and a position x_i, interact with a dilute phase characterized by the volume fraction field ϕ(r, t).

To simplify the theory further, we assume that the size of each droplet is small compared to the length scale of external gradients, so that the local environment of a droplet can be approximated by a linear gradient. These assumptions allow us to calculate the diffusive flux J_i away from each droplet i analytically [7], which is proportional to the local gradient in ϕ. The concentration at the surface of the droplet is fixed to ϕ_eq(R) = ϕ_sat exp[P(R)/(k_BTn_L)], which follows from using the ideal form of the chemical potential of the dilute phase. Here, P(R) = P_C + 2γ/R is the excess pressure inside the droplet of radius R, which is comprised of the Laplace pressure caused by the surface tension γ. While P_C = 5E/6 is a well established threshold value, recent experiments [10] suggest that P_C may be lower far beyond threshold, and closer to E/2.

The dynamics of the dilute phase are governed by a simple diffusion equation with diffusivity, D = 4-5 x 10⁻¹¹m²/s (see Supplemental Information for measurement of D), where the droplets appear as source terms, so the total material in the system in conserved. For simplicity, we discretize ϕ equidistantly in three dimensions with no-flux boundary conditions on all sides and we use a simple Euler scheme for the time stepping.

Note that all parameters in the above description are measured, so we can predict the dynamics once an initial condition is specified. We initialize the droplet positions {x_i} and radii {R_i} directly from the first time point of the measurements. Conversely, we do not have direct measurements of the dilute field ϕ. For simplicity, we initialize ϕ with the equilibrium value ϕ_eq (assuming γ = 0), implying that the background field is locally (but not globally) in equilibrium with the embedded droplets.

The only unknown from the experiments is the precise profile of the elastic modulus E as a function of the coordinate z perpendicular to the interface. Far away from the interface, E assumes the bulk values E_stiff and E_soft, but close to the interface the value can deviate, e.g., due to diffusing cross-linkers. Since we do not know these dynamics, we consider a simple exponential decay characterized by a length δ on the stiff side,

$$E\left(z\right)=\{\begin{array}{ll}\left(E_{\text{stiff}}-E_{\text{soft}}\right)\left(1-e^{-z/\delta }\right)+E_{\text{soft}}\hfill & z>0\hfill \\ E_{\text{soft}}\hfill & z\le 0.\hfill \end{array}$$

Here, δ is our only fitting parameter.

Side by comparisons of all theory and experiments are shown in Figs S10 and S11. The former uses P_C = E/2 and the latter P_C = 5E/6. Figure S12 illustrates the impact of the fitting parameter δ. Figure S13 compares contributions of surface tension and elasticity, showing that surface tension makes a negligible contribution to the observed dynamics.