Design and synthesis of pleated DNA origami nanotubes with adjustable diameters

Abstract

DNA origami allows for the synthesis of nanoscale structures and machines with nanometre precision and high yields. Tubular DNA origami nanostructures are particularly useful because their geometry facilitates a variety of applications including nanoparticle encapsulation, the construction of artificial membrane pores and as structural scaffolds that can uniquely spatially arrange nanoparticles in circular, linear and helical arrays. Here we report a system of parametrization for the design of radially symmetric DNA origami nanotubes with adjustable diameter, length, crossover density, pleat angle and chirality. The system is implemented into a computational algorithm that provides a practical means to navigate the complex geometry of DNA origami nanotube design. We apply this in the design, synthesis and characterization of novel DNA origami nanotubes. These include structures with pleated walls where the same number of duplexes can form nanotubes with different diameters, and to vary the diameter within the same structure. We also construct nanotubes that can be reconfigured into different chiral shapes. Finally, we explore the effect of strain on the local and global geometry of DNA origami nanotubes and demonstrate how pleated walls can provide a strategy to rigidify nanotubes and to construct closely packed parallel duplexes.

INTRODUCTION

DNA nanotechnology utilizes the well-known structural properties and complementary base-pairing rules of DNA (1) for the self-assembly of rationally designed nanoscale structures and machines (2–8). DNA strands at specific sites on these structures can be functionalized to selectively bind to small molecules such as nanoparticles, dyes and proteins to control their spatial organization at resolutions well below 10 nm (9–11). Thus, DNA nanostructures are suitable for a broad range of applications. For example, metallic nanoparticles can be spatially arranged to construct DNA-based plasmonic architectures (12–14) for fluorescence enhancement (15) or surface enhanced Raman scattering (16–18), which can be used as highly sensitive molecular sensors (19–21). In addition, immobilization of biomolecules allows for the construction of multi-enzyme complexes (22–26), as well as the control of biomolecular assembly (27–30) and cellular processes (31–33).

Tubular DNA structures have properties that make them particularly useful (34). Their hollow structure can be used to construct biomimetic membrane channels (30,35–37), to encapsulate proteins for multi-enzyme bioreactors (25,38) or to selectively deliver cargo to, and mediate the activity of, specific cell types (32,39). DNA nanotubes have greater structural rigidity than single DNA duplexes (40). This makes them suitable for such applications as the alignment of proteins in solution for nuclear magnetic resonance spectroscopy (41), the construction of molecular barcodes for calibration of super-resolution microscopy methods (42,43), or for scaffolding extended linear arrays of metallic nanoparticles (44–46), which is useful for the bottom-up construction of nanowires (47,48). In addition, nanotubes can organize nanoparticles into circular arrays and helical arrays, which can be used to construct plasmonic nanostructures (49,50) with distinct optical resonances that depend on their chirality (12).

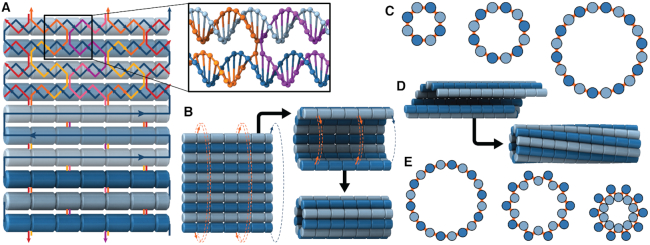
DNA nanotubes with defined diameters can be synthesized from repeating arrays of short DNA motifs (51–54). The length of these nanotubes cannot be controlled however, and each site on the nanotube is not uniquely addressable. Alternatively, nanotubes can be synthesized using the DNA origami method (4), which involves folding a long single-stranded DNA ‘scaffold’ into a desired structure by hybridization to many shorter ‘staple’ strands. This creates arrays of double-stranded DNA duplexes linked by crossovers, which are junctions where staple or scaffold strands cross from one duplex to another (Figure 1A). Each site on a DNA origami structure is unique and hence the structure has fixed dimensions and is fully addressable. DNA nanotubes with larger diameters can be constructed with duplexes aligned radially and bent along the circumference (55–57). Whereas nanotubes with smaller diameters and a higher density of radially symmetric attachment points, which are useful for immobilizing nanoparticles, can be constructed with straight duplexes aligned axially. This latter configuration, can be formed from a canonical DNA origami sheet consisting of a single layer of double-stranded DNA duplexes aligned side-by-side and held together with crossovers (4,58) (Figure 1A). By incorporating additional staple crossovers that link the first and last duplex, a DNA origami sheet can be rolled into a hollow cylinder (Figure 1B), the diameter of which is dependent on the number of duplexes around the circumference (Figure 1C).

Figure 1.

Construction of nanotubes from a DNA origami sheet. (A) Typical configuration of a section of DNA origami sheet. Blue line represents scaffold strand, with arrows indicating 5′ to 3′ direction. Light blue and dark blue cylinders indicate DNA duplexes with rightward and leftward polarity respectively. Coloured lines represent staple strands. Inset: Section showing a typical staple double crossover. (B) Schematic demonstrating how a DNA origami sheet can be ‘rolled’ into a tube by connecting the first and last duplex with crossovers. (C) Along-axis view of several DNA origami nanotubes with different number of duplexes, depicted as circles. (D) Intrinsically curved sheets form nanotubes with a well-defined inside and outside surface, but if radial symmetry is preserved, the tubes are chiral. (E) Along-axis view of pleated nanotube structures.

The intrinsic curvature of the DNA origami sheet can be controlled by altering the dihedral angles formed between three adjacent duplexes. The rules for rationally controlling these angles are non-trivial because they require navigation of complex geometry between staple crossover locations and the natural helicity of a DNA duplex (10.5 base pairs (bp) per 360° turn) (4,59,60). There are a defined set of ‘minimally-strained’ dihedral angles where the staple crossover locations align with the periodicity of DNA. These have been explored theoretically (54,59,61,62) and include angles of 120° and ∼90°, which are commonly used to construct 3D DNA origami with honeycomb (5) and square lattices (63) respectively. For the construction of nanotubes, an intrinsic curvature of ∼34.3° per pair of helices has been applied to control the direction in which the DNA origami sheet rolls. This in turn determines the inside and outside surface, and imposes chirality on the tube (50) (Figure 1D).

The design space however is much larger than has previously been explored. First, because dihedral angles can also be alternated around the circumference of the nanotube to create a pleated wall, which in principle allows for the construction of nanotubes with the same number of duplexes but different diameters (59) (Figure 1E). Second, because alternate dihedral angles can be modified to create different amounts of intrinsic sheet curvature, which in turn can create chiral tubes with different degrees of twist. And third, because internal strain can be incorporated into nanotubes to control their shape and rigidity, but their interdependence is poorly understood.

Here, we distil this complex problem into specific and simple parameters to comprehensively explore the design space for the construction of DNA origami nanotubes. We present a general algorithm for their design and apply this in the synthesis of novel DNA origami nanotubes, which we demonstrate can adopt different diameters with the same number of duplexes. We also present nanotubes with diameters that vary along their length and nanotubes with adjustable chirality. Finally, we demonstrate how strain can increase radial rigidity as well as cause the collapse of nanotube cavities, and how strain affects the local geometry of DNA duplexes.

MATERIALS AND METHODS

Algorithm for determining crossover locations

The NanoCooper algorithm was implemented in Wolfram Mathematica version 11.2. Designs were entered manually into Cadnano v2 (64) to determine staple sequences (See Supplementary Data File 2 for all Cadnano designs and Supplemental Excel Spreadsheet for all DNA staple sequences).

Molecular simulation

Molecular dynamics (MD) simulations were performed with the CUDA implementation of the oxDNA2 model (65,66), which is coarse-grained at the level of single nucleotides. Nucleotides in oxDNA are rigid and interact with each other through several different interaction types: hydrogen bonding between Watson–Crick bases, π–π stacking of bases both within and between DNA strands, backbone connectivity, excluded volume and Debye–Hückel electrostatics. Sequence-averaged parameters for stacking and hydrogen bonding potentials were used, so the architecture of each design was studied independently of sequence-specific effects. Temperature was maintained with an Andersen-like thermostat (67).

Designs of nanotubes were imported as a flat sheet into oxDNA from cadnano and carefully relaxed to a roughly circular cross-section being careful to ensure that the paths of the strands retained the correct intended topology and did not become entangled. Each system underwent a thermal equilibration over 2 × 10⁷ MD steps at 300 K and [Na⁺] = 0.5 M unless otherwise stated, followed by a production run of 10⁸ MD steps at the same conditions. Positions of all nucleotides in the system were recorded every 10⁴ MD steps, allowing us to calculate distances and angles between various base pairs. A range of diameters, radii and angles of pleats was thus determined.

DNA origami synthesis

DNA origami samples were synthesized by mixing 20 nM M13mp18 ssDNA scaffold strands (Bayou Biolabs) with 10-fold molar excess of DNA staple strands (Integrated DNA Technologies) in DNA origami buffer (5 mM Tris, 1 mM EDTA, 16 mM MgCl₂, pH 8.0) and annealing over ∼20 h (65°C for 15 min, then 60–40°C in 200 steps at 5 min/step, then 40–25°C in 150 steps at 1 min/step).

Transmission electron microscopy

DNA origami nanotubes were purified using PEG precipitation (68) and drop cast onto carbon/formvar coated copper grids and given 4 minutes to adsorb. Excess sample was wicked off using filter paper. A drop of 2% aqueous uranyl acetate was then applied to the grid and immediately wicked off using filter paper. Grids were dried overnight or until imaging. Imaging was performed on a Tecnai G2 20 Transmission Electron Microscope (FEI) in bright field mode at 200 kV. Images were analysed in ImageJ (69). Histograms were created in Wolfram Mathematica version 11.2. 2D class averages of TEM micrographs were obtained using Relion (70).

Cryo-electron microscopy

DNA origami nanotubes were imaged with cryo-EM with one of two different conditions. In the first, 4 μl of PEG-precipitation purified DNA origami were applied on glow-discharged Quantifoil R2/2 copper grids (Quantifoil Micro Tools) and plunge frozen in liquid ethane cooled liquid nitrogen using a Lecia EM GP device (Leica Microsystem). The grids were imaged using a Talos Arctica transmission electron microscope (Thermo Fisher Scientific) and operated at 200 kV, with the specimen maintained at liquid nitrogen temperatures. Images were recorded at magnification 92k× on a Falcon 3EC direct detector camera operated in linear mode.

In the second condition, Quantifoil molybdenum 200 mesh R1.2/1.3 holey carbon grids were glow discharged on a grass slide for 20 s. A 3 μl aliquot of the sample solution was applied onto the grid, was blotted by filter papers for 8 s at 100% humidity and 4°C, and the grid was quickly frozen by rapidly plunging it into liquid ethane using Vitrobot Mark IV (Thermo Fisher Scientific). The grid was inserted into a Titan Krios FEG transmission electron microscopy (Thermo Fisher Scientific) operated at 300 kV with a cryo specimen stage cooled with liquid nitrogen. Cryo-EM images were recorded with a FEI Falcon II 4k × 4k CMOS direct electron detector (Thermo Fisher Scientific) at a nominal magnification of ×75 000, corresponding to an image pixel size of 1.07 Å. Images were acquired by collecting seven movie frames with a dose rate of 45 electrons per square angstrom per second and an exposure time of 2 s.

Small angle X-ray scattering

Nanotubes were annealed as previously described, then purified using PEG precipitation. Residual PEG was removed via size exclusion centrifugation in P-30 Bio-spin columns (Bio-Rad) in DNA origami buffer. SAXS data were collected on the SAXS/WAXS Beamline at the Australian Synchrotron, Clayton, Victoria as described previously (60). Briefly, samples were passed through a 1.5-mm quartz capillary at 20°C while exposed to monochromatic X-rays (11 keV) at a flux of 4 × 10¹² photons per second. SAXS data were collected with exposure times of 5 s on a Pilatus 1M photon counting detector (Dectris), and scattering intensity I(q) was collected in the range of 0.0059 < q < 0.53 Å⁻¹, where 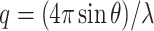, 2θ is the scattering angle and λ is the X-ray wavelength.

RESULTS AND DISCUSSION

Description of system

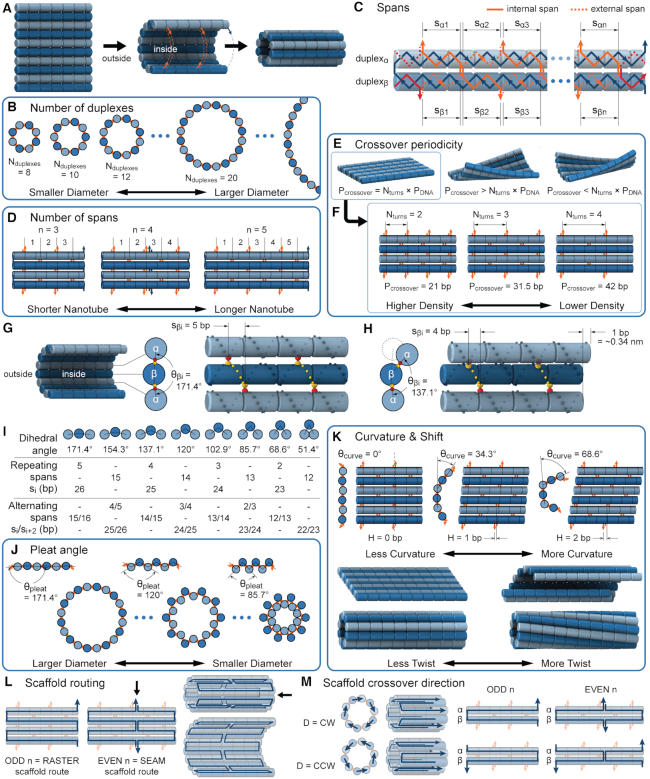
We first define a set of parameters that are sufficient to capture all aspects of the geometry of radially symmetric DNA origami nanotubes. It is helpful to describe these parameters with reference to a ‘flat’ DNA origami sheet, consisting of an array of straight parallel DNA duplexes of identical length that are connected by staple and scaffold crossovers, and how altering these parameters correspondingly alters the geometry of this reference sheet. With duplexes aligned horizontally, the sheet has an arbitrarily defined left and right, and an inside surface around which it can be rolled into a tube (Figure 2A). Each DNA duplex has a polarity, which we define as the direction the scaffold strand takes in the 5′ to 3′ direction. Typically, DNA origami structures are constructed from a circular scaffold strand. To ensure that this can route through the entire structure, it follows that a sheet or nanotube must have an even number of duplexes (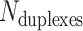), where adjacent duplexes have opposite polarities to allow for scaffold connectivity. Nanotubes are therefore constrained to have 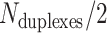radial symmetry (Figure 2B). Moreover, for a radially symmetric nanotube, we constrain all duplexes with the same polarity to have the same crossover locations. Thus, we classify all duplexes in a nanotube as either an α-duplex (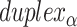), which have a left to right polarity or a β-duplex (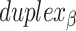), which have a right to left polarity. Duplexes within each class differ only by their DNA sequence (Figure 2C).

Figure 2.

Description of DNA origami nanotube design parameters. (A) A reference DNA origami sheet with an arbitrarily defined inside and outside surface, and the resulting nanotube when top and bottom helices are linked by crossovers. (B) Along-axis view of nanotubes with different even numbers of duplexes (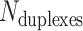). (C) A neighbouring pair of DNA duplexes ( 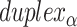and 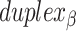), which are repeated around the circumference of the nanotube. Their associated list of staple spans ( 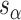and 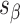), which quantify the number of base pairs between successive staple crossovers are labelled and shown as solid orange lines for internal spans or dotted orange lines for external spans. End-spans are shown as red lines and occur between the scaffold crossover at the end of the nanotube and the proximal staple crossover. (D) DNA origami sheets with different number of spans (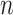), which affects the length of the nanotube. (E) DNA origami sheets each with a different crossover periodicity (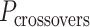). On the left, 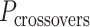is equal to the periodicity of DNA (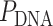) multiplied by an integer number of complete turns (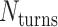) resulting in a flat sheet. Whereas the middle and right depict DNA origami sheets where 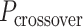is out of phase with 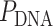in opposite directions resulting in a global twist also in opposite directions. (F) DNA origami sheets with different values of 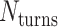where the density of staple crossovers (orange) is inversely proportional to 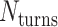. (G) Three adjacent DNA duplexes with an internal span length of 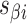= 5 bp resulting in a dihedral angle of 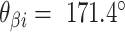relative to the inside of the DNA sheet. 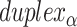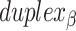Red and yellow spheres show the midpoint between successive C3′ carbon atoms (NEMid) (59) on and respectively (Supplementary Figure S1). (H) Three adjacent DNA duplexes with an internal span length of 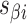= 4 bp resulting in a dihedral angle of 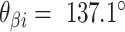and a shift of 1 bp. (I) Table of the eight possible dihedral angles used in this study (including the seven angles between 60° and 180°) and the possible repeated or alternating span lengths required to achieve them. (J) Illustration of how the pleat angle (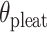) of a sheet or nanotube is defined as the effective dihedral angle of every 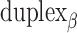, which is proportional to sheet width and nanotube diameter. (K) DNA origami sheets with different curvature angles (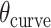) and associated shift values (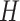). Bottom shows how sheets with intrinsic curvature will also be chiral, and hence are predicted to form chiral tubes. (L) DNA sheet showing scaffold strand following a raster (left) or seamed (middle) routing, where staple crossovers form a seam in the middle of the tube (indicated by arrow in middle panel). In a seamed configuration, two of the duplexes are not connected by scaffold crossovers (arrow in right panel), which may allow the formation of ‘open’ structures. (M) Depiction of nanotubes with different scaffold strand configurations. Top left and bottom left shows nanotubes with scaffold strand crossovers routed in a clockwise (CW) or counter-clockwise (CCW) direction on the left of the nanotube. Middle and right shows nanotubes with an odd and even number of spans (n), which results in a raster and seamed scaffold routing respectively.

Staple crossover locations are defined as a list of spans

We refer to the number of base pairs between successive staple crossovers along a DNA duplex as a ‘span’ (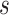) (Figure 2C, Supplementary Figure S1). This allows the location of all staple crossovers along a duplex to be represented by an ordered list of integers 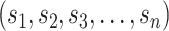, each of which quantifies the length (in bp) of a given span, and where 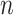is the total number of spans. Thus, the number and length of spans also determines the length of the nanotube (Figure 2D). Moreover, since crossover locations within each and each 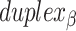are the same, the location of all staple crossovers in a DNA nanotube can be represented by two ordered lists of integers: one for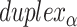 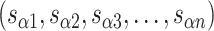and another for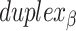 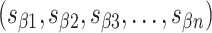. The significance of these two lists of staple spans extends beyond the simple annotation of DNA staple routing. Here, we demonstrate how careful design of span lengths can be used to control the curvature, twist and dimensions of a DNA origami sheet for the construction of novel DNA nanotubes. Moreover, spans encapsulate information on the routing of the scaffold strand.

Global twist and crossover density

In much the same way that crossover locations are repeated in each α- and β-duplex to ensure radial symmetry of the nanotube, we also use periodically repeated span lengths along the duplexes to ensure uniformity along the nanotube's length. In the reference DNA origami sheet, successive staple crossovers along each DNA duplex alternate periodically between those that occur between its top and bottom neighbour (Figure 2C). Thus, in the simplest case, any two successive staple spans define a set of periodic crossovers. The average number of base pairs in these sets defines the global staple crossover periodicity (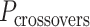). 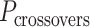determines whether the DNA origami sheet has a global twist. If the average periodicity of these crossovers is in phase with the natural periodicity of DNA ( 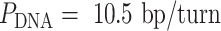), then crossovers between duplexes will be aligned and there will be no twist according to

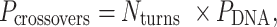(1)

where 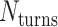defines the integer number of turns between repeating crossovers. Conversely, if 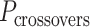does not meet this criterion, crossovers will follow a helical path around each duplex resulting in the pair of duplexes twisting around one another and a global twist in the origami sheet (60) (Figure 2E, Supplementary Figure S2A).

The magnitude of this twist as a function of crossover periodicity and the global shape of a twisted DNA origami sheet is difficult to predict because it depends on the torsional stiffness and bendability of each DNA duplex at each location on the sheet (60,71). Thus, it is desirable to minimize global twist by satisfying equation 1 above. This is straightforward when 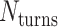is even, as the crossover periodicity 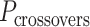is an integer, which we achieve by summing any two successive spans,

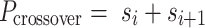(2)

However, when 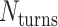is odd, satisfying equation 1 requires that 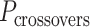is a non-integer (e.g. 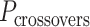= 31.5 bp when 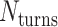= 3), and so cannot be reached with an integer number of base pairs. The solution is to alternate the number of base pairs between every second set of periodic crossovers (e.g. 31 bp followed by 32 bp, Supplementary Figure S2B) so that 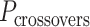is the average number of base pairs between any two successive pairs of periodic crossover sets:

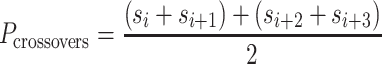(3)

The value of 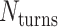affects the structural properties of the nanotube. Smaller values result in a higher density of crossovers along the nanotube, but only allow for staples with shorter span lengths, which have fewer base pairing interactions and are therefore less stable. Conversely, larger values of 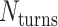allow for longer span lengths but a lower density of crossovers along the tube (Figure 2F). The effects of crossover density in DNA origami structures have been explored in both 2D (4) and 3D structures (72) and larger value of 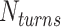has been shown to result in more porous structures with less mechanical stiffness (72). In this study, we therefore limit 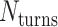to 2, 3, or 4 turns.

Dihedral angles

Dihedral angles formed between 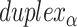or 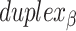and its two neighbours relative to the ‘inside’ surface of the curved sheet or tube ( 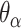or 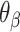respectively), are also determined by span lengths. Successive spans along a duplex alternate between those that we classify as ‘internal’ and those that we classify as ‘external’ spans (Figure 2C). Internal spans occur where a majority of the associated staple nucleotides are on the internal side of the sheet or nanotube. In this case, the first and second crossovers of the span connect the neighbouring DNA helices on the top and bottom respectively, and the staple nucleotides within the span that are immediately adjacent to crossovers, occur on the internal side. The reverse is true for ‘external’ spans. Whether a span is classified as internal or external is relevant because fewer base pairs in an internal span in 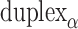(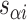) for example, results in a proportionally smaller dihedral angle at this span (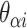) (Figure 2G, H) according to:

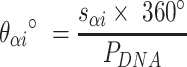(4)

Conversely, fewer base pairs in an external span results in a proportionally larger dihedral angle by the same magnitude. Indeed, successive internal and external spans are coupled such that whenever an internal span is decreased, the neighbouring external span must be increased and vice versa. Otherwise, 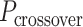would be altered resulting in a global twist rather than a specified dihedral angle (see equations 2 and 3). If the length of all internal spans in 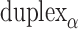are the same, then .

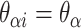It is often impractical to construct DNA origami structures with very short spans because this only allows for staple strands to hybridize at very few base pairs. For example, a span length of 5 bp between crossover pairs results in an approximately ‘flat’ dihedral angle of 171.4°, which can be increased or decreased by ∼34.3° by increasing or decreasing the span length by one base pair respectively (Figure 2G, H). However, a span length of 5 bp is likely too short to result in stable hybridization. Adding 21 bp, or two complete turns, increases the span length to 26 bp while leaving dihedral angle unchanged (891.4° mod 360° = 171.4°). Moreover, adding 10 or 11 bp to the 5 bp span length results in span lengths of 15 or 16 bp. This results in a decrease or increase in dihedral angle of 17.1° and hence dihedral angles of 154.3° or 188.6°. Dihedral angles can thus be altered in increments of ∼17.1° and the range of allowable angles has been comprehensively explored by others (59). Angles that are too small or too large will result in duplexes sterically clashing, which occurs with spans of length 11, 12 or 21 bp. If we set our minimum dihedral angle to 60°, where the centres of the three successive duplexes form an equilateral triangle in layout, there are seven possible acute dihedral angles ranging from 68.6° to 171.4°. These angles and minimal associated span lengths are shown in Figure 2I.

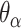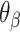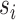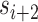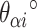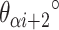Span lengths can be alternated over the length of a duplex so that or is equal to an average, or effective dihedral angle (Figure 2I, Supplementary Figure S1). For example, the same dihedral angle of 171.4° can be approximated with two alternating internal spans ( and ) of length 15 and 16 respectively. These correspond to internal angles of 154.3° and 188.6° for and respectively, where the effective dihedral angle will be the average of the two angles (171.4°). While averaging will result in strain, the approach provides an alternative method to achieving the desired angle using staples of a practical length. To limit the amount of strain caused by this type of averaging, we only permit averaging over spans that differ by one base pair (Supplementary Figure S2C).

In principle, if it were possible to average over an infinite number of spans, arbitrary effective dihedral angles are possible. However, this only works if DNA duplexes have an infinitely low bendability. In practice, DNA duplexes have a persistence length of ∼50 nm (73) and are likely to bend locally to help accommodate torsional strain, which we explore in more depth below. Thus, if we average over more than two pairs of spans, this will likely result in local perturbations to the structure rather than a global effective dihedral angle. In this study, we only consider designs where pairs of spans are repeated up to every second pair and for simplicity, we define the effective dihedral angle to be the average of the two alternating dihedral angles rather than the true average of the angles along the length of the duplex, which may differ if there are an odd number of span pairs.

Pleated sheets

As well as alternating along the length of a duplex, internal and external spans also alternate between adjacent duplexes, so that wherever there is an internal span in 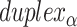there is an external span in 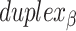and vice versa. Subsequently, if equivalent spans in α- and β-duplexes are constrained to be the same ( 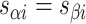) then changing dihedral angles will not result in a curved sheet. With this constraint, reducing the internal spans on 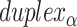and hence 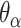will be associated with an increase in 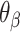of the same magnitude, resulting in a DNA origami sheet with a pleated structure. The pleat angle (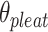), which we define as equal to 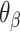(Figure 2J) affects the dimensions of the DNA origami sheet and hence the diameter of the nanotube. Thus, by altering , it is in principle possible to construct different nanotubes with the same number of duplexes, but different diameters. The pleat angle may also affect the flexibility of the nanotube in solution, as more tightly pleated DNA origami sheets have less freedom to move before sterically clashing with neighbouring duplexes.

Intrinsic curvature and shift

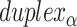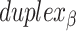To construct a DNA origami sheet with intrinsic curvature around an axis parallel to those of the DNA duplexes, it is necessary to relax this constraint so that the number of base pairs in equivalent spans in and are not the same (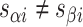). For example, decreasing and increasing successive internal (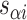) and external (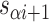) spans on each 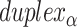but not 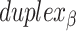, reduces 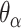by 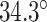per base pair, without a compensating increase in 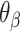. This has two consequences to the geometry of the DNA origami sheet and nanotube. The first is that the sheet will now have an intrinsic curvature. We define the curvature angle as that formed between three α-duplexes relative to a flat sheet (Figure 2K), which is equal to 360° minus the sum of the effective α and β dihedral angles:

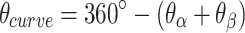(5)

In turn, the total curvature of a sheet can be quantified as the cumulative curvature angle of the duplex pairs where the sign of 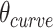determines in which direction an unstrained sheet curves. For example, a 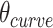of 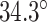in a 20-duplex sheet, the cumulative change in 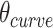of 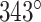and hence the total curvature of the sheet is similar to that of a closed tube (50).

The second consequence is less obvious. Since a DNA duplex is helical, reducing all of the internal spans in any duplex is necessarily associated with a rightward translation or ‘shift’ of the upper neighbouring duplex along the duplex axis, relative to the lower neighbouring duplex (Figure 2G,H). The magnitude of shift in base pair units (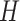) is related to 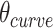according to:

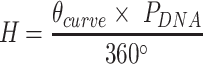(6)

As we can alternate successive span sets to obtain effective dihedral angles, we can also alternate shift over successive sets of spans to allow finer 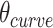increments of ∼17°. This is useful for tubes with larger stoichiometries, for which smaller values of 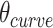are needed to approximate 360° (Supplemental Figure S3).

The shift necessitates that the arrangement of parallel duplexes in DNA origami sheets with intrinsic curvature will also have an intrinsic chirality (Figure 2K). The sheet can nonetheless be forced into a tube with flat ends (50), which will likely result in some twist and internal strain. The greater the magnitude of curvature in the sheet, the greater strain from twisting (Supplementary Note 1). The exact effects of this strain on the local or global geometry of the nanotube depend on an interplay of multiple physical factors and are not well understood (60,71). It is also possible to synthesize a nanotube from a sheet without any intrinsic curvature, but the strain on the duplexes increases as the stoichiometry decreases, and it is impossible to control which surface becomes the inside surface and which the outside.

Pleat and shift

We note that 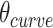and 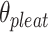can be independently defined and independently influence the geometry of the DNA origami sheet and nanotube. Thus, it is in principle possible to simultaneously design DNA nanotubes with the same number of helices but different diameters, while also controlling the intrinsic curvature of the DNA sheet to control the internal and external surface and degree of twist.

Scaffold strand routing

The path through which the scaffold strand threads through a DNA origami structure is another important design consideration. In a DNA origami sheet, single-strand scaffold crossovers necessarily occur with one neighbouring duplex at either end, and with the other neighbour via a reciprocal double crossover somewhere in the middle of the duplexes. If the double crossover occurs in at the same location on each duplex, this can result in the formation of a seam in the DNA origami sheet (4). This ‘seamed’ configuration is required to accommodate a circular scaffold strand in a DNA origami sheet. However, if the sheet is rolled into a closed tube, the scaffold can follow a raster path with scaffold crossovers alternating between either end of the nanotube (Figure 2L). While it is unlikely that routing the scaffold in either a seamed or raster configuration will affect nanotube geometry, the seamed configuration has two adjacent duplexes without a scaffold crossover, which may make it preferable for applications which require opening the nanotube, for example to release a payload anchored within (39), or reconfiguring its chirality. Another consideration is whether the direction () of the scaffold strand crossovers follow a clockwise (CW) or counter-clockwise (CCW) path through the nanotube at the left end of the nanotube when viewed from the left (Figure 2M).

The scaffold configuration is also encapsulated in the list of 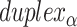and 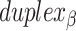spans. First, the total number of spans determines whether the scaffold strand adopts a seamed or raster configuration: if the total number of spans is even, then the first and last crossover occurs between the same duplexes and the scaffold strand must therefore adopt a seamed configuration. Similarly, if the total number of spans is odd, then the first and last crossover occurs between different helices and the scaffold must follow a raster pattern. Second, the direction that the scaffold strand follows (CW or CCW) depends on whether the first span in 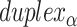is associated with an inner or an outer stretch of DNA staple: If the first span is classified as internal, the first staple crossover occurs with its top neighbour. It follows therefore that the scaffold crossover at the beginning of the duplex must occur with its bottom neighbour resulting in a CW template strand routing. Conversely, if first span is associated with an outer stretch of DNA staple, the template must be threaded in a CCW configuration.

Scaffold strand crossovers

In addition to the list of staple spans, which define the relative location of all staple crossovers, it is also necessary to define the relative location of scaffold strand crossovers. The location of scaffold crossovers at the ends of duplexes can be determined as the number of base pairs corresponding to an odd number of half turns from the closest staple crossover with the same neighbouring duplex (e.g. 5.25 bp or 15.75 bp). We can therefore calculate two additional ‘end-spans’ that occur at the start (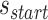) and end (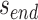) of each duplex, which are defined as the number of base pairs between the scaffold crossover at the end of the duplex and the nearest staple crossover. This also provides a reference point that sets the absolute position of all staple crossovers.

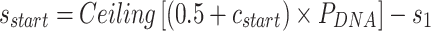(7)

and

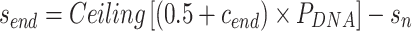(8)

where 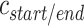is the integer number of whole turns between the scaffold crossover and the closest staple crossover occurring between the same pair of duplexes, and can be adjusted to ensure that 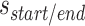is positive and sufficiently large to allow for a stable number of base pairs between staple and scaffold crossovers. As with staple spans, end-spans may differ between α- and β-duplexes and must be defined independently. In some cases, it may be desirable to omit staples at the end of duplexes. This results in a loop of unpaired scaffold strand between pairs of adjoining duplexes, which may be useful for preventing unwanted base stacking interactions (4).

Finally, if the scaffold strand adopts a seamed configuration, the location of the seam (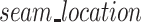) can be defined as the number of base pairs between the first staple crossover and the seam. For a seam approximately in the middle of the sheet, this can be calculated as 5 bp (∼half a turn) from the staple crossover in the middle of the DNA origami sheet:

When n is even:

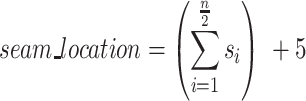(9)

Algorithm

It is not straightforward to convert these numerous principles into practical designs for nanotubes with the desired geometries. Thus, to make nanotube design more generally accessible we developed an algorithm to do so, which was implemented into software named ‘NanoCooper’. This software allows the user to enter desired nanotube parameters into a simple graphical user interface, and presents them with design solutions. These solutions take the form of graphical representations of the nanotube, useful information about its geometry, and relevant span lengths and crossover positions which can then be used to design DNA staples and scaffold routing for the synthesis of nanotubes. A complete description of the algorithm and the NanoCooper software is presented in Supplementary Note 2 with associated Supplementary Figures S5–S9.

Molecular dynamics simulations of 36-duplex DNA origami nanotubes with various pleat angles

We applied the principles described above to design eight different DNA origami nanotubes using the NanoCooper program. Each nanotube had the same number of duplexes ( 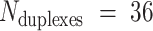) but different pleat angles ranging from 51° to 171° (Figure 3A). Scaffold strands were routed in a raster configuration and 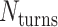was set to three to allow for a reasonably high density of staple crossovers without compromising the number of base pairs stabilizing each staple. To define the inside and outside surface, duplex pairs were designed with a curvature angle of 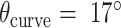, resulting in a total curvature of 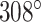, which closely matches a closed tube.

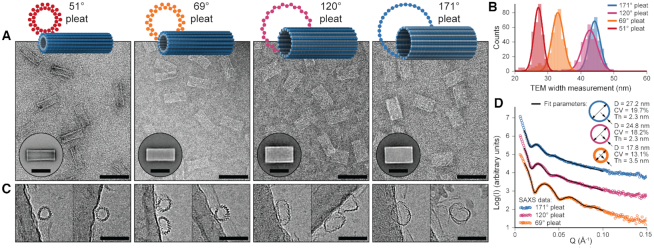
Figure 3.

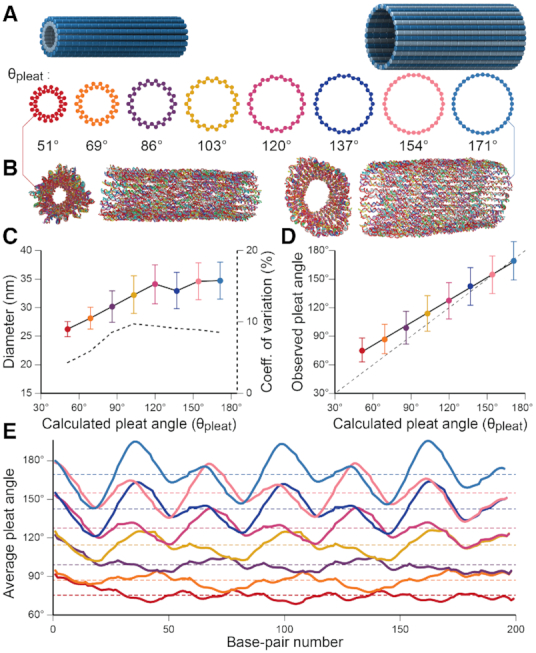
Molecular dynamics simulation of pleated DNA origami nanotubes using oxDNA. (A) Designs for eight 36-duplex nanotubes with a range of pleat angles. 3D models are of nanotubes with a 51° pleat angle (left) and a 171° pleat angle (right) (B) Single-frame images showing end and side views of the 51° pleated (left) and 171° pleated (right) nanotubes. (C) Observed diameters versus designed pleat angle for the 8 designs. Error bars are standard deviation. Dashed line (right axis) indicates coefficient of variation of diameter. Theoretically diameters calculated from idealized models (Supplementary Note 3) are shown in Supplementary Figure S11. (D) Observed average versus designed pleat angles for the with linear fit (solid black line). Dashed line shows equivalent values for reference. (E) Average pleat angle measurements at every base pair location along the length of each nanotube. Dotted lines indicate average pleat angles along the entire length.

These nanotubes were first characterized in silico with molecular dynamics (MD) simulations using the oxDNA coarse-grained model (66). This model has been demonstrated to accurately predict the local and global geometry of DNA nanostructures at a level of detail that is not easily obtainable with experimental methods (71). Here, we visualize the global geometry of the DNA nanotubes, including how pleat angles affect their diameter and flexibility, and how strain from averaging spans lengths to construct effective dihedral angles affects the local geometry of DNA helices. All structures formed hollow tubular structures which appeared to have approximately circular cross sections (Figure 3B, Supplementary Figure S10). The twist in DNA duplexes resulting from the intrinsic curvature of nanotube walls was less than predicted from ideal models (Supplementary Note 1 and Supplementary Figure S4). Fluctuations in average cross-sectional diameters (Supplementary Figure S10) reveal that orthogonal diameters are almost perfectly anti-correlated, with correlation coefficients ranging from -0.84 to -0.92. This indicates that nanotube cross sections are centrosymmetric and fluctuate between circular and elliptical shapes, hence resulting in an average circular cross section. Nanotube diameter increased with pleat angle as expected (Figure 3C), affirming that pleated walls can be used to control nanotube diameters. To quantify how well nanotube geometry matched design, we compared observed and predicted pleat angles for all nanotubes. These were similar for nanotubes with large pleat angles, but deviated linearly from design with decreasing pleat angle (Figure 3D). Increasing the concentration of sodium ions from 0.5 to 5 M only marginally reduced this deviation suggesting that electrostatic forces have a minor influence (Supplementary Figure S12A). A more prominent reduction in pleat angles is observed by lowering temperatures (Supplementary Figure S12B). This indicates that thermal fluctuations, which have been explored previously (71), have a larger effect on nanotube geometry. These give rise to the larger observed variance at larger pleat angles, but are increasingly constrained by electrostatic forces and the excluded volume of duplexes at low pleat angles where α-duplexes on the inside surface are forced to be in closer proximity (Figure 2K). Consequently, there will be a greater repulsive force between inner duplexes at low pleat angles and a larger deviation from design. Subsequently, electrostatic forces likely place increasing torsional strain on duplexes with smaller pleat angles. OxDNA simulations also indicate that nanotubes with small pleat angles have greater radial rigidity. The diameters of nanotubes with larger pleat angles fluctuate more dramatically and with large fluctuations occurring over longer time scales (Supplementary Figure S10). The coefficient of variation (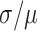) was similar for the diameter of nanotubes designed with pleat angles of 103° and greater (∼10%) but decreased at pleat angles of 86° (9%), 69 (7%) and 51° (5%) (Figure 3C). We attribute this to the more densely packed duplexes and torsional strain, both which provide additional constraints against the deformation of DNA duplexes. This was evident in oxDNA simulations, which also reflect that inter-duplex repulsions have a greater constraining effect on duplex fluctuations at smaller pleat angles. We also observe the local pleat angle changes periodically along the length of a duplex (Figure 3E). This indicates that duplexes bend significantly to accommodate the torsional strain from the alternating span lengths utilized to achieve the effective global dihedral angle. This effect is more pronounced in nanotubes with larger pleat angles where duplexes are less densely spaced confirming that the conformational freedom of duplexes is more restrained with smaller pleat angles.

oxDNA was also used to visualize fluctuations in nanotubes to that were split into an open structure by removing all crossovers between two adjacent helices. As expected, all sheets tended to curve towards the designated inside surface but with significant fluctuations between a nearly flat sheet and a closed tube (Supplementary Figure S13). These data suggest that while intrinsic curvature in nanotube walls may be effective for controlling the designated inside and outside surface, such curvature provides little restraint on the global structure of nanotubes. Indeed, the large fluctuations suggest that a range of intrinsic angles may be tolerated for the construction of nanotubes with the same diameter.

Experimental characterization of 36-duplex DNA nanotubes with various pleat angles

Four 36-duplex nanotubes spanning the range of possible pleat angles (51°, 69°, 120° and 171°) were synthesized and characterized experimentally with transmission electron microscopy (TEM) and cryo-electron microscopy (cryo-EM). In TEM images, the nanotubes appeared mostly as uniform rectangular structures, often with visible striations running along the length of the nanotube, confirming the direction of the DNA duplexes (Figure 4A). There were very few malformed particles and nanotubes formed sharp dominant bands when visualized with agarose gel electrophoresis (Supplementary Figure S14). This indicates that synthesis yields were high as typically observed for DNA origami structures. As expected, the average lengths of all nanotubes were the same (Supplementary Figures S15–S18) whereas their average widths increased with pleat angle (27.1 ± 1.4, 33.0 ± 1.7, 42.7 ± 2.3 and 44.1 ± 1.7 nm for the 51°, 69°, 120° and 171° respectively, Figure 4B). These widths were larger than the diameters observed in MD simulations, suggesting that the nanotubes were somewhat flattened on the carbon grid. Nanotubes were also imaged with cryo-EM. Although most particles tended to be associated with the carbon support, there were sufficient 51° and 69° pleated nanotube particles in the vitreous ice to determine their distribution of widths in solution (Supplementary Figures S17, S18). These widths as measured by cryo-EM were consistent with measurements from oxDNA simulations. Cryo-EM also allowed imaging of nanotubes in an end-on orientation with (Figure 4C). This allowed for the direct visualization of the pleated walls of the nanotubes and confirmation that wider tubes had larger pleat angles. At the largest pleat angles, nanotubes were formed from a single layer of duplexes. Whereas at the smallest pleat angles, parallel inner α-duplexes were closely spaced so that the structure of the wall resembled a triangular lattice (74). Thus, altering pleat angles also provides a means to achieve a range of distances between parallel duplexes in DNA origami structures, which may be useful for tuning the distances between immobilized nanoparticles (75).

Figure 4.

Experimental characterization of 36-duplex nanotubes with various pleat angles. (A) Design schematics and representative TEM micrographs of 36-duplex nanotubes with pleat angles of 51°, 69°, 120° and 171° from left to right respectively (scale bars 100 nm). Inset: 2D class averages (scale bars 50 nm) (B) Histograms of width measurements from TEM micrographs of all four designs overlaid with Gaussian fits. (C) Representative single particles from cryo-EM micrographs captured end-on showing the different pleated structures of each design (scale bars 50 nm). (D) SAXS data and analytical fits for three of the nanotube designs. Inset: Model fit parameters, where ‘D’ and ‘Th’ are the diameter and wall thickness respectively of the model cylinder and ‘CV’ is the coefficient of variation of D.

By comparing the widths of nanotubes on TEM grids to the diameters of nanotubes in oxDNA simulations and cryo-EM images, it is possible to estimate the degree of flattening. This flattening was less pronounced in nanotubes with smaller pleat angles than those with larger pleat angles (Supplemental Figure S19). This was also evident in TEM micrographs in which the narrowest nanotube with a 51° pleat angle had more prominent walls and accumulated uranyl acetate stain in its centre (Figure 4A); indicative of a raised and hollow structure. We also characterized nanotubes with pleat angles of 69°, 120° and 171° using small angle X-ray scattering (SAXS). SAXS provides a measure of nanotube diameter, wall thickness and flexibility in solution. X-ray scattering from hollow tubular structures produces characteristic diffraction peaks where the inter-peak spacing increases with decreasing diameter. These diffraction peaks are also less pronounced with more flexible structures that sample a greater range of diameters (60). Scattering from structures with a larger pleat angle produced diffraction peaks that were less pronounced but more closely spaced, not only confirming that these structures had a larger diameter in solution but also suggesting that wider nanotubes are more flexible (Figure 4D). To quantify these differences, SAXS data were fitted with analytical models of hollow cylinders. As anticipated, nanotube diameters from SAXS measurements were consistent with structures observed in oxDNA simulations. Scattering from nanotubes with a 69° pleat angle were also consistent with a cylinder with a thicker wall than nanotubes with a 120° and 171° pleat angle. Finally, narrower nanotubes had a lower coefficient of variation in their diameters. Along with the greater resistance to flattening on TEM grids, SAXS data are consistent with oxDNA simulations that indicate that nanotubes with smaller pleat angles have greater radial rigidity.

Application for the design and synthesis of additional novel DNA origami nanotubes

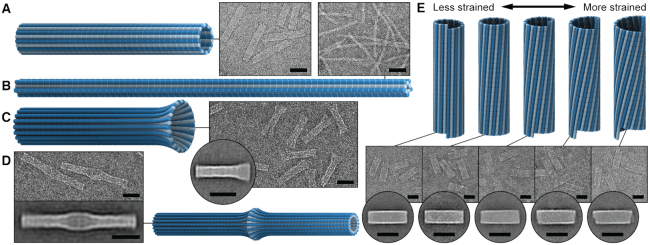
To more broadly explore the applicability of the system, nanotubes with a different number of duplexes were designed and synthesized. These included a 20-duplex minimally-pleated nanotube designed to have a similar diameter to that of the tightly-pleated 36-duplex nanotube (Figure 5A), as well as a much longer 10-duplex nanotube with a pleat angle of 85° and curvature angle of 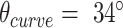, (Figure 5B). TEM images illustrate how both nanotubes appeared as well-formed structures with dimensions similar to those predicted (Supplementary Figures S20, S21). Furthermore, we also designed and synthesized 26-duplex nanotubes with a curvature angle of 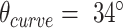, but where the diameter varies over the nanotube's length. This was achieved by incorporating different pleat angles along the length. We created a ‘nanotrumpet’ with tight 69° pleating along most of the tube, flaring into a looser 171° pleating at one end (Figure 5C, Supplementary Figure S22). These nanotrumpets were used to form dimeric structures that form a continuous nanotube with a larger chamber in the centre (Figure 5D). Dimerization was achieved by truncating staples at the end of the first nanotrumpet to leave unpaired scaffold strands, which bound to complementary staple extensions the second nanotrumpet.

Figure 5.

Electron micrographs of additional novel DNA origami nanotubes. 3D models, representative TEM micrographs, and 2D class averages of (A) a 20-duplex, 171°-pleated nanotube, designed to have similar diameter to the 36-duplex, 51°-pleated nanotube, (B) a 10-duplex, 69°-pleated nanotube, (C) the 26-duplex ‘nanotrumpet’, (D) nanotrumpet dimers, and (E) a 26-duplex nanotube with the scaffold strand routed with a seam, allowing for reconfiguration into different chiral shapes with varying degrees of predicted twist and strain. All scale bars are 50 nm.

We next designed and synthesized 26-duplex nanotubes where the scaffold strand was routed in a seamed configuration resulting in one pair of neighbouring ‘seam’ duplexes, which are not linked by scaffold crossovers (Figure 2M). Thus, by replacing the subset of staples that form crossovers between these seam duplexes, their relative positions can be adjusted. To illustrate this, we designed and synthesized a radially symmetric 26-duplex nanotube with flat ends. Then by replacing a subset of crossovers, the nanotube was transformed into a structure in which the array of duplexes follow a right-handed helical path (Figure 5E, Supplementary Figure S23). In this nanotube, the seam duplexes were offset by 10 base pairs in the direction aligned with the shift (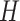) associated with the intrinsic curvature of the sheet (see equation 6). Subsequently, duplexes in this nanotube are likely to be under less strain than a tubular configuration with flat ends. We also synthesized nanotubes in which the helical array of duplexes take left handed chirality where the seam helices were offset in the opposite direction by 11, 21 and 31 bp (Figure 5E). Interestingly, these left-handed nanotubes appeared to form without significant loss of yields despite a probable increase in strain with an increasing offset between seam helices.

OxDNA simulations above suggest that there is substantial flexibility in open DNA origami sheets. We therefore explored the consequence of constructing strained nanotubes from DNA origami sheets with a total curvature that is substantially more or less than that of a closed nanotube (Supplementary Note 4). We designed two 36-duplex pleated nanotubes, the first of which was constructed from a sheet with no intrinsic curvature and the second of which was dramatically over-curved (total curvature = 617.1°, Supplementary Figure S24). Both structures were analysed with oxDNA simulations. The first nanotube formed a tubular structure with a circular cross section and no obvious global twist (Supplementary Figure S24D). These data suggest that while rolling up a flat sheet forfeits control over which side of the sheet forms the inside or outside surface of the nanotube, there is little consequence to the global dimensions of the nanotube. Indeed, torsional strain from the under-curved sheet might be expected to impart expanding forces on the nanotube and prevent collapse. In contrast, oxDNA simulations of the second nanotube indicate that torsional strain in nanotubes formed from sheets with too much curvature may be sufficient to collapse the hollow cavity of the nanotube. These flattened nanotubes tended to form a twisted sheet similar to the blade of a propeller (Supplementary Figure S24I). To test this experimentally, we synthesized the over-curved 36-duplex pleated nanotubes and imaged these. Particles in TEM and cryo-EM micrographs were less uniform and tended to form an hourglass rather than a rectangular shape, consistent with the propeller-like structure observed in oxDNA simulations (Supplementary Figures S24J, S25).

Here we report a system of parameterization for the design of DNA nanotubes and its implementation into an algorithm that yields ideal crossover locations for radially symmetric designs. This provides a facile approach for the construction of nanotubes with an arbitrary even number of helices as well as with a pleated wall structure. We demonstrate how these pleated walls provide an effective strategy to increase the radial rigidity of nanotubes to overcome the inherent flexibility in single-layered DNA origami structures, as well as a greater versatility in nanotube design than previously demonstrated. These include structures whose diameter can be tuned independently from the number of duplexes by altering pleat angles, nanotubes whose diameter can vary within the same structure and nanotubes that can be reconfigured into different chiral shapes. We also explore the effect of strain on the local and global geometry of nanotubes. We demonstrate how torsional strain can be utilized to create structures with the desired global dihedral angles, but also how this torsional strain is in part accommodated by the local bending of DNA duplexes, which likely limits the achievable effective dihedral angles in DNA origami structures. We also demonstrate how hollow tubular structures appear to be resilient to the twisting of duplexes into chiral nanotubes and to torsional strain from rolling up a flat sheet, but can collapse if the intrinsic curvature of the sheet is too great. Combined, these findings increase the design space and provide an accessible approach for the construction of radially symmetric DNA origami nanotubes. We note that this system can potentially be expanded upon to include more elaborate design configurations (Supplementary Figure S26). In addition, this study provides a greater understanding of how DNA origami structures accommodate strain.

Notes

Present address: Lawrence K. Lee, EMBL Australia Node for Single Molecule Science, School of Medical Sciences, UNSW Sydney, NSW 2052, Australia.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Australian Research Council [DP130102219]; Human Frontiers Science Program [RGP0030/2013]; National Health and Medical Research Council [APP1129234]; Australian Research Council Discovery Early Career Research Award [DE140100262 to L.K.L.]. Funding for open access charge: The National Health and Medical Research Council [APP1129234].

Conflict of interest statement. None declared.