Patch-Based Generative Adversarial Neural Network Models for Head and Neck MR-Only Planning

Abstract

Purpose:

To evaluate pix2pix and CycleGAN and to assess the effects of multiple combination strategies on accuracy for patch-based synthetic CT (sCT) generation for MR-only treatment planning in head and neck (HN) cancer patients.

Materials and Methods:

Twenty-three deformably registered pairs of CT and mDixon FFE MR datasets from HN cancer patients treated at our institution were retrospectively analyzed to evaluate patch-based sCT accuracy via the pix2pix and CycleGAN models. To test effects of overlapping sCT patches on estimations, we 1) trained the models for three orthogonal views to observe the effects of spatial context, 2) we increased effective set size by using per-epoch data augmentation, and 3) we evaluated the performance of three different approaches for combining overlapping Hounsfield Unit (HU) estimations for varied patch overlap parameters. Twelve of twenty-three cases corresponded to a curated dataset previously used for atlas-based sCT generation and were used for training with leave-two-out cross-validation. Eight cases were used for independent testing and included previously unseen image features such as fused vertebrae, a small protruding bone, and tumors large enough to deform normal body contours. We analyzed the impact of MR image preprocessing including histogram standardization and intensity clipping on sCT generation accuracy. Effects of mDixon contrast (in-phase vs water) differences were tested with three additional cases.

The sCT generation accuracy was evaluated using Mean Absolute Error (MAE) and Mean Error (ME) in HU between the plan CT and sCT images. Dosimetric accuracy was evaluated for all clinically relevant structures in the independent testing set and digitally reconstructed radiographs (DRRs) were evaluated with respect to the plan CT images.

Results:

The cross-validated MAEs for the whole-HN region using pix2pix and CycleGAN were 66.9±7.3 HU vs. 82.3±6.4 HU, respectively. On the independent testing set with additional artifacts and previously unseen image features, whole-HN region MAEs were 94.0±10.6 HU and 102.9±14.7 HU for pix2pix and CycleGAN, respectively. For patients with different tissue contrast (water mDixon MR images), the MAEs increased to 122.1±6.3 and 132.8±5.5 HU for pix2pix and CycleGAN, respectively.

Our results suggest that combining overlapping sCT estimations at each voxel reduced both MAE and ME compared to single-view non-overlapping patch results.

Absolute percent mean/max dose errors were 2% or less for the PTV and all clinically relevant structures in our independent testing set, including structures with image artifacts. Quantitative DRR comparison between planning CTs and sCTs showed agreement of bony region positions to less than 1 mm.

Conclusions:

The dosimetric and MAE based accuracy, along with the similarity between DRRs from sCTs, indicate that pix2pix and CycleGAN are promising methods for MR-only treatment planning for HN cancer. Our methods investigated for overlapping patch-based HU estimations also indicate that combining transformation estimations of overlapping patches is a potential method to reduce generation errors while also providing a tool to potentially estimate the MR to CT aleatoric model transformation uncertainty. However, because of small patient sample sizes, further studies are required.

1. Introduction

MR imaging provides superior soft-tissue contrast compared to CT imaging and is often considered the standard for tumor delineation in Head and Neck (HN) cancers¹. Its inclusion with CT imaging in radiotherapy (RT) dose planning has shown marked improvements in intra-observer tumor delineation, segmentation, and treatment outcomes in HN cancer^1–4. The current radiotherapy planning process requires delineation of target and organs-at-risk (OAR) structures on MR images followed by the transfer of these contours to CT images via image registration. This process introduces registration uncertainty for the contours. It is, therefore, desirable to move towards MR-only planning since it could potentially reduce unnecessary CT imaging for patients, improve clinical workflow efficiency and reduce anatomical uncertainties stemming from registration errors between CT and MR images. However, the inability to directly calculate the electron density from MR images has, until recently, necessitated CT imaging for dose planning.

The methods and results for estimating Hounsfield Unit (HU) and the electron density indirectly from MR images that have been developed over the last two decades are summarized in three recent review papers for different anatomical sites^5–7. These review articles group the methods into voxel based, registration (atlas) based, and hybrid voxel-and-atlas-based classification. As computational techniques evolve, these categories become harder to fit uniquely, so it can also be helpful to categorize them by their core underlying processing methods. These methods divide into segmentation (including manual and automated), multi-atlas registration, and machine learning including deep-learning approaches.

With regards to the accuracy of the estimations, modern multi-atlas and deep learning methods are promising and active areas of research for synthetic CT (sCT) generation. In multi-atlas-based methods, the computational burden mainly lies in aligning the target MR scan with the set of MR images in the MR-CT atlas set. This process is computationally intense with times ranging from ten minutes to several hours to generate sCT images^8–12. Note also that computational time increases with the number of atlas pairs used. Ultimately, this computational burden makes these methods largely unsuitable for clinical practice at present, especially looking forward to where MR is used for online treatment adaptation. With deep learning methods, a convolutional neural network consisting of several convolutional layers is trained with data from the two modalities prior to sCT generation. While training is computationally intensive and may require several days, once trained, these methods are extremely fast and produce sCT images in seconds to tens of seconds^13–18. Another attractive feature of deep learning techniques is that they can directly extract the relevant set of features from the data without requiring extensive feature engineering. As a result, recent papers have shown promising results from deep learning applied to sCT generation in brain^13–18 and pelvis^{17, 19–23} sites.

A central assumption of all the aforementioned methods to estimate HU values or electron density is that the distribution of MR intensities from the target and the existing set of training (or atlas) images are similar. This is essential particularly for machine learning methods including deep learning, without which the learned models are no longer applicable to the unseen dataset^{24, 25}. Dataset differences can also be problematic for multi-atlas registration, which are typically based on matching the local intensity distributions or features between the target and atlas set. However, MR images are not generally calibrated and typically show variations from scan to scan, and scanner to scanner. Furthermore, the mapping from MR to CT tissue density is non-unique (not a one-to-one mapping) and, due to the short T2* relaxation time for cortical bone, bone is represented with similar image intensity values to air regions for almost all MR sequences. Ultrashort time echo (UTE) MR sequences can mitigate the ambiguity between air and bone since the ultrashort echo time permits bone measurements, but such acquisitions take considerably longer (>10 min)^{26, 27} than pulse sequences such as mDixon (~5 min), thereby making UTE sequences less practical for clinical workflows. For non-UTE MR sequences, bias-field corrections, image standardization, machine learning and/or complex heuristics along with atlas techniques have proven effective in estimating structures^5–7. Therefore, we implemented our methods with image preprocessing including bias-field correction and histogram standardization for training and testing and also tested how the models performed if the input MR images were not standardized.

Unlike prior deep learning studies that have typically focused on brain and pelvis, our work studied the applicability of deep learning based sCT generation for head and neck (HN) cancers, a previously unstudied site for deep learning when including dosimetric evaluations. It is important to note that whereas rigid registration is generally considered acceptable to align scans for brain and pelvis, deformable registration is crucial for HN. Because of this, in this pilot study we compared two Generative Adversarial Network (GAN) based approaches that have differing alignment requirements. The pix2pix²⁸ model requires near perfect alignment between CT and MR images while CycleGAN²⁹ relaxes the constraint of using aligned images or even images acquired from the same patient. For a reference point, we compared the results of the training set to the results from previous work on multi-atlas sCT generation using the same curated dataset¹⁰. To obtain realistic expected performance of these methods, we evaluated the models on a new set of paired data with a variety of clinical conditions. These included: patient cases with strong streak and dental artifacts in the CT images (a common occurrence for head and neck studies around mandible due to dental implants), a case with fused vertebrae, and cases with anatomical features not present in the training set, such as protruding bone from the skull and a large (>100 cm³) tumor protruding from the neck. We performed ablation testing of these methods including orthogonal views as additional channels for processing, epoch-specific data augmentation, and three different post-processing techniques to integrate the overlapping patch-based inferences into a sCT. These patch combination methods are independent of the neural networks used and the results can be applied to any other network model. Finally, we evaluated the dosimetric consequences of generating sCT images with CycleGAN and pix2pix neural networks, as well as generated digitally reconstructed radiographs as a pilot test of the applicability of these neural networks for clinical usage.

2. Methods

We developed and investigated methods to enhance sCT estimations, testing them in the frameworks of the pix2pix and CycleGAN networks. Our methods included (i) utilizing the pix2pix and CycleGAN networks in a 2.5-D manner (three orthogonal views trained independently), (ii) per-epoch data augmentation in training, and (iii) improved HU estimation by combining multiple overlapping sCT patch predictions using three different combination techniques. We investigated the robustness of these trained networks on clinical cases that were challenging due to previously unseen image features and we compared our 2.5-D approach to single axial view based sCT generation. Details of our processing pipeline from patient selection to registration techniques, as well as our implementation enhancements are explained in the following subsections.

We tested the sCT generation accuracy and robustness using Mean Absolute Error (MAE) based on HU for three regions (whole-HN region, which we define as the voxels within the head and neck body region of each patient, as well as the bone, and air subregions within the HN). We used Mean Error (ME) to measure systematic average offset errors in the sCT generation. We evaluated the effects of histogram standardization and input image contrast. We also evaluated the dosimetric uncertainties introduced by using sCTs and tested their accuracy as references for 2D matching by creating digitally reconstructed radiographs (DRRs). Finally, we compared the accuracy of these deep learning methods to a multi-atlas sCT generation method¹⁰.

2.1. Patient Selection

Twenty-three head and neck (HN) mDixon MR and CT image pairs from patients who received external beam radiotherapy were included in this study. Twelve patients were from a curated set used in a previous multi-atlas study¹⁰, to allow direct comparison of the neural networks to multi-atlas methods, and were also used as the training data set for the neural networks. The ages for these patients ranged from 24 to 67, with a median age of 52; ten patients were male and two were female. Eight patients with similar tissue contrast and previously unseen MR image features were added for independent testing, and for evaluating the robustness of the learned models. The ages for this test group ranged from 44 to 77 with a median age of 63; six patients were male and two were female. The image features not present in the training set included a small protruding bone, tumors large enough to visibly deform the normal body contour, necrotic tissue, strong dental artifacts (>4.5 cm in sup-inf direction of MR images), and fused vertebrae. There were no exclusion criteria for the additional eight cases aside from matching scan sequence parameters.

The CT and MR image sets were acquired in radiotherapy treatment position. The MR images were acquired on a Philips 3T Ingenia system using the vendor-supplied phased-array dStream Head-Neck-Spine coil, with mDixon in-phase dual fast field echo (FFE) images (TE1/TE2/TR = 2.3/4.6/6.07 ms, flip angle = 10°, slice thickness of 1.2 mm and in-plane pixel size of approximately 1 mm²). 3D scan sequences were used, but additional undersampling speed enhancements were not used. The scan time was under 4 min. Vendor correction for geometric distortion was applied to the mDixon MR images. The CT images were acquired using a GE CT scanner in helical mode with tube voltage of 140 kVP, and pitch factor 1.675.

As an additional test of contrast sensitivity, three new cases with different mDixon tissue contrast (water instead of in-phase images) were tested with the trained models. The age range for this set was 52 to 77, with median age 66; all patients were male. These patients also included anatomical differences from the training set such as missing multiple molars or an entire row of teeth, and a metal implant at the sternum for one patient.

A table including the original voxel dimensions for the CT and MR images, as well as notes about artifacts and implants is included in Table S-1.

2.2. Image Processing

The workflow for processing images is available in the supplemental information as Figure S-1. Image preprocessing steps are shown in Figure S-1a and the workflow for the processed, registered CT/MR pairs for training and testing the two conditional GANs: pix2pix, and CycleGAN, is shown in Figure S-1b.

2.2.1. MR Image Standardization and Bias Field Correction

The mDixon in-phase FFE MR image intensities may vary between scans and can also be affected by B0 and B1 field nonuniformities. We used a vendor provided software (Philips’ CLEAR, or Constant LEvel AppeaRance) to correct non-uniform receiver coil intensity inhomogeneity as applicable. It uses pre-scan coil sensitivity maps to minimize intensity variations. Additional in-house software based on level set energy minimization to estimate and correct the bias field effects³⁰ was used in sagittal plane views, followed by histogram based image standardization, as described in detail in our previous work¹⁰.

2.2.2. Image Registration

The differences in patient setup position, head tilt/orientation, arm position (affecting the shoulder region of the scans) and usage of bite blocks were enough to preclude using only simple rigid registration. Multi-staged deformable image registration with Plastimatch³¹ was used to register the CT images to the MR images for both the training and testing sets. The CT images were registered to the MR images to minimize the number of deformable (i.e. non-affine) transformations performed on the MR images, which we expected might change local image features including image textures and would adversely impact training and sCT generation accuracy. The curated set from the multi-atlas study that was used for training was deformably registered using a strategy that combined two different cost functions for maximizing mutual information between the MR-CT images and minimizing the mean square error between the MR and bone-suppressed CT images, as described by Farjam et al.¹⁰. Before performing deformable registration on the external data set, the MR images were resampled to isotropic spacing (1.1 mm in each direction).

For the independent, newly added sets following training, the registration method consisted of first registering CT to MR images using affine transformations for a rough alignment of global structures. A coarse-to-fine multi-resolution B-spline deformable registration was then performed at three resolutions with 60 mm grid size at the coarsest level uniformly placed over each direction. The mesh size was reduced by a factor of 2 at each subsequent level. A Broyden–Fletcher–Goldfarb–Shanno (BFGS) optimizer was used to maximize mutual information between two images with a regularization term to penalize discontinuity in deformation vector field³¹. The regularization weight (λ) was set to λ=0.001 and λ=0.1 for the coarser and the finest levels, respectively.

2.3. GAN and Conditional GAN Details

GANs are a class of neural networks that pit two convolutional neural networks, a generator and a discriminator, against each other to allow the generation of realistic looking images with similar statistical properties compared to a sample training set, starting from random noise. These networks are optimized through error backpropagation computed using a cost metric³². The generator and discriminator are trained simultaneously using a min-max (minimize loss in generator and maximize discriminative capacity of discriminator) strategy.

Conditional GANs^{32, 33} extend the standard GAN approach by requiring that the resulting target domain images are dependent on additional information for the network such as a set of segmentations, paired images, or text labels. The network is then optimized to generate images with similar statistical characteristics as the target images given the specific additional information. An example of a conditional GAN is the pix2pix paired image-to-image model²⁸.

CycleGAN²⁹, while sharing some network architecture similarity with pix2pix and using many of the same building blocks, does not have the same paired image constraints. It instead uses cycle consistency and identity losses to constrain the networks and generate images in the second modality based on the original image. There are, by design, no conditional dependencies for the GAN discriminators because the network does not require paired images. In the following subsections we describe these two models in further detail. We also describe our patch-based training and sCT generation implementation for HN cancer cases based on deformably registered CT and MR images.

2.3.1. Image-to-Image Conditional Generative Adversarial Network (pix2pix)

The pix2pix²⁸ model is a conditional image-to-image generative adversarial network that requires paired images from two modalities that are co-registered with voxel-wise correspondence. In addition to the adversarial GAN losses consisting of the generator loss and the discriminator loss (real vs. fake image pairs), it includes an additional loss based on the absolute difference between the generated image and the original paired image (L1 norm loss). The L1 norm loss is expressed as:

$${\mathcal{L}}_{L1}\left(G_S^T\right)={\mathbb{E}}_{x,y}\left(\Vert y-G_S^T\left(x\right){\Vert }_1\right)$$ (1)

where $G_s^T$ is the generator network that produces images to match the target modality from source modality images, and $\mathbb{E}$ is the expectation value dependent on both x, the set of source modality (MR) images, and y, the set of target modality (CT) images. The adversarial loss penalizes at the scale of sub-image patches (e.g. 70 × 70 pixels for a 128 × 128 image) and is expressed as:

$${\mathcal{L}}_{GAN}\left(G_S^T,D_T\right)= {\mathbb{E}}_{x,y}\left(\text{log\hspace{0.17em}}{D}_T\left(x,y\right)\right)+{\mathbb{E}}_x\text{\hspace{0.17em}log}\left(1-D_T\left(x,G_S^T\left(x\right)\right)\right)$$ (2)

where D_T is the target modality discriminator which attempts to distinguish between real and fake image pairs, $\mathbb{E}$ is the expectation value, and the other parameters remain the same as in eq (1). In pix2pix networks the number of samples in the source and target domain are the same due to the requirement for aligned datasets. The adversarial loss for equation (2) is calculated using the binary cross-entropy cost function. The final cost function used to optimize the network is a weighted summation of the aforementioned losses:

$${\theta }_{G,D}=\mathbf{\text{arg }}\underset{G}{\mathbf{\text{min}}}\underset{D}{\mathbf{\text{max}}}\left({\mathcal{L}}_{GAN}\left(G_S^T,D_T\right)+\lambda {\mathcal{L}}_{L1}\left(G_S^T\right)\right)$$ (3)

where λ is the user-defined weighting factor for the L1 loss. This implementation consists of a generator network that is constructed using a U-Net³⁴ and a discriminator composed of a sequence of five convolutional layers. This model is shown in Figure 1a.

Figure 1). (a).

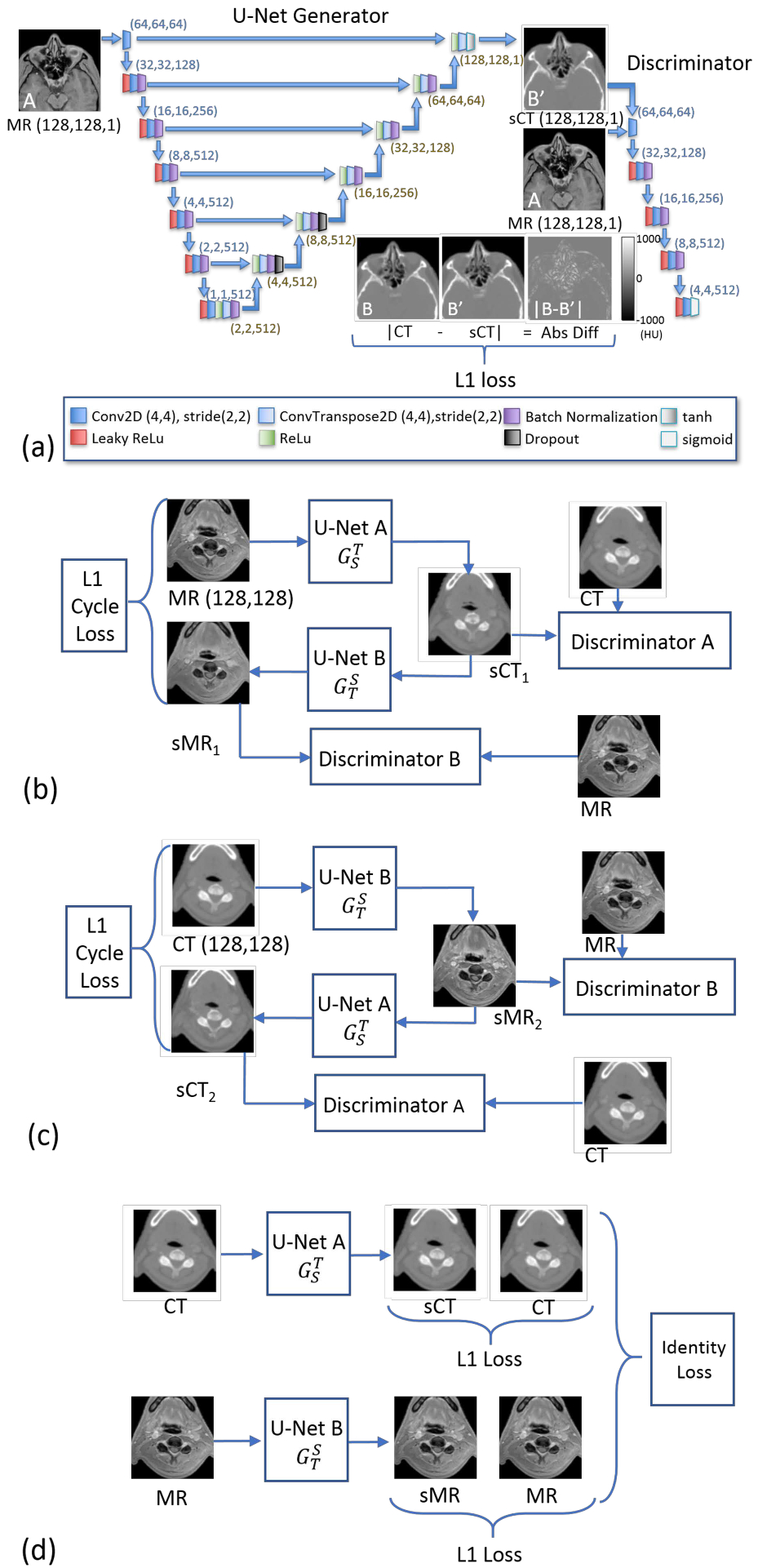
The pix2pix model²⁸ as used in this work, showing the generator U-Net, and the five-level discriminator. In addition to these components, an L1 loss based on the synthetic and real CTs is used. Paired images are required for pix2pix. The identity losses for CycleGAN resemble the L1 loss depicted here in (a), but with the input images matching the target modality of the generator and with generators for both sCT and sMR images. (b) A simplified view of the first half of the CycleGAN model²⁹ showing the cycle comprised of Generators and Discriminators starting with MR images and ending with synthetic MR images. (c) The second half of the CycleGAN model, starting with CT images and ending with synthetic CT images. (d) The identity loss, an L1 loss between the input CT and sCT generated with U-Net A and the L1 loss between the input MR and sMR generated with U-Net B, works to constrain intensity ranges. The networks (b), (c), and (d) are trained simultaneously.

2.3.2. Cycle-consistent Generative Adversarial Network (CycleGAN)

CycleGAN²⁹ is related to pix2pix in that it uses the same basic network blocks, but it only needs images from each modality rather than near-perfectly aligned paired images from the same patient. This matched-image requirement is eliminated by imposing an additional cycle consistency loss such that each image passing through the pair of generators will attempt to reproduce itself. Cycle consistency in both directions is required for this training. For example, using MR mDixon in-phase images and CT scans the cycle of generator networks will produce images MR→sCT₁→sMR₁ and CT→sMR₂→sCT₂. The cycle consistency is enforced by minimizing the L1 norm losses between the final synthesized images (sMR_1, sCT₂) and the corresponding input modality images (MR, CT, respectively). As a result, a single cycle network is composed of a pair of GANs operating on the two imaging modalities. The generators are implemented using U-Nets, and the discriminator networks are composed of five convolutional layers and use a binary cross entropy cost function. The cycle consistency loss is expressed as:

$${\mathcal{L}}_{cyc}\left(G_s^T, G_T^S\right)={\mathbb{E}}_x\left({\Vert x-G_T^S\left(G_S^T\left(x\right)\right)\Vert }_1\right)+{\mathbb{E}}_y\left({\Vert y-G_S^T\left(G_T^S\left(y\right)\right)\Vert }_1\right)$$ (4)

where $G_s^T$ represents the generator in the direction of MR→CT as S represents our primary source modality (MR) and T represents our primary target modality (CT). Correspondingly, $G_T^S$ represents the generator in the direction of CT→MR. The GAN loss is expressed as:

$${\mathcal{L}}_{GAN}\left(G_s^T, G_T^S, D_S, D_T\right)= {\mathbb{E}}_y\left(\text{log}\left(D_T\left(y\right)\right)\right)+{\mathbb{E}}_x\left(\text{log}\left(1-D_T\left(G_s^T\left(x\right)\right)\right)\right)+{\mathbb{E}}_x\left(\text{log}\left(D_S\left(x\right)\right)\right)+{\mathbb{E}}_y\left(\text{log}\left(1-D_S\left(G_T^S\left(y\right)\right)\right)\right)$$ (5)

where D_S represents the primary source modality (MR) discriminator, and D_T represents the primary target modality (CT) discriminator. An additional identity loss, to constrain the intermediate images to have similar intensities to the actual intermediate group is expressed as:

$${\mathcal{L}}_{identity}\left(G_s^T, G_T^S\right)={\mathbb{E}}_y\left({\Vert y-G_S^T\left(y\right)\Vert }_1\right)+{\mathbb{E}}_x\left({\Vert x-G_T^S\left(x\right)\Vert }_1\right)$$ (6)

where the variables remain the same as before, with $G_s^T$ representing the generator from source to target (MR→CT) and $G_T^S$ representing the generator from the target to source modalities (CT→MR). The final cost function to be optimized is:

$${\theta }_{G,D}=\mathbf{\text{arg }}\underset{G}{\mathbf{\text{min}}}\underset{D}{\mathbf{\text{max}}}{\mathcal{L}}_{GAN}\left(G_s^T, G_T^S, D_s, D_T\right)+{\lambda }_{cyc}{\mathcal{L}}_{cyc}\left(G_s^T, G_T^S\right)+{\lambda }_{identity}{\mathcal{L}}_{identity}\left(G_s^T, G_T^S\right)$$ (7)

where λ_cyc and λ_identity represent the weight factors for the cycle and identity losses, respectively. The cyclic constraints are weaker than the voxel-wise constraints of the pix2pix model, but the aim of creating images in the second modality based on the input images remains.

Simplified block diagrams of the two cycles, MR→ sCT→ sMR, and CT → sMR→ sCT, are shown in Figure 1b and 1c, respectively. Each cycle has two U-Nets (labelled with an A and B), and two discriminators (also labeled with A and B) along with the L1 loss for cycle consistency. The identity loss is shown, schematically, in Figure 1d.

2.3.3. Implementation Details

The full volume scans (MR and CT) were resampled and padded with air values to produce isotropically spaced cubes of 512×512×512 voxels with voxel spacing of approximately 1.1 mm on edge, prior to any image scaling performed in the augmentation routines. Training of the pix2pix and CycleGAN networks were performed for all three views (axial, coronal, sagittal) independently on 2D image patches of 128 × 128 pixels, with per-epoch custom augmentation as described in §2.3.4.

Body masks for the CT images were automatically generated based on the largest contiguous regions contained in the axial slices above a specified threshold value (−250 HU). Likewise, body masks for the standardized, bias field corrected (BFC) MR images were created from the largest contiguous voxel regions above a user-defined threshold chosen in the range [0,1000], dependent on the particular MR image set. Holes in the body mask volumes were filled in automatically using a flood fill command for binary masks in MATLAB (2014b and 2018b). The CT masks were dilated in each axial slice using the Matlab function, ‘imdilate’, and a circular disk kernel with radius 4 voxels (4.4 mm). Likewise, the MR masks were dilated in each axial slice by 12 voxels (approximately 13.2 mm) to ensure that any boundary differences between the registered CT and the MR would not exclude portions of the CT data by having too small a mask. Comparisons of sCT and CT data for MAE and ME were based on the expanded CT masks.

We used the pix2pix and CycleGAN models and framework freely available from github at https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix as our starting point. The models were trained starting with the same original HN datasets, though they were augmented to different sets due to the custom augmentation functions that included random image modifications during the training. For training, the standardized, BFC input MR images were clipped with a constant value of 2500. This value corresponds to the 99.5 percentile intensity value of all masked voxels for the combined set of the standardized, BFC MR images. Following intensity clipping, the values were scaled linearly to the range [0,255] as required for input to the augmenter and the network. The CT images were clipped to a range of [−1000 HU, 3000 HU] and were also scaled linearly to the required network input range of [0, 255].

The receptive field for the generator is the full 128 × 128 pixel image patch. Example images showing what this spatial extent (~14 × 14 cm) includes can be seen in Figure 1. The discriminator networks themselves compare subregions of the image patches as an ensemble, in a method called PatchGAN²⁸, with receptive fields of 70 × 70 pixels (7.7 cm × 7.7 cm) for the subregion. This method corresponds to a Markovian discriminator (due to independent estimation of errors across different patches in an image, which corresponds to a Markov random field) and is meant to preserve both low and high spatial frequency image information in the generated images, which is often lost with L1 or L2 loss functions alone²⁸. For image patches of 128 × 128 pixels both the pix2pix and CycleGAN models have over forty-one million parameters for each generator network and over two million parameters for each discriminator in each view.

The models use batch size of one for the input images, batch normalization, and the Adam optimizer (β₁ = 0.5, β₂ = 0.999)³⁵ for the generator and discriminator networks. We used the default value for β₁, 0.5, in the implementations by Zhu et al.²⁹, and Isola et al.²⁸, which lies halfway between the extrema tested by Kingma and Ba³⁵ and which has been shown to help increase training stability by reducing oscillation in training³⁶. The β₂ parameter, 0.999, was chosen for stability in sparse gradients³⁵. The learning rate for the Adam optimizer was set to a constant 0.0001 for the first 100 epochs and decayed to zero over the next 100 epochs. Models were trained to a maximum of 200 epochs. The cross-validation models were stopped at 100 epochs based on the convergence of the L1-loss, to save computational training time (each fold took approximately 1 week of training for 100 epochs). This is justified as the cross-validation results were only used for comparison against the multi-atlas method. Additionally, empirical testing of the networks showed differences in MAE results of less than 2 HU between 100 and 200 epochs for training. Basing our specific case implementation on established code bases^{28, 29} that were already parameter-tuned, we did not have issues with GAN training instability.

The output sCT intensity values were rescaled linearly from the output range of [0,255] to the same range as the intensity clipped input CT images [−1000 HU, 3000 HU]. Combining multiple overlapping estimates allows us to reduce the HU step size from the initial size of 15.625 HU possible from single estimations with 8-bit output, but even with increased precision leaves the potential for a base accuracy uncertainty of 7.8125 HU (half the base HU step size).

The original curated dataset that had been used for multi-atlas studies¹⁰ was the basis of the training set, with two cases left out for testing. This training set was used for all the performance comparisons using both the pix2pix and CycleGAN models, as well as different pre-processing and data augmentation strategies. Eight additional paired sets with a wider range of image features were made available after training and were used as an independent testing set. The two test cases from the curated set were removed from results reporting, aside from comparison with the multi-atlas method, as they were only available pre-standardized with respect to the training set. To observe how these deep learning methods compared to the multi-atlas method, network training was performed on the curated set using leave-two-out cross-validation, requiring the pix2pix and CycleGAN models to be trained six times each, for each orthogonal view.

Three additional water mDixon cases were made available following our full evaluation of the independent testing set, and image-based metrics were also tested for these cases to assess the robustness of the models to tissue contrast differences.

For computations, deep learning training and testing were performed on a Linux based high performance cluster (HPC) with 128 GB RAM per node and Nvidia GeForce 1080 Ti (11 GB RAM) GPUs.

2.3.4. Data Augmentation and Training

In deep learning, an epoch is defined as the computational period for which all of the training images have been propagated through the neural network weight optimization training (both forward and backward) exactly once. The PyTorch (www.pytorch.org) framework that we use allows per-epoch augmentations, so we implemented custom data augmentation routines on the image pairs before each epoch.

Our custom augmentation routines allow us to 1) allow a greater variation of anatomical features, positions, or orientations which may be observed in new patient data, 2) prevent overfitting in the network by giving variation in the data at each epoch, and 3) exclude slices comprised of voxels outside the body that could lead to trivial mappings and network weights.

From each original 512 × 512 slice containing patient data, an additional mirror image along the symmetry axis is created if possible, such as for axial and coronal views. Uniform random numbers are applied for a variety of factors including: angles for rotations in the range [−3.5, 3.5 degrees], scaling in the range [0.9,1.1], and shearing of the image in range [0.97, 1.03] on each slice. From each of these transformed slices five uniform random crops of 128 × 128 pixels are made. The cropped image patch size, 128 × 128 pixels, or a field of roughly 14 cm × 14 cm, was chosen to balance the flexibility of learning multiple scales of physical features with the potential to learning trivial mappings (air-to-air mappings outside of the patient body). If there was no overlap with the patient body mask in a random crop, then the patch was discarded and up to 100 tries were performed before selecting an image pair patch. Thus, from an original set of 2663, 2524, and 4245 slices (512 × 512 pixels) that contain relevant patient data for a 10 patient training set for axial, coronal, and sagittal views, respectively, the network was trained on roughly 2.6 × 10⁶, 2.5 × 10⁶, and 2.1 × 10⁶ image patches (128 × 128 pixels) after data augmentation over 100 epochs of training. The number of patches correspondingly increased with the number of epochs.

2.3.5. Patch Based sCT Generation and Overlapping Estimation Combination Strategies

For sCT generation after training, the 512 × 512 × 512 voxel volumes with isotropic spacing (approximately 1.1 mm on edge) of the eight test cases were processed to create sets of 128 × 128 pixel images, with user specified strides that control the overlapping regions of the generated sCT estimation patches. Accuracy reduction in the sCT from lack of spatial context toward the outside edges of the image patch was addressed by using a tunable ‘pixel crop’ parameter for excluding a number of border pixels during sCT inference. The parameters for stride, s, and cropping, c, are shown with the test workflow in Figure 2. We tested non-overlapping sCT image patches: stride = 128 voxels, crop = 0 voxels; and stride = 96 voxels crop = 16 voxels; as well as overlapping sCT regions: stride = 64 voxels, crop = 16 voxels; stride = 32 voxels, crop = 16 voxels; and stride = 32 voxels, crop = 8 voxels. For the case with stride = 64 voxels, as many as 12 estimations exist at each location, and for stride = 32 voxels, as many as 48 estimations exist at each voxel location using three orthogonal views.

Figure 2).

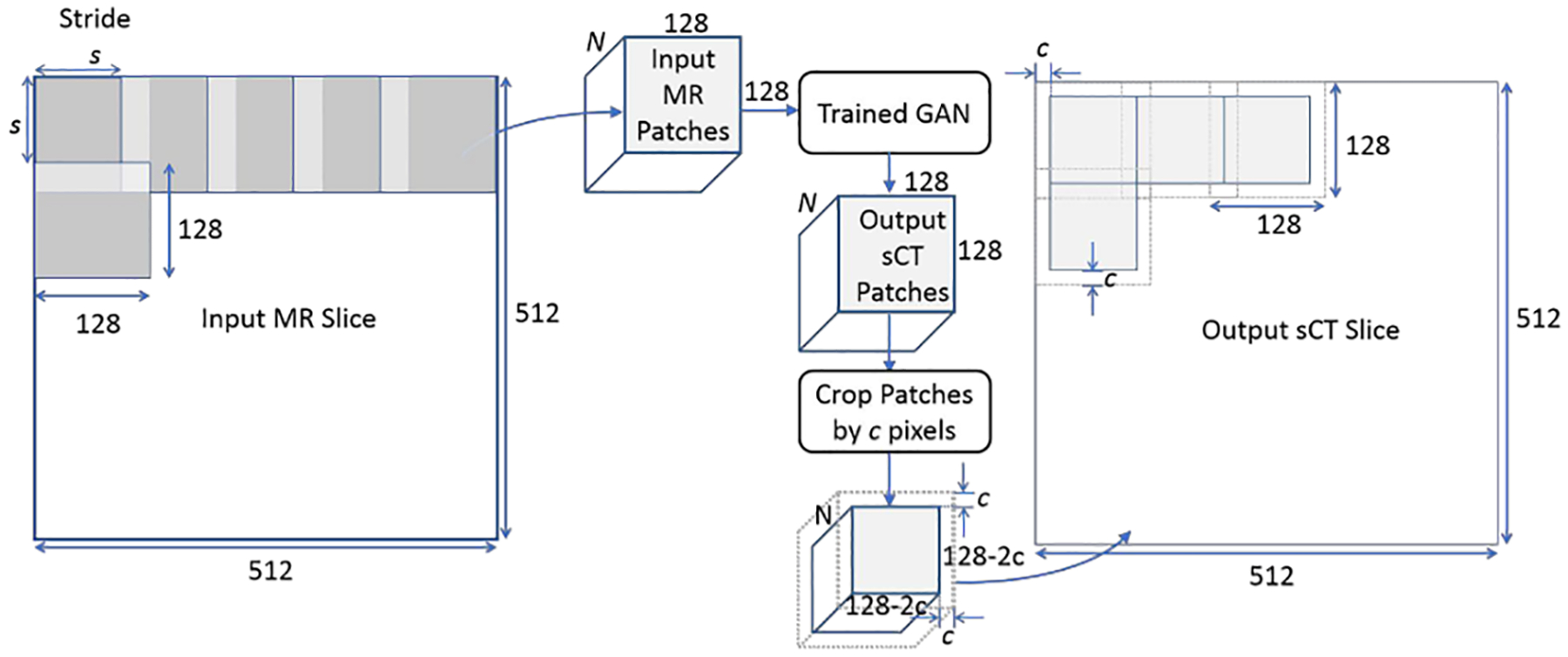
Image processing workflow showing the effects of changing the stride, s, on the number, N, of input patches and the cropped pixels on edge, c, when tiling the resultant sCT patches. This example case shows perfect tiling in the resultant sCT, but changes to s and/or c will result in overlapping sCT patches.

Because the estimated HU values may vary at a given voxel from the overlapping sCT patches based on the context for the patch, three methods to combine the overlapping HU estimations were investigated: averaging, median, and voting. Averaging and median work with the assumption of largely unimodal intensity distributions for HU estimations of a single voxel, while voting has the potential to perform better with multimodal HU intensity distributions (e.g. if air and bone HU values are estimated for a single voxel). We implemented the voting strategy as follows. First, the multiple predicted HU intensity values for a given voxel are classified into three types based on predetermined thresholds: air-like [−1000 HU, −200 HU), tissue-like [−200 HU, 200 HU), and bone/metal like [200 HU, ∞). Next the number of estimations in each classification type at each voxel are compared in a method akin to voting. If the number of overlapping estimations in a classification group surpass the majority-win fraction (e.g. 65%) then the values from the other groups are discarded and the average of the values in the winning group is recorded for that voxel. If there is no majority winner, then if the two largest groups surpass the minority fraction (e.g. 65% as well), then the values for the third group are discarded and the average of the values in the two winning groups are recorded for the voxel. If there is no majority or minority win, the average of all estimations is recorded for the voxel. We use 65% for both the majority and minority win fractions in this study.

Related to the combination methods, we investigated the ranges of the HU estimations at each voxel for the overlapping patches. The number of estimations for each voxel are dependent on the stride and crop factors as shown in the previous section and the estimations vary based on the local context of the individual patches. Thus, for non-overlapping patches for each orthogonal view there would be only three estimations per voxel, and for stride=32, crop=16, there would be as many as 48 estimations per voxel. From this we calculate the per-voxel estimation range as:

$$sCTRange\left(i\right)=\mathbf{\text{max}}\left(x_{MR}^{sCT}\left(i, a\right)\right)-\mathbf{\text{min}}\left(x_{MR}^{sCT}\left(i,a\right)\right)$$ (8)

where for clarity we write $x_{MR}^{sCT}\equiv G_S^T\left(x\right)$ to represent the transformation from MR→CT images, where i denotes voxel indices for the transformed set of images, and a represents the set of source (MR) patches containing voxel i.

The sCT Range is calculated for all voxel indices the results and can be plotted as images. These images are indicative of uncertainty in the HU estimation due to variations in intensities in adjacent patches and approximate the aleatoric (or image-based) uncertainties.

2.4. Evaluation

Evaluation of the synthetic CT images can be broken into quantification of voxel-wise accuracy and overall dosimetric accuracy. The evaluation metrics are described below.

2.4.1. Image-based Metrics

The most common evaluation metrics for comparing new multi-atlas and convolutional neural network sCT generation techniques are the mean absolute error (MAE), and mean error (ME):

$$MAE= \frac{1}{N}\sum _{i=1}^N{\Vert y\left(i\right)-x_{MR}^{sCT}\left(i\right)\Vert }_1$$

$$ME=\frac{1}{N}\sum _{i=1}^N\left(y\left(i\right)-x_{MR}^{sCT}\left(i\right)\right)$$ (9)

where y again represents the set of target modality (reference CT) images, $x_{MR}^{sCT}$ represents the set of sCT images generated from MR images, i represents the voxel indices of the regions/tissues of interest, and N represents the number of voxels in the given region/tissue of interest.

Significant errors often occur in transition or interface regions with bone and air (such as the sinuses, internal ear structure, trachea, and esophagus). In addition to the MAE with standard deviation for the whole head and neck region, we also reported MAE for bone and air regions. These regions were chosen from the deformed CT images using HU thresholds of less than −200 HU [−1000 HU, −200 HU) and greater than 200 HU (200 HU, ∞ HU) for air-like and bone/metal regions, respectively. The whole-HN, air, and bone regions were all expanded by an integer number of voxels using 2D image dilation per axial slice (circular structuring element with radius of 4 voxels) in Matlab that yielded a distance less than 5 mm laterally and in anterior-posterior directions (4 voxels equal ~4.4 mm). This dilation serves to smooth the edges of the automatically generated boundaries and helps to ensure that the complete transition zones were captured in the error metrics. Note that increasing the boundary zone too much would include soft tissue or air outside the body, which, in comparison, are relatively simple mappings in the networks, and would thus artificially lower the error for those zones. Artifacts were not manually masked out in the evaluation of the sCT images compared to the CT images.

2.4.2. Dosimetric Evaluation

To evaluate the accuracy of the HN sCTs for patient treatment planning, the treatment plan and structure set from the original planning CT was transferred to the sCT for all ten patients in the testing dataset and dose was recalculated and compared. Differences in patient setup between the planning CT and MR images prevented the direct transfer of structures between image sets. Therefore, the original planning structures were rigidly transferred to the deformed CT registered to the MR/sCT images using the previously described Plastimatch-based deformable registration method, and then when verified for the deformed CT, they were transferred to the sCT images. The following structures and dosimetric quantities were evaluated: PTV (max dose, D95), parotids (mean dose), submandibular glands (mean dose), brainstem (max dose), cord (max dose), and mandible (max dose).

To evaluate the accuracy of sCT as a reference for 2D head and neck image-guided radiotherapy, DRRs were generated from both the original planning CT and pix2pix as well as CycleGAN sCT for all test patients. The localization accuracy in 2D was evaluated by registering two sets of DRRs (plan CT vs pix2pix and plan CT vs CycleGAN) to each other using a bony match. Pearson Correlation Coefficient metrics were also calculated for all registration results.

3. Results

3.1. Effects of Multi-View and Overlapping Image Patches on MAE and ME

The MAE for sCT images generated when using overlapping and non-overlapping patches when using single view axial input images vs 2.5-D (three views: axial, sagittal, coronal) input MR images for both the pix2pix and CycleGAN sCT generation methods are shown in Figure 3; the corresponding plot for ME is shown in Figure S-2. As observed in Figure 3, for non-overlapping in-plane patches (crop = 0, stride = 128) to generate the sCT images, the average MAE for the whole set of test patients was nearly double for axial-only patches when compared to the MAE from averaging the HU values from sCTs generated from the axial, sagittal, and coronal views. The MAE results for axial only were: pix2pix = 156.3 ± 12.9 HU; CycleGAN = 165.2 ± 14.1 HU, while the MAE results when axial, coronal, and sagittal sCTs were averaged were: pix2pix = 99.8 ± 11.6 HU; CycleGAN = 108.3 ± 13.1 HU. The same trends were observed for the ME with axial MR only non-overlapping patches (pix2pix = 74.6 ± 22.1; CycleGAN = 92.2 ± 22.8 HU) vs. combined three-views based method (pix2pix = 23.3 ± 11.2 HU; CycleGAN = 38.1 ± 14.8 HU).

Figure 3).

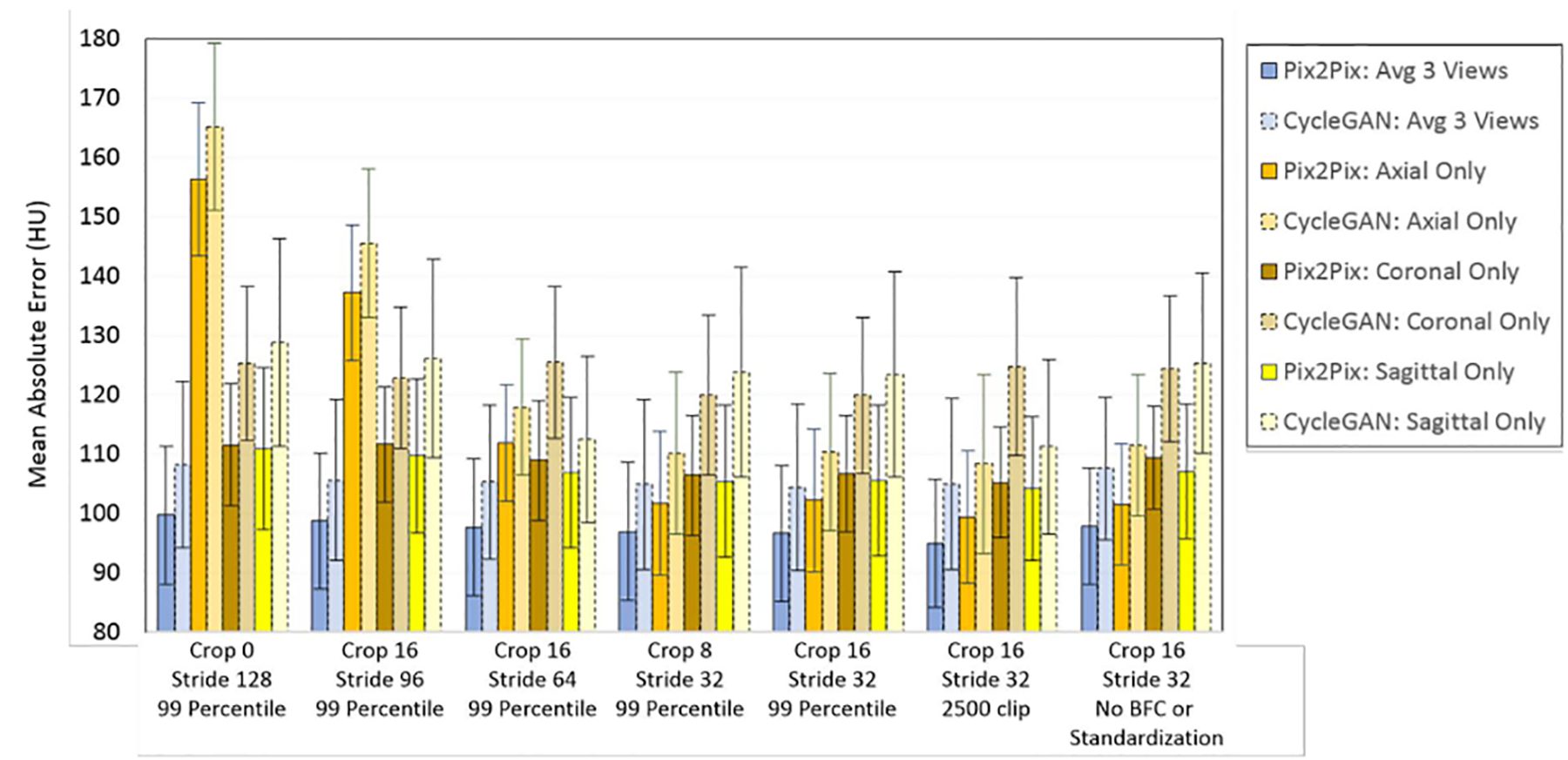
The MAE for the whole-HN region with respect to different crop and stride parameters, as well as effects of clipping the MR input intensities to the 99 percentile value for the image, or for a static post-standardized value for the external test set. This plot shows that when multiple sCT estimations overlap and are averaged, either by using three complementary views or overlapping patches in a single view, the errors decrease, and that standardization prior to sCT generation improves MAE.

As shown in Figure 3, the sCT estimation accuracy improved and the corresponding MAE values decreased even further when using overlapping patches (see Figure S-2 for ME trends). Cropping the sCT patches to reduce the number of voxel estimations that lack local spatial context (i.e. the patch border voxels) also improves the accuracy, but the improvement is more marked when combined with overlapping patches (Figure 3). Using overlapping patches reduces the discrepancy between the single-view axial and multi-view sCT estimations to within one standard deviation for the MAE and ME results. Additionally, when using results comprised of sCT patches from the three views there is little difference between the combination of cropped multiple-view non-overlapping in-plane sCT results (crop = 16, stride = 96) with the multiple-view, overlapping results (agreement within one standard deviation). However, gridding artifacts, caused by mismatches of estimations edges of the individual sCT patches are still pronounced for sCT images when non-overlapping in-plane patches are combined (Figure S-3).

Figure 4 shows CT and MR images, the corresponding sCTs for pix2pix and CycleGAN, their error maps, and the per-voxel estimation range plot for sCTs generated with crop=16, stride=32 voxels. This combination of crop and stride parameters corresponds to as many as 48 overlapping estimations per voxel created from patches each with different spatial context. Note that while large estimation ranges per voxel do not necessarily equate to large errors in the generated sCT, they highlight the more difficult regions in the modality mapping, such as bone-air transition regions, and dental artifacts.

Figure 4).

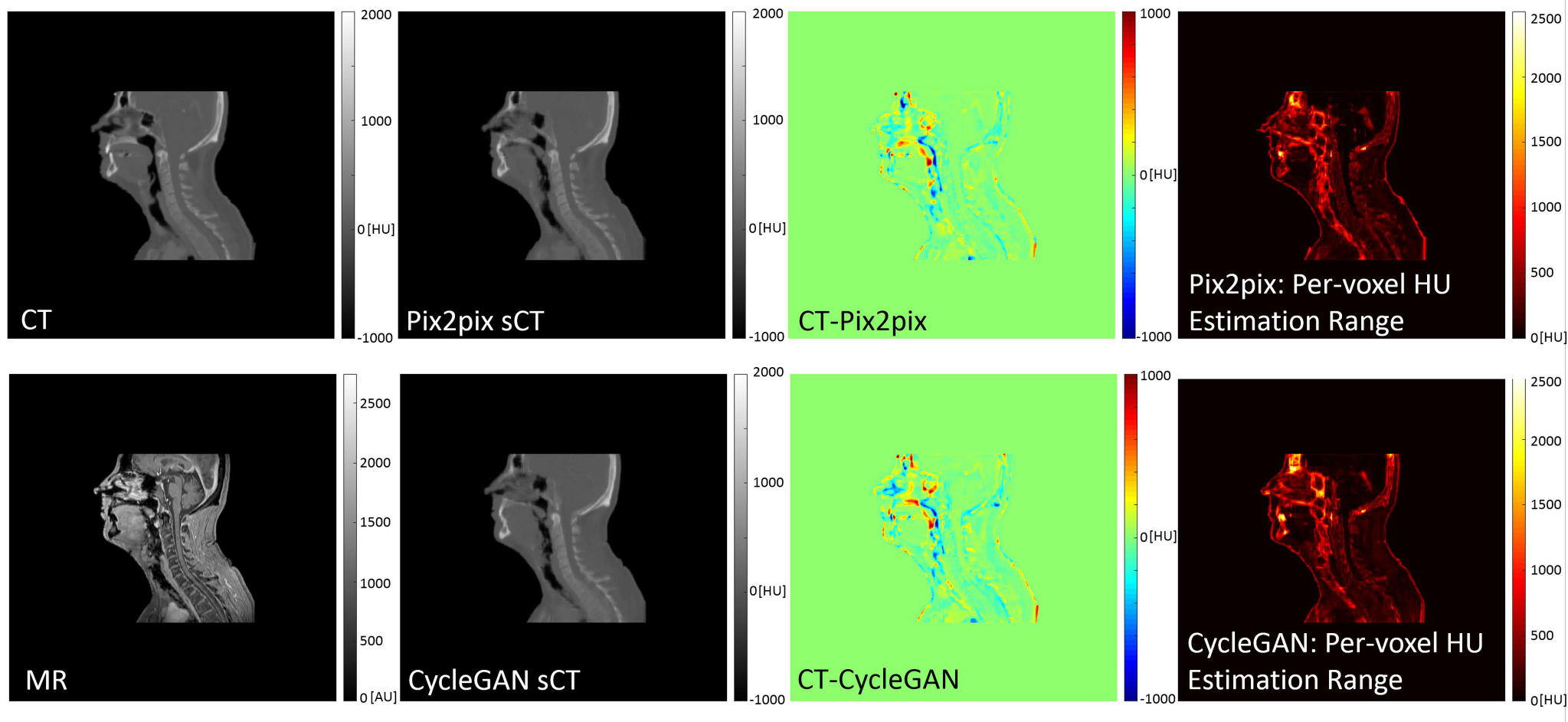
512 × 512 voxel sagittal slices from the isotropically spaced volume cubes of the deformably registered CT and MR pairs, pix2pix and CycleGAN sCTs, difference maps (CT – sCT), and per-voxel HU range estimation for sCTs created from 128 × 128 voxel patches with crop=16, stride=32 for overlapping. This results in as many as 48 unique HU estimations per sCT voxel. The largest values in the range estimation map correspond with tissue transition zones, and materials which are ambiguous in standard classification-based MR-CT transformations. Units for all plots are HU, except the MR, which has arbitrary intensity units.

With increased numbers of overlapping patches, there is an associated increase in computational loads and memory burdens. When there are no overlapping patches per plane (e.g. crop = 0, stride = 128 or crop 16, stride = 96) only three copies of the full matrix (each 512 × 512 × 512 voxels) are required prior to combining the HU estimations for the final sCT. With stride = 64, or half the patch size, there are as many as 4 overlapping estimations per voxel in-plane, so an array with dimensions of 512 × 512 × 512 × 12 is required to store the HU estimations prior to the 2.5-D estimation combination for the final sCT generation. Similarly, with stride = 32, or ¼ the patch size, as many as 16 overlapping estimations per voxel in-plane are generated, so arrays of 512 × 512 × 512 × 48 elements are needed prior to estimation combination for the final sCT image. We found that for typical HN volumes with 1.1 mm isotropic voxels, computing the sCT patches takes approximately 7 s per view for non-overlapping-per-view pix2pix calculations, and 21 s per view for non-overlapping-per-view CycleGAN calculations. The total run time including recombination of the overlapping estimations from the three independent views was approximately 45 s for pix2pix and less than 1.5 min for CycleGAN. As the number of sCT patches increases with the amount of overlapping, the time to generate sCTs scales linearly with the number of patches, but the sorting and combination functions for voting, averaging, or taking the median add additional processing and RAM requirements. If arrays are not stored as compressed or sparse matrices, then the intermediate arrays will require 4 or 16 times the memory for stride = 64 and stride = 32, respectively, compared to the non-overlapping methods. The non-optimized methods to combine overlapping results that were created for this project took an additional approximate 30 mins for the post-generation processing with stride = 32 for an HPC compute node with Xeon processors and 128 GB of RAM.

3.2. Effects of Intensity Standardization and Intensity Clipping on MAE and ME

The effects of MR histogram normalization at different MR image intensity clipping values on MAE and ME for the generated sCT images (using crop = 16, stride = 32 voxels on the image patches) are presented in Table 1. The MR intensity clip values are presented as four possibilities: (i) dynamic 99 percentile, meaning the values are clipped at the 99-percentile intensity value for the masked voxels for each patient starting with the standardized, BFC MR images; (ii) static 2500: clipping at a predetermined MR intensity level of 2500 (i.e. 99.5 percentile for the entire set of standardized, BFC MR images), (iii) static 3500: the average maximum value after standardization with the ability to also a test of reduced image contrast compared to static 2500 for robustness testing; or (iv) dynamic: clipping at the 99^th percentile intensity value for the masked values in the original uncorrected MR images for each patient. The results agree with each other within one standard deviation for each specific network model for both MAE and ME, showing there is robustness against intensity and contrast variation.

Table 1).

Effect of preprocessing input images on MAE and ME for the independent test set (overlapping patches combined via averaging), where BFC stands for bias field corrected images. The 99-percentile intensity value varies for individual MR volumes, even after standardization, so changing from a dynamic to a static clip value will affect the input image set contrast. These results show while the networks are robust against some contrast/intensity variation, there is a dependence on the input MR relative contrast and intensity.

	pix2pix	CycleGAN	pix2pix	CycleGAN
	MAE ± Std Dev (HU)	MAE ± Std Dev (HU)	ME ± Std Dev (HU)	ME ± Std Dev (HU)
Dynamic: 99 percentile on BFC, standardized MR sets	96.6 ± 11.5	104.4 ± 14.0	22.0 ± 13.0	38.9 ± 16.2
Static: 2500 clip value on BFC, standardized MR sets	95.0 ± 10.7	104.1 ± 15.8	24.4 ± 13.8	38.9 ± 15.6
Static: 3500 clip value on BFC, standardized MR sets	99.6 ± 14.3	118.0 ± 31.0	45.8 ± 14.9	38.2 ± 17.1
Dynamic: 99 percentile on unmodified MR sets	97.9 ± 9.8	107.6 ± 12.0	35.1 ± 11.6	51.2 ± 14.1

3.3. Effect of Merging Strategy from Overlapping Image Patches on MAE and ME

The MAE and ME for averaging, calculating the median, or voting (averaging the values from dominant classified ranges of values) to estimate the HU value for a voxel from overlapping patches (crop value = 16 pixels, stride = 32 pixels) with three orthogonal views (2.5-D sCT generation) agree within one standard deviation (Table 2). However, in the sCT images there are visible qualitative differences. The most notable differences are seen at the edges of bone and air sections, and in large uniform HU value regions: the edges of bones and air passages appear less blurred and the uniform regions appear less textured for the median and voting combination methods (Figure S-4). The line cut plot in Figure S-4 shows homogeneous soft tissue regions with errors as large as 80 HU caused by including outlier estimations when averaging values. In addition to poor estimation of the HU values, sCT images computed using only axial-views produced discontinuous interplane estimations with increased noise.

Table 2).

Effect of the combination method for overlapping voxel HU estimations (3 view, stride = 32, crop = 16, MR clip intensity = 2500) on sCT generation for the independent test set. As many as 48 estimations per voxel are combined with the different methods.

	pix2pix	CycleGAN	pix2pix	CycleGAN
	MAE ± Std Dev (HU)	MAE ± Std Dev (HU)	ME ± Std Dev (HU)	ME ± Std Dev (HU)
Averaging Values	95.0 ± 10.7	104.1 ± 15.8	24.4 ± 13.8	38.9 ± 15.6
Voting of Values	94.5 ± 10.8	103.8 ± 15.2	25.4 ± 13.5	40.9 ± 15.0
Median of Values	94.0 ± 10.6	102.9 ± 14.7	25.3 ± 13.5	42.7 ± 14.5

Comparison between the combination methods, as well as 2D averaging results for both CycleGAN and pix2pix is shown in Figure 5a, where the percentage of masked body voxels for the whole set of cross-validation results are plotted against the absolute error in HU. Magnified regions centered on 75%, 50%, 25% and 10% of the masked voxels are shown in Figure 5b–e, respectively, to highlight the differences in errors by using the different combination methods. For our cross-validation data set, the median combination method has lowest absolute error until 31% for CycleGAN and 21% for pix2pix where voting and voting/average combination methods start to perform better than taking the median value for CycleGAN and pix2pix, respectively.

Figure 5).

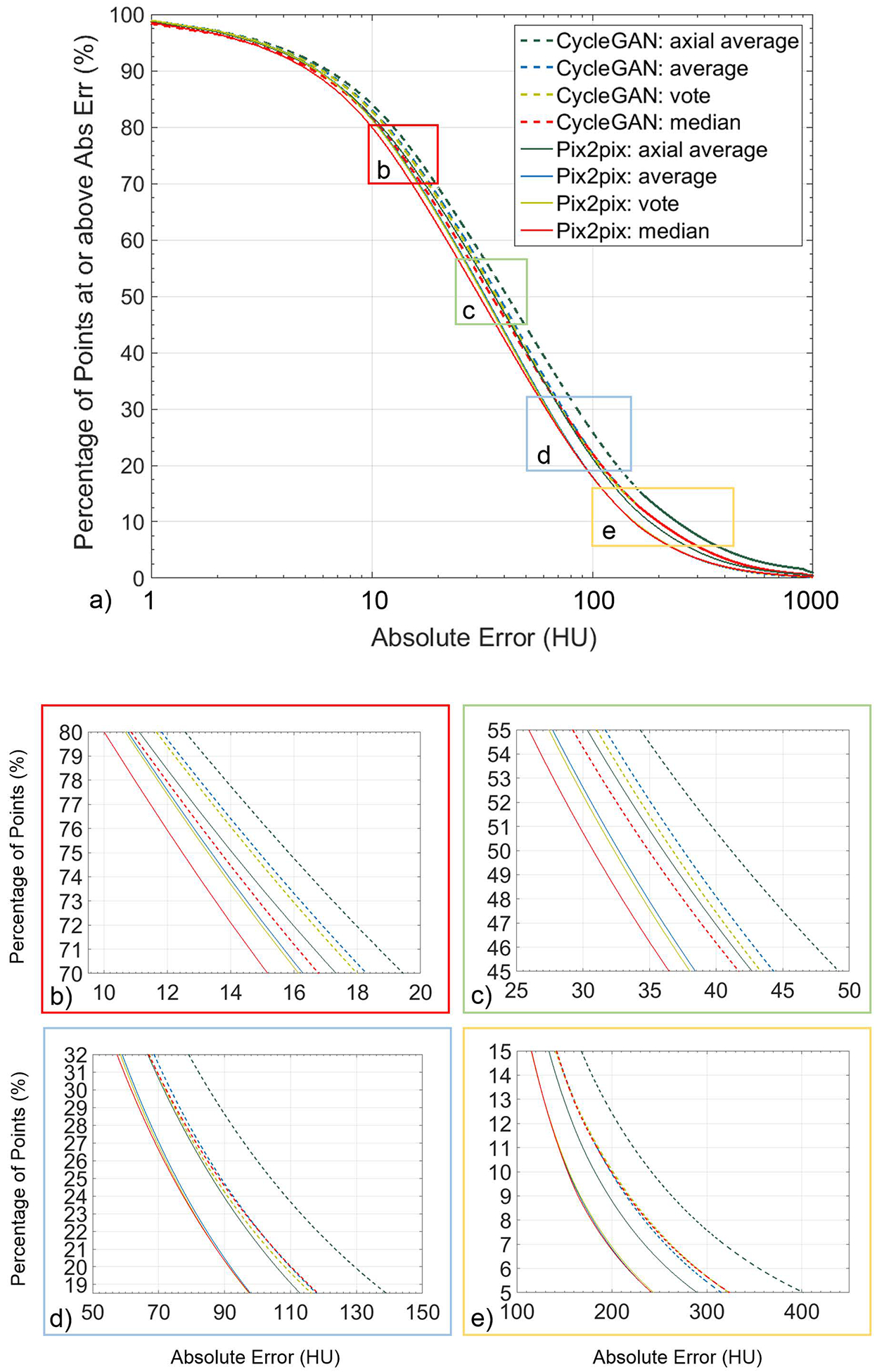
Percentage of masked voxels for the entire cross-validation set vs absolute error in HU for the four combination methods for both CycleGAN and pix2pix. Plots (b-e) show magnified regions centered on 75%, 50%, 25%, and 10% of the masked voxels.

Correlation plots of sCT intensity vs CT intensity for both models are shown in Figure S-5, using 100000 randomly chosen voxels from the body volume. Tightness of the scattered points to the 1:1 line shows how well the models map from MR to CT.

Based on the associated uncertainties, the differences in the composite sCT images constructed with the different combination methods are not significantly different. However, because of the better uniformity of HU estimations for homogenous tissue regions observed when outlier estimations occurred (Figure S-4), the median method to combine overlapping voxel estimations was used for reporting the rest of the results (crop value = 16 pixels, stride = 32 pixels, 3 views).

3.4. MAE/ME Summary for Cross-validation, Independent Testing, and Different Soft-Tissue Contrast Sets

The results from our training and testing of the sets are summarized in Table 3. The full summary tables for the leave-two-out cross validation results for the curated set (patch parameters: crop value = 16, stride = 32 voxels) and the independent test set to test robustness to new features and scans with different tissue contrast can be found in the supplemental information (Tables S-2 to S-5). The increased quantity and volumes of the artifacts and previously unseen features present in the independent test set adversely affected the sCT accuracy. Processing MR images with different soft-tissue contrast showed further reduction in sCT accuracy and showed the limitations of the standardization algorithm as evidenced with lower MAE and ME when this additional set did not get processed with the standardization function.

Table 3).

Summary of Errors (± standard deviation) for the whole-HN region, bone region (original CT value >200 HU, with 4 voxel padding), and air regions (original CT value < −200 HU, with 4 voxel padding). For the three additional tests, because tissue contrast differs between water and in-phase mDixon images, the histogram standardization method failed and the standardized images resulted in higher MAEs than the images that were not standardized prior to being input to the neural networks.

		MAE for Whole-HN Volume: (HU)	ME for Whole-HN Volume: (HU)	MAE for Bones: (HU)	MAE for Air Regions: (HU)
Leave-two-out cross-validation	pix2pix	66.9 ± 7.3	15.7 ± 12.7	109.2 ± 16.3	120.5 ± 12.6
	CycleGAN	82.3 ± 6.4	27.5 ± 15.2	135.3 ± 17.1	132.7 ± 12.5
Independent testing	pix2pix	94.0 ± 10.6	25.3 ± 13.5	176.7 ± 21.7	188.5 ± 29.2
	CycleGAN	102.9 ±14.7	42.7 ± 14.5	197.3 ± 27.2	189.9 ± 33.1
Different Tissue contrast (water) (standardization attempted)	pix2pix	129.1±7.2	17.6±21.3	233.7±15.3	158.3±26.3
	CycleGAN	154.5±11.9	17.4±20.8	246.4±19.7	158.8±22.4
Different Tissue contrast (water) (no standardization)	pix2pix	122.1±6.3	23.9±21.8	238.3±21.9	163.9±32.8
	CycleGAN	132.8±5.5	27.5±20.2	236.1±20.7	162.2±29.6

Example sCT images generated using all three views following bias-field correction and histogram standardization and using the averaging combination method for overlapping image patches are shown for sagittal views in Figure 6 (top). Example results of the patient with a large tumor (Independent Testing Case 6) are shown in Figure 6 (bottom). Additional axial images for the case with the large tumor can be viewed in the supplemental information (Figure S-6).

Figure 6). (Top).

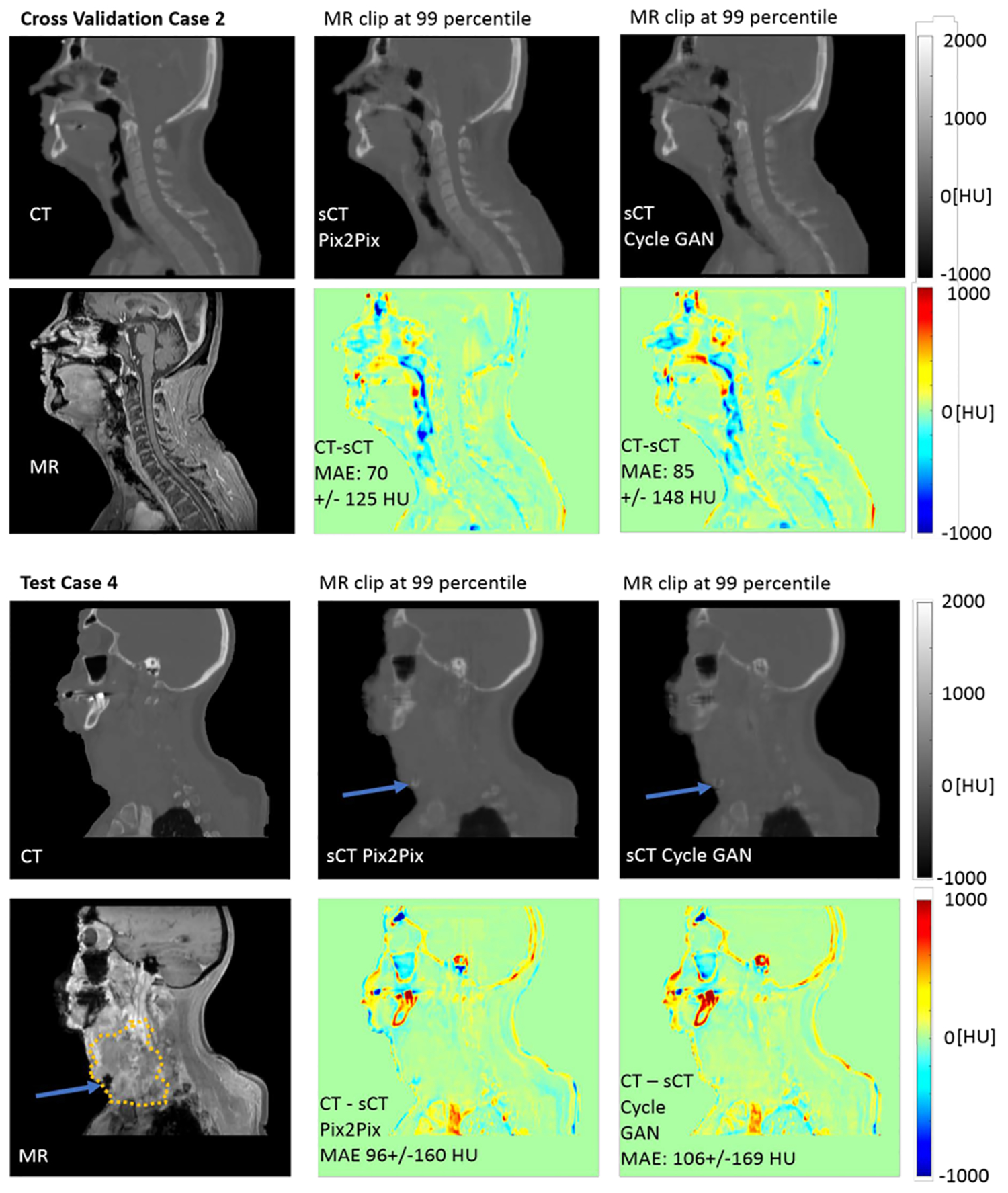
Example sCT images for Cross Validation Case 2 with sCT patches from the three views combined by averaging, showing the similarities and differences between the resultant pix2pix and CycleGAN sCT images. The most notable differences in the sagittal view are in the sinuses, nasopharynx and with the tongue. (Bottom) Example sCT images for Test Case 4, which included a large tumor (GTV highlighted with dotted line). Both pix2pix and CycleGAN estimate the HU values for the soft tissue of the tumor well, except for a small region at the anterior inferior part of the tumor recorded with low intensities in the MR image that was incorrectly transformed to bone-valued HUs.

3.5. Clinical and Dosimetric Results

An example dose volume histogram for Test Case 5 is shown in Figure 7. The sCTs for both the pix2pix and CycleGAN networks agree to within 1% relative to the deformed CT dose-volume statistics for all structures of interest in this case.

Figure 7).

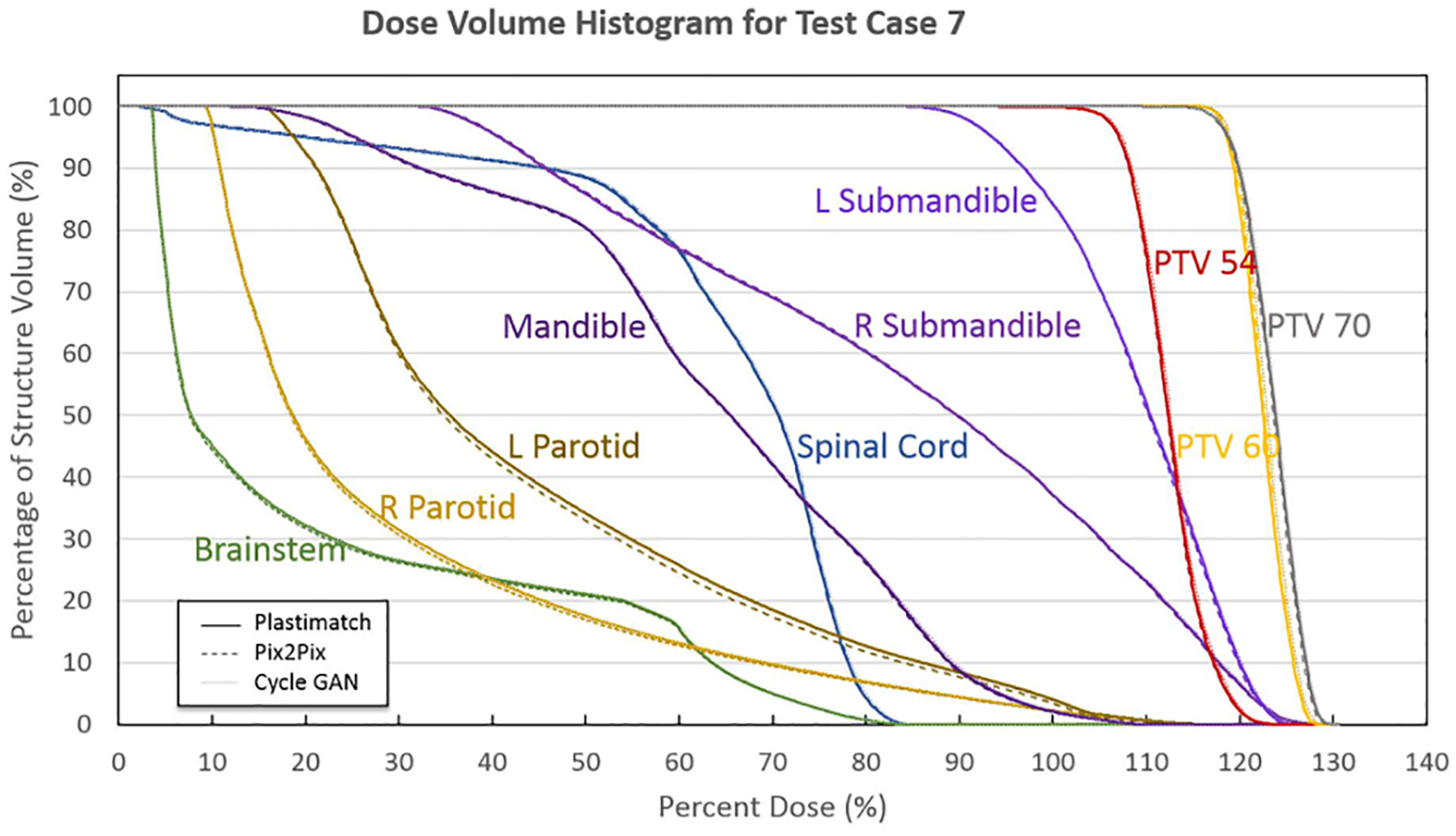
Dose Volume Histogram for all clinically relevant structures for Test Case 5, showing agreement to within 1% for the doses between the sCTs and the deformed CT. Original deformed CT DVHs are plotted with solid lines, pix2pix DVHs are plotted with dashed lines, and CycleGAN DVHs are plotted with dotted lines.

The absolute dose difference and absolute percent dose difference between the pix2pix and CycleGAN sCTs and the deformed CTs for all clinical structures of interest are presented in box whisker plots in Figure 8. For normal structures, the relevant DVH metric, such as mean dose difference or max dose difference, was calculated. Both the pix2pix and CycleGAN models create clinically relevant sCT images, yielding absolute percent dose differences of 2% or less for all clinically relevant structures without discarding any outlier points, and less than 1.65% for all clinically relevant structures when one point in the mandible structure from a case with large dental artifacts is excluded (Test Case 8).

Figure 8).

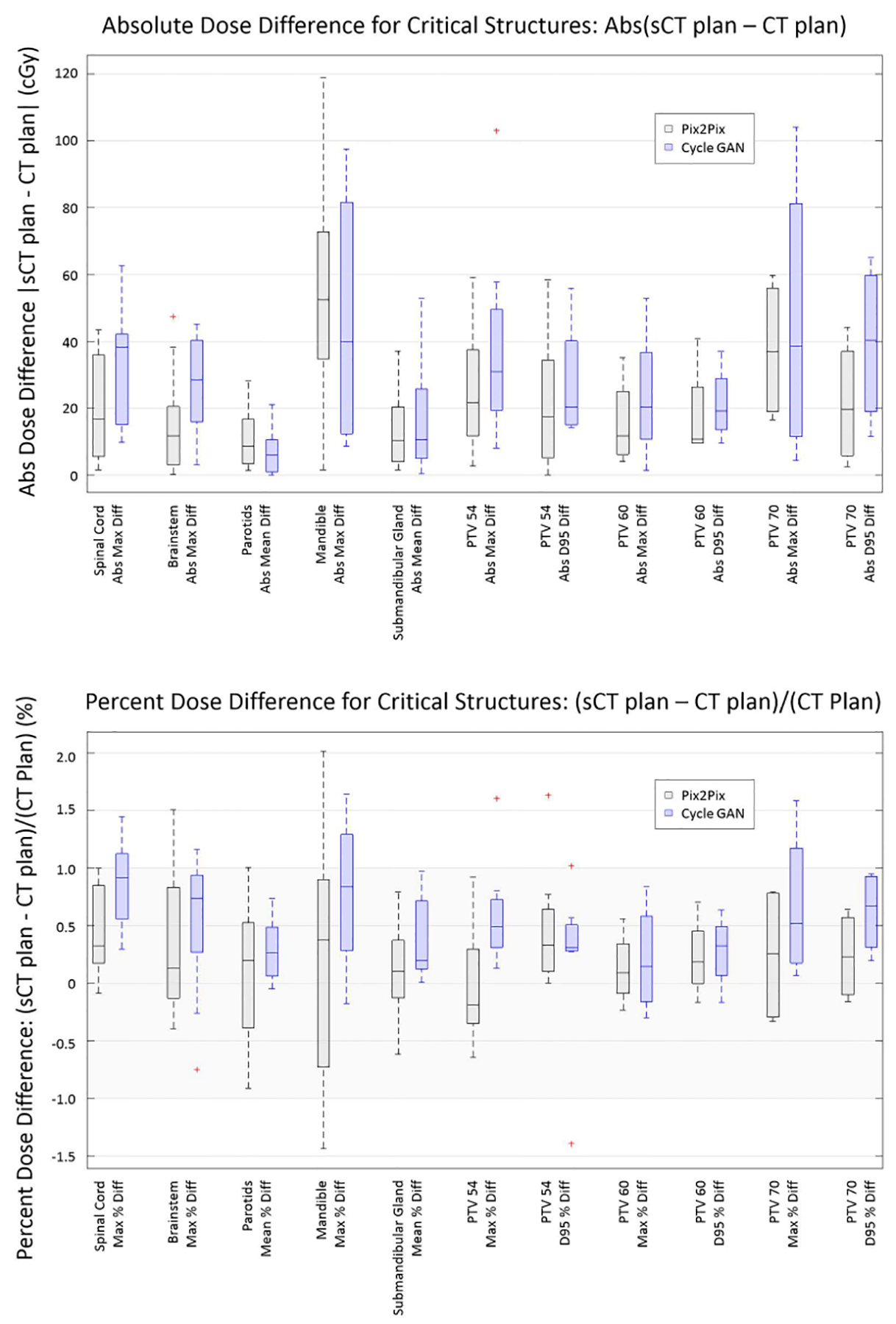
Box Whisker plots showing (a) Absolute Dose Difference and (b) Percent Dose Difference for all clinical structures of interest. The mandible, due to the dental artifacts, has the largest range of uncertainty of all clinically relevant structures for both pix2pix and CycleGAN sCTs.

Bony DRRs were generated from both the planning CT and sCT images. Both pix2pix and CycleGAN methods produced a very strong correlation to the planning CTs with an average PCC of 0.95 ± 0.02 and 0.95 ± 0.03, respectively. For the pix2pix results, the average match for all the patients between planning CT and pix2pix CT was −0.08 ± 0.49 mm, 0.13 ± 0.3 mm, and 0.05 ± 0.18 mm in lateral, anterior-posterior, and superior-inferior directions, respectively. Regarding CycleGAN results, the average match for all the patients between planning CT and CycleGAN sCT were 0.01 ± 0.39 mm, −0.23 ± 0.37 mm, and 0.07 ± 0.10 mm in lateral, anterior-posterior and superior-inferior directions, respectively.

Example DRRs for case 2 of the curated set, from the CT, pix2pix sCT, and CycleGAN sCT images are shown in Figure 9. Differences between bone HU estimations and the HU values from the original CT can lead to observable differences such as blurred edges and less intense bone structures (highlighted with arrows in Figure 9), though the sCT images would still be useful for alignment purposes.

Figure 9).

Sample sagittal and coronal view DRRs for the original CT, the pix2pix sCT, and the CycleGAN sCT for curated set case 2. The largest differences can be seen at the jaw (related to a dental artifact), and for the porous bone near the ear (see arrows).

4. Discussion

The pix2pix and CycleGAN models were investigated for generating head and neck sCTs using the in-phase mDixon FFE sequence. The sCT generation methods were evaluated under conditions typically seen in our clinic including patients with significant dental artifacts leading to voids and local distortions in the MR images and streak artifacts on CT images, as well as different anatomy conditions including a large tumor and a wide range of body masses. Additionally, rigorous evaluation was performed under multiple image pre-processing (processing before analysis using GAN), post-processing (following sCT computation using GAN), as well as implementation conditions namely, one-view (axial, sagittal, or coronal) patch-based sCT vs. multi-view (reformatted views consisting of axial, sagittal, and coronal) patch-based sCT generation. The results of the evaluated implementation conditions are general and should be relevant for informing network design and implementation in other tumor sites.

We found that training and combining results from three separate neural networks, one for each orthogonal view to create a 2.5-D sCT generation method, resulted in lower MAE and ME and better constrained tissue extent compared with axial view training alone, even with in-plane overlapping of generated sCTs. We believe that the improvements in sCT accuracy are predominantly a result of the additional local spatial context provided by the three orthogonal views. Our results indicate potential improvements in sCT estimations, which is important to minimize for dose planning, with increased numbers of overlapping patches. However, the difference between non-overlapping and multiple overlapping patches per-view is not significant based on the large standard deviations on the per-case MAE values. The non-overlapping per-view method also reduces the number of estimates by a factor of 16, resulting in reduced sCT generation computational times and simplified combination calculations.

With regards to the combination methods for overlapping sCT estimations at individual voxels, we tested three methods since it was not clear if the overlapping HU estimations for voxels would have unimodal or multimodal distributions, and estimations, based on context, might produce widely ranging values. Averaging is the simplest combination method for overlapping voxel estimations, but the average value can be strongly affected by outlier HU values leading to variations in soft tissue and blurred transition regions between tissue types (Figure S-4). Calculating the median value works well for suppressing outliers if the HU estimation distributions are unimodal, so soft tissue intensities are homogeneous, but at sinus and inner ear transitions between bone and air regions, the distribution may not be unimodal, and the median value could thus lie between the two tissue types. Transition zones between tissue types are most strongly affected for the median calculation. Voting classifies voxels into general classes (air, soft-tissue, and bone/metal), and then calculates the average of the dominant tissue type(s). This suppresses noise in homogeneous soft-tissues and retains stronger edges at transition zones (Figure S-4). The MAE and ME are not significantly different for the different combination methods, so despite the qualitative differences between the sCT images, the dosimetric results will be similar. While the numerical results are similar, the median and voting methods limit the effect of outlier estimations; an example of this can be seen in Figure S-4, where low-valued estimations pull down the HU estimation created by averaging the values by as much as 80 HU in a homogeneous soft tissue region.

We investigated the uncertainties in the HU estimations resulting from the input imaging variabilities at test time that model a form of aleatoric uncertainties. We computed this by combining overlapping patch estimations of HU enclosing each voxel. As the models are optimized to incorporate the statistical image characteristics at different feature scales, the differences in the HU estimations from the various patches is an indicator of model uncertainty due to imaging variations. Hence, a large agreement of HU estimates (small range of differences in the HU estimates) reflects a higher certainty that the estimate is robust to imaging variations for a voxel, while a small agreement reflected as a large range of HU estimates between patches indicates large uncertainty in the model estimates.

However, this uncertainty is not reflective of the epistemic or model uncertainties itself, which will be studied in the future. Nevertheless, these uncertainty estimates could potentially identify or highlight regions with large estimation uncertainties caused by physical ambiguities (air and bone appear similar in MR images except for UTE images), transitions of tissue type, or features that were previously untrained in the models. Expansion of these techniques with incorporation of additional uncertainties with testing could potentiate an additional tool, akin to a transformation uncertainty map, to highlight regions with potentially inaccurate sCT estimations. This could aid in the evaluation of sCT images, since GANs create images based on optimized statistical properties of features for a set of images, and they may change critical features in a transformation in a way that does not appear incorrect without close inspection³⁷.

There are no other HN deep learning studies with dosimetric results to compare against that we are aware of, but the MAEs reported in this study compare well to the most similar prior works (HN multi-atlas based, and brain cancer deep-learning based sCT generation) (Table 4). Although comparison to methods that used brain as their primary sites are not a fair comparison (we expect higher errors for HN due to a larger number of structures, transition regions, and the need for deformable registration), we wanted to assess how our method fared in comparison to other deep learning studies for sCT generation. Our leave-two-out curated cross-validation set, which still includes cases with dental artifacts, results in MAE = 66.9 ± 7.3 HU for the pix2pix model, which is as good as the best previously reported deep learning results for brain¹⁴ images.

Table 4).

Comparison of the studies with the most similar site (Brain) to our study (HN). The shaded cases had strong exclusion criteria, where cases with large streak/metal artifacts were excluded.

Study	Year	Method	Location	MAE ± Std Dev (HU)	ME ± Std Dev (HU)	# Cases test/total
This Study: Leave-two cross validation		pix2pix	HN	66.9 ± 7.3	15.7 ± 12.7	12
		CycleGAN	HN	82.3 ± 6.4	27.5 ± 15.1	12
This Study: Independent Testing		pix2pix	HN	94.0 ± 10.6	25.3 ± 13.5	8
		CycleGAN	HN	102.9 ±14.7	42.7 ± 14.5	8
10 Leave one-out cross-validation	2017	Multiatlas	HN	64 ± 10		12
13 Two-fold cross validation	2019	Adversarial Semantic Structure (double GAN)	Brain	101 ± 40	−14 ± 18	50
14 Two-fold cross validation	2018	Dilated CNN	Brain	67 ± 11	13 ± 9	52
15 Five-fold cross validation	2018	ResNET	Brain	89.3 ± 10.3		15
16 Six-fold cross validation	2017	U-NET	Brain	84.8 ± 17.3	−3.1 ± 21.6	18
17 Unspecified	2018	3D FCN GAN	Brain	92.5 ± 13.9		16
18 Unspecified	2017	CycleGAN	Brain	73.7 ± 2.3		6/24
	2017	pix2pix	Brain	89.4 ± 6.8		6/24

However, since this set is identical to the set used in an earlier multi-atlas study by our group¹⁰, direct comparison with that study is possible. In addition to the results summarized in Table 4 which shows agreement between the atlas-based method and pix2pix for the body-region, the atlas-based method¹⁰ produced a MAE of 113± 12 HU for the bone region, and 130 ± 28 HU for the air region. In comparison, our best deep learning model, namely, the pix2pix model, produced lower MAEs of 109.2 ± 16 HU and 120.5 ± 12.6 HU for the bone and air regions, respectively. Furthermore, pix2pix has less variation than the multi-atlas model for air regions. We also note that the deep learning methods are more robust to input contrast variation and previously unseen features for the input MR images. The multi-atlas method could not be evaluated on these new cases due to artifacts and the anatomical variabilities. The training data set can also be expanded to many more cases and once training has been performed, sCT generation can be performed in minutes to tens of minutes for pix2pix and CycleGAN, depending on the number of overlapping patches computed, independent of how many cases were used in training. In contrast, the atlas-based method takes more than 1 hour to compute 1 sCT and will slow down with additional reference patients in the database.

Our results indicate that for well-aligned deformably registered image pairs, pix2pix may yield lower MAE, ME, and dosimetric uncertainties compared to CycleGAN, contrary to the results reported by Wolterink et al.¹⁸. This was somewhat unexpected, as inter-modality registrations are not perfect, so a model that is not dependent on pixel-perfect registrations might be expected to be more robust. We should note, however, that there are implementation differences between our study and theirs, as they used single view (sagittal)-based sCT generation and rigid registration for aligning CT with MR images. While well-registered CT-MR pairs are not required for training CycleGAN, they are still required to evaluate the results produced by these methods. Inconsistent or misregistered images can adversely impact both training (in the case of pix2pix) and the evaluation of error essential for training optimization and assessment of method performance, particularly when evaluating regions with bone and air interface. As pointed out in their study, mis-registrations between CT and MR images were present due to the rigid registrations, so we believe this is one potential reason why they noted pix2pix model results had poorer accuracy compared to the CycleGAN model in contrast to what we observed. Another potential reason could be that since loss constraints are stronger for the pix2pix model, small residual geometric distortions remaining after automatic corrections and the deformable registration may have been systematically learned by our pix2pix model. Finally, differences may arise because the image sets differ and because the training and testing sizes are relatively small for both this preliminary study and their study. Increased training and testing sample sets are needed to test this further.

One clear advantage for the CycleGAN model is that it does not require aligned CT-MR image pairs from the same patients which will simplify the preprocessing stages when training larger data sets. This benefit comes at the cost of increased training and sCT generation computational time. However, if training sets are expected to grow or change over time when moving toward a clinical setting, this simplification of the preprocessing stage by relaxing the alignment criteria may ultimately be preferred. One major advantage of both pix2pix and CycleGAN methods, and deep learning methods in general, is that they learn the overall statistical characteristics of tissue correspondences between CT and MR images when producing the translation and are thus robust to presence of noise and small artifacts when generating sCT images. However, this modeling of overall statistical characteristics can also be a disadvantage as these methods do not necessarily preserve local spatial characteristics in the image, especially if training sets differ from test sets and if sufficiently strong loss criteria (such as L1 losses) are not used in training as shown in other works³⁸ including work by our group³⁷. Also, features that occur infrequently may be ignored if additional weighting factors for them are not added. This defect/limitation was observable in an example independent testing case, case 4, with a very large tumor (Figure 6, bottom). While the majority of the tumor was transformed to sCT soft tissue correctly, a small region was incorrectly transformed to bone near the inferior part of the tumor growth by both methods since there were no example cases in the training set to transform the dark necrotic tissue region of the tumor from the MR image.

Ultimately, the afore-mentioned limitation including mis-matching air cavities near bone regions could potentially be resolved with larger training sets, more inputs/different MR sequences including the UTE sequence, higher-resolution image sets, or more advanced deformable image registration methods. Additionally, methods to target easily identifiable artifacts with in-painting techniques may also lead to more accurate sCT HU estimations.

Both methods have been shown to produce clinically feasible dosimetric results for the limited set of independent cases tested here, with ≤2% dose differences for all clinically relevant structures including the mandible even when large dental artifacts were present. Bony matches between the sCT images and the original CT images show positional agreement to less than 1 mm, indicating potential usage for patient alignment.

The results from this pilot study evaluating patch-based sCT image generation with respect to MAE, ME, dosimetric evaluation for PTV and critical structures show promise for both network models and for using overlapping patches to reduce error and estimate modality transformation uncertainty. However, with the small number of training and test cases, even with enhanced augmentation in training it is not possible to represent all possible image features. While the results here are favorable for MR-only planning with either pix2pix or CycleGAN, strong conclusions based off these small training and testing image sets cannot be made and further studies with larger training and testing sets are required to test clinical viability of these methods.

5. Conclusions

In this study, we evaluated the effects of using sub-image patches for synthetic CT image generation for head and neck cancer patients using two different state-of-the art generative adversarial network models, namely, the pix2pix and CycleGAN models. For our independent test sets the dosimetric accuracy of both pix2pix and CycleGAN had absolute percent dose differences of 2% or less. While indicative of sufficient accuracy on a small sample size, these methods, in general, need evaluation on a larger cohort. We also found that modeling aleatoric uncertainties by combining overlapping sub-patch HU estimations may potentially aid in providing estimates of reliability in sCT generation and help to identify regions with potentially problematic domain transformations.