Optical Transduction for Vertical Nanowire Resonators

Abstract

We describe an optical transduction mechanism to measure the flexural mode vibrations of vertically aligned nanowires on a flat substrate with high sensitivity, linearity, and ease of implementation. We demonstrate that the light reflected from the substrate when a laser beam strikes it parallel to the nanowires is modulated proportionally to their vibration, so that measuring such modulation provides a highly efficient resonance readout. This mechanism is applicable to single nanowires or arrays without specific requirements regarding their geometry or array pattern, and no fabrication process besides the nanowire generation is required. We show how to optimize the performance of this mechanism by characterizing the split flexural modes of vertical silicon nanowires in their full dynamic range and up to the fifth mode order. The presented transduction approach is relevant for any application of nanowire resonators, particularly for integrating nanomechanical sensing in functional substrates based on vertical nanowires for biological applications.

Nanomechanical sensing with resonant devices based on semiconductor nanowires (SCNWs) is currently consolidated as one of the most fruitful research lines involving this kind of nanostructure. SCNWs are highly useful as resonators for high-performance applications because of their unique structural and dynamic properties. The former imply an exceptional combination of very low mass, single-crystal quality, and controllable dimensions and geometry.¹ Regarding dynamic properties, the characteristic high aspect ratio of SCNWs results in flexural modes which are extremely sensitive to external perturbations of a different nature.² On one hand, this facilitates detecting their thermomechanical vibrations, as the effect of temperature alone results in relatively large vibration amplitudes; on the other hand, it also simplifies external driving schemes, as external forces of a different nature can be used to drive flexural vibrations even beyond the fundamental mode. These properties provide SCNW resonators with singular sensing capacities which are otherwise impossible to achieve with other structures. Some of the most significant ones are based on the splitting of each flexural mode in a doublet of nearly degenerate orthogonal oscillations, which occurs for both single-clamp^3,4 and double-clamp nanowires.⁵ This effect has indeed already been explored for innovative applications such as simultaneous mass and elasticity sensing of adsorbates,^4,6 vectorial force sensing/imaging,⁷⁻⁹ and the exploration of complex dynamics¹⁰⁻¹³ or optomechanical back-action effects.^14,15

Exploiting the unique properties of SCNW resonators for developing an equally high performance and practical functionalities requires an efficient conversion of the nanowire vibrations into readable signals with high sensitivity, linearity, and minimum constraints regarding the nanowires’ arrangement. Different transduction schemes have been demonstrated so far to that end, but arguably all of them have one severe drawback in common: the need of specific and often complex arrangements or geometry of the nanowires. For instance, most reported optical readout schemes imply perpendicular incidence of a laser beam on the nanowires, which requires placing the nanowires on supporting prefabricated microstructures such as microtips¹⁶ or microtrench sidewalls.^17,18 Also, all electrical readout schemes, either capacitive,^19,20 piezoresistive,^21,22 or magnetomotive,²³ require the ability to precisely place the nanowires with respect to biasing and/or driving electrodes, which is far from a trivial issue. Although several micro-/nanofabrication approaches have been successfully developed to that end,²⁴⁻²⁶ all of them require nontrivial, costly, and often low-yield clean-room processing methods, which imposes important difficulties for a systematic, agile, and efficient development of practical applications. It must be noted that some of the reported SCNW resonator configurations, particularly some of those involving nanowires located at tips or edges, are not motivated exclusively by the need of enabling a vibration readout but also by their appropriateness for specific applications, such as the paradigmatic example of nanowire probe sensors.^8,9,26 Anyhow, it is remarkable that a transduction mechanism that enables the nanowire vibration readout for the simplest disposition of SCNWs, consisting of vertically aligned nanowires with an arbitrary pattern on an unstructured flat substrate, has not been reported yet. Although the measurement of mechanical resonances of vertical SCNWs has been previously achieved, the transduction schemes used imposed important restrictions regarding the nanowire geometry or arrangement. Specifically, laser beam deflection schemes have been demonstrated only for nanowires with micron-sized nanowire tips and inverted cone nanowire geometries.^27,28 Also, an optical Bragg scattering readout has been recently applied to truly nanometer-scaled vertical nanowire arrays,²⁹ but it required a periodic arrangement of the arrays and thus a specific nanofabrication process to provide such an arrangement. Besides these optical schemes, electromechanical coupling of nanomechanical motion to focused electron beams has recently emerged as a feasible approach for transduction of vertical SCNWs without the need of specific arrangements.^30,31 However, in addition to the obvious practical limitations imposed by the operation inside a scanning electron microscope, the reported results indicate the presence of radiation pressure back-action effects that perturb the mechanical response of the nanowires. These effects can be of great interest in fundamental studies regarding dynamical cooling of macroscopic degrees of freedom to the quantum ground state,³⁰ but they may also introduce disadvantageous and complex phenomenology for practical applications.

In this work we describe an optical transduction mechanism that allows the measurement of the flexural vibrations of vertical SCNWs with sub-wavelength-scale diameters and no particular requirements about their geometry and arrangement. The experimental implementation of this mechanism does not involve any fabrication process on the substrates besides the generation of the SCNWs themselves, and it can be applied to both isolated single nanowires and nanowire arrays, either randomly or regularly patterned on the substrate, and without any constraint regarding the array density. Specifically, we show that the light reflected when a laser beam strikes the substrate vertically and sufficiently close to a nanowire (longitudinally parallel to the nanowire) is modulated by the flexural mode vibrations of the nanowire. We show that such modulation is proportional to the amplitude of the nanowire vibrations, and it can be easily detected by a standard photodetector and measured by spectral analysis of the resulting signal. We demonstrate the performance of this transduction mechanism by its application to vertical silicon nanowires (Si NWs) grown by the vapor–liquid–solid (VLS) mechanism on a flat Si (111) substrate without any predetermined pattern. We first analyze the effect of varying the relative nanowire–laser beam position for detecting split flexural modes, and we present results that allow the determination of the positions of maximum sensitivity with respect to the directions of the nanowire vibrations at the split mode resonance frequencies. Then, we present a model for the transduction mechanism that successfully reproduces the experimentally detected mechanical resonances. Furthermore, we demonstrate the highly sensitive and linear performance of the transduction mechanism by providing a complete characterization of our Si NW resonator model devices, including their dynamic range when externally driving flexural modes, high-order mode detection, and frequency stability. Our results determine a detection threshold below the thermomechanical limit of the Si NWs under test. Also, acoustic piezo-driven vibrations of the nanowires allow the detection of the onset of nonlinear oscillations, providing access to the full dynamic range of the nanowires as well as to their nonlinear regime. In addition, high-order flexural modes are detected up to the fifth order, potentially enabling the simultaneous tracking of several modes for enhanced multiparameter nanomechanical sensing.³² Finally, we analyze the signal-to-noise ratio and frequency stability obtained for the Si NW resonators under test as a function of the incident laser power and discuss the influence of this parameter for optimum transduction performance.

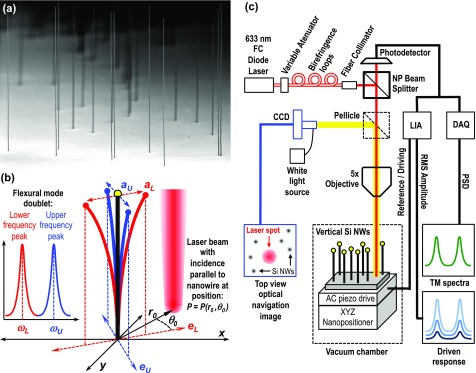
The experimental implementation of the transduction mechanism presented in this work is schematically depicted in Figure 1. A focused laser beam is aligned parallel to vertical Si NWs as those shown in Figure 1a (further images are provided in Figure S1, and experimental details about the used VLS growth technique can be found elsewhere³³). We consider three nanowire sizes: the longest nanowires have lengths (L), base diameters (D_b), and tip diameters (D_t) around L = 50 μm, D_b = 300 nm, and D_t = 60 nm; the medium type corresponds to dimensions around L = 25 μm, D_b = 250 nm, and D_t = 100 nm. The shorter nanowires have typical dimensions around L = 15 μm, D_b = 200 nm, and D_t = 125 nm. Typical deviations of dimensions within each type are below 20%. A notable feature of the parallel laser beam incidence (parallel to the vertically aligned nanowires, perpendicular to the substrate) is its symmetry with respect to the orthogonal vibrations of the nanowires in both the lower and upper-frequency components of their flexural mode doublets (Figure 1b). This results in the advantage of a symmetrical access to the resonance response of both components as well as a straightforward determination of their vibration directions with respect to the X–Y positioning axes. The experimental setup (Figure 1c) uses a fiber-coupled diode laser (TopMode-633, Toptica Photonics AG, λ = 633 nm) whose output power and polarization are manually controlled with a variable attenuator and birefringence loops, respectively. Then, a triplet lens collimator provides a nearly Gaussian free-space beam, with its optical axis oriented parallel to the longitudinal axis of the nanowires. The beam is focused on the substrate using a 5× objective with 0.14 numerical aperture, which results in a laser spot diameter of around 8 μm, approximately constant along the entire length of the nanowire. A positioning stage controls the relative X–Y position of the sample with respect to the probe beam incidence point as well as its focus, and a piezoelectric actuator placed below the sample allows the excitation of flexural modes. The beam reflected from the substrate is collected by an unsegmented Si photoreceiver coupled to a low-noise transimpedance amplifier. The resulting electrical signal is then processed either by a digital acquisition (DAQ) board or by a lock-in amplifier (LIA) whose reference signal is delivered to the piezo-actuator in the case of driven vibrations. The DAQ board is synchronized both with a signal generator, which can also be connected to the actuator, and with the positioning stage, allowing the acquisition of the signal of the photoreceiver as the relative sample–laser beam position is scanned. All the measurements are performed in high vacuum (∼10^–5 mbar) and at room temperature conditions. A CCD camera with white light illumination coupled to the system by a pellicle beamsplitter provides top-view optical images in order to navigate the sample surface and locate nanowires of interest. Besides the use of an unsegmented photodetector, this detection scheme is similar to those previously reported in studies involving nanowires with micron-sized tips and inverted cone geometries.^27,28 The essential difference between those works and the results reported here is the transduction mechanism involved. The transduction principle used with micron-sized tip nanowires was based on the modulation of the reflected light as a consequence of the deflection of a laser beam tightly focused just on top of the micron-sized tip. The transduction mechanism described in this work does not rely on laser beam deflection, so that it can be applied to nanometer-scale cross-section nanowires without particular requirements about tapering geometry or tip size.

Figure 1.

Experimental system and measurement setup. (a) Scanning electron microscopy image of a representative example of the Si nanowires considered in this work as a model system. (b) Representation of the orthogonal vibrations corresponding to the lower- and upper-frequency components of the fundamental flexural mode doublet of a Si nanowire and its relative position with respect to the parallel incidence probe laser beam. (c) Schematic depiction of the measurement setup.

Figure 2 shows an example where thermomechanical spectra corresponding to the fundamental flexural mode doublet of a nanowire of the longest type are shown at different relative nanowire–laser beam positions. In Figure 2a, the radial distance from the incidence point and the nanowire is kept constant (r₀ = 2.5 μm) while the relative angle is varied from 0° to 180°. This angle, denoted as θ₀, is defined so that θ₀ = 0° corresponds to incidence on the lower-frequency resonance vibration axis (e_L) whereas 90° corresponds to incidence on the upper-frequency resonance vibration axis (e_U). As shown in Figure 2a, for θ₀ = 0°, only the lower-frequency peak appears in the spectrum. As the angle θ₀ is increased, the lower-frequency peak decreases in amplitude, whereas the upper-frequency peak first appears and then increases in amplitude. When an angle of θ₀ = 90° is reached, the lower-frequency peak disappears, and the upper-frequency peak takes its maximum amplitude. For angle values varying from 90° to 180°, the peak amplitude evolution is reversed, so that the lower-frequency peak increases back to its maximum amplitude, and the upper-frequency peak is reduced until it vanishes. The observed variations of the amplitude of the fundamental mode doublet peaks are a consequence of the dependence of the transduction sensitivity on the relative nanowire–laser beam position. A more general vision of this dependence can be gathered by measuring the vibration amplitude at resonance at all possible positions. An example of such a measurement is shown in Figure 2b,c for the lower and upper components of the fundamental mode doublet, respectively. These plots allow the determination of the direction of the lower and upper vibration axes, e_L and e_U, respectively, with respect to the X–Y positioning axes. Each plot shows two lobular areas where the amplitude reaches maximum values, so that the lines connecting these two maxima in each case determine the vibration axes. The relative perpendicular orientation of the lobular areas corresponding to the lower- and upper-frequency vibrations is consistent with the expected orthogonality of the doublet components in conservative force fields.⁸ The maximum sensitivity position (maximum amplitude) does not correspond to a laser beam incidence just on top of the nanowire. Instead, maximum sensitivity is obtained around 2.5 μm away from the nanowire along any of the vibration axes for the corresponding resonance frequency component, either e_L or e_U.

Figure 2.

Detection of a fundamental flexural mode doublet and demonstration of the effect of varying the relative nanowire–laser beam position. (a) Resonance spectra of an undriven nanowire at varying angles between the nanowire–laser beam vector and the lower-frequency vibration axis. (b) Mapping of the lower-frequency oscillation amplitude as a function of the relative nanowire–laser beam position. (c) Mapping of the upper-frequency oscillation amplitude as a function of the relative nanowire–laser beam position.

In order to understand the underlying transduction mechanism and, in particular, the observed dependence of the transduction sensitivity with the relative nanowire–laser beam position, we have developed a theoretical model whose main elements are presented in Figure 3. The model is based on the modulation of the light reflected from the substrate by the vibration of the nanowires. In order to verify such a mechanism, we first measure the reflected power from the substrate in the area surrounding a nanowire. A representative experimental result is presented in Figure 3a, which shows a map of the reflected power collected from a 16 × 16 μm² area around the nanowire position. The map shows a symmetric round-shaped area around the central nanowire position where the reflected power progressively decreases down to a minimum of approximately an 80% with respect to the power reflected from the flat plain Si substrate. A cross-section from this map along the X-axis is plotted in Figure 3b, showing a steep dip centered at the nanowire position and extended along a width comparable to the spot size. The observed reduction in reflected power as the relative nanowire–laser beam distance decreases is produced as a consequence of the light scattered by the nanowire.¹⁸ The steep dependence of the reflected power with respect to the relative nanowire–laser beam position implies that nanowire vibrations will produce a modulation of the reflected power, generating an AC signal in the optical power collected in the photodiode with the same frequency as the nanowire vibrations, as schematically depicted in Figure 3b. Thus, the nature of the transduction mechanism relies on the change of light scattered by the nanowire as a function of the relative nanowire–laser beam distance, which is effectively determined by the nanowire deflection. Due to the local intensity gradient given by the Gaussian cross-section of the probe beam, the vibration of the nanowire has the effect of modulating the scattered light and thus also the total optical power reflected from the substrate. Consequently, the amplitude of the generated optical signal will be larger where the change of reflected power with position is steeper. These areas correspond to the regions of maximum reflected power gradient, as calculated in Figure 3c,d. The maximum reflected power gradient is located at around 2.5 μm of radial distance between the nanowire and the point of laser beam incidence, consistent with the relative nanowire–laser beam distance at which the maximum sensitivity is observed in Figure 2b,c. Figure S2 shows simulated optical intensity fields for varying relative nanowire–laser beam positions which are consistent with the provided interpretation of the experimental observations given in Figure 3a–d. Moreover, we can theoretically explain the lobular shape of the areas of maximum sensitivity by considering that the nanowire vibrations do not happen in any radial direction from the nanowire position, but only along the axes corresponding to the lower and upper-frequency vibrations of the flexural mode doublets. Therefore, by projecting the reflected power gradient along these axes, as depicted in Figure 3e–h, we reproduce the lobular shapes of the measured amplitude maps shown in Figure 2b,c with notable agreement.

Figure 3.

Transduction mechanism model and experiment–theory comparison. (a) Mapping of collected optical power as a function of the relative nanowire–laser beam position (the nanowire is located at the center of the map). (b) Cross-section of the previous map showing the variation of reflected power as the laser beam is translated along the nanowire center position. (c) Gradient (absolute value) of the collected optical power shown in part a. (d) Cross-section of the previous map showing the variation of the reflected power gradient when the beam is displaced along the nanowire center position. (e, g) Schematic depiction of the projections along the nanowire–laser position vector of the lower- and upper-frequency vibration amplitudes (a_L, a_U). (f, h) Mapping of the projections of the reflected power gradient along the lower- and upper-frequency vibration axis, respectively. (i, j) Experiment–theory comparison of the thermomechanical resonance spectra of an undriven nanowire for the lower-frequency (i) and upper-frequency (j) components of the fundamental flexural mode doublet.

In consideration of the transduction model described above, we can derive an expression for the measured vibration amplitude signal as a function of the actual nanowire vibration amplitude. We define S_L(ω) and S_U(ω) as the contributions to the total power spectral density (PSD) of the nanowire vibration corresponding, respectively, to the lower- and upper-frequency components of a flexural mode doublet. If only thermomechanical effects are considered, following the fluctuation–dissipation theorem each of these terms can be written as

1

where the subscript i = {L, U} denotes either the lower- or upper-frequency doublet component, S_i^TH = 4k_BTΓ_i is the PSD of the Langevin force given by the product of the Boltzmann’s constant k_B, the temperature T, and Γ_i = m_iω_i/Q_i, with m_i, ω_i, and Q_i being the effective mass, resonance frequency, and quality factor corresponding to each doublet component. According to the proposed transduction model, the nanowire vibration is converted into an optical signal by means of the dependence of the reflected power on the nanowire position. Thus, besides the factor given by the gradient of the reflected light intensity, ∂I/∂r, and its projection along the lower and upper doublet component axes, we need to consider the nanowire vibration mode-shape ψ(z) in order to account for the actual variation of the effective nanowire position. From such considerations, the measured PSD of the reflected optical power signal measured from the photodetector at a relative radial nanowire–laser beam distance r₀ with an angle θ₀ with respect to the lower-frequency vibration axis can be written as

2

Figure 3i,j shows the experiment–theory comparison of results corresponding, respectively, to the PSD of the lower and upper resonance peaks of the fundamental mode doublet of an undriven nanowire. The experimental data represented in these plots correspond to S_R(r₀, θ₀, ω) in μV²/Hz units as measured at the relative nanowire–laser beam position corresponding to the maximum sensitivity for each doublet component, i.e., θ₀ = 0° in Figure 3i and θ₀ = 90° in Figure 3j. The theoretical results correspond to the application of eq 1 for calculating S_i(ω) in m²/Hz units, considering T = 300 K and using the values of m_i, ω_i, and Q_i obtained from the experimental data. In particular, for the calculation of the effective mass m_i we consider the flexural mode shape ψ(z) given by the Euler–Bernoulli equation for a tapered cross-section beam with a normalization so that ψ(L) = 1.⁶ The dimensions and the tapering degree of the nanowire are determined by high-resolution scanning electron microscopy images of the particular nanowire under test (Figure S3 provides further details about the quantification of tapering). For the theoretical estimation of S_R(r₀, θ₀, ω) from the calculated S_i(ω) by the application of eq 2, the reflected light intensity gradient considered is obtained by derivation of the experimental measurement of reflected light intensity vs the relative nanowire–laser beam position. The relative position of the laser beam with respect the lower- and upper-frequency vibration axes is determined by previously obtaining the amplitude maps presented in Figure 2b,c. Remarkably, the experiment–theory agreement is excellent, validating our description of the transduction mechanism.

Equation 2 allows the estimation of the tip displacement and the displacement detection limit in length units. For the same nanowire considered in Figure 3, a thermomechanical spectrum converted into pm/Hz^1/2 units is shown in Figure S4, revealing a detection limit of 27 pm/Hz^1/2 for a laser power of 16.8 μW. This value is well below the PSD peak amplitude obtained, around 0.9 nm/Hz^1/2, which implies an RMS amplitude of 3.5 nm for the actual tip displacement. Lower detection limits down to the order of 1 pm/Hz^1/2 were obtained for shorter nanowires by maximizing optical power (typically up to 350 μW) and increasing the numerical aperture (N.A.) of the objective (up to 0.55), which provides a larger optical gradient but a less uniform laser beam cross-section along the nanowire. Optical power is limited by the onset of back-action effects, and a uniform laser beam cross-section is preferred for a precise application of our model, which does not consider variations of the beam shape along the NW. For all the nanowire sizes considered in this work the displacement detection limit achieved was always at least 1 order of magnitude lower than the thermal noise amplitude at resonance, allowing for a clean detection of the fundamental flexural mode doublet of the nanowires without external driving. Table S1 presents examples of the parameters measured for the different nanowire sizes considered in this work, including PSD peak amplitude and RMS amplitude estimations.

The high sensitivity and stability of the transduction scheme presented in this work allow the characterization of the resonant response of the Si NW resonators considered as a model system in their full dynamic range and for flexural modes of higher order than the fundamental. Examples are presented in Figure 4 for a nanowire of the longest type. Figure 4a shows the upper and lower resonance peaks of the fundamental mode driven by a piezoelectric actuator with increasing voltage amplitude, from the undriven resonance to the onset of the nonlinear regime. This set of measurements demonstrates that no amplitude saturation or frequency shift effects limit the acquisition of the resonant response of the nanowires in their full dynamic range. Moreover, the graphs show that the nonlinear regime becomes available, showing a right-shift of the upper part of the resonance peaks. Such stiffening of the frequency response is a general intrinsic behavior of single-clamp beam resonators produced by geometrical nonlinearities, which appear when large deformations induce a nonlinear relation between strain and curvature and introduce a cubic restoring force in the equation of motion.^34,35 We estimate a nanowire tip RMS amplitude of 1.12 μm at the onset of this nonlinear response. The capacity of the transduction mechanism to provide access to this nonlinear regime enables applications based on the singular dynamics of nanomechanical resonators in this regime.^11,36,37 The behavior of the peak amplitudes of the lower- and upper-frequency doublet components as a function of the piezo voltage driving amplitude is plotted in Figure 4b. The amplitude of both peaks shows a linear dependence with the driving amplitude in a range up to around 300 mV of driving voltage, resulting in a dynamic range of around 50 dB. Shorter nanowires showed a slightly higher dynamic range up to around 60 dB, consistent with the theoretically expected behavior for nanowire resonators.³⁸ In Figure 4c–g, we represent the upper and lower resonance peaks of the doublets from the fundamental to the fifth order flexural modes of a Si NW resonator driven just below the onset of the nonlinear regime. The experimental values of the resonance frequencies for all mode orders are in good agreement with the theoretical values derived from Euler–Bernoulli elastic beam theory for tapered beams, previously reported for the first two mode orders,⁶ and extended here up to the fifth order (see Tables S2 and S3 and Figure S3 of the Supporting Information). It is noteworthy that the signal-to-noise ratio (SNR, ratio of the peak amplitude to the background level of the spectra) is excellent for all mode orders, allowing for plotting the measured amplitudes as a function of the relative nanowire–laser beam position for each mode order (shown as insets in each figure). These plots reveal the relative orientations of the nanowire vibrations in the lower and upper components of each mode order doublet, showing that the orientation remains approximately the same regardless of the mode order. The deviations observed, particularly for the third order, are attributed to the presence of structural defects that may happen at the positions of maximum strain for this particular mode. This is supported by the observation that different nanowires show a different behavior to this respect. Some nanowires show the same orientation for all mode order doublets, while others show deviations at a particular mode order which varies from nanowire to nanowire as a consequence of the random distribution of defects along their lengths.

Figure 4.

Transduction in full dynamic range and high-order flexural modes of vertical Si NW resonators. (a) Resonance spectra showing the lower and upper resonance peaks of the fundamental mode doublet of a Si nanowire driven with varying piezo voltage amplitudes, from 0 V (thermomechanical fluctuations) to 800 mV (slightly above the onset of the nonlinear regime). (b) Peak amplitude vs piezo voltage amplitude obtained from the previous results. (c–g) Resonance spectra and amplitude mappings from the fundamental (c) to the fifth order mode (g) for a Si nanowire driven just below the onset of the nonlinear regime (a full experiment–theory comparison for the resonance frequency values is provided in the Supporting Information). All resonance spectra were measured at θ₀ = 0° for the lower peak and θ₀ = 90° for the upper peak. All amplitude maps are 20 × 20 μm² with a Z-range equivalent to the vertical axis of the corresponding resonance spectra.

Besides the relative nanowire–laser beam position, the optical power of the laser beam is another key factor for the optimization of the transduction performance. Figure 5 presents the influence of optical power on the sensitivity and noise performance of the transduction mechanism. Thermomechanical spectra obtained at different values of the optical power are presented in Figure 5a. The optical power values used span almost 2 orders of magnitude (from 0.4 to 17.7 μW), and the effect of this variation is clearly visible in the evolution of the resonance peak represented, corresponding to the lower component of the fundamental mode doublet of an undriven nanowire. As the optical power increases, two main effects are observed: the signal amplitude increases, and the resonance frequency is shifted to higher values. Figure 5b represents the signal amplitude at resonance vs the optical power, revealing a linear increase. This dependence is given by the effect of the increase of the incident optical power on the reflected power dip observed when varying the relative nanowire–laser beam position (Figure 3a,b): a higher incident power implies a steeper reflected power dip and, thus, a larger reflected power gradient which ultimately determines sensitivity, as expressed in eq 2. However, the signal-to-noise ratio (SNR), plotted in Figure 5c, shows a slight deviation from a linear dependence, which is attributed to the effect of the optical power on the background noise level given by the laser source shot noise. Figure 5d shows the dependence of the relative frequency shift with the optical power, which shows a nonlinear monotonic increase. Such dependence is attributed to the complex balance of forces acting on the nanowire resonators as a consequence of their exposure to the laser beam, which includes thermoelastic forces (arising from both the Young’s modulus dependence on the temperature^17,39 and thermal expansion effects⁴⁰) and optical forces (provided by attractive gradient forces⁴¹ as well as radiation pressure effects⁴²). Figure 5e represents the evolution of the quality factor vs the optical power. The results reveal an asymptotic decrease from slightly higher values at lower optical power that decrease around a 30% to a constant value at higher optical power. This dependence is attributed to an overestimation of Q in the noisier spectra obtained at lower optical power. As the SNR improves for increasing power, the estimation of Q stabilizes at a constant value independent of the optical power. Finally, Figure 5f,g presents the analysis of the frequency stability as a function of the optical power. The lowest Allan deviation achieved (Δf/f = 2 × 10^–7) is obtained at the maximum optical power (17.4 μW) for an acquisition time of 1 ms. These values are comparable to those obtained for other silicon nanoresonators.⁴³ There are two main implications of the observed effects of the optical power: first, a larger optical power implies higher sensitivity and better noise performance in the range considered; and second, the transduction mechanism does not imply any significant back-action effect between the laser beam and the nanowire vibration in the range of optical power considered. The upper limit of the optical power for linear transduction performance optimization is in fact limited by the appearance of back-action effects, which were not observed at optical power values below 75 μW for the longest nanowires and below 350 μW for the shortest.

Figure 5.

Effect of optical power on sensitivity and noise performance. (a) Resonance spectra showing the lower resonance peak of the fundamental mode doublet of an undriven Si nanowire obtained for varying optical power from 0.4 to 17.7 μW. (b–e) Peak amplitude, SNR, resonance frequency, and quality factor vs optical power obtained from the previous results. (f) Resonance frequency fluctuations (Allan deviation) vs acquisition time for a Si nanowire driven just below the onset of the nonlinear regime obtained at different values of the optical power. (g) Resonance frequency fluctuations (Allan deviation) vs optical power at varying acquisition times obtained from the previous result, highlighting the minimum frequency fluctuations achievable as a function of the optical power (red line).

The main conclusions of this work can be summarized in three points. First, the flexural mode vibrations of vertically aligned semiconductor nanowires can be read out by a transduction mechanism based on the nanowire vibration-induced modulation of the reflected optical power from a laser beam with parallel incidence. Second, the main performance characteristics of this transduction mechanism are its high sensitivity and its linearity, demonstrated here by its application for detecting flexural mode doublet vibrations of vertical Si NWs in their full dynamic range, high mode orders, and with a detection limit below their thermomechanical vibrations. Finally, in contrast to all transduction schemes reported so far for semiconductor nanowires, this transduction mechanism requires neither any particular geometry or array pattern for the nanowires nor their positioning in specific supporting structures or close to driving/biasing electrodes, so that the only fabrication process involved is the generation of the nanowires themselves. The availability of such a transduction mechanism can be extremely useful for improving or extending already existing applications and also to stimulate the development of new ones by the absence of the constraints and limitations imposed by specific nanofabrication processes. In particular, a universal transduction scheme for vertical nanowires becomes singularly significant when considering the increasing interest of these nanostructures for biological applications. The interactions between vertical nanowire arrays and cells, bacteria, and several types of biomolecules have been the focus of many works related to the development of substrates with enhanced functionalities regarding cell adhesion/motility,⁴⁴⁻⁴⁷ biomolecular transfection,⁴⁸⁻⁵⁰ characterization of cell forces,⁵¹⁻⁵⁶ bacterial recognition/proliferation,^57,58 and biomolecular detection/analysis.^59,60 The transduction scheme presented in this work, which adds the nanomechanical sensing functionalities of vertical SCNW resonators to this field, opens new research and technology lines including the measurement, tracking, and analysis of nanomechanical properties (vectorial forces, mass, stiffness, viscoelasticity, etc.) of small cells, bacteria, or large biomolecules adsorbed or adjacent to the nanowires.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.9b04909.

• Additional scanning electron microscopy images, 2D finite element simulations, determination of tapering degree of Si nanowires from SEM images, experiment–theory comparison of higher-order to fundamental mode resonance frequency ratios, estimation of displacement detection limit, representative examples of the measured dimensions and dynamic parameters for the fundamental mode of the three types of nanowires considered as a model system, equations for calculating resonance frequencies, full experiment–theory comparison of resonance frequencies for flexural modes from fundamental to 5th order (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.