Neutron Diffraction and Raman Studies of the Incorporation of Sulfate in Silicate Glasses

Abstract

The oxidation state, coordination, and local environment of sulfur in alkali silicate (R₂O–SiO₂; R = Na, Li) and alkali/alkaline-earth silicate (Na₂O–MO–SiO₂; M = Ca, Ba) glasses have been investigated using neutron diffraction and Raman spectroscopy. With analyses of both the individual total neutron correlation functions and suitable doped–undoped differences, the S–O bonds and (O–O)_S correlations were clearly isolated from the other overlapping correlations due to Si–O and (O–O)_Si distances in the SiO₄ tetrahedra and the modifier–oxygen (R–O and M–O) distances. Clear evidence was obtained that the sulfur is present as SO₄^2– groups, confirmed by the observation in the Raman spectra of the symmetric S–O stretch mode of SO₄^2– groups. The modifier–oxygen bond length distributions were deconvoluted from the neutron correlation functions by fitting. The Na–O and Li–O bond length distributions were clearly asymmetric, whereas no evidence was obtained for asymmetry of the Ca–O and Ba–O distributions. A consideration of the bonding shows that the oxygen atoms in the SO₄^2– groups do not participate in the silicate network and as such constitute a third type of oxygen, “non-network oxygen”, in addition to the bridging and non-bridging oxygens that are bonded to silicon atoms. Thus, each individual sulfate group is surrounded by a shell of modifier and is not connected directly to the silicate network. The addition of SO₃ to the glass leads to a conversion of oxygen atoms within the silicate network from non-bridging to bridging so that there is repolymerization of the silicate network. There is evidence that SO₃ doping leads to changes in the form of the distribution of Na–O bond lengths with a reduction in the fitted short-bond coordination number and an increase in the fitted long-bond coordination number, and this is consistent with repolymerization of the silicate network. In contrast, there is no evidence that SO₃ doping leads to a change in the distribution of Li–O bond lengths with a total Li–O coordination number consistently in excess of 4.

1. Introduction

The form and behavior of sulfur in glasses and melts is of interest to multiple research fields, ranging from commercial glass manufacture to radioactive waste vitrification and geology. Sulfur, present in the form of sodium sulfate, Na₂SO₄, is widely used as a refining agent for bubble removal and accelerated silica sand grain dissolution in commercial soda-lime–silica (SLS) glass manufacture.¹⁻⁴ Under oxidizing melting conditions, some of the added sulfate partially dissolves (represented as SO₃ or SO₄^2–) within the glass melt, and SO₃ solubilities of 0.2–1 wt % have been demonstrated for soda-lime–silica (SLS) glasses.^1,2,5−7 The solubility of SO₃ in the melt is strongly affected by the composition, redox conditions, and melting temperatures. Besides sulfates, under strongly reducing conditions, sulfur dissolves in the melt in the form of sulfide (S^2–) and has long been used by SLS container glass industries to provide the well-known Fe³⁺–S^2– amber color.^1,2,8−11 In addition to commercial glass manufacture, sulfur solubility in silicate liquids is also of interest to geologists due to the atmospheric release of large amounts of SO₂ gas during volcanic eruptions.¹²⁻¹⁶

The classical model for sulfur speciation and solubility in oxide melts^15,17 shows the existence of sulfur in (VI) and (−II) oxidation states, occurring as sulfate (SO₄^2–) and sulfide (S^2–) species, respectively. Sulfur solubility is a function of partial pressures of oxygen (pO₂) and sulfur dioxide (pSO₂) and oxygen ion activity in the melt (which is in turn determined by melt composition). Effects of pO₂ and pSO₂ on sulfur solubility and speciation in oxide melts have been widely studied in glass science and technology and geological fields.^2,12,17−21 It is widely accepted that sulfur occurs as S(VI) species (sulfate, SO₄^2–) in oxide glasses prepared under oxidizing conditions. Moretti and Ottonello¹⁹ have indicated that the sulfur capacity of silicate melts can be predicted by combining systemic acidity–basicity (as measured by optical basicity) with a modified Toop-Samis polymeric model, and for many years others,¹¹⁻³⁴ have also been studying different aspects of the complex relationships governing sulfur solubility in a range of oxide melt systems.

Further to its relevance to commercial glass manufacture and geology, sulfate solubility is also of critical importance to the vitrification of certain radioactive wastes. The high concentrations of sulfur present in some low-activity waste (LAW) and/or high-level waste (HLW) streams produced in the United States, India, Russia, and China can be problematic. Sulfur is present as sulfate ions (SO₄^2–) in LAW and HLW radioactive waste streams, often arising due to the addition of ferrous sulfamate as a reprocessing additive to enable separation of reusable transuranic elements such as U, Pu, and Am from spent nuclear fuel.²²⁻²⁴ Sulfur may also arise in the intermediate-level waste (ILW) streams under consideration for vitrification (e.g., in the U.K. and Korea), for example, inorganic cationic exchange resins containing functional sulfonic acid groups combined with polymers.²⁵⁻²⁷ High concentrations of sulfate show low (typically <1 wt % as SO₃) solubility in the different alkali borosilicate glass matrices used globally for radioactive waste vitrification.²⁸⁻³⁴ During melting, the excess sulfate forms an immiscible sulfate salt layer (a yellow color may be imparted due to the presence of chromates in the waste) that floats on the top of melt.³⁵⁻³⁷ This salt layer is typically rich in water-soluble alkali/alkaline-earth sulfates³⁸ and may thus provide a pathway for partitioning of Tc, Sr, and Cs radionuclides into this water-soluble layer during melting. Following geological disposal, this pathway could enable these radionuclides to readily dissolve in groundwater and thus enter the biosphere. In addition to presenting an environmental threat, further problems are associated with the development of sulfate salt phases with the most important being the fact that it can determine upper safe waste loading limits, thereby increasing the total volume of vitrified waste and hence adding greatly to disposal costs.^22,28 The salt formation is also highly detrimental to the waste vitrification process as it is corrosive to the melting vessel refractories, obstructs the release of gas bubbles during vitrification, and also reduces efficiency of melting due to high thermal and electrical conductivity.³⁹⁻⁴¹ Potential solutions to mitigate these issues include (i) decomposing the sulfate segregated layer at a sufficiently high temperature to release the consequently generated SO_x gases through a suitable gas-treating apparatus, (ii) replacing the sulfate-based reprocessing additives with alternative chemicals, (iii) pre-treating the waste to remove or reduce SO₄^2– contents, and (iv) developing new or modified glass compositions with higher SO₄^2– capacities. To improve upon present waste glass compositions, it is critical to understand the factors governing the solubility of SO₄^2– anions in glasses. However, actual LAW, HLW, and ILW glass compositions may contain >20 elements in appreciable concentrations. Many of these elements can have mixed influences on SO₄^2– retention in the molten glass.^28,34,42,43 Spectroscopic investigations have also been carried out to study the sulfur oxidation state and local environment in conventional oxide glasses.⁴⁴⁻⁴⁷ Through Raman spectroscopic studies of SO₃-doped borosilicate and silicate glasses, some of these authors showed that the Raman modes correlating with S–O vibrations in glass Raman spectra exhibited closely similar Raman shifts and relative intensities as in the Raman spectra of corresponding crystalline sulfates. Thus, the Raman studies have indicated that sulfur was present in the glasses as S⁶⁺ in the form of SO₄^2– anions and was associated with network-modifier alkali cations present in the glass to form SO₄^2– clusters. The Raman spectroscopy outcomes were further supported with sulfur K edge EXAFS and XANES studies^48,49 on oxide, silicate, and borosilicate glasses, including high-level nuclear waste glasses. Comparisons between the XANES spectra for SO₄^2– in oxide glasses and corresponding crystalline sulfates again revealed similar environments. Mishra et al.³⁶ studied SO₄^2– environments in sodium–barium borosilicate glasses and concluded that SO₄^2– units preferentially associate with the larger Ba²⁺ ions rather than the Na⁺ ions. Their result was in contrast with that of McKeown et al.^44,50 who concluded that the surrounding chemical environment around SO₄^2– anions consisted of predominantly Na⁺ ions. However, these studies considered different base glass compositions and thus may or may not actually be in disagreement. Therefore, the sequence of preference for SO₄^2– ions to associate with alkali or alkaline-earth ions in multicomponent silicate and borosilicate glasses is still unclear. The current study was undertaken to directly address this knowledge gap. Our neutron diffraction results have revealed the average S–O and O–O interatomic distances and angles for the sulfur units present in simple binary and ternary silicate glasses. A comparison of neutron diffraction and Raman parameters for our glasses with those for a free sulfate (SO₄^2–) tetrahedron and for corresponding alkali/alkaline-earth sulfate crystalline salts provides greater understanding of the local environment around sulfur units in oxide glasses. It also reveals the differences in the capability of modifier cations to provide stabilization and charge compensation of SO₄^2– tetrahedra in oxide glasses, which can be linked to sulfate solubilities.

2. Neutron Diffraction Theory

Neutron diffraction (ND) can accurately determine the distribution of interatomic distances in glasses. It is very informative about the short-range order and, to a lesser extent, the intermediate range order, especially with the aid of modeling. The ND pattern of a noncrystalline material, such as glass, consists of broad peaks and troughs, which can reveal information about the local structure. In a diffraction measurement, all neutrons scattered by the sample are detected, regardless of energy transfer, and the total diffraction pattern measured in this way is the differential cross section:⁵¹⁻⁵³

1

Here, i(Q) is the distinct scattering due to interferences between the waves scattered by pairs of different atoms, and ℏQ is the magnitude of the momentum transfer for elastic scattering. The second term (the average of the squared scattering length) is the self-scattering due to interferences between waves scattered by the same atom. The self-scattering term is featureless for diffraction, and all the relevant information about interatomic distances is contained in i(Q). The total neutron correlation function, T(r), is obtained from the Fourier transform of i(Q):

2

where r is the distance between distinct pairs of atoms. Here, M(Q) is a modification function (such as the Lorch function or a step function) used to take into account the limitation that experimental data can only be measured up to a finite maximum momentum transfer, Q_max, and T⁰(r) is the average density contribution to the correlation function:

3

ρ⁰ is the average atomic number density and ⟨b̅⟩_avg is the average coherent neutron scattering length for the sample. The total correlation function is a weighted sum of all possible pairwise partial correlation functions, t_ll′(r), between atoms of element l and l′ as follows:

4

where c_l and b̅_l are the atomic fraction and coherent neutron scattering length for element l, respectively. If there is a peak in T(r) at a single interatomic distance of r_jk, arising from sites j and k (of elements l and l′, respectively), then this gives rise to a Gaussian contribution⁵⁴ to the partial correlation function t_ll′(r) given by

5

where n_jk is the average coordination number for these sites and 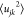is the mean square variation in the interatomic distance r_jk (arising from thermal motion and maybe static disorder). Thus, the coordination number, n_jk, can be determined from the area under a peak in T(r) according to eqs 4 and 5. The peak parameters (r_jk, 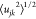, and n_jk) given in this work were determined by least squares fitting of the peak functions given by eqs 4 and 5 with the additional complication that the Gaussian functions were convoluted with real-space resolution (as given by the appropriate Fourier transform of M(Q)).

3. Experimental Procedures

3.1. Glass Preparation

Four sets of glasses were prepared in this study. Each set contained one SO₃-free “undoped” base glass and a corresponding SO₃-“doped” equivalent. The four base glasses comprised two binary systems (R₂O–SiO₂ with R = Li, Na) and two ternary systems (Na₂O–MO–SiO₂ with M = Ca, Ba). The ternary glass compositions were achieved by substituting half of the molar concentration of Na₂O with MO in Na₂O–SiO₂ glasses_. Analytical-grade carbonates and high-purity silica sand (>99.9% purity) were used for glass batch preparation. Sulfate was provided by Na₂SO₄ in the Na₂O-containing glass batches and Li₂SO₄ in the Li₂O–SiO₂–SO₃ glass batch. Batch compositions were prepared to make 125 g of glass and melted in a Pt-ZGS (ZrO₂ grain-stabilized) crucible loosely covered with a Pt-ZGS lid to reduce volatilization losses and minimize contamination. Batches were heated in an electric furnace at a temperature of 1300-1350 °C for 3 h, and after which, the crucibles were removed from the furnace, and the molten glass was poured onto a clean stainless-steel plate and allowed to cool to room temperature. The Li₂O–SiO₂ and Li₂O–SiO₂–SO₃ glasses were splat-quenched between two uniform stainless-steel blocks to maximize cooling rates and avoid crystallization. It was not possible to completely eliminate crystallization of these glasses wherein visible levels of crystallization occurred at the sample edges outside the area between the two steel blocks. The glassy material from between the steel blocks were visually identified and carefully physically separated for further analysis. The cooled glasses were immediately transferred into a vacuum desiccator to minimize any potential hydration or carbonation in consideration of their relatively poor chemical durability. Nominal compositions of all glasses are given in Table 1.

Table 1. Nominal and Analyzed (in Parentheses) Compositions in mol % for the Eight Silicate Glasses (the Melt Temperature and Density Are Also Given).

sample name	SiO2 (mol %)	Li2O (mol %)	Na2O (mol %)	CaO (mol %)	BaO (mol %)	SO3 (mol %)	SiO2/MOx	melt temp (°C)	density (g cm–3)
LiSi	57.50 (62.50)	42.50 (37.50)	0	0	0	0	1.35 (1.67)	1320	2.329
LiSiS	54.63 (59.97)	40.37 (35.50)	0	0	0	5.00 (4.53)	1.35 (1.69)	1320	2.326
NaSi	57.50 (60.35)	0	42.50 (39.65)	0	0	0	1.35 (1.52)	1300	2.519
NaSiS	53.76 (56.32)	0	39.74 (37.23)	0	0	6.50 (6.45)	1.35 (1.51)	1300	2.490
NaCaSi	57.50 (57.92)	0	21.25 (19.77)	21.25 (22.31)	0	0	1.35 (1.38)	1350	2.654
NaCaSiS	56.34 (56.48)	0	20.83 (19.25)	20.83 (22.23)	0	2.00 (2.04)	1.35 (1.36)	1350	2.645
NaBaSi	57.50 (58.62)	0	21.25 (22.40)	0	21.25 (18.98)	0	1.35 (1.41)	1350	3.321
NaBaSiS	54.62 (55.63)	0	20.19 (22.51)	0	20.19 (17.40)	5.00 (4.45)	1.35 (1.39)	1350	3.265

3.2. Compositional Analysis

A Philips Magix Pro PW2440 sequential wavelength dispersive X-ray fluorescence spectrometer, running an Oxide program constructed using multiple certified reference material (CRM) calibration standards, was used for the measurement of the final oxide concentrations in each glass containing Na₂O. Fused glass beads were prepared for XRF analysis by mixing 1 part by weight of the powdered glass sample with eight parts by weight of a 50:50 flux composed of Li₂B₄O₇ and LiBO₂ and melting in a Pt crucible at 1100 °C for 20 min. Inductively coupled plasma atomic emission spectroscopy (ICP-OES) was used to detect oxide concentrations in Li₂O–SiO₂ and Li₂O–SiO₂–SO₃ glasses. Analyzed compositions of all glasses are provided in Table 1.

3.3. Density

Density measurements were conducted on bulk glasses with deionized water as the working fluid using a Mettler Toledo balance installed with density measurement equipment based on Archimedes’ principle. The densities shown in Table 1 are averages of three separate measurements. Estimated uncertainties associated with each density are ±0.01 g cm^–3. The measured densities compare favorably with literature results taken from the SciGlass database.⁵⁵

3.4. Neutron Diffraction

The GEneral Materials diffractometer (GEM) at the ISIS Facility pulsed neutron source, Didcot, U.K., was used for the ND measurements.⁵⁶ Bulk glass samples were crushed to fine particles and placed into cylindrical vanadium foil cans of a wall thickness of 0.004 cm. Vanadium is preferred for this purpose because the scattering from vanadium is almost entirely incoherent, and therefore the Bragg peaks due to the can itself are very small. The height and weight of the sample were measured to obtain the packing fraction of the sample inside each can, and this was used in evaluating the experimental corrections. A rod of vanadium–niobium null alloy was measured as a standard. An empty vanadium can was also measured for appropriate subtraction from the sample measurement. The raw data were reduced, and corrected using GudrunN and ATLAS software.⁵⁷⁻⁵⁹ The correlation function of each sample was obtained by Fourier transforming the distinct scattering using the Lorch modification function⁶⁰ with a maximum momentum transfer of Q_max = 43 Å^–1. The peaks in the correlation functions were fitted using the pfit software package.⁵³The neutron diffraction results (distinct scattering and total correlation functions) are available from the ISIS Disordered Materials Database.⁶¹

3.5. Raman Spectroscopy

Raman spectra were obtained on all glass samples and crystalline sulfate materials (Li₂SO₄, Na₂SO₄, CaSO₄, and BaSO₄, analytical-grade reagents). The Raman data file for glauberite, Na₂Ca(SO₄)₂, a rare sulfate mineral comprising both sodium and calcium, was obtained from the RRUFF database.⁶² Bulk sample surfaces were polished with SiC paper to a finish of 15 μm. A Thermo Scientific DXR 2 Raman spectrometer installed with a laser of a wavelength of 532 nm and 10 mW power was used for analysis. The grating was set to 900 lines/mm, the estimated resolution was 5.5–8.3 cm^–1, and the estimated spot size was 2.1 μm. The instrument was calibrated using a standard polystyrene film prior to each measurement. The glass samples were exposed to the laser for 60 s/scan. Acquisitions were repeated 30 times within the range of 100–3000 cm^–1 and summed to improve spectral signal-to-noise ratios. OMNIC software was used to perform background removal and apply fluorescence corrections to the final spectra.

4. Results and Discussion

4.1. Compositional Analysis

All produced glasses were entirely colorless and transparent. This was consistent with parts-per-million levels or below of iron contamination from raw materials; also, very low levels or the absence of sulfur as S^2– (sulfide) groups within the glass^47,63 since the presence of the latter, even in low quantities, would impart a reddish yellow or amber color to the glasses. No salt phase separation was observed on the surface of the pristine melts during pouring, the presence of which would indicate that the sulfate capacity (solubility) of the glass melt had been exceeded under the preparation conditions used. Therefore, it can be concluded that the sulfate capacities of the glasses studied here are either the same or greater than the analyzed molar content of SO₃ within each glass. Figure 1 shows the analyzed SO₃ content retained within the sulfate-doped glasses as a function of glass composition where all glasses retained >85% of batched SO₃ (within an error limit of ±0.1–0.3 mol %). Table 1 shows the nominal and analyzed compositions for the eight silicate glasses studied. The error bars were generated by calculating the standard deviation of the multiple measurements made per sample. Table 1 shows that there were minor deviations from nominal compositions. This may have resulted from volatilization losses during glass melting and/or fused bead-making process for compositional analysis. However, the analyzed SiO₂/MO_x (modifier oxides) ratios remained almost constant between each set of SO₃-free and SO₃-doped glasses. The resulting compositions were also close to the nominal compositions, a conclusion that is also supported by comparing the densities of the glasses with published data on similar silicate glass compositions.⁵⁵ To ensure minimum volatilization losses of SO₃ and alkali oxides, the platinum crucibles were loosely covered with a Pt-ZGS lid as stated in Section 3.1. Based on our experience, the binary silicate glasses with the compositions studied here are more hygroscopic in atmospheric conditions than the ternary silicate glasses and can visibly change in 2–3 weeks if left at room temperature in atmospheric conditions. To minimize interactions of the glasses with atmospheric moisture or CO₂, all glasses were immediately transferred upon cooling from being molten into a vacuum desiccator with consideration of their relatively poor chemical durability.

Figure 1.

SO₃ capacity as a function of glass composition. The analyzed SO₃ content is also given as a percentage of the nominal SO₃ content above each pair of columns.

4.2. Raman Spectroscopy

The Raman spectra for the sulfate-free and sulfate-doped silicate glasses (Figure 2) show the presence of multiple overlapping contributions centered at Raman shifts of approximately 460, 550–700, 950, 990, and 1080 cm^–1 in all spectra albeit with notable differences in position and intensity between different samples. With the exception of the band at ∼990 cm^–1 for the sulfate-doped silicate glasses in Figure 2, the bands in the range of ∼950 to 1150 cm^–1 originate from Si–O stretching modes in the Qⁿ structural units where Q represents the SiO₄ tetrahedron and n is the number of bridging oxygens (BOs) in the unit.⁶⁴⁻⁶⁷ The Qⁿ structural units in the glasses studied here mainly consist of Q² (900–980 cm^–1) and Q³ (1050–1080 cm^–1) species, as observed in the Raman spectra. It is visible that, with sulfate addition, the intensity of the bands attributed to highly polymerized Q³ (3BOs) and fully polymerized Q⁴ (4BOs) species increases, suggesting polymerization of the silicate network.

Figure 2.

Raman spectra of the SO₃-free and SO₃-doped silicate glasses.

Tsujimura et al.⁴⁷ have reported Raman spectroscopic studies of sodium silicate glasses containing sulfur, and they conclude that the presence of SO₃^2– (sulfite) groups would produce two prominent Raman bands at 970–990 and 950–970 cm^–1 due to the symmetric and asymmetric S–O stretch modes in SO₃^2– groups, respectively. We do not observe such Raman bands but instead observe a sharp and intense band at 980–1000 cm^–1 (superimposed over the main silicate Qⁿ bands), which corresponds closely to the symmetric S–O stretching mode in SO₄^2– (sulfate) anions.^47,68,69 This observation, combined with the absence of any coloration in the samples, is strongly indicative of the presence of sulfur as only SO₄^2– sulfate units within all sulfur-doped glasses studied here. Further supporting evidence for this conclusion is provided, for example, by Morizet et al.^70,71 who showed using micro-Raman spectroscopy that, in aluminosilicate geological melts prepared under oxidizing conditions, S is present only in sulfate groups (SO₄^2–). Several others have also shown that S is present as sulfate groups (SO₄^2–) in oxide melts prepared under oxidizing conditions using a range of techniques including Raman spectroscopy and X-ray absorption spectroscopy.^21,49,72

Our conclusion is yet further supported by data from XANES studies of silicate glasses,⁴⁹ which show that sulfur only exists as sulfate in commercial soda–lime–silica glasses melted under mildly oxidizing conditions. The positions of the intense Raman band at 980–1000 cm^–1 in all of our sulfate-doped glasses (Figure 2) were also compared with the S–O symmetric stretching Raman band positions for corresponding crystalline alkali and alkaline-earth sulfates (Figure 3), and the band positions are consistent with those obtained from many Raman studies of different silicate and borosilicate glasses.^44,45,73 The peak positions for the intense υ₁ S–O symmetric stretch Raman band obtained for the crystalline sulfates and the sulfate-doped glasses are tabulated in Table 2. This approach, comparing and contrasting the υ₁ S–O Raman peak position in glasses with corresponding crystalline sulfate materials, has also been used successfully in previous studies of sulfur solubility, speciation, and structural environments in aluminosilicate geological glasses^70,71 and borosilicate radioactive waste glasses.⁴⁴

Figure 3.

Normalized Raman spectra for crystalline sulfates. The spectrum for Na₂Ca(SO₄)₂ was adapted from the RRUFF Raman spectra database.⁶²

Table 2. Peak Maximum Positions of the υ₁ S–O Symmetric Stretch Raman Band in the SO₃-Doped Silicate Glasses and Corresponding Crystalline Sulfate Salts; Estimated Uncertainty for Each Measurement Is ±0.5 cm^–1.

glass name	peak maximum of υ1 S–O symmetric stretch band (cm–1)	crystal	peak maximum of υ1 S–O symmetric stretch band (cm–1)
LiSiS	1007	Li2SO4	1008
NaSiS	990	Na2SO4	992
		Na2Ca(SO4)74	1002
NaCaSiS	992	CaSO4	1016
NaBaSiS	986	BaSO4	987

The υ₁ S–O bands in the glass Raman spectra are less sharp compared to the corresponding crystalline sulfates, which indicates a wider range of environments around SO₄^2– groups in the glass than in the corresponding crystalline sulfates and is entirely consistent with glass structural models. Based on the υ₁ S–O Raman shift at ∼992 cm^–1 in the Na₂O–CaO–SiO₂ (NaCaSiS) glass spectrum, SO₄^2– anions appear to be more closely associated with Na⁺ ions than Ca²⁺ ions, as evidenced by a comparison of the υ₁ S–O positions for NaCaSiS glass with those for crystalline Na₂SO₄, CaSO₄, and a naturally occurring sodium–calcium mixed-cation sulfate mineral, glauberite (Na₂Ca(SO₄)₂). Contrastingly, in the spectrum for Na₂O–BaO–SiO₂ (NaBaSiS) glass where the υ₁ S–O Raman shift appears at ∼986 cm^–1 and using the same approach, this indicates that SO₄^2– anions are at least partially charge-compensated by the Ba²⁺ ions (so that there are Ba–O–S linkages) with the remainder being partially charge-compensated by Na⁺. The fact that the peak maximum for the NaBaSiS glass is at a lower Raman shift than that of the corresponding Na-only binary glass (NaSiS) and at almost exactly the same Raman shift as the BaSO₄ salt (Table 2) supports the view that Ba²⁺ must at least partially stabilize the sulfate groups in the NaBaSiS glass. This in turn suggests some form of competition between alkali and alkaline-earth cations to stabilize SO₄^2– anions.

4.3. Neutron Diffraction Results

4.3.1. Sulfur Coordination

Figure 4 shows the corrected distinct scattering, i(Q), measured by neutron diffraction for each of the samples. The total correlation functions, T(r), obtained by Fourier transformation of the distinct scattering are shown in Figure 5. T(r) is a measurement of the distribution of interatomic distances weighted by the coherent neutron scattering lengths, b̅, of the elements concerned, and a peak in T(r) indicates a commonly occurring interatomic distance, such as a bond length.⁵³ Reliable normalization of T(r) is essential for identifying and parameterizing the structural role of sulfur in these glasses, and the normalization of the correlation functions was achieved using the method described by Hannon⁵³ and Alderman et al.⁷⁵ The correlation functions for all samples show two prominent peaks at ∼1.62 and ∼2.65 Å. These correspond to the Si–O and (O–O)_Si distances in SiO₄ tetrahedra.⁷⁶⁻⁷⁹ The Na–O bonds give rise to a shoulder before the (O–O)_Si peak at ∼2.33 Å, while Li–O bonds manifest themselves as a peak at ∼1.95 Å that is negative due to the negative neutron scattering length of lithium.⁸⁰ The peaks at a very short distance of ∼0.2 Å are error peaks arising from imperfect corrections of the data, and the lithium-containing samples have the largest error peaks due to the relatively large neutron absorption cross section of Li.⁸⁰ The most obvious difference between correlation functions for sulfate-doped and undoped samples is that sulfate doping leads to some additional intensity at ∼2.4 Å.

Figure 4.

Distinct scattering, i(Q), measured by neutron diffraction for the SO₃-free and SO₃-doped silicate glasses. For clarity, the patterns are shown with suitable vertical offsets.

Figure 5.

Total neutron correlation function, T(r), for the SO₃-free and SO₃-doped silicate glasses. For clarity the functions are shown with suitable vertical offsets. The assignments of some of the peaks to pairs of elements are indicated.

The first peak in the correlation function for each of the undoped samples was fitted with a single symmetric peak using pfit software.⁵³ An example of these fits is shown in Figure 6. The parameters for the fits (mean Si–O bond length, r_SiO, RMS variation in the Si–O bond length, u_SiO, and mean Si–O coordination number, n_SiO) are given in the upper part of Table 3. The Si–O coordination numbers are found to be essentially four within the limitations of the method,⁸¹ as may be expected for tetrahedral SiO₄ units in silicates. Furthermore, the observed (O–O)_Si distance is ∼1.633 (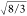) times longer than the Si–O bond length, consistent with tetrahedral geometry. Coordination numbers were determined from the peak areas (eq 5) on the basis of the nominal compositions.

Figure 6.

Total neutron correlation function, T(r), for the (a) SO₃-free and (b) SO₃-doped sodium silicate glasses, together with the fits to the first peak described in the text.

Table 3. Parameters from Fitting the Si–O, S–O, and (O–O)_S Peaks in T(r) and ΔT(r)^a.

parameters		LiSi and LiSiS	NaSi and NaSiS	NaCaSi and NaCaSiS	NaBaSi and NaBaSiS
fit to the first peak of T(r) for the undoped sample	rSiO (Å)	1.6222(2)	1.62491(6)	1.6251(2)	1.62584(5)
	uSiO (Å)	0.0511(3)	0.05844(8)	0.0548(3)	0.05703(6)
	nSiO	4.10(2)	4.016(3)	3.92(1)	3.908(2)
fit to the first peak of T(r) for the doped sample	rSiO (Å)	1.6219(2)	1.6231(2)		1.6262(2)
	nSiO	4.129(6)	4.006(8)		3.91(4)
	rSO (Å)	1.478(3)	1.475(2)		1.54(1)
	uSO (Å)	0.044b	0.044(2)		0.08(1)
	nSO	3.7(1)	3.1(1)		4.7(6)
fit to peaks in the doped–undoped difference	rSO (Å)	1.4686(4)	1.4755(3)	1.522(1)	1.5136(5)
	uSO (Å)	0.0443(6)	0.0313(6)	0.024(2)	0.0556(9)
	nSO	3.74(2)	3.07(1)	3.57(4)	3.02(2)
	rOO(S) (Å)	2.4091(4)	2.4038(4)	2.386(1)	2.4151(7)
	uOO(S) (Å)	0.0626(6)	0.0734(6)	0.081(2)	0.065(1)
	nOO(S)	0.358(2)	0.514(2)	0.130(2)	0.309(3)
	O–Ŝ–O	110.2	109.1	103.2	105.8
predictions
undoped sample	rOO(Si) (Å)	2.6490	2.6535	2.6538	2.6550
	nOO(Si)	4.38	4.38	4.38	4.38
	nOSi	1.46	1.46	1.46	1.46
doped sample	rOO(Si) (Å)	2.6486	2.6505		2.6556
	nOO(Si)	3.98	3.87	4.22	3.98
	nOO(S)	0.364	0.468	0.150	0.364
	nOSi	1.33	1.29	1.41	1.33

^aSee text for details. The SO₃ doping of NaCaSiS is too small to allow a meaningful fitting of two peaks to the first peak in T(r).

^bFor LiSiS, the S–O peak width was fixed at a value taken from NaSiS in order to obtain a meaningful fit. Statistical errors from the fits are given in parentheses. (The parameter r_jk represents the interatomic distance between atoms j and k, while u_jk (written as in eq 5) represents the root mean square variation in r_jk, and n_jk represents the coordination number. For O–O distances, an additional bracket is used to differentiate oxygen pairs in the sulfur (r_OO(S)) and silicon (r_OO(Si)) coordination shells. O–Ŝ–O is the bond angle at the sulfur atom.)

The average Si–O bond lengths in Table 3 are consistently longer than the Si–O bond length in pure SiO₂ glass (1.608(4) Å⁸¹). This lengthening of the average Si–O bond length with the addition of a modifier has been observed before,⁸² and, for example, Clare et al.⁸³ have reported a value of r_SiO = 1.6220 Å for sodium silicate glass with 30.83 mol % Na₂O. The addition of a modifier to the glass leads to the formation of (negatively charged) non-bridging oxygens (NBOs), and Si-NBO bonds are expected to be shorter than Si-BO bonds to bridging oxygens; thus, the observed lengthening of the Si–O bond (compared to pure SiO₂) may seem counterintuitive, but it can be understood by consideration of crystal structures. First, note that diffraction measurements on a glass are usually only able to measure the average bond length, whereas it is possible to determine the exact lengths of individual bonds in a crystal structure. In crystalline α-SiO₂,⁸⁴ the mean bond length is r_SiO = 1.609 Å with a very small standard deviation of 0.001 Å. On the other hand, detailed analysis of the bond lengths in crystalline Li₂Si₂O₅⁸⁵shows that the overall mean Si–O bond length is r_SiO = 1.616 Å, while the mean bond lengths to NBOs and BOs are r_Si-NBO = 1.565 Å and r_Si-BO = 1.633 Å, respectively. Thus, the average bond length becomes lengthened because the shortening of the Si-NBO bonds is outweighed by the lengthening of the Si-BO bonds. The reason for the lengthening of the average Si-BO bond length is that some of the BOs are bonded to modifier cations in addition to two silicon atoms. This behavior gives rise to a greater variation in the lengths of the Si–O bonds on the addition of a modifier, and thus the Si–O peak widths, u_SiO, reported in Table 3 are larger than the corresponding width for pure SiO₂ glass (0.047(4) Å⁸¹).

The first peak in T(r) for the SO₃-doped glass samples shows a small additional signal on the short-distance side at ∼1.5 Å. In phase V of Na₂SO₄,⁸⁶ the sulfur atoms are tetrahedrally coordinated by four oxygens with S–O bonds of a length of 1.472 Å, and hence this signal is assigned as arising from S–O distances in the glasses. The S–O signal is small due to the (relatively) low SO₃ content in the glasses (Table 1) and the fact that the neutron scattering length of sulfur is smaller than that of silicon.⁸⁰ This signal is close to the lower limit of what can be observed in a neutron correlation function, and consequently, the present work extends the boundaries of ND study on glass. We note that the S–O peak could be observed more readily if it did not partially overlap with another peak (namely, the Si–O peak), but on the other hand, it could not be resolved at all if it overlapped fully with another peak. The signal arising from the units around sulfur atoms can be seen more clearly by taking a suitable difference between correlation functions. For each pair of SO₃-doped and undoped samples, the components other than SO₃ are essentially present in the same proportions, irrespective of doping. Therefore, to a good approximation, all of the short-range peaks that are not associated with the presence of SO₃ can be removed by a suitable subtraction:

6

where the SO₃-doped glass contains 100x_SO3 mol % SO₃. Figure 7 shows the difference function ΔT(r) for each pair of samples. Each difference function exhibits two peaks at distances of ∼1.5 and ∼2.4 Å; the magnitude of which appears to depend on the SO₃ content of the glasses (Table 1). According to a simple bond valence calculation,^85,87 a S⁶⁺ ion bonded in a SO₄ unit to four equidistant oxygens has a S–O bond length, r_SO, of 1.474 Å. For comparison, the equivalent S–O bond lengths for SO₃ and SO₅ units with hexavalent sulfur are calculated to be 1.368 and 1.557 Å, respectively. Figure 7 shows a vertical line at the calculated S–O bond length for SO₄ coordination, and the first peak in each difference function is at approximately this distance. For a regular SO₄ tetrahedron with this S–O bond length, the (O–O)_S distance may be calculated as 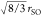≈ 2.407 Å. Figure 7 shows a second vertical line at 2.407 Å, and the second peak in each difference function is at approximately this distance. Thus, the distances at which the peaks in the difference functions occur are consistent with tetrahedral SO₄ units.

Figure 7.

Difference function, ΔT(r), for each pair of samples, shown with suitable vertical offsets (indicated by horizontal black lines) for clarity. The two vertical lines indicate distances of 1.474 and 2.407 Å, the calculated S–O and (O–O)_S distances for regular tetrahedral SO₄ units (see text for details). The peaks fitted to each difference function are shown as thick black lines.

For a successful determination of the difference function, ΔT(r), the correlation functions for the doped and undoped samples must both be normalized well, or else, it will contain residual peaks at ∼1.62 and ∼2.65 Å arising from the Si–O and (O–O)_Si peaks. There is little evidence for such residual peaks in the difference functions shown in Figure 7. Accurate normalization of T(r) is more difficult for the lithium-containing samples because the average scattering length, ⟨b̅⟩_avg, is smaller (due to the negative scattering length of Li), leading to a smaller gradient for T⁰(r) (see eq 2). The difficulty of normalization for lithium-containing samples is also exacerbated by the relatively large error peak in T(r), and the final normalization for LiSiS was refined so as to remove the Si–O and (O–O)_S residuals in the corresponding ΔT(r).

Since the sulfate signal is toward the lower limit of what can be observed in a neutron correlation function, it was parameterized using two different approaches. In the first approach, the first peak of T(r) for the SO₃-doped sample was fitted using two symmetric peaks to represent the distributions of S–O and Si–O distances. In this fit, the width u_SiO of the Si–O peak was held at the same value as for the undoped sample. The parameters for these fits are given in the central part of Table 3, and an example of these fits is shown in Figure 6. The NaCaSiS sample has the lowest SO₃ content of the doped samples, and it was not possible to obtain a two-peak fit for this sample. Furthermore, fitting of this region of T(r) for the LiSiS sample is more complex due to an overlap with the contribution from shorter Li–O distances and is discussed later. The second approach was to fit two peaks to the S–O and (O–O)_S peaks in ΔT(r). The fitted peaks are shown in Figure 7, and the parameters for these fits are given in the lower part of Table 3. An advantage of this approach is that it shows a clear peak for (O–O)_S atom pairs in SO₄ tetrahedra from which the (O–O)_S distance can be determined; contrastingly, if T(r) for the doped sample is considered alone, then this distance cannot be readily determined, even though the contribution from (O–O)_S distances is apparent as a difference between pairs of correlation functions shown in Figure 7. On the other hand, an advantage of the first approach is the fact that information about the Si–O coordination is obtained.

The fits to the first peak of T(r) for the doped samples yield Si–O bond lengths and coordination numbers that are reasonable and consistent with tetrahedral SiO₄ coordination. The S–O bond lengths and coordination numbers are also consistent with tetrahedral coordination (SO₄) but with a much greater scatter of values due to the difficulty of resolving a small peak overlapping almost entirely with a larger peak. Likewise, the S–O bond lengths and coordination numbers from fitting the difference function ΔT(r) are also consistent with tetrahedral SO₄ coordination. Table 3 gives the mean O–Ŝ–O bond angle determined from the two distances fitted to the difference function, and these values are similar to the ideal tetrahedral value of 109.47°.

The (O–O)_S coordination number obtained from fitting the difference function ΔT(r) can also be shown to be consistent with tetrahedral coordination as follows: If cations A^v+ in an oxide have coordination polyhedra that are essentially regular with an average coordination number, n_AO, that is sufficiently low (i.e., tetrahedral or trigonal polyhedra with n_AO ≤ 4), then all pairs of oxygens in these polyhedra are separated by essentially the same distance. It can then be shown that the average O–O coordination number at this distance, arising from these polyhedra, is given by

7

where c_A and c_O are the atomic fractions for the two elements concerned. In this work, we will apply this equation to both SO₄ and SiO₄ units in the glasses (i.e., A = S and A = Si) for which n_OO(A) = 12c_A/c_O. Equation 7 shows that the (O–O)_A coordination number depends only on the A–O coordination number and the relative concentrations of A and O atoms. The penultimate row of Table 3 gives the predicted (O–O)_S coordination number, n_OO(S), according to eq 7 on the assumption that n_SO = 4. There is good agreement between the predicted values and the values determined by fitting. Although n_OO(S) may appear to be a less direct test than n_SO of whether the S–O coordination is tetrahedral, it is actually a better test because the (O–O)_S peak is larger and more clearly observed (Figure 7) due to oxygen having a larger neutron scattering length than sulfur. In contrast, the S–O peak is smaller and suffers from overlap with the adjacent large Si–O peak, so it is more difficult for highly accurate coordination numbers to be obtained. Table 3 also gives the predicted O–Si coordination number, n_OSi = n_SiOc_Si/c_O, assuming that n_SiO = 4 because this is useful for the later discussion of the connectivity of the silicate network.

As discussed in Section 4.2, the Raman spectra, combined with literature and redox conditions, show no evidence for and do not support the presence of tetravalent sulfur in SO₃^2– sulfite groups. However, such groups cannot be entirely ruled out on the basis of the ND results alone. Crystalline Na₂SO₃ contains SO₃ groups with a S–O bond length of 1.505 Å, a (O–O)_S distance of 2.398 Å, and a O–Ŝ–O bond angle of 106°.⁸⁸ The values of these three structural parameters are similar to the corresponding values for SO₄ groups (r_SO = 1.474 Å, r_OO(S) = 2.407 Å, and O–Ŝ–O = 109°), and in fact, the fitted values for NaCaSiS and NaBaSiS are closer to those of the SO₃ group (see Table 3). However, the difference in parameters for the two units is dominated by the different S–O bond lengths, and examination of Figure 7 shows that ΔT(r) for these two samples has large ripples around the S–O peak, limiting the reliability to which r_SO can be determined. (The ripples are experimental artifacts arising from Fourier ripples due to truncation of the diffraction pattern at Q_max, statistical noise, and imperfect corrections and normalizations of the diffraction data.) Thus, the S–O bond length, especially for NaCaSiS and NaBaSiS, is not determined accurately enough to be able to discriminate between SO₃ and SO₄ groups. However, the (O–O)_S peak is more accurately determined by ND than the S–O peak (see, for example, Figure 7) due to its greater intensity, and as shown in Table 3, the fitted n_OO(S) coordination numbers are in good agreement with the values predicted on the basis that sulfur is tetrahedrally coordinated by oxygen. On the other hand, if all of the sulfur in these glasses were in SO₃ units instead of SO₄ units, then the n_OO(S) coordination number would be halved (this result can be seen by considering that a SO₃ unit has half as many O–O pairs as a SO₄ unit, or it can be derived from eq 7). The fitted n_OO(S) coordination numbers are not in good agreement with predictions that are half the values given in Table 3. This is the strongest evidence from ND that the sulfur is present in these glasses in SO₄ groups, not SO₃ groups, implying that sulfur is hexavalent, not tetravalent. This result is fully consistent with the literature for other oxide glasses prepared under similar redox conditions (see Section 1).

4.3.2. Modifier Coordination

For the sodium-containing glass samples, the peaks in T(r) arising from modifier–oxygen bonds overlap significantly with the (O–O)_Si peak arising from O–O distances in SiO₄ tetrahedra, and for the doped samples, there is also an overlap with the (O–O)_S peak arising from O–O distances in SO₄ tetrahedra. Consequently, the determination of information about the modifier coordination requires detailed modeling of this region of T(r), which is aided considerably by taking into account the tetrahedral coordination of silicon and sulfur. First, the coordination numbers for the O–O peaks (and hence their areas according to eq 4) can be calculated from eq 7. Furthermore, the positions for the O–O peaks can be calculated to a good approximation as .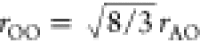

The correlation functions for the NaSi and NaSiS samples were fitted with three and four peaks, respectively, as shown in Figure 8, yielding the parameter values given in Table 4. The peaks were fitted over the distance range from 2.06 to 2.80 Å, and they characterize the Na–O and O–O distributions in this region. The lower limit of the fit range was chosen to exclude any significant influence from the Si–O peak at ∼1.62 Å, while the upper limit was chosen to exclude the overlap with longer distance correlations; the first of which are the shortest cation–cation distances (Si-Si, Si-Na, and Na-Na, for example, it is well known that the Si–Si distance is typically ∼3.12 Å⁸⁹). The same fit range was also used for fitting the modifier–oxygen and O–O distributions for the NaBa and NaCa glass systems, as described below. The positions and areas of the O–O peaks were fixed at the calculated values (given in Table 3), but the widths of these peaks were allowed to vary. Initial subtraction of the simulated O–O peaks from the measured correlation functions showed that the distribution of Na–O bond lengths is asymmetric but can be represented satisfactorily by the sum of two symmetric peaks. None of the parameters for the Na–O peaks were constrained in the fitting. The value obtained for the width of the (O–O)_Si peaks is ∼0.093 Å; this is slightly larger than for pure SiO₂ glass (for which typical values are 0.090–0.091 Å⁸¹) due to the increased static disorder arising from the presence of both BO and NBO in the SiO₄ tetrahedra. The total valence of the bonds to a sodium atom was calculated using the appropriate bond valence parameter,^85,87 and the values obtained (see Table 4) are within an acceptable deviation from the ideal value of 1 (the formal valence of Na⁺), indicating that the bond lengths and coordination numbers obtained are reasonable. The total Na–O coordination numbers (4.7 and 4.8) are similar to the value of 5 found in both crystalline α-Na₂SiO₃⁹⁰ and α-Na₂Si₂O₅,⁹¹ the ambient crystal phases with closest compositions to these glasses. It is also interesting to compare with a molecular dynamics simulation of a 30Na₂O·70SiO₂ glass with a screened shell model potential reported by Tilocca et al.;⁹² an asymmetric nearest-neighbor Na–O peak was predicted with a r_NaO = 2.33 Å and a Na–O coordination number of 5.33, taking 3.1 Å as the cutoff distance.

Figure 8.

Correlation function, T(r), for (a) SO₃-free and (b) SO₃-doped sodium silicate glass (thin black line), together with the fitted Na–O (blue lines) and O–O (red lines) peaks. The thick black line shows the fitted function, which is the sum of all the fitted peaks, and the thick blue line shows the total fitted Na–O distribution.

Table 4. Parameters from Fitting the Modifier–Oxygen and O–O Peaks in T(r)^a.

parameters	NaSi	NaSiS	NaBaSi	NaBaSiS	NaCaSi	NaCaSiS
uOO(Si) (Å)	0.093(1)	0.0934(3)	0.0900(2)	0.091(1)	0.0897(7)	0.091(1)
uOO(S) (Å)		0.056(3)		0.074(3)		0.074b
M	Na	Na	Ba	Ba	Ca	Ca
rMO,1 (Å)	2.297(7)	2.278(3)	2.737(4)	2.695(7)	2.376(3)	2.363(2)
uMO,1 (Å)	0.116(8)	0.096(9)	0.177(4)	0.14(1)	0.130(3)	0.119(3)
nMO,1	2.2(7)	1.6(3)	6.1(1)	5.6(2)	6.1(1)	5.59(9)
rMO,2 (Å)	2.59(6)	2.52(3)
uMO,2 (Å)	0.20(6)	0.21(2)
nMO,2	2.5(9)	3.2(4)
ΣnMO	4.7	4.8	6.1	5.6	6.1	5.59
vMO,1	0.57	0.44	1.81	1.89	2.01	1.92
vMO,2	0.30	0.45
ΣvMO	0.87	0.90	1.81	1.89	2.01	1.92

^aSee table footnote of Table 3 for the description of fit parameters. The valence for each modifier–oxygen peak, v_jk, is calculated using bond valence parameters.^85,87 Statistical errors from the fits are given in parentheses.

^bThe width of the (O–O)_S peak was fixed at a value of 0.074 Å.

The correlation functions for the barium- and calcium-containing glass samples were fitted (see Figures 9 and 10) using a method based on that for the sodium silicate glass samples. The distribution of Na-O distances in each of the barium-containing and calcium-containing samples was assumed to be the same as in the corresponding sodium silicate sample (but note that the resultant Na–O contribution to T(r) is reduced in magnitude due to the lower Na₂O content, see Table 1). Our assumption of the same distribution of Na–O distances occurring in the sodium–calcium silicate and sodium–barium silicate glasses as in the sodium silicate glasses carries uncertainties, which are acknowledged. As summarized by Cormier et al.,⁹³ the literature for several alkali silicate, alkaline-earth silicate, and alkali/alkaline-earth silicate glasses indicates random mixing of cations for alkali silicate and alkaline-earth silicate glasses for which more than one modifier of the same type is present, for example, Na–K or Mg–Ca. However, the literature for alkali/alkaline-earth silicate glasses (e.g., Na–Ba or Na–Ca) indicated forms of cation ordering; the nature of which varied depending on the system. It has also been noted that, in some glasses, modifier–BO bonds can form. Lee and Stebbins⁹⁴ studied SiO₂–Na₂O–CaO glasses using 3Q MAS ¹⁷O NMR, showing nonrandom distributions of Na and Ca ions with preference for dissimilar pairs. Interestingly, they also observed interactions between bridging oxygens (BO) and the Na and Ca cations. Lee et al.⁹⁵ also observed cation ordering in SiO₂–Na₂O–BaO glasses, again using 3Q MAS ¹⁷O NMR. In these glasses, they observed a wide distribution of configurations for Na and Ba cations around non-bridging oxygens (NBO), forming Ba-NBO and Na-NBO as well as substantial intensity of mixed NBO peaks. They concluded that this indicated a preference for dissimilar pairs around NBO or a stronger preference for Ba-O-^[4]Si over Na-O-^[4]Si, and these results from their work and the literature revealed a hierarchy in the NBO preference for different network-modifying cations, resulting from competition between steric (ionic radius) and electrostatic (charge) cation effects. Our Raman and ND results for the sodium–calcium and sodium–barium glasses studied here are qualitatively consistent with these conclusions in that they show different levels of “competition” for stabilization of SO₄^2– groups (which are themselves associated with NBO’s) depending on modifier cations with Ba²⁺ more effectively (or preferentially) stabilizing SO₄^2– groups compared with Ca²⁺ when present in combination with Na⁺ in alkali/alkaline-earth silicate glasses. In the context of our ND results and fitting, it is acknowledged that average Na⁺ environments may not be identical in these different glasses, and this will be investigated further in a future publication.

Figure 9.

Correlation function, T(r), for (a) SO₃-free and (b) SO₃-doped sodium barium silicate glass (thin black line), together with the fitted Ba–O (blue lines) and O–O (red lines) peaks. The thick black line shows the fitted function, which is the sum of the individual peaks, and the thick green line shows the total modeled Na–O distribution (composed of two peaks).

Figure 10.

Correlation function, T(r), for (a) SO₃-free and (b) SO₃-doped sodium calcium silicate glass (thin black line), together with the fitted Ca–O (blue lines) and O–O (red lines) peaks. The thick black line shows the fitted function, which is the sum of the individual peaks, and the thick green line shows the total modeled Na–O distribution (composed of two peaks).

As was carried out for our sodium silicate glass samples, the positions and areas of the O–O peaks were fixed at the calculated values (given in Table 3). The widths of the O–O peaks were allowed to vary with the exception that the width of the (O–O)_S peak for the NaCaSiS sample was fixed at a value of 0.074 Å because this sample has a smaller SO₃ content (see Table 1), so this peak is very small. The Ba–O and Ca–O distributions appeared to be well described by a single symmetric peak, and the parameters obtained are given in Table 4. The valences of the bonds to each of these alkaline-earth ions were calculated, and the values obtained are acceptably close to the ideal value of 2, indicating that the bond lengths and coordination numbers obtained are reasonable. The coordination numbers for the barium-containing glasses are similar to the values for crystalline Na₂BaSi₂O₆,⁹⁶n_BaO = 7 and n_NaO = 5.5. Likewise, the coordination numbers for the calcium-containing glasses are similar to those for crystalline Na₂Ca₃Si₆O₁₆,⁹⁷n_CaO = 5.67 and n_NaO = 5.

For the sodium-containing samples, the modifier–oxygen distribution in T(r) overlaps significantly with the O–O peak(s), but is well-separated from the first peak (Si–O and S–O). However, for the lithium-containing samples, the Li–O distribution overlaps with the first peak as well as with the O–O peak(s), and thus the first peak needs to be taken into account when fitting the Li–O distribution. Furthermore, the Li–O distribution is negative (due to the negative scattering length of lithium), leading to the possibility of “inflation” whereby the fitted Li–O peak area can grow simultaneously with the area of an overlapping positive peak. Therefore, for fitting the Li–O distribution, the coordination numbers of the adjacent peaks were fixed. Figure 11 shows the fits performed to T(r) for the lithium-containing samples over the distance range of 1.11–2.76 Å, and the parameters obtained are given in Table 5.

Figure 11.

Correlation function, T(r), for (a) SO₃-free and (b) SO₃-doped lithium silicate glass (thin black line), together with the fitted S–O, Si–O (green lines), Li–O (blue lines), and O–O (red lines) peaks. The thick black line shows the fitted function, which is the sum of all the fitted peaks, and the thick blue line shows the total fitted Li–O distribution.

Table 5. Parameters from Fitting the Peaks in T(r) for the Lithium-Containing Samples^a.

parameters	LiSi	LiSiS
rSO (Å)		1.474*
uSO (Å)		0.044*
nSO		4.0*
rSiO (Å)	1.6242(3)	1.6239(3)
uSiO (Å)	0.0501(4)	0.0491(4)
nSiO	4.0*	4.0*
rLiO 1 (Å)	1.956(2)	1.951(2)
uLiO 1 (Å)	0.103(2)	0.099(2)
nLiO 1	3.31(6)	3.26(5)
vLiO 1	0.88	0.88
rLiO 2 (Å)	2.236(7)	2.222(6)
uLiO 2 (Å)	0.103†	0.099†
nLiO 2	1.33(5)	1.44
vLiO 2	0.17	0.19
ΣnLiO	4.64	4.69
ΣvLiO	1.05	1.06
r̅LiO (Å)	2.036	2.034
rOO(S) (Å)		2.407†
uOO(S) (Å)		0.074*
nOO(S)		0.364*
rOO(Si) (Å)	2.6523†	2.6518†
uOO(Si) (Å)	0.0885(5)	0.0880(5)
nOO(Si)	4.38*	3.98*

^aSee table footnote of Table 3 for the description of the fit parameters. r̅_LiO is the weighted mean of the two fitted Li–O distances. Fixed values are indicated by an asterisk, and bound values are indicated by a dagger (see text for details). The valence, v_LiO, for each Li–O peak is calculated using bond valence parameters.^85,87 Statistical errors from the fits are given in parentheses.

The S–O peak in T(r) for glass LiSiS is relatively small, and hence all of its parameters were fixed for fitting using values obtained previously. Also, the two O–O distances were bound to be equal to 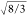times the fundamental distance (S–O or Si–O) in their respective tetrahedron. Similar to the Na–O distribution, the Li–O distribution was found to be asymmetric (see Figure 11) and well represented by the sum of two peaks with a larger Li–O coordination number for the shorter distance peak and a smaller coordination number at a longer distance. The total valence of the bonds to a lithium atom was calculated using the bond valence method,^85,87 and the values obtained (see Table 5) are close to the ideal value of 1, indicating that the bond lengths and coordination numbers obtained are reasonable. The total Li–O coordination number is consistently found to be larger than 4 and almost as large as the values (4.7 and 4.8) found for n_NaO in the sodium silicate samples. In crystal structures, the dominant Li–O coordination is tetrahedral with a mean bond length r̅_LiO of 1.96 Å, but nevertheless the octahedral coordination with r̅_LiO = 2.15 Å and even five-fold coordinated Li are known.⁹⁸ When compared with these values of r̅_LiO, the mean Li–O bond length found in the Li-containing glasses (see Table 5) is consistent with the coordination number being larger than 4 and less than 5. There is very little change in the Li–O coordination shell with SO₃ doping, and this seems to be different in the Na–O coordination shell, which shows evidence for SO₃ doping leading to a shift to longer Na–O bond lengths (see Table 4). There is less distinction between the lengths of Li-NBO and Li-BO bonds than there is for Na–O bonds (for example, see the Li–O bond lengths in crystalline Li₂Si₂O₅⁹⁹), and this may be the reason for the relative lack of change in the Li–O distribution.

4.4. Network Structure of SO₃-Doped Silicate Glass

The results presented above show consistently that SO₃ is incorporated in silicate glass in the form of SO₄^2– sulfate groups. A simple electrostatic bond strength (EBS) consideration of the structural role of an SO₄ group is instructive.^85,100 For a S⁶⁺ ion bonded to four oxygens, the EBS of each S–O bond is 6/4 = 1.5 (valence/coordination number). According to Pauling’s rule,^85,101 the sum of the strengths of the bonds to an oxygen must be exactly or nearly equal to the magnitude of its formal charge of two. This implies that an oxygen atom cannot act as a bridge (S–O–S) between two sulfur atoms. Furthermore, the EBS of an Si–O bond in a SiO₄ tetrahedron is 1 with the consequence that an oxygen atom also cannot act as a bridge (S–O–Si) between a sulfur atom and a silicon atom. On the other hand, the formal charge on a modifier ion (M⁺ or M²⁺) is smaller than that of silicon or sulfur, leading to smaller values for the EBS of M–O bonds of an order of 0.2–0.3. Thus, an oxygen atom in a S–O bond can readily be balanced by (say two) modifier ions, leading to an EBS sum of approximately 2 for the bonds to the oxygen. Therefore, it may be concluded that SO₄ groups in silicate glasses are directly bonded to only modifier ions and not to other SO₄ groups or SiO₄ tetrahedra. It may be that this avoidance of direct bonding to the silicate network is the reason why (to the best of our knowledge) there are no reports of crystal structures in systems such as SiO₂–Na₂O–SO₃. The inability of a sulfate group to bond directly to the silicate network provides a clear reason why SO₃ could not form a glass with glass former SiO₂ alone but is able to do so when the glass also includes a modifier.

The EBS of S–O bonds in SO₄ groups, 1.5, is unusually large for bonds in an oxide glass. In comparison, the bonds to glass former cations (e.g., Si–O bonds) typically have an EBS of approximately 1, while bonds to modifier cations (e.g., Na–O bonds) typically have an EBS that is considerably less than 1. It is thus reasonable that the widths of the S–O peaks in the neutron correlation functions (typically u_SO ≈ 0.044 Å, see Table 3) are smaller than the widths of the other peaks due to their greater strength. A more extreme example of this behavior is found in cyanides for which the neutron correlation function has a peak for the C≡N triple bond with a very small width of u_CN ≈ 0.03 Å.¹⁰²

The avoidance of direct bonding of SO₄^2– groups to the silicate network has consequences for the connectivity of the silicate network. When a unit of SO₃ is incorporated in the glass, a sulfur atom must bond to one additional oxygen atom so that it can form a SO₄ group. Figure 12 shows how this additional oxygen may be obtained; the incorporation of one unit of SO₃ in the glass leads to the conversion of two NBOs to one BO. Thus, the doping of a silicate glass with SO₃ leads to a repolymerization of the silicate network itself in which there is a relative increase in the number of BOs in the silicate network (and a decrease in the number of NBOs). This is consistent with Morizet et al.⁷¹ who reached a similar conclusion on the basis of an NMR study of the effect of sulfur on the structure of silicate melts.

Figure 12.

Schematic showing the repolymerizing effect of SO₃ incorporation on a silicate network. (a) Fragment of the silicate network containing two units of Na₂O, showing the connectivity of the bridging (O_b) and non-bridging (O_nb) oxygen atoms. The incorporation of each unit of Na₂O converts one O_b to two O_nb. (b) Same fragment of the silicate network after the addition of one unit of SO₃. The sulfur atom is at the center of a SO₄ group, directly bonded only to sodium atoms. The formation of the SO₄ group leads to the conversion of two O_nb to one O_b. Note that these diagrams are intended to show only the connectivity of the atoms but not to convey information about the distances between atoms.

In a silicate glass, a BO has six oxygen neighbors, whereas an NBO has three. Thus it may appear counterintuitive that the predicted (O–O)_Si coordination number is smaller for SO₃-doped glasses (see Table 3). Furthermore, the average O–Si coordination number, n_OSi, is smaller for SO₃-doped glasses, and again this may not seem consistent with the relative growth in the number of BOs. The explanation for this behavior is simply found by considering the oxygen atoms, O_S, in the SO₄ groups, which are not actually part of the silicate network (oxygen atoms in a network glass that are not part of the network are sometimes referred to as free oxygen,¹⁰³ but this is arguably less appropriate, especially in this case because S–O bonds are stronger than Si–O bonds; a more appropriate term may be non-network oxygen¹⁰⁴). The oxygen coordination numbers (such as n_OSi and n_OO(Si)) are averages over all oxygen sites in the glass, including the O_S sites, which do not have any silicon or (O–O)_Si neighbors, and this is why the average value for these coordination numbers is reduced when the glass is doped with SO₃.

The correlation function fits for the sodium-containing samples show some evidence that SO₃ doping leads to changes in the form of the distribution of Na–O bond lengths with a reduction in the fitted short-bond coordination number and an increase in the fitted long-bond coordination number (Table 4). It is already known that the distribution of Na–O bonds in silicate glasses is asymmetric⁸² with a long distance tail as observed in this work (Figure 8), and it has been proposed that the short Na–O bonds in this distribution involve NBOs, while the long Na–O bonds involve BOs.⁸² It is thus likely that the change on doping of the two Na–O coordination numbers is due to the growth in the proportion of BOs (and decline in the proportion of NBOs) in the silicate network that occurs when SO₃ is incorporated into the glass. Note that the Na–O distances in crystalline III-Na₂SO₄ are typically ∼2.4 Å; this distance is intermediate between the two fitted Na–O peaks (Table 4), and so, it is unlikely that the lengths of Na–O bonds in Na–O–S linkages have a strong influence on the apparent shift of the Na–O distribution toward the peak at ∼2.5 Å and away from the peak at ∼2.3 Å.

It is worth noting that, in all cases studied, doping with SO₃ leads to a narrowing of the modifier–oxygen peak, which is apparent as a reduction in the value of u_MO where M is Na, Ca, Ba, and Li (see Tables 4 and 5). This may be due to repolymerization of the silicate network; the addition of SO₃ converts some NBOs to BOs, and as a consequence, the network is more heavily dominated by BOs, so there is less variety in the types of oxygen bonded to the M atoms.

Figure 13 shows a two-dimensional representation of the structure of a SO₃-doped sodium silicate glass based on the results from this study. A sulfate group is surrounded by a region that contains only sodium and oxygen, and this region is then surrounded by the silicate network. The local structure around the sulfate group may be similar in character to the structure of sodium sulfate. The need for a “shell” of a modifier around each individual sulfate group may be a contributing reason why the solubility of SO₃ in silicate glasses can be limited.

Figure 13.

Two-dimensional representation of the proposed structure of a SO₃-doped sodium silicate glass. The spheres represent atoms (Na is green, O is red, S is yellow, and Si is blue). The continuous lines represent Si–O and S–O bonds, while the dashed lines represent Na–O bonds. A sulfate group is at the center of the picture, surrounded by a sodium oxide region (shaded green) and then a silicate region (shaded blue). The connectivity of the cations has been reduced to facilitate representation in only two dimensions.

The Raman shift of the υ₁ S–O stretch mode in the naturally occurring mixed-cation compound, Na₂Ca(SO₄)₂ (glauberite), is 1002 cm^–1,⁷⁴ and this value is closer to the shift for crystalline Na₂SO₄ and less close to the shift for crystalline CaSO₄ (see Table 2). In the crystal structure of Na₂Ca(SO₄)₂,¹⁰⁵ the oxygen atoms in the SO₄ group are bonded to about twice as many Na ions as Ca ions. (The exact ratio of O-M coordination numbers depends on what range in interatomic distances is defined to be bonded, but nevertheless, as the chemical composition suggests, oxygen is consistently bonded to ∼2 times as many Na as Ca.) Thus, the υ₁ Raman shift depends closely on the environment of the oxygens in the SO₄ groups. For the NaCaSiS glass, the υ₁ Raman shift is much closer to that of Na₂SO₄ than either Ca₂SO₄ or Na₂Ca (SO₄)₂, indicating a strong preference for the oxygen atoms in SO₄ groups to form Na–O–S linkages. On the other hand, for the NaBaSiS glass, the υ₁ Raman shift is almost exactly the same as for BaSO₄, indicating a strong preference for the formation of Ba–O–S linkages.

5. Conclusions

Sulfate-doped and sulfate-free Na₂O-SiO₂, Li₂O-SiO₂, Na₂O-CaO-SiO₂, and Na₂O-BaO-SiO₂ glasses were prepared and analyzed using neutron diffraction, Raman spectroscopy, and XRF. Comparison of the υ₁ S–O stretching modes for the SO₃-doped ternary silicate glasses Na₂O–CaO–SiO₂–SO₃ and Na₂O–BaO–SiO₂–SO₃ and crystalline Na₂SO₄, BaSO₄, CaSO₄, and CaNa₂(SO₄)₂ shows that the sulfate ions are stabilized either entirely or partially by Ba²⁺ ions in glass Na₂O–BaO–SiO₂–SO₃, whereas in Na₂O–CaO–SiO₂–SO₃ glass, Na⁺ ions predominantly act as charge compensators for the SO₄^2– anions. The influence of the alkaline-earth modifier cation on sulfate solubility, however, is not yet fully understood. The S–O and (O–O)_S distances and coordination numbers were obtained from the neutron correlation function by both direct fitting and a difference method. The results of this analysis and the Raman shift of the symmetric S–O stretch mode observed in the Raman spectra indicate that the sulfur in these glasses is in the form of sulfate SO₄^2– groups. Thus, sulfur exists only as S⁶⁺ in these glasses. A consideration of the bonding shows that individual sulfate groups are surrounded by a shell of modifier cations, making up local units that may be structurally similar to the corresponding crystalline alkaline/alkaline-earth sulfates. The sulfate groups are not directly bonded to the silicate network or to each other, and the oxygens in the sulfate groups are non-network oxygens. The addition of SO₃ to the glasses causes a repolymerization of the silicate network with the conversion of non-bridging oxygens to bridging oxygens. A fitting method was used to determine the distributions of modifier–oxygen bond lengths in the glasses. A clear asymmetry was observed for the Li–O and Na–O distributions, but no evidence of Ca–O or Ba–O asymmetry was found. The addition of SO₃ was observed to cause a change in the form of the Na–O distribution, consistent with repolymerization. No evidence of a change in the form of the Li–O distribution was found with a total Li–O coordination number consistently in excess of 4.

The authors declare no competing financial interest.