Methodology of emergency medical logistics for public health emergencies

Highlights

• •This work addresses the issue of public health emergencies.
• •The proposed model characterizes the differences in survivor infection conditions.
• •Extended model considers spatial interaction relationships among epidemic areas.
• •This work integrates survivor psychology with medical relief emergency logistics.

Abstract

This work presents a novel model of emergency medical logistics for quick response to public health emergencies. The proposed methodology consists of two recursive mechanisms: (1) the time-varying forecasting of medical relief demand and (2) relief distribution. The medical demand associated with each epidemic area is forecast according to a modified susceptible-exposed-infected-recovered model. A linear programming approach is then applied to facilitate distribution decision-making. The physical and psychological fragility of affected people are discussed. Numerical studies are conducted. Results show that the consideration of survivor psychology significantly reduces the psychological fragility of affected people, but it barely influences physical fragility.

1. Introduction

A public health emergency is defined by the U.S. National Disaster Medical System as the emergency need for healthcare or medical services in response to a disaster, the significant outbreak of an infectious disease, bioterrorist attack, and other significant or catastrophic events. Examples of public health emergencies include the outbreak of H1N1 influenza, of the Ebola virus disease in Congo, of severe acute respiratory syndrome (SARS), and of the Marburg hemorrhagic fever in Angola, as well as widespread dysentery, cholera, measles, encephalitis B, and other diseases following significant disasters.

In addition to health threats and economic losses, public health emergencies also result in psychological suffering, such as feelings of helplessness, sorrow, and panic. Studies conducted on the worldwide effects of the SARS outbreak in 2003 suggest that the fear of SARS is a more severe pandemic than the disease itself (Cheng and Tang, 2004).

Most emergencies cannot be avoided, but their influence can be significantly reduced by an efficient framework of emergency medical logistics. Medical logistics that direct responses to public health emergencies are vital. However, the field of emergency logistics faces many challenges that have not been addressed effectively.

Emergency medical logistics has three characteristics that increase the complexity and difficulty of solving logistical problems in contrast to general emergency logistics. First, limited demand-related information, such as the severity of injuries and the number of casualties, challenges distribution-related decision making. In particular, the incubation period results in a time delay in demand (Li et al., 1999, Zhang and Ma, 2003). Second, a disease can spread quickly from one area to another and can even become a large-scale epidemic. Infection, recovery, and mortality rates typically vary across areas because of different physical conditions of individuals, as well as habits, customs and medical services provided by the hospitals in each area (Brauer and van den Driessche, 2001, Capaldi et al., 2012). Third, the substitutability of medical relief is imperfect, unlike other forms of relief such as food. A specific medicine cannot be perfectly substituted by another medicine (Mete and Zabinsky, 2010).

The available literature inadequately addresses emergency medical logistics. Thus, the current work proposes a model of emergency logistics for rapid response to public health emergencies. In particular, a modified epidemic susceptible-exposed-infected-recovered (SEIR) model is developed to forecast time-varying demand as well as a linear programming model that optimizes decisions regarding the distribution of emergency medical reliefs.

Specifically, this work contributes to the decision analysis of logistical responses to public health emergencies in the following ways:

• (1)This interdisciplinary study contributes to the fields of public health and emergency logistics. Emergency medical logistics differs from general emergency logistics in that the former involves many challenges that increase the complexity and difficulty of solving logistical problems.
• (2)This work applies a novel methodology to forecast the demand of multiple urgent medical reliefs and to distribute these reliefs to multiple epidemic areas. The physical and psychological situations of those affected are considered. The modified SEIR model contributes to forecasting by considering not only physical factors, such as the differences in the infection conditions of survivors and the spatial interaction relationships among epidemic areas, but also the psychological demand of exposed and undiagnosed individuals. In the distribution model, psychological fragility is formulated and discussed in detail, unlike in previous studies. The relationship between emergency medical logistics and the psychological effects on affected people is highlighted as well.
• (3)This work conducts a case study using real data and a continuation study with experimental data to demonstrate the applicability of the three proposed models. These models are then compared. Observations are provided and their implements are discussed on this basis.

The remainder of this paper is organized as follows. Section 2 reviews related studies. Section 3 presents the proposed basic methodology, including time-varying demand forecasting according to the epidemic diffusion rule and the distribution of medical reliefs. Section 4 introduces two extended models. Section 5 presents a numerical study and discusses the analytical results. Section 6 provides managerial insights. Finally, Section 7 concludes and discusses the directions for future work.

2. Literature review

Although some studies try to combine medical rescue with emergency logistics (Sheu and Pan, 2014), only a few studies exist on emergency medical logistics for public health emergencies despite its importance and particularity. Only bioterror response logistics, a special case in emergency medical logistics, has been discussed (Kaplan et al., 2003, Craft et al., 2005, Liu and Zhao, 2011). These studies have aided in understanding the problems of evaluating existing proposals for logistics, distributing antibiotics, and providing hospital care after a bioterror attack. Methods such as atmospheric release models, dose–response models, disease progression models and epidemic diffusion models have been used. However, these studies have made limited contribution to medical logistics for public health emergencies. First, a terrorist attack has only two most feared biological agents, namely, smallpox and anthrax (Craft et al., 2005), but other public health emergencies may be aroused by other diseases that are less understood. Second, a terrorist attack focuses on only one or several cities, whereas other public health emergencies may occur in large areas at the same time. Except for the distinctiveness of bioterrorism, these studies ignored the differences in the infection conditions and survivor psychology. In practice, vulnerable groups, such as children and the elderly, face different infection, recovery, and mortality rates. Moreover, the psychological suffering of affected people in a bioterror attack is usually more serious than physical pain.

In addition, this work reviews the related literature by first focusing on demand forecasting and then discussing the approaches to logistics distribution for an emergency and their objective functions.

Typically, demand forecasting is studied based on general supply chain management in business logistics but limited to emergency logistics. The approaches adopted in business logistics forecast are based on historical values, which can be collected easily during business processes. By contrast, emergency medical logistics lacks historical data. Gaur et al. (2007) discussed demand uncertainty in business logistics, but demand history was unavailable. Based on the characteristics of the predictions of emergency resource demand, Sheu (2010) presented a dynamic model of relief-demand management for emergency logistics operations under imperfect information conditions in large natural disasters. Mete and Zabinsky (2010) proposed forecasting and optimization approaches to problems on medical storage and distribution for a wide variety of disaster types and magnitudes. Hasan and Ukkusuri (2011) developed a novel model to understand the cascade of the warning information flow in social networks during the hurricane evacuations. Fajardo and Gardner (2013) used a bi-linear integer program to model diseases spreading through direct human interaction on a social-contact network. Ekici et al. (2014) created an interesting approach to demand forecasting based on the characteristics of disease epidemics. They also developed a SEIR model with a spatial component among communities, age-based structure, heterogeneous mixing, and night/day differentiation to plan food distribution. Few studies have forecast demand in this way (Wang and Wang, 2008, Liu and Zhao, 2011), even though scholars have conducted much research on preventing and controlling epidemics, as well as identifying their characteristics and models.

The mathematical models of epidemic diffusion rules (Brauer and van den Driessche, 2001, Capaldi et al., 2012) can be used to facilitate demand forecasting for public health emergencies. Most models, including the susceptible-infectious, susceptible-infectious-removed, susceptible-infectious-susceptible, susceptible-infectious-removed-susceptible, susceptible-exposed-infectious, and SEIR model, are suitable for studying the general laws of all epidemics. In particular, SEIR model, which considers incubation period, has drawn considerable attention. In the real world, there is some duration between the time that a person is infected and the time that he/she starts infecting others. SEIR model divided the people in epidemic areas into four classes: susceptible, exposed, infectious and recovered. The model describes the transition among these classes with differential equations. Basic reproduction number is an important concept in epidemic model. It determines the global dynamics and the outcome of disease. If it is less than or equal to 1, the disease-free equilibrium is globally stable and the disease always dies out; otherwise, there exists a unique positive endemic equilibrium and the disease persists at an endemic equilibrium state if it initially exists (Hethcote and Tudor, 1980, Greenhalgh, 1992, Li and Muldowney, 1995, Li et al., 1999, Zhang and Ma, 2003).

Based on these standard models, two main types of exploration are used to build multi-class models, but neither is perfectly appropriate for general medical emergency logistics in this work. The first type of exploration covers studies that consider an ecosystem where two disease-affected populations thrive and epidemics can spread among these populations (Han et al., 2001, Chaudhuri et al., 2012). In these studies, the two populations compete for survival resource or have a predator–prey relation. The second type involves age-structured models (Cha et al., 1998, Li and Song, 2011) that are unable to describe the vulnerable people because they can be distinguished not only by age but also by other characteristics, such as gender. Therefore, demand forecasting based on these models, including standard models and previous multi-class models, may forecast demand that differs markedly from the real demand of emergency logistics.

Additionally, considerable effort has been made to optimize logistics under emergencies. Özdamar et al. (2004) constructed a distribution optimization model for a situation in which the supply is limited, current demand is known, future demand can be predicted, and commands on vehicle allocation are composed of a series of breakpoints. Adıvar and Mert (2010) proposed an international relief-planning model that can handle uncertain information while maximizing the credibility of international agencies in the most cost-efficient way. Ben-Tal et al. (2011) applied robust optimization for dynamic evacuation traffic-flow problems with time-dependent uncertainty on demand. Liu and Ye (2014) proposed a sequential approach for humanitarian logistics in natural disasters based on the Bayesian group information updates. Allahviranloo et al. (2014) proposed three new formulations to account for different optimization strategies under uncertain demand or utility level: reliable, robust, and fuzzy selective vehicle routing problems. And they developed three parallel genetic algorithms and a classic genetic algorithm. Stochastic programming is also an appropriate tool for making emergency logistics decisions and has been applied to different cases of emergency management (Barbaroso and Arda, 2004, Beraldi et al., 2004, Chang et al., 2007, Zhan et al., 2014). Han et al. (2013) present a novel approach to consider a vehicle routing problem with uncertain travel times in which a penalty is incurred for each vehicle that exceeds a given time limit.

Existing models can be divided based on their objective characterization. They can be categorized into models that (1) minimize the distribution time or shipping distance (Zografos et al., 2002, Yan and Shih, 2009), (2) minimize cost of logistics (Ben-Tal et al., 2011), (3) minimize the number of wounded and dead people (Fiedrich et al., 2000, Yi and Kumar, 2007), and (4) maximize level of satisfaction of the relief demand (Özdamar et al., 2004, Sheu, 2007). Some studies developed multi-objective models. Tzeng et al. (2007) constructed a relief-distribution model by multi-objective programming to design relief delivery systems for a real case. As a part of the entire disaster salvaging system, sufficiently accurate information is needed before model application. Vitoriano et al. (2009) presented a Humanitarian Aid Distribution System focusing on the transportation problem to distribute humanitarian aid to affected people after a disaster in a developing country. Vitoriano et al. (2011) proposed a new approach to solve humanitarian aid distribution problems, by constructing a goal programming model based upon cost, time, equity, priority, reliability and security. Ortuño et al. (2011) presented a novel lexicographical goal programming model with a first level of priority with the goal of delivering the planned goods in the operation verifying all the hard constraints or to deliver the largest possible quantity of commodity. Then the model concerned other targets in a second level of priority.

Despite remarkable advances in emergency logistics modeling, the relationship between relief distribution and psychological utility or psychological cost for those affected has barely been assessed or formulated, although characterizing this relationship may improve the rationality of models. Disasters have negative psychological effects on affected people and can even manifest as a major depressive episode, acute stress disorder or post-traumatic stress disorder. Hu and Sheu (2013) developed a multi-objective linear programming model to minimize total reverse logistical costs, corresponding environmental and operational risks, and psychological trauma experienced by local residents while they waited for medical treatment and removal of debris. Rooted in survival psychology and cognition theories, Sheu (2014) proposes a emergency logistics operational model that aims at disaster relief-service distribution to maximize survivor resilience. In Hu et al. (2014), a mixed-integer linear program is constructed for multi-step evacuation and temporary resettlement under minimization of panic-induced psychological penalty cost, psychological intervention cost, and costs associated with transportation and building shelters. Negative psychological effects of widespread disease epidemics are usually more significant. For the public, the psychological effect of an epidemic may be greater than the danger to physical health (Cheng and Tang, 2004). Maunder et al. (2003) examined the psychological and the occupational effects of SARS in a large hospital in Canada in 2003. Their study showed that patients with SARS reported fear, loneliness, boredom and anger and worried about the adverse effects of quarantine and their contagiousness on family members and friends. The patients experienced anxiety about fever and the effects of insomnia. Healthy people were also adversely affected by the fear of contagion and infecting their family, friends, and colleagues. Other studies on SARS have reported similar findings (Wang and Luo, 2003, Cheng and Cheung, 2005, Leung et al., 2005). These studies have identified approaches that can alleviate psychological suffering, such as symmetric information, on-time treatment, effective prophylactic methods, and social support. Most approaches have been considered part of medical logistics.

3. Model formulation

This section presents the proposed methodology. A modified SEIR model is developed based on a specification of an emergency medical relief system, including the sequence of operational procedures and basic assumptions, to forecast time-varying demand. The final part of this section presents the model for medical relief distribution.

3.1. System specification

The hypothetical network of emergency medical logistics is a specific two-layer supply chain that involves (1) local Emergency Medical Reserve Centers (EMRCs) that serve as emergency medical logistics hubs, and (2) medical demand areas, namely epidemic areas. EMRCs gather medical reliefs and distribute them appropriately to epidemic areas.

The government decides whether or not to issue an emergency medical response shortly after an infectious disease has established itself. EMRCs then initiate a mechanism to forecast time-varying medical relief demand by collecting and estimating epidemic characteristics. The mechanism of medical relief distribution is then triggered based on updated information. Fig. 1 lists the sequence of the operation.

Fig. 1.

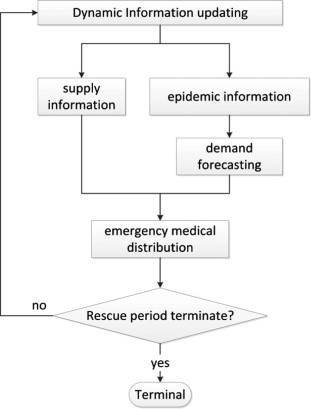
Sequence of operational procedures in emergency medical logistics.

This figure presents the recurrent calculation time step in emergency medical logistics. Supply and epidemic information (e.g., mortality, recovery, exposure, and infection rates) is updated at the beginning of each step.

Five basic assumptions are made to facilitate model formulation:

• (1)The number of and geographic information on epidemic areas are available, and the location of EMRCs is known because they have been established before emergencies.
• (2)The corresponding socioeconomic statistics (e.g., population size, population composition, and natural mortality and birth rates) are determined for each epidemic area. Such data can generally be obtained from government databases.
• (3)Emergency medical suppliers are known. The number and the type of available medical suppliers are identified at the beginning of each time step.
• (4)Different medical reliefs can be loaded on a vehicle that serves affected areas. Correspondingly, a vehicle is allowed to load multiple medical reliefs for any distribution mission.
• (5)Recovered individuals acquire permanent immunity.

On the basis of these assumptions, Sections 3.2, 3.3 present a demand forecasting model and a distribution model, respectively. Table 1 lists the notations used:

Table 1.

Notations.

A	A set of epidemic areas, A = {a1, a2, … , aJ}
B	A set of EMRCs, B = {b1, b2, … , bI}
M	A set of medical reliefs, M = Mp + Mt. Mp and Mt are sets of prophylactic and treatment reliefs, respectively. Mp = {m1, m2, … , ml}, Mt = {$m_{l+1}$, ml+2, … , ml+k}
$Q_{\mathit{it}}^p$	Available amount of relief p in EMRC i in time period t
$W_{\mathit{it}}$	Available transportation capacity in EMRC i in time period t
Ct	Maximum budget in time period t
$c_{\mathit{ijt}}^p$	Unit distribution cost of relief p from EMRC i to area j in time period t
${\theta }^p$	Demand of medical relief p needed per unit time per demander
${\alpha }^p$	Mortality increase caused by unit dissatisfaction of medical relief $p\text{,}p\in \mathit{Mt}$
${\beta }^p$	Infection rate increase caused by unit dissatisfaction of medical relief $p\text{,}p\in \mathit{Mp}$
${\alpha }_M$	The highest mortality rate that can be withstood
${\beta }_M$	The highest infection rate that can be withstood
$S_j^c(t)\text{,}{S}_j^v\left(t\right)$	Numbers of common and vulnerable susceptible people in area j at moment t
$E_j^c\left(t\right)\text{,}{E}_j^v\left(t\right)$	Numbers of common and vulnerable exposed people in area j at moment t
$I_j^c\left(t\right)\text{,}{I}_j^v\left(t\right)$	Numbers of common and vulnerable infectious people in area j at moment t
$R_j^c\left(t\right)\text{,}{R}_j^v\left(t\right)$	Numbers of common and vulnerable recovered people in area j at moment t
$S_{\mathit{jt}}^c\text{,}{S}_{\mathit{jt}}^v$	The approximate average numbers of common and vulnerable susceptible people in area j in time period t
$E_{\mathit{jt}}^c\text{,}{E}_{\mathit{jt}}^v$	The approximate average numbers of common and vulnerable exposed people in area j in time period t
$I_{\mathit{jt}}^c\text{,}{I}_{\mathit{jt}}^v$	The approximate average numbers of common and vulnerable infectious people in area j in time period t
$A_j^c\text{,}{A}_j^v$	Constant net input of common and vulnerable people to area j
${\beta }_j^c\text{,}{\beta }_j^v$	Common and vulnerable infection rate in area j
${\delta }_j$	Contact coefficient in area j
ε	Exposure rate (the rate at which exposed individuals become infectious)
${\gamma }_j^c\text{,}{\gamma }_j^v$	Common and vulnerable recovery rate in area j
${\mu }_j$	Diagnosis rate in area j
$d_j^c\text{,}{d}_j^v$	Natural mortality rate of common and vulnerable people in area j
${\alpha }_j^c\text{,}{\alpha }_j^v$	Disease mortality rate of common and vulnerable people in area j
$D_{\mathit{jt}}^p$	Demand for medical relief p in area j in time period t
${\mathit{Inv}}_{\mathit{jt}}^p$	The inventory of relief p in area j at the beginning of time period t
$x_{\mathit{ijt}}^p$	The amount of medical relief p sent from EMRC i to area j in time period t

3.2. Medical demand forecasting model

This mechanism forecasts the time-varying emergency medical demand of each affected area based on epidemic diffusion rules. On the basis of previous models, this study constructs a modified SEIR epidemic diffusion model that accommodates the differences between vulnerable and non-vulnerable or common groups to enhance forecast accuracy given that vulnerable groups usually report different infection, recovery, and mortality rates. The SEIR model is considered because it reflects the practical phenomena observed in incubation periods.

Fig. 2 shows the relationship and transition among different groups in a specific area.

Fig. 2.

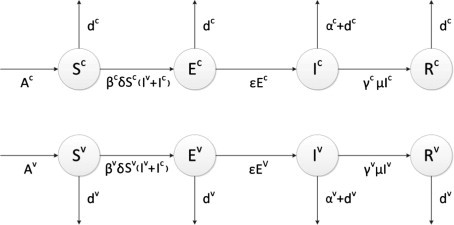
Modified SEIR model.

where S, E, I, and R denote the number of susceptible, exposed, infectious, and recovered people in an area, respectively. Superscripts c and v are the common and the vulnerable groups, respectively. $S^c$ and $S^v$ represent those who are susceptible to infection. $E^c$ and $E^v$ correspond to those who are subject to incubation periods (or latent periods). The incubation period is the time interval between exposure to a disease and the manifestation of initial signs or symptoms. An individual in this period has been infected but is not yet infectious himself/herself. $I^c$ and $I^v$ represent those who are infectious. $R^c$ and $R^v$ denote those who are cured and have permanent immunity. Generally, $\mu >0$, $\delta >0$, ε  > 0, $A^c⩾0$, $A^v⩾0$ and $d^v>d^c>0\text{,}{\beta }^v>{\beta }^c>0\text{,}{\alpha }^v>{\alpha }^c>0\text{,}{\gamma }^c>{\gamma }^v>0$. These coefficients may vary with the increase in knowledge regarding an epidemic disease. For instance, diagnosis rate may increase and mortality rate may decrease as doctors amass knowledge.

The modified SEIR model in this study is formulated as follows:

$$\frac{{\mathit{dS}}_j^c(t)}{\mathit{dt}}=A_j^c-d_j^c{S}_j^c\left(t\right)-{\beta }_j^c{\delta }_j{S}_j^c\left(t\right)\left(I_j^c\left(t\right)+I_j^v\left(t\right)\right)$$ (1)

$$\frac{{\mathit{dS}}_j^v(t)}{\mathit{dt}}=A_j^v-d_j^v{S}_j^v\left(t\right)-{\beta }_j^v{\delta }_j{S}_j^v\left(t\right)\left(I_j^c\left(t\right)+I_j^v\left(t\right)\right)$$ (2)

$$\frac{{\mathit{dE}}_j^c(t)}{\mathit{dt}}={\beta }_j^c{\delta }_j{S}_j^c\left(t\right)\left(I_j^c\left(t\right)+I_j^v\left(t\right)\right)-\epsilon E_j^c\left(t\right)-d_j^c{E}_j^c\left(t\right)$$ (3)

$$\frac{{\mathit{dE}}_j^v(t)}{\mathit{dt}}={\beta }_j^v{\delta }_j{S}_j^v(t)\left(I_j^c\left(t\right)+I_j^v\left(t\right)\right)-\epsilon E_j^v(t)-d_j^v{E}_j^v(t)$$ (4)

$$\frac{{\mathit{dI}}_j^c(t)}{\mathit{dt}}=\epsilon E_j^c\left(t\right)-\left({\alpha }_j^c+d_j^c\right)I_j^c\left(t\right)-{\gamma }_j^c{\mu }_j{I}_j^c\left(t\right)$$ (5)

$$\frac{{\mathit{dI}}_j^v(t)}{\mathit{dt}}=\epsilon E_j^v\left(t\right)-\left({\alpha }_j^v+d_j^v\right)I_j^v\left(t\right)-{\gamma }_j^v{\mu }_j{I}_j^v\left(t\right)$$ (6)

$$\frac{{\mathit{dR}}_j^c(t)}{\mathit{dt}}={\gamma }_j^c{\mu }_j{I}_j^c\left(t\right)-d_j^c{R}_j^c\left(t\right)$$ (7)

$$\frac{{\mathit{dR}}_j^v(t)}{\mathit{dt}}={\gamma }_j^v{\mu }_j{I}_j^v(t)-d_j^v{R}_j^v(t)$$ (8)

Eqs. (1), (2) describe how the number of susceptible people varies in epidemic area j. This number increases because of net input (such as susceptible input from non-epidemic areas and newborns) and decreases as susceptible people die naturally or are exposed. Eqs. (3), (4) indicate the transition from susceptible to exposed groups and from exposed to infectious groups. Eqs. (5), (6) describe the transition from exposed to infectious groups and from infectious to recovered groups. Eqs. (7), (8) indicate how the number of recovered people varies.

The modified SEIR model operates under continuous time forecasting, and distribution decisions are made in discrete time periods (as explained in Section 3.1 and depicted in Fig. 1). Therefore, this study uses aggregation to approximate medical demand further. t represents the tth time period, and the length of each time period depends on specific emergencies. Time periods usually range from 4 h to 6 h for an anthrax attack and one to several days for an influenza outbreak.

In this study, two types of emergency medical reliefs are considered: prophylactic reliefs for susceptible people to reduce the infection rate (denoted as Mp) and treatment reliefs for infectious people to lower the mortality rate (denoted as Mt).

Notably, this work forecasts demand based on both the physical and psychological effects of reliefs. Demand for prophylactic reliefs is strongly correlated with the numbers of susceptible, exposed, and undiagnosed people. Prophylactic medicines do not affect exposed and undiagnosed people physically, but demand remains because susceptible, exposed, and infectious but undiagnosed individuals are impossible to distinguish. Demand for treatment reliefs is strongly correlated with the number of infectious and diagnosed individuals. Medical reliefs are consumed continuously; therefore, demand for both types is related to the length of each time period. Thus, the following demand forecasting model is established:

$$D_{\mathit{jt}}^p=\left\{\begin{array}{cc}{\theta }^p{\int }_{t_0}^{t_0+L}\left[S_j\left(t\right)+E_j\left(t\right)+(1-{\mu }_j)I_j\left(t\right)\right]\mathit{dt}-{\mathit{Inv}}_{\mathit{jt}}^p\text{,}\hfill & p\in \mathit{Mp}\hfill \\ {\theta }^p{\int }_{t_0}^{t_0+L}{\mu }_j{I}_j\left(t\right)\mathit{dt}-{\mathit{Inv}}_{\mathit{jt}}^p\text{,}\hfill & p\in \mathit{Mt}\hfill \end{array}\right)$$ (9)

where $S_j\left(t\right)=S_j^c\left(t\right)+S_j^v\left(t\right)\text{;}{E}_j\left(t\right)=E_j^c\left(t\right)+E_j^v\left(t\right)\text{;}{I}_j\left(t\right)=I_j^c(t)+I_j^v(t)\text{;}{t}_0$ is the beginning moment of period $t\text{;}L$ is the length of a time period.

3.3. Distribution decision model

In this section, a linear programming model is formulated and applied to distribute urgent medical reliefs from multiple EMRCs to multiple epidemic areas.

The objective function of the distribution model considers the physical fragility of affected individuals. This function is represented by mortality and infection rates.

The objective function is:

$$\min F_{\mathit{phy}}={\displaystyle \sum _{j=1}^J}({\sigma }_1{\overline{\beta }}_{\mathit{jt}}^c{S}_{\mathit{jt}}^c+{\sigma }_2{\overline{\beta }}_{\mathit{jt}}^v{S}_{\mathit{jt}}^v+{\sigma }_3{\overline{\alpha }}_{\mathit{jt}}^c{I}_{\mathit{jt}}^c+{\sigma }_4{\overline{\alpha }}_{\mathit{jt}}^v{I}_{\mathit{jt}}^v)$$ (10)

where

$${\overline{\alpha }}_{\mathit{jt}}^v={\alpha }_j^v+{\displaystyle \sum _{p=l+1}^{l+k}}{\alpha }^p\frac{D_{\mathit{jt}}^p-{\sum }_{i=1}^I{x}_{\mathit{ijt}}^p}{D_{\mathit{jt}}^p}\text{,}\forall j\text{,}t$$ (11)

$${\overline{\alpha }}_{\mathit{jt}}^c={\alpha }_j^c+{\displaystyle \sum _{p=l+1}^{l+k}}{\alpha }^p\frac{D_{\mathit{jt}}^p-{\sum }_{i=1}^I{x}_{\mathit{ijt}}^p}{D_{\mathit{jt}}^p}\text{,}\forall j\text{,}t$$ (12)

$${\overline{\beta }}_{\mathit{jt}}^v={\beta }_j^v+{\displaystyle \sum _{p=1}^l}{\beta }^p\frac{D_{\mathit{jt}}^p-{\sum }_{i=1}^I{x}_{\mathit{ijt}}^p}{D_{\mathit{jt}}^p}\text{,}\forall j\text{,}t$$ (13)

$${\overline{\beta }}_{\mathit{jt}}^c={\beta }_j^c+{\displaystyle \sum _{p=1}^l}{\beta }^p\frac{D_{\mathit{jt}}^p-{\sum }_{i=1}^I{x}_{\mathit{ijt}}^p}{D_{\mathit{jt}}^p}\text{,}\forall j\text{,}t$$ (14)

The proposed objective function minimizes the aforementioned physical fragility ($F_{\mathit{phy}}$), which is given by a function of variable $x_{\mathit{ijt}}^p$.

The weights $({\sigma }_1\text{,}{\sigma }_2\text{,}{\sigma }_3\text{,}{\sigma }_4)$ in Eq. (10) reflect the priorities of different groups. These weights are set by the decision maker (usually the government or experts) based on the trend and the characteristic of the spreading disease, as drawn from the modified SEIR model (Eqs. (1), (2), (3), (4), (5), (6), (7), (8)). For example, the priority of prophylactic medicines should be not lower than that of treatment medicines (${\sigma }_1⩾{\sigma }_3\text{and}{\sigma }_2⩾{\sigma }_4$) at the beginning because in this situation, the major object of emergency medical logistics is to avoid a large-scale epidemic. Furthermore, the priority of vulnerable groups should be not lower than that of common groups (${\sigma }_2⩾{\sigma }_1\text{and}{\sigma }_4⩾{\sigma }_3$) for humanitarian reasons. Recovered people are not included in Eq. (10) because they are healthy. Exposed people are not included because they are no longer at risk of infection and do not suffer illness until they become infectious.

In Eqs. (11), (12), (13), (14), the demand for medical reliefs and the number of people in each group are forecasted using Eqs. (1), (2), (3), (4), (5), (6), (7), (8), (9). ${\overline{\alpha }}_{\mathit{jt}}^v$ and ${\overline{\alpha }}_{\mathit{jt}}^c$ are adopted to measure physical fragility. These variables refer to the expected epidemic mortality rates of vulnerable and common infectious individuals, respectively, after distribution in area j during time period t. Both variables are related to the amount of treatment reliefs sent to epidemic area j in a specific time period. Similarly, ${\overline{\beta }}_{\mathit{jt}}^v$ and ${\overline{\beta }}_{\mathit{jt}}^c$ indicate the expected epidemic infection rates of vulnerable and common susceptible people after distribution, respectively. These variables are related to the amount of prophylactic medical reliefs sent to epidemic area j in time period t.

The following constraints are proposed:

$${\displaystyle \sum _{j=1}^J}{x}_{\mathit{ijt}}^p⩽Q_{\mathit{it}}^p\text{,}\forall i\text{,}p\text{,}t$$ (15)

$${\displaystyle \sum _{i=1}^I}{x}_{\mathit{ijt}}^p⩽D_{\mathit{jt}}^p\text{,}\forall j\text{,}p\text{,}t$$ (16)

$${\displaystyle \sum _{j=1}^J}{\displaystyle \sum _{p=1}^{l+k}}{x}_{\mathit{ijt}}^p⩽W_{\mathit{it}}\text{,}\forall i\text{,}t$$ (17)

$${\displaystyle \sum _{i=1}^I}{\displaystyle \sum _{j=1}^J}{\displaystyle \sum _{p=1}^{l+k}}{c}_{\mathit{ijt}}^p{x}_{\mathit{ijt}}^p⩽C_t\text{,}\forall t$$ (18)

$${\overline{\alpha }}_{\mathit{jt}}^v\text{,}{\overline{\alpha }}_{\mathit{jt}}^c⩽{\alpha }_M\text{,}\forall j\text{,}t$$ (19)

$${\overline{\beta }}_{\mathit{jt}}^v\text{,}{\overline{\beta }}_{\mathit{jt}}^c⩽{\beta }_M\text{,}\forall j\text{,}t$$ (20)

$$x_{\mathit{ijt}}^p⩾0\text{,}\forall i\text{,}j\text{,}p\text{,}t$$ (21)

Among the constraints discussed above, Eq. (15) ensures that the aggregate amount of medical relief p sent from EMRC i does not exceed the corresponding amount available in this EMRC in the given time period t. Eq. (16) guarantees that the aggregate amount of medical relief p sent to a given area j does not exceed the corresponding demand in the given time period t. Eq. (17) ensures that the aggregate amount of medical reliefs distributed from any given EMRC i does not exceed the corresponding transportation capacity. Eq. (18) guarantees that the aggregate distribution cost does not exceed the budget in time period t. Eqs. (19), (20) consider fairness and ensure that the mortality and infection rates in all epidemic areas do not exceed the limit. These equations balance these rates among different areas to avoid the situation in which some areas receive enough reliefs, whereas other areas report high rates because of a lack of medicines. Eq. (21) characterizes a feasible numerical domain associated with $x_{\mathit{ijt}}^p$.

In addition, two theorems are proposed for further discussion (proved in Appendix A). Theorem 1 helps analyze the trend of epidemic diffusion after relief distribution. Theorem 2 shows the condition in which the effectiveness and fairness of emergency medical logistics can be balanced.

Disease-free and endemic equilibrium are discussed, and Theorem 1 is proposed to explore the effects on the epidemic diffusion of emergency logistics.

An equilibrium is defined as a state where $\frac{{\mathit{dX}}_i}{\mathit{dt}}=0$ for all compartments $X_i\subseteq \left\{S_j^c\left(t\right)\text{,}{E}_j^c\left(t\right)\text{,}{I}_j^c\left(t\right)\text{,}{R}_j^c\left(t\right)\text{,}{S}_j^v\left(t\right)\text{,}{E}_j^v\left(t\right)\text{,}{I}_j^v\left(t\right)\text{,}{R}_j^v\left(t\right)\right\}$ in a specific epidemic area j. In the system of Eqs. (1), (2), (3), (4), (5), (6), (7), (8), let $N_j^c\left(t\right)=S_j^c\left(t\right)+E_j^c\left(t\right)+I_j^c\left(t\right)+R_j^c(t)$ , $N_j^v\left(t\right)=S_j^v\left(t\right)+E_j^v\left(t\right)+I_j^v\left(t\right)+R_j^v(t)$ and $\Gamma =\left\{\left(E_j^c\left(t\right)\text{,}{I}_j^c\left(t\right)\text{,}{R}_j^c\left(t\right)\text{,}{N}_j^c\left(t\right)\text{,}{E}_j^v\left(t\right)\text{,}{I}_j^v\left(t\right)\text{,}{R}_j^v\left(t\right)\text{,}{N}_j^v\left(t\right)\right)\subseteq R_{+}^8\right\}$. In each area $j\text{,}$ a disease free equilibrium can be found at E ₁  = (0, 0, 0, 0, 0, 0, 0, 0) and E ₂  = (0, 0, 0, $N_{\mathit{je}}^c$, 0, 0, 0, $N_{\mathit{je}}^v)$ and they exist for all nonnegative values of their parameters.

Theorem 1

In the system of Eqs. (1), (2), (3), (4), (5), (6), (7), (8) ,

• 1.
  ${\Lambda }_j^c-{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c>0$ and ${\Lambda }_j^v-{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v>0\text{,}$

  • (a)
    and if $R_j^0>1$ , there is one and only one positive equilibrium $E_3=(E_{\mathit{je}}^c\text{,}{I}_{\mathit{je}}^c\text{,}{R}_{\mathit{je}}^c\text{,}{N}_{\mathit{je}}^c\text{,}{E}_{\mathit{je}}^v\text{,}{I}_{\mathit{je}}^v\text{,}{R}_{\mathit{je}}^v\text{,}{N}_{\mathit{je}}^v)\text{.}$
  • (b)
    and if $R_j^0⩽1$ , there is no positive equilibrium.
• 2. if ${\Lambda }_j^c-{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c<0$ and ${\Lambda }_j^v-{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v<0$ , there is one and only one positive equilibrium E ₃ .
• 3. if $({\Lambda }_j^c-{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c)({\Lambda }_j^v-{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v)⩽0$ , there is one and only one positive equilibrium E ₃ .

where ${\Lambda }_j^k=\frac{1}{\epsilon }\left({\gamma }_j^k{\mu }_j+{\alpha }_j^k+d_j^k\right)\left(d_j^k+\epsilon \right)\text{,}k\in \left\{c\text{,}v\right\}$ and $R_j^0=\frac{{\delta }_j^2{\beta }_j^c{\beta }_j^v{N}_{\mathit{je}}^c{N}_{\mathit{je}}^v}{({\Lambda }_j^c-{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c)\left({\Lambda }_j^v-{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v\right)}$.

The three cases described in Theorem 1 are mutually exclusive and collectively exhaustive. $R_j^0$ is the basic reproduction number of the epidemic in epidemic area j and represents the number of cases that one case generates on average over the course of its infectious period. This metric is useful because it helps determine whether an epidemic can spread through a population.

Instead ${\alpha }_j^c\text{,}{\alpha }_j^v\text{,}{\beta }_j^c$ and ${\beta }_j^v$ in Theorem 1 by ${\overline{\alpha }}_j^c\text{,}{\overline{\alpha }}_j^v\text{,}{\overline{\beta }}_j^c$ and ${\overline{\beta }}_j^v$ respectively, we can deduce there is no positive equilibrium under the Conditions 1(b), that is, ${\Lambda }_j^c-{\delta }_j{\overline{\beta }}_j^c{N}_{\mathit{je}}^c>0,{\Lambda }_j^v-{\delta }_j{\overline{\beta }}_j^v{N}_{\mathit{je}}^v>0$ and $\overline{R_j^0}=\frac{{\delta }_j^2{\overline{\beta }}_j^c{\overline{\beta }}_j^v{N}_{\mathit{je}}^c{N}_{\mathit{je}}^v}{(\overline{{\Lambda }_j^c}(t)-{\delta }_j{\overline{\beta }}_j^c(t)N_{\mathit{je}}^c)\left(\overline{{\Lambda }_j^v}(t)-{\delta }_j{\overline{\beta }}_j^v(t)N_{\mathit{je}}^v\right)}<1$, where ${\bar{\Lambda }}_j^k\left(t\right)=\frac{1}{\epsilon }\left({\gamma }_j^k{\mu }_j+{\overline{\alpha }}_j^k\left(t\right)+d_j^k\right)\left(d_j^k+\epsilon \right)\text{,}k\in \left\{c\text{,}v\right\}$.

Epidemic diseases die out in the long run if no positive equilibrium exists, and diseases can continue to spread in a population under other situations. Theorem 1 can facilitate emergency medical logistics by (1) setting “no positive equilibrium” as another constraint in the distribution model or by (2) checking Condition 1(b) after distribution decisions have been made by the models regardless of equilibrium. This work applies the theorem in the second manner. Equilibrium is disregarded in the distribution model (Eqs. (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), (20), (21)). The existence of a positive equilibrium is then determined. If equilibrium exists in some areas, then the government should adjust relevant policies (not logistics policies) to prevent diseases from spreading in the long run. An example of such adjustments involves investments in exogenous parameters, such as diagnosis rate and contact coefficient. Equilibrium is not set as a constraint because this behavior is less important than the transient behavior for a particular application to a sudden emergency related to a new strain of epidemic disease. Therefore, this work regards equilibrium condition as a consequence and not a constraint of emergency logistics.

Theorem 2

Under the constraint of the given model, if ${\alpha }_M<{\alpha }_U$ or ${\beta }_M<{\beta }_U$ then the problem has no feasible solution, in which

$${\alpha }_U={\alpha }_{\mathit{jt}}^v+{\displaystyle \sum _{p=l+1}^{l+k}}\left[{\alpha }^p\times \max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}\right]\text{,}\forall j\text{,}t$$

$${\beta }_U={\beta }_{\mathit{jt}}^v+{\displaystyle \sum _{p=1}^l}\left[{\beta }^p\times \max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}\right]\text{,}\forall j\text{,}t$$

The objective function of the model involves effectiveness. Eqs. (19), (20) are concerned with fairness, which is achieved by ensuring that the mortality and infection rates do not exceed ${\alpha }_M$ and ${\beta }_M$ in all areas. A feasible solution cannot be obtained when extreme fairness ( ${\alpha }_M<{\alpha }_U$ or ${\beta }_M<{\beta }_U$ ) is required. Therefore, we can balance effectiveness and fairness only to some extent.

4. Model extension

In this section, the model is extended to improve its representation of real problems. The mechanism for demand forecasting is improved in the first part, and the distribution mechanism is enhanced in the subsequent part.

4.1. Extended Model 1

The basic model assumes that epidemic areas are independent and that all of the people moving into these areas are susceptible. In reality, an epidemic area is affected by another in a public health emergency given the infectiousness of an epidemic. Therefore, an extension that considers the spatial interaction relationships among epidemic areas is developed in this section.

A migration matrix H is adopted.

$$H=\left[\begin{array}{ccccc}\hfill h_{11}\hfill & \hfill \cdots \hfill & \hfill h_{1j}\hfill & \hfill \cdots \hfill & \hfill h_{1J}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill h_{j1}\hfill & \hfill \hfill & \hfill h_{\mathit{jj}}\hfill & \hfill \hfill & \hfill h_{\mathit{jJ}}\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill h_{J1}\hfill & \hfill \cdots \hfill & \hfill h_{\mathit{Jj}}\hfill & \hfill \cdots \hfill & \hfill h_{\mathit{JJ}}\hfill \end{array}\right]\text{,}{h}_{j_1{j}_2}⩾0$$ (22)

where $h_{j_1{j}_2}$ is the rate at which the population in $j_1$ moves to $j_2$. Moreover, $h_{11}=h_{22}=\dots =h_{\mathit{JJ}}=0$ and ${\sum }_{m=1}^J{h}_{\mathit{jm}}⩽1\text{,}\forall j$. The corresponding epidemic model is formulated as follows:

$$\frac{{\mathit{dS}}_j^c(t)}{\mathit{dt}}={\displaystyle \sum _{m=1}^J}{h}_{\mathit{mj}}{S}_m^c(t)-{\displaystyle \sum _{m=1}^J}{h}_{\mathit{jm}}{S}_j^c\left(t\right)-d_j^c{S}_j^c\left(t\right)-{\beta }_j^c{\delta }_j{S}_j^c\left(t\right)I_j\left(t\right)$$ (23)

$$\frac{{\mathit{dS}}_j^v(t)}{\mathit{dt}}={\displaystyle \sum _{m=1}^J}{h}_{\mathit{mj}}{S}_m^v(t)-{\displaystyle \sum _{m=1}^J}{h}_{\mathit{jm}}{S}_j^v(t)-d_j^v{S}_j^v(t)-{\beta }_j^v{\delta }_j{S}_j^v(t)I_j(t)$$ (24)

$$\frac{{\mathit{dE}}_j^c(t)}{\mathit{dt}}={\displaystyle \sum _{m=1}^J}{h}_{\mathit{mj}}{E}_m^c(t)-{\displaystyle \sum _{m=1}^J}{h}_{\mathit{jm}}{E}_j^c\left(t\right)+{\beta }_j^c{\delta }_j{S}_j^c(t)I_j(t)-\epsilon E_j^c(t)-d_j^c{E}_j^c(t)$$ (25)

$$\frac{{\mathit{dE}}_j^v(t)}{\mathit{dt}}={\displaystyle \sum _{m=1}^J}{h}_{\mathit{mj}}{E}_m^v(t)-{\displaystyle \sum _{m=1}^J}{h}_{\mathit{jm}}{E}_j^v\left(t\right)+{\beta }_j^v{\delta }_j{S}_j^v(t)I_j(t)-\epsilon E_j^v(t)-d_j^v{E}_j^v(t)$$ (26)

$$\frac{{\mathit{dI}}_j^c(t)}{\mathit{dt}}={\displaystyle \sum _{m=1}^J}{h}_{\mathit{mj}}{I}_m^c(t)-{\displaystyle \sum _{m=1}^J}{h}_{\mathit{jm}}{I}_j^c\left(t\right)+\epsilon E_j^c(t)-({\alpha }_j^c+d_j^c)I_j^c(t)-{\gamma }_j^c\mu I_j^c(t)$$ (27)

$$\frac{{\mathit{dI}}_j^v(t)}{\mathit{dt}}={\displaystyle \sum _{m=1}^J}{h}_{\mathit{mj}}{I}_m^v(t)-{\displaystyle \sum _{m=1}^J}{h}_{\mathit{jm}}{I}_j^v\left(t\right)+\epsilon E_j^v(t)-({\alpha }_j^v+d_j^v)I_j^v(t)-{\gamma }_j^v\mu I_j^v(t)$$ (28)

$$\frac{{\mathit{dR}}_j^c(t)}{\mathit{dt}}={\displaystyle \sum _{m=1}^J}{h}_{\mathit{mj}}{R}_m^c(t)-{\displaystyle \sum _{m=1}^J}{h}_{\mathit{jm}}{R}_j^c\left(t\right)+{\gamma }_j^c\mu I_j^c(t)-d_j^c{R}_j^c(t)$$ (29)

$$\frac{{\mathit{dR}}_j^v(t)}{\mathit{dt}}={\displaystyle \sum _{m=1}^J}{h}_{\mathit{mj}}{R}_m^v(t)-{\displaystyle \sum _{m=1}^J}{h}_{\mathit{jm}}{R}_j^v(t)+{\gamma }_j^v\mu I_j^v(t)-d_j^v{R}_j^v(t)$$ (30)

As with Eqs. (1), (2), (3), (4), (5), (6), (7), (8), Eqs. (23), (24) describe how the numbers of susceptible individuals vary in epidemic area j. ${\sum }_{m=1}^J{h}_{\mathit{mj}}{S}_m^c(t)$ and ${\sum }_{m=1}^J{h}_{\mathit{mj}}{S}_m^v(t)$ indicate the numbers of common and vulnerable susceptible people moving to j from other epidemic areas, respectively, whereas ${\sum }_{m=1}^J{h}_{\mathit{jm}}{S}_j^c\left(t\right)$ and ${\sum }_{m=1}^J{h}_{\mathit{jm}}{S}_j^v(t)$ are the numbers of common and vulnerable susceptible people that move from j to other areas, respectively. Similar migration is also formulated in Eqs. (25), (26), (27), (28), (29), (30).

The demand forecasting model is:

$$D_{\mathit{jt}}^p=\left\{\begin{array}{cc}{\theta }^p{\int }_{t_0}^{t_0+L}\left[S_j\left(t\right)+E_j\left(t\right)+(1-{\mu }_j)I_j\left(t\right)\right]\mathit{dt}-{\mathit{Inv}}_{\mathit{jt}}^p\text{,}\hfill & p\in \mathit{Mp}\hfill \\ {\theta }^p{\int }_{t_0}^{t_0+L}{\mu }_j{I}_j\left(t\right)\mathit{dt}-{\mathit{Inv}}_{\mathit{jt}}^p\text{,}\hfill & p\in \mathit{Mt}\hfill \end{array}\right)$$ (31)

The definitions of other notations are similar to those provided for the basic model.

4.2. Extended Model 2

This section extends the model by integrating survivor psychology with medical relief logistics.

As mentioned in Sections 1, 2, previous studies presented strong evidence for the adverse psychological effects of public health emergencies on affected people. These studies also suggest that providing on-time treatment and applying an effective prophylactic method help alleviate psychological suffering. These approaches are closely related to on-time logistics and a sufficient amount of medical relief.

A distribution time threshold is set on the basis of the results of previous studies; that is, emergency medical distribution is completely effective only when it is delivered within the time limit. Affected people suffer extra psychological distress, such as anxiety, anger, panic, and fear if distribution time exceeds its limit. Therefore, a “suffering” coefficient is adopted to represent additional psychological suffering as a result of distribution delay. Similarly, an insufficient amount of medical reliefs can also increase psychological suffering. The mental states of different groups vary. Three additional “suffering” coefficients are then adopted to denote suffering due to the insufficient amount of relief. The new notations are as follows:

• ${\phi }_1$: suffering coefficient for diagnosed people caused by unsatisfactory amounts of treatment reliefs

• ${\phi }_2$: suffering coefficient for susceptible, exposed, and infectious but undiagnosed people caused by unsatisfactory amounts of treatment reliefs

• ${\phi }_3$: suffering coefficient for susceptible, exposed, and infectious but undiagnosed people caused by unsatisfactory amounts of prophylactic reliefs

• ${\phi }_4$: suffering coefficient caused by delay

• $T_M$: transportation time threshold

• $T_{\mathit{ijt}}$: transportation time from EMRC i to epidemic area j in time period t

The objective of the extended model is formulated as follows:

$$\min F=F_{\mathit{phy}}+(1-\omega )F_{\mathit{psy}}$$ (32)

where $F_{\mathit{phy}}$ is given as in Eq. (10) and $F_{\mathit{psy}}$ is the psychological fragility of affected people.

$$F_{\mathit{psy}}={\phi }_1{\displaystyle \sum _{j=1}^J}{\displaystyle \sum _{p=l+1}^{l+k}}\left({\alpha }^p\frac{D_{\mathit{jt}}^p-{\sum }_{i=1}^I{x}_{\mathit{ijt}}^p}{D_{\mathit{jt}}^p}\right){\mu }_j{I}_{\mathit{jt}}+{\phi }_2{\displaystyle \sum _{j=1}^J}{\displaystyle \sum _{p=l+1}^{l+k}}\left({\alpha }^p\frac{D_{\mathit{jt}}^p-{\sum }_{i=1}^I{x}_{\mathit{ijt}}^p}{D_{\mathit{jt}}^p}\right)(S_{\mathit{jt}}+E_{\mathit{jt}}+(1-{\mu }_j)I_{\mathit{jt}})+{\phi }_3{\displaystyle \sum _{j=1}^J}{\displaystyle \sum _{p=1}^l}\left({\beta }^p\frac{D_{\mathit{jt}}^p-{\sum }_{i=1}^I{x}_{\mathit{ijt}}^p}{D_{\mathit{jt}}^p}\right)(S_{\mathit{jt}}+E_{\mathit{jt}}+(1-{\mu }_j)I_{\mathit{jt}})+{\phi }_4{\displaystyle \sum _{j=1}^J}{\displaystyle \sum _{i=1}^I}\left(\max \left\{0\text{,}{T}_{\mathit{ijt}}-T_M\right\}\times {\displaystyle \sum _{p=1}^{l+k}}{x}_{\mathit{ijt}}^p\times \left(S_{\mathit{jt}}+E_{\mathit{jt}}+I_{\mathit{jt}}\right)\right)$$ (33)

The first two terms in Eq. (33) reflect the additional psychological suffering caused by unsatisfactory amounts of treatment reliefs. Disease-caused mortality increases as unsatisfied demand increases. Thus, the fear of disease-caused death increases. That is, psychological fragility increases as unsatisfied demand for treatment relief increases. The third term in Eq. (33) reflects the additional psychological fragility of individuals who are susceptible, exposed, and infectious but undiagnosed as a result of the unsatisfactory amounts of prophylactic reliefs. Exposed people have already been infected, and prophylactic reliefs do not have physical effects on them. However, psychological effects remain because these individuals are impossible to distinguish from the susceptible group. The psychological suffering of infectious people who have not been diagnosed is also affected by prophylactic reliefs because they do not realize that they have been infected. The fourth term corresponds to the additional pain caused by delayed distribution. A long transportation time increases the psychological fragility of all affected individuals.

The other denotations and constraints are similar to those presented in the basic model.

5. Numerical study

This section conducts a case study using real data and a continuation study with experimental data to demonstrate the applicability of the proposed methodology. The case study involves the SARS outbreak in China during the first quarter of 2003. All computational processes are conducted with MATLAB on a personal computer with a 2.53 Hz CPU and 2G RAM. Following an introduction of the case background, the main procedures executed in this numerical study are the validation of forecasting model, testing with real data, and experimental testing.

5.1. Background

The SARS outbreak originated in Guangdong Province, China, in November 2002. The epidemic spread across almost the entire country. When the severity of this public health emergency was determined, the Chinese central government responded. The government reported 305 cases and 5 deaths to the World Health Organization on 10th February 2003.

The numerical study focuses on Guangdong. It is also known as Canton or Kwangtung Province and is located on the South China Sea coast. Guangdong is among the most populous provinces in China and registers 79.1 million permanent residents, as well as 31 million migrants who lived in the province for at least six months of the year. These numbers account for 7.79% of Mainland China’s population. Given the epidemic-related information and the basic state of the distribution network, the proposed methodology is used to forecast the trend of the spread of SARS and to make medical logistics decisions for Guangdong. The unit interval is one day.

Cases of SARS infection were reported in the following prefectures in Guangdong: Guangzhou, Foshan, Jiangmen, Heyuan, Zhongshan, and Shenzhen. The province has four EMRCs. Fig. 3 shows the simplified geographical relationships among these affected areas and among the EMRCs. Three types of treatment and two types of prophylactic reliefs were provided as urgently needed. The four EMRCs concentrated their supplies of reliefs and distributed them to the six epidemic areas. The case background indicates that a simplified 5  $\times$  4  $\times$  6 medical logistics network is formed (5 types of medical reliefs, 4 EMRCs, and 6 epidemic areas). People older than 45 are regarded as the vulnerable ones in this case.

Fig. 3.

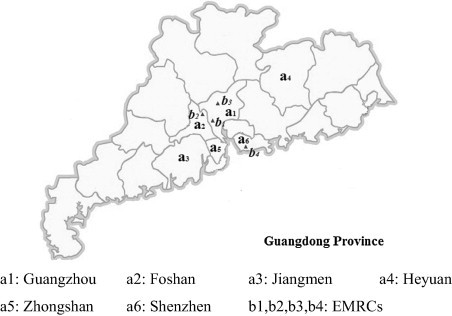
Study areas.

To elucidate the methodology, this work explains the decisions made on 10th February 2003 in detail as an example.

5.2. Testing of the forecasting model

Demand is forecasted using Eqs. (9), (31). These two forecasting models are compared with moving average method and standard SEIR model, which are presented in Appendix D.

This study uses Eqs. (1), (2), (3), (4), (5), (6), (7), (8) and (23), (24), (25), (26), (27), (28), (29), (30) to compare the numbers of corresponding demanders instead of comparing demands because demands for both types of prophylactic reliefs are positively correlated with the numbers of susceptible, exposed, and undiagnosed people. Moreover, demands for all three types of treatment reliefs are correlated with the number of infectious and diagnosed individuals.

The parameters are presented in Table B.1, and they are set as follows: (1) the parameters for population are set (National Bureau of Statistics of P.R. China, 2004). (2) The parameters for disease (recovery rate, diagnosed rate, mortality, and incubation period) are set. Dctors and medical experts can generally estimate the expected values of these parameters shortly after a new disease is recognized in a region. In this study, they are obtained from several medical reports and statistics (National Health and Family Planning Commission of P.R. China, 2004; Chinese Center for Disease Control and Prevention; Kamps and Hoffmann, 2003). (3) Infection rates are set with two methods. First, these rates can be obtained by fitting the forecasting curve with observations given epidemic areas with adequate infectious cases. In this study, the infection rates in Guangzhou (j  = 1) and Zhongshan (j  = 5) are set in this manner. The objective function of fitting is to minimize $\sqrt{{\sum }_{k=1}^N{\left({\mathit{obs}}_k-{\mathit{est}}_k\right)}^2}/\left(\sqrt{{\sum }_{k=1}^N{\mathit{obs}}_k^2}+\sqrt{{\sum }_{k=1}^N{\mathit{est}}_k^2}\right)$, where ${\mathit{obs}}_k$ refers to the kth observed value and ${\mathit{est}}_k$ refers to the kth estimated value. Given epidemic areas with a few infectious cases, these rates can also be set by comparing specific areas with the areas listed above in terms of previous cases of similar epidemic outbreak. In this study, infection rates in the other four areas (j  = 2, 3, 4, 6) are set in this manner. For example, the infection rates of influenza and pneumonia in Guangzhou (j  = 1) is 0.05 lower than those in Foshan (j  = 2). Thus ${\beta }_2^c={\beta }_1^c+0.05$ and ${\beta }_2^v={\beta }_1^v+0.05$.

The following table compares demand forecasting in Guangzhou (j  = 1) as an example. Although accurate parameters can be obtained at present, this study attempts to recreate a specific situation in which a new, little-know epidemic outbreak is reported.

Table 2 shows that all four models are valid in terms of forecasting prophylactic demanders. In combination with Fig. 4 , this table illustrates that the performance of these models differ with respect to forecasting the numbers of treatment demanders. The methods proposed in this paper perform better than standard SEIR model and moving average method in the initial two weeks, but then the error rate increases rapidly. The main reason for this trend is the development of preventive and therapeutic methods as doctors amass additional knowledge about SARS. Nonetheless, accurate forecasting for two weeks is enough to facilitate distribution decision-making. In addition, the models proposed in this paper can forecast every group in the population, unlike the moving average method. This advantage is useful in distributional decision-making.

Table 2.

Comparison of different forecasting methods.

Forecasting methods	Average forecasting error of prophylactic demanders			Average forecasting error of treatment demanders
	In one week (%)	In two weeks (%)	In one month (%)	In one week (%)	In two weeks (%)	In one month (%)
Basic model	0.01	0.03	0.06	3.55	3.99	45.84
Extended Model 1	0.01	0.03	0.06	3.54	3.96	44.80
Standard SEIR model	0.02	0.03	0.05	12.02	13.75	43.07
Moving average method	0.02	0.03	0.05	11.61	8.17	13.10

^∗ The original point of forecasting is 10th February.

Fig. 4.

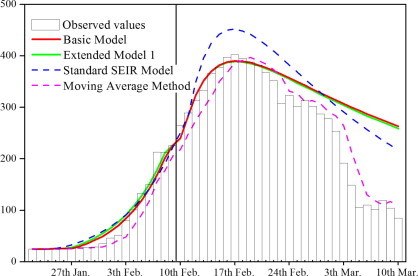
Forecasting of treatment demanders.

5.3. Testing with real data

In this section, the three models proposed in Sections 3, 4 are solved and their results compared. This paper summarizes and compares the numerical analysis results for these three models. The parameters and statistics are reported in the appendix.

Table 3 shows the main indices of the three models. Extended forecasting method (proposed in Section 5.2) is adopted in Extended Model 2. The psychological fragility determined with the basic model and with Extended Model 1 are also calculated for comparison. The computation times for solving these three models are 1.94, 2.48 and 2.53 s, respectively.

Table 3.

Numerical results of testing with real data.

Model	Basic model	Extended Model 1	Extended Model 2
Average mortality ratea	0.497	0.497	0.091
Average infection ratea	0.573	0.572	0.571
Total amount of prophylactic reliefs	436,994	436,980	436,405
Total amount of treatment reliefs	181	195	770
Cost	443,342	520,878	461,523
Physical fragility	3,869,667	3,862,785	3,881,985
Psychological fragility	2,269,299	2,291,386	1,172,696

^aAverage mortality rate is the average of mortality rates of all areas after distribution, that is, the average of ${\overline{\alpha }}_j^m(j=1\text{,}2\text{,}\dots \text{,}6\text{;}m=c\text{,}v)$; and average infection rate is the average of infection rates of all areas after distribution, that is, the average of ${\overline{\beta }}_j^m(j=1\text{,}2\text{,}\dots \text{,}6\text{;}m=c\text{,}v)$.

The horizontal axis in Fig. 5 shows four EMRCs, whereas the vertical axis indicate epidemic areas. Circles with different colors correspond to the five types of reliefs, and the colored areas refer to the corresponding distributed amounts (specific numbers are reported in Table C.1).

Fig. 5.

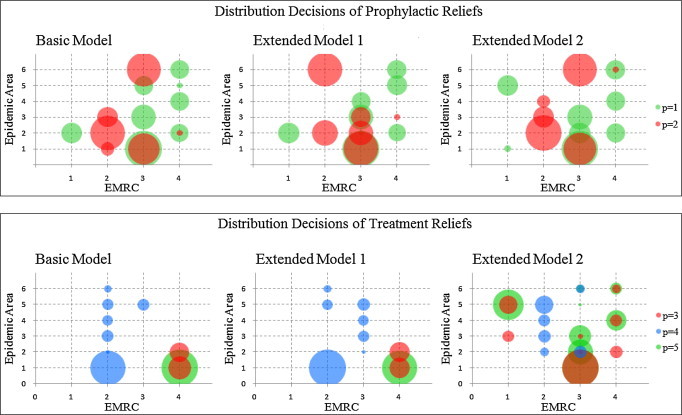
Comparison of three models.

The following observations are made based on the analytical results presented above.

• (1)The amounts of prophylactic reliefs distributed to specific epidemic areas differ when the spatial interaction relationships among epidemic areas are considered. As a result, the average infection rate decrease slightly although the total distributed amount does not increase.
• (2)The total amount of treatment reliefs distributed increases when survivor psychology is considered. In the process, psychological fragility declines significantly.
• (3)The amount of reliefs distributed increase for epidemic areas with a large input population that originates from severely infected areas when the spatial interaction relationships among epidemic areas are considered. In this case, additional prophylactic reliefs are sent to Shenzhen (j  = 6) to avoid the spread of SARS. The reason for this outcome is that this area has a large input population coming from Guangzhou (j  = 1) and Zhongshan (j  = 5). These areas are the most severely. Moreover, the number of residents in Shenzhen (j  = 6) is small. Guangzhou (j  = 1) is less affected although the input from Zhongshan (j  = 5) to this area (j  = 1) is larger given that Guangzhou (j  = 1) has much more residents.
• (4)The amount of prophylactic reliefs distributed increases for epidemic areas with low diagnosis rates when survivor psychology is considered. In this case, the diagnosis rate of Heyuan (j  = 4) is the lowest and many infectious people have not realized that they are infected. Infectious but undiagnosed individuals share a physical state with those who have been diagnosed, but their psychological characteristics differ. Therefore, more prophylactic relief is sent to Heyuan (j  = 4) in Extended Model 2 than in Extended Model 1.
• (5)The number of distribution paths that report long transportation times decreases when survivor psychology is considered. A long distribution time increases psychological fragility. In this case, the distribution paths from EMRC 4 to Guangzhou (j  = 1) and to Jiangmen (j  = 3) are avoided in Extended Model 2, unlike in the other two models. In a case of emergency medical logistics following a large-scale disaster, the effect of survivor psychology on path selection is strengthened because destroyed infrastructure may increase transportation time.

5.4. Experimental testing

Four observations are made based on the analysis presented with actual SARS data. An analysis using experimental data is conducted to test these observations in different epidemic situations.

We test four typical types of situations as follows. Situation 1: not easily spread and not especially lethal (small α and small β); Situation 2: easily spread but not especially lethal (small α and large β); Situation 3: not easily spread but especially lethal (large α and small β); and Situation 4: easily spread and especially lethal (large α and large β).

The effects of α and β alone are reported and discussed in this section to induce brief observations given the similar effects of δ and β, as well as the inverse effects of α and γ.

The other parameters are similar to those in Section 5.3. We make distribution decisions in the four situations as in the analysis with real data. The main indices and specific decisions are summarized in Table C.2, Table C.3, Table C.4, Table C.5, Table C.6, Table C.7, Table C.8, Table C.9 in Appendix C.

The following four observations are made based on the results of experimental testing:

• (1)All four situations exhibit results similar to those in the first and second observations made by analyzing real data. That is, the amounts of prophylactic reliefs distributed to specific epidemic areas differ when the spatial interaction relationships among epidemic areas are considered, although the total amount does not increase. Moreover, the total amount of treatment reliefs distributed increases when survivor psychology is considered, thus reducing psychological fragility considerably.
• (2)All four situations show the results similar to those in the third observation made by analyzing real data. That is, more prophylactic reliefs are distributed to epidemic areas with large input populations that originate from severely infected areas when the spatial interaction relationships among such areas are considered.
• (3)Situations 2 and 4 display results similar to those in the fourth observation made by analyzing real data. More prophylactic reliefs are sent to areas with low diagnosis rates when survivor psychology is considered. However, Situations 1 and 3 fail to provide strong evidence for these changes. The effect of the variation in prophylactic relief on physical and psychological fragility is insignificant in these situations given the low infection rate.
• (4)In all four experimental situations, distribution paths that report long transportation times are avoided when survivor psychology is considered, as in the analysis with real data.

6. Implications

Academic literature and popular press both indicate that the decision-makers for public health emergencies have long been advised to control physical factors, such as mortality and infection rates, and economic factors, such as transportation cost. This study underscores the importance of survivor psychology in such emergencies and provides suggestions on efficient, effective, and fair medical rescue.

This work highlights the necessity and feasibility of reducing the psychological fragility of affected people during emergency medical logistics. Aside from inducing health threats and economic losses, public health emergencies also have negative psychological effects on both patients and healthy people. Affected people may feel helplessness, sorrow, panic, anxiety, and fear. Such individuals may even develop mental illnesses. Widespread serious psychological problems may also threaten economic order and public security. Numerical results show that the consideration of survivor psychology significantly reduces the psychological fragility of affected people and that it hardly affects the physical fragility. Aside from highlighting survivor psychology, this work also indicates the benefits of considering the spatial interaction relationships among epidemic areas, especially in response to public health emergencies with high infection rates in areas with high population density.

In addition, the specific effects of incubation period and diagnosis rate are emphasized in the discussion of the relationship between logistics and survivor psychology. Additional treatment reliefs generally help improve psychological states. Conversely, prophylactic reliefs are significant to epidemics with long incubation periods. Such reliefs do not exert physical effects on exposed people, and such individuals cannot infect others. However, psychological effects remain. Similarly, the psychological suffering of infectious but undiagnosed people is affected by prophylactic rather than treatment reliefs. Therefore, additional prophylactic but not treatment reliefs are sent to areas with low diagnosis rates. The increase in diagnosis rate lowers the demand for prophylactic reliefs and the corresponding logistics capacity.

Overall, this work provides managerial insights to improve decisions made on medical distribution as per demand forecasting for quick response to public health emergencies. These insights also enhance the physical and psychological status of affected individuals.

7. Conclusions

This work presents a novel model of emergency medical logistics for rapid response to public health emergencies. The proposed model consists of two mechanisms: (1) medical demand forecasting and (2) relief distribution. The medical demand associated with each epidemic area is forecast using a modified SEIR model. This process is followed by a linear programming approach to making distribution decisions. On the basis of a basic model that applies the proposed method, two extended models are generated by assessing (1) the spatial interaction relationships among epidemic areas and (2) survivor psychology.

A numerical study conducted on a real SARS outbreak in China demonstrates the applicability of the proposed method. The numerical results of the three models are compared to identify the advantages of each model. The psychological status of affected people improves significantly when survivor psychology is considered. Four experimental situations are tested to support and supplement the analysis with real data. Managerial insights are also provided.

The performance of emergency medical logistics may be improved significantly. The first mechanism of the proposed model is used in demand forecasting and supports the distribution mechanism in which the government is the real decision-maker. Nevertheless, the forecast demand information can be shared with non-governmental organizations and local charities for medical logistics coordination. This issue is worthy of further research. Furthermore, survivor psychology is discussed on the basis of providing the public with transparent information. However, emergency logistics may influence affected people in different ways as a result of imperfect information. Therefore, additional research must be conducted to explain this issue. Such research is particularly important for medical logistics and rescue in large public health emergencies.

Finally, the proposed approach to emergency medical logistics not only improves the performance of medical relief distribution but also clarifies the importance of further research in the fields of emergency logistics and public health. Thus, the physical and psychological fragility of affected people can be minimized.

Appendix A. Proofs of theorems

A.1. Proof of Theorem 1

Proof 1

For an equilibrium in system of Eqs. (1), (2), (3), (4), (5), (6), (7), (8), we can obtain

$$I_j^v\left(t\right)=\frac{1}{{\delta }_j{\beta }_j^c}\left(\frac{\left(d_j^c+\epsilon \right)E_j^c\left(t\right)}{N_{\mathit{je}}^c-E_j^c\left(t\right)-I_j^c\left(t\right)-R_j^c\left(t\right)}-{\delta }_j{\beta }_j^c{I}_j^c\left(t\right)\right)\text{,}$$

$$E_j^c\left(t\right)=\frac{1}{\epsilon }\left({\gamma }_j^c{\mu }_j+{\alpha }_j^c+d_j^c\right)I_j^c\left(t\right)\text{,}{R}_j^c\left(t\right)=\frac{{\gamma }_j^c{\mu }_j}{d_j^c}{I}_j^c\left(t\right)\text{,}$$

$$I_j^c\left(t\right)=\frac{1}{{\delta }_j{\beta }_j^v}\left(\frac{(d_j^v+\epsilon )E_j^v\left(t\right)}{N_{\mathit{je}}^v-E_j^v\left(t\right)-I_j^v\left(t\right)-R_j^v\left(t\right)}-{\delta }_j{\beta }_j^v{I}_j^v\left(t\right)\right)\text{,}$$

$$E_j^v\left(t\right)=\frac{1}{\epsilon }\left({\gamma }_j^v{\mu }_j+{\alpha }_j^v+d_j^v\right)I_j^v\left(t\right)\text{,}{R}_j^v\left(t\right)=\frac{{\gamma }_j^v{\mu }_j}{d_j^v}{I}_j^v\left(t\right)\text{,}$$

Let ${\mathrm{\Upsilon }}_j^c=1+\frac{1}{\epsilon }\left({\gamma }_j^c{\mu }_j+{\alpha }_j^c+d_j^c\right)+\frac{{\gamma }_j^c{\mu }_j}{d_j^c}$ and ${\mathrm{\Upsilon }}_j^v=1+\frac{1}{\epsilon }\left({\gamma }_j^v{\mu }_j+{\alpha }_j^v+d_j^v\right)+\frac{{\gamma }_j^v{\mu }_j}{d_j^v}$

We can deduce

$$\left\{\begin{array}{cc}{I}_j^c\left(t\right)=\frac{\left({\Lambda }_j^v-{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v\right)I_j^v\left(t\right)+{\mathrm{\Upsilon }}_j^v{\delta }_j{\beta }_j^v{I}_j^v{\left(t\right)}^2}{{\delta }_j{\beta }_j^v(N_{\mathit{je}}^v-{\mathrm{\Upsilon }}_j^v{I}_j^v\left(t\right))}\text{,}\hfill & I_j^v\left(t\right)\in \left[0\text{,}\frac{N_{\mathit{je}}^v}{{\mathrm{\Upsilon }}_j^v}\right)\hfill \\ I_j^v\left(t\right)=\frac{\left({\Lambda }_j^c-{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c\right)I_j^c\left(t\right)+{\mathrm{\Upsilon }}_j^c{\delta }_j{\beta }_j^c{I}_j^c{\left(t\right)}^2}{{\delta }_j{\beta }_j^c(N_{\mathit{je}}^c-{\mathrm{\Upsilon }}_j^c{I}_j^c\left(t\right))}\text{,}\hfill & I_j^c\left(t\right)\in \left[0\text{,}\frac{N_{\mathit{je}}^c}{{\mathrm{\Upsilon }}_j^c}\right)\hfill \end{array}\right)$$ (A.1)

An equilibrium exists $\iff$ curve $I_j^c\left(t\right)$ intersect with curve $I_j^v\left(t\right)$ in the first quadrant of the plane whose dimensions are $I_j^c\left(t\right)$ and $I_j^v\left(t\right)$.

with Eqs. (1), (2), (3), (4), (5), (6), (7), (8) we can obtain

$$\begin{array}{cc}\hfill & \frac{{\mathit{dI}}_j^c\left(t\right)}{{\mathit{dI}}_j^v\left(t\right)}=\frac{\left({\Lambda }_j^v-{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v\right)N_{\mathit{je}}^v+{\mathrm{\Upsilon }}_j^v{\delta }_j{\beta }_j^v{I}_j^v\left(t\right)(2N_{\mathit{je}}^v-{\mathrm{\Upsilon }}_j^v{I}_j^v\left(t\right))}{{\delta }_j{\beta }_j^v{(N_{\mathit{je}}^v-{\mathrm{\Upsilon }}_j^v{I}_j^v\left(t\right))}^2}\text{and}\frac{d^2{I}_j^c\left(t\right)}{{\mathit{dI}}_j^v{\left(t\right)}^2}=\frac{2{\mathrm{\Upsilon }}_j^v{\Lambda }_j^v{N}_{\mathit{je}}^v}{{\delta }_j{\beta }_j^v{(N_{\mathit{je}}^v-{\mathrm{\Upsilon }}_j^v{I}_j^v\left(t\right))}^3}\text{;}\hfill \\ \hfill & \frac{{\mathit{dI}}_j^v\left(t\right)}{{\mathit{dI}}_j^c\left(t\right)}=\frac{\left({\Lambda }_j^c-{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c\right)N_{\mathit{je}}^c+{\mathrm{\Upsilon }}_j^c{\delta }_j{\beta }_j^c{I}_j^c\left(t\right)(2N_{\mathit{je}}^c-{\mathrm{\Upsilon }}_j^c{I}_j^c\left(t\right))}{{\delta }_j{\beta }_j^c{(N_{\mathit{je}}^c-{\mathrm{\Upsilon }}_j^c{I}_j^c\left(t\right))}^2}\text{and}\frac{d^2{I}_j^v\left(t\right)}{{\mathit{dI}}_j^c{\left(t\right)}^2}=\frac{2{\mathrm{\Upsilon }}_j^c{\Lambda }_j^c{N}_{\mathit{je}}^c}{{\delta }_j{\beta }_j^c{\left(N_{\mathit{je}}^c-{\mathrm{\Upsilon }}_j^c{I}_j^c\left(t\right)\right)}^3}\text{.}\hfill \end{array}$$

Since $\frac{{\mathit{dI}}_j^c\left(t\right)}{{\mathit{dI}}_j^v\left(t\right)}>0$ and $\frac{d^2{I}_j^c\left(t\right)}{{\mathit{dI}}_j^v{\left(t\right)}^2}>0\text{,}{I}_j^c\left(t\right)$ is a monotonically increasing convex function when $I_j^v\left(t\right)\in \left[0\text{,}\frac{N_{\mathit{je}}^v}{{\mathrm{\Upsilon }}_j^v}\right)$, and ${\lim }_{I_j^v\left(t\right)\to \frac{N_{\mathit{je}}^v}{{\mathrm{\Upsilon }}_j^v}}{I}_j^c\left(t\right)=\infty$. Similarly, $I_j^v\left(t\right)$ is a monotonically increasing convex function when $I_j^c\left(t\right)\in [0\text{,}\frac{N_{\mathit{je}}^c}{{\mathrm{\Upsilon }}_j^c})$, and ${\lim }_{I_j^c\left(t\right)\to \frac{N_{\mathit{je}}^c}{{\mathrm{\Upsilon }}_j^c}}{I}_j^v\left(t\right)=\infty$. and since if $I_j^v\left(t\right)=0\text{,}\frac{{\mathit{dI}}_j^c\left(t\right)}{{\mathit{dI}}_j^v\left(t\right)}=\frac{{\Lambda }_j^v}{{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v}-1$; if $I_j^c\left(t\right)=0\text{,}\frac{{\mathit{dI}}_j^v\left(t\right)}{{\mathit{dI}}_j^c\left(t\right)}=\frac{{\Lambda }_j^c}{{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c}-1\text{,}{R}_j^0>1$, curve $I_j^c\left(t\right)$ intersects with curve $I_j^v\left(t\right)$ only once in the first quadrant. That is, there exists only one positive equilibrium E₃ in the system of Eqs. (1), (2), (3), (4), (5), (6), (7), (8). With $R_j^0⩽1$, no equilibrium exists. □

Proof 2

From Proof 1 we get E₃ exists $\iff$ curve $I_j^c\left(t\right)$ intersects with curve $I_j^v\left(t\right)$ in the first quadrant when $I_j^c\left(t\right)\in \left(0\text{,}\frac{{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c-{\Lambda }_j^c}{{\mathrm{\Upsilon }}_j^c{\delta }_j{\beta }_j^c}\right)\text{,}{I}_j^v\left(t\right)<0$.

$I_j^v\left(t\right)$ is a monotonically increasing convex function if $I_j^c\left(t\right)\in \left[\frac{{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c-{\Lambda }_j^c}{{\mathrm{\Upsilon }}_j^c{\delta }_j{\beta }_j^c}\text{,}\frac{N_{\mathit{je}}^c}{{\mathrm{\Upsilon }}_j^c}\right)$ and ${\lim }_{I_j^c\left(t\right)\to \frac{N_{\mathit{je}}^c}{{\mathrm{\Upsilon }}_j^c}}{I}_j^v\left(t\right)=\infty$.

When $I_j^v\left(t\right)\in \left(0\text{,}\frac{{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v-{\Lambda }_j^v}{{\mathrm{\Upsilon }}_j^v{\delta }_j{\beta }_j^v}\right)\text{,}{I}_j^c\left(t\right)<0$.

$I_j^c\left(t\right)$ is a monotonically increasing convex function if $I_j^v\left(t\right)\in \left[\frac{{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v-{\Lambda }_j^v}{{\mathrm{\Upsilon }}_j^v{\delta }_j{\beta }_j^v}\text{,}\frac{N_{\mathit{je}}^v}{{\mathrm{\Upsilon }}_j^v}\right)$ and ${\lim }_{I_j^v\left(t\right)\to \frac{N_{\mathit{je}}^v}{{\mathrm{\Upsilon }}_j^v}}{I}_j^c\left(t\right)=\infty$.

Thus, curve $I_j^c\left(t\right)$ and $I_j^v\left(t\right)$ have one and only one intersection point ($I_{\mathit{je}}^c\text{,}{I}_{\mathit{je}}^v$) in the first quadrant. That is, there is one and only one positive equilibrium E ₃. □

Proof 3

In the similar way of Proof 2, we can prove there is one and only one positive equilibrium E ₃ if $({\Lambda }_j^c-{\delta }_j{\beta }_j^c{N}_{\mathit{je}}^c)({\Lambda }_j^v-{\delta }_j{\beta }_j^v{N}_{\mathit{je}}^v)<0$.

A.2. Proof of Theorem 2

Since

$$0⩽x_{\mathit{ijt}}^p⩽{\displaystyle \sum _{j=1}^J}{x}_{\mathit{ijt}}^p⩽Q_{\mathit{it}}^p\text{,}\forall i\text{,}p\text{,}t$$

$$0⩽{\displaystyle \sum _{i=1}^I}{x}_{\mathit{ijt}}^p⩽{\displaystyle \sum _{i=1}^I}{Q}_{\mathit{it}}^p\text{,}\forall j\text{,}p\text{,}t$$

$${\alpha }^p\max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}⩽{\alpha }^p\left(1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right)⩽{\alpha }^p\frac{D_{\mathit{jt}}^p-{\sum }_{i=1}^I{x}_{\mathit{ijt}}^p}{D_{\mathit{jt}}^p}\text{,}\forall j\text{,}p\text{,}t$$

$${\alpha }_{\mathit{jt}}^v+{\displaystyle \sum _{p=l+1}^{l+k}}\left[{\alpha }^p\max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}\right]⩽{\alpha }_{\mathit{jt}}^v+{\displaystyle \sum _{p=l+1}^{l+k}}\left({\alpha }^p\frac{D_{\mathit{jt}}^p-{\sum }_{i=1}^I{x}_{\mathit{ijt}}^p}{D_{\mathit{jt}}^p}\right)={\overline{\alpha }}_{\mathit{jt}}^v\text{,}\forall j\text{,}t$$

If ${\alpha }_M<{\alpha }_{\mathit{jt}}^v+{\sum }_{p=l+1}^{l+k}\left[{\alpha }^p\max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}\right]$ then the problem has no feasible solution as constrain ${\overline{\alpha }}_{\mathit{jt}}^v⩽{\alpha }_M$ is insatiable.

In a similar manner, one can prove that if ${\alpha }_M<{\alpha }_{\mathit{jt}}^c+{\sum }_{p=l+1}^{l+k}\left[{\alpha }^p\max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}\right]$ or ${\beta }_M<{\beta }_{\mathit{jt}}^v+{\sum }_{p=1}^l\left[{\beta }^p\max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}\right]$ or ${\beta }_M<{\beta }_{\mathit{jt}}^c+{\sum }_{p=1}^l\left[{\beta }^p\max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}\right]$, then the problem has no feasible solution.

Since ${\alpha }_{\mathit{jt}}^v>{\alpha }_{\mathit{jt}}^c$ and ${\beta }_{\mathit{jt}}^v>{\beta }_{\mathit{jt}}^c$, one can obtain

$${\alpha }_U={\alpha }_{\mathit{jt}}^v+{\displaystyle \sum _{p=l+1}^{l+k}}\left[{\alpha }^p\max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}\right]\text{,}\forall j\text{,}t$$

$${\beta }_U={\beta }_{\mathit{jt}}^v+{\displaystyle \sum _{p=1}^l}\left[{\beta }^p\max \left\{0\text{,}1-\frac{{\sum }_{i=1}^I{Q}_{\mathit{it}}^p}{D_{\mathit{jt}}^p}\right\}\right]\text{,}\forall j\text{,}t\square$$

Appendix B. Parameters in the numerical study

See Table B.1, Table B.2, Table B.3, Table B.4, Table B.5 .

Table B.1.

Parameters for epidemic and population.

Area	j = 1	j = 2	j = 3	j = 4	j = 5	j = 6
$A_j^c$	504	229	114	80	92	556
$A_j^v$	80	16	−8	−1	6	84
${\beta }_j^c$	0.4	0.45	0.46	0.5	0.48	0.4
${\beta }_j^v$	0.5	0.55	0.56	0.6	0.58	0.55
${\delta }_j$	1.02 × 10−8	1.14 × 10−8	0.33 × 10−8	0.13 × 10−8	1.05 × 10−8	3.11 × 10−8
ε	0.23	0.23	0.23	0.23	0.23	0.23
${\gamma }_j^c$	0.1	0.13	0.1	0.08	0.1	0.1
${\gamma }_j^v$	0.05	0.08	0.05	0.03	0.05	0.05
${\alpha }_j^c$	0.003	0.003	0.006	0.01	0.008	0.005
${\alpha }_j^v$	0.005	0.005	0.008	0.015	0.01	0.007
${\mu }_j$	0.8	0.7	0.6	0.5	0.7	0.6
$d_j^c$	1.00 × 10−5	0.996 × 10−5	1.03 × 10−5	1.01 × 10−5	0.991 × 10−5	1.00 × 10−5
$d_j^v$	3.00 × 10−5	2.99 × 10−5	3.00 × 10−5	2.98 × 10−5	2.99 × 10−5	3.01 × 10−5
$S_j^c$(0)	6,875,080	4,174,889	2,738,309	1,657,264	1,739,502	5,898,274
$S_j^v$(0)	2,971,785	1,391,632	1,288,616	823,680	643,378	1,567,896
$E_j^c$ (0)	316	41	22	29	50	10
$E_j^v$ (0)	136	20	10	15	15	3
$I_j^c$ (0)	198	12	17	15	29	8
$I_j^v$ (0)	85	7	8	7	11	2

Table B.2.

Parameters for medical reliefs.

Area	j = 1	j = 2	j = 3	j = 4	j = 5	j = 6
m1(p = 1)	${\theta }^1=0.01\text{,}{\beta }^1=0.3$
${\text{Inv}}_t^1$	24,000	12,000	6000	5000	1500	3000
$c_{1\mathit{jt}}^1$	0.04	0.24	0.94	2.07	0.91	1.63
$c_{2\mathit{jt}}^1$	0.23	0.11	0.78	2.23	0.74	1.91
$c_{3\mathit{jt}}^1$	0.10	0.28	1.03	2.05	1.04	1.73
$c_{4\mathit{jt}}^1$	1.63	1.91	2.63	1.70	2.54	0.06
m2(p = 2)	${\theta }^2=0.02\text{,}{\beta }^2=0.1$
${\text{Inv}}_t^2$	131,000	41,000	57,000	10,000	200	85,000
$c_{1\mathit{jt}}^2$	0.08	0.48	1.88	4.14	1.82	3.26
$c_{2\mathit{jt}}^2$	0.46	0.22	1.56	4.46	1.48	3.82
$c_{3\mathit{jt}}^2$	0.20	0.56	2.06	4.10	2.08	3.46
$c_{4\mathit{jt}}^2$	3.26	3.82	5.26	3.40	5.08	0.12
m3(p = 3)	${\theta }^3=1\text{,}{\beta }^3=0.1$
${\text{Inv}}_t^3$	21	5	0	0	0	2
$c_{1\mathit{jt}}^3$	0.04	0.24	0.94	2.07	0.91	1.63
$c_{2\mathit{jt}}^3$	0.23	0.11	0.78	2.23	0.74	1.91
$c_{3\mathit{jt}}^3$	0.10	0.28	1.03	2.05	1.04	1.73
$c_{4\mathit{jt}}^3$	1.63	1.91	2.63	1.70	2.54	0.06
m4(p = 4)	${\theta }^4=1\text{,}{\beta }^4=0.3$
${\text{Inv}}_t^4$	20	0	0	0	0	0
$c_{1\mathit{jt}}^4$	0.12	0.72	2.82	6.21	2.73	4.89
$c_{2\mathit{jt}}^4$	0.69	0.33	2.34	6.69	2.22	5.73
$c_{3\mathit{jt}}^4$	0.30	0.84	3.09	6.15	3.12	5.19
$c_{4\mathit{jt}}^4$	4.89	5.73	7.89	5.10	7.62	0.18
m5(p = 5)	${\theta }^5=3\text{,}{\beta }^5=0.2$
${\text{Inv}}_t^5$	300	8	0	0	6	2
$c_{1\mathit{jt}}^5$	0.04	0.24	0.94	2.07	0.91	1.63
$c_{2\mathit{jt}}^5$	0.23	0.11	0.78	2.23	0.74	1.91
$c_{3\mathit{jt}}^5$	0.10	0.28	1.03	2.05	1.04	1.73
$c_{4\mathit{jt}}^5$	1.63	1.91	2.63	1.70	2.54	0.06

Table B.3.

Parameters for EMRCs.

	$Q_{\mathit{it}}^1$	$Q_{\mathit{it}}^2$	$Q_{\mathit{it}}^3$	$Q_{\mathit{it}}^4$	$Q_{\mathit{it}}^5$	$W_{\mathit{it}}$
i = 1	25,000	0	50	0	100	25,000
i = 2	0	100,000	0	75	0	110,000
i = 3	130,000	175,000	150	25	270	300,000
i = 4	60,000	2000	40	0	60	100,000

Table B.4.

Migration matrix for Extended Model 1.

$h_{j_1{j}_2}$	j2 = 1	j2 = 2	j2 = 3	j2 = 4	j2 = 5	j2 = 6
j1 = 1	0	4.57 × 10−7	9.04 × 10−7	5.27 × 10−7	2.88 × 10−7	13.75 × 10−7
j1 = 2	6.00 × 10−7	0	2.94 × 10−7	1.71 × 10−7	0.93 × 10−7	4.46 × 10−7
j1 = 3	44.82 × 10−7	11.14 × 10−7	0	12.84 × 10−7	7.01 × 10−7	33.51 × 10−7
j1 = 4	49.57 × 10−7	12.32 × 10−7	2.44 × 10−7	0	7.76 × 10−7	37.06 × 10−7
j1 = 5	14.92 × 10−7	3.71 × 10−7	7.34 × 10−7	4.28 × 10−7	0	11.16 × 10−7
j1 = 6	0.93 × 10−7	0.23 × 10−7	0.46 × 10−7	0.27 × 10−7	0.15 × 10−7	0

Table B.5.

Additional parameters for Extended Model 2.

$T_{\mathit{ijt}}$	j = 1	j = 2	j = 3	j = 4	j = 5	j = 6		$T_M$
i = 1	0.25	0.40	1.57	2.78	1.52	2.05		2
i = 2	0.88	0.52	1.30	3.38	1.23	3.18
i = 3	0.67	0.47	1.72	3.42	4.13	2.08
i = 4	2.72	2.35	4.38	2.83	4.23	0.43

Appendix C. Results of the numerical study

See Fig. C.1 and Table C.1, Table C.2, Table C.3, Table C.4, Table C.5, Table C.6, Table C.7, Table C.8, Table C.9 .

Table C.1.

Optimal solutions of three models with real data.

		j = 1	j = 2	j = 3	j = 4	j = 5	j = 6
Basic model	i = 1			m1:25,000
	i = 2	m2:10,285	m2:66,175	m2:23,540	m4:4.983	m4:5.867	m4:2.567
		m4:54.72	m4:0.5867	m4:6.403
	i = 3	m1:75,475		m1:34,270		m1:20,225	m2:64,329
		m2:55,665				m4:6.259
	i = 4	m3:23.00	m1:18,666		m1:19,810	m1:2075	m1:19,449
		m5:60.00	m2:2000
			m3:17.00
Extended Model 1	i = 1		m1:25,000
	i = 2	m4:66.20	m2:35,586			m4:5.871	m2:64,414
							m4:2.933
	i = 3	m1:74,480	m1:1486	m1:34,244	m1:19,790	m4:7.569
		m2:65,960	m2:32,533	m2:21,487	m4:5.750
			m4:0.6667	m4:6.403
	i = 4	m3:20.00	m1:17,185	m2:2000		m1:22,328	m1:20,487
		m5:60.00	m3:20.00
Extended Model 2	i = 1	m1:2522		m3:14.00		m1:22,328
						m3:36.00
						m5:100
	i = 2		m2:67,694	m2:23,487	m2:8819	m4:35.00
			m4:8.000	m4:17.00	m4:15.00
	i = 3	m1:71,958	m1:23,798	m1:34,244			m2:62,414
		m2:57,141	m3:3.000	m3:3.000			m4:8.000
		m3:144.0	m4:17.00	m5:52.00			m5:7.000
		m5:144.0	m5:66.00
	i = 4		m1:19,873		m1:19,790		m1:20,337
			m3:17.00		m3:15.00		m2:2000
					m5:45.00		m3:8.000
							m5:15.00

Table C.2.

Optimal solutions of three models in Situation 1.

		j = 1	j = 2	j = 3	j = 4	j = 5	j = 6
Basic model	i = 1	m1:25,000
	i = 2	m2:31,821	m2:68,179	m4:4.524	m4:4.767	m4:11.41	m4:2.450
		m4:51.63
	i = 3	m1:32,254	m1:43,666	m1:34,270	m1:19,810		m2:62,329
		m2:34,129		m2:23,540
				m4:1.596
	i = 4	m1:18,221	m3:17.00			m1:22,330	m1:19,449
		m3:23.00					m2:2000
		m5:60.00
Extended Model 1	i = 1	m1:25,000
	i = 2	m2:35,586				m4:9.511	m2:64,414
		m4:62.69					m4:2.800
	i = 3	m1:33,154	m2:68,114	m1:34,245	m1:19,790		m1:20,483
		m2:30,381		m2:21,489	m4:5.500	m1:22,328
				m4:6.480
	i = 4	m1:16,329	m1:43,671	m2:2000
		m3:20.00	m3:20.00
		m5:60.00
Extended Model 2	i = 1	m1:2522	m3:3.000			m1:22,328
		m3:11.00				m3:36.00
						m5:100.0
	i = 2	m2:65,967	m2:34,033	m4:18.00	m4:15.00	m4:34.00
			m4:8.000
	i = 3		m1:23,794				m2:62,414
		m3:132.0	m2:33,652	m2:23,489			m4:8.000
		m5:142.0	m4:17.00	m3:18.00			m5:7.000
			m5:66.00	m5:54.00
	i = 4		m1:19,877		m1:19,790		m1:20,333
			m3:17.00		m3:15.00		m2:2000
					m5:45.00		m3:8.000
							m5:15.00

Table C.3.

Numerical results of experimental testing in Situation 1.

Model	Basic model	Extended Model 1	Extended Model 2
Average mortality rate	0.498	0.498	0.089
Average infection rate	0.373	0.372	0.372
Total amount of prophylactic reliefs	436,998	436,984	436,455
Total amount of treatment reliefs	177	191	770
Cost	481,090	610,594	464,306
Physical fragility	2,425,069	2,418,231	2,420,013
Psychological fragility	2,297,467	2,323,959	1,149,958

Table C.4.

Optimal solutions of three models in Situation 2.

		j = 1	j = 2	j = 3	j = 4	j = 5	j = 6
Basic model	i = 1		m1:5190		m1:19,810
	i = 2	m2:12,131		m2:23,540	m4:4.767	m4:11.41	m2:64,329
		m4:52.92		m4:4.229			m4:2.450
	i = 3	m1:74,475	m1:33,195	m4:1.891		m1:22,330
		m2:51,820	m2:68,178
	i = 4	m2:2000	m1:5282	m1:34,270			m1:20,448
		m3:23.00	m3:17.00
		m5:60.00
Extended Model 1	i = 1	m1:25,000
	i = 2	m2:35,586		m4:6.480	m4:5.500	m4:12.84	m2:64,414
		m4:47.13					m4:2.800
	i = 3	m1:32,294	m1:43,671	m1:34,245	m1:19,790
		m2:28,374	m2:68,121	m2:23,489
		m4:15.93
	i = 4	m1:17,186	m3:20.00			m1:22,328	m1:20,486
		m2:2000
		m3:20.00
		m5:60.00
Extended Model 2	i = 1	m1:2522	m3:3.000			m1:22,328
		m3:11.00				m3:36.00
						m5:100.0
	i = 2	m2:30,417	m2:67,692	m4:18.00	m2:1891	m4:34.00
			m4:8.000		m4:15.00
	i = 3	m1:71,958	m1:23,797	m1:34,245		m5:1.000	m2:62,414
		m2:33,652	m4:17.00	m2:23,489			m4:8.000
		m3:132.0	m5:66.00	m3:18.00			m5:7.000
		m5:142.0	m5:54.00
	i = 4		m1:19,874		m1:19,790		m1:20,336
			m3:17.00		m3:15.00		m3:8.000
					m5:45.00		m3:8.000
							m5:15.00

Table C.5.

Numerical results of experimental testing in Situation 2.

Model	Basic model	Extended Model 1	Extended Model 2
Average mortality rate	0.498	0.498	0.089
Average infection rate	0.772	0.772	0.772
Total amount of prophylactic reliefs	436,998	436,984	436,405
Total amount of treatment reliefs	177	191	770
Cost	527,057	539,718	451,672
Physical fragility	5,307,370	5,307,397	5,312,915
Psychological fragility	2,171,765	2,314,800	1,156,000

Table C.6.

Optimal solutions of three models in Situation 3.

		j = 1	j = 2	j = 3	j = 4	j = 5	j = 6
Basic model	i = 1		m1:25,000
	i = 2	m2:35,671	m4:11.20			m4:27.20	m2:64,329
		m4:31.55					m4:5.050
	i = 3	m1:74,475	m1:15,266	m2:21,540	m1:19,810		m1:20,449
		m2:30,280	m2:67,781	m4:13.65	m4:11.00
		m3:103.6
		m5:270.0
	i = 4	m3:25.00	m1:3400	m1:34,270		m1:22,330
		m5:60.00	m3:15.00	m2:2000
Extended Model 1	i = 1	m1:25,000
	i = 2	m2:12,097	m4:1.320	m2:23,489	m4:11.92	m4:27.20	m2:64,414
		m4:29.16					m4:5.400
	i = 3	m1:49,480	m1:3461	m1:34,245		m1:22,328	m1:20,486
		m2:53,863	m3:16.00	m4:14.56
		m3:177.0	m4:10.44
		m5:270.0
	i = 4	m3:40.00	m1:40,210		m1:19,790
		m5:60.00	m2:2000
Extended Model 2	i = 1	m1:2522		m5:24.28		m1:22,328
		m3:50.00
		m5:75.72
	i = 2	m2:32,308	m2:67,692		m4:13.00	m4:27.20
		m4:16.80	m4:18.00
	i = 3	m1:71,958	m1:23,797	m1:34,245			m2:62,414
		m2:33,652	m4:3.000	m2:23,489			m4:6.000
		m3:134.0	m5:11.00	m3:16.00
		m5:259.0		m4:16.00
	i = 4	m3:5.000	m1:19,874		m1:19,790		m1:20,336
			m3:16.00		m3:13.00		m2:2000
			m5:44.00				m3:6.000
							m5:16.00

Table C.7.

Numerical results of experimental testing in Situation 3.

Model	Basic model	Extended Model 1	Extended Model 2
Average mortality rate	0.472	0.472	0.303
Average infection rate	0.372	0.372	0.372
Total amount of prophylactic reliefs	436,601	436,572	436,405
Total amount of treatment reliefs	574	603	770
Cost	767,627	555,226	443,918
Physical fragility	2,418,860	2,418,920	2,419,981
Psychological fragility	1,942,086	1,776,862	1,151,773

Table C.8.

Optimal solutions of three models in Situation 4.

		j = 1	j = 2	j = 3	j = 4	j = 5	j = 6
Basic model	i = 1	m1:25,000
	i = 2	m2:65,951	m2:10,509	m2:23,540		m4:27.20	m4:5.05
		m4:31.55	m4:11.20
	i = 3	m1:29,734	m1:43,667	m1:34,269	m4:11.00	m1:22,330	m2:64,329
		m3:89.59	m2:55,272	m4:13.65
		m5:270.0	m3:15.00
	i = 4	m1:19,741	m2:2000		m1:19,810		m1:20,449
		m3:40.00
		m5:60.00
Extended Model 1	i = 1		m1:25,000
	i = 2	m2:65,960	m4:1.320		m4:11.92	m4:27.20	m2:34,040
		m4:29.16					m4:5.400
	i = 3	m1:74,480	m1:18,671	m1:34,245		m1:2604	m2:28,374
		m3:136.7	m2:67,706	m2:23,489
		m5:270.0	m4:10.44	m4:14.56
	i = 4	m3:24.00	m3:16.00		m1:19,790	m1:19,724	m1:20,486
		m5:60.00					m2:2000
Extended Model 2	i = 1	m1:2522	m5:11.00	m3:16.00		m1:23,328
		m3:34.00		m5:21.67
		m5:67.33
	i = 2	m2:65,153	m2:10,551	m2:23,489	m2:1807	m4:27.20
		m4:16.80	m4:18.00		m4:13.00
	i = 3	m1:71,958	m1:23,797	m1:34,245			m2:62,414
		m3:150.0	m2:57,141	m4:16.00			m4:6.000
		m5:270.0	m4:3.000
	i = 4	m3:5.000	m1:19,874		m1:19,790		m1:20,336
			m3:16.00		m3:13.00		m2:2000
			m5:44.00				m3:6.000
							m5:16.00

Table C.9.

Numerical results of experimental testing in Situation 4.

Model	Basic model	Extended Model 1	Extended Model 2
Average mortality rate	0.472	0.472	0.304
Average infection rate	0.772	0.772	0.772
Total amount of prophylactic reliefs	436,601	436,569	436,405
Total amount of treatment reliefs	574	606	770
Cost	472,774	487,172	467,576
Physical fragility	5,308,059	5,308,123	5,312,750
Psychological fragility	1,759,643	1,742,787	1,161,607

Fig. C.1.

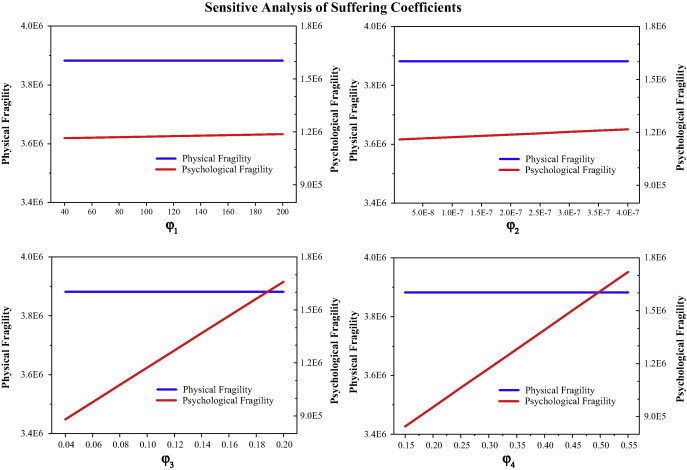
Sensitive analysis of suffering coefficients with real data.

Appendix D.

Standard SEIR model

$$\left\{\begin{array}{c}\frac{{\mathit{dS}}_j(t)}{\mathit{dt}}=A_j-d_j{S}_j\left(t\right)-{\beta }_j{\delta }_j{S}_j\left(t\right)I_j\left(t\right)\hfill \\ \frac{{\mathit{dE}}_j(t)}{\mathit{dt}}={\beta }_j{\delta }_j{S}_j\left(t\right)I_j\left(t\right)-d_j{E}_j\left(t\right)-\epsilon E_j\left(t\right)\hfill \\ \frac{{\mathit{dI}}_j\left(t\right)}{\mathit{dt}}=\epsilon E_j\left(t\right)-d_j{I}_j\left(t\right)-{\alpha }_j{I}_j\left(t\right)-{\gamma }_j{I}_j\left(t\right)\hfill \\ \frac{{\mathit{dR}}_j(t)}{\mathit{dt}}={\gamma }_j{I}_j\left(t\right)-d_j{R}_j\left(t\right)\hfill \end{array}\right)$$

The number of prophylactic demanders in time period t is ${\int }_{t_0}^{t_0+L}\left[S_j\left(t\right)+E_j\left(t\right)\right]\mathit{dt}$ and the number of treatment demanders in time period t is ${\int }_{t_0}^{t_0+L}{I}_j\left(t\right)\mathit{dt}$, where $t_0$ refers to the beginning moment of period t and Lis the length of a time period.

Parameters are set as follows (j = 1): $A_1=584\text{,}{d}_1=0.00002\text{,}{\alpha }_1=0.0045\text{,}{\beta }_1=0.4\text{,}{\delta }_1=$1.02 × 10⁻⁸, $\epsilon =0.23\text{,}{\gamma }_1=0.08\text{,}{S}_1\left(0\right)=9847978\text{,}{E}_1\left(0\right)=452\text{,}{I}_1\left(0\right)=283\text{,}{R}_1\left(0\right)=0$.

Moving average model

$$N_{\mathit{jt}}=0.7N_{\mathit{jt}-1}+0.2N_{\mathit{jt}-2}+0.1N_{\mathit{jt}-3}$$

where $N_{\mathit{jt}}$ refers to the number of demanders in area j in time period t.