Analytical considerations associated with implementing M²⁺ correction factors to address false positives on As and Se within U.S. EPA method 200.8

Abstract

Rare earth elements (REE) can produce M²⁺ ions in ICP-MS and ¹⁵⁰Nd²⁺, ¹⁵⁰Sm²⁺, and ¹⁵⁶Gd²⁺ can produce false positives on ⁷⁵As and ⁷⁸Se. Alternative instrumental tuning conditions, that utilize lower He flows within the collision cell, reduce these false positives by a factor of 2 (to 0.8 ppb As and 19 ppb Se in solutions containing 50 ppb Nd and Gd) with comparable ¹⁶O³⁵Cl⁺ reduction (<100 ppt false ⁵¹V in 0.4% HCl) and Se sensitivity (DL < 1 ppb). Further reduction of these false positives is achieved by estimating the M²⁺ correction factors and utilizing them in the interference-correction software. Approaches to estimating the M²⁺ correction factor were evaluated with an emphasis on techniques that tolerate daily variability in end-user backgrounds and their ability to reduce the initial and ongoing purity requirements associated with the rare earth standards used to estimate the M²⁺ correction factor. The direct elemental and polyatomic overlaps associated with unit-mass approaches tend to overcorrect as non-rare-earth signals as small as 30 cps at the unit mass can induce bias relative to the <300 cps signals associated with the M²⁺ from a 50 ppb REE standard solution. Alternatively, shifting the M²⁺ estimate to a half mass (i.e., m/z 71.5: ¹⁴³Nd²⁺) eliminates the direct overlap source of bias and allows the unit mass signal to approach 150000 cps before it bleeds over on the 1/2 mass because of abundance sensitivity limitations. The performance of the half-mass approach was evaluated in reagent water and regional tap waters fortified with Nd, Sm, and Gd at 2 ppb and 50 ppb. In addition, a half-mass in-sample approach was also evaluated. This approach was found to be beneficial relative to the external or fixed-factor half-mass approach as it could compensate for instrument drift and matrix-induced shifts in the M²⁺ factors. Finally, all results were evaluated relative to the As and Se concentrations determined using an ICP-QQQ in mass shift mode and a high-resolution ICP-MS.

Introduction

Rare earth elements (REEs) are relatively abundant in the earth’s crust (Ce, the most abundant REE is more common than Cu or Pb), but finding a minable deposit that is both economically and environmentally friendly is challenging.^1–3 REEs have unique properties that make them almost irreplaceable in the electronics, nuclear, medical, and glass industries,^1,4 while their chemical similarity adds to the difficulty of purifying them from a mineral deposit.^2,3 The use of REEs in light-emitting diode lighting and hybrid car technology and their potential use as refrigerants indicate a growing role for REEs^1,2 as industries look for more sustainable processes.² As these REE-oriented technologies are adopted, the occurrence of REEs in environmental assessment samples is likely to increase.⁵

In an argon plasma, REEs such as neodymium, samarium, gadolinium, and dysprosium can produce M²⁺ ions (¹⁵⁰Nd²⁺, ¹⁵⁰Sm²⁺, ¹⁵⁶Gd²⁺, and ¹⁵⁶Dy²⁺), leading to false positives on ⁷⁵As and ⁷⁸Se if inductively coupled plasma mass spectrometry (ICP-MS) methodologies are used for compliance monitoring.⁶ ICP-MS is rapidly becoming the method of choice for metals compliance monitoring because of its sensitivity and multielement capability. The impact of M²⁺ ions as interferences in ICP-MS has been recognized since its inception.^7,8 Even today, the formation of M²⁺ ions such as Ba²⁺ and Ce²⁺ is commonly documented as a performance specification by instrument manufacturers in an attempt to minimize this as a source of false positives. These false positives in both water and waste are not common but can make the difference between compliance and costly treatment. In a 4 month review of ICP-MS data, US EPA Region 4 laboratory found that 7% of their Se results in water (91% in soil) and 5.4% of their As results in water (59% in soil) would have been altered by 20% or more without implementation of a M²⁺ correction.⁹ Recently, doubly charged polyatomic argon species, for example, BaAr²⁺, have been added to the list of M²⁺ potential interferences.¹⁰ Merging these M²⁺ oriented interferences with the list of plasma- and matrix-induced polyatomics¹¹ makes it increasingly more difficult to imagine a universal interference-reduction approach that maintains a multi-element mind-set while tolerating a diversity of sample matrices. Reaction cell approaches can provide enhanced interference reduction and analyte signal preservation by understanding and optimizing the gas- phase chemistry between the reaction gas and the analyte/interfering ion that facilitates the separation.^12–17 This increased specificity is attractive in some analytical arenas, but this specificity is targeted and limited to a few elements in a fairly well-defined matrix.^17,18 Admittedly, some of these limitations are addressed or at least minimized by the added selectivity achieved by specifying a single mass to enter the reaction cell (ICP-QQQ) versus the initial band pass associated with the dynamic reaction cell (DRC). Alternatively, He-collision cell approaches only address polyatomics and typically do not generate the same level of interference reduction; however, they are generally beneficial to a wider set of interferences, making them more amenable to a multi-element-based analysis.¹⁹

The inclusion of an interference-reduction technology that preserves the multi-element capability while addressing the wide spectrum of plasma- and matrix-dependent polyatomic interferences such as ¹⁶O³⁵Cl⁺, ⁴⁰Ar¹²C⁺, ⁴⁰Ar³⁵Cl⁺, and ⁴⁰Ar³⁸Ar⁺ (ref. 19–21) is analytically attractive from an environmental compliance monitoring perspective. However, the almost universal benefits of polyatomic interference reduction associated with an He-collision cell are not favorable for M²⁺ interferences.^22–25 These and other M²⁺ interferences, although not as common as matrix induced polyatomic interferences, they are a source of false positives and have fueled interest in addressing this shortcoming through the use of reaction gases in combination with the earlier DRC instruments.^26,27 This is done through the use of H₂ for Gd²⁺ (ref. 28) and, more recently, use of ICP-QQQ technology.^22,23,29,30 While ICP-QQQ reaction-oriented technologies are very effective in eliminating REEs as M²⁺ interferences, they come with an added instrumental cost. Therefore, updating a single quadrupole method such as U.S. Environmental Protection Agency (EPA) method 200.8 to include He-collision cell technology while formally addressing the false positives from M²⁺ ions through the use of M²⁺ correction factors would benefit the compliance monitoring community.

There are different approaches to estimate and apply M²⁺ correction factors in ICP-MS. Fixed-external-unit-mass approaches that are element specific are the most common. These approaches use the response at the unit mass associated with the M²⁺ interference (i.e., m/z 75 for Nd²⁺) and the response at the mass used to monitor that same element (i.e., m/z 143 for Nd¹⁺) to directly estimate a fixed M²⁺ correction factor for a specific element using an external solution. The M²⁺ correction factors are typically entered into the instrument interference-correction software and are applied uniformly to all the samples in a batch similar to the correction used in the U.S. Food and Drug Administration Elemental Analysis Manual, Section 4.7.³¹ In addition to the above approaches, there are indirect element-specific approaches that use unit-mass or half-mass²⁴ oriented data; these approaches can use data from either normal or narrow resolution modes. However, the unit-mass approaches are more susceptible to elemental, polyatomic overlap and end-user-specific blank control issues. Half-mass-based approaches with narrow resolution data collection avoid these sources of bias²⁴ and should produce a more robust M²⁺ estimate across a wide variety of users, making them beneficial in a compliance monitoring method.

In this manuscript, we show the traditional instrumental optimization that balances polyatomic interference reduction and analyte sensitivity needs to be expanded to include M²⁺ as interferences. The authors compare half-mass and unit-mass approaches to estimate M²⁺ correction factors and demonstrate the added utility of using narrow resolution mode to generate M²⁺ estimates. Additionally, we provide data that indicate that some bias is generated by not adopting end-user and tune-specific isotopic ratio (i.e., ¹⁴³Nd/¹⁵⁰Nd) estimates within indirect M²⁺ correction approaches. The work also shows that there is a bias between M²⁺ correction factors estimated in normal resolution mode and narrow resolution mode and that the magnitude of this bias is dependent on He flow. Finally, the authors compare the As and Se concentrations in reagent water and regional tap waters fortified with Nd, Sm, and Gd to concentrations obtained from an ICP-QQQ in mass shift mode and a high-resolution ICP-MS.

Experimental

Standards and reagents

Single-element rare earth solutions containing Nd, Sm, and Gd that were used to fortify both standard and drinking water matrices were obtained from Spex (Metuchen, NJ). The multi-element calibration standard 1A (Spex) was used to calibrate the ICP-MS instrument. EPA method 200.8 Standard 2 from High Purity (Charleston, SC), along with NIST 1643e Trace Elements in Water were used as secondary sources. Single-element standards (Spex) of As and Se were used to fortify the reagent water samples. The 10 ppb internal standard mixture of Li, Sc, Ge, Y, In, Tb, and Bi was purchased from Agilent (Palo Alto, CA). The nitric and hydrochloric acids (Ultrex® II Ultrapure Reagent) used to acidify standard solution and drinking water samples were purchased from J. T. Baker (Center Valley, PA). All solutions were prepared by diluting the primary stocks with 18 MΩ water (Millipore, Burlington, MA), and all dilutions were made gravimetrically using Rainin (Oakland, CA) pipettes on either a Mettler (Columbus, OH) PM 1200 or an AG204 balance. Samples were made and stored in class 100 clean benches (Labconco, Kansas City, MO). Drinking water samples were collected from different regions in the United States.

Instrumentation

All single quadrupole-based data were collected on an Agilent 7700 ICP-MS equipped with a helium collision cell, torch shield, and bonnet. The autosampler used was an Agilent ASX-500. Oxides were minimized by using low sample uptake (0.1 rps) in combination with a sampling depth of 8 mm and a double-pass spray chamber held at 2 °C. These tuning conditions typically produced a CeO⁺/Ce⁺ ratio of <0.6% with the He flow optimized. The energy discrimination (ED, is the difference in potential between the octopole and the quadrupole) was set at 5 V in order to capitalize on the kinetic energy difference between analyte ions and polyatomic ions and to minimize the potential impact of any polyatomic ion formation in the cell.²⁰ The ED of 5 V was used in combination with an octopole bias of −12 V unless otherwise noted. The collision cell He was an ultra high-purity grade (99.999%, Indiana Oxygen, Indianapolis, IN) and was passed through a triple filter (Agilent, part number 5182–9705) prior to entering the cell. This triple filter cartridge is a single carrier filter that removes hydrocarbon, moisture and oxygen. Data were collected in normal resolution mode (0.8 amu at 10% peak height) and narrow resolution mode (0.4 amu at 10% peak height) to evaluate the abundance-sensitivity implication of utilizing half-mass integration to estimate M²⁺ correction factors. The resolution mode is often a variable; for this reason, this information was included in the footnotes associated with each figure to ensure clarity. The deflect lens located downstream of the collision cell and before the plate bias voltage was optimized to reduce the M²⁺. In general, the deflect lens voltage works in combination with the cell exit voltage and the plate bias voltage to determine ion trajectory post collision cell. In this work, several experiments are performed in which the deflect lens potential was varied while maintaining a consistent exit cell and plate bias voltage to monitor the effect of deflect lens voltage changes on M²⁺ and analyte sensitivity. All half-mass data were exported and integrated using a 0.15 amu integration window in Excel. This external integration was necessary to estimate some of the M²⁺ correction factors prior to use in the instrument’s interference-correction software. All concentrations were determined using indium as an internal standard after adding the necessary M²⁺ correction factors in the interference-correction software. Fig. 1 highlights the experimental factors (e.g., mass selection, acquisition mode) that impact the formulation of the appropriate M²⁺ correction factor applied to the Agilent 7700 data. Fig. 1 includes an example of the associated M²⁺ calculation for an Nd correction on arsenic using a narrow resolution mode and an external rare earth standard solution to estimate the response at m/z 71.5 (Nd²⁺) and 143 (Nd¹⁺). In Fig. 1, these experimental factors are denoted using subscripts and superscripts to ensure clarity. A complete set of example calculations is included in the ESI‡ section entitled: M²⁺ correction equations for figures and data tables.

Figure 1.

Experimental parameters that impact the formulation of the M²⁺ correction equation¹ Notes: 1. The ¹⁵⁰Nd²⁺ correction on m/z 75 is used as an example, while the approaches can be applied to Sm²⁺ and Gd²⁺ corrections as well. 2. The rare earth M²⁺ and M¹⁺ pairs used in this paper were 71.5/143, 74.5/149, and 77.5/155 for Nd, Sm, and Gd, respectively. 3. A rare earth odd mass isotope is used in half-mass M²⁺ corrections, and this was the only type of correction used in presented in this paper to generate recovery data. 4. Narrow and normal resolution modes can be used to estimate half-mass M²⁺ correction factors, but only the narrow mode approach was used to generate recovery data. 5. M²⁺ correction factors can be estimated using an external rare earth standard solution or they can be estimated in the sample matrix (in-sample). 6. Samples are analyzed using normal resolution to preserve sensitivity when using an external rare earth solution to estimate the M²⁺ correction. In-sample M²⁺ estimates require the analysis be conducted in narrow resolution mode to minimize the impact of elemental overlap and abundance-sensitivity issues in actual samples. 7. Normal resolution is defined as 0.8 amu at 10% peak height. 8. Narrow resolution is defined as 0.4 amu at 10% peak height. 9. This is an abbreviation that summarizes the experimental details associated with a ¹⁵⁰Nd²⁺ correction on m/z 75. Once this factor is estimated, it is used directly in the Agilent interference-correction software. 10. This factor is only used when the M²⁺ correction factors are estimated using narrow resolution and the samples are analyzed in normal resolution mode.

All ICP-QQQ data were collected using an Agilent 8800 ICP-MS. Both As and Se were analyzed in a mass-shift mode using oxygen (0.5 mL min⁻¹) as a reaction gas at m/z 91 and 94, respectively. Yttrium (YO⁺, 89 → 105) was used as an internal standard for the mass-shifted analytes because of the increased sensitivity of the oxygen reaction product ions compared to other commonly used internal standards. The short term reproducibly of the 89 → 105 mass-shift was determined by analyzing multiple yttrium fortified calibration standards over the course of one hour. Based on the plasma conditions used in this work less than a 3% change in cps (counts per second) for the 89 → 105 mass-shift was measured. All data were collected using selective ion monitoring with a 0.99 s per amu integration time with yttrium (YO⁺, 89 → 105) as an internal standard.

High-resolution data were collected using a Thermo Finnigan Element2 double-focusing magnetic sector ICP-MS equipped with a 100 μL min⁻¹ PFA micronebulizer and a cyclonic quartz spray chamber (Elemental Scientific, Omaha, NE). Both ⁷⁵As and ⁷⁸Se were analyzed in the high-resolution mode to provide resolution between the analyte and the associated M²⁺ ions. The sensitivity for ⁷⁵As and ⁷⁷Se are 1166 and 127 cps μg⁻¹ L⁻¹, respectively in high resolution mode. All data were collected using 40 samples per peak over a 0.200 s sampling time, 30% search and 60% integration windows, and indium as the internal standard over 3 runs and 2 passes (n = 6). The Auto Lock Mass feature was active during analysis.

Results and discussion

Fig. 2 is an ICP-MS mass spectrum (using 0.4 amu at 10% peak height) of a solution containing 50 ppb Nd, Sm, and Gd. The brackets in the figure indicate the corresponding mass range of the Nd²⁺, Sm²⁺, and Gd²⁺ interferences in the solution. At this resolution setting, the odd mass isotopes of Nd, Sm, and Gd produce baseline distinguishable signals at the corresponding half-masses, while some of the even isotopes produce signals at the masses commonly used for quantification (⁷⁵As, ⁷⁸Se), thereby producing false positives for the respective analytes. In this solution, the As and Se concentrations were determined to be 17 ppt and 41 ppt; respectively, using an ICP-QQQ. Ge was added as an internal standard at a concentration of 4.6 ppb. Therefore, it is reasonable to attribute most of the signal at these masses to the M²⁺ ions. The M²⁺ ions that overlap with Ge isotopes can also produce bias but for a much wider spectrum of analytes because it is commonly used as an internal standard. These M²⁺ ions can be classified as isobaric interferences for theses analyte masses, but they cannot be dissociated in the He-collision cell and do not respond to kinetic energy discrimination like most polyatomic ions²⁰ (e.g., ArCl⁺). In fact, the M²⁺/M¹⁺ percentage has been shown to be enhanced relative to polyatomic or elemental ions of the same mass to charge as He flow increases.²² Therefore, increased He flow that is beneficial to polyatomic interference reduction increases the need for accurate M²⁺ correction factors estimates. Ideally, He-collision cell optimization approaches that balance polyatomic reduction and analyte sensitivity preservation should be expanded to consider the impact of M²⁺ ions as false positives.

Figure 2.

Isobaric interferences produced from Nd²⁺, Sm²⁺, and Gd²⁺ ions in ICP-MS–based analysis¹ Note: 1. This mass spectrum was collected in scan mode (2 seconds per amu) using narrow resolution (0.4 amu at 10% peak height) with an Octopole of −12V and an energy discrimination of 5 V. 2. The As and Se concentrations were determined to be 17 ppt and 41 ppt; respectively, using an ICP-QQQ. Ge was added as an internal standard at a concentration of 4.6 ppb.

Fig. 3A is a contour plot of Se sensitivity and ¹⁶O³⁵Cl⁺ (reported as V equivalence) response as a function of He flow and deflect lens potential. Se sensitivity is used in this plot because its ICP-MS sensitivity relative to compliance monitoring requirements is low (relative to other elements); ¹⁶O³⁵Cl⁺ is used because its false positive at m/z 51 is reduced but often not eliminated in a 0.4% HCl acid matrix that is characteristic of digested samples within method 200.8.⁶ In Fig. 3A, low He flow rates produce poor ¹⁶O³⁵Cl⁺ reduction, while high He and high deflect potentials result in poor Se sensitivity. A compromised set of tuning conditions surrounds the line starting at 2.5 mL He per min per deflect 20 V and ending at 4.5 mL He per min per deflect 5 V. In this region, the false positive from ¹⁶O³⁵Cl⁺ has been minimized (<100 ppt as V equivalence, approximately 180-fold reduction relative to the corresponding no He tune) and an appropriate selenium detection limit for compliance monitoring under method 200.8 (MDL < 1.0 ppb) was achieved. In Fig. 3B, the Nd²⁺ response at m/z 71.5 is converted (see footnotes for Fig. 3B) to an As equivalent concentration and overlaid on the ¹⁶O³⁵Cl⁺ contour reported in Fig. 3A. In Fig. 3B, the As equivalence produced by the Nd²⁺ is about 0.5 ppb at a He flow rate of 0 mL min⁻¹, and it steadily increases as the He flow is increased at a fixed deflect potential. However, if we focus on the region that produced a compromise between Se sensitivity and ¹⁶O³⁵Cl⁺ reduction in Fig. 3A, the As equivalence increases from 0.9 ppb (2.5 mL He per deflect, 20 V) to 1.9 ppb (4.5 mL He per deflect 5 V) at the two endpoints. These data indicate that there are instrument-tuning conditions that reduce M²⁺ false positives; these tunes also produce adequate ¹⁶O³⁵Cl⁺ reduction and Se sensitivity that is compatible with compliance monitoring.

Figure 3A.

Se detection limit and ¹⁶O³⁵Cl⁺ reduction as a function of He flow and deflect potential^1–3 Notes: 1. The Se detection limit is estimated using 3 times the standard deviation of the background divided by the slope of the calibration and the unit of measure is ppb. 2. The vanadium equivalence is calculated based on the response from a 10 ppb V standard associated with that specific He flow and deflect potential and the unit of measure is ppb. 3. The data are collected in narrow resolution mode (0.4 amu at 10% peak height) using selective ion monitoring with a dwell time of 0.3 sec/amu at an Octopole of −12V and an energy discrimination of 5 V.

Figure 3B.

Arsenic equivalence from ¹⁵⁰Nd²⁺ and ⁵¹V equivalence from ¹⁶O³⁵Cl⁺as a function of He flow and deflect potential^1–3 Notes: 1. The m/z 75 response from ¹⁵⁰Nd²⁺ is estimated by using the response at m/z 71.5 and multiplying it by the tune-specific ¹⁵⁰Nd to ¹⁴³Nd ratio. This response is converted to As equivalence based on the response from an As standard associated with that specific He flow and deflect potential. The unit of measure is ppb. 2. The vanadium equivalence is calculated based on the response from a 10 ppb V standard associated with that specific He flow and deflect potential. The unit of measure is ppb. 3. The data are collected in narrow resolution mode (0.4 amu at 10% peak height) using selective ion monitoring with a dwell time of 0.3 sec/amu at an Octopole of −12V and an energy discrimination of 5 V.

The effect of alternative octopole potential on these contour plots is shown in ESI Fig. S1.‡ In all cases, an increased deflect potential produces a further reduction of the ¹⁶O³⁵Cl⁺ at a fixed He flow, while increased He flow at a fixed deflect potential also reduces the amount of ¹⁶O³⁵Cl⁺ interference independent of octopole settings. The net effect at both −12 V and −18 V octopole settings is that if the deflect potential is not used to reduce ¹⁶O³⁵Cl⁺ and the optimization relies purely on He flow for its reduction; the resulting tune will generate more M²⁺ interferences. Therefore, tuning approaches that capitalize on the deflect potential to reduce polyatomics are beneficial because they do not have the negative consequence of added M²⁺ transmission that is associated with increased He flow. It should also be noted that the As equivalence difference across the two tunes is larger at an octopole setting of −18 V. Finally, the residual M²⁺ signal associated with all instrumental tunes was evaluated, and these residual signals indicate that further reduction could be achieved using mathematical M²⁺ corrections.

A second goal of our research was to evaluate procedures for estimating M²⁺ factors, with a focus on approaches that will tolerate a variety of end user-specific instrumental backgrounds (m/z approximately 65–80) and minimizing the initial and ongoing end-user based purity requirements for the external solutions used to estimate the M²⁺ correction factors. In Fig. 4, the Gd²⁺ correction factor is estimated as a function of He flow rate using both unit-mass and half-mass data²⁴ that were collected in both narrow and normal resolution modes. Fig. 4 indicates that any source of residual signal at m/z 78 (⁴⁰Ar³⁸Ar⁺, ⁷⁸Kr⁺, ⁷⁸Se⁺) is going to produce a positive bias in estimating a unit mass-based Gd²⁺ correction factor. The underlying problems are that day-to-day cell optimization can produce a variable residual ⁴⁰Ar³⁸Ar⁺ signal, krypton content can vary across argon dewars, and some end-users may also suffer from Se blank control issues. Estimating the impact of the non-¹⁵⁶Gd²⁺ sources of signal at m/z 78 on an ongoing basis is possible. However, having the end-user sorting through the potential sources of non-¹⁵⁶Gd²⁺ signal on a daily basis is difficult to implement within the context of a standardized method. The sources of error mentioned above are unique to unit-mass approaches and m/z 78; however, similar sources of error exist for Nd²⁺ and Sm²⁺ (m/z 75; ⁴⁰Ar³⁵Cl, ⁷⁵As) depending on the unit mass selected to estimate the numerator (M²⁺ response) in the M²⁺ correction factor. The half-mass approaches shown in Fig. 4 produce Gd²⁺ correction factors that are more consistent with respect to He flow because they avoid direct overlaps and are more tolerant of non-¹⁵⁶Gd²⁺ signals (⁷⁸Kr⁺, ⁴⁰Ar³⁸Ar⁺, and ⁷⁸Se⁺).

Figure 4.

Estimating Gd²⁺ correction factors as a function of He flow rate using unit- and half-mass correction approaches in both normal and narrow resolution^1–3Notes:1. Normal resolution mode is defined as 0.8 amu at 10% peak height, and narrow resolution mode is defined as 0.4 amu at 10% peak height. 2. Five instrument replicates were averaged using a dwell time of 0.1 sec/point. Each point represents 0.05 amu. The estimate for the response was obtained from a 0.15-amu integration window. 3. A second more concentrated Gd solution was used to estimate the M²⁺ factors at a He flow rate greater than 2.5 mL/min because of the decreased sensitivity at these higher He flow rates.

The abundance-sensitivity limitations associated with half-mass approaches using normal resolution mode can be further enhanced by adopting a narrow resolution-based tune to make the estimate. In Fig. 4, this is evident by the consistent Gd²⁺ correction factor (<1%) estimates even at low He flows where signals from ⁴⁰Ar³⁸Ar⁺ are present. The abundance-sensitivity considerations between normal and narrow resolution modes are further defined in ESI Fig. S2A,‡ where the signal from the more abundant ¹⁴⁴Nd²⁺ is beginning to bleed over into the 0.15 amu wide integration window of 71.5 (¹⁴³Nd²⁺) in normal resolution mode. The amount of bleed-over will depend on the Nd concentration (¹⁴⁴Nd²⁺), the Ge impurity in the external solution (⁷²Ge), and any end user-specific background at m/z 72. ESI Fig. S2B‡ illustrates the impact of Ge impurity on the Nd²⁺ correction factor (71.5/143) in both narrow and normal resolution modes by sequentially increasing the concentration of Ge. ESI Fig. S2B‡ indicates that the signal at m/z 72 can exceed 150000 cps in narrow resolution mode with little change in the Nd²⁺ correction factor, while the same 150000 cps produces an approximately 300% increase in the correction factor if normal resolution mode is used. Clearly, the half-mass approaches are abundance-sensitivity limited but they are beneficial relative to a unit-mass approach by minimizing the purity constraints associated with the solution used to estimate the M²⁺ and by providing added protection against end user-specific backgrounds. Similar half-mass protections are experienced in estimating Sm and Gd M²⁺ factors (data not shown), while the list of elemental overlaps and ions responsible for abundance-sensitivity-induced limitations are dependent on which M²⁺ correction factor is being determined. In Fig. 4, the smallest M²⁺ correction factor is generated when the instrument is optimized to reduce both polyatomic and M²⁺ interference (see Fig. 3B). These tunes have smaller M²⁺ false positives associated with them and, when they are coupled with narrow resolution-based M²⁺ correction factor estimates, the end user is provided a greater tolerance against the sources of bias induced by M²⁺ ions, which is beneficial within the context of a compliance monitoring method. In this context, a shift from unit-mass to narrow resolution half-mass approaches relaxes the initial and ongoing purity constraints of the external solution from <200 ppt to <20 ppb. This can be analytically attractive across a diverse set of users with variable blank control capabilities.

Finally, Fig. 4 indicates that half-mass approaches that use narrow resolution instrument tune conditions provide added protections in estimating the numerator (M²⁺ response) in the M²⁺ correction; however, approaches that exclusively use a narrow resolution mode may experience sensitivity limitations. Using a method approach that allows the M²⁺ factors to be estimated in narrow resolution mode while analyzing samples in a normal resolution setting circumvents the sensitivity limitation but requires that the M²⁺ factors associated with the two modes (normal versus narrow) be correlated.

Fig. 5 provides estimates for the correlation between the two modes for Nd, Sm, and Gd as a function of He flow rate. All the element-specific data in Fig. 5 produce negative linear least squares (LLS) slopes with respect to He flow, indicating a movement away from a 1:1 correlation between narrow and normal resolution settings with increased He flows. To correct for this difference, the He flow associated with the batch analysis was used to obtain the element-specific correction factor from the LLS in Fig. 5. This LLS-based narrow-to-normal correction factor was incorporated into the overall M²⁺ correction equation used in Tables 1 and 2 and is part of the overall correction equation outlined in Fig. 1.

Figure 5.

Correlation of M²⁺ factors as a function of He flow rate for Nd, Sm, and Gd using both narrow and normal resolution^1–2 Notes: 1. The data were collected in both narrow resolution mode (0.4 amu at 10% peak height, 1.65 sec/amu) and normal resolution mode (0.8 amu at 10% peak height, 1.75 sec/amu). The element-specific error bars are estimated based on seven replicate analyses. 2. The data collected using 2 mL/min He and less were collected using a lower concentration of REE. The data for He flows greater than 2 mL/min were collected using a higher rare earth concentration to help compensate for the reduced signal intensities at the half-mass with increased He flow. 3. Data are presented using the box and whisker plot with outliers within Excel.

Table 1.

An evaluation of M²⁺ interference-correction approaches on m/z 75 in reagent and regional tap water matrices fortified with Nd and Sm

Reagent Water Fortified with Low and High Rare Earth Spikes	m/z 75, No Correction1,2	m/z 75, No Correction1,3	m/z 75, External Correction1,3,4	m/z 75, In-Sample Correction5	m/z 91, 8800 ICP-MS6	High Resolution ICP-MS7
	4.5mL He ([ppb] ± 2σ)	2.5mL He ([ppb] ± 2σ)	2.5mL He ([ppb] ± 2σ)	2.5mL He ([ppb] ± 2σ)	75→91 As [O2] ([ppb] ± 2σ)	75As ([ppb] ± 2σ)
2 ppb Nd	0.05 ± 0.03	0.04 ± 0.04	0.00 ± 0.04	0.00 ± 0.04	−0.002 ± 0.001	−0.012 ± 0.002
2 ppb Nd + spike8	0.10 ± 0.06	0.10 ± 0.03	0.06 ± 0.03	0.05 ± 0.07	0.05 ± 0.01	0.043 ± 0.005
50 ppb Nd	1.44 ± 0.21	0.84 ± 0.13	−0.02 ± 0.12	0.06 ± 0.22	0.000 ± 0.001	−0.0111 ± 0.0004
50 ppb Nd +spike8	1.51 ± 0.12	0.92 ± 0.18	0.06 ± 0.18	0.05 ± 0.22	0.05 ± 0.01	0.045 ± 0.009
2 ppb Sm	0.06 ± 0.04	0.03 ± 0.02	0.00 ± 0.02	0.01 ± 0.05	0.003 ± 0.002	−0.009 ± 0.001
2 ppb Sm + spike8	0.09 ± 0.04	0.09 ± 0.06	0.05 ± 0.07	0.07 ± 0.06	0.05 ± 0.01	0.044 ± 0.001
50 ppb Sm	1.36 ± 0.16	0.79 ± 0.13	−0.07 ± 0.12	−0.03 ± 0.20	0.000 ± 0.001	−0.01 ± 0.01
50 ppb Sm + spike8	1.45 ± 0.14	0.84 ± 0.12	−0.01 ± 0.11	0.05 ± 0.11	0.05 ± 0.01	0.034 ± 0.007
Regional tap waters9
Water A + 50 ppb Gd, Nd, Sm	3.01 ± 0.31	1.74 ± 0.22	−0.22 ± 0.24	0.52 ± 0.46	0.45 ± 0.02	0.48 ± 0.14
Water B + 50 ppb Gd, Nd, Sm	2.47 ± 0.34	1.27 ± 0.27	−0.73 ± 0.29	0.08 ± 0.25	0.18 ± 0.01	0.15 ± 0.05
Water C + 50 ppb Gd, Nd, Sm	4.85 ± 0.47	3.38 ± 0.51	1.60 ± 0.54	2.27 ± 0.47	2.03 ± 0.03	2.11 ± 0.48
Water D + 50 ppb Gd, Nd, Sm	2.83 ± 0.65	1.53 ± 0.34	−0.46 ± 0.40	0.20 ± 0.33	0.23 ± 0.02	0.17 ± 0.05
Water E + 50 ppb Gd, Nd, Sm	2.77 ± 0.32	1.44 ± 0.40	−0.62 ± 0.46	0.10 ± 0.52	0.11 ± 0.01	0.07 ± 0.02
Water F + 50 ppb Gd, Nd, Sm	2.91 ± 0.52	1.53 ± 0.15	−0.51 ± 0.15	0.29 ± 0.28	0.35 ± 0.02	0.32 ± 0.06

^1.Data were collected in normal resolution mode (0.8 amu at 10% peak height) using In as an internal standard with a 0.3-sec/amu integration time in selective ion monitoring mode. All estimates are based on 10 instrument replicates.

^2.The calibration blank and 50 ppt standard associated with the analysis of reagent waters (4.5 mL He) produced 3 cps and 45 cps, respectively. The calibration blank and 100 ppt standard associated with the regional waters (4.5 mL He) produced 6 cps and 60 cps, respectively.

^3.The calibration blank and 50 ppt standard associated with the analysis of reagent waters (2.5 mL He) produced 6 cps and 41 cps, respectively. The calibration blank and 100 ppt standard associated with the regional waters (2.5 mL He) produced 12 cps and 56 cps respectively.

^4.The M²⁺ correction factors were estimated in narrow resolution mode (0.4 amu at 10% peak height) using an external rare earth standard and applied as a fixed correction factor to all samples. This correction also incorporated a narrow to normal conversion factor (see Figure 5). No additional correction was required for the ⁴⁰Ar³⁵Cl interference.

^5.Data were collected in narrow resolution mode (0.4 amu at 10% peak height) using In as an internal standard with a 0.3-sec/amu integration time in selective ion monitoring mode. All estimates are based on 10 instrument replicates. The M²⁺ correction factors were estimated in each sample. The solutions fortified with 2 ppb rare earth produced about 30 cps at the corresponding half-mass with percent relative standard deviation (RSD) across the 10 replicates of about 25%. The solutions fortified with 50 ppb rare earth produced about 300–500 cps at the corresponding half-mass with %RSD across the 10 replicates of about 12%. A 50 ppt As standard in narrow resolution mode using 2.5 mL He produces 25 cps with a 3 cps blank. All in-sample M²⁺ estimates required manual abundance-sensitivity evaluations at the adjacent masses to the M²⁺ ion. No additional correction was required for the ⁴⁰Ar³⁵Cl interference.

^6.Data were collected at m/z 91 in oxygen mode using 0.5 mL/min with a 0.99-sec/amu integration time in selective ion monitoring mode. All estimates are based on n = 5 using Y as an internal standard (YO⁺, 89→105). The calibration blank and 50 ppt standard produced 6 cps and 465 cps, respectively.

^7.Arsenic data used a mass range of 74.916–94.926 amu, 40 samples per peak, 0.200 sampling time, and 30% search and 60% integration windows over 3 runs and 2 passes (n = 6). All data were collected in high-resolution mode, and concentrations were determined relative to the ¹¹⁵In internal standard. The Auto Lock Mass feature was active during analysis.

^8.This sample was fortified with 0.050 ppb As and 1 ppb Se.

^9.All regional waters were prepared to reflect the 0.4% HCl concentration that results from an acid digestion according to Method 200.8.

Table 2.

An evaluation of M²⁺ interference-correction approaches on m/z 78 in reagent and regional tap water matrices fortified with Gd

Reagent Water Fortified with Low and High Rare Earth Spikes	m/z 78, No Correction1,2	m/z 78, No Correction1,3	m/z 78, External Correction1,3,4	m/z 78, In-Sample Correction5	m/z 94, 8800 ICP-MS6	High Resolution7
	4.5mL He ([ppb] ± 2σ)	2.5mL He ([ppb] ± 2σ)	2.5mL He ([ppb] ± 2σ)	2.5mL He ([ppb] ± 2σ)	78→94 Se [O2] ([ppb] ± 2σ)	78Se ([ppb] ± 2σ)
2 ppb Gd	2.3 ± 0.7	0.7 ± 0.6	−0.1 ± 0.6	0.0 ± 0.8	0.01 ± 0.04	−0.03 ± 0.02
2 ppb Gd + spike8	3.1 ± 1.3	1.6 ± 0.9	0.8 ± 0.9	1.5 ± 1.3	1.0 ± 0.1	0.924 ± 0.004
50 ppb Gd	53.0 ± 5.7	19.1 ± 1.9	−1.0 ± 2.0	−0.1 ± 1.2	−0.04 ± 0.03	−0.01 ± 0.12
50 ppb Gd+ spike8	54.0 ± 7.0	20.3 ± 1.8	0.0 ± 1.8	0.6 ± 2.3	1.1 ± 0.1	0.94 ± 0.06
Regional tap waters9
Water A + 50 ppb Gd, Nd, Sm	51.2 ± 7.3	15.5 ± 2.9	−9.6 ± 3.2	−1.0 ± 2.6	0.18 ± 0.10	0.36 ± 0.03
Water B + 50 ppb Gd, Nd, Sm	51.1 ± 7.8	16.2 ± 2.0	−9.3 ± 1.8	−1.0 ± 3.9	1.35 ± 0.24	1.33 ± 0.12
Water C + 50 ppb Gd, Nd, Sm	51.8 ± 4.2	17.9 ± 4.3	−7.3 ± 4.6	1.2 ± 4.2	2.29 ± 0.23	2.17 ± 0.26
Water D + 50 ppb Gd, Nd, Sm	53.3 ± 5.8	15.8 ± 2.5	−9.6 ± 2.9	−2.4 ± 3.5	−0.03 ± 0.05	0.15 ± 0.02
Water E + 50 ppb Gd, Nd, Sm	53.2 ± 6.3	15.8 ± 3.6	−10.3 ± 4.3	−2.8 ± 4.2	−0.01 ± 0.09	0.21 ± 0.01
Water F + 50 ppb Gd, Nd, Sm	52.5 ± 6.7	16.3 ± 3.8	−9.6 ± 3.9	−2.1 ± 1.9	0.33 ± 0.07	0.46 ± 0.05

^1.Data were collected in normal resolution mode (0.8 amu at 10% peak height) using In as an internal standard with a 0.3-sec/amu integration time in selective ion monitoring mode. All estimates are based on 10 instrument replicates.

^2.The calibration blank and 1 ppb standard associated with the analysis of reagent water (4.5 mL He) produced 9 cps and 67 cps, respectively. The calibration blank and 5 ppb standard associated with the analysis of regional waters (4.5 mL He) produced 12 cps and 169 cps, respectively.

^3.The calibration blank and 1 ppb standard associated with the analysis of reagent waters (2.5 mL He) produced 23 cps and 87 cps, respectively. The calibration blank and 5 ppb standard associated with the analysis of regional waters (2.5 mL He) produced 31 cps and 279 cps, respectively.

^4.The M²⁺ correction factors were estimated in narrow resolution mode (0.4 amu at 10% peak height) in an external rare earth standard and applied as a fixed correction factor to all samples. This correction also incorporated a narrow to normal conversion factor (see Figure 5).

^5.Data were collected in narrow resolution mode (0.4 amu at 10% peak height) using In as an internal standard with a 0.3-sec/amu integration time in selective ion monitoring mode. All estimates are based on 10 instrument replicates. The M²⁺ correction factors were estimated in each sample. The solutions fortified with 2 ppb rare earth produced about 30 cps at the corresponding half-mass with %RSD across the 10 replicates of about 25%. The solutions fortified with 50 ppb rare earth produced about 300–500 cps at the corresponding half-mass with %RSD across the 10 replicates of 12%. A 1 ppb Se standard in narrow resolution mode using 2.5 mL He produces 51 cps with a 19 cps blank. All in-sample M²⁺ estimates required manual abundance-sensitivity evaluations at the adjacent masses to the M²⁺ ion.

^6.Data were collected using m/z 94 in oxygen mode at 0.5 mL/min with a 0.99-sec/amu integration time in selective ion monitoring mode. All estimates are based on n = 5 using Y as an internal standard (YO⁺, 89→105). The calibration blank and 1 ppb Se standard produced 7 cps and 351 cps, respectively.

^7.Selenium data were collected with an EScan over the mass range of 77.912–77.922 amu with a sampling time of 0.200 sec, 40 samples per peak, and 30% search and 60% integration windows over 3 runs and 2 passes (n = 6). All data were collected in high-resolution mode, and concentrations were determined relative to the ¹¹⁵In internal standard. The Auto Lock Mass feature was active during analysis.

^8.This sample was fortified with 0.050 ppb As and 1 ppb Se.

^9.All regional waters were prepared to reflect the 0.4% HCl concentration that results from an acid digestion according to Method 200.8.

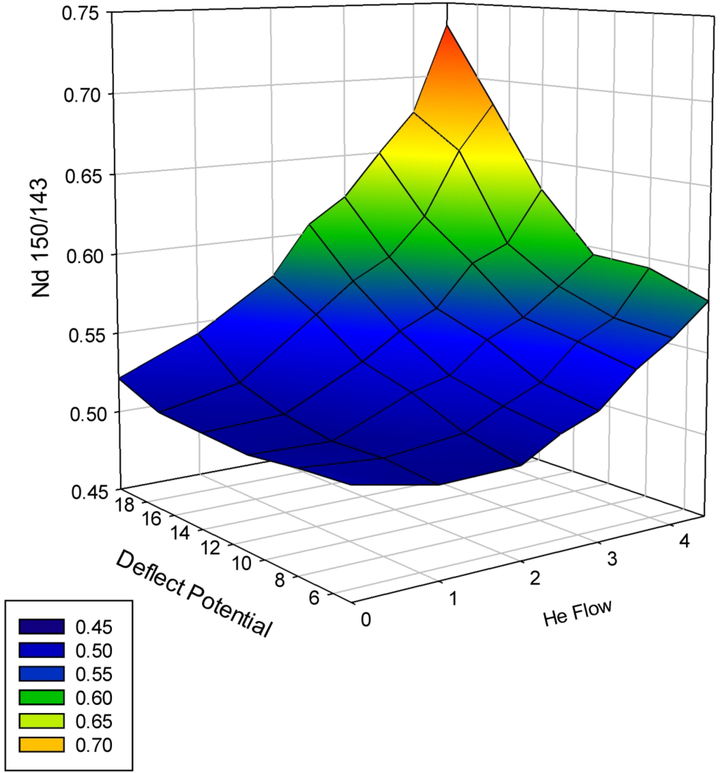
The half-mass approaches to estimate M²⁺ factors are indirect approaches. This means that in a quadrupole instrument with a collision cell, the response at a monitoring isotope (i.e., ¹⁴³Nd, ¹⁴⁹Sm, or ¹⁵⁵Gd) needs to be converted to a signal equivalence at the isotope producing the M²⁺ interference (i.e., ¹⁵⁰Nd, ¹⁵⁰Sm, or ¹⁵⁶Gd). In Fig. 6, the ¹⁵⁰Nd/¹⁴³Nd ratio is estimated as a function of He flow rate and deflect lens potential using a 50 ppb Nd standard. High He flow with high deflect potential tends to produce the highest ¹⁵⁰Nd/¹⁴³Nd ratio. This ratio was chosen because it represents the largest mass differences between the monitored mass (m/z 143) and the isotope associated with the interference (m/z 150) and, for that reason, likely has the largest mass bias associated with it. All 150/143 ratio estimates in Fig. 6 are biased high relative to the theoretical ratio of 0.463. Potential sources of bias at m/z 150 from ¹⁵⁰Sm, ¹³⁴Ba¹⁶O, and ¹³⁴Xe¹⁶O were evaluated and shown to be insignificant relative to the bias reported in Fig. 6. Similar experiments were conducted using a secondary source of Nd (secondary source produced results within 1% of the primary stock, data not shown) as well as in a second laboratory (data not shown); all of these experiments produced results comparable to those shown in Fig. 6. The use of ¹⁴⁹Sm to predict ¹⁵⁰Sm and ¹⁵⁵Gd to predict ¹⁵⁶Gd produced significantly smaller (2–6%) sources of bias and are much smaller relative to those reported in Fig. 6. The element- and tune-specific isotopic ratios estimated from the external solution were utilized in Tables 1 and 2. Finally, the data in Fig. 6 indicate the need for the end-user to determine a tune-specific isotopic ratio for Nd if an indirect correction of ¹⁵⁰Nd²⁺ on ⁷⁵As is to be used.

Figure 6.

¹⁵⁰Nd¹⁺/¹⁴³Nd¹⁺ ratio as a function of He flow rate and deflect potential^1–2 Notes: 1. The data were collected in narrow resolution mode (0.4 amu at 10% peak height) using selective ion monitoring with a 0.3 sec/amu dwell time. 2. Using 4.0 mL of He, the ¹³⁷Ba was 6 cps and the ¹²⁹Xe was 174 cps, indicating the ¹³⁴BaO and ¹³⁴XeO were not contributing to the signal significantly at m/z 150 when compared to the Nd standard, which produced >10,000 cps at m/z 150 for all tunes except 4.5 mL He/deflect 20.

The above data outline some of the sources of bias in generating M²⁺ correction factors within the context of a He-collision cell method. By incorporating some of these approaches, the end user should minimize the number of situations where an over correction is evident. The inherent variability of incorporating these M²⁺ corrections cannot be avoided, and this variability is especially problematic when the M²⁺ is large and the target analyte is small.³² In Tables 1 and 2, this variability is evaluated in reagent and drinking water matrices for Nd, Sm, and Gd. In the top half of Table 1, the ability to recover a 50 ppt As spike is evaluated in reagent waters fortified at two Sm and Nd concentrations (2 ppb and 50 ppb). The As concentrations are estimated with and without M²⁺ corrections. These results are compared to concentrations determined using mass-shift (ICP-QQQ) and magnetic sector-based ICP-MS instruments. The lower half of Table 1 lists regional tap waters fortified with 50 ppb Sm and Nd. The uncorrected and M²⁺ corrected estimates are compared again to those obtained from mass-shift and magnetic sector-based ICP-MS instruments. A comparison of the uncorrected data (columns 2 and 3) indicates that a smaller false positive is produced by the Sm and Nd at m/z 75 if a lower He flow and a higher deflect potential are used. This tune-induced reduction of M²⁺ interferences is consistent with the data in Fig. 3B. This approach reduces the size of the M²⁺ correction that needs to be addressed by the interference-correction software. A comparison of the uncorrected data in column 3 to the external (column 4) and in-sample (column 5) M²⁺ corrected data indicates that the false positives produced by Sm and Nd are further reduced by the M²⁺ correction. The difference associated with these two M²⁺ correction approaches only becomes evident when instrument drift or the sample matrix influences the M²⁺ correction factor. The external approach assumes the correction is fixed (constant) across all sample analyses, while the in-sample approach attempts to compensate for these changes on a sample-by-sample basis. The inability for the external approach to compensate for shifts in the M²⁺ correction is most evident in the over corrections in the regional waters relative to the in-sample, mass-shift, and magnetic sector-based estimates.

Table 2 has the same format as Table 1. The only difference is that the analyte is ⁷⁸Se and the corresponding rare earth interference is ¹⁵⁶Gd²⁺. The similarities between the two tables include: (1) the low helium, high deflect tune reduces the false positives from M²⁺ in the uncorrected data. (2) The M²⁺ correction further reduces the false positive produced by ¹⁵⁶Gd²⁺ on m/z 78. (3) The external approach to estimating the M²⁺ correction tends to overcorrect (generating negative concentrations in Table 2) while the in-sample approach captures some of the instrument drift and matrix-induced shifts in the M²⁺ factor and for this reason produces less overcorrection. The ability to correct for instrumental drift and matrix-induced shift is key and a second paper is in progress in which the variability of the M²⁺ correction is investigated using multiple instrument tunes over four non-consecutive analysis days with a wider collection of REE and sample matrices. (4) The in-sample estimates (column 5) are more in line with the mass shift and magnetic sector ICP-MS results relative to the external M²⁺ results in column 4; however, all the Se results are near the detection limit.

Conclusions

The minimization of false positives produced by ¹⁵⁰Nd²⁺, ¹⁵⁰Sm²⁺, and ¹⁵⁶Gd²⁺ on ⁷⁵As and ⁷⁸Se need to be considered in the optimization of a He-collision cell ICP-MS. Low He flow tuning conditions can produce comparable ¹⁶O³⁵Cl⁺ reduction and Se sensitivity relative to high He tuning conditions after discrimination energy and lenses are optimized. However, the low He tune has the added benefit of producing (approximately 50% reduction) less false signal and a smaller M²⁺ correction factor. All tuning conditions have some residual M²⁺ response that could be further reduced by using a M²⁺ correction within the interference-correction software. Estimation of the M²⁺ correction using half-mass approaches (narrow and normal) are advantageous relative to unit-mass approaches because half-mass approaches avoid direct elemental (As⁺, ⁷⁸Se⁺, ⁷⁸Kr⁺) and polyatomic (⁴⁰Ar³⁵Cl⁺, ⁴⁰Ar³⁸Ar⁺) isobaric sources of bias. If the half-mass estimates are made in narrow resolution mode, the sources of bias are limited to abundance-sensitivity issues that relax the external solution purity requirements from hundreds of ppt to 10–20 ppb while providing added tolerance of a blank control by the end user. Both external and in-sample M²⁺ correction approaches can reduce the bias induced by the co-occurrence of M²⁺ ions on As and ⁷⁸Se. However, the in-sample approach can compensate for some instrumental drift or matrix-induced shifts in the M²⁺ correction factor. Finally, the best approach to minimizing the impact of false positives from M²⁺ ions likely involves a change in the instrument optimization procedures (which incorporates M²⁺ reduction as a optimization factor) while concurrently adopting approaches to estimating M²⁺ correction factors that compensate for the shifts in both the M¹⁺ and M²⁺ response induced by instrumental drift and matrix.